1. Introduction
Global warming has become the most severe environmental issue of the world. As greenhouse gas (GHG) is the main factor for temperatures rising, countries around the world have realized the urgency of low-carbon development. As the largest emitter of GHG, China aims to reduce 60%~65% GHG emissions per unit of GDP by 2030 compared to 2005. Emission mitigation should start with its sources. Industry is recognized as the main source of GHG emissions, while agriculture also releases significant amounts of CO
2, CH
4 and N
2O to the atmosphere [
1]. GHG emissions from agriculture in China, accounting for 17% of the total amount [
2] and predicted to increase by another 30% in 2050 [
3], should not be neglected. Meanwhile, the agricultural ecosystem also plays an important role in absorbing GHG [
4], which influences the total amount, too. The complicated process of agricultural production makes it impossible to judge the net effect of GHG directly. In addition, because of the vast territory of China, natural resources and agricultural development may be completely different among regions, broadening the gaps of agricultural net GHG amount, but the geographical environment and industrial structure of neighboring provinces are usually similar, which may cause the net amount to correlate spatially. Therefore, what is the spatial–temporal characteristic of agricultural net GHG amount in China? Will it show spatial correlation? How is it evolving? Perhaps which regional emission mitigation measures to take can be addressed by answering the above questions.
To clarify the sources and to estimate the amount of GHG from agriculture, scholars have carried out relevant research. They have agreed that agricultural GHG emission comes from the process of agricultural production, mainly involving crop and livestock production, forestry and farmland use [
3], also including agricultural waste, agricultural energy use and bio-burning [
1,
4]. There are two major perspectives for estimating: one is to focus on sources of a certain category, such as the cropping system [
5,
6,
7], farmland use [
8], agricultural burning [
9], waste products [
10] and livestock [
11,
12,
13]. The other is to measure the total amount of a variety of sources from agriculture, which takes a certain country or region as the research object [
14,
15,
16,]. As for the GHG-absorption function of the agro-ecosystem, scholars generally believe that the absorption is contributed by forest, grassland and farmland. Research of Europe and the United States focus on forest, including soil carbon sequestration [
17,
18] and forest carbon sinks [
19,
20,
21]. In China, scholars mainly consider absorption of cropping system, that is, the GHG absorption of crops by photosynthesis during the growth cycle [
22,
23]. In general, related studies are consistent in the coefficients of crops’ absorption [
4]. Based on the estimation of GHG emission and absorption, scholars have begun to link them up and explore the net effect in different countries or regions [
24,
25,
26,
27,
28]. In the representative research of China, Duan et al. study the carbon emissions, absorption and footprint of farmland ecosystems, and find that they all show an increasing trend [
29]. Chen et al. measure the carbon absorption and emission of agricultural systems from 1991 to 2011, deeming the system is a sink of GHG [
30]. The existing studies have laid a foundation for thorough exploration on the net GHG emissions from agriculture. However, the consideration of sources and estimation methods have not been unified, resulting in different conclusions.
After understanding the sources and amount of agricultural GHG emission, scholars have paid attention to its regional disparities [
31,
32], finding several factors that lead to the regional difference, such as technical progress [
33], production mode [
34], agricultural practitioners, disaster degree, industrial structure, economic development and public investment [
35], and then proposing a series of potential mitigation options [
36,
37]. With the research deepening, the convergence test, a tool to investigate the evolution of regional disparities, is applied to analyze the regional difference of GHG emissions [
38,
39,
40]. Yang estimates the amount and intensity of agricultural carbon emissions in China from 1993 to 2011, and confirms that there is no α convergence and conditional β convergence in the intensity [
41]. Cheng et al. study the convergence trend of agricultural carbon productivity in China from 1997 to 2012, whose results show that there is no α convergence but absolute β convergence [
42]. While Wu et al. take the slack based measure under undesirable outputs (SBM-Undesirable) to evaluate China’s agricultural carbon emissions’ performance from 2000 to 2014 and believe that there is no stochastic convergence in carbon emissions or its performance [
43]. As seen from the convergence study, scholars concentrate on agricultural GHG emission, paying insufficient attention to absorption, and seldom consider the net effect. Besides, scholars assume that emissions are independent in different regions, so they apply ordinary panel econometric methods when conducting the β convergence test. In fact, agricultural GHG is more likely to correlate spatially because of the similar resource endowments, industrial structure and the emission-mitigation policy imitation in neighboring provinces. If the potential spatial correlation is ignored, it may affect the accuracy of the results [
44].
To make up for the existing research, we comprehensively took 21 sources of agricultural GHG emissions into consideration, and linked up the emission and absorption of agricultural ecosystem, to estimate the net GHG emissions of 30 provinces in China from 2007 to 2016. Then, we chose the Moran’s I based on the distance reciprocal square matrix to explore the spatial agglomeration of the emissions. Finally, the convergence theory and spatial econometric methods were used to analyze the emissions’ convergence, aiming to offer a reference for controlling the emissions from both temporal and spatial perspectives. The article is structured as:
Section 2 introduces the method and data involved in this study. The third section presents the empirical analysis. The fourth section discusses the results and the last section gives the conclusions.
4. Discussion
4.1. Implication
Agricultural GHG emissions plays an important role in global warming. As can be seen from the analysis, the situation of agricultural GHG in China is not optimistic, which reveals the urgency to accelerate the pace of emission mitigation.
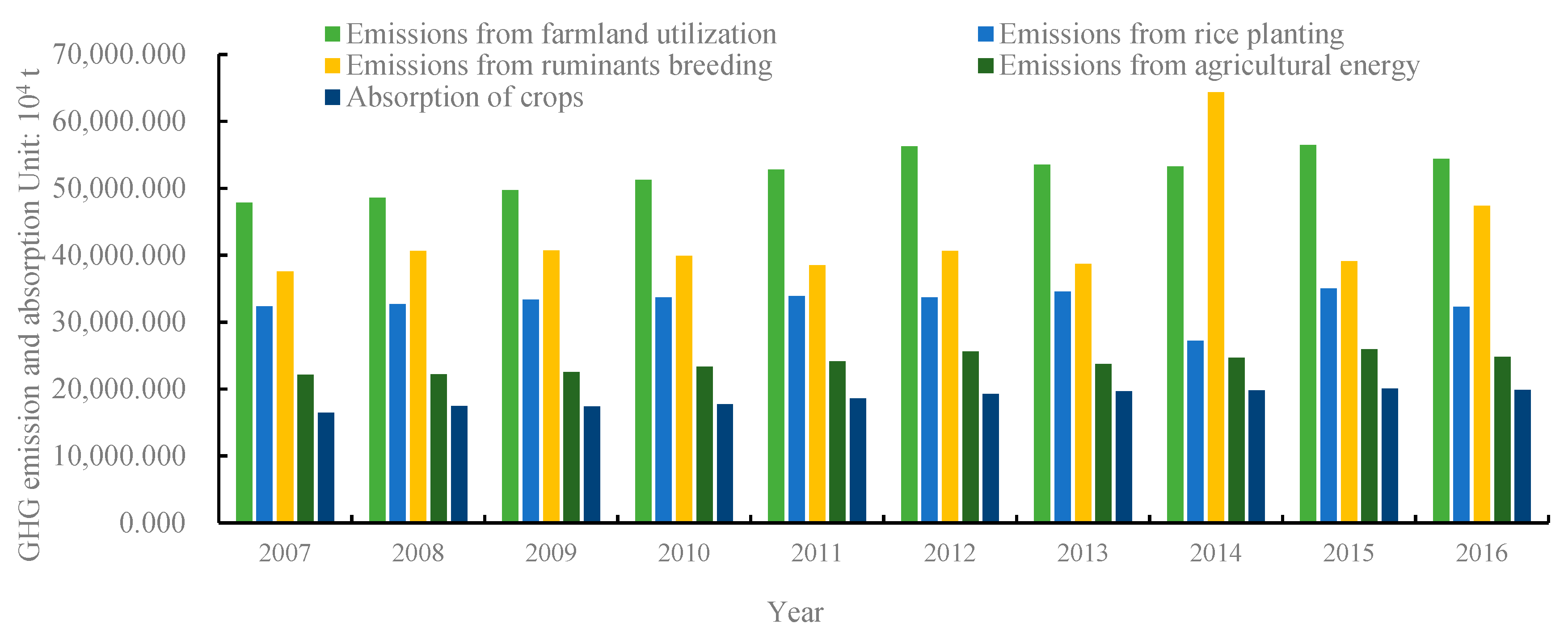
(1) Although agricultural net GHG emissions in China had experienced some ups and downs in the sample years, it showed an overall upward trend. Moreover, based on the evolution, we could predict the net emissions may continue to grow in the next few years, manifesting the necessity to take measures for emissions mitigation. From the structure, GHG emissions from farmland utilization, ruminant breeding and agricultural energy all showed growing trends, especially those from farmland utilization, accounting for 34.494% of the total amount, should be paid more attention.
(2) Due to the obvious provincial difference, when formulating regional agricultural GHG emission mitigation policies, it is essential to establish differentiated emission reduction targets based on local conditions. The key is to apply the low-carbon development mode of farming: adjust agricultural production structure and plant low-emission and high-sink crops that adapt to local resources, increase investment in technology to enhance the efficiency of agricultural machinery and the utilization rate of energy, encourage agricultural practitioners to learn conservation-oriented fertilization techniques, use pesticides rationally and recycle the waste plastic mulch.
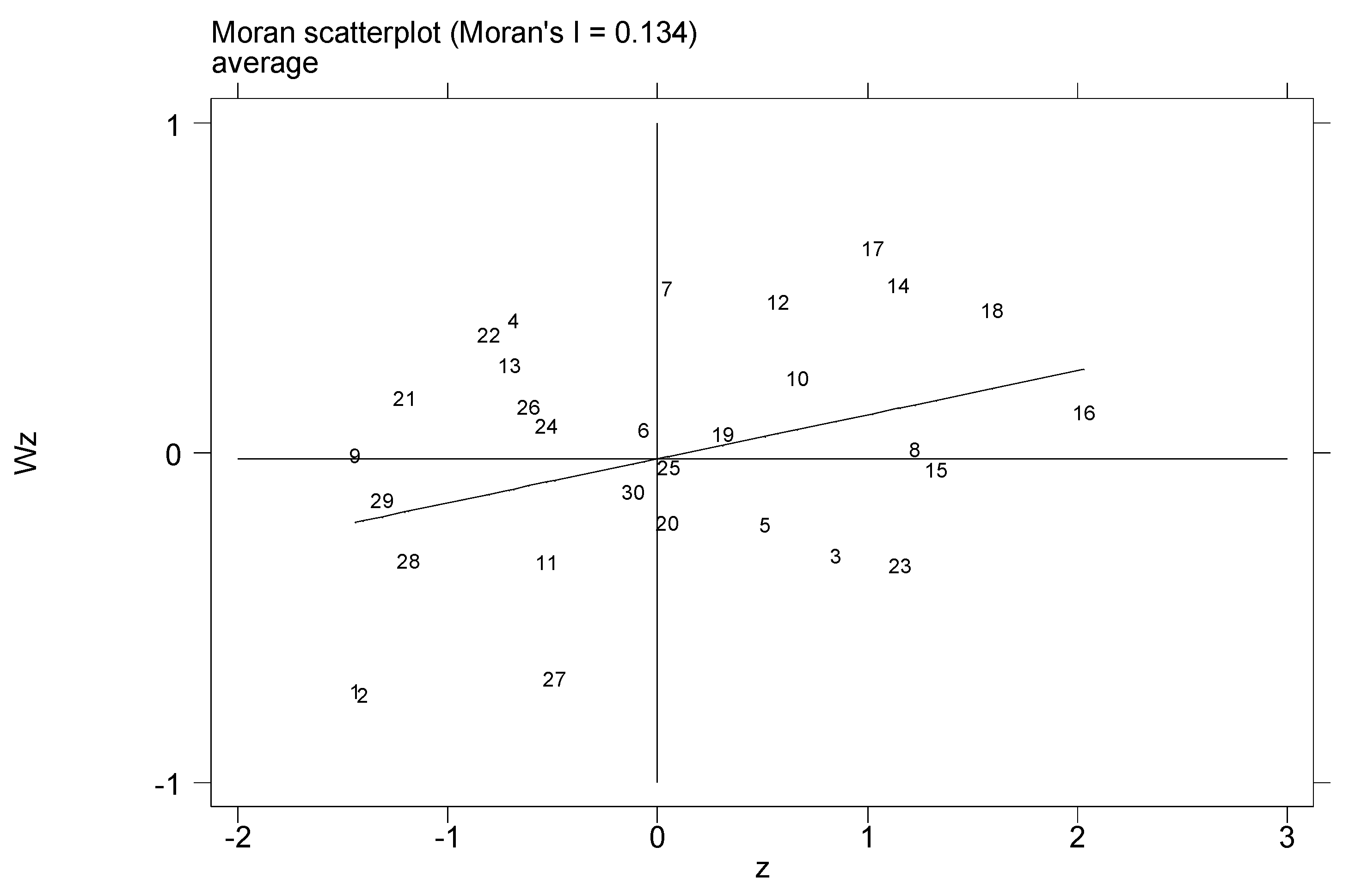
(3) Based on the results of two convergence tests, there is no convergence nationwide, so it is hard for the net emissions to reduce naturally. On the contrary, taking effective reduction measures is a possible way to bridge the provincial gaps. Besides, the net emissions showed spatial correlation, which interact and influence each other among provinces, suggesting that there is a possibility of regional cooperation. It is necessary for all regions to strengthen cooperation and share low-carbon technology, so as to cut down the net emissions coordinately through provincial correlation.
(4) A series of studies showed that some technologies may act in carbon sequestration and negative emission of carbon may be achieved [
49]. Technologies and techniques as biochar [
49], agroforestry systems [
50] and conservational agriculture measurements [
51,
52] may act as additional benefit methods for reduce carbon emission in agriculture. At present, low-carbon technology is relatively insufficient for agriculture in China, and most of them are staying in the experimental stage. In the future, China should attach importance to the development of the technologies and techniques and apply them to practice as soon as possible.
4.2. Comparison
Comparing with the existing estimation of China, we find that difference in categories and sources of agricultural GHG leads to the diversity of the results. Taking Chen’s estimation for example, he deems that China’s agriculture served as a net GHG sink from 1991 to 2011 [
30], while we believe that it was a GHG source from 2007 to 2016. Observing the calculation procedure, Chen calculates the GHG absorption from 15 kinds of crops, whose categories and corresponding coefficients are the same as our study, but there is a difference when calculating the emissions: Chen’s research is on the basis of six sources of GHG emission source, inclusive of fertilizer, pesticide, plastic mulch, sheep, cow and pig, less than our study that considers 21 sources of GHG emissions. Therefore, there is little difference in the estimation of absorption between the two studies, but the emissions we estimated are much more than Chen’s, consequently causing a significant difference in the net amount.
As for convergence, previous research focus on GHG emissions and relative indicators, and some scholars have agreed that the agricultural GHG emissions of China does not achieve convergence nationwide, neither does the intensity or performance [
41,
43], while the national agricultural carbon productivity has absolute β convergence [
42]. Instead, we took the net emissions as the target, and found that neither of α convergence or conditional β convergence existed in the whole country, which is a complement to the existing research.
4.3. Improving Direction
It should be noted that there are some limitations of this study. First, it lacks the consideration for GHG effect of soil. The emission and sequestration of soil is closely related to the farming system, where the soil carbon loss caused by no-tillage, less tillage or complete cultivation often has a world of difference [
34]. Some scholars adopt the test data of a certain region as GHG emission coefficient of soil, and applied it to the whole country [
4,
53]. However, China has a vast territory, and its geographical conditions and production patterns are quite different. Therefore, the application of such a simple way is unscientific. Based on the above reasons, GHG emission and sequestration of soil have not been considered in our measurement system of the agricultural GHG net emission.
Second, the impact of different farming methods was not considered. The agricultural practices, such as cover crops and straw returning, may also influence the carbon sequestration in the soil, resulting in a completely different net effect of GHG. As the major mode in China is smallholder production, it was hard to consider the influence of cultivation modes in different regions. For this reason, this paper did not consider different agricultural practices, which may have led to deviation in the result.
To refine the measurement system and ensure the accuracy of results, we will focus on taking the GHG effect of soil into research in the future. In addition, assessing the influence of different agricultural practices also becomes the next direction.
5. Conclusions
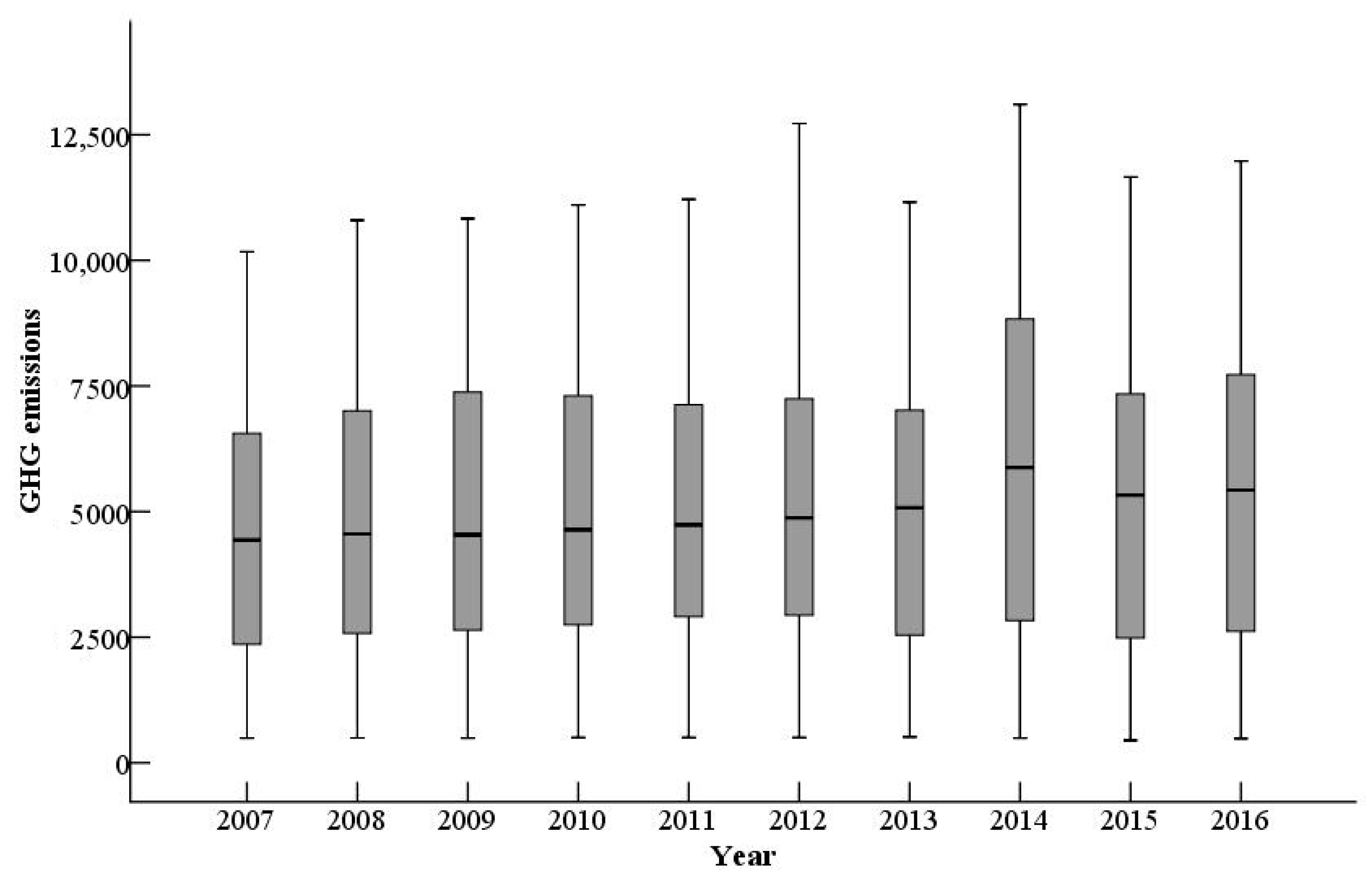
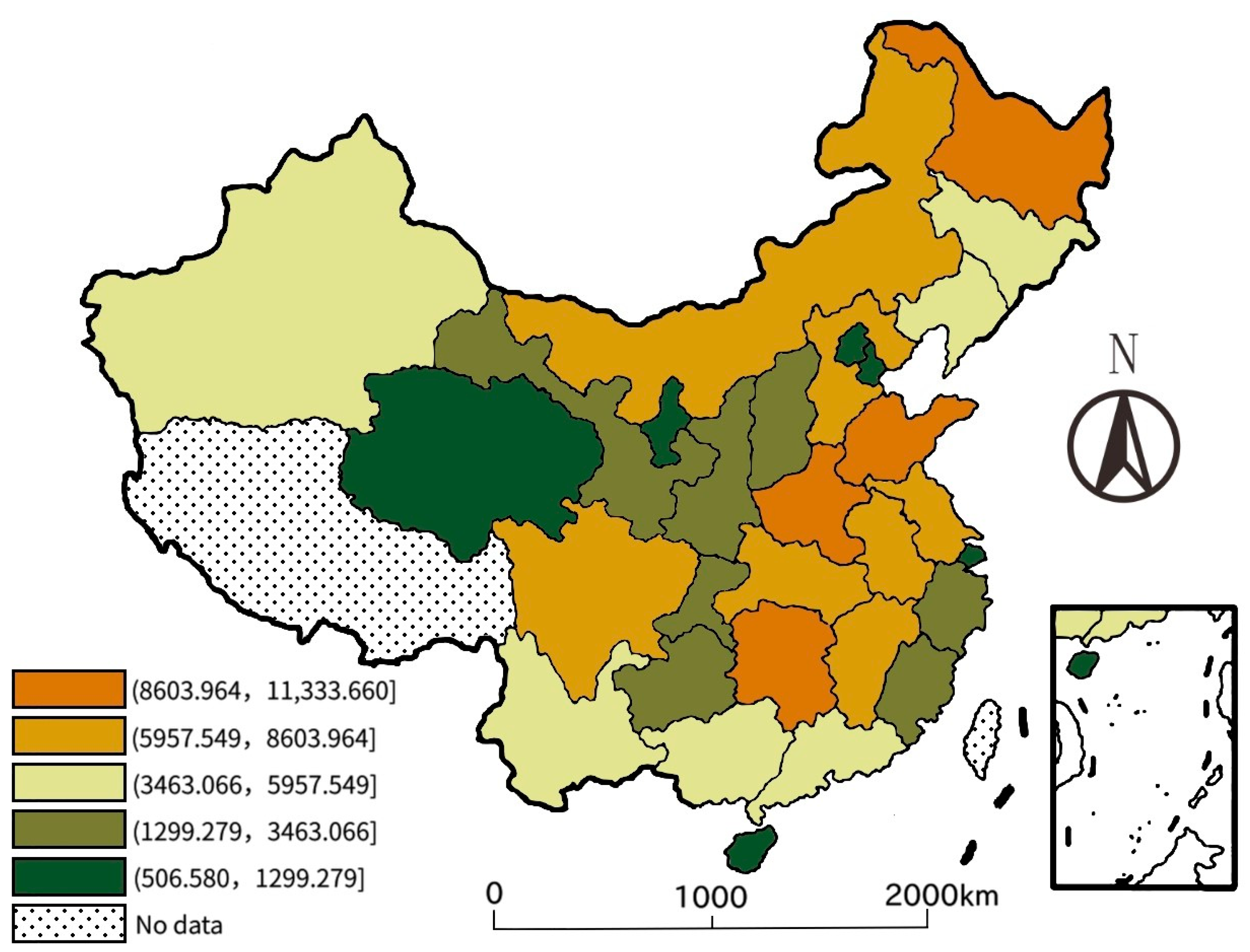
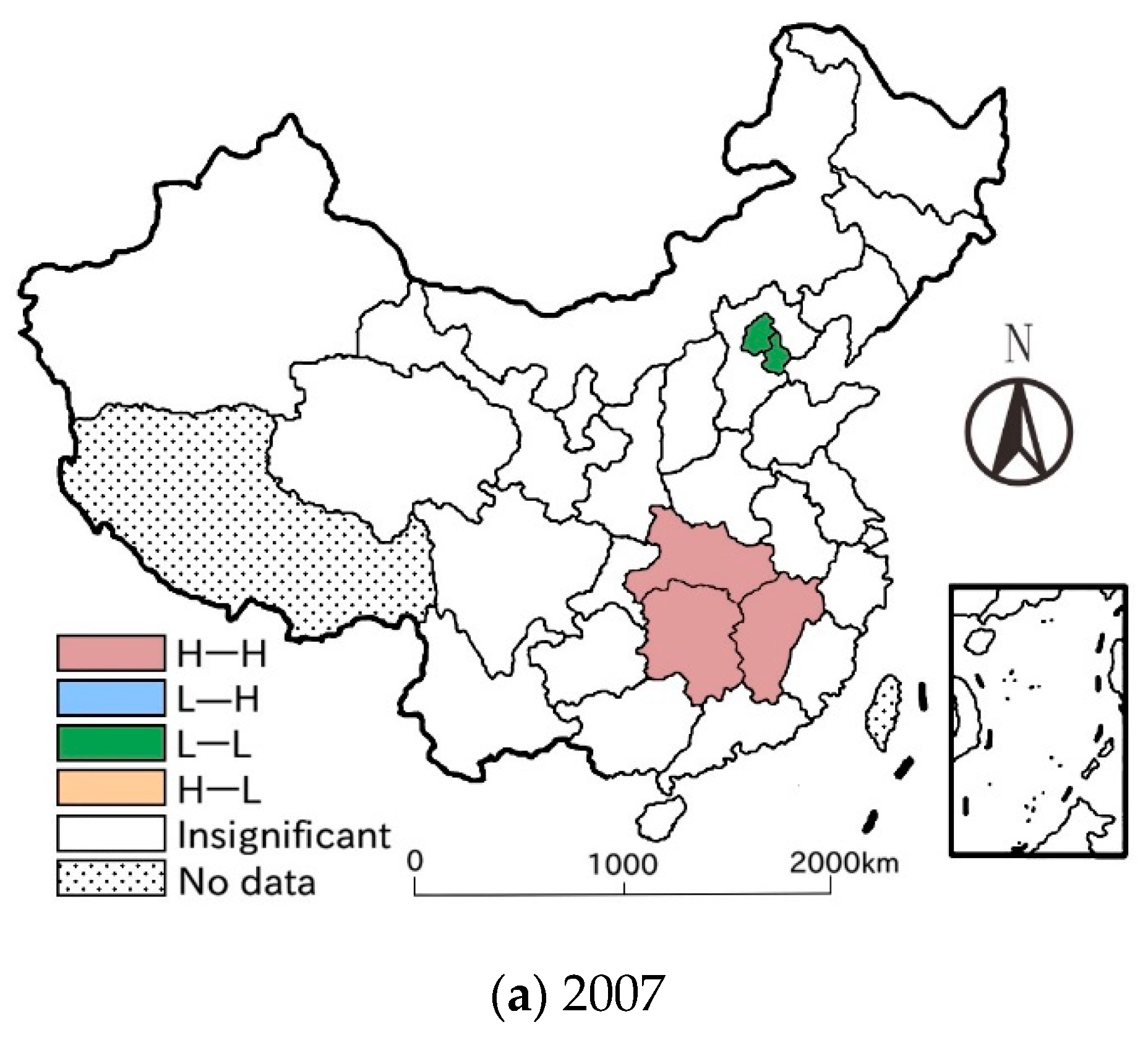
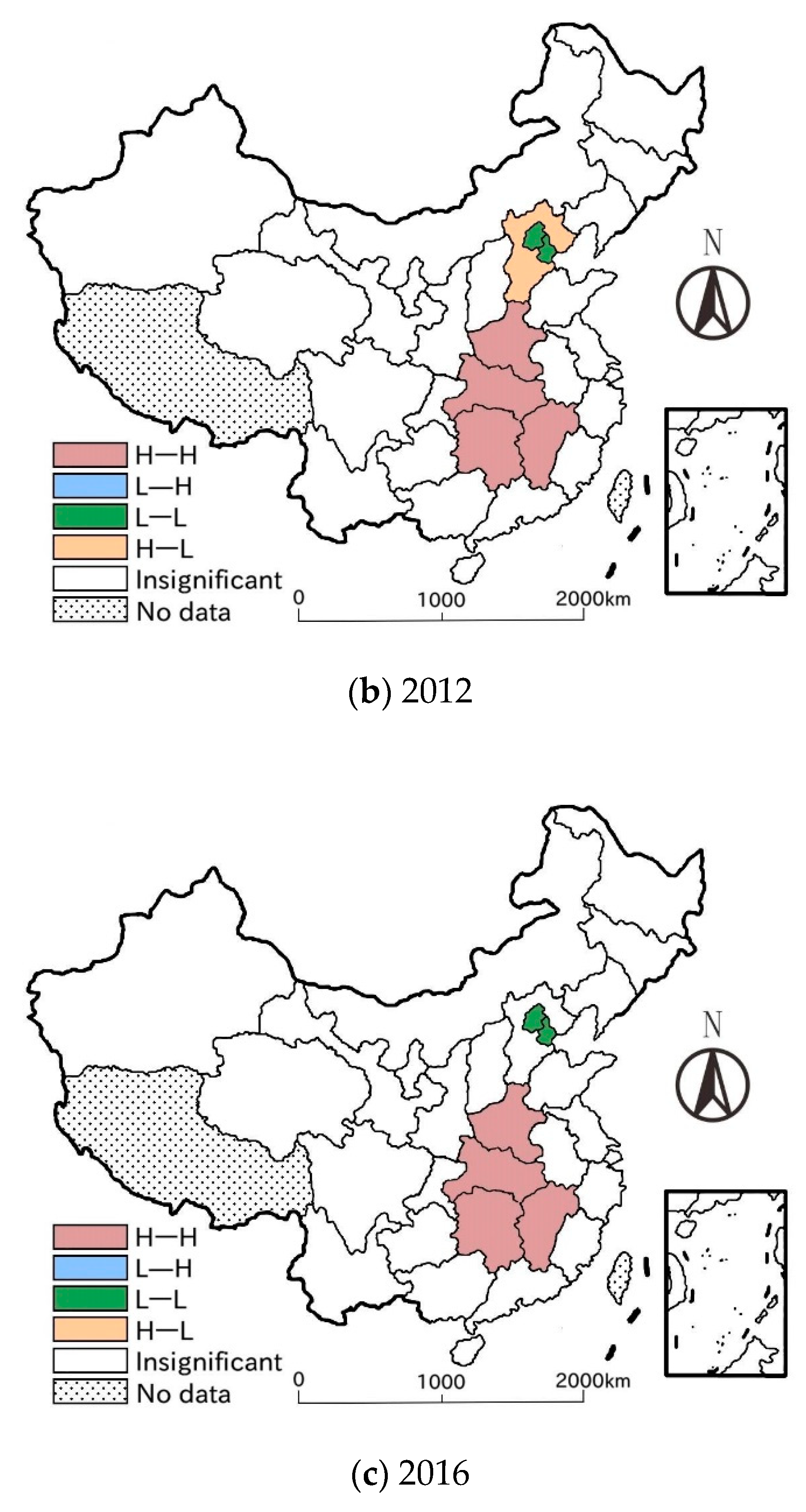
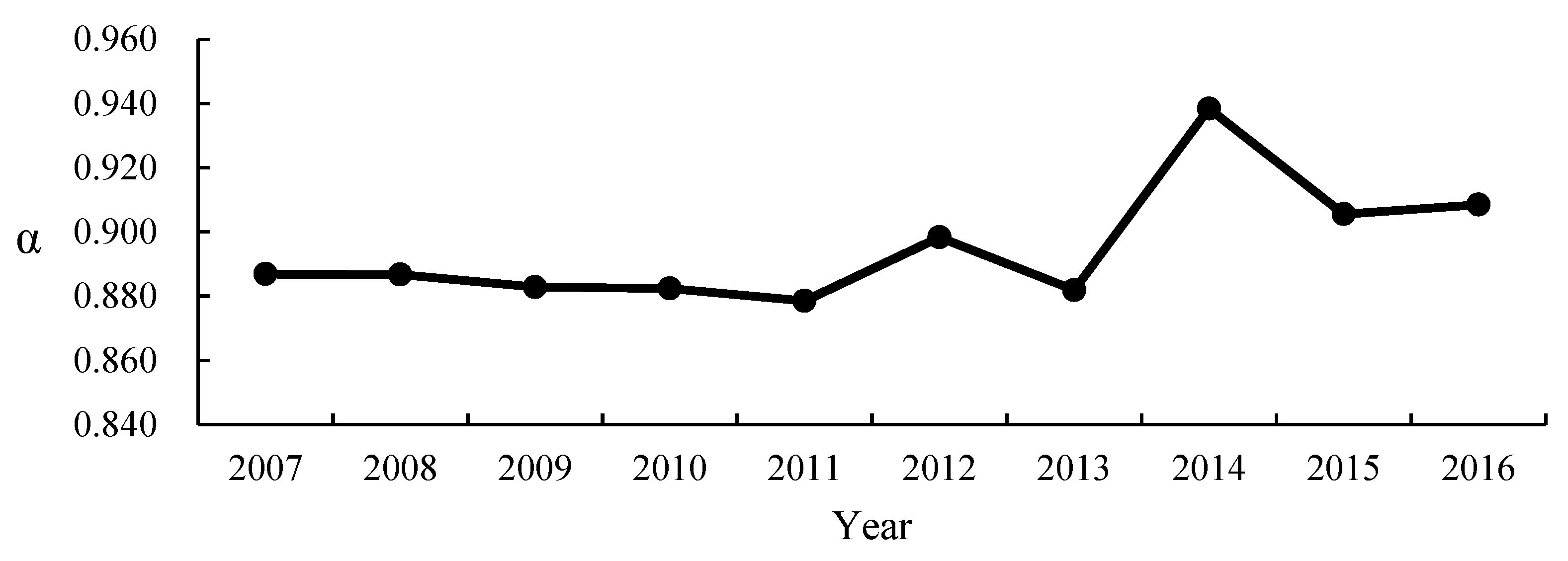
Based on the Moran’s I, convergence tests and spatial econometric models, the study analyzed the spatial correlation and convergence of agricultural net GHG emissions in China. From 2007 to 2016, the average of the net emissions of all provinces was 4999.916 × 104 t, showing a fluctuating growth trend as a whole, and the gaps among provinces had been gradually widening. Most of the provinces with large emissions belonged to the middle reaches of the Yangtze River, while the provinces with low emissions were mainly located in the northwest of China. As for the spatial correlation, the global Moran’s I of agricultural net GHG emissions was all over 0.100, implying the net emissions were spatially correlated, whose correlation level showed an inverted U-shaped curve as a whole. There was an obvious polarization of the net emissions, mainly exhibiting “high–high” and “low–low” agglomeration, whose agglomerating centers were situated in the middle reaches of the Yangtze River and the northern coastal region respectively. With the passage of time, the spatial correlation pattern had changed greatly. In terms of convergence, agricultural net GHG emissions did not show α convergence or conditional β convergence in the whole country. With time going by, the gaps among different provinces broadened, and there was no “chase effect” in the emissions’ growth rate among provinces. In addition, the growth rate had a significant positive spatial spillover effect in close provinces, and the agricultural force and economic development had negative impact on the growth rate of the net emissions.