1. Introduction
Mobile phones have become essential parts of daily life and the most commonly manufactured electronic equipment [
1]. Since China became the largest producer and seller of mobile phones in 2004, the total number of mobile phone users has achieved 1.5 billion in 2018 [
2]. The life expectancy of a mobile phone is shorter than 3 years according to studies from many scholars [
3,
4,
5]. Obviously, the generation of waste mobile phones (WMPs) is huge and now they have become an environmental problem as a part of waste electrical and electronic equipment (WEEE). In 2017, there were approximately 1 billion WMPs in China, and the recycling rate was only 2% [
6]. However, WEEE management has been implemented in developed countries since 2000 [
7,
8,
9], and many compulsory laws and directives such as the EU Directive on WEEE (2002/96/EC) [
10], its revised version (2008/34/EC) [
11], and the newest one (2012/19/EU) [
12] have been enacted based on extended producer responsibility (EPR) principles. The Directive (2012/19/EU) requires that 75% of WMPs should be recovered, and 55% of WMPs should be reused and recycled by 2018 [
12]. The EPR principles require producers including manufacturers and importers to take responsibility for the whole lifespan of a product, especially for the collecting, dismantling, and recycling at its end-of-life stage [
13].
The collection of WMPs in the reverse supply chain (RSC) is mainly conducted by formal collectors in many developed countries. Switzerland first established a formal and comprehensive management system of WEEE, which is well operated with producer responsibility organizations (PROs) [
14]. Manufacturers, importers, distributors, and retailers collect WMPs through established collection points and retail locations supported by the Swiss Association for Information, Communication and Organization Technology, which is one of the most important PROs [
15]. In Japan, the
Law on the Promotion of Recycling and Reuse of Used Small Electronic Equipment was enacted to support the tack-back of 28 types of small electronic products including WMPs in 2012 [
16]. Under the guidance of related laws, retailers and mobile phone operators have collected WMPs through recycling bins at their business outlets [
17].
In many developing countries including China, the collection of WMPs is conducted by formal and informal collectors [
18,
19,
20]. Street peddlers and repairers in China dismantle WMPs harmfully and crudely and put them into the market with rough refurbishment, who are the leading collectors in the informal collection. As to the formal collection, there are mainly two ways in China. One is the manufacturer’s collection, such as the Old-for-New (OFN) service of Mi (
http://huanxin.mi.com), and the other is the collector’s collection like the third-party collection platform represented by Aihuishou (
https://www.aihuishou.com/shouji). They have a competitive and cooperative relationship for WMPs collection. The collector can be served for the manufacturer. On the other hand, they also compete for the surplus value of WMPs such as remanufacturing materials. One of main reasons why they engage in e-waste collection is to recapture the value of the recycled materials and end-of-life products [
21]. Their coopetition (cooperative competition) relationship continues throughout the whole game process, and they adjust with each other’s strategy according to opponent’s responses and their own payoffs.
The relationship between the manufacturer and the collector can be presented by evolutionary game theory (EGT) which assumes the man of bounded rationality [
22]. It is more in line with the reality because of incomplete information and changing environment. The EGT emphasizes the behavioral interaction among players which can affect their payoffs directly. The behavioral interaction between the manufacturer and the collector in the WMPs collection is who will do the collection and how to bind them with a contract. They develop their own strategies in the process of the interaction. The EGT can entirely reflect the relationship between strategies change and payoffs fluctuation, can also effectively reflect their complex coopetition relationships. Rosas [
23] pointed out that social scientists usually exploit the EGT to study human cooperation. Ji et al. [
24] argued that the EGT can effectively observe the changing of cooperation tendency among multi-stakeholders. Some studies have exploited the EGT to analyze the collection of WEEE. Esmaeili et al. [
25] adapted the EGT to discuss whether performing collection or not for the manufacturer and the retailer. Wu and Xiong [
26] studied cooperation behavior between manufacturers and collectors under a government subsidy mechanism with the EGT.
Except for the subsidy mechanism, the reward-penalty mechanism (RPM) made by the government in a closed-loop supply chain is examined by Wang et al. [
27,
28,
29,
30]. The RPM is one of incentive mechanisms which are usually used to coordinate forward and reverse supply chains. The producers will face penalties if they cannot achieve the target collection rate set by the EU Directives on WEEE. Unlike this, the Chinese government prefers subsidies or rewards, which set up a WEEE treatment fund in 2012 [
31] and added the WMPs to the
Waste Electrical and Electronic Equipment Treatment Directory (2014 Edition) in 2015 [
32]. The EPR principles were adopted in this fund. Specifically, the government levies funds on the electrical and electronic equipment producers and provides subsidies or rewards to authorized WEEE dismantling companies according to their actual disposal quantity. The RPM for the manufacturer and the collector is conducive to enhancing collection rate and increasing their payoffs. In addition, the RPM can be used to promote positive strategy evolution. Therefore, we examine an internal RPM negotiated by the manufacturer and the collector, which is rare in other literature.
Based on the theory and practice of the RSC, EGT, RPM, and the motivating example, we investigate an RSC comprising one manufacturer and one collector under an RPM. This paper uses the evolutionary game to discuss the relationships between members in the RSC and to analyze the evolution mechanism of their collection strategies, meanwhile, an optimal RPM is obtained. Finally, we take the collection of Chinese WMPs as an example to conduct the simulation of the RPM. Specifically, we address the following research questions:
- (1)
What kind of relationship between the manufacturer and the collector is beneficial to them?
- (2)
How does the evolution mechanism of their collection strategies affect their coopetition?
- (3)
What kind of RPM should be negotiated by them?
This paper exploits the EGT to discuss the coopetition relationship between a manufacturer and a collector in the collection and to examine the evolution mechanism and the optimal RPM for their collection strategies. Their strategy changes, evolution trends, and payoff fluctuations have been thoroughly studied, which is rare in other literature. The majority of incentive mechanisms is imposed by the government in a closed-loop supply chain (CLSC); there are few internal RPMs from players. However, this paper provides the internal RPM negotiated by the manufacturer and the collector.
The remainder of this paper is organized as follows. In the next section, we provide a literature review. The coopetition evolutionary game model (CEGM) is given in
Section 3.
Section 4 provides the analysis of evolutionary stability strategy (ESS) and the detailed analysis of the model including the optimal RPM. The simulation of the RPM is conducted in
Section 5.
Section 6 concludes this paper, discusses managerial implications, and proposes future research opportunities. List of acronyms in this paper is shown in
Appendix A.
3. Coopetition Evolutionary Game Model
3.1. Problem Definition
The manufacturer such as Mi can collect waste phones by himself and can also authorize the third-party collector such as Aihuishou to undertake the collecting tasks. This paper will refer to the manufacturer as “he” and to the third-party collector as “she” hereinafter. Their choices of strategy are presented in
Table 1. When he chooses the competitive strategy, he will undertake the task of self-collection, i.e., take into account both manufacturing and collecting; When he chooses the cooperation strategy, he will authorize her to undertake the collection, but there may be some risks of cooperation such as uncontrollable collecting process and difficult to guarantee service quality. When she chooses the competitive strategy, she will collect his waste phones for other manufacturers, which will reduce his remanufacturing materials; Otherwise, she will collect the waste phones for him.
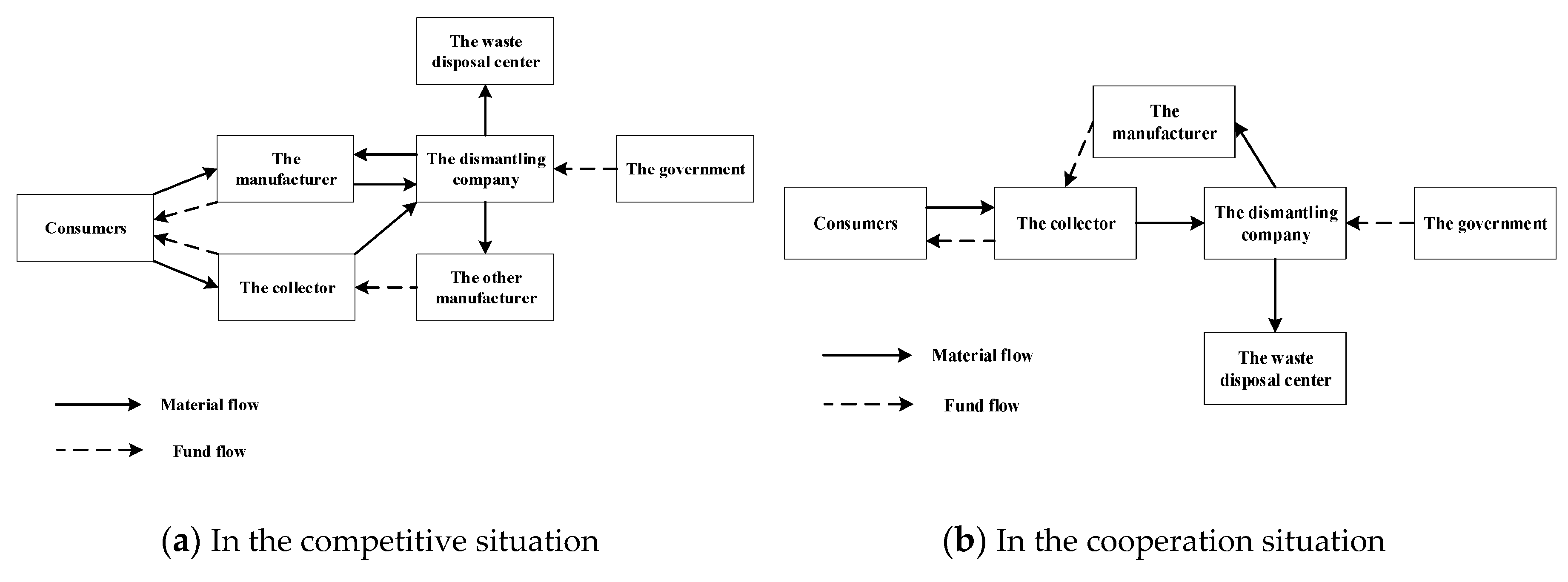
There are several parties including the manufactures, the collector, the dismantling company, the waste disposal center, the government, and consumers to achieve the collection in the RSC. Consumers’ waste phones would be bought back by the manufacturer and the collector for collection, then the waste ones would be disassembled by the dismantling company. The company will deliver remanufacturing materials to the corresponding manufacturer according to the collecting source of the waste phones, namely, returning them to him who takes the self-collection or to the manufacturer who cooperates with her. Here we assume that the other manufacturer does not take the collection. The government funds the dismantling company for environmental protection and resources conservation, and the cooperative manufacturer pays the collector collecting fees. The RSC structure in the competitive and cooperation situation is shown in
Figure 1.
As shown in
Figure 1, they compete for the collection of consumers’ WMPs in the competitive situation, and she collects his WMPs for the other manufacturer. Then the dismantling company delivers remanufacturing materials to the manufacturers according to the source of the waste. While in the case of cooperation, all the waste ones are collected by her for him. Then the dismantling company only delivers the remanufacturing materials to him. The key point of this RSC structure lies in their choice of collection strategies. Thus, we study the RSC consisting of one manufacturer and one collector.
3.2. Notations and Assumptions
The following notations in
Table 2 are used throughout the paper:
The following assumptions are made in the light of the actual situation and the characteristics of the model.
- (1)
The total amount and quality of collected phones would not be changed by their different strategies.
- (2)
His basic income is greater than the sum of the operating cost of his self-collection and the risk cost of his cooperation, namely, ; Her basic income is greater than the initial cost of her cooperation, that is, .
- (3)
To ensure that the both sides have the potential to cooperate, their potential profits are higher than cooperative risk inputs, namely, , .
3.3. Modeling
To improve their cooperative quality and protect their interests, this paper introduced an RPM
under cooperation, which is negotiated by them and implemented by him. Their payoff matrix of the CEGM is set up based on the model descriptions and assumptions above, as shown in
Table 3.
As can be seen in
Table 3, when they both adopt the competitive strategy, his income is the basic income excluding the operating cost of self-collection, namely
, and her income is the basic income
; When he takes the competition strategy and she takes the opposite one, his income is still
, but her income is the basic income excluding the initial cost of choosing cooperation, i.e.,
. In addition, when he adopts the cooperation strategy and she is the opposite, his income is the basic income excluding the sum of the operating cost of self-collection and the risk cost of choosing cooperation, i.e.,
, and her income is the basic income
; When they both adopt the cooperation strategy, his income depends on the RPM, cooperative risk cost, and his potential profit in a cooperative strategy, that is,
, and her income relies on the RPM, her operating cost of collection, her initial cost of cooperation, and her potential profit in a cooperative strategy, i.e.,
.
If she takes the competitive strategy, his income set (competition, cooperation) is (, ), and he will obviously choose the competitive strategy. However, if she adopts the cooperative strategy, his income set (competition, cooperation) is (). Since the latter is bigger, he will choose to cooperate with each other. Similarly, when he chooses the cooperation strategy, she also adopts the cooperation strategy; When he adopts the competition strategy, she adopts the same one. Therefore, the pure strategy Nash equilibriums of the CEGM are (competition, competition), (cooperation, cooperation).
When both of them choose cooperation, their income set (he, she) is (), which both reach the maximum value. Besides, the integration of resources caused by cooperation is beneficial to the overall interests of the RSC. Thus, the best choice for them is to adopt cooperative strategies.
In reality, when being under competition, they will vigorously pursue cooperation for greater interests. That is because he needs more remanufacturing materials and she pursues more profits. When they are under cooperation, he would doubt her operation capacity not matched with expenses, and she may dissatisfy their RPM. Therefore, it is not eternally immutable for their cooperative or competitive relationship with each other. In the long run, they will choose a competitive or cooperative strategy randomly.
4. Model Analysis and Discussion
4.1. Analysis of ESS
To obtain the evolution mechanism and the stability state of the coopetition relationship in the RSC, this paper analyzes ESSs.
It can be available from
Table 3 that his expected income of cooperative strategy is:
and his expected income of competitive strategy is:
Then his average expectation of expected income can be showed as:
Similarly, her expected income of cooperative strategy is:
her expected income of competitive strategy is:
Then her average expectation of expected income can be represented as:
The replicator dynamics [
69] was used to obtain the ESS. The replicator dynamic equation of his cooperative strategy is:
Put his expected incomes into Equation (7), can obtain:
Similarly, the replicator dynamic equation of her cooperative strategy is:
When is simultaneous, it can obtain , .
In the plane
N = {(
p,
q); 0 ≤
p,
q ≤ 1}, there are five equilibrium points including
O (0, 0),
A (0, 1),
B (1, 0),
C (1, 1), and
. The local stability of the RSC system is analyzed at these five equilibrium points by analyzing the local stability of Jacobian matrix. The partial derivatives of
and
are taken with respect to
and
respectively, and the Jacobian matrix is given as:
where
, , , .
Denote the determinant of
as
, and
. Denote the trace of
as
, and
. According to the method proposed by Friedman [
62], the criteria for judging the local stability of the Jacobian matrix are as follows:
The necessary and sufficient condition for the equilibrium point to be an evolutionary stable point is , ; The necessary and sufficient condition for the equilibrium point to be an instability point is , ; The necessary and sufficient condition for the equilibrium point to be a saddle point is .
The local stability of the equilibrium points in the RSC system can be obtained by calculation, as shown in
Table 4.
In
Table 4, “+” represents more than 0, and “-” represents less than 0.
It can be seen from
Table 4 that
O (0, 0),
C (1, 1) are evolutionary stable points;
A (0, 1),
B (1, 0) are instability points;
is a saddle point. Therefore, the ESSs of this CEGM are (competition, competition), (cooperation, cooperation).
4.2. Coopetition Evolution Analysis
In combination with
Table 3 and
Table 4, point
A corresponds to the case where he chooses cooperation and she chooses the opposite one. Her competitive strategy is because she is not satisfied with the RPM. Point
B corresponds to the case where he chooses the competitive strategy and she is the opposite. He dissatisfies with her service and adopts a competitive strategy. Their cooperation in these two cases ends in failure. However, they hope to achieve the maximization of their interests by means of cooperation. Therefore, point
A and
B are instability points.
Point O corresponds to the situation that they both choose competition, and point C corresponds to the cooperation situation. When they do not trust each other, they will be in competition for collection. However, when they reach an agreement, he will be not involved in the collecting business and she will provide quality services for him.
Denote his mixed strategy set as
, denote her mixed strategy set of as
, where
represents the pure strategy of competition,
represents that of cooperation. It is easy to verify that
is concave in
and
is concave in
from Equations (8) and (9), resulting in the income of
and
for any
and
. According to the definition of the mixed strategy Nash equilibrium [
70], when he chooses the strategy of
and she chooses
, they are just the best response to each other, achieving the mixed strategy Nash equilibrium. Thus,
is the mixed strategy Nash equilibrium of the CEGM.
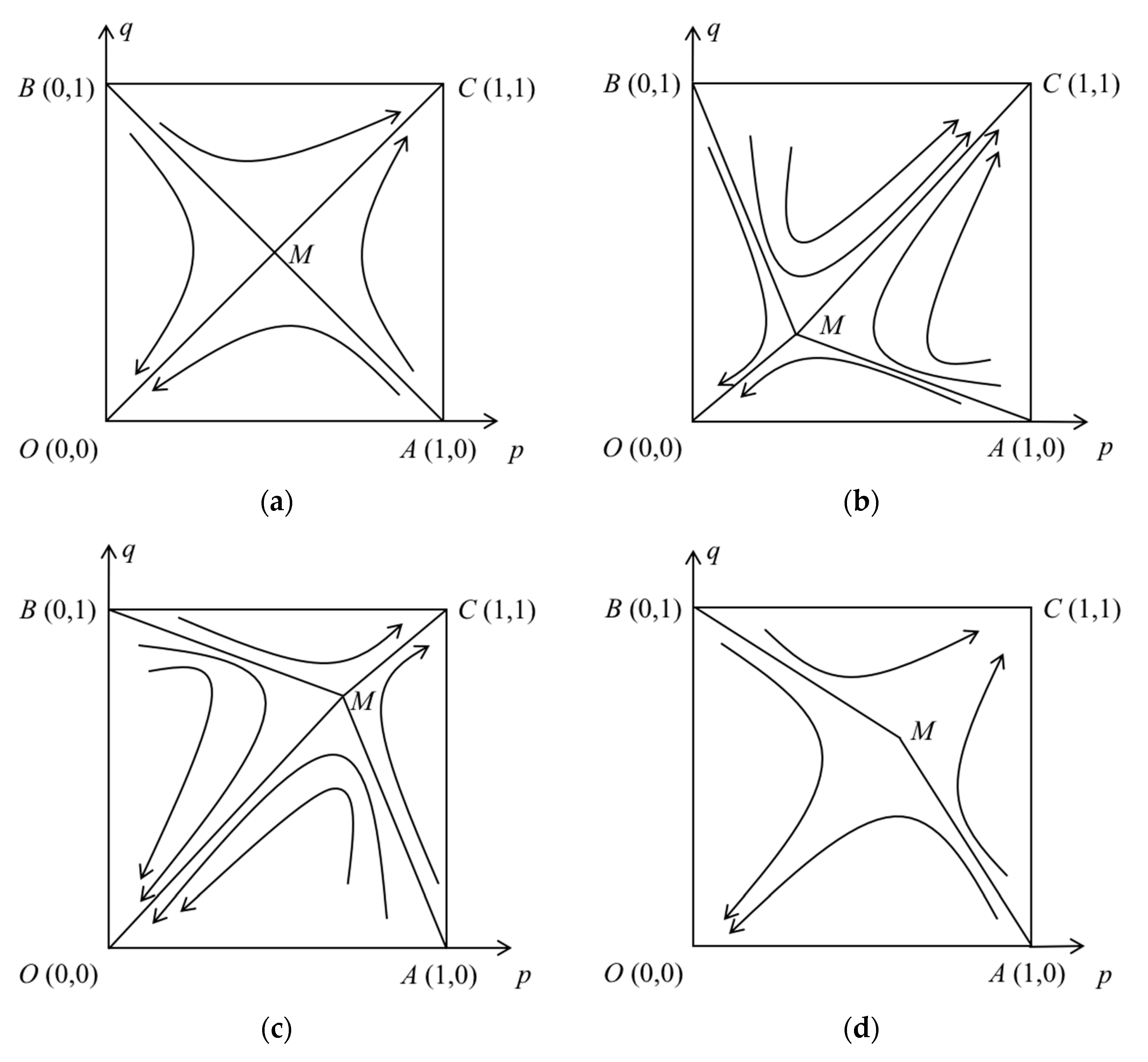
In the long-term evolution, they will alternate the situation of competition and cooperation, and achieve a dynamic equilibrium in the saddle point
. The evolution laws of the RSC system at different positions of point
M are shown in
Figure 2.
In
Figure 2a, the point
M is in the position (0.5, 0.5), and they have the same probability of overall competition or cooperation here; The point
M is in the position (
0.5,
0.5) in
Figure 2b, and they are more convergent to point
C (
cooperation), that is, more likely to choose the comprehensive cooperation strategy; In
Figure 2c, it is in the position (
0.5,
0.5), and here they are more convergent to point
O (
competition), namely, more likely to choose overall competition; The position of point
M is to be determined in
Figure 2d, and it is necessary to determine whether the system converges to point
O or point
C by means of further analysis.
Denote the area of quadrilateral
AMBO as
, the area of quadrilateral
AMBC as
. Then
The probability of the system convergence to the equilibrium point
O is higher than
C when
, as shown in
Figure 2c; The probability of the system convergence to
O is lower than
C when
, as shown in
Figure 2b; The probability of the system convergence to
O is equal to
C when
, as shown in
Figure 2a. Therefore, the probability of their competition is positively related to
, and the probability of cooperation is positively related to
.
It can be seen from Equations (11) and (12) that the factors that influence and are , , , , , , , , and in this game model. The detailed analysis will be presented below.
4.3. Sensitivity Analysis
Combining Equations (11) and (12) and the previous model assumptions, we can get the sensitivity analysis of the related parameters in the CEGM, as illustrated in
Table 5.
In
Table 5, the signs + and − represent an increase and decrease in equilibrium, in response to a marginal increase of the corresponding parameter, respectively. The sign
indicates that the equilibrium climbs up and then declines with a marginal increase of the corresponding parameter; The sign
indicates that the equilibrium decreases first and then increases with a marginal increase of the corresponding parameter. The superscripts
denote the different turning points of corresponding parameters.
As shown in
Table 5, the bigger
, the smaller
and the bigger
, that is, the probability of the system convergence to
O is smaller, but to
C is greater. Similarly, the bigger
, the smaller the probability of the system convergence to
O and the greater to
C. That means the greater the potential profit, the smaller the barrier to cooperation, and the probability of the waste phone RSC system evolved into cooperation is greater. It implicates that she should increase the collection quantity and quality of WMPs, and he should comply with the contract of cooperation.
The bigger , the bigger and the smaller , namely, the probability of the system convergence to O is greater, but to C is smaller. Similarly, the bigger , the greater the probability of the system convergence to O and the smaller to C. In other words, the greater the initial cost or risk cost of the cooperation strategy, the lower the willingness to cooperate, and the probability of the system evolved into competition is greater. It shows that she should improve operational management capability to reduce the risk cost of his cooperation strategy. She should also make full use of their resources, for example, take advantage of his sales outlets to conduct collection. He should evaluate her carefully according to her contractual history and operational capability.
The greater the operating cost of his self-collection and the smaller the operating cost of her collection , the greater the willingness to cooperate, and the probability of the system evolved into cooperation is greater. It indicates that she should improve operational management capability to reduce her operating costs.
The greater his reward to her, the greater the probability of her cooperation, but the smaller that of his cooperation. The greater his penalty to her, the smaller the probability of her cooperation, but the greater one of his cooperation. That means there are some contradictions that complicate the effects of the reward implemented by him for her successful service
and the penalty implemented by him for her failed service
on the probability of cooperation. These contradictions implicate that they have an optimal RPM to promote the cooperation tendency. As shown in
Table 5,
decreases first and then increases as
or
increases, and
is the opposite, namely, the system first tends to converge to
C and then to
O. In this case, both
and
have an optimal value, making the probability of the system evolved into cooperation to the maximum. The probability of her service failure
has a direct impact on the implementation of
and
, and its change is consistent with
.
It can be obtained by solving Equation (11) that the optimal reward implemented by him for her successful service is , and the optimal penalty implemented by him for her failed service is . The probability of her service failure that is most conducive to cooperative evolution is .
In conclusion, the optimal RPM is , .
5. Simulation of RPM
Although the theoretical solution of the optimal RPM has been analyzed in
Section 4.3, to enhance understanding, a simulation of the RPM is conducted to further clarify the meaning of the optimal RPM. Therefore, we investigated a famous mobile phone manufacturer A and a prosperous third-party collector B as a case study. The parameters, as shown in
Table 6, in the following simulation experiments were collected from them, but were modified for the confidentiality reason. These experiments were conducted on the simulation platform of MATLAB R2017b.
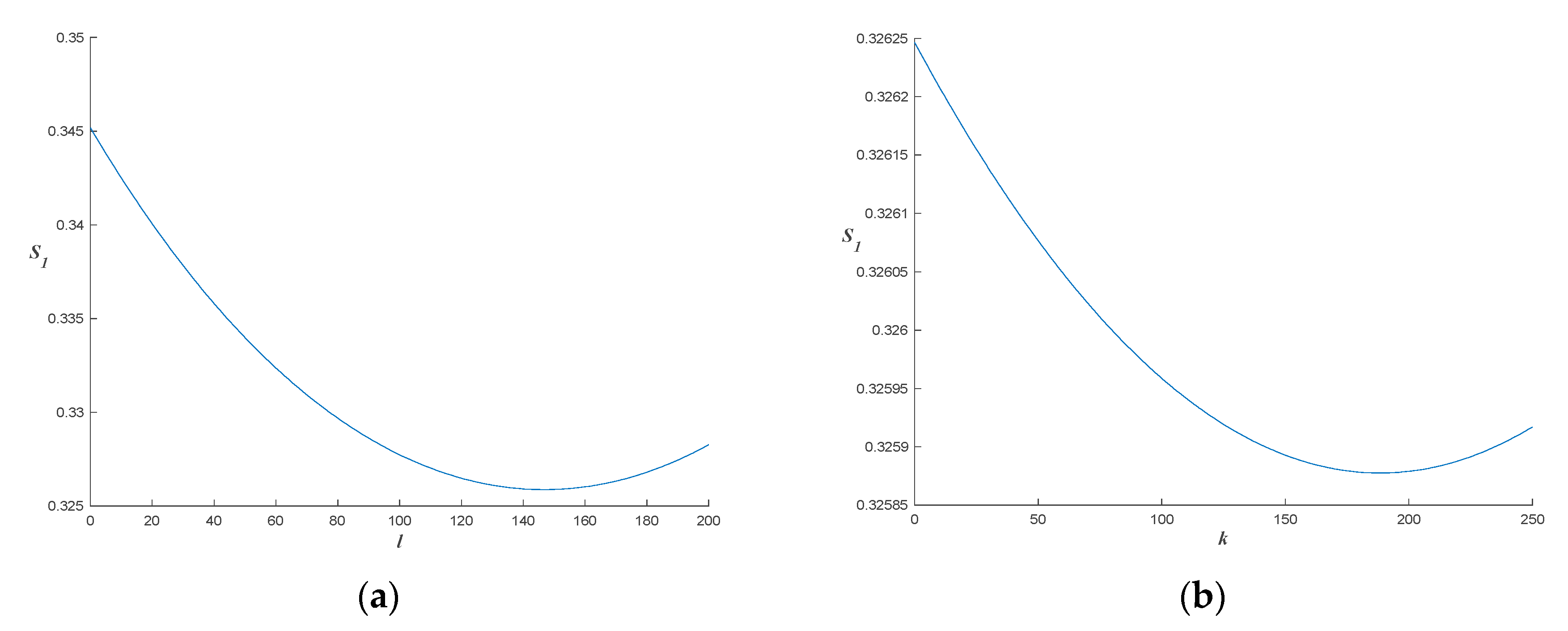
To obtain the optimal reward implemented by him for her successful service
, we made the range of
0–200, and the simulation result is shown in
Figure 3a. Similarly, to obtain the optimal penalty implemented by him for her failed service
, we made the range of
0–250, and the result is shown in
Figure 3b.
It can be seen from
Figure 3a that
decreases first and then increases as
increases. In this case, when
, the value of
is the minimum, that is, it is the largest for the probability of the system evolved into cooperation.
has the similar effect on
as
, which is shown in
Figure 3b. When
, the value of
is the minimum in this case, namely, it is the largest for the probability of the system evolved into cooperation.
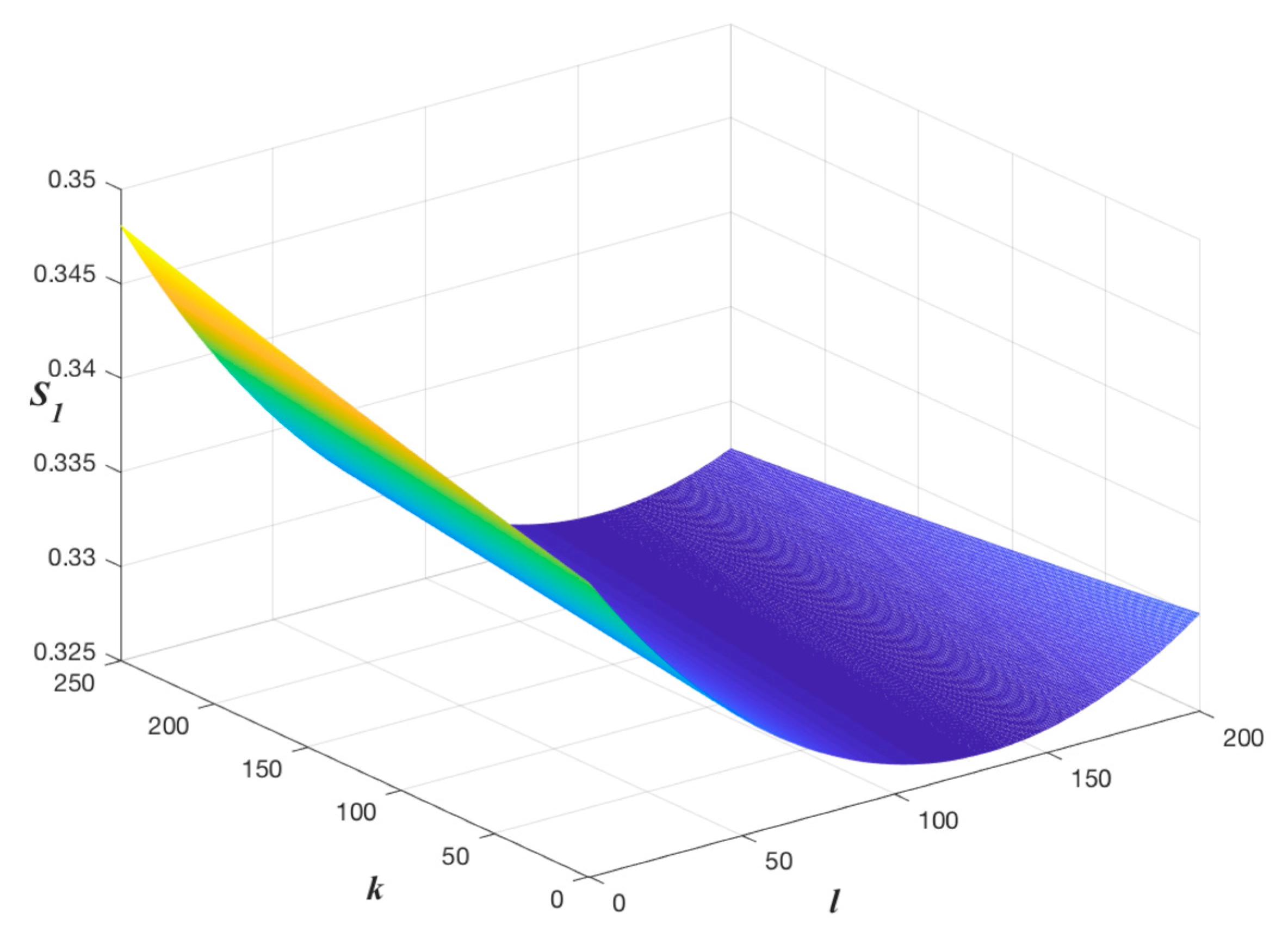
We also made the simulation of
with the ranges of
0–200 and
0–250, the result is shown in
Figure 4.
It can be seen from
Figure 4 that
is under the double influence of
and
. When
is low,
increases with the increase of
, otherwise,
decreases with the increase of
. However,
decreases first and then increases as
increases no matter whether
is big or small. It shows that the optimal RPM consisting of the optimal reward and penalty is interrelated, and they need to be developed at the same time, which is the same as the implication of their formulas. According to the calculated results, the optimal reward and penalty here are 147 and 143, respectively.
6. Conclusions, Insights, and Future Research
This paper presents a CEGM to discuss the coopetition relationship between members in an RSC comprising one manufacturer and one collector and examines the evolution mechanism and the internal RPM for their collection strategies. The pure strategy Nash equilibriums in this model are obtained which show their collection strategy choices of perfect competition or cooperation. However, their cooperative or competitive relationship is not eternally immutable. In the long run, they will choose a competitive or cooperative strategy randomly. The mixed strategy Nash equilibrium and the optimal RPM are obtained in the model analysis and discussion. Finally, this paper takes the example of WMPs in China to examine the simulation of the RPM.
The contributions of this paper include two parts: Firstly, it examines the coopetition relationship between the manufacturer and the collector. It provides common collection strategies and then analyzes the evolution of them, which is of practical significance to implement their collection of WMPs. Secondly, it discusses the two-sided RPM negotiated by the manufacturer and the collector in the RSC, which is beneficial to promote their cooperation tendencies and then to increase their payoffs.
We find that cooperation is the best choice for the manufacturer and the collector to increase their payoffs. There is an optimal RPM for them to propel the cooperation tendency. We provide some practical insights for the manufacturer and the collector as follows. They need to simultaneously negotiate the two-sided RPM consisting of the optimal reward and penalty. The manufacturer should evaluate the potential partner carefully according to her contractual history and operational capability. Once cooperation is reached, he should faithfully perform it. The collector should improve operational management capability to reduce her operating costs and the risk cost of his cooperation strategy and to increase the collection quantity and quality of WMPs. She should also make full use of their resources, for example, take advantage of his sales outlets to conduct collection.
This paper adopts the failure probability of the collector’s service instead of the quantitative analysis of her service to define her success or failure. However, the latter is more feasible to implement the RPM, because to obtain the failure probability of her service needs accurate evaluation and prediction. Thus, the future research should quantitatively analyze her service and provide more specific RPM. In addition, other competitors are neglected in this paper, it is more practical to deal with internal and external competition from members in the RSC.