3. Thermal Balance of the Greenhouse
Thermal balance aims to determine the losses and heat gains of each partition in an examined object. For this purpose, calculations of losses by the lateral surface, the upper surface and the ground, as well as the gains from solar radiation that reaches the object during sunny days, known as radiation heat, were conducted.
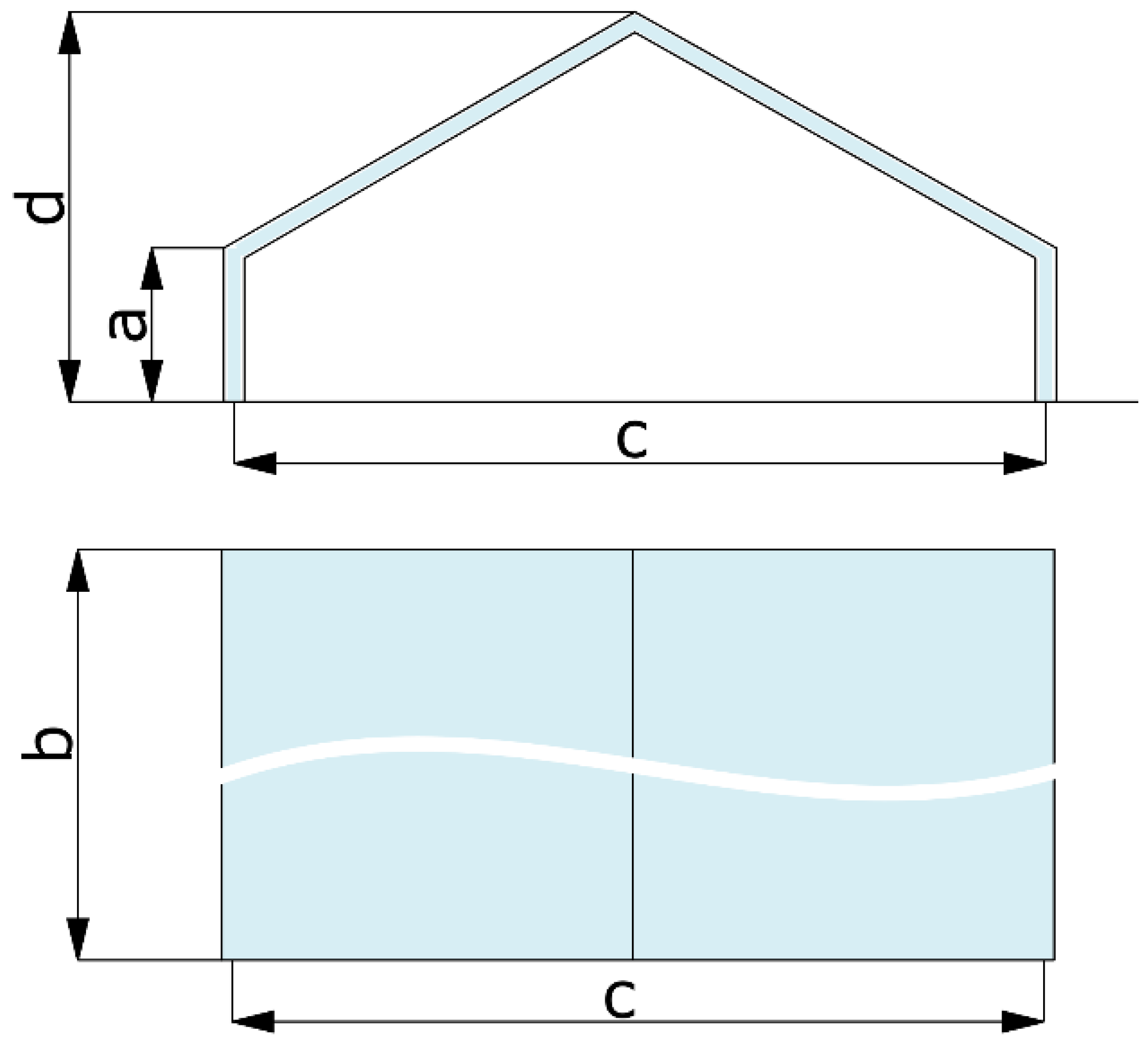
Figure 2 presents the dimensions of the analyzed roof surfaces.
Calculations of the heat gains and losses were made with the assumption that the air between the glass layer and the cell foil, as well as that found inside the greenhouse, is stationary, and therefore there is natural convection. Due to small changes in wind speed in the analyzed period, it was assumed that the average wind speed outside the greenhouse was equal to 2 m/s. This value corresponds to the averaged meteorological data for the given area.
By knowing the dimensions of the walls, the characteristic linear dimensions should be determined. For the front wall, it is expressed by the formula for the arithmetic mean of the sidewall height a and the height of the greenhouse
d (Equation (1)).
The internal roof slope length
was assumed as the characteristic linear dimension of the roof surface (Equation (2)).
For the side walls, the height of a side wall
was assumed as the characteristic linear dimension (Equation (3)).
For the ground surface, the diagonal of the surface is assumed as the characteristic linear dimension (Equation (4)), where
is its width and
is its length.
To characterize the heat exchange process, it was necessary to determine the Reynolds number for the air parameters outside the greenhouse, which was described using Equation (5).
The obtained values of the Reynolds number (
Table 1) show the turbulent movement of air outside the greenhouse, and also determine the selection of subsequent equations. The equation for the Nusselt number for the outer surface of the greenhouse is described using Equation (6).
There is a free convection inside the greenhouse, which is why the Nusselt number
is determined using Equation (7). It depends on the coefficient
, the Grashof number
, the Prandtl number
(
Table 1) and the coefficient
, the value of which is equal to
[
28].
The value of constant
in Equation (8) is an indispensable element for determining Nusselt numbers for individual vertical partitions from the inside of an object, and it depends on the Prandtl number
, the value of which is in
Table 1.
The compressibility of fluid in Equation (9) is determined for the layer next to a wall. It is a value that depends on the temperature inside an object
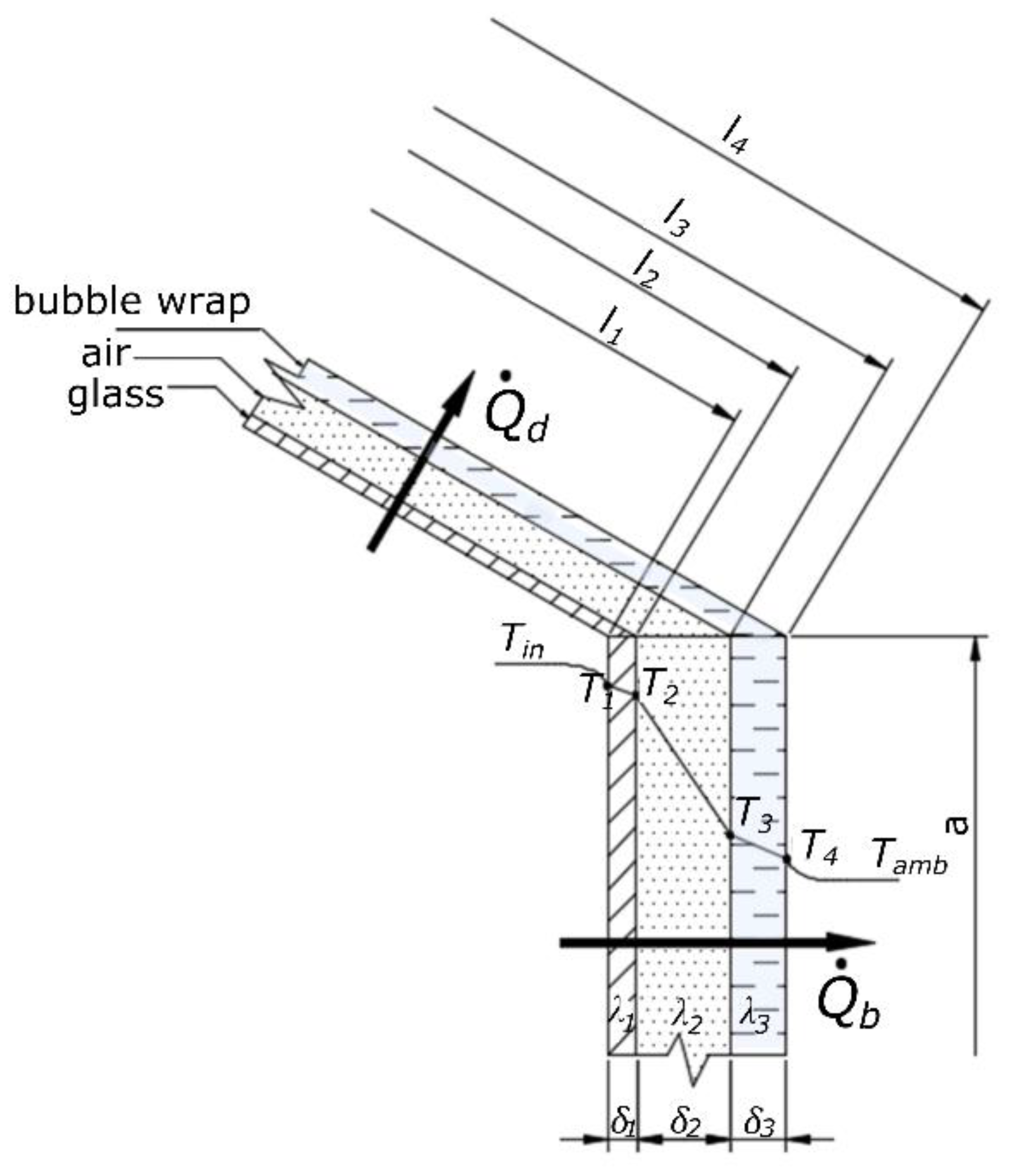
and the temperature of the partition that is directly in contact with the liquid
. In the analyzed case, this temperature is the temperature of the inner surface of the glass for the front partition and for each of the other partitions.
The Grashof number (Equation (10)) depends on: the compressibility of fluid
(Equation (9)), the temperature inside a greenhouse
, the characteristic dimensions
(Equations (1)–(3)), the acceleration of gravity
g, the inner temperature of the glass layer
, and the kinematic viscosity of the air inside the greenhouse
(
Table 1).
For a flat partition inclined at an angle of
, the Nusselt number is calculated from Equation (11).
The coefficient of heat transfer from the inside of the greenhouse to the wall for individual partitions depends on the Nusselt number
(Equations (7) and (11)), the thermal conductivity coefficient
for the liquid in the object (
Table 1), and the characteristic dimension of the partition
(Equations (1)–(3)). It is expressed using Equation (12).
The heat transfer coefficient outside the greenhouse depends on the Nusselt number (Equation (6)), the thermal conductivity coefficient
(
Table 1) of the fluid surrounding the object, and the characteristic dimension
(Equations (1)–(3)), and is described using Equation (13).
The heat transfer coefficient
depends on the thickness of the individual layers of the partition, the conductivity coefficients of the materials from which the partition was constructed (
Table 1), and heat transfer coefficients (Equations (12) and (13)), and is described using Equation (14).
The heat flux through the partition depends on the heat transfer coefficient
(Equation (14)), the difference between internal temperature
and external temperature
, and the heat transfer area
(
Table 1), and is described using Equation (15).
The heat flux transmitted between the fluid and the inner wall of the greenhouse (Equation (16)) depends on the coefficient of heat transfer
(Equation (12)), the temperature difference between the temperature inside an object
and the temperature of the inner glass layer
, as well as the surface of heat exchange
(
Table 1).
For the roof, the heat transfer coefficient
(Equation (12)) is increased by 30% in relation to the coefficient calculated for the lateral surface [
26]. This is due to the heat flow direction that results from the difference in fluid density, and therefore, for this surface, Equation (16) takes the form of Equation (17).
Heat of radiation is a result of solar radiation that reaches the interior of an object, and it depends on the intensity of solar radiation that directly falls on a given surface , and also the coefficients of transparency of individual partition layers .
The values of transparency coefficients of the individual layers of a partition of the greenhouse were taken from literature [
29]. Their values are given in
Table 1.
The volume of the greenhouse
(Equation (18)) is the value that determines the volume of air inside the object. It can be estimated when knowing the geometric dimensions of the greenhouse (
Table 1) and the basic formulas for the surfaces of flat figures.
By knowing both the volume of air inside the greenhouse
(Equation (18)) and the air density
, it is possible to determine the air mass (Equation (19)).
It was assumed that solar radiation reaches half of the roof surface
. Therefore, this area is calculated from the length of the greenhouse side
and the outer length of the roof
(
Table 1).
The heat flux penetrating into the greenhouse due to radiation (Equation (21)) depends on the transparency coefficients of the individual layers of a partition
(
Table 1), the surface of heat exchange (Equation (20)), radiation intensity
, and the efficiency of the conversion process
that defines the amount of radiation energy converted into sensible heat, which takes the value of
[
29].
The loss of heat to the ground is calculated from heat exchange equation [
28] for heat penetration into the ground surface. For this purpose, the series of variables that make this loss are determined. The heat flux depends on the surface of heat exchange
and the difference between the ground temperature
and the temperature inside the object
, as well as the soil conductivity coefficient
and the heat transfer coefficient
.
The compressibility of fluid (Equation (22)) next to the ground surface depends on both the temperature inside the greenhouse
and the ground temperature
.
The Grashof number depends on the compressibility of fluid
, the difference between the temperature inside the greenhouse
and the ground temperature
, kinematic viscosity
(
Table 1) and the characteristic linear dimension
(Equation (4)). It is expressed by Equation (23).
The Nusselt number inside the greenhouse for the ground surface (Equation (24)) depends on the coefficient
[
26], the Grashof number
(Equation (23)), the Prandtl number
(
Table 1) and coefficient
, the value of which is equal to
[
30].
The coefficient of heat transfer to the ground
(Equation (25)) depends on the Nusselt number
(Equation (24)), the air conductivity coefficient
(
Table 1) and the characteristic linear dimension of the ground
(Equation (2)).
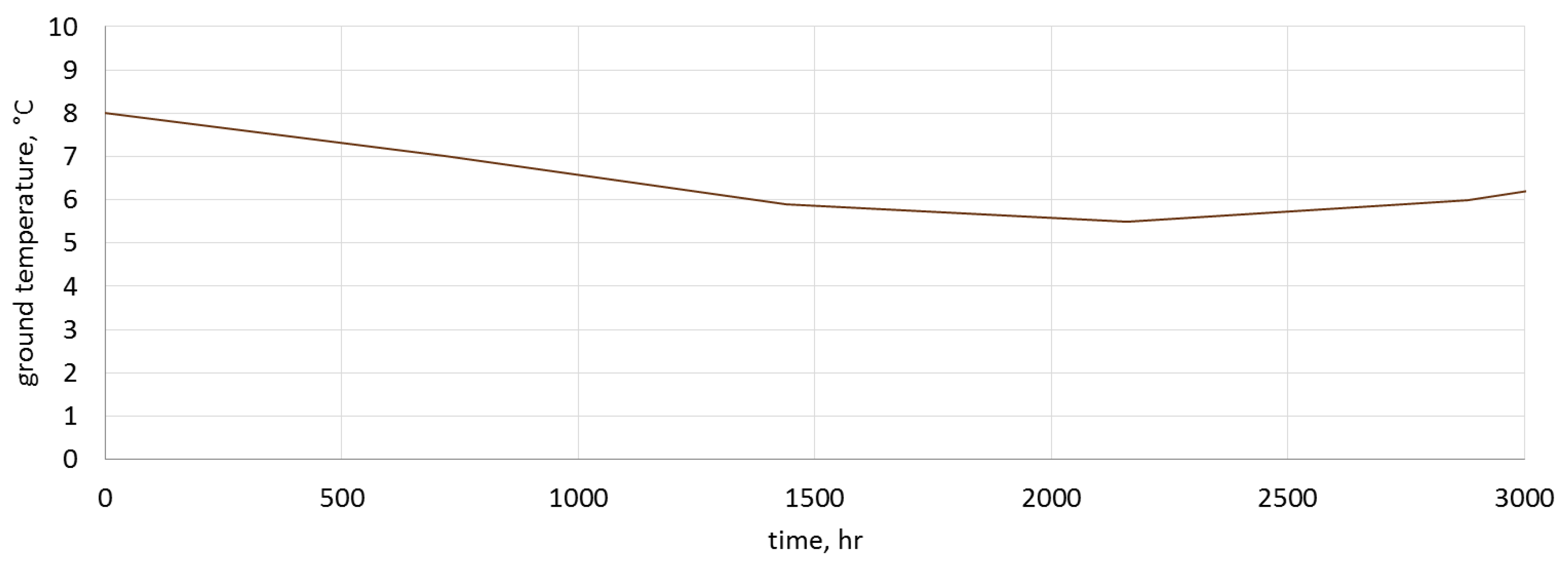
The heat flux that penetrates the ground is expressed by Equation (26), where the ground temperature
is assumed to be the ambient temperature
. The flux depends on the surface of heat exchange
(
Table 1) and the difference between the temperature inside an object
and the ground temperature
, as well as the heat transfer coefficient
, the ground heat conductivity coefficient
and the equivalent ground thickness
, the value of which is assumed to be 2 m [
25].
The heat flux of ventilation that was caused by greenhouse leaks is related to the specificity of this type of facility and depends on the total area of covers
and the resistance to heat transfer that is associated with the air exchange
, as well as the difference between the temperature inside the greenhouse
and the temperature outside
. The total area of the covers
(Equation (27)) is the sum of the surfaces of the side walls
, the front and back walls
and also the roof surface
(
Table 1).
The heat flux that is associated with the ventilation of the object
is expressed by Equation (28), where the value of the thermal resistance is equal to
[
25].
The computational algorithm that allows the above heat exchange equations to be solved was prepared in Mathcad 15 software. It enabled the heat flux that penetrates the individual partitions, as well as the temperature of the inner wall
and the final temperature inside the object
to be determined. The above-mentioned activities allowed the balance in Equation (29) to be written, which in turn enabled the temperature in the greenhouse
after the specific time step
to be determined.
3.1. Calculation of the Temperature Inside the Greenhouse
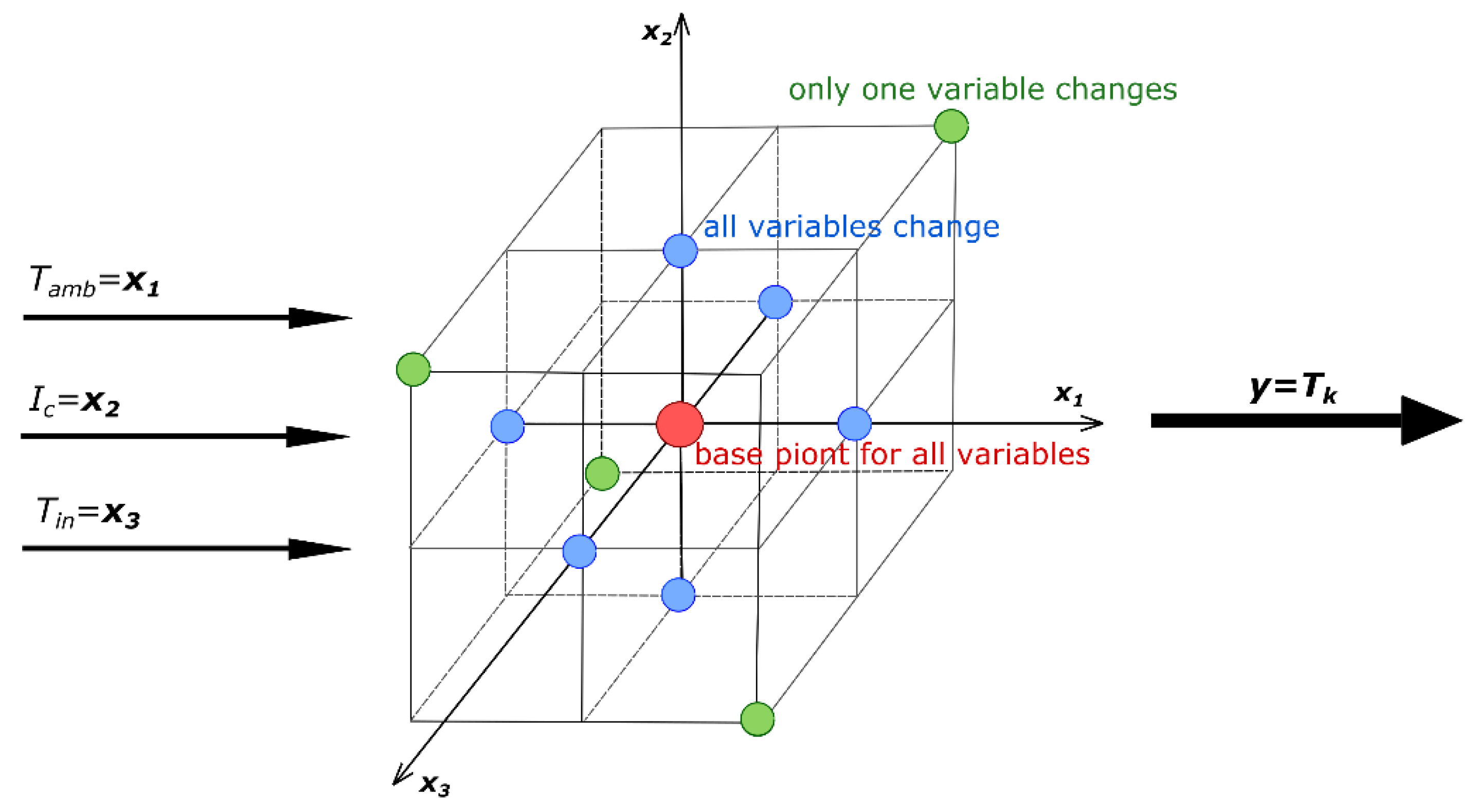
To determine the final temperature inside the greenhouse, techniques of planning an experiment were used. A three-level plan for three input factors on three levels of variation, called the Hartley plan [
31], was chosen for the analysis. The use of it enabled the dependence between the final temperature inside the greenhouse
and the three following input factors to be determined (
Figure 3):
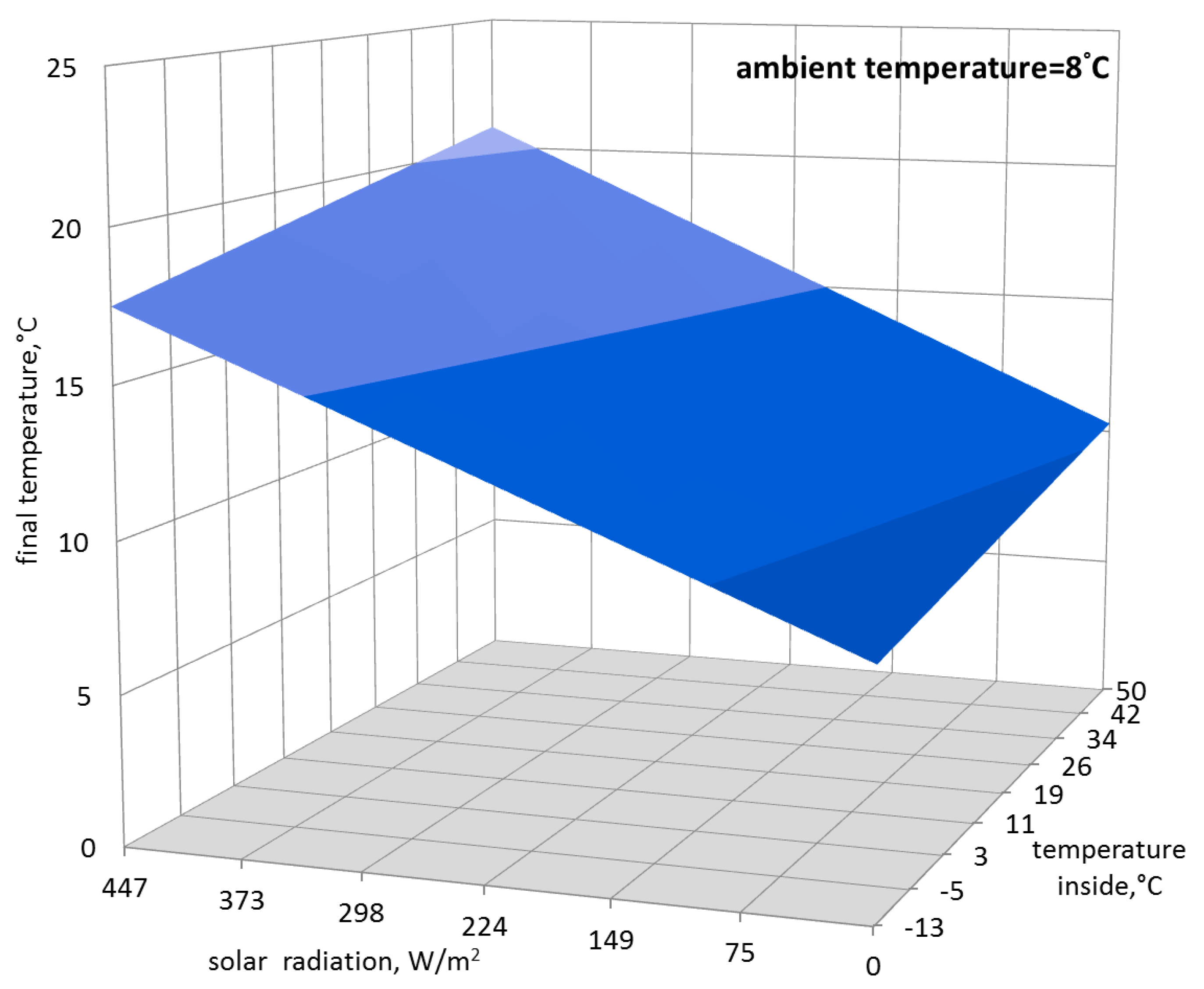
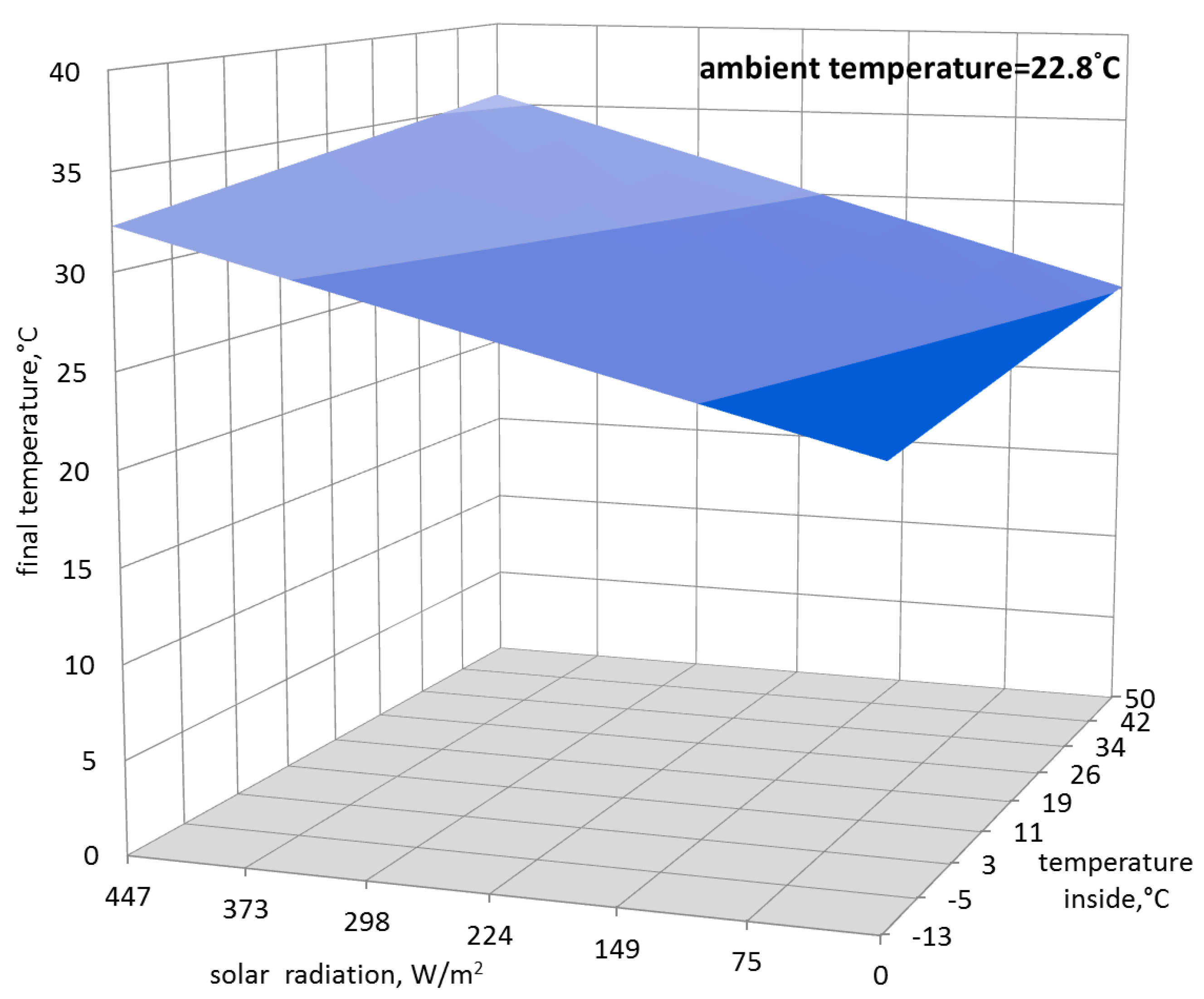
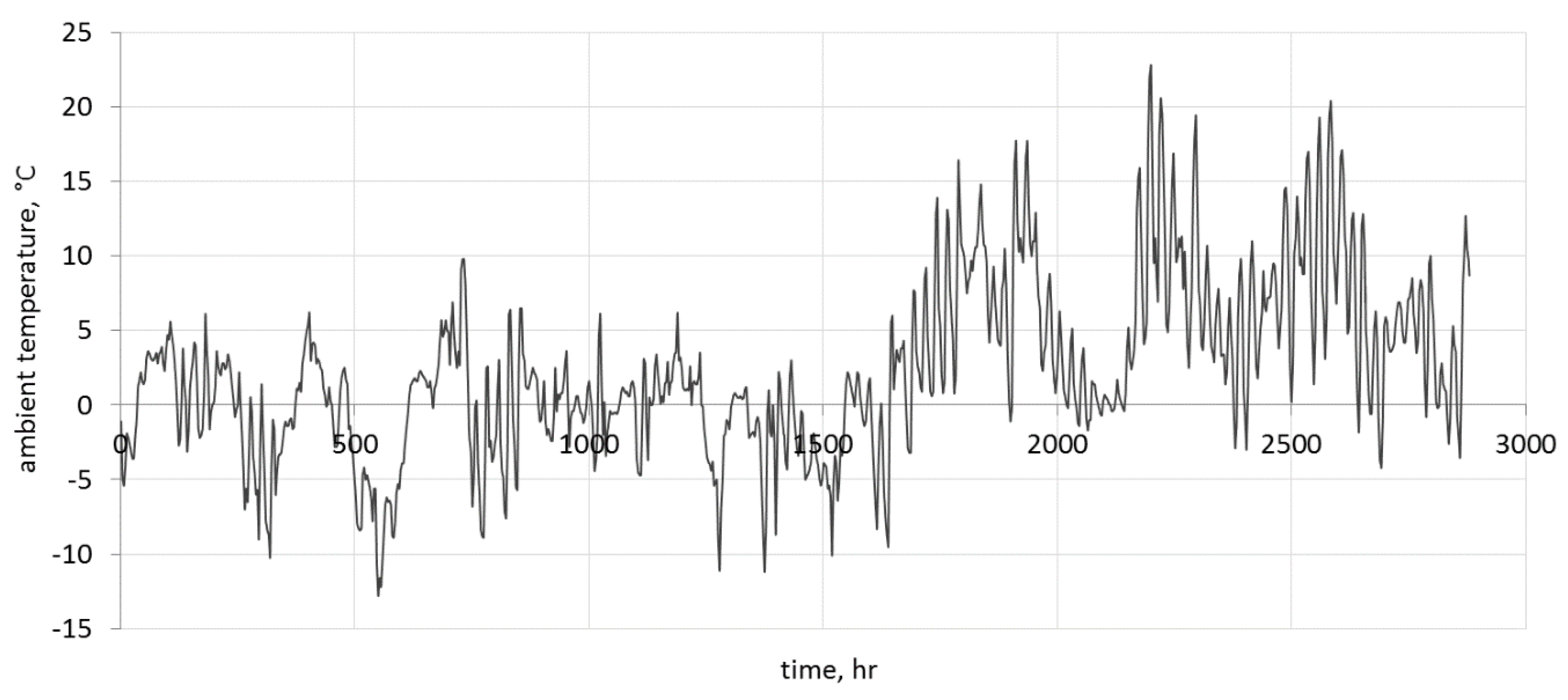
—ambient temperature that varies within the range from −12.8 to 22.8 °C;
—intensity of solar radiation that covers the range from 0 to 447.3 W/m2; and
—temperature inside the greenhouse , which can take values from −12.8 to 50 °C.
The Hartley Plan matrix for the three input factors, which is built on the hypercube, is shown in
Table 2.
The implementation of Hartley’s plan allows a mathematical model that describes the temperature changes inside the greenhouse with regards to the input factors, which is expressed by means of the second degree polynomial (Equation (30)), to be determined.
Determination of the linear-quadratic equation starts with the calculation of the central values (Equations (31)–(33)), thus the determination of the input variables that assumes the 0 level.
Table 3 presents the values of individual variables that assume the three levels of +1, 0 and −1 successively.
The values of individual linear-quadratic equation coefficients (Equation (30)) were determined using matrix markers, and their values are presented in
Table 4.
Table 4 also shows the simulation results for individual combinations of input variables according to the Hartley matrix.
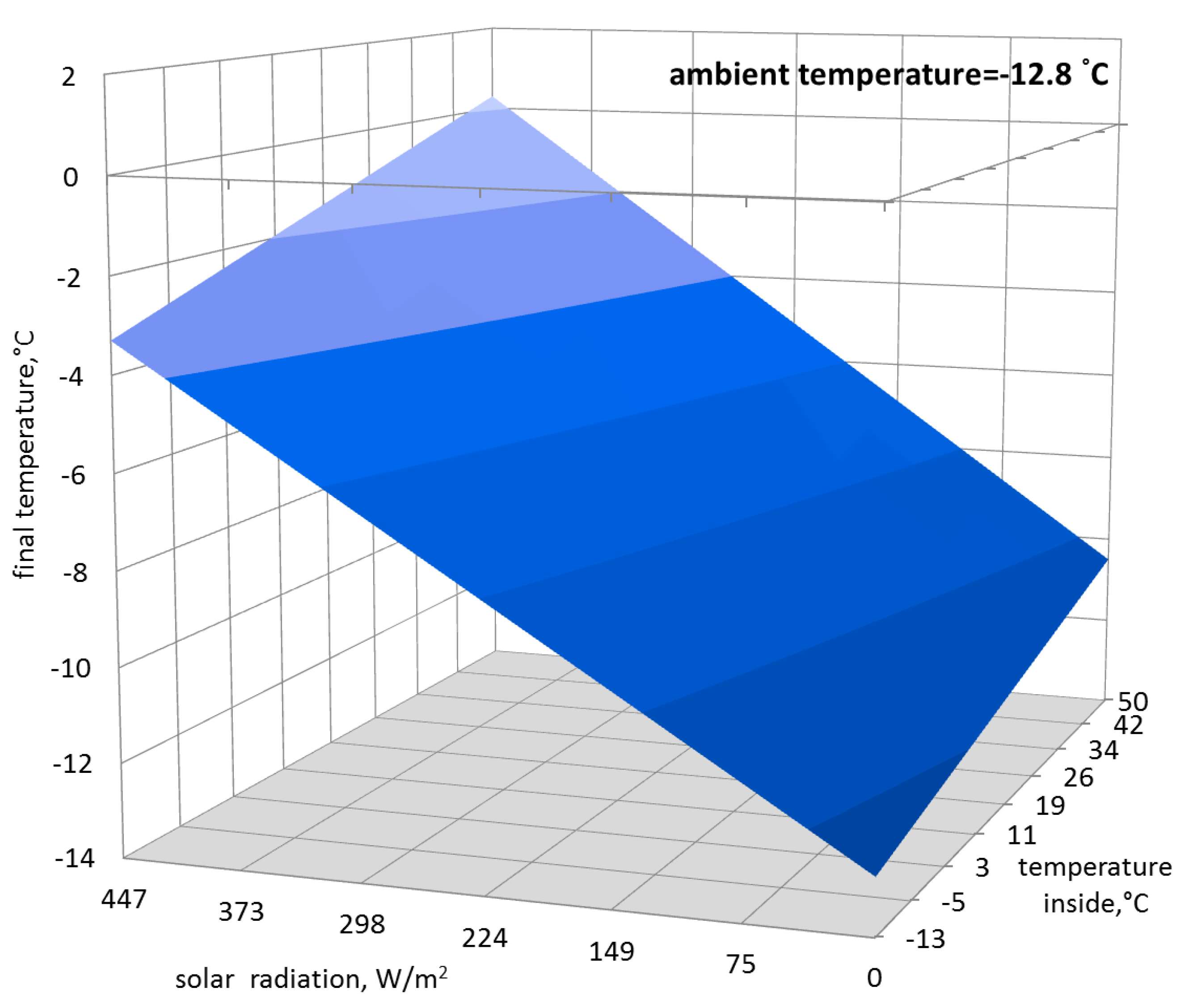
Based on the obtained function, it was possible to determine the final temperature inside the greenhouse with regards to the three above-mentioned input parameters, which is shown in
Figure 4,
Figure 5 and
Figure 6.
The obtained equation for the temperature inside the greenhouse was used to prepare the heat demand for the analyzed heating period.
3.2. The Greenhouse’s Heat Demand
To determine heat demands, statistical data published by the Ministry of Investment and Development of the Republic of Poland [
32] were used for the energy calculations of buildings for the given location of the greenhouse.
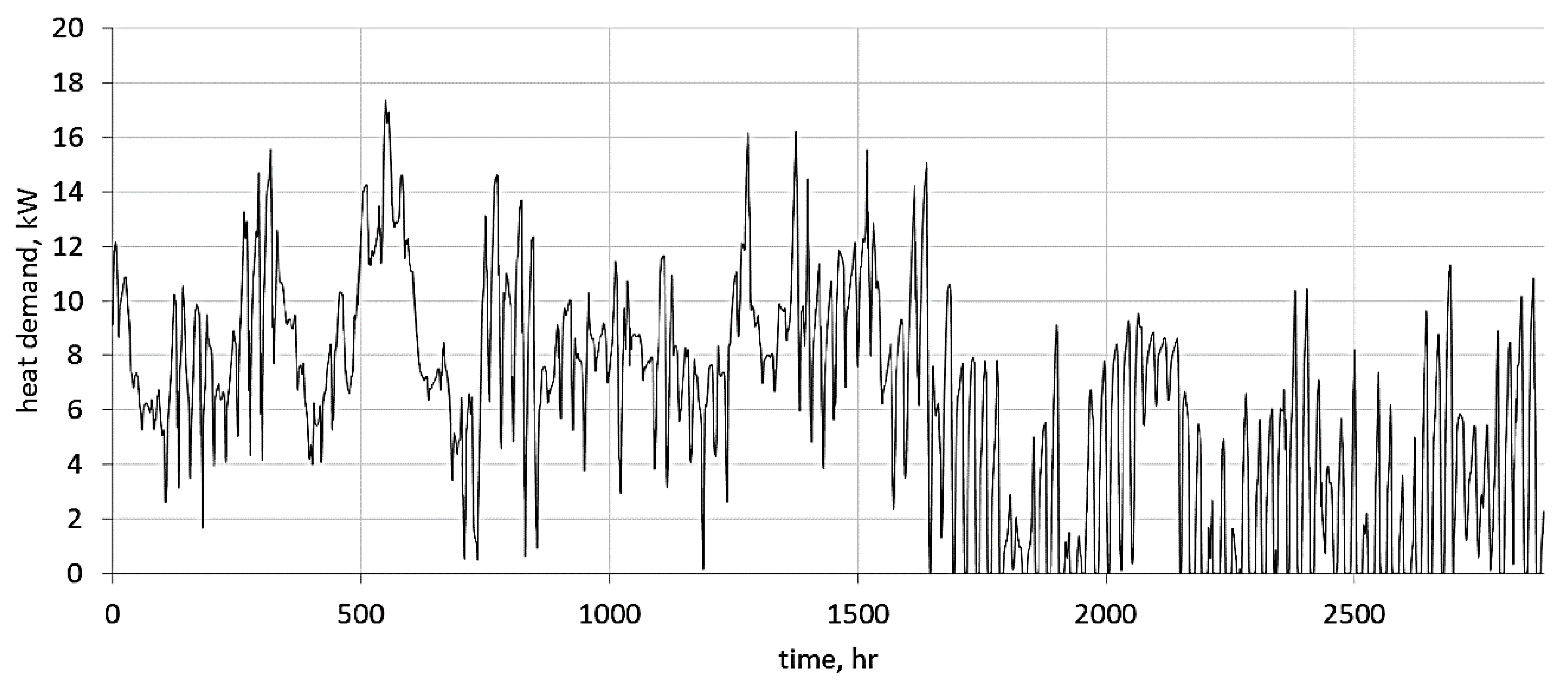
Figure 7 shows the change in the temperature inside the object during the day from the beginning of January until the end of April. In the analyzed period, the temperature inside the greenhouse is lower than the reference temperature of 12 °C. This proves that a heating system needs to be used during this time.
Figure 8 presents the characteristics of the greenhouse’s heat demand, which was created on the basis of the thermal balance equations of the greenhouse.
The obtained characteristics determine the minimum power of the heating system and are the basis for determining the operating costs.
5. Economic Analysis
The cost of a heating installation includes fixed and variable costs. For the analyzed heating system, the heat pump is a fixed cost. The price of the chosen ground source heat pump, according to the company’s price list, is equal to €10,049 gross. The price of executing a horizontal collector is around €4285. The cost of the entire investment of €14,334 is obtained by adding the cost of purchasing a ground source heat pump and installing a ground collector. Calculated per unit of the greenhouse area that amounts to 419.92 m2, it is equal to €34/m2. The cost of an air source heat pump is equal to €4952 gross, and when it is calculated per unit of the greenhouse area, it is equal to €12/m2. The cost of producing a boiler room equipped with a coal-fired boiler with an 18 kW feeder is approximately €1904.5 gross. The total cost of assembly is about €1190, and therefore the total investment cost is estimated to be €3094.5, which, when calculated per unit of the greenhouse area, is equal to €7.4/m2.
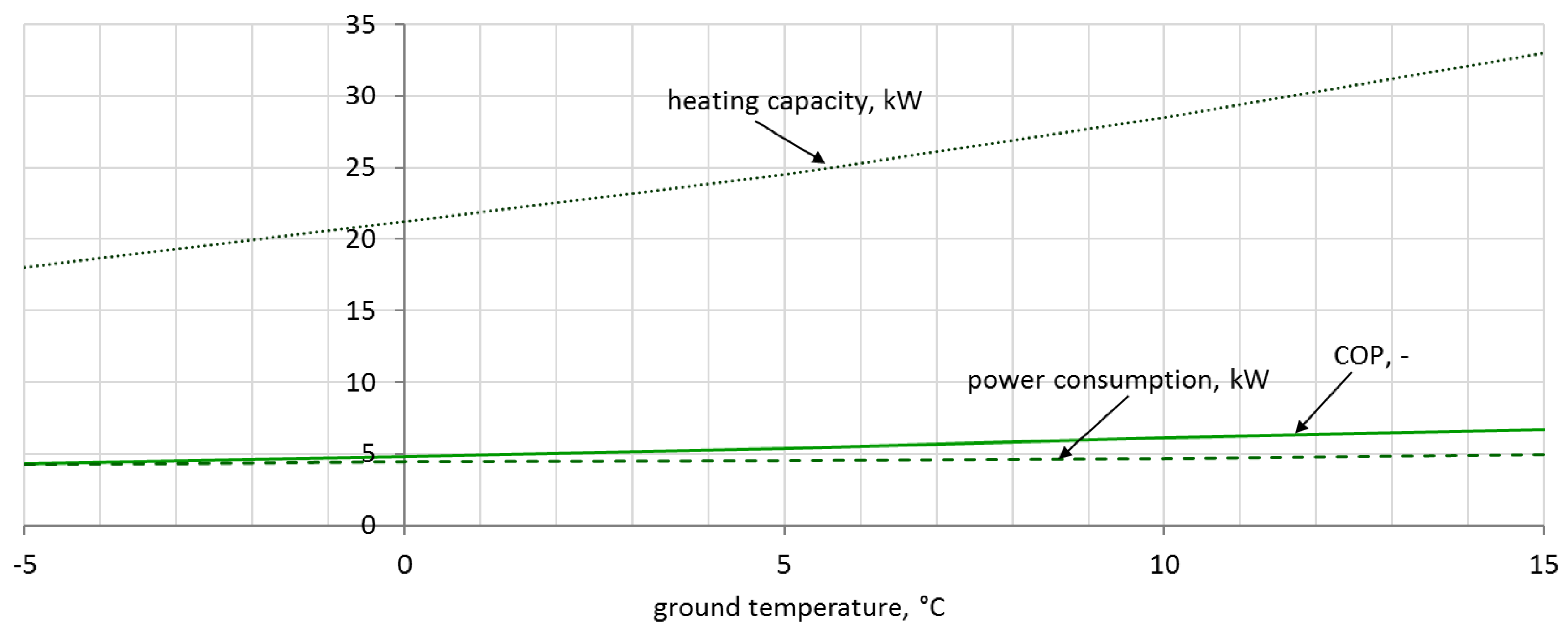
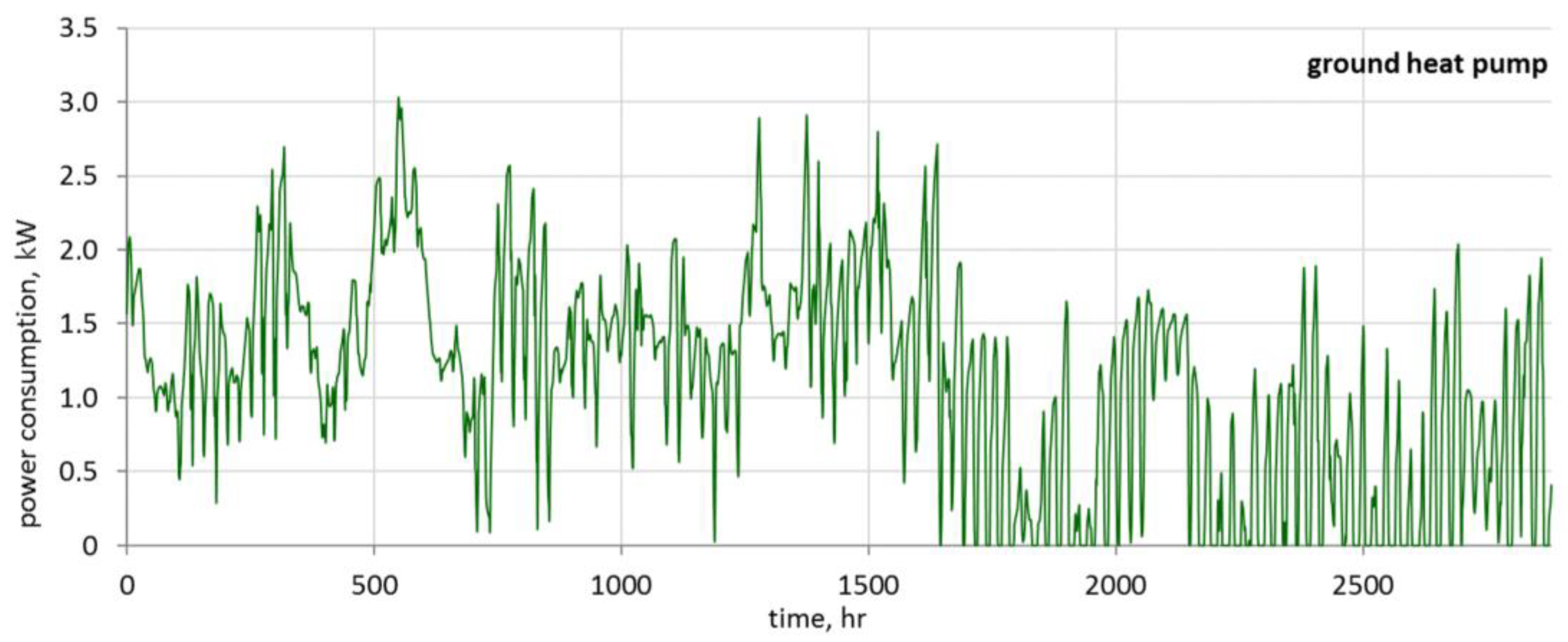
The cost of running a ground source heat pump is calculated on the basis of the characteristics of the consumed electricity (
Figure 12). Assuming that 1 kWh costs €0.12, then the cost for the entire heating period
is equal to €385.60/year. Using the characteristics presented in
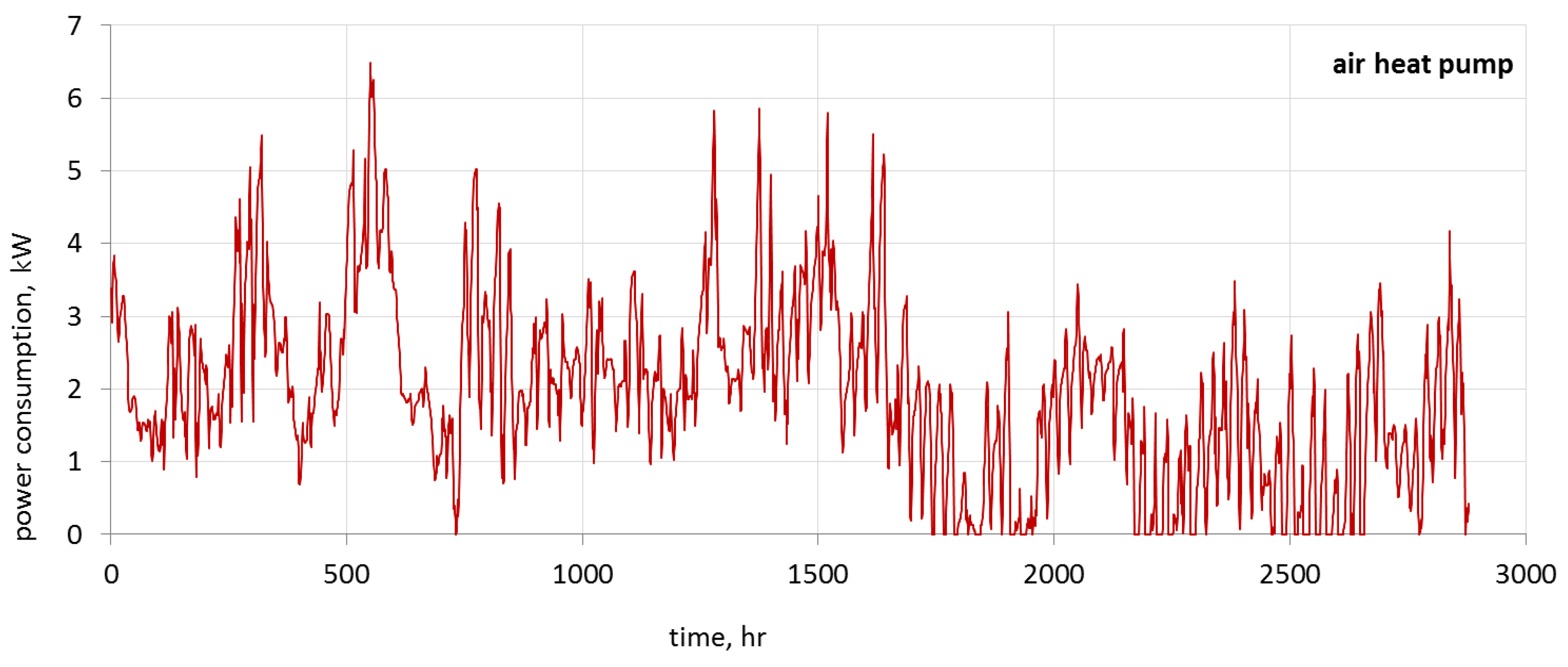
Figure 16, the cost of the air source heat pump
is equal to €678.64/year.
To calculate the simple payback time of the investment, the costs of the heat pumps’ operation were compared to the costs incurred when heating the boiler with fine coal. Fuel consumption for heating the greenhouse with the existing 25 kW fine coal boiler for the designated heat demands is determined using Equation (35).
The calorific value of fine coal is assumed to be 18–26 MJ/kg, and therefore the following value is assumed for the calculations:
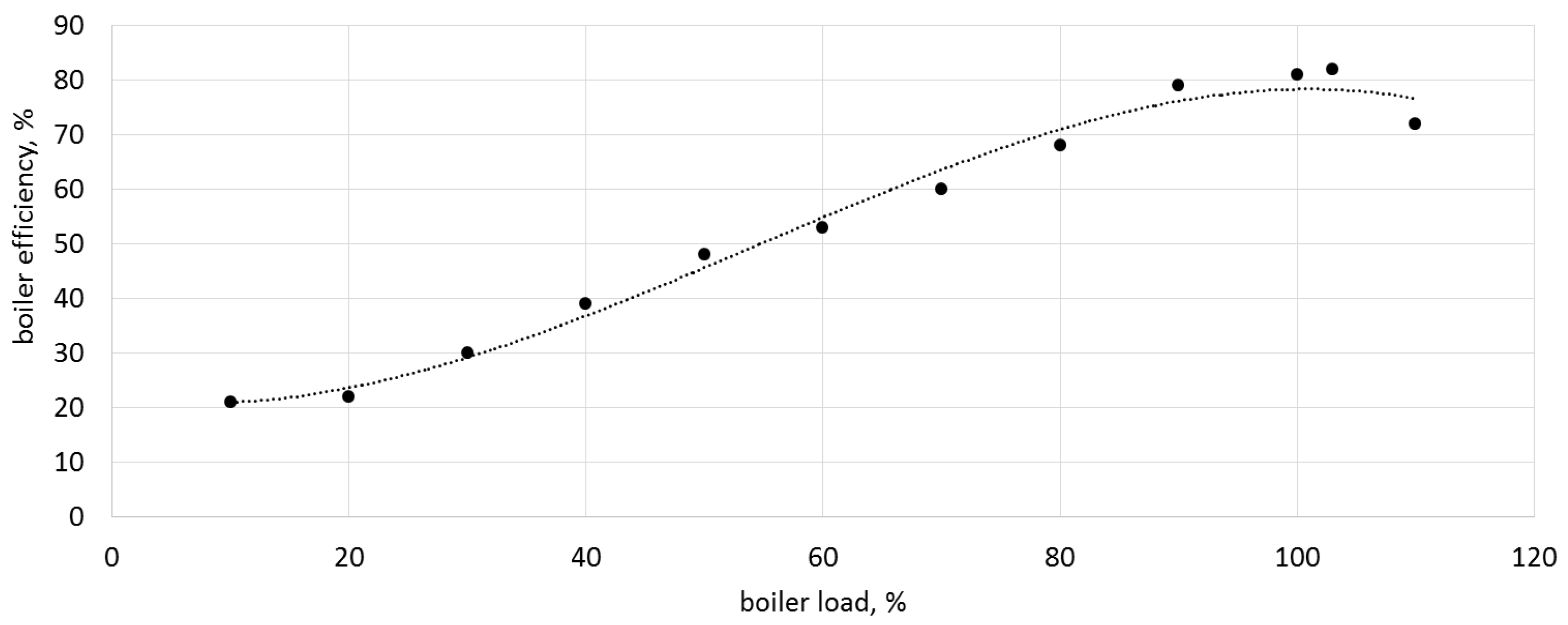
. It corresponds to the most common value of coal in this region. The efficiency of the boiler
strictly depends on its load. Therefore, based on the boiler efficiency characteristics, a function describing this dependence was determined, which allows the amount of burned fuel (
Figure 17) to be more accurately analyzed.
The consumption of coal dust in the analyzed period of four months amounted to 7670 kg, therefore, considering the average price of coal dust of €135.71 per tonne, it is estimated that the cost of heating the greenhouse was equal to
€1040.90/year. This value is consistent with the costs borne by the owners of the greenhouse. The obtained profit
Z (Equation (36)) is the amount of money that the facility user would have to bear for its heating in the case of a lack of installation that uses a heat pump. It is the difference between the costs incurred for the coal boiler
and the operating costs related to heating the greenhouse with the heat pump
.
The simple payback time for the investment
(Equation (37)) is the quotient of investment costs
, which are the difference between the cost of a boiler room using the heat pump
and that equipped with a boiler with a feeder
, and profits
:
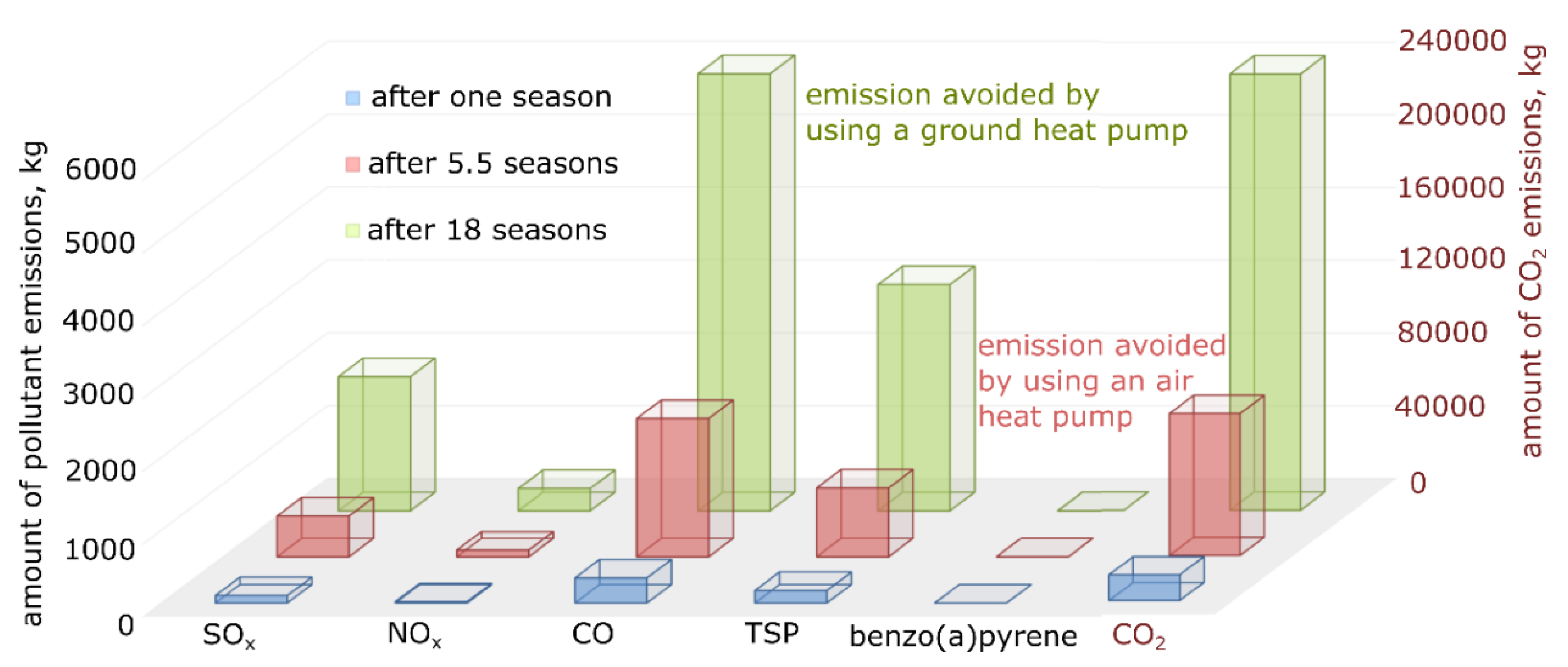
A simple payback time for a ground source heat pump for the analyzed greenhouse facility is 18 years. The lifetime of the heat pump compressor is estimated at around 90,000 operating hours, and in the analyzed facility the operation time of the pump is about 2688 h. Considering the average annual time of 2700 h of using the device, the heat pump should theoretically work without failure for about 33 years. The simple payback time for an air source heat pump is 5.5 years. The working time is the same as for a ground source heat pump, and therefore trouble-free working time should also be around 33 years.
7. Summary and Conclusions
The analysis presented in the article concerned the heating of a greenhouse facility in Polish climatic conditions. The thermal balance of the greenhouse included all inflows of heat from the environment resulting mainly from solar radiation, as well as losses due to heat transfer through the partitions, and also those resulting from the natural ventilation of the greenhouse, which in turn depends on the difference between the interior temperature and the ambient temperature.
The created balance was used to perform a simulation according to the specific assumptions of the Hartley plan. This allowed temperature changes in the facility, assuming a time step of 1 h for the four analyzed months, to be described in detail.
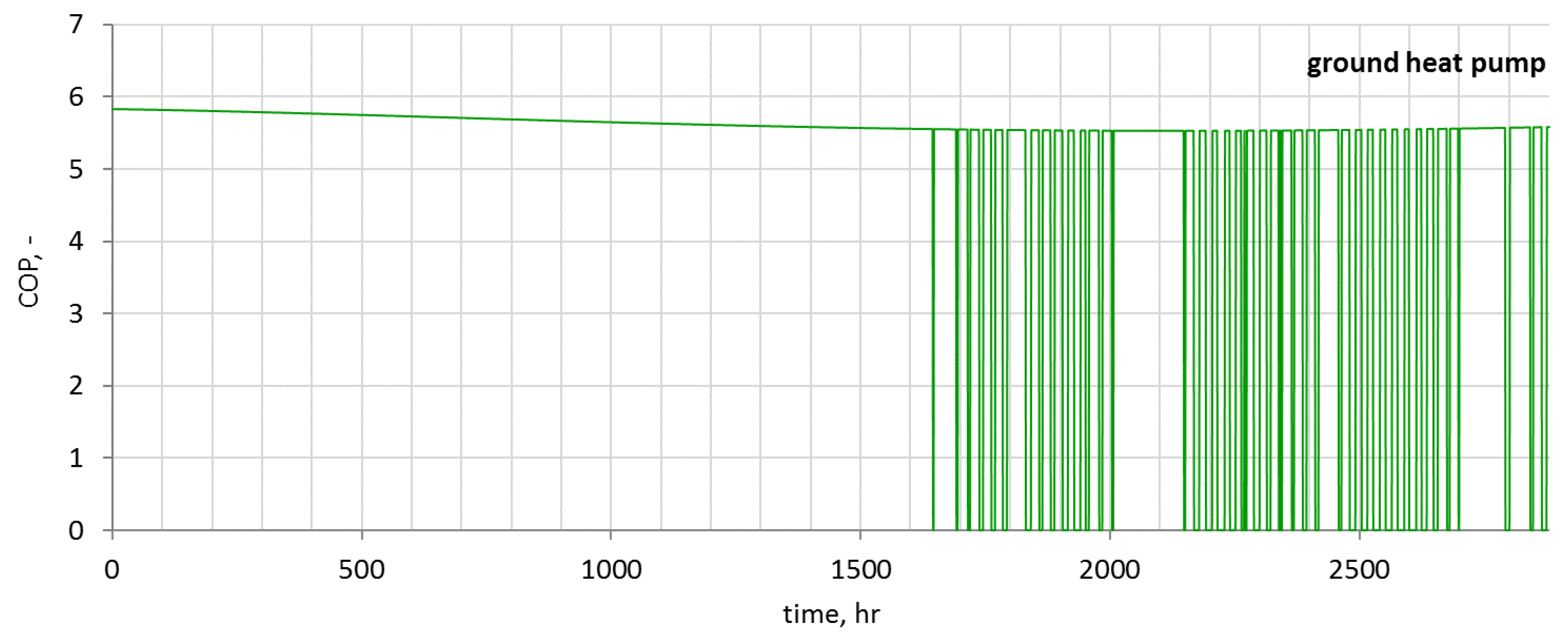
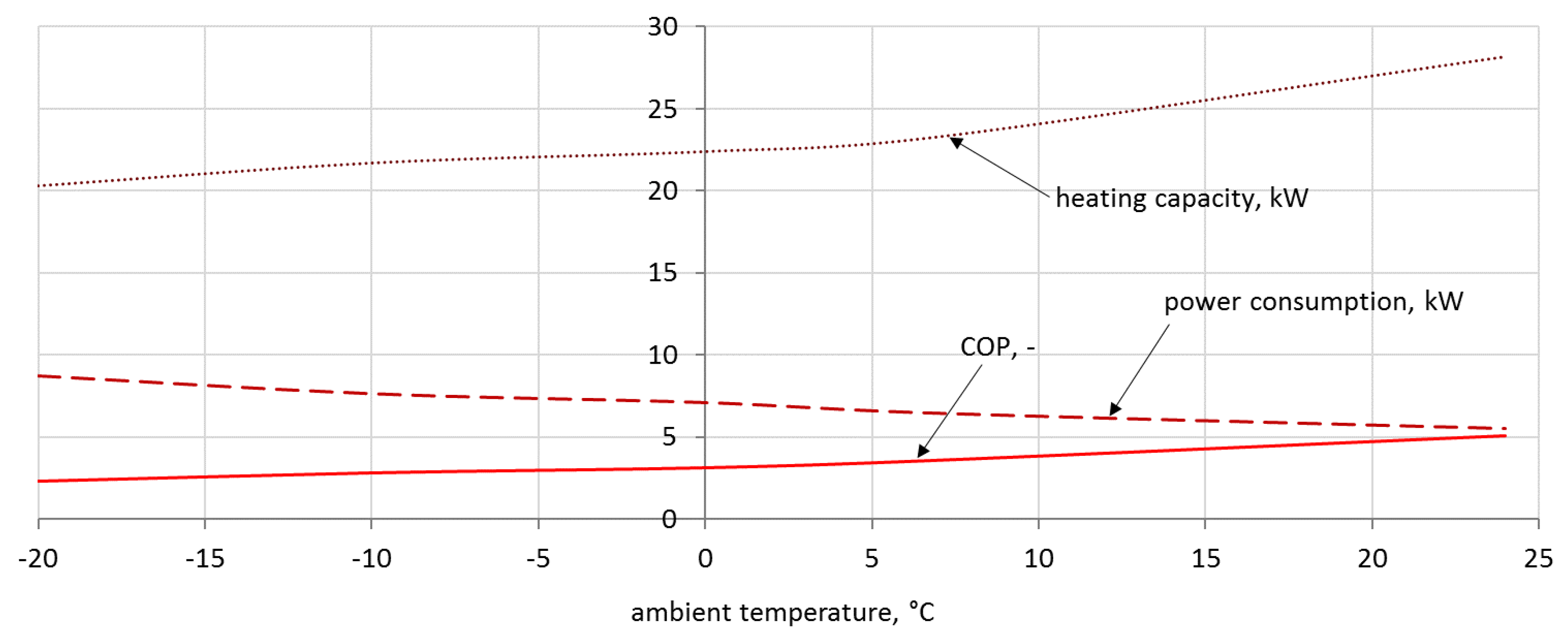
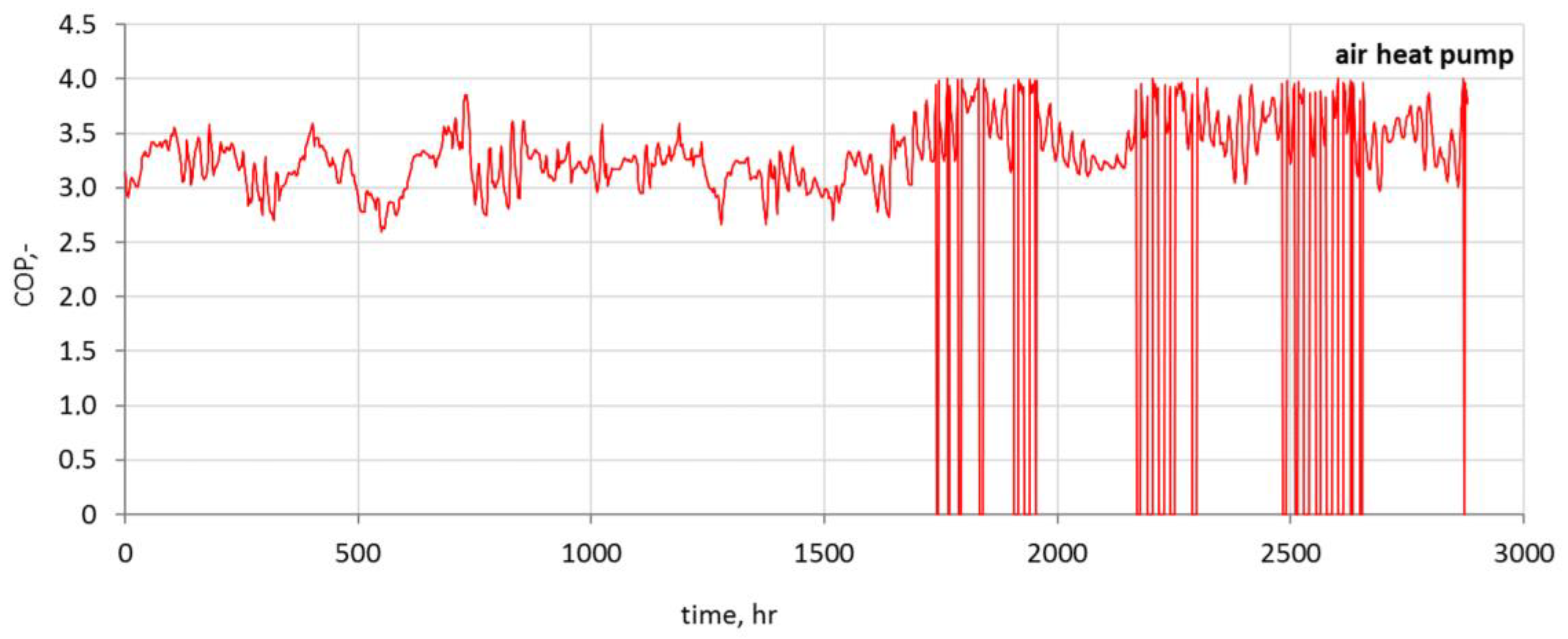
Due to the legal regulations regarding environmental protection, and also the general interest in the use of heat pumps, it was decided to use and analyze ground and air source heat pumps in the greenhouse. The rated power of the selected glycol–water ground source heat pump was equal to 21.5 kW. The analysis showed that the ground source heat pump will work with a COP within the range of 5.53–5.83. For a selected 23 kW air source heat pump, the COP varied 2.59–4.00. Significantly higher changes in ambient temperature, when compared to the ground temperature, resulted in higher energy demands, and therefore in higher operating costs. For the air source heat pump, it amounted to €678.64/year, and for the ground source heat pump it amounted to only €385.60/year.
To estimate the profitability of using a certain heating system, it was necessary to perform economic analysis and calculate the simple payback time of the investment. When comparing the cost of operating a heating system that uses a ground source heat pump with an existing heating system that uses a coal-fired boiler, annual profits reached 62%. The calculation of the simple payback time also included the investment cost, which is more than 3.5 times higher for the ground source heat pump. Therefore, such an investment will pay back after about 18 years. Annual savings from the use of the air source heat pump are smaller and amounted to 32%. However, a much lower investment cost means that the payback time of such an investment is only 5.5 years.
Taking into account all the advantages and disadvantages of a heating system based on a heat pump, and the analysis of the system’s operation, it can be considered as a competitive method of heating greenhouse facilities when compared to traditional coal boilers with regards to the economy and especially with regards to environmental protection.
The air source heat pump has the unstable temperature of the lower heat source. However, this temperature in the analyzed period of time is so high that the device is profitable. The shorter payback time for the air source heat pump means that it should be more often chosen as a greenhouse heating system in Poland’s climatic conditions.