Systematic Planning of Electric Vehicle Battery Swapping and Charging Station Location and Driver Routing with Bi-Level Optimization
Abstract
1. Introduction
2. Literature Review
3. Problem Description and Design of the Solving Scheme
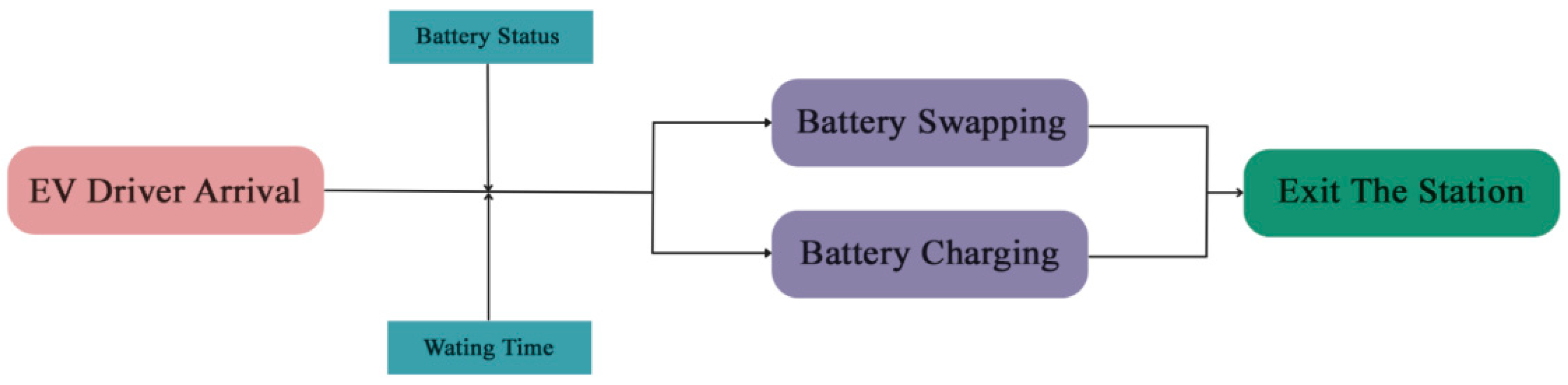
3.1. Problem Description
- (1)
- All EVs are battery electric vehicles and capable of both charging and battery swapping.
- (2)
- The battery capacity of each EV has no significant variation.
- (3)
- EV arrivals follow a bimodal Poisson distribution.
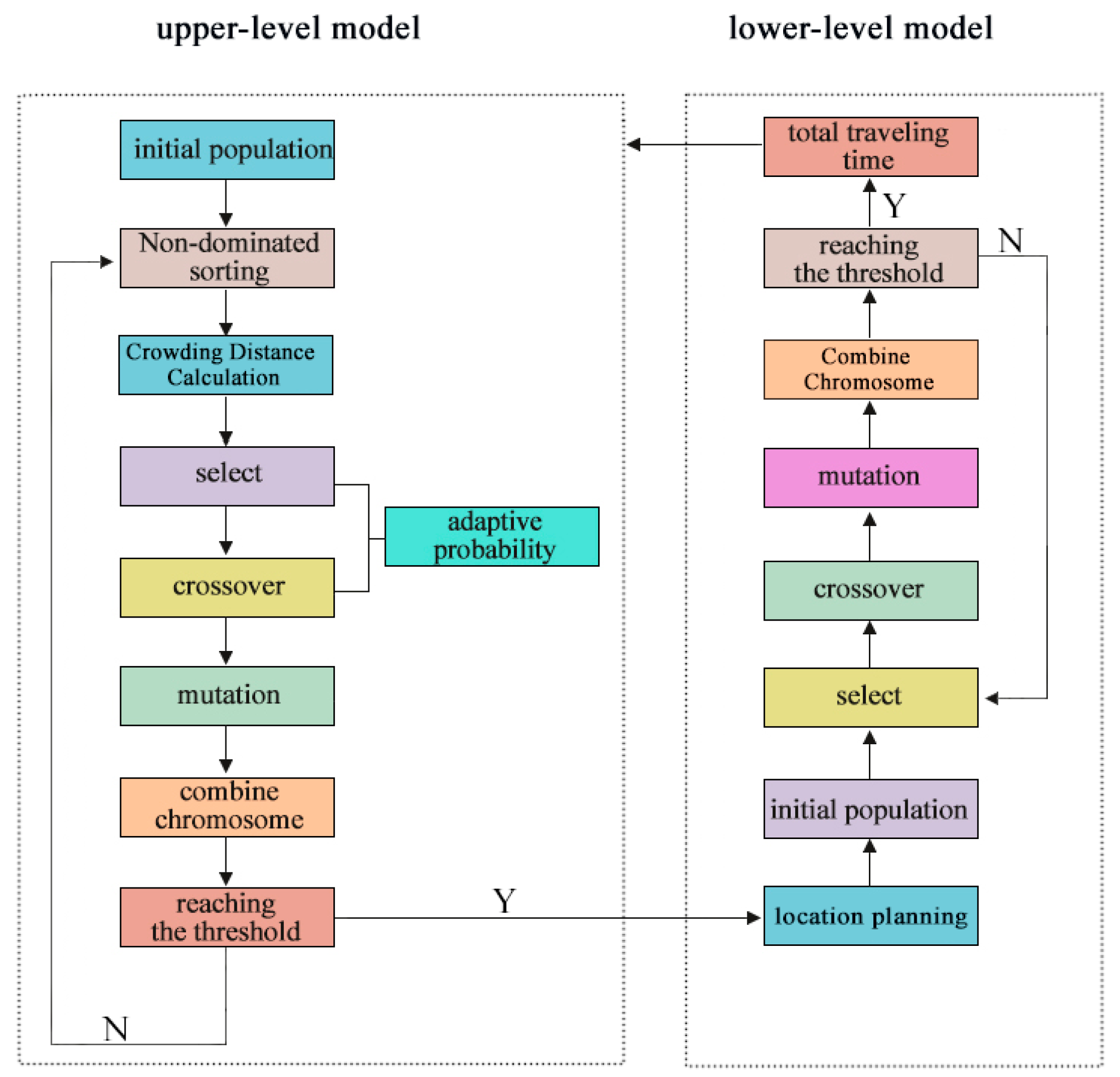
3.2. Design of Bi-Level Solving Scheme
4. Formulation of a Bi-Level Optimization Model for Location and Route Planning of BSCSs
4.1. Upper-Level Model of Location
- 1.
- Minimize total costs: This includes the fixed investment for constructing stations, operational costs, and costs associated with component usage and battery distribution.
- 2.
- Minimize service delay for drivers: Efficient service reduces waiting times and improves user satisfaction. The model evaluates service delays based on drivers’ arrival times and the times when they actually receive charging or swapping services.
- 3.
- Satisfy practical constraints: Station capacity, geographic coverage, and the maximum number of stations are explicitly considered to ensure feasibility and operational reliability.
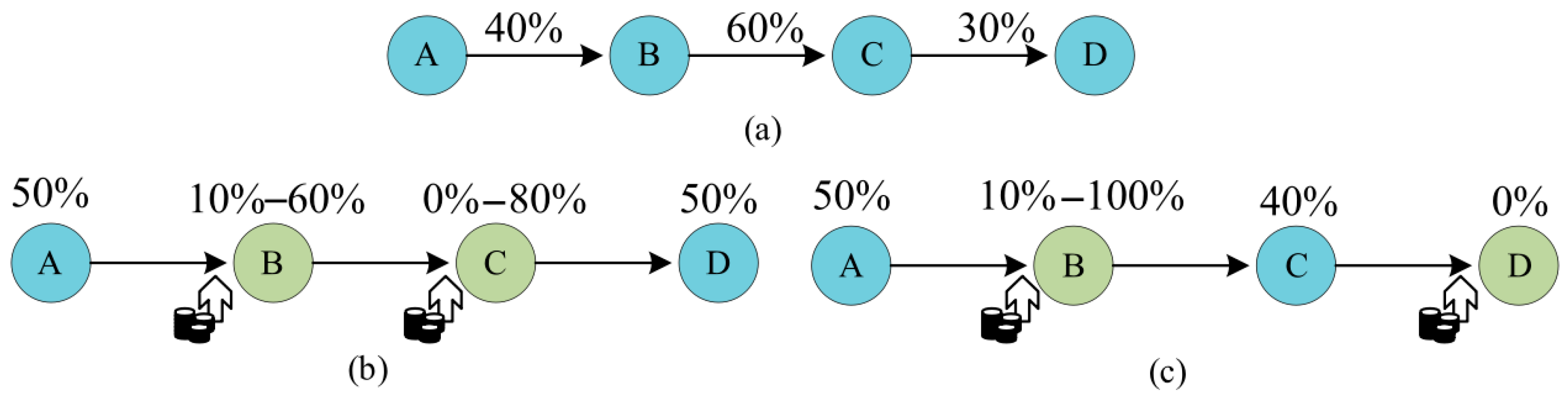
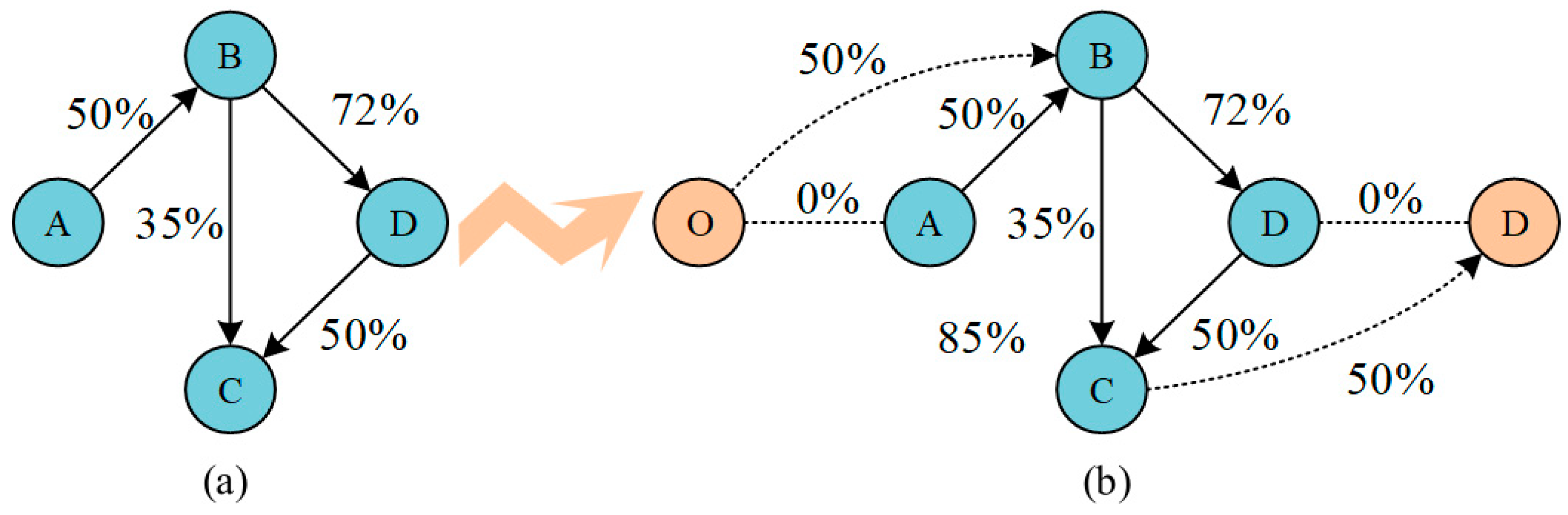
4.2. Lower-Level Model of Routing
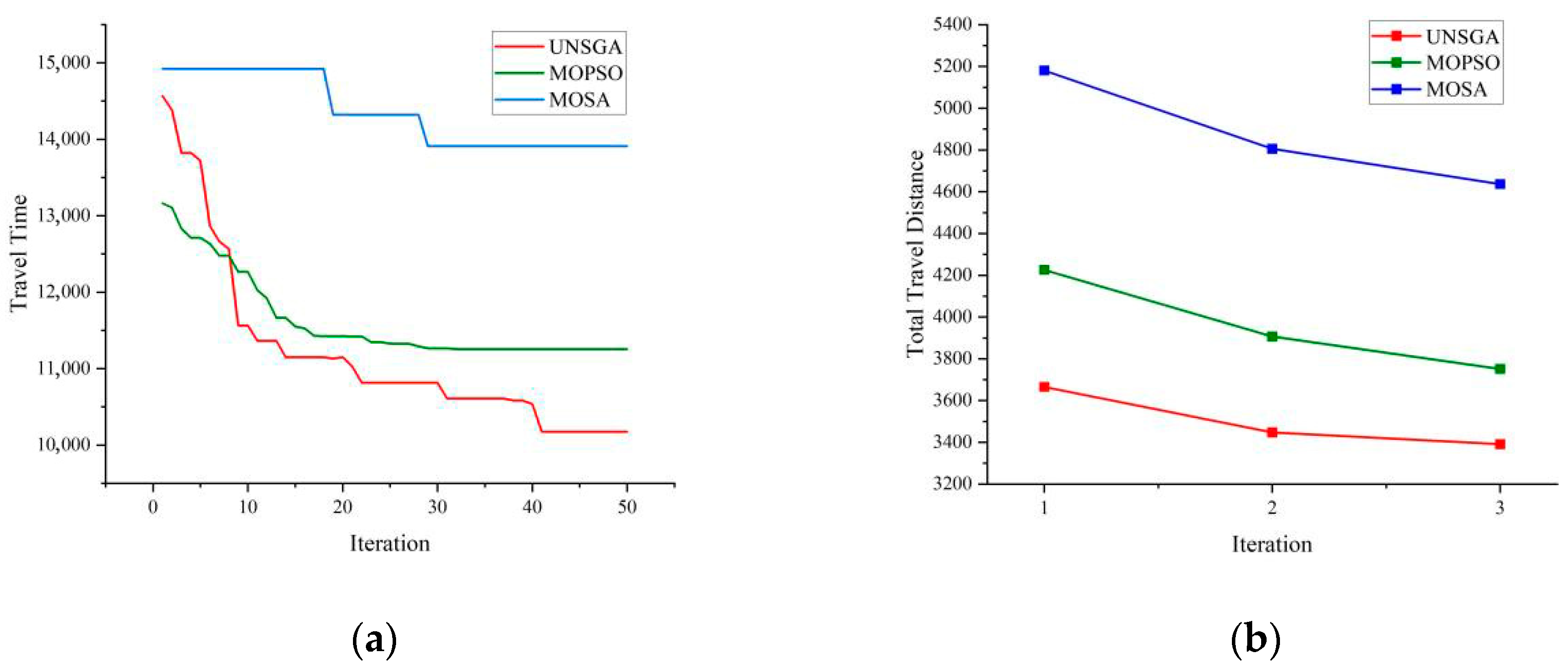
5. Design of an Updated NSGA
6. Case Study
6.1. Basic Information and Data
6.1.1. System Cost Analysis
6.1.2. User Travel Behavior Analysis
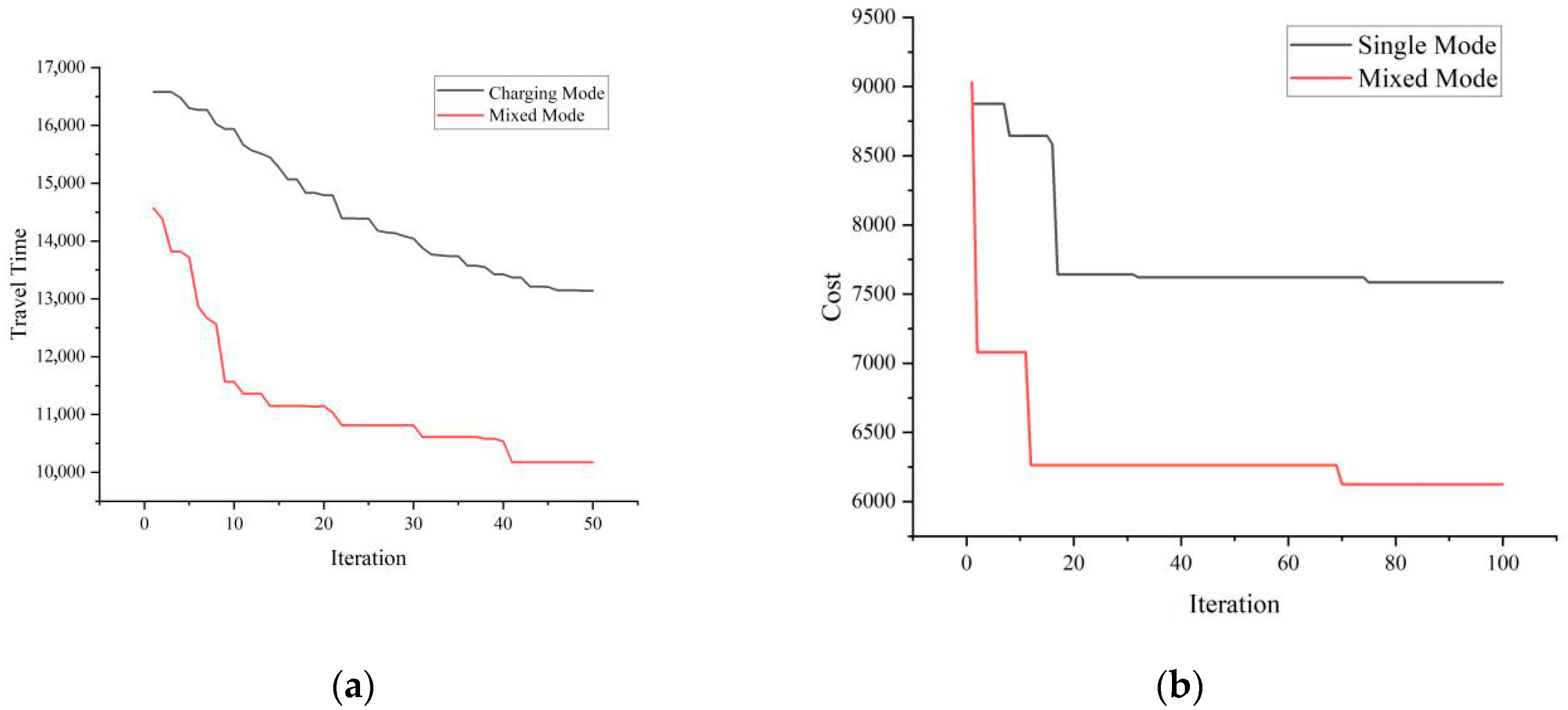
6.2. Performance Tests for BSCS Mode and CS Mode
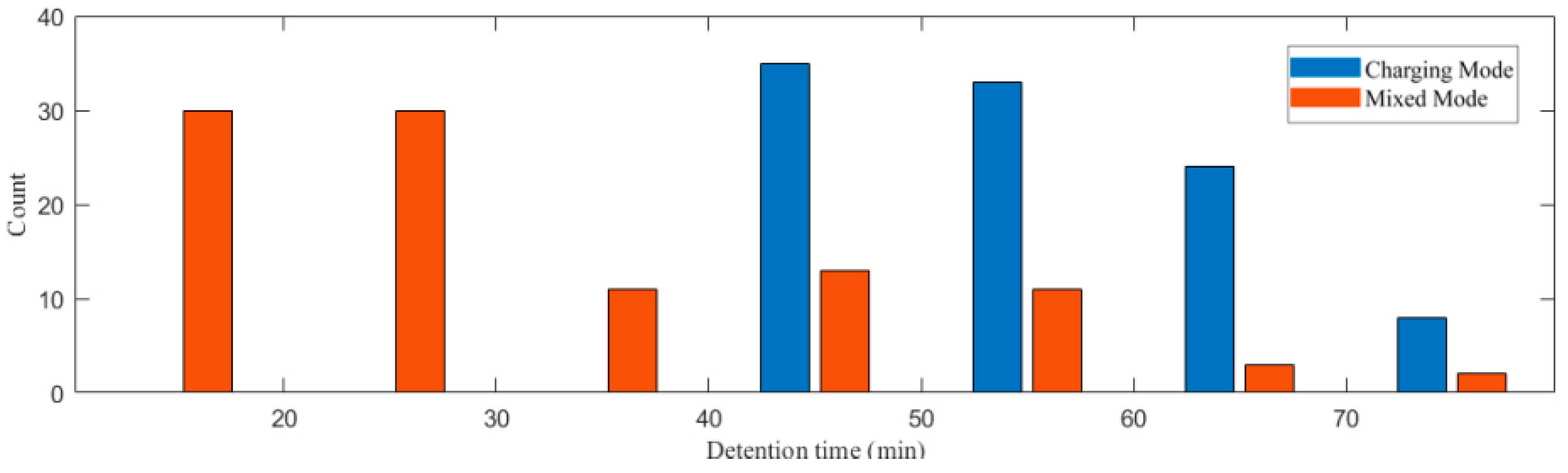
6.2.1. Cost and Detention Time Analysis
6.2.2. Performance of Satisfaction Rate Between CSs and BSCSs
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Yu, H.; Zhang, G.; Ma, T. Optimal planning of flood-resilient electric vehicle charging stations. Comput. Aided Civ. Infrastruct. Eng. 2023, 38, 489–507. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Zhang, C.; Li, J.; Li, X.; Zhao, Y. Electric vehicle charging station location model considering charging choice behavior and range anxiety. Sustainability 2022, 14, 4213. [Google Scholar] [CrossRef]
- Hu, D.; Huang, L.; Liu, C.; Liu, Z.W.; Ge, M.F. Data driven optimization for electric vehicle charging station locating and sizing with charging satisfaction consideration in urban areas. IET Renew. Power Gener. 2022, 16, 2630–2643. [Google Scholar] [CrossRef]
- Guillet, M.; Hiermann, G.; Kröller, A.; Schiffer, M. Electric vehicle charging station search in stochastic environments. Transp. Sci. 2022, 56, 483–500. [Google Scholar] [CrossRef]
- Ademulegun, O.O.; MacArtain, P.; Oni, B.; Hewitt, N.J. Multi-stage multi-criteria decision analysis for siting electric vehicle charging stations within and across border regions. Energies 2022, 15, 9396. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, M.; Hu, X. Location planning of electric vehicle charging station with users’ preferences and waiting time: Multi-objective bi-level programming model and HNSGA-II algorithm. Int. J. Prod. Res. 2023, 61, 1394–1423. [Google Scholar] [CrossRef]
- Xu, D.; Pei, W.; Zhang, Q. Optimal planning of electric vehicle charging stations considering user satisfaction and charging convenience. Energies 2022, 15, 5027. [Google Scholar] [CrossRef]
- Banegas, J.; Mamkhezri, J. A systematic review of geographic information systems based methods and criteria used for electric vehicle charging station site selection. Environ. Sci. Pollut. Res. 2023, 30, 68054–68083. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Li, J.; Zhou, Y. Optimal planning of hybrid charging and battery swapping stations for electric vehicles. Appl. Energy 2023, 345, 121229. [Google Scholar] [CrossRef]
- Lai, Z.; Li, S. Towards a multimodal charging network: Joint planning of charging stations and battery swapping stations for electrified ride-hailing fleets. Transp. Res. Part B Methodol. 2024, 183, 102928. [Google Scholar] [CrossRef]
- Ben Abbes, S.; Rejeb, L.; Baati, L. Route planning for electric vehicles. IET Intell. Transp. Syst. 2022, 16, 875–889. [Google Scholar] [CrossRef]
- Froger, A.; Jabali, O.; Mendoza, J.E.; Laporte, G. The electric vehicle routing problem with capacitated charging stations. Transp. Sci. 2022, 56, 460–482. [Google Scholar] [CrossRef]
- Mahmoudian, F.; Moghaddam, A.H.; Davachi, S.M. Genetic-based multi-objective optimization of alkylation process by a hybrid model of statistical and artificial intelligence approaches. Can. J. Chem. Eng. 2022, 100, 90–102. [Google Scholar] [CrossRef]
- Fang, C.; Chen, X.; Li, X.; Fang, Y.; Li, S.; Shao, S.; Samorani, M.; Lu, H. Strategic XFC Charging Station Placement in Equilibrium Traffic Networks. IEEE Trans. Intell. Transp. Syst. 2025, 26, 4865–4877. [Google Scholar] [CrossRef]
- Soczówka, P.; Lasota, M.; Franke, P.; Żochowska, R. Method of Determining New Locations for Electric Vehicle Charging Stations Using GIS Tools. Energies 2024, 17, 4546. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Wu, B.; Dedeoglu, M.; Zhang, J.; Trajkovic, L. Stochastic modeling and analysis of public electric vehicle fleet charging station operations. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9252–9265. [Google Scholar] [CrossRef]



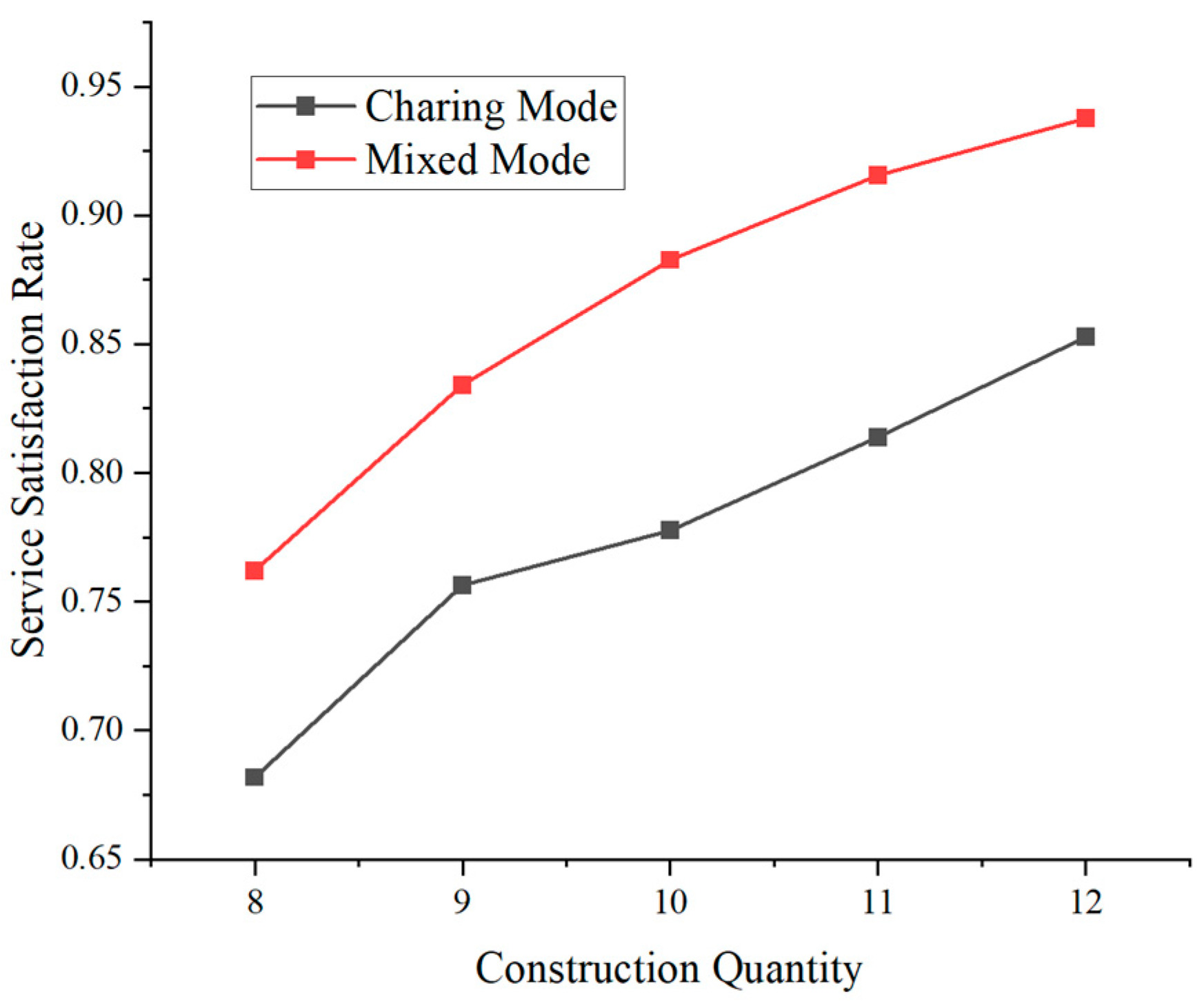
| Quantity of CSs | Satisfied Rate of Charging Service | Total Cost |
|---|---|---|
| 8 | 68.18% | 2238.64 |
| 9 | 75.64% | 2597.35 |
| 10 | 77.76% | 2774.47 |
| 11 | 81.39% | 3097.98 |
| 12 | 85.27% | 3469.25 |
| Quantity of BSCSs | Satisfied Rate of Charging Service | Total Cost |
|---|---|---|
| 8 | 76.21% | 2784.92 |
| 9 | 83.42% | 3132.66 |
| 10 | 88.27% | 3481.16 |
| 11 | 91.55% | 3828.71 |
| 12 | 93.76% | 4176.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, J.; Feng, H. Systematic Planning of Electric Vehicle Battery Swapping and Charging Station Location and Driver Routing with Bi-Level Optimization. World Electr. Veh. J. 2025, 16, 499. https://doi.org/10.3390/wevj16090499
Chen B, Chen J, Feng H. Systematic Planning of Electric Vehicle Battery Swapping and Charging Station Location and Driver Routing with Bi-Level Optimization. World Electric Vehicle Journal. 2025; 16(9):499. https://doi.org/10.3390/wevj16090499
Chicago/Turabian StyleChen, Bowen, Jianling Chen, and Haixia Feng. 2025. "Systematic Planning of Electric Vehicle Battery Swapping and Charging Station Location and Driver Routing with Bi-Level Optimization" World Electric Vehicle Journal 16, no. 9: 499. https://doi.org/10.3390/wevj16090499
APA StyleChen, B., Chen, J., & Feng, H. (2025). Systematic Planning of Electric Vehicle Battery Swapping and Charging Station Location and Driver Routing with Bi-Level Optimization. World Electric Vehicle Journal, 16(9), 499. https://doi.org/10.3390/wevj16090499








