Advancing Energy Management Strategies for Hybrid Fuel Cell Vehicles: A Comparative Study of Deterministic and Fuzzy Logic Approaches

Abstract

The increasing depletion of fossil fuels and their environmental impact have led to the development of fuel cell hybrid electric vehicles. By combining fuel cells with batteries, these vehicles offer greater efficiency and zero emissions. However, their energy management remains a challenge requiring advanced strategies. This paper presents a comparative study of two developed energy management strategies: a deterministic rule-based approach and a fuzzy logic approach. The proposed system consists of a proton exchange membrane fuel cell (PEMFC) as the primary energy source and a lithium-ion battery as the secondary source. A comprehensive model of the hybrid powertrain is developed to evaluate energy distribution and system behaviour. The control system includes a model predictive control (MPC) method for fuel cell current regulation and a PI controller to maintain DC bus voltage stability. The proposed strategies are evaluated under standard driving cycles (UDDS and NEDC) using a simulation in MATLAB/Simulink. Key performance indicators such as fuel efficiency, hydrogen consumption, battery state-of-charge, and voltage stability are examined to assess the effectiveness of each approach. Simulation results demonstrate that the deterministic strategy offers a structured and computationally efficient solution, while the fuzzy logic approach provides greater adaptability to dynamic driving conditions, leading to improved overall energy efficiency. These findings highlight the critical role of advanced control strategies in improving FCHEV performance and offer valuable insights for future developments in hybrid-vehicle energy management.

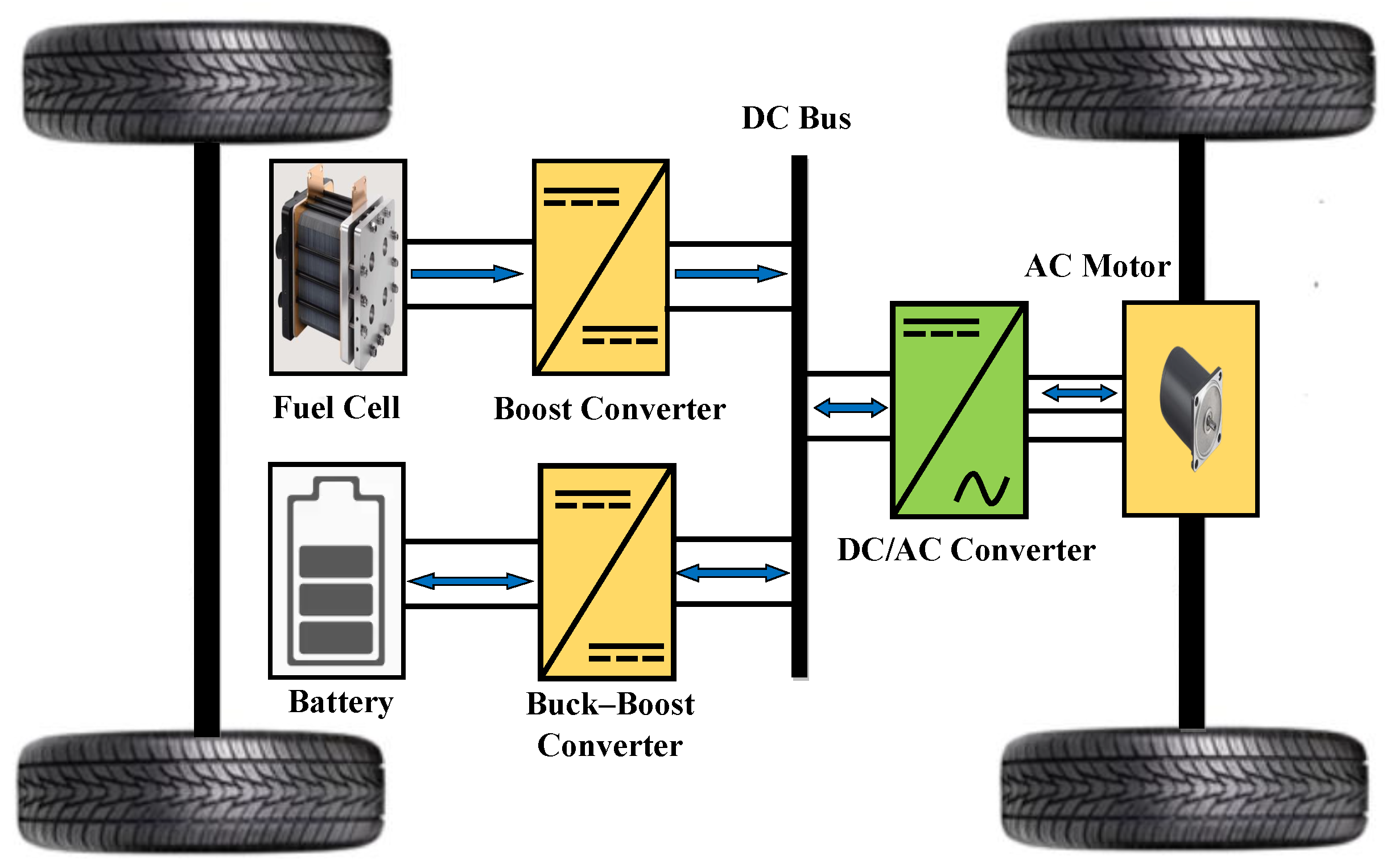
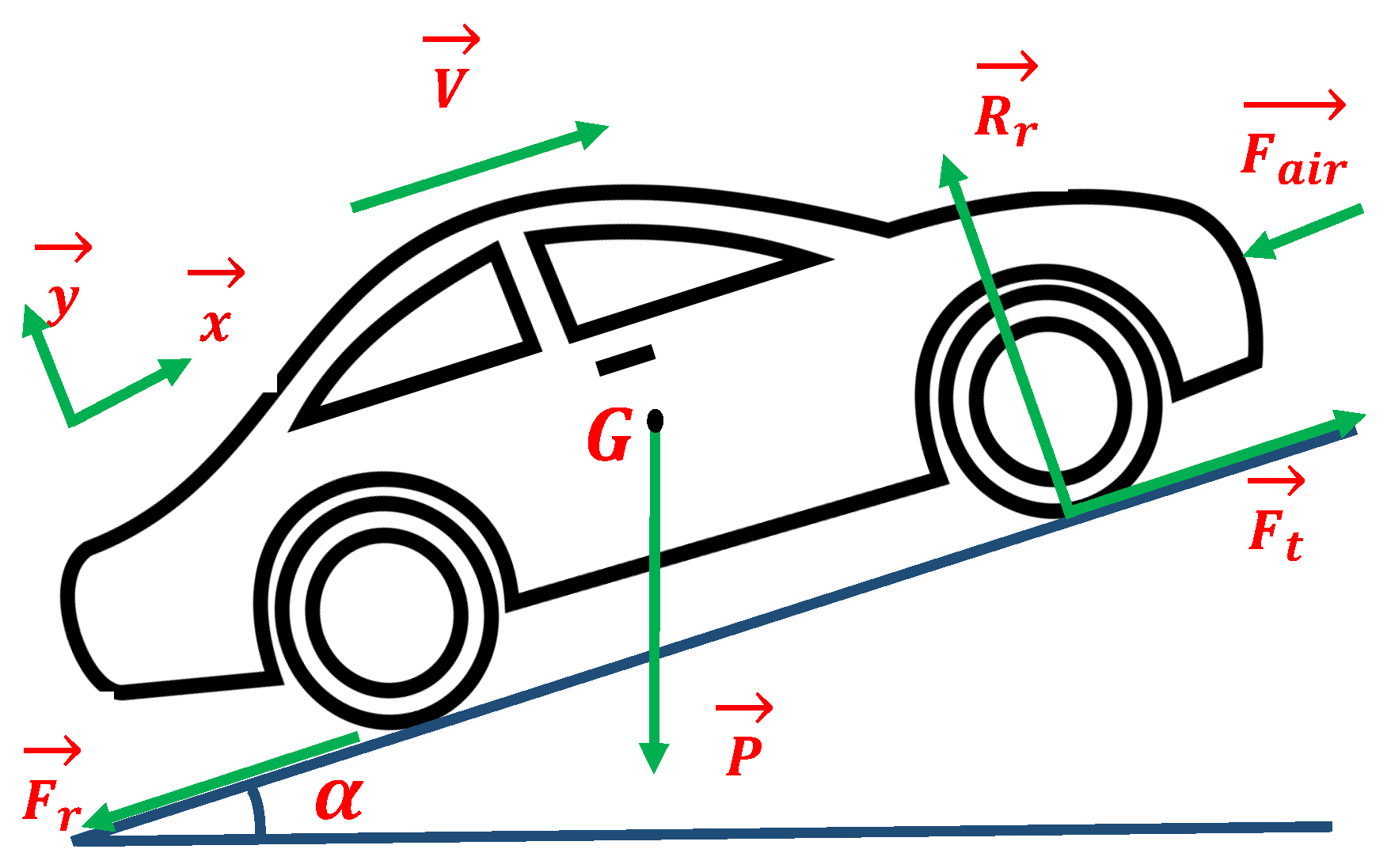
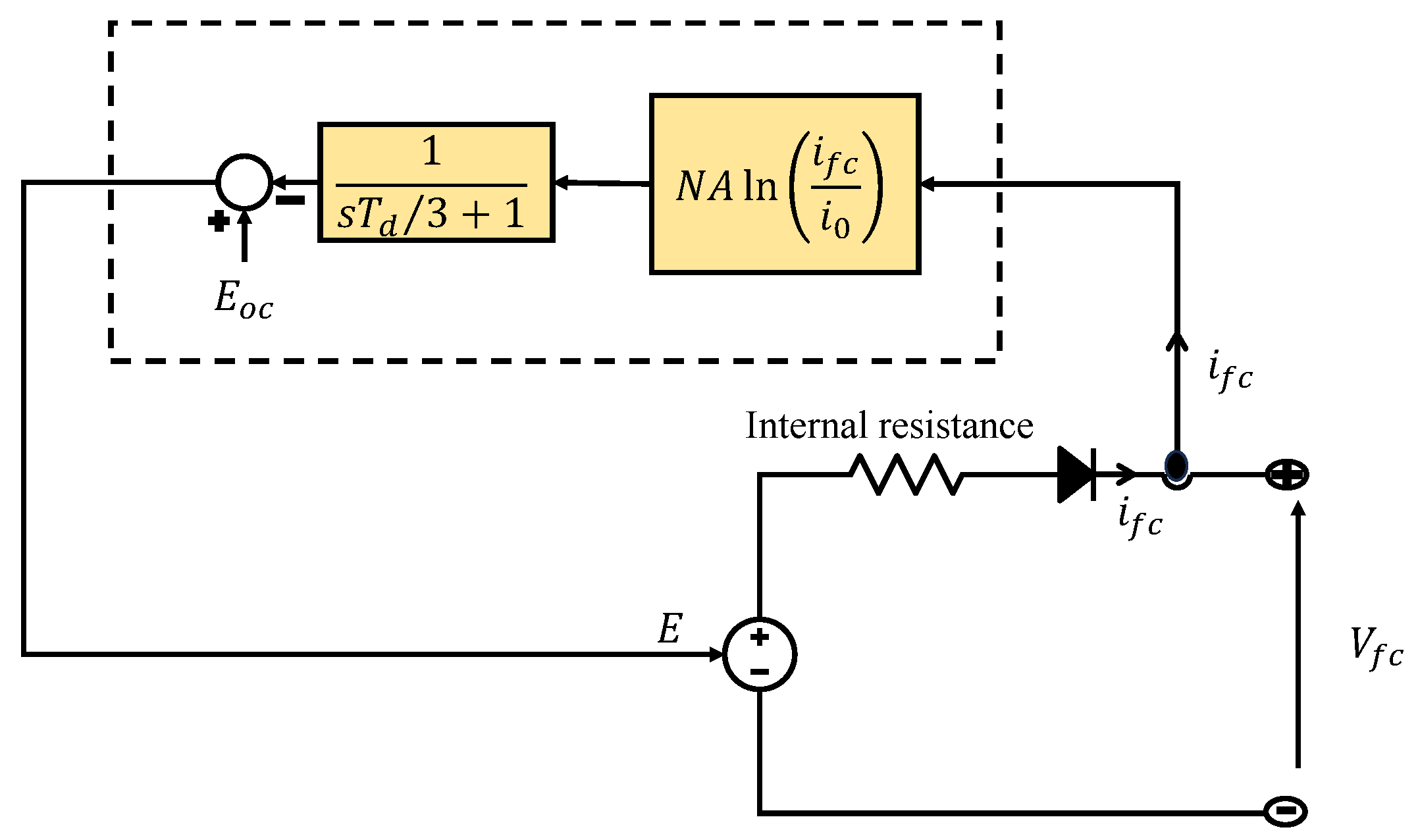
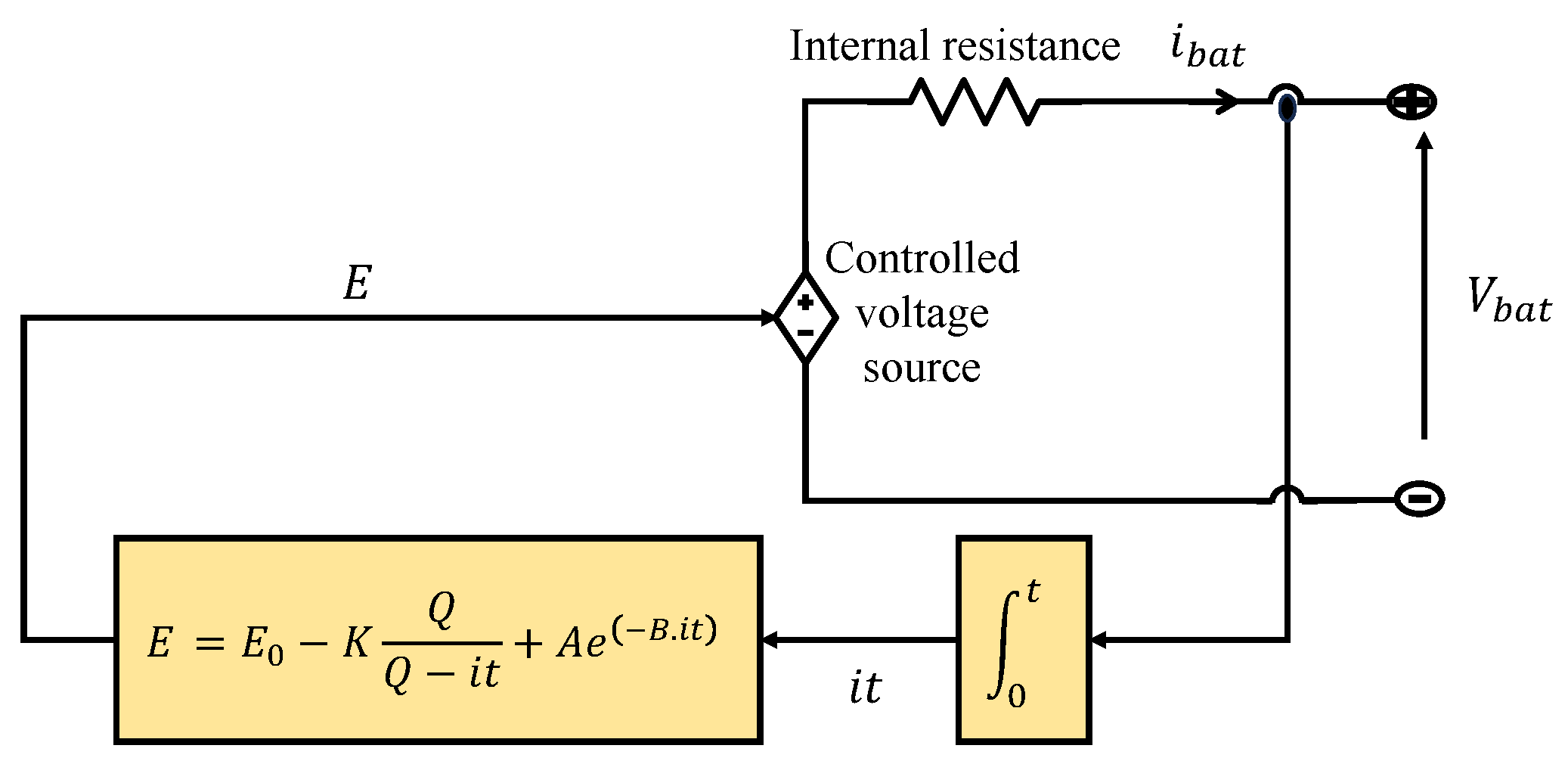
1. Introduction

The environmental consequences of fossil fuel consumption, particularly its contribution to global warming and air pollution, have become a major global concern. Fossil fuels have historically played a central role in powering industry and transport, but they are now widely recognised as a primary source of greenhouse gas (GHG) emissions. The transport sector alone contributes around 16.2% of total global GHG emissions, with road transport alone accounting for 11.9%. In addition to ${\mathrm{CO}}_2$, the combustion of fossil fuels releases harmful pollutants that degrade air quality and threaten public health [1,2].

In response to these environmental and energy challenges, considerable efforts have been made to promote cleaner alternatives to conventional vehicles. Battery electric vehicles (EVs) have emerged as a promising solution, offering zero emissions and reduced dependence on fossil fuels [3]. However, their widespread adoption is still hindered by practical limitations, including limited driving range, long recharging times, and degraded performance in extreme conditions [4].

Hydrogen fuel cell vehicles (FCVs) represent another attractive alternative. These vehicles offer several crucial advantages: zero emissions during vehicle use, refuelling times comparable to those of diesel vehicles, and greater range [5]. In addition, hydrogen, one of the most abundant elements on Earth, is a sustainable energy solution, especially when produced in an environmentally friendly way using renewable sources such as solar or wind power. This green hydrogen production guarantees a clean, sustainable fuel supply chain, which significantly reduces environmental impact and supports the transition to more sustainable transport systems [6]. However, the limited lifespan of proton exchange membrane fuel cells (PEMFCs) is a major obstacle to the large-scale commercialisation of fuel cell vehicles.

Despite these advantages, FCVs face technical limitations, particularly their slow dynamic response and unidirectional nature, which reduce their ability to efficiently handle rapid power fluctuations and regenerative braking. To overcome these challenges, they are often combined with batteries or supercapacitors, forming a hybrid configuration. This combination maximises the advantages of both sources: the fuel cell provides constant power, while the batteries or supercapacitors manage transient loads and store regenerative energy. However, this hybridization requires an effective energy management system (EMS), which coordinates energy flows to improve overall energy efficiency and reduce consumption [7].

To ensure optimum coordination between the various energy sources, the energy management system (EMS) generates specific power references for each source. These references are then converted into actual actions by the power converters, which play an essential role in interfacing between the energy sources and the DC bus. Power converters are essential for efficiently regulating energy transfer, maintaining system stability and optimizing overall efficiency. Their control, supervised by a dedicated controller, ensures compliance with the energy management system’s instructions, while guaranteeing the correct operation of the components. This control process contributes not only to the accurate management of energy flows, but also to the protection and sustainability of energy sources, consolidating the reliability of the energy system [5].

A variety of energy management strategies have been developed to optimise energy flow in hybrid electric vehicles. These strategies, which are widely studied in the literature, can be classified into three main categories: rule-based strategies, optimisation-based strategies and artificial intelligence-based strategies [8]. These strategies not only meet the vehicle’s energy demand, but they also exploit the full potential of energy sources and coordinate them to minimise fuel consumption, extend component life, reduce economic costs, and more. Each type has its own specific operating methods, scope of application, advantages, and disadvantages.

Rule-based strategies are based on predefined rules to manage the distribution of power between the fuel cell and the battery. These strategies can be divided into several sub-categories. The first is the rule-based strategy, which uses fixed, predefined rules that remain unchanged whatever the driving conditions. These rules are generally based on human intelligence and experience. In [9], the authors use PID controllers to maintain the battery state of charge at 60% and manage the battery and fuel cell currents. Du et al. [10] combine rule-based and dynamic programming to reduce hydrogen consumption and extend battery life. A rule-based approach optimised by genetic algorithm is proposed in [11] that balances several objectives but lacks online recognition of driving cycles. Wang et al. [12] use a Bayes Monte Carlo technique to improve fuel economy and component lifetime. Yang Li et al. [13] integrate Q-learning and deterministic rules to reduce current fluctuations, but the intensive training and model dependence make real-time applications difficult. The second is fuzzy rule-based strategy, which uses fuzzy logic to manage uncertainties and imprecise information [14]. In [15], an approach using fuzzy logic aims to keep the fuel cell in a high-efficiency zone while responding to fast demands. Luciani and Tonoli [16] compare several control strategies, highlighting fuzzy logic, which improves fuel cell efficiency by up to 33% for low-load cycles. In [17], a type-2 fuzzy strategy is used for a hybrid system integrating fuel cell, battery, and supercapacitor. This method improves stability and efficiency through robust control. Zhang et al. [18] integrate driving mode recognition via a neural network with fuzzy adaptive control, optimizing energy distribution in real time. In [19], a strategy combining fuzzy logic, flatness theory, and rule-based algorithms improves energy distribution and stabilizes output voltage. In [20], Ahmadi et al. propose an optimised management approach integrating fuzzy logic and genetic algorithms, balancing fuel economy and performance. The third is the strategy based on frequency separation, which is particularly well suited to FCHEVs due to the fuel cell’s low dynamic response characteristics [21]. These strategies separate the power demand into high-frequency and low-frequency components. High-frequency components, corresponding to rapid variations in power demand, are managed by the battery, while low-frequency components, corresponding to steady-state or slow variations, are managed by the fuel cell [22,23,24,25,26,27].

Optimisation-based strategies, using mathematical models, are being developed to manage the energy of hybrid vehicles by balancing the distribution of power between fuel cells and batteries [28]. These strategies aim to improve performance in terms of fuel economy, sustainability of energy sources, emissions reduction, and vehicle efficiency [29]. Energy management is based on a cost function that integrates these objectives, and the optimisation process can be achieved via two methods: global (offline) or local (online) optimisation. Global optimisation strategies play a crucial role in hybrid vehicle energy management, despite their high computational demands and dependence on prior knowledge of the driving cycle [30]. These strategies aim to identify optimal solutions in the entire search space, minimising or maximising a cost function while respecting predefined constraints. Although they are difficult to implement directly in real scenarios, they serve as a valuable reference for evaluating other control approaches [31]. In addition, global optimisation techniques help refine rule-based strategies and optimise the sizing of vehicle components, thus contributing to advances in the theoretical and practical design of energy management systems [32,33,34]. Local optimisation strategies, designed for real-time energy management, replace global optimisation with instantaneous decisions, reducing the computational load and enabling rapid adaptation to the dynamic requirements of hybrid vehicles [35]. Among the key approaches, the Equivalent Consumption Minimization Strategy (ECMS) optimises global consumption by translating electrical energy into fuel equivalent [36]. The Pontryagin Minimum Principle (PMP) solves the Hamiltonian function to minimise instantaneous costs while managing the non-linearities of hybrid systems [37]. Model predictive control (MPC), although more computationally demanding, anticipates future states and adjusts power distribution to optimise energy utilization under complex conditions [38,39].

Artificial intelligence-based energy management strategies use advanced algorithms, machine learning techniques and real-time data processing to improve decision-making in fuel cell hybrid electric vehicles (FCHEVs) [40]. These intelligent systems offer significant advantages over traditional methods by constantly learning from data and adapting to changing conditions, ensuring optimum performance and efficiency [41]. These strategies can be divided into several categories depending on the feedback available to the algorithm to learn over time. In the literature, various learning-based strategies, such as supervised learning, unsupervised learning, and reinforcement learning, are used to supervise the energy flow in a fuel cell hybrid electric vehicle [42,43,44,45,46].

Rule-based energy management strategies are widely preferred by the automotive industry due to their simplicity and ease of implementation in real time. Although they are not based on complex optimisation techniques, they continue to attract significant interest and are still being actively developed and refined to achieve near-optimal performance, particularly in fuel cell hybrid vehicle applications where reliability and computational efficiency are essential.

In this work, the development of advanced energy management strategies for hybrid fuel cell vehicles, combining several rule-based approaches, is proposed. In particular, the power tracking method and the optimal efficiency region strategy are integrated to design an adaptive algorithm based on deterministic rules. In order to improve the system’s adaptability and robustness, a fuzzy logic algorithm is also exploited. This enables more flexible and reactive management, taking into account uncertainties and dynamic variations in driving conditions.

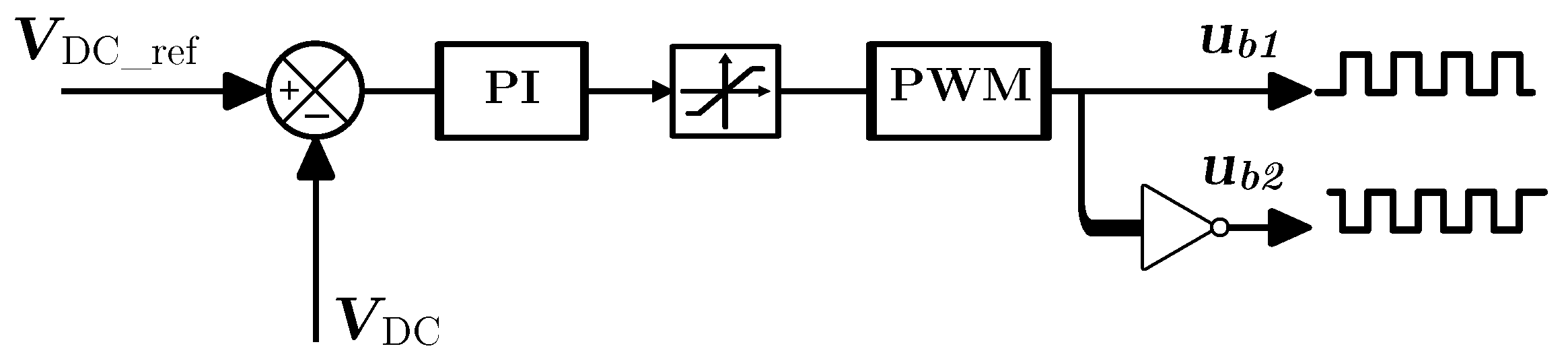
In addition, precise control of the converters associated with each source is implemented to optimise energy transfer. A PI controller is used to control the buck–boost converter of the battery, guaranteeing DC bus voltage stability, while a model predictive controller (MPC) is employed to control the boost converter of the fuel cell, ensuring improved responsiveness and energy efficiency.

Finally, an extensive comparative analysis is performed to evaluate the performance of the different strategies in terms of energy consumption, battery state-of-charge maintenance, and system dynamic response. This study highlights the advantages and limitations of each approach, enabling the selection of optimal strategies for improved energy efficiency and extended component lifetime.

This paper is structured as follows: Section 2 describes system architecture, modelling, and converter control. Section 3 presents energy management strategies based on deterministic rules and fuzzy logic. Section 4 analyses the simulation results, while Section 5 compares the two approaches in terms of energy efficiency, component preservation, and reactivity. Finally, Section 6 concludes the study by summarizing the main contributions and proposing improvement perspectives for future work.

2. System Configuration and Modelling

2.1. Proposed Hybrid Topology

The topology illustrated in Figure 1 was selected for the fuel cell–battery hybrid electric vehicle (FCHEV). In this configuration, the proton exchange membrane fuel cell (PEMFC) acts as the main energy source, delivering practically constant power. It is connected to the DC bus via a unidirectional DC/DC power converter. The secondary power source, the battery, is connected to the DC bus via a bidirectional DC/DC power converter. The DC power supplied by these two energy sources is converted into AC power by a DC/AC converter, which then drives the AC motor to propel the vehicle. In addition, the AC motor can also function as a generator, enabling the vehicle’s braking energy to be recovered. This architecture is the most preferred because it offers two degrees of freedom, allowing independent control of the DC bus voltage, better protection of the energy sources, and efficient regulation of the energy flow. It ensures optimum energy management and system performance by taking advantage of the complementary strengths of each energy source under varying driving conditions.

2.2. Vehicle Model

All the forces acting on a moving vehicle are illustrated in Figure 2. Vehicle dynamics takes into account the specific characteristics and coefficients of the vehicle under study, as well as the required dynamic performance. Based on Newton’s second law and as shown in Figure 2, vehicle motion can be expressed mathematically by Equation (1):

$$\begin{array}{c}\hfill M_v{\displaystyle \frac{d\overrightarrow{v}}{dt}}=\overrightarrow{R_r}+\overrightarrow{F_{air}}+\overrightarrow{F_r}+\overrightarrow{F_t}+\overrightarrow{P}\end{array}$$

(1)

The principal forces acting on the vehicle are:

$$\overrightarrow{F_{air}}=-{\displaystyle \frac{1}{2}}{\rho }_{\mathrm{air}}{V}^{2}A{C}_x\overrightarrow{x}$$

(2)

$$\overrightarrow{F_r}=-P{C}_{r}cos\left(\alpha \right)\overrightarrow{x}$$

(3)

$$\overrightarrow{P}=-M_{v}gsin\left(\alpha \right)\overrightarrow{x}$$

(4)

where

• $\overrightarrow{F_{air}}$ is the aerodynamic force, which is the air resistance in the direction of the vehicle’s motion;
• $\overrightarrow{F_r}$ is the rolling resistance force between the wheels and the ground;
• $\overrightarrow{P}$ is the gravitational force of the vehicle;
• $M_v$ is the total mass of the vehicle;
• $\overrightarrow{R_r}$ is the rolling resistance force vector due to tire–road interaction;
• $\overrightarrow{F_t}$ is the mechanical tensile force.

The mechanical tensile force $\overrightarrow{F_t}$ is expressed by Equation (5):

$$F_t=M_v{\displaystyle \frac{dv}{dt}}+{\displaystyle \frac{1}{2}}{\rho }_{\mathrm{air}}{V}^{2}A{C}_x+M_{v}gsin\alpha +M_{v}g{C}_{r}cos\alpha$$

(5)

The mechanical power required is given by Equation (6), which describes the power required to propel the vehicle, taking into account the resisting forces:

$$P_m=v\left(M_v{\displaystyle \frac{dv}{dt}}+{\displaystyle \frac{1}{2}}{\rho }_{\mathrm{air}}{V}^{2}A{C}_x+M_{v}gsin\alpha +M_{v}g{C}_{r}cos\alpha \right)$$

(6)

The parameters used to simulate the behaviour of the fuel cell hybrid electric vehicle are shown in

Table 1. Parameters of the vehicle used.

Description	Value	Unit
Vehicle mass	$M_v=3000$	kg
Number of wheels per axle	2
Horizontal distance between centre of gravity and front axle	1.56	m
Horizontal distance between centre of gravity and rear axle	1.56	m
Frontal area	2.31	${\mathrm{m}}^2$
Friction coefficient	0.26
Gravitational acceleration	9.81	${\mathrm{m}/\mathrm{s}}^2$
Air density	1.18	${\mathrm{kg}/\mathrm{m}}^3$
Unloaded tire-wheel radius	0.25	m

.

2.3. Fuel Cell Model

Figure 3 illustrates the dynamic fuel cell model [47]. This model is represented as a controlled voltage source in series with an internal resistor and a diode, which serves to protect the fuel cell from reverse currents. The output voltage of the fuel cell is determined by Equation (7):

$$V_{\mathrm{FC}}=E-R_{\mathrm{ohm}}·i_{\mathrm{FC}}$$

(7)

where the controlled voltage source E is defined by Equation (8):

$$E=E_{\mathrm{oc}}-N·A·ln\left({\displaystyle \frac{i_{\mathrm{FC}}}{i_0}}\right)·{\displaystyle \frac{1}{s{T}_d/3+1}}$$

(8)

To quantify the hydrogen consumption rate, we use the relationship between fuel cell current and hydrogen consumption rate (Equation (9)) [48]:

$$m_{{\mathrm{H}}_2}={\int }_0^t{\displaystyle \frac{M_{{\mathrm{H}}_2}{N}_{\mathrm{cell}}}{2F}} i_{\mathrm{FC}}\left(t\right) dt$$

(9)

2.4. Battery Model

Battery modelling forms the basis of battery design and control. A large number of battery models have been developed in the literature. These models can generally be classified into electrochemical models or equivalent electrical circuit models.

The equivalent electrical circuit model of the battery used in this study is shown in Figure 4 [49].

Figure 4 shows the battery model with a controlled voltage source in series with an internal resistor. The model is used to calculate the battery’s output voltage ($V_{\mathrm{bat}}$), which varies according to the battery’s charging or discharging mode. During discharge, the output voltage is calculated by Equation (10). During charging, however, the output voltage is determined by Equation (11).

Discharge mode:

$$V_{\mathrm{discharge}}=E_0-Ri-K{\displaystyle \frac{Q}{Q-it}}·(it+i^{*})+A{e}^{-Bit}$$

(10)

Charge mode:

$$V_{\mathrm{charge}}=E_0-Ri-K{\displaystyle \frac{Q}{it-0.1Q}}·i^{*}-K{\displaystyle \frac{Q}{Q-it}}·it+A{e}^{-Bit}$$

(11)

The estimated state of charge ($SO{C}_{\mathrm{bat}}$) of the battery is calculated by Equation (12):

$$SO{C}_{\mathrm{batt}}=100\left(1-{\displaystyle \frac{\int i\left(t\right) dt}{Q}}\right)$$

(12)

2.5. Control of DC/DC Converters

2.5.1. DC Bus Voltage Control

The proposed method aims to maintain the DC bus voltage at 500 V using a proportional–integral (PI) controller, as illustrated in Figure 5. This controller compares the reference voltage with the measured voltage in real time and corrects the deviation by generating the control signals $u_{b1}$ and $u_{b2}$ required to control the bidirectional buck–boost converter. This process ensures the stability and precision of the DC bus, even in the presence of load fluctuations. As a result of this dynamic control, the battery can stock or deliver energy optimally, improving the system’s overall energy efficiency.

2.5.2. Fuel Cell Current Control

The boost converter associated with the fuel cell is controlled using model predictive control (MPC). In the MPC design, the prediction horizon is set to ($N=1$), enabling the determination of the next optimal switching state. The cost function, which incorporates system states, reference values, and future control actions, is defined by Equation (13):

$$g=f\left(x\right(k),u(k),\dots ,u(k+N-1\left)\right)$$

(13)

The total cost function is derived using the discrete-time MPC method, which involves three steps:

• Converter modelling:
  The boost converter model used is described by dynamic Equations (14) and (15):

  $${\displaystyle \frac{d{i}_L}{dt}}={\displaystyle \frac{V_{\mathrm{in}}}{L}}-{\displaystyle \frac{r_L}{L}}{i}_L+{\displaystyle \frac{V_{\mathrm{DC}}}{L}}(u-1)$$

  (14)

  $${\displaystyle \frac{d{V}_{\mathrm{DC}}}{dt}}={\displaystyle \frac{i_L}{C}}(1-u)-{\displaystyle \frac{V_{\mathrm{DC}-\mathrm{ref}}}{CR}}$$

  (15)

• Discrete-time model development:
  The forward-difference Euler approximation method is employed. By combining Equations (14) and (16), Equation (17) is derived to predict the next value of the inductor current.

  $${\displaystyle \frac{d{i}_L}{dt}}\approx {\displaystyle \frac{i_L(k+1)-i_L\left(k\right)}{T_s}}$$

  (16)

  $$i_L(k+1)={\displaystyle \frac{T_s}{L}}\left(V_{\mathrm{in}}\left(k\right)-V_{\mathrm{DC}}\left(k\right)(1-u)\right)+i_L\left(k\right)$$

  (17)

  where $T_s$ is the sampling time, k is the iteration number, and $i_L(k+1)$ is the predicted current value.

• Defining cost functions:
  The main cost function presented in Equation (18) aims to minimise the difference between the inductor current and its reference.

  $$g_i(k+1)={[i_{\mathrm{L}-\mathrm{ref}}-i_L(k+1)]}^2$$

  (18)
  An additional cost function, presented in Equation (19), is introduced to reduce the switching frequency.

  $$g_{\mathrm{sw}}(k+1)=\lambda {[u_{(k+1)}-u_{\left(k\right)}]}^2$$

  (19)

  where ($\lambda =0.1$) is an adjustable weighting factor.
  The total cost function combining these two objectives is expressed by Equation (20):

  $$g_t(k+1)=g_i(k+1)+g_{\mathrm{sw}}(k+1)$$

  (20)

The MPC selects the optimal control $u^{*}\left(k\right)$ presented by Equation (21), by minimising the cost function among the possible switching states.

$$u^{*}\left(k\right)=arg\underset{u\left(k\right)}{min}{g}_t(k+1)$$

(21)

3. Energy Management System

Hybridization of fuel cell electric vehicles with batteries offers a promising solution for improving overall system efficiency and extending the lifespan of energy sources. However, this potential can only be fully exploited by implementing an appropriate energy management strategy that optimally distributes power between the sources to ensure energy efficiency and performance. In this context, two critical degradation factors are specifically considered in this study: the frequent and rapid variation in the fuel cell’s reference power, and its operation outside the optimum efficiency range. These conditions impose dynamic stress on the membrane–electrode assembly and accelerate ageing by increasing irreversible losses, highlighting the crucial role of power management in protecting the longevity of fuel cells.

Two approaches for energy management in hybrid fuel cell vehicles are then developed and compared: a deterministic rule-based and a fuzzy logic-based strategy.

3.1. Deterministic Energy Management Strategy

The principle of deterministic rule-based energy management strategies for fuel cell and battery electric vehicles is based on the use of predefined “if-then” rules to manage energy distribution between the fuel cell, battery, and electric motor. These rules are established on the basis of prior knowledge of the system and technical experience, to ensure reliable operation under various driving conditions. The strategy consists in determining the energy source according to certain predefined conditions, such as battery state of charge, power demand, and vehicle speed.

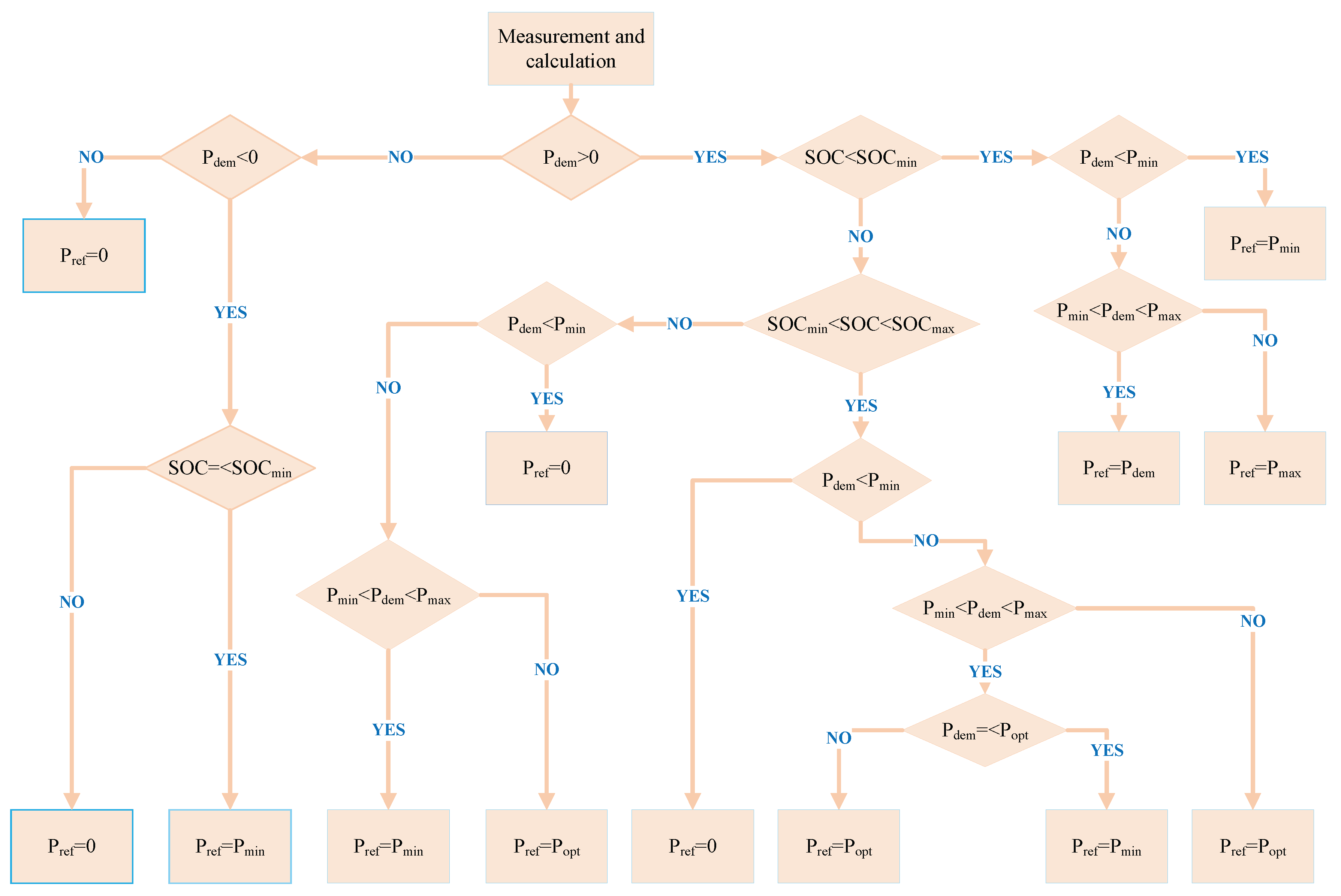
An energy management strategy (EMS) was developed, combining two deterministic rule-based approaches—power tracking and optimal efficiency region—with critical state-of-charge (SOC) management. This integration guaranteed operational efficiency, power balance, and optimal battery condition.

The power tracking method aims to effectively balance the power distribution between the fuel cell and the battery to meet the vehicle’s energy demand $P_{\mathrm{dem}}$. When $P_{\mathrm{dem}}>0$, the system evaluates the battery’s state of charge ($SOC$) against defined thresholds and adjusts the fuel cell’s power, taking into account its minimum and maximum limits. In the event of regenerative braking, the energy recovered is stored in the battery. This mechanism guarantees optimum energy distribution, keeps the SOC within an ideal range, and preserves the battery’s health. The fundamental formula for this method is defined by Equation (22):

$$P_{\mathrm{dem}}=P_{\mathrm{fc}}+P_{\mathrm{bat}}$$

(22)

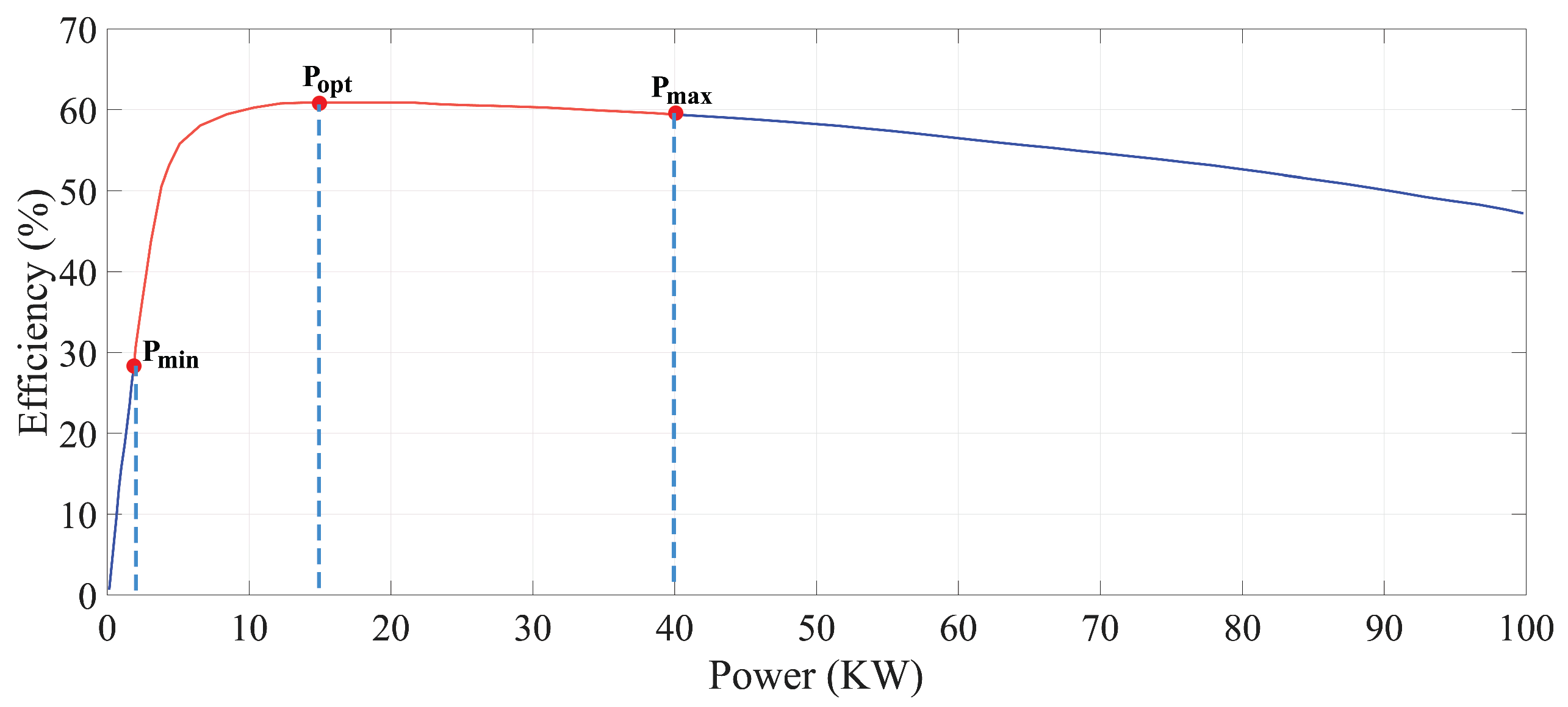
The optimal efficiency region algorithm aims to maximise energy efficiency by keeping the fuel cell in its optimal power range (Figure 6). When the power demand is between the limits of efficient operation, the fuel cell responds directly to that demand. If ($P_{\mathrm{dem}}$) exceeds ($P_{\max }$), the battery supplies the surplus, ensuring that the fuel cell remains within its optimum efficiency range (highlighted in red in the figure). This coordination between fuel cell and battery reduces hydrogen consumption, minimises energy losses, and improves overall system efficiency. By prioritizing $P_{\mathrm{opt}}$, this approach ensures a sustainable balance between fuel cell energy production and battery support.

The last consideration in designing the energy management strategy was to maintain the battery’s state of charge (SOC) around a target of 60% at the end of each drive cycle, regardless of its initial state, in order to optimise battery health and reduce degradation. This strategy guaranteed a delta SOC ($\mathrm{\Delta }\mathrm{SOC}$) of zero when the SOC started at 60%, indicating efficient energy management. The rules aimed to keep the SOC within a safe operating range of 40% to 80% to avoid extreme cycle conditions and extend battery life.

Based on the previously defined objectives for optimizing energy management in fuel cell electric vehicles, the deterministic rules algorithm is illustrated in Figure 7.

3.2. Fuzzy Logic Energy Management Strategy

A fuzzy logic rule-based energy management strategy for a fuel cell hybrid electric vehicle exploits the strengths of fuzzy logic to effectively manage the uncertainties and non-linearities inherent in the system. Contrary to traditional deterministic rule-based approaches that follow fixed if–then instructions, fuzzy logic uses a more flexible and adaptive control strategy. This flexibility is achieved through the use of fuzzy sets and membership functions, which allow the system to manage different degrees of truth and integrate a wider range of input conditions.

In a fuel cell–battery electric vehicle, power demand and battery state of charge can fluctuate considerably depending on driving conditions, load requirements, and other dynamic factors. Fuzzy logic is excellent in this context, as it enables smooth transitions between different energy sources (fuel cell and battery) and nuanced control of energy distribution. This ability to adapt is essential for optimizing vehicle performance, as it ensures that the powertrain operates efficiently under diverse and changing conditions.

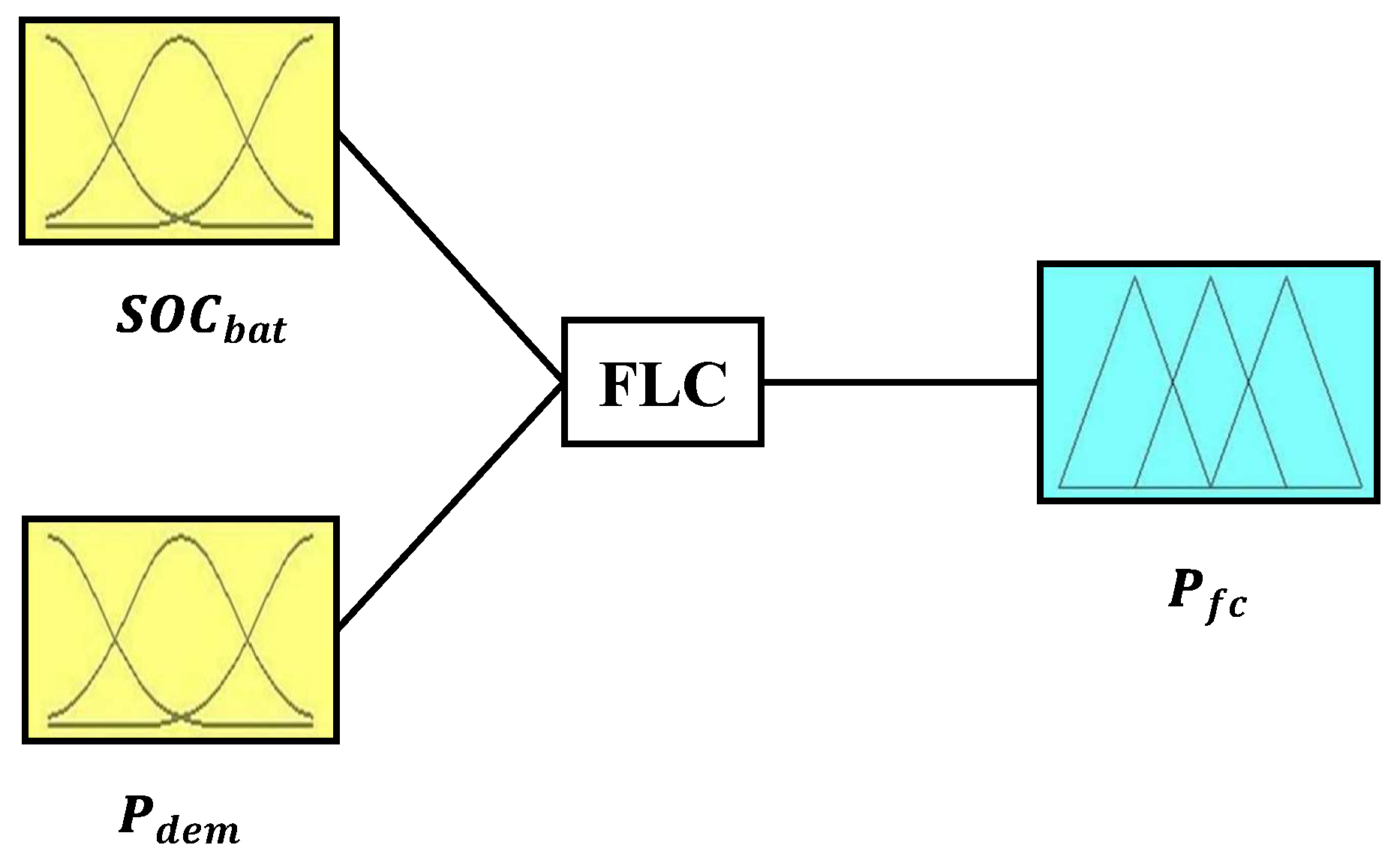
The fuzzy controller shown in Figure 8 was employed. That controller uses two inputs: the power demand and the battery state of charge. The output of the fuzzy controller is the fuel cell’s reference power, which determines the power to be delivered by the fuel cell at any given time to optimise system performance and efficiency.

The fuzzy logic rules were designed using the same methodology as that applied to the deterministic rule-based strategy. That approach was based on expert knowledge and analysis of system behaviour, incorporating criteria such as fuel cell efficiency zones, battery state-of-charge limits, and energy demand characteristics. Both strategies used predefined thresholds derived from the power tracking and the optimal efficiency region approach to ensure that the fuel cell operated within its ideal dynamic range while preserving the state of health of the battery. This ensured consistency between the two EMS designs and enabled a close comparison of performance.

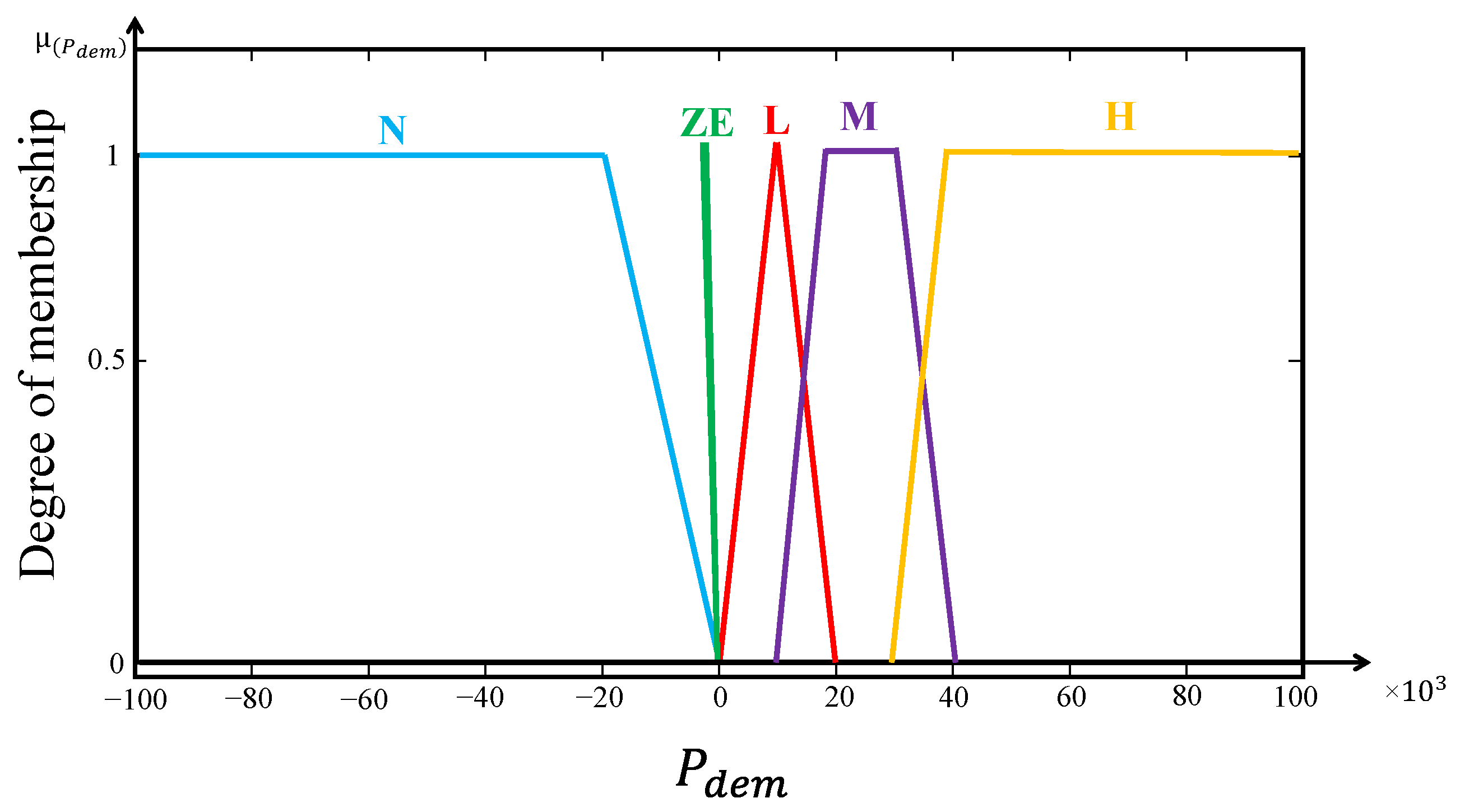
Figure 9 shows the membership functions of the input variable “power demand”. The power demand on a vehicle’s motor can vary considerably depending on driving conditions. To manage this variability, power demand was divided into different linguistic categories covering all possible cases.

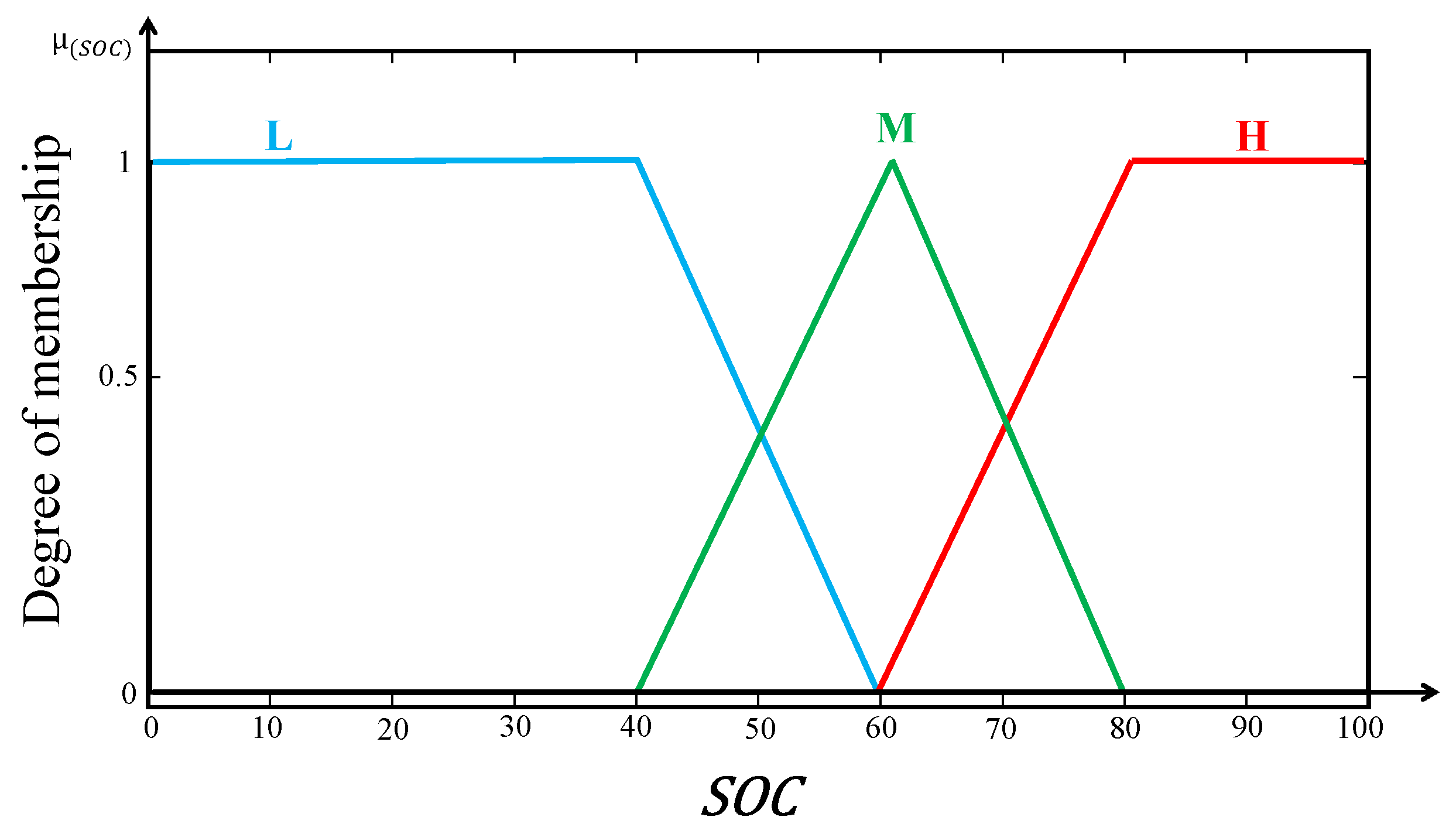
Figure 10 illustrates the membership functions of the input variable “Battery state of charge”. The battery’s state of charge is another essential indicator of the battery’s current state of charge.

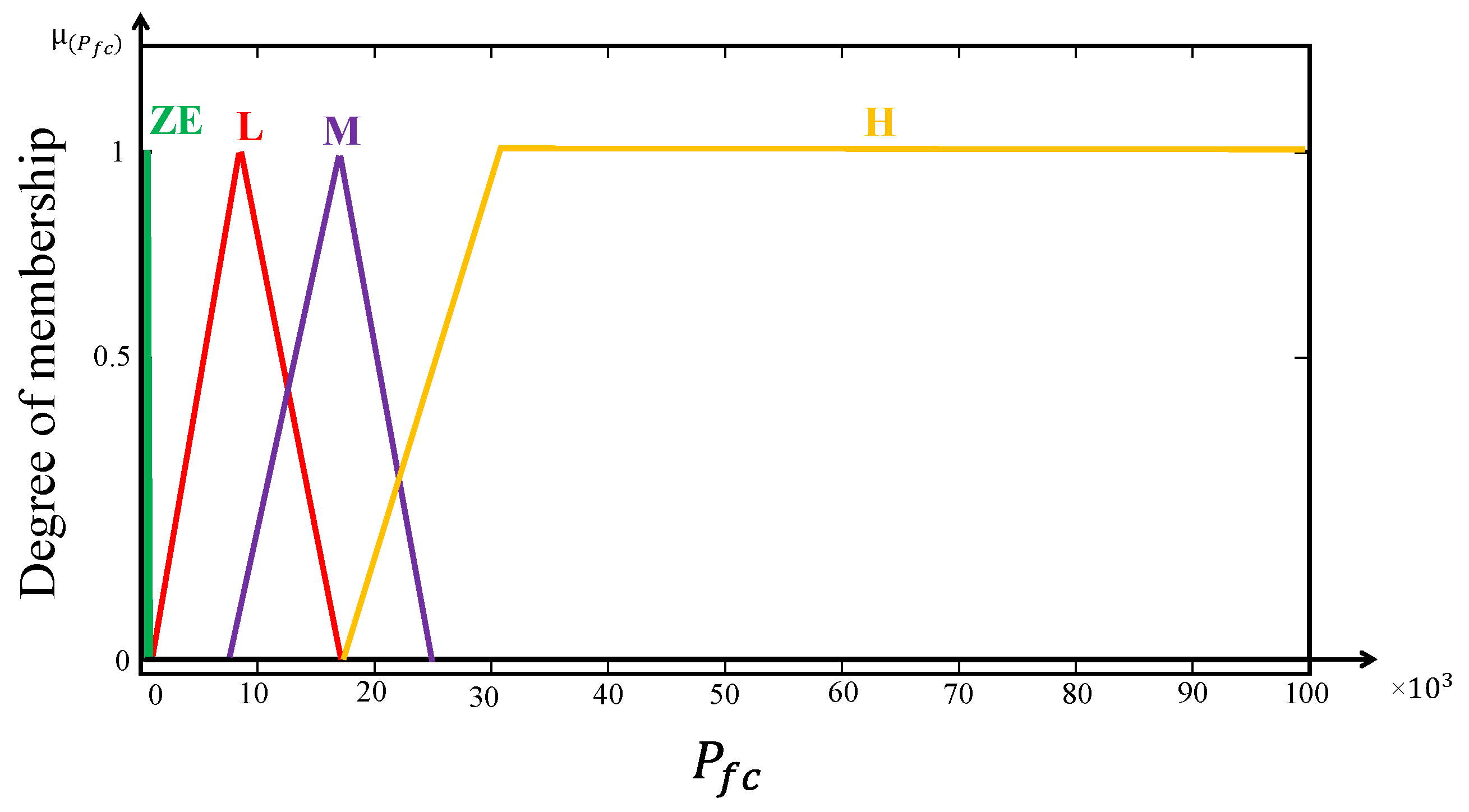
Figure 11 presents the membership functions of the output variable “Fuel cell reference power”. Fuel cell power output was determined to ensure optimum performance and efficiency. The membership functions associated with the fuel cell’s reference power were defined according to the optimal efficiency region.

Fuzzy rules determined how the fuel cell should react to different combinations of power demand and state of charge. These rules ensured that the system optimised energy utilization, balancing power between the fuel cell and the battery.

Table 2. Fuzzy logic controller rules.

		SOC
		L	M	H
Pdem	N	ZE	ZE	ZE
	ZE	L	ZE	ZE
	L	M	L	ZE
	M	H	M	L
	H	H	M	M

shows the fuzzy logic rules for the energy management strategy proposed for the fuel cell hybrid electric vehicle under study.

4. Simulation Results and Discussion

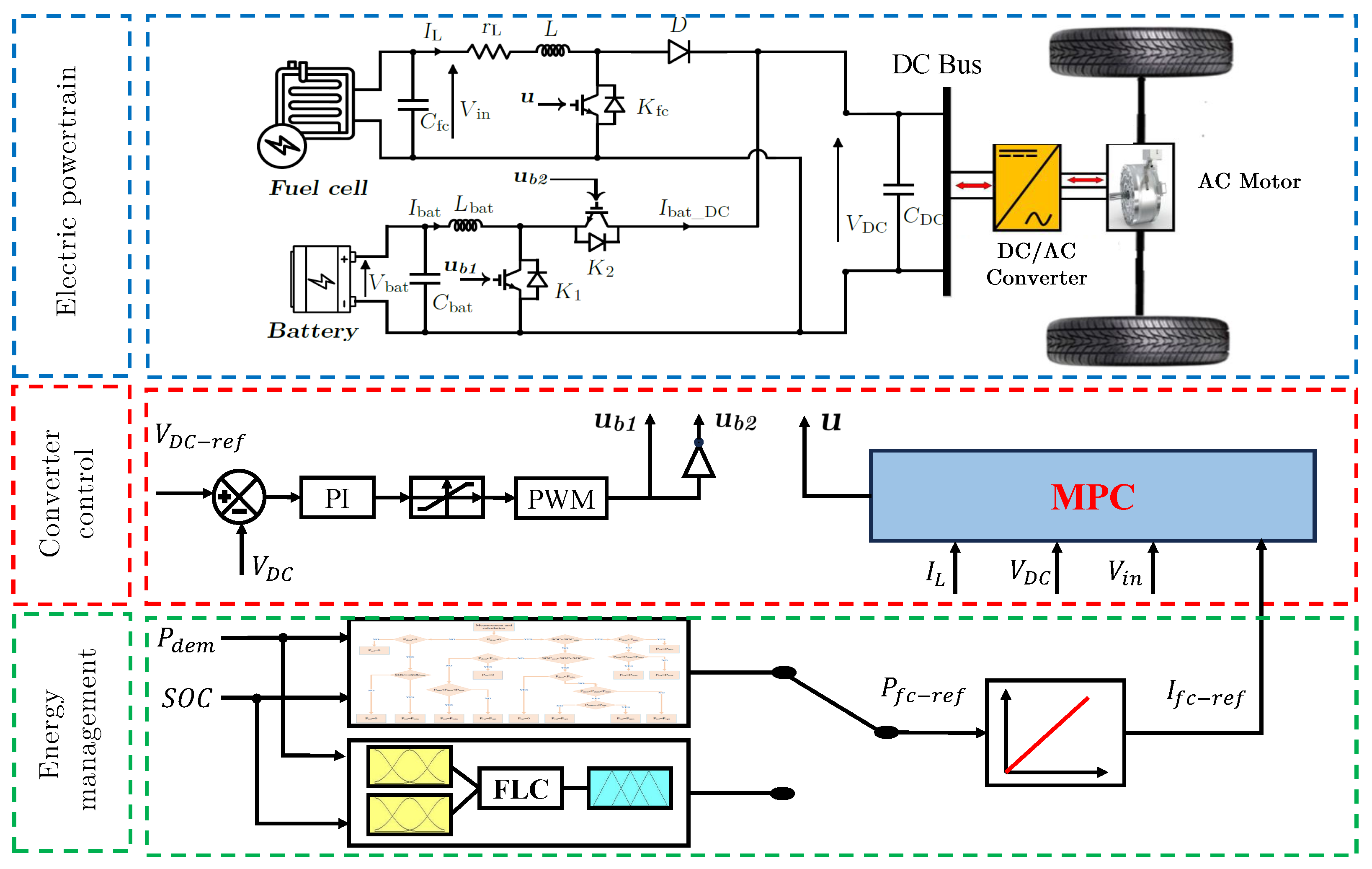
The simulation model for the energy management system of a fuel cell–battery hybrid vehicle, developed in MATLAB Simulink R2016a, is presented in Figure 12. It is based on a three-layer architecture, enabling in-depth analysis and optimisation of energy management strategies. The first layer, dedicated to the energy management system (EMS), uses two algorithms, the first based on deterministic rules and the second based on fuzzy rules. A look-up table converts this power into a reference current, serving as input to the second layer. The second layer generates PWM signals to control the converters via model predictive control (MPC) and a PI controller, guaranteeing a stable voltage of 500 V on the DC bus and efficient energy conversion. The third layer, called the powertrain, integrates the energy sources, converters, and motor, converting electrical energy into mechanical energy to propel the vehicle. This model was tested with two standard driving cycles, the NEDC and the UDDS, offering a variety of scenarios for evaluating the performance and efficiency of the energy management strategy under dynamic and stable load conditions.

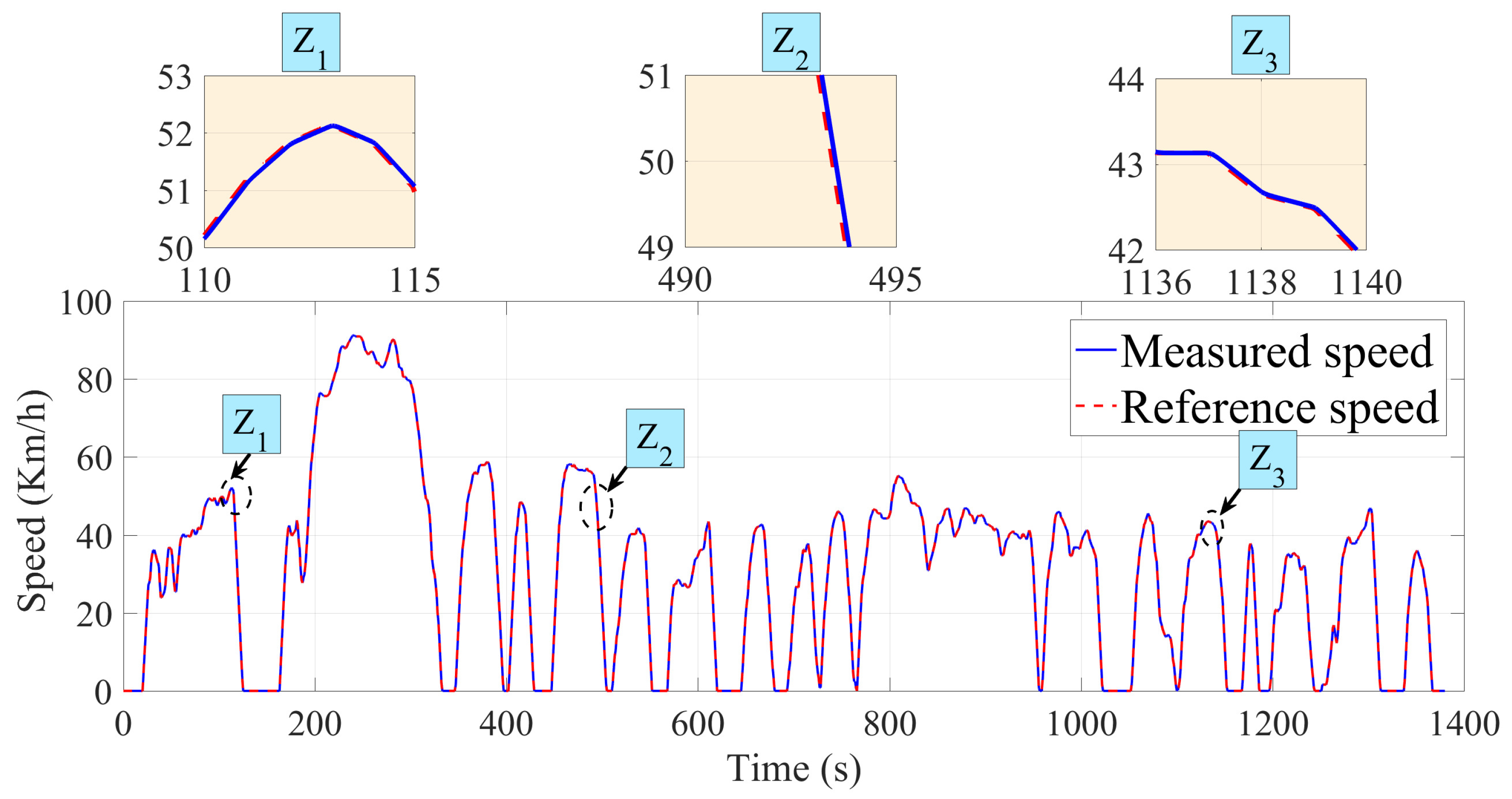
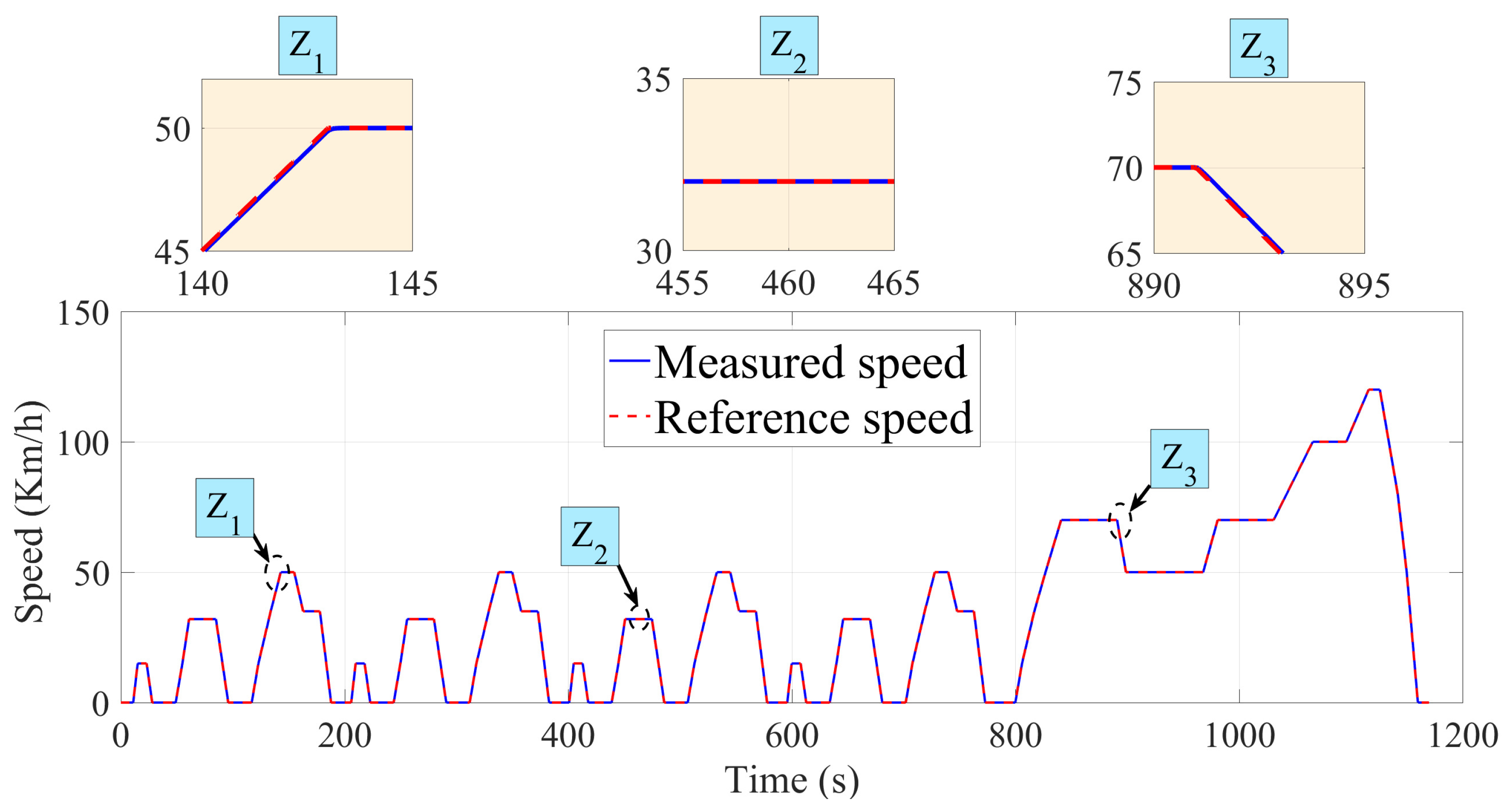
Figure 13 and Figure 14 present vehicle speeds for the UDDS and NEDC driving cycles, respectively.

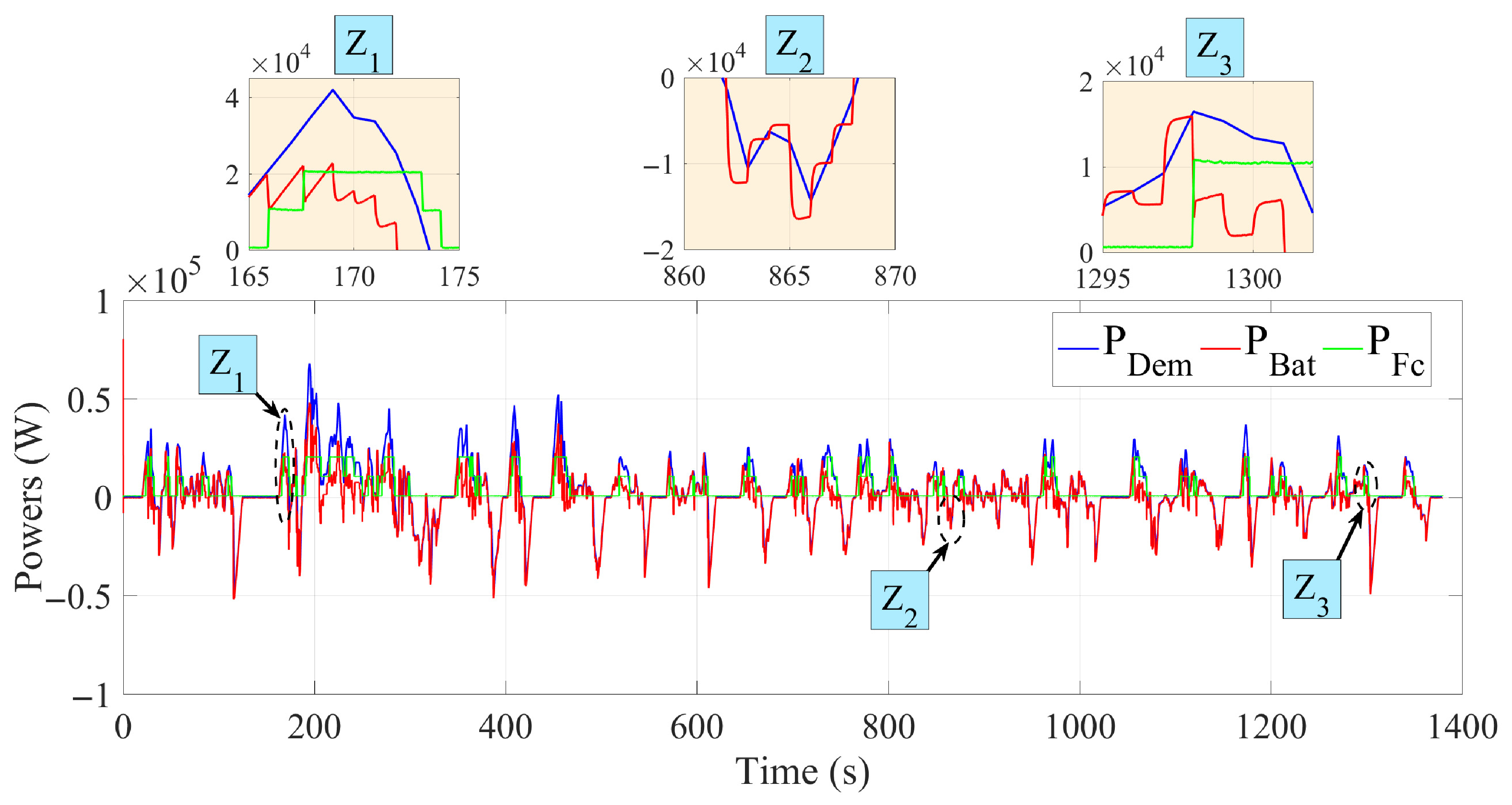
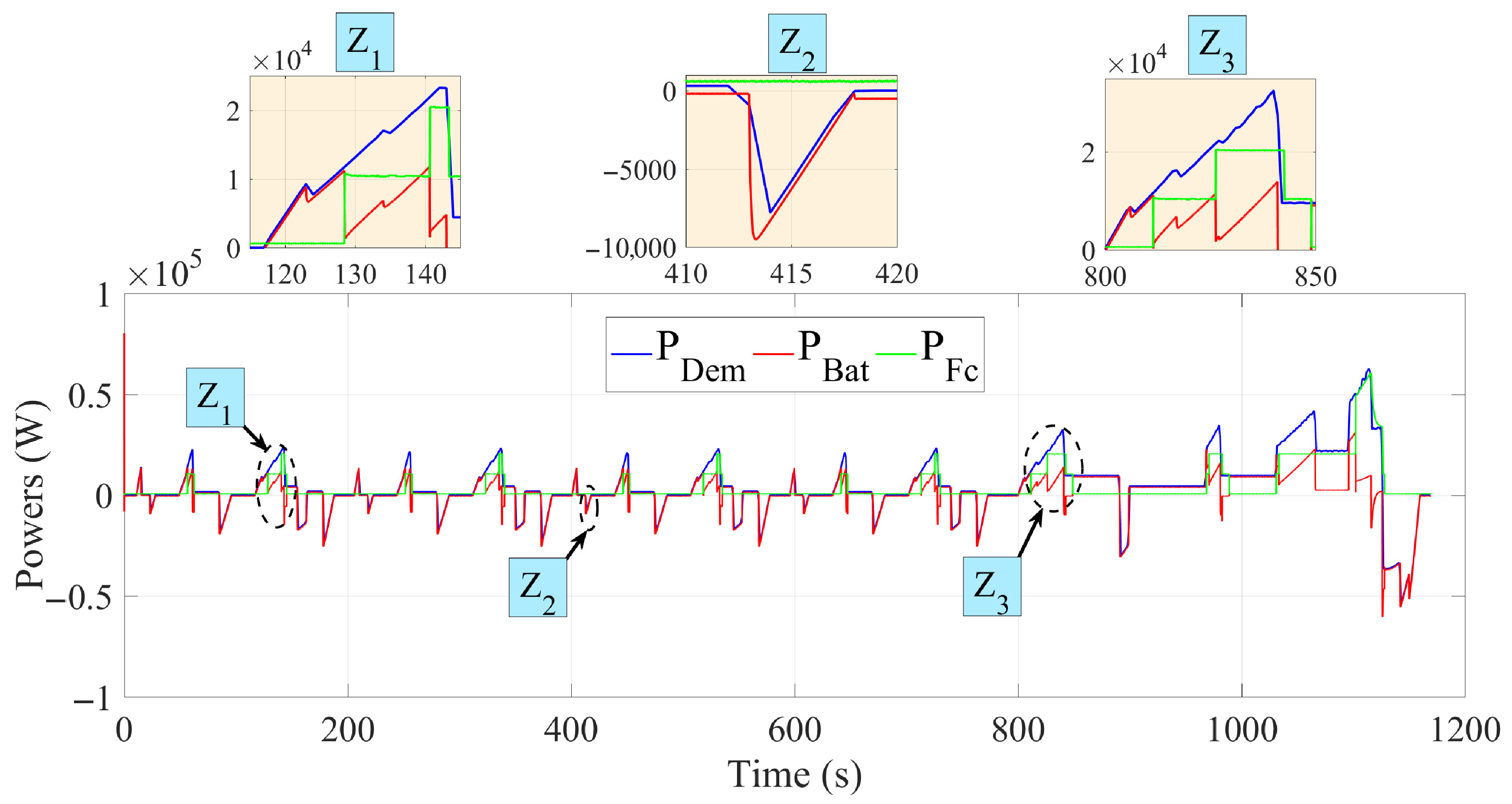
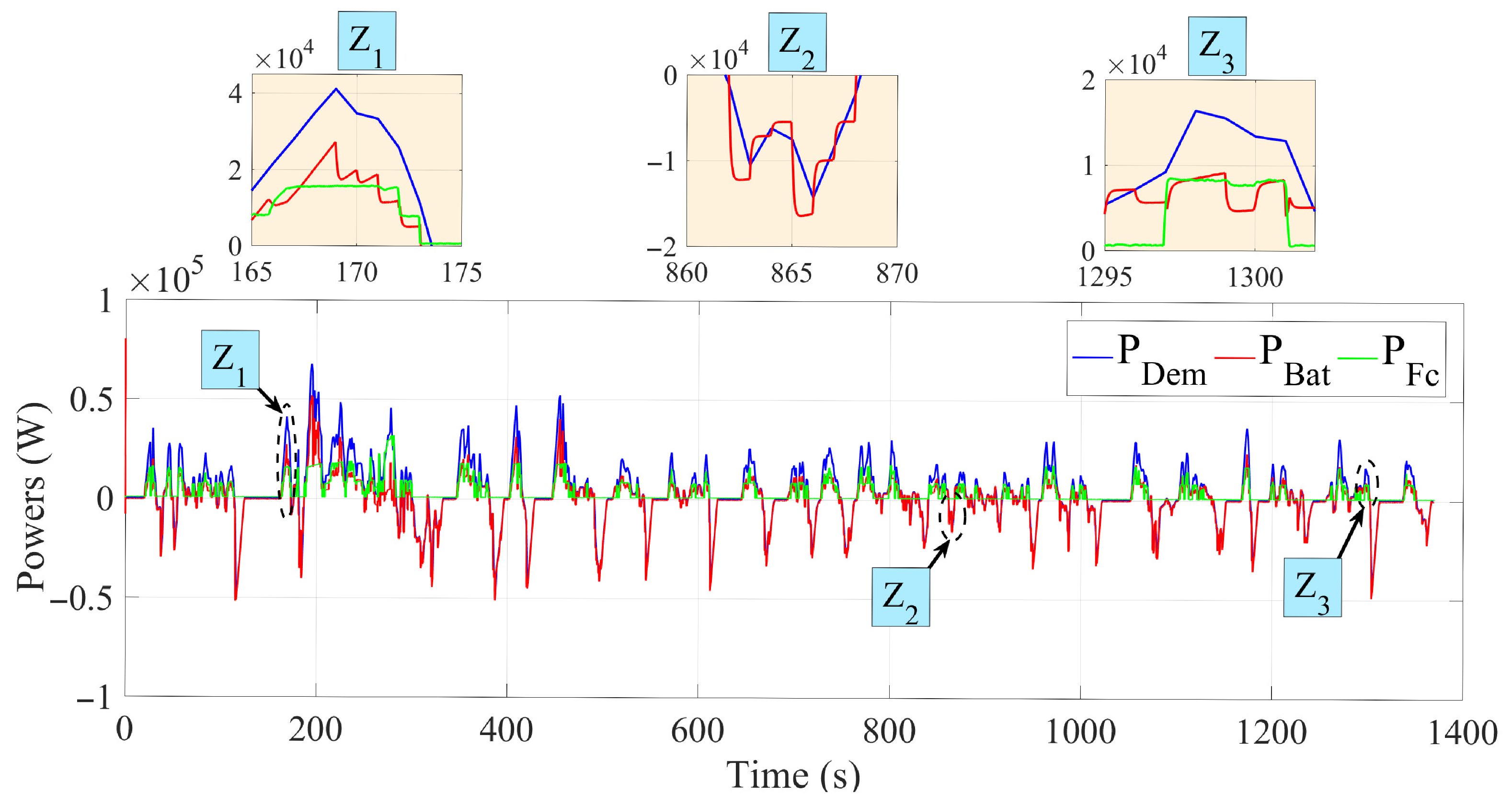
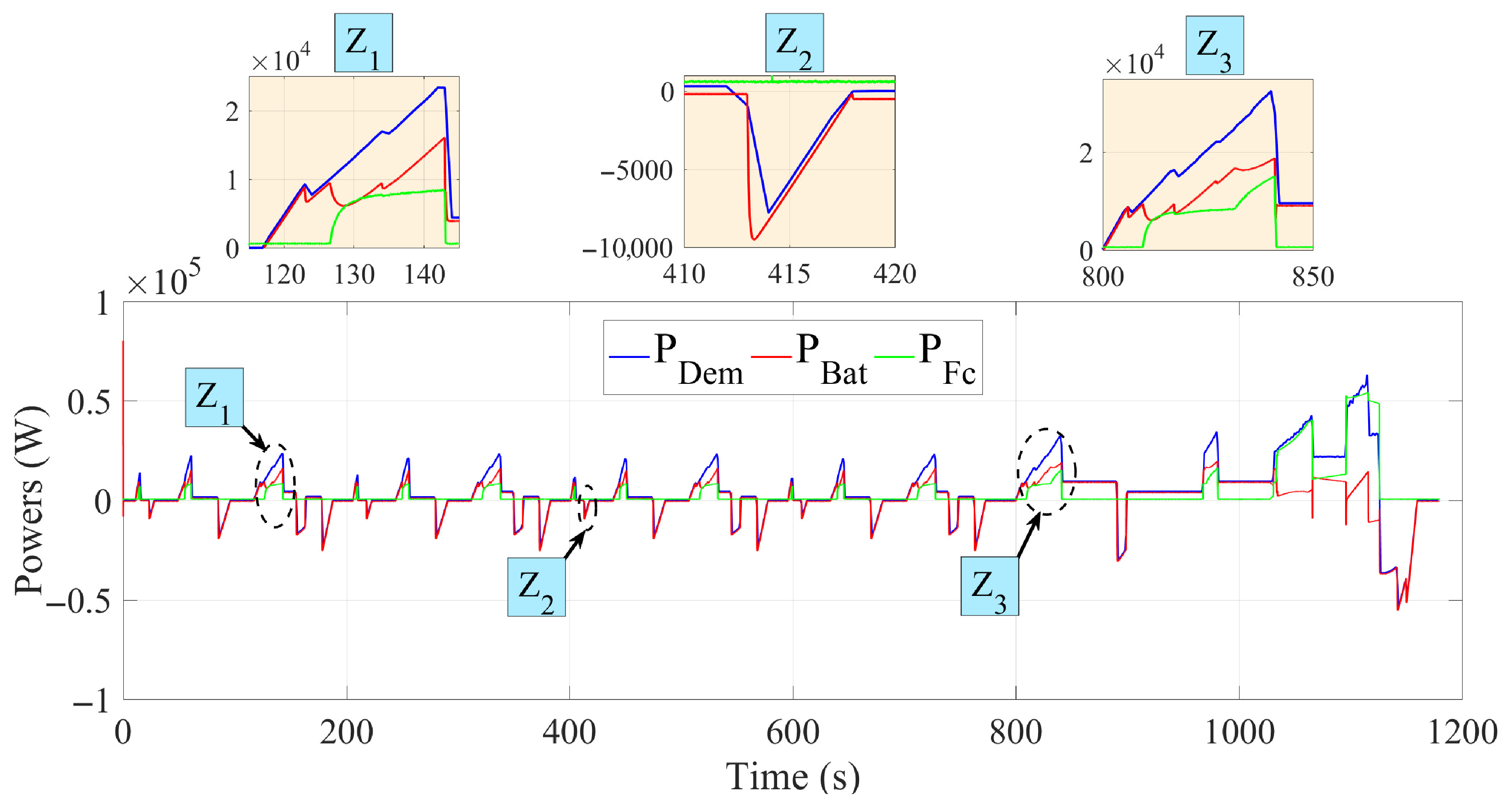
In both cases, the vehicle speed closely followed the reference speed with minimal error, demonstrating the high performance of the system. The figures also highlight three zones: Z1, Z2, and Z3. Each zone illustrates a crucial aspect of vehicle control, from achieving maximum speed to precise response under hard deceleration, as well as smooth management of speed reductions. Together, these zones demonstrate the precision and reliability of our control system in handling real-life urban and extra-urban driving scenarios.

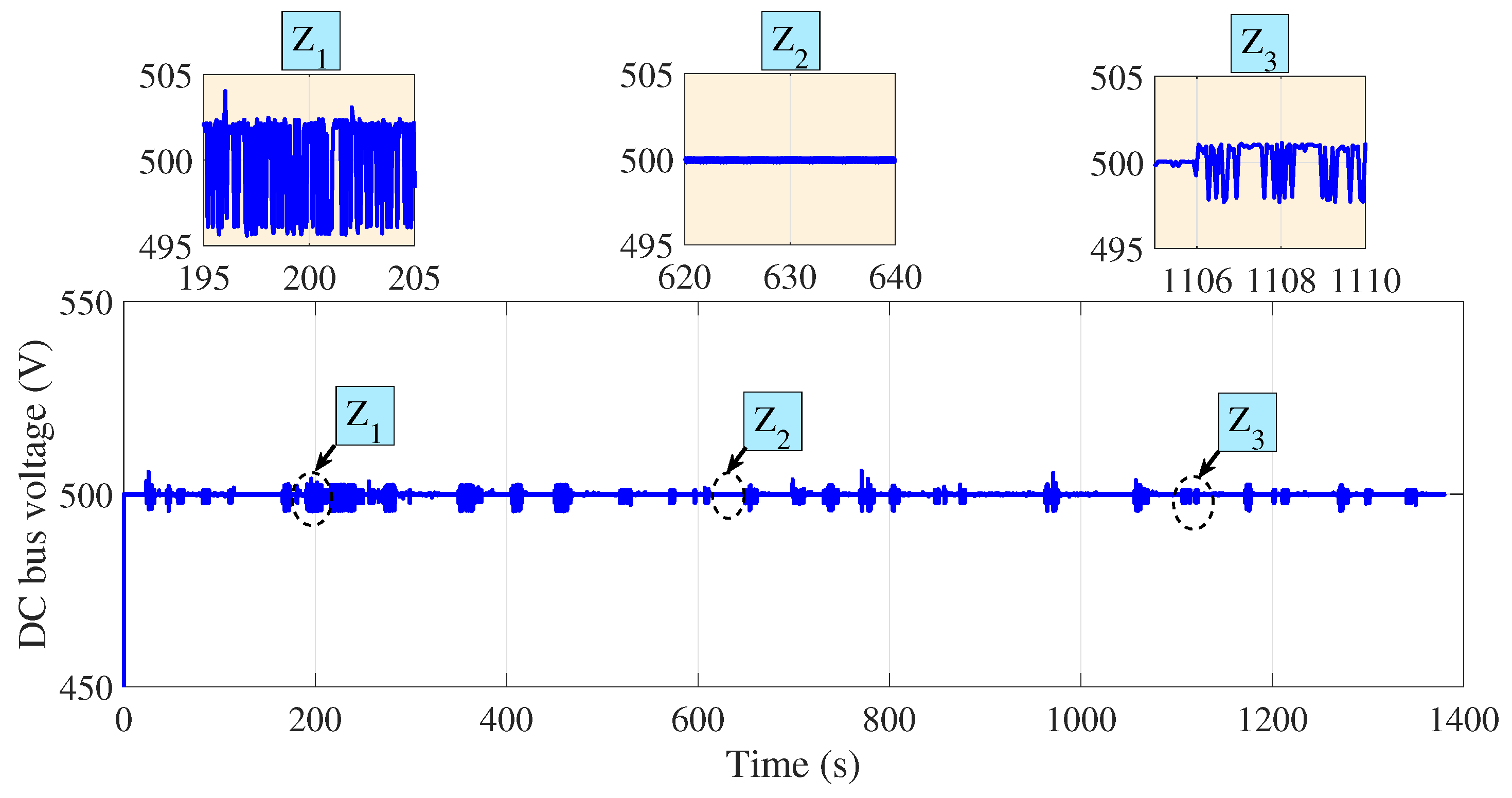
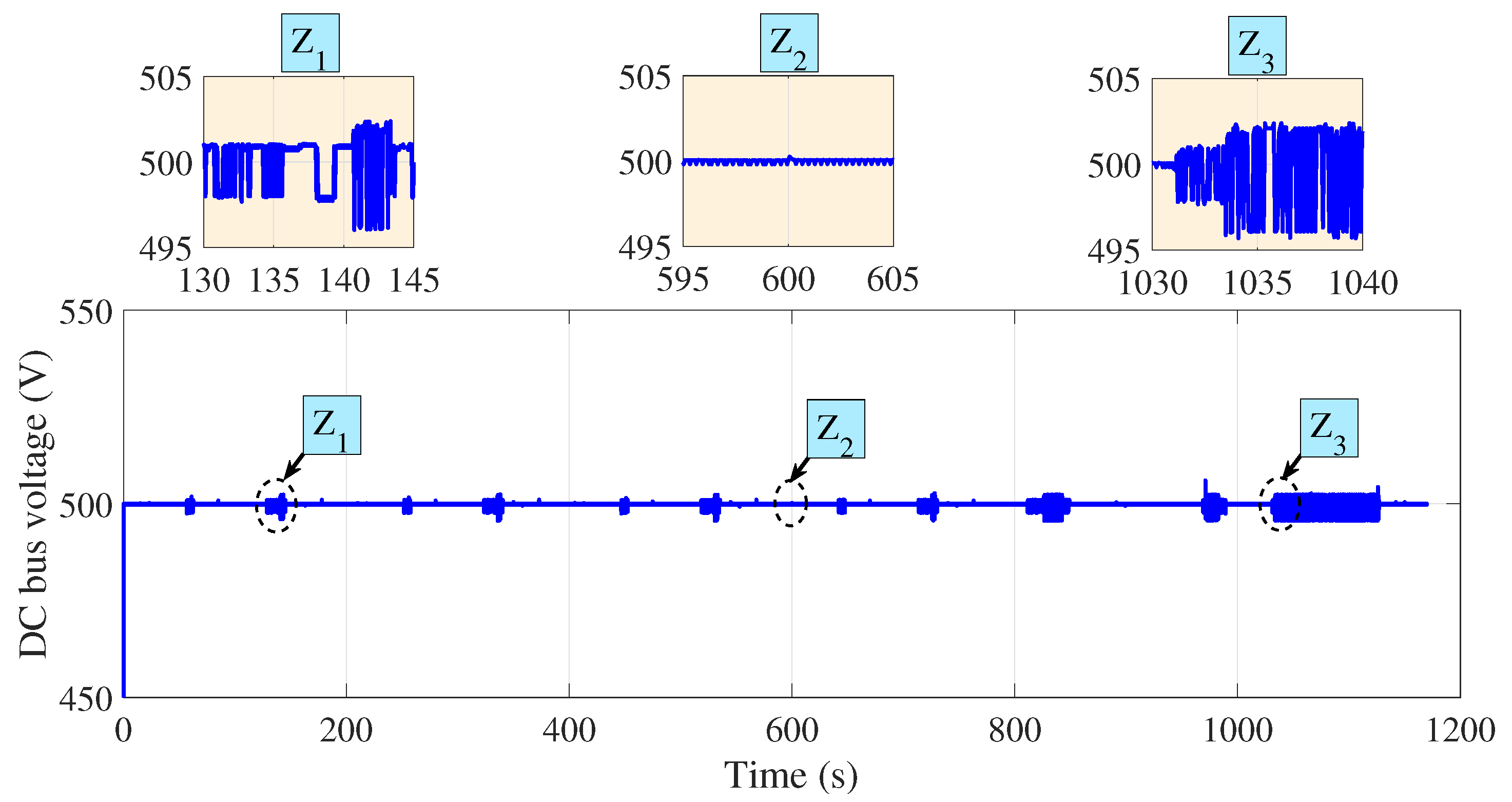
Figure 15 and Figure 16 illustrate the DC bus voltage variation for the UDDS and NEDC driving cycles, respectively. In both cases, the DC bus voltage remained stable and closely tracked the reference value of 500 V, with only minor fluctuations, characterized by a voltage ripple of approximately 1%. This stability demonstrates the effectiveness of the PI controller in regulating the buck–boost DC/DC converter, ensuring that the voltage remains within the required operational limits despite varying power demands. Maintaining a consistent voltage level underscores the robustness and reliability of the control system, which is crucial for enhancing overall vehicle efficiency and performance.

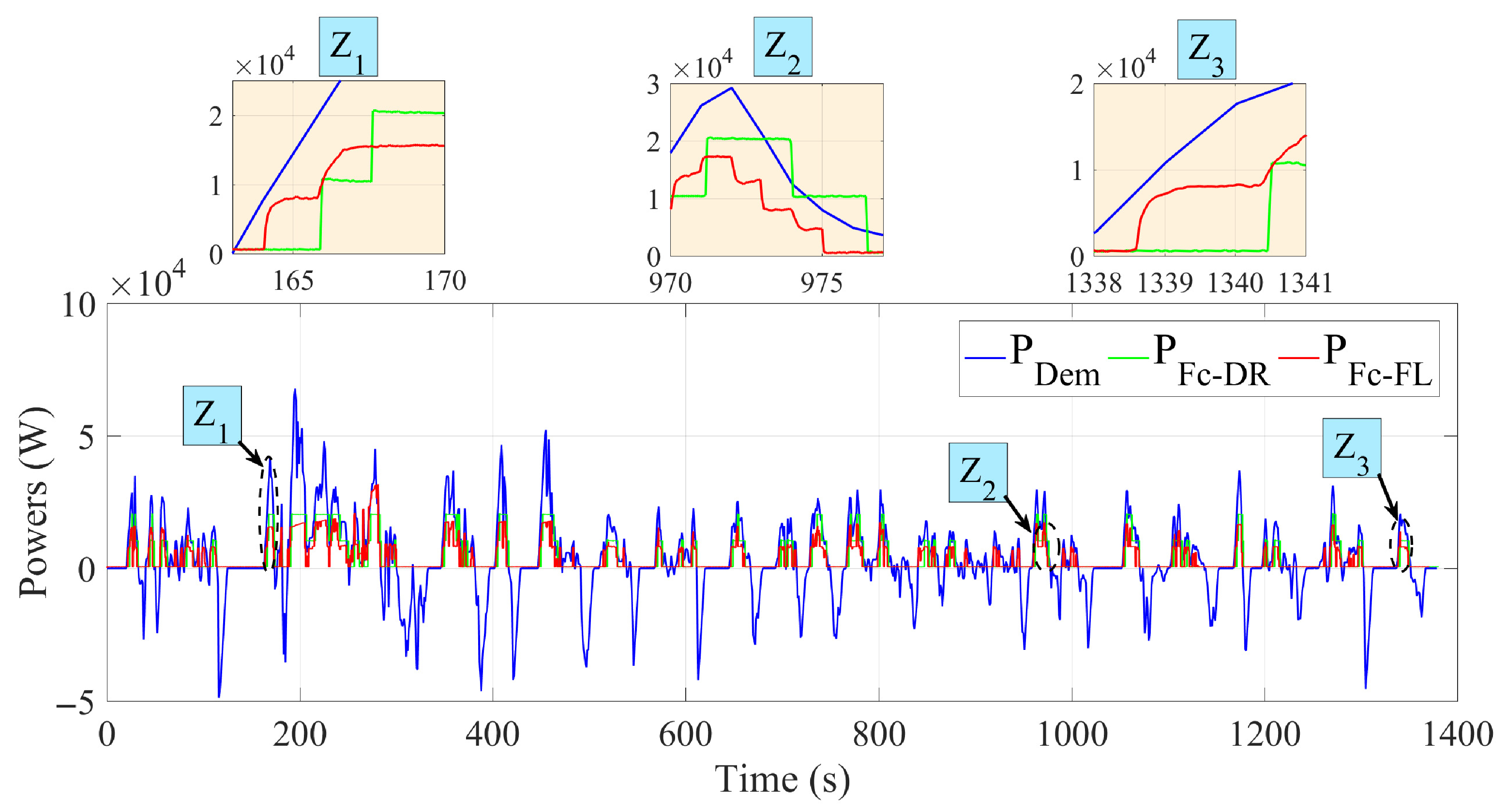
Figure 17 and Figure 18 illustrate the power evolution of the fuel cell, battery, and electric motor during the UDDS and NEDC driving cycles. They show the dynamic interaction between these power sources, regulated by a strategy based on deterministic rules. The battery assisted the fuel cell by providing surplus energy during acceleration and recovering energy during braking. Zoomed-in areas highlight the critical moments when the system adjusted energy distribution to ensure smooth transitions. These results demonstrate the system’s ability to manage energy distribution in real time and optimise consumption in a variety of driving scenarios.

Figure 19 and Figure 20 illustrate the power evolution of the fuel cell, battery and electric motor using a fuzzy logic-based energy management strategy, applied to the UDDS and NEDC cycles. In contrast to deterministic strategies, this approach ensured smoother power variations, enhancing the system’s adaptability. The fuel cell adjusted its power smoothly, while the battery compensated acceleration and recovered energy from braking. Zoomed-in areas highlight critical transitions, showing how fuzzy logic optimised energy distribution. These results confirm improved flexibility and energy performance in different driving scenarios.

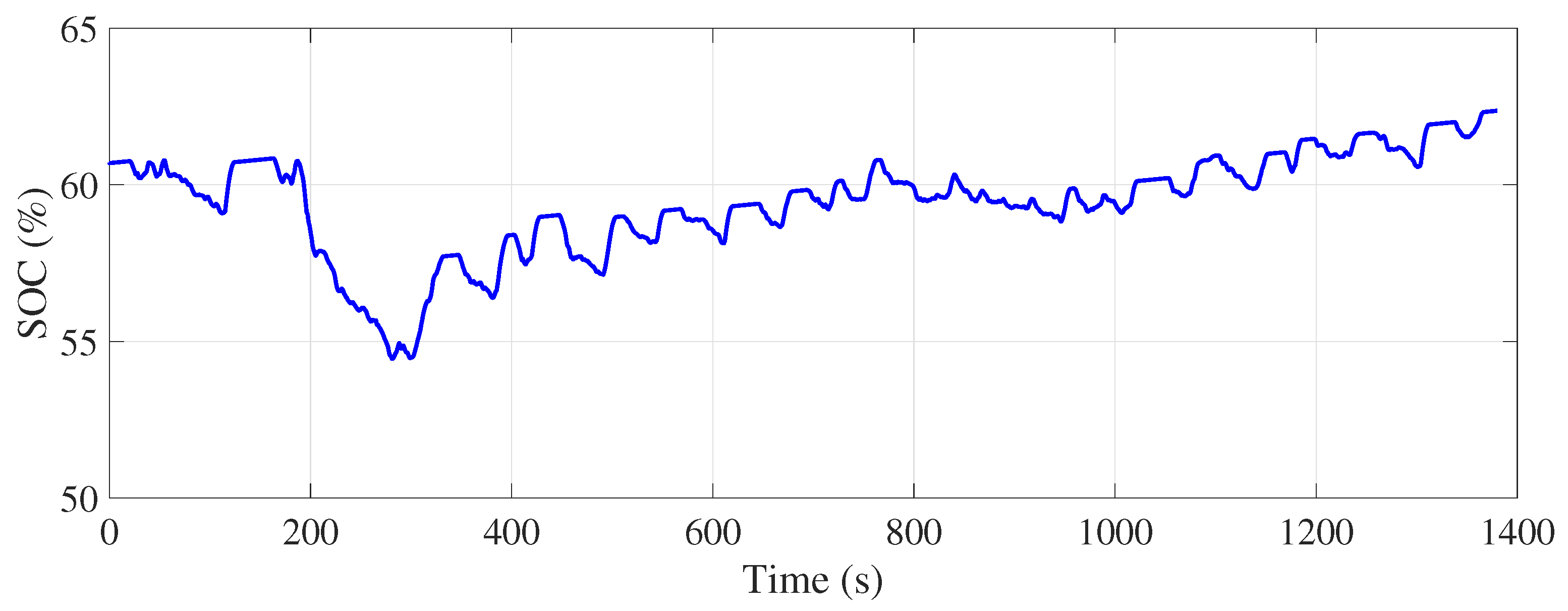
Figure 21 and Figure 22 show the evolution of the battery’s state of charge (SOC) during the UDDS and NEDC driving cycles, respectively. In both figures, the state of charge remains within the predefined range of 40% to 80%, fluctuating around an average state of charge (60%), demonstrating the effectiveness of the energy management strategy in maintaining the state of charge within a safe and efficient operating range. The difference in state of charge between the initial and final state of charge was +3% for the UDDS cycle and −4% for the NEDC cycle. These results demonstrate the ability of the energy management system to adapt to different driving conditions, while maintaining the battery’s SOC within the desired range.

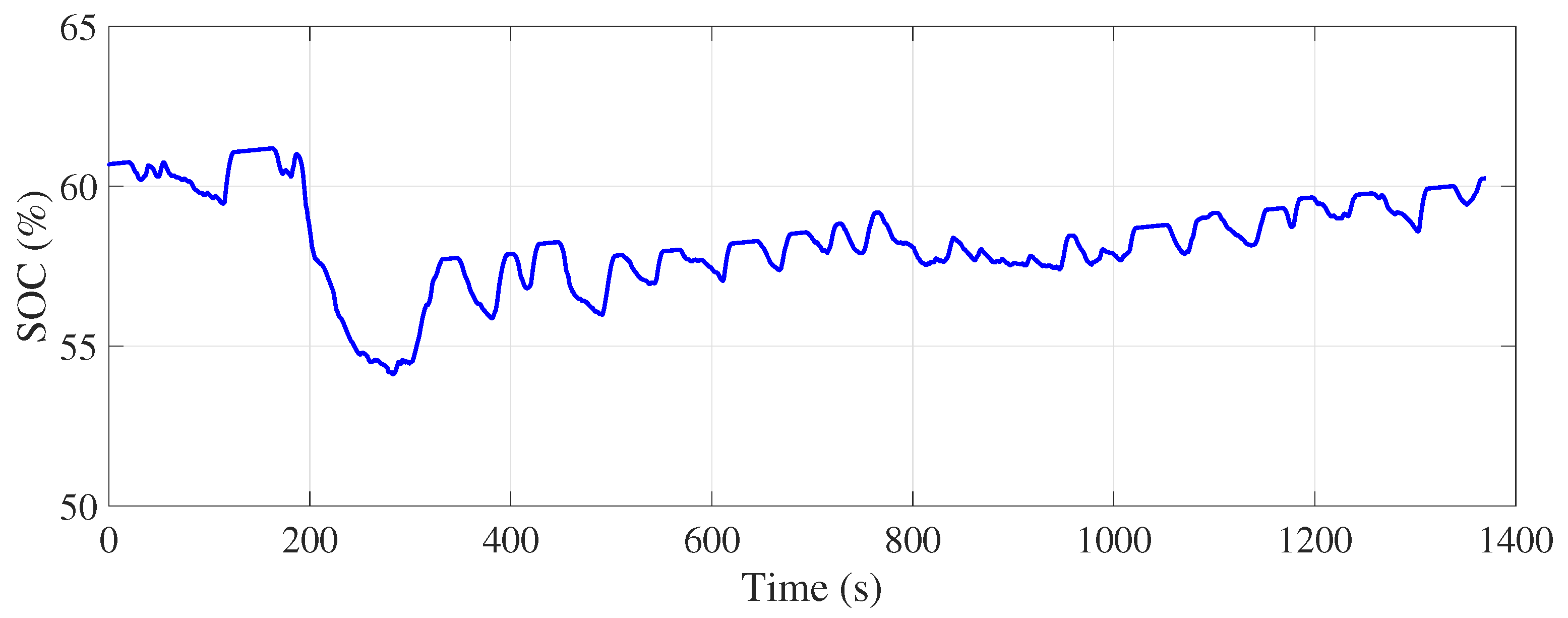
Figure 23 and Figure 24 illustrate the evolution of the battery state of charge during the UDDS and NEDC driving cycles using a fuzzy logic-based energy management strategy. The state of charge in both cases remained within the predefined range of 40% to 80%, fluctuating around an average value of 60%. This demonstrates the effectiveness of the system in adaptively regulating the state of charge, guaranteeing safe and optimal vehicle operation. The variation in state of charge between the start and end of cycles was −0.5% for the UDDS cycle and −1% for the NEDC cycle. These results clearly demonstrate the ability of fuzzy logic to adapt to the dynamic conditions of different driving cycles, maintaining the battery’s state of charge within the desired limits while adapting to the vehicle’s fluctuating energy requirements.

In order to test the robustness of the energy management strategy, different initial state of charge (SOC) values were simulated, with the objective of achieving 60% SOC at the end of each cycle. This approach also aimed to ensure that the state of charge remained within the safe operating range of 40% to 80%, thus avoiding deep discharge and overcharge conditions, which can degrade the battery’s state of health.

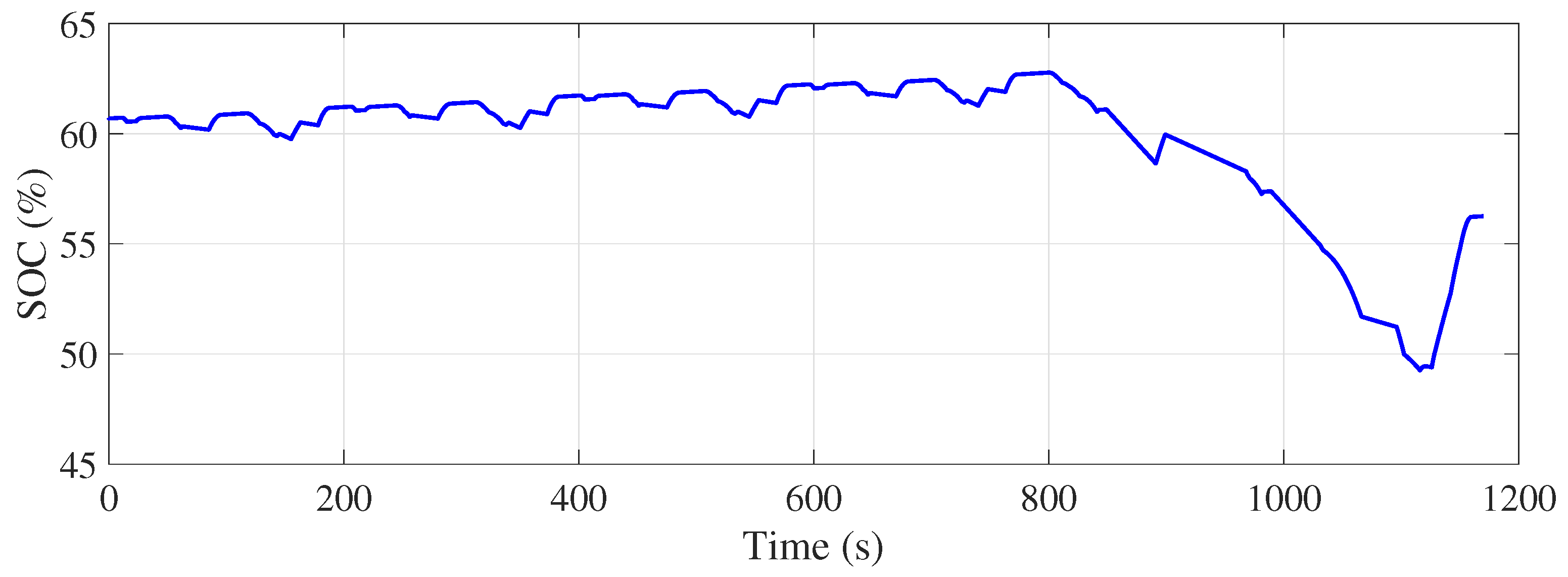
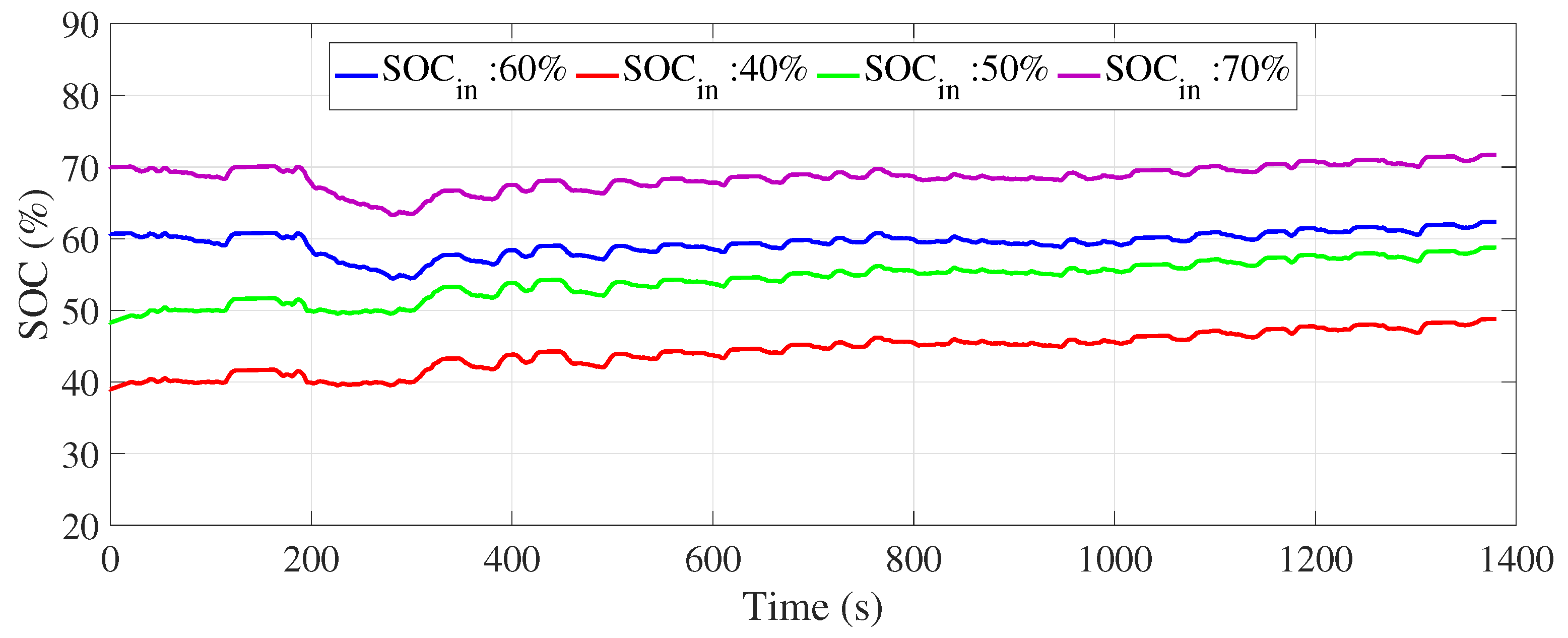
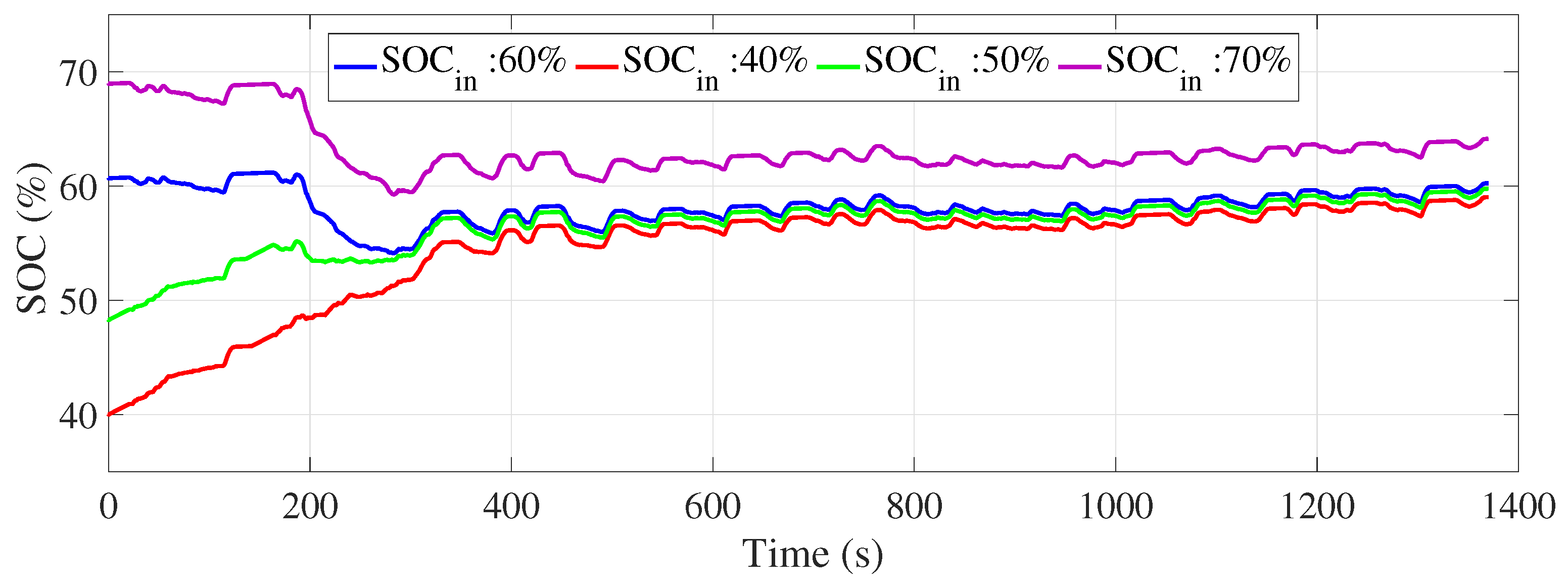
Figure 25 and Figure 26 illustrate the evolution of the SOC for the UDDS and NEDC driving cycles, respectively, from different initial SOC values (40%, 50%, 60%, and 70%) using a deterministic rule-based energy management strategy. These figures provide a clear visual representation of how the energy management system adjusted its behaviour according to the initial SOC and managed to converge towards the ideal SOC of 60% at the end of the driving cycles.

Simulation results show that the strategy based on deterministic rules failed to achieve the 60% SOC target at the end of the UDDS cycle, revealing challenges associated with frequent variations in urban energy demand. In contrast, for the NEDC cycle, the strategy proved more effective, returning the SOC close to target with low error, due to more stable driving conditions. These differences underline the need to adapt the strategy according to driving profiles and to explore more flexible approaches, such as the integration of fuzzy logic-based rules, to improve SOC management in dynamic urban environments.

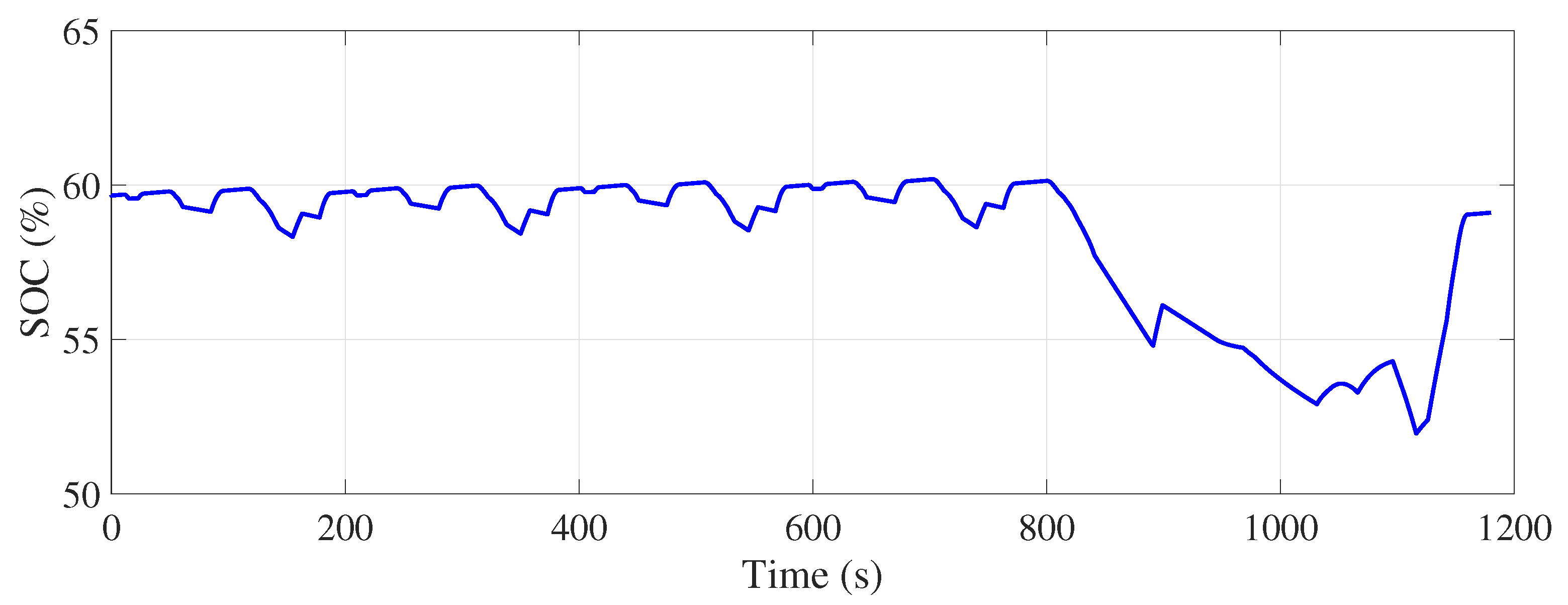
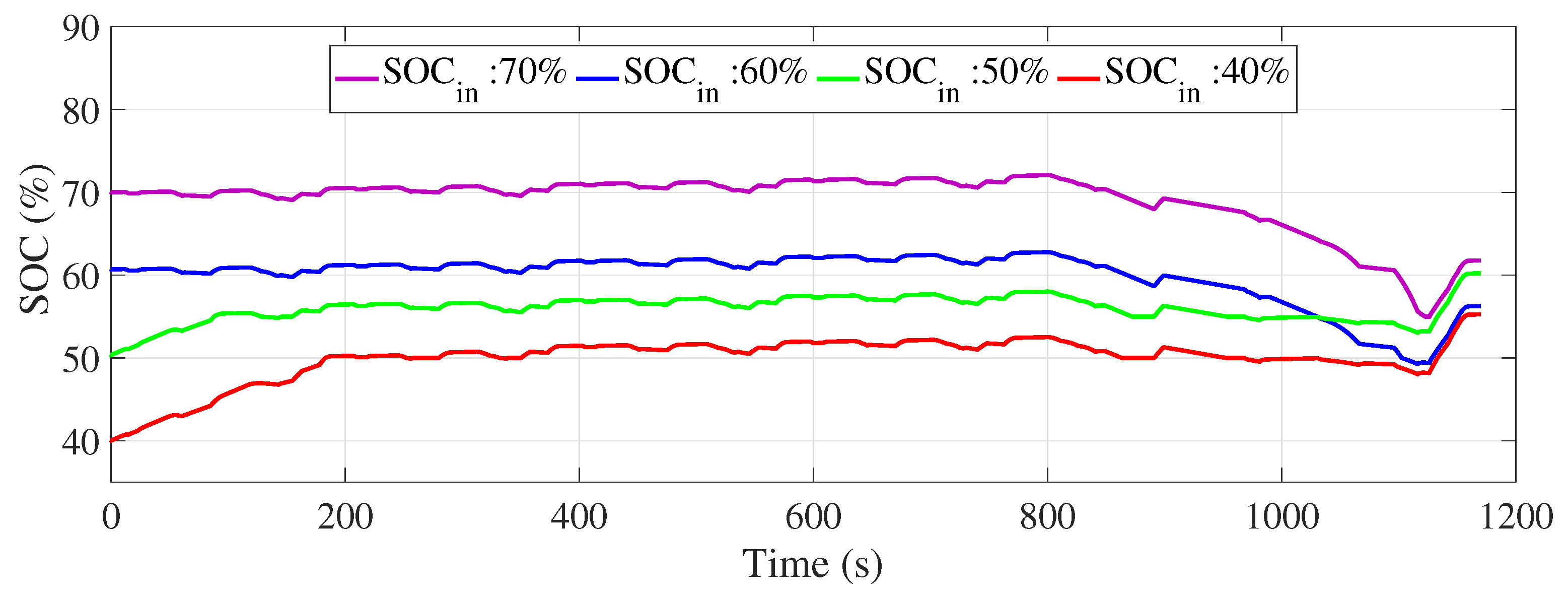
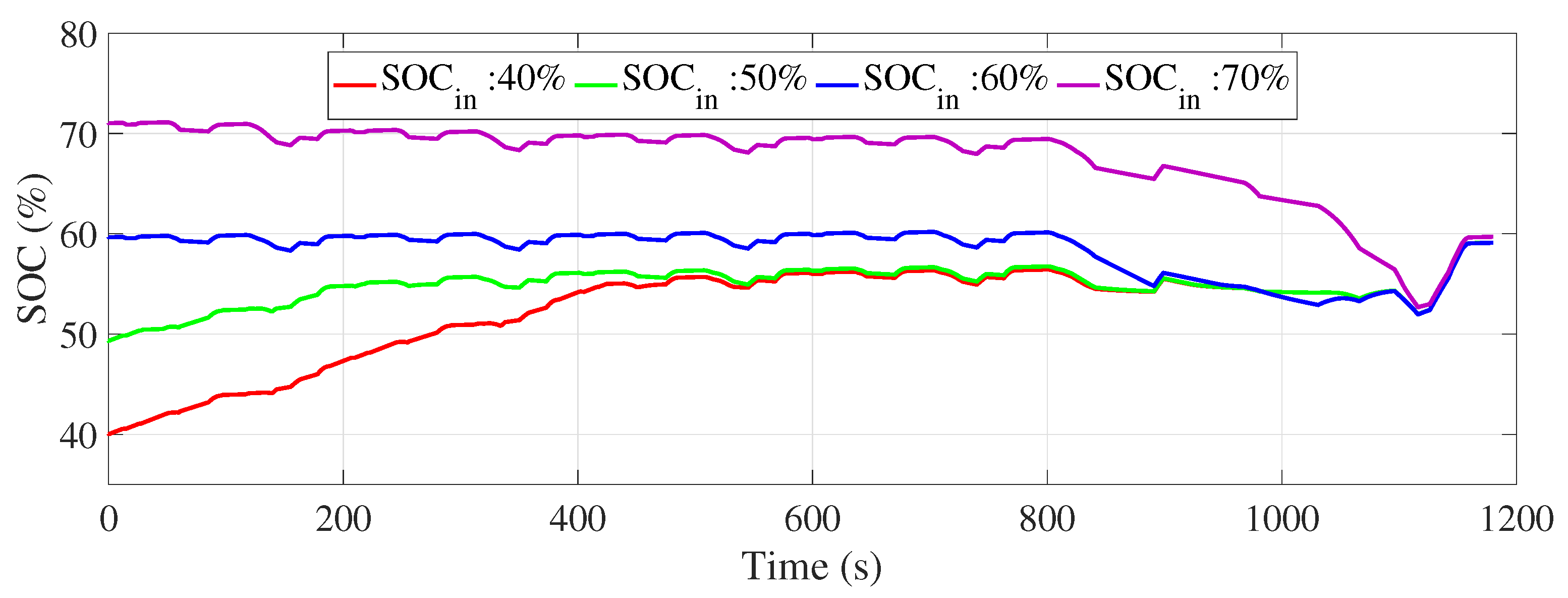
Figure 27 and Figure 28 show the evolution of the SOC for the UDDS and NEDC driving cycles, respectively, starting from different initial SOC values (40%, 50%, 60%, and 70%). These figures clearly demonstrate that the fuzzy logic energy management system effectively adjusts its energy behavior according to the initial SOC and systematically achieves the targeted SOC of 60% at the end of the cycles, whatever the initial value.

Simulations showed that fuzzy logic-based energy management effectively regulated the SOC to 60% at the end of the UDDS cycle when the initial SOC was 40%, 50%, or 60%. However, a small deviation (final SOC of 64%) was observed for an initial SOC of 70%, indicating the need for improvements to better manage high levels under dynamic urban conditions. In the NEDC cycle, on the other hand, the SOC systematically reached 60%, whatever its initial level, confirming the system’s effectiveness in more stable driving conditions.

5. Comparison and Evaluation of the Two Approaches

The evaluation of the two approaches developed, based on deterministic rules (DR) and fuzzy logic (FL), was based on several key criteria: hydrogen consumption, maintenance of the battery’s state of charge (SOC), and the ability to adapt to variable driving conditions, specifically in the UDDS and NEDC cycles. These two cycles presented different driving conditions: the UDDS cycle was used to simulate urban environments with frequent variations in power, while the NEDC cycle was considered more representative of extra-urban driving, with less frequent phases of acceleration and deceleration.

In both approaches, a crucial objective was that the battery’s state of charge should reach 60% at the end of every driving cycle. In addition, during the cycle, the state of charge had to always remain within a safe range of 40–80% to protect the battery from the damaging effects of deep discharge or overcharging.

Figure 29 and Figure 30 highlight the significant differences between the two strategies in adjusting the fuel cell’s reference power to meet the vehicle’s power demand.

For the UDDS driving cycle, the fuzzy logic (FL) strategy ensured smooth power transitions, reducing sudden variations and stress on the fuel cell, particularly in critical zones (Z1, Z2, Z3). In contrast, the deterministic rule-based (DR) strategy presented more rigid transitions, with sudden variations in power, resulting in higher hydrogen consumption and greater stress on the fuel cell.

For the NEDC driving cycle, characterized by more stable driving, the fuzzy logic (FL) strategy ensured progressive power transitions, optimizing energy efficiency and preserving the fuel cell. Adjustment in critical zones (Z1, Z2, Z3) ensured more controlled hydrogen consumption. In comparison, the deterministic rule-based (DR) strategy offered acceptable performance but remained less flexible, with more marked power peaks, impacting load management and hydrogen consumption.

Table 3. Performance comparison of FL and DR energy management strategies for UDDS and NEDC driving cycles.

Strategy	Cycle	Speed (km/h)	Dyn. FC	${\mathbf{SOC}}_{\mathit{min}}$	${\mathbf{SOC}}_{\mathit{moy}}$	${\mathbf{SOC}}_{\mathit{max}}$	${\mathbf{SOC}}_{\mathit{final}}$	H2 (g)	Rob.
Ref.			Yes	40	60	80	60	Min	Yes
DR	UDDS	0–91.2	No	54.44	59.32	62.4	62.36	62.49	No
	NEDC	0–120	No	49.26	59.21	62.77	56.25	61.30	No
FL	UDDS	0–91.2	Moderate	54.12	58.24	61.18	60.24	57.65	Yes
	NEDC	0–120	Moderate	51.95	57.79	60.18	59.10	68.42	Yes

presents an overall comparison of the performance of the two energy management strategies, FL and DR, for both the UDDS and NEDC driving cycles in terms of key criteria such as initial and final SOC, hydrogen consumption, quality of power transitions, and system reactivity.

The strategy based on fuzzy logic (FL) was more respectful of fuel cell dynamics, offering progressive power adjustments, while the strategy based on deterministic rules (DR) was more rigid and led to sudden variations that put more stress on components.

In regard to battery state-of-charge management, the FL strategy approached the 60% target at the end of cycles, with final state-of-charge values of 60.24% for the UDDS and 59.10% for the NEDC, thus extending battery lifetime. In comparison, the DR strategy showed a lower final state of charge in the NEDC cycle, at 56.25%, indicating that the battery had compensated for some of the energy required, thus reducing apparent hydrogen consumption. The target of 60% state of charge was chosen as a compromise between energy availability and preserving the health of the battery. Operating the battery within an intermediate SOC window helps to minimise degradation mechanisms such as lithium plating and electrolyte decomposition, which are more pronounced at the high and low SOC extremes. Maintaining the state of charge around that level reduces stress on the battery and extends its life, helping to improve SOH over a long period of use. This choice is aligned with industry practice for improving battery durability in hybrid systems.

Robustness was another strong point of the FL strategy, which adapted better to rapid variations in energy demand, making it better suited to dynamic urban environments. In summary, the FL strategy was characterized by better energy optimisation, reduced hydrogen consumption, and more respectful management of the SOC, while the DR strategy remained effective under stable conditions but was limited under variable driving conditions.

6. Conclusions

In this paper, we investigated the impact of deterministic and fuzzy logic energy management strategies on the performance of fuel cell hybrid electric vehicles (FCHEVs). By developing a detailed model of the hybrid powertrain—including the fuel cell, battery, and power converters—we evaluated how these strategies influenced energy distribution, fuel consumption, and system stability under standard driving cycles. Model predictive control (MPC) was implemented to regulate the boost converter, while a PI controller was used for the bidirectional converter, ensuring stable voltage regulation and efficient energy flow management.

The comparative analysis revealed that deterministic rule-based strategies, while simple and effective under stable conditions, lacked adaptability to rapid fluctuations in energy demand. As shown in Table 3, the deterministic rule (DR) approach maintained a higher final state of charge (SOC) of 62.36% for the UDDS cycle and 56.25% for the NEDC cycle, compared to 60.24% and 59.10% for the fuzzy logic (FL) approach, respectively. However, the deterministic strategy failed to dynamically adjust fuel cell power, resulting in sudden power variations and sub-optimal hydrogen consumption. In contrast, the fuzzy logic (FL) controller enabled smoother power transitions by avoiding sudden variations in the fuel cell’s reference power. This smoother behaviour reduced the number of start–stop cycles and helped to maintain operation in the fuel cell’s optimum efficiency range. As a result, transient losses and dynamic stresses on the fuel cell were minimised, leading to improved hydrogen economy. This was reflected in the UDDS cycle, where the FL strategy reduced hydrogen consumption to 57.65 g, compared with 62.49 g for the deterministic rule-based (DR) strategy.

In contrast, the fuzzy logic approach proved more flexible and better suited to variable driving conditions, generating a more progressive and smoother power reference. This adaptability was particularly evident in the NEDC cycle, where the FL strategy achieved a higher final SOC of 59.10% while also ensuring improved system robustness. However, despite its ability to provide smoother power transitions, fuzzy logic control remains constrained by the slow natural dynamics of the fuel cell, particularly due to the limitations imposed by components such as electrovalves and compressors.

These findings highlight the importance of advanced power management strategies for optimizing the performance of fuel cell hybrid electric vehicles (FCHEVs). In particular, hybrid control approaches that combine the advantages of fuzzy logic and frequency separation—while respecting the natural dynamics of the fuel cell—represent a promising future research direction. Although deterministic rule-based methods and fuzzy logic controllers are simpler to compute than optimisation-based strategies, fuzzy logic introduces additional computational steps (fuzzification, rule evaluation, defuzzification). Nevertheless, the fuzzy logic controller developed in this study was carefully designed with a limited number of inputs, membership functions, and rules (as shown in Table 2), ensuring its compatibility with standard automotive embedded control units (ECUs). Future work should therefore aim to validate these strategies through real-time implementation and experimental testing, including hardware-in-the-loop (HIL) simulations, in order to assess their practical feasibility and support their adoption in next-generation hybrid vehicles. Furthermore, the integration of artificial intelligence techniques—in particular reinforcement learning—offers a promising route for the development of adaptive energy management strategies.