Multi-Objective Optimal Design of 200 kW Permanent Magnet Synchronous Motor Based on NSGA-II

Abstract

Interior permanent magnet synchronous motors (IPMSMs) are widely applied as drive motors in electric vehicles because they have the advantages of high power density, high efficiency, and excellent dynamic performance. This paper introduces a framework for multi-objective optimization, tailored for the demands of V-Shaped IPMSMs, which involves high-dimensional variables. The framework is divided into three parts. Firstly, a proportional parametric finite element analysis (FEA) model for V-Shaped IPMSMs was established to reduce the probability of size interference among motor design parameters. Secondly, a surrogate model was trained using the design of experiments (DOE) approach and was utilized to substitute the FEA model. The accuracy of the surrogate model was then verified. Thirdly, the surrogate model was used as a fitness function, and a non-dominated sorting genetic algorithm II (NSGA-II) was employed as the optimization method to acquire the optimal goals rapidly. Based on the optimal design parameters, a prototype of the electrical motor was fabricated. Finally, the effectiveness of optimization was proven by experimental testing.

1. Introduction

The permanent magnet synchronous motor (PMSM) is a critical technology in electric vehicles, recognized for its high power density, efficiency, and superior dynamic performance. Research indicates that PMSMs offer strong overload capacity, fast response, and smaller volume, making them ideal for electric vehicle drive systems. When compared to surface-mounted permanent magnet synchronous motors, interior permanent magnet synchronous motors (IPMSMs) boast high reluctance torque and a wide range of constant power operation, achieved through flux-weakening techniques. Therefore, IPMSMs are widely applied as drive motors in electric vehicles [1,2].

In recent years, the field of motor optimization has seen significant advancements, with multi-objective optimization methods emerging as a key research focus to enhance the overall performance of electric motors. For instance, multi-objective optimization techniques are extensively applied in motor design to balance various objectives such as efficiency, cost, volume, and weight, as detailed in the motor design application of multi-objective optimization [3,4,5,6,7,8]. These methods enable designers to identify a set of optimal solutions that represent a trade-off among conflicting objectives, thereby improving the general performance of electrical motors. Junguo Cui et al. applied a combined DOE and Taguchi approach to optimize the design of a submersible PMSM, aiming to achieve peak efficiency and significantly reduce cogging torque [9]. Pin Lv et al. adopted an improved Multi-Objective Salp Swarm Optimization Algorithm (IMOSSA) and Spearman correlation analysis to weaken the torque ripple caused by cogging torque and increase the output torque of PMSMs [10]. Yinquan Yu et al. presented a hybrid multi-objective optimization scheme combining the Taguchi method and particle swarm optimization (PSO) algorithm; the motor’s output torque, torque ripple, and core losses were optimized [11]. Xu Wang et al. presented a radial–axial hybrid excitation machine with consequent poles for electric vehicles and optimized the torque output, flux-regulation ability, and torque ripple using the non-dominated sorting genetic algorithm II (NSGA II) [12].

Besides the optimization method, the choice of the mapping method between design properties and objectives is another key issue. Currently, there are three main methods. The first one is the finite element analysis (FEA) model [13]. FEA is a computational method that accurately models the relationships between design parameters and objectives. However, the FEA model requires substantial computational resources and execution time. The second one is an equivalent model based on several electromagnetic field theory models such as the subdomain field model [14], the equivalent magnetic circuit model [15], and the equivalent magnetic network model [16]. Although equivalent models can achieve objectives swiftly, their calculation accuracy falls short of that provided by FEA. Furthermore, when the topology undergoes changes, the equivalent model requires reconstruction. The third one is the surrogate model, which is based on data-driven approaches like response surface methodology (RSM) [17], the Kriging surrogate model [18], artificial neural networks (ANNs) [19], and so on. Although the surrogate model requires a lot of input data in the early stage, the results can be obtained quickly after the model is established. Focusing on non-linear systems, ANNs are the most beneficial among them.

From the studies in Refs. [9,10,11,12,13,14,15,16,17,18,19], most optimization research has always aimed at improving existing electrical motors. The optimization variable dimensions were limited and optimization design was infrequently initiated at the onset of the design process. This paper introduces a multi-objective optimization framework tailored for V-Shaped IPMSM demands, which involve high-dimensional variables. Initially, a proportional parametric FEA model tailored for V-Shaped IPMSMs was developed. This FEA model boasts advantages stemming from its high-dimensional variables, particularly focusing on the aspect of design variables; it has strong versatility and can effectively reduce the possibility of size interference between design variables. The relations between design variables and objectives were confirmed by a design of experiments (DOE) approach, and the sensitivities of the design variables to the objectives were analyzed. Then, a back-propagation (BP) neural network was trained as a surrogate model using DOE results to replace the FEA model. Focusing on a specific demand of V-Shaped IPMSMs, optimal design parameters were acquired by combining the surrogate model and NSGA-II. Finally, a prototype of the electrical motor was fabricated, and the results of the conducted experiments confirmed the effectiveness of the optimization framework.

2. Topology and Design Specifications of Parametric Model

FEA methods can address the non-linearity of the magnetization process in the electrical motor design process, which has multiple variables and strong coupling properties. Therefore, it is necessary to establish a parametric FEA model to accurately evaluate output performance under different design parameters. This is the basis of the subsequent DOE.

The structure of a V-Shaped IPMSM is shown in Figure 1. In order to reduce the probability of size interference between electrical motor design parameters, a proportional parametric model is established. The design parameters of the proportional parametric model are shown in

Table 1. Design parameter specification of a V-Shaped IPMSM.

Design Parameters	Defining Formula
kd	Dsi/Dso
kt	bt/(π·Dsi/Q)
ky	by/[(1 − kd)·Dso/2]
khm	hm/g
αp	θp/(360°/2p)
kwm	Wm/[(αp·Dro·π)/2p]
Vm	π·(Dso/2)2·Ls

. D_so is the stator outer diameter, D_si is the stator inner diameter, D_ro is the rotor outer diameter, Q is the slot number, p represents the pole pairs, g is the air gap length, b_t is the tooth width of the stator, b_y is the yoke height of the stator, h_m is the magnet thickness, W_m is the magnet width, θ_p is the pole arc angle, and L_s is the iron core length.

In addition, the excitations in armature windings are assigned as in Equation (1).

$$\left\{\begin{array}{l}{i}_{\mathrm{A}}(t)=\sqrt{2}{F}_{\mathrm{s}}\sin ({\omega }_{\mathrm{elc}}t+\gamma )\\ i_{\mathrm{B}}(t)=\sqrt{2}{F}_{\mathrm{s}}\sin ({\omega }_{\mathrm{elc}}t-{\displaystyle \frac{2}{3}}\pi +\gamma )\\ i_{\mathrm{C}}(t)=\sqrt{2}{F}_{\mathrm{s}}\sin ({\omega }_{\mathrm{elc}}t+{\displaystyle \frac{2}{3}}\pi +\gamma )\end{array}\right.$$

(1)

where F_s represents the magnetomotive force expressed in Equation (2), ω_elc represents the electrical angular frequency, and γ is the primary phase angle.

$$F_s={\displaystyle \frac{I_{\mathrm{rms}}·N_{\mathrm{s}}·Q}{m·a}}$$

(2)

where I_rms is the root-mean-square value of the phase current, N_s is the conductor number per slot, m is the phase number, and a is the number of parallel branches for armature winding.

3. Surrogate Model Design

3.1. Design of Experiment

DOE technology is the key to constructing the surrogate model. The principle is to obtain the data characteristics in the global search space by selecting more typical design points. A reasonable experimental design can improve the sampling efficiency and the accuracy of the surrogate model.

The Latin hypercube sampling (LHS) method and the orthogonal sampling method are the most common methods used in surrogate models for electric motors. The orthogonal sampling experiment method is also called the Taguchi method, which can be used to obtain more useful information with fewer experiments. For high-dimensional design parameters, the effect of the orthogonal sampling method for decreasing experiment numbers is not useful, and the orthogonal sampling method cannot produce an arbitrary number of design points. However, the basis of LHS is a full stratification of the sampled distribution with a random selection inside each stratum. According to the value range of the influence factors of the experiment, the probability distribution function of the experiment factors is divided into non-overlapping sub-regions, and finally, independent equal-probability sampling is carried out at each sub-interval. Compared with the orthogonal sampling method, the number of experiments can be manually controlled by LHS [20].

In this paper, the LHS method is employed as the sample method. The design parameters’ variation range and constraint value are shown in

Table 2. Design parameters’ variation range and constraint value.

Properties	Parameters	Value
Variation	αp	[0.5~0.8]
	Dso	[150~300] mm
	Fs	[1920~19,200] A
	γ	[0~90]°
	kd	[0.5~0.8]
	khm	[4~8]
	kt	[0.5~0.8]
	kwm	[1~2]
	ky	[0.15~0.4]
	p	[3~10]
Constraint	Q	12p
	g	0.8 mm
	Vm	4.249 × 10−3 m3
	Ns	1
	m	3
	a	1

. The results of copper loss, core loss, and average torque with a speed of 10,000 r/min are used as responses. They directly reflect the output characteristics of the electrical motor.

Copper loss can be calculated using Equations (3) and (4) when the design parameters are fixed. ρ_Cu is the electrical resistivity of copper, l_half is the half-turn length of the armature coil, and A_c is the area of the conductor.

$$P_{C\mathrm{u}}=m·I_{rms}^2·R_{\mathrm{ph}}$$

(3)

$$R_{\mathrm{ph}}={\rho }_{\mathrm{Cu}}·{\displaystyle \frac{N_{\mathrm{s}}·Q·l_{\mathrm{half}}}{m·a·A_{\mathrm{c}}}}$$

(4)

The number of samples is set to 4000, and the number of effective samples is 2502. The results of LHS are shown in

Table 3. Results of LHS.

	αp	Dso/mm	Fs/A	γ/°	kd	khm	kt	kwm	ky	p	PCu/W	PFe/W	Tavg/Nm
1	0.542	169.481	4099.440	20.531	0.705	5.097	0.723	1.149	0.387	4	2092.022	2820.707	86.733
2	0.665	289.144	11,210.160	41.254	0.790	7.103	0.730	1.682	0.207	6	3266.113	7494.592	135.221
3	0.673	217.406	5982.960	47.869	0.773	5.056	0.542	1.745	0.244	4	1421.681	3963.566	69.326
4	0.610	183.244	16,376.880	16.144	0.594	4.128	0.750	1.418	0.207	3	13,232.336	3074.359	141.019
5	0.602	283.444	7214.160	47.734	0.544	6.969	0.621	1.407	0.229	4	532.788	3311.562	84.015
…	…	…	…	…	…	…	…	…	…	…	…	…	…
2498	0.695	298.556	2094.960	50.209	0.799	6.421	0.614	1.661	0.262	4	115.334	3255.099	14.495
2499	0.531	221.006	14,372.400	64.766	0.729	5.912	0.532	1.565	0.328	8	5972.671	6004.758	169.600
2500	0.625	269.831	17,560.560	14.861	0.636	6.942	0.742	1.404	0.383	10	6114.775	14,968.234	213.809
2501	0.698	181.031	12,735.120	68.861	0.759	5.473	0.701	1.528	0.366	7	17,986.196	4015.358	174.326
2502	0.628	258.169	8475.600	17.381	0.748	7.021	0.586	1.315	0.200	10	1177.983	9232.935	133.253

. P_Fe is core loss, and T_avg is average torque; they are calculated by FEA.

3.2. Sensitivity Analysis

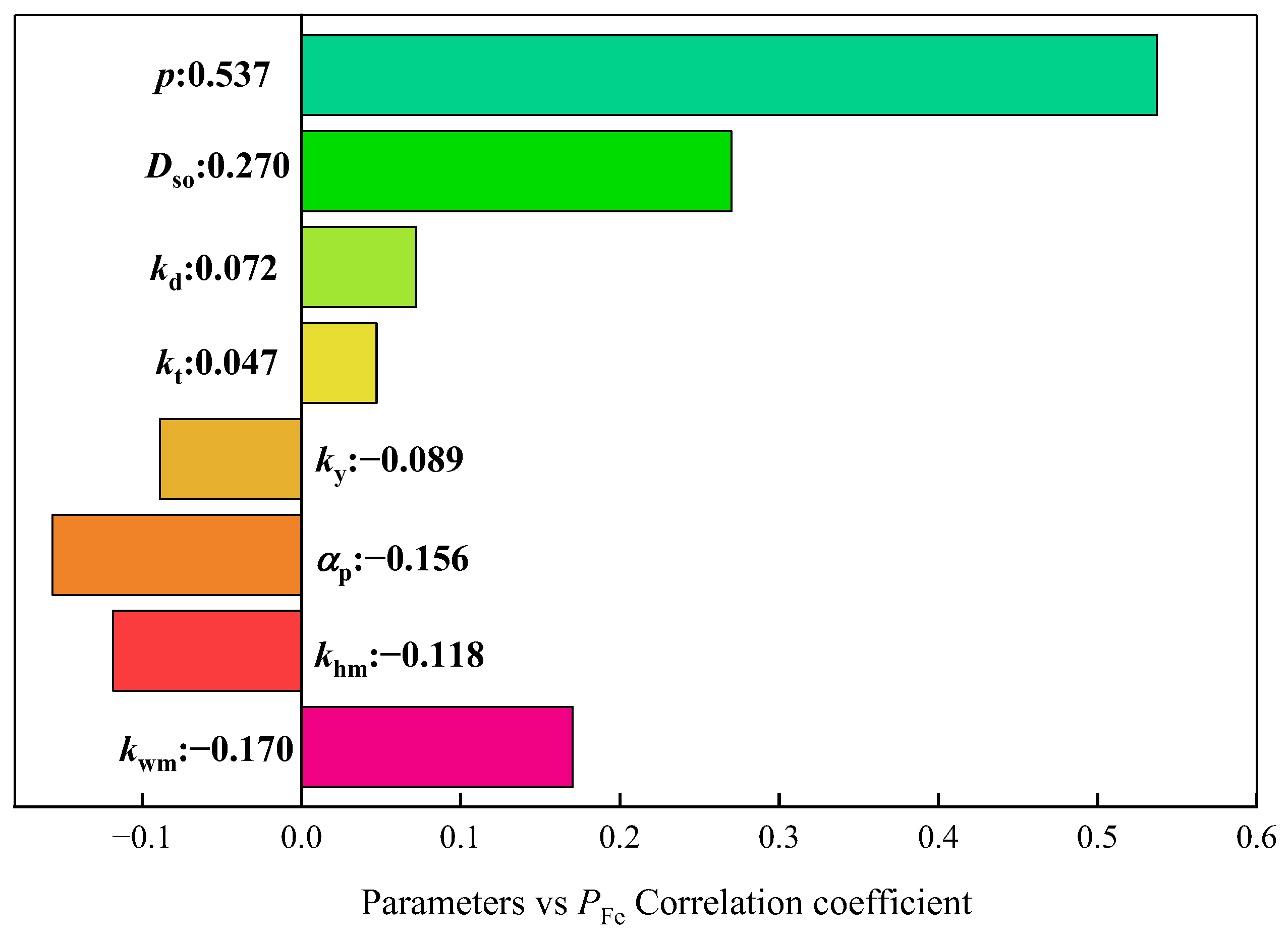
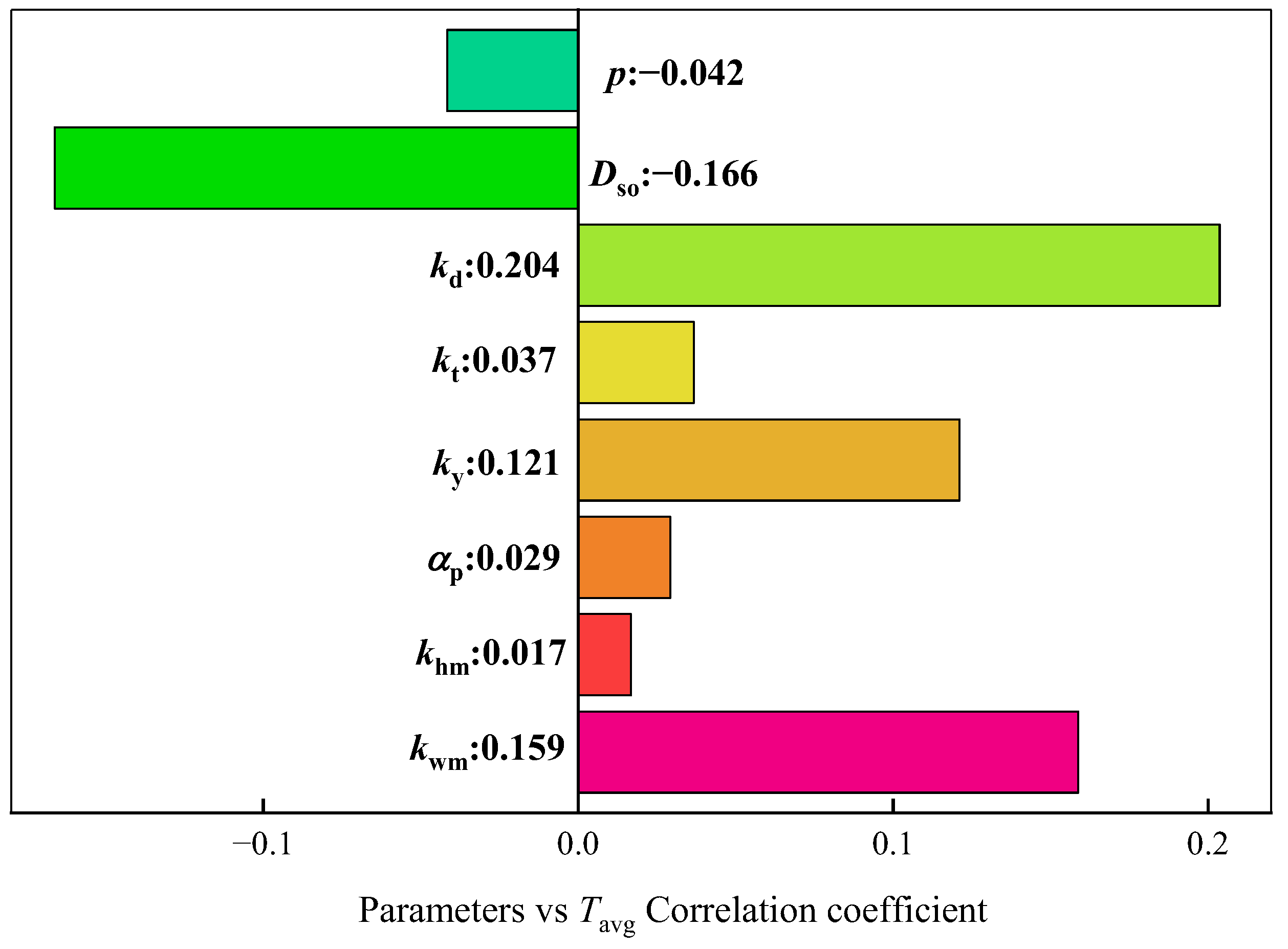
Obviously, the excitation parameters must have a strong correlation with the response results. Greater attention is given to the relationship between structure parameters and response results. Therefore, the Pearson correlation analysis is used to analyze the sensitivity between structure parameters and response results. Figure 2 shows the sensitivity between the structure parameters and P_Cu, Figure 3 shows the sensitivity between the structure parameters and P_Fe, and Figure 4 shows the sensitivity between the structure parameters and T_avg. The plus sign represents a parameter that has a positive influence on the response result, and the minus sign represents a parameter that has a negative influence on the response result. The absolute value of the coefficient represents the strength of the correlation.

The above analysis shows that the absolute correlation coefficients of p, D_so, k_d, k_t,, and k_y are above 0.03 for all response results; they exhibit strong sensitivity to all response outcomes. While α_p and k_hm primarily affect P_Fe and display lower sensitivity to the other two response results, their influences on P_Fe and T_avg are in opposite directions. k_wm has a greater impact on P_Fe and T_avg, with the least effect on P_Cu. It is impossible to accurately obtain three response results at the same time when any design parameter is missing. Therefore, to describe the loss characteristics and output torque characteristics of the motor accurately, all design parameters should participate in the surrogate model construction.

3.3. ANN Training

The BP neural network stands as one of the most prevalent algorithms within ANNs, offering particular advantages in non-linear systems. A BP neural network is used to establish the surrogate model in this paper. A BP neural network comprises one input layer, multiple hidden layers, and one output layer. To introduce the principle of the BP neural network, a simple model is shown in Figure 5. The simple model has an input layer with three input parameters, a hidden layer with three neurons, and an output layer with two output objectives [21].

x₁~x₃ are variables of the input layer; w_i11~w_i33 represent the weight factors from the input layer to the hidden layer; z₁₂, z₂₂, and z₃₂ represent the weighted input variables of the hidden layer; b₁₂, b₂₃, and b₃₂ are the biases of the hidden layer; a₁₂, a₂₂, and a₃₂ represent the output variables of the hidden layer; w_h11~w_h32 represent the weight factors from the hidden layer to the output layer; z₁₃ and z₂₃ represent the weighted input variables of the output layer; b₁₃ and b₂₃ are the biases of the output layer; and y₁ and y₂ are output objectives.

The mathematical relationships of the parameters above are expressed as Equations (5)–(8). The s function is an activation function, as shown in Equation (9).

$$\left[\begin{array}{l}{z}_{12}\\ z_{22}\\ z_{32}\end{array}\right]=\left[\begin{array}{ccc}{w}_{i11}& w_{i21}& w_{i31}\\ w_{i12}& w_{i22}& w_{i32}\\ w_{i13}& w_{i23}& w_{i33}\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\\ x_3\end{array}\right]+\left[\begin{array}{l}{b}_{12}\\ b_{22}\\ b_{32}\end{array}\right]$$

(5)

$$\left\{\begin{array}{l}{a}_{12}=s(z_{12})\\ a_{22}=s(z_{22})\\ a_{23}=s(z_{23})\end{array}\right.$$

(6)

$$\left[\begin{array}{l}{z}_{13}\\ z_{23}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{l}{w}_{h11}\\ w_{h12}\end{array}& \begin{array}{l}{w}_{h21}\\ w_{h22}\end{array}& \begin{array}{l}{w}_{h31}\\ w_{h32}\end{array}\end{array}\right]\left[\begin{array}{l}{a}_{12}\\ a_{22}\\ a_{32}\end{array}\right]+\left[\begin{array}{l}{b}_{13}\\ b_{23}\end{array}\right]$$

(7)

$$\left\{\begin{array}{l}{y}_1=s(z_{13})\\ y_2=s(z_{23})\end{array}\right.$$

(8)

$$s(x)={\displaystyle \frac{1}{1+{\mathrm{e}}^{-x}}}$$

(9)

P_Fe and T_avg are trained by BP, respectively, in this paper. Based on the experience and sample data size, the designed BP neural network has one input layer, three hidden layers, and one output layer. The input layer contains all of the variation parameters shown in Table 2. The first hidden layer has 40 neurons, the second hidden layer has 25 neurons, and the third hidden layer has 20 neurons. Of the samples in Table 3, 70% were used to train the BP neural network, 15% were used to verify the effectiveness of the BP neural network, and 15% were used to test the BP neural network. Before BP neural network training, the input data and output data were all normalized. The BP neural network was trained in MATLAB R2021a, and Bayesian Regularization was adopted as the training algorithm.

Finally, the mean squared error (MSE) between the results predicted by the trained BP neural network and from the samples of P_Fe is 7.3662 × 10⁻⁵, while the MSE between the results predicted by the trained BP neural network and from the samples of T_avg is 1.8443 × 10⁻⁵. To validate the effectiveness of the trained BP neural network, 10 sets of data from the test set were selected randomly. The T_avg comparison results between the BP neural network and FEA are shown in

Table 4. T_avg comparison results between BP neural network and FEA.

	αp	Dso/mm	Fs/A	γ/°	kd	khm	kt	kwm	ky	p	Tavg/Nm (BP)	Tavg/Nm (FEA)	Difference
327	0.703	266.981	11,724.240	35.449	0.738	7.749	0.641	1.377	0.299	5	193.287	192.238	0.52%
486	0.609	260.081	4665.360	29.126	0.602	7.816	0.699	1.178	0.267	5	64.270	65.803	2.33%
817	0.707	200.944	7045.680	19.001	0.617	4.016	0.608	1.346	0.398	6	121.386	121.511	0.10%
984	0.709	291.694	10,052.400	65.846	0.571	4.566	0.782	1.122	0.361	9	55.492	54.607	1.62%
1245	0.613	189.769	18,739.920	78.221	0.680	4.356	0.566	1.413	0.223	9	92.909	97.172	4.39%
1362	0.588	242.194	8056.560	9.259	0.621	6.613	0.525	1.329	0.235	10	87.769	86.348	1.65%
1488	0.538	276.206	8505.840	30.971	0.559	5.308	0.722	1.616	0.246	7	102.262	102.931	0.65%
1805	0.758	198.056	17,055.120	8.134	0.534	4.024	0.599	1.058	0.234	3	127.589	128.807	0.95%
1925	0.518	284.419	15,076.560	73.271	0.550	4.716	0.761	1.937	0.224	8	70.250	72.083	2.54%
2402	0.614	269.681	1956.720	68.434	0.668	4.529	0.738	1.970	0.325	8	13.814	14.120	2.17%

. The P_Fe comparison results between the BP neural network and FEA are shown in

Table 5. P_Fe comparison results between BP neural network and FEA.

	αp	Dso/mm	Fs/A	γ/°	kd	khm	kt	kwm	ky	p	PFe/W (BP)	PFe/W (FEA)	Difference
327	0.703	266.981	11,724.240	35.449	0.738	7.749	0.641	1.377	0.299	5	5057.593	5081.255	−0.47%
486	0.609	260.081	4665.360	29.126	0.602	7.816	0.699	1.178	0.267	5	3386.454	3373.200	0.39%
817	0.707	200.944	7045.680	19.001	0.617	4.016	0.608	1.346	0.398	6	3974.767	3984.775	−0.25%
984	0.709	291.694	10,052.400	65.846	0.571	4.566	0.782	1.122	0.361	9	4234.767	4222.164	0.30%
1245	0.613	189.769	18,739.920	78.221	0.680	4.356	0.566	1.413	0.223	9	6572.774	6471.177	1.57%
1362	0.588	242.194	8056.560	9.259	0.621	6.613	0.525	1.329	0.235	10	8162.633	8159.807	0.03%
1488	0.538	276.206	8505.840	30.971	0.559	5.308	0.722	1.616	0.246	7	6519.608	6492.925	0.41%
1805	0.758	198.056	17,055.120	8.134	0.534	4.024	0.599	1.058	0.234	3	2979.354	2976.806	0.09%
1925	0.518	284.419	15,076.560	73.271	0.550	4.716	0.761	1.937	0.224	8	8080.939	8057.535	0.29%
2402	0.614	269.681	1956.720	68.434	0.668	4.529	0.738	1.970	0.325	8	8139.650	8138.040	0.02%

. The order number in the first column of Table 4 and Table 5 is the same as the order number in Table 3. In Table 4, all the differences are less than 5%. In Table 5, all the differences are less than 1%, except for a single point with a difference of 1.57%. From the value of MSE, the overall accuracy of the BP neural network is very high, but there may still be relatively high errors at individual points.

4. Optimization Design

A specific electrical motor design requirement is shown in

Table 6. Specific electrical motor requirements.

Properties	Values
Rated bus voltage	800 V
Rated power	200 kW
Rated torque	191 Nm
Rated speed	10,000 r/min
Coolant method	Water cooling
Coolant temperature	25 °C
Coolant flow	10 L/min

. The variation range of the design parameters and constraint values is presented in Table 2. The objectives are to optimize the highest efficiency of the electrical motor and achieve the lowest temperature of the armature winding under rated working conditions.

Focusing on the requirements above, the surrogate model trained by BP was used instead of FEA to predict P_Fe and T_avg. P_Cu is calculated by Equations (3) and (4). The maximum temperature of armature winding is calculated by the thermal circuit method using MotorCAD based on values of P_Fe and P_Cu, and the efficiency is calculated using Equations (10) and (11). n is the speed of the electrical motor.

$$\eta ={\displaystyle \frac{P_{\mathrm{mec}}}{P_{\mathrm{mec}}+P_{\mathrm{Cu}}+P_{\mathrm{Fe}}}}$$

(10)

$$P_{\mathrm{mec}}={\displaystyle \frac{T_{\mathrm{avg}}·n}{9.55}}$$

(11)

NSGA-II is used as the multi-objective optimization method in this paper, which is a fast non-dominated sorting procedure, an elitist strategy, a parameterless approach, and a simple yet efficient constraint-handling method [22]. The objective function is defined by Equations (12) and (13), where T_w is the temperature of the armature winding.

$$\mathrm{Objective}:\left\{\max (\eta ),\min (T_{\mathrm{w}})\right\}$$

(12)

$$\mathrm{Constraint}:T_{\mathrm{avg}}\ge 191$$

(13)

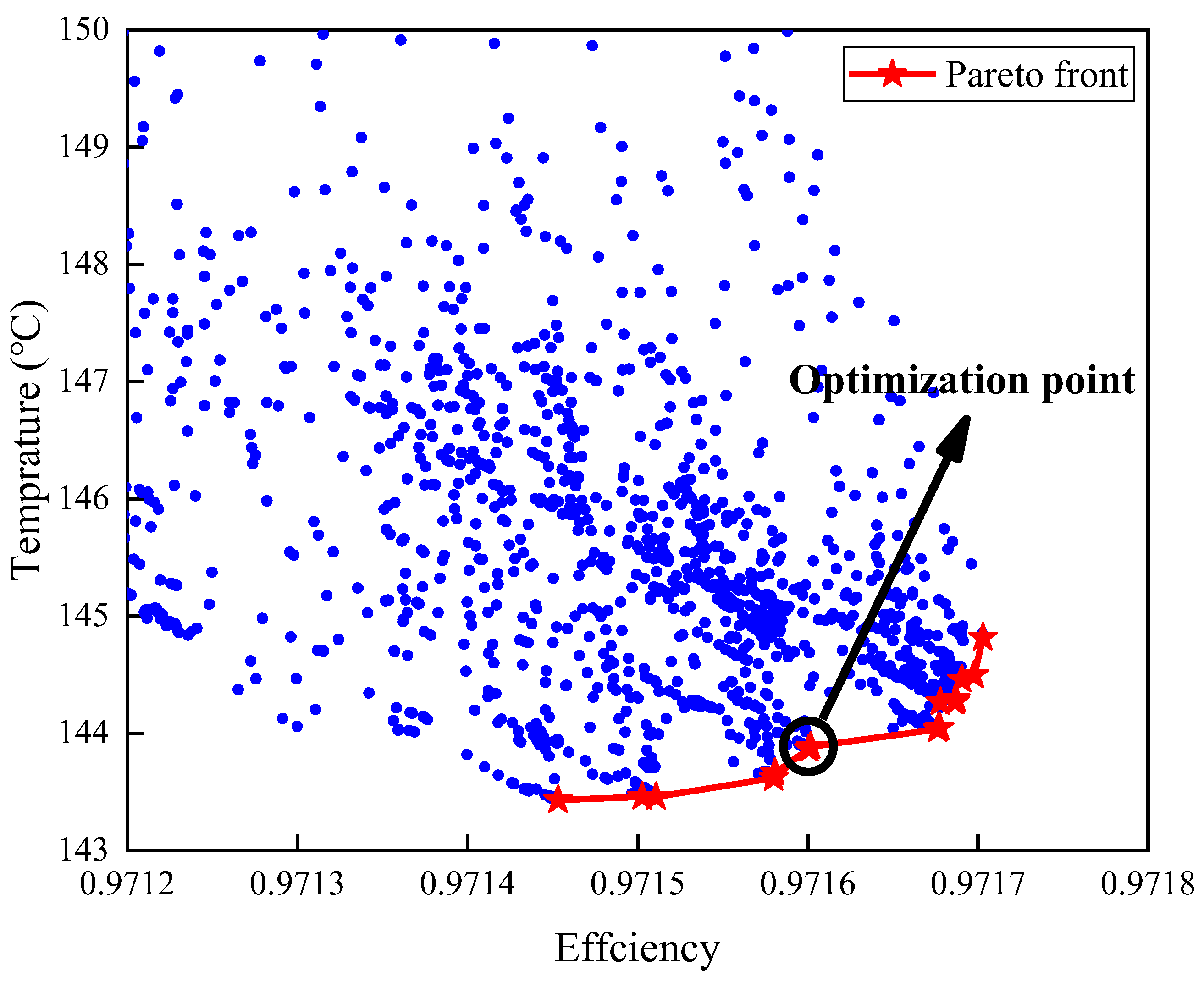
The optimization results are depicted in Figure 6, where the red line with stars represents the Pareto front. To trade off the efficiency of the electrical motor and temperature of armature winding, the optimal result should be selected from the middle position of the Pareto frontier. The point indicated with the arrow is selected as the final optimization result.

The parameters of the final optimization result point are shown in

Table 7. The parameters of the final optimization result point.

Properties	Parameters	Value
Variation	αp	0.6713
	Dso	175.55 mm
	Fs	7548 A
	γ	25°
	kd	0.6286
	khm	6.8625
	kt	0.6715
	kwm	1.9687
	ky	0.2929
	p	4

. The results of the surrogate model and FEA are compared in

Table 8. Result comparison of the surrogate model and FEA.

	Surrogate Model	FEA	Difference
Tavg	191.9	191.5	0.21%
η	0.9716	0.9709	7 × 10−4
Tw	143.8	153.4	6.26%

.

The parameters of the final optimization result point are determined from the sample data in Table 3. Although the surrogate model has high accuracy compared with sample data, a difference is inevitable when predicting points using sample data with a surrogate model. The results of the surrogate model for T_avg and η are nearly equal to those obtained by FEA, and the difference in T_w is less than 10%. Thus, the validity of the surrogate model is proven again.

5. Results of Experiment

A prototype of an electrical motor is fabricated according to the optimization results. Photos of the electrical motor are shown in Figure 7.

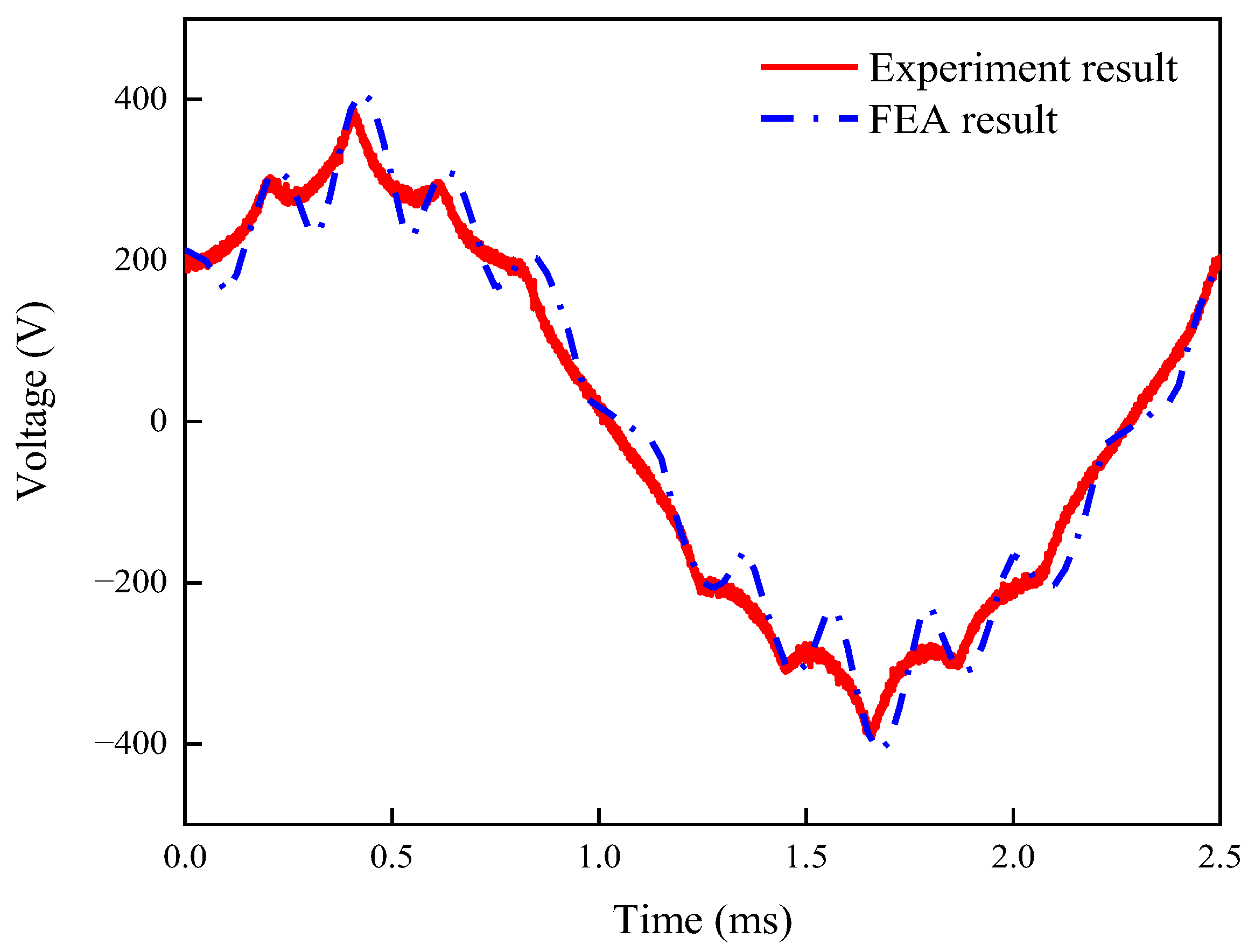
A comparison of no-load back-EMF at 6000 r/min between the experimental and FEA results is shown in Figure 8. The root-mean-square value (RMS) of the experimental model is 230.29 V, and the RMS of FEA is 229.68 V. The error between them is 0.27%.

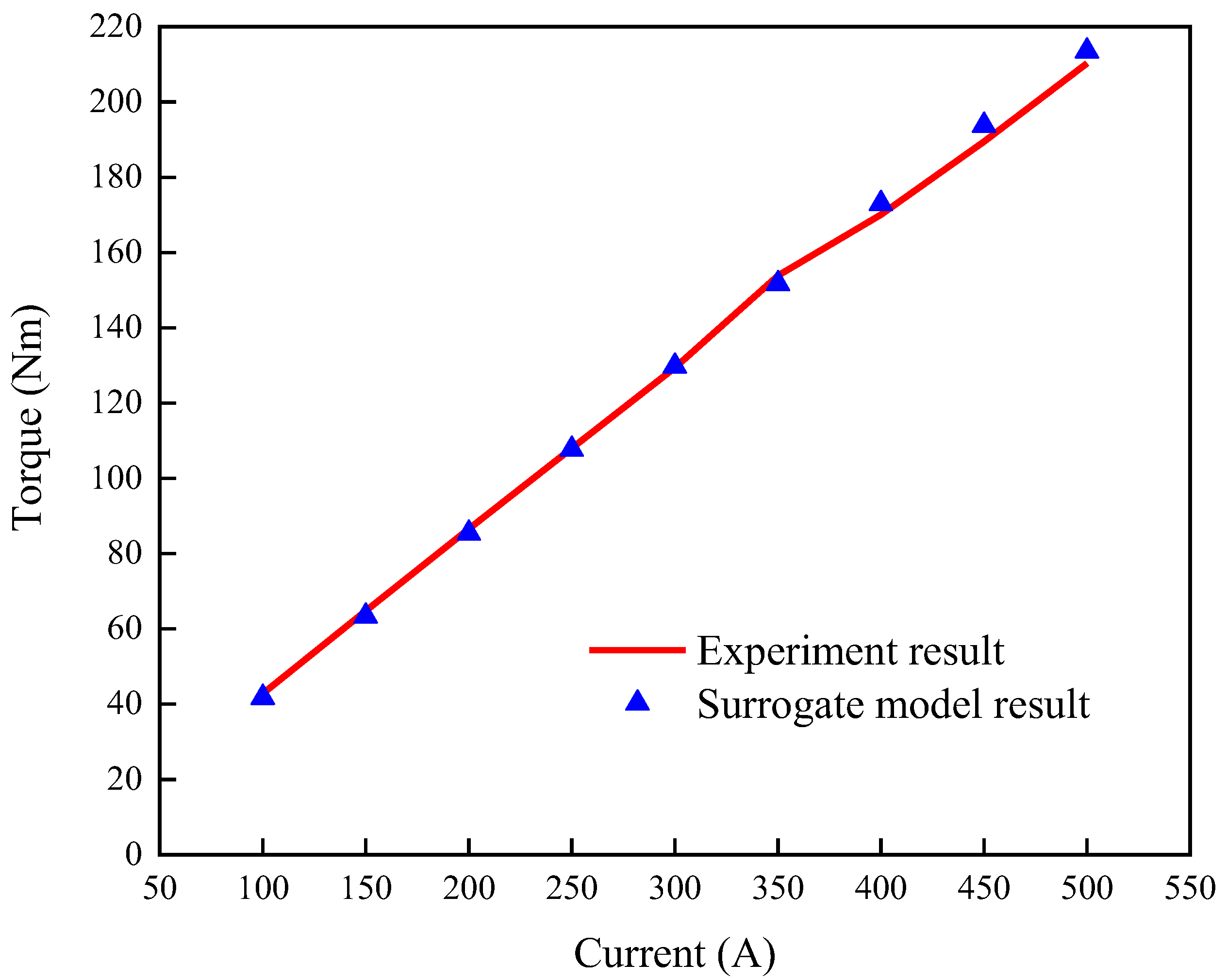
The average torque versus amplitude currents of the experimental and surrogate models are compared in Figure 9. The rated torque appears at 450 A. The average torque of the experimental model is 189.5 Nm, and the average torque of the surrogate model is 193.8 Nm. The error between them is 2.27%.

Two load tests were conducted. The first test’s load condition was set to 500 r/min, and the amplitude of the phase current was set to 300 A. The thermal test time was set as 1800 s. The three-phase current waveforms are shown in Figure 10a, and the maximum temperatures of the experiment, acquired by the thermal circuit method using MotorCAD, are compared in Figure 10b. The temperature curves stabilize around 600 s. The final temperature of the experiment is 60.9 °C, while the temperature calculated by the thermal circuit is 60.0 °C, resulting in an error of 1.5%.

The second test’s load condition was set to 6000 r/min, and the amplitude of the phase current was set as 450 A. The thermal test time was set as 1800 s. The three-phase current waveforms are shown in Figure 11a, and the maximum temperatures obtained from the experiment and the thermal circuit method using MotorCAD are compared in Figure 11b. The final temperature of the experiment is 119.2 °C, while the final temperature calculated by the thermal circuit is 116.0 °C, resulting in an error of 2.76%.

Based on the analysis of the existing test results, the simulation results are consistent with the test results. Therefore, it can be inferred that the optimization results are reliable.

6. Conclusions

This paper introduces a multi-objective optimization framework tailored for the demands of V-Shaped IPMSMs, which involves high-dimensional variables. This optimization framework offers robust support for the selection of design parameters during the initial design phase of an electrical motor. The optimization framework is divided into three parts.

The first part involves the establishment of a proportional parametric FEA model for V-Shaped IPMSMs. This parametric model incorporates 10 design parameters, comprising 8 structural design parameters and 2 excitation parameters. The proposed model effectively reduces the likelihood of interference among motor design parameters, thereby enhancing the precision and efficiency of the design process.

The second part involves training a BP neural network as a surrogate model, using results from the DOE to replace the FEA model. When the design parameters are fixed, P_Cu can be calculated directly; P_Fe and T_avg can be obtained through FEA. Since P_Cu, P_Fe, and T_avg directly reflect the output characteristics of the electrical motor, they are selected as the objectives for the surrogate model, providing greater flexibility in subsequent analyses. Based on the sensitivity analysis, the surrogate model, which incorporates all proposed parameters, accurately describes the loss characteristics and output torque characteristics of the electrical motor. Finally, the MSE between the predictions of the trained BP neural network and the P_Fe samples is 7.3662 × 10⁻⁵, while the MSE between the predicted results and the T_avg samples is 1.8443 × 10⁻⁵. These results validate the effectiveness and accuracy of the trained BP neural network model.

The third part involves optimization design, specifically addressing a particular electrical motor design requirement. The surrogate model serves as the fitness function, while NSGA-II is employed as the optimization method. The objectives are to maximize η and minimize T_w under rated working conditions. Since η and T_w are indirectly determined by P_Cu, P_Fe, and T_avg, these parameters play a critical role in the optimization process. The optimal design parameters have been identified, and the comparison results between the surrogate model and FEA validate the efficacy of the optimization.

After the optimization process, a prototype of the electrical motor was fabricated. The simulation results exhibit strong consistency with the test results, thereby validating the reliability of the optimization outcomes.