Abstract
High-frequency (HF) injection is a widely used technique for low-speed implementation of position sensorless permanent magnet synchronous motor control. A key component of this technique is the tracking loop control system, which extracts rotor position error and utilizes proportional–integral regulation as a position observer for estimating the rotor position. Generally, this process relies on band-pass filters (BPFs) and low-pass filters (LPFs) to modulate signals in the quadrature current to obtain rotor position error information. However, limitations in filter accuracy and dynamic response lead to prolonged convergence times and timing inconsistencies in the estimation process, which affects real-time motor control performance. To address these issues, this study proposes an exponential moving average (EMA)-based scheme for rotor position error extraction, offering a rapid response under dynamic conditions such as direction reversals, step speed changes, and varying loads. EMA is used to pass the original rotor position information carried by the quadrature current signal, which contains HF components, with a specified smoothing factor. Then, after the synchronous demodulation process, EMA is employed to extract rotor position error information for the position observer to estimate the rotor position. Due to its computational simplicity and fast response in handling dynamic conditions, the proposed method can serve as an alternative to BPF and LPF, which are commonly used for rotor position information extraction, while also reducing computational burden and improving performance. Finally, to demonstrate its feasibility and effectiveness in improving rotor position estimation accuracy, the proposed system is experimentally validated by comparing it with a conventional system.
1. Introduction
The permanent magnet synchronous motor (PMSM) has gained widespread attention as a reliable electric drive system. The motor offers advantages such as high power density, high efficiency, and low maintenance, making it a preferred alternative in various sectors, including home appliances, medical equipment, transportation, robotics, and aviation [1]. The electric drive system comprises electrical motors and their controllers, which directly affect the dynamic performance of motor drive applications [2]. To achieve high-performance PMSM drive systems, the vector control method is commonly applied. This method requires precise rotor position and motor speed information [3]. Typically, mechanical sensors such as encoders are used to detect the rotor position. However, the use of encoders not only increases volume, wiring complexity, and production costs but also reduces system reliability. One of the most critical challenges of incremental encoder-based position detection occurs during start-up conditions and at low speeds. Under these conditions, mechanical noise and movement limitations influence the incremental sampling rate, leading to inaccurate rotor position information. Therefore, research on position sensorless control has attracted significant attention in recent decades [4,5].
In general, position sensorless control methods can be categorized into two main approaches: fundamental model-based observers and magnetic saliency-based methods. The first approach, fundamental model-based observers, is employed by estimating the motor’s Back-EMF using techniques such as the Sliding Mode Observer (SMO) [6,7], Extended Kalman Filter (EKF) [8,9], and others. This method performs well when the motor operates at medium to high speeds, where the Back-EMF can be clearly observed to obtain rotor position information [10]. However, at low speeds, the Back-EMF becomes too small due to the voltage drop across the stator resistance, making it difficult to observe. Consequently, this method may not perform well and can even fail [11]. To enable sensorless PMSM control over an extended speed range, adaptive filters have been introduced in the sensorless control strategy. However, these filters face an inherent trade-off between low-frequency attenuation and passband bandwidth. A wider bandwidth ensures fast dynamic response, but it compromises low-frequency attenuation, allowing DC components to leak through and cause estimation offsets [12]. The second approach, the magnetic saliency-based method, utilizes the high-frequency (HF) injection technique, which has been developed for motor operation from standstill to low speeds [13]. Based on the injection technique used, this method can be classified into two types: rotating injection [14,15] and pulsating injection [16,17]. Due to its higher accuracy in rotor position estimation and lower sensitivity to inverter nonlinearity, HF pulsating injection is preferred over HF rotating injection [18]. In its implementation, the HF pulsating injection technique consists of three main stages to obtain rotor position information: HF voltage injection, position error signal extraction, and rotor position estimation [19]. The injected HF voltage is usually fixed to establish the estimated rotating reference frame, while the modulated signal is employed to extract the position error signal, which contains essential information related to the difference between the actual and estimated rotor positions. Furthermore, rotor position estimation is performed through a proportional–integral (PI) control loop to obtain accurate position information. Therefore, the performance of rotor position error information extraction and rotor position estimation has a direct impact on the overall implementation of position sensorless control systems.
In order to provide a responsive approach for obtaining accurate position error information under dynamic conditions, an improved position error signal extraction system is required in real-time motor control applications. Generally, a low-pass filter (LPF) is used to extract the rotor position error signal, which is processed through a band-pass filter (BPF) and demodulated via heterodyne techniques [20,21]. However, the accuracy of the LPF under dynamic conditions depends on the filter order and bandwidth, leading to long convergence times and potential timing mismatches in the rotor position estimation process. To eliminate filters, square-wave injection is presented [22,23], enabling rotor position extraction without LPF. Nevertheless, higher audible noise is not only undesirable in industrial applications but also affects the speed information used as feedback in the control process. Instead of eliminating audible noise, Ref. [24] utilized this noise for sensorless control by replacing position sensors with a microphone to capture motor behavior related to rotor position during injection, enabling estimated rotor position through complex signal processing. A direct extraction method in the stationary reference frame, as discussed in Ref. [25], eliminates the BPF by leveraging HF αβ currents in the estimation process to obtain rotor position information. Nonetheless, inverter nonlinearity should be considered to maintain estimation accuracy. A Notch Filter (NF) is used in the amplitude observer of the injected HF current modulation, replacing both BPF and LPF, as seen in Ref. [26]. However, its narrow bandwidth requires precise tuning to the target harmonic. Under varying conditions, such as parameter changes or inverter noise, mismatched NF parameters may degrade estimation performance. In Refs. [27,28], a Second-Order Generalized Integrator (SOGI) is presented, which reduces filter dependency but introduces multiple integration stages, affecting the dynamic response. Meanwhile, the Sliding Discrete Fourier Transform (SDFT) for extracting the rotor position error is explained in Ref. [29]. In addition to increasing the computational burden, additional processing is required before integration into the PI-based rotor position estimation.
By adopting a data-smoothing technique commonly used in forecasting systems to analyze fluctuations and respond rapidly to data variations for more accurate results [30], the exponential moving average (EMA) is utilized in the modulation process of the rotor position error signal extraction system. The smoothing factor (α) is designed to have an adaptive response by weighting the most recent data in response to changes while maintaining effectiveness in smoothing the acquired data. This is intended to maintain the accuracy of rotor position estimation during dynamic conditions. In addition, unlike other rotor position error information extraction systems that utilize some filters, multiple integral functions, and complex signal processing, which increase the computational load, EMA offers a lightweight system because its calculation method only uses a moving average of data while prioritizing the most recent data. Therefore, EMA can be used as an alternative to filter-based data-processing methods with a lower computational burden. Its responsiveness in handling data changes becomes an advantage in obtaining more accurate data during rapid changes, addressing common issues that arise from dependence on filter performance. In the HFI technique, the rotor position information is contained in the quadrature current signal including HF components. In this study, EMA is proposed to process the quadrature current signal carrying the rotor position information. Then, the heterodyne synchronous modulation method is applied to extract the AC and DC components. Finally, EMA is used to pass the DC component carrying the rotor position error information. This information is then used in the observer tracking loop control system to obtain a more accurate rotor position estimate, even under dynamic conditions. Therefore, the main contributions of this study are as follows:
- A simplified filter structure is proposed for extracting rotor position error signals, effectively reducing system complexity.
- The influence of signal-to-noise ratio (SNR) on the sensorless control system is minimized to maintain robust control performance, particularly under low-speed operating conditions.
- A responsive signal extraction method is introduced to enable accurate rotor position estimation during dynamic conditions.
- The accuracy of rotor position estimation in real-time sensorless control systems is significantly improved, even under varying dynamic scenarios.
- A lightweight implementation is achieved to reduce DSP resource utilization on FPGA hardware, thereby improving computational efficiency for real-time control.
The rest of this article is organized as follows. The HF injection for PMSM position sensorless control is explained in Section 2. In Section 3, the improved tracking loop control systems with the position error information extraction method based on EMA for sensorless implementation is discussed. To demonstrate the performance of the proposed strategies, analysis and verification using experimental systems are presented in Section 4. Finally, Section 5 concludes this article.
2. Analysis of High-Frequency Pulsating Injection Technique for Position Sensorless PMSM
The basics of dynamic equations for a PMSM are represented in the d–q rotating frame, which is expressed in the following mathematical model [3]:
where , and represent the stator voltages and currents in the d–q axis, as well as the motor resistance and inductances in the d–q axis, respectively. Meanwhile p, and represent the differential operator, the rotational speed of the motor, and the permanent linkage of the motor, respectively.
The sensorless strategy using high-frequency injection operates in the low-speed region, and the Back-EMF and cross-coupling effects as correlated in Equation (1) can be neglected. Therefore, the equation for the PMSM can be simplified as follows:
During the frequency injection signal, the injected frequency is higher than the motor frequency itself and the voltage drop across the stator resistance. Consequently, the PMSM equation is equivalent to the pure inductance model, which can be expressed as follows:
where and represent the stator voltages and currents in the d–q axis of the high frequency, respectively. Although this condition may seem like an inductive circuit that could potentially cause a temperature increase, resulting in changes to the inductance parameters, it does not affect the accuracy of the rotor position estimation in this study because the estimation does not rely on those parameter values.
Furthermore, when a HF pulsating voltage signal is injected into the d-axis of the estimated synchronous reference frame in Equation (4), the resulting current response can be analyzed to estimate the rotor position.
where and represent the amplitude and frequency of the injected voltage, respectively. By applying the rotational matrix in Equation (5) to the estimated synchronous reference frame, the current response in the estimated d–q axis can be expressed as follows:
To reflect the effect of the injected pulsating voltage in the synchronous reference frame, the voltage response in the actual d–q axis after HF signal injection can be obtained by rewriting Equation (3) as follows:
The current response of the estimated d–q axis can be obtained by substituting Equation (3) into Equation (6), as follows:
Then, by substituting Equation (7) into Equation (8), when the HF signal is injected into the estimated d-axis, the position information can be derived from the induced current signal, as expressed in the following equation.
where and are expressed, as seen in the equation below:
In general, the estimation process in the HF injection technique using the tracking loop control system is illustrated in Figure 1. A BPF is used to extract the HF carrier quadrature current , which contains rotor position information, as shown in Equation (9). This equation may face sensitivity challenges when is small. So far, providing a clear and undistorted rotor position error signal has been useful for accurately capturing the amplitude, thereby maintaining estimation accuracy.
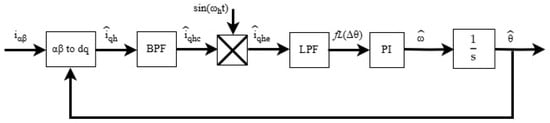
Figure 1.
Tracking loop control system with BPF and LPF-based extraction.
- Then, the synchronous demodulation process is applied by multiplying sin). After the signal modulation process, secondary harmonics, consisting of AC and DC components, appear in the resulting current. Thus, the HF quadrature current after the modulation process can be expressed as follows:
The BPF was designed using a second-order filter, where is the damping ratio and the natural frequency is and , which can be expressed as follows:
Then, LPF is used to filter out the AC component, allowing for the signal position error information to be extracted using the following equation:
Typically, the LPF is developed using either a first-order or second-order filter, which are expressed in Equation (14) and Equation (15), respectively.
Finally, when is regulated to zero by the PI controller, the actual reference frame aligns with the estimated synchronous reference frame, indicating that the estimated rotor position matches the actual rotor position. This is the working principle of the HF injection technique.
3. Proposed Implementation of Tracking Loop Control Systems for Sensorless PMSM Using the HF Injection Technique
This section presents an improvement in the extraction scheme in the tracking loop control system to estimate rotor position and motor speed. The tracking loop control system consists of two main parts: modulation signal processing, which extracts rotor position estimation error, and the PI regulator, which serves as an observer to estimate the rotor position. These components are discussed in detail throughout this section.
The rapid extraction of rotor position error information during dynamic changes has a positive impact on the tracking loop control system, enabling the control system to respond quickly and estimate the rotor position more accurately. In this extraction scheme, filter performance also plays a critical role in the demodulation process. Conventional signal demodulation techniques typically rely on a BPF and LPF, which may potentially narrow the bandwidth of sensorless PMSM control systems. In addition, the use of a low-order BPF can degrade the signal-to-noise ratio (SNR) of high-frequency signals, leading to unstable rotor position estimation. Conversely, a high-order BPF tends to deteriorate the dynamic response, especially during sudden changes such as speed variations, direction reversals, or abrupt load additions. Meanwhile, the design of the LPF also faces two conflicting demands. First, a wide bandwidth is required to enhance the system’s ability to respond quickly to dynamic changes. Second, the bandwidth needs to be narrowed to suppress high-frequency harmonic components. This contradiction creates a technical dilemma in the design of the demodulation system for the extraction scheme.
To address these challenges, this paper proposes an alternative demodulation technique that is more effective and can serve as a replacement for the conventional combination of BPF and LPF. The EMA is proposed due to its high responsiveness to dynamic changes and superior computational efficiency. EMA continuously updates values based on recent data by assigning greater weight to newer samples, thereby improving the system’s responsiveness to changing conditions without depending on filter level order, bandwidth, and SNR. Moreover, since EMA performs simple weighted averaging on recent data, this method significantly reduces the complexity and computational burden in digital signal processing. The transfer function of EMA in the continuous domain can be expressed as follows:
Interestingly, the EMA model resembles the LPF, as shown in Equation (14). However, the main difference between the two approaches lies in the method of determining their coefficients: the LPF operates based on a specified cut-off frequency, with coefficients chosen according to the frequency attenuation characteristics; whereas the EMA calculates a weighted average of the input signal, where the weight of the most recent data is greater, and the weight of the previous data decreases exponentially. The smoothing factor α determines the relative weighting between the most recent and previous data, which can be obtained from the number of samples in a time window based on the frequency characteristics of the signal to be passed. Therefore, in hardware implementation, the EMA offers a simpler structure, where the value of α can be directly determined using equations in the discrete-time system, as follows:
where is the number of samples used to calculate the average with a window length determined based on the time–frequency of the data is chosen according to the characteristic frequency of the signal to be passed so that , is the sampling time. Therefore, the EMA in the discrete domain can be expressed as:
In this proposed scheme, the demodulation technique for the tracking loop control system is implemented using multiple EMA stages, as illustrated in Figure 2. The first EMA, referred to as the pre-EMA stage, is designed to set the upper and lower limit functions instead of the BPF, as expressed in Equation (19). This approach serves as a replacement for the conventional BPF, aiming to achieve improved dynamic response without depending on the filter order level or SNR.
where and represent the pre-EMA signals used to set the lower and upper limits of the filtered signal, respectively. Meanwhile, denotes the high-frequency quadrature current that carries rotor position information to be modulated. The parameters and are the smoothing factor settings for the lower and upper limits, respectively. For instance, if the window length is set to 0.002 s, the resulting characteristic frequency of the window length is 500 Hz. According to Equation (17), the α value can then be calculated for this frequency to ensure that signals below this threshold are effectively attenuated.
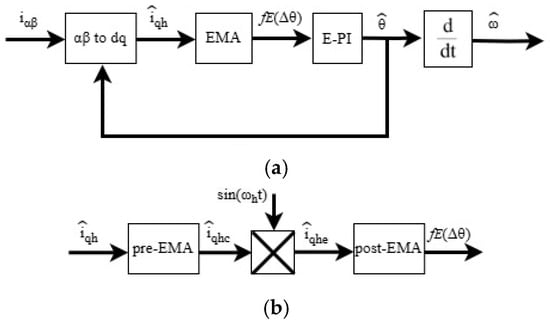
Figure 2.
Proposed EMA-based extraction scheme. (a) Tracking loop control system. (b) Block diagram of EMA.
In this study, the injected HF signal is set to 1 kHz. The demodulation technique is performed by modulating the HF quadrature current, which carries rotor position information due to the frequency injection. Therefore, the pre-EMA system is designed to pass signals in a frequency range around the injection frequency, with the lower limit set at 900 Hz and the upper limit set at 1.1 kHz. Since is the EMA for the lower limit, which is obtained by subtracting between the input signal and the reduced signal, the reduced signal must be in the 100 Hz range to obtain signals around 900 Hz. Thus, when the sampling time is set to 0.0001 s, the window length for the lower limit can be set to 0.01 s, giving an value of 0.019 to obtain the desired lower limit. Meanwhile, is the EMA used to define the upper limit of the passed signal. Since this stage processes the output of the lower-limit EMA and passes signals below 1.1 kHz, the window length can be set to 0.0009 s. Based on this value, can be set to 0.198, effectively passing signals in this upper frequency range. Consequently, the HF quadrature current signal passed through the pre-EMA stage can be utilized for the synchronous demodulation process. As a result, Equation (11) can be rewritten as follows:
Since the rotor position error contains both AC and DC components resulting from the synchronous demodulation process, the second-stage EMA, referred to as the post-EMA, is applied to suppress the AC component as a replacement for the conventional LPF. Accordingly, the rotor position estimation error can be expressed by rewriting Equation (13) as follows:
In this case, the AC component introduces a specific frequency into the rotor position error. To eliminate this component, the window length can be set to the lower limit at 50 Hz, which corresponds to a window length of 0.02 s, resulting in a post-EMA smoothing factor of 0.001. Accordingly, the post-EMA is employed to extract the DC component by calculating the average values within the defined window length. Thus, rotor position information can be expressed by rewriting Equation (21) as follows:
Furthermore, to observe the responsiveness of the proposed system under dynamic conditions that require quick adaptation to input signal changes, a simulation is conducted using a suddenly changed input signal to compare the performance of both extraction systems, as shown in Figure 3.
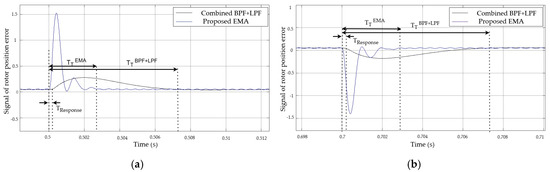
Figure 3.
Performance comparison between combined BPF+LPF-based and EMA-based methods in the extraction scheme. (a) The input signals representing the rotor position error changed abruptly at 0.5 s. (b) The input signals representing the rotor position error changed abruptly at 0.7 s.
The input signal, representing the quadrature current component in the high-frequency (HF) frame, is set to within the time interval . It is then changed to during the interval and returns to the initial signal in the interval . Here, 1000 Hz is the injection frequency, while 20,000 Hz represents the switching frequency. Figure 3a shows that the input signal changes at t = 0.5 s. The conventional system requires a response time (TResponse) of approximately 0.25 ms and a transient time (TT) of about 7 ms to reach stability. This response needs to be shortened to maintain accurate rotor position estimation under dynamic conditions. In contrast, the proposed system demonstrates a faster response, with a TResponse less than 0.125 ms and a TT of only 3 ms, indicating a significant improvement despite a slight overshoot during the transition. Subsequently, at t = 0.7 s, the system is changed while in a steady-state condition, as shown in Figure 3b. The proposed system exhibits a faster response with TResponse and did not exceed 0.2 ms, compared to 0.35 ms in the conventional system. The transient time TT2 also has a shorter time, at 2.8 ms compared to 7.5 ms in the conventional system. The statistical analysis shows that the standard deviation of the TT is below 0.15 ms, confirming the consistency of the system’s faster dynamic performance. In this case, EMA is not exactly a filter that suppresses the signal, but rather a signal-smoothing technique that assigns greater weight to more recent data within a defined window length. Although the EMA output still contains slight ripples, these are eliminated in the appropriate control loop systems through parameter design that considers the cut-off frequency. Therefore, rotor position information can still be extracted quickly and accurately under dynamic conditions.
As a further process within the tracking loop control system, a PI controller with extended integration (E-PI) is adopted, where the rotor position error information is used as input to obtain the rotor position estimate , which can be expressed by the following equation:
where are the proportional coefficient, integral coefficient, cut-off frequency of the extraction scheme, and angular margin, respectively.
In contrast to conventional methods, the rotor position estimation in Equation (23) is performed earlier to avoid potential noise that may arise when the estimated motor speed is used as feedback in the speed control system, particularly at low speeds. In addition, to ensure that the estimated theta quickly reaches a stable condition and remains unaffected by noise in the estimated motor speed, this approach is expected to provide better performance in rotor position estimation, even under low-speed dynamic conditions. Therefore, the rotor position can be derived by a differential equation to obtain the motor speed. Then, an LPF is employed to reduce noise introduced during the differentiation process, so that the expression of the estimated motor speed, which is represented as the estimated rotor omega , can be expressed in Equation (25). Thus, the obtained estimated rotor position and motor speed information can be used to implement real-time PMSM control without a position sensor.
In order to realize the proposed sensorless scheme, an FPGA is selected. Due to its capability in hardware control implementation, which enables parallel processing and fast execution, a wider control-loop bandwidth can be achieved. This is beneficial for minimizing delays that may occur in the sensorless control process, such as ADC control, vector control, the estimation process, and filtering, as shown in Figure 4.
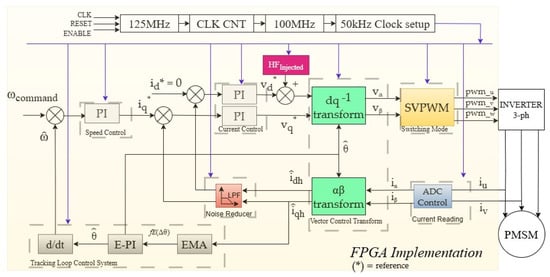
Figure 4.
Block diagram of proposed position sensorless PMSM implementation using HFI technique.
On the other hand, to observe the efficiency of resource utilization in real-time motor control implementation using FPGA, a system-processing comparison is presented in the FPGA utilization resources between the conventional system and the proposed system, as shown in Table 1. According to this, the system using EMA shows a reduction of DSP and LUT utilization, indicating a computational system with a lighter workload. This proves that the proposed system has better efficiency in implementing real-time motor control compared to conventional systems using BPF and LPF while providing better responsiveness under dynamic conditions to improve the performance of the sensorless control technique.

Table 1.
FPGA resource utilization.
Furthermore, the detailed parameters used in hardware implementation are presented in Table 2, where the value of α is determined based on the window length. This window length can be calculated according to the frequency characteristics of the signal to be passed, as described in Equation (17). Meanwhile, the proportional and integral constants used in the E-PI controller for the tracking loop estimation process are not tuned empirically. Instead, they are analytically derived based on the cutoff frequency and the angular margin, as shown in Equation (24). These analytical formulations eliminate the need for manual parameter adjustment, thereby improving the reproducibility of the implementation in real-time sensorless control systems.

Table 2.
Parameters values used in hardware implementation.
4. Experimental Results
4.1. Experimental Apparatus
In this section, the experimental setup was conducted to verify the effectiveness of the proposed position sensorless control strategy through a series of tests. The experimental apparatus, shown in Figure 5, consists of a PMSM, a designed inverter board with a sensor module, an FPGA board, a DC power supply, and an electronic load. The electrical parameters of the PMSM are listed in Table 3. An encoder was used to evaluate the accuracy of the estimation results by monitoring the actual position and speed. Furthermore, the control bandwidth was set to 50 kHz, and the PWM switching frequency was 20 kHz. In this sensorless strategy, the injection frequency was set to 1 kHz with an amplitude of 5 V. In addition, the cut-off frequencies of the BPF were 900 Hz and 1.1 kHz, while the cut-off frequency of the LPF was 100 Hz in the conventional extraction scheme. Meanwhile, the α for the proposed EMA-based scheme is described in Section 3.

Figure 5.
Experimental apparatus.

Table 3.
Specifications of PMSM.
Since HF injection-based methods are categorized as low-speed sensorless control schemes [25], the experimental tests in this study were conducted at a speed range of approximately 5% of the motor’s rated speed. The estimation performance of each method is discussed in detail in the following subsection, and the results are compared in Table 4 and Table 5.

Table 4.
Maximum position estimation errors in steady state response for different tests.

Table 5.
Maximum position estimation errors in transient response for different tests.
4.2. Sensorless Control Performance Comparison Under Speed Change Conditions
In this section, a test was conducted to evaluate the performance of position estimation during sudden speed increases and decreases. The position estimation accuracy was compared between two methods: a BPF+LPF-based conventional extraction scheme and an EMA-based proposed extraction scheme, both of which demonstrated effectiveness in observing rotor position in a sensorless control strategy. As illustrated in Figure 6, the speed was increased from 17.5 min−1 to 35 min−1. The position error is defined as the difference between the actual position and the estimated position. The maximum steady-state error during speed variations was calculated, indicating that the conventional method has a maximum steady-state error of 7.45° (0.13 rad), with a maximum error in the transient response during a sudden speed change condition of 16.6° (0.29 rad), while the proposed method does not exceed 0.5° (0.0087 rad), with a maximum error in the transient response of 9.91° (0.173 rad). Meanwhile, Figure 7 presents the results of the test with a speed decrease from 50 min⁻1 to 25 min⁻1. Based on these results, the conventional method produced a maximum steady-state error of 8.89° (0.155 rad), with a maximum error in the transient response during a sudden speed change condition of 17.19° (0.3 rad), whereas the proposed method reduced the e error to 1.32° (0.023 rad), with a maximum error in the transient response of 10.89° (0.19 rad). Thus, these results show that the proposed method improves accuracy by reducing position error during sudden speed changes.
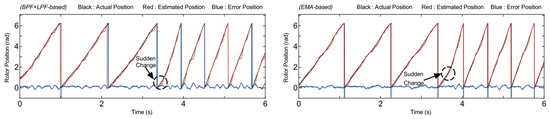
Figure 6.
Comparison performance under step response from 17.5 min−1 to 35 min−1.
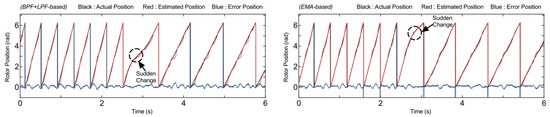
Figure 7.
Comparison performance under step response from 50 min−1 to 25 min−1.
4.3. Sensorless Control Performance Comparison Under Reverse Speed Conditions
Further observation of sensorless system performance was conducted during abrupt changes in motor direction. The experimental results, presented in Figure 8 and Figure 9, demonstrate that both methods perform well in estimating rotor position across bidirectional speed changes. From the waveform results, when the direction changes from 15 min−1 to −15 min−1, as shown in Figure 8, the maximum steady state error using the conventional method is approximately 13.47° (0.23 rad). In contrast, the proposed method significantly reduces the estimation error to 8.65° (0.15 rad). Moreover, during the transient response in the speed reversal condition, the proposed method has a maximum error of 11.46° (0.2 rad), which is smaller than that of the general method, at 17.7° (0.31 rad). Similarly, Figure 9 illustrates a sudden direction change from −15 min−1 to 15 min−1 to evaluate performance under reverse conditions. The results indicate that the proposed method achieves a lower maximum steady-state estimation error of 9.88° (0.172 rad), with a maximum error in the transient response during speed reversal of 13.18° (0.13 rad), compared to 10.17° (0.177 rad) and a maximum error during the transient response of 18.91° (0.33 rad) using the general method. Hence, the proposed method provides smaller estimation errors, improving the accuracy of rotor position estimation.
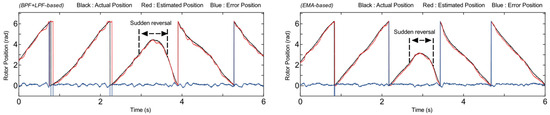
Figure 8.
Comparison performance under reversal speed from 15 min−1 to −15 min−1.
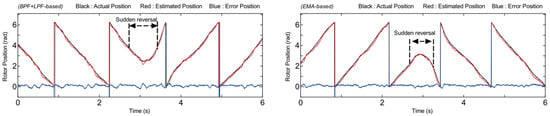
Figure 9.
Comparison performance under reversal speed from −15 min−1 to 15 min−1.
4.4. Sensorless Control Performance Comparison Under Sudden Load
To evaluate the performance of the sensorless system under load conditions, a test was conducted by suddenly applying a load. Figure 10 shows that the load was applied at 1 s when the motor operated at 100 min−1. These results show a desirable phase current response with a more sinusoidal waveform. During sudden load addition, the motor current increases, and the tracking-loop control in the position estimation process is still able to accurately track the actual rotor position, allowing for the system to remain stable even under dynamic conditions. This indicates that both sensorless systems were able to operate well while adding the load to the system, demonstrating their capabilities in handling dynamic conditions. Based on the experimental results, the proposed method performed effectively under loaded conditions, with an average rotor position estimation error of 0.57° (0.01 rad) and a maximum error in the transient response during load application of 16.62° (0.29 rad). This represents a reduction compared to the conventional method, which had an average estimation error of 0.85° (0.015 rad) and a maximum error in the transient response during a load application of 28.66° (0.5 rad). In this study, the E-PI method demonstrates effective tracking-loop control performance in the rotor position estimation process, delivering accurate estimation results with smaller estimation errors even under sudden load conditions. This clearly contributes positively to the overall control system, especially in maintaining system stability during load disturbances. Thus, the proposed system is not only resilient to sudden load changes but also provides more accurate rotor position estimation than the conventional method.
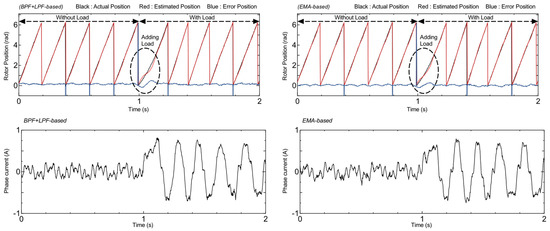
Figure 10.
Comparison performance under sudden load at 100 min−1.
4.5. Performance Comparison with Existing Methods
A comparison between the proposed method and several recent techniques is presented in Table 6, focusing on the maximum estimation error as the performance metric under dynamic conditions involving sudden increases and decreases in motor speed. The results clearly indicate that the proposed method achieves superior estimation accuracy, exhibiting a significantly lower maximum error compared to other methods. This improvement highlights the effectiveness of the proposed sensorless PMSM control scheme.

Table 6.
Comparison of HF injection techniques for sensorless PMSM.
4.6. Observation of Performance Comparison Under Sudden Changes from Sensor-Based to Sensorless Modes
In the final test, the control mode was switched during motor operation at 45 min−1 to demonstrate the feasibility of the sensorless control strategy. As shown in Figure 11, the motor operated in sensorless mode from 0 s to 1.5 s and then switched to sensor mode from 1.5 s to 3 s. The experimental waveform indicates that both sensorless control methods performed well. The analyzed average steady-state error of the conventional method was 3.43° (0.06 rad) in sensorless mode, while that of the proposed method was 1.54° (0.027 rad), indicating that the proposed method achieves better accuracy in reducing estimation error. Additionally, there was no significant change in performance, demonstrating that the sensorless and sensor-based modes achieve nearly identical control performance. Thus, the sensorless control strategy can be successfully implemented in a real-time PMSM drive system without a position sensor.
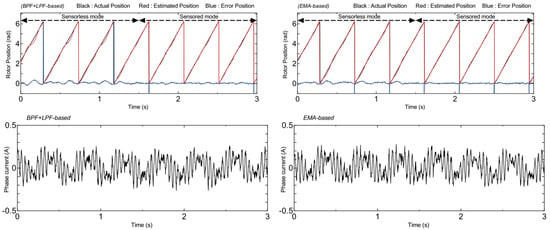
Figure 11.
Comparison performance of sensor-based and sensorless modes under speed for 45 min−1.
5. Conclusions
This study proposes a method for extracting rotor position error information in a tracking loop system for rotor position estimation with the HFI technique using EMA. Generally, BPF and LPF are used in tracking loop control systems to obtain rotor position error information. However, in real-time motor control, such systems may suffer from limitations in filter accuracy and dynamic response, potentially leading to time imbalances in the position error extraction and estimation process. By leveraging the responsiveness of EMA, which offers a quick response to adapt to sudden changes in dynamic conditions by weighting recent data through a smoothing factor α, along with simple calculations and independence from filter order and bandwidth, the proposed method significantly improves accuracy compared to conventional systems, particularly under varying motor speed, direction, and load conditions. Thus, in practical applications, the proposed EMA-based approach provides three key advantages: reduced reliance on filters and their performance limitations, simplified calculations that lower computational burden, and high responsiveness for accurate estimation even under sudden condition changes. Experimental verification shows that the proposed system reduces estimation errors under all tested conditions. The conventional system exhibits a maximum error of 13.47° in a steady state, while the proposed system achieves a lower error of 9.88°, representing a 26.64% reduction. Additionally, the maximum error in transient response is reduced by 42%, from 28.66° to 16.62°. Thus, the proposed system demonstrates its effectiveness and feasibility as an alternative for the real-time implementation of position sensorless PMSM control.
Author Contributions
The manuscript preparation including system design and experiments was carried out by I.F. under the supervision of T.H. The analysis of data was performed by I.F. and T.H., who also contributed to manuscript correction. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, G.; Xiao, F.; Lian, C. A Position Sensorless Control Strategy for PMSM Drives with Single-Phase Current Sensor. IEEE Trans. Trans. Electrif. 2024, 10, 4678–4688. [Google Scholar] [CrossRef]
- Yan, K.; Hu, Z.; Hu, J.; Li, J.; Zhang, B.; Song, J.; Li, J.; Chen, L.; Li, H.; Xu, L.; et al. A critical review of radial field in-wheel motors: Technical progress and future trends. eTransportation 2024, 22, 100353. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z.; Chen, Z.; Liu, J.; Lu, Y. An Enhanced Sensorless Control Scheme for PMSM Drives Considering Self-inductance Asymmetry. CES Trans. Electr. Mach. Syst. 2022, 6, 384–392. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position sensorless permanent magnet synchronous machine drives—A review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Li, Y.; Hu, H.; Shi, P. A review of position sensorless compound control for PMSM drives. World Electr. Veh. J. 2023, 14, 34. [Google Scholar] [CrossRef]
- Liang, J.; Wu, J.; Wang, Y.; Zhong, Z.; Bai, X. Sensorless Control for a Permanent Magnet Synchronous Motor Based on a Sliding Mode Observer. Eng 2024, 5, 1737–1751. [Google Scholar] [CrossRef]
- Sreejith, R.; Singh, B. Sensorless predictive control of SPMSM-driven light EV drive using modified speed adaptive super twisting sliding mode observer with MAF-PLL. IEEE Trans. Emerg. Sel. Topics Ind. Electron. 2021, 2, 42–52. [Google Scholar]
- Yang, H.; Yang, R.; Hu, W.; Huang, Z. FPGA-Based Sensorless Speed Control of PMSM Using Enhanced Performance Controller Based on the Reduced-Order EKF. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 289–301. [Google Scholar] [CrossRef]
- Dilys, J.; Stankevic, V.; Luksza, K. Implementation of Extended Kalman Filter with Optimized Execution Time for Sensorless Control of a PMSM Using ARM Cortex-M3 Microcontroller. Energies 2021, 14, 3491. [Google Scholar] [CrossRef]
- Filho, C.J.V.; Xiao, D.; Vieira, R.P.; Emadi, A. Observers for High-Speed Sensorless PMSM Drives: Design Methods, Tuning Challenges and Future Trends. IEEE Access. 2021, 9, 56397–56415. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Duan, W.; Jiang, J. Research on sensorless control system of low speed and high power PMSM based on improved high frequency signal injection. Energy Rep. 2021, 7, 499–504. [Google Scholar] [CrossRef]
- Tian, L.; Zhao, J.; Sun, J. Sensorless Control of Interior Permanent Magnet Synchronous Motor in Low-Speed Region Using Novel Adaptive Filter. Energies 2016, 9, 1084. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, D.; Zhang, G.; Li, C.; Zhang, X.; Xu, D. Sensorless control scheme of IPMSMs using HF orthogonal square-wave voltage injection into a stationary reference frame. IEEE Trans. Power Electron. 2019, 34, 2573–2584. [Google Scholar] [CrossRef]
- IIioudis, V.C. Sensorless Control of Permanent Magnet Synchronous Machine with Magnetic Saliency Tracking Based on Voltage Signal Injection. Machines 2020, 8, 14. [Google Scholar] [CrossRef]
- Naderin, M.; Markadeh, G.A.; Karimi-Ghartemani, M.; Mojiri, M.; Li, X.; Yan, Y.; Xu, Y.; Chen, W.; Shi, T. Improved Sensorless Control Strategy for IPMSM Using an ePLL Approach With High-Frequency Injection. IEEE Trans. Ind. Electron. 2024, 71, 2231–2241. [Google Scholar] [CrossRef]
- Tang, Q.; Shen, A.; Luo, X.; Xu, J. PMSM sensorless control by injecting HF pulsating carrier signal into ABC frame. IEEE Trans. Power Electron. 2017, 32, 3767–3776. [Google Scholar] [CrossRef]
- Mao, Y.; Du, Y.; He, Z.; Quan, L.; Zhu, X.; Zhang, L.; Zuo, Y. Dual Quasi-Resonant Controller Position Observer Based on High Frequency Pulse Voltage Injection Method. IEEE Access. 2020, 8, 213266–213276. [Google Scholar] [CrossRef]
- Wu, X.; Huang, S.; Liu, P.; Wu, T.; He, Y.; Zhang, X.; Chen, K.; Wu, Q. A reliable initial rotor position estimation method for sensorless control of interior permanent magnet synchronous motors. J. ISA Trans. 2020, 97, 116–129. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Yang, S.; Ma, M. Improved initial rotor position estimation for PMSM drives based on HF pulsating voltage signal injection. IEEE Trans. Ind. Electron. 2018, 65, 4702–4713. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Yang, S.; Liu, S. Unified Graphical Model of High Frequency Signal Injection Methods for PMSM Sensorless Control. IEEE Trans. Ind. Electron. 2020, 67, 4411–4421. [Google Scholar] [CrossRef]
- Szalai, T.; Berger, G.; Petzoldt, J. Stabilizing Sensorless Control Down to Zero Speed by Using the High-Frequency Current Amplitude. IEEE Trans. Power Electron. 2014, 29, 3646–3656. [Google Scholar] [CrossRef]
- Benevieri, A.; Formentini, A.; Marchesoni, M.; Passalacqua, M.; Vaccaro, L. Sensorless Control with Switching Frequency Square Wave Voltage Injection for SPMSM with Low Rotor Magnetic Anisotropy. IEEE Trans. Power Electron. 2023, 38, 10060–10072. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Q.; Xiao, J.; Liang, T.; Lin, Z.; Chen, W. High-Frequency Square Wave Injection Sensorless Control Method of IPMSM Based on Oversampling Scheme. World Electr. Veh. J. 2022, 13, 217. [Google Scholar] [CrossRef]
- Malekipour, A.; Corne, A.; Garbuio, L.; Granjon, P.; Gerbaud, L. A Closed-Loop PMSM Sensorless Control Based on the Machine Acoustic Noise. IEEE Trans. Ind. Electron. 2023, 70, 9859–9869. [Google Scholar] [CrossRef]
- Wang, A.; Yang, K.; Chen, K. An improved position-sensorless control method at low speed for PMSM based on high-frequency signal injection into a rotating reference frame. IEEE Access. 2019, 7, 86510–86521. [Google Scholar] [CrossRef]
- Mai, Z.; Xiao, F.; Fu, K.; Liu, J.; Lian, C.; Li, K.; Zhang, W. HF Pulsating Carrier Voltage Injection Method Based on Improved Position Error Signal Extraction Strategy for PMSM Position Sensorless Control. IEEE Trans. Power Electron. 2021, 36, 9348–9360. [Google Scholar] [CrossRef]
- Lu, Q.; Wanf, Y.; Mo, L.; Zhang, T. Pulsating High Frequency Voltage Injection Strategy for Sensorless Permanent Magnet Synchronous Motor Drives. IEEE Trans. Appl. Supercond. 2022, 31, 5204204. [Google Scholar] [CrossRef]
- Li, X.; Cui, Y.; Wu, X. Sensorless Control of Surfaced-Mounted Permanent Magnet Synchronous Motor in a Wide-Speed Range. Electronics 2024, 13, 1131. [Google Scholar] [CrossRef]
- Jiang, Y.; Cheng, M. An improved initial rotor position estimation method using high frequency pulsating voltage injection for PMSM. Def. Technol. 2024, 33, 19–29. [Google Scholar] [CrossRef]
- Yu, J.; Kim, S.B.; Bai, J.; Han, S.W. Comparative Study on Exponentially Weighted Moving Average Approaches for the Self-Starting Forecasting. Appl. Sci. 2020, 10, 7351. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).