A Road-Adaptive Vibration Reduction System with Fuzzy PI Control Approach for Electric Bicycles
Abstract
1. Introduction
- Structural integrity: Excessive vibrations contribute to material fatigue, especially in welded joints and electronic mounting points, which can shorten the lifespan of the frame and internal components.
- Electronic reliability: Vibrations can negatively impact sensitive components such as batteries, controllers, and PCBs (printed circuit boards), increasing the risk of failure under repeated mechanical stress.
- User comfort and safety: Vibrations degrade ride comfort and may reduce control stability, especially at higher speeds or on uneven terrain, which can compromise rider safety.
- Energy efficiency: Vibrations introduce mechanical inefficiencies in the drivetrain and rolling resistance, which, in turn, affect power consumption and reduce the effective range.
2. Related Work
3. Proposed Road-Adaptive Vibration Reduction System
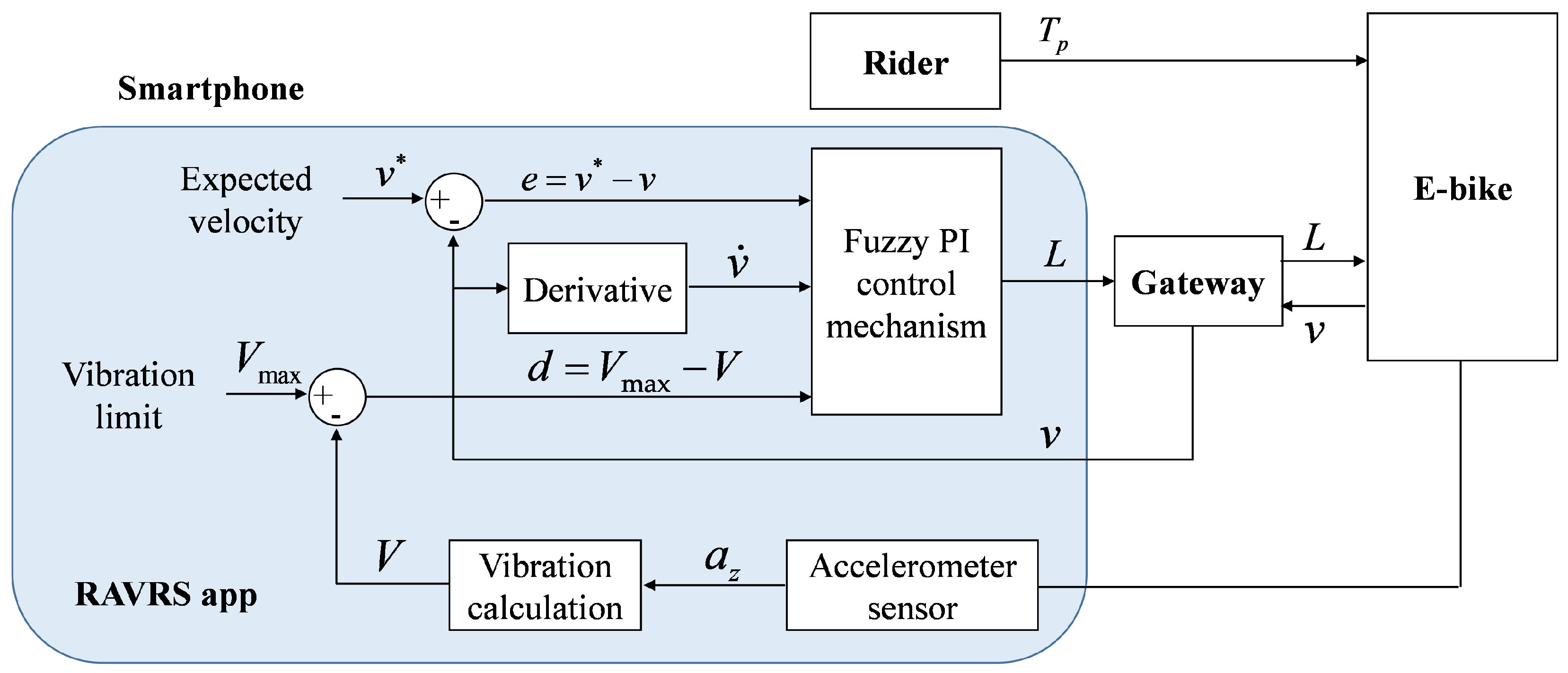
3.1. System Overview
3.2. System Architecture of the RAVRS
3.3. E-Bike Dynamic Model
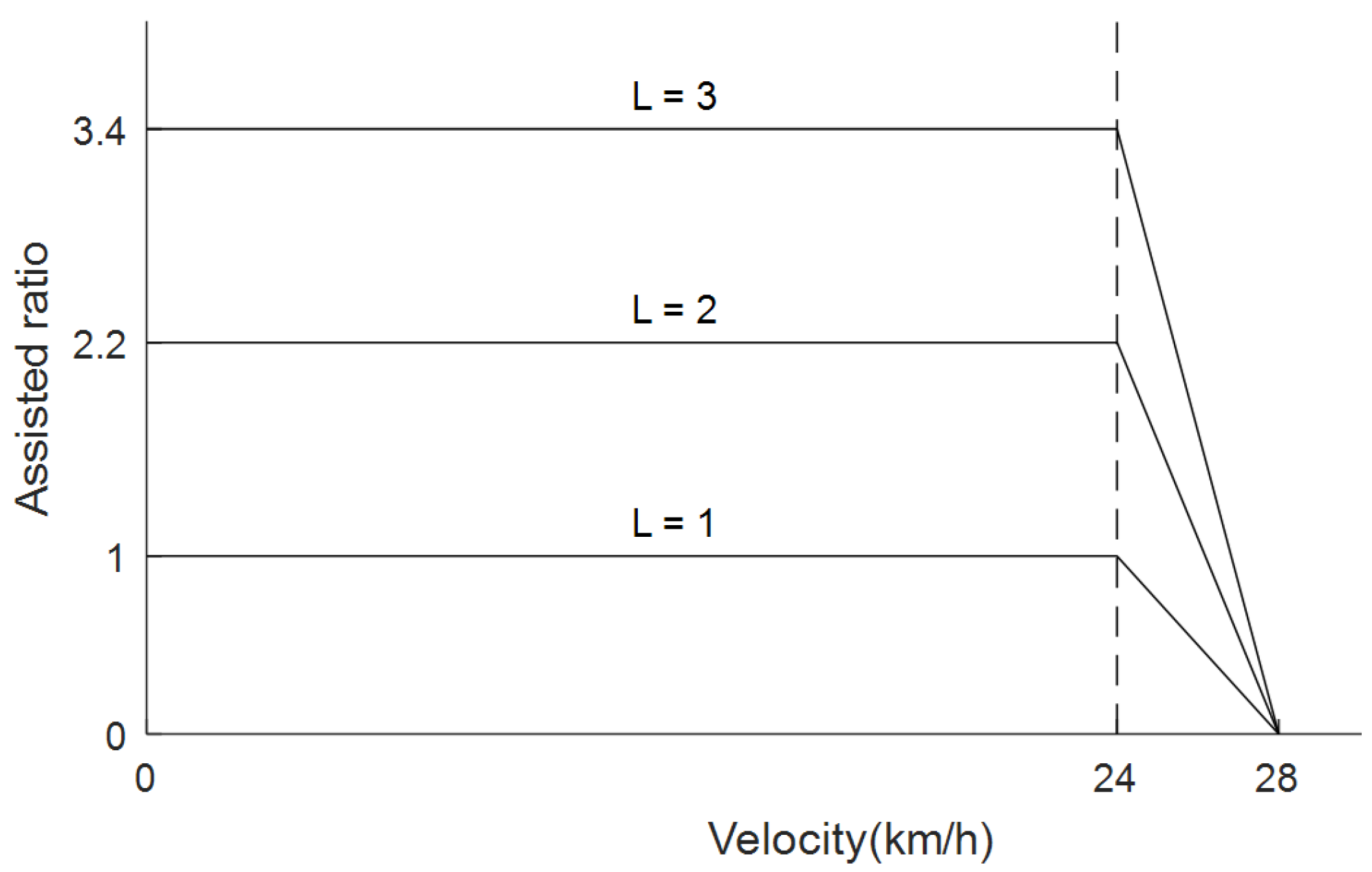
3.4. PAP Method for E-Bikes
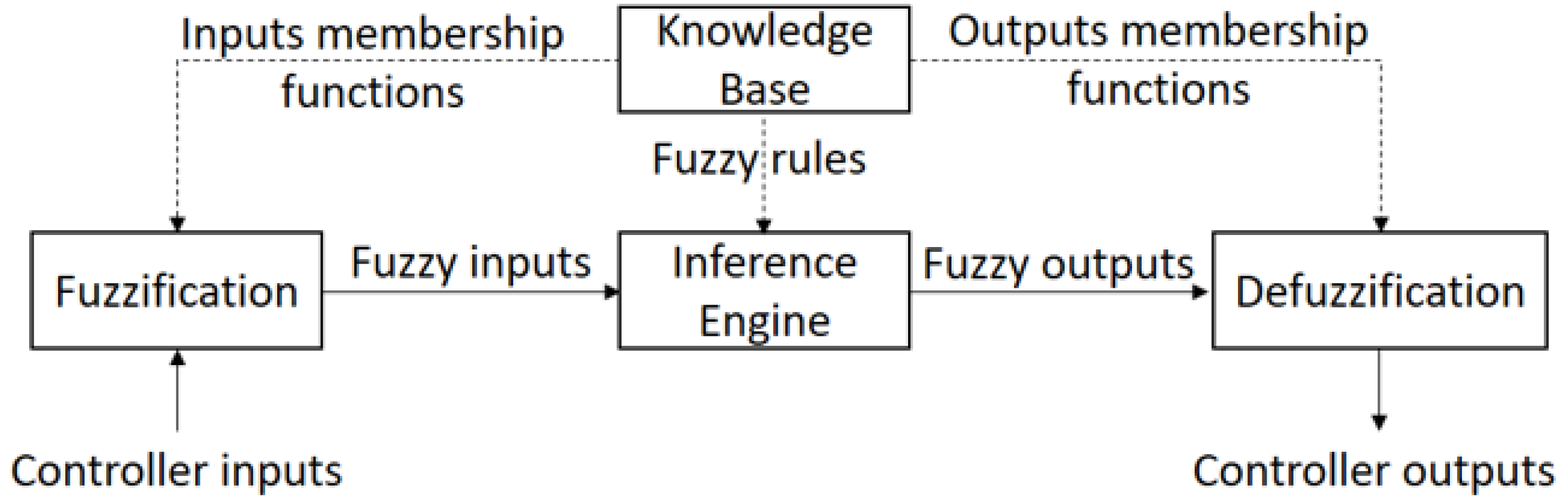
4. Fuzzy PI Control Mechanism of the RAVRS
4.1. Control Structure
4.2. Fuzzification
4.3. Inference Rules and Defuzzification
4.4. RAVRS Application Implementation
5. Experimental Results
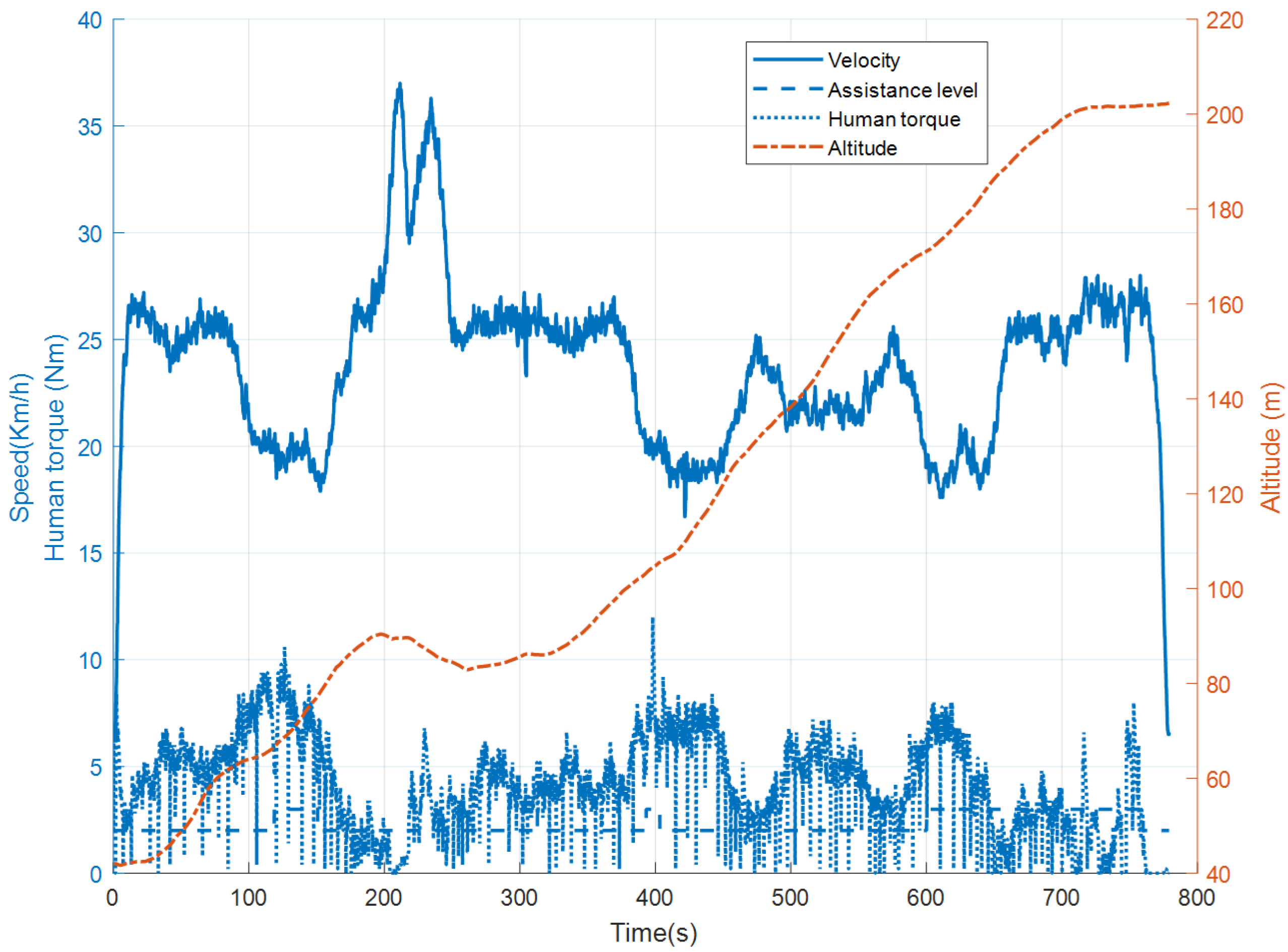
5.1. Experimental Setup
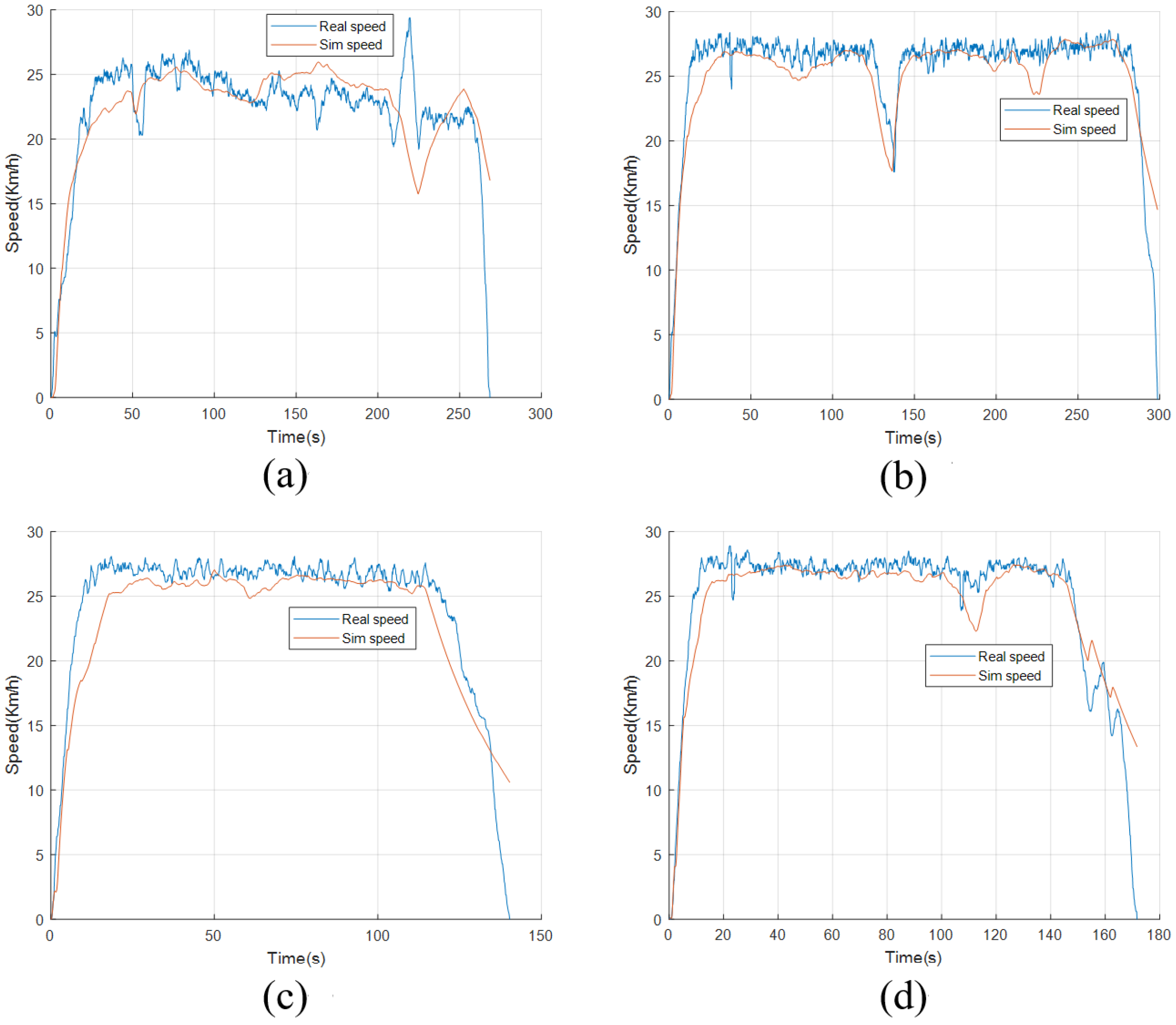
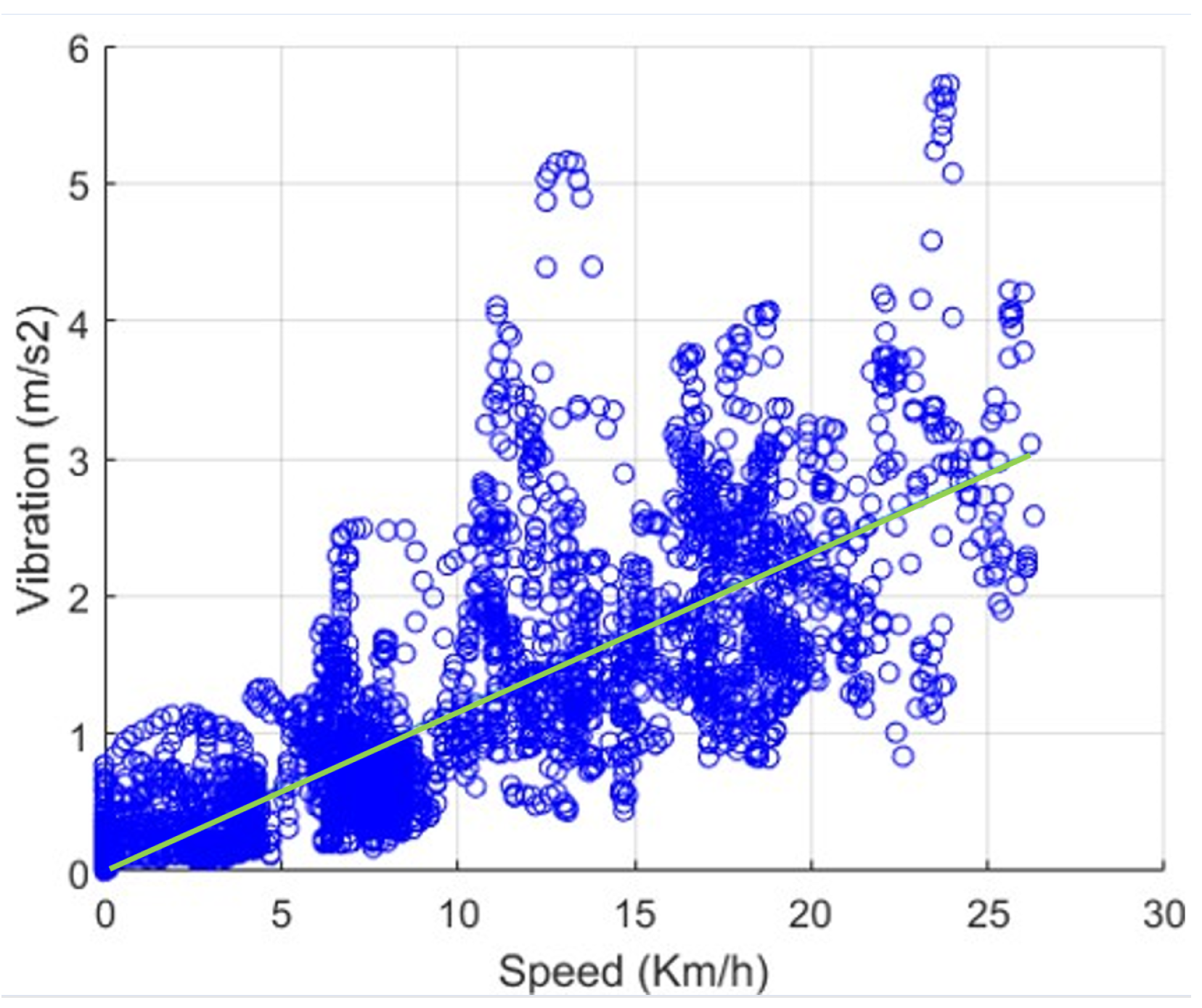
5.2. E-Bike Model Validation
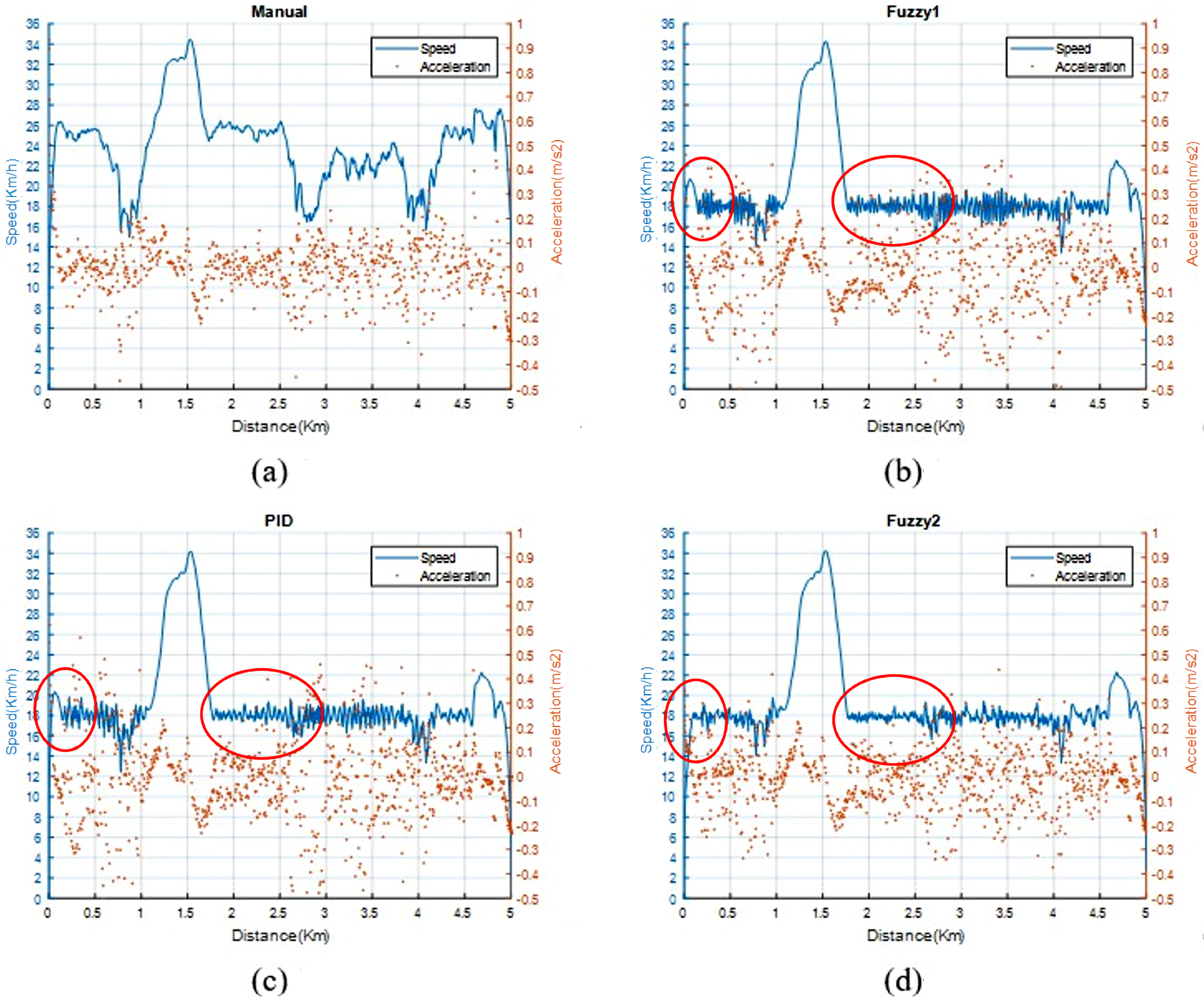
5.3. Quality of Riding at the Starting Stage
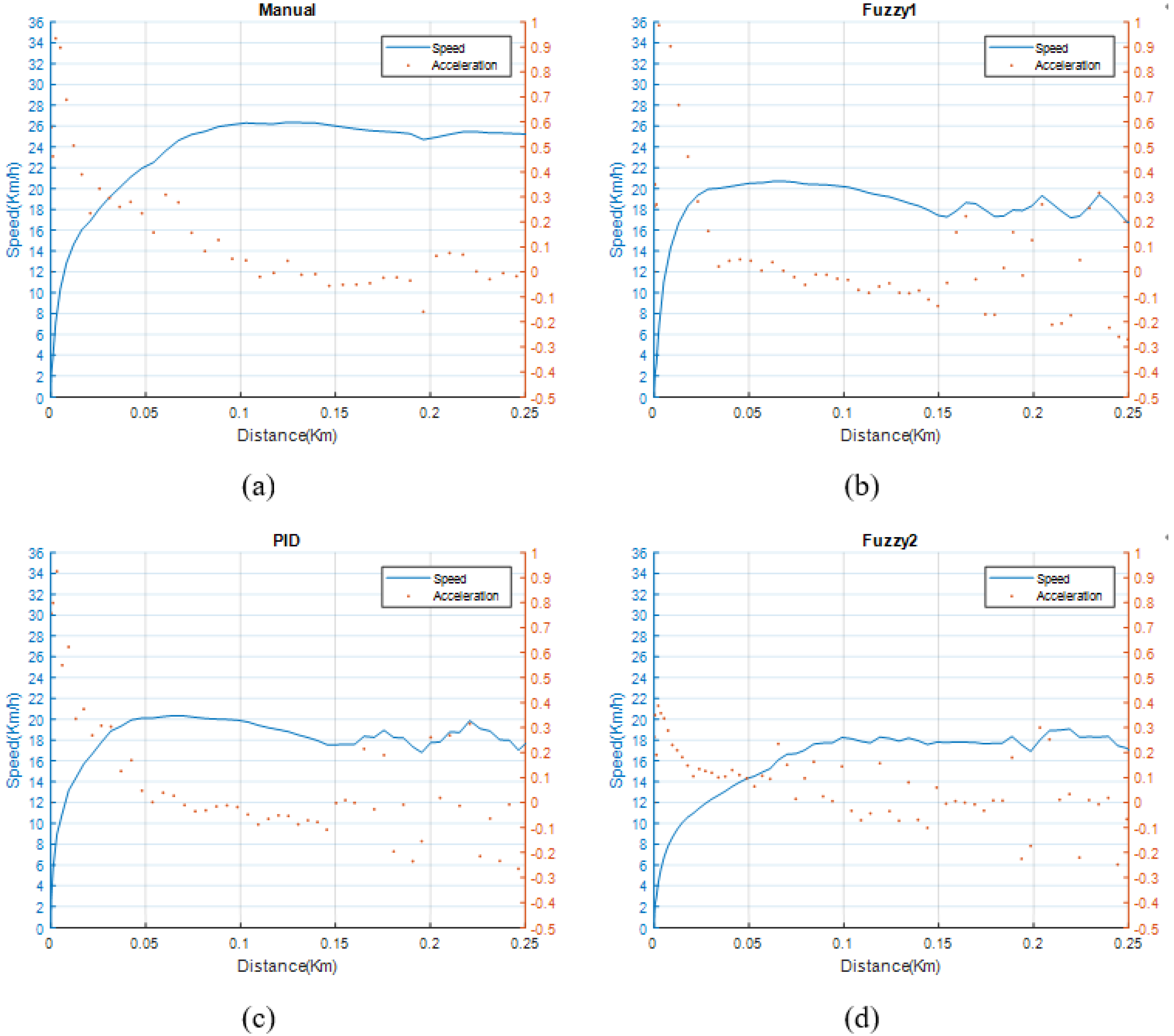
5.4. Velocity and Acceleration Control Performance
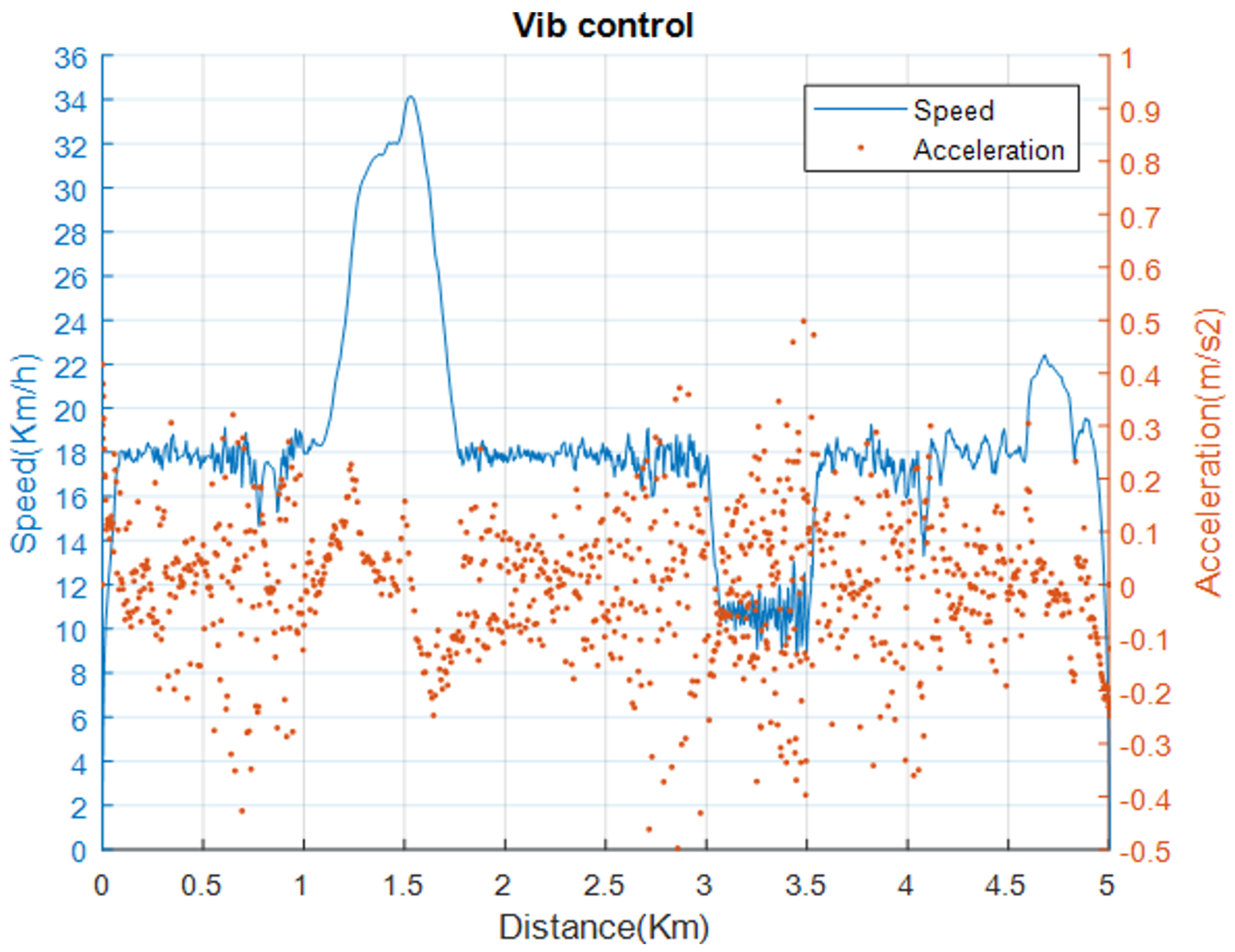
5.5. Vibration Reduction Control Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taiwan’s Pathway to Net-Zero Emissions in 2050. Available online: https://www.ndc.gov.tw/en/Content_List.aspx?n=B154724D802DC488 (accessed on 20 April 2023).
- Chen, W.H.; Chen, I.; Lin, J.C.M.; Hsieh, I.Y.L. Role of hydrogen fuel cells in achieving road transport decarbonization: A case study from Taiwan. Int. J. Hydrogen Energy 2024, 80, 1182–1196. [Google Scholar] [CrossRef]
- Liao, F.; Correia, G. Electric carsharing and micromobility: A literature review on their usage pattern, demand, and potential impacts. Int. J. Sustain. Transp. 2022, 16, 269–286. [Google Scholar] [CrossRef]
- Bourne, J.E.; Leary, S.; Page, A.; Searle, A.; England, C.; Thompson, D.; Andrews, R.C.; Foster, C.; Cooper, A.R. Electrically assisted cycling for individuals with type 2 diabetes mellitus: A pilot randomized controlled trial. Pilot Feasibility Stud. 2023, 9, 60. [Google Scholar] [CrossRef] [PubMed]
- Boland, P.; Connell, L.; Thetford, C.; Janssen, J. Exploring the factors influencing the use of electrically assisted bikes (e-bikes) by stroke survivors: A mixed methods multiple case study. Disabil. Rehabil. 2022, 44, 1389–1398. [Google Scholar] [CrossRef]
- Bourne, J.E.; Kelly, P.; Armstrong, M.E.G. A Theory and Evidence-Informed e-Cycling Intervention for Individuals Diagnosed With Cancer: Development Study. JMIR Cancer 2024, 10, e54785. [Google Scholar] [CrossRef]
- Cairns, S.; Behrendt, F.; Raffo, D.; Beaumont, C.; Kiefer, C. Electrically-Assisted Bikes: Potential Impacts on Travel Behaviour. Transp. Res. Part A Policy Pract. 2017, 103, 327–342. [Google Scholar] [CrossRef]
- Bourne, J.E.; Cooper, A.R.; Kelly, P.; Kinnear, F.J.; England, C.; Lear, S.; Page, A. The Impact of E-Cycling on Travel Behaviour: A Scoping Review. J. Transp. Health 2020, 19, 100910. [Google Scholar] [CrossRef]
- Jiao, G.; Zhai, S. Design and Research of Real-Time Perception for Intelligent Power-Assisted Bicycles Based on Fuzzy Control. In Proceedings of the 2024 China Automation Congress (CAC), Qingdao, China, 1–3 November 2024. [Google Scholar]
- Genç, M.O. Data-driven model predictive control using road-based disturbance estimations in longitudinal driving of e-bike. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 204. [Google Scholar] [CrossRef]
- Lee, J.S.; Chen, Z.H.; Hong, Y. Enhancing Urban Mobility with Self-Tuning Fuzzy Logic Controllers for Power-Assisted Bicycles in Smart Cities. Sensors 2024, 24, 5. [Google Scholar] [CrossRef]
- Abagnale, C.; Cardone, M.; Iodice, P.; Strano, S.; Terzo, M.; Vorraro, G. Model-based Control for an Innovative Power-assisted Bicycle. Energy Procedia 2015, 81, 606–617. [Google Scholar] [CrossRef]
- Uyar, O.; Çunkaş, M.; Karaca, H. Enhanced intelligent control with adaptive system for electrically assisted bicycle. Eng. Sci. Technol. 2022, 30, 101047. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Huang, X.; Xiao, H. Research on Vibration Comfort of Non-Motorized Lane Riding Based on Three-Axis Acceleration. Appl. Sci. 2024, 14, 441. [Google Scholar] [CrossRef]
- Chitra, L.; Devabalaji, K.; Manobala, M.K.; Yogesh, S.; Raj, N. Design and Optimization of Light Weight Materials for E bike Chassis. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024. [Google Scholar]
- Li, F.; Ma, P.; Wen, B. Optimization design and vibration reduction performance analysis of vehicle suspension structure. J. Vib. Control 2025. [Google Scholar] [CrossRef]
- Cui, B.Y.; Zhang, G.; Ma, Q.L. A stable velocity control strategy for a discrete-time car-following model. Phys. A Stat. Mech. Its Appl. 2021, 571, 125846. [Google Scholar] [CrossRef]
- Du, Y.C.; Chen, J.; Zhao, C.; Liu, C.L.; Liao, F.X.; Chan, C.Y. Comfortable and Energy-Efficient Speed Control of Autonomous Vehicles On Rough Pavements Using Deep Reinforcement Learning. Transp. Res. Part C Emerg. Technol. 2022, 134, 103489. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Ocktaeck, L. A Review of History, Development, Design and Research of Electric Bcycles. Appl. Energy 2020, 260, 114323. [Google Scholar]
- Contò, C.; Bianchi, N. E-Bike Motor Drive: A Review of Configurations and Capabilities. Energies 2022, 16, 160. [Google Scholar] [CrossRef]
- Ebnealipour, S.; Tehrani, M.M.; Nazemian, H. A novel e-bike energy management for improvement of the rider metabolism. IET Intell. Transp. Syst. 2023, 17, 1925–2113. [Google Scholar] [CrossRef]
- Bravo, E.G.A.; de Sousa, F.A.S.F.; Escriba, C.; Acco, P.; Giraud, F.; Fourniols, J.Y.; Romero, G.S. Design and Validity of a Smart Healthcare and Control System for Electric Bikes. Sensors 2023, 23, 4079. [Google Scholar] [CrossRef]
- Neuber, H.; Strube, M. Closed-Loop heartrate Control with Electric Bicycles for Cardiac Rehabilitation. In Proceedings of the 2020 21st International Conference on Research and Education in Mechatronics (REM), Cracow, Poland, 9–11 December 2020. [Google Scholar]
- Meyer, D.; Körber, M.; Senner, V.; Tomizuka, M. Regulating the Heart Rate of Human–Electric Hybrid Vehicle Riders Under Energy Consumption Constraints Using an Optimal Control Approach. IEEE Trans. Control Syst. Technol. 2019, 27, 2125–2138. [Google Scholar] [CrossRef]
- Sweeney, S.; Ordóñez-Hurtado, R.; Pilla, F.; Russo, G.; Timoney, D.; Shorten, R. A Context-Aware E-Bike System to Reduce Pollution Inhalation While Cycling. IEEE Trans. Intell. Transp. Syst. 2019, 20, 704–715. [Google Scholar] [CrossRef]
- Iglesia, D.H.D.L.; Paz, J.F.D.; González, G.V.; Barriuso, A.L.; Bajo, J.; Corchado, J.M. Increasing the Intensity over Time of an Electric-Assist Bike Based on the User and Route: The Bike Becomes the Gym. Sensors 2018, 18, 220. [Google Scholar] [CrossRef] [PubMed]
- Tal, I.; Ciubotaru, B.; Muntean, G. Vehicular-Communications-Based Speed Advisory System for Electric Bicycles. IEEE Trans. Veh. Technol. 2016, 65, 4129–4143. [Google Scholar] [CrossRef]
- Morchin, W.C. Battery-powered electric bicycles. Proceedings of NORTHCON ’94, Seattle, WA, USA, 11–13 October 1994; pp. 269–274. [Google Scholar]
- E-Bike Instruction Manual Bosch Components; Riese & Müller GmbH: Weiterstadt, Germany, 2016. Available online: https://www.r-m.de/media/filer_public/0e/68/0e68a9ce-63ff-4529-b4d5-78ec67163f30/rum_ba_bosch_2017_en_160628_download.pdf (accessed on 11 May 2025).
- Precup, R.E.; Nguyen, A.T.; Blažič, S. A survey on fuzzy control for mechatronics applications. Int. J. Syst. Sci. 2024, 55, 771–813. [Google Scholar] [CrossRef]
- Hsu, R.C.; Liu, C.; Chan, D. A Reinforcement-Learning-Based Assisted Power Management with QoR Provisioning for Human–Electric Hybrid Bicycle. IEEE Trans. Ind. Electron. 2012, 59, 3350–3359. [Google Scholar] [CrossRef]
- Hsu, R.C.; Liu, C.; Lee, W.; Chen, C. A Reinforcement Learning Based Power Assisted Method with Comfort of Riding for Light Electric Vehicle. In Proceedings of the in 2010 IEEE 71st Vehicular Technology Conference, Taipei, Taiwan, 16–19 May 2010; pp. 1–5. [Google Scholar]
- Bui, V.-T.; Dow, C.-R.; Huang, Y.-C.; Liu, P.; Thai, V.D. A CANopen-Based Gateway and Energy Monitoring System for Electric Bicycles. Energies 2020, 13, 3766. [Google Scholar] [CrossRef]
- Schirmer, M.; Höpfner, H. Smartphone Hardware Sensors. Available online: https://www.uni-weimar.de/kunst-und-gestaltung/wiki/images/Zeitmaschinen-smartphonesensors.pdf (accessed on 11 May 2025).
- Múčka, P. International Roughness Index Thresholds Based on Whole-Body Vibration in Passenger Cars. Transp. Res. Rec. 2021, 2675, 305–320. [Google Scholar] [CrossRef]
- Zhao, Z.; Taghavifar, H.; Du, H.P.; Qin, Y.C.; Dong, M.M.; Gu, L. In-Wheel Motor Vibration Control for Distributed-Driven Electric Vehicles: A Review. IEEE Trans. Transp. Electrif. 2021, 7, 2864–2880. [Google Scholar] [CrossRef]
- Doria, A.; Marconi, E.; Munoz, L.; Polanco, A.; Suarez, D. An Experimental-Numerical Method for the Prediction of On-Road Comfort of City Bicycles. Veh. Syst. Dyn. 2021, 59, 1376–1396. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Sahandabadi, S.; Bhawya; Ahamed, M.J. Application of MEMS Accelerometers in Dynamic Vibration Monitoring of a Vehicle. Micromachines 2023, 14, 923. [Google Scholar] [CrossRef]
- Wang, L. PID Control System Design and Automatic Tuning Using MATLAB/SIMULINK; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020. [Google Scholar]


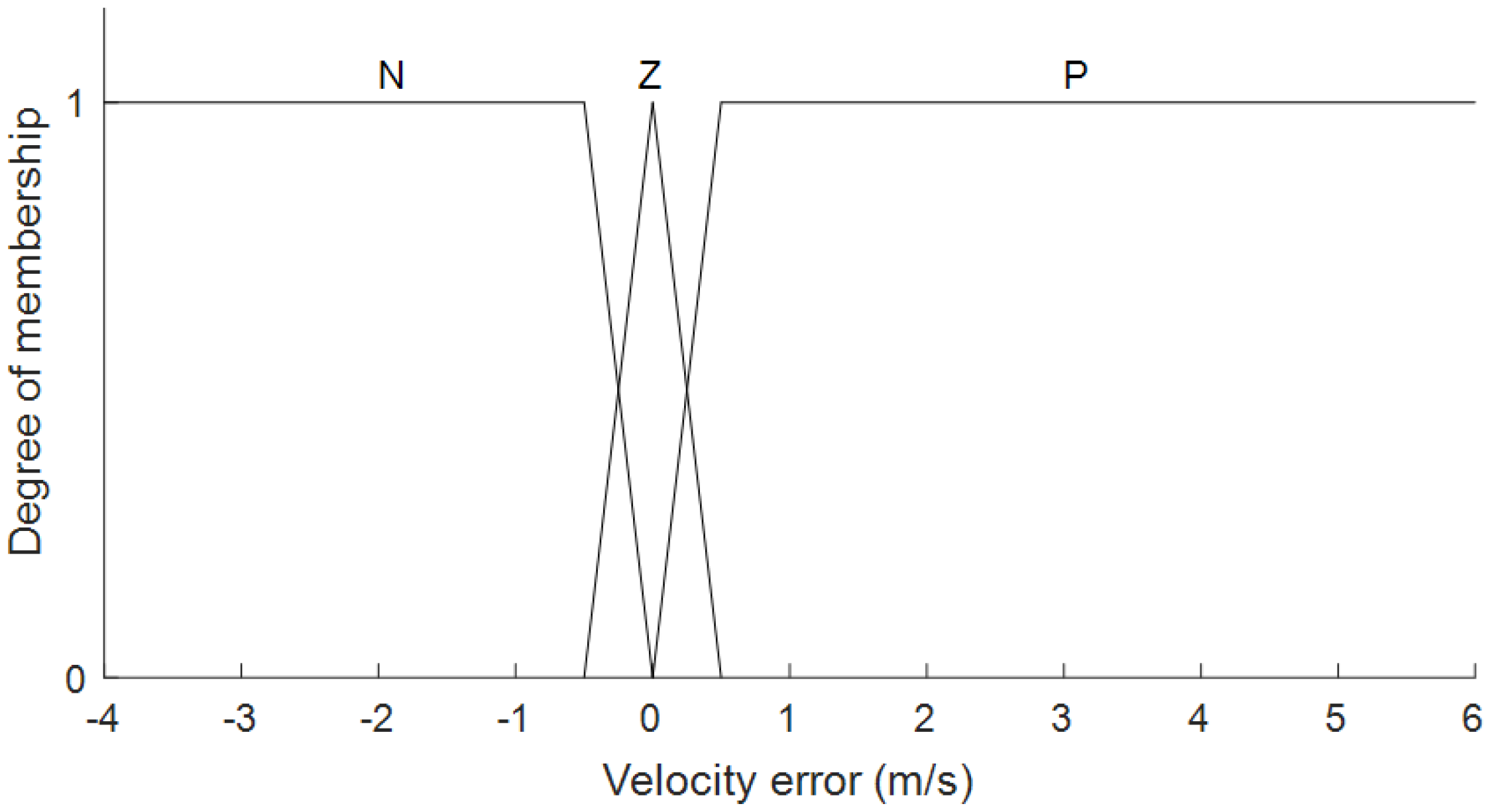
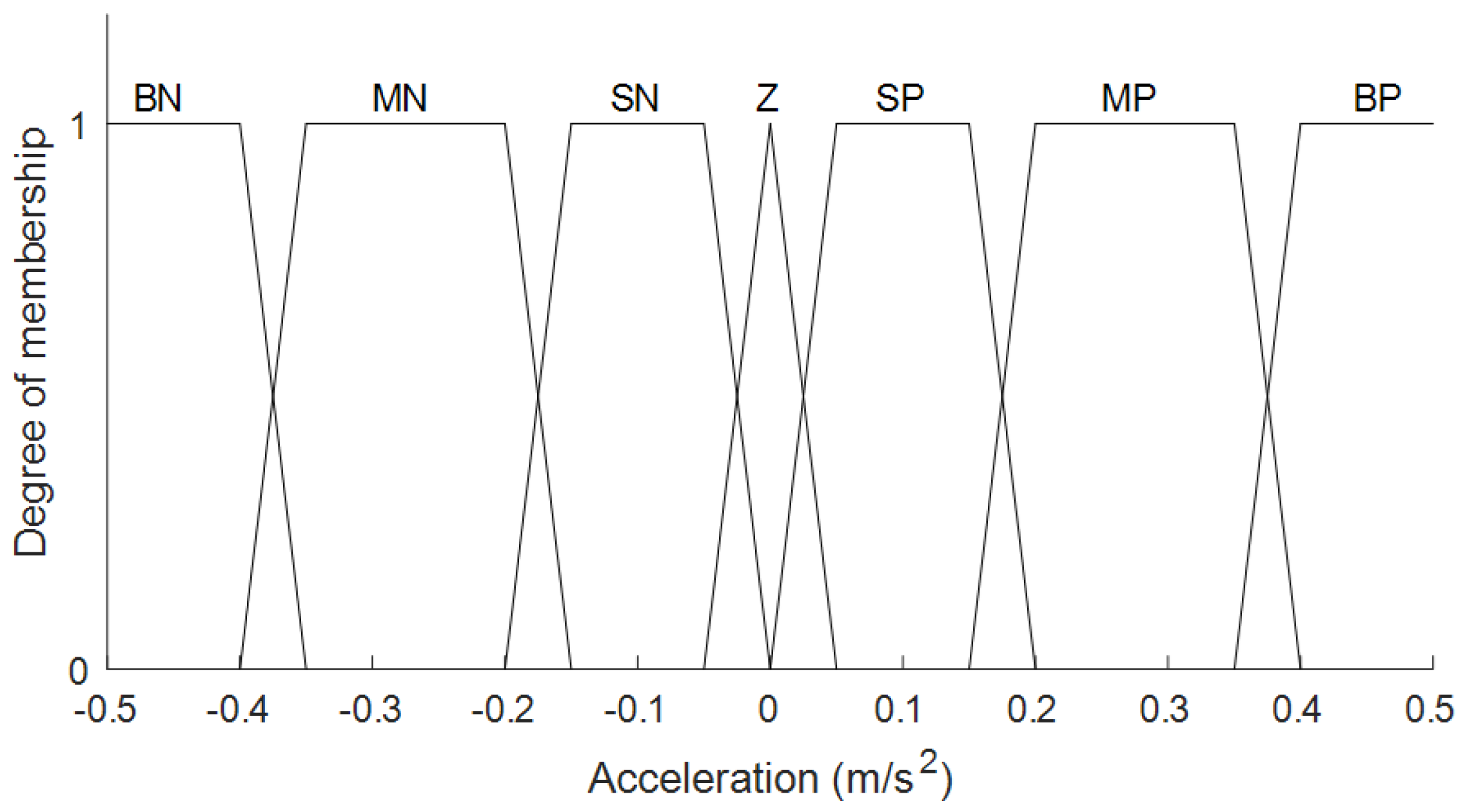



| Output | |
| Negative | −1 |
| Zero | 0 |
| Positive | Table 2 |
| Acceleration | Velocity Error | ||
|---|---|---|---|
| Negative | Zero | Positive | |
| Big negative | +0.4 | +0.6 | +1.0 |
| Medium negative | +0.2 | +0.4 | +0.8 |
| Small negative | +0.2 | +0.6 | |
| Zero | +1.0 | ||
| Small positive | +0.6 | ||
| Medium positive | |||
| Big positive | |||
| Parameter | Description | Value |
|---|---|---|
| Maximum of assistance-level output L | 3 | |
| Expected velocity | 18 km/h | |
| k | Ratio between middle gear and rear gear | 4 |
| CZ | Comfortable zone | 16 to 20 km/h |
| SZ | Safety zone | −0.4 to 0.4 m/ |
| Vibration limit | 1.2 m/ | |
| T | Controller cycle time | 1 s |
| n | Number of samples of vibration per controller cycle time | 50 |
| Parameter | Description | Value |
|---|---|---|
| E-bike mass | 22 kg | |
| Radius of the rear wheel | 27 in | |
| k | Ratio between middle gear and rear gear | 4 |
| N | Number of assistance levels | 4 |
| Velocity point from that the assistance ratio decreases | 24 km/h | |
| Velocity point from that the assistance ratio is zero | 28 km/h | |
| Maximum assistance ratio when L = 0 | 0% | |
| Maximum assistance ratio when L = 1 | 100% | |
| Maximum assistance ratio when L = 2 | 220% | |
| Maximum assistance ratio when L= 3 | 340% |
| Parameter | Description | Value |
|---|---|---|
| Rolling friction coefficient | 0.008 | |
| g | Gravitational acceleration | 9.8 m/ |
| Atmospheric drag coefficient | 0.5 | |
| Vehicle frontal area | 1 | |
| Air density | 1.18 kg/ |
| Method | Ratio of Speed Control (%) | Ratio of Acceleration Control (%) |
|---|---|---|
| Manual | - | 99.37 |
| PID | 80.67 | 95.30 |
| Fuzzy1 | 82.13 | 98.01 |
| Our proposed | 83.97 | 99.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, C.-L.; Bui, V.-T.; Dow, C.-R.; Chang, S.-M.; Lu, Y.-E. A Road-Adaptive Vibration Reduction System with Fuzzy PI Control Approach for Electric Bicycles. World Electr. Veh. J. 2025, 16, 276. https://doi.org/10.3390/wevj16050276
Meng C-L, Bui V-T, Dow C-R, Chang S-M, Lu Y-E. A Road-Adaptive Vibration Reduction System with Fuzzy PI Control Approach for Electric Bicycles. World Electric Vehicle Journal. 2025; 16(5):276. https://doi.org/10.3390/wevj16050276
Chicago/Turabian StyleMeng, Chao-Li, Van-Tung Bui, Chyi-Ren Dow, Shun-Ming Chang, and Yueh-E (Bonnie) Lu. 2025. "A Road-Adaptive Vibration Reduction System with Fuzzy PI Control Approach for Electric Bicycles" World Electric Vehicle Journal 16, no. 5: 276. https://doi.org/10.3390/wevj16050276
APA StyleMeng, C.-L., Bui, V.-T., Dow, C.-R., Chang, S.-M., & Lu, Y.-E. (2025). A Road-Adaptive Vibration Reduction System with Fuzzy PI Control Approach for Electric Bicycles. World Electric Vehicle Journal, 16(5), 276. https://doi.org/10.3390/wevj16050276








