Improving State-of-Health Estimation for Lithium-Ion Batteries Based on a Generative Adversarial Network and Partial Discharge Profiles
Abstract
1. Introduction
- Lack of task-specific datasets for SOH estimation under partial and low-SOC conditions. The existing studies largely depend on full-cycle data, which is not feasible for real-time EV monitoring. Public datasets rarely capture low-SOC partial discharge profiles in a volume sufficient for effective model training.
- Insufficient robustness and accuracy of existing SOH estimation models under low-SOC conditions. While models such as TCNs are effective in some scenarios, their accuracy degrades in sparse or low-voltage regions. Moreover, few studies integrate data augmentation techniques, such as GANs, to address these limitations.
- A data augmentation strategy based on the GAN is proposed to address the limitation of insufficient training data. The GAN model was tailored to match the distributional characteristics of battery discharge data, enabling the generation of high-quality synthetic datasets.
- A TCN-based SOH estimation framework was developed for partial discharge profiles. The proposed method significantly improved the prediction accuracy in both constrained low-SOC scenarios and broader applications involving full-range SOC profiles.
- An integrated framework is presented for SOH estimation from partial discharge profiles under data-scarce conditions, combining synthetic data generation, segmentation, and temporal modeling to achieve robust and accurate predictions.
2. The Analysis of the Dataset
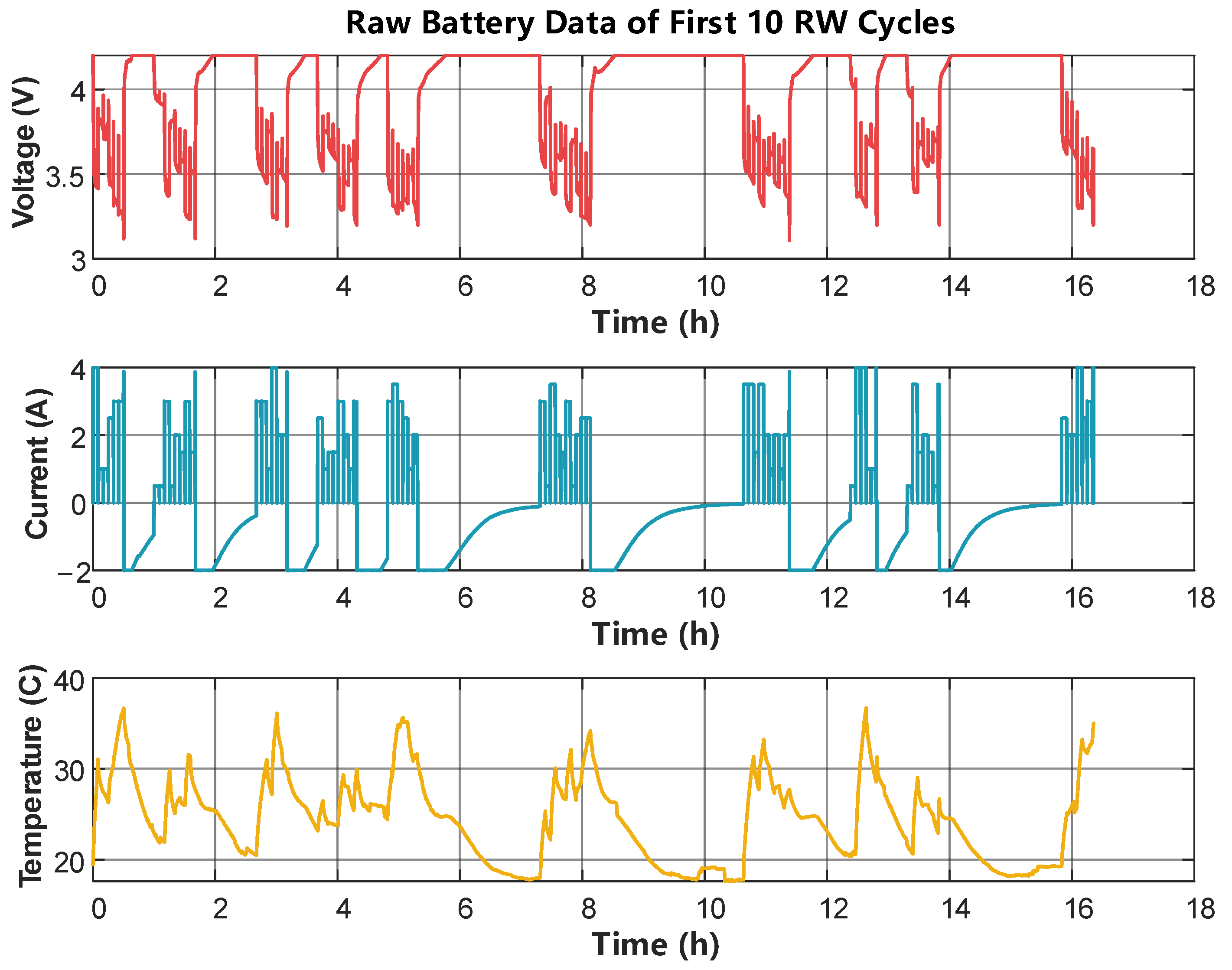
2.1. Dataset Introduction
2.2. Definition of SOH
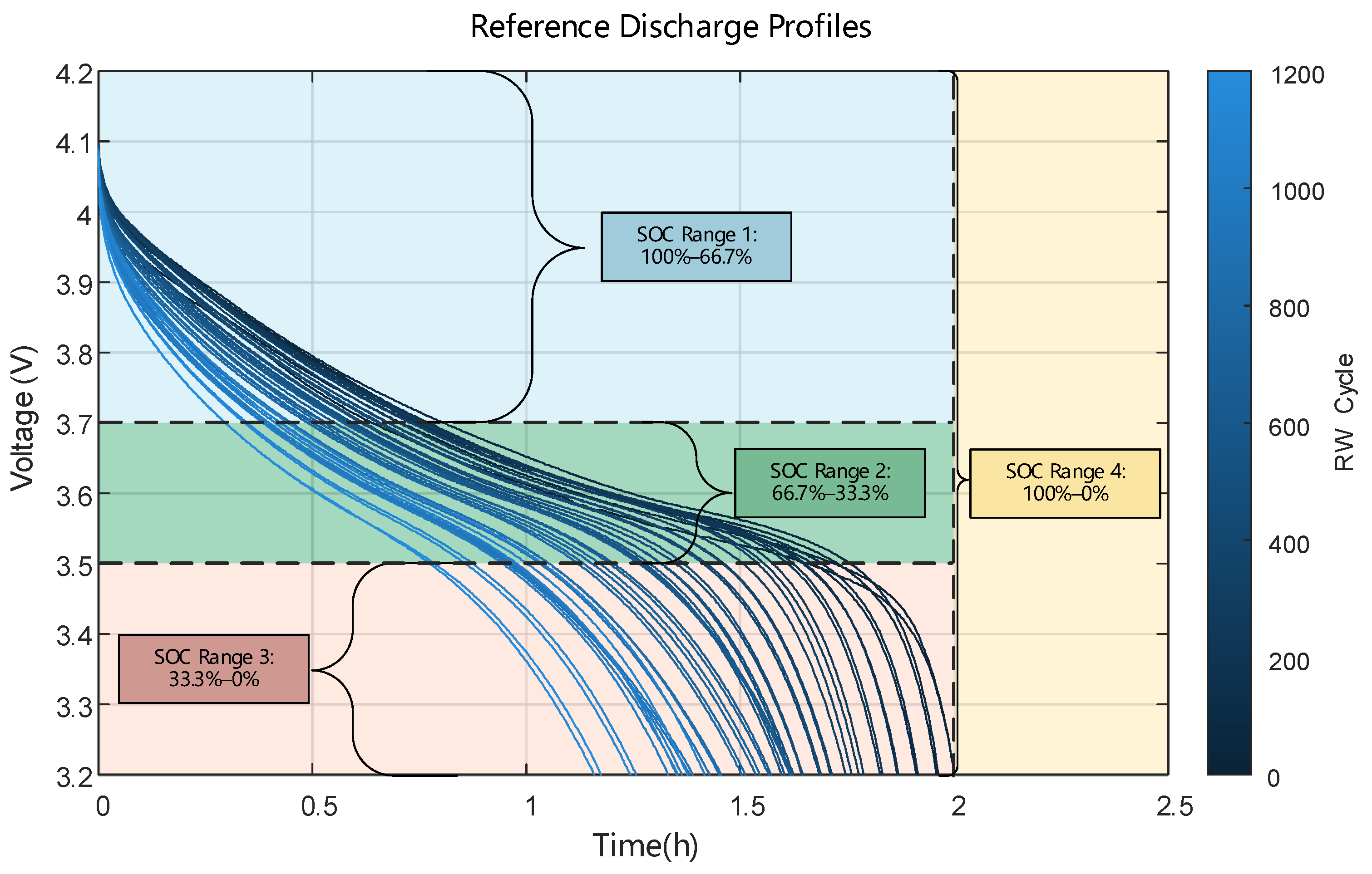
2.3. Partial Discharge Profiles
3. Data Augmentation Using GAN
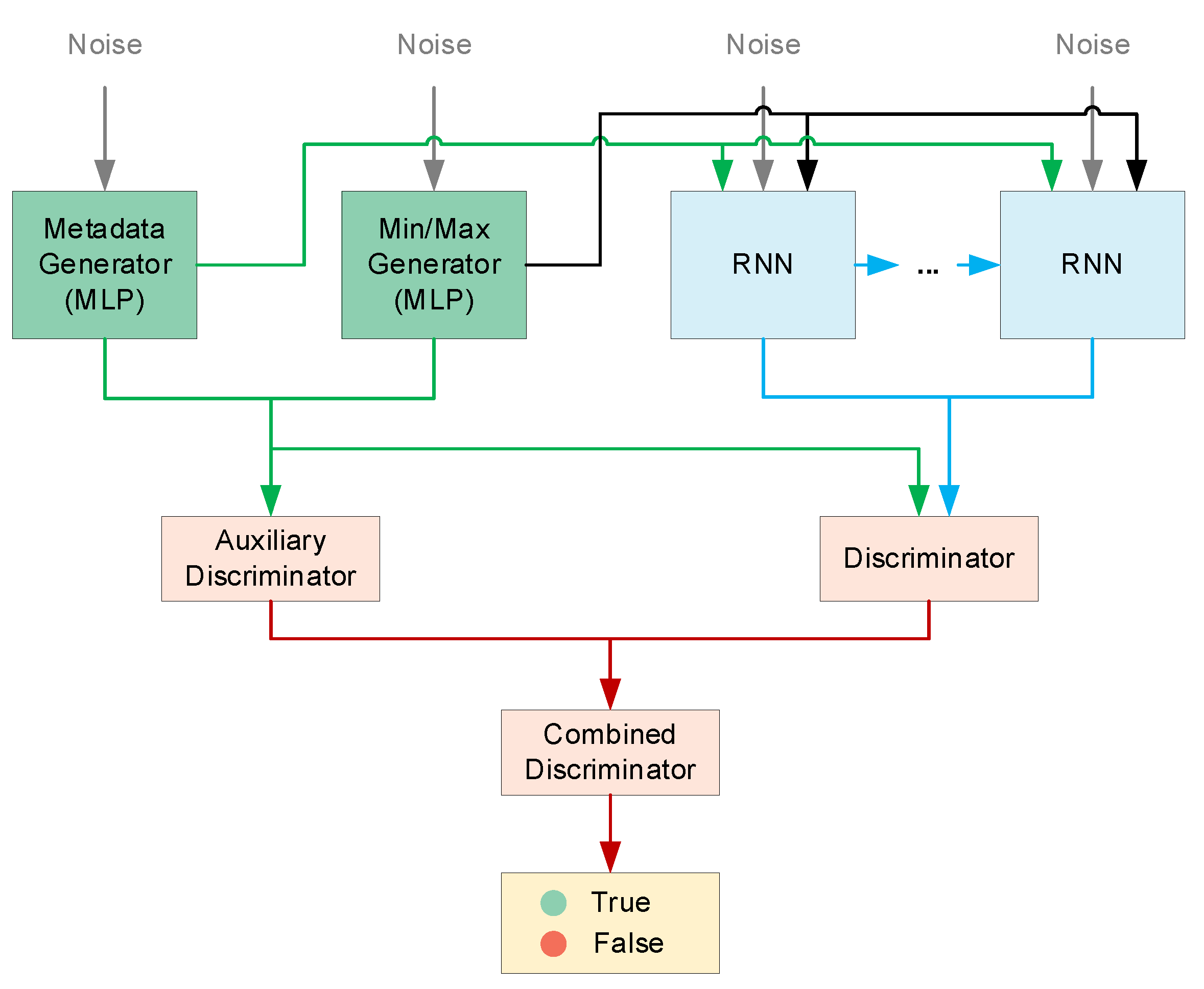
3.1. Metadata Generator
3.2. Time Series Generator
3.3. Discriminator
3.4. Normalization Mechanism and Mode Collapse Prevention
4. Estimation of SOH Through TCN
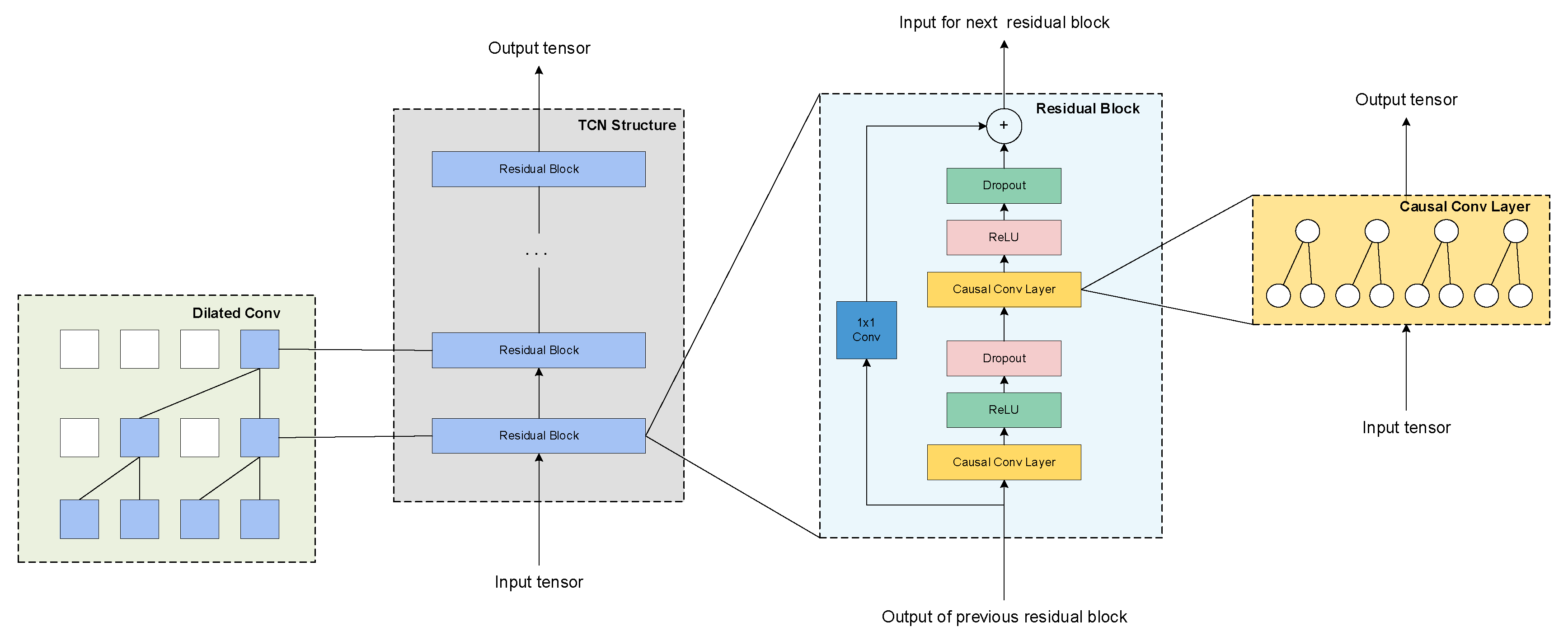
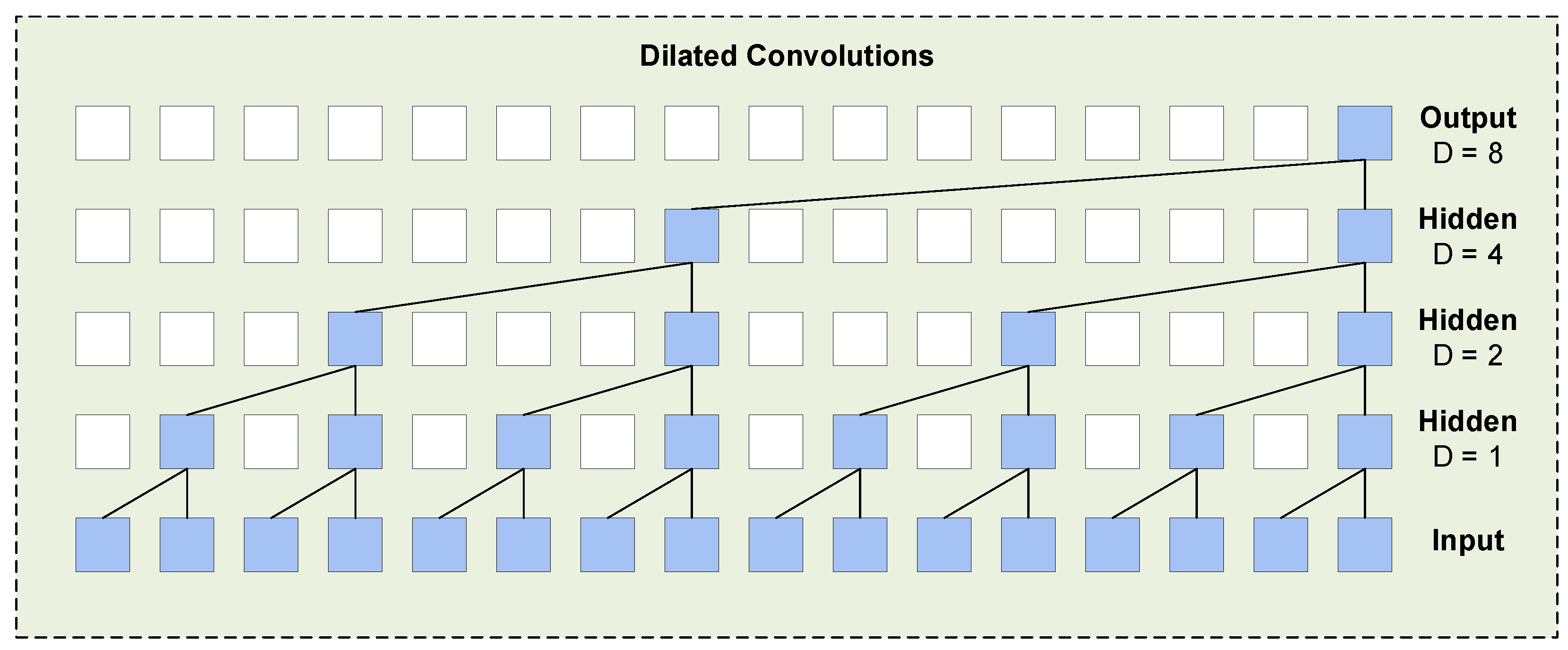
4.1. Dilated Convolutional Networks
4.2. Causal Convolutional Networks
4.3. Residual Blocks
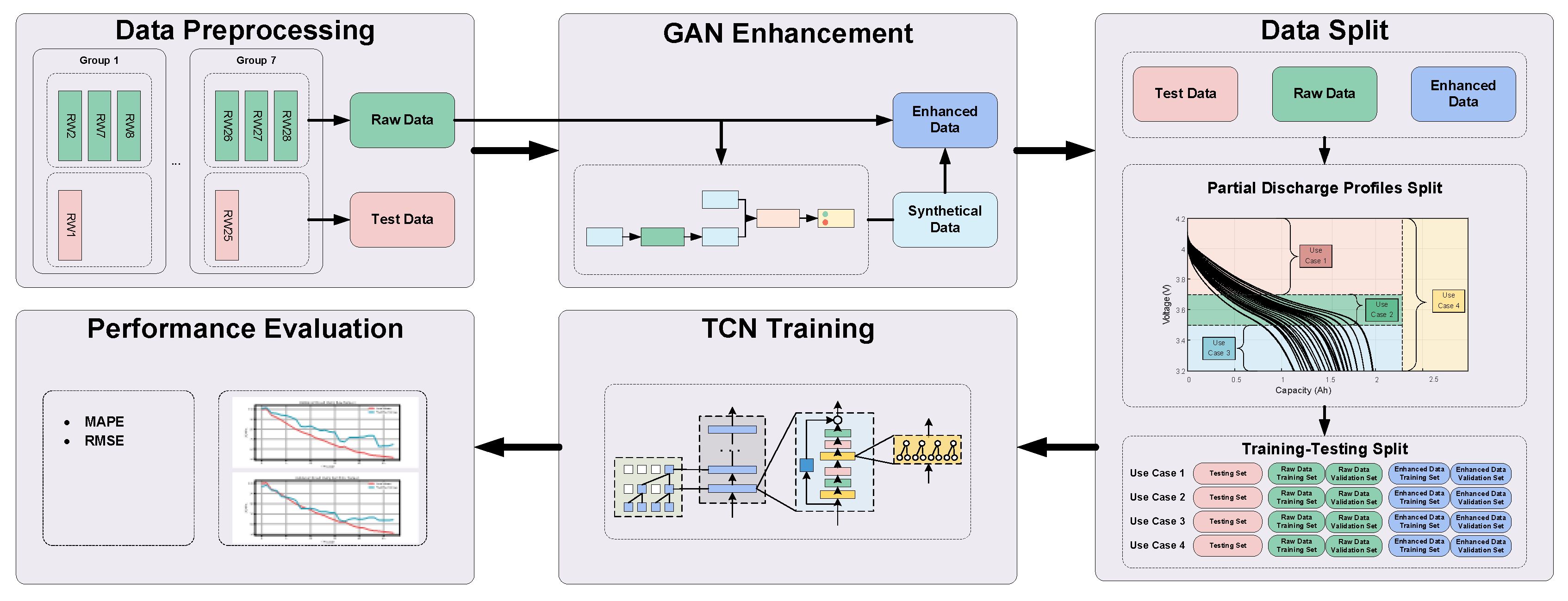
5. Method and Procedure
5.1. Data Preprocessing
5.2. GAN Enhancement
5.3. Data Split
5.4. TCN Training
5.5. Performance Evaluation
6. Experimentation and Analysis
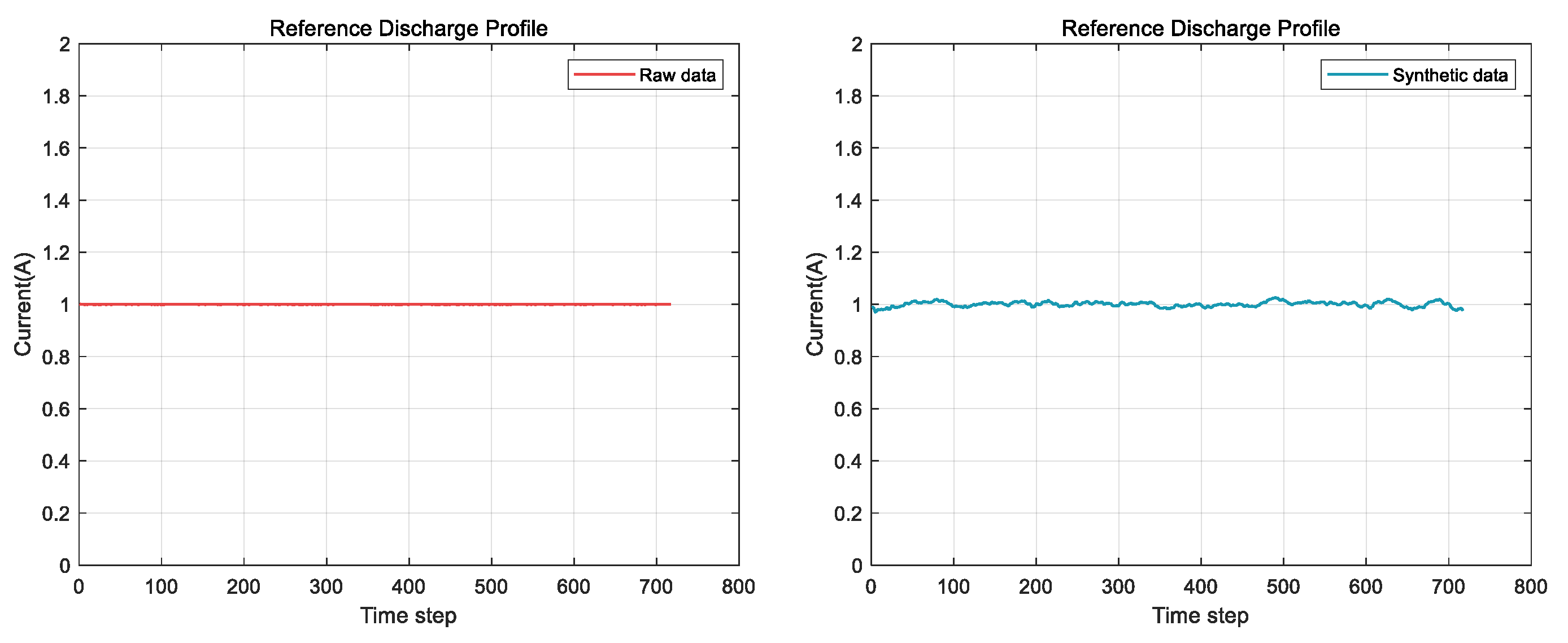
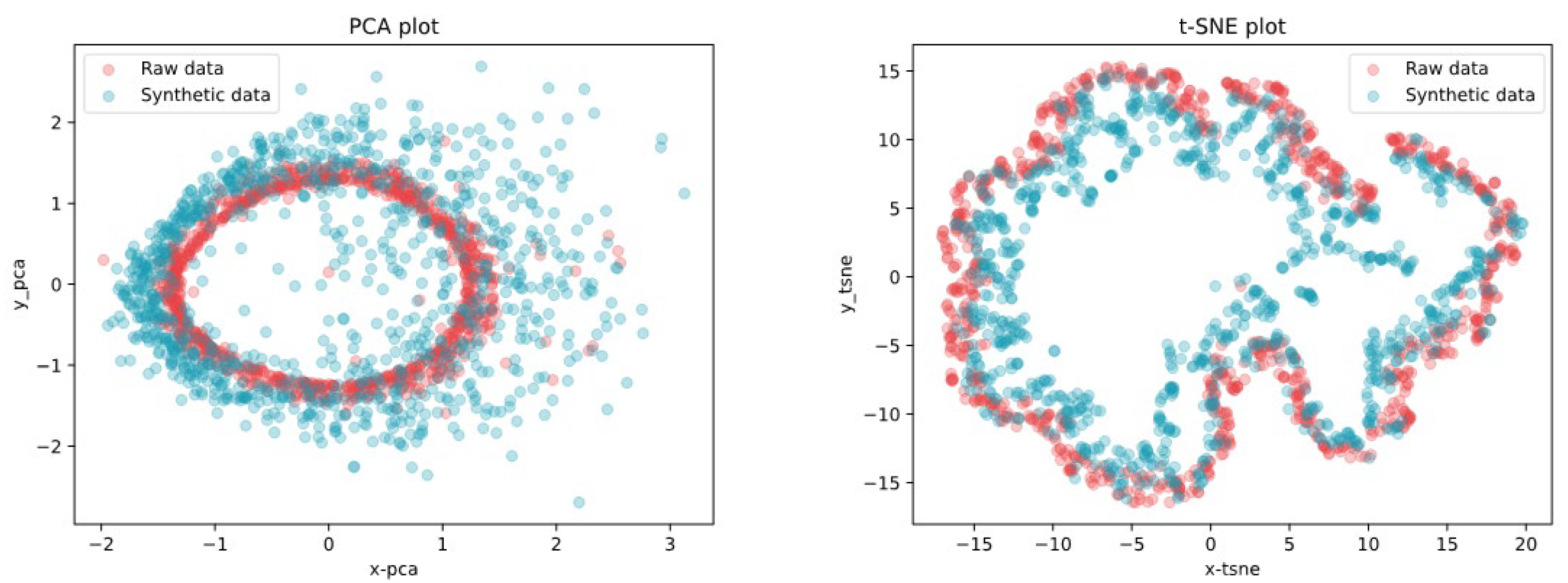
6.1. GAN-Based Synthetic Data Generation and Evaluation
6.2. TCN-Based SOH Estimation Using Partial Discharge Profiles
7. Conclusions
- The framework only incorporated voltage and current, excluding other relevant indicators, such as temperature, impedance, or internal resistance.
- The evaluation was validated solely on the NASA dataset, and the generalizability of the proposed method to other battery types or operational environments has yet to be tested.
- Integrating multi-modal sensor data to further enhance the reliability of SOH estimation;
- Verifying the transferability of the approach to different datasets and real-world usage scenarios;
- Investigating more advanced temporal architectures, such as attention-based models and graph neural networks to improve the modeling of battery degradation patterns.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Chen, S.; Dai, F.; Cai, M. Opportunities and Challenges of High-Energy Lithium Metal Batteries for Electric Vehicle Applications. ACS Energy Lett. 2020, 5, 3140–3151. [Google Scholar] [CrossRef]
- Niu, H.; Zhang, N.; Lu, Y.; Zhang, Z.; Li, M.; Liu, J.; Zhang, N.; Song, W.; Zhao, Y.; Miao, Z. Strategies toward the Development of High-Energy-Density Lithium Batteries. J. Energy Storage 2024, 88, 111666. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A Single Particle Model with Chemical/Mechanical Degradation Physics for Lithium Ion Battery State of Health (SOH) Estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Lin, M.; Yan, C.; Wang, W.; Dong, G.; Meng, J.; Wu, J. A Data-Driven Approach for Estimating State-of-Health of Lithium-Ion Batteries Considering Internal Resistance. Energy 2023, 277, 127675. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of Health-State Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D.U. Characterization of High-Power Lithium-Ion Batteries by Electrochemical Impedance Spectroscopy. I. Experimental Investigation. J. Power Sources 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Li, C.; Yang, L.; Li, Q.; Zhang, Q.; Zhou, Z.; Meng, Y.; Zhao, X.; Wang, L.; Zhang, S.; Li, Y.; et al. SOH Estimation Method for Lithium-Ion Batteries Based on an Improved Equivalent Circuit Model via Electrochemical Impedance Spectroscopy. J. Energy Storage 2024, 86, 111167. [Google Scholar] [CrossRef]
- Demirci, O.; Taskin, S.; Schaltz, E.; Acar Demirci, B. Review of Battery State Estimation Methods for Electric Vehicles-Part II: SOH Estimation. J. Energy Storage 2024, 96, 112703. [Google Scholar] [CrossRef]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-Board State of Health Monitoring of Lithium-Ion Batteries Using Incremental Capacity Analysis with Support Vector Regression. J. Power Sources 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, J.; Chen, Z.; Liu, Y. Online Diagnosis of State of Health for Lithium-Ion Batteries Based on Short-Term Charging Profiles. J. Power Sources 2020, 471, 228478. [Google Scholar] [CrossRef]
- Lyu, C.; Lai, Q.; Ge, T.; Yu, H.; Wang, L.; Ma, N. A Lead-Acid Battery’s Remaining Useful Life Prediction by Using Electrochemical Model in the Particle Filtering Framework. Energy 2017, 120, 975–984. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Feng, X. State-of-Health Estimation and Remaining-Useful-Life Prediction for Lithium-Ion Battery Using a Hybrid Data-Driven Method. IEEE Trans. Veh. Technol. 2020, 69, 10854–10867. [Google Scholar] [CrossRef]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Sun, S.; Sun, J.; Wang, Z.; Zhou, Z.; Cai, W. Prediction of Battery SOH by CNN-BiLSTM Network Fused with Attention Mechanism. Energies 2022, 15, 4428. [Google Scholar] [CrossRef]
- Petkovski, E.; Marri, I.; Cristaldi, L.; Faifer, M. State of Health Estimation Procedure for Lithium-Ion Batteries Using Partial Discharge Data and Support Vector Regression. Energies 2024, 17, 206. [Google Scholar] [CrossRef]
- Saxena, S.; Hendricks, C.; Pecht, M. Cycle Life Testing and Modeling of Graphite/LiCoO2 Cells under Different State of Charge Ranges. J. Power Sources 2016, 327, 394–400. [Google Scholar] [CrossRef]
- Zhao, C.; Andersen, P.B.; Træholt, C.; Hashemi, S. Data-Driven Battery Health Prognosis with Partial-Discharge Information. J. Energy Storage 2023, 65, 107151. [Google Scholar] [CrossRef]
- Yu, P.; Zhou, C.; Yu, Y.; Chang, Z.; Li, X.; Huang, K.; Yu, J.; Yan, K.; Jiang, X.; Su, Y. Improved PSO-TCN Model for SOH Estimation Based on Accelerated Aging Test for Large Capacity Energy Storage Batteries. J. Energy Storage 2025, 108, 115031. [Google Scholar] [CrossRef]
- Fan, C.; Sun, J.; Wang, H. SOH Estimation of Lithium-Ion Batteries Based on Raw Charging Data and TCN. In Proceedings of the 2024 4th International Conference on Energy, Power and Electrical Engineering (EPEE), Wuhan, China, 20–22 September 2024; pp. 699–702. [Google Scholar]
- Bockrath, S.; Lorentz, V.; Pruckner, M. State of Health Estimation of Lithium-Ion Batteries with a Temporal Convolutional Neural Network Using Partial Load Profiles. Appl. Energy 2023, 329, 120307. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Li, Q. Generative Adversarial Network and Transfer-Learning-Based Fault Detection for Rotating Machinery with Imbalanced Data Condition. Meas. Sci. Technol. 2022, 33, 045103. [Google Scholar] [CrossRef]
- Bui, V.; Pham, T.L.; Nguyen, H.; Jang, Y.M. Data Augmentation Using Generative Adversarial Network for Automatic Machine Fault Detection Based on Vibration Signals. Appl. Sci. 2021, 11, 2166. [Google Scholar] [CrossRef]
- Shangguan, A.; Xie, G.; Fei, R.; Mu, L.; Hei, X. Train Wheel Degradation Generation and Prediction Based on the Time Series Generation Adversarial Network. Reliab. Eng. Syst. Saf. 2023, 229, 108816. [Google Scholar] [CrossRef]
- Seol, S.; Lee, J.; Yoon, J.; Kim, B. Improving SOH Estimation for Lithium-Ion Batteries Using TimeGAN. Mach. Learn. Sci. Technol. 2023, 4, 045007. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.S.; Daigle, M. Adaptation of an Electrochemistry-Based Li-Ion Battery Model to Account for Deterioration Observed Under Randomized Use. Annu. Conf. PHM Soc. 2014, 6, 1–9. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.S.; Daigle, M. “Randomized Battery Usage Data Set”. NASA Prognostics Data Repository. NASA Ames Research Center, Moffett Field, CA, USA, 2014. Available online: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/ (accessed on 10 July 2024).
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Curran Associates, Inc.: New York, NY, USA, 2014; Volume 27. [Google Scholar]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-Valued (Medical) Time Series Generation with Recurrent Conditional GANs. Available online: https://arxiv.org/abs/1706.02633v2 (accessed on 23 April 2025).
- Yoon, J.; Jarrett, D.; van der Schaar, M. Time-Series Generative Adversarial Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Lin, Z.; Jain, A.; Wang, C.; Fanti, G.; Sekar, V. Using GANs for Sharing Networked Time Series Data: Challenges, Initial Promise, and Open Questions. In Proceedings of the ACM Internet Measurement Conference, New York, NY, USA, 27 October 2020; Virtual Event USA; ACM: New York, NY, USA, 2020; pp. 464–483. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shen, S.; Sadoughi, M.; Li, M.; Wang, Z.; Hu, C. Deep Convolutional Neural Networks with Ensemble Learning and Transfer Learning for Capacity Estimation of Lithium-Ion Batteries. Appl. Energy 2020, 260, 114296. [Google Scholar] [CrossRef]
- State-of-Health Estimation of Li-Ion Batteries in Electric Vehicle Using IndRNN under Variable Load Condition. Available online: https://www.mdpi.com/1996-1073/12/22/4338 (accessed on 23 April 2025).
- A Computationally Efficient Approach for the State-of-Health Estimation of Lithium-Ion Batteries. Available online: https://www.mdpi.com/1996-1073/16/14/5414 (accessed on 23 April 2025).
- Ye, J.; Xie, Q.; Lin, M.; Wu, J. A Method for Estimating the State of Health of Lithium-Ion Batteries Based on Physics-Informed Neural Network. Energy 2024, 294, 130828. [Google Scholar] [CrossRef]



| Battery Key Characteristics | Specifications |
|---|---|
| Manufacturer | LG Chem |
| Battery chemistry | Lithium cobalt oxide vs. graphite |
| Nominal capacity | 2.1 Ah |
| Lower cut-off voltage | 3.2 V |
| Upper threshold voltage | 4.2 V |
| Group (Cells Id) | Test Conditions |
|---|---|
| Group 1 (RW1, RW2, RW7, RW8) | Randomized charging (0.5–3 h) to 4.2 V and discharging to 3.2 V, with currents between −0.5 A and −4 A. Reference tests every 50 cycles. |
| Group 2 (RW3–RW6) | Non-randomized charging to 4.2 V and discharging to 3.2 V, with randomized currents (−0.5 A to −4 A). Reference tests every 50 cycles. |
| Group 3 (RW9–RW12) | Charging and discharging with randomized current pulses (30 min–3 h). Discharging currents between −0.5 A and −4 A. Reference tests every 1500 cycles. |
| Group 4 (RW13–RW16) | Charging to 4.2 V and discharging to 3.2 V, with customized probability distribution (peak at 4 A). Load points are updated every minute. Tests at ~40 °C. Reference tests every 50 cycles. |
| Group 5 (RW17–RW20) | Same as Group 4, but the ambient temperature was not strictly controlled (lower than 40 °C). Reference tests every 50 cycles. |
| Group 6 (RW21–RW24) | Same as Group 4, but the probability distribution skewed toward lower currents (peak at 2 A). Tests at ~40 °C. Reference tests every 50 cycles. |
| Group 7 (RW25–RW28) | Same as Group 6, but the ambient temperature was not strictly controlled (lower than 40 °C). Reference tests every 50 cycles. |
| Use Case | SOC Ranges | Voltage Ranges |
|---|---|---|
| 1 | 100% to 66.7% | 4.2 V to 3.7 V |
| 2 | 66.7% to 33.3% | 3.7 V to 3.5 V |
| 3 | 33.3% to 0% | 3.5 V to 3.2 V |
| 4 | 100% to 0% | 4.2 V to 3.2 V |
| Hyperparameters | Values |
|---|---|
| max_sequence_len | 700 |
| sample_len | 500 |
| batch_size | 1000 |
| generator_learning_rate | 1 × 10−4 |
| discriminator_learning_rate | 1 × 10−4 |
| Epochs | 5000 |
| Data Source | Wasserstein Distance (<0.05) | KL Divergence (<2) |
|---|---|---|
| voltage | 0.0094 | 0.6817 |
| current | 0.0267 | 1.2137 |
| Hyperparameters | Values |
|---|---|
| input_size | 1 |
| output_size | 1 |
| kernel_size | 3 |
| dropout | 0.33 |
| Dilation | [1, 2, 4, 8, 16, 32, 64] |
| earning_rate | 0.001 |
| epochs | 5000 |
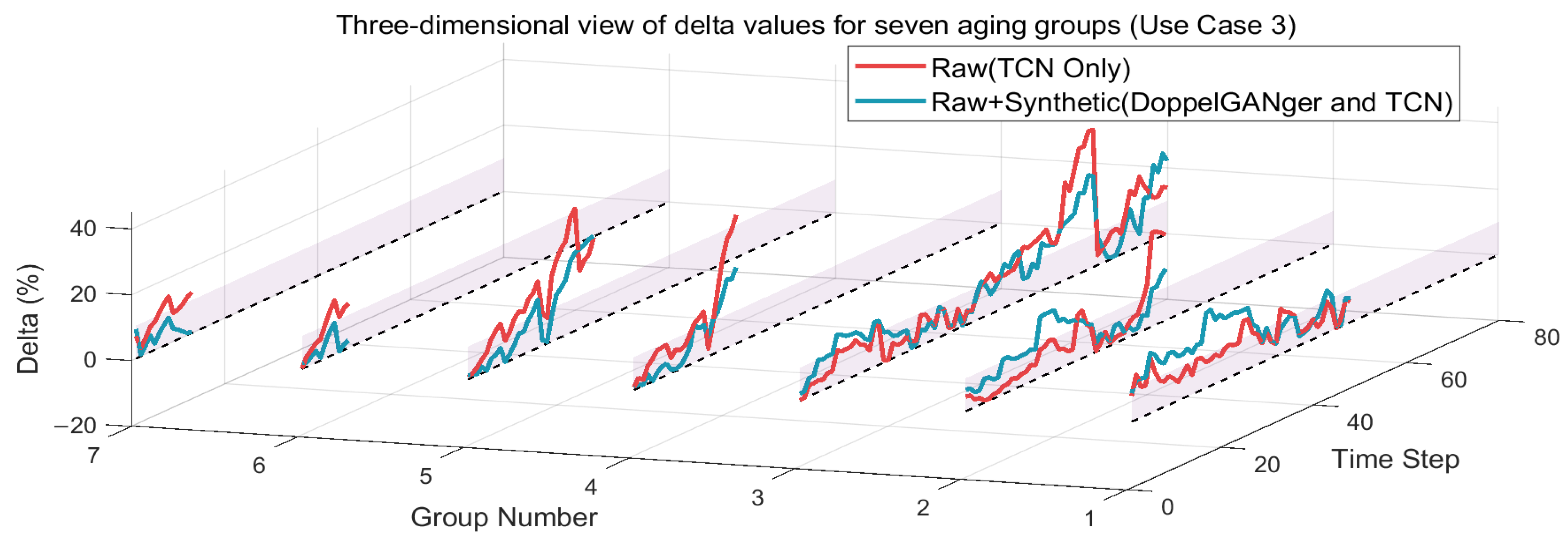
| Group | Raw Data (TCN Only) | Raw + Synthetic Data (DoppelGANger and TCN) | ||
|---|---|---|---|---|
| MAPE | RMSE | MAPE | RMSE | |
| 1 | 8.2710% | 0.0749 | 11.9831% | 0.1121 |
| 2 | 6.9889% | 0.0624 | 8.8346% | 0.0772 |
| 3 | 11.0467% | 0.0745 | 10.0822% | 0.0684 |
| 4 | 12.2142% | 0.0936 | 7.1604% | 0.0571 |
| 5 | 15.2889% | 0.1065 | 9.8016% | 0.0741 |
| 6 | 8.8731% | 0.0825 | 3.2651% | 0.0359 |
| 7 | 9.1879% | 0.0819 | 3.6310% | 0.0409 |
| References | Methods | Conditions | RMSE |
|---|---|---|---|
| [22] | TCN | Partial discharge profiles (Use Case 3) | 0.131 |
| Present work | DoppelGANger and TCN | Partial discharge profiles (Use Case 3) | 0.078 |
| [34] | DCNN | Full discharge profiles | 0.015~0.037 |
| [35] | IndRNN | Full discharge profiles | 0.017~0.03 |
| [36] | LightGBM-WQR | Full discharge profiles | 0.0136~0.0286 |
| [37] | Physics-informed Model | Full discharge profiles | 0.008–0.015 |
| [22] | TCN | Full discharge profiles (Use Case 4) | 0.01 |
| Present work | DoppelGANger and TCN | Full discharge profiles (Use Case 4) | 0.0061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Lai, Y.-H. Improving State-of-Health Estimation for Lithium-Ion Batteries Based on a Generative Adversarial Network and Partial Discharge Profiles. World Electr. Veh. J. 2025, 16, 277. https://doi.org/10.3390/wevj16050277
Zhang H, Lai Y-H. Improving State-of-Health Estimation for Lithium-Ion Batteries Based on a Generative Adversarial Network and Partial Discharge Profiles. World Electric Vehicle Journal. 2025; 16(5):277. https://doi.org/10.3390/wevj16050277
Chicago/Turabian StyleZhang, Hangyu, and Yi-Horng Lai. 2025. "Improving State-of-Health Estimation for Lithium-Ion Batteries Based on a Generative Adversarial Network and Partial Discharge Profiles" World Electric Vehicle Journal 16, no. 5: 277. https://doi.org/10.3390/wevj16050277
APA StyleZhang, H., & Lai, Y.-H. (2025). Improving State-of-Health Estimation for Lithium-Ion Batteries Based on a Generative Adversarial Network and Partial Discharge Profiles. World Electric Vehicle Journal, 16(5), 277. https://doi.org/10.3390/wevj16050277








