Abstract
To optimize the modulated vibration generated by the integer-slot interior permanent magnet synchronous motor (IPMSM), a stepwise segmented skewed pole method was proposed, using an 8-pole 48-slot IPMSM as an example. First, the vibration characteristics of the motor were studied, and the theoretical mechanisms of the magnetic field modulation effect and radial force modulation effect were explained. The study showed that high-order radial forces can excite larger low-order vibrations under the influence of radial force modulation. Then, in response to the axial spacing in the linear skewed pole structure when canceling the 48th-order radial force, a stepwise skewed pole structure was proposed. The suppression mechanism of this skewed pole structure on the motor’s modulated vibration was analyzed, and the optimization effect of different segment numbers on the motor’s vibration acceleration at was discussed. Finally, models for the motor’s magnetic field, structural field, and acoustic field before and after skewing were established, and simulations were conducted to compare the magnitudes of the radial forces at each order and their vibration noise performance. The results showed that after stepwise skewed pole optimization, the radial force that excites the modulated vibration was reduced by 68%, the maximum vibration acceleration on the casing surface was reduced by 84%, and the overall noise was reduced by 7.491 dB, effectively suppressing electromagnetic vibration noise.
1. Introduction
To meet the high torque density requirements of electric vehicle drive motors, the d-axis and q-axis magnetic circuits of the motor rotor are often severely coupled, which can lead to a complex airgap flux distribution and generate additional electromagnetic force harmonics, resulting in increased motor vibration and noise. Therefore, the demand for research on vibration and noise in electric vehicle IPMSMs has been growing increasingly [1].
The electromagnetic vibration of IPMSMs is primarily caused by radial excitation forces. Accurately calculating the excitation forces and determining the correlation between excitation forces and electromagnetic vibration are prerequisites for reducing vibration and noise in electric vehicle drive motors [2]. Li et al. [3] comprehensively analyzed the effects of windings, frame end caps, and temperature on the intrinsic frequency of the stator system and experimentally verified how each factor affects the intrinsic frequency of the motor. Yang et al. [4] studied the effect of low-order radial force components on vibration and demonstrated that the minimum nonzero order of the radial force is equal to the greatest common divisor (GCD) of the motor’s pole and slot numbers. Typically, the amplitudes of the zeroth-order and minimum nonzero-order radial forces are large, leading to significant vibration, while higher-order radial forces have smaller amplitudes and contribute less to the vibration, often being ignored [5]. With the development of the general airgap field modulation theory, the analysis of the motor’s physical significance has become increasingly clear [6]. Fang et al. [7] investigated the effect of high-order radial forces on the vibration of fractional-slot permanent magnet motors, finding that high-order radial forces can excite larger low-order vibrations under modulation. Wang et al. [8] analyzed the effect of slot number order radial forces on the motor’s zeroth-order slot-frequency vibration using a 6-pole 36-slot IPMSM as an example. The results showed that, under modulation effects, slot number order radial forces can excite significant zeroth-order vibration.
The ultimate goal of analyzing radial excitation forces and establishing vibration mechanisms is to reduce the electromagnetic vibration of the motor. Methods such as stator skewing, stator tooth slot auxiliary slots, and segmented skewed rotor poles have been widely applied to vibration optimization in PMSMs. Wang et al. [9] proposed a serrated skew structure to address the shortcomings of linear skewed poles and experimentally verified the effectiveness of this structure in suppressing motor vibration. Hong et al. [10] introduced a permanent magnet pole structure with continuous skewed edges to reduce pole-frequency and slot-frequency vibrations, addressing the limitations of the skew slot method in vibration reduction. Peng et al. [11] proposed a rotor segment structure with varying pole widths to reduce the zeroth-order vibration amplitude, overcoming the limitations of traditional skew slots and skewed pole methods in suppressing zeroth-order and pole-multiple order vibrations. Feng et al. [12] analyzed the effect of skew slots on the suppression of sideband noise, compared it with a straight-slot motor, and experimentally validated the effectiveness of the skew slot method in reducing sideband noise. While these methods effectively suppress electromagnetic vibration in motors, they do not consider the impact of tooth modulation effects. Fang et al. [13] proposed a hybrid vibration synthesis analysis method, considering both tooth modulation effects and tangential forces. Zhao et al. [14] comprehensively evaluated the effects of magnetic field modulation, tooth modulation, and other factors, ultimately proposing an unequal tooth design to reduce the seventh-order harmonics generated by evenly distributed fractional-slot concentrated winding permanent magnet synchronous motors, thereby reducing the electromagnetic vibration produced by the motor. Wang et al. [15] proposed a rotor structure with asymmetric magnetic poles and compared the oblique slot and linear oblique pole methods, the results show that the oblique slot method has the best optimization effect and the linear oblique pole has the worst optimization effect, which side by side reflects the limitation of the linear oblique pole on the optimization of vibration and noise performance of the motor.
This paper uses an 8-pole 48-slot IPMSM as an example to introduce in detail the modulated vibration characteristics of this type of motor. Then, a stepwise segmented skewed pole structure is proposed to suppress the modulated vibration excited by high-order radial forces, and its vibration reduction mechanism is analyzed. Finally, simulation analyses of the motor’s vibration and noise levels before and after optimization are conducted to validate the effectiveness of the proposed structure in suppressing motor vibration and noise.
2. Motor Modulated Vibration Mechanism
2.1. Motor Structure
To analyze the vibration characteristics of the integer-slot motor, a dual-V-type 8-pole 48-slot IPMSM designed for electric vehicles is developed. The motor rotor adopts a dual-V-type permanent magnet layout, and a reasonable structural topology is implemented to optimize the magnetic circuit. The two-dimensional structure of the motor is shown in Figure 1. Some important parameters of the motor are shown in Table 1. (In Figure 1, the black part is the positive pole of the magnet, the red part is the A-phase winding, the yellow part is the C-phase winding, and the green part is the B-phase winding).
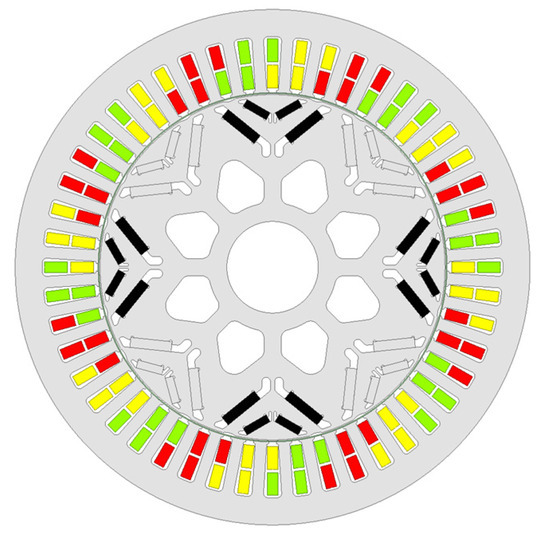
Figure 1.
Two-dimensional cross-sectional view of the motor.

Table 1.
Main parameters of the motor.
To ensure accurate simulation of motor performance parameters, appropriate mesh sizing and solver settings were implemented in ANSYS 2022 R1. The simulation domain employs a 3.5 mm inside mesh for both the motor body and zero-flux boundaries. Considering the critical importance of airgap region for electromagnetic performance evaluation, a refined onside mesh with 0.25 mm element size was specifically applied to the airgap to enhance solution accuracy, as depicted in Figure 2.
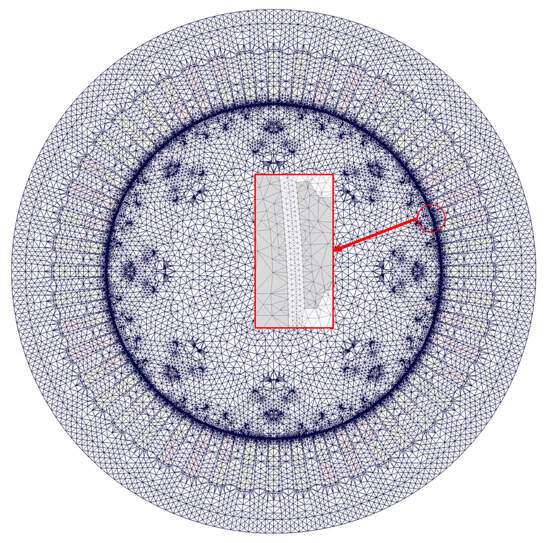
Figure 2.
Finite element mesh.
2.2. Vibration Characteristics
The multi-physical field vibration and noise simulation process of the motor is shown in Figure 3. The finite element method (FEM) is used to calculate the radial force of the motor and the structural modes of the stator housing. Then, the modal superposition method is employed to estimate the harmonic response of the motor [16].
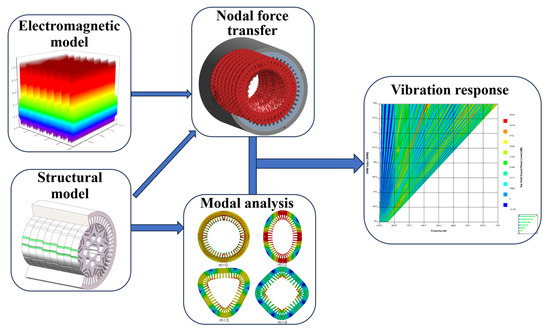
Figure 3.
Flowchart of multi-physics vibration simulation model.
In traditional analysis, the amplitude of low-order radial forces is large and significantly contributes to the vibration of the IPMSM. As shown in Figure 4, except for (where is the supply frequency), the amplitude of the 8th-order radial force is the largest. Therefore, it can be inferred that the 8th-order radial force will excite the dominant vibration of the motor.
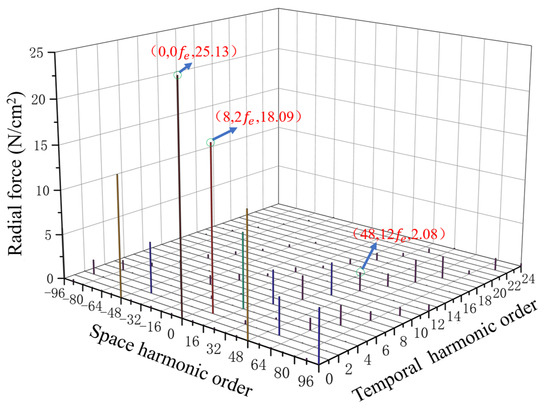
Figure 4.
Two-dimensional fast Fourier decomposition of radial electromagnetic forces.
However, the multi-speed vibration results of the motor under load, simulated using ANSYS software (as shown in Figure 5), indicate that the equivalent radiated sound power level is highest at . Although the amplitude of the radial force at the 48th-order is much smaller than that at the 8th-order , the radial force at this frequency range has a significant impact on the vibration.
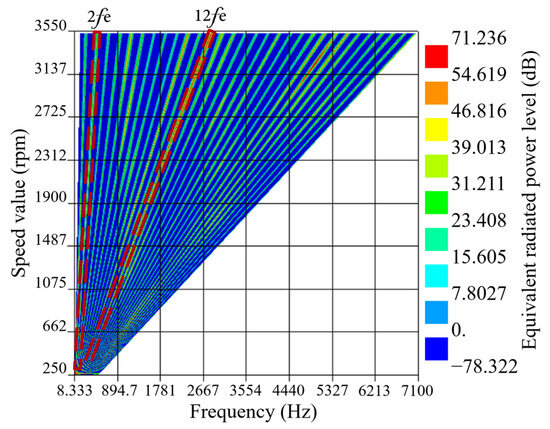
Figure 5.
Equivalent radiant power waterfall diagram.
The amplitude of the stator deformation when the electromagnetic force order can be expressed as follows:
where is the inner radius of the stator; is the average radius of the stator yoke; is the radial thickness of the stator yoke; is the Young’s modulus; is the amplitude of the zeroth-order electromagnetic force; and m is the spatial harmonic order of the electromagnetic force, which is a non-negative integer.
The amplitude of the stator deformation for can be written as follows:
According to Equation (2), it can be seen that when the order of the electromagnetic force is greater than 2, the deformation amplitude of the stator is almost inversely proportional to the fourth power of the electromagnetic force’s spatial order. Typically, the minimum non-zero order of the electromagnetic force is the greatest common divisor (GCD) of the motor’s pole and slot numbers. For an 8-pole, 48-slot IPMSM, the minimum non-zero order is 8, so the deformation amplitude caused by non-zero order electromagnetic forces in this type of motor is minimal.
However, Equations (1) and (2) were established by Jordan based on a two-dimensional toothless cylindrical model [17]. Under the cylindrical approximation theory framework, the slotted stator is simplified as a smooth cylindrical shell for motor vibration analysis. The theory initially assumes perfect matching between the stator deformation mode orders and the spatial orders of radial electromagnetic force waves. Based on Jordan’s formula, it derives an inverse quartic relationship (vibration amplitude ∝ 1/n4) between vibration magnitude and the spatial order of electromagnetic forces, thereby focusing the analysis on low-order force waves. However, this theoretical approach completely neglects the modulation effects induced by stator slotting structures, failing to explain the phenomenon where high-order force waves undergo aliasing into equivalent low-order wave numbers through tooth-slot sampling effects. With the improvement in the accuracy of finite element models and the refinement of airgap field modulation theory, research has shown that, due to the stator slotting effect, the wave number of the stator deformation does not match the wave number of the airgap force. Under the slotting effect, when the spatial order of the electromagnetic force corresponding to the slot number matches the number of stator teeth, it will be modulated into a zeroth-order electromagnetic force wave, thereby generating a zeroth-mode vibration [8].
2.3. Magnetic Modulation Effect
According to the magnetic field modulation effect, each component of the IPMSM must be defined during the modulation process [17]. First, the internal permanent magnets and armature windings are considered as the excitation source of the magnetomotive force (MMF). Then, the slotted stator and the convex rotor are treated as field modulators, and the initial MMF generated by the excitation source is modulated by the field modulator along the air gap, resulting in a uniformly distributed magnetic density.
The process of the excitation source being modulated by the modulator is shown in Figure 6. Due to the simple salient pole rotor, the modulator’s impact on the modulation is minimal. Ignoring the rotor modulator, the magnetic field modulation function can be represented as follows:
where is the stator modulation function; represents the mechanical angle; is the DC component of the stator modulation function; is the amplitude of the k-th order modulation function; and is the number of stator teeth.
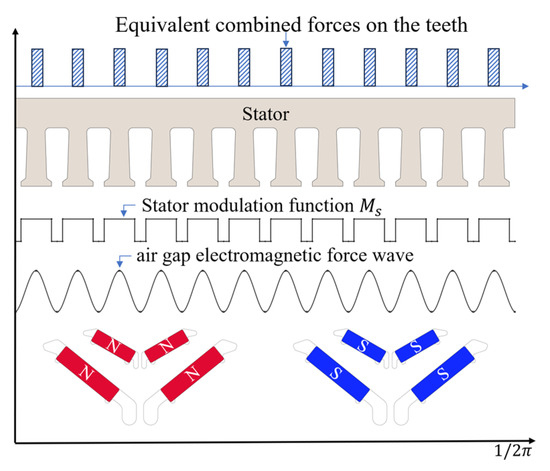
Figure 6.
Schematic diagram of modulation principle.
The airgap flux density includes the permanent magnet field flux density and the armature reaction field flux density. When magnetic flux saturation is neglected, the radial flux density is expressed as follows:
where is the permanent magnet flux density and is the armature flux density.
Using Fourier series, and can be written as follows:
where is the harmonic order of the permanent magnet MMF; is the amplitude of the -th order permanent magnet MMF; is the number of poles; is the rotor mechanical angular velocity; and is time.
where is the harmonic order of the armature MMF; is the amplitude of the -th order armature MMF; and is the phase angle of the -th order armature flux density.
2.4. Analysis of Radial Force Modulation
Ignoring the tangential airgap magnetic flux density, and applying Maxwell’s stress tensor method, the airgap radial force density can be expressed as follows:
where is the vacuum permeability.
Substituting Equations (3) to (6) into Equation (7) yields the radial force for each spatial and temporal order:
where is the magnetic flux density generated by the interaction of the permanent magnet MMF with ; is the magnetic flux density generated by the interaction of the permanent magnet MMF with ; is the magnetic flux density generated by the interaction of the armature MMF with ; is the magnetic flux density generated by the interaction of the armature MMF with ; and is the airgap magnetic permeability harmonic number, which is a non-negative integer.
From Equation (7), it can be seen that the radial force during load is generated by three components: , the magnetic flux density generated by the permanent magnet field acting alone; , the magnetic flux density generated by the interaction between the permanent magnet field and the armature field; and , the magnetic flux density generated by the armature field acting alone. Expanding Equation (8), since the radial force generated by the interaction of the -th order modulation function has a smaller amplitude, such radial forces are neglected, and only the larger amplitude radial forces are retained, resulting in the following formula:
When , or , or , it can be seen from Equations (10), (12) and (14) that the resulting radial force wave order is 0. For the 8-pole 48-slot IPMSM, taking Equation (10) as an example, the zeroth-order radial force density is the result of the interaction between the fundamental magnetic field, the 11th-order permanent magnet MMF harmonic field, and the 1st-order tooth harmonic, i.e., .
From Equations (9), (11) and (13), the order of these radial force harmonics will be the multiple of stator teeth. According to the Nyquist–Shannon sampling theorem, when the spatial order of the radial force is more than Z/2, “force wave aliasing” or modulation effects occur [7]. In this process, high-order radial forces will be modulated into lower-order radial forces under the influence of the stator slotted magnetic field. As shown in Equation (15), the modulated radial force order is :
where is the modulated radial force; is the amplitude of the modulated radial force; is the electrical angle; and is the phase of the modulated radial force.
It can be observed that when the initial spatial order of the radial force is a multiple of the number of teeth, it will be modulated into zeroth-order and tooth-multiple orders. According to Equation (1), the modulated zeroth-order radial force component will cause significant stator deformation, contributing significantly to motor vibration. Meanwhile, the zeroth-order and tooth-multiple radial forces modulated from the tooth-order radial force will have the same frequency and phase but different amplitudes. In this case, the stator will undergo uniform compression and expansion deformation, resembling a “breathing” zeroth-mode vibration (breathing mode) [8], as shown in Figure 7.
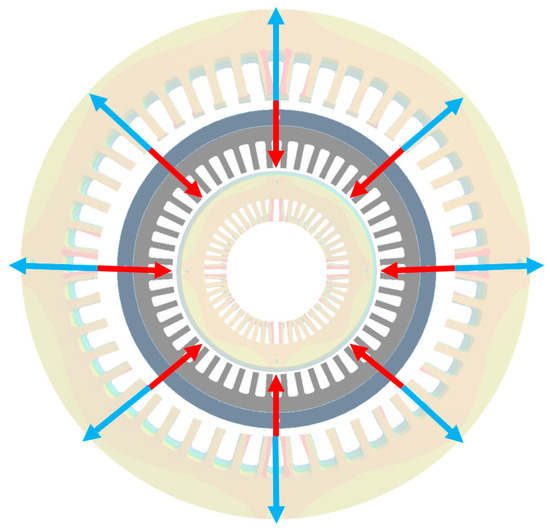
Figure 7.
Schematic of the “breathing” mode.
3. Segmented Oblique Pole Modulation Vibration Damping Design
Different rotor deflection angles and segment numbers lead to varying improvements in the motor’s vibration performance. To achieve the best optimization effect, the total skew angle of the rotor segments is typically set to the angle of one stator tooth. For a 48-slot motor, the angle of one stator tooth is , and the optimal basic deflection angle between rotor segments can be calculated using Equation (16):
where is the basic deflection angle between rotor segments and is the number of rotor segments (this paper takes the case of the rotor being evenly divided into 8 segments as an example).
After the rotor is segmented and skewed, the phase of the permanent magnet field is altered, but it does not affect the armature magnetic field. As the phase of the permanent magnet field changes, the radial magnetic flux density generated by the permanent magnet field also changes, and its average value can be expressed as follows:
From Equation (17), Equations (9) to (15) can be derived again. Under load conditions, the phase of the radial force harmonics generated by the term and the term will change, as shown in Table 2.

Table 2.
Phase shift in radial force harmonics for each rotor segment.
When , the 48th-order radial force generated by the motor will be deflected. If a linear segmented skewed pole structure is used, the deflection of the 48th-order radial force is shown in Figure 8. It can be seen that, when using the linear segmented skewed pole structure, the 48th-order radial forces generated by segments 1 and 5, 2 and 6, 3 and 7, and 4 and 8 cancel each other out in the circumferential direction. However, in the axial direction, for example, between segments 1 and 5, there exists an axial spacing of 3 rotor segments, which reduces the ideal cancelation effect of the 48th-order radial force.
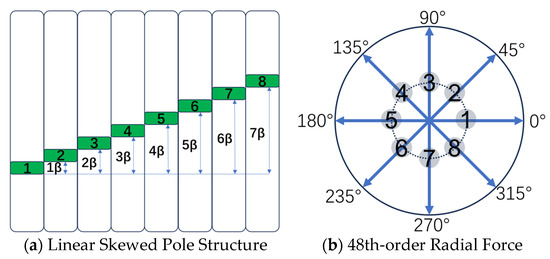
Figure 8.
Illustration of linear skewed pole and 48th-order radial force deflection for each rotor segment.
To address the issues with the linear skewed pole structure, the arrangement order of the rotor segments is changed to form a stepwise segmented rotor skew structure, as shown in Figure 9. Unlike the linear segmented skew structure, in the circumferential direction, the 48th-order radial forces generated by segments 1 and 2, 3 and 4, 5 and 6, and 7 and 8 cancel each other out, and there is no axial spacing between rotor segments.
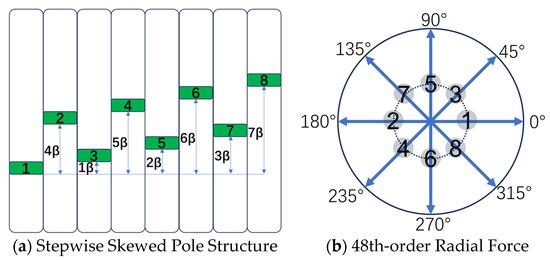
Figure 9.
Illustration of stepwise skewed pole and 48th-order radial force deflection for each rotor segment.
To validate the advantages of the stepwise skew configuration, a comparative simulation analysis was conducted to evaluate the vibration acceleration amplitudes on the motor surface between linear skew and stepwise skew designs. The simulation implementation of segmented skew differs slightly from conventional methods, where both linear and stepwise skew angles for each rotor segment were configured in Maxwell 2D Model Settings while the 3D stator model was equally divided into eight axial sections. Additionally, to ensure accurate acquisition of vibration acceleration results, the maximum frequency was set to 7100 Hz. The simulation results are presented in Figure 10, demonstrating the effectiveness of the stepwise skew design in vibration suppression while maintaining torque performance. The analysis shows that the vibration acceleration at the stator surface at the , caused by the 48th-order radial force, is 4687.3 mm/s2. However, after adopting the stepwise skewed pole structure, the vibration acceleration at the is reduced to 853.15 mm/s2, which further validates the significant optimization effect of the stepwise structure on the motor’s . Furthermore, significant reductions in vibration acceleration amplitudes were observed at the , , and , while the remaining harmonic components exhibited relatively minor magnitudes that did not warrant detailed comparative analysis.
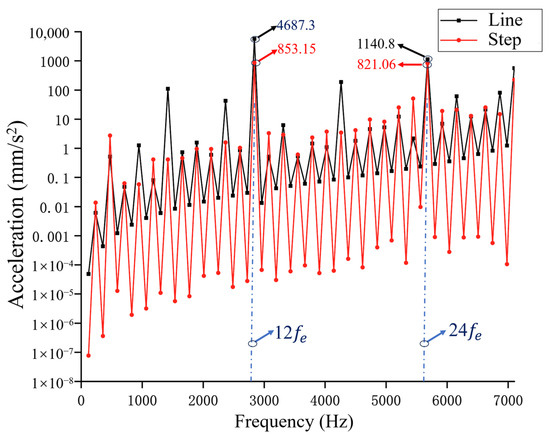
Figure 10.
Comparison of vibration acceleration spectrum on the motor surface with different skewed pole structures.
Additionally, the optimization performance of the stepwise skewed pole structure when the rotor is divided into 6, 7, and 8 segments was analyzed, as shown in Figure 11 and Figure 12. When the rotor is divided into an odd number of 7 segments, the radial force does not completely cancel in the circumferential direction, so the vibration acceleration at is higher than the result with 6 segments. However, when the rotor is divided into 8 segments, the cancelation effect of the 48th-order radial force is ideal, and the vibration acceleration at is minimized.
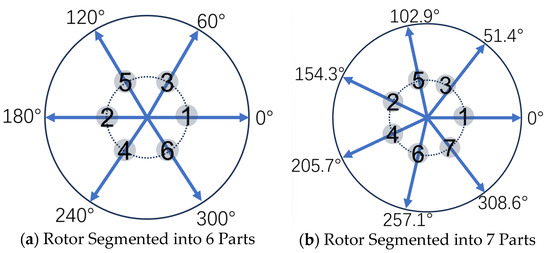
Figure 11.
Illustration of 48th-order radial force deflection for each rotor segment with different segment numbers.
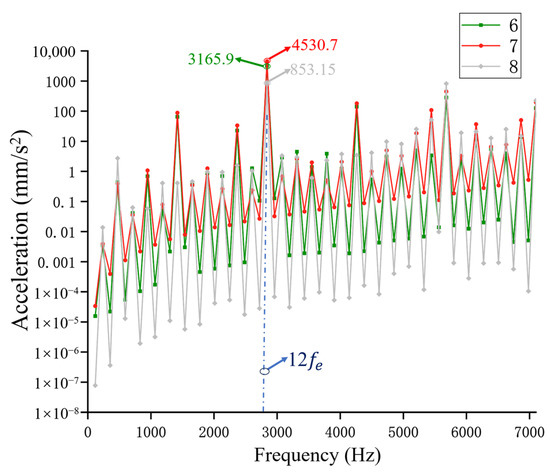
Figure 12.
Comparison of vibration acceleration spectra of motor surfaces with different number of segments.
4. Analysis of Optimization Results
4.1. Analysis of Radial Force Optimization
According to the two-dimensional motor model shown in Figure 13, the radial electromagnetic force before and after optimization was simulated using the finite element method under the same load conditions. After segmentation of the skewed poles, the radial electromagnetic force density was calculated by averaging each segment’s radial force densities and performing a 2D fast Fourier decomposition on the results, as shown in Figure 14.
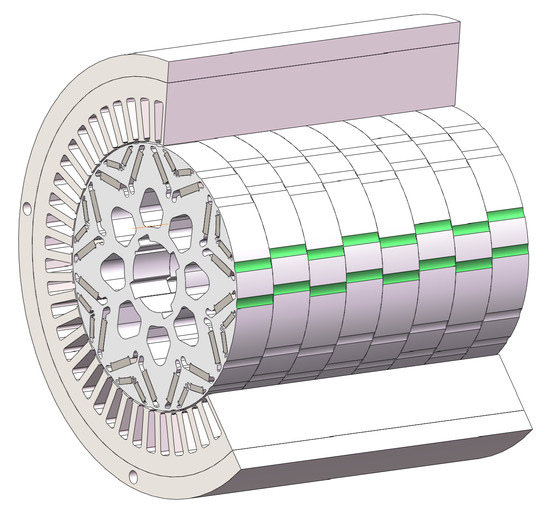
Figure 13.
Illustration of the skewed pole on the motor.
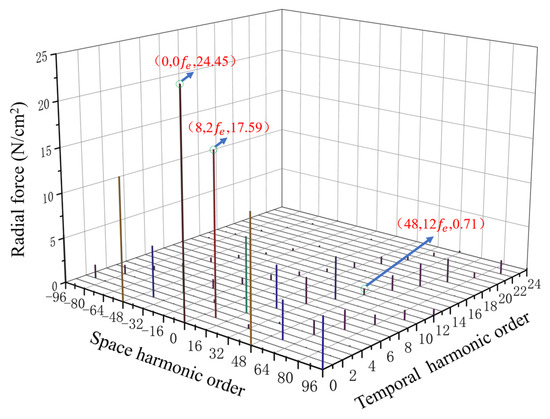
Figure 14.
Harmonic distribution of radial electromagnetic force density after skewing.
The results shown in Figure 4 and Figure 14 show that by adopting the stepwise segmented rotor skewed pole structure, the 48th-order radial electromagnetic force density during load conditions is significantly reduced. Under the same load conditions, its value decreases from 2.08 N/cm2 to 0.71 N/cm2, a reduction of 68%. At the same time, the amplitudes of radial electromagnetic forces at higher harmonics (such as 0th, 8th, etc.) are also reduced, though these are not listed individually.
Additionally, after applying the stepwise segmented skewed pole structure, significant improvements were observed in the motor’s no-load back EMF harmonics, load torque fluctuations, and cogging torque, as shown in Figure 15.
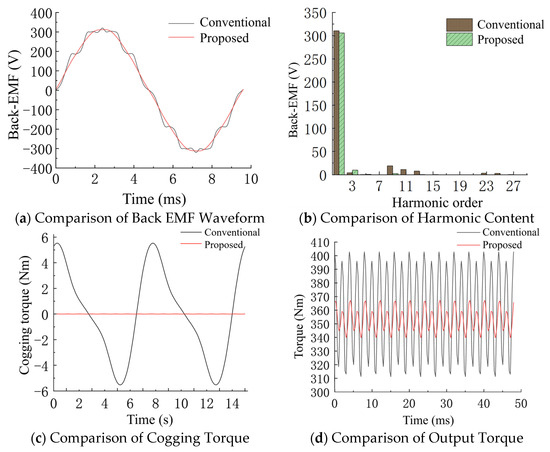
Figure 15.
Performance comparison of the motor after skewing.
Typically, no-load back EMF harmonics, cogging torque, and load torque fluctuations all contribute to motor vibrations. From the comparison shown in Figure 14, it can be seen that after the stepwise segmented rotor skewed pole structure is applied, the back EMF waveform of the motor exhibits better sinusoidal characteristics; the amplitudes of the various harmonics are also reduced. The peak-to-peak value of cogging torque is reduced from 11.39 Nm before optimization to 4.9 mNm after optimization; the output torque fluctuation is reduced from 87.25 Nm to 25.52 Nm. These optimizations in the data also indirectly indicate an improvement in the motor’s vibration performance.
4.2. Analysis of Vibration Performance Optimization
A simulation analysis of the motor’s vibration behavior before and after skewing was conducted to further verify the improvement in the motor’s vibration performance from the stepwise segmented rotor skewed pole structure. First, modal analysis of the stator and simplified housing models was performed, with the material properties of each component shown in Table 3. The stator is made by laminating silicon steel sheets, and to make the simulation closer to actual conditions, anisotropic materials were assigned to the stator [8].

Table 3.
Material properties.
Table 4 shows the natural frequencies of the stator housing’s modal shapes under both unconstrained and constrained (with the constraint applied to the circular hole in the housing shown in Figure 13) conditions. It can be seen that the vibration frequency of the stator housing is not the same in the unconstrained (free mode) and constrained cases. When the fixed constraint is added at the circular hole mentioned above, it is equivalent to adding an infinite stiffness to the local area. The effective stiffness of the overall structure is also increased. Hence, the frequencies of the modes of each order of the constrained modes are higher than those of the unconstrained ones. The motors are usually fixedly mounted, so the constrained modes are utilized to carry out the next step of the vibration simulation.

Table 4.
Mode shapes and natural frequencies.
Next, based on the simulation process in Figure 3, the electromagnetic forces after segmented skewing were imported into the structural field for coupled simulation. At the same time, the vibration acceleration results on the motor casing surface before and after optimization were observed at peak speed (3550 r/min), as shown in Figure 16. When the motor operates at peak speed, the electrical frequency corresponding to is 2840 Hz. According to the analysis of radial force modulation effects, the 48th-order radial force is the primary excitation source for the vibration. The vibration acceleration at the casing surface in this frequency range is 5635 mm/s2, indicating that the vibration induced by the 48th-order radial force is significant, consistent with the theoretical analysis.
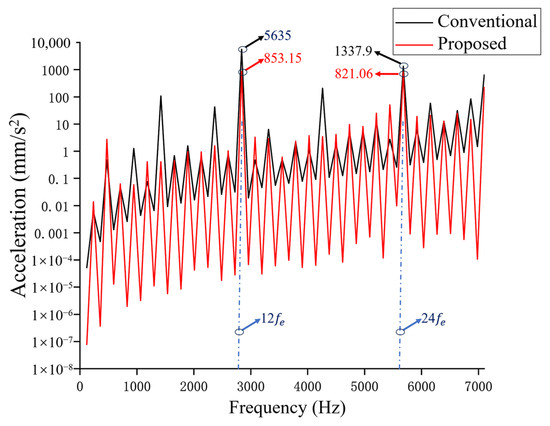
Figure 16.
Comparison of vibration acceleration spectrum at peak speed.
At the same time, the electrical frequency corresponding to is 5680 Hz, which, similar to the analysis of radial force modulation effects at , shows that the primary excitation source for the vibration is the 96th-order radial force. The vibration acceleration at this frequency is 1337.9 mm/s2, and the vibration induced by the 96th-order radial force is also significant. After optimization using the stepwise segmented skewed pole structure proposed in this paper, the radial force vectors of slot-multiple orders generated by each rotor segment (such as the 48th-order radial force and the 96th-order radial force) are shifted and canceled out. The corresponding radial electromagnetic force density is reduced, and the excitation vibration acceleration decreases from 5635 mm/s2 at to 853.15 mm/s2, and from 1337.9 mm/s2 at to 821.06 mm/s2, representing reductions of 84% and 38%, respectively.
Finally, an air domain with a radius of 1 m is established centered on the motor, and the vibration results from the structural field are mapped to the acoustic field. The noise level caused by sound wave propagation is calculated through simulation. Figure 17 shows the noise waterfall diagram across the full speed range of the motor before optimization, after linear skewed pole optimization, and after stepwise skewed pole optimization.
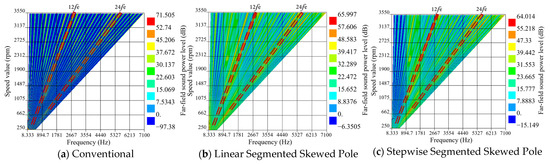
Figure 17.
Far-field sound power level waterfall diagram.
The maximum electromagnetic noise generated by the motor is located in the frequency range, while the noise in the frequency range is relatively smaller but still warrants attention. Before optimization, the maximum electromagnetic noise was 71.505 dB, and after optimization, the maximum electromagnetic noise was reduced to 64.014 dB, showing a significant improvement in noise level. It should be noted that this step-skewing technique demonstrates excellent vibration and noise suppression for integer-slot permanent magnet synchronous motors (PMSMs). As this method is specifically designed for the structural configuration of integer-slot PMSMs, it is applicable not only to traction motors for electric vehicles but also to PMSMs for other applications. However, the method proves ineffective for fractional-slot PMSMs. Furthermore, during high-speed operation, the rotor’s mechanical strength and the motor’s thermal management system face significant challenges, making mechanical integrity tests and thermal analysis essential when necessary.
5. Conclusions
This study provides a detailed description of the generation mechanism of modulated vibration in the integer-slot IPMSM and the suppression mechanism of modulated vibration by the stepwise segmented skewed pole structure, and the following conclusions are drawn:
- Due to the modulation effect in the integer-slot IPMSM, high-order radial forces are modulated into low-order radial forces under the influence of the stator slotted magnetic field, leading to larger vibrations. For the 8-pole 48-slot IPMSM studied in this paper, the 48th-order radial force is modulated into a zeroth-order radial force. Even though the amplitude of this order’s radial force is small, it will still cause significant vibration and noise.
- The stepwise segmented rotor skewed pole method can suppress the motor’s modulated vibration. After skew optimization, the vibration acceleration at the harmonic on the motor casing surface is reduced from 5635 mm/s2 to 853.15 mm/s2, a reduction of 84%; the maximum electromagnetic noise is reduced from 71.505 dB to 64.014 dB, a decrease of 7.491 dB. The vibration and noise at the harmonic are also well suppressed.
- Compared with the traditional linear skewed pole structure, the stepwise skewed pole structure does not increase the difficulty in motor manufacturing and assembly. Still, it offers better optimization of modulated vibration for the integer-slot permanent magnet synchronous motor. This skewed pole structure provides an additional option for vibration optimization design in motors.
In addition, this study has certain limitations. For example, only the stepwise segmented skewed pole structure was simulated, and no experimental validation was conducted. Future research could consider using experimental methods to further verify the accuracy of the simulation results and investigate the effects of control factors on motor vibration. In the future, based on the current simulation results, a prototype will be fabricated to test its output performance, etc. The simulation results will be de-calibrated based on the tested inverse electromotive force results. The simulation input parameters will be adjusted to narrow down the error to a reasonable range. At the same time, under the free boundary conditions (hanging the motor with a soft rope), the frequency response of several test points on the surface of the stator and the shell is tested by the hammering method. The results are fitted and compared with the simulation results. Then, the material properties inputted during the modal simulation test are adjusted. The simulation is performed several times to narrow the error, to make the simulation results of the vibration noise more in line with the actual situation.
Author Contributions
Conceptualization, S.L.; data curation, S.L.; funding acquisition, H.W.; investigation, S.L.; methodology, S.L., H.W. and X.Z.; software, S.L.; supervision, H.W., W.L. and J.P.; visualization, S.L.; writing—original draft, S.L.; writing—review and editing, H.W., X.Z., W.L. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant Nos. 52472405), the Hubei Province Central Guiding Local Science and Technology Development Special Project (2024CSA081), the Natural Science Foundation of Hubei Province (Grant Nos. 2024AFB219, 2024AFD042, 2024AFD045), the Open Fund of Hubei Longzhong Laboratory (2024KF-22), and the Special Fund of Hubei Longzhong Laboratory of Xiangyang Science and Technology Plan (2024KF-22).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Weiye Li was employed by the company Xiangyang CRRC Motor Technology Co., Ltd. Author Jianping Peng was employed by the company Dongfeng Electric Drive Systems Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Cheng, Y.; Ding, L.; Zhao, T.; Cui, S. Design and Optimization of Electric Vehicle Traction Motor Considering Rotor Topology and Manufacturing Uncertainty. IEEE Trans. Ind. Electron. 2024, 71, 5034–5044. [Google Scholar] [CrossRef]
- Kim, C.; Ha, N. A Study on the Vibration and Noise Reduction of Scrolling-Type Electric Compressor for Electric Vehicles. World Electr. Veh. J. 2025, 16, 126. [Google Scholar] [CrossRef]
- Li, X.; He, W.; Zhao, R.; Feng, A.; Liu, Y.; Lu, Y. Modal analysis of the stator system of a permanent magnet synchronous motor with integer slot multi-pole pair for electric vehicles. IET Electr. Power Appl. 2022, 16, 1–14. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y. Influence of radial force harmonics with low mode number on electromagnetic vibration of PMSM. IEEE Trans. Energy Convers. 2014, 29, 38–45. [Google Scholar] [CrossRef]
- Cheng, M.; Wen, H.; Han, P.; Zhu, X. Analysis of Airgap Field Modulation Principle of Simple Salient Poles. IEEE Trans. Ind. Electron. 2019, 66, 2628–2638. [Google Scholar] [CrossRef]
- Cheng, M.; Han, P.; Hua, W. General Airgap Field Modulation Theory for Electrical Machines. IEEE Trans. Ind. Electron. 2017, 64, 6063–6074. [Google Scholar] [CrossRef]
- Fang, H.; Li, D.; Qu, R.; Yan, P. Modulation effect of slotted structure on vibration response in electrical machines. IEEE Trans. Ind. Electron. 2019, 66, 2998–3007. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Analysis of zeroth-mode slot frequency vibration of integer slot permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2020, 67, 2954–2964. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Effect comparison of zigzag skew PM pole and straight skew slot for vibration mitigation of PM brush DC machines. IEEE Trans. Ind. Electron. 2020, 67, 4752–4761. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Sun, Y.; Sun, X.; Cao, H. Piecewise Stagger Poles with Continuous Skew Edge for Vibration Reduction in Surface-Mounted PM Synchronous Machines. IEEE Trans. Ind. Electron. 2021, 68, 8498–8506. [Google Scholar] [CrossRef]
- Peng, C.; Wang, D.; Wang, B.; Li, J.; Wang, C. Different Rotor Segmented Approaches for Electromagnetic Vibration and Acoustic Noise Mitigation in Permanent Magnet Drive Motor: A Comparative Study. IEEE Trans. Ind. Electron. 2023, 71, 1223–1233. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, D.; Peng, C.; Feng, W.; Wang, B. Investigation and Experimental Validation of Sideband Harmonic Vibration of IPMSM with and without Skewed Slots for EVs. World Electr. Veh. J. 2021, 12, 223. [Google Scholar] [CrossRef]
- Fang, H.; Li, D.; Guo, J.; Xu, Y.; Qu, R. Hybrid Model for Electromagnetic Vibration Synthesis of Electrical Machines Considering Tooth Modulation and Tangential Effects. IEEE Trans. Ind. Electron. 2020, 68, 7284–7293. [Google Scholar] [CrossRef]
- Zhao, W.; Zhu, S.; Ji, J.; Liu, G.; Mao, Y. Analysis and Reduction of Electromagnetic Vibration in Fractional-Slot Concentrated-Windings PM Machines. IEEE Trans. Ind. Electron. 2021, 69, 3357–3367. [Google Scholar] [CrossRef]
- Wang, D.; Peng, C.; Li, J.; Wang, C. Comparison and Experimental Verification of Different Approaches to Suppress Torque Ripple and Vibrations of Interior Permanent Magnet Synchronous Motor for EV. IEEE Trans. Ind. Electron. 2023, 70, 2209–2220. [Google Scholar] [CrossRef]
- Torregrossa, D.; Peyraut, F.; Fahimi, B.; M’boua, J.; Miraoui, A. Multiphysics Finite-Element Modeling for Vibration and Acoustic Analysis of Permanent Magnet Synchronous Machine. IEEE Trans. Energy Convers. 2011, 26, 490–500. [Google Scholar] [CrossRef]
- Zhou, Y.; Ji, J.; Zhao, W.; Zhu, S.; Liu, H. Modulated Vibration Reduction Design for Integral-Slot Interior Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2022, 69, 12249–12260. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).