A Novel Method of Parameter Identification for Lithium-Ion Batteries Based on Elite Opposition-Based Learning Snake Optimization
Abstract
1. Introduction
- (1)
- Development of the new EOLSO algorithm, which achieves better global search capability and faster convergence.
- (2)
- Verification of EOLSO’s performance superiority compared to leading optimization methods through standardized testing.
- (3)
- Application of EOLSO to the 2-RC battery model, resulting in more accurate and stable parameter identification.
- (4)
- Introduction of a practical solution to the accuracy and adaptability challenges faced by traditional parameter identification methods in battery modeling.
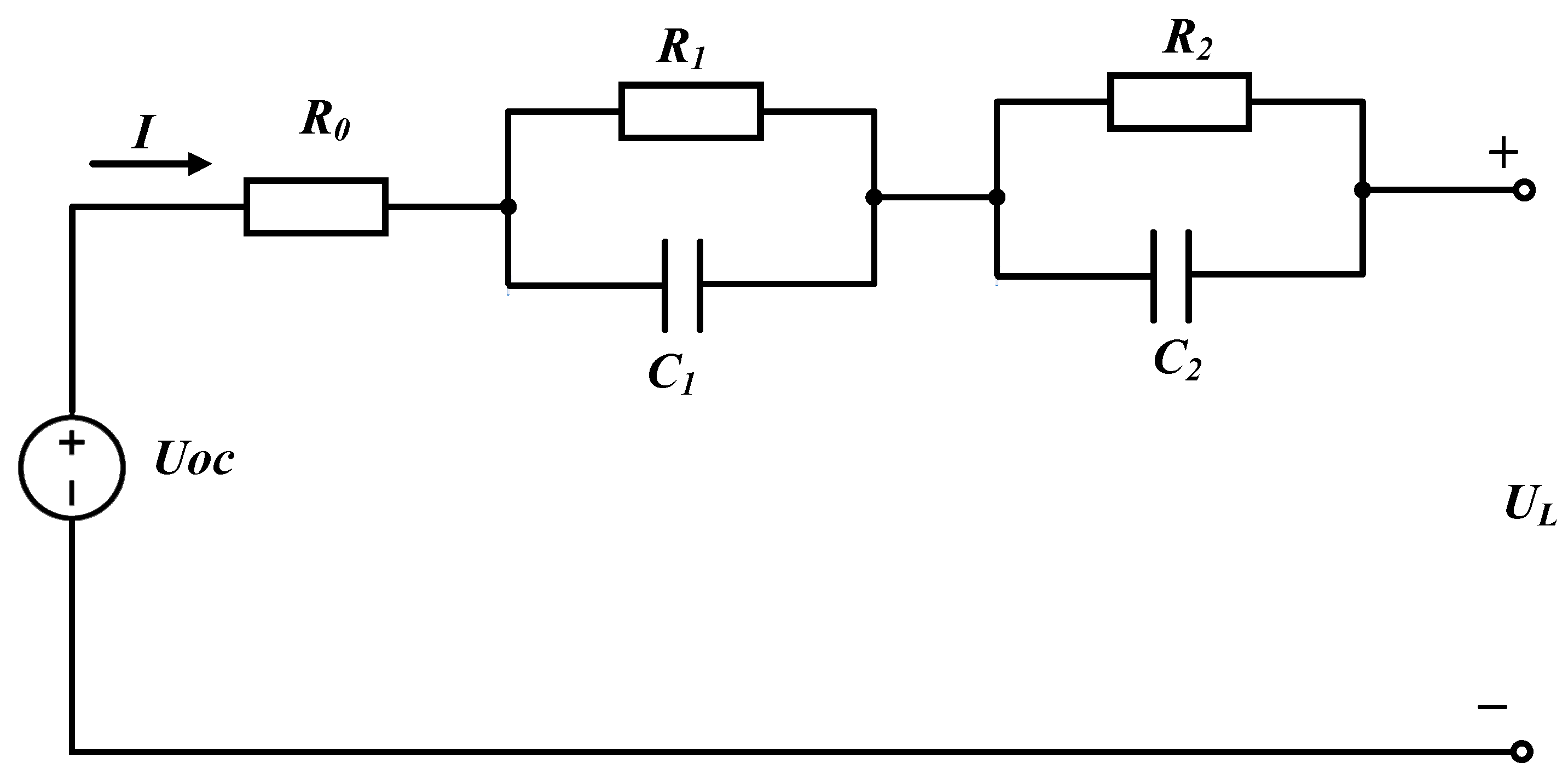
2. Second-Order RC Equivalent Circuit Model of Lithium-Ion Batteries
2.1. Model Structure
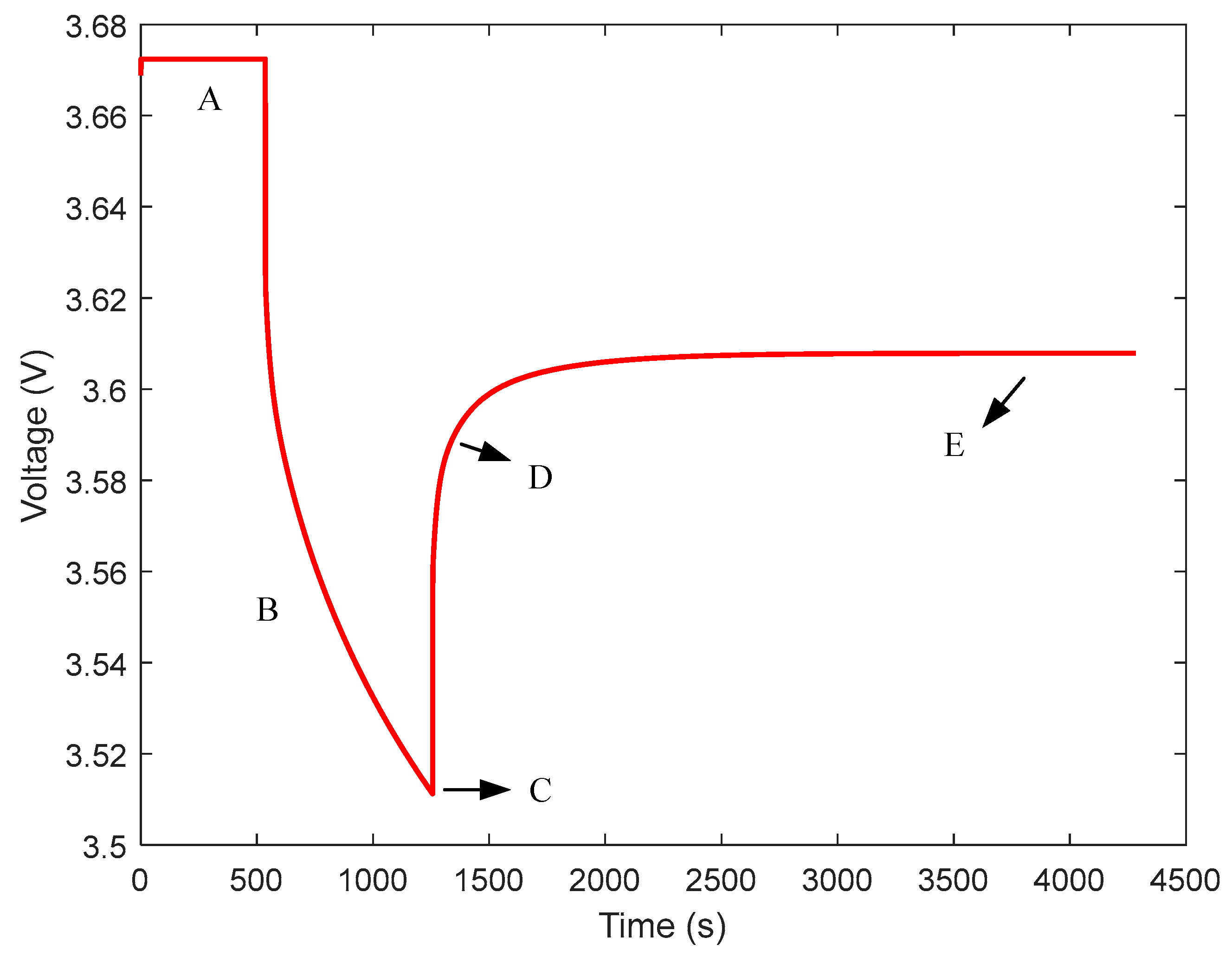
2.2. Parameter Identification for Lithium-Ion Batteries
2.3. Objective Function of Parameter Identification
3. Parameter Identification Methods
3.1. Basic Concepts of the Snake Optimizer (SO)
3.2. Improvements in the Snake Optimization
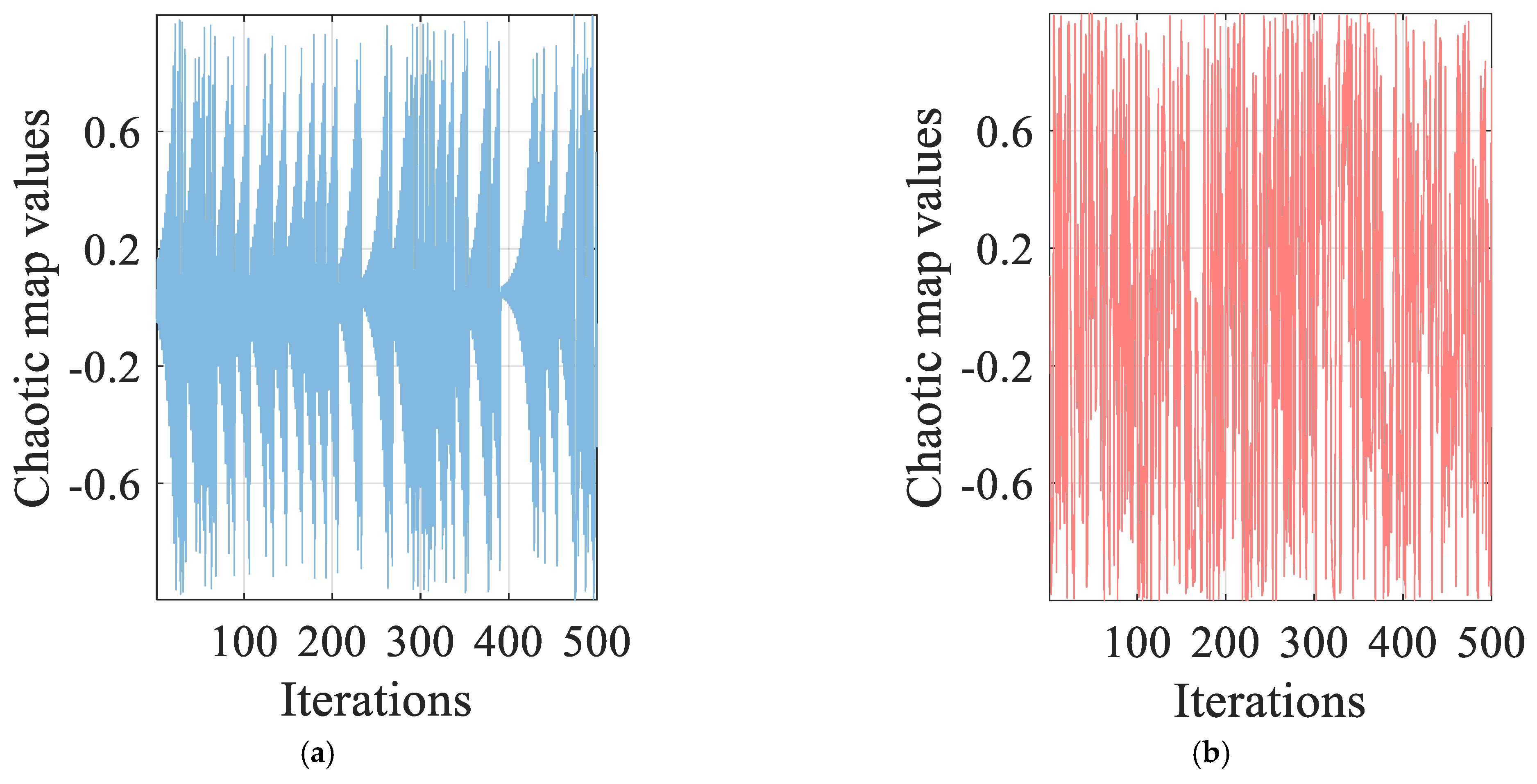
3.2.1. Chebyshev Population Initialization
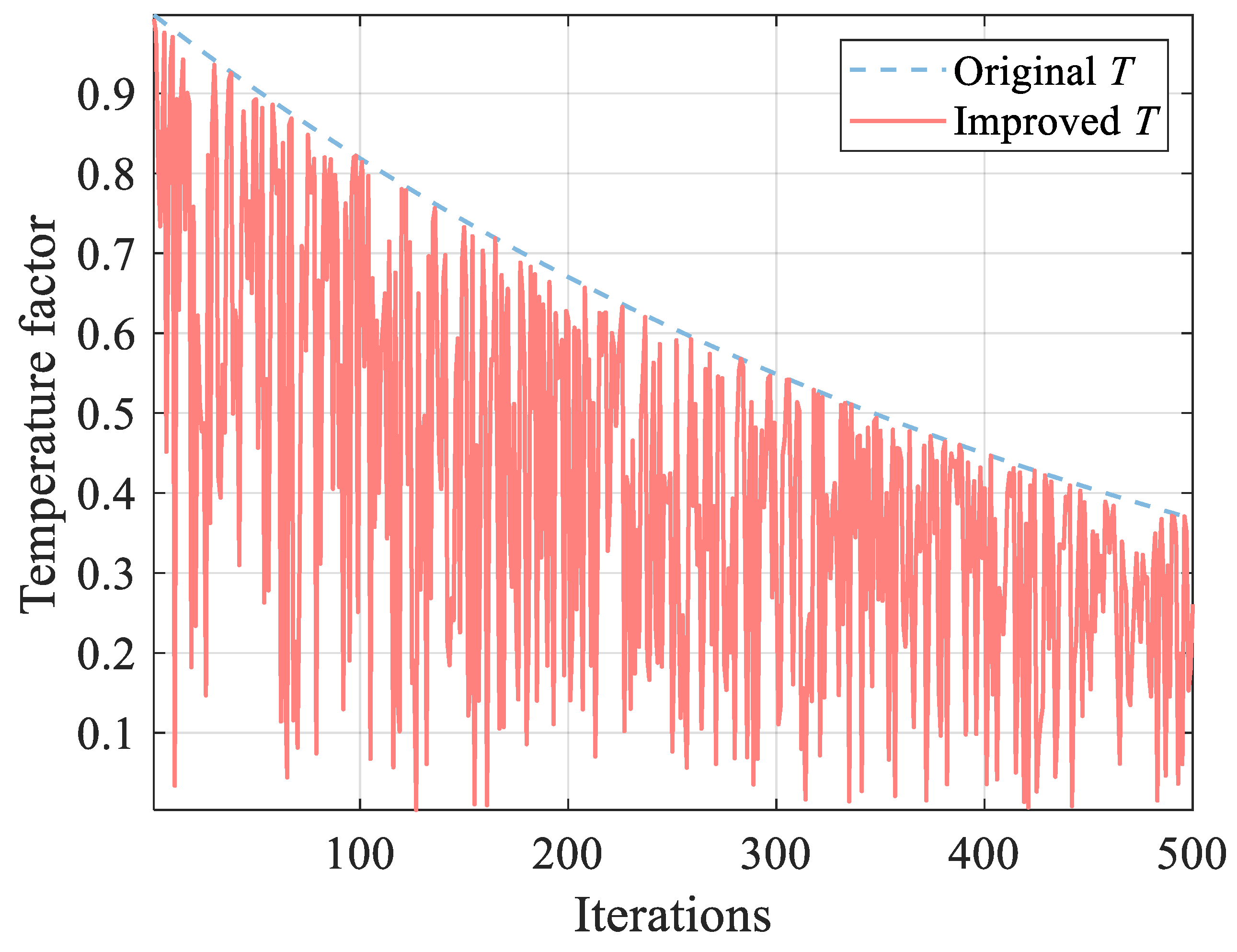
3.2.2. Non-Monotone Decreasing Temperature Factor
3.2.3. Elite Opposition-Based Learning
3.2.4. Parameter Identification of the Lithium-Ion Battery Model with EOLSO
| Algorithm 1: EOLSO |
| Input: Population Size N, Lower Bound lb, Upper Bound ub, Max Iterations tmax, Dimension D |
| Output: Best solution and its fitness |
| 1. Initialize: |
| a. Set iteration count t = 0 |
| b. Generate a chaotic initial population (Equation (22)) |
| c. Divide population into male and female groups of size N/2 |
| 2. While t < tmax do: |
| a. Set control parameters |
| -Set the food quantity Q using Equation (8) |
| -Set the temperature factor T using Equation (23) |
| b. For each individual in the population: |
| i. Exploration Phase: |
| - If Q < 0.25 update positions using Equation (9) |
| ii. Operation Phase: |
| -If T > 0.6, update positions using Equation (11) (with non-monotonic Temp) |
| -If Pr > 0.6 (Pr is a random value in (0, 1), conduct mating using Equation (17) |
| update males using Equation (16) |
| update females using Equation (17) |
| -Otherwise |
| update males using Equation (12) |
| update females using Equation (13) |
| iii. replace worst individuals using Equations (20) and (21) |
| c. if t % Tp == 0: (Periodically execute elite opposition-based learning) |
| -generate elite opposition-based learning using Equation (24) |
| -evaluate and select best solutions |
| -update male_positions and female_positions |
| d. Calculate the best fitness for male and female groups |
| 3. Output: |
| -Best solution in the population |
| -Best fitness value |
4. Experimental Simulation and Result Analysis
- (1)
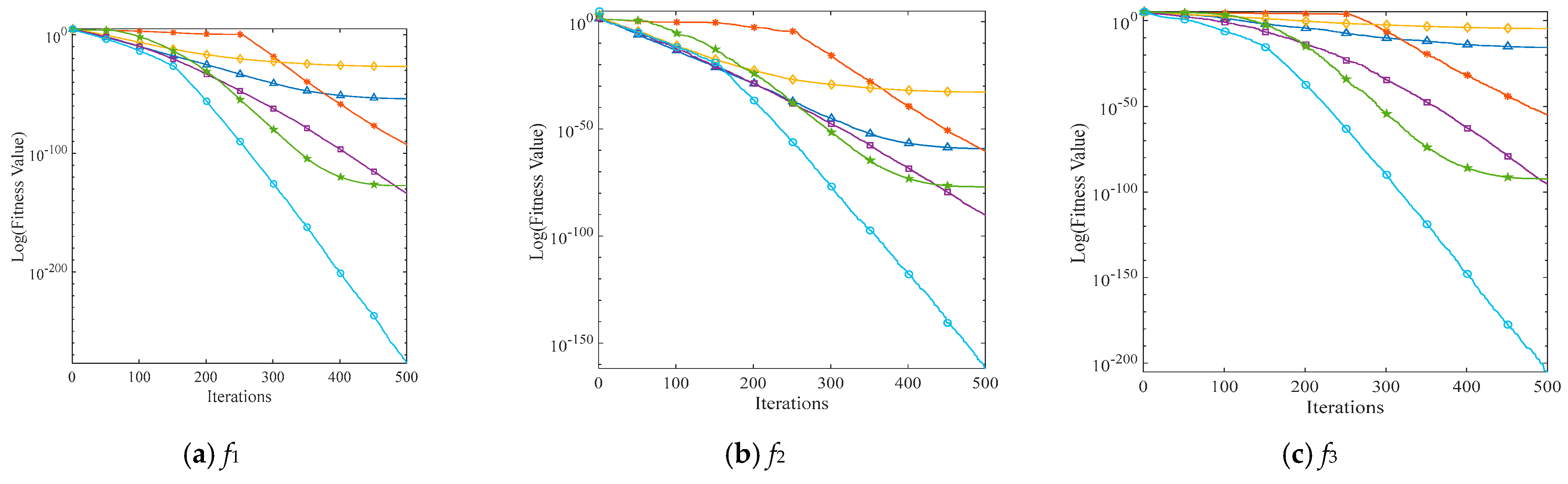
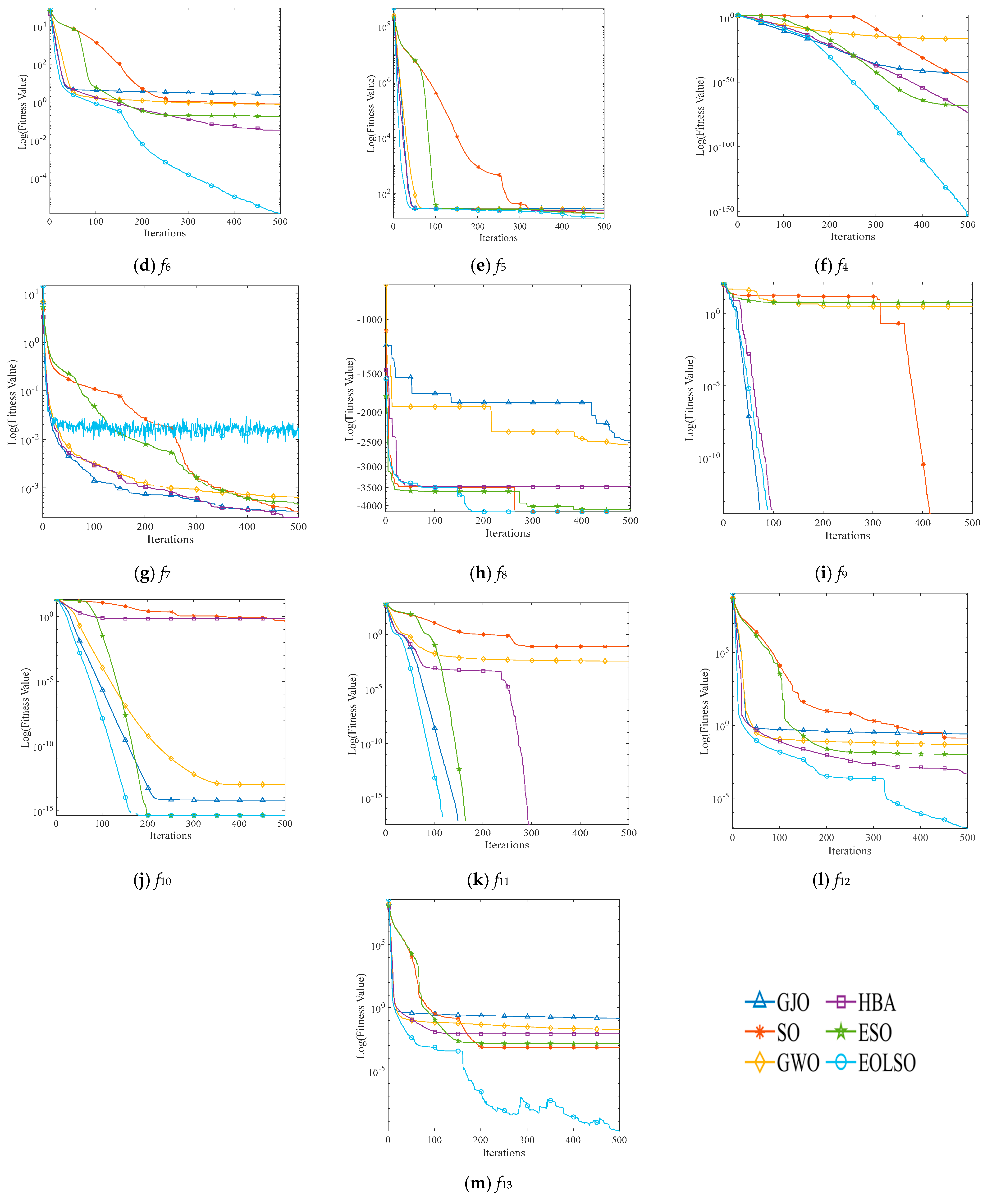
- Benchmark Test Functions: We select several benchmark test functions to compare the convergence speed and optimization precision of different algorithms. This comparison aims to verify whether EOLSO has a stronger capability to escape local optima when handling large-scale optimization problems.
- (2)
- Parameter Identification Simulation: We compare the performance of different algorithms in parameter identification of a lithium-ion battery model to further validate the feasibility of EOLSO in solving practical issues.
4.1. Comparative Experiments with Benchmark Test Functions
4.2. Battery Model Parameter Identification Experiments Based on EOLSO
4.2.1. Experimental Setup and Data Collection
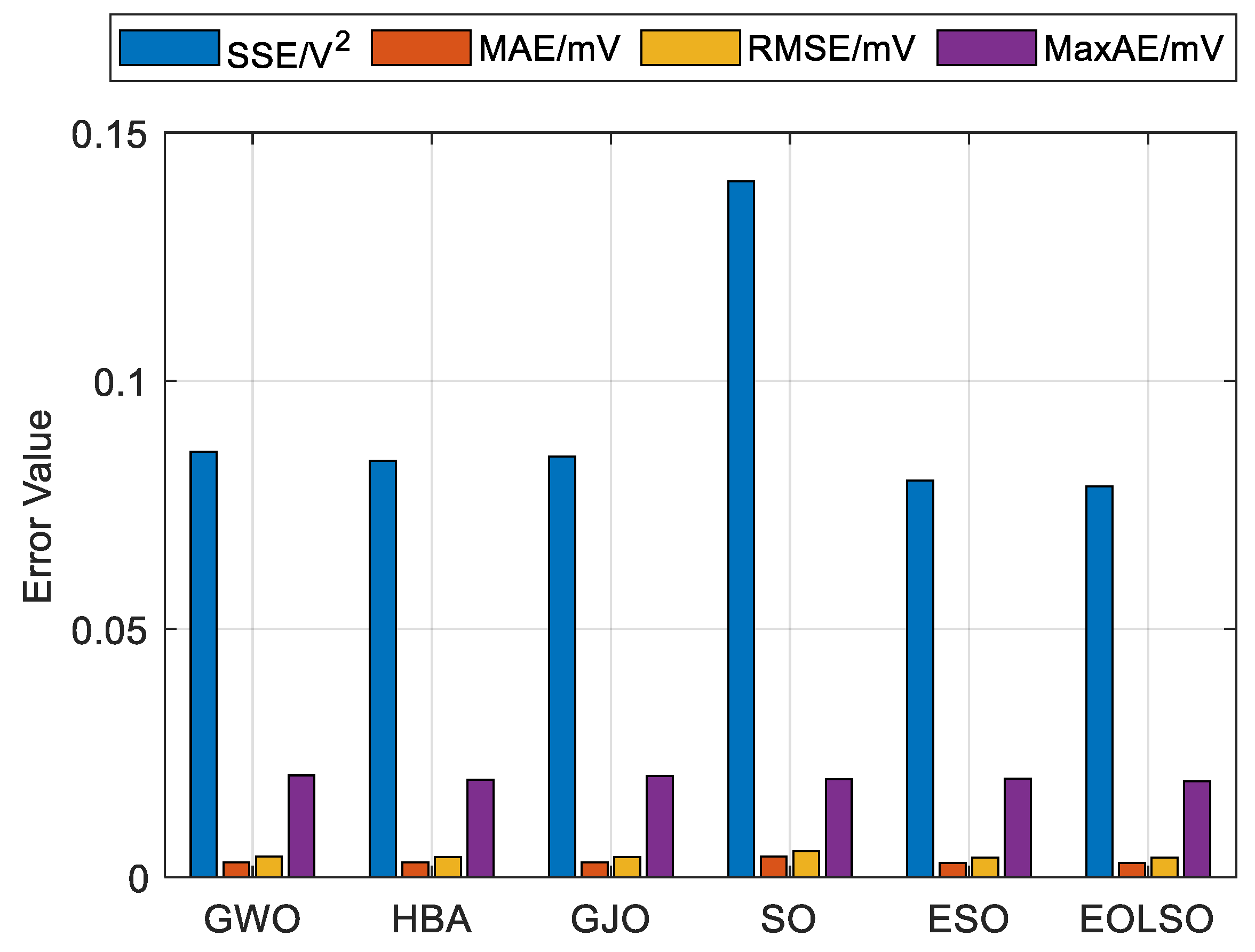
4.2.2. Parameter Identification Results from the HPPC Test
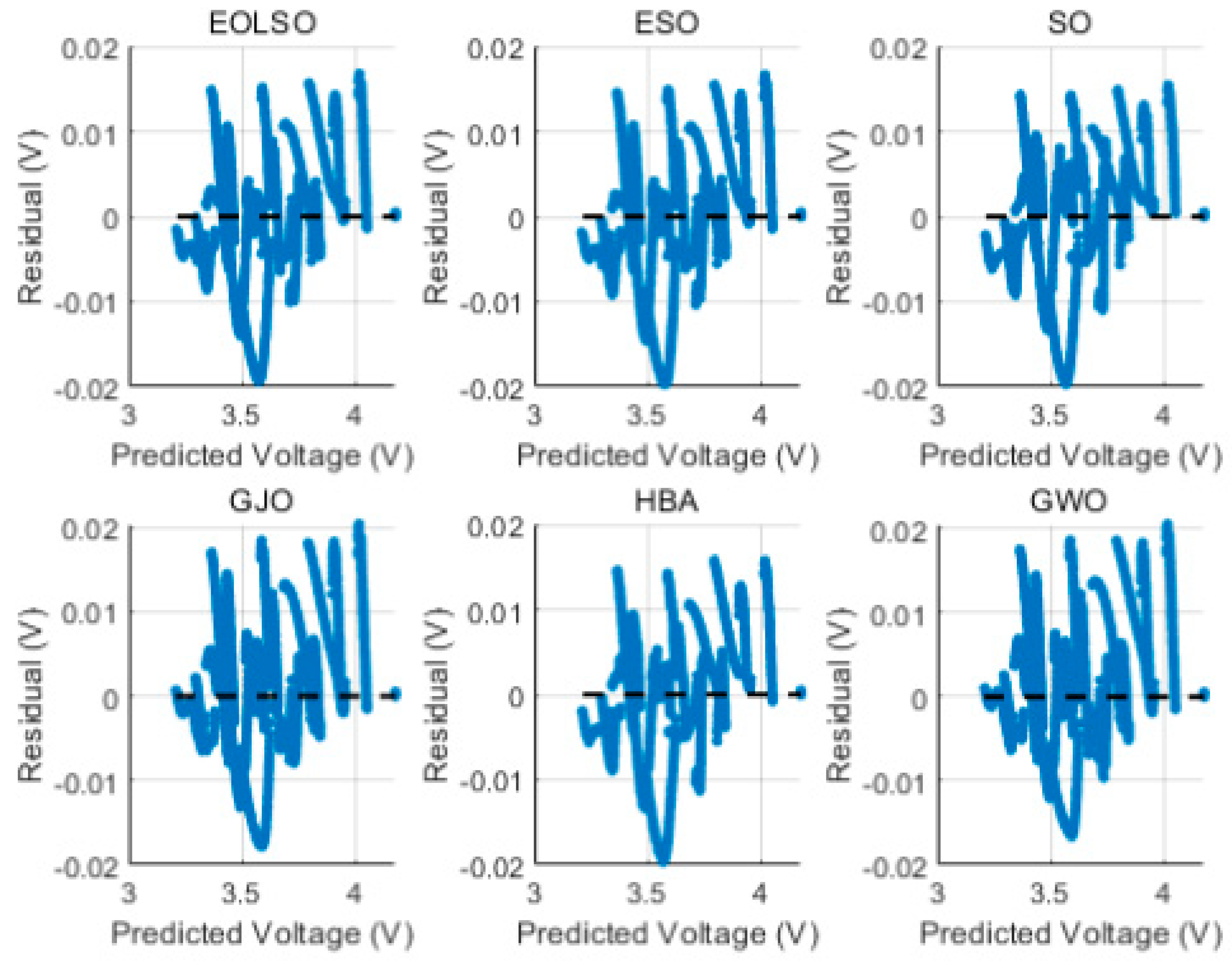
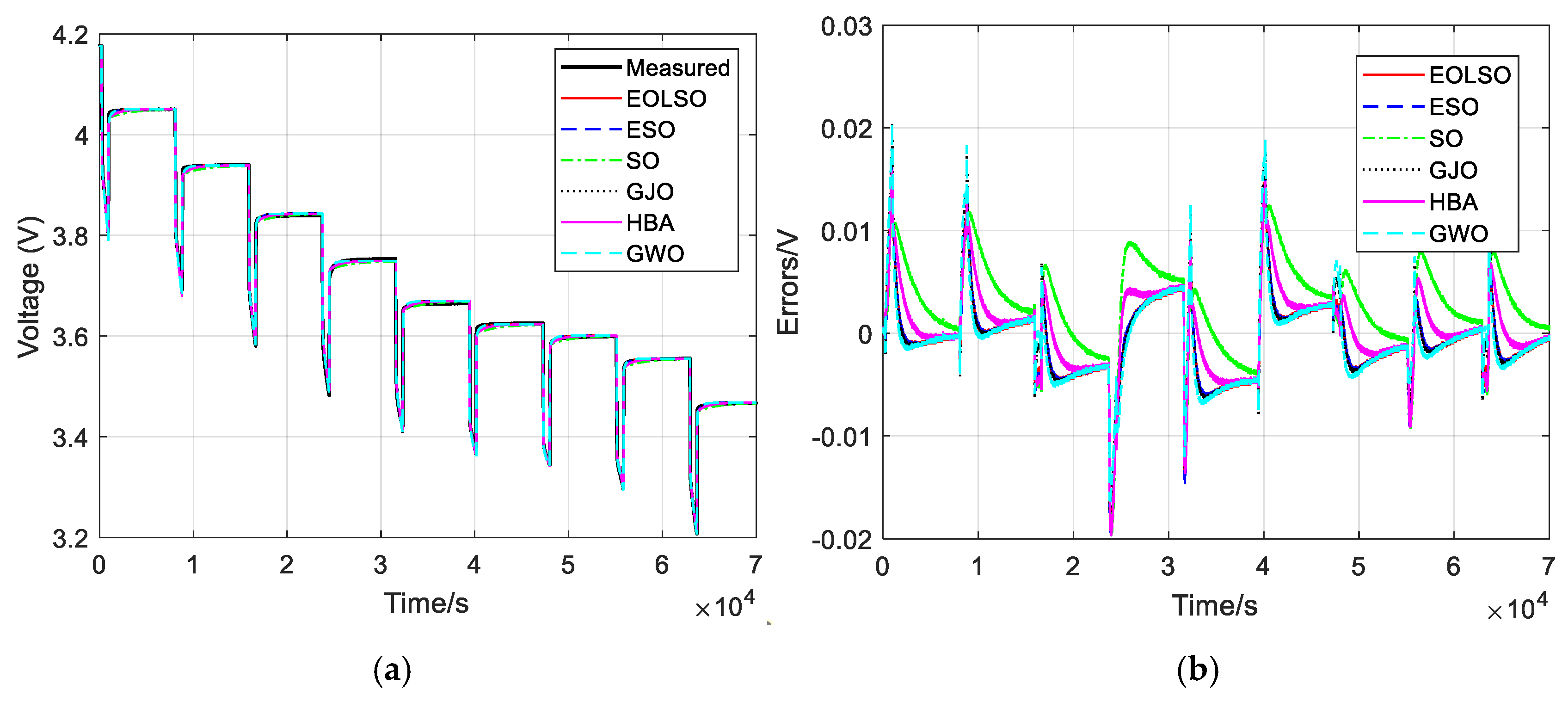
- (1)
- All algorithms achieve high prediction accuracy, with residuals predominantly within ±0.02 V (20 mV);
- (2)
- The residual patterns reveal the systematic behavior of errors across different voltage ranges;
- (3)
- EOLSO shows a slightly tighter residual distribution, aligning with its superior RMSE (0.00594 V) in Table 6.
4.2.3. Ablation Study
- EOLSO-C: Replaces the Chebyshev chaotic initialization with standard random initialization;
- EOLSO-T: Substitutes the non-monotonic temperature factor with a monotonic temperature schedule;
- EOLSO-E: Operates without the elite opposition-based learning mechanism.
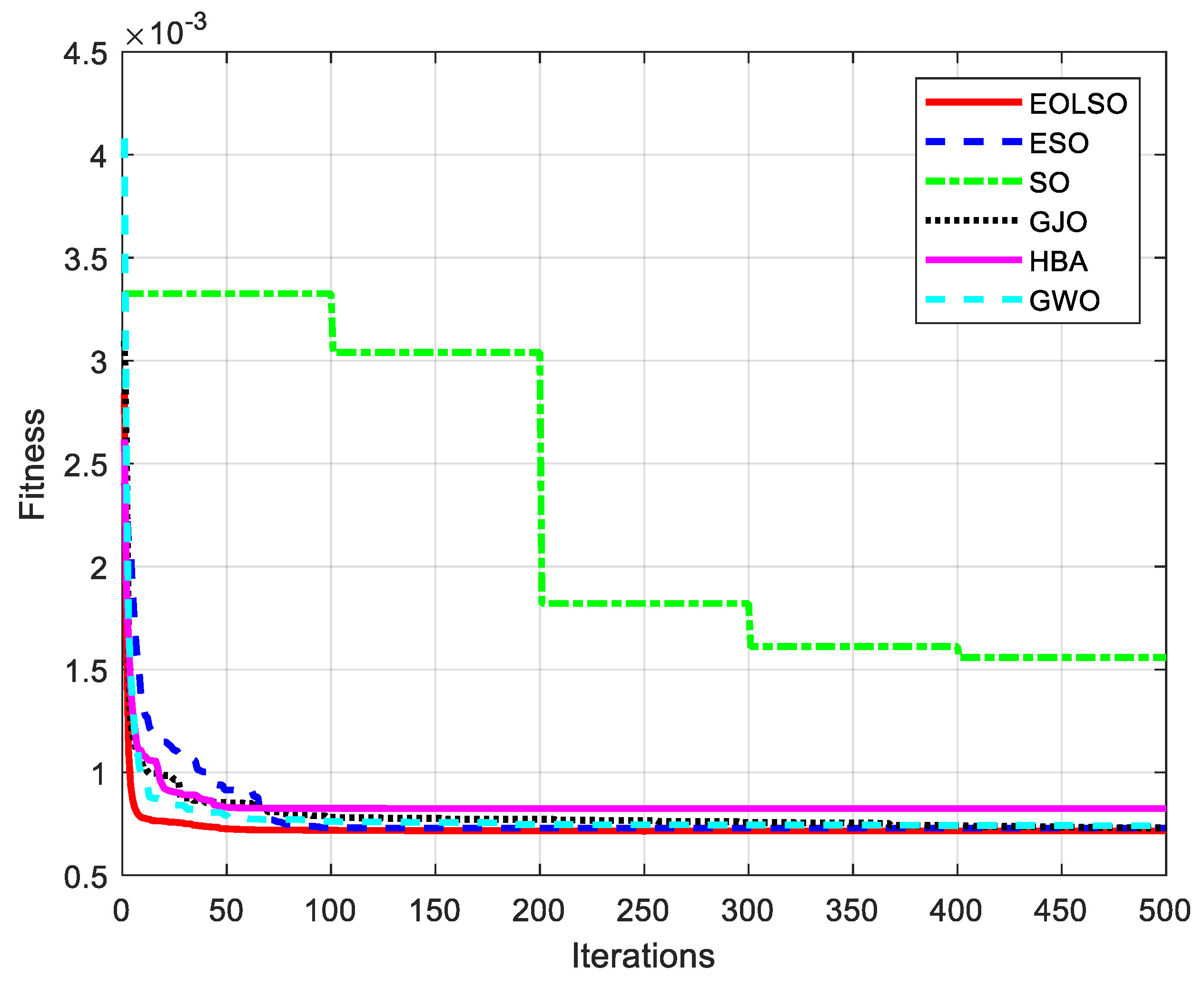
- Chebyshev chaotic initialization contributes most significantly (a 4.6% SSE increase when removed), ensuring optimal initial population distribution.
- The non-monotonic temperature factor helps prevent trapping in local optima (a 1.4% SSE degradation with monotonic replacement), while also serendipitously achieving the best MaxAE performance.
- Elite opposition learning provides marginal but consistent refinement (≤0.11% error increases).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| EOLSO | Elite Opposition-Based Learning Snake Optimization |
| GWO | Gray Wolf Optimizer |
| HBA | Honey Badger Algorithm |
| GJO | Golden Jackal Optimizer |
| ESO | Enhanced Snake Optimizer |
| SO | Snake Optimizer |
| HPPC | Hybrid Pulse Power Characterization |
| SSE | Sum of Squares Error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| SOC | State Of Charge |
| SOH | State Of Health |
| BMS | Battery Management System |
| ECM | Equivalent Circuit Model |
| OCV | Open-Circuit Voltage |
| OBL | Opposition-Based Learning |
| EOL | Elite Opposition-Based Learning |
References
- Nasajpour-Esfahani, N.; Garmestani, H.; Bagheritabar, M.; Jasim, D.; Toghraie, D.; Dadkhah, S.; Firoozeh, H. Comprehensive review of lithium-ion battery materials and development challenges. Renew. Sustain. Energy Rev. 2024, 203, 114783. [Google Scholar] [CrossRef]
- Xu, X.; Han, X.; Lu, L.; Wang, F.; Yang, M.; Liu, X.; Wu, Y.; Tang, S.; Hou, Y.; Hou, J.; et al. Challenges and opportunities toward long-life lithium-ion batteries. J. Power Sources 2024, 603, 234445. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-energy lithium-ion batteries: Recent progress and a promising future in applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Selvaraj, V.; Vairavasundaram, I. A comprehensive review of state of charge estimation in lithium-ion batteries used in electric vehicles. J. Energy Storage 2023, 72, 108777. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A review on thermal management of lithium-ion batteries for electric vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Lai, X.; Chen, Q.; Tang, X.; Zhou, Y.; Gao, F.; Guo, Y.; Bhagat, R.; Zheng, Y. Critical review of life cycle assessment of lithium-ion batteries for electric vehicles: A lifespan perspective. Etransportation 2022, 12, 100169. [Google Scholar] [CrossRef]
- Shafique, M.; Rafiq, M.; Azam, A.; Luo, X. Material flow analysis for end-of-life lithium-ion batteries from battery electric vehicles in the USA and China. Resour. Conserv. Recycl. 2022, 178, 106061. [Google Scholar] [CrossRef]
- Habib, A.K.M.A.; Hasan, M.K.; Issa, G.F.; Singh, D.; Islam, S.; Ghazal, T.M. Lithium-ion battery management system for electric vehicles: Constraints, challenges, and recommendations. Batteries 2023, 9, 152. [Google Scholar] [CrossRef]
- Tian, J.; Liu, X.; Li, S.; Wei, Z.; Zhang, X.; Xiao, G.; Wang, P. Lithium-ion battery health estimation with real-world data for electric vehicles. Energy 2023, 270, 126855. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, S.; Yang, Z.; Chen, Y. A reliable data-driven state-of-health estimation model for lithium-ion batteries in electric vehicles. Front. Energy Res. 2022, 10, 1013800. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of battery management systems (BMS) development and industrial standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Yang, S.; Liu, X.; Li, S.; Zhang, C. Thermal Management and Thermal Safety. In Advanced Battery Management System for Electric Vehicles; Springer Nature Singapore: Singapore, 2022; pp. 197–212. [Google Scholar]
- Waseem, M.; Ahmad, M.; Parveen, A.; Suhaib, M. Battery technologies and functionality of battery management system for EVs: Current status, key challenges, and future prospectives. J. Power Sources 2023, 580, 233349. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, Y.; Zhang, B.; Liu, M.; Wang, J.; Liu, C.; Hao, X. Review of state estimation and remaining useful life prediction methods for lithium–ion batteries. Sustainability 2023, 15, 5014. [Google Scholar] [CrossRef]
- Huang, C.-S. An online condition-based parameter identification switching algorithm for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2022, 72, 1701–1709. [Google Scholar] [CrossRef]
- Hamida, M.A.; El-Sehiemy, R.A.; Ginidi, A.R.; Elattar, E.; Shaheen, A.M. Parameter identification and state of charge estimation of Li-Ion batteries used in electric vehicles using artificial hummingbird optimizer. J. Energy Storage 2022, 51, 104535. [Google Scholar] [CrossRef]
- Shi, H.; Wang, S.; Wang, L.; Xu, W.; Fernandez, C.; Dablu, B.E.; Zhang, Y. On-line adaptive asynchronous parameter identification of lumped electrical characteristic model for vehicle lithium-ion battery considering multi-time scale effects. J. Power Sources 2022, 517, 230725. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Jin, J.; Geng, Y.; Liu, K. Review of lithium-ion battery state of charge estimation methods based on electrochemical models. Trans. China Electrotech. Soc. 2022, 37, 1703–1725. [Google Scholar]
- Liang, Y.; Li, S.; Yan, C.; Li, M.; Jiang, C. Explaining the black-box model: A survey of local interpretation methods for deep neural networks. Neurocomputing 2021, 419, 168–182. [Google Scholar] [CrossRef]
- Amir, S.; Gulzar, M.; Tarar, M.O.; Naqvi, I.H.; Zaffar, N.A.; Pecht, M.G. Dynamic equivalent circuit model to estimate state-of-health of lithium-ion batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
- Chen, C. Research progress on lithium-ion battery models. Model. Simul. 2024, 13, 941. [Google Scholar] [CrossRef]
- Deufel, F.; Freund, M.; Gauterin, F. A Novel Approach for a Predictive Online ECMS Applied in Electrified Vehicles Using Real Driving Data. World Electr. Veh. J. 2023, 14, 353. [Google Scholar] [CrossRef]
- Ji, Y.; Qiu, S.; Li, G. Simulation of second-order RC equivalent circuit model of lithium battery based on variable resistance and capacitance. J. Cent. South Univ. 2020, 27, 2606–2613. [Google Scholar] [CrossRef]
- Xu, D. Analysis of the dynamic characteristics of the first-order RC equivalent circuit model for lithium batteries. Power Technol. 2021, 45, 1448–1452. [Google Scholar]
- Hou, J.; Wang, X.; Su, Y.; Yang, Y.; Gao, T. Parameter identification of lithium battery model based on chaotic quantum sparrow search algorithm. Appl. Sci. 2022, 12, 7332. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Zhang, W.; Lopes, A.M.; Wu, X.; Chen, L. Improved parameter identification for lithium-ion batteries based on complex-order beetle swarm optimization algorithm. Micromachines 2023, 14, 413. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Ganesan, N.; Rudolph, G.J.; Daniel, H.D. Modeling of lithium-ion cells—A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar]
- Johnson, V.H. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Ma, C.; Wu, C.; Wang, L.; Chen, X.; Liu, L.; Wu, Y.; Ye, J. A Review of Parameter Identification and State of Power Estimation Methods for Lithium-Ion Batteries. Processes 2024, 12, 2166. [Google Scholar] [CrossRef]
- Li, J.; Peng, Y.; Wang, Q.; Liu, H. Status and prospects of research on lithium-ion battery parameter identification. Batteries 2024, 10, 194. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hashim, F.A.; Ferahtia, S.; Rezk, H. Battery parameter identification strategy based on modified coot optimization algorithm. J. Energy Storage 2022, 46, 103848. [Google Scholar] [CrossRef]
- Kim, J.; Chun, H.; Baek, J.; Han, S. Parameter identification of lithium-ion battery pseudo-2-dimensional models using genetic algorithm and neural network cooperative optimization. J. Energy Storage 2022, 45, 103571. [Google Scholar] [CrossRef]
- Shi, N.; Chen, Z.; Niu, M.; He, Z.; Wang, Y.; Cui, J. State-of-charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification. J. Energy Storage 2022, 45, 103518. [Google Scholar] [CrossRef]
- Abdelhafiz, S.M.; Fouda, M.E.; Radwan, A.G. Parameter identification of li-ion batteries: A comparative study. Electronics 2023, 12, 1478. [Google Scholar] [CrossRef]
- Yu, Z.; Xiao, L.; Li, H.; Zhu, X.; Huai, R. Model parameter identification for lithium batteries using the coevolutionary particle swarm optimization method. IEEE Trans. Ind. Electron. 2017, 64, 5690–5700. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Al-Betar, M.A.; Abu Doush, I.; Awadallah, M.A.; Kassaymeh, S.; Mirjalili, S.; Abu Zitar, R. Recent advances in Grey Wolf Optimizer, its versions and applications. IEEE Access 2023, 12, 22991–23028. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Ahandani, M.A.; Kharrati, H. A corporate shuffled complex evolution for parameter identification. Artif. Intell. Rev. 2020, 53, 2933–2956. [Google Scholar] [CrossRef]
- Turgut, M.S.; Sağban, H.M.; Turgut, O.E.; Özmen, Ö.T. Whale optimization and sine–cosine optimization algorithms with cellular topology for parameter identification of chaotic systems and Schottky barrier diode models. Soft Comput. 2021, 25, 1365–1409. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Yao, L.; Yuan, P.; Tsai, C.-Y.; Zhang, T.; Lu, Y.; Ding, S. ESO: An enhanced snake optimizer for real-world engineering problems. Expert Syst. Appl. 2023, 230, 120594. [Google Scholar] [CrossRef]
- Wang, L.; Liu, S.; Wang, J.; Tian, Y. Snake optimization algorithm combined with elite initialization and K-nearest neighbor. Res. Comput. Appl. 2024, 41, 2712–2721. [Google Scholar]
- Wu, T.-Y.; Li, H.; Chu, S.-C. CPPE: An improved phasmatodea population evolution algorithm with chaotic maps. Mathematics 2023, 11, 1977. [Google Scholar] [CrossRef]
- Tizhoosh, H.R.; Rahnamayan, S. Learning opposites with evolving rules. In Proceedings of the2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–8. [Google Scholar]
- Jiao, C.; Yu, K.; Zhou, Q. An opposition-based learning adaptive chaotic particle swarm optimization algorithm. J. Bionic Eng. 2024, 21, 3076–3097. [Google Scholar] [CrossRef]
- Si, T.; Miranda, P.B.; Bhattacharya, D. Novel enhanced Salp Swarm Algorithms using opposition-based learning schemes for global optimization problems. Expert Syst. Appl. 2022, 207, 117961. [Google Scholar] [CrossRef]
- Khishe, M. Greedy opposition-based learning for chimp optimization algorithm. Artif. Intell. Rev. 2023, 56, 7633–7663. [Google Scholar] [CrossRef]
- Farahmand-Tabar, S.; Shirgir, S. Boosting the efficiency of metaheuristics through opposition-based learning in optimum locating of control systems in tall buildings. In Handbook of Formal Optimization; Springer: Singapore, 2024; pp. 313–330. [Google Scholar]
- Mohapatra, S.; Mohapatra, P. Fast random opposition-based learning Golden Jackal Optimization algorithm. Knowl.-Based Syst. 2023, 275, 110679. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Naseem, R. Common benchmark functions for metaheuristic evaluation: A review. JOIV Int. J. Inform. Vis. 2017, 1, 218–223. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Metzler, R.; Klafter, J.; Gonchar, V.Y. Introduction to the theory of Lévy flights. In Anomalous Transport: Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 129–162. [Google Scholar]
- CALCE Battery Dataset. Available online: https://calce.umd.edu/battery-data (accessed on 22 December 2024).

| Num. | Name | Range | fmin |
|---|---|---|---|
| f1 | Sphere Function | [−100, 100] | 0 |
| f2 | Schwefel 2.22 Function | [−10,10] | 0 |
| f3 | Schwefel 1.2 Function | [−100,100] | 0 |
| f4 | Schwefel 2.21 Function | [−100,100] | 0 |
| f5 | Rosenbrock Function | [−30,30] | 0 |
| f6 | Step 2 Function | [−100,100] | 0 |
| f7 | Quartic Function | [−1.28, 1.28] | 0 |
| f8 | Schwefel 2.26 Function | [−500, 500] | −2094 |
| f9 | Rastrigin Function | [−5.12, 5.12] | 0 |
| f10 | Ackley 1 Function | [−32, 32] | 0 |
| f11 | Griewank Function | [−600, 600] | 0 |
| f12 | Penalized 1 Function | [−50,50] | 0 |
| f13 | Penalized 2 Function | [−50, 50] | 0 |
| Algorithms | Parameters |
|---|---|
| EOLSO | Th1 = 0.25, Th2 = 0.6, Tp = 50 |
| ESO | Th1 = 0.25, Th2 = 0.6; cstart1 = 0.5, cstart2 = 0.05, cstart3 =2; cend1 =cend2 = cend3 = 0.5 |
| SO | Th1 = 0.25, Th2 = 0.6 |
| GJO | c1 = 1.5, β = 1.5 |
| HBA | C = 2, β = 6 |
| GWO | a ∈ [0, 2] |
| Num | GJO Ave (Std)/win | SO Ave (Std)/win | GWO Ave (Std)/win | HBA Ave (Std)/win | ESO Ave (Std)/win | EOLSO Ave (Std)/win |
|---|---|---|---|---|---|---|
| f1 | 9.67 × 10−106 (5.29 × 10−105)/+ | 1.71 × 10−112 (5.97 × 10−112)/+ | 4.04 × 10−56 (1.64 × 10−55)/+ | 5.90 × 10−163 (3.14 × 10−162)/+ | 5.51 × 10−145 (1.54 × 10−144)/+ | 5.48 × 10−310 (0) |
| f2 | 1.42 × 10−60 (2.07 × 10−60)/+ | 6.14 × 10−57 (2.07 × 10−56)/+ | 6.02 × 10−33 (1.15 × 10−32)/+ | 4.83 × 10−87 (1.33 × 10−86)/+ | 1.26 × 10−76 (1.81 × 10−76)/+ | 1.47 × 10−159 (7.93 × 10−159) |
| f3 | 5.41 × 10−55 (2.89 × 10−54)/+ | 8.60 × 10−77 (4.63 × 10−76)/+ | 1.89 × 10−24 (9.81 × 10−24)/+ | 7.85 × 10−130 (3.73 × 10−129)/+ | 1.44 × 10−115 (5.66 × 10−115)/+ | 6.38 × 10−249 (0) |
| f4 | 1.08 × 10−39 (3.55 × 10−39)/+ | 4.29 × 10−48 (1.31 × 10−47)/+ | 3.97 × 10−18 (8.23 × 10−18)/+ | 1.57 × 10−73 (6.68 × 10−73)/+ | 3.37 × 10−67 (5.39 × 10−67)/+ | 8.39 × 10−147 (3.94 × 10−146) |
| f5 | 7.30 (0.59)/+ | 5.44 (2.86)/+ | 6.60 (0.71)/+ | 2.34 (0.47)/− | 3.93 (2.24)/+ | 2.77 (2.14) |
| f6 | 1.98 × 10−1 (2.20 × 10−1)/+ | 3.46 × 10−6 (9.59 × 10−6)/+ | 8.40 × 10−3 (4.60 × 10−2)/+ | 1.65 × 10−15 (5.70 × 10−15)/− | 7.84 × 10−10 (3.33 × 10−9)/+ | 2.64 × 10−13 (3.72 × 10−13) |
| f7 | 2.53 × 10−4 (2.06 × 10−4)/+ | 3.42 × 10−4 (2.69 × 10−4)/+ | 5.07 × 10−4 (3.99 × 10−4)/+ | 3.28 × 10−4 (2.07 × 10−4)/+ | 5.05 × 10−4 (3.88 × 10−4)/+ | 9.41 × 10−5 (9.51 × 10−5) |
| f8 | −2240.99 (328.06)/+ | −4168.35 (47.91)/= | −2727.38 (276.86)/+ | −3351.09 (335.15)/+ | −4178.27 (16.92)/= | −4189.83 (2.89 × 10−3) |
| f9 | 0 (0)/= | 1.80 (3.05)/+ | 0.78 (1.65)/+ | 0 (0)/= | 2.31 (3.70)/+ | 0 (0) |
| f10 | 3.88 × 10−15 (6.49 × 10−16)/+ | 1.98 × 10−15 (1.79 × 10−15)/+ | 7.43 × 10−15 (1.74 × 10−15)/+ | 4.44 × 10−16 (0)/= | 4.44 × 10−16 (0)/= | 4.44 × 10−16 (0) |
| f11 | 0 (0)/= | 8.74 × 10−2 (6.95 × 10−2)/+ | 2.21 × 10−2 (3.38 × 10−2)/+ | 0 (0)/= | 4.20 × 10−3 (1.44 × 10−2)/+ | 0 (0) |
| f12 | 3.28 × 10−2 (3.28 × 10−2)/+ | 1.32 × 10−2 (2.87 × 10−2)/+ | 3.05 × 10−3 (6.92 × 10−3)/+ | 1.30 × 10−16 (5.34 × 10−16)/+ | 3.39 × 10−10 (1.14 × 10−9)/+ | 3.13 × 10−14 (3.19 × 10−14) |
| f13 | 1.15 × 10−1 (1.15 × 10−1)/+ | 1.10 × 10−3 (3.35 × 10−3)/+ | 1.97 × 10−2 (4.82 × 10−2)/+ | 2.19 × 10−2 (3.76 × 10−2)/+ | 1.10 × 10−3 (3.35 × 10−3)/+ | 3.75 × 10−10 (8.64 × 10−10) |
| R1/Ω | R2/Ω | C1/F | C2/F | |
|---|---|---|---|---|
| Minimum | 0.01 | 0.01 | 1 | 1000 |
| Maximum | 0.1 | 0.1 | 10,000 | 75,000 |
| GWO | HBA | GJO | SO | ESO | EOLSO | |
|---|---|---|---|---|---|---|
| R1/Ω | 0.021341 | 0.019197 | 0.019221 | 0.019700 | 0.016443 | 0.017022 |
| R2/Ω | 0.023364 | 0.037190 | 0.027344 | 0.062188 | 0.028298 | 0.027731 |
| C1/F | 2562.030 | 1447.514 | 2596.315 | 1548.089 | 1965.741 | 1853.342 |
| C2/F | 17,740.982 | 27,669.715 | 17,858.170 | 35,101.853 | 18,360.233 | 18,395.515 |
| Time Cost | 1.120(s) | 1.199(s) | 1.162(s) | 0.021(s) | 1.106(s) | 2.932(s) |
| GWO | HBA | GJO | SO | ESO | EOLSO | |
|---|---|---|---|---|---|---|
| SSE/V2 | 0.085683 | 0.083871 | 0.084746 | 0.140143 | 0.079870 | 0.078756 |
| MAE/mV | 0.002946 | 0.002972 | 0.002929 | 0.004147 | 0.002884 | 0.002873 |
| RMSE/mV | 0.004099 | 0.004056 | 0.004077 | 0.005242 | 0.003958 | 0.003930 |
| MaxAE/mV | 0.020531 | 0.019624 | 0.020360 | 0.019696 | 0.019850 | 0.019319 |
| EOLSO-C | EOLSO-T | EOLSO-E | SO | EOLSO | |
|---|---|---|---|---|---|
| SSE/V2 | 0.082352 | 0.079843 | 0.078843 | 0.140143 | 0.078756 |
| MAE/mV | 0.002896 | 0.002887 | 0.002874 | 0.004147 | 0.002873 |
| RMSE/mV | 0.004019 | 0.003957 | 0.003932 | 0.005242 | 0.003930 |
| MaxAE/mV | 0.021419 | 0.018623 | 0.019371 | 0.019696 | 0.019319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Xiong, Y.; Zhang, S.; Fan, X.; Wang, R.; Wong, P. A Novel Method of Parameter Identification for Lithium-Ion Batteries Based on Elite Opposition-Based Learning Snake Optimization. World Electr. Veh. J. 2025, 16, 268. https://doi.org/10.3390/wevj16050268
Li W, Xiong Y, Zhang S, Fan X, Wang R, Wong P. A Novel Method of Parameter Identification for Lithium-Ion Batteries Based on Elite Opposition-Based Learning Snake Optimization. World Electric Vehicle Journal. 2025; 16(5):268. https://doi.org/10.3390/wevj16050268
Chicago/Turabian StyleLi, Wuke, Ying Xiong, Shiqi Zhang, Xi Fan, Rui Wang, and Patrick Wong. 2025. "A Novel Method of Parameter Identification for Lithium-Ion Batteries Based on Elite Opposition-Based Learning Snake Optimization" World Electric Vehicle Journal 16, no. 5: 268. https://doi.org/10.3390/wevj16050268
APA StyleLi, W., Xiong, Y., Zhang, S., Fan, X., Wang, R., & Wong, P. (2025). A Novel Method of Parameter Identification for Lithium-Ion Batteries Based on Elite Opposition-Based Learning Snake Optimization. World Electric Vehicle Journal, 16(5), 268. https://doi.org/10.3390/wevj16050268






