Abstract
As lithium batteries are widely used in mobile electronic devices and electric vehicles, accurately assessing the Remaining Useful Life (RUL) of lithium-ion batteries is crucial to ensure the stable operation of the devices, improve energy efficiency, and safeguard user safety. Although data-driven methods show good prediction potential without the need to understand the reaction mechanism inside the battery, they face the problems of high data demand and feature redundancy that may reduce the model learning accuracy in practical applications. To this end, this paper proposes a data-driven lithium-ion battery life prediction method based on residual network (ResNet) and genetic algorithm (GA) optimization, which is designed to screen the features of the lithium-ion battery training data in order to effectively reduce the redundant features and improve the prediction performance of the model. Fourteen health features were first extracted during the charging and discharging phases of the battery. In order to reduce the usage of the dataset, only the first 100 cycles of the battery data were used, and the prediction error was about 9%. Secondly, the deep feature extraction capability of ResNet is utilized to effectively capture the complex patterns and subtle changes during battery decline to alleviate the problem of gradient disappearance. Meanwhile, in order to reduce the influence of redundant information, GA is used for health feature selection and optimization to screen out the most representative health features and enhance the generalization ability of the model. The experimental results obtained using the test set provided by the Massachusetts Institute of Technology (MIT), demonstrated the effectiveness and superiority of the proposed method.
1. Introduction
In the context of the new energy era, lithium-ion batteries have become a prevalent component of energy-storage devices, playing a pivotal role in domains such as urban transportation and smart grids. These batteries offer several advantages including prolonged cycle life, enhanced safety measures, and high energy density [1,2]. However, it is important to note that the battery capacity undergoes an irreversible decline during operation. Especially at the end of the battery’s service life, continued use will lead to excessive battery aging [3], raising potential safety issues. Consequently, an accurate estimation of the Remaining Useful Life of lithium batteries is imperative to ensure the safety of power users and equipment.
The residual lifetime of a battery cannot be measured directly; instead, state estimation can only be performed indirectly through the mapping relationship between the variation in internal battery parameters and parameters such as current, voltage, and temperature. Commonly used state estimation methods can be categorized into two types: model-based methods and data-driven methods [4]. Model-based methods primarily employ Kalman filtering, particle filtering, and their variants to update the parameters of the aging model [5,6] for RUL prediction. The accurate modeling of the electrochemical degradation characteristics of batteries poses a significant challenge due to the complex physical and chemical changes occurring during the charging and discharging process, compounded by noise interference from the external environment.
Data-driven methods provide a viable solution that eliminates the need for complex mechanistic studies and utilizes extensive datasets to extract implicit battery state information to facilitate RUL prediction. Common data-driven methods include Support Vector Machines (SVMs), Relevant Vector Machines (RVMs), Artificial Neural Networks (ANNs), and deep learning methods such as Recurrent Neural Networks (RNNs) and Deep Neural Networks (DNNs).
The SVM model is simple, less computationally intensive, and faster to train but cannot handle large amounts of data, Shu et al. [7] proposed a generalized SOH estimation framework by using least squares support vector machine.
ANN has strong nonlinear learning ability [8], but the network structure is complex and computationally inefficient, Zhang et al. [9] proposed a method to combine partial incremental capacity with ANN to estimate battery SOH and predict RUL online under constant current discharge conditions, which has good generalization ability and high prediction accuracy.
RNN in deep learning methods can effectively deal with time series data, but there are problems such as gradient vanishing and high computational complexity, Ansari et al. [10] increased the input data dimension of the RNN algorithm and used a dataset consisting of voltage, current, and temperature of each cycle to predict RUL.
On the other hand, DNN performs well in handling nonlinear and high-dimensional data but tends to fall into local optima. Khumprom et al. [11] used DNN to predict the health status and remaining lifetime of batteries and compared their prediction results with other machine learning algorithms and outperformed these traditional machine learning algorithms in terms of prediction accuracy. But it cannot provide uncertainty in the prediction results.
In order to overcome the limitations of a single approach, some studies have used a fusion approach with an optimization strategy. Wang et al. utilized support vector regression (SVR) to predict RUL and concurrently employed an artificial bee colony to optimize the SVR kernel parameters. However, the kernel function and loss function of the SVR algorithm are typically challenging to ascertain [12]. Xue et al. established a biexponential state-space model for lithium battery degradation, introduced an adaptive trace-free Kalman filter algorithm to adaptively update the process noise covariance and observation noise covariance, and used a genetic algorithm to optimize the key parameters of the support vector machine to achieve multistep prediction [13]. SVR in conjunction with particle systems as a measurement equation allows for forward-looking predictions [14]. Furthermore, SVR can be used as an enhancement tool to improve the prediction accuracy of BiLSTM-AM models [15]. However, integrating the model and data-driven methods has the problems of high computational volume, numerous parameters, and poor model generalization ability.
Based on existing research, this study proposes a method for estimating the Remaining Useful Life of lithium-ion batteries based on the ResNet-GA-MLR fusion model, which significantly improves the prediction accuracy and model applicability by integrating the advantages of the residual network, genetic algorithm and multiple linear regression (MLR). The method first extracts 14 types of multidimensional health features, such as voltage, current, capacity, etc., from the battery charging and discharging process, which breaks through the traditional limitation of relying on a single indicator, and only needs the data of the first 100 cycles to realize a prediction error of about 9%, which dramatically reduces the data requirement. In the core framework, ResNet captures the complex patterns and microscopic changes in battery degradation through the residual connection structure, effectively mitigating the problem of gradient disappearance, while GA dynamically removes redundant information and optimizes the parameter combinations in the feature selection stage, enhancing the model generalization capability. Compared with traditional methods, this model has multiple advantages: (1) compared with SVM, its deep feature extraction capability is more adaptable to the nonlinear pattern of battery degradation; (2) compared with ANN, it reduces the complexity of manual parameter tuning through automatic feature selection; (3) for the characteristics of non-time-series data, it utilizes feature optimization to make up for the deficiencies of the RNN in terms of gradient disappearance and computational efficiency; (4) compared with DNN, it introduces the residual connection structure to reduce the complex patterns and microscopic changes in battery degradation. The risk of local optimization is avoided. Experimental validation shows that ResNet-GA-MLR can still maintain high accuracy and strong robustness in small sample scenarios.
2. Data Analysis
2.1. Dataset
In this paper, 40 sets of battery data were extracted from MIT’s battery dataset for the study. The dataset contains 124 full-life-cycle battery datasets using 72 different rapid charge/discharge techniques to reduce the battery capacity to 80% of its rated capacity. The dataset is based on a commercial lithium iron phosphate/graphite battery (A123 system, model APR18650M1A, rated capacity 1.1 Ah), which was subjected to cyclic charge/discharge experiments using different fast-charging conditions at 30 °C. The cycle life information was obtained by varying the charging and discharging multipliers, and the cycle life ranged from 150 to 2300 cycles.
2.2. Health Feature Extraction
The selection of health features has been demonstrated to have a significant impact on the prediction accuracy of the data models [16]. In this study, a series of physical and chemical battery properties were selected as health features based on battery expertise. Figure 1 shows the linear relationship between capacity (discharge) and number of charge/discharge cycles for the same battery type under different charging strategies. It is evident from the figure that the battery capacity exhibits a nonlinear decline with an increase in the number of cycles. Furthermore, the curves demonstrate local fluctuations and capacity regeneration characteristics, which significantly affect RUL estimation of RUL. Therefore, in this paper, 14 health characteristics related to battery cycle life are selected for battery RUL estimation based on specialized knowledge.
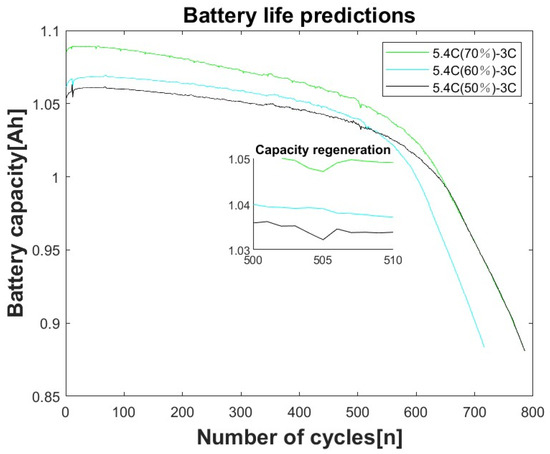
Figure 1.
Trend of battery capacity with increasing number of cycle charging under different charging strategies.
The 14 health characteristics can be categorized into five groups:
- Group 1: Discharge capacity is a capacity indicator reflecting the capacity of the battery, and the change in the battery capacity in different cycle stages has reference significance for predicting the battery life. In this study, the discharge capacity in the second cycle was designated as health characteristic 1, the discharge capacity of the 50th cycle was used as health characteristic 2, and the discharge capacity in the one-hundredth cycle was designated as health characteristic 3. The variation in battery capacity is a significant indicator of a battery’s health status, and the discrepancy in battery capacity may be indicative of battery degradation. Thus, this study selected the variation in battery capacity from the 98th to the 100th cycle as health characteristic 4.
- Group 2: Based on the feature of a gradual decrease in charging time in repeated charge/discharge cycles of the battery, the change in average charging time reflects the change in physical and chemical performance of the battery, which can be used as a health characteristic to express the performance status of the battery. In this study, the average charging time from the second to the sixth cycle is designated as health feature 5, The average charging time from the 94th to the 100th cycle was used as the health characteristic 6, and the average charging time from the second to the hundredth cycle is designated as health feature 7.
- Group 3: As the number of charge/discharge cycles increases, the internal resistance of the battery will continue to increase. This change in resistance is a pivotal metric for gauging a battery’s health status. In this study, the minimum internal resistance from the 2nd to 100th cycles was employed as the health feature 8; the difference in internal resistance from the 2nd to 100th cycles was utilized as the health feature 9, and the maximum internal resistance from the 2nd to 100th cycles was designated as the health feature 10.
- Group 4: As illustrated in Figure 2, it can be seen that the discharge capacity and voltage of the battery gradually shift with the increase in the number of cycles, and this shift tends to increase with the increase in the number of cycles. To describe this trend, the variance of the offset between the 100th cycle curve and the 10th cycle curve and the minimum value of the offset were selected as health features 11 and 12 in this study.
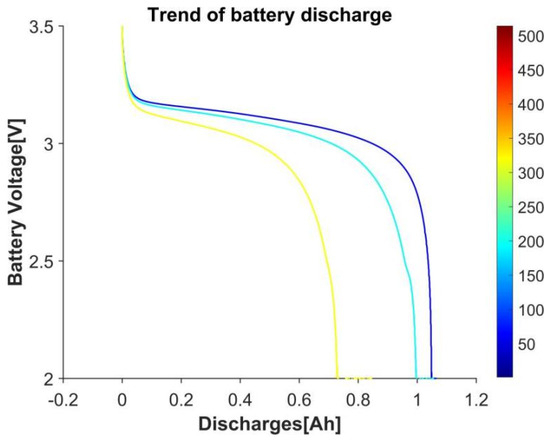 Figure 2. Curve of discharging capacity and voltage of battery with the number of cycles.
Figure 2. Curve of discharging capacity and voltage of battery with the number of cycles. - Group 5: Figure 3 shows the trend curve of the change in battery discharge capacity with the number of discharge cycles during the first 100 cycles. The orange circle denotes the slope of the fitting result of this trend curve, and it can be deduced that the change in slope can roughly reflect the changing trend of the discharge capacity with the number of cycles. Consequently, in this study, the slope and intercept of the trend of the battery discharge capacity change were designated as health characteristics 13 and 14, respectively.
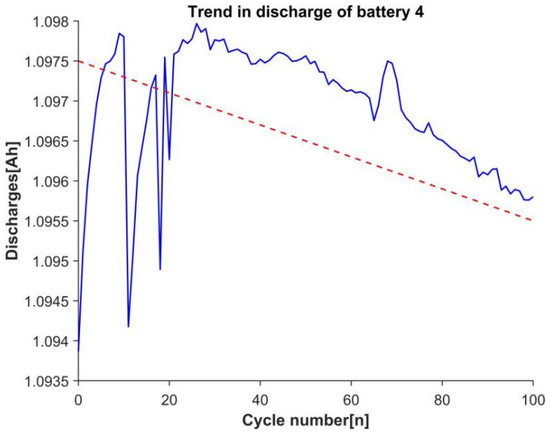 Figure 3. Trend of discharge capacity of battery 4 with cycling factor.
Figure 3. Trend of discharge capacity of battery 4 with cycling factor.
3. Experimental Methods
As previously referenced, 14 sets of features were collectively identified through data analysis and expert consensus. However, in practice, the number of features employed in the training of a machine-learning model is not as high as it should be. Typically, augmenting the number of features can enhance the performance of a machine-learning model and improve the accuracy of the model’s fit to the data. However, it should be noted that an increase in the number of features can lead to an increase in the training complexity of the model and computational burden. Furthermore, the introduction of features that are irrelevant to the problem (i.e., noise) and redundant information may reduce the predictive performance of the model. Consequently, it can be concluded that preprocessing and feature selection of raw data can help to reduce computational cost, decrease model complexity, and improve the generalization ability and prediction accuracy of machine learning models.
In this paper, an integrated machine learning approach for battery life prediction is used with the aim of leveraging the strengths of different algorithms to achieve end-to-end optimization from data processing to prediction. A residual network is utilized to extract deep features from preprocessed data [17]. Residual networks effectively mitigate the gradient vanishing problem in deep networks by introducing residual connectivity, which enables them to learn the complex features in the data in a deeper way and capture the key implicit information in the battery life prediction, thus possessing a powerful deep feature extraction capability. To further improve the model performance, genetic algorithm is used to select the extracted features. By simulating the natural selection and genetic mechanism, the genetic algorithm has a powerful global search capability [18], which can efficiently find the optimal solution in the huge feature space, screen out the subset of features that contribute the most to the model performance, effectively remove the redundant information, and improve the generalization capability and prediction accuracy of the model. as shown in Figure 4.
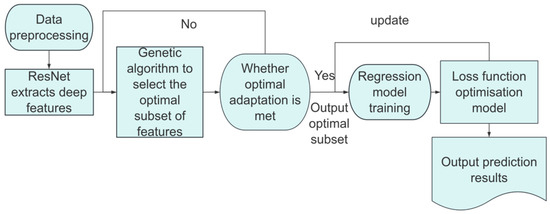
Figure 4.
Machine learning flowchart.
3.1. Extract Features
In this paper, a deep feature extraction method based on the residual network is proposed [19], aiming to extract representative features from the complex charge/discharge data of lithium-ion batteries in order to achieve an accurate prediction of the battery’s Remaining Useful Life. The method designs an improved residual block centered on the use of a LeakyReLU activation function and an adaptive mean pooling layer. The LeakyReLU activation function allows negative values to pass through, which effectively mitigates the problem of gradient vanishing brought by the traditional ReLU activation function, and thus accelerates the model training process. On the other hand, the adaptive average pooling layer reduces the spatial dimension of the feature map to 1 × 1, converts it into a fixed-length feature vector, and prepares it for subsequent processing of the fully connected layer. Each residual block first extracts the local features of the battery data through two 3 × 3 convolutional layers and then passes the input information directly to the output through cross-layer connections, further alleviating the problem of gradient vanishing in deep networks. In addition, a batch normalization layer is introduced in each residual block to normalize the convolutional outputs, thereby accelerating training and improving model stability, while the dropout technique is utilized to randomly discard neurons, thereby preventing the model from overfitting and enhancing its generalization capability. To further enhance the robustness of the features, a shallow network (Shallownet) containing a convolutional layer, an ELU activation function, and a dropout layer were employed for the initial feature extraction prior to the first residual block. The extracted local features are then projected and transformed into dimensions using a feature-projection layer. A shrinkage network is then introduced in each residual block to perform absolute value computation, scaling, and soft thresholding operations on the features to remove the effects of noise and outliers [20]. Finally, a deep ResNet architecture containing three of the above residual blocks and a fully connected layer is constructed to extract high-level deep features from the battery charge/discharge data, which provides a reliable database for subsequent RUL prediction. A flowchart of the algorithm is presented in Figure 5.
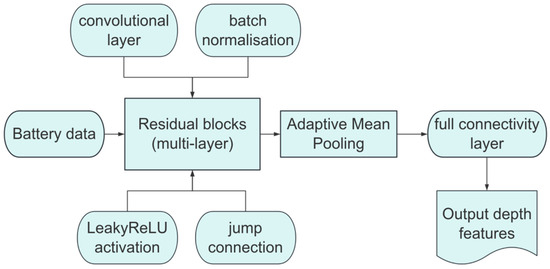
Figure 5.
Flowchart of the residual network.
3.2. Extract Feature Subsets
To enhance the efficacy of the model, this study employs a genetic algorithm to select the deep features extracted from the residual network to identify the subset of features that contribute most to battery life prediction [21]. The fundamental principle of the genetic algorithm is to simulate natural selection and genetic mechanisms to identify the subset of features that contribute most to the target problem through an iterative evolutionary process.
3.2.1. Genetic Design
The genetic algorithm randomly generates N chromosomes, each represented by a gene sequence, similar to the structure of a biological chromosome, by simulating natural selection and genetic mechanisms. Each gene sequence consisted of 14 alleles, with each allele representing a healthy trait. A value of 0 indicates that the health trait is not selected, whereas a value of 1 indicates that the health trait is selected; the structure of the chromosomes is shown in Table 1.

Table 1.
Chromosome structure.
The genes of each chromosome represent a set of feature selection schemes, and if n alleles are activated (i.e., have a value of 1) in the gene sequence, it means that the chromosome selects n health features for use in training the model.
3.2.2. Calculation of Adaptation
In genetic algorithms, the Fitness Function is a key metric for evaluating the merit of each chromosome (i.e., a subset of features). It directly determines which chromosomes are more likely to be selected for crossover and mutation, thus affecting the convergence speed and the final results of the algorithm. To ensure that the Fitness Function accurately reflects the impact of feature subsets on model performance, the Fitness Function designed in this study is shown in Equation (1).
where is the predicted lifetime of the ith cell and is the true lifetime of the ith cell. where Err is the error percentage of the proposed model.
3.2.3. Generation of Children
Each chromosome in the population was evaluated based on the Fitness Function, and individuals in the population were selected for single-point crossover and mutation operations using roulette wheel selection to select parents according to the size of their fitness values. During this time a position-by-position mutation was used to generate a new offspring to maintain the diversity and evolutionary capacity of the population. The selection, crossover, and mutation operations are repeated over several iterations until a predetermined number of iterations is reached or a termination condition is satisfied, and the chromosomes with the highest fitness are selected as the optimal feature subset [22]. This method has the advantages of a strong global search ability, high parallelism, good scalability, and robustness, which can effectively improve the generalization ability and prediction accuracy of the model and provide more reliable feature support for battery life prediction (see Figure 6 for the flow chart).
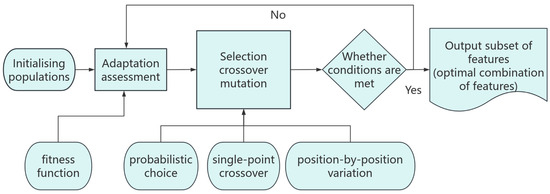
Figure 6.
Flowchart of genetic algorithm.
3.3. Regression Model
The regression model utilized in this study is a multiple linear regression model that is employed to predict battery life. The multiple linear regression model assumes a linear relationship between the target variable (battery life) and the multiple characteristic variables. This relationship is shown in Equation (2).
where is the predicted lifetime of the ith cell, is the p-feature of the ith cell, and is the p-dimensional coefficient vector of the model.
The training process of the linear regression model is to solve for the optimal weight vector by minimizing the loss function. The main loss function used in this study is the mean square error (MSE), which is given in Equation (3).
Meanwhile, to enhance the robustness of the model, this paper also introduces the mean absolute error (MAE) and Huber’s loss as auxiliary loss functions, as illustrated in Equations (4) and (5).
where n is the number of samples, is the predicted battery life of the ith sample, and is the predicted battery life of the ith sample. δ is the hyperparameter.
3.4. Model Training
The deep features extracted from ResNet were selected using a genetic algorithm to filter the subset of features that contributed the most to RUL prediction. The filtered features are then input into a linear regression model for training. The 40 sets of battery data are divided into two parts: D1 is used to train the model, and D2 is used to test the quality of the gene individuals. The evaluation process is shown in Figure 7. The error of a gene can be characterized by its fitness if n healthy features are selected, and subsequent training of the machine learning model on the health features selected by gene X in the population of Table 1, the data of D2 are substituted into Equations (3)–(5) to test the error. This error was combined with the MSE, MAE, and Huber loss to improve the robustness and accuracy of the model.

Figure 7.
Flowchart of training model.
4. Experimental Verification
This section presents a study that utilized a portion of an experimental dataset of lithium-ion batteries from the Massachusetts Institute of Technology. The study employed a decrease in battery capacity to 80% of its initial capacity as the criterion for the conclusion of battery life and the number of cycles the battery underwent as a measure of its longevity. Lithium-ion batteries are known for their long lifespan, a characteristic that brings many application advantages but also leads to high time and economic costs when performing life testing on them. To effectively address this challenge and to validate the effectiveness of the prediction methodology proposed in the preceding section, this section will exclusively analyze the characteristic parameters of each cell during the initial 100 discharge cycles. Through in-depth analysis of these early cycling data, we aim to build a reliable prediction model to assess and predict the remaining lifetime of lithium-ion batteries as early as possible, in order to optimize their use and maintenance strategies while ensuring battery performance and safety.
4.1. Parameter Setting
To extract features from the dataset based on the residual network, the selected parameter settings were as follows:
- Number of input channels: 1;
- Number of output channels: 1;
- Number of residual blocks: 3;
- Learning rate: 0.0005;
- Optimizer: AdamW;
- Weight decay: 0.00012.
The features of the dataset were screened using a genetic algorithm, and the selected parameters were set as follows:
- Population size: 15;
- Chromosome length: 14;
- Number of iterations: 30;
- Mutation rate: 0.1;
- Crossover probability: 0.8;
- D1 Data capacity: 14 × 19;
- D2 Data capacity: 14 × 21.
4.2. Experimental Results
To validate the effectiveness of the proposed method, we used all 40 test sets for validation, labeling the data for which the model was trained by feature selection as Q1 and the results of the real data as Q. In the figure, the horizontal coordinate is the real battery life of the test set, and the vertical coordinate is the battery life predicted by the model after feature selection. The black straight line denotes the baseline, and the proximity of the blue circle to this baseline is indicative of enhanced prediction accuracy. The feature selection training process yields model predictions, as illustrated in Figure 8.
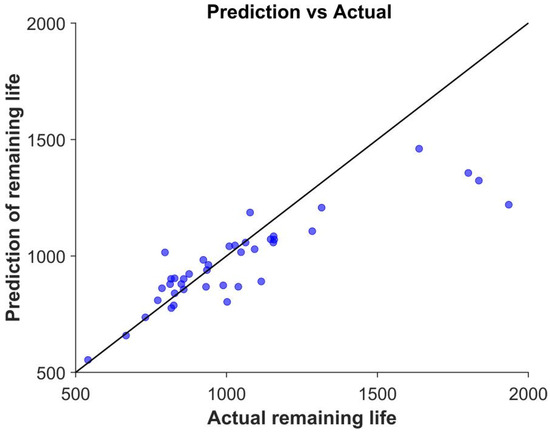
Figure 8.
Feature selection model predictions.
4.3. Ablation Experiments
In order to further verify the superiority of the method, the data that have been used in training to obtain the model only by residual network is labeled as Q2, and label the data for which the model was obtained by training with features extracted by a genetic algorithm without selecting a subset of features as Q3. The results predicted by SVR are labeled as Q4. To ensure the fairness of the comparison experiments, all the models were trained using the 14 features proposed in this study, and the final results are shown in Figure 9, Figure 10 and Figure 11. Compared to the results in Figure 8, the deviation of these models from the baseline is larger, further demonstrating the superiority of the present method.
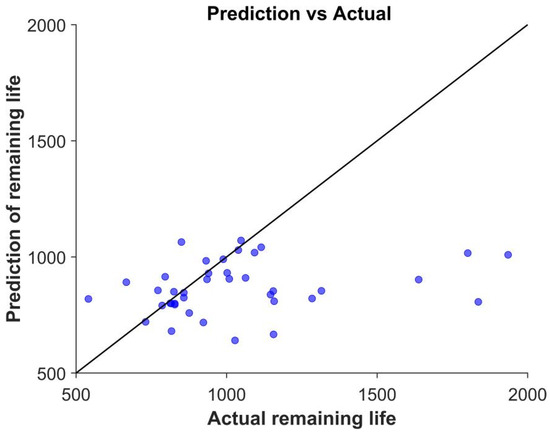
Figure 9.
Residual network training model.
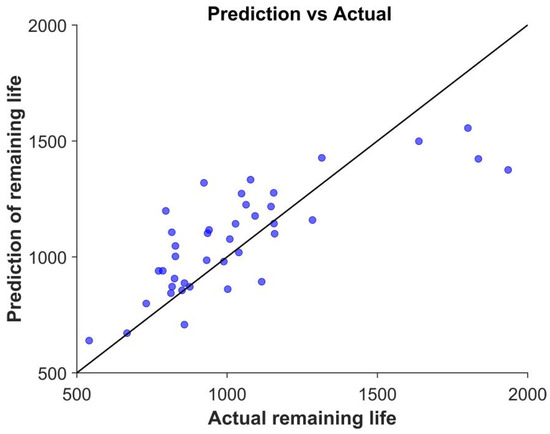
Figure 10.
Training model for extracting feature subsets without genetic algorithm.
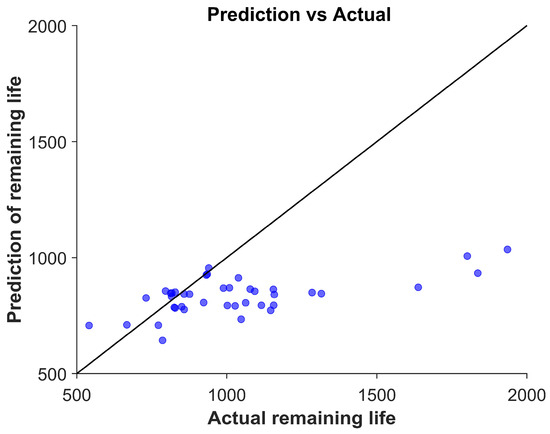
Figure 11.
SVR prediction models.
The experimental results of testing all 40 sets of batteries under different methods are recorded in Table 2, where Q1 represents the experimental results using the feature selection strategy, Q2 represents the experimental results after the residual network feature selection strategy only, and Q3 represents the experimental results after extracting the features by the genetic algorithm without selecting the feature subset, Q4 is the experimental results of the SVR model, and Q is the real lithium-ion battery life. The findings demonstrate that the data-driven battery life prediction strategy based on the data achieves favorable experimental outcomes, with a prediction accuracy of over 75% when utilizing only the feature data of the initial hundred cycles. Furthermore, the experimental results demonstrate that the error of the feature selection strategy was consistently reduced, with an overall experimental error of 8.97%, which is a marked improvement over the data obtained without the feature selection method. This outcome substantiates the efficacy of the proposed approach. With the same data and feature training, the prediction error of the feature subset selection strategy without genetic algorithm extraction is 14.2%, and the prediction method with only residual network training achieves a prediction error of 24.1%, and the prediction error of the SVR model is 18.1%, which is significantly worse than the method proposed in this paper. In addition, the literature used a regression setup and obtained a prediction error of 9.1% using only the first 100 cycles. A comparison of the results presented in Table 2 with those reported in the literature [23] further substantiates the superiority of the proposed methodology.

Table 2.
Comparison of experimental results.
5. Conclusions
In this paper, a data-driven lithium-ion battery life research method based on a linear regression model and 14 health features is proposed, and a feature selection strategy of residual network and genetic algorithm is introduced to further improve the prediction accuracy of the model. The experimental results of 40 sets of test sets show that the accuracy of the method in this paper reaches 91.03% when only the data of the first 100 charging cycles are used. In order to further verify the superiority of the proposed estimation method, under the same data and feature training, the proposed estimation model is compared with the prediction method trained by ResNet only, the prediction method not trained by genetic algorithm to extract the feature subset, and the SVR prediction method, and it is verified that the proposed estimation model has higher accuracy.
The ResNet + GA method proposed in this paper demonstrates high prediction accuracy and robustness in RUL prediction for lithium-ion batteries. Nevertheless, in practical applications, online real-time monitoring of lithium-ion batteries remains challenging, primarily due to the following factors:
- Real-time monitoring necessitates high-performance sensors and data acquisition equipment, which increases the hardware cost. Additionally, the ResNet model is complex and requires substantial computational resources for online real-time computation.
- The research is based on laboratory validation and has not yet been put into application. In order to achieve the industrialization of the method, it is necessary to obtain a large amount of battery data in real scenarios while reducing the hardware and computational costs. If the method is to be integrated into existing battery management systems or electronic devices, software and hardware compatibility issues must be addressed.
In order to develop more robust models, a Deep Residual Shrinkage Network (DRSN) is recommended to suppress data noise by shrinkage mapping and adaptive thresholding. Meanwhile, Deep Reinforcement Learning (DRL) can be employed to dynamically adjust the hyperparameters or structure of ResNet to adapt to different battery data features. In addition, redundant neurons can be pruned through a resource-oriented mechanism to streamline the number of model parameters and reduce the computational cost. However, how to achieve the optimal adaptation of arithmetic power consumption and prediction accuracy is also an issue to be considered.
Author Contributions
J.Z.: writing—original draft, investigation, conceptualization, methodology. W.H.: visualization, formal analysis, data curation. H.D.: supervision, formal analysis. C.W.: writing—review and editing. Y.Z.: formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the non-competitive scientific research project “Study on the Thermal Runaway Mechanism of High-Rate Charging and Discharging in High-Capacity Lithium Batteries” (2024KTSCX158), approved by the Department of Education of Guangdong Province, and the Guangzhou City University of Technology project “Research on Data-Driven Estimation Methods for SOC and SOH of Power Lithium Batteries” (K0224007).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, J.; Zhang, S.; Li, C.; Wu, L.; Wang, Y. A Data-Driven Method With Mode Decomposition Mechanism for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Power Electron. 2022, 37, 13684–13695. [Google Scholar] [CrossRef]
- Cheng, W.; Cai, Y.P.; Su, Y.Z.; Jiang, K.; Huang, H. Review of remaining useful life prediction for lithium-ion batteries. Chin. J. Power Sources 2021, 45, 678–682. [Google Scholar]
- Ding, G.; Wang, W.; Zhu, T. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on CS-VMD and GRU. IEEE Access 2022, 10, 89402–89413. [Google Scholar] [CrossRef]
- Lin, M.Q.; Wu, D.G.; Zheng, G.F.; Wu, J. Health state estimation of lithium battery based on surface temperature and incremental capacity. Automot. Eng. 2021, 43, 1285–1290. [Google Scholar]
- Zhang, L.; Mu, Z.; Sun, C. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Duong, P.L.T.; Raghavan, N. Heuristic Kalman optimized particle filter for remaining useful life prediction of lithium-ion battery. Microelectron. Reliab. 2018, 81, 232–243. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Shen, J.; Lei, Z.; Chen, Z.; Liu, Y. A uniform estimation framework for state of health of lithium-ion batteries considering feature extraction and parameters optimization. Energy 2020, 204, 117957. [Google Scholar] [CrossRef]
- Sterkens, W.; Diaz-Romero, D.; Goedemé, T.; Dewulf, W.; Peeters, J.R. Detection and recognition of batteries on X-Ray images of waste electrical and electronic equipment using deep learning. Resour. Conserv. Recycl. 2021, 168, 105246. [Google Scholar] [CrossRef]
- Zhang, S.; Zhai, B.; Guo, X.; Wang, K.; Peng, N.; Zhang, X. Synchronous estimation of state of health and remaining useful lifetime for lithium-ion battery using the incremental capacity and artificial neural networks. J. Energy Storage 2019, 26, 100951. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Hossain Lipu, M.S.; Hussain, A.; Saad, M.H.M. Remaining useful life prediction for lithium-ion battery storage system: A comprehensive review of methods, key factors, issues and future outlook. Energy Rep. 2022, 8, 12153–12185. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Lu, S.; Wang, J.; Zhang, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee Colony. IEEE Trans. Veh. Technol. 2019, 68, 9543–9553. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, Y.; Cheng, C.; Ma, G. Remaining useful life prediction of lithium-ion batteries with adaptive unscented kalman filter and optimized support vector regression. Neurocomputing 2020, 376, 95–102. [Google Scholar] [CrossRef]
- Li, X.; Ma, Y.; Zhu, J. An online dual filters RUL prediction method of lithium-ion battery based on unscented particle filter and least squares support vector machine. Measurement 2021, 184, 109935. [Google Scholar] [CrossRef]
- Wang, F.K.; Amogne, Z.E.; Tseng, C.; Chou, J.H. A hybrid method for online cycle life prediction of lithium-ion batteries. Int. J. Energy Res. 2022, 46, 9080–9096. [Google Scholar] [CrossRef]
- Li, Q.; Xue, W. A review of feature extraction toward health state estimation of lithium-ion batteries. J. Energy Storage 2025, 112, 115453. [Google Scholar] [CrossRef]
- Xiao, Y.; Lu, Z.; Huang, C.; Yang, F. Battery State of Health Estimation Based on Energy Features and ResNet-SVR Model. Qual. Reliab. Eng. Int. 2025, 1–15. [Google Scholar] [CrossRef]
- Wang, L.; Wang, F.; Xu, L.; Li, W.; Tang, J.; Wang, Y. SOC estimation of lead-carbon battery based on GA-MIUKF algorithm. Sci. Rep. 2024, 14, 3347. [Google Scholar] [CrossRef] [PubMed]
- Alwabli, A. From data to durability: Evaluating conventional and optimized machine learning techniques for battery health assessment. Results Eng. 2024, 23, 102445. [Google Scholar] [CrossRef]
- Khan, M.K.; Houran, M.A.; Kauhaniemi, K.; Zafar, M.H.; Mansoor, M.; Rashid, S. Efficient state of charge estimation of lithium-ion batteries in electric vehicles using evolutionary intelligence-assisted GLA-CNN-Bi-LSTM deep learning model. Heliyon 2024, 10, e35183. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; He, C.; Lin, X.; Li, C.; Huang, J. Research on remaining useful life prediction method for lithium-ion battery based on improved GA-ACO-BPNN optimization algorithm. Sustain. Energy Technol. Assess. 2025, 73, 104142. [Google Scholar] [CrossRef]
- Chang, C.; Wang, Q.; Jiang, J.; Wu, T. Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm. J. Energy Storage 2021, 38, 102570. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).