Machine Learning Techniques for Battery State of Health Prediction: A Comparative Review
Abstract
1. Introduction
- i.
- A comprehensive literature review of four widely used ML algorithms in SOH prediction, namely support vector regression (SVR), long short-term memory (LSTM), convolution neural networks (CNNs), and random forest (RF), including relevant mathematical formulations.
- ii.
- An evaluation of the strengths, limitations, and recent advancements of each algorithm.
- iii.
- A MATLAB R2025a-based simulation to assess and compare the performance of the four selected ML models in SOH prediction.
2. Machine Learning Algorithms in State of Health Prediction
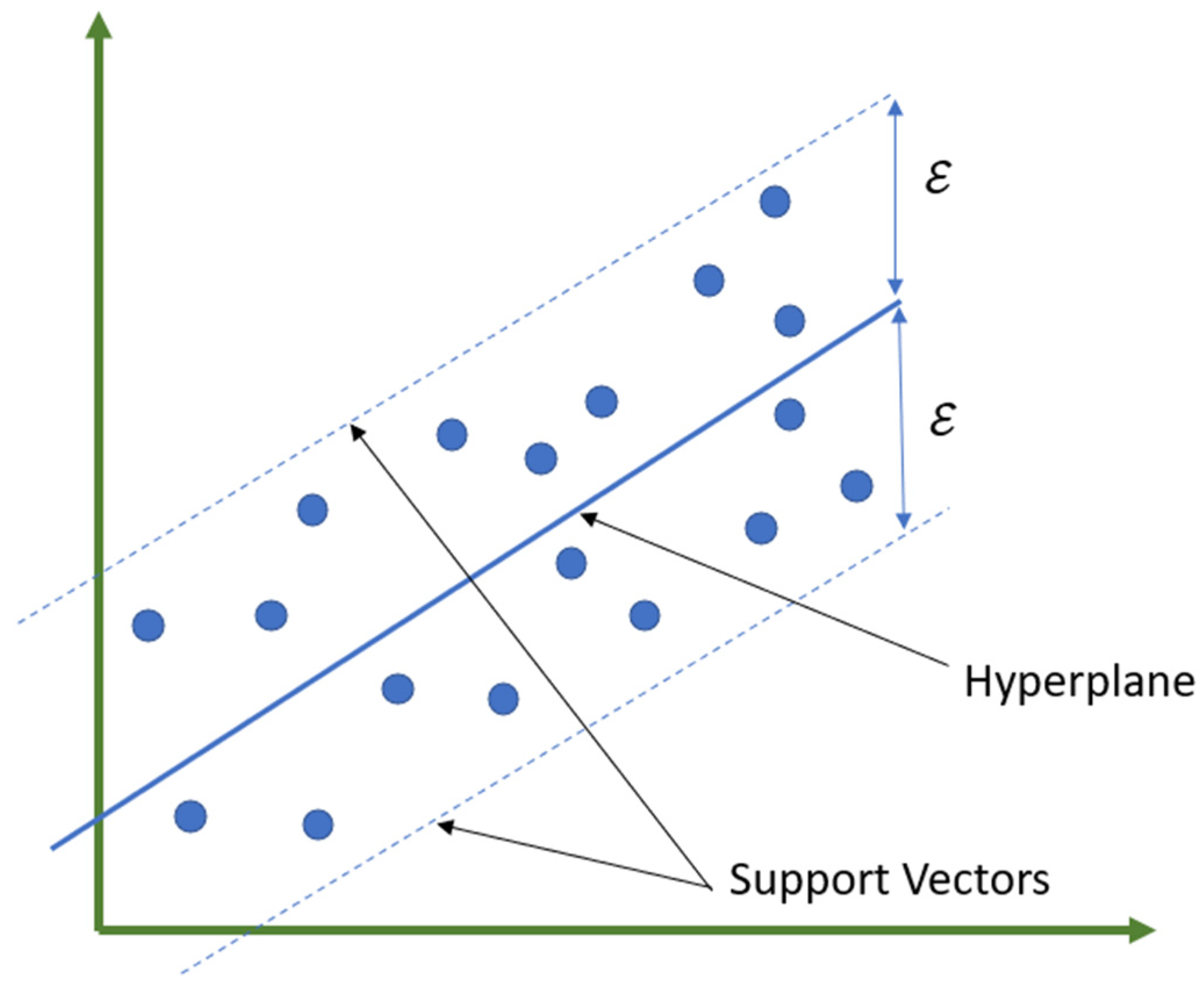
2.1. Support Vector Regression
2.2. Long Short-Term Memory
- A memory cell that maintains a cell state , which carries information across time steps, enabling long-term memory.
- Gates that control the flow of information. The gates are as follows:
- ○
- Forget gate: Decides what to discard from the previous cell state.
- ○
- Input gate: Determines what new information to store.
- ○
- Output gate: Selects what to output at the current time step.
- Each gate uses sigmoid (σ) and tanh activations to regulate information.

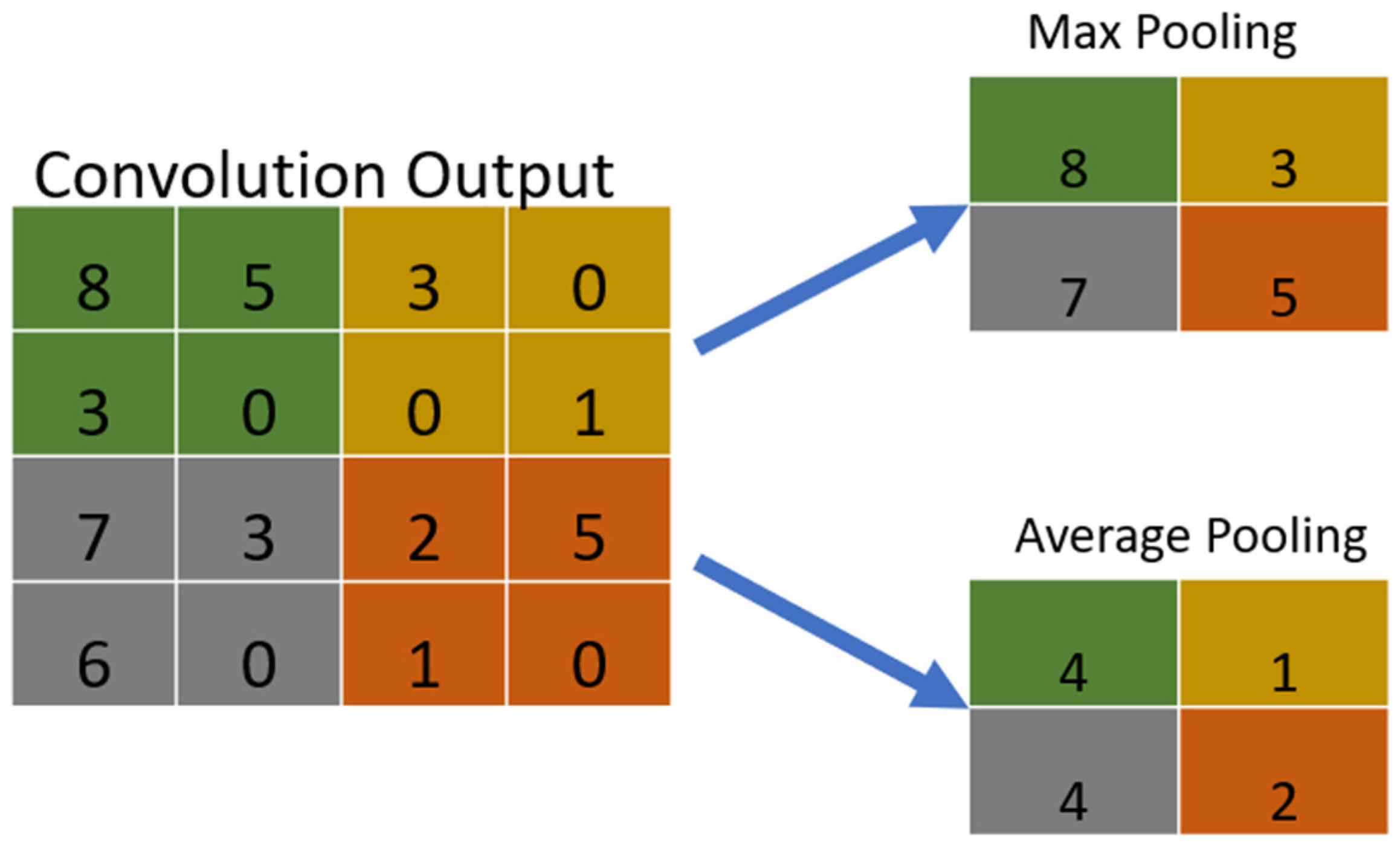
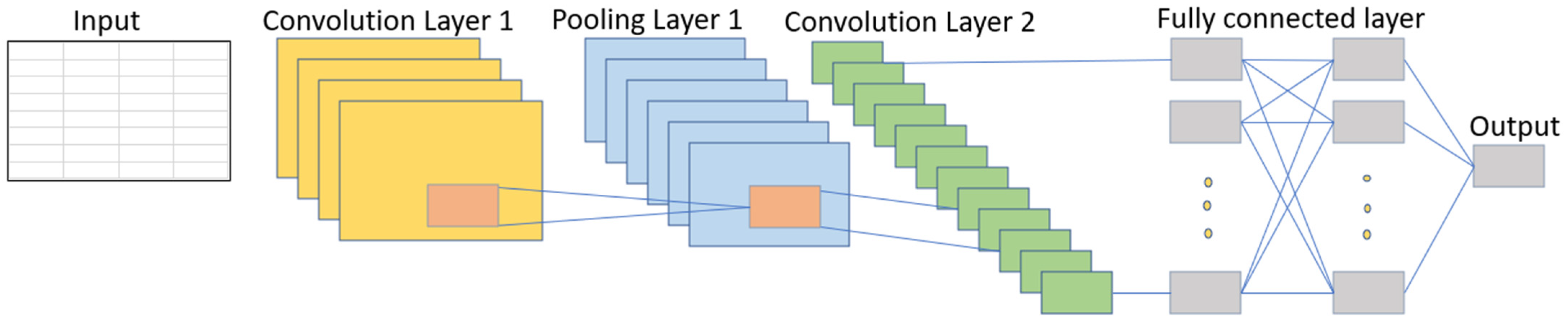
2.3. Convolution Neural Network (CNN)
2.4. Random Forest
3. Discussion
4. MATLAB Simulations
4.1. Introduction to the Datasets
4.2. Health Features Extraction
- i.
- Resampling to a fixed lengthThe raw dataset contains discharge cycles that have varying time steps because of different sampling rates and cycle lengths. To make the cycles comparable, all signals were resampled to 120 uniformly spaced points along a normalised time axis (0 to 1). The normalisation process maintains the original degradation patterns while removing the effects of varying cycle lengths.
- ii.
- Measurement signalsFrom the resampled signals, six synchronised sequences were constructed: the raw measurements of voltage (V), current (I), and temperature (T), together with their first-order derivatives with respect to time (dV/dt, dI/dt, dT/dt). This produced a 6 × 120 representation per cycle, capturing both the original signal values and their time-dependent variations.
- iii.
- Use across models
- CNN and LSTM: The full 6 × 120 sequences were provided directly as inputs, enabling the networks to learn both local patterns (via convolution) and temporal dependencies (via recurrent layers).
- SVR and RF: Since these models require vectorised features rather than full sequences, summary statistics were computed from the same 6 × 120 representation. These features are shown in Table 3, which gives a summary of the health features that were used in the SVR and RF models.
4.3. Model Training
- CNN: A 1D convolutional neural network with three convolutional layers, batch normalisation, global average pooling, and fully connected layers, trained for 100 epochs with early stopping on validation loss
- LSTM: A stacked bi-directional LSTM network, followed by fully connected and dropout layers, trained for 60 epochs with similar validation protocol.
- SVR: The RBF kernel was used with grid search performed over the hyperparameters (C, ε, kernel scale) tuned via 5-fold cross validation, and the best model refit on full training data.
- RF-TreeBagger regression with hyperparameters (number of trees, minimum leaf size) chosen via grid search and out-of-bag RMSE minimisation.
4.4. Evaluation
- (a)
- Mean Absolute Error (MAE)
- (b)
- R-squared (R2)
- (c)
- Root Mean Squared Error (RMSE)
4.5. SOH Estimation Results and Discussion
4.5.1. Performance Metrics
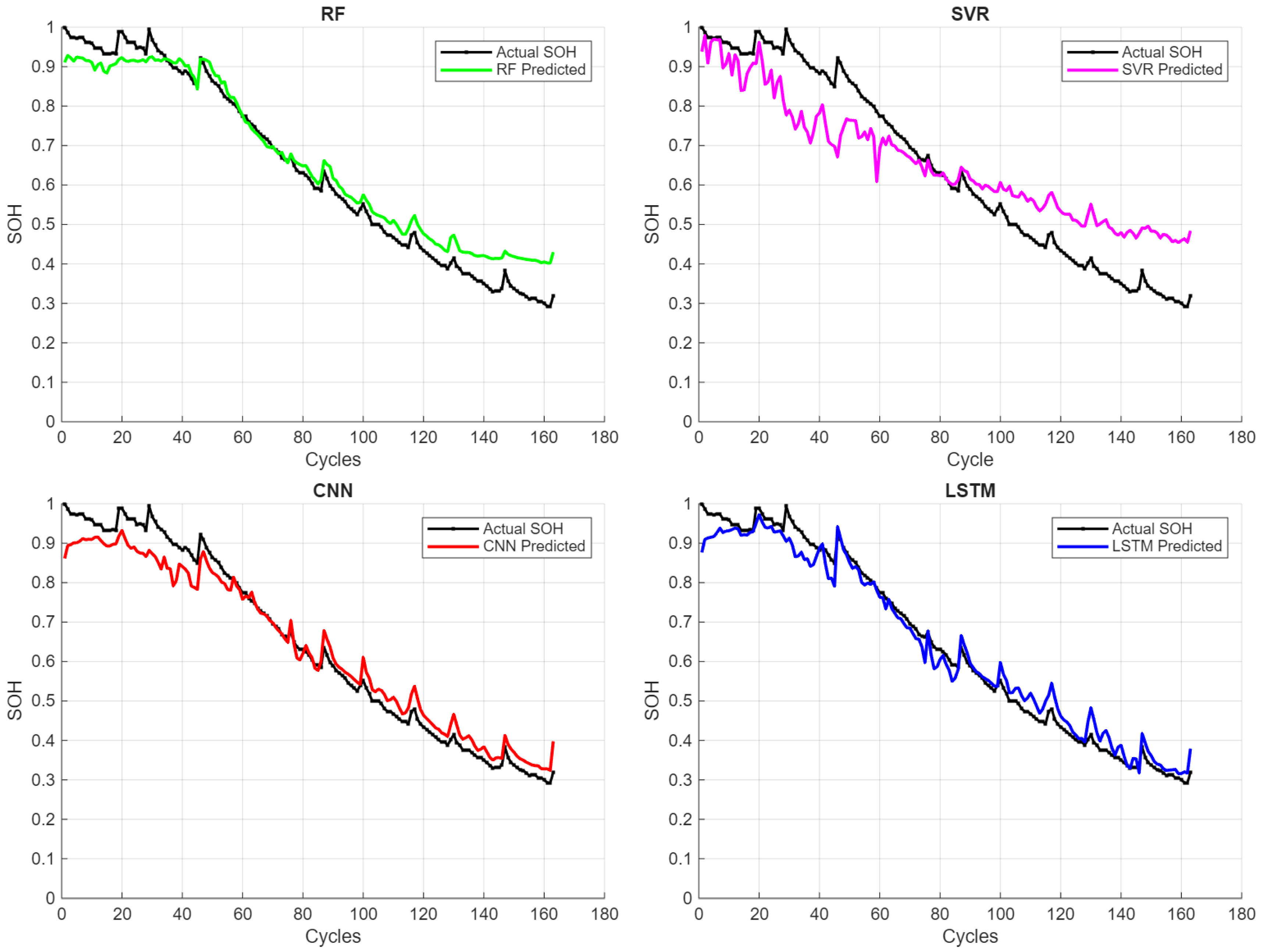
4.5.2. Predicted vs. Actual SOH Across the Different ML Models
4.5.3. Training Time
5. Conclusions
- Interpretability and Trust: Deep models such as LSTM and CNN remain black box in nature. Incorporating explainable AI techniques (e.g., SHAP, LIME) [70] can enhance transparency and facilitate adoption in safety-critical applications.
- Model Robustness and Real-World Applicability: The simulations in this study used only the controlled NASA PCoE dataset (25 °C, fixed charge/discharge protocols), which does not fully represent real-world EV conditions such as fluctuating temperatures, dynamic load profiles, and irregular charging. Future work should validate these models on field datasets to assess robustness. Transfer learning and domain adaptation should be further explored to improve generalisation across chemistries and usage conditions [71].
- Hybrid and Physics-Informed Models: Combining machine learning with physics-informed features [72] or models can improve accuracy while reducing data requirements, creating more generalisable frameworks.
- Resource-Constrained Deployment: Simplified models (e.g., RF or lightweight neural networks) should be optimised for embedded deployment in battery management systems (BMSs), especially in low-cost EVs and grid storage applications.
- Long-Term Prognostics: Future work should extend beyond short-term SOH estimation to include reliable prediction of remaining useful life (RUL) [62], which is critical for lifecycle optimisation and predictive maintenance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Global EV Outlook 2025 Expanding Sales in Diverse Markets. Available online: www.iea.org (accessed on 15 August 2025).
- Padder, S.G.; Ambulkar, J.; Banotra, A.; Modem, S.; Maheshwari, S.; Jayaramulu, K.; Kundu, C. Data-Driven Approaches for Estimation of EV Battery SoC and SoH: A Review. IEEE Access 2025, 13, 35048–35067. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Wang, H. Battery degradation diagnosis under normal usage without requiring regular calibration data. J. Power Sources 2024, 608, 234670. [Google Scholar] [CrossRef]
- Li, G.; West, A.C.; Preindl, M. Characterizing degradation in lithium-ion batteries with pulsing. J. Power Sources 2023, 580, 233328. [Google Scholar] [CrossRef]
- Lee, J.; Won, J. Enhanced Coulomb Counting Method for SoC and SoH Estimation Based on Coulombic Efficiency. IEEE Access 2023, 11, 15449–15459. [Google Scholar] [CrossRef]
- Bourelly, C.; Vitelli, M.; Milano, F.; Molinara, M.; Fontanella, F.; Ferrigno, L. EIS-Based SoC Estimation: A Novel Measurement Method for Optimizing Accuracy and Measurement Time. IEEE Access 2023, 11, 91472–91484. [Google Scholar] [CrossRef]
- Merrouche, W.; Lekouaghet, B.; Bouguenna, E.; Himeur, Y. Parameter estimation of ECM model for Li-Ion battery using the weighted mean of vectors algorithm. J. Energy Storage 2024, 76, 109891. [Google Scholar] [CrossRef]
- Kara, A. A data-driven approach based on deep neural networks for lithium-ion battery prognostics. Neural Comput. Appl. 2021, 33, 13525–13538. [Google Scholar] [CrossRef]
- Wang, R.; Xu, X.; Zhou, Q.; Zhang, J.; Wang, J.; Ye, J.; Wu, Y. State of Health Estimation for Lithium-Ion Batteries Using Enhanced Whale Optimization Algorithm for Feature Selection and Support Vector Regression Model. Processes 2025, 13, 158. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, L.; Li, X.; Hu, Y.; Huang, K.; Xue, B.; Wang, Y.; Yu, Y. State-of-health estimation for the lithium-ion battery based on gradient boosting decision tree with autonomous selection of excellent features. Int. J. Energy Res. 2022, 46, 1756–1765. [Google Scholar] [CrossRef]
- Xu, H.; Wu, L.; Xiong, S.; Li, W.; Garg, A.; Gao, L. An improved CNN-LSTM model-based state-of-health estimation approach for lithium-ion batteries. Energy 2023, 276, 127585. [Google Scholar] [CrossRef]
- Khaleghi, S.; Hosen, M.S.; Van Mierlo, J.; Berecibar, M. Towards machine-learning driven prognostics and health management of Li-ion batteries. A comprehensive review. Renew. Sustain. Energy Rev. 2024, 192, 114224. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Awad, M., Khanna, R., Eds.; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar] [CrossRef]
- Wilson, M.D. Support Vector Machines. In Encyclopedia of Ecology, Five-Volume Set; Jørgensen, S.E., Fath, B.D., Eds.; Academic Press: Cambridge, MA, USA, 2008; Volume 1–5, pp. 3431–3437. [Google Scholar] [CrossRef]
- Zhao, Q.; Qin, X.; Zhao, H.; Feng, W. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries. Microelectron. Reliab. 2018, 85, 99–108. [Google Scholar] [CrossRef]
- Si, Q.; Matsuda, S.; Yamaji, Y.; Momma, T.; Tateyama, Y. Data-Driven Cycle Life Prediction of Lithium Metal-Based Rechargeable Battery Based on Discharge/Charge Capacity and Relaxation Features. Adv. Sci. 2024, 11, 2402608. [Google Scholar] [CrossRef]
- Feng, R.; Wang, S.; Yu, C.; Hai, N.; Fernandez, C. High precision state of health estimation of lithium-ion batteries based on strong correlation aging feature extraction and improved hybrid kernel function least squares support vector regression machine model. J. Energy Storage 2024, 90, 111834. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Y.; Zhu, Q.; Rashid, H.; Li, H. A novel battery health indicator and PSO-LSSVR for LiFePO4 battery SOH estimation during constant current charging. Energy 2023, 282, 128782. [Google Scholar] [CrossRef]
- Vedhanayaki, S.; Indragandhi, V. A Bayesian Optimized Deep Learning Approach for Accurate State of Charge Estimation of Lithium Ion Batteries Used for Electric Vehicle Application. IEEE Access 2024, 12, 43308–43327. [Google Scholar] [CrossRef]
- Xia, X.; Chen, Y.; Shen, J.; Liu, Y.; Zhang, Y.; Chen, Z.; Wei, F. State of health estimation for lithium-ion batteries based on impedance feature selection and improved support vector regression. Energy 2025, 326, 136135. [Google Scholar] [CrossRef]
- Liu, S.; Fang, L.; Zhao, X.; Wang, S.; Hu, C.; Gu, F.; Ball, A. State-of-health estimation of lithium-ion batteries using a kernel support vector machine tuned by a new nonlinear gray wolf algorithm. J. Energy Storage 2024, 102, 114052. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Stighezza, M.; Bianchi, V.; De Munari, I. FPGA Implementation of an Ant Colony Optimization Based SVM Algorithm for State of Charge Estimation in Li-Ion Batteries. Energies 2021, 14, 7064. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, S.; Fan, Y.; Hai, N.; Huang, Q.; Fernandez, C. An improved dung beetle optimizer-hybrid kernel least square support vector regression algorithm for state of health estimation of lithium-ion batteries based on variational model decomposition. Energy 2024, 306, 132464. [Google Scholar] [CrossRef]
- Valizadeh, A.; Amirhosseini, M.H. Machine Learning in Lithium-Ion Battery: Applications, Challenges, and Future Trends. SN Comput. Sci. 2024, 5, 717. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, X.; Gao, D.; Li, H.; Yan, L.; Peng, J.; Huang, Z. State-of-health estimation of lithium-ion batteries based on improved long short-term memory algorithm. J. Energy Storage 2022, 53, 105046. [Google Scholar] [CrossRef]
- Wang, F.K.; Amogne, Z.E.; Chou, J.H.; Tseng, C. Online remaining useful life prediction of lithium-ion batteries using bidirectional long short-term memory with attention mechanism. Energy 2022, 254, 124344. [Google Scholar] [CrossRef]
- Yang, N.C.; Chen, W.C. State of health prediction method for battery cells using bidirectional long short-term memory neural network with time-varying filter empirical mode decomposition. J. Power Sources 2025, 656, 238007. [Google Scholar] [CrossRef]
- Peng, S.; Wang, Y.; Tang, A.; Jiang, Y.; Kan, J.; Pecht, M. State of health estimation joint improved grey wolf optimization algorithm and LSTM using partial discharging health features for lithium-ion batteries. Energy 2025, 315, 134293. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Cao, L.; Gopaluni, B.; Cao, Y. Long Short-Term Memory Network with Transfer Learning for Lithium-ion Battery Capacity Fade and Cycle Life Prediction. Appl. Energy 2023, 350, 121660. [Google Scholar] [CrossRef]
- Yang, G.; Ma, Q.; Sun, H.; Zhang, X. State of Health Estimation Based on GAN-LSTM-TL for Lithium-ion Batteries. Int. J. Electrochem. Sci. 2022, 17, 221128. [Google Scholar] [CrossRef]
- Hu, W.Y.; Zhang, C.L.; Luo, L.J.; Jiang, S.H. Integrated Method of Future Capacity and RUL Prediction for Lithium-Ion Batteries Based on CEEMD-Transformer-LSTM Model. Energy Sci. Eng. 2024, 12, 5272–5286. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Li, Y.; Liu, Y.; Chen, Y.; Zhang, Y. Lithium-ion battery health prognosis via electrochemical impedance spectroscopy using CNN-BiLSTM model. J. Mater. Inform. 2024, 4, 9. [Google Scholar] [CrossRef]
- Xiang, N.; Zhang, T.; Liu, Y. State of health prediction for Lithium-Ion batteries using extended long Short-Term memory network and frequency enhanced channel attention mechanism with Variational mode Decomposition. Measurement 2025, 249, 117084. [Google Scholar] [CrossRef]
- Krichen, M.; Mihoub, A. Long Short-Term Memory Networks: A Comprehensive Survey. AI 2025, 6, 215. [Google Scholar] [CrossRef]
- Mchara, W.; Manai, L.; Khalfa, M.A.; Raissi, M. Intelligent health state diagnosis of lithium-ion batteries for electric vehicles using wavelet-enhanced hybrid deep learning integrated with an attention mechanism. Clean Energy 2025, 9, 64–79. [Google Scholar] [CrossRef]
- Liang, M.; Gan, Y.; Chang, Z.; Wan, Z.; Schlangen, E.; Šavija, B. Microstructure-informed deep convolutional neural network for predicting short-term creep modulus of cement paste. Cem. Concr. Res. 2022, 152, 106681. [Google Scholar] [CrossRef]
- Lu, Z.; Fei, Z.; Wang, B.; Yang, F. A feature fusion-based convolutional neural network for battery state-of-health estimation with mining of partial voltage curve. Energy 2024, 288, 129690. [Google Scholar] [CrossRef]
- Chen, S.Z.; Liang, Z.; Yuan, H.; Yang, L.; Xu, F.; Fan, Y. A novel state of health estimation method for lithium-ion batteries based on constant-voltage charging partial data and convolutional neural network. Energy 2023, 283, 129103. [Google Scholar] [CrossRef]
- Liang, C.; Tao, S.; Huang, X.; Wang, Y.; Xia, B.; Zhang, X. Stochastic state of health estimation for lithium-ion batteries with automated feature fusion using quantum convolutional neural network. J. Energy Chem. 2025, 106, 205–219. [Google Scholar] [CrossRef]
- Xing, Q.K.; Sun, X.W.; Fu, Y.P.; Wang, K. Lithium-ion battery health estimate based on electrochemical impedance spectroscopy and CNN-BiLSTM-Attention. Ionics 2025, 31, 1389–1403. [Google Scholar] [CrossRef]
- Zraibi, B.; Okar, C.; Chaoui, H.; Mansouri, M. Remaining Useful Life Assessment for Lithium-Ion Batteries Using CNN-LSTM-DNN Hybrid Method. IEEE Trans. Veh. Technol. 2021, 70, 4252–4261. [Google Scholar] [CrossRef]
- Yao, Q.; Song, X.; Xie, W. State of health estimation of lithium-ion battery based on CNN–WNN–WLSTM. Complex Intell. Syst. 2024, 10, 2919–2936. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Zhang, R.; Liu, X.M.; Chen, S.; Sun, Z.; Jiang, H. Lithium-ion battery SOH estimation method based on multi-feature and CNN-KAN. Front. Energy Res. 2024, 12, 1494473. [Google Scholar] [CrossRef]
- Peng, C.; Wang, M.; Li, C.; Lv, Y. A speedily-accurately prediction model based on convolutional neural network enhanced feature extraction for lithium-ion batteries remaining life. J. Energy Storage 2025, 133, 118055. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, X.; Wang, Z.; Tan, C.; Wang, Y.; Wang, L. State of health estimation of lithium-ion batteries based on the Kepler optimization algorithm-multilayer-convolutional neural network. J. Energy Storage 2025, 122, 116644. [Google Scholar] [CrossRef]
- Liu, P.; Liu, C.; Wang, Z.P.; Wang, Q.S.; Han, J.L.; Zhou, Y.P. A Data-Driven Comprehensive Battery SOH Evaluation and Prediction Method Based on Improved CRITIC-GRA and Att-BiGRU. Sustainability 2023, 15, 15084. [Google Scholar] [CrossRef]
- Li, Y.; Qin, X.; Chai, M.; Wu, H.; Zhang, F.; Jiang, F.; Wen, C. SOH evaluation and RUL estimation of lithium-ion batteries based on MC-CNN-TimesNet model. Reliab. Eng. Syst. Saf. 2025, 261, 111125. [Google Scholar] [CrossRef]
- Ding, P.; Xia, M.; Wang, X.; Pan, H.; Gao, Q.; Guo, W.; Shi, P.; Min, Y. Advanced lithium-ion battery health state estimation using a Bayesian optimization hybrid neural network model. J. Energy Storage 2025, 123, 116562. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, M.; Shu, X.; Shen, J.; Xiao, R. On-board state of health estimation for lithium-ion batteries based on random forest. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 1754–1759. [Google Scholar] [CrossRef]
- Amamra, S.A. Random Forest-Based Machine Learning Model Design for 21,700/5 Ah Lithium Cell Health Prediction Using Experimental Data. Physchem 2025, 5, 12. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, R.; Zhan, X.; Li, Y.; Xiao, Y. Lithium-Ion Battery State-of-Health Prediction for New-Energy Electric Vehicles Based on Random Forest Improved Model. Appl. Sci. 2023, 13, 11407. [Google Scholar] [CrossRef]
- Lamprecht, A.; Riesterer, M.; Steinhorst, S. Random Forest Regression of Charge Balancing Data: A State of Health Estimation Method for Electric Vehicle Batteries. In Proceedings of the 2020 International Conference on Omni-layer Intelligent Systems (COINS), Virtually, 31 August–2 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Hu, B.; Su, X.; Xu, L.; Zhu, D. State of Health estimation for lithium-ion batteries using Random Forest and Gated Recurrent Unit. J. Energy Storage 2024, 76, 109796. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Lu, D.; Cui, N.; Li, C. A Novel Transfer Learning Framework Combining Attention Mechanisms and Random Forest Regression for State of Health Estimation of Lithium-Ion Battery with Different Formulations. IEEE Trans. Ind. Appl. 2024, 60, 5726–5736. [Google Scholar] [CrossRef]
- Garse, K.M.; Bairwa, K.N.; Roy, A. Hybrid Random Forest Regression and Artificial Neural Networks for Modelling and Monitoring the State of Health of Li-Ion Battery. J. Electr. Syst. 2024, 20, 2231–2243. [Google Scholar] [CrossRef]
- Chen, J.; Kollmeyer, P.; Ahmed, R.; Emadi, A. Battery state-of-health estimation using CNNs with transfer learning and multi-modal fusion of partial voltage profiles and histogram data. Appl. Energy 2025, 391, 125923. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z. State of charge estimation for electric vehicles using random forest. Green Energy Intell. Transp. 2024, 3, 100177. [Google Scholar] [CrossRef]
- Duan, W.; Song, S.; Xiao, F.; Chen, Y.; Peng, S.; Song, C. Battery SOH estimation and RUL prediction framework based on variable forgetting factor online sequential extreme learning machine and particle filter. J. Energy Storage 2023, 65, 107322. [Google Scholar] [CrossRef]
- Shu, X.; Yang, H.; Liu, X.; Feng, R.; Shen, J.; Hu, Y.; Chen, Z.; Tang, A. State of health estimation for lithium-ion batteries based on voltage segment and transformer. J. Energy Storage 2025, 108, 115200. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; He, Y.; Zhang, S.; Cai, Y. Edge–cloud collaborative estimation lithium-ion battery SOH based on MEWOA-VMD and Transformer. J. Energy Storage 2024, 99, 113388. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Y.; Yang, D.; Feng, X.; Sun, Y.; Zhao, Y.; Wu, C.; Pan, R. Enhanced CNN-based state-of-health estimation framework for lithium-ion batteries using variable-length charging segments and transfer learning. J. Energy Storage 2025, 128, 117214. [Google Scholar] [CrossRef]
- Arbaoui, S.; Samet, A.; Ayadi, A.; Mesbahi, T.; Boné, R. Data-driven strategy for state of health prediction and anomaly detection in lithium-ion batteries. Energy AI 2024, 17, 100413. [Google Scholar] [CrossRef]
- Jafari, S.; Byun, Y.C. Interpretable AI for explaining and predicting battery state of health using PSO-enhanced deep learning models. Energy Rep. 2025, 14, 1779–1798. [Google Scholar] [CrossRef]
- Karthikeyan, M.; Anirudh, N.; Columbus, C.; Aravind, C.K. Optimizing battery health monitoring in electric vehicles using interpretable CART–GX model. Results Eng. 2025, 27, 106043. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery Data Set; NASA Ames Research Center Moffett Field: Mountain View, CA, USA, 2007. Available online: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/ (accessed on 3 October 2025).
- Etem, T. Interpretable machine learning for battery health insights: A LIME and SHAP-based study on EIS-derived features. Bull. Pol. Acad. Sci. Tech. Sci. 2025, 73, e155033. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, W.; Fu, Y.H.; Kurdkandi, N.V.; Mi, C. A general framework for lithium-ion battery state of health estimation: From laboratory tests to machine learning with transferability across domains. Appl. Energy 2025, 381, 125086. [Google Scholar] [CrossRef]
- Tang, A.; Xu, Y.; Hu, Y.; Tian, J.; Nie, Y.; Yan, F.; Tan, Y.; Yu, Q. Battery state of health estimation under dynamic operations with physics-driven deep learning. Appl. Energy 2024, 370, 123632. [Google Scholar] [CrossRef]


| Linear Kernel | |
| Polynomial Kernel | |
| Radial Basis Function Kernel (Gaussian Kernel) | |
| Sigmoid Kernel |
| 1 | Zhao et al. (2018) [15] | SVR (RBF) | NASA + CALCE | MAE < 2% SOH; epsilon-insensitive loss helped robustness to outliers/noisy voltage–capacity data. |
| 2 | Si et al. (2024) [16] | SVR | Lab datasets | R2 up to 0.962 on test sets with full discharge; strong performance on partial windows except at high-voltage ranges. |
| 3 | Feng et al. (2024) [17] | Hybrid-kernel LSSVR (poly + RBF) | CALCE | Hybrid kernel improved learning/generalisation and helped avoid overfitting vs. single-kernel SVMs. |
| 4 | Chen et al. (2023) [18] | PSO-LSSVR (LiFePO4, CC charging) | Partial charge V/I; 2 test cells | Reported MSE < 0.00052, MARE < 0.93%; PSO improved kernel/penalty tuning; robustness to noise/outliers. |
| 5 | Liu et al. (2024) [21] | KSVM tuned by nonlinear GWO | Cambridge Cavendish Lab dataset (>20,000 EIS spectra, 12 LR2032 LIBs, 25–45 °C) | GWO-tuned KSVM improved accuracy/stability; longer runtime with larger data. |
| 6 | Li et al. (2022) [22] | Improved ant lion optimisation + SVR | NASA | Meta-heuristic tuning enhanced SVR SOH accuracy. |
| 7 | Stighezza et al. (2021) [23] | ACO-based SVM (FPGA) | Panasonic 18650PF dataset (NN driving cycle + US06) | Focus is SoC (not SOH); demonstrates hardware feasibility of ACO-SVM. |
| 8 | Zhu et al. (2024) [24] | Improved dung beetle optimiser + hybrid-kernel LSSVR (+ VMD) | NASA + CALCE | Hybrid LSSVR + decomposition achieved high SOH accuracy; robust modelling. |
| 9 | Gong et al. (2022) [27] | PSO-optimised LSTM (RMSProp + dropout) | Experimental Li-ion; 4 HIs via GRA | ~5% accuracy improvement vs. vanilla LSTM; better convergence/overfitting control. |
| 10 | Wang, Amogne, Chou, Tseng (2022) [28] | BiLSTM + attention | NASA + Univ. Maryland | Noise-reduced capacity + attention to critical time steps ⇒ improved online RUL/SOH robustness across battery types; higher compute cost. |
| 11 | Wang et al. (2023) [31] | Transfer-learning LSTM (NCA→NCM) | NASA + custom (NCA/NCM) | Accurate cross-chemistry SOH/cycle life prediction; depends on source-target similarity and pretraining data size. |
| 12 | Hu et al. (2024) [33] | CEEMD–transformer-LSTM | Two lab datasets | Robust accuracy across operating conditions; framework complexity; lacks field validation. |
| 13 | Liu et al. (2024) [34] | CNN-BiLSTM (EIS) | Raw EIS | Outperformed GPR, CNN, and LSTM; achieved R2 up to 0.89 for SOH estimation; enabled early-life RUL prediction from first 50 cycles. |
| 15 | Chen et al. (2018) [52] | RF (OOB-tuned) | Sandia National Lab public LFP dataset | RF SOH feasible on partial on-board data; optimisation via OOB; tested on two cells. |
| 16 | Amamra (2025) [53] | RF (grid search) | 21,700/5 Ah cells | R2 = 0.92, RMSE = 0.06; compared against SVR. |
| 17 | Liang et al. (2023) [54] | PSO-optimised RF (LiFePO4 modules) | Charge/discharge features | Improved SOH, but heavy manual feature extraction; limited automation/portability. |
| 18 | Wang et al. (2024) [56] | RF + GRU (hybrid) | Not specified | Hybrid improved estimation accuracy by ≥15.84% vs. standalone RF. |
| 19 | Yang et al. (2022) [57] | CNN + RF (hybrid) | Public datasets | 34–46% MAE reduction vs. baselines; cautions on generalisation across chemistries/form factors. |
| 20 | Bairwa & Roy (2024) [59] | RF + ANN (hybrid) | V/I/T + cycle features | RF for nonlinear features + ANN refinement; does not model long-range sequence dynamics. |
| 22 | Xing et al. (2025) [42] | CNN-BiLSTM–attention (EIS) | EIS | Attention + BiLSTM with CNN improves temporal modelling and accuracy under varied conditions. |
| 23 | Zraibi et al. (2021) [43] | CNN-LSTM-DNN (hybrid) | NASA + CALCE | Hybrid deep network for RUL/SOH achieved strong performance. |
| 24 | Yao et al. (2024) [44] | CNN-WNN-WLSTM (hybrid) | NASA battery datasets (No. 5, 6, 7) | Combines WNN’s fast convergence/stability with WLSTM; robust SOH estimation. |
| 25 | Zhang et al. (2024) [45] | CNN-KAN (hybrid) | Lab-generated CC–CV battery cycling data (4 charge rates) | CNN fused with KAN for SOH; improved performance with multi-feature inputs. |
| 26 | Wu et al. (2025) [47] | Multilayer CNN + Kepler optimisation (KOA) | Lab datasets | KOA-tuned CNN cut MAE by up to 58.97%; depth > 2 layers degraded accuracy. |
| 27 | Liu et al. (2023) [48] | Att-BiGRU (improved GWO) | Real-world EV operational data | Attention-BiGRU with improved GWO delivered comprehensive SOH evaluation/prediction. (GRU noted in CNN section as related.) |
| 28 | Li et al. (2025) [49] | MC-CNN-TimesNet + TPE | Multi-cycle time series (2D tensors) | Avg. RMSE within 1.5% by leveraging inter-timescale dependencies. |
| 29 | Ding et al. (2025) [50] | Bayesian-optimised hybrid NN (CNN + LSTM) | NASA + lab | BO prevented local minima; RMSE < 1% in joint validation. |
| 30 | Chen, Kollmeyer, Ahmed, Emadi (2025) [60] | CNN with TL + multi-modal fusion | Partial voltage profiles + histograms | Transfer learning + multi-modal fusion improved SOH; supports re-use across datasets. |
| 31 | Vedhanayaki & Indragandhi (2025) [19] | Bayesian optimised SVR (BO-SVR) with Gaussian kernel | NASA B0005 | Achieved RMSE = 0.0082, outperforming standard SVR and GPR; Bayesian optimisation improved efficiency. |
| 32 | Peng et al. (2025) [46] | Convolutional-ProbSparse-transformer (CPT) | NCM (BN-74, BN-100) + public datasets | 3.2× faster training vs. transformer; accuracy ↑ 112%; robust for long-term prediction |
| 33 | Chen et al. (2023) [40] | CNN with partial CV charging + TL | Multi-chemistry dataset | Only first 1000 s of CV data needed; accurate SOH prediction; transfer learning improved generalisation |
| 34 | Lu et al. (2024) [39] | Feature fusion CNN (capacity–voltage + derivatives) | 18 batteries, 3 datasets | MAE ≤ 0.0028, MAPE ≤ 0.32%; intra-cycle + inter-cycle features improved accuracy. |
| 35 | Yang et al. (2022) [32] | GAN-LSTM–transfer learning | NASA+ CALCE | Errors < 3%; GAN mitigated data scarcity, TL improved cross-dataset adaptation |
| 36 | Xiang et al.(2025) [35] | VMD + xLSTM + FECAM hybrid | CALCE+ NASA | MAE = 0.0049, RMSE = 0.0085, outperformed LSTM, GRU, transformer. |
| 37 | Yang and Cheng (2025) [29] | TVF-EMD + BiLSTM with BOHB tuning | NASA B0005-B0007 | RMSE < 0.0016, R2 > 0.999, better than CNN-LSTM, SVR; robust across datasets. |
| 38 | Xia et al. (2025) [20] | Sine-SSA optimised SVR with EIS-based feature selection | Commercial EIS dataset (>20 k samples, 25–45 °C) | Max error = 2.58%, outperforming LSTM, GPR; robust under varying temperatures. |
| 39 | Lamprecht et al. (2020) [55] | RF regression | Simulated Tesla Model S battery pack (96S74P, 85 kWh) with aging + charge balancing framework | Achieved 1.94% error for capacity SOH and 4.28% for resistance SOH, outperforming other ML methods. |
| 40 | Lu et al. (2024) [58] | CNN + attention + random forest with transfer learning | Oxford dataset (LCO pouch cells), Sandia dataset (LFP, NCA 18,650 cells) | Reduced estimation errors by 80.9% (LCO), 41.3% (LFP), and 25.6% (NCA). Achieved very low RMSE (0.46% for LFP). |
| Feature Name | Mathematical Expression | Definition of Symbols |
|---|---|---|
| Mean | ;
T: number of samples | |
| Standard deviation | mean of signal | |
| 10th percentile | values | |
| 90th percentile | values | |
| Quartile slopes | : voltages at 25%, 50%, and 75% of discharge | |
| Overall voltage slope | : voltages at 10% and 90% of discharge | |
| Maximum rate of change | : voltage derivative | |
| Peak-to-peak derivative amplitude | : peak-to-peak derivative voltage | |
| Correlation (V, I, T) | : covariance between signals |
| ML Model | Hyperparameters | Hyperparameters Search Space | Final Value Used |
|---|---|---|---|
| Random Forest (RF) | Number of trees | {300, 600, 800} | 600 |
| Minimum leaf size | {1, 2, 4} | 2 | |
| Support Vector Regression (SVR) | C | {1, 10, 100} | 10 |
| ε | {0.01, 0.03, 0.1} | 0.03 | |
| Kernel | {0.3, 1, 3} | 1 | |
| CNN | Convolution filters | Conv filters: [64 (k = 7), | Conv1D(64,7) |
| 128 (k = 5), 128 (k = 3)]; | Conv1D(128,5) | ||
| Conv1D(128,3) | |||
| FC layer size | {128, 256} | 256 | |
| Dropout | {0.2, 0.3} | 0.3 | |
| Epochs | {80, 100, 120} | 100 | |
| Batch size | {16, 32} | 32 | |
| BiLSTM | Hidden units | {64, 128} | biLSTM(128, sequence) |
| biLSTM(64, last) | |||
| Layers | {1, 2} | 2 | |
| Dropout | {0.25, 0.3} | 0.25/0.3 | |
| FC layer size | {64, 128} | 128 | |
| Epochs | {50, 60, 80} | 60 | |
| Batch size | {8, 16} | 16 |
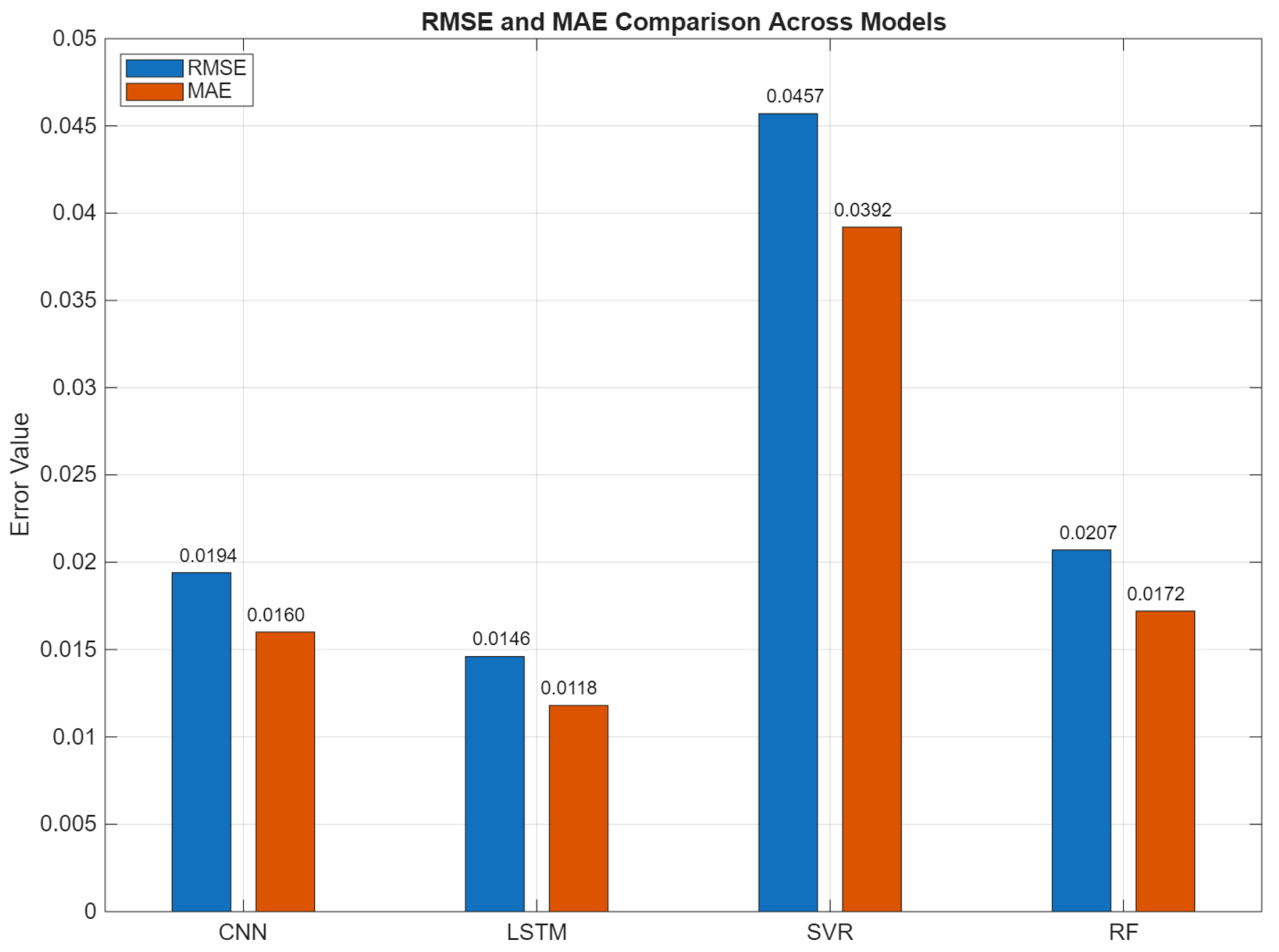
| Model | RMSE | MAE | R2 | MAPE (%) |
|---|---|---|---|---|
| CNN | 0.0194 | 0.0160 | 0.964 | 1.84 |
| LSTM | 0.0146 | 0.0118 | 0.980 | 1.39 |
| SVR | 0.0457 | 0.0392 | 0.800 | 4.80 |
| RF | 0.0207 | 0.0172 | 0.959 | 2.15 |
| ML Model | Training Time (s) |
|---|---|
| CNN | 57.95 |
| SVR | 5.29 |
| RF | 26.11 |
| LSTM | 201.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mbagaya, L.; Reddy, K.; Botes, A. Machine Learning Techniques for Battery State of Health Prediction: A Comparative Review. World Electr. Veh. J. 2025, 16, 594. https://doi.org/10.3390/wevj16110594
Mbagaya L, Reddy K, Botes A. Machine Learning Techniques for Battery State of Health Prediction: A Comparative Review. World Electric Vehicle Journal. 2025; 16(11):594. https://doi.org/10.3390/wevj16110594
Chicago/Turabian StyleMbagaya, Leila, Kumeshan Reddy, and Annelize Botes. 2025. "Machine Learning Techniques for Battery State of Health Prediction: A Comparative Review" World Electric Vehicle Journal 16, no. 11: 594. https://doi.org/10.3390/wevj16110594
APA StyleMbagaya, L., Reddy, K., & Botes, A. (2025). Machine Learning Techniques for Battery State of Health Prediction: A Comparative Review. World Electric Vehicle Journal, 16(11), 594. https://doi.org/10.3390/wevj16110594






