Abstract
This paper presents the design and simulation of a neural sliding mode controller (NSMC) for a regenerative braking system in an electric vehicle (EV). The NSMC regulates the required current and voltage of the bidirectional DC-DC buck–boost converter, an element of the auxiliary energy system (AES), to improve the state of charge (SOC) of the battery of the EV. The controller is based on a recurrent high-order neural network (RHONN) trained using the extended Kalman filter (EKF) and the unscented Kalman filter (UKF) as the tools to train the neural networks to obtain a higher SOC in the battery. The performance of the controller with the two training algorithms is compared with a proportional integral (PI) controller illustrating the differences and improvements obtained with the EKF and the UKF. Furthermore, robustness tests considering Gaussian noise and varying of parameters have demonstrated the outcome of the NSMC over a PI controller. The proposed controller is a new strategy with better results than the PI controller applied to the same buck–boost converter circuit, which can be used for the main energy system (MES) efficiency in an EV architecture.
1. Introduction
The energy storage in electric vehicles (EVs) fully operated with clean fuels is an extremely relevant issue in the automotive industry despite their huge contribution to the environmental impact. In [1], an environmental study of many EVs has demonstrated the advantages and positive impact that result in a lower number of CO2 emissions in a certain period of analysis compared to conventional fossil fuel vehicles. The commitment with the environmental impact has developed new strategies to recycle battery packs such as lithium ion batteries [2], for which demand has increased in recent years. The lead acid battery recycling process has demonstrated great performance, as well as the necessary chemical procedure.
In recent years, many approaches to improve energy consumption have been developed and new alternatives to fuel EVs have emerged. The primary goal of implementing regenerative braking systems in EVs is to recover the kinetic energy produced during motor deceleration, resulting in increased energy storage capacity and increased driving distance [3]. In [4], a regenerative braking system with one single braking pedal decreased the energy consumption and improved the commercial cost of EVs.
The combination of a supercapacitor and battery bank as an energy supply for an EV has demonstrated an improvement in regenerative braking performance, saving energy and increasing efficiency [5].
In [6], a proposed design of a boost converter significantly reduces the number of elements compared to existing models, improving energy performance and reducing cost and size. Furthermore, it allows for the adjustment of converter parameters such as pulse width modulation (PWM) to achieve the power required for the system. DC converters have been implemented with good results in many applications. In [7] a sliding mode control (SMC) is implemented in DC-DC converters such as the buck and boost circuit. The control law is proposed, considering the continuous-time buck and boost converter mathematical model. To reduce chattering, a multiphase controller is developed. However, the analysis of these converters is made separately, and only current control can guarantee stability, as it is the main dynamic to ensure the tracking of a desired voltage reference. In [8], a bidirectional DC-DC converter is operated in a photovoltaic system to take its energy and charge a battery through the converter.
Extensive work is presented in [9], where possible failures that can affect a photovoltaic system, such as the shading fault that leads to the output voltage being lower than expected, and the failure of the DC converter to provide the desired voltage, are studied. Thus, an SMC with the IncCond technique is designed to track the desired voltage under both failures, providing the maximum available solar power. Additionally, a global SMC based on Lyapunov stability analysis is presented in [10], where the main goal of applying this controller is to track the desired output voltage value of a buck converter and reduce the chattering generated with the conventional SMC.
Another study is presented in [11], where a strategy based on inverse optimal control is employed to adjust the output voltage of a boost converter. In addition, the design of two observers is developed to reduce the quantity of sensors. Furthermore, the inverse optimal controller is compared to an SMC. An extremely interesting work is presented in [12], where the two training filters are implemented to obtain the optimal SOC to avoid overcharge of a Li-ion battery used in commercial electric vehicles. Many approaches have been developed to enhance the performance of the EV and the energy use in the DC converters. One of the more important properties of electric vehicles is the ability to regeneratively brake as a bridge that allows for the recovery of energy while braking and the improvement of the efficiency of the storage system [13].
A PI was used to adjust the dynamics of a bidirectional buck-boost in a regenerative braking system with a supercapacitor as an auxiliary energy device in [14]. In [15], the mileage of an EV has been increased by implementing a nonlinear predictive control strategy with two stages to regulate the torque needed during braking. In addition, the optimization of the torque improves the energy conservation during braking.
To minimize chattering produced by the control to regulate the optimal slip value in an antilock braking system, a sliding mode fuzzy controller is implemented using an exponential reaching law. Furthermore, the results are compared to a bang–bang controller, with the SM controller outperforming the bang–bang controller in [16].
Another interesting case is the one depicted in [17], where artificial intelligence is the main tool to develop a “comfort regenerative braking” using neural networks with the backward propagation algorithm, taking data from the acceleration and deceleration limits and using them to map the optimal behavior of the EV. Regenerative braking has also been improved in [18], where state estimation is achieved using neural networks and the least squares algorithm, and is later used in the proposed control. This study demonstrated an improvement in the recovery of 9.62% energy under specified conditions. Moreover, an NSMC with an EKF identifier is being developed to improve the EV system with regenerative braking without considering the DC motor behavior and solely managing the current and voltage of the buck–boost converter within the EV system in [19]. Finally, in an EV framework, a neural inverse optimal control (NIOC) is accomplished by employing a reference generator with the speed of a DC motor that only decelerates once during the entire operation in [20].
The simulation of an EV with a regenerative braking system is presented in this paper, where the above-mentioned system is controlled employing a neural sliding mode controller (NSMC) based on system identification implementing RHONNS trained with EKF and UKF training algorithms to reduce the state estimation error and achieve good performance of the EV system. In this work, the NSMC is used to track the full dynamics of the regenerative braking system using a reference generator that is related to a DC motor that operates at different speeds, resulting in a signal that changes between acceleration and deceleration, and allows us to appreciate the operating modes of the bidirectional DC-DC buck–boost converter more accurately. Considering these changes in the speed of the motor is important, as these approximate the simulation to a real case of an EV driving performance. Furthermore, this approach will enable us to analyze the regenerative braking system of electric vehicles utilizing multiple robust intelligent control techniques based on Kalman filters, leading to novel findings.
The proposed NSMC regulates the required current and voltage of the DC-DC buck–boost converter, an element of the AES, in order to improve the MES efficiency, particularly in the SOC of the EV battery. Successful energy recovery during braking system operation is ensured when correct NSMC performance is achieved.
This article’s main novelty is the use of intelligent control algorithms, such as the NSMC, which is developed using RHONN identification and the EKF and UKF as training tools for neural networks, resulting in a higher SOC in the EV battery. The controller has been validated in simulation for various tasks, including tracking of a varying time–signal trajectory and tracking of a trajectory generated from a DC motor with multiple acceleration and deceleration changes. The performance of the RHONN with the two training algorithms, EKF and UKF, is validated using a chirp signal. The initial weights of the RHONN are chosen randomly. Afterwards, the performance of the proposed NSMC with EKF and UKF identifiers is compared to a PI controller demonstrating the differences and improvements obtained, including Gaussian noise and varying parameters.
The structure of this paper is outlined in Section 2, which explains the steps taken to obtain the results of the simulation and the procedure followed in this study. Section 3 presents the electrical circuit of the DC converter, including a brief explanation of its operation. Section 4 outlines the mathematical preliminaries, including the equations used to design the neural controller. Section 5 describes the modeling of the buck–boost converter system and the integration of RHONN identification into the NSMC design. Section 6 shows the simulation results for each step of the article, including the neural controller test and a comparison of neural identification with EKF and UKF. Additionally, a robustness test of the NSMC controller is done under two scenarios. Section 7 presents the mean square error (MSE) and energy of the error signal (EES), comparing their results obtained during the tracking with the UKF, EKF, and PI considering the arrangement used in [14]. Finally, Section 8 discusses the obtained results and proposes future work. The conclusions of this work based on the results are presented in Section 9.
2. Materials and Methods
The simulation has followed particular steps to obtain the results presented in this article.
- The main objective of this paper is to improve the energy storage and power consumption of the regenerative brake system. To achieve this, the current and voltage dynamics can be controlled using a bidirectional converter. The regenerative braking system and the neural controller have been simulated and verified using the Simscape Electrical from Matlab (Matlab R2020a, Simulink, 1994–2024 ©The MathWorks, Inc., Natick, MA, USA).
- The simulation implements the mathematical representation of the buck–boost converter from [21].
- The system identification is developed taking the RHONN philosophy in [22,23] to identify the dynamics to regulate the buck–boost converter. The RHONN is validated using a chirp signal with initial weights chosen randomly in the range of (0, 1).
- The RHONN philosophy is employed to design the identification process, which is then trained with the EKF and UKF algorithms.
- The NSMC is developed to track the trajectories in the AES chosen for the case study. In the first scenario, a signal is selected to validate the identification and regulation of the buck–boost converter dynamics. The signal is variable, and designed to operate within the range of the AES (supercapacitor) and MES (battery bank) parameters. In the second scenario, the complete control framework implemented in the simulation is verified. The DC motor parameters are considered for building a reference generator that tracks the EV system requirements.
- The results of the NSMC with EKF and UKF are presented, and the enhancement of the battery banks with the implemented AES is demonstrated.
- The NSMC with EKF and UKF is validated to demonstrated the robustness of the system under different conditions. Additionally, the comparison of the NSMC’s robustness with a PI controller based on the control strategy [14] is presented.
- The MSEs and EESs obtained with UKF and EKF are compared with a PI control strategy [14] to identify the best performance in regenerative braking simulation and robustness of the control strategies.
3. DC-DC Bidirectional Buck–Boost Converter
A fundamental device in the regenerative braking system is the power converter, such as the boost converter, buck converter, step-down converter, step-up converter, etc. However, the buck–boost converter is chosen in this case. Additionally, this converter is a fundamental element of the AES, which helps reduce the energy consumption during braking.
Buck–boost converters are the result of the combination of two configurations of DC power converters, which generally work separately in different applications. Furthermore, the configuration selected for the converter can be a bidirectional DC buck–boost converter related to the requirements of the power system [24], and this configuration is perfectly coupled with energy storage and the control of battery charge and discharge applications.
The regenerative braking system contains several elements that allow it to operate correctly. First of all, there is a battery bank, which is responsible for powering the DC motor that moves the vehicle. Next, we have the responsible elements of growing or reducing the voltage supplied to the EV. These elements are the supercapacitor and the DC buck–boost converter. The connections of the system are illustrated in Figure 1.
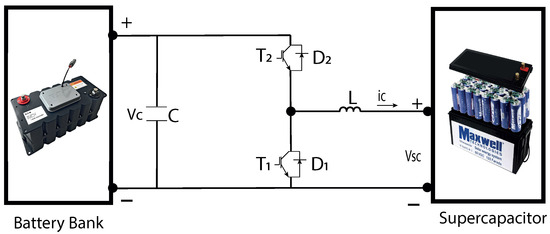
Figure 1.
DC buck-boost converter circuit.
Here, L is an inductor, C is a capacitor, and represent the insulated gate bipolar transistors (IGBT), and the and represent the diodes. A regulated signal such as the PWM is the input of the transistors that transfer the current from or to the supercapacitor.
Buck mode: When this mode is activated, there is a reduction in the output voltage related to the input voltage. is deactivated and is activated, resulting in the transfer of the energy coming from the capacitor voltage to the supercapacitor voltage . Once is deactivated, the energy stored in the capacitor flows C to the supercapacitor employing the current capacitor . Furthermore, the inductor L is charged with a fragment of the same current capacitor energy. Likewise, when is deactivated, the L current is discharged into via , guiding this current energy in the flow of C [14].
Boost operation: During activation of this mode, the output voltage increases concerning the input voltage. is ON and is OFF, and the energy coming from supercapacitor is transferred to battery bank . As soon as is activated, the capacitor’s energy is taken and stored in L. On the other hand, when is activated, the energy in L is driving into the capacitor C across into the battery bank.
While the braking operation is occurring, the electricity generated in the DC motor is managed with the brake into the battery bank or supercapacitor. The boost function is turned ON when the EV is accelerating, while the buck function is activated when the EV is decelerating. The DC-DC converter operating in both modes makes it easier for the supercapacitor to increase and decrease energy. Consequently, the SOC in the battery bank is improved.
4. Mathematical Preliminaries
4.1. Discrete-Time Sliding Mode Control
The SMC allows it to work with robustness over some perturbations, being one of their more attractive properties over the last few decades. Consider the following nonlinear system [25]:
with a , function, which is a bounded constant and a switching function u as the control law, which is used to reduce the error to zero, where the reference input is r, and u is established as
where and are defined as the sliding surface and the upper control bound, respectively. Figure 2 describes a continuous-time system with scalar SMC, where the state starts from an initial point achieving the trajectory of the sliding surface within finite time and remaining on the surface afterwards.
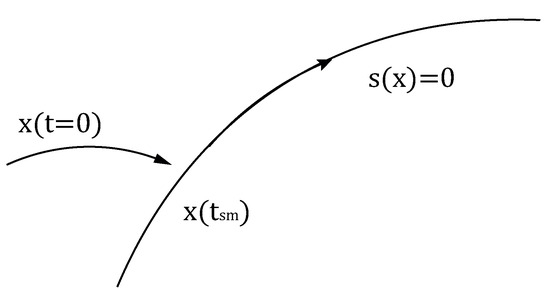
Figure 2.
Continuous-time system trajectory when SMC is applied.
When for each sampling point , the function is derived, and a representation in discrete-time of the continuous time system (1) is
with the starting condition , the trajectory equated to the sliding manifold when , or [25].
This operation can be defined as discrete-time sliding mode. Afterwards, from (1), and considering a scenario in which for any constant control u and whatever initial condition , its closed solution can be written as [26]:
For the constant state control signal to attain , it is required to identify at each sample point k. The corresponding discrete-time representation of the system is the following [26]:
At each sample point, the sliding manifold is achieved, that is, is completed. This can be corroborated since tends to as ; the function may need more control resources than are available for . Using the discrete-time SMC, the sliding manifold is described as
Evaluating at sample time , the sliding manifold is determined:
Now is calculated the equivalent control , as in [25]:
A stabilizing term, determined as , should be added to asymptotically achieve the sliding manifold [26].
where is the Schur matrix.
The following control law is determined considering the boundedness of the control signal , [25]:
where represents the Euclidean norm of and is defined as:
4.2. Discrete-Time Recurrent High-Order Neural Networks
Recurrent neural networks (RNNs) have been utilized in recent times to approximate and identify the mathematical models of complex systems, according to [22]. RHONNs have proven that they are effective at identifying nonlinear systems, where identification is achieved through modifying the parameters of a suitable system representation attached to an adaptive law. The approximated state variable of a nonlinear system using a RHONN identifier with a series-parallel configuration is obtained by [23]:
where is defined as the state of the ith neuron that identifies the ith component of the state vector , where , are the neural networks’ adjustable synaptic weights and are fixed weights, and are linear functions of the state vector, and is the vector input of the RHONN model. Moreover, and is defined as [22]
with defined as non-negative integers; as the number of the connection; as a collection of non-ordered subsets ; n determined as the state dimension; m as the input dimension; and defined as [22]:
where u is the network’s input vector. Additionally, the hyperbolic function is defined as
where is set as the state variable; while and are positive constants.
A ith RHONN identifier scheme is presented in Figure 3.
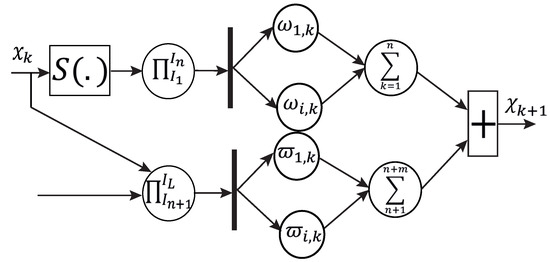
Figure 3.
Scheme of a RHONN identifier.
To reduce the error between the estimation of states, the RHONN identifier requires a training algorithm. The explanation of the two training methods proposed is presented below.
4.3. Extended Kalman Filter
The EKF has turned into a typical method applied in many nonlinear systems’ identification. Only if the state equations of the system have determined the linearization, considering a Gaussian random, can variable operation be possible [27,28].
The algorithm model is defined as follows:
where is defined as the identification error to be minimized, is a parameter of the training algorithm design, is the Kalman matrix, and are set as positive definite constant matrices, and is an adjustable diagonal matrix. Finally, is an adjustable matrix, which is defined as the resulting state derivative with respect to the adjustable weights of the neural identifiers. More extensive details and a stability proof explanation of the RHONN and the EKF training algorithm are presented in [22,29].
4.4. Unscented Kalman Filter
The EKF leverages Jacobian matrices for linear approximations. Its effectiveness hinges on two key factors: firstly, accurate “first-order” approximations give rise to suboptimal terms directly affected by the nonlinearity of the system. Secondly, the computation of Jacobian matrices in practical applications can become complex. Such disparities can cause low performance or divergence. The UKF addresses the limitations generated by the EKF using a deterministic sampling approach. The limitations generated by the EKF are addressed with the UKF employing a deterministic sampling approach.
A method used to calculate the statistics of a random variable that undergoes a nonlinear transformation is defined by Juliar Uhlmann in [30] and defined as the unscented transformation (UT). This is used as an extension of the recursive estimation of states in the UKF, considering the Kalman filter framework.
The UKF identification algorithm equations can be described as follows:
with
where is the identification error, is the matrix of prediction error covariance, is the covariance of predicted output matrix, is the output matrix and the cross-covariance of state, is the -th weight of the -th subsystem, is a parameter of design, is the j-th state of the plant, and is the j-th state of the neural network. L is defined as the number of states while is the Kalman gain matrix, is the measurement noise covariance matrix, is the state noise covariance matrix, is the predicted state mean, is the predicted output mean, and and are sigma-points propagated through prediction and observation, respectively.
Table 1 explains the implementation step-by-step and the comparison of the EKF and UKF. More extensive details and the stability analysis of the UKF training algorithm for neural identification are explained in [31].

Table 1.
Differences between EKF and UKF training algorithms.
5. System Modeling and Sliding Mode Neural Control
5.1. Buck–Boost Converter Model
In this application, boost and buck converters were combined for developing the DC-to-DC converter. The first is used in charge-only situations, whereas the second is utilized in discharge-only situations. The work in [21] is used for the definition of the boost converter model.
The buck converter model is also defined by [21]:
where the converter output voltage is defined as , the output current is , is the voltage in the battery, is the set as the input vector, L is the inductance measured in Henry , R is the load resistance measured in ohms , C is the capacitor in measured in farads , and finally, is the sample time.
5.2. Neural Controller Design
Following the procedures established in Section 4 and using Equation (14), a RHONN has been employed to close in on the buck–boost converter behaviors in order to manage the current flow and assure the charging and discharging operating modes. Given the RHONN’s adaptive nature and the similarity of the buck and boost converter models, a single identifier is suggested for both situations as
where the estimated dynamics of the vector are . As defined above, is the measured voltage in the converter’s output, and is set as the converter output current. the control signal chosen for each state of the system is u, and are constant fixed weights. A representation of the identification design configuration is shown in Figure 4.
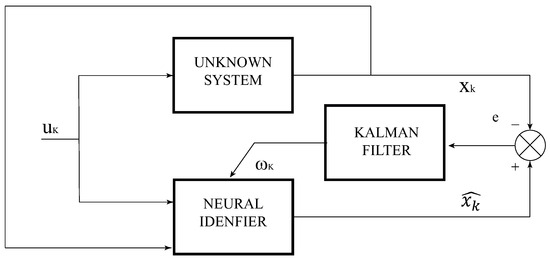
Figure 4.
Neural identification representation strategy.
5.3. Discrete Time Sliding Mode Control
The sliding mode controller is synthesized once the buck–boost converter’s system identification is carried out. Due to the presented neural model’s triangular construction, only the final dynamics require control [25].
For the converter to function effectively in transferring energy to the battery bank, both voltage and current dynamics have to be controlled.
Following the steps in (6)–(13), the sliding surface at the sample point of the dynamics control is obtained as
Voltage NSMC
The equivalent control is calculated as follows:
The is set as
with and is defined as a square matrix with real entries and eigenvalues conditioned with , and is the control upper bound with the condition .
Current NSMC
The sliding surface an control development for is obtained as
Then, the equivalent current control is obtained as follows:
and the NSMC is implemented as follows
The is set as
with , where is again considered as a square matrix with real entries and eigenvalues conditioned with , and is the control upper bound with the established condition of .
5.4. Reference Generator Development
The regenerative braking system results in energy consumption through DC motor behavior and requires the required voltage and current in the AES. A reference generator has been implemented in the simulation to put the whole regenerative braking system in motion.
A reference generator was created to provide the intended value for the buck−boost current and voltage. The energy stored in the supercapacitor as a function of the energy produced by the DC motor is described as the charge reference. A definition considering the work and energy theorem can be consulted in [32]. The mathematical formula for the statement “the work done between point A and point B on a particle increases the kinetic energy” is described as:
Applying this theorem on the DC motor, for a time the energy can calculated as [14]:
is the DC motor power, with the torque and speed defined as and , respectively. The supercapacitor can operate in two modes, charge and discharge. The equation below determines the supercapacitor energy during charging mode as
The following equation defines the supercapacitor energy during discharging:
with , and defined as the reference energy charge, the reference energy discharge, and the lost energy, respectively. represents a function restricted in , and represents the same function with the restriction in . The sum of both energies in the capacitor references (41) and (42), results in the supercapacitor energy reference.
Finally, the obtained reference for the buck−boost converter voltage is written as
where is defined as the reference signal computed for the voltage in the supercapacitor, is the stored energy in the supercapacitor, and C is the capacitance value of the supercapacitor. After the is developed, this can be used in the buck–boost converter control, where the resulting is used to estimate the duty cycle in the transistor and . The duty cycle is determined as follows:
Figure 5 shows a representation of the regenerative braking system, which includes the developed reference generator block and the NSMC. This representation is subsequently introduced into the simulation. The performance of the DC motor determines how effectively the regenerative braking systems work; therefore, a PI controller whose gains are calculated based on the Ziegler–Nichols method and the experience is used to help the DC motor follows a specific speed reference.
where is the speed motor reference and and are the controller gains, respectively.
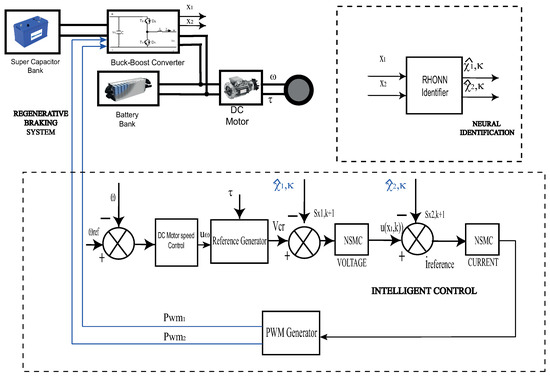
Figure 5.
Regenerative braking system control representation.
6. Simulation Results
The results of different analyses made in this work are described in this section. First, the validation of the RHONN with both UKF and EKF is illustrated using a chirp signal to guarantee the correct operation and estimation of the identifier over a rapidly varying signal.
Subsequently, two scenarios are presented, in which the developed NSMC is applied. In the first simulation test, the control and identification of the system is validated using a time-varying signal operating in a voltage range that the AES and MES can allow. This part illustrates the trajectory tracking of the NSMC without a voltage and current reference generated through the “reference generator”, explained in Section 5.
The final section of the simulation results demonstrates the complete operation of the regenerative braking system, including the simultaneous operation of the identification, NSMC, reference voltage and current generators, and the DC motor. Additionally, a robustness test is implemented in order to validate the correct operation of the NSMC controllers with some changes in the signal dynamics and the parameters of the buck–boost converter.
The proposed control schemes, including the corresponding energy systems used, are implemented and validated with the help of the Matlab/Simulink toolbox “Simscape Electrical” of Matlab. In addition, the simulation parameters used for the build-up of the energy systems AES and MES are enumerated in Table 2.

Table 2.
Parameters of the AES and MES.
6.1. RHONN Validation
The RHONN developed in Section 4 is validated using a chirp signal with the parameters shown in Table 3 for each estimated dynamics. The initial weights of RHONN are randomly chosen in a range of .

Table 3.
Chirp signal parameters.
The aim of identifying chirp signals is to guarantee the correct functioning of the RHONN with both training algorithms. Figure 6 and Figure 7 show the identification of the proposed signal for the UKF, where and are the chirp signals used as the voltage and current input, respectively, and and are the estimated dynamics with the RHONN. On the other hand, the validation of the identification with EKF is illustrated in Figure 8 and Figure 9 using the same chirp signals as described in Table 3.
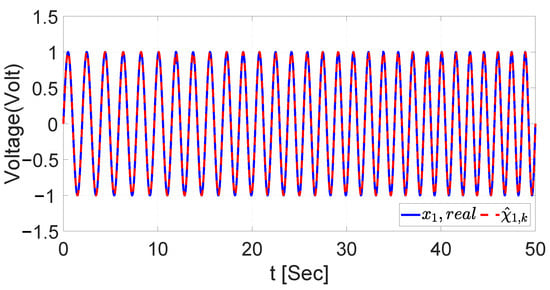
Figure 6.
Chirp signal identification for voltage with UKF.
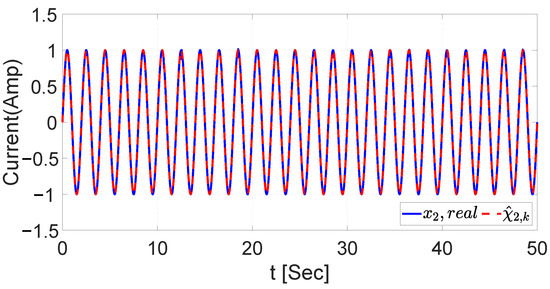
Figure 7.
Chirp signal identification for current with UKF.
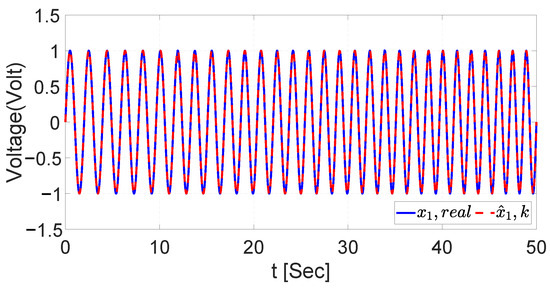
Figure 8.
Chirp signal identification for voltage with EKF.
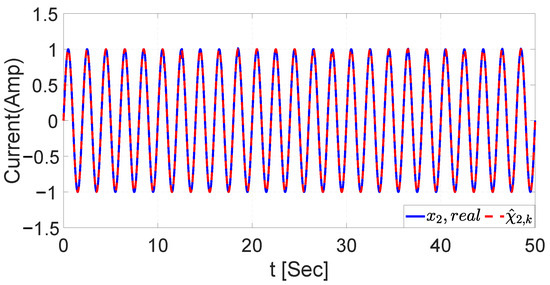
Figure 9.
Chirp signal identification for current with EKF.
6.2. NSMC Trajectory Tracking Results Using UKF
This test allows for the corroboration of the neural controller with the RHONN trained with UKF. The objective here is that the controller could track a desired trajectory operated in a permitted range of the AES. The chosen signal to track works in a range of 350 V to 380 V. First, the signal starts at 355 V for 10 s; after that, the voltage decreases to 350 V and lasts to t = 20 s. Then, the signal increases the value to 365 V. Finally, at t = 30 s, the signal operates as a sine wave between 355 V and 375 V and stops at t = 50 s.
The outcome of the trajectory tracking is shown in Figure 10, where the signal control is tracked with a minimum error at t = 20 s, where the controller adjustment works fast to reach the desired value. The current tracking trajectory is shown in Figure 11, where the current operates related to the controlled voltage, resulting in a signal that operates between −200 and 200 Amps. Furthermore, the controller did not show significant behavior during fast changes in the signal, as seen around t = 20 s.
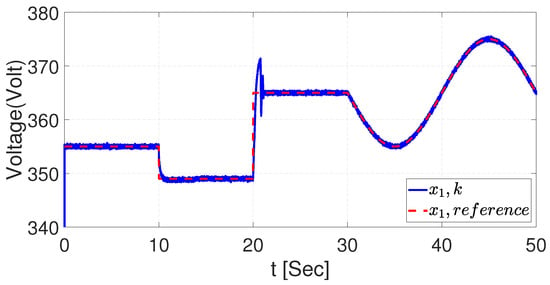
Figure 10.
Voltage dynamics trajectory tracking with UKF.
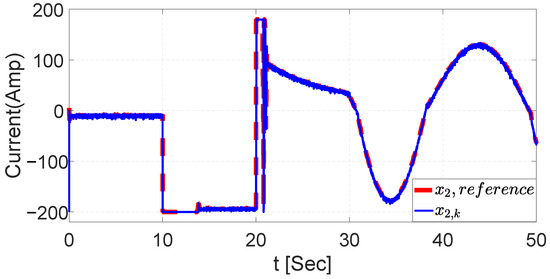
Figure 11.
Current dynamics trajectory tracking with UKF.
Additionally, during the control of the dynamics, the weights of the identifier are adjusted over the tracking of the desired trajectory. The data obtained from the weight adjustment are illustrated in Figure 12, and represent the computation made during the tracking of the trajectory. Furthermore, the identification of the voltage and current dynamics is illustrated in Figure 13. It is important to note that the states identified are the dynamics that take place over the AES, and are tracked subsequently with the NSMC. The proper development of the identification enables the controller’s proper operation, which leads to the improvement of the braking system’s energy recovery capacity.
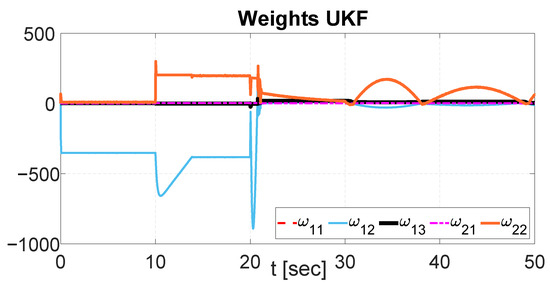
Figure 12.
Weight adjustment with UKF.
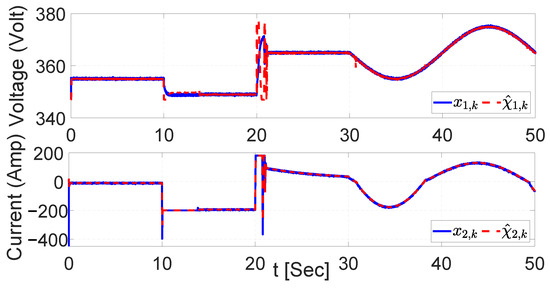
Figure 13.
System dynamics identification with UKF.
The calculation and explanation of the MSE and EES results can be found in Section 7, comparing the UKF and EKF with a PI identification differences during the control trajectory tracking with the NSMC.
6.3. NSMC Trajectory Tracking Results Using EKF
The implementation of the NSMC using the EKF is presented. Figure 14 illustrates the tracking trajectory of the proposed signal where the adjustments made by the controller when the signal changes their parameters are more significant that the one with the UKF.
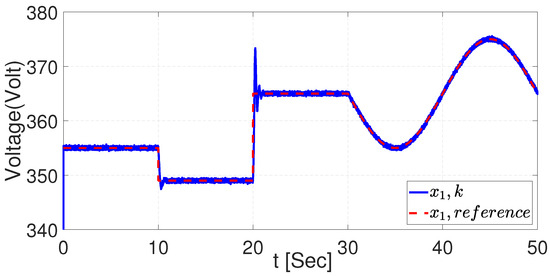
Figure 14.
Voltage dynamics trajectory tracking with EKF.
Figure 15 illustrates the trajectory of current dynamics tracking using the NSMC with the EKF. The controller results demonstrated a great performance to achieve the values of the tracked signal.
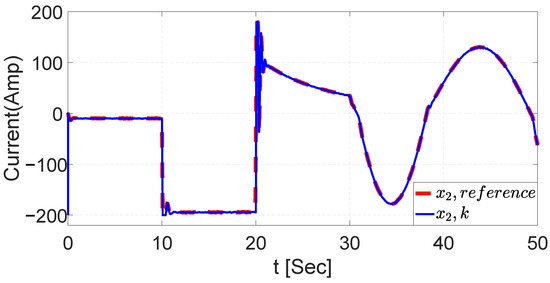
Figure 15.
Current dynamics trajectory tracking with EKF.
The weights of the RHONN identifier during the control of the desired signal with varying time and the adjustments made by the neural network to acquire the required weight values are presented in Figure 16. Additionally, the identified dynamics with the EKF are shown in Figure 17.
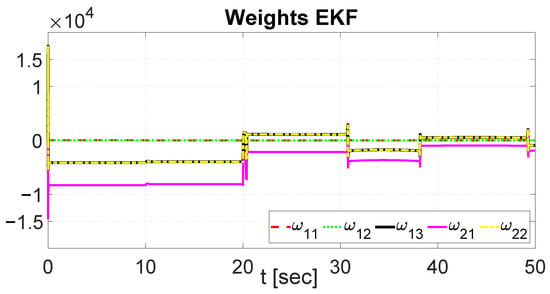
Figure 16.
Weight adjustment with EKF.
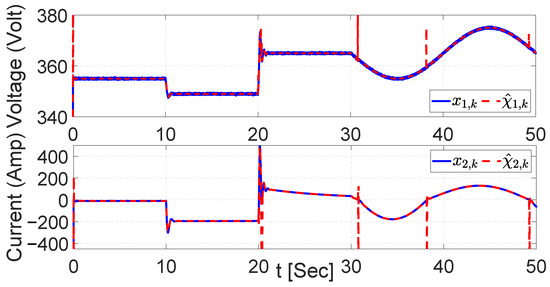
Figure 17.
System dynamics identification with EKF.
6.4. Regenerative Braking System Control Using a Reference Generator with UKF
The complete functioning of the regenerative braking system will be addressed in this section of the simulation results. This test is significant because it relates the entire regenerative braking system by using the DC motor’s speed variations to provide a signal that can be employed to determine and then implement the NSMC. The DC motor parameters are described in Table 4. First, the DC motor operates by varying the speed, which works in the range of 0 to 80 rad/s, with the objective of replicating an EV driving operation where the speed increases and decreases in different instants. In order to ensure the correct calculation of the reference generator is necessary to control the DC motor speed. A PI controller is applied to control the motor speed, as depicted in Figure 18.

Table 4.
Parameters of the DC motor.
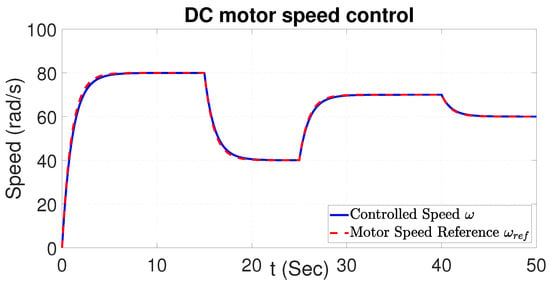
Figure 18.
Motor speed control with PI.
After the desired speed of the motor is controlled, the reference generator block computes the voltage required to operate the AES system and tracks the signal of voltage provided through the reference obtained. The neural controller in this case uses the UKF to identify the system as the first step, and then with the estimated dynamics, the tracking of the system dynamics related to the DC motor speed action is accomplished. The tracking voltage is the reference obtained with the reference generator block, and Figure 19 shows the tracking of accomplished voltage related to the motor speed trajectory. Moreover, we can highlight that when the speed in the motor increases, the voltage decreases. On the other hand, when the speed of the motor decreases, the voltage increases.
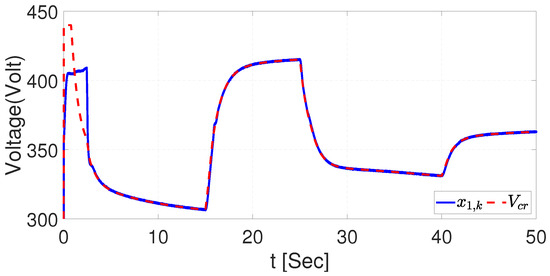
Figure 19.
AES voltage during regenerative braking with UKF.
In addition, Figure 20 illustrates the performance of the current dynamics during the regulation with NSMC. The current reference is obtained through the reference generator, as described in Figure 5.
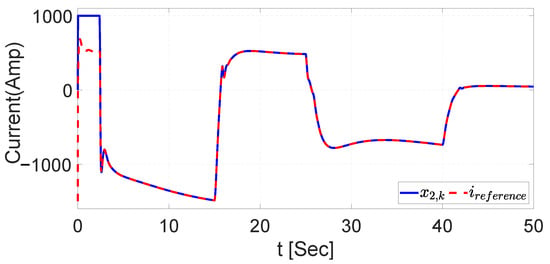
Figure 20.
AES current during regenerative braking with UKF.
After that, the trajectory tracking is acquired over the 50 s of simulation time. The SOC of the battery has been compared with and without AES. The importance of the AES is that it allows for slow discharge on the battery. The results obtained are illustrated in Figure 21, where the achieved signal in the AES and the regenerative braking system are operating, which results in a better SOC in the battery. At the beginning of the simulation, the system achieves the desired reference voltage in approximately 2 s, as seen in Figure 10. However, during the rest of the signal tracking, the results overtake the SOC obtained without the AES connected to the EV bank of batteries.
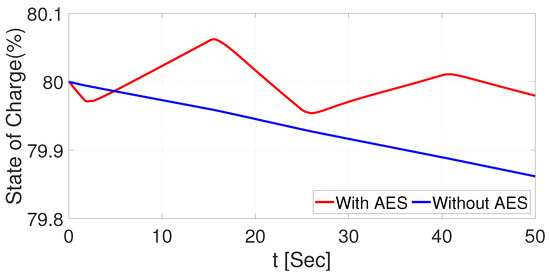
Figure 21.
SOC comparison of the battery with and without AES using UKF.
The battery voltage is compared in Figure 22 with and without the AES. From the results, we can observe that the battery decreases its voltage when the AES is not connected. Moreover, the voltage in the battery increases and maintains its voltage value above the initial 500 v when the AES is connected.
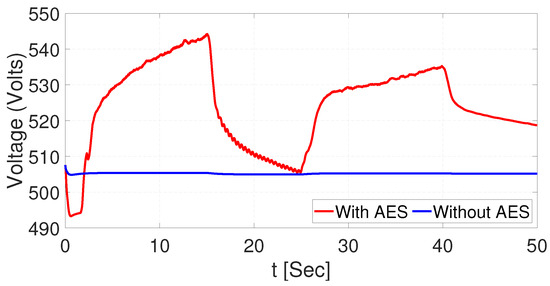
Figure 22.
Comparison of the battery bank voltage with and without AES using UKF.
6.5. Regenerative Braking System Control Using a Reference Generator with EKF
To compare the results later, we used the identical signals in this section of the project’s tests as we did with the UKF. Figure 23 illustrates that the first trajectory tracking of the has a difference in the adjustment during the first seconds due to the initial conditions of and has another behavior compared with the one in the Figure 19. Similarly, the current tracking trajectory displays a similar behavior in the same section of the simulation.
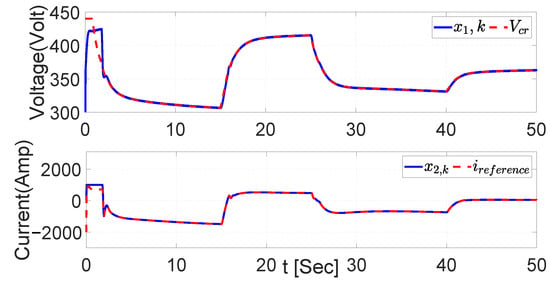
Figure 23.
AES voltage and current during regenerative braking using EKF.
The SOC and voltage in the battery are described in Figure 24 and Figure 25, respectively, and display a similar behavior as the NSMC with the UKF. However, the differences in NSMC with UKF and NSMC with EKF are quantitatively compared in Section 7.
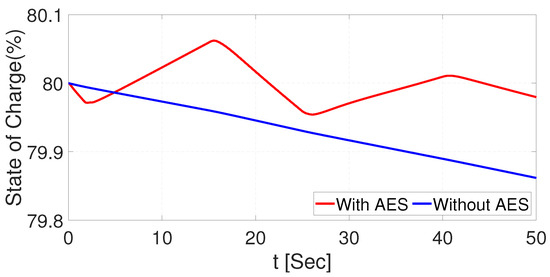
Figure 24.
MES battery bank SOC comparison with and without AES using EKF.
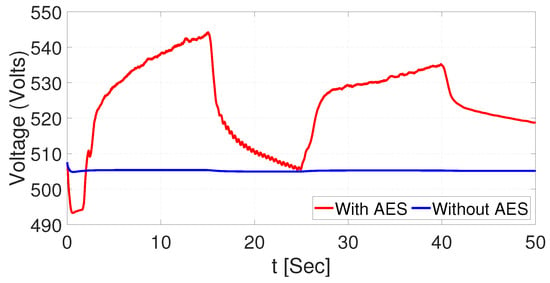
Figure 25.
MES battery bank voltage comparison with and without AES using EKF.
6.6. Robustness Test
The reliability of a control system is very important to assure the correct performance of the proposed scheme during variations on the system and disturbances that are not considered initially in the system’s proposed model. To validate the robustness of the NSMC, two scenarios have been applied. The first one is the system operated by adding noise to the buck–boost converter using a Gaussian random signal, while the second is a variation of the parameters of the buck–boost converter circuit.
6.6.1. Gaussian Noise
The Gaussian random signal is used to generate random values that will help to validate the robustness of the NSMC, and for this test, the chosen mean value is equal to 0 and variance is 1. The noise is added to the measured voltage and current output, and Equations (25)–(28) of the buck–boost converter model, considering the Gaussian noise signal, can be defined as
The buck converter model is also defined as
where is the Gaussian noise added to the dynamics of the buck–boost converter.
Robustness Test with NSMC and UKF
The voltage dynamics affected by the Gaussian noise signal are depicted in Figure 26 a,b, which are a closer view of the real signal compared with the signal with noise. Additionally, Figure 27 describes the dynamics of the current, where the noise signal in (a) and (b) is a closer look at the signal affected by the Gaussian noise.
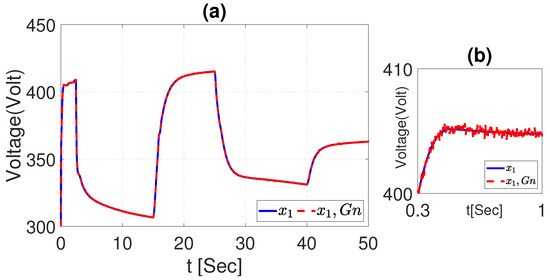
Figure 26.
(a) Voltage dynamics with Gaussian noise signal. (b) is a zoom of (a).
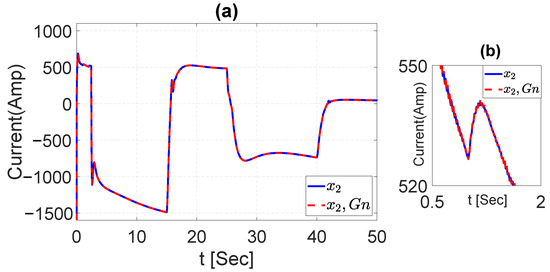
Figure 27.
(a) Current dynamics with Gaussian noise signal. (b) is a zoom of (a).
The control signal of the voltage dynamics is illustrated in Figure 28 and the current dynamics in Figure 29. The results demonstrated the robustness of the NSMC using UKF where the desired trajectory is followed still without issues. Additionally, in Section 7, the MSE and EES analysis supports the illustrated results.
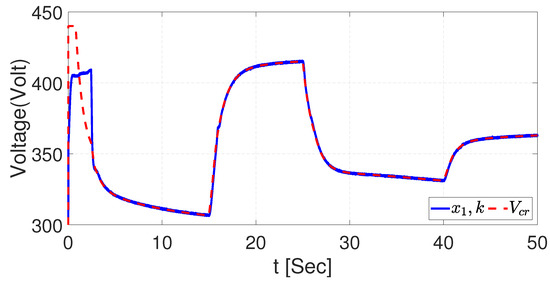
Figure 28.
Tracking trajectory with noise signal for voltage with UKF.
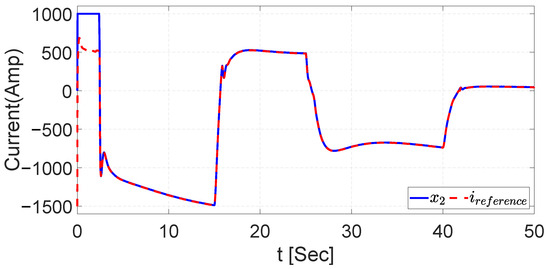
Figure 29.
Tracking trajectory with noise signal for current with UKF.
Robustness Test with NSMC and EKF
The robustness of the NSMC with the EKF has been tested for the current and voltage of the buck–boost converter. Figure 30 and Figure 31 are the signals of the dynamics with the Gaussian noise added to the output signal. Additionally, Figure 32 and Figure 33 illustrate good results in the control of the voltage and current with the noise added to the converter.
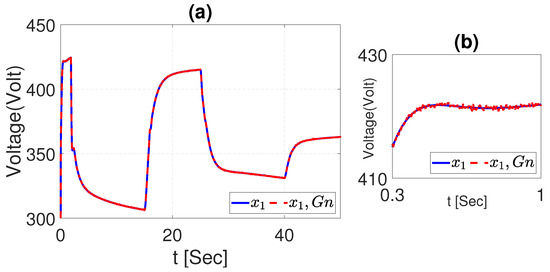
Figure 30.
(a) Voltage dynamics with Gaussian noise signal. (b) is a zoom of (a).
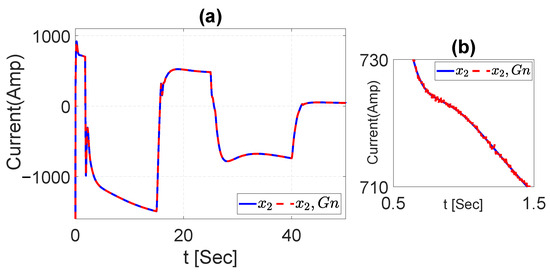
Figure 31.
(a) Current dynamics with Gaussian noise signal. (b) is a zoom of (a).
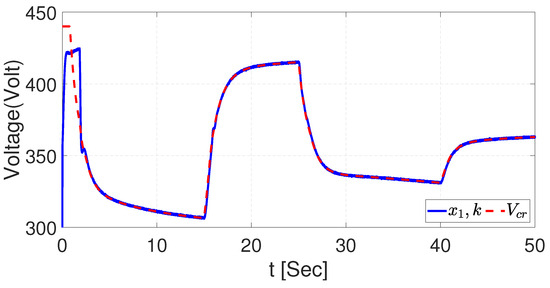
Figure 32.
Tracking trajectory with noise signal for voltage with EKF.
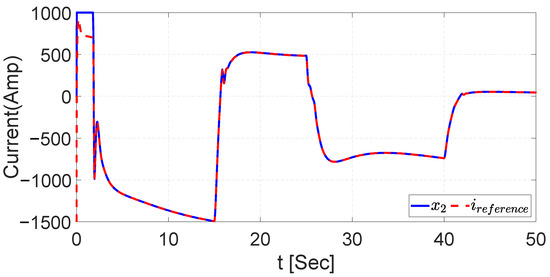
Figure 33.
Tracking trajectory with noise signal for current with EKF.
Robustness Test with PI
Using the same signal illustrated in Figure 30 and Figure 31, a PI controller based on the control strategy presented in [14], which is not an intelligent controller because the neural identifier is not performed to estimate the dynamics of the buck–boost converter, is used for the robustness test. The voltage and current are controlled each, with a PI controller resulting in some issues for the dynamics control, as illustrated in Figure 34 and Figure 35. The results demonstrated that the PI is not completely reliable for the tracking trajectory considering Gaussian noise. In addition, Section 7 presents the MSE and EES for the three configurations of the NSMC.
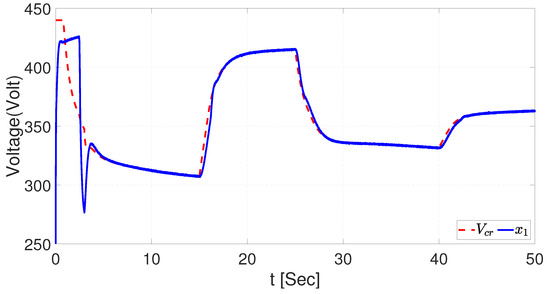
Figure 34.
Tracking trajectory with noise signal for voltage with PI.
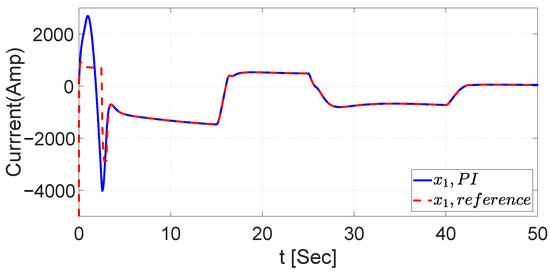
Figure 35.
Tracking trajectory with noise signal for current with PI.
6.6.2. Changes in the Parameters of the Buck–Boost Converter
The second scenario consists of changing the buck–boost converter parameters, which have been used during the different stages of the paper without changes. Now, a variation of its capacitance values is applied to verify the robustness of the NSMC. The new values are illustrated in Table 5. The same NSMC with UKF and EKF is used for the robustness test. The PI controller arrangement of the first robustness test is performed again in this second scenario.

Table 5.
Parameters of the AES and MES with changes for the robustness test.
NSMC with UKF for the tracking of dynamics with changes in buck-boost converter
The results of the validation of the NSMC are illustrated in Figure 36 and Figure 37 for voltage and current, respectively. The NSMC still regulates the dynamics of the buck–boost converter, ensuring the energy consumption.
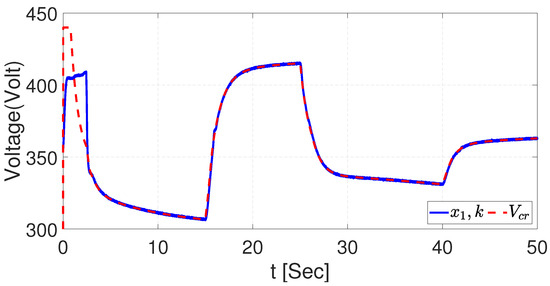
Figure 36.
Tracking trajectory with changes in the buck–boost converter for voltage with UKF.

Figure 37.
Tracking trajectory with changes in the buck–boost converter for current with UKF.
NSMC with EKF for the tracking of dynamics with changes in buck–boost converter
The same parameters described in Table 5 are used to validate the robustness of the NSMC with EKF illustrated in Figure 38 and Figure 39. As expected, the controller still regulates the dynamics of the buck–boost converter despite the changes in its parameters.

Figure 38.
Tracking trajectory with changes in the buck–boost converter for voltage with EKF.

Figure 39.
Tracking trajectory with changes in the buck–boost converter for current with EKF.
The results obtained from the test to validate the robustness of the NSMC demonstrate its correct operation under non-ideal scenarios. This includes scenarios where noise and other signals not initially considered are added to the signal for regulation. However, it is important to note that the NSMC, when used with UKF and EKF, operates differently, and provides results that require further analysis, as does the PI controller. In Section 7, we conduct a detailed analysis where we calculate the MSE and EES.
7. Comparative Analysis between Proposed NSMC Variants and PI Controller
To validate the simulation results and draw a comprehensive conclusion of the work presented in this paper, it is essential to compute the MSE and EES values. The primary objective of this comparison is to determine which of the two filtering techniques, UKF or EKF, provides better results for the electric vehicle regenerative braking system by calculating a numerical value. Furthermore, the results obtained are compared with those of a PI controller with the same structure in [14].
The MSE is obtained as follows:
and the EES is calculated as follows:
where MSE is the calculated mean square error, EES is the calculated energy of the error signal, and in both cases, n is the number of data points to evaluate the computation, represents the values obtained evaluated at the data points, and represents the reference values at the data points.
In this case, we use the values of the proposed reference signal and the real values of the states and to obtain the following results.
7.1. MSE and EES of a Time-Varying Signal Controlled with NSMC
First, the MSE and EES results correspond to the control results obtained with the time-varying signal of Section 6.2 and Section 6.3. The tracking trajectory with the NSMC using EKF performs better than the NSMC using UKF and PI. On the other hand, the PI controller has a better outcome than the NSMC with UKF in the tracking trajectory for the dynamic. Figure 40 presents the three methods compared for the dynamic, while Figure 41 shows the three methods applied in the track trajectory for .
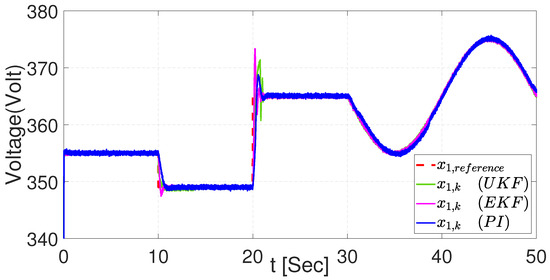
Figure 40.
Tracking trajectory with the three controllers for voltage .
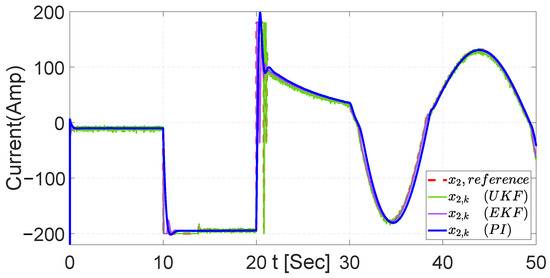
Figure 41.
Tracking trajectory with the three controllers for current .
Table 6 displays the MSE results for the tracking trajectory, where the NSMC with EKF has better results over the NSMC with UKF and PI. However, the PI controller offers better performance than the NSMC with UKF.

Table 6.
MSE and EES in without regenerative braking system.
Moreover, MSE and EES results for the tracking trajectory are illustrated in Table 7, where EKF again presents better performance compared to the NSMC with UKF and PI. However, PI again illustrates better results over the NSMC with UKF.

Table 7.
MSE and EES in without regenerative braking system.
The error signals in both dynamics of the system are demonstrated in Figure 42, Figure 43 and Figure 44 taking the results obtained during the tracking trajectory with UKF, EKF, and PI, respectively. The error signal shows that the values obtained remain around zero throughout the entire simulation. Although the error signal in has some instants where the value moves away from zero, the error values remain around zero.
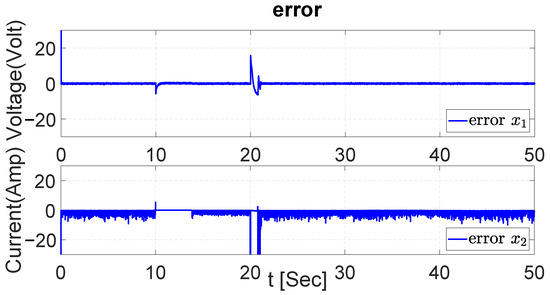
Figure 42.
Error in both dynamics with UKF.
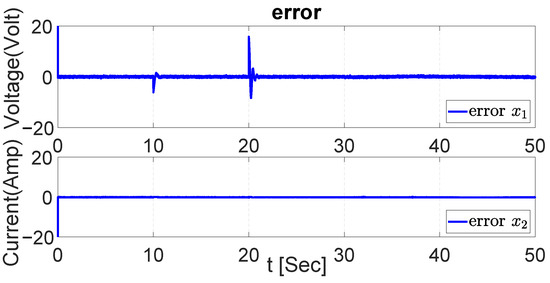
Figure 43.
Error in both dynamics with EKF.
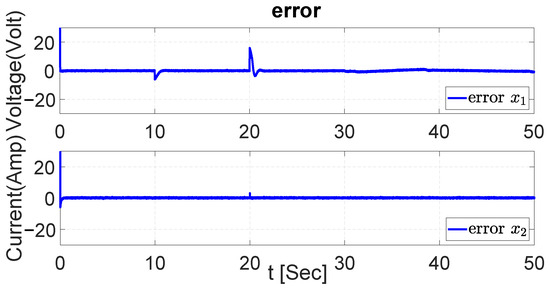
Figure 44.
Error in both dynamics with PI.
7.2. MSE and EES of the Complete Regenerative Braking System Controlled with NSMC
In this part, the compared results have been taken when the whole connected regenerative braking system is operating. As explained in Section 6, the results and are from the reference generator block, using the parameters provided during the acceleration and deceleration of a DC motor. Two figures of the tracking trajectory, considering the parameters of the described scenario, are illustrated in Figure 45 and Figure 46 for and , respectively.
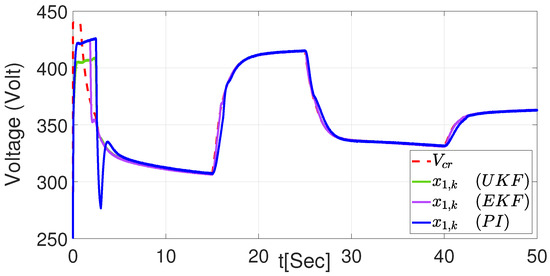
Figure 45.
Tracking trajectory with the three controllers for voltage with regenerative braking system.
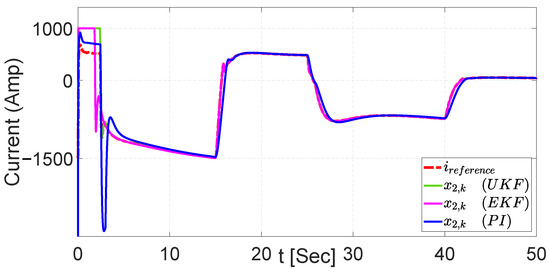
Figure 46.
Tracking trajectory with the three controllers for current with regenerative braking system.
In Table 8, the tracking of the voltage trajectory with the regenerative braking system is presented. In addition, the NSMC with the EKF presents significantly better performance than the NSMC with the UKF and the PI controller. These results are different concerning those presented in Table 6 and Table 7; the NSMC with UKF showed better results compared to the PI.

Table 8.
MSE and EES in with regenerative braking system.
In Table 9, the tracking of the current trajectory is presented. Additionally, NSMC with UKF performs much better than NSMC with the EKF and PI controller.

Table 9.
MSE and EES in with regenerative braking system.
With the results obtained during the UKF, EKF, and PI tracking trajectory, the error signals of the EV system dynamics are demonstrated in Figure 47, Figure 48 and Figure 49. The error signal shows that the values obtained remain around zero during most of the simulation and present only a small adjustment at the beginning. On the other hand, the error values also present an adjustment during the first seconds of the simulation, but eventually, the value of the error is maintained around zero.
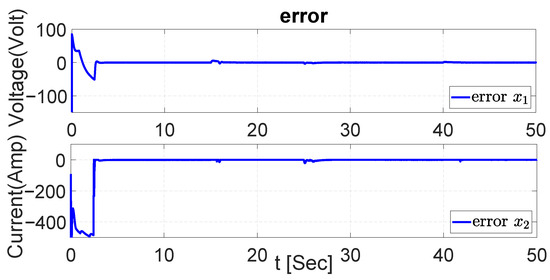
Figure 47.
Error in both dynamics during regenerative braking with UKF.
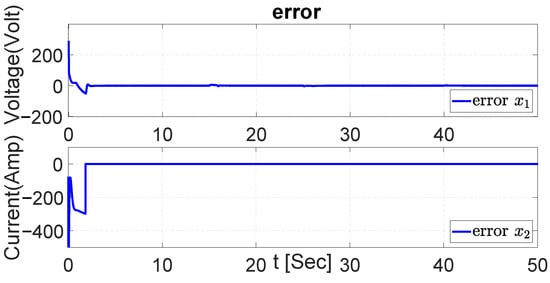
Figure 48.
Error in both dynamics during regenerative braking with EKF.
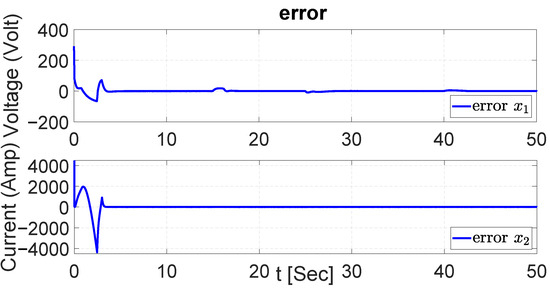
Figure 49.
Error in both dynamics during regenerative braking with PI.
7.3. MSE and EES of Robustness Test
The results of the MSE and EES of the robustness test presented in Section 6 are presented. Two new tables were added to compare the obtained results. Table 10 presents the results of the voltage dynamics with Gaussian noise for UKF, EKF, and PI. Furthermore, Table 11 shows the MSE and EES of the tracking trajectory with the same additional noise to the signal. In addition, similar to the case in Table 8, the NSMC with EKF presents significantly better performance than the NSMC with UKF and the PI controller for .

Table 10.
MSE and EES in with Gaussian noise.

Table 11.
MSE and EES in with Gaussian noise.
Additionally, in the obtained results the NSMC with the UKF performs much better than NSMC with the EKF and PI controller for . The error signals of the system dynamics with Gaussian noise and UKF, EKF and PI are demonstrated in Figure 50, Figure 51 and Figure 52.
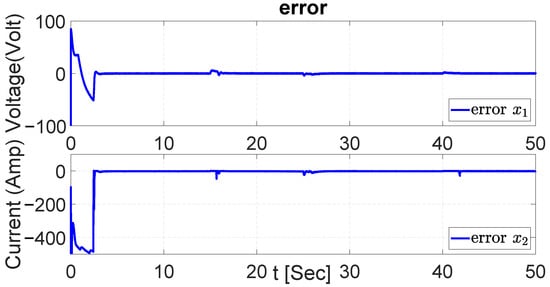
Figure 50.
Error in both dynamics with Gaussian noise with UKF.
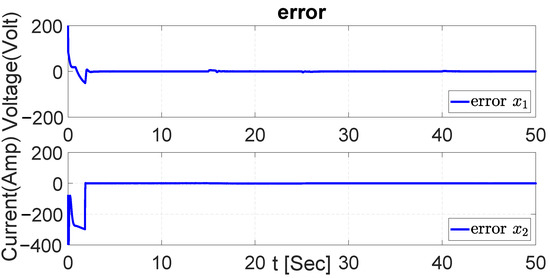
Figure 51.
Error in both dynamics with Gaussian noise with EKF.
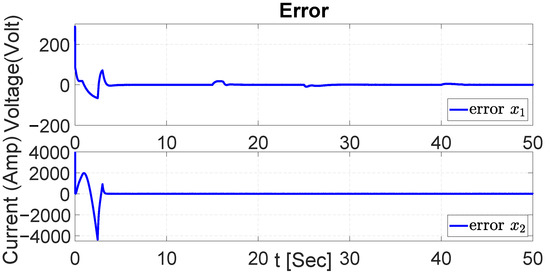
Figure 52.
Error in both dynamics with Gaussian noise with PI.
7.4. MSE and EES of Robustness Test with Changes in the Buck–Boost Converter Parameters
The MSE and EES obtained for the test made with the parameters of the buck–boost converter changed in Section 6 are presented in Table 12 for the voltage dynamics and in Table 13 for the current dynamics. As a result, regarding the voltage , similar to the case in Table 8 the NSMC with EKF presents significantly better performance than the NSMC with UKF and the PI controller for .

Table 12.
MSE and EES in with changes in buck–boost converter parameters.

Table 13.
MSE and EES in with changes in buck–boost converter parameters.
Furthermore, the MSE and EES for the current dynamics are depicted in Table 13, where the results conclude that the NSMC with UKF performs much better than NSMC with the EKF and PI controller for . The error signals for the system dynamics with the UKF, EKF and PI with the buck–boost converter parameters changes are illustrated in Figure 53, Figure 54 and Figure 55.
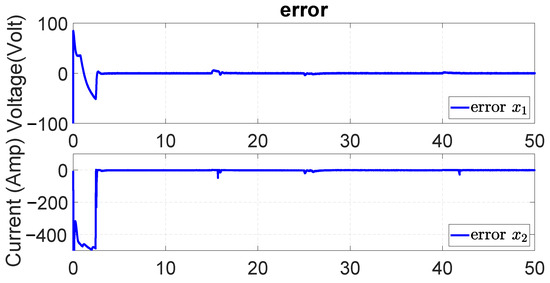
Figure 53.
Error in both dynamics with changes in buck–boost converter parameters with UKF.
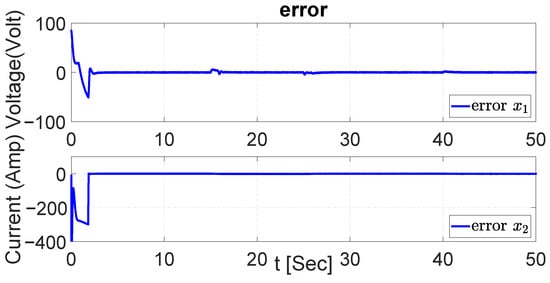
Figure 54.
Error in both dynamics with changes in buck–boost converter parameters with EKF.
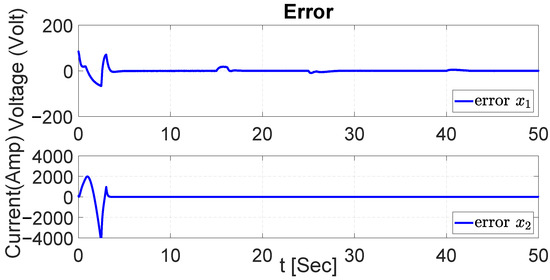
Figure 55.
Error in both dynamics with changes in buck–boost converter parameters with PI.
8. Discussion
This paper presented the comparison of the performance of three controllers: NSMC with EKF, NSMC with UKF, and the PI controller. The novelty of the paper is the design and application via simulation of a hybrid intelligent control scheme using sliding modes and RHONNs trained with EKF and UKF. Our stated control strategy manages the AES, defined as a combination of a supercapacitor and buck–boost converter, to recoup the energy lost during braking and power the MES.
The proposed intelligent controller is a new strategy with better results than a PI controller applied to the same bidirectional buck–boost converter circuit, which can be used for a regenerative braking system in an EV. The performance of three controllers is compared using two scenarios: the first one without considering a reference generator for trajectory tracking and the second one with a reference generator for trajectory tracking for regenerative braking. For both scenarios, NSMC trained with EKF has better performance, improving the SOC of the battery of the EV.
The states of the AES have been approximated successfully using an RHONN identifier trained by an EKF and UKF for different operation modes. The decision to use an RHONN for the identifier was based on the nonlinear systems dynamics estimation facilities. The RHONN has been validated with a chirp signal for both training algorithms.
To make an extensive study of the NSMC and the EKF and UKF training algorithms, different tests have been achieved. The identifier using EKF and UKF is implemented for tracking trajectories without the DC motor considered in the EV system during different AES operation modes. The system identification and synaptic weight adjustment figures help to corroborate the correct performance of the RHONN identifier.
The NSMC takes the estimated states from the RHONN identifier to define the sliding manifold where the controller will operate. The objective of this controller is to manage the DC buck–boost converter’s dynamics during charging and discharging operation modes. In the first scenario, time-varying signals are employed to validate the NSMC without still taking into consideration the DC motor in the EV system but considering the system’s operation range.
In a second scenario, the NSMC is implemented to operate with a completely connected regenerative braking system where the speed of the DC motor is the main parameter to define a reference with the desired trajectory to provide the necessary energy to supply the EV during the acceleration and deceleration. Although this research focuses mainly on simulating the proposed control scheme, from this perspective, this particular case enables us to confirm the effectiveness of the suggested NSMC in a scenario that is closer to the actual operation of regenerative braking.
Additionally, in both cases, the NSMC was shown to enhance the EV regenerative braking system when the car is accelerating and decelerating. Furthermore, the neural controller with UKF and EKF present different and motivating results with and without the reference generator block but the one with better results has been the NSMC with EKF. The most important advantage obtained is in the SOC, which presents a better performance where the percent of charge decreases slowly with the regenerative braking system in comparison without the regenerative braking system.
9. Conclusions
The MSE results obtained in Section 7 allow us to determine the framework in which EKF and UKF offer better control synthesis results than a conventional control technique such as PI. This can be a result of the favorable differences between the two scenarios presented in the simulation. The first case employed a time-varying signal with bounded values to track, while the second case used a signal that is the result of other dynamics that can induce fast adjustments to achieve the EV requirements during the acceleration and deceleration.
To validate the robustness of the NSMC, two scenarios have been applied. The first one is the system operated adding a Gaussian random signal, where the mean value is equal to 0 and the variance is 1 for and .
The noise is added to the measured voltage and current output. The second scenario involves varying parameters on the converter buck–boost circuit. Results are consistent with the tracking trajectory without the Gaussian noise and the variation of the parameters.
We are encouraged to extend the results of this study to obtain an NIOC based on the UKF algorithm to train a RHONN identifier and to control the AES dynamics enhancing the regenerative braking and energy consumption behavior in more scenarios, as well as to carry out a comparative study between NSMC and NIOC based on Kalman filters.
As a future work, the authors and coworkers will continue this project by considering the parameters and dimensions of an EV, as well as the typical driving cycles and new challenges and problems to solve.
Author Contributions
Conceptualization, J.A.R.-H.; methodology, J.A.R.-H.; software, M.A.R.C., R.G.-H. and J.F.G.; investigation, J.R.V.-F., M.A.R.C. and J.A.R.-H.; formal analysis, M.A.R.C., R.G.-H., J.F.G. and J.A.R.-H.; validation, J.A.R.-H., J.-L.R.-L. and R.G.-H.; writing—original draft preparation, M.A.R.C.; writing—review and editing, M.A.R.C., J.F.G., J.A.R.-H., R.G.-H., J.R.V.-F. and J.-L.R.-L.; funding acquisition, J.A.R.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universidad Autónoma del Carmen. Project number FING/1ERP2023/03.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The first author thanks to Universidad Autonoma del Carmen for the support and providing the facilities to develop this project.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NSMC | Neural Sliding Mode Controller |
| SMC | Sliding Mode Controller |
| NIOC | Neural Inverse Optimal Controller |
| IOC | Inverse Optimal Control |
| PWM | Pulse Width Modulation |
| UKF | Unscented Kalman Filter |
| EKF | Extended Kalman Filter |
| EV | Electric Vehicle |
| RHONN | Recurrent High-Order Neural Network |
| MES | Main Energy System |
| AES | Auxiliary Energy System |
| DC | Direct Current |
| PI | Proportional–Integral |
| SOC | State of Charge |
| MSE | Mean Squared Error |
| EES | Energy of the Error Signal |
| Variable | Description |
| index for name states | |
| index for name RHONN states | |
| neural network adjustable synaptic weights | |
| fixed weights | |
| state vector | |
| state of the ith neuron that identifies the ith component of the state vector | |
| , | linear functions of the state vector |
| vector input of the RHONN model | |
| non-negative integers | |
| number of the connection | |
| collection of non-ordered subsets | |
| n | the state dimension |
| m | the input dimension |
| defined as [23] | |
| Extended Kalman Filter | |
| the identification error to be minimized | |
| a parameter of the training algorithm design | |
| the Kalman gain matrix | |
| the measurement noise covariance matrix | |
| the state noise covariance matrix | |
| the prediction error matrix | |
| the measurement matrix, which is defined as the resulting state derivative with respect to the adjustable weights of the neural identifiers | |
| Unscented Kalman Filter | |
| the identification error | |
| the prediction error covariance matrix | |
| the covariance of predicted output matrix | |
| the output matrix | |
| the j-th weight of the i-th subsystem | |
| a parameter of design | |
| the j-th state of the plant | |
| the j-th state of the neural network | |
| L | the number of states |
| the Kalman gain matrix | |
| the measurement noise covariance matrix | |
| the state noise covariance matrix | |
| the predicted state mean | |
| the predicted output mean | |
| sigma-points propagated through prediction | |
| sigma-points propagated through observation | |
| Buck–Boost Converter Model | |
| the buck–boost converter output voltage | |
| the buck–boost converter output current | |
| the voltage in the battery | |
| L | the inductance in henry (H) |
| R | the load resistance in ohms () |
| C | the capacitor in farads (F) |
| the sample time | |
| Gaussian Noise |
References
- Wang, N.; Tang, G. A Review on Environmental Efficiency Evaluation of New Energy Vehicles Using Life Cycle Analysis. Sustainability 2022, 14, 3371. [Google Scholar] [CrossRef]
- Hantanasirisakul, K.; Sawangphruk, M. Sustainable Reuse and Recycling of Spent Li-Ion batteries from Electric Vehicles: Chemical, Environmental, and Economical Perspectives. Glob. Chall. 2023, 7, 2200212. [Google Scholar] [CrossRef] [PubMed]
- Yoong, M.K.; Gan, Y.; Gan, G.; Leong, C.; Phuan, Z.; Cheah, B.; Chew, K. Studies of Regenerative Braking in Electric Vehicle; IEEE: Kuala Lumpur, Malaysia, 2010; pp. 40–45. [Google Scholar] [CrossRef]
- Li, Z.; Shi, Z.; Gao, J.; Xi, J. Research on Regenerative Braking Control Strategy for Single-Pedal Pure Electric Commercial Vehicles. World Electr. Veh. J. 2023, 14, 229. [Google Scholar] [CrossRef]
- Indragandhi, V.; Selvamathi, R.; Gunapriya, D.; Balagurunathan, B.; Suresh, G.; Chitra, A. An efficient regenerative braking system based on battery-ultracapacitor for electric vehicles. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 27–29 November 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Khalid, H.; Mekhilef, S.; Mubin, M.B.; Seyedmahmoudian, M.; Stojcevski, A.; Rawa, M.; Horan, B. Analysis and design of series-LC-switch capacitor multistage high gain DC-DC boost converter for electric vehicle applications. Sustainability 2022, 14, 4495. [Google Scholar] [CrossRef]
- Utkin, V. Sliding mode control of DC/DC converters. J. Frankl. Inst. 2013, 350, 2146–2165. [Google Scholar] [CrossRef]
- Pandey, K.K.; Kumar, M.; Kumari, A.; Kumar, J. Bidirectional DC-DC buck-boost converter for battery energy storage system and PV panel. In Proceedings of the Modeling, Simulation and Optimization: Proceedings of CoMSO 2020, Silchar, India, 3–5 August 2020; Springer: Singapore, 2021; pp. 681–693. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Determination of maximum solar power under shading and converter faults—A prerequisite for failure-tolerant power management systems. Simul. Model. Pract. Theory 2016, 62, 14–30. [Google Scholar] [CrossRef]
- Mobayen, S.; Bayat, F.; Lai, C.C.; Taheri, A.; Fekih, A. Adaptive global sliding mode controller design for perturbed DC-DC buck converters. Energies 2021, 14, 1249. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Riffo, S.; Restrepo, C.; González-Castaño, C. A Sensorless Inverse Optimal Control plus Integral Action to Regulate the Output Voltage in a Boost Converter Supplying an Unknown DC Load. IEEE Access 2023, 11, 49833–49845. [Google Scholar] [CrossRef]
- Priya, R.P.; Sakile, R. State of charge estimation of lithium-ion battery based on extended Kalman filter and unscented Kalman filter techniques. Energy Storage 2023, 5, e408. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, X. Control strategy of regenerative braking system in electric vehicles. Energy Procedia 2018, 152, 496–501. [Google Scholar] [CrossRef]
- Manríquez, E.Q.; Sanchez, E.N.; Toledo, M.E.A.; Muñoz, F. Neural control of an induction motor with regenerative braking as electric vehicle architecture. Eng. Appl. Artif. Intell. 2021, 104, 104275. [Google Scholar] [CrossRef]
- Salari, A.H.; Mirzaeinejad, H.; Mahani, M.F. A new control algorithm of regenerative braking management for energy efficiency and safety enhancement of electric vehicles. Energy Convers. Manag. 2023, 276, 116564. [Google Scholar] [CrossRef]
- Guo, J.; Jian, X.; Lin, G. Performance evaluation of an anti-lock braking system for electric vehicles with a fuzzy sliding mode controller. Energies 2014, 7, 6459–6476. [Google Scholar] [CrossRef]
- Hwang, M.H.; Lee, G.S.; Kim, E.; Kim, H.W.; Yoon, S.; Talluri, T.; Cha, H.R. Regenerative braking control strategy based on AI algorithm to improve driving comfort of autonomous vehicles. Appl. Sci. 2023, 13, 946. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cai, X.; Wang, Z.; Yang, R. Regenerative Braking Control Strategy for Distributed Drive Electric Vehicles Based on Slope and Mass Co-Estimation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14610–14619. [Google Scholar] [CrossRef]
- Ruz-Canul, M.A.; Djilali, L.; Ruz-Hernandez, J.A.; Sanchez-Camperos, E.N. Neural Sliding mode control of a regenerative braking system for electric vehicles. J. Innov. Des. 2022, 6, 6–15. [Google Scholar] [CrossRef]
- Ruz-Hernandez, J.A.; Djilali, L.; Ruz Canul, M.A.; Boukhnifer, M.; Sanchez, E.N. Neural Inverse Optimal Control of a Regenerative Braking System for Electric Vehicles. Energies 2022, 15, 8975. [Google Scholar] [CrossRef]
- Djilali, L.; Sanchez, E.N.; Ornelas-Tellez, F.; Avalos, A.; Belkheiri, M. Improving Microgrid Low-Voltage Ride-Through Capacity Using Neural Control. IEEE Syst. J. 2020, 14, 2825–2836. [Google Scholar] [CrossRef]
- Sanchez, E.N.; Alanis, A.Y.; Loukianov, A.G. Discrete-Time High Order Neural Control: Trained with Kalman Filtering; Springer Science & Business Media: Cham, Switzerland, 2008. [Google Scholar] [CrossRef]
- Alanis, A.Y.; Sanchez, E.N.; Loukianov, A.G. Discrete-time adaptive backstepping nonlinear control via high-order neural networks. IEEE Trans. Neural Netw. 2007, 18, 1185–1195. [Google Scholar] [CrossRef]
- Majumder, R.; Ghosh, A.; Ledwich, G.; Zare, F. Power management and power flow control with back-to-back converters in a utility connected microgrid. IEEE Trans. Power Syst. 2009, 25, 821–834. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Sanchez, E.; Djilali, L. Neural Control of Renewable Electrical Power Systems; Springer Nature: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Chui, C.K.; Chen, G.; Chui, C.K.; Chen, G. Extended Kalman filter and system identification. In Kalman Filtering: With Real-Time Applications; Springer: Cham, Switzerland, 2017; pp. 115–137. [Google Scholar] [CrossRef]
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No. 00EX373), Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]
- Rovithakis, G.A.; Chistodoulou, M.A. Adaptive Control with Recurrent High-Order Neural Networks: Theory and Industrial Applications; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–25 April 1997; SPIE: Bellingham, WA, USA, 1997; Volume 3068, pp. 182–193. [Google Scholar] [CrossRef]
- Guerra, J.F.; Garcia-Hernandez, R.; Llama, M.A.; Santibañez, V. UKF-Based Neural Training for Nonlinear Systems Identification and Control Improvement. IEEE Access 2022, 10, 114501–114513. [Google Scholar] [CrossRef]
- Zohuri, B. Scalar Wave Driven Energy Applications; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).