Fuzzy Logic Control of External Heating System for Electric Vehicle Batteries at Low Temperature
Abstract
1. Introduction
2. System Modeling
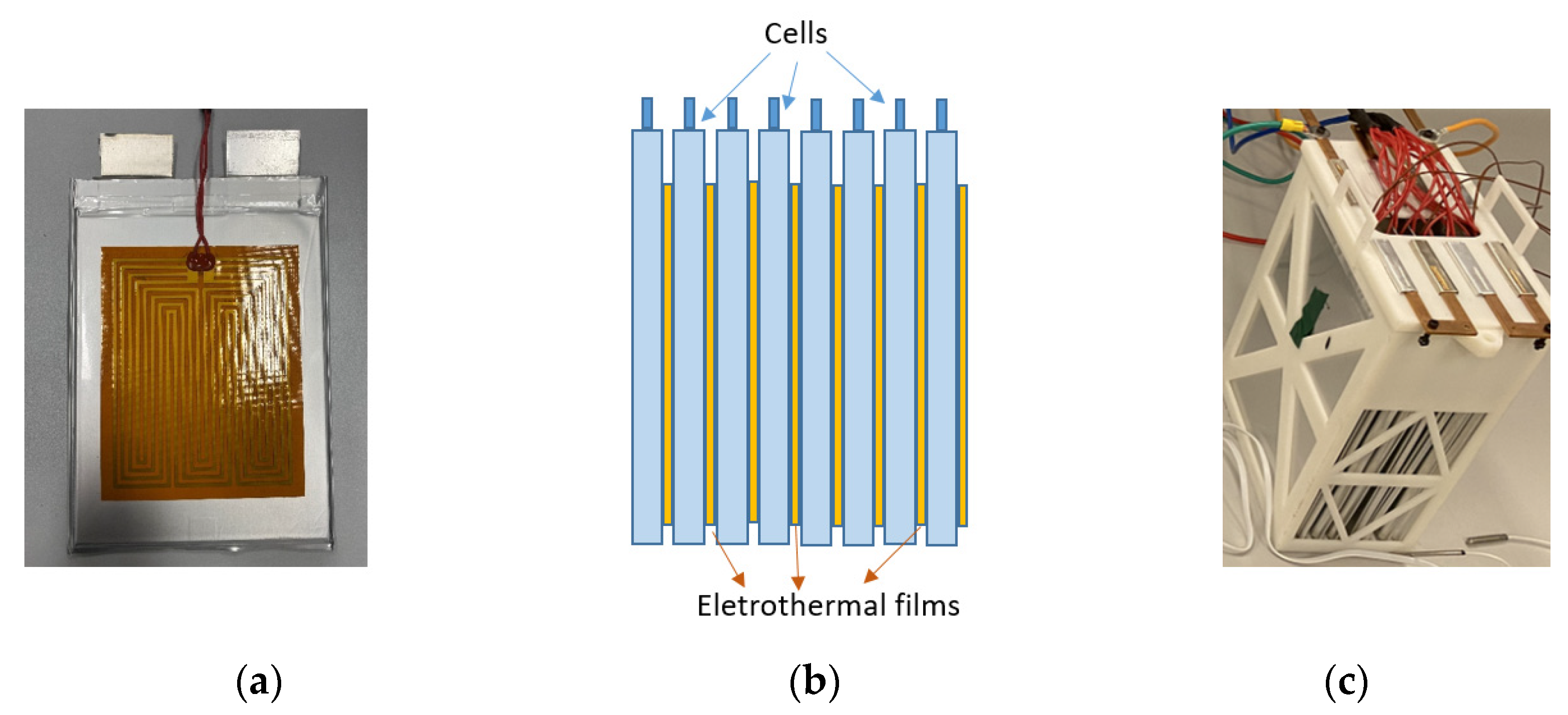
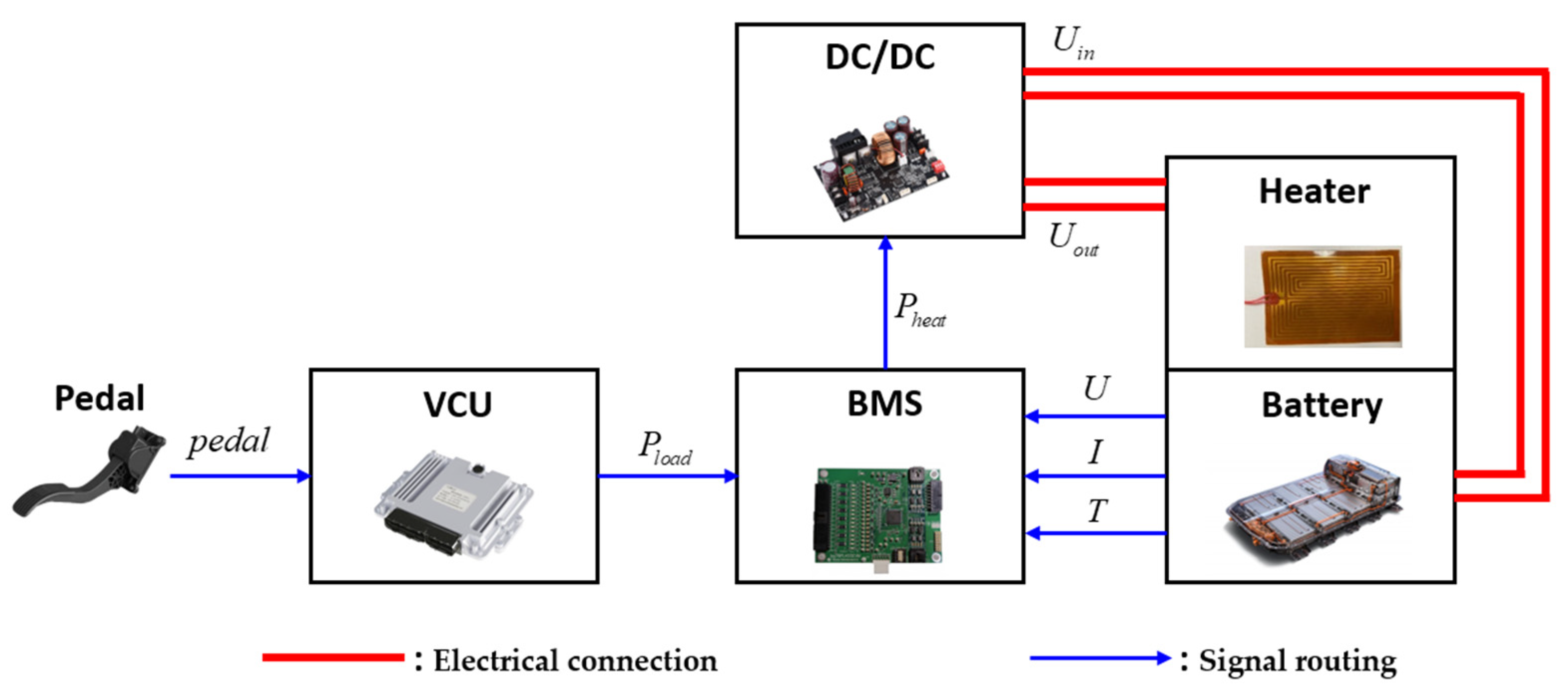
2.1. System Configuration
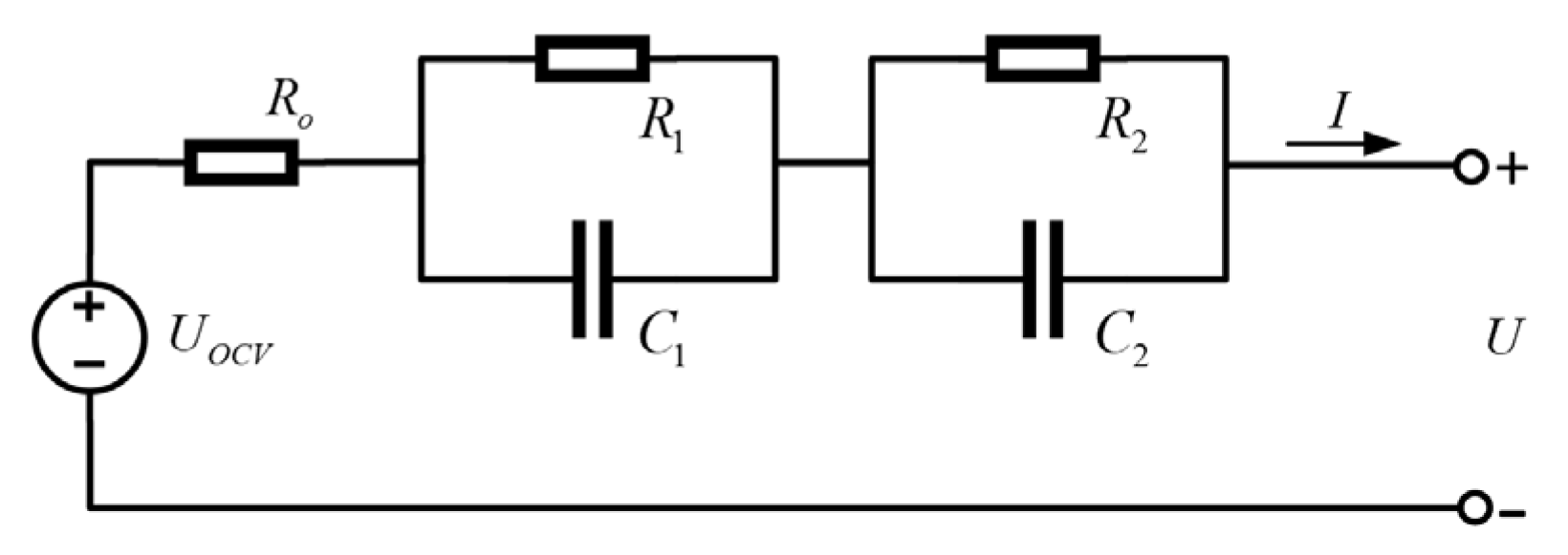
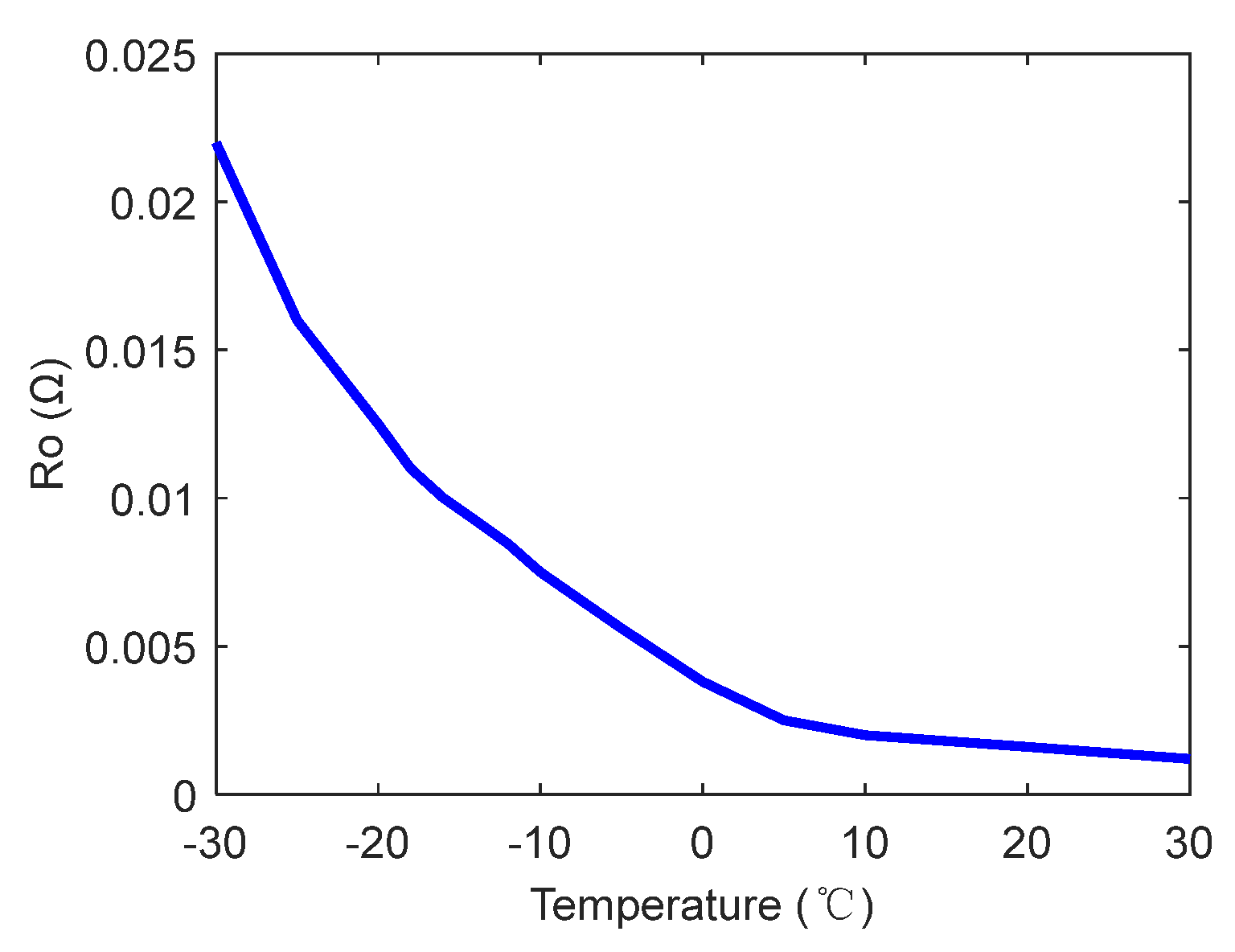
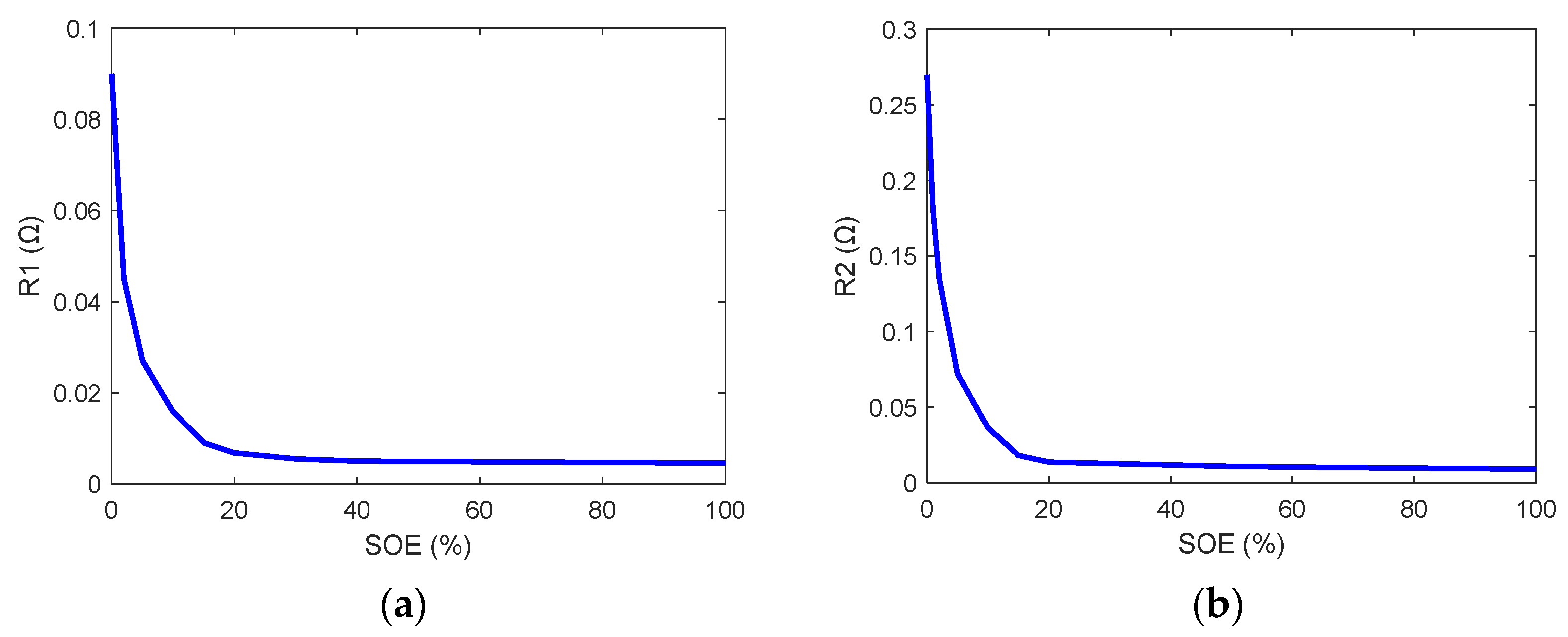
2.2. Equivalent Circuit Model
2.3. Thermal Model
3. Fuzzy Logic External Heating Control
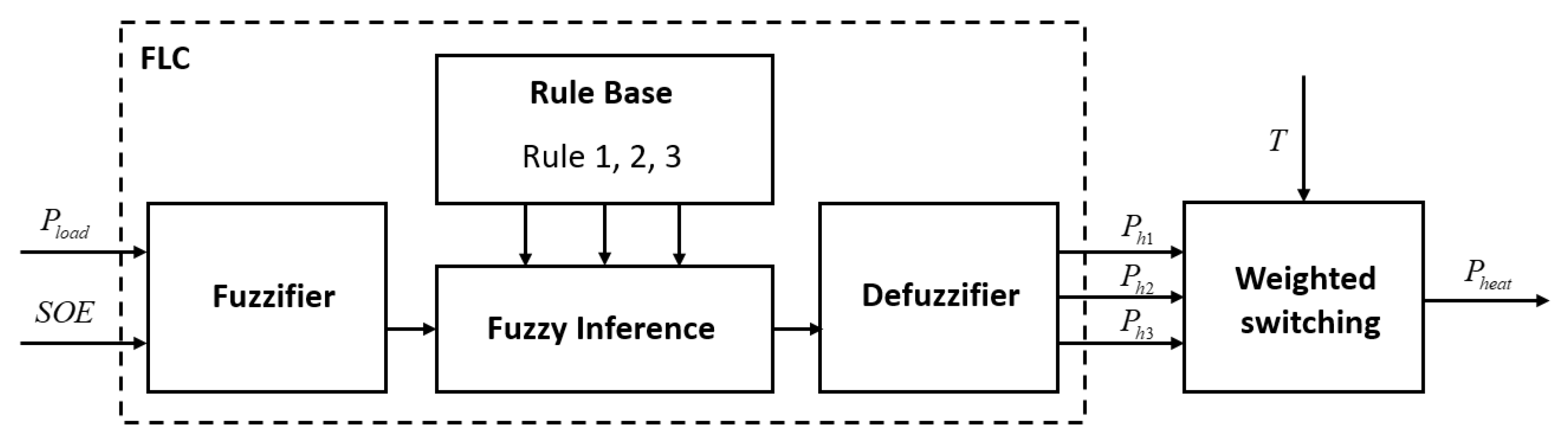
3.1. Control Structure
3.2. Fuzzy Logic Control Design
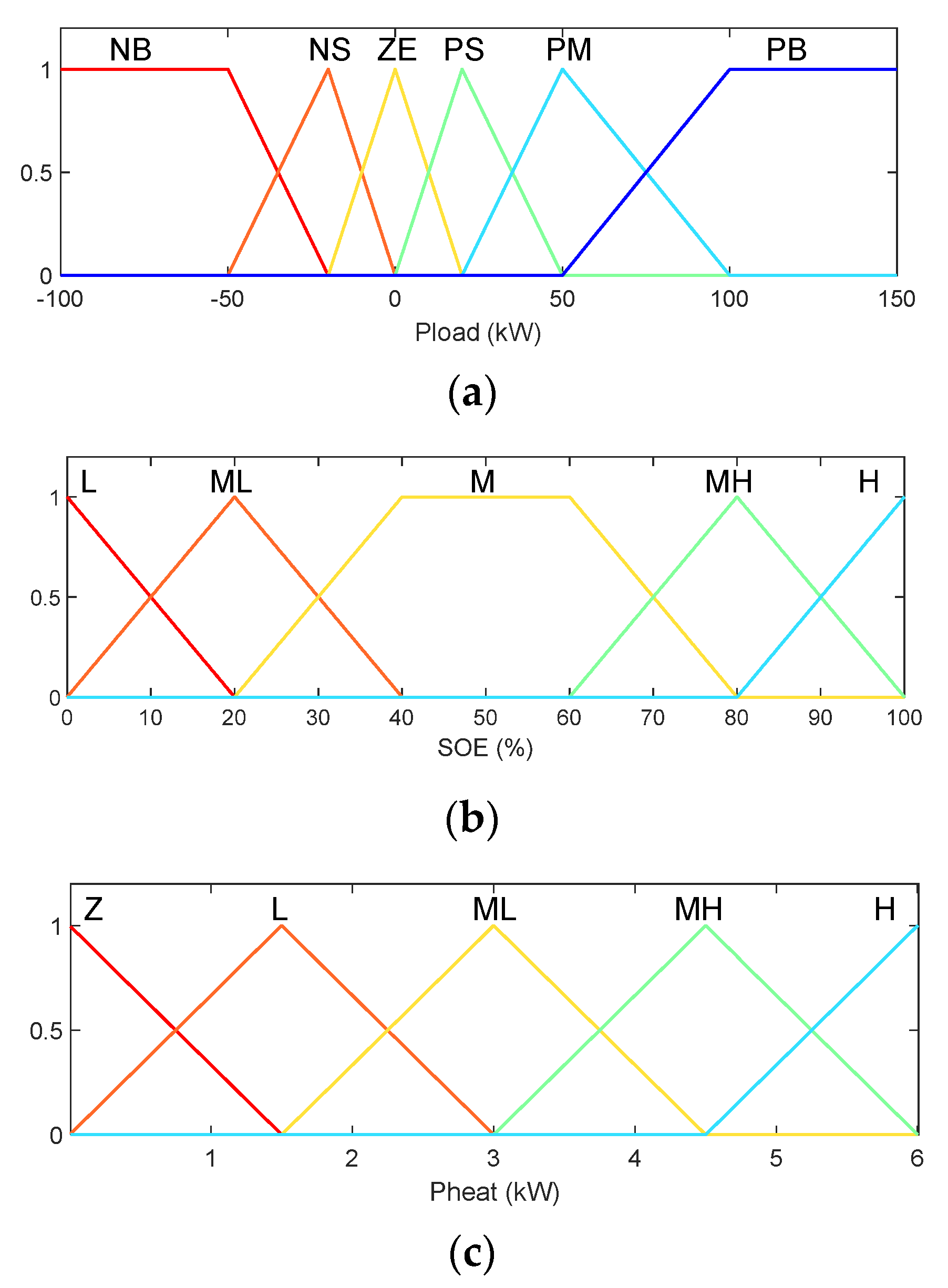
3.2.1. Membership Functions
3.2.2. Fuzzy Control Rules
3.2.3. Defuzzification
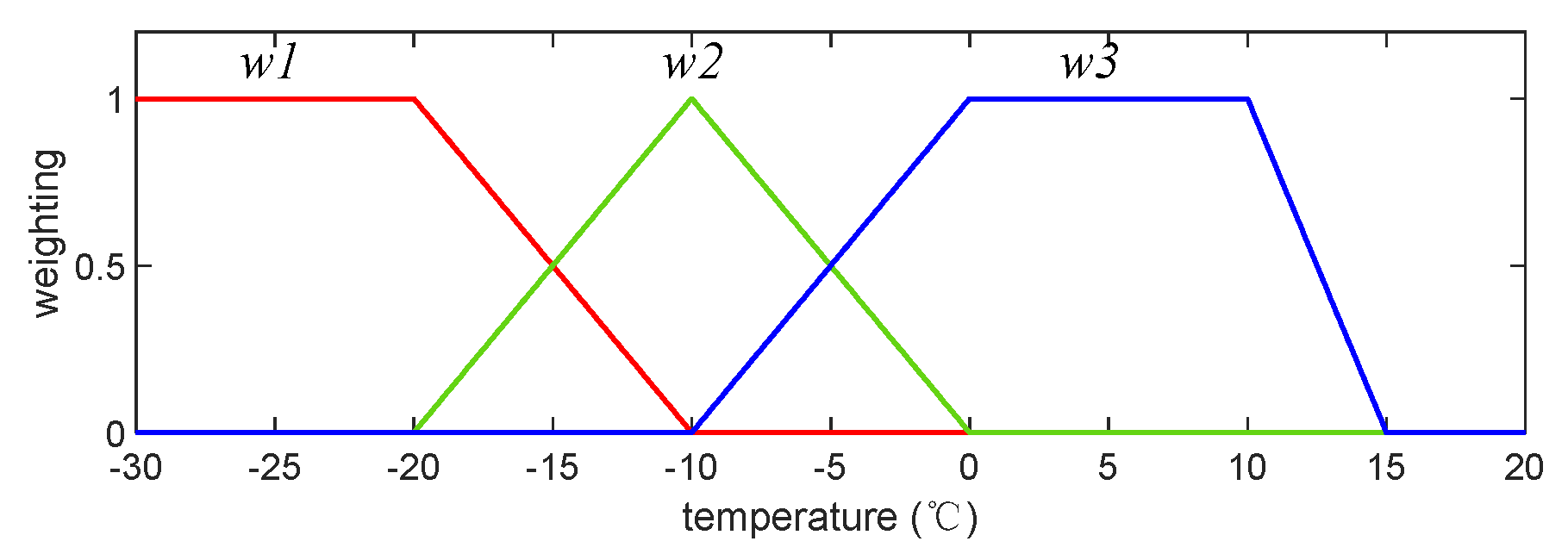
3.3. Weighted Switching
4. Results and Discussions
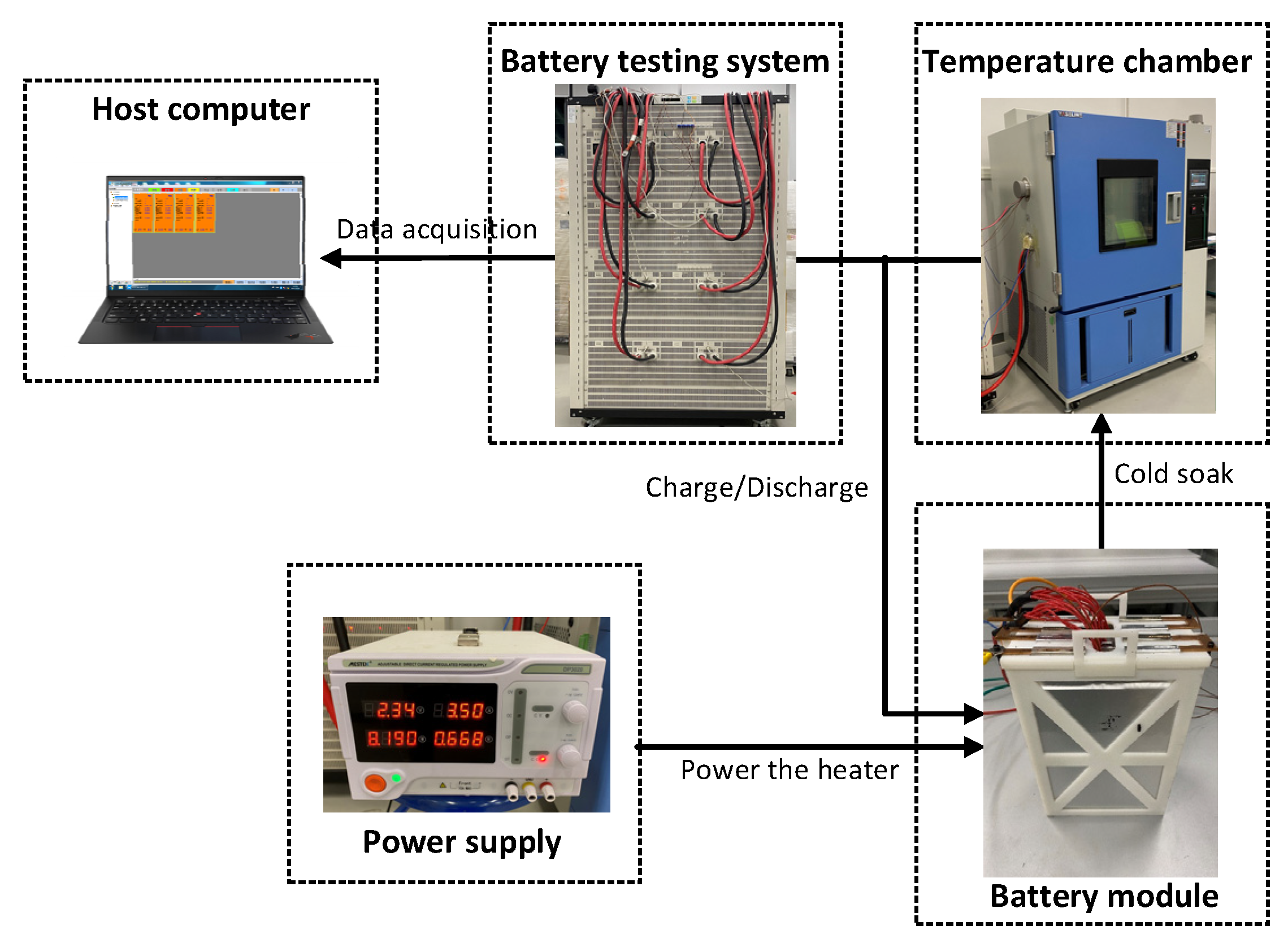
4.1. Test Setup
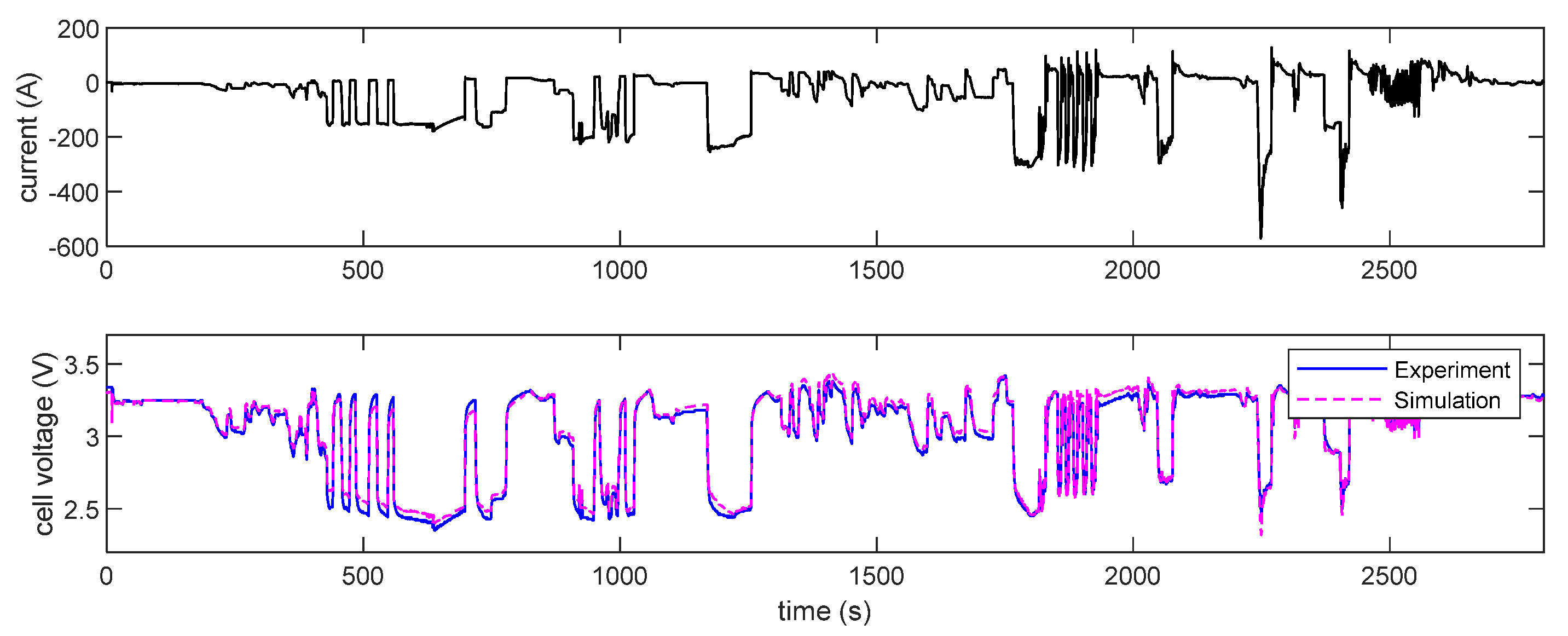
4.2. Experimental Results
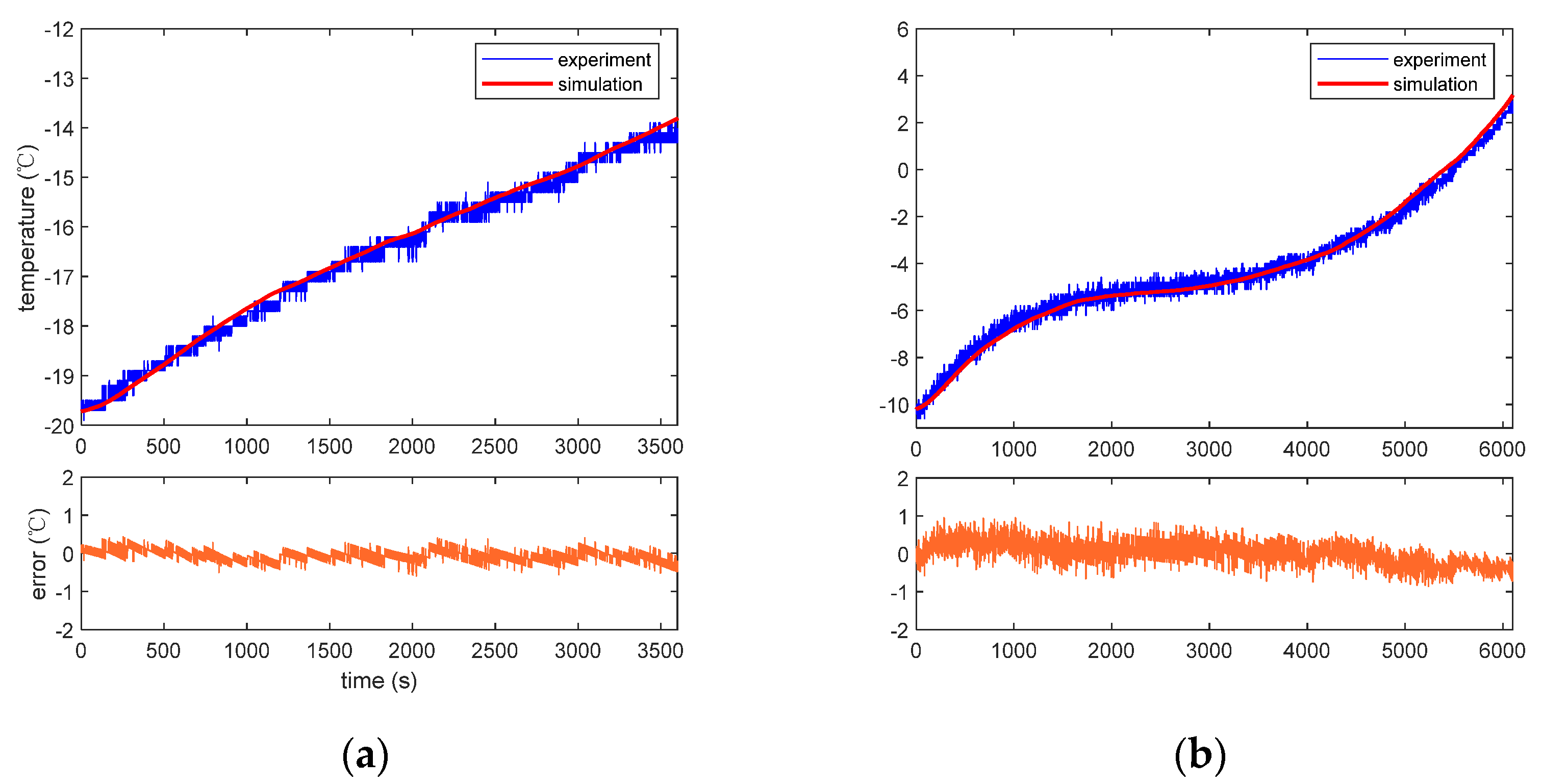
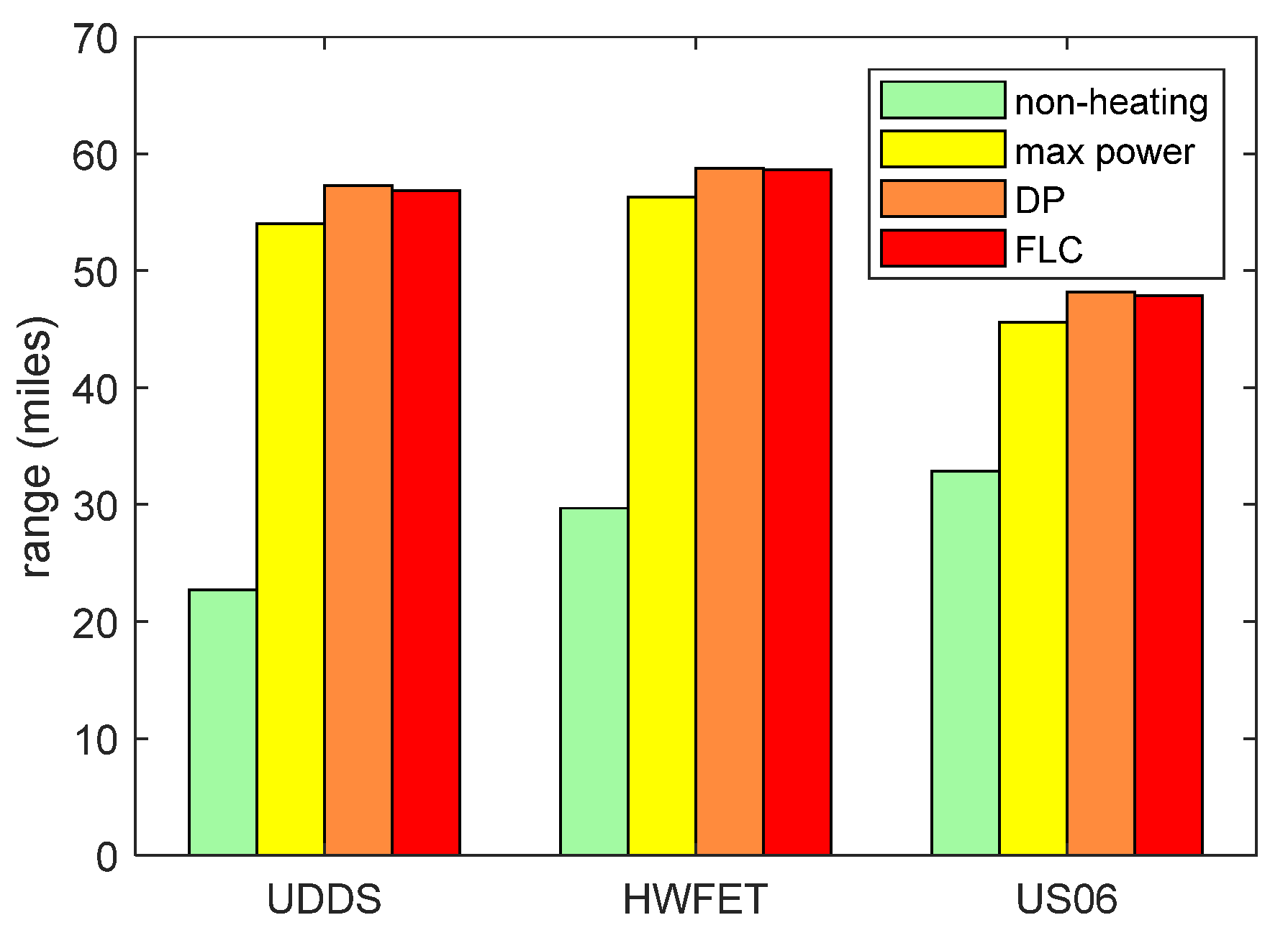
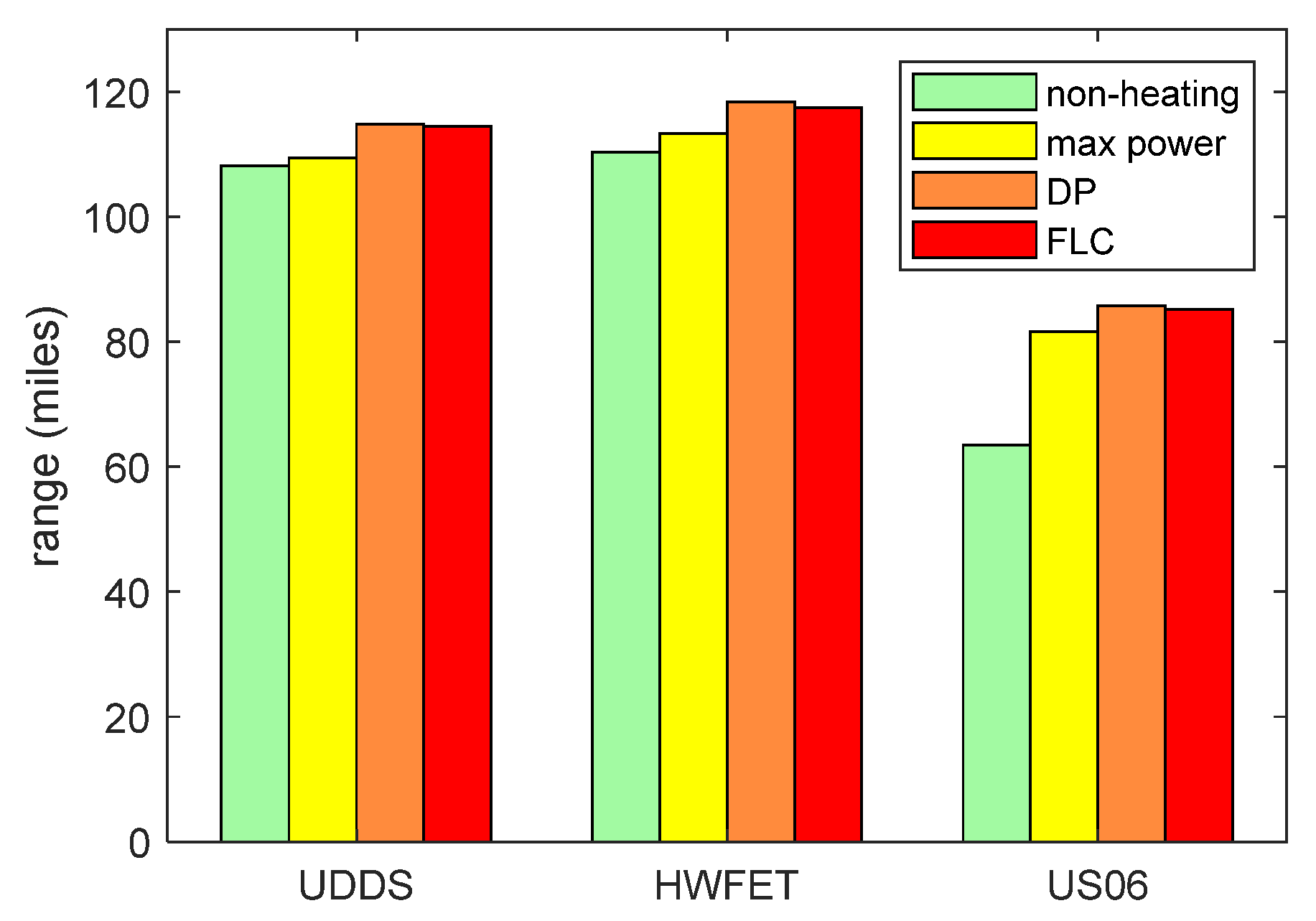
4.3. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Wilberforce, T.; El-Hassan, Z.; Khatib, F.N.; Makky, A.A.; Baroutaji, A.; Carton, J.G.; Olabi, A.G. Developments of electric cars and fuel cell hydrogen electric cars. Int. J. Hydrogen Energy 2017, 42, 25695–25734. [Google Scholar] [CrossRef]
- Capasso, C.; Veneri, O. Experimental analysis on the performance of lithium based batteries for road full electric and hybrid vehicles. Appl. Energy 2014, 136, 921–930. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Meyer, N.; Whittal, I.; Christenson, M.; Loiselle-Lapointe, A. The Impact of Driving Cycle and Climate on Electrical Consumption & Range of Fully Electric Passenger Vehicles. In Proceedings of the EVS26 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium, Los Angeles, CA, USA, 6–9 May 2012. [Google Scholar]
- Reyes, J.R.M.D.; Parsons, R.V.; Hoemsen, R. Winter Happens: The Effect of Ambient Temperature on the Travel Range of Electric Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4016–4022. [Google Scholar] [CrossRef]
- Smart, M.C.; Ratnakumar, B.V.; Behar, A.; Whitcanack, L.D.; Yu, J.S.; Alamgir, M. Gel polymer electrolyte lithium-ion cells with improved low temperature performance. J. Power Sources 2007, 165, 535–543. [Google Scholar] [CrossRef]
- Senyshyn, A.; Mühlbauer, M.J.; Dolotko, O.; Ehrenberg, H. Low-temperature performance of Li-ion batteries: The behavior of lithiated graphite. J. Power Sources 2015, 282, 235–240. [Google Scholar] [CrossRef]
- Liu, K.; Kang, L.I.; Peng, Q.; Zhang, C. A brief review on key technologies in the battery management system of electric vehicles. Front. Mech. Eng. 2018, 14, 47–64. [Google Scholar] [CrossRef]
- Wu, S.; Xiong, R.; Li, H.; Nian, V.; Ma, S. The state of the art on preheating lithium-ion batteries in cold weather. J. Energy Storage 2020, 27, 101059.1–101059.13. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, C. Heating strategies for Li-ion batteries operated from subzero temperatures. Electrochim. Acta 2013, 107, 664–674. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Hou, J.; Zhang, X.; Ouyang, M. The optimization of a hybrid energy storage system at subzero temperatures: Energy management strategy design and battery heating requirement analysis. Appl. Energy 2015, 159, 576–588. [Google Scholar] [CrossRef]
- Li, G.; Huang, X.; Fu, X. Design Research on Battery Heating and Preservation System Based on Liquid Cooling Mode. J. Hunan Univ. 2017, 44, 26–33. [Google Scholar]
- Zhang, J.; Sun, F.; Wang, Z. Heating character of a LiMn2O4 battery pack at low temperature based on PTC and metallic resistance material. Energy Procedia 2017, 105, 2131–2138. [Google Scholar] [CrossRef]
- Su, Z.A. Lithium Ion Power Battery Heating Device. China Patent CN101710630A, 10 August 2011. [Google Scholar]
- Lei, Z.; Zhang, C.; Li, J.; Fan, G.; Lin, Z. Preheating method of lithium-ion batteries in an electric vehicle. J. Mod. Power Syst. Clean Energy 2015, 3, 289–296. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Q.; Zhang, Z.; Hua, Y. Pre-Heating Simulation of Lithium-ion Battery Module for Electric Vehicles. J. Comput. Simul. 2021, 5, 85–89. [Google Scholar]
- Hu, X.; Zheng, Y.; Howey, D.A.; Perez, H.E.; Pecht, M. Battery warm-up methodologies at subzero temperatures for automotive applications: Recent advances and perspectives. Prog. Energy Combust. Sci. 2020, 77, 100806. [Google Scholar] [CrossRef]
- Alaoui, C.; Salameh, Z.M. A novel thermal management for electric and hybrid vehicles. IEEE Trans. Veh. Technol. 2005, 54, 468–476. [Google Scholar] [CrossRef]
- Chen, M.; Li, J. Experimental study on heating performance of pure electric vehicle power battery under low temperature environment. Int. J. Heat Mass Transf. 2021, 172, 121191. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, J.; Wang, L. Design of electric air-heated box for batteries in electric vehicles. Chin. J. Power Sources 2013, 37, 1184–1187. [Google Scholar]
- Jin, X.; Li, J.Q.; Zhang, C.N.; Wu, P.E. Researches on Modeling and experiment of liionbattery ptc self-heating in electric vehicles. Energy Procedia 2016, 104, 62–67. [Google Scholar] [CrossRef]
- Qu, Z.G.; Jiang, Z.Y.; Wang, Q. Experimental study on pulse self-heating of lithium-ion battery at low temperature. Int. J. Heat Mass Transf. 2019, 135, 696–705. [Google Scholar] [CrossRef]
- Guo, S.; Xiong, R.; Wang, K.; Sun, F. A novel echelon internal heating strategy of cold batteries for all-climate electric vehicles application. Appl. Energy 2018, 219, 256–263. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Sun, B.; Su, X.; He, X.; Zhao, K. An optimal internal-heating strategy for lithium-ion batteries at low temperature considering both heating time and lifetime reduction. Appl. Energy 2019, 256, 113797. [Google Scholar] [CrossRef]
- Gang, N.; Haran, B.; Popov, B.N. Capacity fade study of lithium-ion batteries cycled at high discharge rates. J. Power Sources 2003, 117, 160–169. [Google Scholar]
- Qin, Y.; Du, J.; Lu, L.; Gao, M.; Ouyang, M. A rapid lithium-ion battery heating method based on bidirectional pulsed current: Heating effect and impact on battery life. Appl. Energy 2020, 280, 115957. [Google Scholar] [CrossRef]
- Lin, C.; Kong, W.; Tian, Y.; Wang, W.; Zhao, M. Heating lithium-ion batteries at low temperatures for onboard applications: Recent progress, challenges and prospects. Automot. Innov. 2022, 5, 3–17. [Google Scholar] [CrossRef]
- Bao, S.; Sun, P.; Zhu, J.; Ji, Q.; Liu, J. Improved multi-dimensional dynamic programming energy management strategy for a vehicle power-split hybrid powertrain. Energy 2022, 256, 124682. [Google Scholar] [CrossRef]
- Wang, X.; Hua, Q.; Liu, P.; Sun, L. Stochastic dynamic programming based optimal energy scheduling for a hybrid fuel cell/PV/battery system under uncertainty. Process Saf. Environ. Prot. 2022, 165, 380–386. [Google Scholar] [CrossRef]
- Du, J.; Chen, Z.; Li, F. Multi-objective optimization discharge method for heating lithium-ion battery at low temperatures. IEEE Access 2018, 6, 44036–44049. [Google Scholar] [CrossRef]
- Antonio, G.; Nagano, M.S.; Rolim, G.A. Dynamic programming algorithms and their applications in machine scheduling: A review. Expert Syst. Appl. 2022, 190, 116180. [Google Scholar]
- Chen, J.; Xu, C.; Wu, C.; Xu, W. Adaptive Fuzzy Logic Control of Fuel-Cell-Battery Hybrid Systems for Electric Vehicles. IEEE Trans. Ind. Inform. 2018, 14, 292–300. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Lipu, M.S.H.; Uddin, M. Fuzzy Based Charging-Discharging Controller for Lithium-ion Battery in Microgrid Applications. IEEE Trans. Ind. Appl. 2021, 57, 4187–4195. [Google Scholar] [CrossRef]
- Chen, G.; Pham, A. Introduction to Fuzzy Sets, Fuzzy Logic, and Fuzzy Control Systems; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Zhao, Z. Improved fuzzy logic control-based energy management strategy for hybrid power system of fc/pv/battery/sc on tourist ship. Int. J. Hydrogen Energy 2022, 47, 9719–9734. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Mass (kg) | 1.2 |
| Length (mm) | 227 |
| Width (mm) | 161 |
| Thickness (mm) | 15 |
| Nominal voltage (V) | 3.29 |
| Charge cut-off voltage (V) | 3.65 |
| Discharge cut-off voltage (V) | 2.00 |
| Capacity (Ah) | 60 |
| Energy capacity (Wh) | 193.63 |
| Operating temperature range (°C) | −30–55 |
| Specific heat capacity (J/Kg·K) | 1130 |
| Parameter | Value |
|---|---|
| Mass (g) | 37.5 |
| Length (mm) | 150 |
| Width (mm) | 120 |
| Thickness (mm) | 0.15 |
| Rated voltage (V) | 12 |
| Rated power (W) | 20 |
| Specific heat capacity (J/Kg·K) | 1220 |
| Operating temperature range (°C) | −190~205 |
| Ph1 | Pload | ||||||
|---|---|---|---|---|---|---|---|
| NB | NS | ZE | PS | PM | PB | ||
| SOE | H | H | MH | Z | L | L | ML |
| MH | H | MH | Z | L | L | MH | |
| M | H | MH | Z | L | ML | MH | |
| ML | H | MH | L | ML | H | H | |
| L | H | MH | L | M | H | H | |
| Ph2 | Pload | ||||||
|---|---|---|---|---|---|---|---|
| NB | NS | ZE | PS | PM | PB | ||
| SOE | H | H | ML | Z | Z | Z | L |
| MH | MH | ML | Z | Z | L | ML | |
| M | MH | ML | Z | Z | L | ML | |
| ML | MH | ML | Z | L | ML | MH | |
| L | MH | ML | L | ML | MH | H | |
| Ph3 | Pload | ||||||
|---|---|---|---|---|---|---|---|
| NB | NS | ZE | PS | PM | PB | ||
| SOE | H | ML | Z | Z | Z | Z | Z |
| MH | L | Z | Z | Z | Z | Z | |
| M | L | Z | Z | Z | Z | L | |
| ML | L | Z | Z | Z | L | ML | |
| L | L | Z | Z | Z | ML | MH | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Li, T.; Chen, L. Fuzzy Logic Control of External Heating System for Electric Vehicle Batteries at Low Temperature. World Electr. Veh. J. 2023, 14, 99. https://doi.org/10.3390/wevj14040099
Zhang S, Li T, Chen L. Fuzzy Logic Control of External Heating System for Electric Vehicle Batteries at Low Temperature. World Electric Vehicle Journal. 2023; 14(4):99. https://doi.org/10.3390/wevj14040099
Chicago/Turabian StyleZhang, Shupeng, Tao Li, and Liqun Chen. 2023. "Fuzzy Logic Control of External Heating System for Electric Vehicle Batteries at Low Temperature" World Electric Vehicle Journal 14, no. 4: 99. https://doi.org/10.3390/wevj14040099
APA StyleZhang, S., Li, T., & Chen, L. (2023). Fuzzy Logic Control of External Heating System for Electric Vehicle Batteries at Low Temperature. World Electric Vehicle Journal, 14(4), 99. https://doi.org/10.3390/wevj14040099





