Abstract
Dual three-phase motors have the problem of a large generation of harmonic currents while driving due to small inductance for certain harmonics. The purpose of this paper is to theoretically clarify the effect of the winding structure of dual three-phase motors on harmonic currents. Analytical calculations considering the spatial harmonics of the magnetomotive force are used to formulate the inductance that depends on the winding structure and the harmonic order. The validity of the formulated theoretical expression of the inductance is confirmed by finite element analysis. In addition, drive simulations of the coil pitch 5/6 dual 3-phase motor and the coil pitch 1 dual 3-phase motor are performed, and it is found that the magnitude of the generated harmonic currents can be explained using the formulated inductance values. In conclusion, it is found that dual three-phase motors with large winding factors for fifth and seventh order spatial harmonics can reduce the harmonic currents.
1. Introduction
In recent years, the realization of a low-carbon society has become an urgent issue. The electrification of automobiles and all other fields is accelerating, and further performance improvement of motors is required.
Against this background, dual inverter drive systems have been attracting attention for improving motor performance. The advantages of this system include a higher torque and power using two inverters of conventional ratings [1,2,3,4,5,6,7], and an increased degree of control freedom and reliability by increasing the number of phases [1,2,3,4,5,6,7,8]. The winding arrangement of the motor applied in this system can be broadly classified into 3 types with a phase difference between 2 sets of 3-phase windings of 0 degrees, 30 degrees, and 60 degrees in electrical angle [5]. In particular, the dual 3-phase motor with a phase difference of 30 degrees in the electrical angle shown in Figure 1 has attracted more attention because it completely eliminates the 6th harmonic component of the torque ripple, in addition to the above advantages of the dual inverter drive system [3,4,5,8].
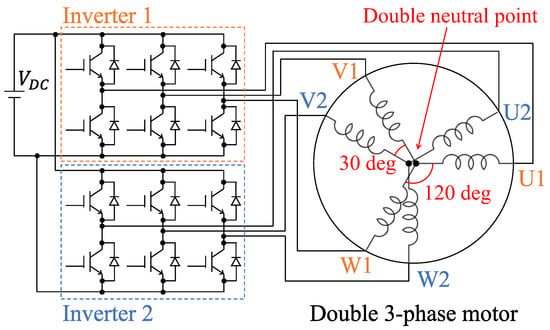
Figure 1.
Dual 3-phase motor.
However, dual three-phase motors have the problem of generating more harmonic currents during driving than conventional three-phase motors [1,2,3,4,6,7]. The cause of this problem can be explained using vector space decomposition (VSD), as proposed in [1]. As described in detail below, the harmonic components of phase voltage and phase current are decomposed into three linearly independent two-dimensional Cartesian coordinate systems (α-β subspace, z1-z2 subspace, o1-o2 subspace) by a Cartesian coordinate transformation based on VSD. Assuming a sinusoidal distribution winding, the magnetizing inductance component is decomposed into only the α-β subspace, and the inductance in the z1-z2 subspace is only the leakage component. Therefore, the inductance in the z1-z2 subspace is small, and large harmonic currents are generated even if the harmonic voltage in the z1-z2 subspace is small [2,3,4]. The harmonic currents in the z1-z2 subspace do not contribute to the generation of torque ripple but must be suppressed because they cause increased losses and inverter current ratings [2,3,4,6]. Since the o1 and o2 phases are the zero sequence of the first and second windings, respectively, separating the neutral points of the first and second windings, as shown in Figure 1, can prevent the generation of harmonic currents in the o1-o2 subspace, such as 3rd order harmonic currents [1,7].
The harmonic currents that are the problem can be broadly classified into low-order harmonic currents (mainly fifth and seventh harmonics) caused by harmonic components of the back electromotive force (back-EMF) and nonlinearity of the inverter, and high-order carrier harmonic currents caused by the pulse width modulation (PWM) of the inverter [4,7]. Many studies have focused on control approaches, proposing low-order harmonic current suppression methods using proportional-integral control with resonant control (PI-R) and multiple synchronous reference frames (MSRFs) [3,4], and carrier harmonic current suppression methods using space vector pulse width modulation (SVPMW) [1,2,7].
On the other hand, the cause of large harmonic currents is the small inductance in the z1-z2 subspace as described above, and an approach to reduce harmonic currents by designing the windings with a large inductance in the z1-z2 subspace is also possible. However, as far as the author has been able to find, there are few studies that clarify how the inductance in the z1-z2 subspace changes depending on the winding structure.
Only in [6], the characteristics of the slot leakage inductance in the α-β and z1-z2 subspaces with respect to the coil pitch are clarified analytically. However, these inductances have not been formulated using a more basic parameter, the winding factor. There is also room for further study of the relationship between the inductance in each subspace and the magnitude of harmonic currents. In particular, the short-pitch winding with the coil pitch of 5/6 is known to have small winding factors for 5th and 7th spatial harmonics. This reduces the fifth and seventh harmonic components of the back-EMF, which is an advantage compared to conventional three-phase motors because the fifth and seventh harmonic currents can be reduced. However, it has been reported that the fifth and seventh harmonic currents conversely increase in the case of dual three-phase motors [6]. To explain the cause of this, it is necessary to clarify the inductance analytically using the winding factor and the relationship with the back-EMF.
In this paper, the inductance of dual three-phase motors, which varies depending on the winding structure and subspaces, is analytically clarified. The validity of the formulated inductances is confirmed by finite element analysis (FEA) and the magnitude of the harmonic currents generated during drive is quantitatively evaluated using these inductance values. The model used in the FEA and simulation is an interior permanent magnet synchronous motor (IPMSM) for electric vehicles.
2. Coordinate System of Dual Three-Phase Motors
2.1. Stationary Orthogonal Subspaces
The original transformation matrix based on VSD is a 6 × 6 matrix, which maps the current, voltage, and flux linkage to three two-dimensional stationary subspaces: α-β subspace, z1-z2 subspace, and o1-o2 subspace. On the other hand, as mentioned above, separating the neutral points of the 1st and 2nd windings prevents the generation of harmonic currents in the o1-o2 subspace, such as 3rd order harmonic currents, so this paper considers a winding structure with the separated neutral points of the 1st and 2nd windings. In this case, the mapping to the o1-o2 subspace can be omitted, and the orthogonal coordinate transformation in this paper uses the 4 × 6 matrix shown in the following Equation (1).
The orthogonal subspaces used in this paper are shown in Figure 2. As an example, the currents in each phase are mapped to the α-β and z1-z2 subspaces as follow (Equation (2)).
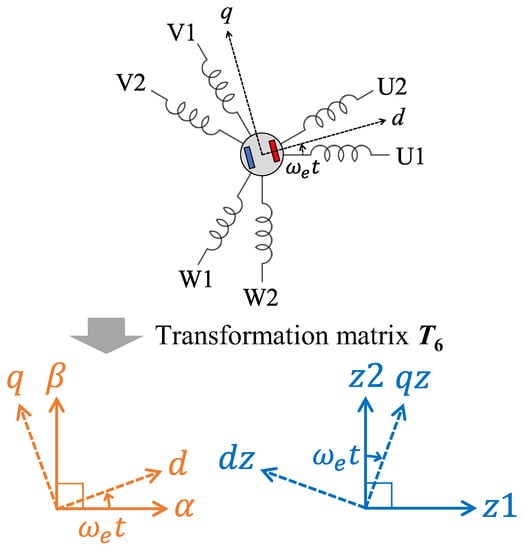
Figure 2.
Orthogonal subspaces.
is the phase current vector, and are the current vectors in the α-β and z1-z2 subspaces. Where , , , , , and are currents in each phase; , and are currents in the α-β subspace; and are currents in the z1-z2 subspace; and , , and are expressed as (Equations (3) and (4)).
Similarly, the voltage and the flux linkage can be transformed to the α-β subspace and the z1-z2 subspace.
The harmonic components in the currents, voltage, and flux linkage of each phase are mapped to either the α-β subspace or the z1-z2 subspace, depending on their orders. As an example, the orthogonal coordinate transformation is performed for the kth order harmonic currents, as shown in the following equation:
where I is the amplitude of currents and is the fundamental electric angular frequency. Furthermore, k is an odd number. The expression for the kth harmonic currents in the stationary orthogonal subspaces, obtained by substituting (5) into (2), can be divided into the following four cases depending on the value of k.
- k = 1, 13, 25, …, 12 m + 1 (m = 0, 1, 2, …):
From (6a), it can be seen that the above harmonic orders, including the fundamental and 13th order, represent the positive sequence components of the α-β subspace.
- 2.
- k = 11, 23, 35, …, 12 m + 11 (m = 0, 1, 2, …):
From (6b), it can be seen that the above harmonic orders, including 11th and 23rd order, represent the negative sequence components of the α-β subspace.
- 3.
- k = 5, 17, 29, …, 12 m + 5 (m = 0, 1, 2, …):
From (6c), it can be seen that the above harmonic orders, including the 5th and 17th order, represent the positive sequence components of the z1-z2 subspace.
- 4.
- k = 7, 19, 31, …, 12 m + 7 (m = 0, 1, 2, …):
From (6d), it can be seen that the above harmonic orders, including the 7th and 19th order, represent the negative components of the z1-z2 subspace.
Note that k = 3, 9, 15, ..., 6 m + 3 (m = 0, 1, 2, ...) are not included above because they are components that are mapped to the o1-o2 subspace. Table 1 shows a comparison of the harmonic distributions in conventional 3-phase motors and dual 3-phase motors. As shown in Table 1, in conventional 3-phase motors, harmonic components of orders such as k = 5, 7, ... are superimposed in the α-β subspace which is the fundamental axes. On the other hand, in dual three-phase motors, these harmonic components are superimposed in the z1-z2 subspace, which is the coordinate system unique to dual 3-phase motors. As described above, it should be noted that the harmonics of dual three-phase motors show a different distribution from those of conventional three-phase motors.

Table 1.
Comparison of harmonic distributions.
2.2. Rotational Orthogonal Subspaces
The transformation from the stationary orthogonal subspaces, α-β and z1-z2 subspaces, to the rotational orthogonal subspaces uses the following matrix [4]:
As an example, currents in the α-β and z1-z2 subspaces are transformed to the d-q and dz-qz subspaces, respectively, as follows:
where and are currents in the d-q subspace, and and are currents in the dz-qz subspace. As is clear from (8), the components in the α-β subspace are mapped to the d-q subspace only, and the components in the z1-z2 subspace are mapped to the dz-qz subspace only. Therefore, the transformation matrix (7) does not change the harmonic distribution discussed in the previous section.
3. Mathematical Model of Dual Three-Phase IPMSM
IPMSMs have saliency in inductance, and it is common to consider inductance saliency in mathematical models. However, the inductance saliency causes interference between harmonic orders [9], which complicates the discussion when considering the relationship between harmonic current amplitude and inductance value for each harmonic order. Therefore, in this chapter, we first define a model that takes into account inductance saliency, and then present a model that ignores inductance saliency to simplify the discussion in the following sections.
3.1. Model with Inductance Saliency
The voltage equation for a dual 3-phase IPMSM is shown below in Equation (9):
where R is the phase resistance and p is the differential operator. Furthermore, where is the phase voltage vector, is the flux linkage vector by an armature current, is the flux linkage vector by a permanent magnet, , , and are expressed as:
The flux linkage vector by armature current is:
where is the overall inductance matrix, is the inductance matrix of the first winding, is the inductance matrix of the second winding, and is the mutual inductance matrix of the first and second windings, respectively. For each inductance component, a model that takes into account the mutual inductance between the first and second windings is used [5]. For the inductance matrices in (15a,b),
For the inductance matrix in (15c),
where is the leakage inductance, and are the DC and AC components of the magnetizing inductance, and are the DC and AC components of mutual inductance between different phases in the same winding set, and are the DC and AC components of mutual inductance among different phases in different winding sets, and are the phase differences between the d-axis and phases i and j (i and j are U1, V1, W1, U2, V2, or W2, and i ≠ j).
The flux linkage in phase i by the permanent magnet is expressed by the following equation when harmonic components are taken into account:
where is the amplitude of the kth harmonic component of the flux linkage by the permanent magnet and is the phase of phase i. In this paper, we consider up to k = 13.
Transforming (9) into the rotational orthogonal subspaces using (1) and (7) yields
where and are the voltages in the d-q subspace and and are the voltages in the dz-qz subspace. The inductances and in the d-q subspace, and and in the dz-qz subspace are:
where is the inductance in the α-β subspace, is the inductance in the z1-z2 subspace, and are:
In the case of sinusoidal distribution winding, and in (16a–c). In this case, (19) and (20) can be expressed as:
From the above equation, the inductance in the z1-z2 or dz-qz subspaces is only the leakage component in the case of sinusoidal distribution winding, as described in Chapter 1.
3.2. Model Ignores Inductance Saliency
For a model that ignores the inductance saliency, it is sufficient to set L2 = 0, M2 = 0, and M2′ = 0 in (16a–c). In this case, transforming (9) to the stationary orthogonal subspaces using (1) yields:
where and are the voltages in the α-β subspace, and and are the voltages in the z1-z2 subspace. From (22), it can be confirmed that the voltage equation in the stationary orthogonal subspaces when ignoring the inductance saliency is not only free from interference between harmonic orders (the frequency of the output current matches the frequency of the input voltage), but also free from interference between axes. In Chapter 6, when analyzing the magnitude of the harmonic currents generated using inductance values, Equation (22) is used for simplifying.
4. Design Method for Inductance of Dual Three-Phase Motors
This chapter describes a method for formulating the inductance and in the α-β and z1-z2 subspaces.
4.1. Definition of Winding Distribution Function
Let the winding distribution function be the magnetomotive force (MMF) distribution when DC 1 [A] is energized in the U1 phase winding, where is the position (electric angle) on the stator. Assuming that the MMF distribution generated by the coil is a square wave, for the winding with the number of phase a, the coil pitch γ, and the number of slots per pole per phase q can be expressed as follows by Fourier series expansion:
where N is the number of turns and kwn is the winding factor for nth spatial harmonics. Furthermore, the winding factor kwn is:
where kpn is the pitch factor for nth spatial harmonics and kdn is the distribution factor for nth spatial harmonics. In this paper, the number of slots per pole per phase q is assumed to be an integer. Figure 3 shows the waveform of the winding distribution function when and only the pitch factor kpn is considered. From Figure 3, the MMF distribution of the winding with the coil pitch γ can be seen.
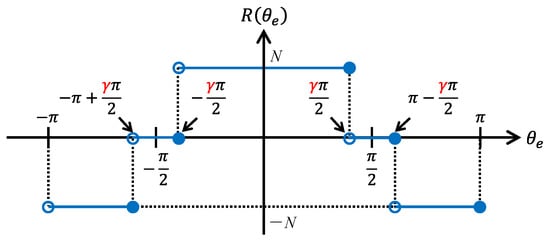
Figure 3.
Winding distribution function R(θe) when kdn = 1.
4.2. Magnetomotive Force Distribution for Harmonic Currents
The synthetic MMF distribution by the armature currents of a dual three-phase motor is:
The synthetic MMF distribution when the kth harmonic current is energized can be obtained by substituting (5) into (25), and, as in (6a–d), it can be divided into the following 4 cases depending on the value of k.
- k = 1, 13, 25, …, 12 m + 1 (m = 0, 1, 2, …):
The energizing currents are the positive sequence of the α-β subspace, and is:
- 2.
- k = 11, 23, 35, …, 12 m + 11 (m = 0, 1, 2, …):
The energizing currents are the negative sequence of the α-β subspace, and is:
- 3.
- k = 5, 17, 29, …, 12 m + 5 (m = 0, 1, 2, …):
The energizing currents are the positive sequence of the z1-z2 subspace, and is:
- 4.
- k = 7, 19, 31, …, 12 m + 7 (m = 0, 1, 2, …):
The energizing currents are the negative sequence of the z1-z2 subspace, and is:
In (26a–d), and represent nth spatial harmonic components of the MMF, the former being a magnetic field rotating with speed kωe in the positive direction and the latter with speed kωe in the negative direction.
As an example, Figure 4 shows the waveforms of (26a–d) when γ = 1 and q = 1. In Figure 4, the waveform at t = 0 is shown as a solid line and the waveform at t = T/4k (where T = 2π/ωe) as a dotted line. From Figure 4a,b, it can be seen that the amplitude of the MMF is large when the energizing currents are in the α-β subspace. On the other hand, Figure 4c,d shows that the amplitude of the MMF is small when the energizing currents are in the z1-z2 subspace. The reason for this can be explained by focusing on the coefficient kwn/n in (26a–d). Since |kwn| is always less than one, the larger n is, the smaller the nth spatial harmonic component of the MMF becomes. Here, the minimum n in (26a,b) is 1, while the minimum n in (26c,d) is 5. Therefore, the amplitude of the synthetic MMF is smaller in the latter case.
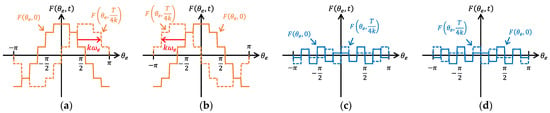
Figure 4.
MMF distribution for kth harmonic currents: (a) k = 12 m + 1 (α-β/positive sequence); (b) k = 12 m + 11 (α-β/negative sequence); (c) k = 12 m + 5 (z1-z2/positive sequence); (d) k = 12 m + 7 (z1-z2/negative sequence).
Equation (26a,b) are similar to the expressions for the synthetic MMF distribution in conventional 3-phase motors. The difference is that when the currents in the α-β subspace (see Table 1) are energized in a conventional 3-phase motor, the spatial orders included in the synthetic MMF are n = 1, 5, 7, 11, 13, ..., whereas in a dual 3-phase motor n = 1, 11, 13, … In the case of a dual 3-phase motor, n = 5, 7, ... are included in the MMF when the current in the z1-z2 subspace are energized (see (26c,d)).
4.3. Calculation of Inductance
The air gap magnetic flux density distribution is obtained by the following equation, where the permeance distribution density is :
Essentially, the permeance distribution density, depends on the shape of the slot and rotor. However, taking these into account complicates the calculation of . Since the purpose of this chapter is to formulate the inductance and , ignoring the inductance saliency, a simple model shown in Figure 5 is used to model . As shown in Figure 5, the shape of the rotor is assumed to be a disk without the inductance saliency and the air gap width δ is uniform regardless of the position. In this model, if the magnetic resistance and magnetic saturation of the steel plate are neglected, can be approximated as only the permeance distribution density in the gap area.
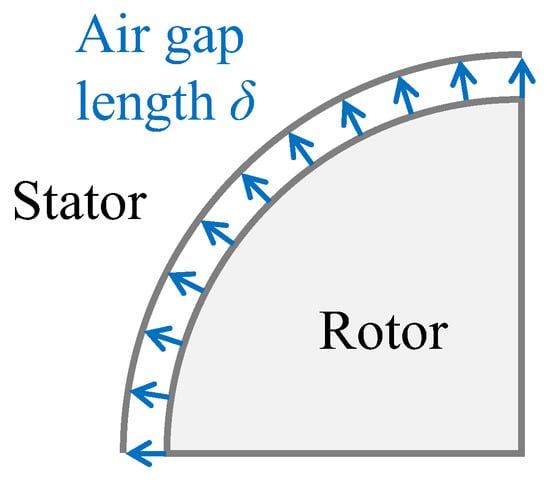
Figure 5.
Simplified model of permeance distribution.
The magnetic flux linked to the coil of one pole pair in phase i (i is one of U1, V1, W1, U2, V2, or W2), , is obtained by the following equation, noting that the coil pitch γ and the number of slots per pole per phase q are considered:
where l is the stack length, r is the stator inner diameter, and P is the number of pole pairs. Furthermore, is the phase of phase i and is:
where represents the phase of the xth coil of phase i.
In the following, P-pole pairs of coils are assumed to be connected in parallel number b. We substitute in (26a–d) and in (28) into (27) to obtain . Furthermore, we substitute into (29) to obtain the flux linkage in each phase. Furthermore, we use the orthogonal coordinate transformation matrix in (1) to transform the flux linkage in the α-β subspace and the z1-z2 subspace. The calculation results are shown in (31a–d).
- k = 1, 13, 25, …, 12 m + 1 (m = 0, 1, 2, …):
- 2.
- k = 11, 23, 35, …, 12 m + 11 (m = 0, 1, 2, …):
- 3.
- k = 5, 17, 29, …, 12 m + 5 (m = 0, 1, 2, …):
- 4.
- k = 7, 19, 31, …, 12 m + 7 (m = 0, 1, 2, …):
Here, in the mathematical model neglecting the inductance saliency, the flux linkage by the armature currents can be expressed from (22) as:
Therefore, by substituting the expressions for the kth harmonic currents shown in (6a–d) and the expressions for the flux linkage when the kth harmonic currents are energized, as shown in (31a–d) into (33), the inductances Lαβ and Lz1z2 in the α-β and z1-z2 subspaces are obtained as follows:
Lαβ and Lz1z2 for the coil pitch γ and the number of slots per pole per phase q are normalized by L and shown in Figure 6. From Figure 6, it can be confirmed that Lz1z2 is basically smaller than Lαβ regardless of the values of γ and q. The reason for this is that Equation (34a,b) are heavily influenced by the inverse of n2, with the former dominated by the term at n = 1 and the latter by the terms at n = 5 and 7.
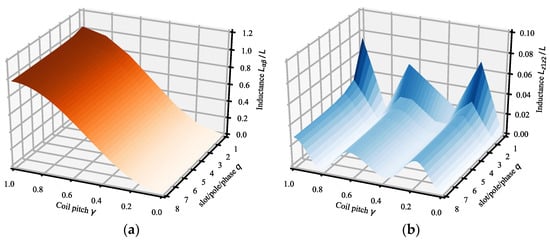
Figure 6.
Theoretical value of inductance for coil pitch γ, number of slots per pole per phase q: (a) in α-β subspace; (b) in z1-z2 subspace.
The magnitude of Lαβ depends on the winding factor kw1 for the first spatial order, and the magnitude of Lz1z2 depends on the winding factors kw5 and kw7 for the fifth and seventh spatial order. Figure 7 shows the pitch factor kpn for the coil pitch γ and Figure 8 shows the distribution factor kdn for the number of slots per pole per phase q. From Figure 6a, we can see that Lαβ is larger when the coil pitch γ is larger. From Figure 7, it can be seen that the trend of Lαβ is similar to that of the pitch factor kp1 for the 1st spatial order. The fact that Lαβ does not show much dependence on the number of slots per pole per phase q is also similar to that of the distribution factor kd1 for the 1st spatial order in Figure 8. On the other hand, Figure 6b shows that the magnitude of Lz1z2 has valleys around the coil pitch γ of 2/6 (=0.333) and 5/6 (=0.833) and peaks around 1/6 (=0.167), 4/6 (=0.667), and 1. From Figure 7, it can be seen that this trend is influenced by the pitch factors kp5 and kp7 for the 5th and 7th spatial order. Furthermore, the larger the number of slots per pole per phase q, the smaller Lz1z2 is, and this tendency is also similar to the distribution factors kd5 and kd7 for the 5th and 7th spatial order in Figure 8.
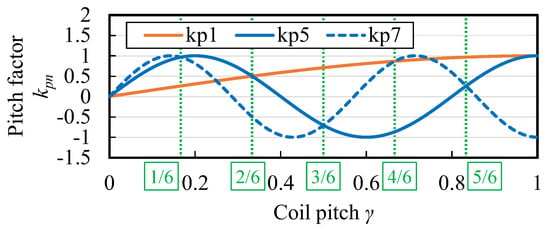
Figure 7.
Pitch factor kpn versus coil pitch γ.
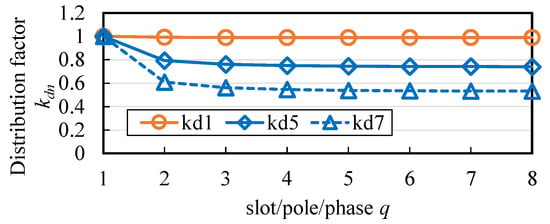
Figure 8.
Distribution factor kdn versus number of slots per pole per phase q.
As mentioned in Chapter 1, in order to reduce the harmonic currents during driving in a dual 3-phase motor, the inductance Lz1z2 in the z1-z2 subspace must be designed to be large. Figure 6b shows that Lz1z2 can be maximized when the coil pitch γ = 1 and the number of slots per pole per phase q = 1. On the other hand, the short-pitch winding with the coil pitch γ = 5/6, which is often used in conventional 3-phase motors, has small pitch factors kp5 and kp7, which means that the 5th and 7th order components of the back-EMF can be reduced when applied to a dual 3-phase motor, but at the same time Lz1z2 is also reduced.
5. Verification by Finite Element Analysis
To verify the validity of the theoretical inductance equations presented in (34a,b), comparisons were made between the theoretical and FEA values. The parameters of the motor for evaluation are shown in Table 2. Since the motor for evaluation is a dual 3-phase motor with 48-slots/8-poles, the number of slots per pole per phase is q = 1. The model used for FEA is shown in Figure 9. For the shape of the rotor, Ld, Lq, Ldz, and Lqz are obtained for the interior magnet model with the saliency in Figure 9a, and Lαβ and Lz1z2 are obtained for the disk model without the saliency in Figure 9b. The purpose of this is to confirm that the parameters Ld, Lq, Ldz, and Lqz, which take into account the inductance saliency, show the same trend as Lαβ and Lz1z2, which ignore the saliency. The analysis was performed for the cases of the coil pitch γ = 1/6, 2/6, 3/6, 4/6, 5/6, and 1, with a two-layer structure where two coils fit in one slot, as shown in Figure 9.

Table 2.
Parameters of motor for evaluation.
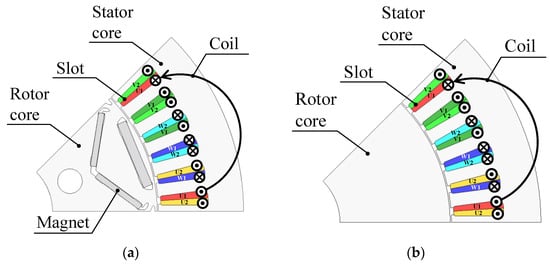
Figure 9.
Model used for FEA: (a) interior magnet rotor with the saliency; (b) disk rotor without the saliency.
Figure 10 shows a comparison of the theoretical and FEA values. Note that in the calculation of the theoretical values, the permeance distribution is given approximately as in (28) and the errors due to differences from the exact permeance of the FEA model are introduced. Therefore, the theoretical values of Lαβ and Lz1z2 in Figure 10 are multiplied by the correction factors Kαβ and Kz1z2, respectively, to the values calculated by (34a,b). From Figure 10, the theoretical values of Lαβ and Lz1z2 are in good agreement with the FEA values. Figure 10a also shows that Lαβ and Lq are close to each other. This is because Lαβ obtained using the model in Figure 9b is the ideal q-axis inductance. On the other hand, Ld is smaller than Lαβ because the magnetic resistance of the d-axis magnetic path is larger due to the presence of the magnet region. Figure 10b also shows that Ldz and Lqz are not affected by the saliency and are consistent with Lz1z2. These results confirm the validity of the theoretical inductance equations presented in (34a,b). It was also confirmed that the inductance values Ld, Lq, Ldz, and Lqz, which take into account the saliency, show the same tendency as the inductance values Lαβ and Lz1z2, which ignore the saliency.
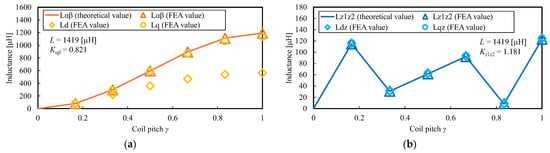
Figure 10.
Comparison of theoretical and FEA values of inductance: (a) in α-β subspace; (b) in z1-z2 subspace.
6. Verification by Circuit Simulation
In this chapter, the magnitude of the harmonic currents is studied by a simulation of the IPMSM drive. The magnitude of the harmonic component superimposed on the current obtained from this simulation is quantitatively evaluated using the inductance Lαβ and Lz1z2 in the α-β and z1-z2 subspaces.
6.1. Simulation Method
Figure 11 shows the simulation configuration. In this simulation, the controller and ideal voltage-source inverter are implemented in the circuit simulator (MATLAB/Simulink), and the voltage and currents are inputted and outputted to the FEA model of the IPMSM (JMAG). The parameters of the IPMSM model are the same as in Table 2, and the shape of the rotor is the same as in Figure 9a. In this chapter, simulations are performed for coil pitch γ = 5/6 and 1.
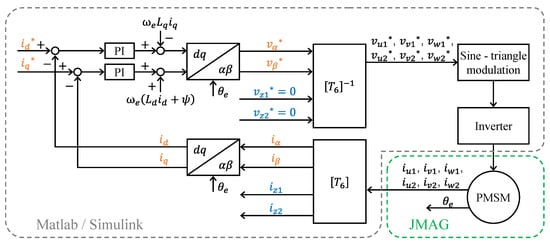
Figure 11.
Simulation configuration.
Next, the control configuration is described. As shown in Figure 11, PI control was applied to the fundamental superimposed on the α-β subspace. In this simulation, the harmonic currents are not controlled for the purpose of obtaining the magnitude of the generated harmonic currents. Therefore, the cutoff frequency of the controller is determined so that the voltage applied to the motor is sinusoidal. For the z1-z2 subspace, where the 5th and 7th order harmonics are superimposed, open-loop control was used with voltage reference values vz1* = 0 and vz2* = 0. The drive conditions are shown in Table 3.

Table 3.
Drive conditions.
6.2. Simulation Results
As simulation results, the waveforms of the phase U1 currents and the FFT results are shown in Figure 12 and Figure 13, respectively. The α-axis and z1-axis currents were calculated using (2), and the FFT results are shown in Figure 14. In Figure 13 and Figure 14, the kf [Hz] component on the horizontal axis indicates the kth harmonic component, and the fc ± 2f and 2fc ± f [Hz] components indicate the carrier harmonic sideband components. From Figure 12 and Figure 13, it can be seen that the phase currents contain large harmonic components for both coil pitch γ = 5/6 and 1. For the coil pitch γ = 1, the phase currents contain mainly 5th and 7th harmonics. At coil pitch γ = 5/6, in addition to the 5th and 7th harmonics, the phase currents also contain large fc ± 2f [Hz] components. Figure 14 shows that these large harmonic components are decomposed into the z1-z2 subspace by the orthogonal coordinate transformation.
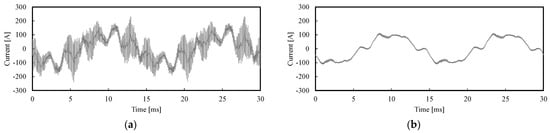
Figure 12.
Waveforms of phase U1 currents: (a) Coil pitch γ = 5/6; (b) Coil pitch γ = 1.
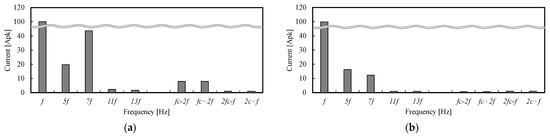
Figure 13.
FFT results of phase U1 currents: (a) Coil pitch γ = 5/6; (b) Coil pitch γ = 1.
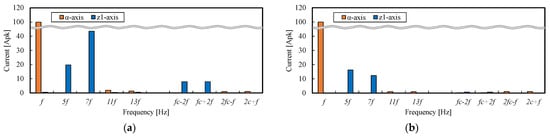
Figure 14.
FFT results of α-axis and z1-axis currents: (a) Coil pitch γ = 5/6; (b) Coil pitch γ = 1.
6.3. Consideration of the Relationship between the Magnitude of Harmonic Currents and Inductance Value
The voltage equation in the stationary orthogonal subspace shown in (22), which ignores the inductance saliency, is used. In (22), the left side corresponds to the voltage applied by the inverter and the second term on the right side corresponds to the back-EMF by the permanent magnet. Therefore, in the α-β and z1-z2 subspaces, respectively, Equation (22) can be regarded as an RL circuit with the applied voltage by the inverter and the back-EMF by the permanent magnet as the voltage input, and and as the current output. Here, the impedance, which is the ratio of the voltage and currents, is expressed by the following equation:
where ω is an arbitrary angular frequency. Figure 15 shows the frequency characteristics of Zαβ(ω) and Zz1z2(ω). From Figure 15, it can be seen that the impedance Zz1z2(ω) is small even in the high frequency band, basically due to the inductance Lz1z2 being smaller than Lαβ, regardless of the coil pitch γ. This results in large harmonic currents in the z1-z2 subspace even when the harmonic components in the voltage input of the z1-z2 subspace are small.
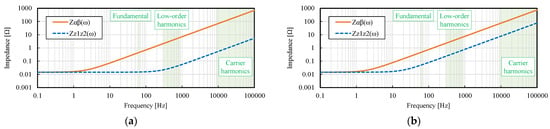
Figure 15.
Frequency characteristic of impedance in α-β and z1-z2 subspaces: (a) Coil pitch γ = 5/6; (b) Coil pitch γ = 1.
First, we discussed the cause of the excessive carrier harmonic currents (fc ± 2f [Hz] component) in the z1-z2 subspace for γ = 5/6 in Figure 14a. The FFT results of the applied voltage by the inverter are shown in Figure 16. From Figure 16, we see that for both γ = 5/6 and 1, the fc ± 2f [Hz] component is included in the z1-z2 subspace. On the other hand, Figure 15a shows that the impedance Zz1z2(ω) around fc ± 2f [Hz] for γ = 5/6 is very small, about 1 [Ω], despite the high frequency. This is thought to cause large harmonic currents at the corresponding frequencies.
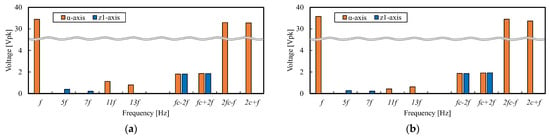
Figure 16.
FFT results of applied voltage by the inverter: (a) Coil pitch γ = 5/6; (b) Coil pitch γ = 1.
Next, we discussed the reason why the 5th and 7th harmonic currents are larger for the coil pitch γ = 5/6 than for the coil pitch γ = 1. The FFT results of the no-load back-EMF are shown in Figure 17. Figure 17 shows that for coil pitch γ = 5/6, the 5th and 7th harmonic components of the back-EMF are smaller than for γ = 1. This is because, in general, the 5th and 7th harmonic components of the back-EMF can be reduced by a factor of |kp5/5| and |kp7/7| for the winding with the coil pitch γ, and, as shown in Figure 7, the pitch factors kp5 and kp7 are particularly small when γ = 5/6. On the other hand, from Figure 15, the impedance Zz1z2(ω) for γ = 5/6 is about 1/10 of that for γ = 1 in the 5th and 7th harmonic frequency bands. This is because, from (34b), the magnitude of the inductance Lz1z2 is strongly influenced by (kp5/5)2 and (kp7/7)2. Therefore, for the coil pitch γ = 5/6, even though the 5th and 7th harmonic components of the no-load back-EMF can be smaller than for γ = 1, the inductance Lz1z2 decrease is more dominant, and large 5th and 7th harmonic currents are generated.
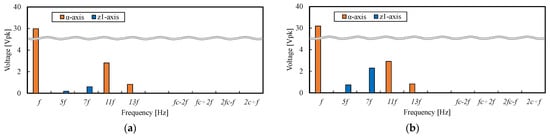
Figure 17.
FFT results of the no-load back-EMF: (a) Coil pitch γ = 5/6; (b) Coil pitch γ = 1.
7. Conclusions
In this paper, the inductance in the α-β and z1-z2 subspaces for dual 3-phase motors, which varies depending on the winding structure, was formulated. The validity of the formulated inductance was confirmed by FEA. Furthermore, using these inductance values, it was clarified that the magnitude of the generated harmonic currents could be quantitatively explained. In conclusion, it was theoretically shown that dual 3-phase motors with large winding factors for 5th and 7th spatial harmonics have a relatively large inductance in the z1-z2 subspace, which can reduce the harmonic currents.
Author Contributions
Writing—original draft, A.Y.; Writing—review & editing, K.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, Y.; Lipo, T.A. Space vector PWM control of dual three-phase induction machine using vector space decomposition. IEEE Trans. Ind. Appl. 1995, 31, 1100–1109. [Google Scholar] [CrossRef]
- Marouani, K.; Baghli, L.; Hadiouche, D.; Kheloui, A.; Rezzoug, A. A New PWM Strategy Based on a 24-Sector Vector Space Decomposition for a Six-Phase VSI-Fed Dual Stator Induction Motor. IEEE Trans. Ind. Electron. 2008, 55, 1910–1920. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, Z.Q.; Qi, J.; Ren, Y.; Gan, C.; Brockway, S.; Hilton, C. Suppression of Major Current Harmonics for Dual Three-Phase PMSMs by Virtual Multi Three-Phase Systems. IEEE Trans. Ind. Electron. 2022, 69, 5478–5490. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, Z.; Liu, K. Current Control for Dual Three-Phase Permanent Magnet Synchronous Motors Accounting for Current Unbalance and Harmonics. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 272–284. [Google Scholar]
- Hu, Y.; Zhu, Z.Q.; Odavic, M. Comparison of Two-Individual Current Control and Vector Space Decomposition Control for Dual Three-Phase PMSM. IEEE Trans. Ind. Appl. 2017, 53, 4483–4492. [Google Scholar] [CrossRef]
- Hadiouche, D.; Razik, H.; Rezzoug, A. On the modeling and design of dual-stator windings to minimize circulating harmonic currents for VSI fed AC machines. IEEE Trans. Ind. Appl. 2004, 40, 506–515. [Google Scholar] [CrossRef]
- Ye, D.; Li, J.; Qu, R.; Jiang, D.; Xiao, L.; Lu, Y.; Chen, J. Variable Switching Sequence PWM Strategy of Dual Three-Phase Machine Drive for High-Frequency Current Harmonic Suppression. IEEE Trans. Power Electron. 2020, 35, 4984–4995. [Google Scholar] [CrossRef]
- Kallio, S.; Andriollo, M.; Tortella, A.; Karttunen, J. Decoupled d-q Model of Double-Star Interior-Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2013, 60, 2486–2494. [Google Scholar] [CrossRef]
- Okajima, Y.; Akatsu, K. Complex Vector form PI Control for Harmonic Current Control of a PMSM. IEEJ Trans. Ind. Appl. 2017, 137, 238–245. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).