Dynamic Performance Enhancement of a Direct-Driven PMSG-Based Wind Turbine Using a 12-Sectors DTC
Abstract
:1. Introduction
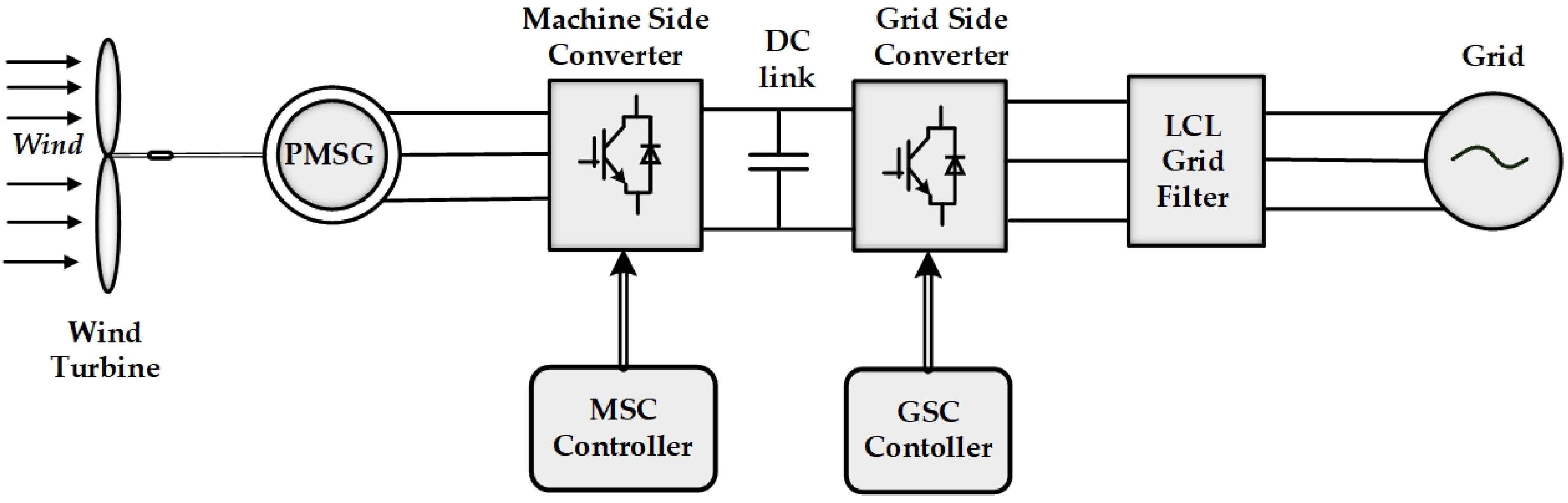
2. WECS System Modeling
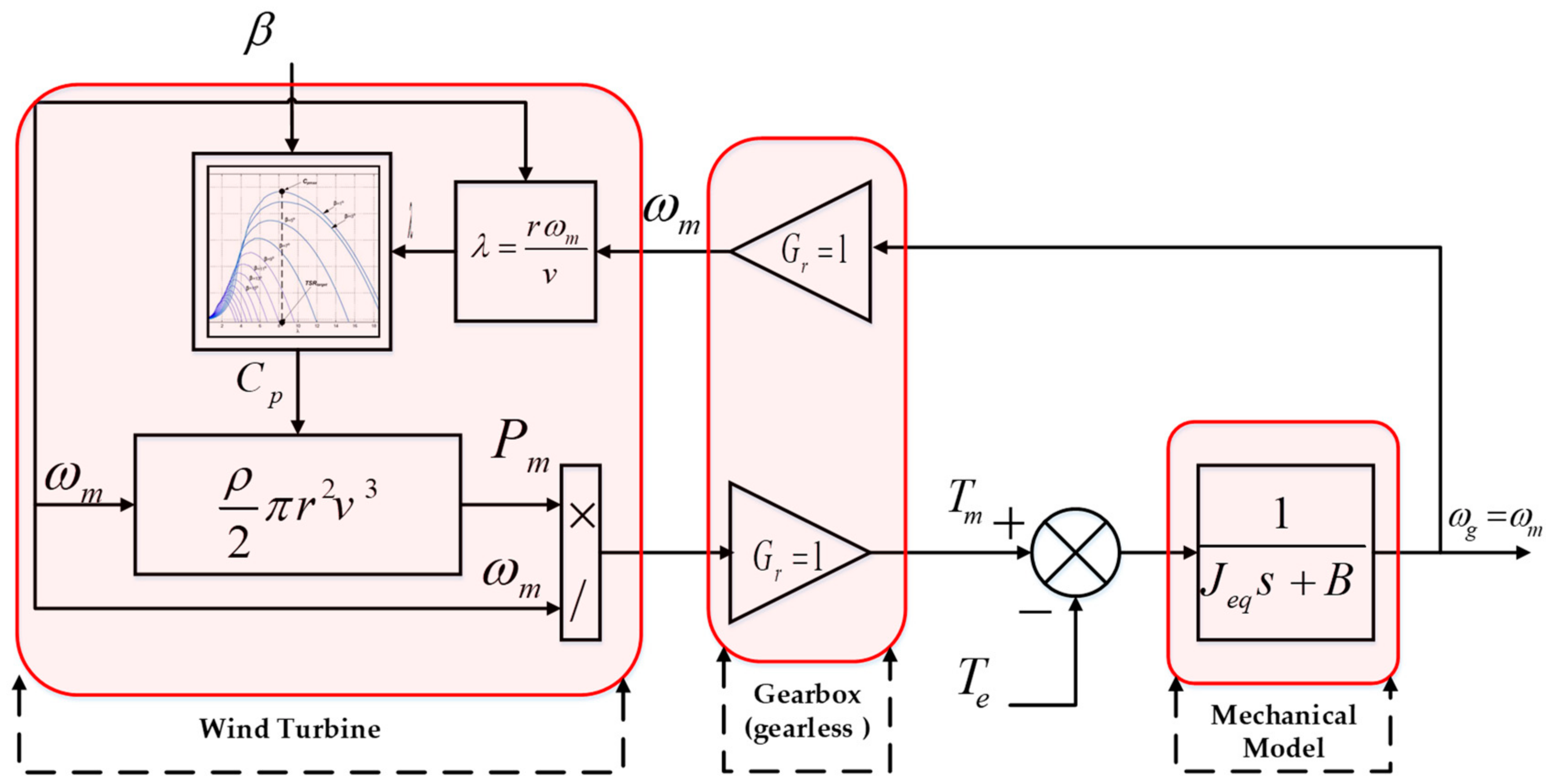
2.1. Mechanical Model of a Wind Turbine
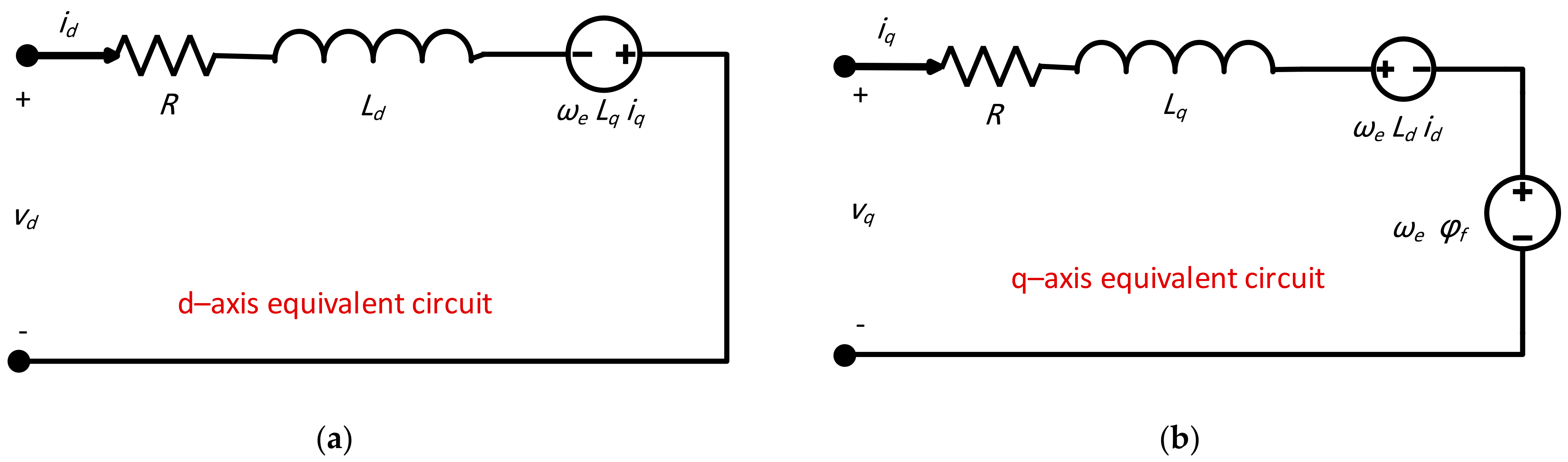
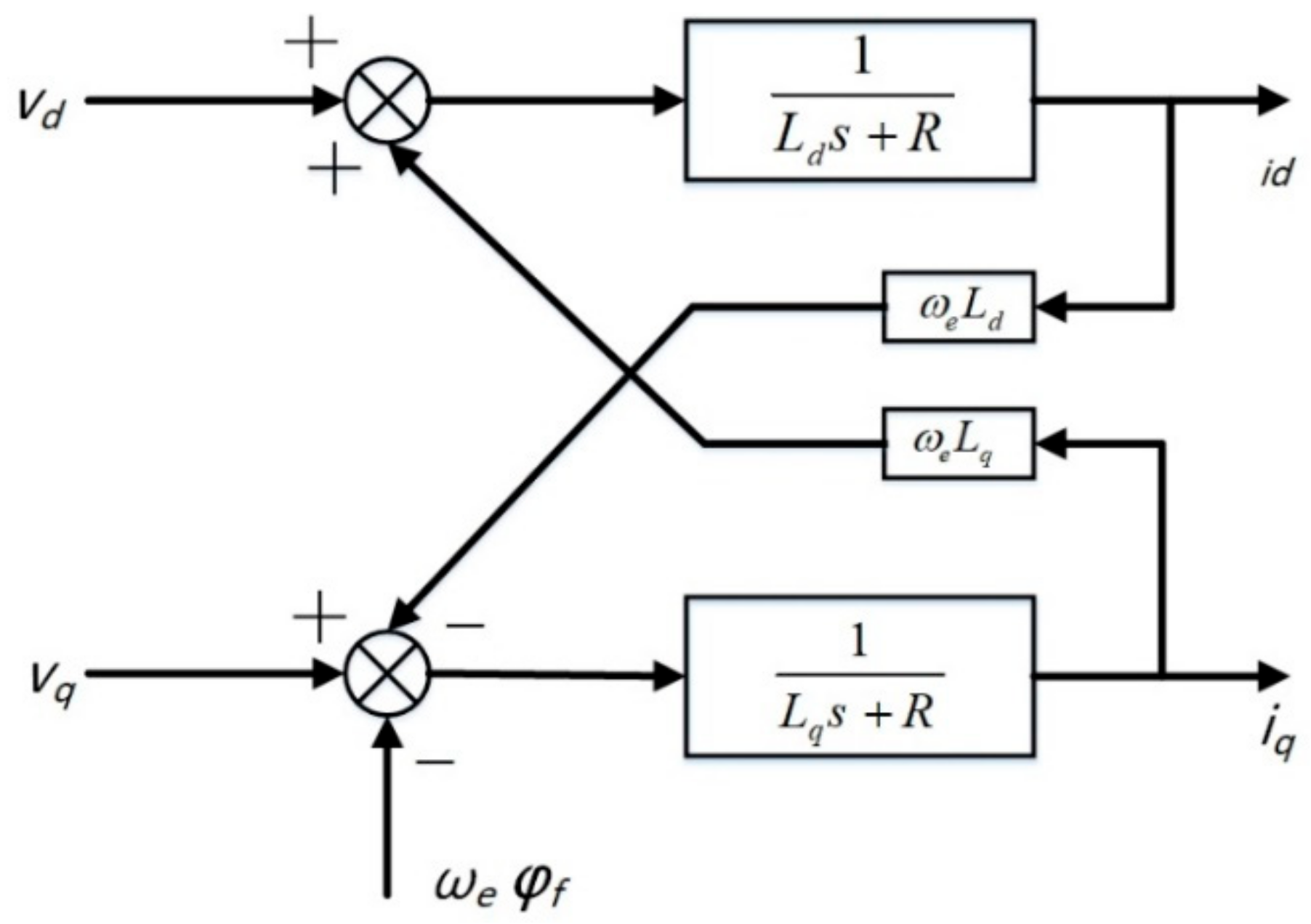
2.2. PMSG Modeling
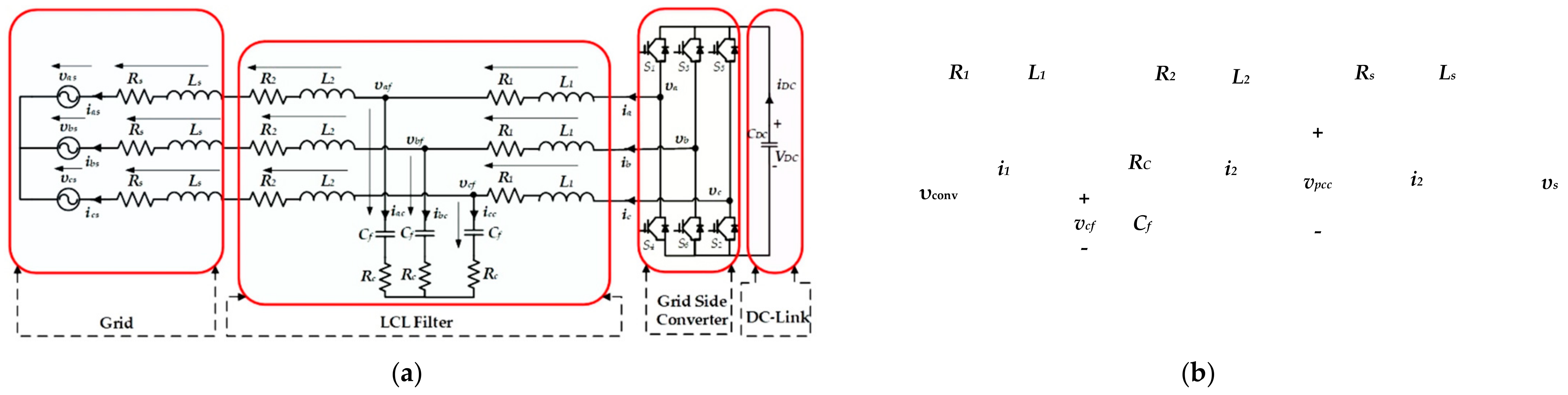
2.3. LCL Filter
2.3.1. Two-Level Converter with LCL Filter
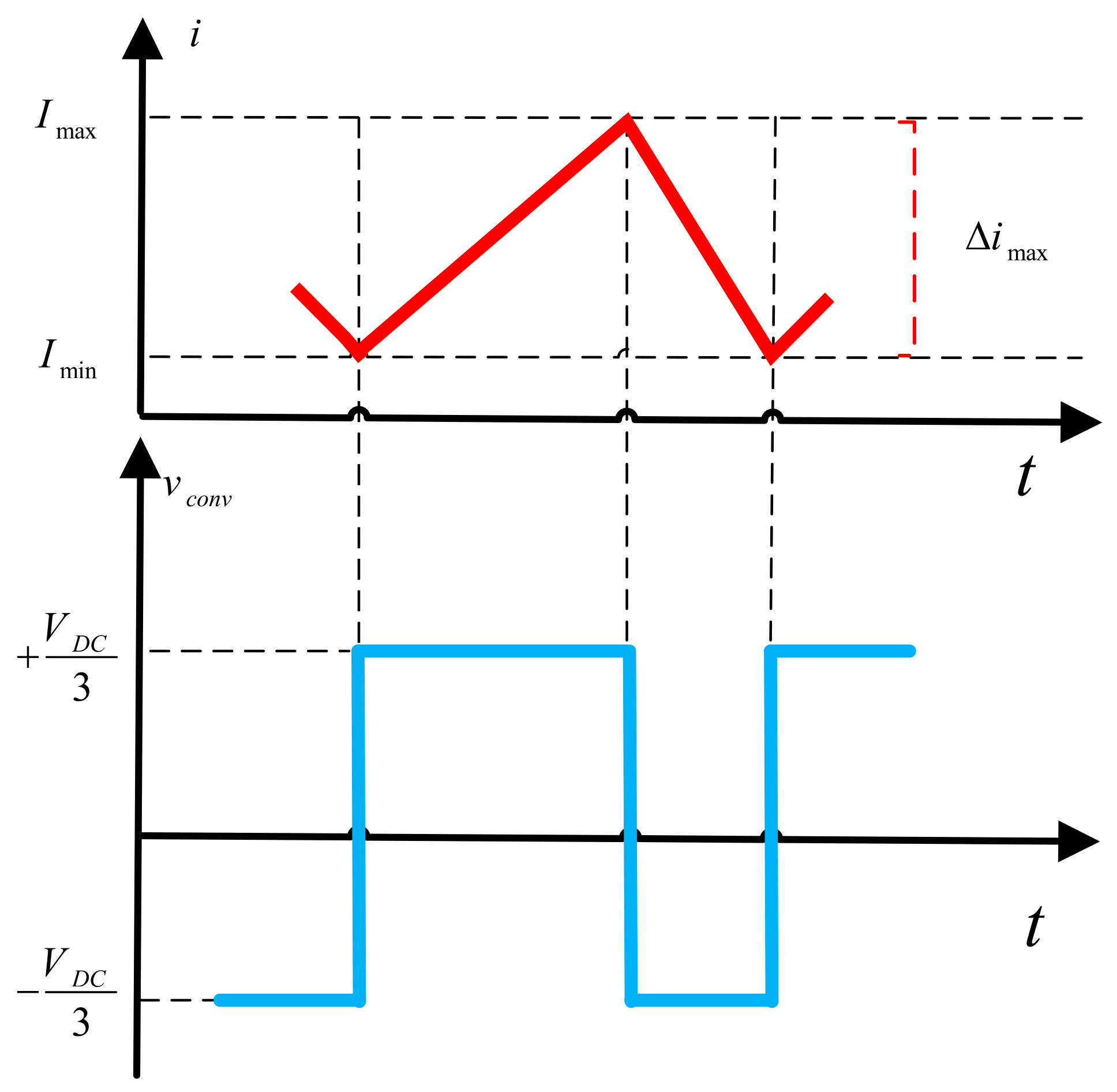
2.3.2. Filter Parameters Design
- The converter-side inductor was calculated based on the desired current ripple attenuation;
- The filter capacitance (Cf) was designed based on the filter’s resonance frequency;
- The capacitor series resistance (Rc) was selected based on the required damping factor.
2.4. Modeling of the DC Link
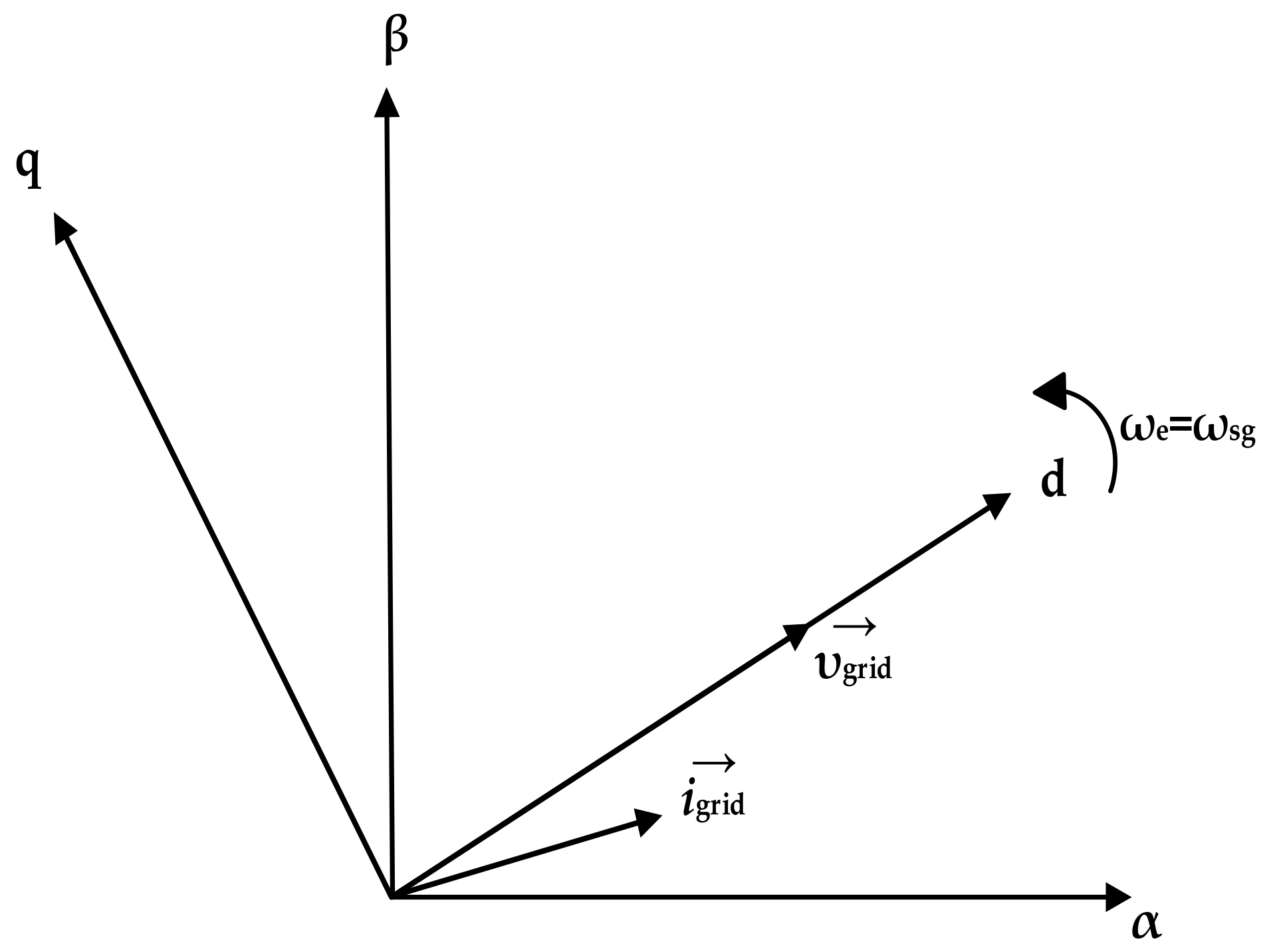
3. Control of the GSC
4. Direct Torque Control (DTC)
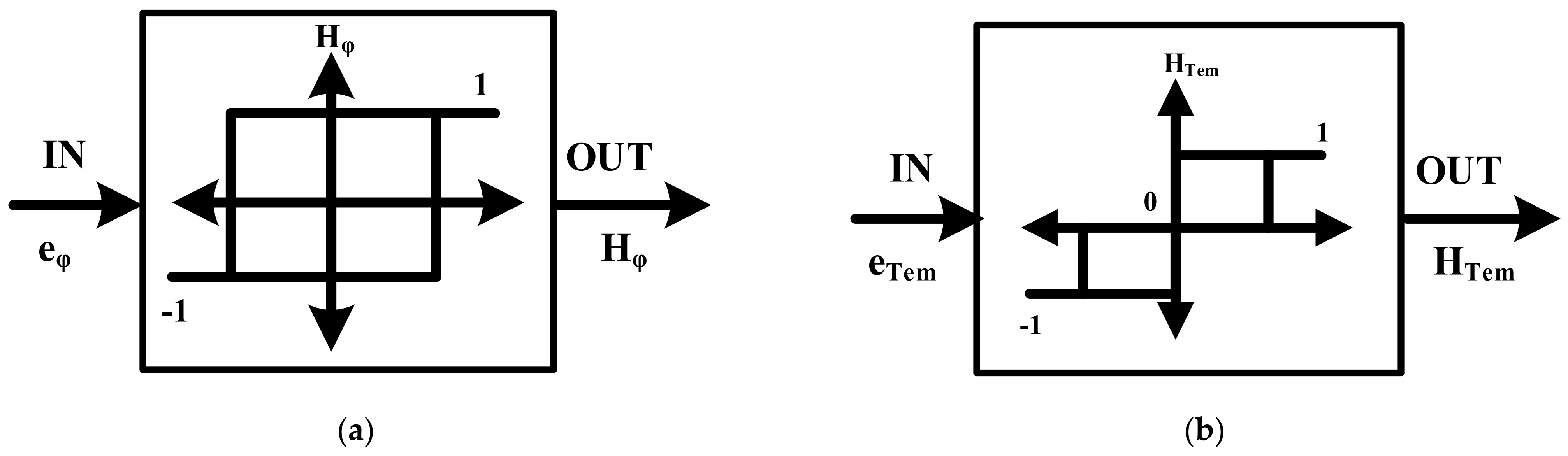
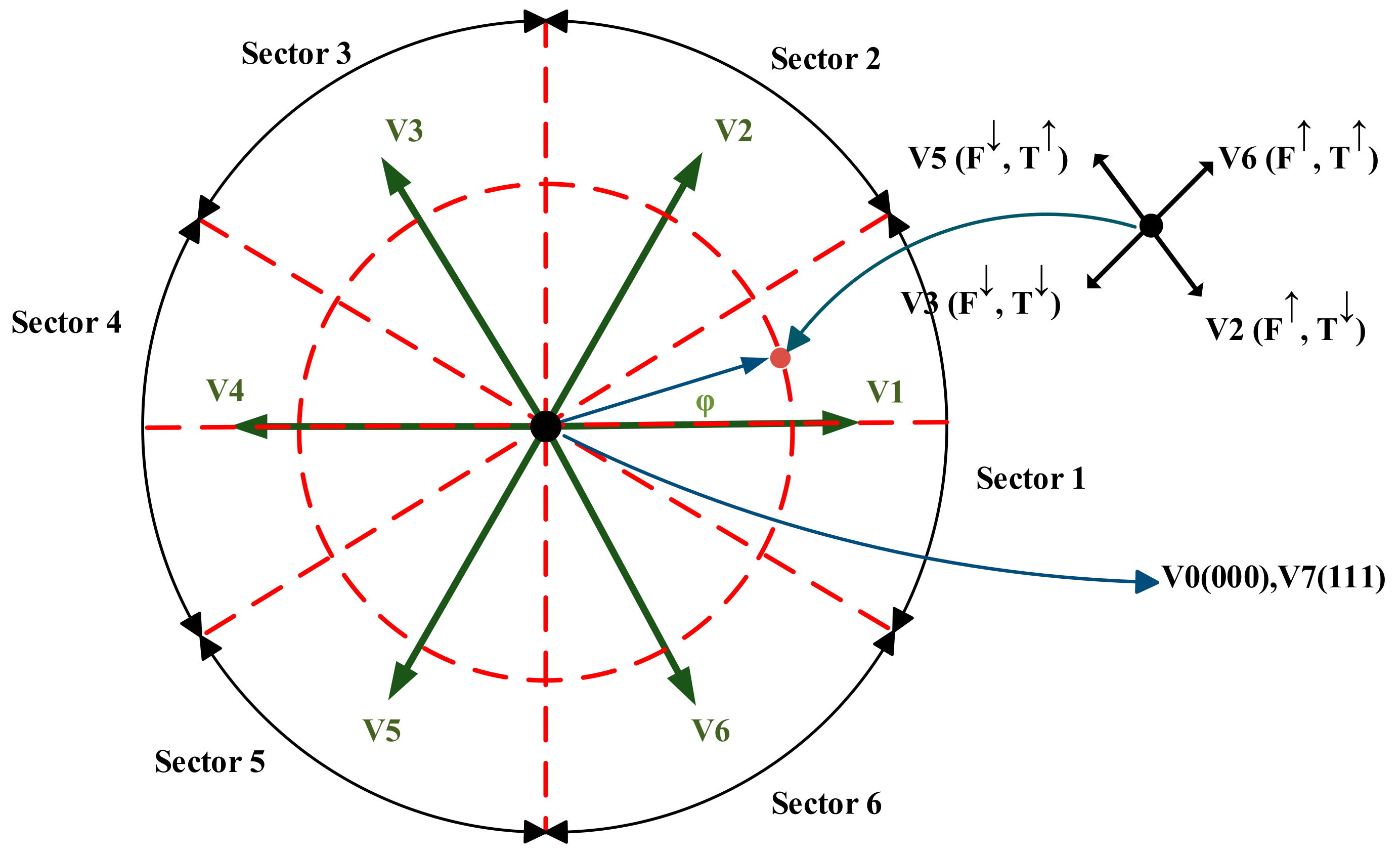
4.1. Conventional 6-Sectors DTC
4.2. Torque and Flux Reference Values Definition
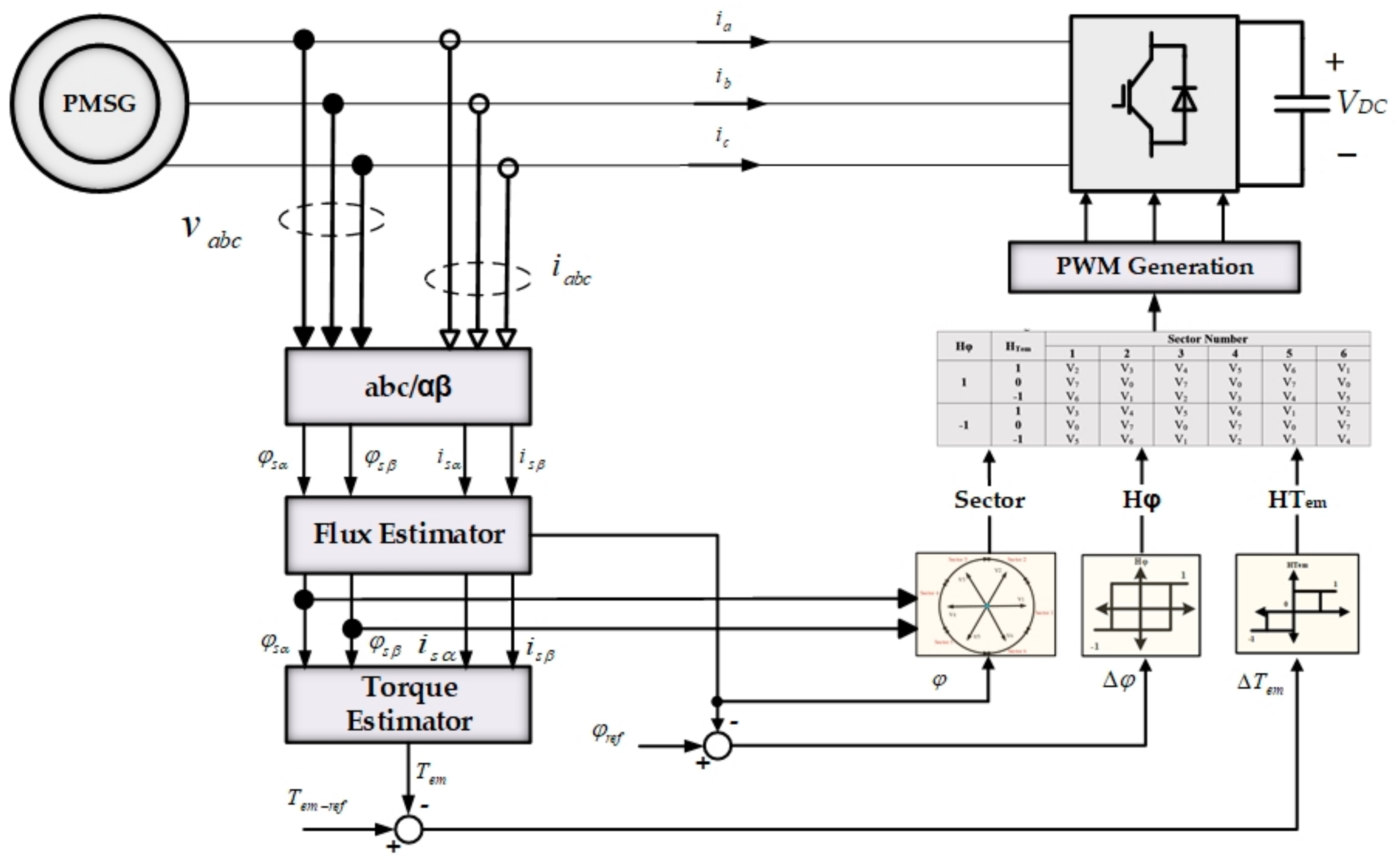
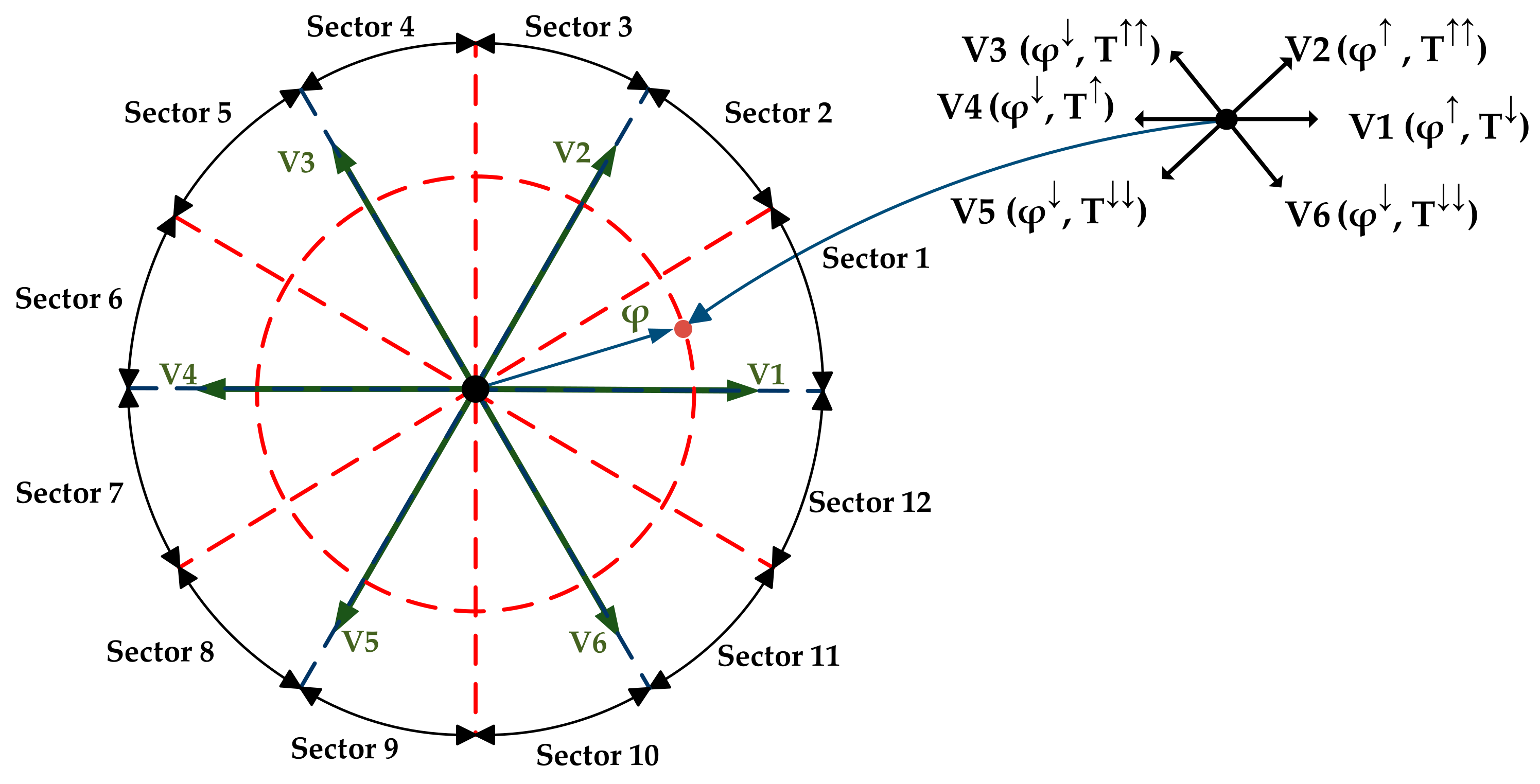
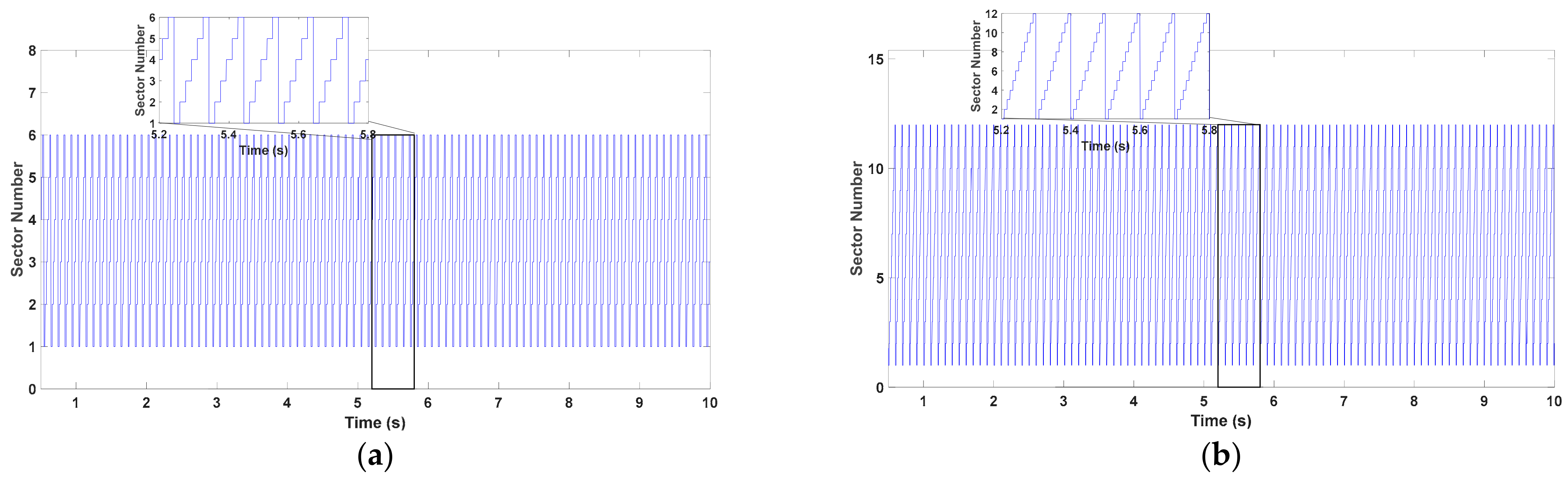
4.3. Proposed 12-Sectors DTC of the PMSG
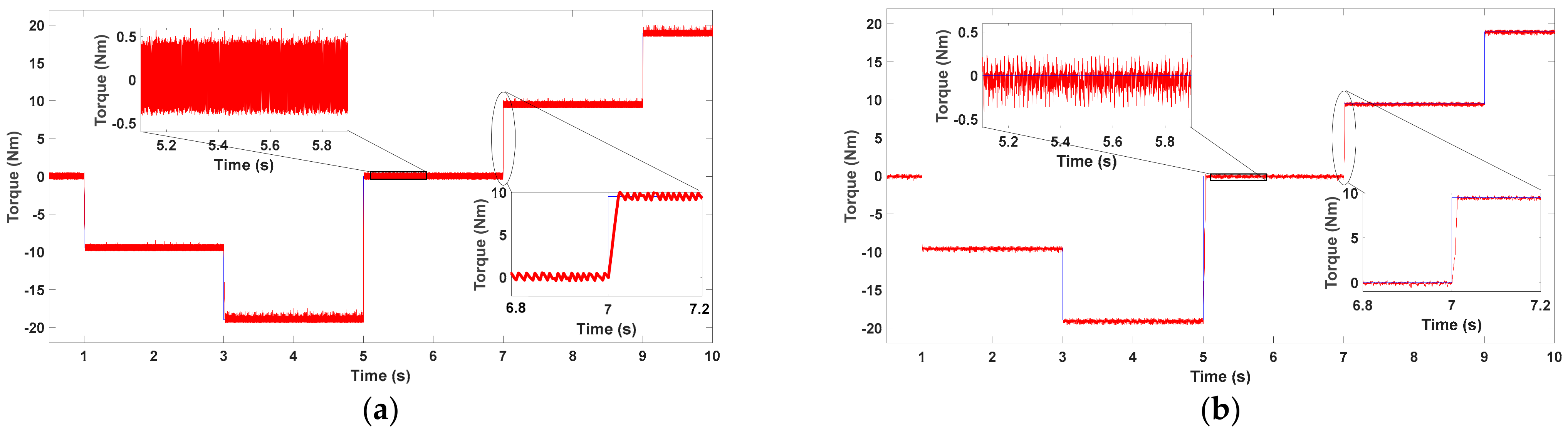
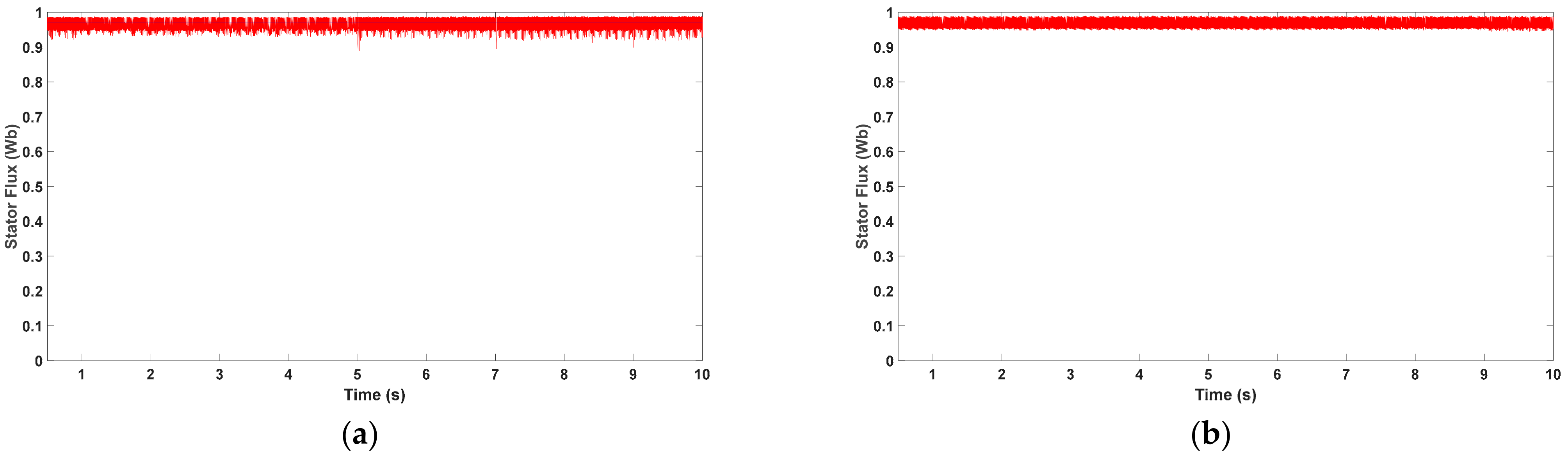
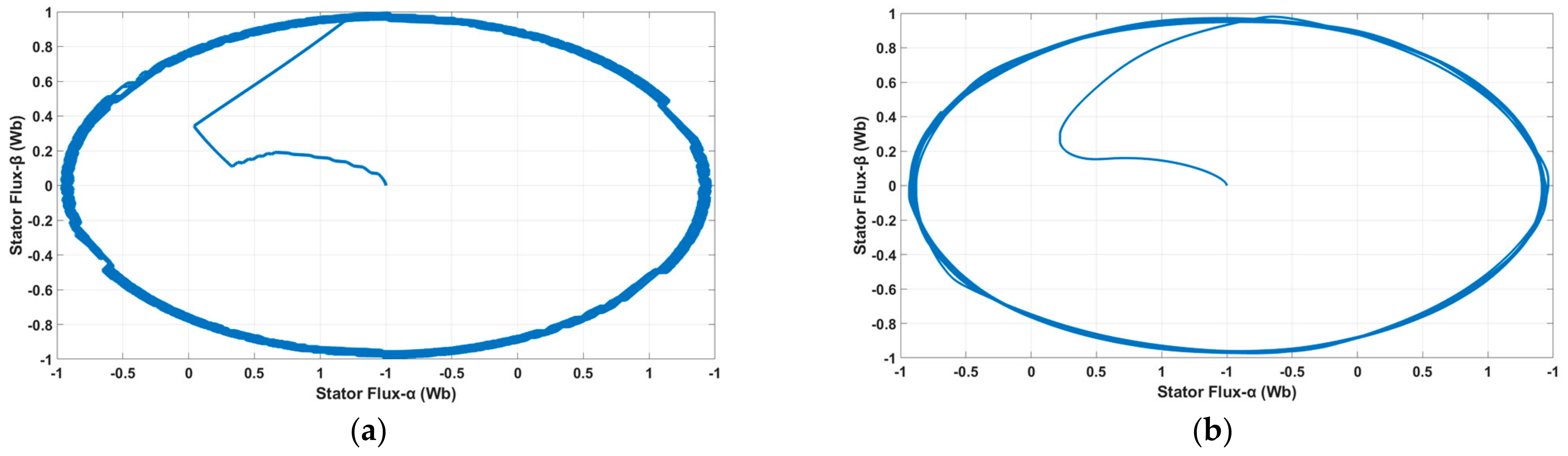
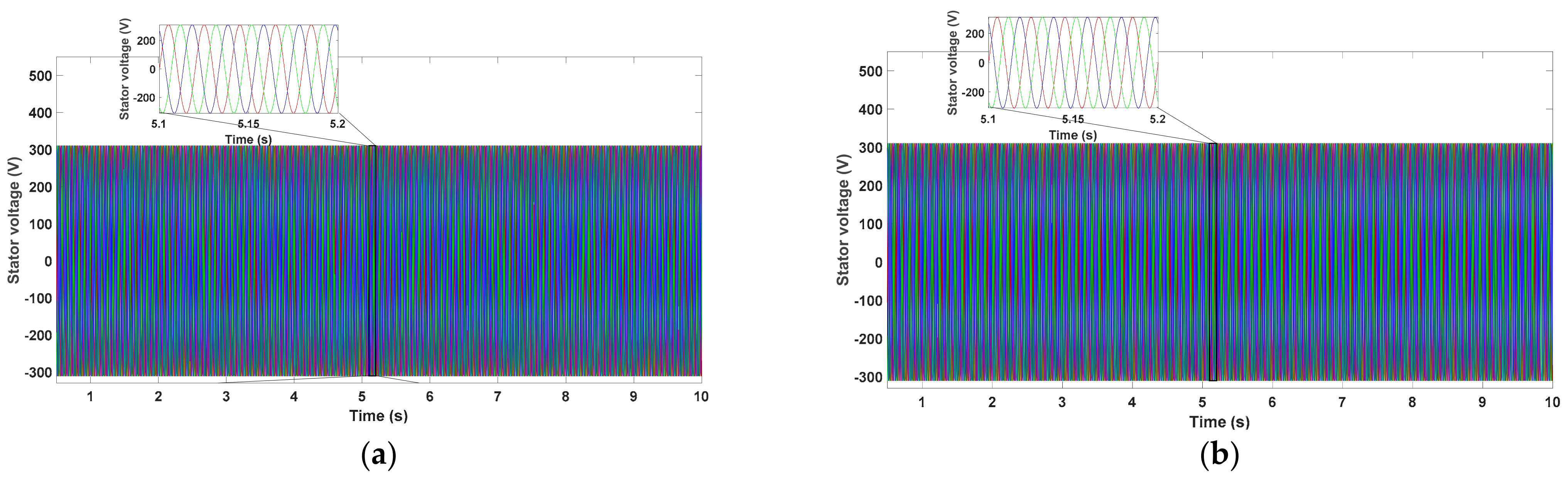
5. Results and Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rasul, M.G.; Azad, A.K.; Sharma, S.C. Clean Energy for Sustainable Development Comparisons and Contrasts of New Approaches; Academic Press is an imprint of Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-805423-9. [Google Scholar]
- Polinder, H.; van der Pijl, F.; de Vilder, G.-J.; Tavner, P.J. Comparison of Direct-Drive and Geared Generator Concepts for Wind Turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Xu, D.; Ji, J.; Zhao, W.; Jiang, Q. Field-oriented control and direct torque control for a five-phase fault-tolerant flux-switching permanent-magnet motor. Chin. J. Electr. Eng. 2018, 4, 48–56. [Google Scholar] [CrossRef]
- Busca, C.; Stan, A.-I.; Stanciu, T.; Stroe, D.I. Control of Permanent Magnet Synchronous Generator for large wind turbines. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics (ISIE 2010), Bari, Italy, 4 July 2010–7 July 2010; pp. 3871–3876. [Google Scholar]
- Abosh, A.H.; Zhu, Z.Q.; Ren, Y. Reduction of Torque and Flux Ripples in Space Vector Modulation-Based Direct Torque Control of Asymmetric Permanent Magnet Synchronous Machine. IEEE Trans. Power Electron. 2017, 32, 2976–2986. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, J.-W.; Park, B.-G.; Lee, D.-H. A Novel Predictive Direct Torque Control Using an Optimized PWM Approach. IEEE Trans. Ind. Appl. 2021, 57, 2537–2546. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, X.; Yang, S.; Xie, Z.; Wang, L.; Cao, R. Simplified model predictive direct torque control method without weighting factors for permanent magnet synchronous generator-based wind power system. IET Electr. Power Appl. 2017, 11, 793–804. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model Predictive Direct Torque Control With Finite Control Set for PMSM Drive Systems, Part 1: Maximum Torque Per Ampere Operation. IEEE Trans. Ind. Inf. 2013, 9, 1912–1921. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Predictive Control of a Three-Level Boost Converter and an NPC Inverter for High-Power PMSG-Based Medium Voltage Wind Energy Conversion Systems. IEEE Trans. Power Electron. 2014, 29, 5308–5322. [Google Scholar] [CrossRef]
- Golnary, F.; Moradi, H. Dynamic modelling and design of various robust sliding mode controls for the wind turbine with estimation of wind speed. Appl. Math. Model. 2019, 65, 566–585. [Google Scholar] [CrossRef]
- Beltran, B.; Benbouzid, M.E.H.; Ahmed-Ali, T. Second-Order Sliding Mode Control of a Doubly Fed Induction Generator Driven Wind Turbine. IEEE Trans. Energy Convers. 2012, 27, 261–269. [Google Scholar] [CrossRef] [Green Version]
- Do, T.D. Disturbance Observer-Based Fuzzy SMC of WECSs Without Wind Speed Measurement. IEEE Access 2017, 5, 147–155. [Google Scholar] [CrossRef]
- Watil, A.; El Magri, A.; Raihani, A.; Lajouad, R.; Giri, F. Multi-objective output feedback control strategy for a variable speed wind energy conversion system. Int. J. Electr. Power Energy Syst. 2020, 121, 106081. [Google Scholar] [CrossRef]
- Errami, Y.; Ouassaid, M.; Maaroufi, M. A performance comparison of a nonlinear and a linear control for grid connected PMSG wind energy conversion system. Int. J. Electr. Power Energy Syst. 2015, 68, 180–194. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, F.; Si, G.; Kennel, R. Predictive encoderless control of back-to-back converter PMSG wind turbine systems with Extended Kalman Filter. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5 December 2016–8 December 2016; pp. 1–7. [Google Scholar]
- Mousa, H.H.; Youssef, A.-R.; Mohamed, E.E. Hybrid and adaptive sectors P&O MPPT algorithm based wind generation system. Renew. Energy 2020, 145, 1412–1429. [Google Scholar] [CrossRef]
- Shang, L.; Hu, J. Sliding-Mode-Based Direct Power Control of Grid-Connected Wind-Turbine-Driven Doubly Fed Induction Generators Under Unbalanced Grid Voltage Conditions. IEEE Trans. Energy Convers. 2012, 27, 362–373. [Google Scholar] [CrossRef]
- Toumi, I.; Meghni, B.; Hachana, O.; Azar, A.T.; Boulmaiz, A.; Humaidi, A.J.; Ibraheem, I.K.; Kamal, N.A.; Zhu, Q.; Fusco, G.; et al. Robust Variable-Step Perturb-and-Observe Sliding Mode Controller for Grid-Connected Wind-Energy-Conversion Systems. Entropy 2022, 24, 731. [Google Scholar] [CrossRef]
- Fateh, F.; White, W.N.; Gruenbacher, D. A Maximum Power Tracking Technique for Grid-Connected DFIG-Based Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 957–966. [Google Scholar] [CrossRef]
- Abdellatif, W.S.E.; Hamada, A.M.; Abdelwahab, S.A.M. Wind speed estimation MPPT technique of DFIG-based wind turbines theoretical and experimental investigation. Electr Eng 2021, 103, 2769–2781. [Google Scholar] [CrossRef]
- Nasiri, M.; Milimonfared, J.; Fathi, S.H. A review of low-voltage ride-through enhancement methods for permanent magnet synchronous generator based wind turbines. Renew. Sustain. Energy Rev. 2015, 47, 399–415. [Google Scholar] [CrossRef]
- Ashourianjozdani, M.; Lopes, L.A.C.; Pillay, P. Power Electronic Converter Based PMSG Emulator: A Testbed for Renewable Energy Experiments. IEEE Trans. Ind. Applicat. 2018, 54, 3626–3636. [Google Scholar] [CrossRef]
- Prakash, M.; Joo, Y.-H. Fuzzy Event-triggered Control for Back to Back Converter involved PMSG-based Wind Turbine Systems. IEEE Trans. Fuzzy Syst. 2021, 30, 1409–1420. [Google Scholar] [CrossRef]
- Said-Romdhane, M.; Naouar, M.; Belkhodja, I.; Monmasson, E. An Improved LCL Filter Design in Order to Ensure Stability without Damping and Despite Large Grid Impedance Variations. Energies 2017, 10, 336. [Google Scholar] [CrossRef] [Green Version]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems. Wiley: Chichester, UK, 2011; ISBN 047066 7052. [Google Scholar]
- Reznik, A.; Simoes, M.G.; Al-Durra, A.; Muyeen, S.M. LCL Filter Design and Performance Analysis for Grid-Interconnected Systems. IEEE Trans. Ind. Appl. 2014, 50, 1225–1232. [Google Scholar] [CrossRef]
- Lu, M.; Al-Durra, A.; Muyeen, S.M.; Leng, S.; Loh, P.C.; Blaabjerg, F. Benchmarking of Stability and Robustness Against Grid Impedance Variation for LCL -Filtered Grid-Interfacing Inverters. IEEE Trans. Power Electron. 2018, 33, 9033–9046. [Google Scholar] [CrossRef] [Green Version]
- Sanatkar-Chayjani, M.; Monfared, M. Design of LCL and LLCL filters for single-phase grid connected converters. IET Power Electron. 2016, 9, 1971–1978. [Google Scholar] [CrossRef] [Green Version]
- Xue, C.; Zhou, D.; Li, Y. Hybrid Model Predictive Current and Voltage Control for LCL-Filtered Grid-Connected Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5747–5760. [Google Scholar] [CrossRef]
- Rockhill, A.A.; Liserre, M.; Teodorescu, R.; Rodriguez, P. Grid-Filter Design for a Multimegawatt Medium-Voltage Voltage-Source Inverter. IEEE Trans. Ind. Electron. 2011, 58, 1205–1217. [Google Scholar] [CrossRef] [Green Version]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Zhan, P.; Lin, W.; Wen, J.; Yao, M.; Li, N. Design of LCL filters for the back-to-back converter in a Doubly Fed Induction Generator. In Proceedings of the IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Tianjin, China, 21 May 2012–24 May 2012; pp. 1–2. [Google Scholar]
- Bansal, R.C. Handbook of Distributed Generation: Electric Power Technologies, Economics and Environmental Impacts; Ramesh, B., Ed.; Springer: Cham, Switzerland, 2017; ISBN 9783319513430. [Google Scholar]
- Xu, D.a.; Xu, D.; Blaabjerg, F.; Chen, W.; Zhu, N. Modelling and Control of Doubly Fed Induction Generator Wind Power System under Non-Ideal Grid, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2016; ISBN 978-1-119-17208-6. [Google Scholar]
- Al-Quteimat, A. Control Layout of Doubly Fed Induction Generator with Respect to Low Voltage Ride through for Wind Energy Conversion System. 2018. Available online: https://depositonce.tu-berlin.de//handle/11303/8209 (accessed on 1 February 2022). [CrossRef]
- Xu, Z.; Rahman, M.F. Direct torque and flux regulation of an IPM synchronous motor drive using variable structure control approach. In Proceedings of the IECON 2004, 30th Annual Conference of the IEEE Industrial Electronics Society, Busan, South Korea, 2–6 November 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 2487–2498. [Google Scholar]
- Rahman, M.F.; Zhong, L.; Lim, K.W. A direct torque-controlled interior permanent magnet synchronous motor drive incorporating field weakening. IEEE Trans. Ind. Appl. 1998, 34, 1246–1253. [Google Scholar] [CrossRef]
- Al-Quteimat, A.; Roccaforte, A.; Schafer, U. Performance improvement of direct torque control for doubly fed induction generator with 12 sector methodology. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 242–246. [Google Scholar] [CrossRef]




| Hφ | HTem | Sector Number | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 1 | V2 | V3 | V4 | V5 | V6 | V1 |
| 0 | V7 | V0 | V7 | V0 | V7 | V0 | |
| −1 | V6 | V1 | V2 | V3 | V4 | V5 | |
| −1 | 1 | V3 | V4 | V5 | V6 | V1 | V2 |
| 0 | V0 | V7 | V0 | V7 | V0 | V7 | |
| −1 | V5 | V6 | V1 | V2 | V3 | V4 | |
| Hφ | HTem | Sector Number | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 1 | 2 | V2 | V3 | V3 | V4 | V4 | V5 | V5 | V6 | V6 | V1 | V1 | V2 |
| 1 | V2 | V2 | V3 | V3 | V4 | V4 | V5 | V5 | V6 | V6 | V1 | V1 | |
| −1 | V1 | V1 | V2 | V2 | V3 | V3 | V4 | V4 | V5 | V5 | V6 | V6 | |
| −2 | V6 | V1 | V1 | V2 | V2 | V3 | V3 | V4 | V4 | V5 | V5 | V6 | |
| −1 | 2 | V3 | V4 | V4 | V5 | V5 | V6 | V6 | V1 | V1 | V2 | V2 | V3 |
| 1 | V4 | V4 | V5 | V5 | V6 | V6 | V1 | V1 | V2 | V2 | V3 | V3 | |
| −1 | V7 | V5 | V0 | V6 | V7 | V1 | V0 | V2 | V7 | V3 | V0 | V4 | |
| −2 | V5 | V6 | V6 | V1 | V1 | V2 | V2 | V3 | V3 | V4 | V4 | V5 | |
| Parameter | Value |
|---|---|
| Rated power, Pn | 3.5 kW |
| Power frequency, fn | 50 Hz |
| Number of pole pairs, P | 4 |
| Stator voltage, VGrid | 380 V |
| Nominal torque, Tn | 23.7 N·m |
| Stator resistance, R | 0.997 Ω |
| Maximum switching frequency, fsw-MAX | 20 kHz |
| 6-Sectors DTC | 12-Sectors DTC | |||
|---|---|---|---|---|
| Tref | Tripple | φripple | Tripple | φripple |
| −0.8∙Tn | 8.72% | 4.22% | 2.95% | 2.35% |
| −0.4∙Tn | 7.33% | 3.10% | 5.23% | 2.10% |
| +0.8∙Tn | 10.72% | 7.22% | 2.11% | 3.11% |
| +0.4∙Tn | 9.82% | 8.12% | 3.26% | 2.21% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eial Awwad, A. Dynamic Performance Enhancement of a Direct-Driven PMSG-Based Wind Turbine Using a 12-Sectors DTC. World Electr. Veh. J. 2022, 13, 123. https://doi.org/10.3390/wevj13070123
Eial Awwad A. Dynamic Performance Enhancement of a Direct-Driven PMSG-Based Wind Turbine Using a 12-Sectors DTC. World Electric Vehicle Journal. 2022; 13(7):123. https://doi.org/10.3390/wevj13070123
Chicago/Turabian StyleEial Awwad, Abdullah. 2022. "Dynamic Performance Enhancement of a Direct-Driven PMSG-Based Wind Turbine Using a 12-Sectors DTC" World Electric Vehicle Journal 13, no. 7: 123. https://doi.org/10.3390/wevj13070123
APA StyleEial Awwad, A. (2022). Dynamic Performance Enhancement of a Direct-Driven PMSG-Based Wind Turbine Using a 12-Sectors DTC. World Electric Vehicle Journal, 13(7), 123. https://doi.org/10.3390/wevj13070123






