Abstract
This study examines the potential role that an Electric Vehicle Battery (EVB) can play in Home Energy Management System (HEMS) based on a future development on the performance and costs of batteries. The value of EVB in an HEMS with different home connection settings and energy consumption/storage/generation capacities are investigated to advise the optimal future HEMS setups. Solar PV are considered as the residential renewal energy supply, which is the main resource of uncertainty of the system. A novel forecasting model is deployed which incorporates geographical information, solar radiation forecast and weather-related conditions into an exponential-based method to simulate day-ahead solar PV output. Optimal flows of energy and usage of storage (batteries) are then captured by a Stochastic Programming (SP) model and solved by CPLEX. Managerial insights and optimal designs of the HEMS are drawn based on the results obtained.
1. Introduction
Renewable energy and energy storage technologies have been developed for decades to conserve natural resources and to reduce global fossil-fuel carbon emissions [1,2]. Many global energy leaders tend to change the direction of production from fossil energy sources to renewables such as solar, wind, hydro, biomass, etc., which are often referred to as clean energies. For instance, renewable energy provided more than one-fourth of global electricity consumption by the end of 2018, and, moreover, its capacity grew by 8% compared to the previous year, which is led by wind and solar [3]. In 2019, the UK’s electricity generated from renewables contributed to 35.8% of the total supply, which is led by wind power, bio-energy, solar photo-voltaic (PV), and hydro-power [4]. In addition, renewable energy sources are characterized in a particular location by considering the existing energy flows and the spatial and time variations [5]. For example, the suitable residential renewable energy deployments in the UK are known as solar panels and small wind turbines [6,7]. In particular, solar PV adoption has expanded rapidly over the past few years as the International Energy Agency (IEA) declared that solar PV power is the new king of electricity since it is consistently cheaper than fossil-fuel power plants [8].
It is well understood that significant uncertainties lie in the renewable power generation, e.g., residential or grid-scale solar power and wind turbine systems largely relying on the weather conditions. In addition, such renewable generations are usually not matching the typical daily consumption patterns of households. For household electric end-uses, there is a variety of home appliances including kitchen and cooking appliances, washing machine and tumble dryer, fridges and freezer, microwaves, ovens, toasters, humidifiers, coffeemakers, TVs, DVD players, video games, telephones, laptops and so on. Electricity consumption of these end-uses depends on lighting and house space, local temperature, utility price, consumer lifestyles, etc. The survey results of 250 British household consumption 2010–2011 [9,10] are shown in Figure 1, which illustrates the usage profile of home appliances and peak periods throughout the day. It can be seen that daily electricity profiles and peak demand occur between 6:00 p.m.–9:00 p.m., which is the time for cooking, lighting and audiovisual demands after working hours, which also falls into the period of high (peak load) prices. To reduce electricity bills, one way is to buy electricity when it is cheap and carry it to meet the peak hour demands, and another is to maximize self-consumption when the household has its own renewable energy generators such as solar panels. Both aims can be achieved by installing some electricity storage (e.g., batteries).
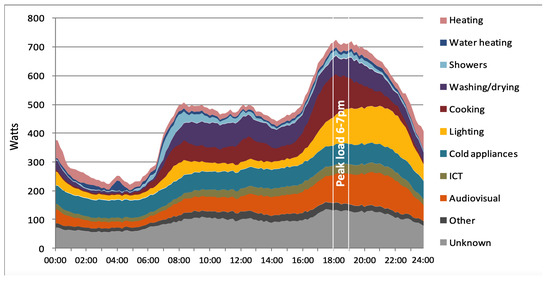
Figure 1.
The average household electricity consumption profile for a typical UK home [10].
As claimed by many publications [11,12,13,14,15], self-consumption, i.e., the power usage on its generation site, is one of the most efficient energy consumption modes, and its level can be increased by deploying energy storage. With the advances of technology and materials, solar PV panels and energy storage have became available at increasingly lower costs [11,12,13,16]. The key factors that affect the renewable energy deployment at household level can then be concluded as the quality of the weather forecasting and the optimal usage of energy storage.
On the other hand, Electric Vehicles (EVs) play a critical role in meeting the environmental goals to reduce local air pollution and to address climate change. In many countries, there is an effort to promote EV development and usage so as to reduce pollution levels by introducing EV policy support measures in various types of Government policies, e.g., financial benefit, tax incentive, etc. [17,18]. Over the last decade, the global EV market expanded rapidly driven by supportive policies and technology advances at all governance levels [19]. Besides these policies, as EV is driven by a battery and it comes home together with the driver, which leads to discussions of using the EV battery to supply home devices, namely EV-to-home power supply. For example, Mitsubishi Motors Corp and the Electricity Generating Authority of Thailand have agreed to cooperate in developing a system to enable electric vehicles to power homes for other purposes in 2021 [20]. Moreover, recently, Tesla’s battery supplier, as one of the leaders of energy storage and EV technologies, plans to launch a lower-cost and million-mile lifespan battery [21].
Based on the above analysis, given the uncertain distributed renewable generation (e.g., micro wind turbines, on-roof solar panels for local communities and households), different clean energy technologies (e.g., EVs, battery storage), and various consumption needs, it is important to have an optimal control system to coordinate the operations of the residential renewable energy system. The home energy management system (HEMS), which could serve such a role, can be seen as a demand response tool conceptualized based upon solar energy management system [22]. Existing literature on HEMS has presented several optimization models and techniques such as stochastic dynamic programming (SDP) [23], convex programming [24], mixed integer linear programming (MILP) [25] and stochastic programming (SP) [26,27] to optimize energy usage in smart homes with renewable energy, energy storage system (ESS) and plug-in electric vehicle (PEV). For instance, Schram et al. [28] proposed a simulation model to optimize the home battery with different household load profiles and PV systems. Moreover, stochastic management of energy storage is one of the important areas to explore to reveal the potential that lies in renewable energy sources [28]. Mathematical optimization, model predictive control and heuristic control are used to improve the efficiency of energy operation in households [29]. The operating policies have been efficiently proposed and applied including vehicle-to-home supply [25] and peak-load shifting [25]. Although our research question comes within the context of home energy management, it is worth mentioning that other research problems in similar or different context could be closely related. For instance, the energy management of microgrids and nanogrids (e.g., buildings) equipped with EVs, energy storage, and PV [30,31] is a closely relevant research problem. Along this direction, Ref. [32] developed a stochastic programming framework to the integrated demand and supply energy management for microgrids. Ref. [33] further extended the framework to multi-energy microgrid equipped with the combined heat and power unit (CHP). Ref. [34] further studied the potential of using a second-life battery as storage in the microgrid system. Ref. [35] developed an Internet-of-things (IOT) based system to monitor the battery status in the microgrid.
Most existing works formulate and optimize the system based on the communication between devices and smart meters for real-time uses so as to monitor electricity consumptions in households with real-time pricing (RTP). In this work, however, we assume that the hourly charging rate of batteries can be pre-set in smart meters according to a forecast of weather condition, electricity price and demand in the following 24 h. We also look at the supportive policies of energy storage systems whether it be electric vehicle battery (EVB) or home energy storage by managing day-ahead electricity usage. The research challenges therefore lie in not only modelling the HEMS as a demand response tool to improve the energy load consumption according to electricity price, but also developing an efficient solar PV forecasting for dealing with system parameter uncertainty.
To this end, this paper aims to propose and investigate the different residential energy connections of EV Battery (EVB) to the residential solar PV system and to home appliances so as to explore the effectiveness of deploying EV batteries in future households. The remainder of this paper is organized as follows: Section 2 summarizes the problem settings and system parameters to be used in our system models. Section 3 presents a forecasting model on electric generation from solar panels. In Section 4, we develop and formulate the EVB-supported systems under a time-of-use tariff in a normal situation on weekdays by stochastic programming (SP). Section 5 summarizes the results of the optimization models under different generation and battery capacities. Finally, in Section 6, we conclude on the optimal settings of the EVB-supported system under different scenarios.
2. Default Setting and System Parameters
Figure 2 represents the electricity flow inside a household which has a solar PV system, a home battery and an EV. Demands are classified into three categories, i.e., EV, typical home appliances and small appliances. It shows the default system where all devices are connected to the grid. A home battery is installed and connected to the solar panel to increase self-consumption. Electricity generated by solar panels or pulled from the grid can directly supply home appliances and/or charge the home battery, while home battery can supply the appliances as well. We assume that solar panels can directly supply home appliances without going through the home battery. A stochastic programming model will be developed in this work to explore the optimal usage of batteries under this connection setting under different solar PV generation levels and home battery capacities. The EV is driven by its own battery which can be charged from the grid. Due to the voltage and existing restrictions, direct charge from solar panel to the EV battery is prohibited by this default layout. In later discussions, however, we will lift this restriction to explore the potential usage of EV batteries in balancing demands and supply, and look into the possibilities of replacing home batteries by EV battery in a household with renewable energy supply.
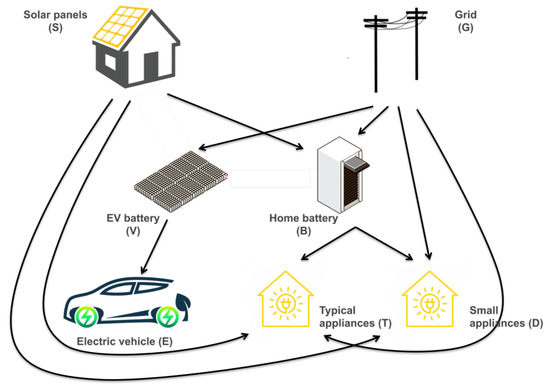
Figure 2.
Graphical representation of home energy consumption and battery usage concepts.
In Section 4, we will develop a stochastic programming model to optimize the usage of batteries in energy shifting so as to minimize household bills. Based on the developed model, further discussion will be carried out on the role of EV and home batteries and the potential integration of them. To feed in the uncertainties of the stochastic programming model, in Section 3, we will develop a novel forecasting approach to estimate the renewable energy generation levels.
3. Day-Ahead Probabilistic PV Generation Forecast
In this work, we develop a forecasting model with exogenous variables at the day ahead horizon to generate scenarios of the hourly output of the peak-PV generation for the next 24 h. For the solar PV power forecasting, the time-series methodology is one of the three major categories for a micro-scale and intra-day resolution [36]. In particular, exponential-based and AutoRegressive Integrated Moving Average (ARIMA) based approaches [37,38,39,40,41] are suitable for the short-term solar PV planning. Most of these methods consist of meteorological data as exogenous variables such as solar radiation, sunshine hour, weather and cloud conditions, etc. The intensity of solar radiation or sunlight, which is a direct input of Photovoltaics (PV) via solar panels, reaches the earth surface that has a strong relation to satellite (images) data [42,43], historical solar radiation data [27,44], cloud conditions [16,27,44], and sunshine duration [43,45]. It also depends on a variety of factors including latitude, season, time of day, cloud cover, and altitude.
A forecasting model proposed by Chitsuphaphan et al. (2020) [27] (Section 2(E)) incorporates local information, such as coordinate, solar radiation forecast, and weather-related conditions into an exponential-based method that can be used to simulate day-ahead solar PV output. To forecast the day-ahead solar PV output in micro-scale resolution for residential energy consumption as a stochastic variable, we focus on statistical probabilistic forecasting [46] by adding the main factors in solar radiation at the earth surface [47], including geographic location, time of day, and local weather into the model [27].
In our analysis, we consider the cloud cover, including five available levels such as sunny, partly cloudy, mostly cloudy, cloudy, and rainy, being an independent variable (as an indicator variable that represents categorical data). Cloud cover is captured by a category variable with five levels. In the regression analysis, we transform it to a four-dimensional dummy variable , with standing for sunny, standing for partly cloudy, standing for mostly cloudy, standing for cloudy and standing for rainy, where indicates the location and j denotes the jth day.
Let represent a historical data set of the peak-PV generation and a cloud forecast vector at position on day j, and denotes an amount of hourly-t solar electricity generation given . Therefore, the forecasting model with five levels of cloudiness used to simulate the scenarios of hourly electricity supply for the second-stage problem of the SP model is
where represents the magnitude forecast at -position on day j when given, denote regression coefficients, denotes a normally distributed disturbance term, s.t. denote sunrise and sunset time index, calculated by and , respectively, denotes a frequency of sine wave function s.t. denotes a PV generation time index on day j, s.t. .
The historical time series and cloud cover conditions (five levels of cloudiness) are serviced to download by the PVOutput platform (see https://pvoutput.org/, accessed on 24 May 2022). The data set is used to estimate the parameters of the forecasting model and simulate the scenarios afterward. In the UK, a 3 kWh solar panel system, which requires at least 21 square metres of surface area to install, can sufficiently generate electricity for daily consumption of a small household size (1–3 residents) [48]. Therefore, we will generate three sets of solar electricity scenarios () based on 1, 2 and 3 kWh peak PV system.
4. Optimization Model
4.1. Notations and Parameters
To develop a stochastic programming model, we firstly declare parameters, decision variables and abbreviations in Table 1.

Table 1.
Abbreviations and system notations.
4.2. System Layouts and Models
To understand the different role played by each component of the household energy system, we look into different systems with respect to the availability of batteries and/or connections between batteries and devices. Table 2 summarizes the detailed systems we are examining with the connection links demonstrated in Figure 3. These scenarios are going to be compared with the default setting as displayed in Figure 2.

Table 2.
Household power system setups.
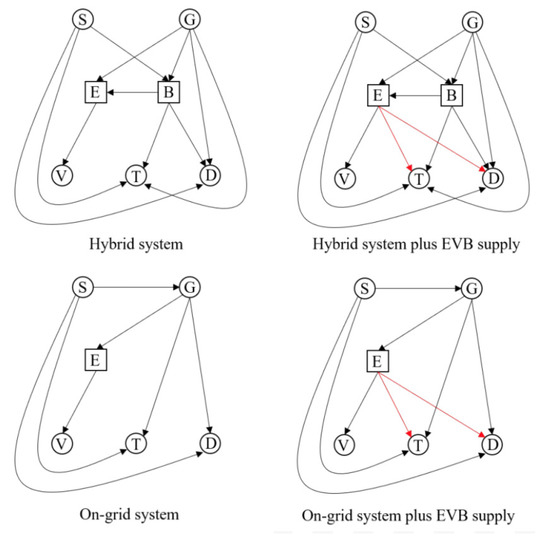
Figure 3.
Alternative layouts of home electric systems.
Note that these systems are proposed with a joint consideration of current practicality and potential future developments of the solar PV and energy storage devices. In detail, the on-grid system is the simplest system for a household with solar PV and EV, which is connected to the grid and all consumption are pulled directly from the grid while needed. To investigate how batteries help in carrying energy from generation phase (cheap hours) to demand phase (peak hours) so as to maximize self-consumption, the default system (Figure 2) is proposed, which reflect the standard setup of a household with solar PV, EV and home energy storage (battery) with the state-of-the-art technology. The hybrid system, on the other hand, improves the default system by allowing power transmission from home battery to EV batteries so that, if the solar PV generation is higher than standard household consumption, the excess will not be wasted.
The other two systems are proposed by adding extra transmission possibilities from the EV battery to home appliances, on top of the structure of hybrid system and the on-grid system. By doing this, we create possibilities of integrating/replacing the home battery with/by EV battery. Considering EV is a global trend of the next generation vehicles, and these systems inform us about the optimal usage of EV batteries in a wider household energy settings. Note that all the links connecting to EV batteries are valid only when the EV is parked at home.
4.2.1. SP Model for the Default Setting
Default system, as shown in Figure 2, is a modern PV system that combines solar panels and battery storage in one place. The electricity generated from solar panels can be consumed right away or be stored in a home battery for later usage. This can improve self-consumption and ease the load and pressure on the grid. In addition, the home battery can also be used as a route to reduce energy bills by carrying electricity from off-peak hours to peak hours. We assume that the EV battery can only be charged at home from the grid, so essentially the two storage systems are not interacting with each other and the EV system is not influenced by the power supply from solar panels.
To simplify the problem structure, a two-stage SP is designed, with the first-stage deciding proactively the best amount to pull from the grid into the energy storage (EV and home battery), and the second stage reacting to the actual supply and demand to minimize the overall cost. Note that, in the formulation in this and subsequent subsections, we model the energy levels of battery directly as (for battery storage) and (for EV battery), instead of the relative measure of energy level (i.e., State of charge (SoC)). Such a modelling approach has been widely used in existing studies, e.g., [32,33].
Let and be the first-stage variables and be second-stage recourse variables, where denotes the outcome of the random weather condition. The two-stage SP model is expressed by
s.t.
EV battery flows:
EV battery capacity:
EV battery daily power cycle:
Non-negativity:
where represents the optimal objective of the second-stage problem under scenario . The second-stage problem can thus be written as
s.t.
Solar PV supply:
Home battery flow:
Electricity demands:
Home battery supply:
Home battery daily power cycle:
Home battery capacity:
Non-negativity:
where represents the 24-h PV output that are generated by the forecasting model in Section 3, which only become available in second stage.
4.2.2. SP Model for (a) Hybrid System
(a) Hybrid System is an extension of the default system by allowing EV battery to be charged by home battery. This system is proposed considering the possibility of a high generation from the solar panel beyond the daily household consumption. The remaining amount can then be used to charge the EV battery so as to save electricity bills. This scenario should work well when the solar generation is high and the home battery is relatively large. Major differences from the default system lie in five constraints:
EV battery flows (moved to the second stage as it now depends on scenario ()):
EV battery capacity (moved to the second stage as it now depends on scenario ()):
EV battery daily power cycle (moved to the second stage as it now depends on scenario ()):
Home battery flow:
Home battery supply:
where denotes the electricity flow from home battery to EV battery in hour t.
4.2.3. SP Model for (b) Hybrid System with EVB Supply
(b) Hybrid System with EVB Supply is an extension of the hybrid system by allowing home appliances to be supplied from the electric vehicle battery (EVB). This system is motivated by the fact that normally the house occupiers come back home together with the EV, so that the EVB connection is available during the peak demand hours. By pushing remaining energy from EVB to supply home appliances when parking at home, one can further reduce the electricity purchase from the grid during peak rate hours. This would enable the maximum usage of the EV battery as an energy storage, which is available to be charged during the off-peak night hours and to be discharged to supply home appliances during the peak hours. This scenario should work well when the home battery is relatively small. Major differences from system (a) lie in three constraints:
EV battery flow:
EV battery supply:
Electricity demands:
where denotes the electricity flow from EV battery to home appliances in hour t.
4.2.4. SP Model for (c) On-Grid System
(c) On-grid System is a benchmark system which has no home battery installed. The excess solar electricity after supplying home appliances at time t, denoted by , can be uploaded to the grid to get power credits. This is shown by the link between the solar panel and the grids in Figure 3. Provided that the surplus can be sold back to the grid at a discounted price with discount rate , the objective function for second stage problem has to be updated to include the income.
s.t.
EV battery flow:
EV battery daily power cycle:
EV battery capacity:
with the second-stage problem written as
s.t.
Solar PV supply:
Electricity demands:
Non-negativity:
where denotes the surplus electricity generated from solar panels in hour t. Note that, as there is no storage available, this surplus has to be uploaded to the grid regardless of whether this uploading is paid or not.
4.2.5. SP Model for (d) On-Grid System with EVB Supply
(d) On-grid System with EVB Supply is an extension of the on-grid system. It assumes no home battery but allows home appliances to be driven by EV battery. Essentially, we assume that the EV battery takes the role of home battery. A major difference lies in the fact that the EV battery is not available throughout the day and it can only be charged/used when the EV is parked at home, so it will miss the peak hours of solar generation and therefore has limited ability to store surplus solar power generations. The EV battery is more likely to serve only as a tool to bring cheaper electricity to peak hours. The SP model can be modified based on the one for an on-grid system.
EV battery flow (moved to the second stage as it now depends on scenario ()):
EV battery daily power cycle (moved to the second stage as it now depends on scenario ()):
Electricity demands:
5. Numerical Results
5.1. Experiment Settings and System Parameters
To draw valuable insights from solving the proposed SP model, we set the problem parameters to reflect practical situations according to reliable sources.
Electricity supply: In practice, the electricity grid can supply as much energy as what is needed by a household, so this problem has no constraints on the amount of electricity from the grid (). On the other hand, how much electricity we can generate from the PV system installed at home is under significant uncertainty, which has to be predicted to feed into the model.
The electricity output from solar panels depends on several factors such as size, capacity, location, and weather conditions. In the UK, most residential solar PV systems installed typically have a capacity between 1 kWh and 4 kWh by taking around 8–28 square metres (m) of space. In this study, we will examine three different peak PV generation capacities at 1 kWh, 2 kWh and 3 kWh in clear sky conditions (sunny day) and study how electricity storage would act in these three settings. Re-scaled according to the chosen capacities, the spatial exponential smoothing model as presented in Section 3 is used to generate 20 random scenarios of the 24-h electricity generation, which are used as the {} values in the model.
Electricity demand: The households consumption data (without EV), i.e., and , are extracted from the household electricity survey [9]. In this study, we deploy the average household consumption data over all household types, in order to explore the optimal household electricity system settings under the typical UK consumption pattern. Devices (excluding EV) in households are categorised into two groups, i.e., major appliances (white goods) and small appliances and electronic devices (brown goods). Figure 4 summarises the hourly consumption level of these two categories (green and orange lines), together with other key information of the system like average daily PV generation and electricity price patterns. It can be seen that the peak demand occurs between 6:00 p.m.–9:00 p.m., which is the typical cooking and family entertaining time after working hours. High peak-load price applies to this period’s consumption, which forms the major part of high electricity bills.
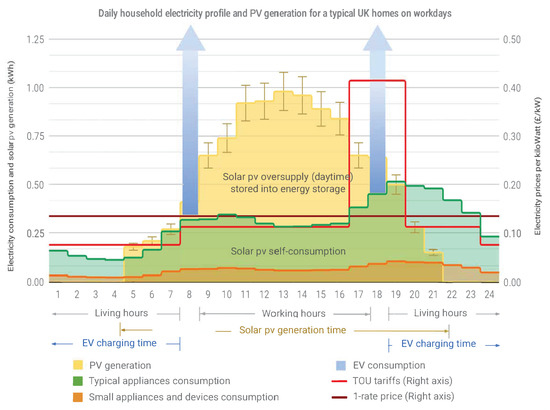
Figure 4.
Average 24-h UK household electricity profile and PV generation curves on summer weekdays.
For the EV consumption (), we consider urban commuter driving profiles by assuming specifications as follows: (a) the household has an EV with 30 kWh battery, with a typical daily consumption of 10 kW, (b) the EV is only charged at home and its available time ranges from 7:00 p.m. to 7:00 a.m. the next morning. Let be binary indicators stating the available charging time at home for the EV, which is set to one between 7:00 p.m.–7:00 a.m.
Electricity prices: For electricity prices, we take a typical time-of-use (TOU) electricity tariff that is provided by the eastern region household electricity surveys [9]. A day is divided into four time intervals, and each has its own electricity prices () as shown by the red line in Figure 4. On the other hand, we assume that the electricity generated by solar panels () is free of charge by ignoring the installation and maintenance costs. When customers upload energy back to the grid, they receive credits for doing so, and this is called Feed-in-tariff. In this study, we test through different levels of Feed-in-tariff, , between 0–60% of the lowest price of the TOU tariffs.
Energy storage capacity: Being consistent with industrial production, here we assume that a 30 kWh () lithium-ion electric-vehicle battery is installed, which provides up to 160 km range per charge. As for the home battery , we are aiming to find the influence of it so we examine the options ranging from 0–30 kWh. The battery round-trip efficiency is the fraction of energy put into the storage that can be retrieved afterwards. Here, we set it to 80% according to [49].
5.2. Scenarios of Solar PV Generation
In this subsection, we fit the forecasting model of Section 3 to a real dataset recorded at a solar farm in Cambridge during 1–30 June 2019. This dataset consists of 1440 observations of half-hourly PV outputs with cloud cover conditions (five levels of cloudiness). The fitted model is then rescaled according to home PV capacity so as to generate simulation scenarios for our stochastic programming models. In the regression analysis (first stage of the proposed model), the aggregated-daily PV output, the dependent variable, is modeled with the independent variables weather conditions using the forward variable selection method.
The parameter estimation results of the forecasting model are presented in Table 3, which is used to simulate possible PV supplies via (1). Then, to feed in the stochastic programming model, we generate 20 random trajectories of hourly solar PV output for a specific weather condition, e.g., sunny, which form the inputs of the second-stage optimization model, which is presented in the following subsection.

Table 3.
Parameter estimation of the forecasting model.
5.3. Results of SP Models
In order to investigate the energy efficiency of the systems proposed, we test them with the aforementioned parameters. Experiments are carried out using ILOG CPLEX V12.9.0 on an Intel Core i9-7940X 3.1 GHz machine. Figure 5 shows a comparison of the energy bills under different system settings as presented in Section 4.2.
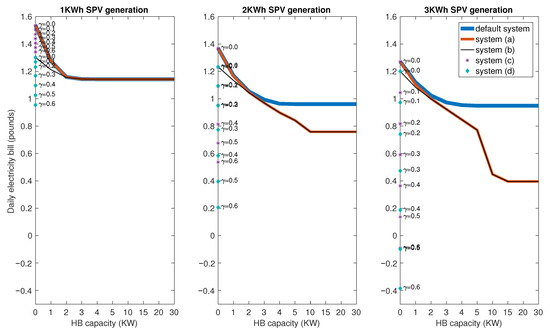
Figure 5.
Daily household consumption costs by solar PV and battery capacities.
Figure 5 shows the daily energy bills payable by the household under different system settings with different levels of Solar PV (SPV) generation and Home Battery (HB) capacities. Note that some results are the same for different systems; to display them clearly, some lines are thickened in Figure 5 and have another line drawn on top of it.
Not surprisingly, the daily usage cost decreases with increased size of solar PV capacity. The cost also decreases with an increased size of home battery, under the same solar PV generation. Upper limits on the home battery capacity can be identified for each system setting from the results. The larger the solar PV generation is, the higher HB should be installed to facilitate full usage of the power generated. According to Figure 5, suitable capacity of HB for 1 kWh, 2 kWh, and 3 kWh SPV under the default systems are, respectively, 3 kWh, 4 kWh, and 5 kWh. Higher home battery capacity will not decrease the electricity bill further. In addition, the best capacity of HB under systems (a) and (b) are, 3 kWh, 10 kWh, and 15 kWh for 1 kWh, 2 kWh, and 3 kWh SPV generation, respectively.
Through future analysis, we find that system (b) (allowing EVB supply to home appliances) reduces the electricity bill by 5.6–15% when no HB is installed in the household, and by 3.3–5% when HB capacity is very low (HB = 1). This is achieved by using the EVB to carry low-cost electricity from off-peak hours to peak hours. The reduction in bill slows down as the solar PV generation is getting higher. If we take a closer look, we can see that the electricity bills are roughly the same for system (b) when HB = 0, regardless of the size of the solar PV. This is because the EVB operates independently from the solar system if there is no home battery connecting them. On the other hand, the cost of the default system when HB = 0 decreases with the increased generation capacity of solar PV, so the gap between system (b) and the default system becomes less significant.
For system (a) (allowing transmission from HB to EVB), it converges to a default system when home battery capacity is low and converges to system (b) when home battery capacity is high. Indeed, when HB capacity is low, it carries less energy than the household demands so there will not be surplus to supply the EVB. When HB capacity is high, however, allowing EVB supply to home appliances will not add further value to the system. In addition, savings achieved by system (a) become more significant when solar system gets larger; it saves 21% (58%) on the daily electricity bill by allowing transmission from HB to EVB on top of the default system with 2 kWh (3 kWh) solar generation capacity. After a future examining of results with solar generation capacity of 2 kWh and 3 kWh, it is not hard to see that both systems are restricted by the battery size until the HB capacity reaches 5 kWh (they have the same decreasing pattern until HB = 5 kWh). Further savings can only be achieved with higher solar generation.
For systems (c) and (d), their results are shown in the figures by the scatters aligned on the left of each graph because they do not have home batteries (HB = 0). The scatters are labelled with the selling price rate considered, e.g., representing one can sell the surplus electricity at a price of . When selling price is zero, system (c) is identical to the default system (and system (a)) with HB = 0, while system (d) is identical to system (c) with HB = 0. We can see from the results that, when selling back electricity is allowed, the daily bill decreases approximately linearly with the increase of the selling price. System (d) saves around on system (c) by allowing EVB supply to home appliances when , and the savings increase with the size of solar panels. When , system (d) leads to a similar daily bill to systems (a) and (b) with the highest possible home battery installed, and system (d) is certainly better than system (a) and (b) when or higher. This means that, supposing selling electricity in the future at a fixed price is allowed, replacing a home battery with an EVB battery becomes feasible at no extra daily usage cost. However, we also note that this increases the pressure and uncertainty of the grid management.
5.4. Managerial Insights
Based on the analysis above, we can obtain some managerial insights:
- In general, EV batteries cannot fully replace HB because: (a) It cannot be charged by solar PV in our experimental setting; (b) It is not at home when solar PV generation reaches the maximum level.
- Supposing that considerable rewards are paid for “selling” back electricity, e.g., at a rate of of the lowest tariff, HEMS without home battery outperforms those with home batteries, and depends less on the solar generation level.
- When home battery is not installed, allowing EVB supply to home appliances saves 5–15% of the daily bill. Therefore, once EV replaces petrol/diesel cars in the future, households having solar PV but no home battery installed can benefit from using their EVB as alternative home energy storage.
- When home battery is large (over 10 kWh), allowing transmission from HB to EVB saves 21–58% of the daily bill with minimum 2 kWh solar generation. This suggests the future development directions of battery charging/discharging routes.
6. Conclusions and Future Work
In this study, we deploy a forecasting model that incorporates spatial information and weather-related conditions to predict solar PV generation for the following 24 h, in order to facilitate proactive management of electricity flows in a residential renewable energy system equipped with solar panels, home battery, EVs, and various types of loads. Several settings (connections) of the residential energy system are proposed and investigated, including allowing electricity transfer from home battery to EVB, and/or allowing EVB to supply home appliances where needed. Stochastic programming models are developed for every connection scenario, which are simplified to two-stage models to be solvable with CPLEX. Discussions around the possibility of replacing a home battery with EVB in future households, and the best connection setup in different supply and consumption scenarios is carried out according to the numerical results obtained.
In addition to this, our approach and the stochastic programming model can also be extended to cover more complicated system setups. We also note that, to capture the full dynamics of the system and for more accurate solutions, one can consider using a multi-stage stochastic model (instead of two stage) or Markov Decision Process (MDP). Another future research direction could be developed around the EV modelling including the statistical modelling of EV departure/arrival times and charging duration such as in [50], and considering different application scenarios such as solar-charging the EV at workplace during the daytime at a lower electricity price, and discharging to power home appliances in the evening [51].
Author Contributions
Conceptualization, X.Y.; methodology, X.Y., T.C. and H.D.; programming, T.C.; validation, T.C. and F.M.; formal analysis, T.C. and X.Y.; resources, T.C.; data curation, T.C. and H.D.; writing—original draft preparation, T.C. and X.Y.; writing—review and editing, X.Y., F.M. and H.D.; visualization, T.C. and X.Y.; supervision, X.Y. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The historical PV time-series and cloud coverage data that support the findings of this study are openly available on the PVOUTPUT.ORG website at https://pvoutput.org. The household’s consumption profiles (without EV information) are extracted from the English Housing Survey HOUSEHOLDS 2010-11: Annual Report on England’s Households available at https://www.gov.uk/government/statistics as cited in Department for Communities and Local Government (2012).
Conflicts of Interest
The authors declare no conflict of interest.
References
- RENA. Renewable Capacity Statistics 2020; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2020; pp. 75–174. [Google Scholar]
- Owusu, P.A.; Asumadu-Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 2016, 3, 1167990. [Google Scholar] [CrossRef]
- REN21. Renewables 2019 Global Status Report; Technical Report; REN21: Paris, France, 2019. [Google Scholar]
- Department for Business, Energy & Industrial Strategy. UK Energy Statistics; Q1 2019; Department for Business, Energy & Industrial Strategy: London, UK, 2019.
- Contreras Montoya, L.T.; Lain, S.; Issa, M.; Ilinca, A. 4—Renewable energy systems. In Hybrid Renewable Energy Systems and Microgrids; Kabalci, E., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 103–177. [Google Scholar] [CrossRef]
- Department for Business, Energy & Industrial Strategy. UK Renewable Electricity Capacity and Generation; Department for Business, Energy & Industrial Strategy: London, UK, 2020.
- Sharifzadeh, M.; Lubiano-Walochik, H.; Shah, N. Integrated renewable electricity generation considering uncertainties: The UK roadmap to 50% power generation from wind and solar energies. Renew. Sustain. Energy Rev. 2017, 72, 385–398. [Google Scholar] [CrossRef]
- Stoker, L. IEA: Solar the ‘New King’ of Power, Will Break Records for Decades to Come. 2020. Available online: https://www.pv-tech.org/news/iea-solar-the-new-king-of-power-will-break-records-for-decades-to-come (accessed on 12 December 2020).
- Department for Communities and Local Government. English Housing Survey HOUSEHOLDS 2010-11: Annual Report on England’s Households; Department for Communities and Local Government: London, UK, 2012.
- Palmer, J.; Terry, N.; Firth, S.; Kane, T.; Godoy-Shimizu, D.; Pope, P. Energy Use at Home: Models, Labels and Unusual Appliances; Further Analysis of the Household Electricity Survey, Reference 475/09/2012; Loughborough University: Loughborough, UK, 2014. [Google Scholar]
- Quoilin, S.; Kavvadias, K.; Mercier, A.; Pappone, I.; Zucker, A. Quantifying self-consumption linked to solar home battery systems: Statistical analysis and economic assessment. Appl. Energy 2016, 182, 58–67. [Google Scholar] [CrossRef]
- Litjens, G.; Kausika, B.; Worrell, E.; van Sark, W. A spatio-temporal city-scale assessment of residential photovoltaic power integration scenarios. Sol. Energy 2018, 174, 1185–1197. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Goy, S.; Sancho-Tomás, A. 4—Load management in buildings. In Urban Energy Systems for Low-Carbon Cities; Eicker, U., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 137–179. [Google Scholar] [CrossRef]
- Schmela, M.; Döring, T.; Gómez, A.P.B.; Roesch, A. 3—Solar Power in Europe: Status and Outlook. In A Comprehensive Guide to Solar Energy Systems; Letcher, T.M., Fthenakis, V.M., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 37–52. [Google Scholar] [CrossRef]
- El-Baz, W.; Tzscheutschler, P.; Wagner, U. Day-ahead probabilistic PV generation forecast for buildings energy management systems. Sol. Energy 2018, 171, 478–490. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Hao, Y.; Fan, J.L.; Wei, Y.M. The impact of government policy on preference for NEVs: The evidence from China. Energy Policy 2013, 61, 382–393. [Google Scholar] [CrossRef]
- Dialogue, A. The Impact of Government Policy on Promoting New Energy Vehicles (NEVs)—The Evidence in APEC Economies; Report APEC#217-CT-01.3; Beijing Capital Energy Technology Co., Ltd.: Beijing, China, 2017. [Google Scholar]
- IEA. Global EV Outlook 2020; Technical Report; IEA: Paris, France, 2020. Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 24 May 2022).
- OUTLANDER PHEV Debuts in Thailand to Offer a New Environmentally-Friendly Option. 2020. Available online: https://www.mitsubishi-motors.com/en/newsrelease/2020/detail1303 (accessed on 1 December 2020).
- Mullaney, T. Tesla and the Science Behind the Next,-generation, Lower-Cost, ‘Million-Mile’ Electric-Car Battery. 2020. Available online: https://www.cnbc.com/2020/06/30/tesla-and-the-science-of-low-cost-next-gen-ev-million-mile-battery (accessed on 1 December 2020).
- Mahapatra, B.; Nayyar, A. Home energy management system (HEMS): Concept, architecture, infrastructure, challenges and energy management schemes. Energy Syst. 2019. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Moura, S.; Yin, X.; Pickert, V. Stochastic control of smart home energy management with plug-in electric vehicle battery energy storage and photovoltaic array. J. Power Sources 2016, 333, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Hou, X.; Wang, J.; Wang, P.; Wang, T. Smart Home Energy Management Optimization Method Considering ESS and PEV. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 101–106. [Google Scholar] [CrossRef]
- Kleywegt, A.J.; Shapiro, A. Stochastic Optimization. In Handbook of Industrial Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001; Chapter 102; pp. 2625–2649. [Google Scholar] [CrossRef] [Green Version]
- Chitsuphaphan, T.; Yang, X.; Dai, H. Stochastic Programming for Residential Energy Management with Electric Vehicle under Photovoltaic Power Generation Uncertainty. In Proceedings of the 2020 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Liege, Belgium, 18–21 August 2020; pp. 1–6. [Google Scholar]
- Schram, W.L.; Lampropoulos, I.; van Sark, W.G. Photovoltaic systems coupled with batteries that are optimally sized for household self-consumption: Assessment of peak shaving potential. Appl. Energy 2018, 223, 69–81. [Google Scholar] [CrossRef]
- Beaudin, M.; Zareipour, H. Home energy management systems: A review of modelling and complexity. Renew. Sustain. Energy Rev. 2015, 45, 318–335. [Google Scholar] [CrossRef]
- Torres-Moreno, J.L.; Gimenez-Fernandez, A.; Perez-Garcia, M.; Rodriguez, F. Energy management strategy for micro-grids with PV-battery systems and electric vehicles. Energies 2018, 11, 522. [Google Scholar] [CrossRef] [Green Version]
- Sulaeman, I.; Chandra Mouli, G.R.; Shekhar, A.; Bauer, P. Comparison of AC and DC Nanogrid for Office Buildings with EV Charging, PV and Battery Storage. Energies 2021, 14, 5800. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Zhu, W.; Zeng, X.J. A stochastic MPC based approach to integrated energy management in microgrids. Sustain. Cities Soc. 2018, 41, 349–362. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Kazemtabrizi, B.; Shi, J. Uncertainty-resistant stochastic MPC approach for optimal operation of CHP microgrid. Energy 2019, 179, 1265–1278. [Google Scholar] [CrossRef]
- Lacap, J.; Park, J.W.; Beslow, L. Development and Demonstration of Microgrid System Utilizing Second-Life Electric Vehicle Batteries. J. Energy Storage 2021, 41, 102837. [Google Scholar] [CrossRef]
- González, I.; Calderón, A.J.; Folgado, F.J. IoT real time system for monitoring lithium-ion battery long-term operation in microgrids. J. Energy Storage 2022, 51, 104596. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Alexiadis, M.C.; Vagropoulos, S.I.; Simoglou, C.K.; Biskas, P.N.; Bakirtzis, A.G. Application of time series and artificial neural network models in short-term forecasting of PV power generation. In Proceedings of the 2013 48th International Universities’ Power Engineering Conference (UPEC), Dublin, Ireland, 2–5 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M. Photovoltaic power forecasting using statistical methods: Impact of weather data. IET Sci. Meas. Technol. 2014, 8, 90–97. [Google Scholar] [CrossRef]
- Yang, C.; Thatte, A.A.; Xie, L. Multitime-Scale Data-Driven Spatio-Temporal Forecast of Photovoltaic Generation. IEEE Trans. Sustain. Energy 2015, 6, 104–112. [Google Scholar] [CrossRef]
- Bouzerdoum, M.; Mellit, A.; Massi Pavan, A. A hybrid model (SARIMA–SVM) for short-term power forecasting of a small-scale grid-connected photovoltaic plant. Sol. Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Chen, C.-R.; Rahman, H.A. A Novel Hybrid Model for Short-Term Forecasting in PV Power Generation. Int. J. Photoenergy 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
- Hammer, A.; Heinemann, D.; Lorenz, E.; Lückehe, B. Short-term forecasting of solar radiation: A statistical approach using satellite data. Sol. Energy 1999, 67, 139–150. [Google Scholar] [CrossRef]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washom, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Sol. Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Gooi, H.; Wang, M. Solar radiation forecast based on fuzzy logic and neural networks. Renew. Energy 2013, 60, 195–201. [Google Scholar] [CrossRef]
- Chen, J.L.; Li, G.S.; Wu, S.J. Assessing the potential of support vector machine for estimating daily solar radiation using sunshine duration. Energy Convers. Manag. 2013, 75, 311–318. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Wald, L. Basics In Solar Radiation At Earth Surface—Revised Version 3; HAL: Bengaluru, India, 2019. [Google Scholar]
- How Many Solar Panels Do I Need to Power My Home or Business? Available online: https://www.expertsure.com/uk/home/how-many-solar-panels/ (accessed on 24 May 2022).
- U.S. Energy Information Administration. Utility-Scale Batteries and Pumped Storage Return about 80% of the Electricity They Store; U.S. Energy Information Administration: Washington, DC, USA, 2021.
- Develder, C.; Sadeghianpourhamami, N.; Strobbe, M.; Refa, N. Quantifying flexibility in EV charging as DR potential: Analysis of two real-world data sets. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, NSW, Australia, 6–9 November 2016; pp. 600–605. [Google Scholar]
- Erickson, L.; Ma, S. Solar-powered charging networks for electric vehicles. Energies 2021, 14, 966. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).