1. Introduction
In recent years, joint efforts to mitigate issues such a global warming and greenhouse emissions have been put in place, and several working plans have been designed following recommendations and discussions such as those of the COP20 [
1]. One of the main focuses has been the use of cleaner energy sources, such as wind and solar, setting up some key goals by 2030 and 2050.
For instance, in Germany, considerable investment and a series of milestones have been designed with the objective of transitioning to full energy production by renewable energy sources by 2050 [
2]. These efforts naturally require multidisciplinary collaboration from many different agents: better infrastructure is needed (e.g., transmission lines), as well as better technology (e.g., batteries), but also related policies that, for instance, allow new participants to be motivated to engage in production. An example of this is the so-called contract for differences (CfD), used for off-shore wind farms [
2,
3].
Ashour Novirdoust et al. [
2] argue that from a market design perspective, the electricity spot market plays a crucial role. In this market, adequate allocations and pricing rules have to be implemented, taking into consideration a growing market share of renewables, as well as a more active demand side. Pricing in electricity spot markets is a delicate subject, especially under the highly uncertain environments given by a strong presence of variable renewable energy (VRE) sources. Participants of the wholesale market will use the spot prices as a reference to hedge risk in the future and forward markets (e.g., contracts for 10 years). Spot market prices then have to represent correctly the market’s underlying conditions.
Price formation has been an ongoing discussion in many different countries; even though their markets are built in intrinsically different ways (e.g., US markets vs. European markets), they still aim to have spot market prices (public information) that correctly represent the costs associated with production and distribution. The so-called
uplifts generally refer to individual side-payments to market participants (which can be positive or negative, depending on the pricing scheme) for the purpose of achieving certain economic properties (e.g., competitive equilibrium). Those uplifts distort those markets in the sense that they are not part of the public prices, and they may lead to biased investment signals: producers may think is not economically sustainable to participate, or have the wrong expectations regarding future profits [
3,
4,
5].
In order to tackle the intrinsic uncertainty associated with VRE sources, researchers and practitioners argue than one of the key elements is a more active demand side (e.g., [
6,
7,
8]) that can react and accommodate the required demand, for instance, shifting it to other times of the day. In a domestic setting, this could be to delay the use of a washing machine, and in an industrial setting, to only use the energy-intensive machines overnight. At the same time, we have observed a growing interest in electric vehicles (EVs) in many countries around the world. Better battery technology has allowed an increasing number of companies to sell these types of cars. As part of their net-zero plans, countries such as the UK announced that by 2030, no more new petrol or diesel cars will be sold, with the aim to eventually phase out those cars by 2050 [
9]. We also see an increasing trend of the EVs’ market share in many countries, where for instance, in 2020 the sales of new EVs in the following countries were as follows: Germany, 295,000; France, 185,000; UK, 175,000; the Netherlands, 89,000; and Norway, 77,000 [
10]. It is worth noting that in the case of Norway, its numbers correspond to nearly the 65% of the total new cars in the country in 2020 (and a total of 86% if we consider hybrid cards). This is mainly justified by the special rules of the country, where EV buyers did not have to pay import duties and had free parking [
11].
What makes EVs so interesting is that they can act as mobile storage, charging in one place, travelling, and then discharging in another [
12]. In the literature, this model is often called the vehicle-to-grid (V2G) model, a concept originally introduced by Kempton and Letendre [
13]. In recent years, V2G models have been studied from many different perspectives. We can find, for example, articles studying the problem of optimal allocation for charging/discharging stations [
14], the problem of optimal charging strategies considering battery degradation [
15], how to operate with EV aggregators [
16], and the use of photovoltaic (PV)-powered car parks for EVs [
17]. Nunes et al. [
18] and Hoarau and Perez [
19] present relevant reviews of the interaction between both types of systems (PV and EVs), tackling issues of technical infrastructure as well as the necessary coordination required for them. The authors highlight that economic conditions for an appropriate synergy are critical and have been under-studied in the literature. In recent years, researchers have focused on problems such as the economic viability of PV car parks (e.g., [
17,
20]), developing, for example, dynamic scheduling systems that consider supply and demand uncertainty or pricing policies for demand management (lower prices during the day).
For the purpose of this paper, we will focus on wholesale markets and the effects of incorporating EVs in them. We are particularly interested in understanding how different pricing policies behave in the presence of EVs. This is relevant because some articles and technical reports [
21] have claimed that current electricity spot markets are not well-suited for EVs, arguing that operating rules were not designed considering them, particularly if battery degradation is not taken into account [
22], and therefore new implementations need to be designed. Hanemann and Bruckner [
23] take a step towards those issues, developing a model that incorporates EVs into the spot market and analysing their effect on the prices. These prices are computed following one of the most common pricing schemes, which is, after O’Neill et al. [
24], typically called integer programming (IP) pricing.
In our paper, we consider a similar allocation model that, in addition to directly including EVs, also accommodates different pricing rules. We explore some of the most popular pricing rules used in this type of market, and we discuss the economic properties those pricing rules can ensure, with a special focus on the conditions that provide minimal uplifts. We complement these results with a series of experiments, where we consider three different scenarios: The first scenario serves as a baseline. In the second scenario, we incorporate EVs using a V2G model. In the third scenario, in addition to EVs, we incorporate a recurrent concept in electricity markets, namely demand flexibility. Our results showcase the behaviour of two main pricing rules under those scenarios, depicting their potential suitability for future electricity markets where EVs and an active demand side can participate.
The rest of our paper is structured as follows:
Section 2 is dedicated to the related literature.
Section 3 provides a simple example to showcase why deciding on a pricing rule is a complicated problem. In
Section 4, we explain the main components of electricity market design, with a particular focus on pricing. In
Section 5, we develop our market model, that will be tested in the numerical analysis from
Section 6, using the pricing schemes defined in
Section 4. Finally in
Section 7, we discuss the open problems, future research, and conclusions.
2. Related Literature
The literature on EVs has grown substantially in recent years. For example, Sovacool et al. [
25] present a review of about 200 papers dating from 2015–2017. The authors conclude that a large majority of the reviewed papers only focused on the technical and economical aspects of V2G systems, such as storage, batteries, load balance, and minimisation of costs. However, other related issues, such as environmental consequences and social impacts, have a much smaller presence in the literature. In the case of our paper, we will not cover such a large variety of sources; instead, we will just focus on those papers that deal with market-related questions involving EVs.
Mwasilu et al. [
26], back in 2014, created a comprehensive review of the (at the time) state-of-the-art research on the integration of EVs into the power grid. Many different approaches are discussed there, such as the functionality of EVs acting as ancillary services (e.g., voltage regulation and peak power regulation leading to reduced operational costs), which has been extensively studied in many countries. The authors also include papers proposing the deployment of EVs in a smart grid system, but in order to work properly, advanced (real-time) communication and control are required (such as the later suggestion by Englberger et al. [
12]). In [
26], the authors suggest that there is no clear evidence to justify a V2G system over other types of energy storage systems. It is worth mentioning that the global numbers of EVs were quite small in 2014 compared to 8 years later: a 0.4% of market share in 2014 and a 8.3% in 2021 [
27]. This might justify some of the conclusions of the articles mentioned by Mwasilu et al. [
26].
Gunkel et al. [
28] present an interesting study of different levels of flexibility that EVs can offer, namely passive charging, smart charging, and V2G. The first of these corresponds to uncoordinated drivers that (only) charge their cars whenever they need to. Smart charging refers to a coordinated version of drivers acting only as demand but accommodating their charging times optimally. Finally, the V2G model includes both smart charging and discharging. The authors study the potential impacts of these levels in European markets, and they discover that the increasing level of flexibility helps to reduce system costs and affects spot market prices.
Both passive charging and smart charging are sometimes grouped into the category of unidirectional charging (EVs acting only as demand), as opposed to bidirectional charging (such as a V2G system). Bidirectional charging is intrinsically more complicated, but that does not mean that unidirectional models are simple. For instance, Kühnbach et al. [
29] focus on issues associated with the combination of unidirectional charging for EVs and demand response. Wu and Lin [
30] deal with a similar problem, but for the bidirectional case, studying the effects of reduced electricity costs caused by incorporating EVs in a V2G system, in comparison with other charging policies (random charging and controlled charging). Wu and Lin [
30] argue that policies will need to change to allow them to participate as a power source. This is an ongoing discussion across different countries, and not only policies and regulations are involved; appropriate infrastructure is also needed (e.g., [
31,
32]).
Uddin et al. [
33] deal with the sensitive topic of battery degradation in a V2G system, which has been discussed in the literature with seemingly contradictory conclusions. Two different influential papers are discussed there [
34,
35], and the authors manage to conciliate their conclusions with respect to the negative and positive effects (respectively) on battery life due to participation on V2G systems. According to Uddin et al. [
33], the key to optimizing battery life is through the use of smart control, which optimally formulates the minimisation of battery degradation.
Englberger et al. [
12] provide an overview of the growing popularity of EVs. Some of the key points include quick response time, geographical and temporal flexibility, and the ability to act as mobile storage that can help to meet the demand in a system with an increasing share of renewables. The authors also discuss the issue of degradation of batteries and their lifetime in a V2G system, and how in the smart grid literature, EVs enable more efficient management of electricity resources. A detailed model to incorporate bidirectionally chargeable EVs and the potential revenues associated with such participation are proposed by Kern et al. [
36]. Their results suggest that those revenues depend on how many EVs are available, the user behaviour, and the implemented rules/policies. Kühnbach et al. [
37] study whether private EVs may affect those prices. Their estimates of EV market participation by 2030 show how the additional demand in a unidirectional model can cover specific costs and reduce electricity prices.
Zoltowska and Lin [
38] consider a bid/offer optimal power flow model where EVs can be incorporated in the wholesale market. In a way, aggregators can adopt a similar bidding parameter to conventional generators, adapting accordingly: for instance, in an EV aggregator, there are no start-up costs, but travel costs can act in a similar way. Unlike other research papers on this topic, which seek to minimise costs or maximise the state of charge (SoC) of the EVs, the authors aim for a social welfare maximisation problem. They account for what they call availability bids, which consider physical constraints (arrive on time to a place where energy is required), technical constraints (whether or not it is feasible for the car to provide the required energy, considering they need to return to their origins with a certain level on their batteries), and economic constraints (whether the market price will cover the associated costs or not).
The closest paper to our research is Hanemann and Bruckner [
23]. The authors create a unit commitment model where they incorporate EVs directly, leading to a mixed integer program. They explore many scenarios with different charging strategies, as well as the associated costs and sensitivities, but they stick to a single pricing rule (IP pricing). In our case, the focus is on modifying the different pricing rules but having a common allocation model where EVs can participate in the spot market. In this way, the main pricing schemes used in the literature and in practice can be tested and compared.
In the following section, we will introduce some preliminary concepts that will be useful throughout the paper. We start with a general description of why developing a pricing scheme for electricity spot markets is a very complex problem. Some key sources of complexity are the intrinsic non-convex nature of the costs functions, and the dual role (supply and demand) of EVs in a V2G system.
3. Preliminaries
We introduce a pricing problem similar to that of Azizan et al. [
39]. An auction with multiple market participants on the supply and demand side is considered; we refer to these participants as
suppliers and
demanders. Formally, they are described by the sets
G and
D, indexed by
g and
d, respectively. Each market participant
g/
d has a cost/value function
/
for producing/consuming quantity
/
and is willing to sell/buy up to the upper limit or capacity
/
. Once market participants have placed their bids (how much they want to buy/sell at which min/max price), the following allocation problem is solved:
is the dual variable associated with the market-clearing constraint (
1b), and
are the dual variables associated with the capacity constraints of each supplier (
1c) and demander (
1d). The objective (
1a) is to allocate the quantities such that social welfare is maximised.
The welfare function and constraints are assumed to be continuously differentiable. The solution is only optimal if the necessary
Karush–Kuhn–Tucker (KKT) conditions hold [
40,
41,
42]. The marginal cost (MC) price corresponds to the optimal dual variable
, which is the same as the marginal cost(s)/value(s) of the underutilised supplier(s) or demander(s). This can also be interpreted as the cost/value for generating/demanding the next 1 MWh.
If
/
are convex functions, then the whole problem is convex and there is no duality gap (strong duality). Therefore, the central allocation is optimal to each individual, and MC prices support a competitive equilibrium under the welfare-maximizing, efficient outcome [
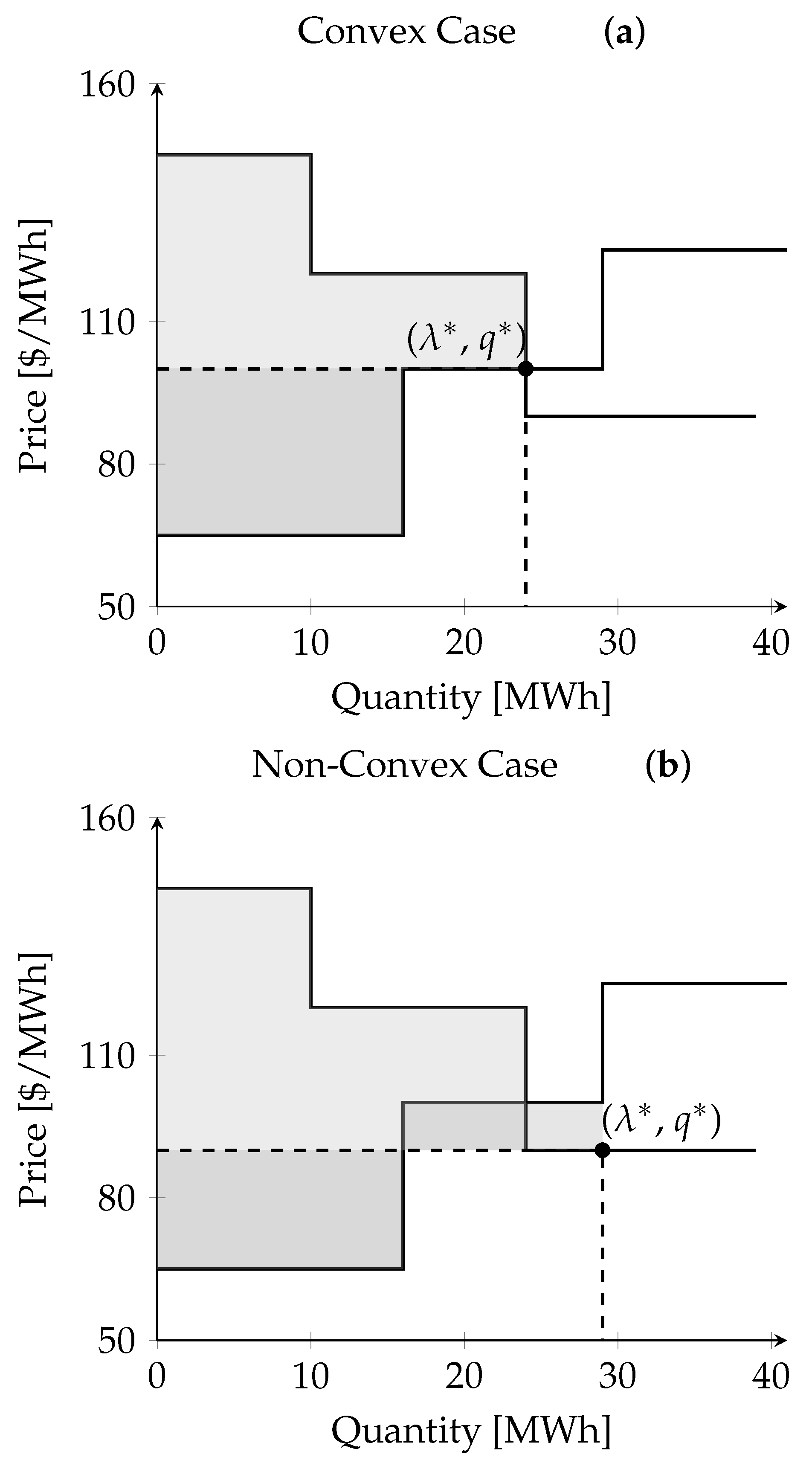
43]. In a convex setting, the MC prices can be graphically determined by aggregating the market participants’ bidding curves to construct the industry supply and demand curves (see
Figure 1). The optimal traded quantity and the MC price are given by the intersection of the two curves. Unfortunately in electricity markets, where cost functions are generally non-convex, this convenient property does not hold.
Similar to Madani et al. [
44] and Araoz and Jörnsten [
45], the following small example demonstrates the potential problems in the presence of non-convexities. Consider an example with three suppliers and buyers each, who submit the bidding curves described by
Table 1. Excluding the last row in
Table 1, the bidding curves of the suppliers and demanders are convex. As shown in
Figure 1a, the optimal outcome is to fully allocate D1, D2, and G1, as well as to allocate a fraction of G2. The market-clearing price is set to USD 100/MWh. Given the MC price, G1, D1, and D2 will maximise their profit/utility if they produce/consume at full capacity. In contrast, D3 and G3 are not willing to participate in the market since they would lose money. G2 is indifferent about the quantity to produce, because their marginal costs are equal to the market price. The profit will be zero in any case. This implies that the MC price supports a competitive equilibrium in that every market participant intends to follow this central allocation. The resulting surpluses of suppliers and demanders are marked by grey areas in
Figure 1.
Let us now impose a minimum production requirement of 13 MW on G2, meaning that G2 can only be allocated as a whole (see
Table 1). The industry supply and demand curves do not cross anymore, because the previous point of intersection is technically unfeasible. Therefore, the market operator has to determine a different allocation. As reported in
Figure 1b, it is optimal to fully allocate G1, G2, D1, and D2, and allocate a fraction of D3. The market-clearing price corresponds to the marginal value of D3, which is USD 90/MWh. However, G2 operates at a loss under the MC price and is willing to leave the market. Increasing the price is not an option either since the utility of D3 would become negative. This exemplifies the evidence of many authors that MC pricing may not support a competitive equilibrium in the presence of non-convexities (e.g., [
46]), and furthermore, that uniform linear pricing (linear: price per MWh; uniform: everyone gets the same price) is generally not capable of guaranteeing this property (e.g., [
47,
48]). The non-existence of a competitive equilibrium, in practical terms, could imply that some useful agents will not be willing to participate.
5. Market Model
This section presents the allocation problem for which the pricing schemes are evaluated. We focus on day-ahead auctions in pool markets for several reasons. First, pool models are more efficient in the coordination of system resources, which becomes more relevant with VRE and flexible resources. Second, pricing rules can be assessed more clearly when there is no market layer through a decentralised market organisation and scheduling decisions. Third, the evaluation of pricing rules in pool markets ties in with existing research that has been primarily conducted for pool markets.
The allocation problem represents a multiple-period, double-sided auction, where market participants submit multi-part bids for generation resources, demand resources, and EVs. Likewise, a TSO specifies technical costs and constraints for the transmission network. Every participant will communicate their preferences and constraints through these multi-part bids to the market operators. For instance, EV aggregators might communicate the number of available vehicles for different nodes, their energy requirements, and the vehicles’ charging capacities. After receiving the market participants’ bids, the market operator centrally allocates the resources such that welfare is maximised.
Formally, there is a set of time periods T indexed by t and a set of network nodes N indexed by n. The generation and demand resources are reflected by the sets G and D, indexed by g and d, respectively. Notice that any type of prosumers such as EVs can be considered part of both sets. Therefore, we denote them separately by index v and set V. Finally, the system resources located in node n are assigned to the subsets , , and . is a subset of N and includes each node m that is directly connected to node n.
The following outlines the bidding language and the allocation problem for the different resource types. The allocation problem is adapted from various models found in the literature (e.g., [
44,
69,
81,
82]), while the formulation of EVs is explicitly based on Hanemann and Bruckner [
23] and Zoltowska and Lin [
38]. All the sets, variables, and parameters mentioned in the following subsections can be found in the
Table A1,
Table A2 and
Table A3 in
Appendix A.
5.1. Generation Resources
The bidding language for generation resources we use here represents only the most basic constraints that any type of generation should consider. We opt for an abstract and simple model that can represent any type of generation to keep the complexity low. However, to fully represent a particular type of generation resource, extra constraints would need to be included (e.g., ramping constraints for gas, and curtailment constraints for VRE such as solar). We leave such tasks for future research, and focus instead on how to accommodate pricing rules under our simpler allocation model.
The capacity of each generation resource is given by
(
), and the minimum output level by
(
). The generated power
(
) must thus lie in between:
where
(
) describes the commitment decision.
Every generation resource has a cost function
, which consists of fixed and variable cost components. These include commitment costs and marginal generation costs, which are given by
(
), and
(
). The total costs for each generation resource can be written as follows:
5.2. Demand Resources
Demanders can submit multi-part bids including different load parts, namely fixed loads and elastic loads. Fixed loads represent short-term inelastic demand. They must be fulfilled under any circumstances and can neither be adjusted in quantity nor shifted in time. Elastic loads are flexible in the sense that they can be adjusted within the minimum and maximum output restrictions of the demand resource. They are only fulfilled when it is economically viable to do so. The total load per demand resource d and time period t is the aggregate of the two load parts.
The notation of the power quantities are
(
) for fixed loads, and
(
) for elastic loads. The total load must lie in between the minimum consumption requirement
(
) and the capacity
(
). Given the commitment status
(
), the following inequality must hold:
Demanders perceive fixed loads as basic needs and thus will accept any price. In contrast, demanders only want to consume elastic loads if their valuation
(
) exceeds the electricity price. Hence, the total valuation
is solely a function of elastic loads:
5.3. Electric Vehicles
The bidding language for EVs essentially takes into account technical restrictions for the state of charge and the (dis-)charging quantities. The state of charge for each EV
v and period
t is denoted by the decision variable
(
). Likewise, the charging quantity of EV
v in period
t is defined by
(
), and the discharging quantity by
(
). Given the capacity requirements
(
) and
(
), the electricity demand for driving
(
), as well as the (dis-)charging efficiencies
(
) and
(
), the state of charge is defined by the following equations:
Constraints (2e) and (2f) formulate the state of charge as a function of scheduled (dis-)charge plus unscheduled power demand (i.e., driving). By Equation (2g), it is assumed that the vehicles are fully charged at the end of each day. (This condition can be easily changed. We designed in this way to fit in the experimental setting. An alternative is to consider them fully charged before departure.) Constraint (2h) establishes that the state of charge is limited by the minimum and maximum capacity requirements of the vehicle’s battery.
For the (dis-)charging processes, a limit on the maximum (dis-)charged power
(
) must be maintained. Note that the parameter has a value of zero when EV
v is unplugged in period
t. Furthermore, it is only possible to either charge or discharge an EV
v in period
t. This binary decision is denoted by the variable
(
), which equals one if EV
v is charging in period
t and zero if it is discharging.
M is a parameter described by the following equations:
5.4. Transmission Network
The transmission network is modelled as a lossless
direct current (DC) power flow model. The power flows
on the transmission lines
are defined through
Kirchhoff’s second law. Given the phase angles
(
) and the susceptance
(
), the mesh rule can be stated as:
In order to obtain a unique solution for phase angles, the phase angle of the reference node
is fixed to zero, as follows:
Kirchhoff’s first law ensures that the power supply and inflows equal the power demand and outflows. We assume that negative values on line
are outflows (
) and positive values on line
are inflows (
). The power balance is thus enforced by:
Finally, the power flows are restricted by line capacities
(
), as follows:
5.5. Allocation Problem
Given the technical costs and restrictions of all power system resources, the market operator determines the optimal allocation by solving the following mixed integer linear programming problem:
The objective is a negative representation of the social welfare, including suppliers’ costs and demanders’ values. The constraints (
2a)–(
2o) represent the technical restrictions of all power system resources described above.
6. Numerical Experiments
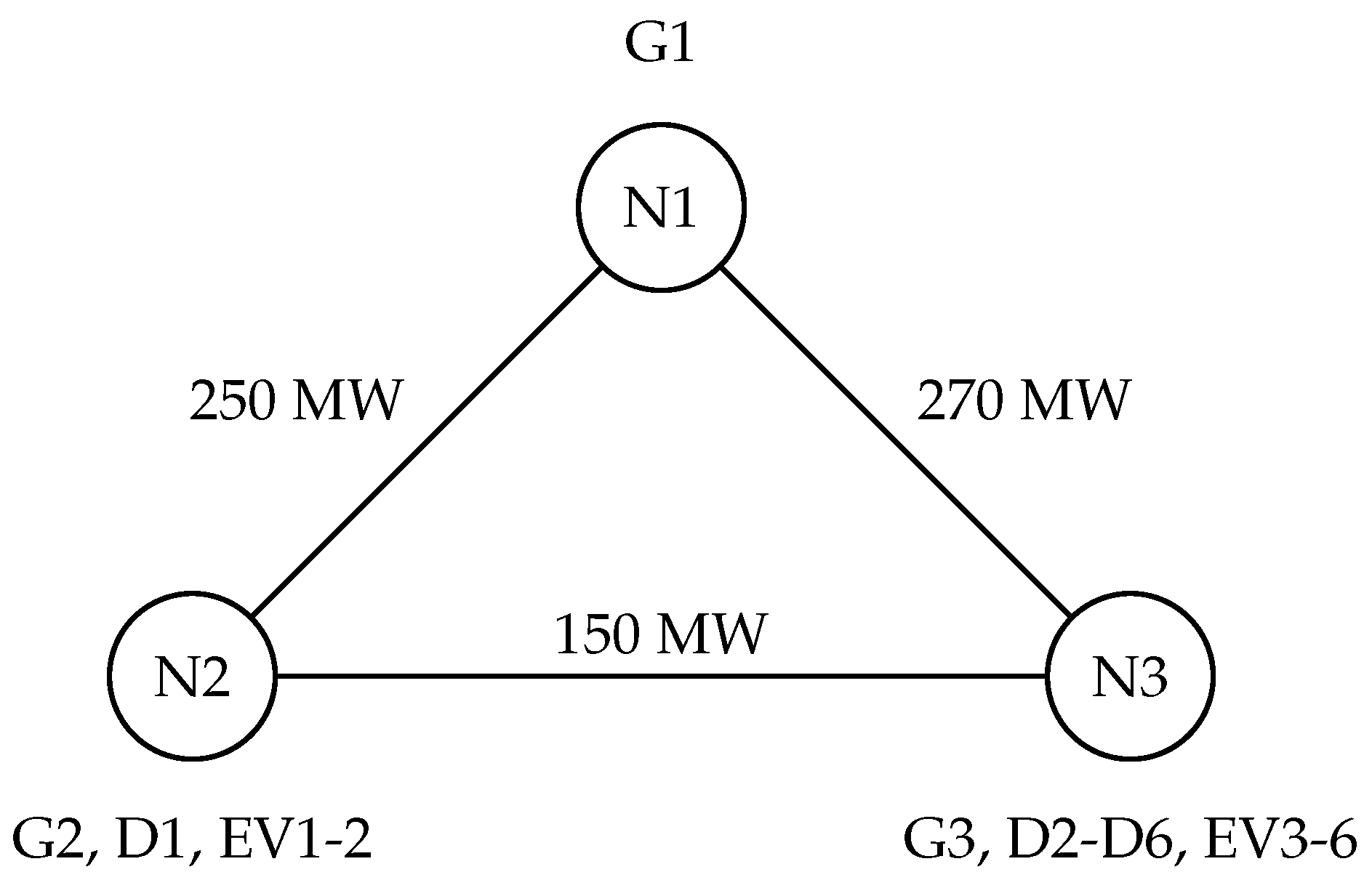
In our implementation, IP and ELM pricing schemes are only applied to a simple three-node, 24 h example (see
Figure 2). In order to analyse the impact of EVs on pricing and their potential interference with other endeavours, such as demand flexibility, we consider three different scenarios:
Scenario 1 (reference case): absence of EVs, absence of demand flexibility;
Scenario 2: presence of EVs, absence of demand flexibility;
Scenario 3: presence of EVs, presence of demand flexibility.
The data, code, computed values, and respective plots can be found in the online repository [
83]. Given the size of the problem we analyse here, computing both the allocation problem and the IP/ELM pricing problems (using OR-Tools [
84] in Python) takes just a few seconds (on a Mac Mini 2020 with M1 processor).
More realistic settings (e.g., smart-grid with dozens of nodes, incorporating travel distance, losses, specific generation resources, etc.) will be intrinsically more complex, and would require more computational power. Kotzur et al. [
85] provide a detailed discussion of techniques to handle more complex environments, where things such as decomposition methods play an important role in more real scenarios. Exact methods for mixed integer programs may struggle in larger settings. However, as reported by [
85], certain extra constraints, such as ramping, might even be beneficial in terms of computational complexity, because they narrow down the search space.
6.1. Numerical Example
The instance of our allocation problem is a modification of the numerical example of Wu [
86], also used by Zoltowska [
81]. It consists of a three-node network with three generation resources (G1–G3) and six demand resources (D1–D6). The network topology is presented in
Figure 2. We assume the susceptance
of every transmission line to be 1. Each auction round spans 24 h (instead of Wu’s two hours) in order to account for typical load profiles and driving characteristics of EVs.
Table 2 reports the multi-part offers of generation resources. As in Wu [
86], all generation resources have time-constant costs and output constraints. To obtain typical demand profiles for 24 h, we calculated the average of the total grid load in Germany on all weekdays in 2021 (based on data available at [
87]). Subsequently, we scaled the load profile to the numerical example using the peak demand of each demand resource in Wu’s original example. The visualisation of the load profiles for each node is included in
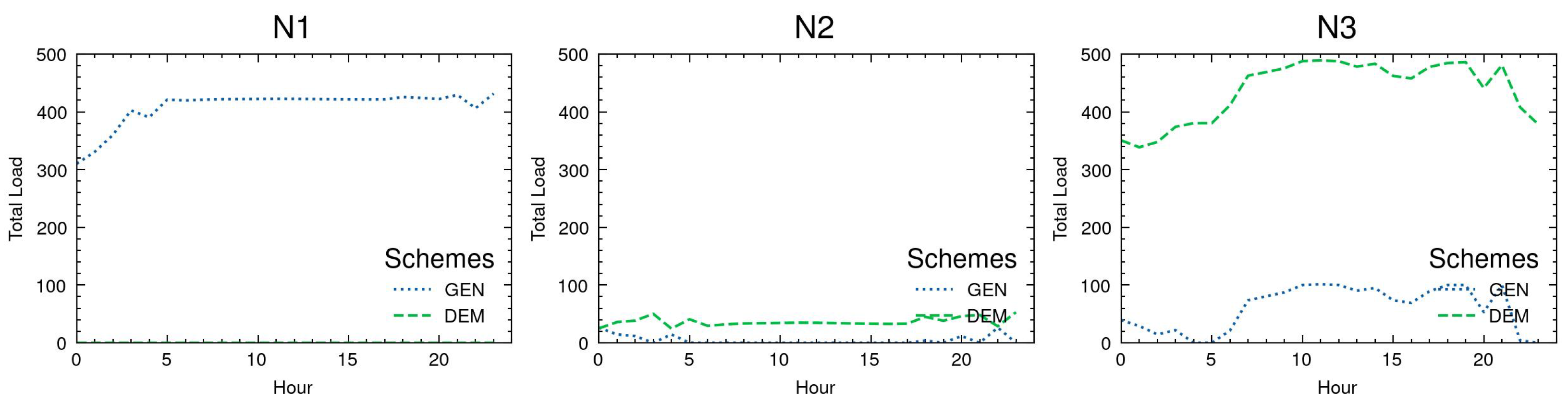
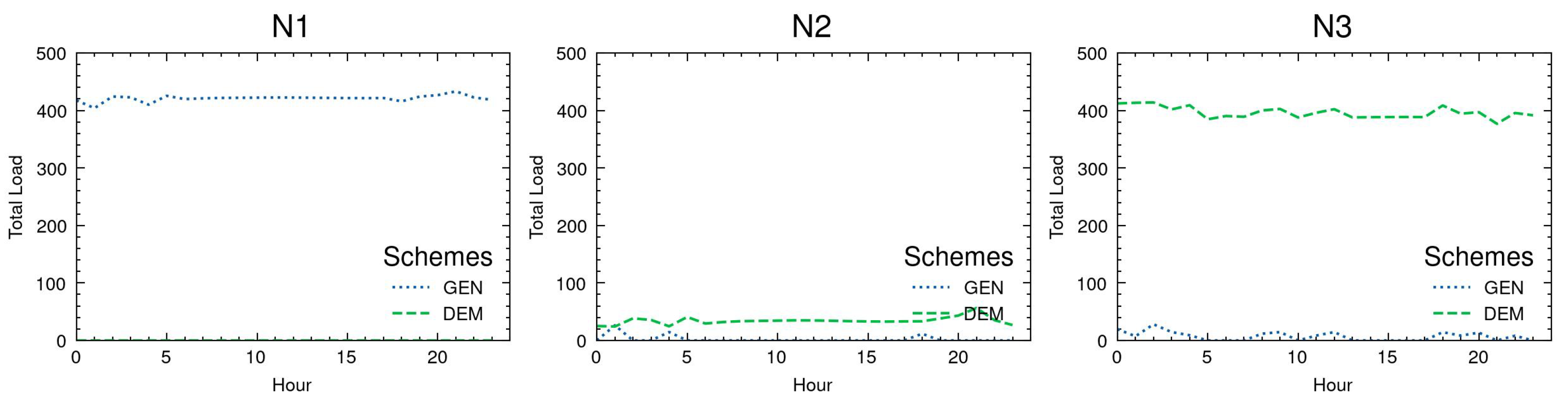
Figure 3. D2–D6 share the same load profile and thus account for one fifth of the total demand in N3.
For Scenarios 2 and 3, EVs with similar driving characteristics are grouped into fleets.
Table 3 reports the relevant parameters, which are essentially based on the case study of Zoltowska and Lin [
38], which is itself a modification of the numerical example of Khodayar et al. [
88]. We include a sixth fleet that is parked 24 h a day and thus serves as a full-time storage solution. The (dis-)charging efficiencies
/
are set to 100%. We further assume that EVs only have a (dis-)charging option at their own nodes. As pointed out in
Section 5, the maximum (dis-)charge in
Table 3 is zero when the EV is not plugged in.
In Scenario 3, D2–D6 are willing to provide demand flexibility through elastic loads. The demand of D1 remains inflexible. Following Wu [
86] and Zoltowska [
81], we reduce the fixed load parts of D2–D6 to 80% of the values in Scenario 1 and convert the other 20% into elastic load parts. The valuations
for flexible demand are USD 20.80/MWh for D2, USD 18.40/MWh for D3, USD 16.00/MWh for D4, USD 13.60/MWh for D5, and USD 11.20/MWh for D6. Besides, we assume that there is no minimum output requirement
, only a maximum capacity
of 100 MW. This is slightly higher than the peak demand of 97.80 MWh in Scenario 1.
6.2. Results
In this section, we compare the prices and uplifts of the IP and ELM pricing schemes across all three scenarios. For better understanding, we also discuss the optimal allocation in each case.
It is important to notice that in practical terms, both IP and ELM pricing are based on current implementations from real electricity markets. For instance, in the real-time electricity markets in the US, allocation and pricing problems are solved every 5 min considering thousand of nodes [
89]. For this purpose, similar methods to the ones described in our experiments are used, but with the appropriate computational resources.
6.2.1. Scenario 1
Scenario 1 is the reference case without EVs and without demand flexibility.
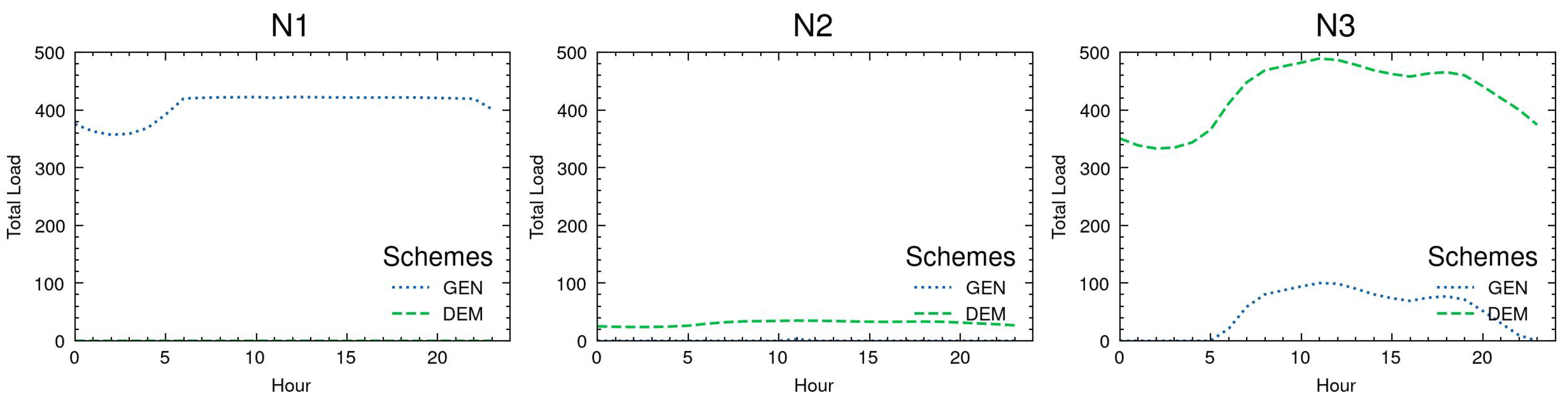
Figure 3 displays the respective demand and supply curves. The results show that G1 essentially covers the base load in N2 and N3. In hours 6 to 22, G3 supplies additional power to meet the increased demand requirements. G2 is only dispatched at peak load in hour 11.
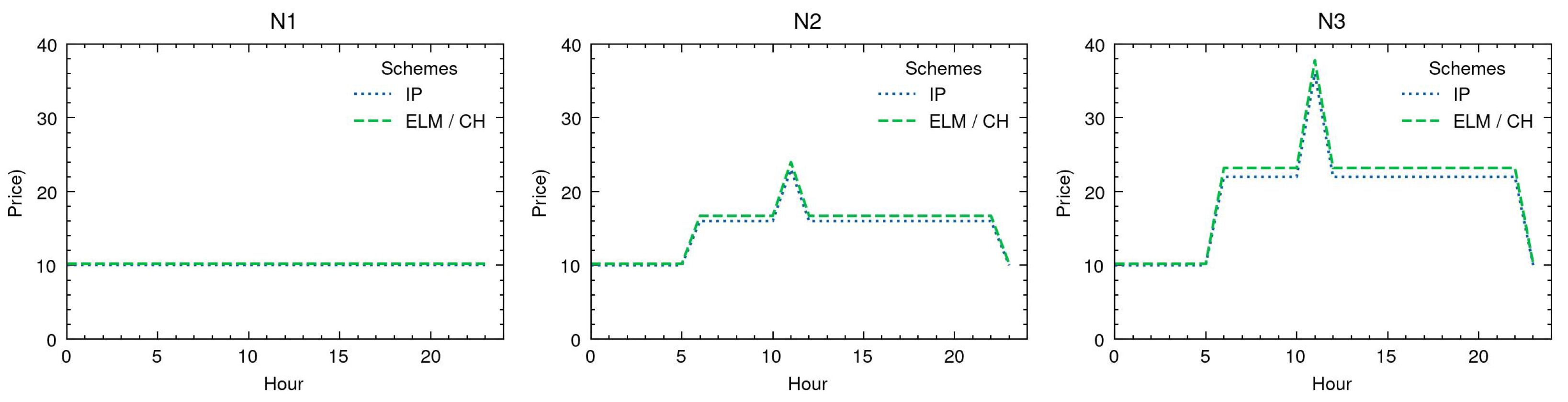
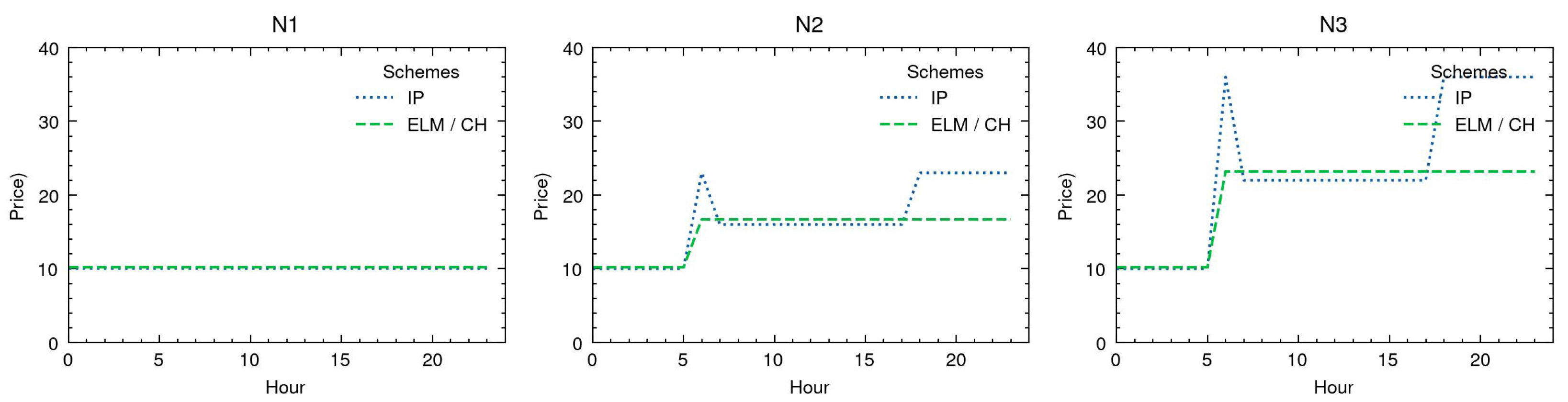
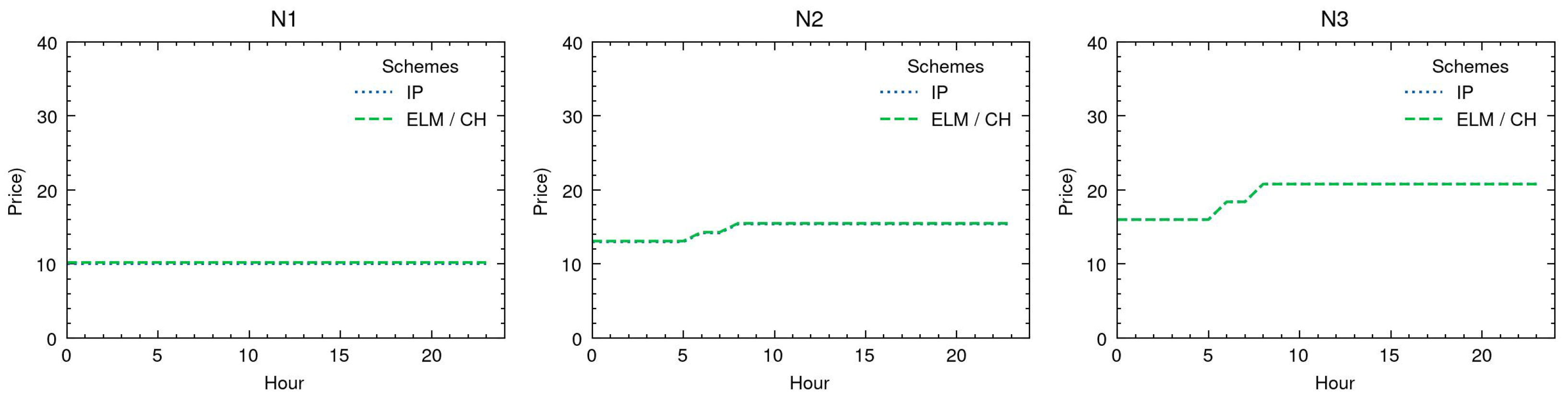
Figure 4 depicts the corresponding IP and ELM prices. They generally show the same pattern and differ only slightly in value. The IP prices correspond to the marginal costs and the ELM prices to average costs at full capacity of producing/consuming 1 MWh more. Accordingly, ELM prices include a proportion of the commitment costs and are slightly larger than IP prices [
63].
In N1, there is only one price level equivalent to the cost of G1, that is, USD 10.00/MWh for IP pricing and USD 10.20/MWh for ELM pricing. In N2 and N3 there are three price levels each. The IP prices are USD 23.00/MWh in hour 11, USD 16.00/MWh in hours 6–22, and USD 10.00/MWh in the remaining hours. The ELM prices are USD 24.00/MWh, USD 16.70/MWh, and USD 10.20/MWh. The prices correspond (in this order) to the cost of producing 1 MWh more with G2, equal parts of G1 and G3, and G1. In N3, the IP scheme derives the prices USD 36.00/MWh, USD 22.00/MWh, and USD 10.00/MWh. With ELM, the prices are USD 37.80/MWh, USD 23.20/MWh, and USD 10.20/MWh. The price peak results from a binding transmission constraint, which leads to a situation where the generation of one additional unit of output requires 2 MWh more of G2 and 1 MWh less of G1. The middle price corresponds to the cost of G3 and the low price to the cost of G1.
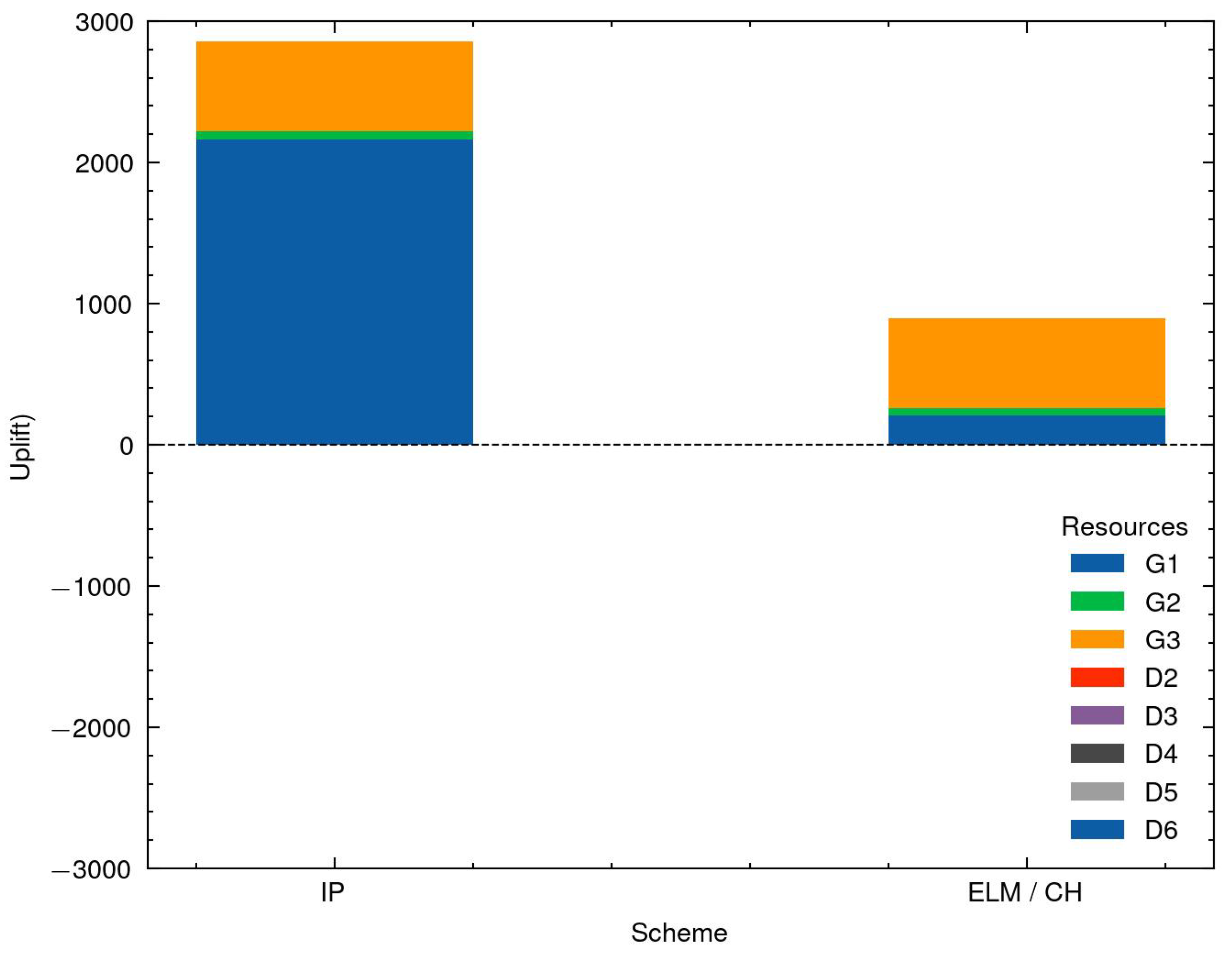
The respective uplifts for Scenario 1 are displayed in
Figure 5. ELM pricing provides considerably smaller uplifts than IP pricing. The main reason is presumably that the IP prices are lower than the ELM prices. Higher side-payments are needed to compensate the suppliers for losses. In particular, IP pricing requires USD 2860.00 for uplifts, while it is only USD 897.65 with ELM.
An important remark is that uplifts are not public information, meaning that any non-participant will only observe the public prices in
Figure 4. As in this particular case, IP prices have smaller values than ELM prices, so they might seen more attractive for the demand side. In reality, a share of the necessary uplifts is typically collected from the demanders.
6.2.2. Scenario 2
In Scenario 2, we incorporate EVs in a bidirectional model (acting as demand and supply). For one thing, this increases the total daily demand from 10.95 GWh to 11.33 GWh due to additional energy requirements for driving. For another, it adds a storage option for electricity to the allocation model.
Figure 6 reports the respective demand and supply curves. Overall, the demand in N2 and N3 is very similar to Scenario 1. The extra demand in Scenario 2 is most evident in the off-peak-hours of Scenario 1 and/or the afternoon. The dispatch of generation resources changes in that G2 is only dispatched in hour 21 (instead of 11) and G3 is online in hours 7–19 and 21 (instead of 6–22). The remaining power supply in
Figure 6 comes from discharging EV batteries, for example, in hours 0 to 6 in N2 and N3.
The prices of Scenario 2 are depicted in
Figure 7. In N1, the prices remain the same as in Scenario 1. However, some differences emerge in N2 and N3. For IP pricing, the times of the price peaks shift to hour 6 and hours 18–23. Interestingly, the price peaks do not coincide with peak loads but result from the interaction of supply, demand, and storage over time. Apart from this, the low prices continue to be in hours 0–5, and the middle prices are in the remaining hours 7–17. For ELM pricing, there are no longer price peaks. The low prices are in hours 0–5, and the middle prices in hours 6 to 23.
The different price patterns can be explained by the underlying models. In the IP pricing scheme, the integer variables are relaxed and fixed by additional constraints to the solution values of the allocation problem. In the ELM pricing scheme, the integer variables are relaxed and can take any value between their lower and upper bound. Therefore, IP pricing produces a solution equivalent to the allocation problem, while ELM pricing might produce a different solution. The additional flexibility reduces the often criticised price volatility of IP pricing and prevents price spikes in our numerical experiments.
Figure 8 shows the uplifts of Scenario 2. IP pricing results in a large positive uplift for G1 (USD 2160.00), a small positive uplift for G2 (USD 60.00), and a large negative uplift for G3 (USD −2520.00). The positive uplifts compensate G1’s and G2’s losses under the respective IP prices, while the negative uplift offsets G3’s high revenues from generation at peak prices. The financial imbalance is USD −300. With ELM pricing, the total uplifts are USD 474.97, about half those of Scenario 1. Accordingly, the financial balance has been improved with the participation of EVs.
6.2.3. Scenario 3
In Scenario 3, in addition to the EVs, we also allow demanders to have a portion of flexible demand. This increases the flexibility in the allocation problem and further allows one to decrease the total daily demand from 11.33 GWh in Scenario 2 to 10.27 GWh.
Figure 9 reports the respective demand and supply curves. The load profiles in N2 and N3 are significantly smoothed compared to the previous scenarios. In fact, the demand is fully met by G1 and discharging of EV batteries. G2 and G3 stay offline.
Figure 10 presents the corresponding prices. In general, the prices are lower and less volatile than in Scenarios 1 and 2. Between IP and ELM prices, there are only little to no differences. In N1, the prices remain the same as in the previous scenarios. In N2, the IP prices are USD 13.00/MWh in hours 0–5, USD 14.20/MWh in hours 6 and 7, and USD 15.40/MWh in hours 8–23. Respectively, the ELM prices are USD 13.10/MWh in hours 0–5, USD 14.30/MWh in hours 6 and 7, and USD 15.50/MWh in hours 8–23. The prices are based on both G1’s cost and the demanders’ valuations. In N3, both pricing schemes produce a price of USD 16.00/MWh in hours 0–5, USD 18.40/MWh in hours 6 and 7, and USD 20.80/MWh in hours 8–23. These prices are solely set by the demanders’ marginal valuations. Because there are no fixed costs, the marginal and average costs/valuations are equivalent, and thus the IP and ELM schemes produce the same prices.
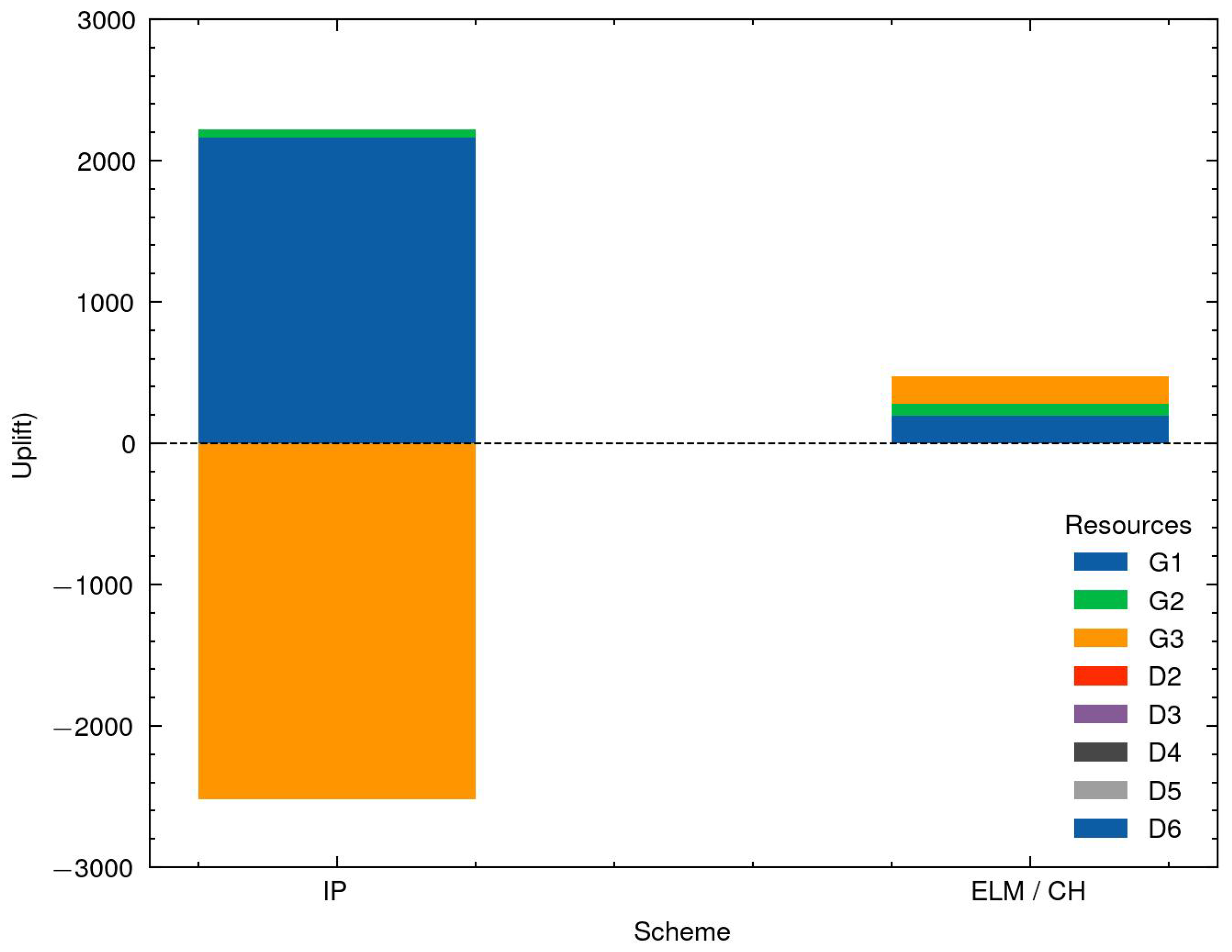
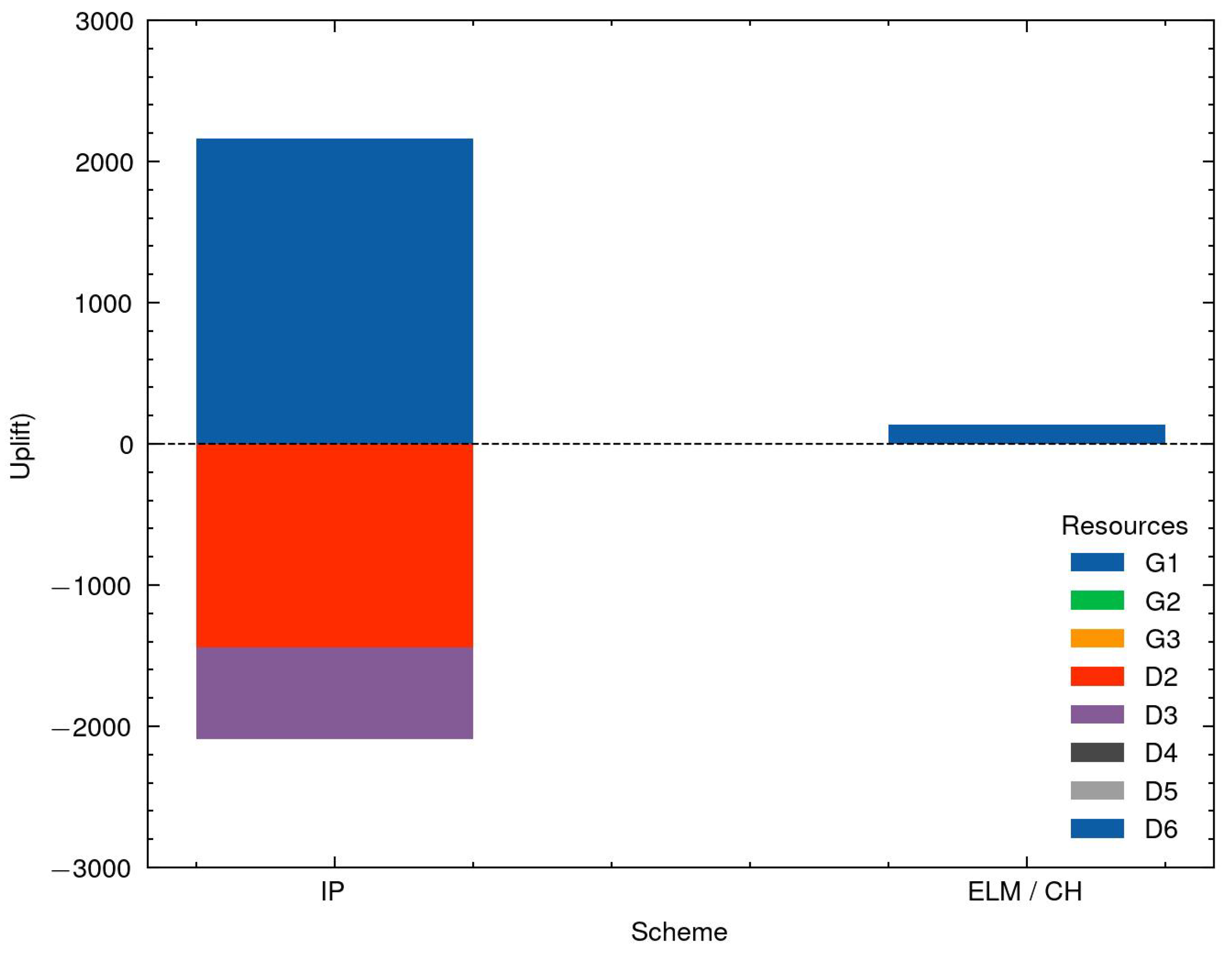
The uplifts of Scenario 3 are displayed in
Figure 11. On the supply side, G1 receives an IP uplift of USD 2160.00. No money is paid to G2 or G3, because they are offline and under the given prices there are no lost opportunity costs for dispatch. On the demand side, the IP uplift for D2 is USD −1442.87 and for D3 USD −646.44 in order to offset their profits. The financial imbalance is USD 70.68. With ELM pricing, only G1 receives an uplift of USD 139.05. There are no opportunity costs for any other market participants to deviate from the market allocation. In absolute terms, the ELM uplifts in Scenario 2 and 3 are significantly lower than for IP, whereas the financial imbalance is higher. However, this seems more like a coincidence compared to Scenario 1 and what is typically reported (see e.g., [
2,
5,
63,
70]).
7. Discussion
The goal of this paper was to asses a variety of pricing schemes in electricity markets with EV penetration. Because we designed this model on a nodal system, it could easily fit in a smart-grid context, where several allocation and pricing problems are solved within a region. In our model, we discussed a few of those pricing schemes, prioritizing the ones that currently work in electricity markets around the world. We discussed some economic properties of them and particularly focused on the concepts of competitive equilibrium (if participants want to deviate from the proposed solution) and financial balance (if extra money is needed to ensure participation), as well as the price signals those schemes send.
In order to incorporate different pricing schemes, we start with an allocation model based on the literature, where we consider general constraints for generation, demand, and transmission for the wholesale market. It is possible to build upon our model, creating a more complex environment where specific type of generation resources (such as solar) can be incorporated through the inclusion of extra constraints (e.g., ramping, curtailment, etc.). We leave such extensions for future work, and in our paper, we instead focus more on an active demand side and prosumers:
Participation of EV aggregators in a V2G model;
Demanders that have a a fixed load that they want to fulfil regardless of the price, and another demand component that is only fulfilled when it is economically viable.
For our experiments, we selected some of the most used pricing schemes in pool models such as most US electricity markets, namely IP pricing and ELM pricing. In terms of their economic properties, both pricing schemes support competitive equilibria under the definition we consider in this paper, and both violate financial balance. This imbalance can be substantial, as seen in Scenario 1 of our experiments. It is important to notice that Bichler et al. [
71] considers a definition of competitive equilibrium more in line with economic theory, where financial balance is required. Therefore, under their definition, both IP and ELM pricing do not support competitive equilibria.
IP pricing distributes the positive and negative uplifts (which can be very large, as seen in
Figure 11, for example), whereas ELM pricing compensates the differences between potential deviations and the optimal allocation. Even though the total financial imbalance of ELM pricing is bigger than the one from IP pricing in two of three scenarios, ELM pricing seems to provide a less risky option, because individual uplifts are smaller and do not show extreme values as in the case of IP pricing. Additionally, ELM prices seem to better reflect the additional flexibility of EVs (see
Figure 7), smoothing the prices throughout the day (compared with the spikes in prices associated with IP pricing), providing a more suitable option for EV aggregators to be incorporated.
A very critical point that we discuss in this paper regards the price signals these two schemes send. Uplifts are not public information, and they are only dealt internally; for instance, in IP pricing, we collect the surpluses from some generators and give it to others that make losses under the public prices. Those uplifts, even in very reduced settings such as the scenarios we studied in our experiments, are substantial (see
Figure 8, for example) compared to what ELM prices present. Large uplifts distort the market, as new participants may be discouraged to participate under current prices (low prices), or they may have the wrong expectations in terms of future revenues (high prices).
This issue is without a doubt one of the most important for a future integration of EVs and the increasing share of renewable energy sources. Recently, the President of the European Commission, Ursula von der Leyen stated “[…] this market system does not work anymore!” [
90]. Arguing that the rules that operate for most European electricity markets were designed when generation, transmission, and demand were very different. A drastic change seems inevitable and correct pricing rules are at the core of such changes—after all, most of the investment decisions are driven by that.
There are several open questions derived for our current paper. Large-scale experiments in a smart-grid would certainly help to observe other patterns driven by different pricing rules. We are particularly interested in understanding how to deal with EVs moving from one node to another when it is economically convenient (cheaper to charge, more expensive to discharge). A more realistic experiment would also help to understand the interaction of more complex types of flexibility (e.g., shiftable loads: those loads that can be moved to different times of the day, for example the use of a washing machine) and a V2G model in a smart-grid. Additionally, it would be interesting to address particular generation resources such as solar. In this regard, we would need to add to our model the respective technical constraints as well as the associated legislation and local policies.
Naturally, those more complex environments will lead to more complicated allocation and pricing problems to be solved. In particular, an active demand side with flexibility types such as shiftable loads and a V2G model impacts heavily on the allocation problem, adding (exponential) extra binary variables (for instance, a shiftable load allocated to any 30 min timeslot during the day). Without testing them, it is unclear how much these conditions would affect the efficiency of the proposed algorithms, and whether some compromises on the exactness of methods are needed or not.