Research on Pressure Control Algorithm of Regenerative Braking System for Highly Automated Driving Vehicles
Abstract
:1. Introduction
2. Materials and Methods
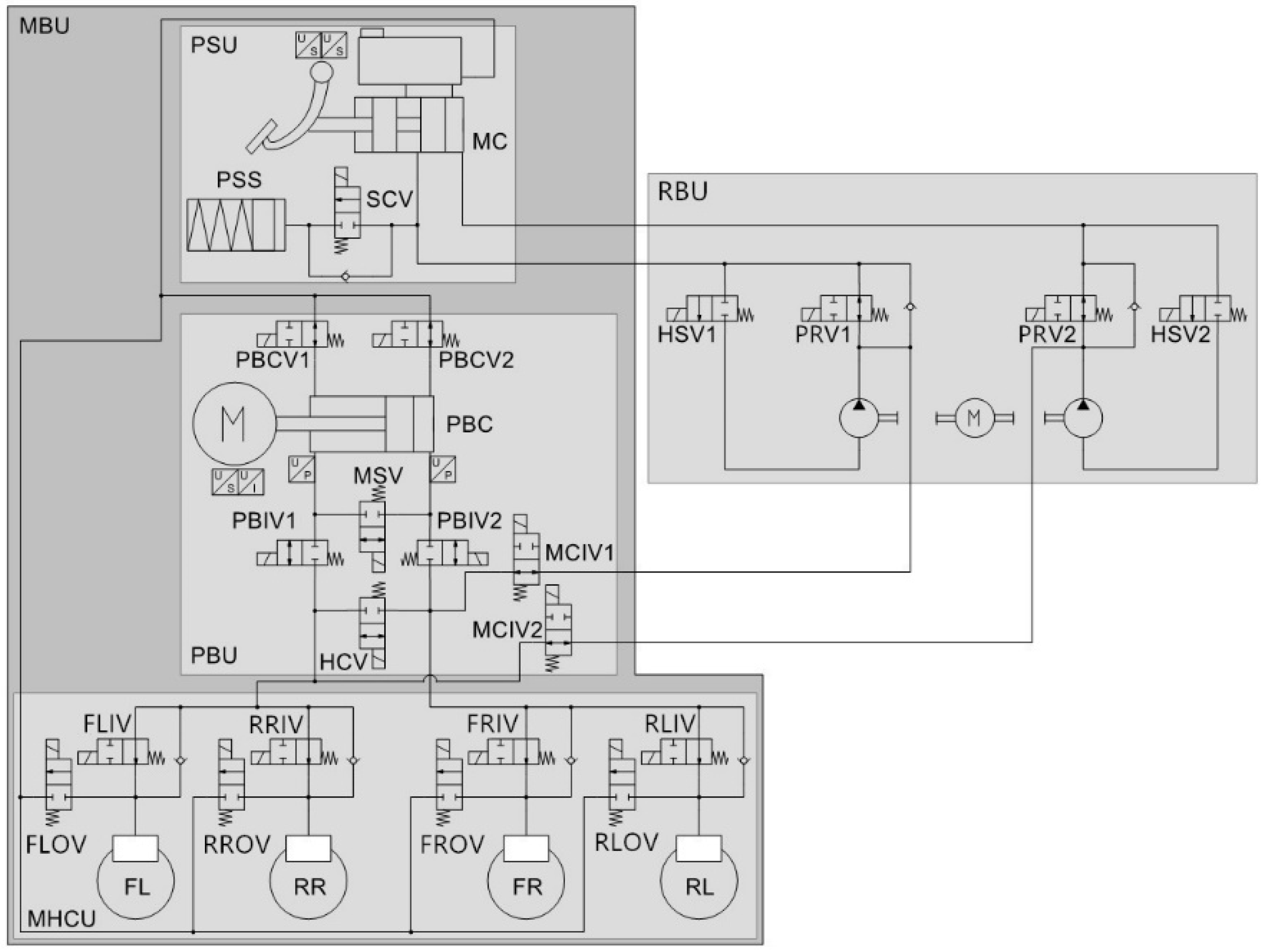
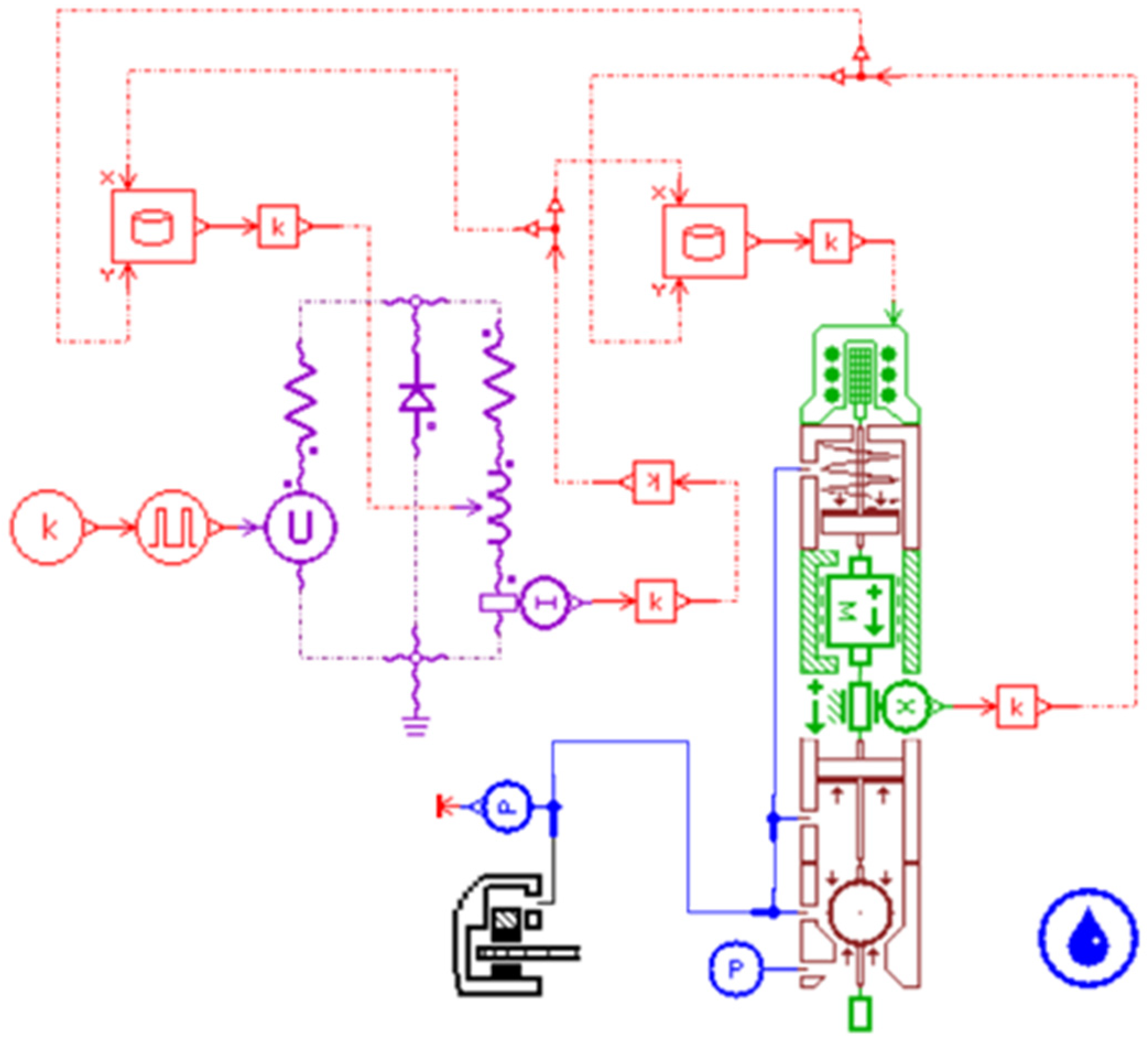
2.1. Regenerative Braking System
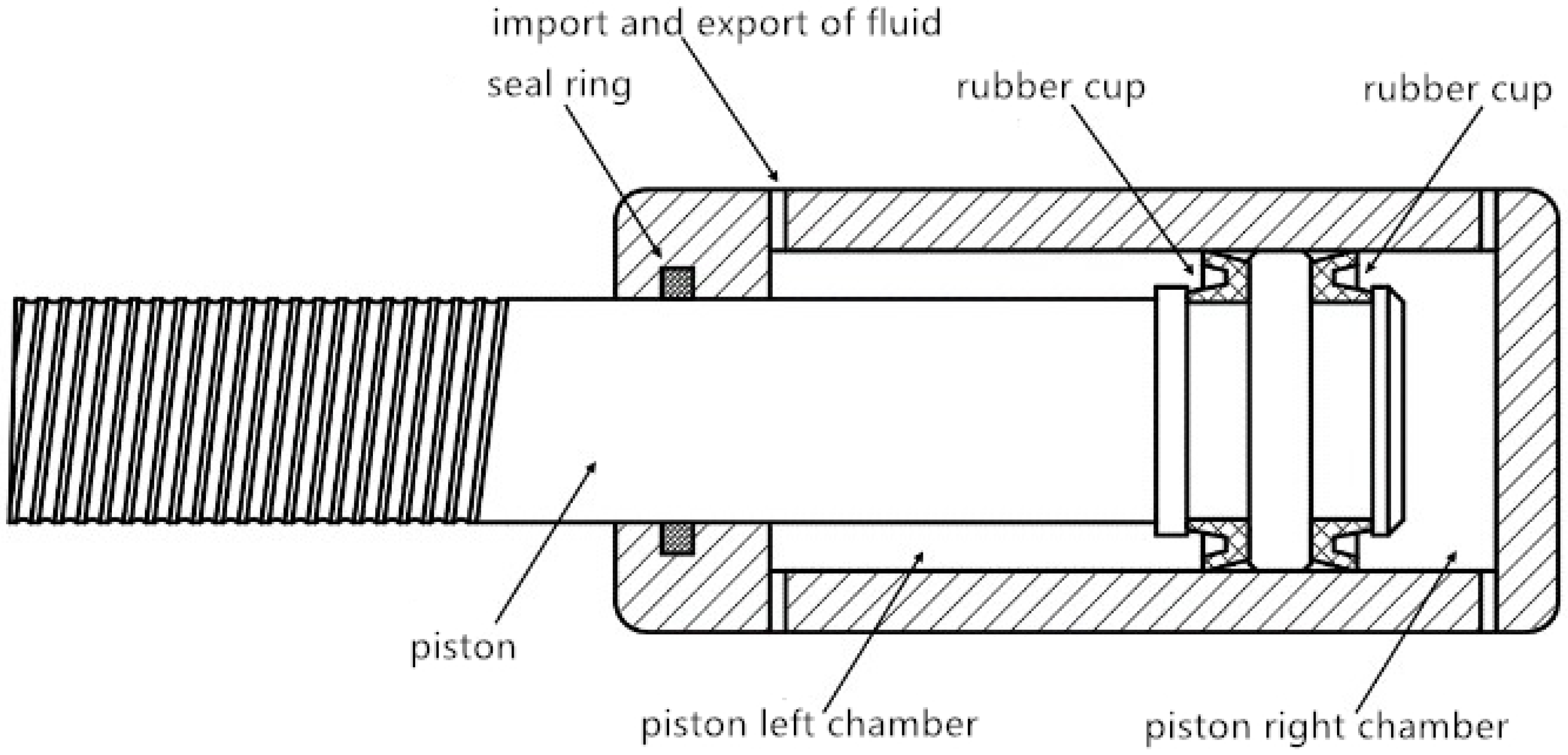
2.1.1. Mechanical Structure of the Regenerative Braking System
2.1.2. Working Principle of the Regenerative Braking System
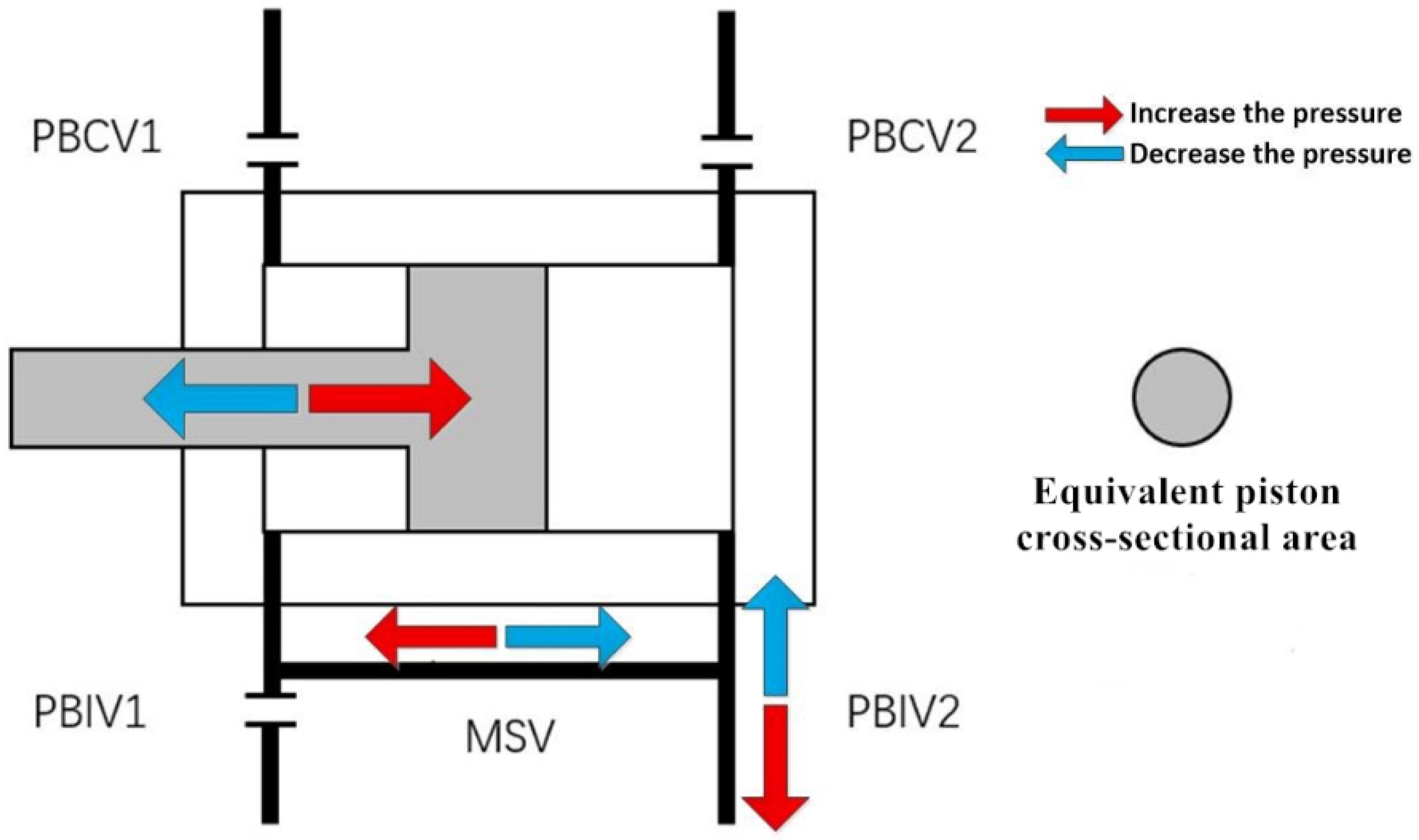
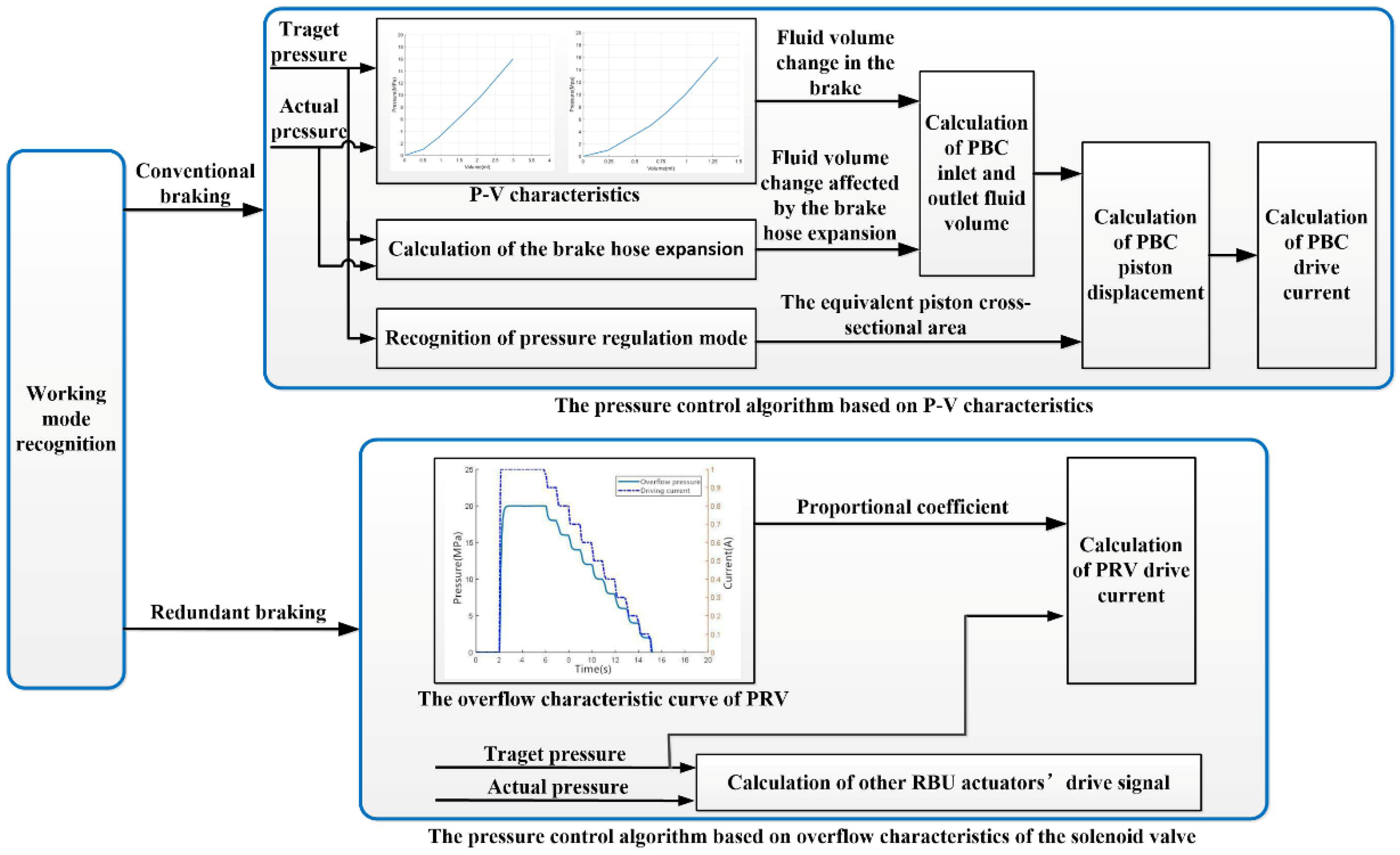
2.2. Pressure Control Algorithm
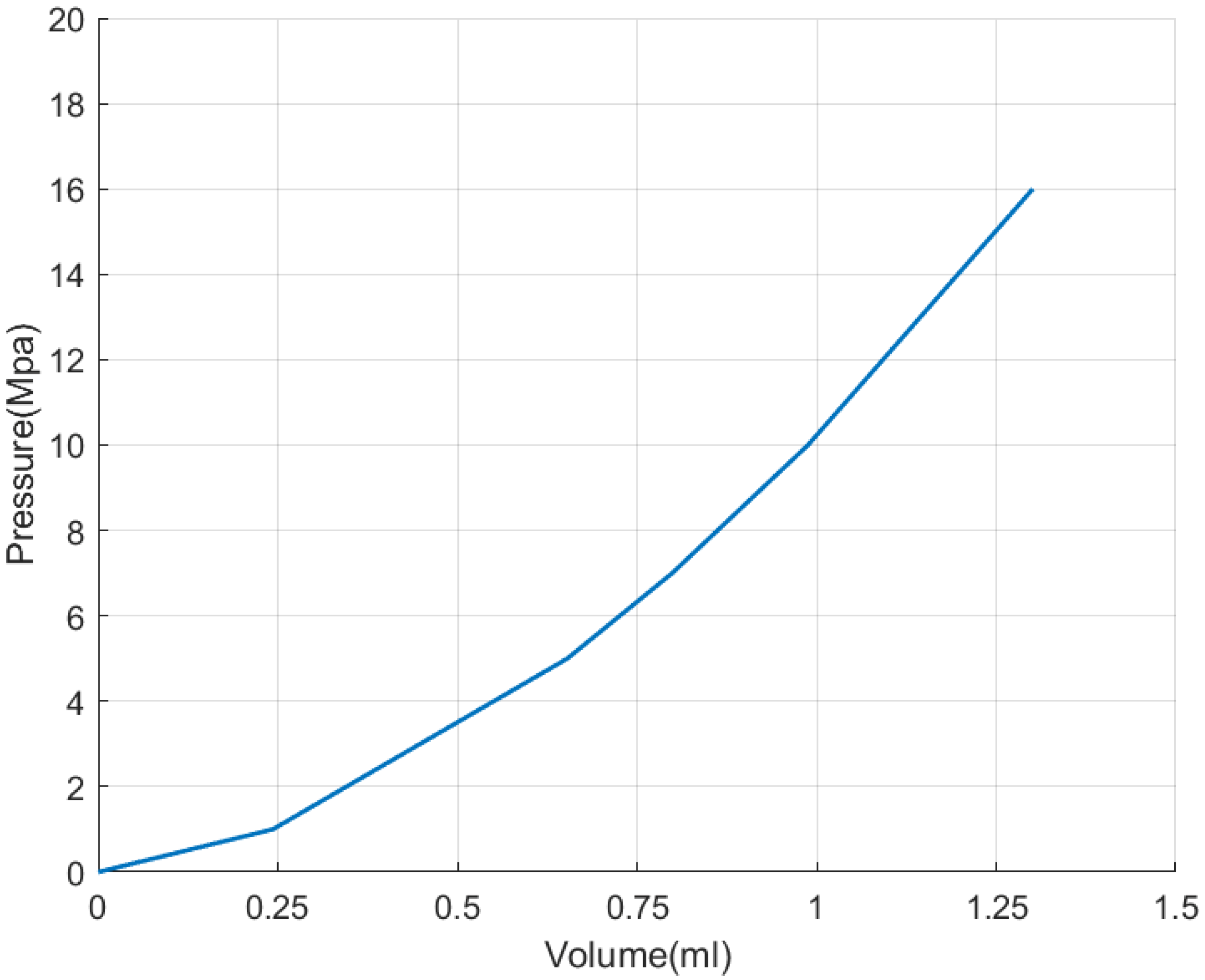
2.2.1. The Pressure Control Algorithm Based on P-V Characteristics
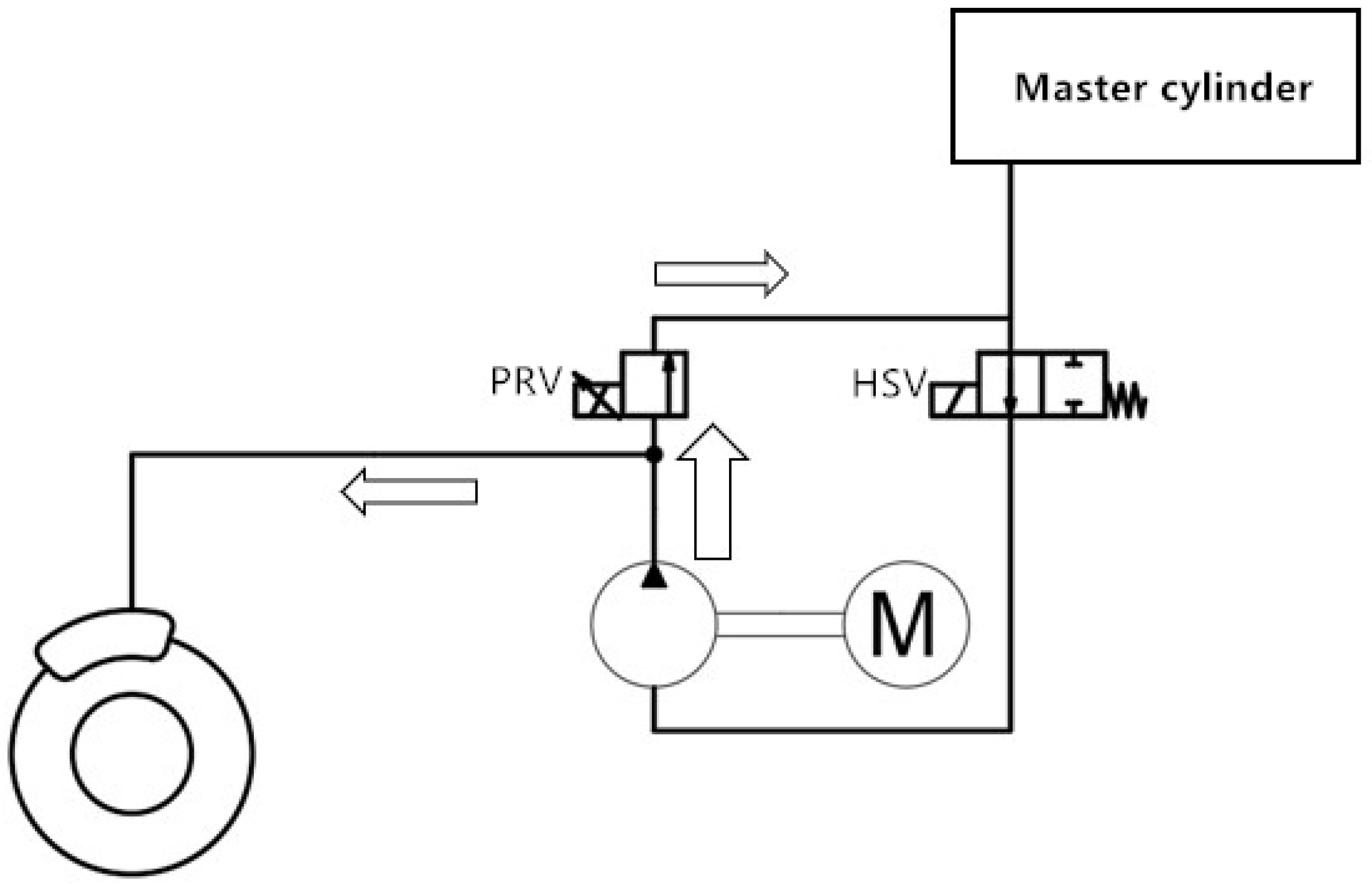
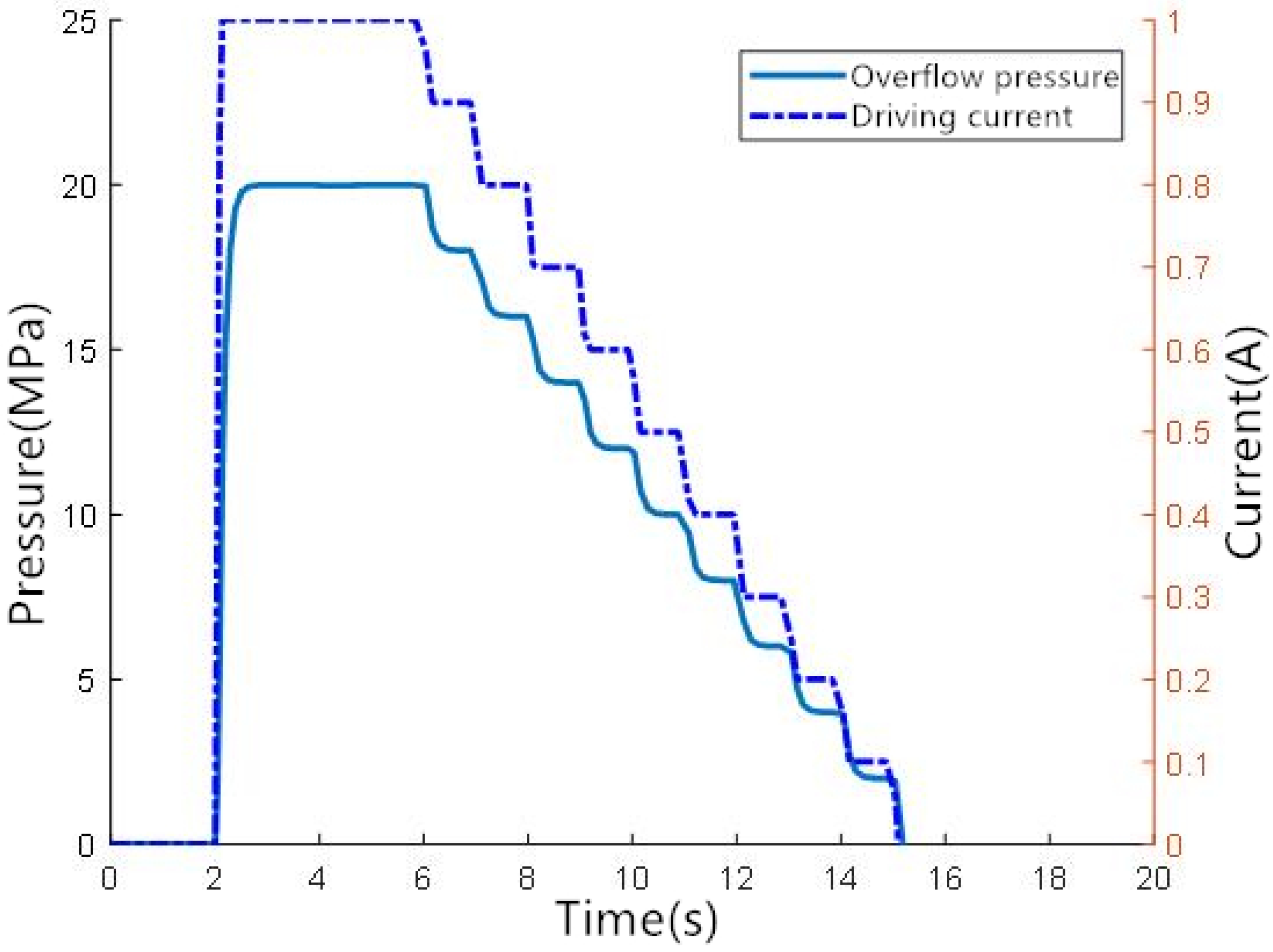
2.2.2. The Pressure Control Algorithm Based on Overflow Characteristics of the Solenoid Valve
3. Results and Discussion
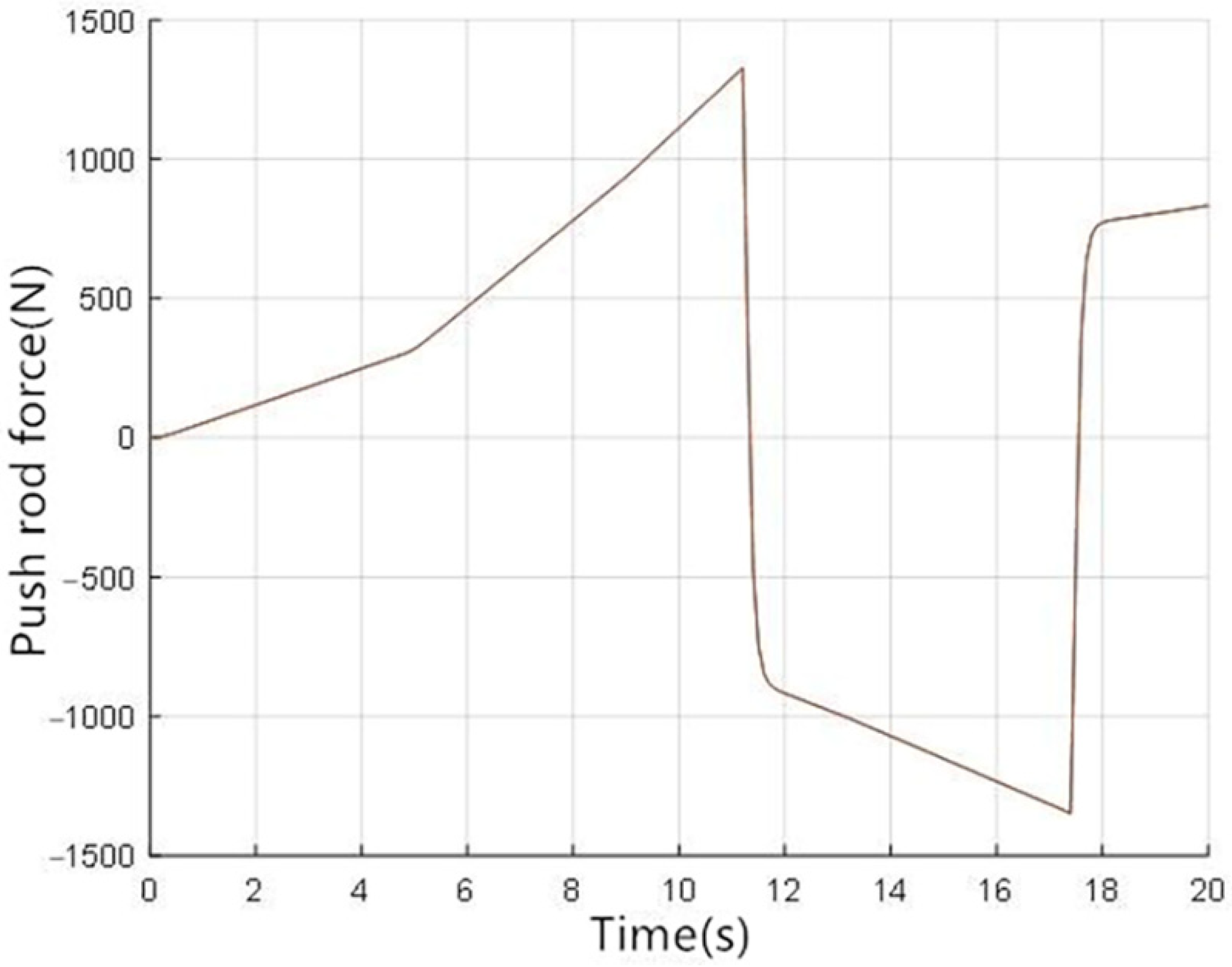
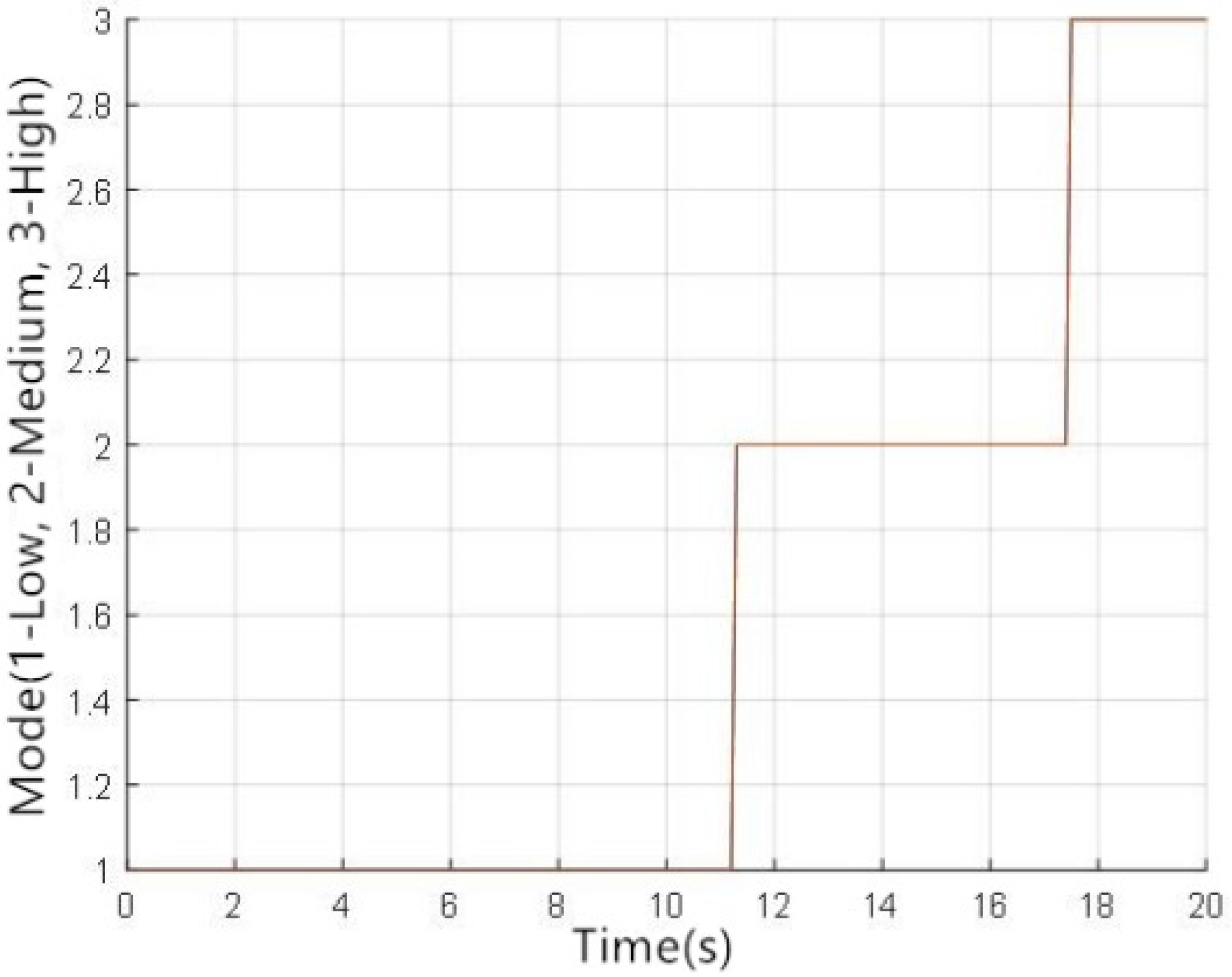
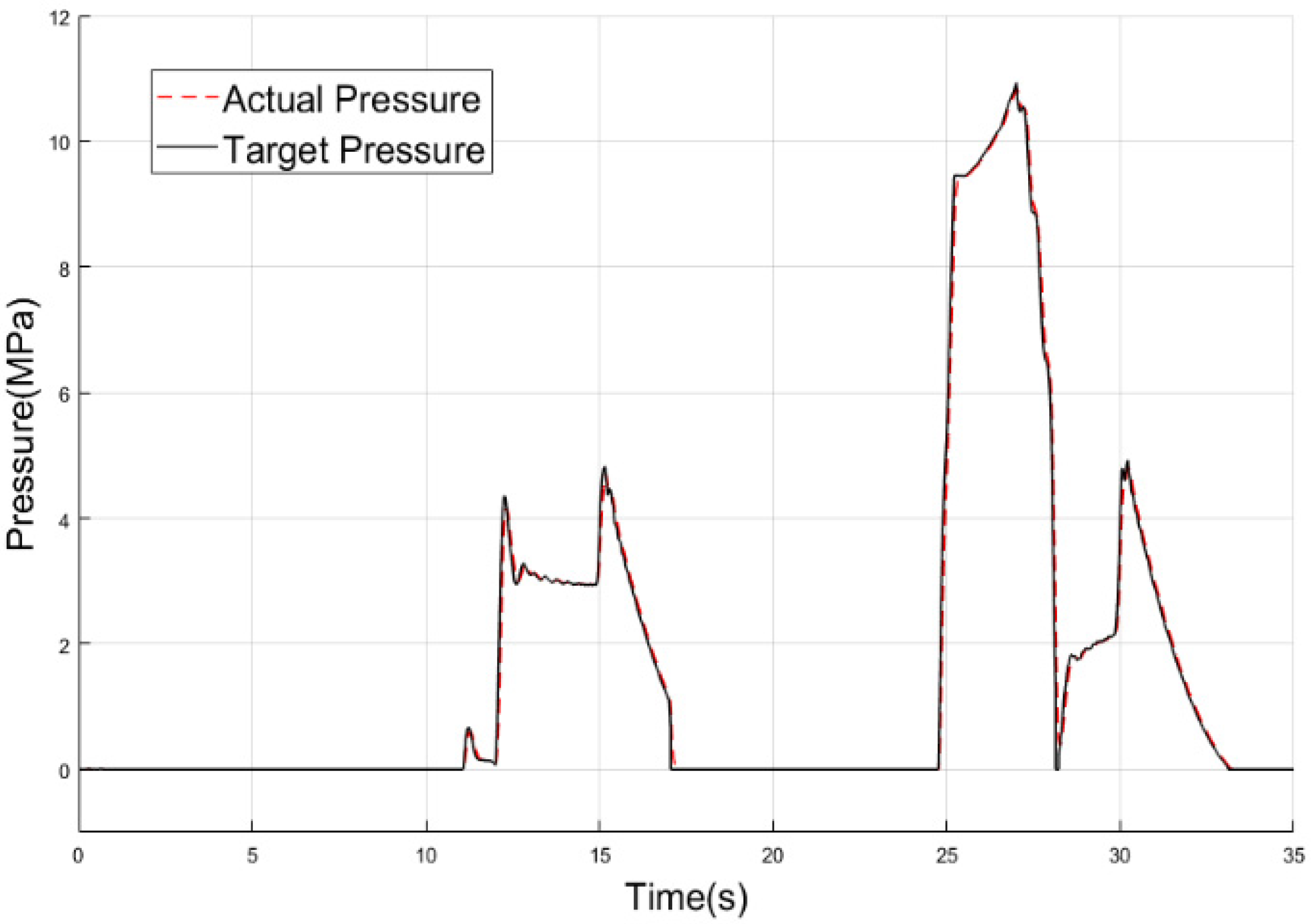
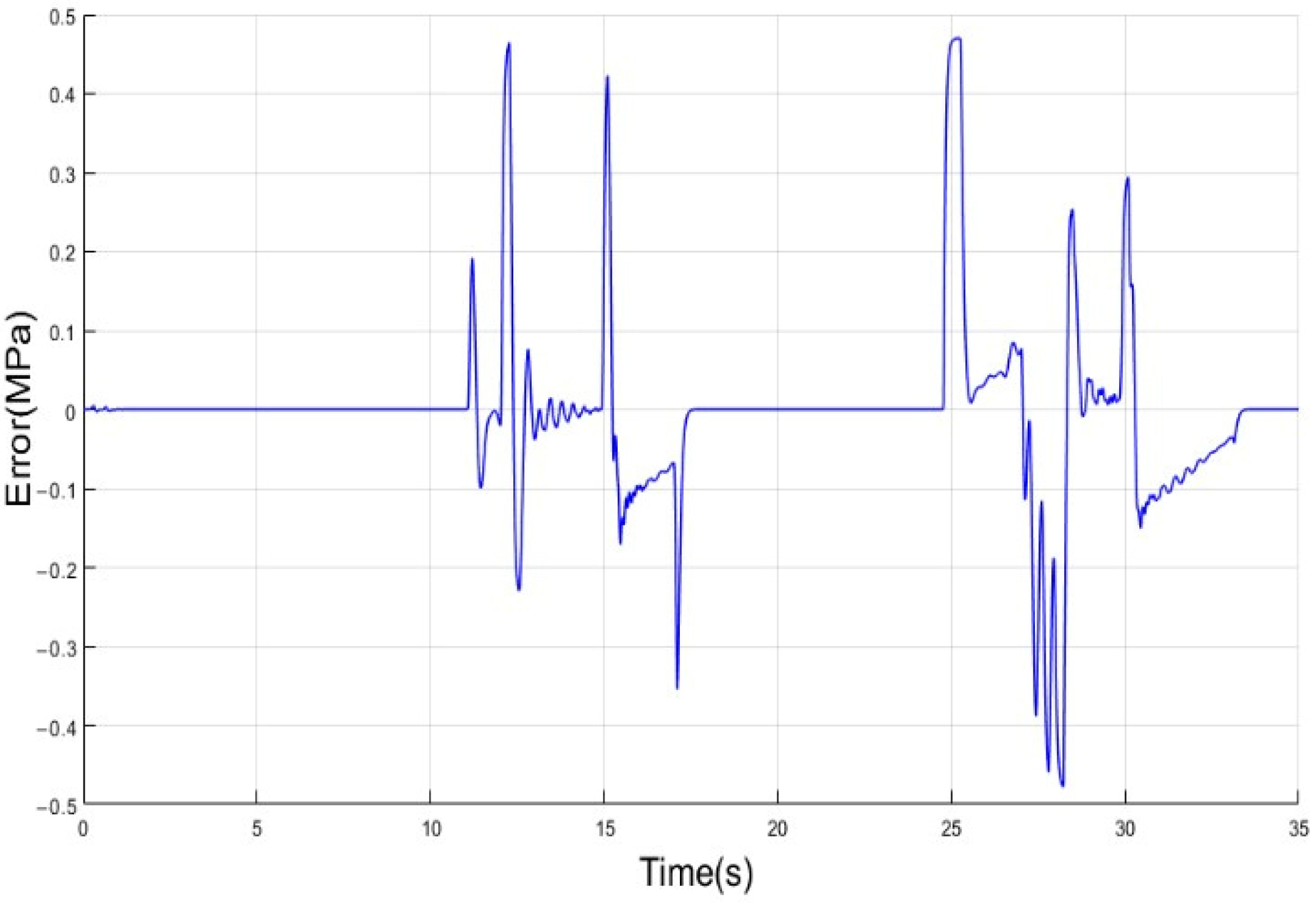
3.1. Results and Discussion of Conventional Braking Mode
3.2. Results and Discussion of Redundant Braking Mode
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Fernandes, P.; Nunes, U. Multiplatooning leaders positioning and cooperative behavior algorithms of communicant automated vehicles for high traffic capacity. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1172–1187. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Chen, D.; Ahn, S.; Hegyi, A. Analysis of driver response and traffic evolution under variable speed limit control. Transp. Res. Rec. 2015, 2490, 1–10. [Google Scholar] [CrossRef]
- Maimaris, A.; Papageorgiou, G. A review of intelligent transportation systems from a communications technology perspective. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Rio de Janeiro, Brazil, 1–4 November 2016; pp. 54–59. [Google Scholar]
- Zhang, J.; Wang, F.Y.; Wang, K.; Lin, W.H.; Xu, X.; Chen, C. Data-driven intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1624–1639. [Google Scholar] [CrossRef]
- Sun, C.; Chu, L.; Guo, J.; Shi, D.; Li, T.; Jiang, Y. Research on adaptive cruise control strategy of pure electric vehicle with braking energy recovery. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Ma, H.; Chu, L.; Guo, J.; Wang, J.; Guo, C. Cooperative Adaptive Cruise Control Strategy Optimization for Electric Vehicles Based on SA-PSO with Model Predictive Control. IEEE Access 2020, 8, 225745–225756. [Google Scholar] [CrossRef]
- Yang, D.G.; Jiang, K.; Zhao, D.; Yu, C.L.; Cao, Z.; Xie, S.C.; Xiao, Z.Y.; Jiao, X.Y.; Wang, S.J.; Zhang, K. Intelligent and connected vehicles: Current status and future perspectives. Sci. China Technol. Sci. 2018, 61, 1446–1471. [Google Scholar] [CrossRef]
- Meier, J.N.; Kailas, A.; Adla, R.; Bitar, G.; Moradi-Pari, E.; Abuchaar, O.; Ali, M.; Abubakr, M.; Deering, R.; Ibrahim, U.; et al. Implementation and evaluation of cooperative adaptive cruise control functionalities. IET Intell. Transp. Syst. 2018, 12, 1110–1115. [Google Scholar] [CrossRef]
- Depner, N.; Graaf, R.; Spahl, R.; Wielgos, S. Vehicle Concept with Electric Wheel Hub Drives. ATZ Worldw. 2016, 118, 42–47. [Google Scholar] [CrossRef]
- Conti, R.; Galardi, E.; Meli, E.; Nocciolini, D.; Pugi, L.; Rindi, A. Energy and wear optimisation of train longitudinal dynamics and of traction and braking systems. Veh. Syst. Dyn. 2015, 53, 651–671. [Google Scholar] [CrossRef]
- Pugi, L.; Malvezzi, M.; Papini, S.; Vettori, G. Design and preliminary validation of a tool for the simulation of train braking performance Luca Pugi Monica Malvezzi Susanna Papini. J. Mod. Transp. 2013, 21, 247–257. [Google Scholar] [CrossRef] [Green Version]
- Ganzel, B.J. Hydraulic Brake System with Controlled Boost. U.S. Patent 8544962, 29 October 2008. [Google Scholar]
- Akita, K.; Yamamoto, T.; Miyazaki, T.; Uraoka, T.; Watanabe, K. Brake Control System. U.S. Patent 9238454, 4 February 2011. [Google Scholar]
- Kunz, A.; Kunz, M.; Vollert, H.; Förster, M. Electromechanical Brake Booster for all Drive Concepts and Automated Driving. ATZ Worldw. 2018, 120, 58–61. [Google Scholar] [CrossRef]
- Matsushita, S. Vehicle Braking Device. U.S. Patent 8746813, 6 May 2010. [Google Scholar]
- Ohkubo, N.; Matsushita, S.; Ueno, M.; Akamine, K.; Hatano, K. Application of electric servo brake system to plug-in hybrid vehicle. SAE Int. J. Passeng. Cars Electron. Electr. Syst. 2013, 6, 255–260. [Google Scholar] [CrossRef]
- Xiong, Z.; Guo, X.; Yang, B.; Pei, X.; Zhang, J. Modeling and pressure tracking control of a novel electro-hydraulic braking system. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Continental Mk C1. Available online: https://www.continental-automotive.com/en-gl/Passenger-Cars/Safety/Products/Brakes/Electronic-Brakes/MK-C1 (accessed on 3 March 2020).
- Zhao, D.; Chu, L.; Xu, N.; Sun, C.; Xu, Y. Development of a cooperative braking system for front-wheel drive electric vehicles. Energies 2018, 11, 378. [Google Scholar] [CrossRef] [Green Version]
- Lv, C.; Zhang, J.; Li, Y. Extended-Kalman-filter-based regenerative and friction blended braking control for electric vehicle equipped with axle motor considering damping and elastic properties of electric powertrain. Veh. Syst. Dyn. 2014, 52, 1372–1388. [Google Scholar] [CrossRef]
- Lee, C.H.; Lee, J.M.; Choi, M.S.; Kim, C.K.; Koh, E.B. Development of a semi-empirical program for predicting the braking performance of a passenger vehicle. Int. J. Automot. Technol. 2011, 12, 193–198. [Google Scholar] [CrossRef]
- Vasilevsky, M.; Razva, A.; Grebenkov, Y. Determination of tension of friction of piston of dispersible material is in a pipeline. In Proceedings of the MATEC Web of Conferences, Tomsk, Russian Federation, 22–23 April 2015. [Google Scholar]
- Zhang, J.; Lv, C.; Yue, X.; Li, Y.; Yuan, Y. Study on a linear relationship between limited pressure difference and coil current of on/off valve and its influential factors. ISA Trans. 2014, 53, 150–161. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.S. Electromagnetic force calculation method in finite element analysis for programmers. Univers. J. Electr. Electron. Eng. 2019, 6, 62–67. [Google Scholar] [CrossRef]
- Chu, L.; Zhao, D.; Li, W. Modeling and dynamic characteristics simulation for fast-switching solenoid valves in electro-hydraulic braking systems. Qiche Gongcheng/Automot. Eng. 2017, 39, 61–65. [Google Scholar] [CrossRef]
- Tomasikova, M.; Tropp, M.; Gajdosik, T.; Krzywonos, L.; Brumercik, F. Analysis of Transport Mechatronic System Properties. In Proceedings of the Procedia Engineering, High Tatras Grand Hotel Bellevue, Vysoké Tatry Slovakia, 31 May 2017; pp. 881–886. [Google Scholar]







| Parameter | Value | Units |
|---|---|---|
| Cross-sectional area of PBC piston | 329 | mm2 |
| Cross-sectional area of PBC piston rod | 119 | mm2 |
| Diameter of front wheel cylinder | 57.15 | mm |
| Diameter of rear wheel cylinder | 37.68 | mm |
| Diameter of master cylinder | 20.5 | mm |
| Peak power of PBC motor | 450 | W |
| Peak torque of PBC motor | 2.2 | Nm |
| Rated speed of PBC motor | 4000 | r/min |
| Flexibility of the brake hose | 6.25 × 10−3 | ml/MPa |
| Ball screw lead | 0.005 | m |
| Transmission ratio of the first stage gear | 1.8 | / |
| Ball screw efficiency | 0.96 | / |
| Proportional coefficient of PRV | 19.8 | MPa/A |
| Diameter of PSS | 15 | mm |
| Stiffness of PSS spring(1st stage) | 9.03 | N/mm |
| Stiffness of PSS spring(2nd stage) | 42.16 | N/mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, L.; Xu, Y.; Zhao, D.; Chang, C. Research on Pressure Control Algorithm of Regenerative Braking System for Highly Automated Driving Vehicles. World Electr. Veh. J. 2021, 12, 112. https://doi.org/10.3390/wevj12030112
Chu L, Xu Y, Zhao D, Chang C. Research on Pressure Control Algorithm of Regenerative Braking System for Highly Automated Driving Vehicles. World Electric Vehicle Journal. 2021; 12(3):112. https://doi.org/10.3390/wevj12030112
Chicago/Turabian StyleChu, Liang, Yanwu Xu, Di Zhao, and Cheng Chang. 2021. "Research on Pressure Control Algorithm of Regenerative Braking System for Highly Automated Driving Vehicles" World Electric Vehicle Journal 12, no. 3: 112. https://doi.org/10.3390/wevj12030112
APA StyleChu, L., Xu, Y., Zhao, D., & Chang, C. (2021). Research on Pressure Control Algorithm of Regenerative Braking System for Highly Automated Driving Vehicles. World Electric Vehicle Journal, 12(3), 112. https://doi.org/10.3390/wevj12030112







