Advanced Control Method of 5-Phase Dual Concentrated Winding PMSM for Inverter Integrated In-Wheel Motor
Abstract
:1. Introduction
2. Target In-Wheel Motor System
3. Motor Design
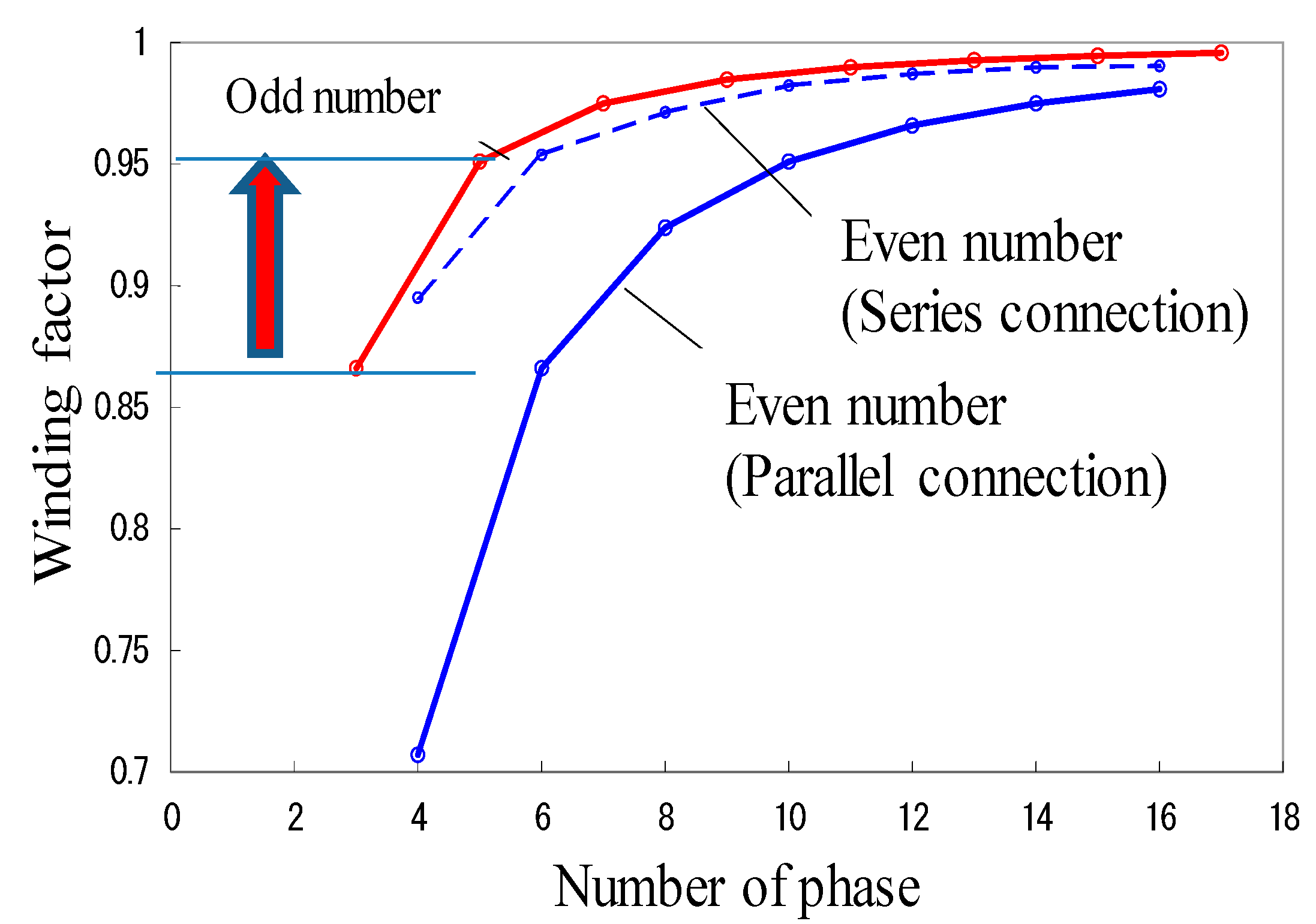
3.1. Phase Number and Pole Number Selection
3.2. Winding Change over Technique
4. Motor Control Design
4.1. Current Control
4.2. 3rd Harmonics Current Control
4.3. PWM Phase Shift Control
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jahns, T.M.; Sarlioglu, B. The Incredible Shrinking Motor Drive: Accelerating the Transition to Integrated Motor Drives. IEEE Power Electron. Mag. 2020, 7, 18–27. [Google Scholar] [CrossRef]
- Rahman, K.; Patel, N.; Ward, T.; Nagashima, J.; Caricchi, F.; Crescimbini, F. Application of direct drive wheel motor for fuel cell electric and hybrid electric vehicle propulsion system. IEEE Trans. Ind. Appl. 2004, 42, 1185–1192. [Google Scholar] [CrossRef]
- Chen, Q.; Shao, H.; Huang, J.; Sun, H.; Xie, E.J. Analysis of Temperature Field and Water Cooling of Outer Rotor In-Wheel Motor for Electric Vehicle. IEEE Access 2019, 7, 140142–140151. [Google Scholar] [CrossRef]
- Ifedi, C.J.; Mecrow, B.C.; Brockway, S.T.M.; Boast, G.S.; Atkinson, G.J.; Kostic-Perovic, D. Fault-Tolerant In-Wheel Motor Topologies for High-Performance Electric Vehicles. IEEE Trans. Ind. Appl. 2013, 49, 1249–1257. [Google Scholar] [CrossRef]
- Akatsu, K.; Tanimoto, S. Air-Cooled Multi-Phase Dual-Winding In-Wheel Motor Integrated with Ultra Small SiC Module. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 41–46. [Google Scholar] [CrossRef]
- Swamy, M.M.; Kume, T.J.; Maemura, A.; Morimoto, S. Extended high speed operation via electronic winding change method for ac motors. IEEE Trans. Ind. Appl. 2004, 42, 742–752. [Google Scholar] [CrossRef]
- Takatsuka, Y.; Hara, H.; Yamada, K.; Maemura, A.; Kume, T. A Wide Speed Range High Efficency EV Drive System Using Winding Changeover Technique and SiC Device. In Proceedings of the 2014 International Power Electronics Conference, Hiroshima, Japan, 18–21 May 2014; pp. 1898–1903. [Google Scholar]
- Nakano, M.; Akatsu, K. An Onboard Heat Transfer Measurement System for The Thermal Design of Air Cooled In-Wheel-Motor. In Proceeding of the SICE Annual Conference, Tsukuba, Japan, 20–23 September 2016. [Google Scholar]
- Suzuki, T.; Yamashita, M.; Mori, T.; Araki, S.; Tanimoto, S.; Iizuka, S.; Niitsuma, Y.; Akatsu, K. A Built-In High Temperature Half-Bridge Power Module with Low Stray Inductance and Low Thermal Resistance for In-Wheel Motor Application. Mater. Sci. Forum 2017, 897, 677–680. [Google Scholar] [CrossRef]
- Beik, O.; Yang, R.; Emadi, A. Design of a 5-Phase IPM Machine for Electric Vehicles. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 168–172. [Google Scholar] [CrossRef]
- Zhu, D.; Qiu, X.; Zhou, N.; Yan, Y. A comparative study of winding factors between distributed windings and non-overlapping concentrated windings. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 2725–2729. [Google Scholar] [CrossRef]
- Akatsu, K.; Wakui, S. Torque and Power Density Comparison between Fractional-slot Concentrated Winding SPMSMs. In Proceedings of the International Conference on Electric Machines and Systems, Nagasaki, Japan, 20–23 November 2006. [Google Scholar]
- Aslan, B.; Semail, E. New 5-phase concentrated winding machine with bi-harmonic rotor for automotive application. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2114–2119. [Google Scholar] [CrossRef]
- Hijikata, H.; Sakai, Y.; Akatsu, K.; Miyama, Y.; Arita, H.; Daikoku, A. Wide Speed Range Operation by Low-Voltage Inverter-Fed MATRIX Motor for Automobile Traction Motor. IEEE Trans. Power Electron. 2017, 33, 6887–6896. [Google Scholar] [CrossRef]
- Fukuda, K.; Akatsu, K. 5-phase double winding PMSM with integrated SiC inverter for In-Wheel Motor. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Gopalarathnam, T.; Toliyat, H.A.; Moreira, J.C. Multi-phase fault-tolerant brushless DC motor drives. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference, Rome, Italy, 8–12 October 2000; Volume 3, pp. 1683–1688. [Google Scholar] [CrossRef]
- Fu, J.-R.; Lipo, T.A. Disturbance-Free Operation of a Multiphase Current-Regulated Motor Drive with an Opened Phase. IEEE Trans. Ind. Appl. 1994, 30, 1267–1274. [Google Scholar] [CrossRef]
- Ryu, H.-M.; Kim, J.-W.; Sul, S.-K. Synchronous frame current control of multi-phase synchronous motor part I. modeling and current control based on multiple d-q spaces concept under balanced condition. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, 2004. 39th IAS Annual Meeting, Seattle, WA, USA, 3–7 October 2004; p. 63. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Parsa, L.; Serra, G.; Casadei, D. High-Torque-Density Control of Multiphase Induction Motor Drives Operating Over a Wide Speed Range. IEEE Trans. Ind. Electron. 2015, 62, 814–825. [Google Scholar] [CrossRef]






















| Parameter | Value |
|---|---|
| Torque [Nm] | 72 |
| Max. speed [rpm] | 20,000 |
| DC bus voltage [V] | 360 |
| Current [Arms] (peak) | 55 (78) |
| Max. Output power [kW] | 40 |
| Motor diameter [mm] | 159 |
| Motor length [mm] | 82 |
| Parameter | Without PWM Shift | With PWM Shift |
|---|---|---|
| Efficiency [%] | 92.44 | 95.08 |
| Total loss [W] | 440.1 | 278.7 |
| Cupper loss [W] | 263.3 | 253.4 |
| Iron loss [W] | 176.8 | 25.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akatsu, K.; Fukuda, K. Advanced Control Method of 5-Phase Dual Concentrated Winding PMSM for Inverter Integrated In-Wheel Motor. World Electr. Veh. J. 2021, 12, 61. https://doi.org/10.3390/wevj12020061
Akatsu K, Fukuda K. Advanced Control Method of 5-Phase Dual Concentrated Winding PMSM for Inverter Integrated In-Wheel Motor. World Electric Vehicle Journal. 2021; 12(2):61. https://doi.org/10.3390/wevj12020061
Chicago/Turabian StyleAkatsu, Kan, and Keita Fukuda. 2021. "Advanced Control Method of 5-Phase Dual Concentrated Winding PMSM for Inverter Integrated In-Wheel Motor" World Electric Vehicle Journal 12, no. 2: 61. https://doi.org/10.3390/wevj12020061
APA StyleAkatsu, K., & Fukuda, K. (2021). Advanced Control Method of 5-Phase Dual Concentrated Winding PMSM for Inverter Integrated In-Wheel Motor. World Electric Vehicle Journal, 12(2), 61. https://doi.org/10.3390/wevj12020061







