1. Introduction
Advances in computing technology are transforming the way people execute computational tasks for daily applications like stock trading [
1], gaming [
2], etc. Usage of traditional desktop computers for large computational works has been expanded to various ways of computing such as cloud computing. For example, cloud gaming platforms PlayStation Now [
3] and GameFly [
4] execute most gaming computational tasks on the cloud, which frees gamers from having to update their computing devices frequently. Stock market investors are now able to manipulate stock trading on their mobile devices by offloading most computational tasks to the cloud [
1].
In recent years, with the explosion of smart mobile devices and their capacities in terms of computing power, storage, data transmission efficiency, etc., the concept of fog computing [
5] and D2D offloading has been facilitated to overcome high cloud service costs and mobility constraints. Although it is widely adapted contemporarily with offloading of computational tasks to the cloud as the fog does not have as high a “density” (i.e., calculation and storage capacities), fog computing and D2D offloading prevent high carrier data transmission cost and cloud service costs, and its presence in users’ vicinity can prevent high communication latency. Intermittent access to cellular data and non-seamless wireless coverage in the mobile environments are also discouraging factors for users to completely rely on the cloud. Faster and more responsive task cooperation and offloading in the D2D network becomes even more necessary in extreme situations like earthquake response.
The work in [
6] shows that despite increasing usage of mobile devices in our daily lives, most of the computational power of these smart devices is still in the idle state and wasted, e.g., only email notification listeners and other low consumption applications run in the background for most of the time. If we can take advantage of the computational power of these idle devices together with their storage and data layover abilities, cost-effective task cooperation in D2D networks is highly feasible. Such a task cooperation and offloading context was first presented in Serendipity [
7], a system that allows a mobile initiator to utilize computational resources available in other mobile systems in its surroundings to accelerate computing and save energy, whose performance is further analysed in [
8] to see significant potential gain in both execution time and device energy. The authors of [
9] proposed a mobile application that enables the cooperation of computationally-intensive applications by making use of computational powers of mobile devices in a nearby cloudlet.
While many previous works tried to exploit how idle computational power can be effectively utilized in D2D networks, the mobility aspects of users, especially the task cooperation scheduling in mobile environments, still remain open issues. Previous work in [
10] illustrated a computational task cooperation system in the D2D network that provides users with significantly lowered task execution time without turning to cloud services that may introduce high monetary costs. However, this work does not consider the incentive for a user to share the computational resource of her/his device even though her/his device might be idle, neither is the fairness among users considered.
The work in [
11] presented a reputation system incorporated with an ad hoc cloud gaming system. Without such a reputation system, unfairness will present as the players with higher network quality will be sacrificing significantly higher bandwidth that may lead to much higher monetary cost than those with lower network quality. In a D2D computation offloading system, similarly, unfairness may also result if users who contribute many computational resources are offered little, or even none, when in need. Therefore, it becomes important for us to build a reliable credit system on top of our computational resource sharing system to provide incentives for users to share their spare computational resources and enforce fairness while not affecting system effectiveness too much. Among various possible ways to implement a credit system for our computational resource sharing system, the recent upsurge of attention toward de-centralized blockchain technology has inspired us. Blockchain technology features de-centralized autonomy, anonymity, transparency, immutability, etc. [
12], naturally meeting our system needs and becoming the choice as the basis of our credit system. In this work, we will be the first to propose a task outsourcing and scheduling scheme that is probabilistically based on the mobility of smart mobile device users in a D2D network, with a blockchain-based credit system to enforce fairness among users in the system.
The remaining parts of this work are organized as follows.
Section 2 conducts a review on related works.
Section 3 presents the system overview, and
Section 4 models the proposed system.
Section 5 illustrates the problem formulation of our proposed scheme, and
Section 6 shows corresponding experimental evaluation results.
Section 7 discusses the benefits and limitations of the proposed scheme.
Section 8 concludes our work in this paper.
2. Related Work
2.1. Abundance of Spare Resources in D2D Networks
To relieve the burden of wireless cellular networks and the cloud, mobile data and computational traffic can be delivered through other means to the users (e.g., WiFi, D2D communications). This is known as mobile data and computation offloading. Several works have identified the benefits of WiFi data offloading [
13,
14,
15]. The work in [
13] showed that deferring the uploading tasks until WiFi access points are available can save the energy of smartphones. By jointly considering the power consumption and link capacity of wireless network interfaces, Ding et al. in [
14] studied the criterion of downloading data from WiFi, as well as the WiFi access point selection problem.
However, mobile data traffic cannot always be offloaded to WiFi networks since the number of open-accessible WiFi access points is limited [
14], just as the availability of affordable cloud computing services may be quite limited [
5]. To fully exploit the benefits of data and computation offloading, mobile traffic and computational works can also cooperate in D2D networks. Specifically, mobile devices in close proximity can be connected via WiFi Direct [
16], Bluetooth, etc., in a D2D manner for data and task cooperation between users. This is referred to as D2D data and computation offloading. The works in [
7,
8] explore task cooperation of mobile devices in the D2D network and showed that significant execution time and device energy can be saved. The authors of [
17] presented a framework for opportunistic storage and processing in the mobile cloud. The work in [
18] considers D2D technologies as candidates to deal with most local communications and time-sensitive computations in the near future. A D2D network should make use of Bluetooth, WiFi-Direct and other protocols to more efficiently provision services to applications such as video gaming and image processing.
It has been shown in [
6] that the computational power of our smart mobile devices is idle and wasted for most of the time before these devices become outdated and replaced with newer models. The work in [
19] presents that contemporary smart devices (mostly quad-core devices) use less than two cores on average in their non-idle states with the consideration of simultaneously running applications in the background, not to mention the computing power that these devices can provide in their idle states. It is generally true that building more data centres can provision more computational power for end users. However, a data centre needs to be built and maintained at a very high cost, which encourages us to exploit the task cooperation possibilities in D2D networks bearing users’ mobility.
Considering the mobile nature of smart device users in ad hoc networks, Wang et al. in [
20] proposed a metric, expected available duration (EAD), based on the mobility and similarities of users’ interests in the D2D network. EAD indicates the statistically determined expected duration of each user’s files of interest in the D2D network. With this metric, this work presents an optimization and performance promotion of a file sharing system in the D2D network to reduce the expensive data charge from cellular carriers and download more data from neighbours.
The work in [
11] presented a reputation system incorporated with an ad hoc cloud gaming system that can reduce system players’ overall bandwidth consumption while keeping fairness among them, without which players with higher network quality will be sacrificing significantly higher bandwidth. Similarly, if a user in our D2D computation offloading system can choose not to share spare computational resources while only receiving help from peers, it is unfair for those helpers contributing their computational resources. Consequently, we need to add a reliable credit system for our computational resource sharing system to enforce fairness among users, but not affecting system effectiveness too much. Multiple candidates are available for building a credit system, among which de-centralized blockchain technology seems to meet our system needs most.
2.2. Fairness and Blockchain
The authors in [
21] presented a blockchain-based reputation system framework for joint cloud computing services, which evaluates the credibility of cloud service vendors in terms of service quality. The blockchain-based information database stores vendor reputation values in a distributed manner and prevents the reputation values from being artificially tampered with, which benefits agnostic end users. The recent upsurge of attention toward de-centralized blockchain technology resulted because traditional credit systems like centralized banking and membership services are losing user confidence because users are agnostic and not truly in charge of their accounts. For example, if the cloud service vendor in [
21] can easily tamper with it and increase its reputation value, the system is not trustworthy with respect to its customers. To build up a fair and trustworthy computational resource sharing system, blockchain technology naturally becomes the key cornerstone of our credit system. First, the blockchain needs to be maintained by mining (to be explained below), which can be performed by any of our system nodes. Second, the blockchain is available to all users, which is transparent and immutable so that users are in charge of their own accounts and transactions. Third, the transactions on the blockchain are anonymized, which provides user privacy, just to name a few. In this section, we describe the key concepts related to blockchain technology in general.
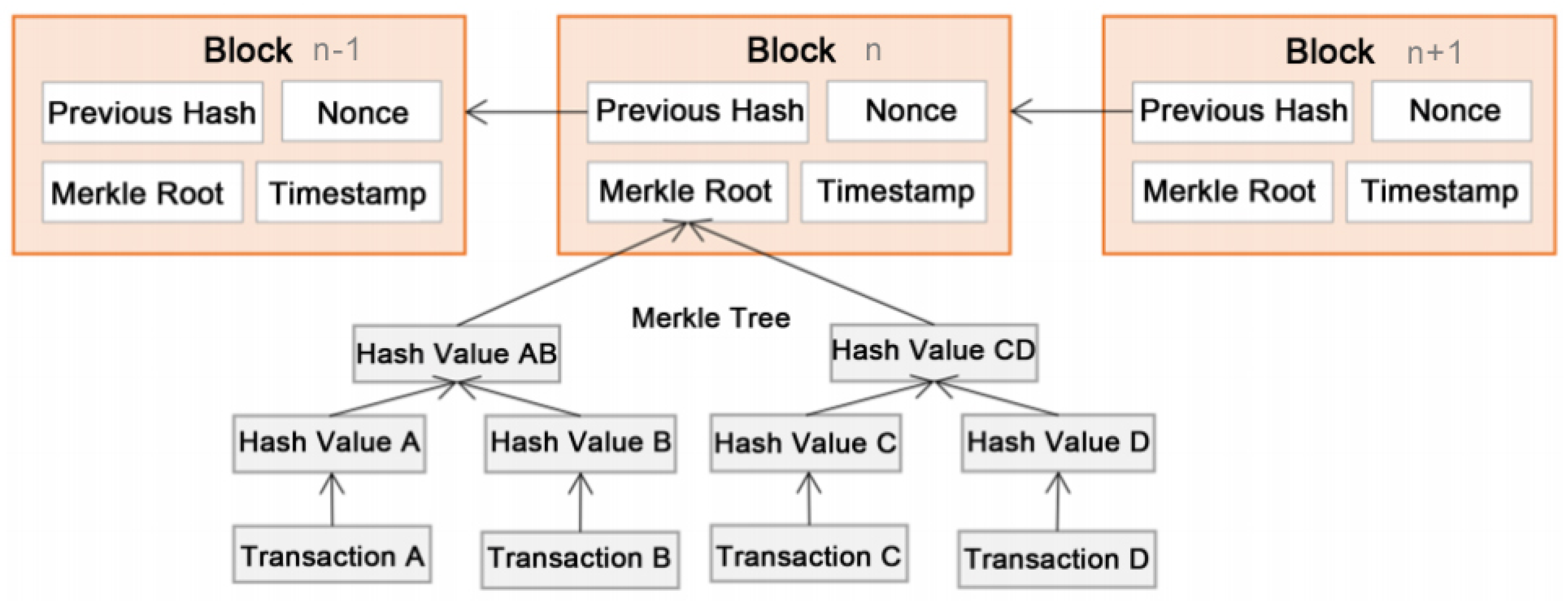
Blockchain: Blockchain is a distributed data structure consisting of a chain of blocks. Blockchain works as a distributed database or a public ledger that keeps records of all transactions in the blockchain network. The transactions are time-stamped and listed into blocks where each block is identified by a unique cryptographic hash. Each block links to it previous block by referencing the hash value of the previous block, forming a chain of blocks and thus called a blockchain. A blockchain is maintained by a network of nodes, and every node records the same transactions. The blockchain is publicly accessible among the nodes in the blockchain network.
Figure 1 illustrates the structure of a blockchain.
Blocks: The transactions in a blockchain network are bundled into blocks. These blocks are executed and maintained by all nodes in the network. A block consists of its hash, the hash of its previous block, a nonce that is used to avoid malicious nodes from flooding the network, a transaction list and a timestamp. In order to save storage space, the transaction list is typically stored in a Merkel root [
22] format in each block. Only one of the conflicting transactions (e.g., transactions trying to double spend) will be taken as a part of the block. The blocks are added to the blockchain at regular intervals by miners.
Transactions: A transaction is between two nodes in the blockchain network. Each transaction mainly includes the addresses of the sender and recipient, as well as a transaction value. In a valid transaction, the transaction value is transferred from the sender to the recipient. All transactions are signed by the sender’s private key as a digital signature. Transactions are chosen and included in the blocks in the mining process. All transactions on a blockchain can be accessed by all participant nodes in the network.
Mining: Transactions in a blockchain network are verified in a process called mining. Incentives, in the form of credit or crypto-currency, are provided to participating nodes to perform the mining operations. Nodes participating in mining are called miners. A miner typically is required to select new transactions from a transaction pool, include them in a candidate new block and perform a mathematical computation to determine an appropriate nonce for the new block. This process of performing the mathematical computation is referred to as “proof of work” (PoW) [
23], which is mainly used to prevent malicious nodes from arbitrarily adding new blocks to the blockchain or “flooding” the network. The first miner to come up with a valid nonce and thus a valid new block gets the block reward. Miners produce blocks that are then verified by other miners in the network for validity. Once a new winning block is selected, all other miners update to that new block. The longer the blockchain becomes, the harder for a malicious node to tamper with it. Therefore, mining is typically the key to keep data safety in blockchain applications. While mining is prevalent in contemporary blockchain applications, it is not necessary, and the discussion of this remains beyond the scope of this work.
3. System Overview
Our system consists of two major parts: the cooperative task scheduling to enhance effectiveness (e.g., average task execution time) among users and a blockchain-based credit system to provide fairness and incentives to users. Specifically, as the recent upsurge of interest in de-centralized blockchain technology suggests, traditional credit system like centralized banking and membership services are losing user confidence because users are not truly in charge of their accounts. The central power is able to modify user credit or create credit out of nothing, which can lead to user losses. Consequently, our credit system will be empowered by blockchain technology to enforce fairness and other benefits, e.g., autonomy and anonymity, among users, which effectively enhances user QoE in a fair manner.
3.1. Cooperative Task Scheduling and Roles of System Users
As shown in
Figure 2, our D2D network consists of users with smart devices and a supernode at the base station (BS). Communications between user devices are through direct D2D links like Bluetooth or WiFi Direct, and communications between user devices and the supernode (e.g., reporting mobility and task information) are through a cellular link like 4G or LTE. D2D task cooperation is coordinated by the supernode bearing the mobility and task information among users in mind. In this paper, we assume that some necessary information related to a properly sliced task piece (including some overhead and necessary execution files, which are assumed to be of limited size not comparable to large multimedia content) will be sent from a requester to a helper, and the calculation result (which is even smaller) will be sent back to the requester once the helper has finished. The information exchanged between a user node and the supernode will be of a much more limited size, whose transmission time can also be negligible compared to the cooperative task execution time. More importantly, the D2D task cooperation is coordinated and assigned by the supernode at the base station, meaning that each helper is assigned specific time slots (to be elaborated in
Section 5) and a corresponding amount of work to help each requester. Thus, we do not emphasize the difficulty of assigning dedicated in-band channels for the D2D communications in our system. Instead, we emphasize the difficulty of a user executing her/his own task in a timely manner, and since our system is not proposed for content sharing that is bandwidth significant, we assume that D2D communications between user nodes use dedicated in-band channels assigned by the supernode. Hence, mutual interference is not emphasized in our work.
At any moment, we may further divide system users into computational resource users and miners. Miners will write transactions into the main blockchain and grant credits for keeping our blockchain-based credit system safe. Computational resource users consist of requesters and helpers: requesters in an task period are devices in need of computational assistance, and helpers are devices that may offer help requesters. Each successful computational assistance will be recorded as a transaction and will be written into the blockchain. Therefore, a requester will need to pay the corresponding amount of credit to a helper after receiving the computational assistance from that helper.
3.2. Supernode Coordination and Working Process
In our system, the supernode will not only assign task assignments to devices in the D2D network, it will also work as a coordinator between a requester and worker pair by acknowledging their cooperation work. As shown in
Figure 2, the step-by-step working process is as follows: (1) A requester notifies the supernode at the BS about the need for a cooperative task
T; (2) After calculation and analysis of the system conditions, the supernode will assign, say, 30% of cooperative task
T to one helper and 70% of
T to another helper around the requester. The supernode will notify the requester and each related helper about the cooperation assignment information. The requester then will send corresponding task portions to each assigned helper; (3) Each helper executes the task portion on the device; (4) Upon completion, each helper will notify the supernode and send back the result to the requester; (5) When the requester gets back the computational result from a helper, she/he will notify the supernode about the successful reception of the result; (6) A transaction of the requester paying each related helper is confirmed by all three: the requester, the helper and the supernode. All three of them will store this transaction into their own transaction pool, waiting for a miner to put this transaction into the blockchain.
3.3. Transaction Pool and Mining
After cooperation is performed between a requester and a helper, both of them will have an identical transaction generated. They will store this transaction into their own transaction pool on their own device and also broadcast to nearby peers. Each peer will then store the transaction into her/his own transaction pool upon reception of the broadcast transaction. Note that the supernode has the information of all transactions in the D2D network, so the supernode holds the publicly assessable full transaction pool for all users in the network. The storage space of the transactions is negligible.
Figure 3 is a typical part of the blockchain of our system. Each block is identified with a 256-bit unique hash value and links to its previous block. Each block contains transactions, also identified with a 256-bit unique hash value, that contain information about the cooperative work in the D2D network. For example, Transaction 1 in the left block is recording that User 1 paid 2000 credits to User 2 for receiving the corresponding amount of helper work from User 2. As a safety feature, each transaction needs to point to the source of the income of the credit, as a proof of enough credit. For instance, Transactions 1 and 2 at the right block both point to Transaction 1 in the left block since this is an indication that User 2 does have enough credit to pay the total of 1600 credits in the right block. Similarly, Transaction 3 at the right block also points to Transaction 2 in the left block, indicating that User 4 has enough credit. Note that for demonstration purposes, users are labelled as
,
, etc., in the figure. In fact, these users are actually represented as 256-bit unique digital addresses to provide anonymity. Users are also able to change their addresses to further enhance anonymity.
A user will switch between a helper and a miner according to whether task cooperation is needed in the surrounding area. When a device is assigned work to help a requester in the D2D network, the device will switch to helper mode; otherwise, i.e., when no task is assigned to assist a helper in the current period, the device will switch to miner mode in search for a mining possibility. The debate between how secure the mining algorithm is compared to those used in Bitcoin or Ethereum remains beyond the scope of this work.
4. System Modelling
In this section, the basic system settings, connectivity model, dynamic program slicing, task cooperation scheduling background and the credit balance system that is blockchain based are illustrated.
4.1. Basic System Settings
Apart from the set of all miners in the D2D network, there is a computational resource user set U consisting of u users in our system, where in each task period p, u users are requesters and the rest are helpers. We divide the user set U into two member sets, namely requester set P and helper set H. There are p requesters in P and h helpers in H, where and . Each requester is denoted as , and each helper is denoted as , where . The smart device of a requester or helper is subject to a D2D communication range or , respectively, above which D2D direct link connection is not possible. or is used to denote the available computational power of a requester or helper, indicating how fast or how much computation the smart device is able to handle per second for our cooperative scheme. Typically, this type of computational power is represented by how many clock cycles the device can run per second, 2.6 GHz for example. At any task period , each requester initializes a task of complexity in clock cycles (indicating how many clock cycles need to be run to get the result of the task) with its maximum wait time in seconds (indicating the maximum time will wait for the result until he/she has to do the assigned uncompleted task slices by himself/herself).
4.2. Connectivity Model
Assuming the connection between a requester
and a helper
to be symmetric, we denote the random variable
(or
) to represent that
and
are connected (or disconnected) at time
. Moreover, let random variable
denote the sojourn time that
and
are in the connected state and
denote that in the disconnected state. We consider that both
and
follow the exponential distribution with parameters
and
, respectively. Therefore, we have the cumulative distribution functions (CDF) of
and
given by:
and:
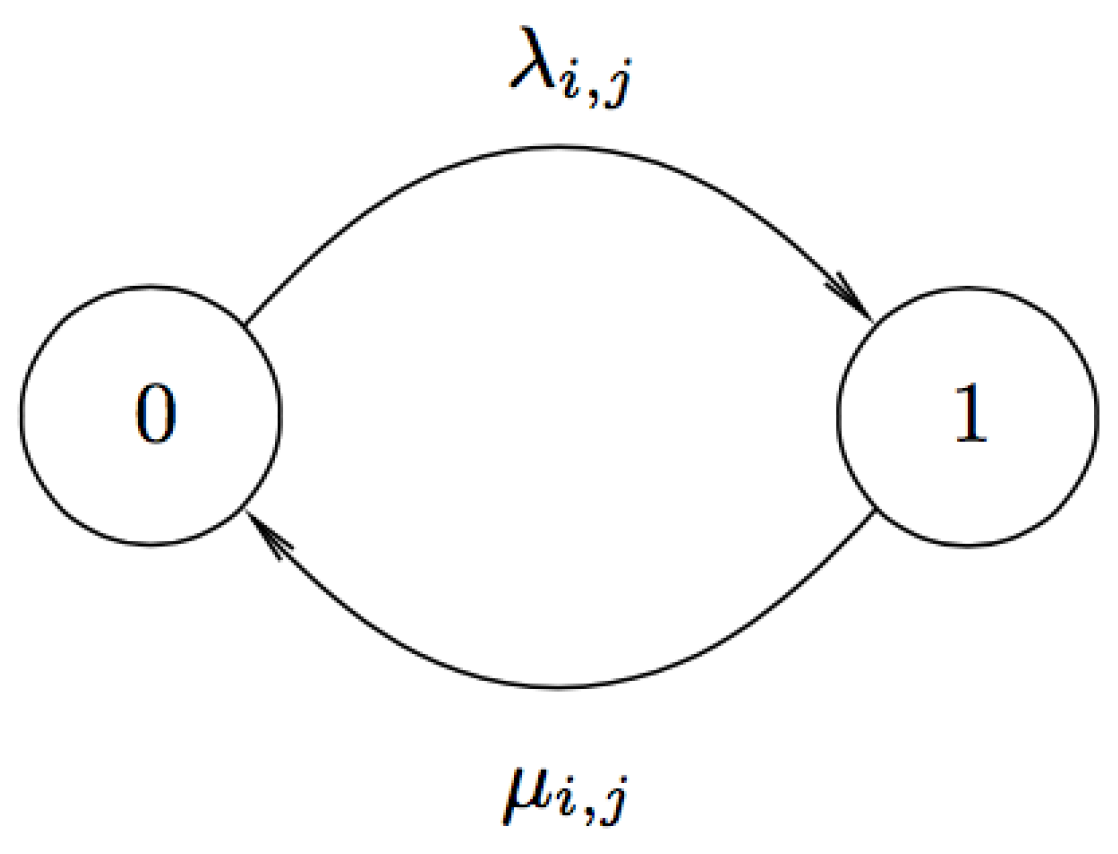
We represent the continuous time Markov chain (CTMC) model with two states illustrated in
Figure 4 and let
denote the
matrix with entries
, where
. Referring to [
24], we have the solution of
given by:
where
and
.
The parameters
and
used in (
3) for
and
can be obtained by maximum likelihood estimation (MLE) on each of them. Specifically, without loss of generality, consider that
and
were disconnected initially, and the connectivity between
and
has changed
m times before the current time
. Therefore,
and
have recorded a vector of time
, where each element
represents the time when the connectivity between
and
changed. Assume
and
are currently connected (then,
m must be an odd number, and the case that
and
are currently disconnected can be analysed via following approach similarly);
and
estimated by MLE up to current time
are given by:
and:
Because the connections between
and
are assumed symmetric, the same results are obtained on
and
. For the people who study or work together,
is kept being recorded by both
and
as the system time increases. According to (
4) and (
5),
and
will converge. We denote
and
, which are the MLE of
and
, respectively. Given the connection station
between
and
at time
, the probability that they are connected at future time
is given by:
4.3. Dynamic Program Slicing
In general, computational tasks cannot be arbitrarily sliced into different parts. However, many dynamic program slicing techniques are facilitating our need for the distribution of tasks [
25]. For example, MapReduce [
26] allows Google to slice and run an average of one hundred thousand MapReduce jobs every day from 2004–2008. Without the availability of dynamic program slicing, a large load of tasks may not be sent back to the requester in a timely manner, and this increases the risk of the helper being out of the device communication range of the requester on completion of the task execution. Therefore, we adopt the assumption that tasks can be sliced in an arbitrary manner in our system.
4.4. Task Cooperation Scheduling
In our system, we assume that a computing unit, which we refer to as a supernode, with enough capacity to perform task cooperation scheduling for all devices is available at the cellular BS covering the D2D network. At the beginning of each task period, the supernode collects task and connectivity information sent wirelessly from the devices and computes the task scheduling for requesters and helpers in the D2D network based on the probability of connection among them according to (
6). Note that the task and connectivity information sent to the supernode is very limited in size and transmission time, which are assumed to be negligible for simplicity. Each task period is divided into discrete time slots for scheduling to ensure accuracy and latency and to lower the chance of losing computation results due to changes in connectivity. This computation will be based on an effective light-weight algorithm elaborated in
Section 5.5.
4.5. Blockchain-Empowered Credit System
In contrast to a Bitcoin system, where later, the user is discouraged from joining due to the significantly increased difficulty to obtain a new coin, our system offers the same initial credit, , to any new user to the system. Users need to pay credits from their own balance to get help from peers and will earn credits after helping peers on computational tasks. At the beginning of each task period , the credit balance of each user is obtained by the supernode by referring to the blockchain. For each user in period , we denote the amount of help received by peers as , the amount of work contributed to peers as and the block reward as . For simplicity, we limit a user to be either a requester, a helper or a miner within a given task period . In our blockchain-empowered credit system, needs to pay from and is rewarded to the balance ; therefore,
5. Problem Formulation
As mentioned in the previous section, we assume that a supernode with enough capacity is present at the BS covering the D2D network of our interest. At the beginning of each task period, the supernode will, with the knowledge of all devices and tasks in the D2D network, calculate the probability distribution of the connectivities between devices and assign computational tasks to each helper or requester device accordingly. The task assignment also takes into account users’ credit balance when our blockchain-based credit system is adopted. Connectivity awareness, computational task assignment, selfishness avoidance and response delay optimization are mathematically formulated in this section.
5.1. Connectivity Awareness
To analyse the connectivity between requesters and helpers for more accurate and cost-effective computation assignment, we first define a
probability matrix
at each time slot
. For a given
t, the element
is the probability of connection between
and
if
and
indicating the probability of connection between
and herself/himself. Obviously,
. At the start of each task period, i.e.,
, we randomly generate
based on the pre-defined initial connection probability. Thereafter, according to Equation (
6), we generate
for each
-
pair.
At any given time slot , we define a p-element vector with its element representing the amount of self-computing computational task assigned to and a matrix with element representing the amount of assisting computational task assigned to for . By concatenating and , we get a computation assignment matrix at time slot t. Joining all where , we get a three-dimensional system computation assignment matrix, M, containing the computation assignment in a task period . Consequently, where is the amount of computational task assigned to for and is the amount of self-computing computational task assigned to at time slot .
Note that the element-wise product between
R and
M,
is the matrix indicating the expected amount of computational task done and the result sent back to requesters. For example,
is the expected amount of assisting task done by
and sent back to
at time slot
.
5.2. Computation Assignment and Maximum Wait Time
At the start of each task period, all requesters will specify to the supernode at the BS the amount of computation, in clock cycles, required for the coming task period. We represent these tasks with a
p-element vector
with
corresponding to the total amount of task required by
. Meanwhile, for an ensured QoE,
is also subject to a maximum wait time in each task period for the result of the computational task. We use another
p-element vector
with
corresponding to the maximum wait time for
in seconds. Apparently,
. Therefore, the computation assignment needs to ensure that a task is expected to be completed before the maximum wait time for all requesters, that is:
5.3. Computation Capacity of Mobile Devices
Each mobile device is subject to a computation capacity denoted as
for
’s mobile device and
for
’s mobile device where
. When talking about the computation capacity of a device, one typically will refer to its CPU. CPU processing capacity is typically referred to in terms of megahertz (MHz) or gigahertz (GHz). Professionals talk about clock speed, which is the standard ability of the CPU to cycle through its operations over time. Therefore, a 1-GHz CPU is able to tick its clock around one billion times per second, which in turn can perform more complicated computational tasks. Without loss of generality, we regulate these computational power values in clock cycles to a scale of 0–100, i.e.,
and
, for simplicity. Each entry of the computation assignment matrix,
, refers to the number of clock cycles required to perform the corresponding task section. For example,
means that at
,
is assigned to help
for 1000 clock cycles worth of computational task. If
Hz, then it takes
s to perform the task. Therefore, each device is subject to an amount of computational task in clock cycles at each time slot as a higher limit, that is:
for all helper devices, and:
for all requester devices as the
column of the computation assignment matrix is representing the amount of self-computing tasks.
5.4. Selfishness Avoidance
As derived in
Section 4.5, the balance of each user is updated as represented in (
7). When computing cooperative task assignment for the D2D network at each task period, the supernode needs to make sure that each requester has enough balance for the task period according to the task assignment matrix
M in that period
. Since the exact amount of
and
for user
is not known at the beginning of task period
, the supernode ideally needs to make sure that:
where
. However, though the exact amount of
and
for user
is not known at the beginning of task period
, their expected value, namely
and
, can easily be obtained in advance from
in that period
:
and:
For simplicity, we will relax the constraint (
12) to the following:
This way, user connectivity has been taken into account, and more cooperation is expected to be done, while leaving the possibility that a user’s balance becomes lower than zero after task period such that the user will need to earn back enough credit before asking for more help.
5.5. Response Delay Optimization
In our work, we emphasize the importance of low task execution time towards a requester’s QoE. In each task period, there is
time slots, and we define the expected completion time,
, for each requester
as follows:
where
. Therefore, our optimization problem becomes:
Calculation of the optimal computation assignment matrix
M is similar to the famous knapsack problem that is NP-hard [
27]. Here, the computational powers of helper devices are like knapsacks with different sizes, and the computational tasks from requesters are like items with different sizes. Solving for the optimal solution for the task scheduling resembles solving for an optimal solution for the knapsack problem: it is NP-hard. For effectiveness, especially considering the trend of an increasingly massive number of smart mobile devices in D2D networks, we proposed a light-weight heuristic algorithm to efficiently find the sub-optimal solution for the computation assignment matrix
M illustrated in Algorithm 1. Note that we make substantial use of the linprog function [
28] in MATLAB for calculating the computation assignment matrix
M by transforming
M element-wise into a one-dimensional unknown vector
with
entries from elements in
M. According to linprog [
28],
A,
b in Algorithm 1 represent the inequality constrains for
, and
,
represent the equality constrains for
. The function get_linprog_parameter in Algorithm 1 is transforming the constraint functions in (
17) from a matrix from to a one-dimensional vector form, which is basically a simple reshaping of the matrix. There is no upper bound for
, and the lower limit for elements of
is zero. The maximum wait time of a requester is the longest time the requester can wait before she/he needs to compute the task result herself/himself. However, it is possible that the task can be completed much sooner than the maximum wait time. Each iteration of Algorithm 1 tries to find lower feasible task assignment solutions by halving (up to an integer value) a randomly-selected requester’s maximum wait time. Since the duration of each task period is limited, the maximum wait time is up to the length of a task period. Therefore, the complexity of Algorithm 1 is subject to
where
p is the number of requesters at the task period and
represents the complexity of MATLAB’s linprog function [
28]. Unfortunately, MATLAB claims improvement on efficiency of linprog over time, but releases no detail about the complexity. Yang in [
29] claims that his algorithm on top of linprog may achieve polynomial complexity with the best known complexity bound on linear programming problems.
| Algorithm 1: The algorithm to obtain , which corresponds to a sub-optimal solution for (17). |
Input: Maximum wait vector
Output: Modified maximum wait vector that corresponds to a sub-optimal solution for (17)
![Futureinternet 09 00085 i001]() |
6. Experiment
In a D2D network, a variety of factors may affect the performance of our cooperative network with the credit system. In this section, we will examine the following effects:
Effect of initial credit: we vary the initial credit provided to each user to see how our system will be affected.
Effect of mean maximum wait time: we vary the mean maximum wait time during the random generation to see how the performance will be affected.
Effect of mean task size: we vary the mean task size of each requester in a task period during the random generation to see how the performance will be affected.
Effect of time elapsed: we run the simulation on multiple task periods and see how system performance changes over time.
In our simulation, we compare the performance of the computational resource sharing system in four different cases:
Greedy D2D task cooperation without our credit system: Without connectivity awareness, each helper device will equally contribute its available computing power to all connecting requesters at the beginning of a task period. For example, helper will assign computing power to each of , , for the current task period if and only if , , are the only requesters in connection with at time .
Greedy D2D task cooperation with our credit system: This is very similar to the above case, except that our blockchain-based credit system is added in to enforce fairness. Therefore, the supernode at BS will check on requester balances before task assignment, ensuring that the assistance expected to be received by a requester will not exceed her.his available balance in that task period.
Connectivity-aware task scheduling without our credit system: At the start of each task period, the supernode at BS will perform task scheduling calculation according to Algorithm 1 without our blockchain-based credit system.
Connectivity-aware task scheduling with our credit system: This is very similar to the above case, except that our blockchain-based credit system is added in to enforce fairness, as illustrated in (
15).
Apart from being a reasonable incentive for users to provide help and gain credit for future needs, the blockchain credit also provides selfishness avoidance to our system. That is, it prevents certain users who only want to get help from peers, but not contribute to other users’ need. We define hereof the level of selfishness,
, to reflect whether users have been contributing relatively equally over task periods
:
In the following experimental illustrations, we show the comparison of
in a normalized way: with respect to the greedy D2D task cooperation without our credit system case since
for this case is much larger than the other three cases and it appears to be stable over the changing factors. For simplicity, the mining process is simplified to a random selection of idle users to be miners in the network. To validate the performance of our proposed system, we set up the following experiment. Default simulation parameters are illustrated in
Table 1, where the uniform distribution between two values
a,
b is denoted as
. We used three real-world traces “Intel” (Trace 1), “Cambridge” (Trace 2) and “Infocom” (Trace 3) in the Cambridge/Haggle dataset in [
30] for our simulations. Traces 1–3 were recorded by 8, 12 and 41 mobile iMotes using Bluetooth with a 30-metre radio range, respectively. Although these iMotes were not smartphones or tablets, the connection states recorded in these traces can be used to reproduce the dynamic topology for mobile users. The interval of each iMote sending a beacon (i.e., hello message) is 120 ± 12 s.
The connectivity between mobile users is assumed to be symmetric in our work. However, the connect and disconnect events in traces were recorded by each iMote individually. Thus, we consider that a pair of iMotes was connected (or disconnected) as long as one of them detected a connect (or disconnect) event. In the real-world traces, an iMote has recorded a connect event with a zero contact duration when it was connected with another iMote for a short period of time such that the iMote failed to receive two or more consecutive beacons. Thus, for a record with the zero contact duration, we assume that the actual contact duration is uniformly distributed on [0 s, 120 s]. We concatenate the contact and inter-contact durations recorded by each pair of iMotes in a chronological order to reproduce the connect and disconnect events for both of them. We then run trace-driven simulations with the D2D topologies reproduced by all iMote pairs in each trace.
6.1. Effect of Initial Credit
The choice of initial credit is a rather significant factor in our system. The initial credit is an indication of how much helper work can be received before a requester has to help others or perform mining to get system credits. If the initial credit is set too low, users are discouraged from performing D2D cooperation. In the extreme case in
Figure 5, where initial credit is set to zero, the users cannot perform any D2D cooperation, resulting in a self-computing performance with a high average task execution time and no selfishness.
As initial credit increases, users are encouraged to perform D2D cooperation, leading to a fast drop in average task execution time in the two cases with our credit system. Particularly, the average task execution time of the heuristic case with our credit system drops to <5% more than that without our credit system, while remaining 20% less selfish. This is an indication that with a proper selection of initial credit, a little sacrifice on average task execution time can be exchanged for a much higher level of fairness. The greedy-credit case has much lower than that without the credit system, but its performance is much worse than the heuristic-credit case, implying the importance of our heuristic algorithm.
6.2. Effect of Mean Maximum Wait Time
During a task cooperation in the D2D network, the requester typically wants the task to be done in a timely manner. For example, if a requester wishes to perform a neural network-based stock index prediction task [
31] that predicts the price of a stock in 30 s, this requester will want to get the computation result within 30 s (could be 20 s, 25 s, etc., depending on the specific application logic and handling behind).
As shown in
Figure 6a, two heuristic cases started with a decrease in average runtime from mean maximum wait time changing from 15 s to 20 s. This may be due to the fact that when the mean maximum wait time is too low, the probability of finding a feasible solution in the cases with our heuristic algorithm is much lower. As mean maximum wait time continues to increase thereafter, the average task execution time increases in all four cases: the enlarged solution space is increasing the difficulty of our heuristic algorithm in finding the optimal solution; and in the greedy cases, the helpers cannot focus on helping fewer requesters since most requesters have similarly high mean maximum wait time. Particularly, the performance on the average task execution time of the greedy-credit case deteriorates approximately 36% from 14 s–19 s, while that for our heuristic case with our credit system deteriorates only 9% for the same change. This further proves the necessity of our heuristic algorithm. However, the normalized level of selfishness decreases with respect to the greedy-non credit case, with the two heuristic cases scaling down faster. Comparing the heuristic cases with and without our credit system, the sacrifice of around 10–15% of average task execution can bring us at least 40% less selfishness at a 50-s mean maximum wait time and almost 100% less at a 15-s mean maximum wait time.
6.3. Effect of Mean Task Size
The generation of task sizes in a period T is a uniform distribution . Note that it is possible that the mean task size for a requester within a period is over the computing capacity of the requester device itself. Therefore, a D2D cooperation is necessary if the task needs to be done within the maximum wait time.
As illustrated in
Figure 7a, the average task execution time increases with respect to the mean task size almost directly proportionally. The performance of our heuristic cases starts at a very close performance at the beginning when the mean task size is small; a requester does not need too much assistance work from helpers, leading to a relatively lower level of selfishness and average task execution time. When the mean task demand from requesters increases, the level of selfishness in the heuristic case without our credit system increases much faster than that with our credit system. When the normalized mean task size is 60, though the heuristic case without our credit system is 15% better on the average task execution time, it is yet more than 250% higher in the level of selfishness. This shows how important it is to use our credit system to enforce fairness among users.
6.4. Effect of Time Elapsed
Here, time elapsed is represented in the unit of the number of task periods elapsed. Effect of time elapsed generally gives an idea of how the performance of the four cases will stabilize over time.
As shown in
Figure 8, the performance of our credit system starts to stabilize beyond the point of the 50th period. As the task period goes on, our blockchain-empowered credit system maintains a good level of selfishness with decreasing normalized selfishness, while the cooperative system without the blockchain-empowered credit system, regardless of whether or not our heuristic algorithm is used, builds up more and more selfishness. Although the performance of the heuristic-credit case on the average task execution time is around 20% worse than that without our credit system, the level of selfishness of the case without our credit system is more than three-times higher. Therefore, the adoption of our credit system is highly recommended to enforce fairness in the network.
7. Discussion
As shown in
Section 6, our blockchain-empowered D2D computational resource sharing system is able to achieve lower average task execution time while enforcing fairness among users. Possible application scenarios include computation virtualization [
32] in the D2D network. The authors in [
33] presented the feasibility of computational resource virtualization within a personal cloud so that a weak device can utilize computational resources from stronger devices for graphics rendering and other applications. The authors clearly claimed one of the key challenges to be the dynamic nature of a personal cloud caused by the mobility of the user. With our proposed system in this paper, we can extend the idea of computational resource virtualization presented in [
33] to a D2D network. A cooperative computational task may be executed in a virtual machine and migrated to different devices in the D2D network. Although virtualization introduces performance and management overhead, the flexibility it can bring to network resource management still makes it very appealing. The fact that virtual machines can be migrated to a different physical host while keeping applications alive makes the computational resource virtualization and sharing in the D2D network even more fascinating [
34]. Furthermore, our system enforces fairness among users by incorporating the blockchain-based credit system.
Apart from the pros and cons explained in the
Section 6, the benefits of adopting the blockchain-base credit system for our proposed D2D computational resource sharing system are as follows:
Decentralized and trustless: The blockchain is a public ledger of all transactions in the network. This public ledger is maintained by all participating nodes, and this consensus mechanism makes central authority unnecessary. Therefore, blockchain technology enables a decentralized and trustless network where peers do not need any trusted third party to interact with each other. Note that the supernode in our system mainly works to assign computational resource sharing in an efficient and fair way by considering user mobility and credit balances. Our supernode also provides a public transaction pool as a reference to system users, but the supernode in no way participates in the mining operations. All mining operations are performed by system users in the D2D network.
Autonomous: Blockchain technology can enable devices in the D2D network to communicate with each other and perform transactions autonomously, since each device can assess the blockchain and a trusted intermediary is not needed. Again, although the supernode helps system users by assigning cooperation tasks in an efficient and fair way, the credit balance system is not controlled by the supernode and remains autonomous.
Our system also faces a few challenges as follows:
Efficiency: Since all miners in the network perform the same computations trying to get the next block reward from the blockchain, there remains efficiency concerns. In our proposed blockchain-empowered D2D computational resource sharing system, the block reward is credits that could be used to exchange for computational resources, which can also be granted when helping peers computing in the D2D network. Therefore, users in the system are not merely encouraged to compete for the block rewards, but also encouraged to assist other peers, which enhances the efficiency of users’ idle computational resources.
Privacy: Because the blockchain is a public ledger and any node can see all transactions in the network, privacy concerns remain for the transacting parties.
Interference in the D2D network: In this work, we de-emphasized the effect of mutual interference in the D2D network due to the limited D2D communications’ duration and the coordination from the supernode. To realize a more realistic model, we will elaborate on how mutual interference can be tackled by supernode coordination in future works.
8. Conclusions
In this work, we build a blockchain-empowered credit system on top of the connectivity-aware computational resource sharing system in the D2D network. A supernode at the base station, with knowledge of user mobilities and thus the probability model of device connectivities, will perform task scheduling to reduce average task execution time for requesters in the network and enhance user quality of experience. Based on the blockchain-based credit system, selfish users who only want to get help from peers, but not contribute, will not be assigned any helper assistance if their balance is not sufficient. The supernode also possesses a publicly accessible transaction pool for miners’ reference on building up a trustworthy blockchain network. Simulation results based on a realistically examined mobility model show that our system substantially reduces average task execution time for requesters in the D2D network. Sacrificing a minor amount of average task execution time allows the system to remain at a rather low level of selfishness. To enforce fairness and encourage users, the adoption of our credit system is highly recommended. With the help of blockchain technology, our system becomes more favourable for users by providing incentives to helpers and enforces fairness among users.