Predicting Timber Board Foot Volume Using Forest Landscape Model and Allometric Equations Integrating Forest Inventory Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Model Parameterization and Simulation
2.3. Board Foot Volume Calculation and Verification
3. Results
3.1. The Red Oak Group
3.2. The White Oak Group
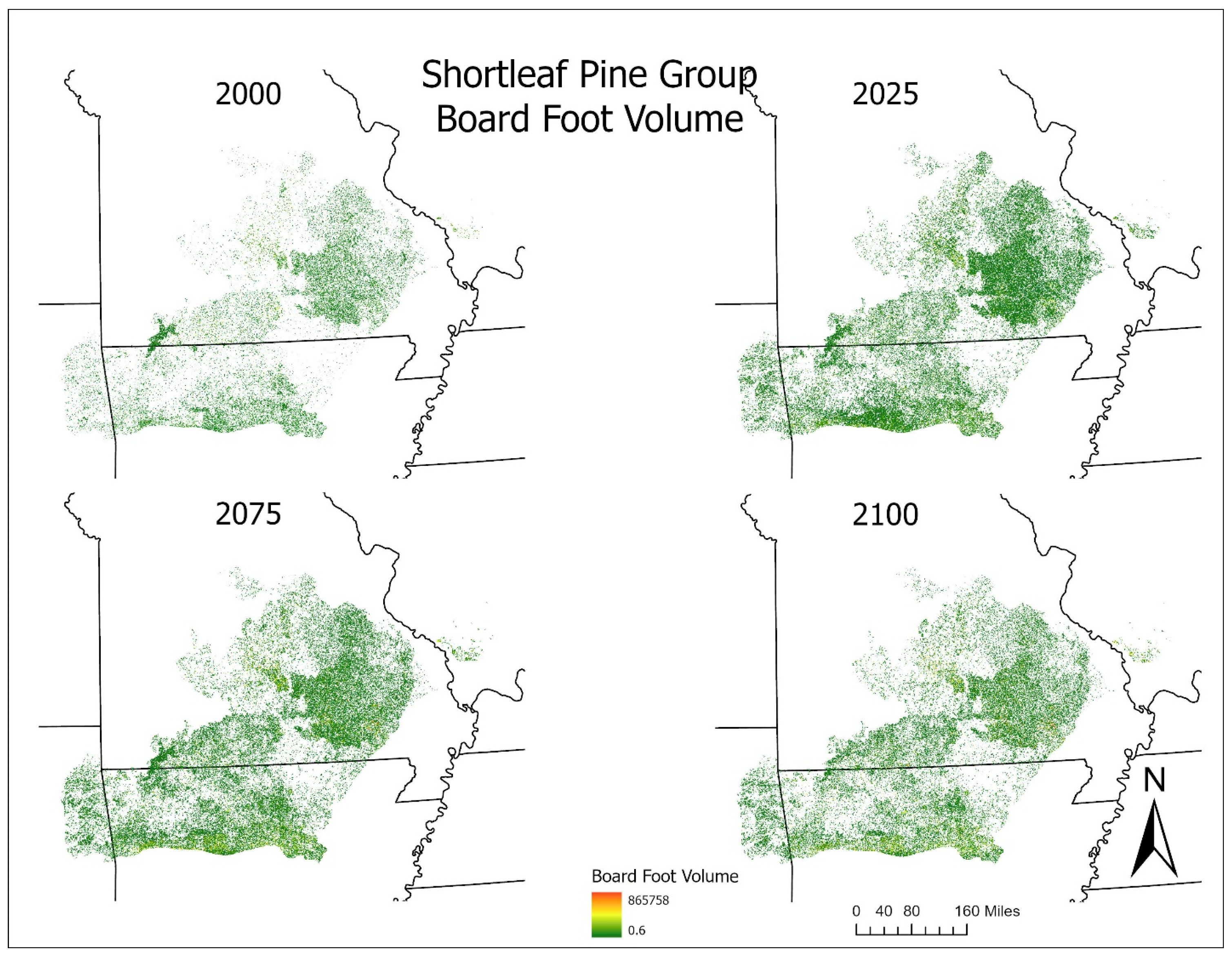
3.3. Shortleaf Pine Group
3.4. The Complete Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NLCD | National Land Cover Database |
| FIA | Forest Inventory and Analysis |
| QMD | Quadratic mean Diameter |
| USDA | United States Department of Agriculture |
Appendix A
References
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Klingenberg, T.F.; Astrup, R. Above-ground biomass change estimation using national forest inventory data with Sentinel-2 and Landsat 8. arXiv 2020, arXiv:2010.14262. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Patenaude, G.; Milne, R.; Dawson, T.P. Synthesis of remote sensing approaches for forest carbon estimation: Reporting to the Kyoto Protocol. Environ. Sci. Policy 2005, 8, 161–178. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Muhairwe, C.K. Taper equations for Eucalyptus grandis and Pinus patula in South Africa. South. Hemisph. For. J. 1999, 195, 13–21. [Google Scholar]
- He, H.S. Forest landscape models: Definitions, characterization, and classification. For. Ecol. Manag. 2008, 254, 484–498. [Google Scholar] [CrossRef]
- Scheller, R.M.; Mladenoff, D.J. An ecological classification of forest landscape simulation models: Tools and strategies for understanding broad-scale forested ecosystems. Environ. Model. Softw. 2007, 22, 733–739. [Google Scholar] [CrossRef]
- Wang, W.J.; He, H.S.; Fraser, J.S.; Thompson, F.R., III; Shifley, S.R.; Spetich, M.A. LANDIS PRO: A landscape model that predicts forest composition and structure changes at regional scales. Ecography 2014, 37, 225–229. [Google Scholar]
- Fraser, J.S.; Thompson, F.R.; He, H.S.; Wang, W.J. Simulating stand-level harvest prescriptions across landscapes: LANDIS PRO harvest module design. Can. J. For. Res. 2013, 43, 972–978. [Google Scholar] [CrossRef]
- Shifley, S.R.; Moser, W.K. (Eds.) Future Forests of the Northern United States; General Technical Report NRS-151; USDA Forest Service: Newtown Square, PA, USA, 2016.
- Wear, D.N.; Greis, J.G. (Eds.) The Southern Forest Futures Project: Summary Report; General Technical Report SRS-168; USDA Forest Service: Newtown Square, PA, USA, 2013.
- Adamski, J.C. Environmental and Hydrologic Setting of the Ozark Plateaus Study Unit, Arkansas, Kansas, Missouri, and Oklahoma; National Water-Quality Assessment Program; U.S. Geological Survey: Little Rock, AR, USA, 1995; Volume 94.
- Dijak, W.D.; Hanberry, B.B.; Fraser, J.S.; He, H.S.; Wang, W.J.; Thompson, F.R. Revision and application of the LINKAGES model to simulate forest growth in central hardwood landscapes in response to climate change. Landsc. Ecol. 2016, 32, 1365–1384. [Google Scholar] [CrossRef]
- Jenness, J. Topographic Position Index (TPI). An ArcView 3. x Tool for Analyzing the Shape of the Landscape; Jenness Enterprises: Flagstaff, AZ, USA, 2006. [Google Scholar]
- Dijak, W. (USDA Forest Service, Retired, Columbia, MO, USA). Personal Communication, 2024.
- Dijak, W. Landscape Builder: Software for the creation of initial landscapes for LANDIS from FIA data. Comput. Ecol. Softw. 2013, 3, 17. [Google Scholar]
- Wang, W.J.; He, H.S.; Thompson, F.R., III; Fraser, J.S.; Hanberry, B.B.; Dijak, W.D. Importance of succession, harvest, and climate change in determining future composition in US Central Hardwood Forests. Ecosphere 2015, 6, 1–18. [Google Scholar]
- Curtis, R.O.; Marshall, D.D. Why quadratic mean diameter? West. J. Appl. For. 2000, 15, 137–139. [Google Scholar] [CrossRef]
- Hahn, J.T.; Hansen, M.H. Cubic and Board Foot Volume Models for the Central States. North. J. Appl. For. 1991, 8, 47–57. [Google Scholar] [CrossRef]
- Zmigrod, R.; Vieira, T.; Cotterell, R. Exact Paired-Permutation Testing for Structured Test Statistics. arXiv 2002, arXiv:2205.01416. [Google Scholar]
- Good, P. Permutation, Parametric and Bootstrap Tests of Hypotheses, 3rd ed.; Springer: Huntington Beach, CA, USA, 2005. [Google Scholar]
- Goff, T.C.; Albright, T.A.; Butler, B.J.; Crocker, S.J.; Kurtz, C.M.; Lister, T.W.; McWilliams, W.H.; Morin, R.S.; Nelson, M.D.; Piva, R.J.; et al. Missouri Forests 2018: Summary Report; Resource Bulletin NRS-122; U.S. Department of Agriculture, Forest Service, Northern Research Station: Madison, WI, USA, 2021; 13p. [CrossRef]
- Legacy Tree Data. Virginia Polytechnic Institute and State University. Available online: https://charcoal2.cnre.vt.edu/nsvb_factsheets/index.html (accessed on 8 February 2024).
- Westfall, J.A.; Coulston, J.W.; Gray, A.N.; Shaw, J.D.; Radtke, P.J.; Walker, D.M.; Weiskittel, A.R.; MacFarlane, D.W.; Affleck, D.L.R.; Zhao, D.; et al. A National-Scale Tree Volume, Biomass, and Carbon Modeling System for the United States; General Technical Report WO-104; U.S. Department of Agriculture, Forest Service: Washington, DC, USA, 2024; 37p. [CrossRef]
- Scheller, R.M.; Mladenoff, D.J. A forest growth and biomass module for a landscape simulation model, LANDIS: Design, validation, and application. Ecol. Model. 2004, 180, 211–229. [Google Scholar] [CrossRef]
- Simons-Legaard, E.; Legaard, K.; Weiskittel, A. Predicting aboveground biomass with LANDIS-II: A global and temporal analysis of parameter sensitivity. Ecol. Model. 2015, 313, 325–332. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dijak, J.; He, H.; Fraser, J. Predicting Timber Board Foot Volume Using Forest Landscape Model and Allometric Equations Integrating Forest Inventory Data. Forests 2025, 16, 543. https://doi.org/10.3390/f16030543
Dijak J, He H, Fraser J. Predicting Timber Board Foot Volume Using Forest Landscape Model and Allometric Equations Integrating Forest Inventory Data. Forests. 2025; 16(3):543. https://doi.org/10.3390/f16030543
Chicago/Turabian StyleDijak, Justin, Hong He, and Jacob Fraser. 2025. "Predicting Timber Board Foot Volume Using Forest Landscape Model and Allometric Equations Integrating Forest Inventory Data" Forests 16, no. 3: 543. https://doi.org/10.3390/f16030543
APA StyleDijak, J., He, H., & Fraser, J. (2025). Predicting Timber Board Foot Volume Using Forest Landscape Model and Allometric Equations Integrating Forest Inventory Data. Forests, 16(3), 543. https://doi.org/10.3390/f16030543





