Experiments and Simulation on the Effects of Arch Height Variation on the Vibrational Response of Paulownia Wood
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Tests
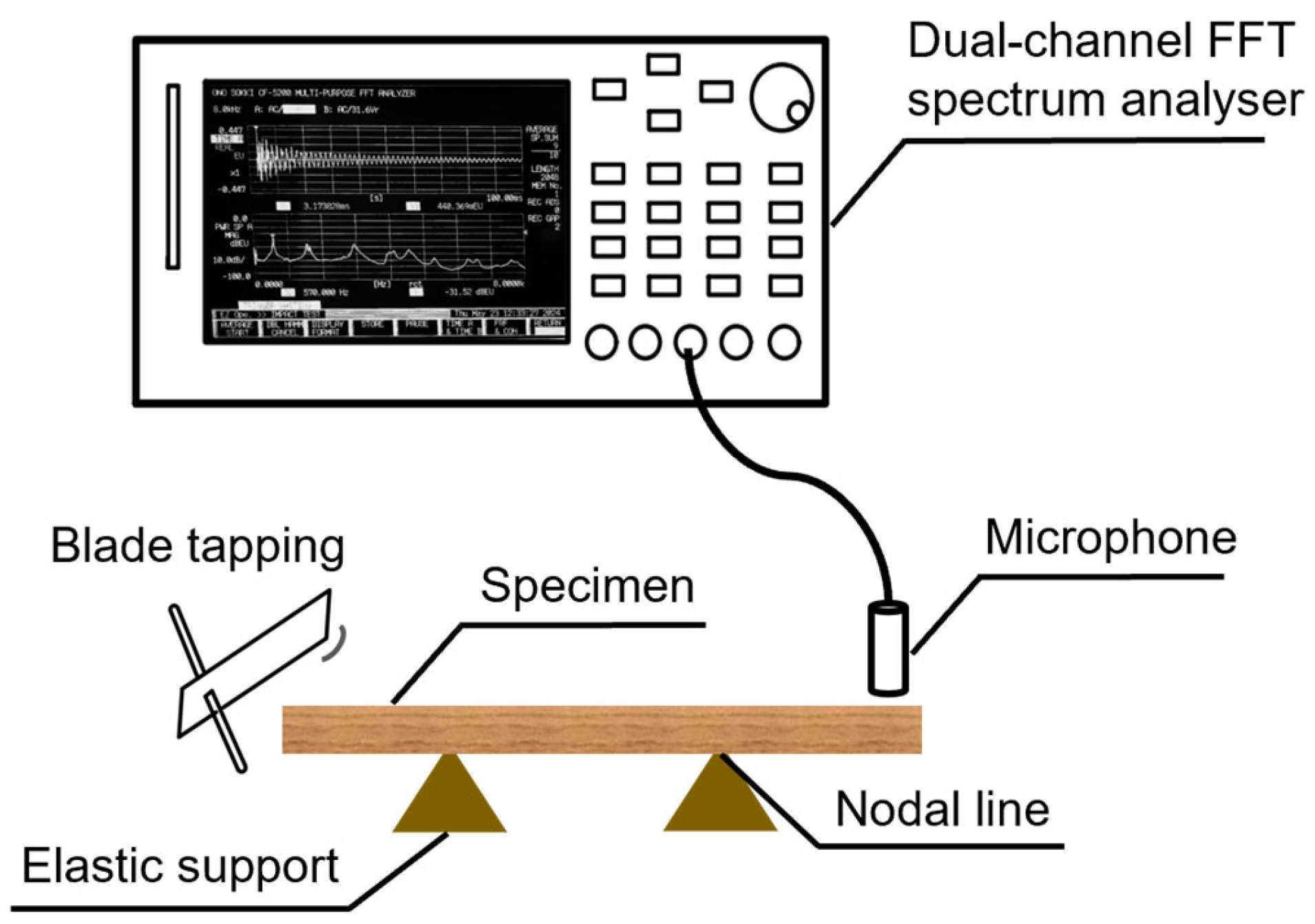
2.2.1. Frequency Spectral Measurement
2.2.2. Time-Domain Feature Extraction
2.3. Finite Element Simulation
3. Results and Discussion
3.1. Results of the Experimental Tests
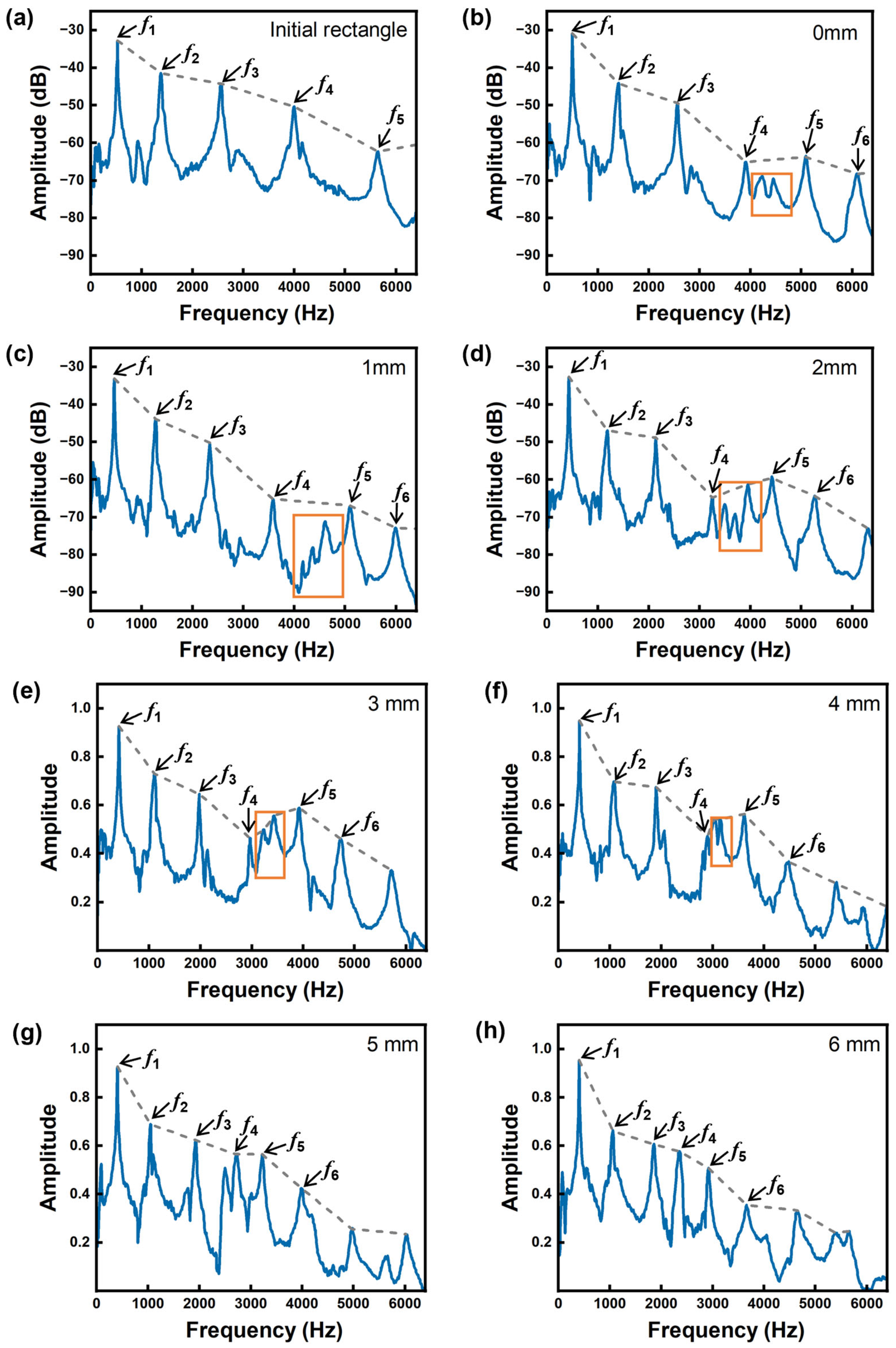
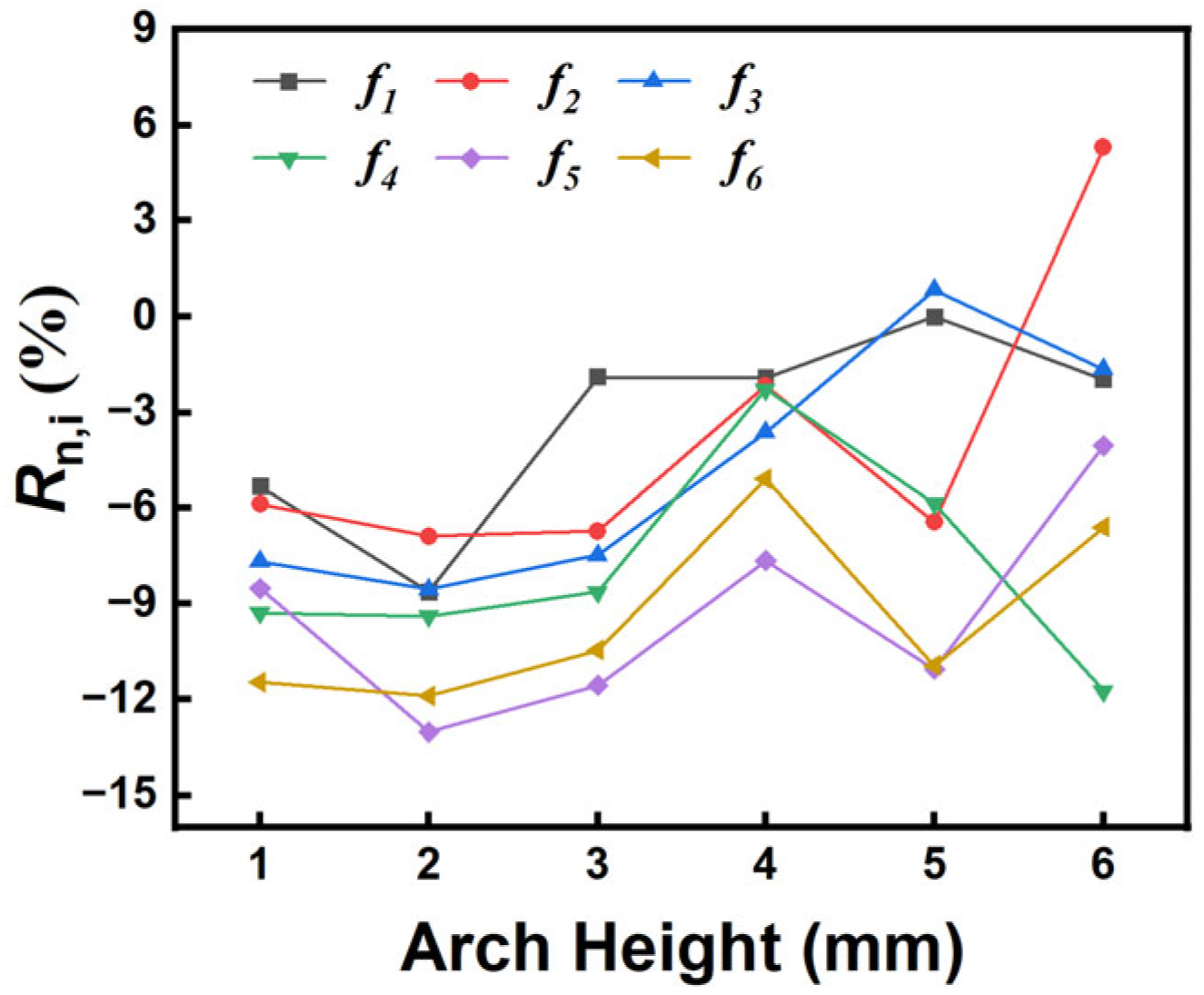
3.1.1. Frequency Domain
3.1.2. Time Domain
3.2. Results of Finite Element Simulation
3.2.1. Modal Shapes
3.2.2. Harmonic Response
3.2.3. Reliability Evaluation of the Finite Element Simulation Results
4. Conclusions
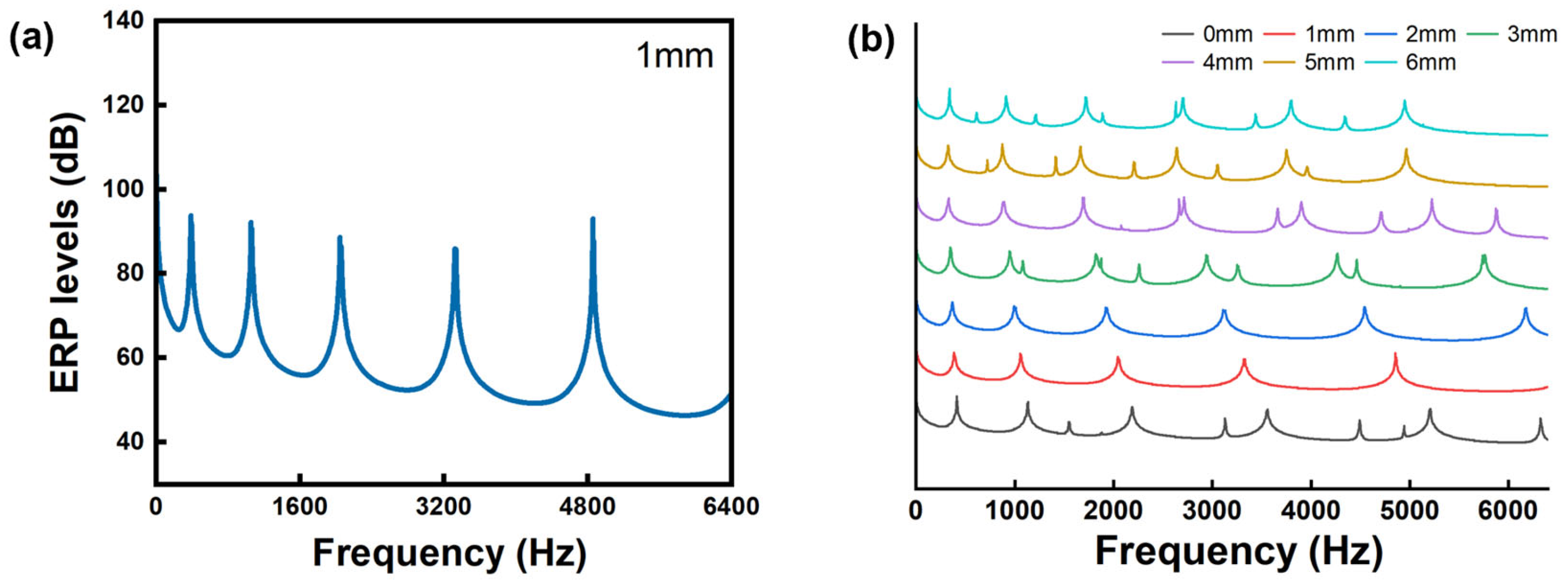
- Variations in arch height influenced the frequency spectrum response of the vibrations of Paulownia wood. Changes in arch height resulted in the emergence of more peaks between f4 and f5, which became increasingly concentrated as the arch height increased, ultimately disappearing when the arch height reached 6 mm. The high arch (3–6 mm) has a small effect on the fundamental frequency, and the low arch (0–2 mm) has a large effect on the fundamental frequency, with R1,1 and R1,2 being 5.31% and 8.62%, respectively. As the arch height increases, the change in the fundamental frequency stabilizes, decreasing by approximately 2% after each 1 mm thinning. In contrast, adjustments to the arch height have a pronounced effect on the higher-order frequencies (f4, f5, f6), which decrease by approximately 9%–13% with each 1 mm thinning in the range of 1–3 mm.
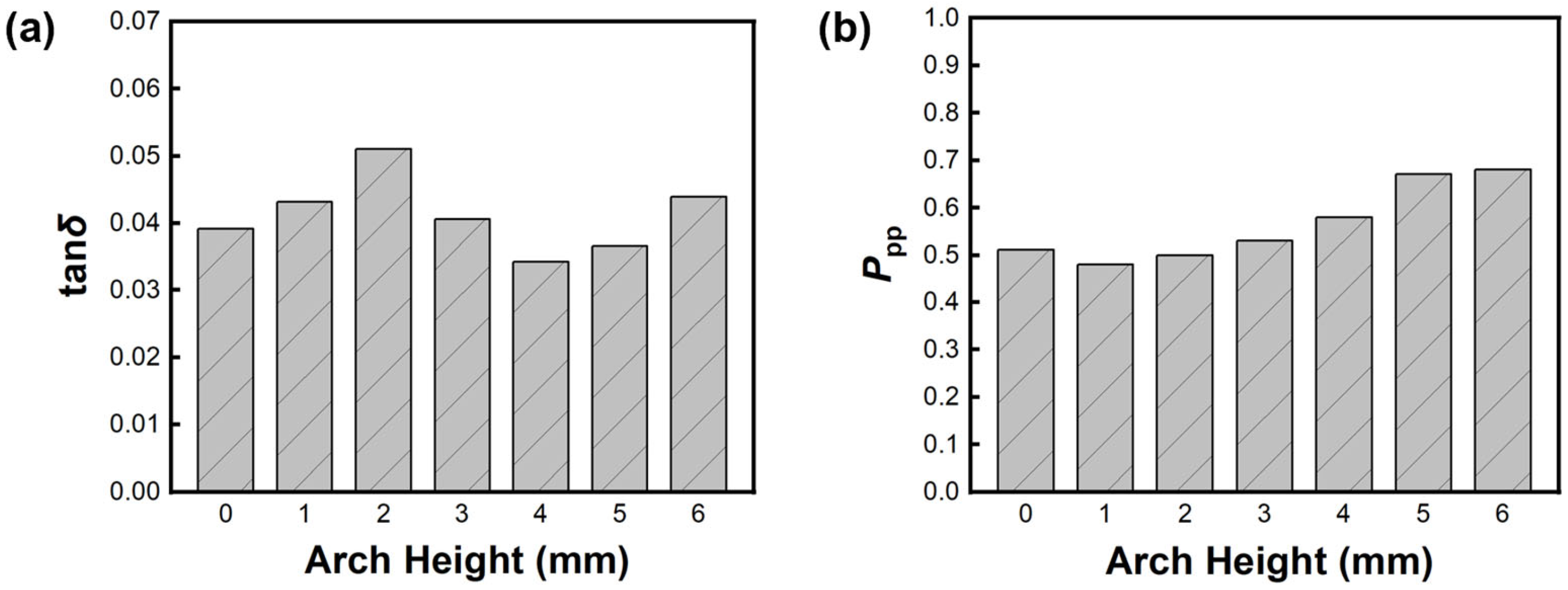
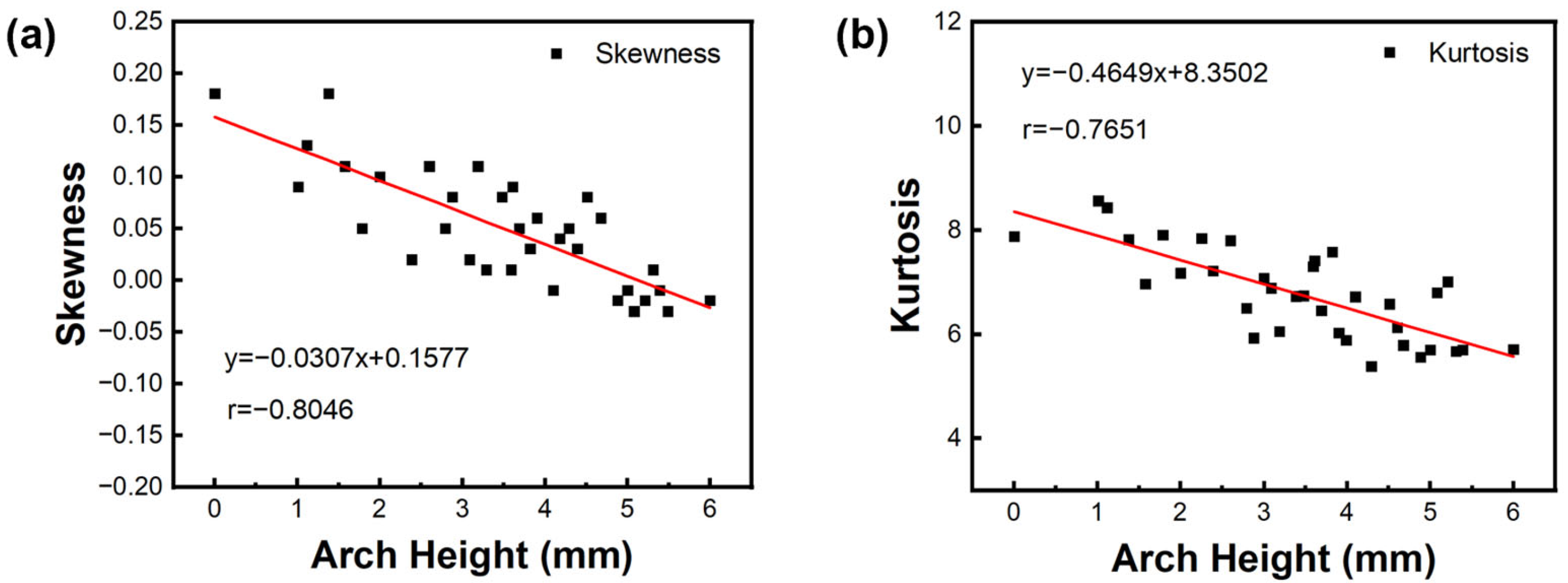
- The adjustment of arch height alters the acoustic radiation efficiency of resonance boards. There is a negative correlation between the skewness and kurtosis and the arch height of the wood. The vibration energy is released more when ΔH exceeds 3.06. The results of harmonic response also confirm this point. The number of peaks increases as the arch height increases to 3 mm, indicating that more energy in the frequency range is radiated.
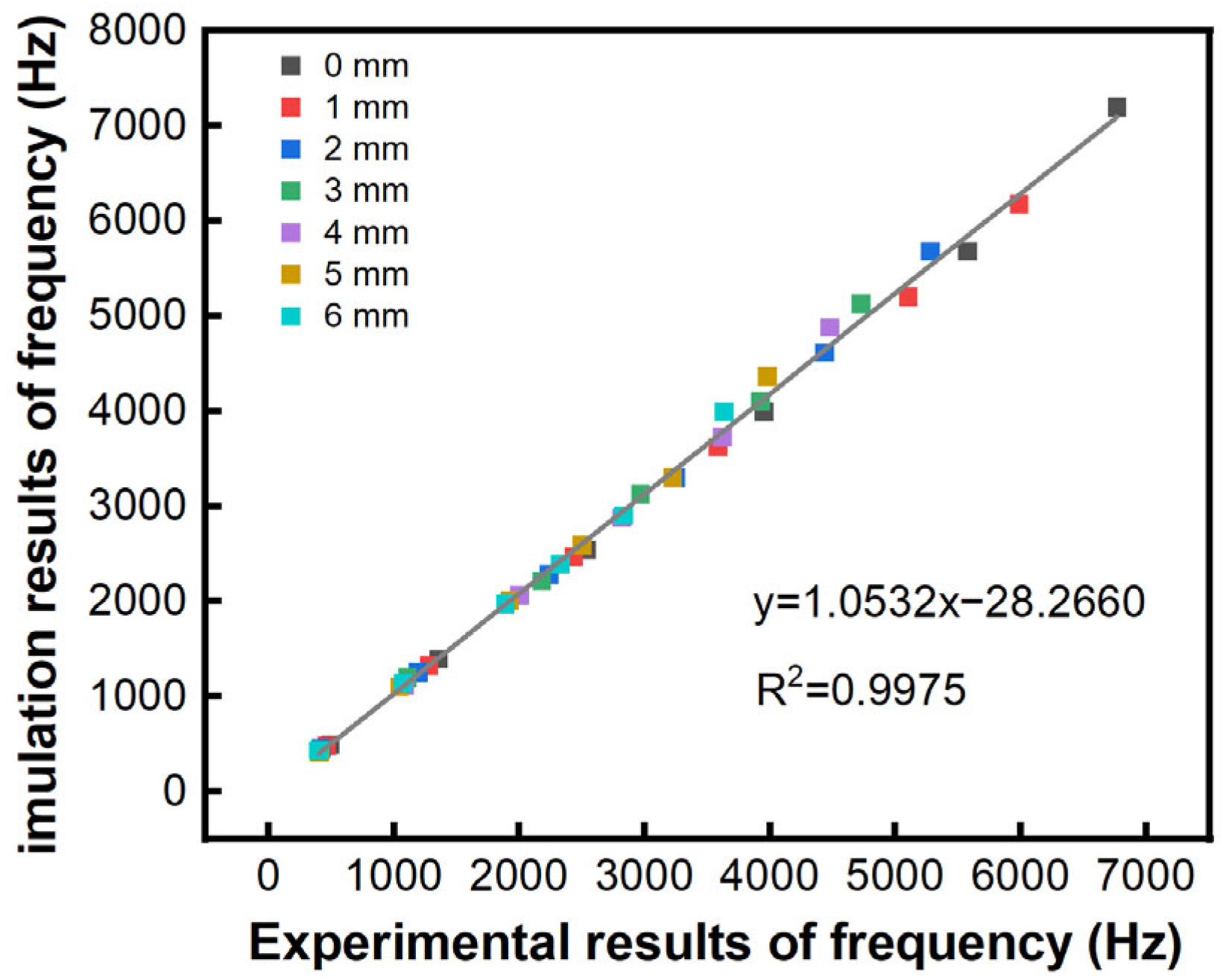
- Under free boundary conditions at both ends, the arch height significantly influenced the vibrational modes of the resonance board. Both frequency-domain and time-domain analyses demonstrated strong agreement with finite element simulation results. Experimental measurements exhibited high correlation with numerical predictions, validating the reliability of computational modal analysis for characterizing the modal vibration patterns of arched specimens. For future research, we suggest exploring a broader range of arch heights, as well as investigating the effects of different boundary conditions, such as clamped or simply supported edges. This could provide a more comprehensive understanding of how these factors interact with arch height to influence vibrational behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Castellanos, J.R.S.; Aguilar, J.M.V. Material properties and acoustic performance indexes of twenty-two Mexican woods. Measurement by ultrasound. Madera Bosques 2018, 24, e2431132. [Google Scholar] [CrossRef]
- Wegst, U.G.K. Bamboo and Wood in Musical Instruments. Ann. Rev. Mater. Res. 2008, 38, 323–349. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Deng, L.P.; Song, R.Z.; Chen, F.M.; Liu, X.G. Research Progress on the Acoustic Vibration Performance of Wood and Bamboo. World For. Res. 2021, 34, 1–7. [Google Scholar] [CrossRef]
- Ke, W.; Jing, Z.; Yixin, Z.; Haiyang, Z.; Zhenbo, L.; Wenshuai, C. Effect of Crack Length on Acoustic Vibration Properties of Paulownia Wood-All Databases. J. For. Eng. 2023, 8, 55–62. [Google Scholar] [CrossRef]
- Fedyukov, V.; Saldaeva, E.; Chernova, M. Different Ways of Elastic Modulus Comparative Study to Predict Resonant Properties of Standing Spruce Wood. Wood Res. 2017, 62, 607–614. [Google Scholar]
- Stoel, B.C.; Borman, T.M. A Comparison of Wood Density between Classical Cremonese and Modern Violins. PLoS ONE 2008, 3, e2554. [Google Scholar] [CrossRef]
- Dinulica, F.; Stanciu, M.D.; Savin, A. Correlation between Anatomical Grading and Acoustic-Elastic Properties of Resonant Spruce Wood Used for Musical Instruments. Forests 2021, 12, 1122. [Google Scholar] [CrossRef]
- Gonzalez, S.; Salvi, D.; Baeza, D.; Antonacci, F.; Sarti, A. A Data-Driven Approach to Violin Making. Sci. Rep. 2021, 11, 9455. [Google Scholar] [CrossRef]
- LeBlanc, J.; Shukla, A. Underwater Explosion Response of Curved Composite Plates. Compos. Struct. 2015, 134, 716–725. [Google Scholar] [CrossRef]
- Ramteke, P.M.; Panda, S.K. Free Vibrational Behaviour of Multi-Directional Porous Functionally Graded Structures. Arab. J. Sci. Eng. 2021, 46, 7741–7756. [Google Scholar] [CrossRef]
- Danihelova, A.; Stafura, A.; Culik, M.; Gergel, T. Influence of Wood and Thickness of Back Wall of Wooden Organ Pipe and Air Pressure in Windchest on Sound. Appl. Sci. 2024, 14, 7897. [Google Scholar] [CrossRef]
- Bissinger, G. Structural Acoustics of Good and Bad Violins. J. Acoust. Soc. Am. 2008, 124, 1764–1773. [Google Scholar] [CrossRef] [PubMed]
- Fritz, C.; Curtin, J.; Poitevineau, J.; Borsarello, H.; Wollman, I.; Tao, F.-C.; Ghasarossian, T. Soloist Evaluations of Six Old Italian and Six New Violins. Proc. Natl. Acad. Sci. USA 2014, 111, 7224–7229. [Google Scholar] [CrossRef]
- Li, D.; Zhao, X.; Hu, X.; Ma, G.; Hu, K.; Ma, H. Influence of Sectional Dimension of Stabilizing Piles on Soil Arching Characteristics. J. Eng. Geol. 2018, 26, 484–493. [Google Scholar] [CrossRef]
- Li, D.; Hu, X.; Zhao, X.; Yue, Z. Variation of Horizontal Arch Height of Granite Residual Soil Slope in Vertical Direction. J. Southwest Jiaotong Univ. 2016, 51, 1024–1032. [Google Scholar] [CrossRef]
- Xue, W.; Yiping, G.; Wei, Z. Analysis on the Three-Dimensional Measurement of Panels Shapes of Guzheng. Print. Digit. Media Technol. Study 2023, 6, 30–37. [Google Scholar] [CrossRef]
- Miranda Valiente, P.; Squicciarini, G.; Thompson, D.J. Influence of Soundboard Modelling Approaches on Piano String Vibration. J. Acoust. Soc. Am. 2024, 155, 3213–3232. [Google Scholar] [CrossRef]
- Waltham, C.; Lan, Y.; Koster, E. An Acoustical Study of the Qin. J. Acoust. Soc. Am. 2016, 139, 1592–1600. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, Y.T.; Wan, K.; Miao, Y.Y.; Li, Y.X.; Tian, M.L.; Guo, L.G.; Liu, Z.B. Vibration Mode of Guzheng Resonance Panel with Whole Board Structure-All Databases. J. Beijing For. Univ. 2021, 43, 107–116. [Google Scholar] [CrossRef]
- Ege, K.; Boutillon, X.; Rebillat, M. Vibroacoustics of the Piano Soundboard: (Non)Linearity and Modal Properties in the Low- and Mid-Frequency Ranges. J. Sound Vibr. 2013, 332, 1288–1305. [Google Scholar] [CrossRef]
- Bissinger, G. Structural Acoustics Model of the Violin Radiativity Profile. J. Acoust. Soc. Am. 2008, 124, 4013–4023. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; He, L.; Liang, Y.; Zhang, J.; Zhang, H.; Zhou, J.; Cui, H.; Li, M.; Miao, Y.; Liu, Z. Modulating the Acoustic Vibration Performance of Wood by Introducing a Periodic Annular Groove Structure. Forests 2023, 14, 2360. [Google Scholar] [CrossRef]
- Gonzalez, S.; Chacra, E.; Carreno, C.; Espinoza, C. Wooden Mechanical Metamaterials: Towards Tunable Wood Plates. Mater. Des. 2022, 221, 110952. [Google Scholar] [CrossRef]
- Gough, C.E. A Violin Shell Model: Vibrational Modes and Acoustics. J. Acoust. Soc. Am. 2015, 137, 1210–1225. [Google Scholar] [CrossRef]
- Gliga, V.G.; Stanciu, M.D.; Nastac, S.M.; Campean, M. Modal Analysis of Violin Bodies with Back Plates Made of Different Wood Species. BioResources 2020, 15, 7687–7713. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, Y.; Miao, Y.; Liu, Z.; Li, Y.; Tian, M.; Li, X.; Wang, C. Vibration Mode of Guzheng Soundboard with Composite Structure. J. Beijing For. Univ. 2022, 44, 132–141. [Google Scholar] [CrossRef]
- Salvi, D.; Gonzalez, S.; Antonacci, F.; Sarti, A. Modal Analysis of Free Archtop Guitar Top Plates. J. Acoust. Soc. Am. 2021, 150, 1505–1513. [Google Scholar] [CrossRef]
- Sun, L.; Miao, Y.; Zhai, X.; Li, M.; Liu, Z. Effect of Excitation Force on Wood Vibration Damping Coefficient. J. Northeast For. Univ. 2020, 48, 91–95. [Google Scholar] [CrossRef]
- Jia, N.; Guo, L.; Wang, R.; Liu, J. Design of Vibration and Noise Reduction for Ultra-Thin Cemented Carbide Circular Saw Blades in Woodworking Based on Multi-Objective Optimization. Forests 2024, 15, 1554. [Google Scholar] [CrossRef]
- Yang, Y. Research on GRNN Prediction Model for Acoustic Quality of Yueqin Based on Wood Vibration Characteristics. For. Eng. 2024, 40, 160–167. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Dinulica, F.; Bucur, V.; Gliga, V.G.; Nastac, S.M.; Campean, M. Changing the Vibrational Behavior of the Wooden Thin Arched Plates-The Maestro Violins Experimental Study Case. Thin-Walled Struct. 2022, 174, 109042. [Google Scholar] [CrossRef]
- Deng, X.; Yu, Z.; Yao, W.; Chen, M. Simulation Analysis of Vibro-Acoustic Characteristics of Traditional Guzheng. J. Shanghai Jiaotong Univ. 2016, 50, 300–305. [Google Scholar] [CrossRef]
- Miao, Y.; Liu, Z.; Liu, Y.; Shen, J. Effect of Vibration Properties of a Resonance Board on Piano Timbre. For. Prod. J. 2016, 66, 126–133. [Google Scholar] [CrossRef]
- Mania, P.; Skrodzka, E. Modal Parameters of Resonant Spruce Wood (Picea abies L.) after Thermal Treatment. J. King Saud Univ. Sci. 2020, 32, 1152–1156. [Google Scholar] [CrossRef]
- Yin, Y.; Miao, Y.; Wan, K.; Wang, X.; Zhai, X.; Liu, Z. Analysis and Evaluation of Wood Acoustic Vibration Signal Based on Daubechies Wavelet Base. J. For. Eng. 2021, 6, 68–75. [Google Scholar] [CrossRef]
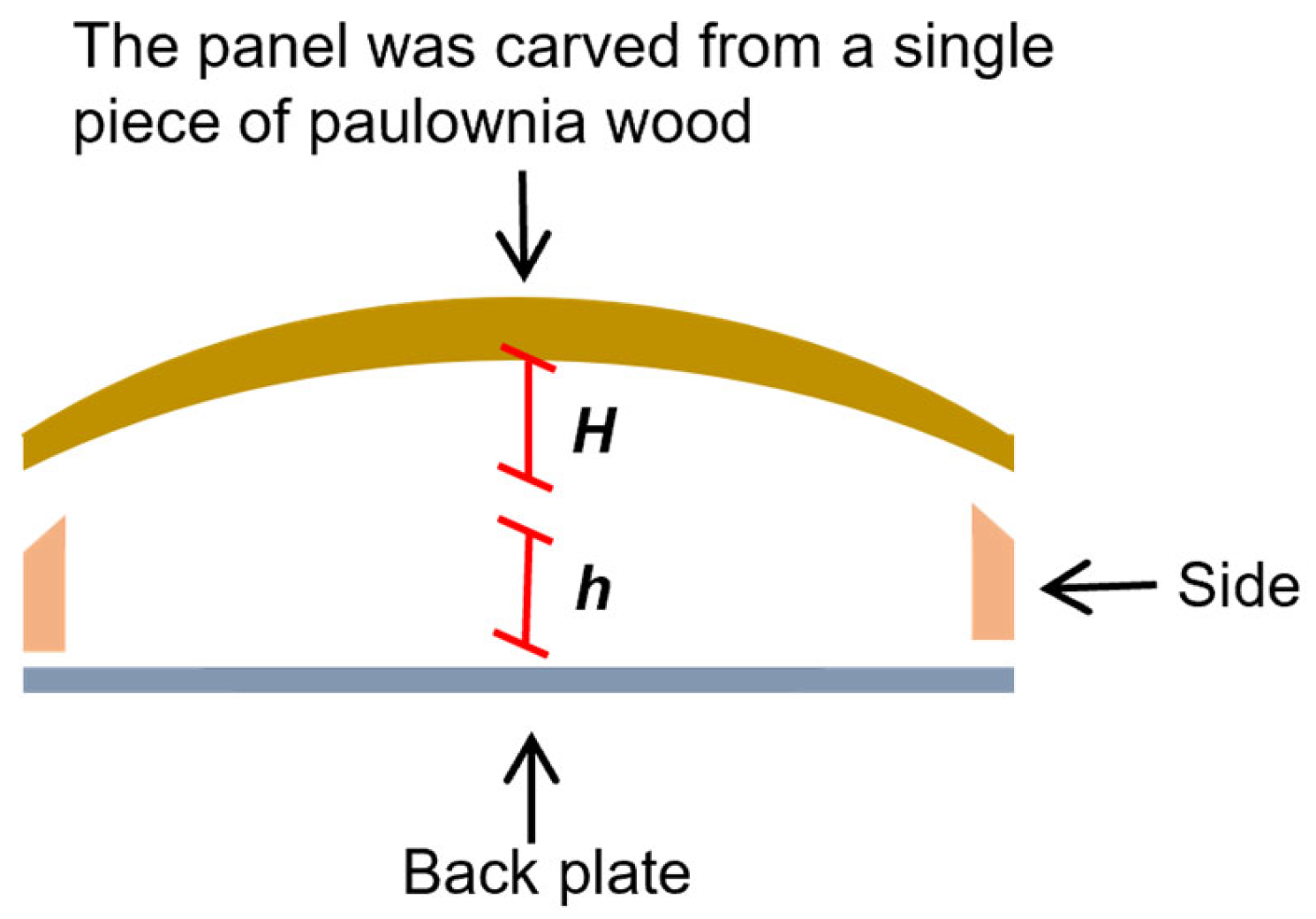




| Design Arch Height H (mm) | Measured Arch Height H (mm) | Errors (mm) | L × R (mm) | T1 (mm) | T2 (mm) | Density ρ (g·cm−3) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 300.01 × 50.20 | 3.09 | 3.05 | 0.27 |
| 1 | 0.98 | ±0.02 | ||||
| 2 | 2.01 | ±0.01 | ||||
| 3 | 3.00 | ±0.01 | ||||
| 4 | 3.99 | ±0.01 | ||||
| 5 | 5.04 | ±0.04 | ||||
| 6 | 6.01 | ±0.01 |
| Density (g·cm−3) | Damping Ratio | Young’s Modulus (GPa) | Shear Modulus (GPa) | Poisson’s Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EL | ET | ER | GLT | GLR | GRT | μLT | μLR | μRT | ||
| 0.27 | 0.05 | 4.20 | 1.03 | 2.96 | 0.300 | 0.200 | 0.033 | 0.15 | 0.02 | 0.08 |
| Range Minimum (Hz) | Range Maximum (Hz) | Solution Intervals | Excitation Direction | Stress (MPa) |
|---|---|---|---|---|
| 0 | 8000 | 2048 | Z | 0.01 |
| Resonant Order | Results | 0 mm | 1 mm | 2 mm | 3 mm | 4 mm | 5 mm | 6 mm |
|---|---|---|---|---|---|---|---|---|
| f1 | Measured value/Hz | 490 | 464 | 424 | 416 | 408 | 404 | 400 |
| Simulation value/Hz | 494 | 485 | 458 | 437 | 409 | 406 | 424 | |
| Errors/% | 0.82 | 4.33 | 7.42 | 4.81 | 0.24 | 0.49 | 5.66 | |
| f2 | Measured value/Hz | 1360 | 1280 | 1192 | 1112 | 1088 | 1048 | 1072 |
| Simulation value/Hz | 1392 | 1325 | 1250 | 1188 | 1110 | 1096 | 1141 | |
| Errors/% | 2.35 | 3.52 | 4.87 | 6.83 | 2.02 | 4.58 | 6.44 | |
| f3 | Measured value/Hz | 2530 | 2436 | 2236 | 2176 | 2004 | 1920 | 1888 |
| Simulation value/Hz | 2541 | 2461 | 2280 | 2216 | 2066 | 2002 | 1965 | |
| Errors/% | 0.43 | 1.03 | 1.97 | 1.84 | 3.09 | 4.27 | 4.07 | |
| f4 | Measured value/Hz | 3950 | 3584 | 3248 | 2968 | 2816 | 2500 | 2330 |
| Simulation value/Hz | 3991 | 3628 | 3301 | 3124 | 2874 | 2589 | 2390 | |
| Errors/% | 1.04 | 1.22 | 1.63 | 5.26 | 2.06 | 3.56 | 2.58 | |
| f5 | Measured value/Hz | 5570 | 5096 | 4432 | 3920 | 3616 | 3220 | 2832 |
| Simulation value/Hz | 5682 | 5203 | 4616 | 4100 | 3727 | 3294 | 2906 | |
| Errors/% | 2.01 | 2.10 | 4.15 | 4.60 | 3.07 | 2.30 | 2.61 | |
| f6 | Measured value/Hz | 6760 | 5984 | 5272 | 4720 | 4472 | 3980 | 3632 |
| Simulation value/Hz | 7193 | 6173 | 5683 | 5130 | 4877 | 4365 | 3992 | |
| Errors/% | 6.41 | 3.14 | 7.80 | 8.67 | 9.10 | 9.67 | 9.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, S.; Guo, Y.; Zhang, J.; He, L.; Zhou, J.; Miao, Y.; Liu, Z. Experiments and Simulation on the Effects of Arch Height Variation on the Vibrational Response of Paulownia Wood. Forests 2025, 16, 545. https://doi.org/10.3390/f16030545
Li X, Wang S, Guo Y, Zhang J, He L, Zhou J, Miao Y, Liu Z. Experiments and Simulation on the Effects of Arch Height Variation on the Vibrational Response of Paulownia Wood. Forests. 2025; 16(3):545. https://doi.org/10.3390/f16030545
Chicago/Turabian StyleLi, Xiyue, Siyuan Wang, Yaqing Guo, Juncheng Zhang, Lan He, Jing Zhou, Yuanyuan Miao, and Zhenbo Liu. 2025. "Experiments and Simulation on the Effects of Arch Height Variation on the Vibrational Response of Paulownia Wood" Forests 16, no. 3: 545. https://doi.org/10.3390/f16030545
APA StyleLi, X., Wang, S., Guo, Y., Zhang, J., He, L., Zhou, J., Miao, Y., & Liu, Z. (2025). Experiments and Simulation on the Effects of Arch Height Variation on the Vibrational Response of Paulownia Wood. Forests, 16(3), 545. https://doi.org/10.3390/f16030545







