Development and Evaluation of a Thinning Tree Selection System Using Optimization Techniques Based on Multi-Platform LiDAR
Abstract
1. Introduction
- Construction of individual tree position, DBH, and tree height information for large-scale areas using LiDAR;
- Optimization of thinning tree selection utilizing precise forest structural information and genetic algorithms;
- Evaluation of system applicability through comparison with tree selection results by forestry experts.
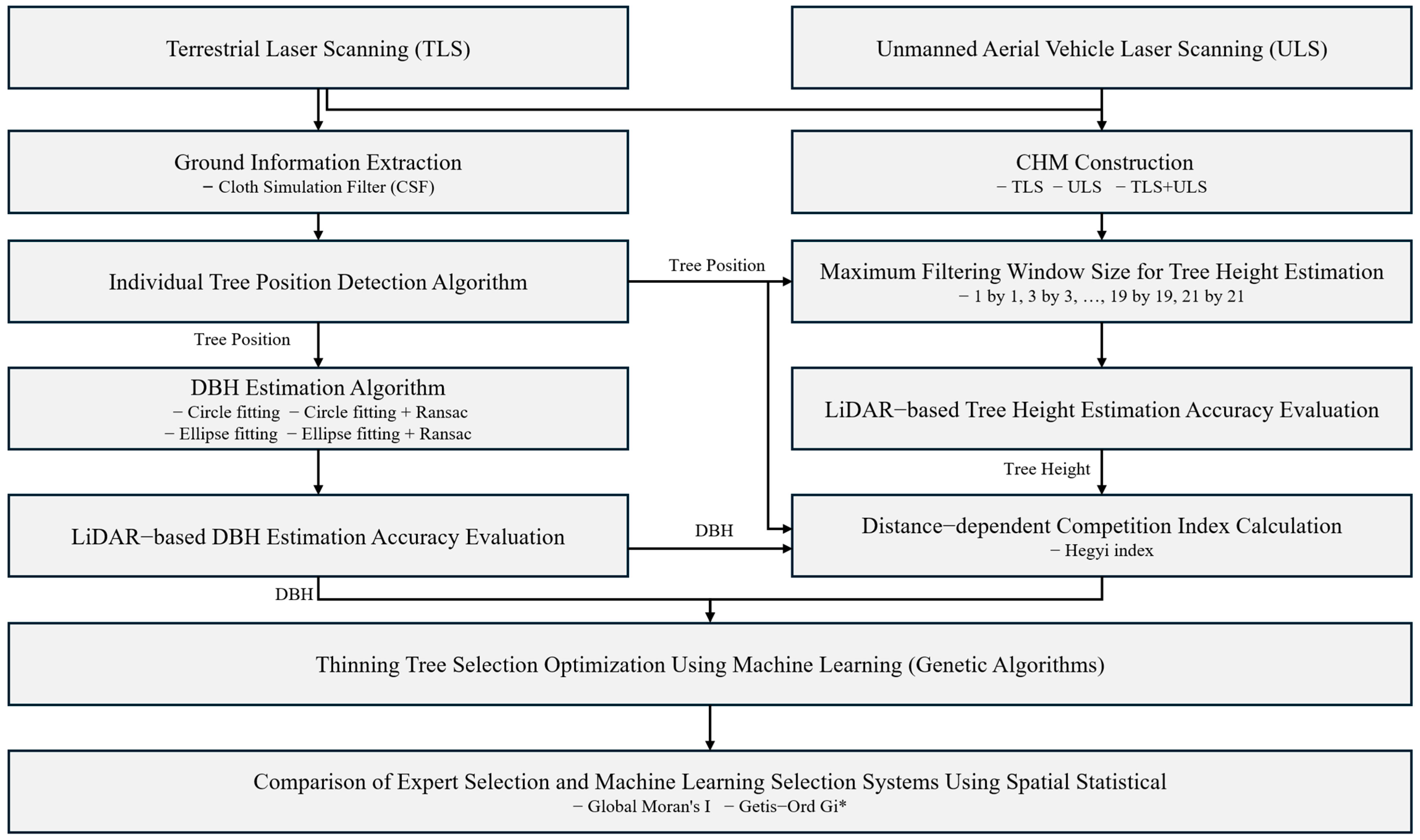
2. Materials and Methods
2.1. Study Area
2.2. Materials
2.3. Methods
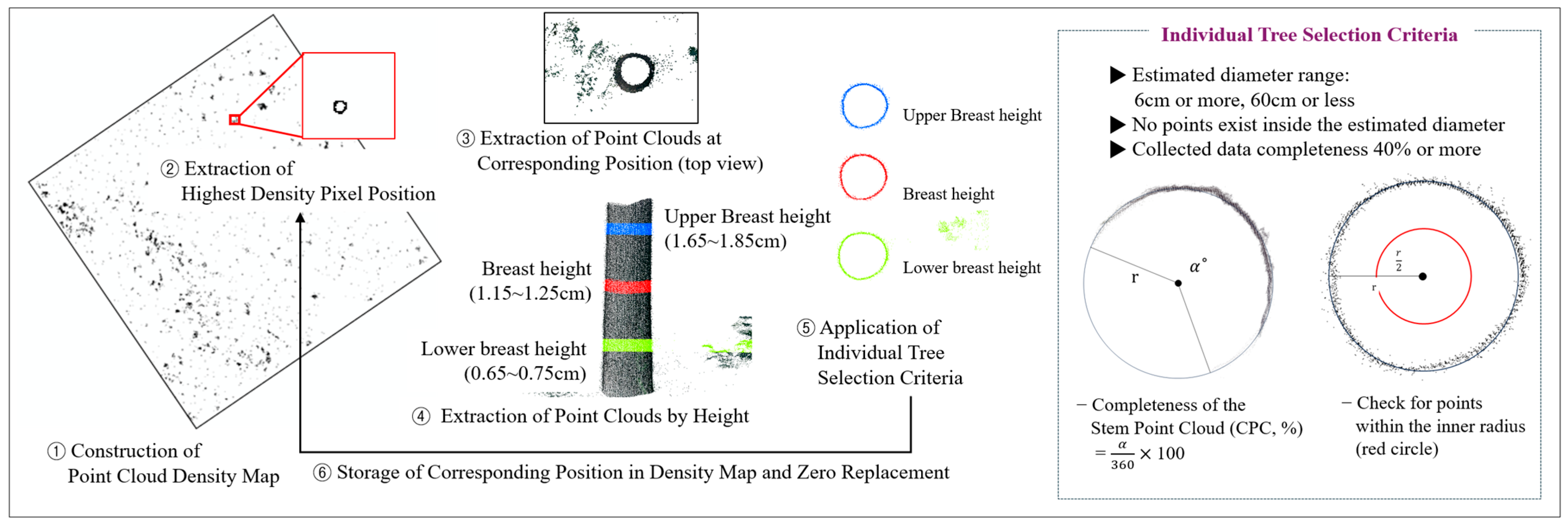
2.3.1. Individual Tree Position Detection Using LiDAR Data
2.3.2. DBH Estimation Using LiDAR Data
2.3.3. Tree Height Estimation Using LiDAR Data
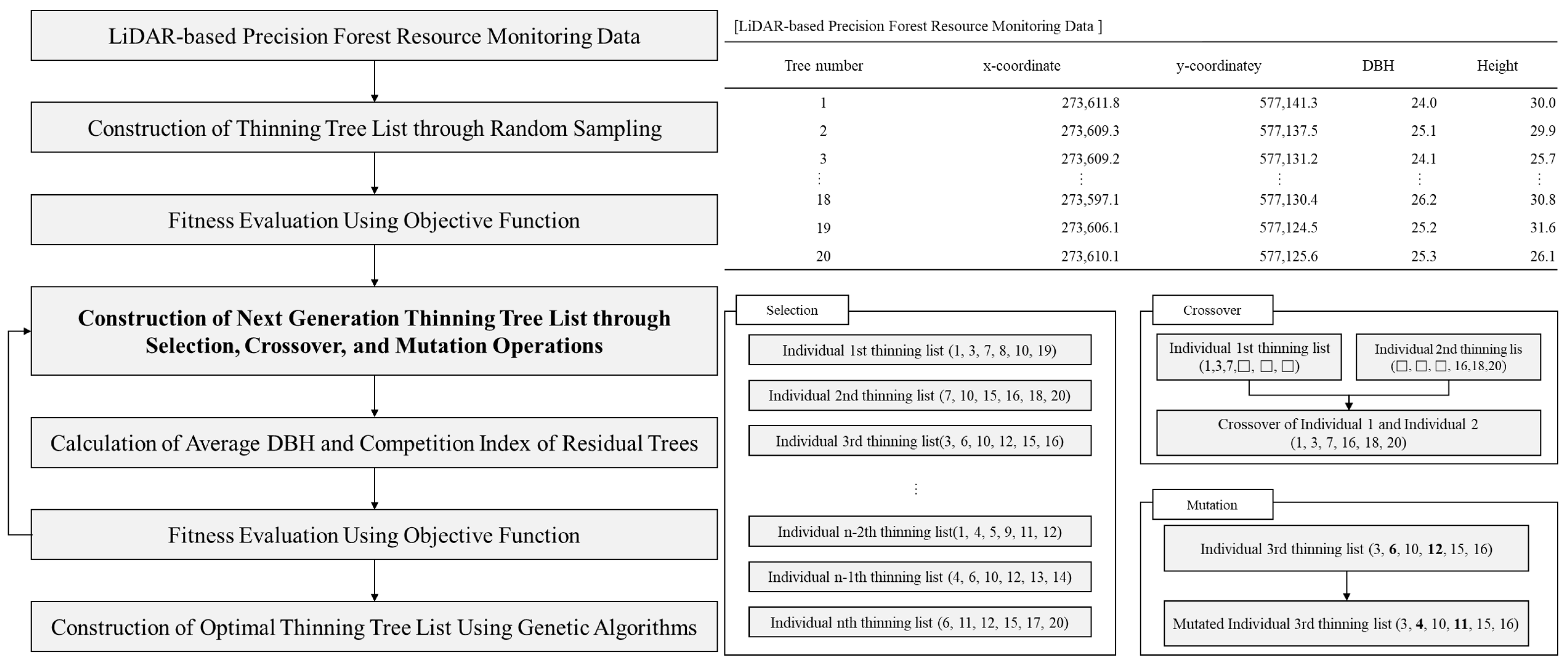
2.3.4. Variable Setting for Thinning Tree Selection Optimization
2.3.5. Optimization of Thinning Tree Selection Using Genetic Algorithms
| Category | DBH Weight (w0) | Competition Index Weight (w1) |
|---|---|---|
| Scenario 1 | 0.2 | 0.8 |
| Scenario 2 | 0.4 | 0.6 |
| Scenario 3 | 0.6 | 0.4 |
| Scenario 4 | 0.8 | 0.2 |
2.3.6. Comparison and Evaluation of Thinning Tree Selection Results Using Expert and Machine Learning Tree Selection Systems
3. Results and Discussion
3.1. Individual Tree Detection Using LiDAR
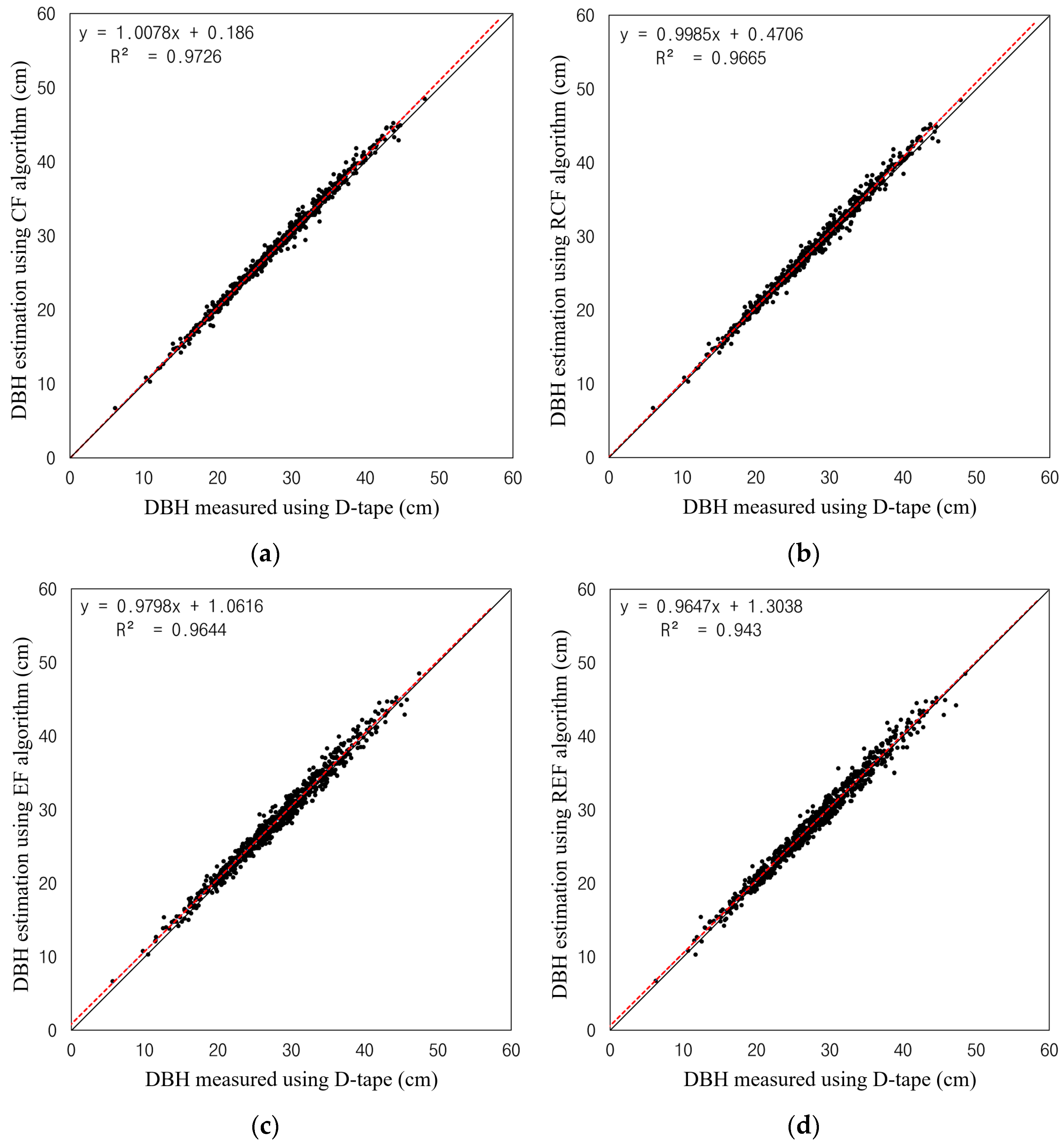
3.2. Evaluation of DBH Estimation Accuracy According to Circle Fitting Algorithms
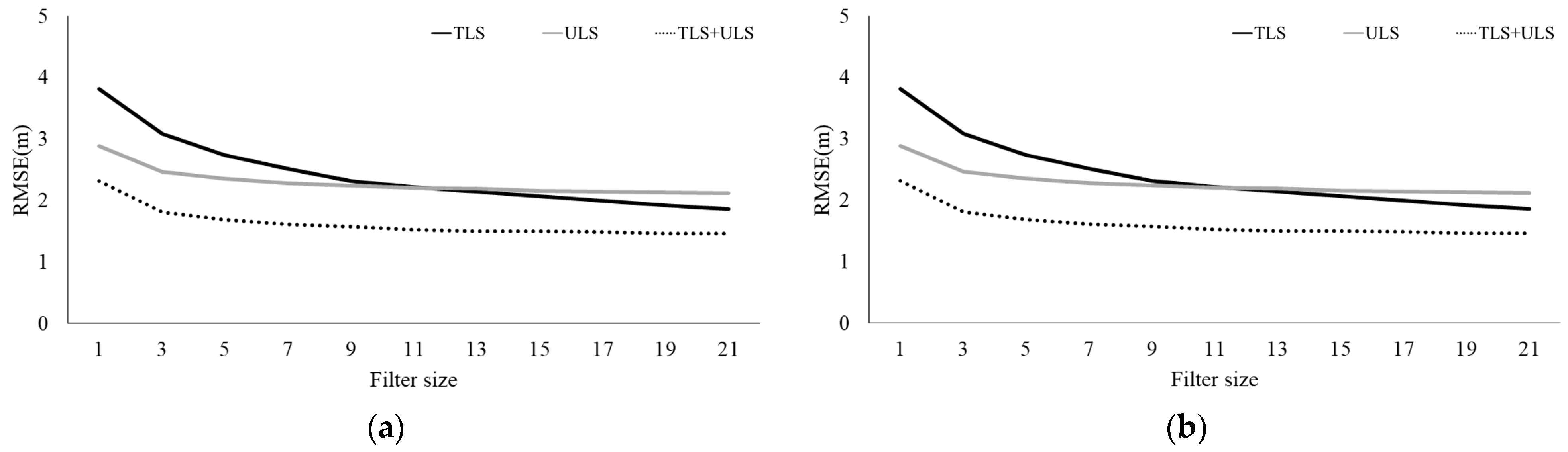
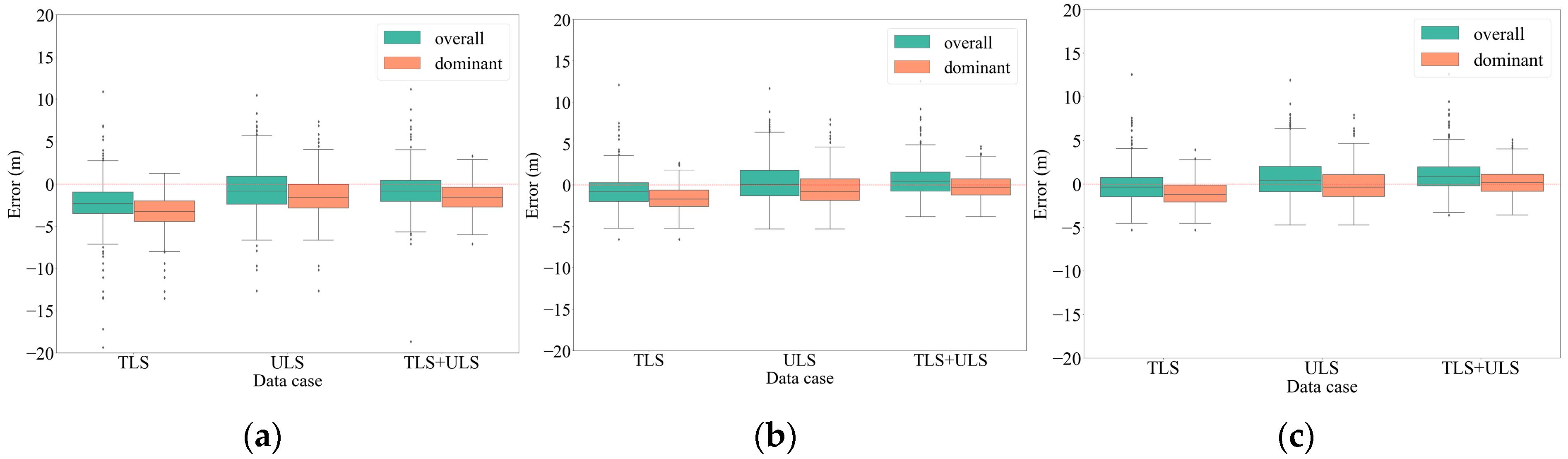
3.3. Tree Height Estimation and Accuracy Evaluation Using Multi-Platform LiDAR Data
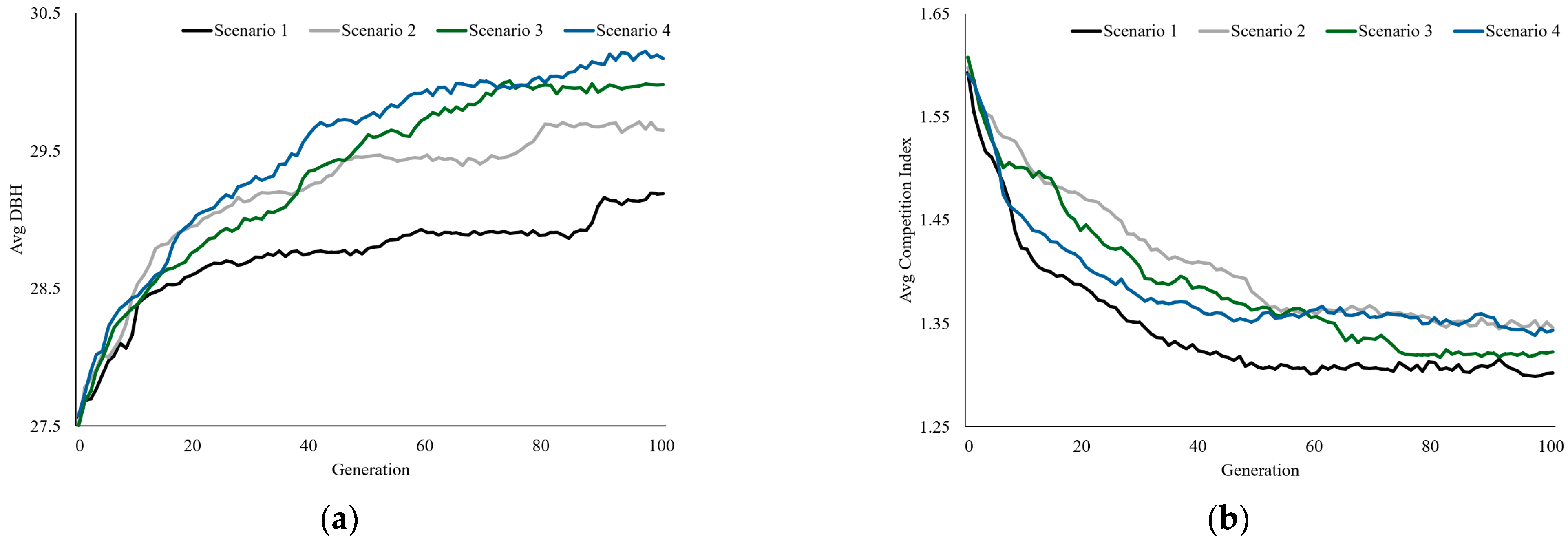
3.4. Optimal Thinning Tree Selection and Evaluation Using Genetic Algorithms
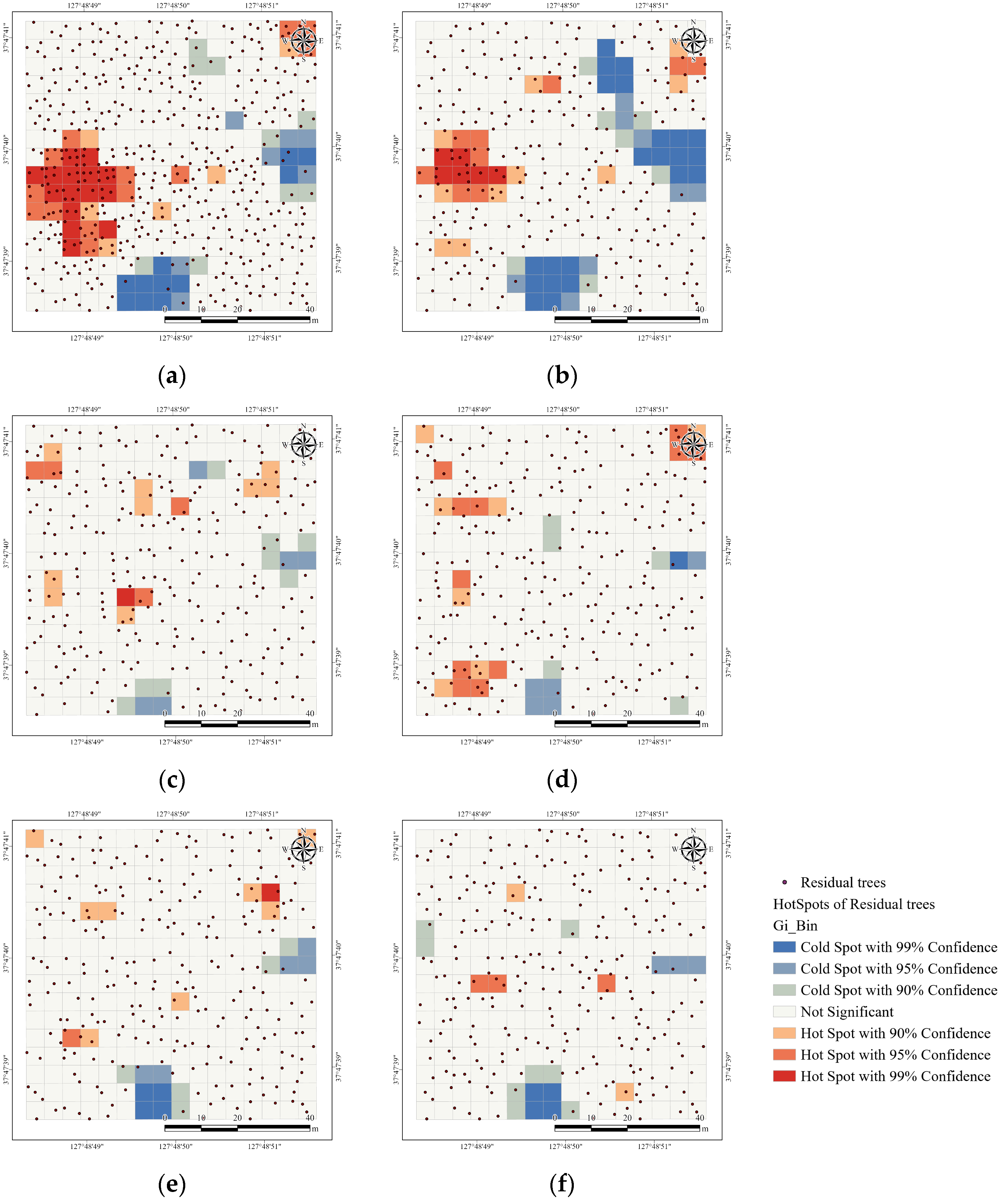
3.5. Comparison of Expert Selection and Machine Learning Tree Selection System Using Spatial Statistical Techniques
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TLS | Terrestrial Laser Scanning |
| ULS | Unmanned Aerial Vehicle Laser Scanning |
| DBH | Diameter at Breast Height |
| RMSE | Root Mean Square Error |
| GCP | Ground Control Point |
| DSM | Digital Surface Models |
| DEM | Digital Elevation Models |
| CHM | Canopy Height Models |
References
- Fuller, M.R.; Ganjam, M.; Baker, J.S.; Abt, R.C. Advancing forest carbon projections requires improved convergence between ecological and economic models. Carbon Balance Manag. 2025, 20, 2. [Google Scholar] [CrossRef]
- Loehle, C.; Miller, D.A.; Kovach, A.I.; Larsen-Gray, A.L.; Akresh, M.E.; McDonald, J.E.; Cheeseman, A.E.; King, D.; Petzinger, S.M.; Kanter, J. Forest Management Is Key for Conserving Biodiversity and Providing Ecosystem Services in the United States. Forests 2024, 15, 2087. [Google Scholar] [CrossRef]
- Ameray, A.; Bergeron, Y.; Valeria, O.; Girona, M.M.; Cavard, X. Forest Carbon Management: A Review of Silvicultural Practices and Management Strategies Across Boreal, Temperate and Tropical Forests. In Current Forestry Reports; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Lundholm, A.; Black, K.; Corrigan, E.; Nieuwenhuis, M. Evaluating the impact of future global climate change and bioeconomy scenarios on ecosystem services using a strategic forest management decision support system. Front. Ecol. Evol. 2020, 8, 200. [Google Scholar] [CrossRef]
- Moreau, G.; Chagnon, C.; Achim, A.; Caspersen, J.; D’Orangeville, L.; Sánchez-Pinillos, M.; Thiffault, N. Opportunities and limitations of thinning to increase resistance and resilience of trees and forests to global change. Forestry 2022, 95, 595–615. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.; Yu, J.; Li, J.; Shangguan, Z.; Deng, L. Thinning increases forest ecosystem carbon stocks. For. Ecol. Manag. 2024, 555, 121702. [Google Scholar] [CrossRef]
- Pretzsch, H. Density and growth of forest stands revisited. Effect of the temporal scale of observation, site quality, and thinning. For. Ecol. Manag. 2020, 460, 117879. [Google Scholar] [CrossRef]
- Lee, D.S.; Choi, J.K. Comparison of stand structure and growth characteristics between Korean white pine plantation and oak-dominated natural deciduous forest by thinning treatment. J. Ecol. Environ. 2022, 46, 85–98. [Google Scholar] [CrossRef]
- Spinelli, R.; Magagnotti, N.; Pari, L.; Soucy, M. Comparing tree selection as performed by different professional figures. For. Sci. 2016, 62, 213–219. [Google Scholar] [CrossRef]
- Park, J.K.; Lee, K.W. Individual tree detection and modeling using terrestrial and drone-mounted laser scanners. J. Korea Acad.-Ind. Coop. Soc. 2022, 23, 36–41. [Google Scholar] [CrossRef]
- Šporčić, M.; Landekić, M.; Šušnjar, M.; Pandur, Z.; Bačić, M.; Mijoč, D. Deliberations of forestry workers on current challenges and future perspectives on their profession—A case study from Bosnia and Herzegovina. Forests 2023, 14, 817. [Google Scholar] [CrossRef]
- Liu, T.; Sun, Y.; Wang, C.; Zhang, Y.; Qiu, Z.; Gong, W.; Lei, S.; Tong, X.; Duan, X. Unmanned aerial vehicle and artificial intelligence revolutionizing efficient and precision sustainable forest management. J. Clean. Prod. 2021, 311, 127546. [Google Scholar] [CrossRef]
- Singh, R.; Gehlot, A.; Akram, S.V.; Thakur, A.K.; Buddhi, D.; Das, P.K. Forest 4.0: Digitalization of forest using the Internet of Things (IoT). J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 5587–5601. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J.; Janicka, J. Tree position estimation from TLS data using hough transform and robust least-squares circle fitting. Remote Sens. Appl. Soc. Environ. 2023, 29, 100863. [Google Scholar] [CrossRef]
- Hui, Z.; Lin, L.; Jin, S.; Xia, Y.; Ziggah, Y.Y. A reliable dbh estimation method using terrestrial lidar points through polar coordinate transformation and progressive outlier removal. Forests 2024, 15, 1031. [Google Scholar] [CrossRef]
- Lee, Y.K.; Lee, J.S. Advancing Stem Volume Estimation Using Multi-Platform LiDAR and Taper Model Integration for Precision Forestry. Remote Sens. 2025, 17, 785. [Google Scholar] [CrossRef]
- Fransson, P.; Franklin, O.; Lindroos, O.; Nilsson, U.; Brännström, Å. A simulation-based approach to a near-optimal thinning strategy: Allowing harvesting times to be determined for individual trees. Can. J. For. Res. 2020, 50, 320–331. [Google Scholar] [CrossRef]
- Niemi, M.T.; Vauhkonen, J.; Uusitalo, J. Trade-off analysis for multi-objective boreal forest thinning. For. Int. J. For. Res. 2025, cpaf027. [Google Scholar] [CrossRef]
- Wardius, Y.; Hein, S. Terrestrial laser scanning vs. manual methods for assessing complex forest stand structure: A comparative analysis on plenter forests. Eur. J. For. Res. 2024, 143, 635–649. [Google Scholar] [CrossRef]
- Zimmerman, T.; Jansen, K.; Miller, J. Analysis of UAS Flight Altitude and Ground Control Point Parameters on DEM Accuracy along a Complex, Developed Coastline. Remote Sens. 2020, 12, 2305. [Google Scholar] [CrossRef]
- Storch, M.; Jarmer, T.; Adam, M.; de Lange, N. Systematic approach for remote sensing of historical conflict landscapes with UAV-based laserscanning. Sensors 2021, 22, 217. [Google Scholar] [CrossRef]
- Iheaturu, C.J.; Hepner, S.; Batchelor, J.L.; Agonvonon, G.A.; Akinyemi, F.O.; Wingate, V.R.; Speranza, C.I. Integrating UAV LiDAR and multispectral data to assess forest status and map disturbance severity in a West African forest patch. Ecol. Inform. 2024, 84, 102876. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J. Evaluation of Accuracy in Estimating Diameter at Breast Height Based on the Scanning Conditions of Terrestrial Laser Scanning and Circular Fitting Algorithm. Forests 2024, 15, 313. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Bailey, G.; Li, Y.; McKinney, N.; Yoder, D.; Wright, W.; Herrero, H. Comparison of ground point filtering algorithms for high-density point clouds collected by terrestrial LiDAR. Remote Sens. 2022, 14, 4776. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating individual tree height and diameter at breast height (DBH) from terrestrial laser scanning (TLS) data at plot level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the RANSAC algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Rodríguez-Puerta, F.; Gómez-García, E.; Martín-García, S.; Pérez-Rodríguez, F.; Prada, E. UAV-Based LiDAR Scanning for Individual Tree Detection and Height Measurement in Young Forest Permanent Trials. Remote Sens. 2022, 14, 170. [Google Scholar] [CrossRef]
- Xiang, B.; Wielgosz, M.; Kontogianni, T.; Peters, T.; Puliti, S.; Astrup, R.; Schindler, K. Automated forest inventory: Analysis of high-density airborne LiDAR point clouds with 3D deep learning. Remote Sens. Environ. 2024, 305, 114078. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, T.; Zhu, J.; Wu, F.; Li, X.; Lu, D.; Yu, F. Individual Tree Segmentation and Tree Height Estimation Using Leaf-Off and Leaf-On UAV-LiDAR Data in Dense Deciduous Forests. Remote Sens. 2022, 14, 2787. [Google Scholar] [CrossRef]
- Sačkov, I. Forest inventory based on canopy height model derived from airborne laser scanning data. Cent. Eur. For. J. 2022, 68, 224–231. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Lisiewicz, M.; Kamińska, A.; Kraszewski, B.; Stereńczak, K. Correcting the results of CHM-based individual tree detection algorithms to improve their accuracy and reliability. Remote Sens. 2022, 14, 1822. [Google Scholar] [CrossRef]
- Lee, Y.K.; Lee, J.S.; Park, J.W. A study on classification of crown classes and selection of thinned trees for major conifers using machine learning techniques. J. Korean Soc. For. Sci. 2022, 111, 302–310. [Google Scholar]
- Moore, J.A.; Budelsky, C.A.; Schlesinger, R.C. A new index representing individual tree competitive status. Can. J. For. Res. 1973, 3, 495–500. [Google Scholar] [CrossRef]
- Martin, G.L.; Ek, A.R. A comparison of competition measures and growth models for predicting plantation red pine diameter and height growth. For. Sci. 1984, 30, 731–743. [Google Scholar] [CrossRef]
- Lee, Y.K.; Lee, J.S.; Han, S.K.; Ji, H.V.; Park, J.W. Selection of Trees for Thinning Using Machine Learning Algorithms and Competition Indices. Forests 2025, 16, 65. [Google Scholar] [CrossRef]
- Miller, B.L.; Goldberg, D.E. Genetic algorithms, tournament selection, and the effects of noise. Complex Syst. 1995, 9, 193–212. [Google Scholar]
- Fotakis, D.G.; Sidiropoulos, E.; Myronidis, D.; Ioannou, K. Spatial genetic algorithm for multi-objective forest planning. For. Policy Econ. 2012, 21, 12–19. [Google Scholar] [CrossRef]
- Kaya, A.; Bettinger, P.; Boston, K.; Akbulut, R.; Ucar, Z.; Siry, J.; Merry, K.; Cieszewski, C. Optimisation in forest management. Curr. For. Rep. 2016, 2, 1–17. [Google Scholar] [CrossRef]
- Castro, I.; Salas-González, R.; Fidalgo, B.; Farinha, J.T.; Mendes, M. Optimising Forest Management Using Multi-Objective Genetic Algorithms. Sustainability 2024, 16, 10655. [Google Scholar] [CrossRef]
- Thompson, M.P.; Hamann, J.D.; Sessions, J. Selection and penalty strategies for genetic algorithms designed to solve spatial forest planning problems. Int. J. For. Res. 2009, 2009, 527392. [Google Scholar] [CrossRef]
- Shanin, V.; Hökkä, H.; Grabarnik, P. Testing the performance of some competition indices against experimental data and outputs of spatially explicit simulation models. Forests 2021, 12, 1415. [Google Scholar] [CrossRef]
- Korea Forest Service. Sustainable Forest Resource Management Guidelines; Directive No. 1454, Partially Amended; Korea Forest Service: Daejeon, Republic of Korea, 2020. Available online: https://www.law.go.kr (accessed on 14 October 2024).
- Rossi, F.; Becker, G. Creating forest management units with Hot Spot Analysis (Getis-Ord Gi*) over a forest affected by mixed-severity fires. Aust. For. 2019, 82, 166–175. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Lin, Y.C.; Shao, J.; Shin, S.Y.; Saka, Z.; Joseph, M.; Manish, R.; Fei, S.; Habib, A. Comparative analysis of multi-platform, multi-resolution, multi-temporal LiDAR data for forest inventory. Remote Sens. 2022, 14, 649. [Google Scholar] [CrossRef]
- Kuželka, K.; Surový, P. Noise Analysis for Unbiased Tree Diameter Estimation from Personal Laser Scanning Data. Remote Sens. 2024, 16, 1261. [Google Scholar] [CrossRef]
- Martínez-Otzeta, J.M.; Rodríguez-Moreno, I.; Mendialdua, I.; Sierra, B. Ransac for robotic applications: A survey. Sensors 2022, 23, 327. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. 3D point cloud fusion from UAV and TLS to assess temperate managed forest structures. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102917. [Google Scholar] [CrossRef]
- Zhou, R.; Sun, H.; Ma, K.; Tang, J.; Chen, S.; Fu, L.; Liu, Q. Improving estimation of tree parameters by fusing ALS and TLS point cloud data based on canopy gap shape feature points. Drones 2023, 7, 524. [Google Scholar] [CrossRef]
- Stovall, A.E.; MacFarlane, D.W.; Crawford, D.; Jovanovic, T.; Frank, J.; Brack, C. Comparing mobile and terrestrial laser scanning for measuring and modelling tree stem taper. For. Int. J. For. Res. 2023, 96, 705–717. [Google Scholar] [CrossRef]
- Compeán-Aguirre, J.L.; López-Serrano, P.M.; Silván-Cárdenas, J.L.; Martínez-García-Moreno, C.A.; Vega-Nieva, D.J.; Corral-Rivas, J.J.; Pompa-García, M. Evaluation of two-dimensional DBH estimation algorithms using TLS. Forests 2024, 15, 1964. [Google Scholar] [CrossRef]
- He, M.; Hu, Y.; Zhao, J.; Li, Y.; Wang, B.; Zhang, J.; Noguchi, H. Exploring Stand Parameters Using Terrestrial Laser Scanning in Pinus tabuliformis Plantation Forests. Remote Sens. 2025, 17, 1228. [Google Scholar] [CrossRef]
- Shimizu, K.; Nishizono, T.; Kitahara, F.; Fukumoto, K.; Saito, H. Integrating terrestrial laser scanning and unmanned aerial vehicle photogrammetry to estimate individual tree attributes in managed coniferous forests in Japan. Int. J. Appl. Earth Obs. Geoinf. 2022, 106, 102658. [Google Scholar] [CrossRef]
- Nègre, P.; Mahé, K.; Cornacchini, J. Unmanned aerial vehicle (UAV) paired with LiDAR sensor to detect bodies on surface under vegetation cover: Preliminary test. Forensic Sci. Int. 2025, 369, 112411. [Google Scholar] [CrossRef]
- Lee, Y.K.; Woo, H.S.; Lee, J.S. Forest Inventory Assessment Using Integrated Light Detection and Ranging (LiDAR) Systems: Merged Point Cloud of Airborne and Mobile Laser Scanning Systems. Sens. Mater. 2022, 34, 4583–4597. [Google Scholar] [CrossRef]
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and evaluating different LiDAR-derived canopy height model generation methods for tree height estimation. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 132–143. [Google Scholar] [CrossRef]
- Weiser, H.; Schäfer, J.; Winiwarter, L.; Krašovec, N.; Fassnacht, F.E.; Höfle, B. Individual tree point clouds and tree measurements from multi-platform laser scanning in German forests. Earth Syst. Sci. Data 2022, 14, 2989–3012. [Google Scholar] [CrossRef]
- Henrich, J.; van Delden, J.; Seidel, D.; Kneib, T.; Ecker, A.S. TreeLearn: A deep learning method for segmenting individual trees from ground-based LiDAR forest point clouds. Ecol. Inform. 2024, 84, 102888. [Google Scholar] [CrossRef]
- Sparks, A.M.; Smith, A.M. Accuracy of a lidar-based individual tree detection and attribute measurement algorithm developed to inform forest products supply chain and resource management. Forests 2021, 13, 3. [Google Scholar] [CrossRef]
- Jurjević, L.; Liang, X.; Gašparović, M.; Balenović, I. Is field-measured tree height as reliable as believed–Part II, A comparison study of tree height estimates from conventional field measurement and low-cost close-range remote sensing in a deciduous forest. ISPRS J. Photogramm. Remote Sens. 2020, 169, 227–241. [Google Scholar] [CrossRef]
- Tenzin, J.; Tenzin, K.; Hasenauer, H. Individual tree basal area increment models for broadleaved forests in Bhutan. For. Int. J. For. Res. 2017, 90, 367–380. [Google Scholar] [CrossRef]

| Actual | |||
|---|---|---|---|
| True | False | ||
| Predicted | Positive | 735 | 4 |
| Negative | 1 | 0 | |
| Overall accuracy | 99.32% | ||
| Precision | 99.46% | ||
| Recall | 99.86% | ||
| F1-score | 99.66% | ||
| Estimation Method | With Outliers | Without Outliers | RMSE Difference | ||
|---|---|---|---|---|---|
| Number of Trees | RMSE | Number of Trees | RMSE | ||
| CF | 736 | 1.21 | 727 | 0.74 | 0.47 |
| RCF | 736 | 1.76 | 726 | 0.82 | 0.94 |
| EF | 735 | 1.39 | 722 | 1.04 | 0.36 |
| REF | 736 | 1.68 | 727 | 1.02 | 0.66 |
| Tree Group | Overall | Dominant | ||||
|---|---|---|---|---|---|---|
| Window size | 1 | 11 | 21 | 1 | 11 | 21 |
| TLS | 3.27 | 2.00 | 1.84 | 3.81 | 2.22 | 1.86 |
| ULS | 2.64 | 2.34 | 2.38 | 2.89 | 2.21 | 2.12 |
| TLS + ULS | 2.24 | 1.93 | 2.06 | 2.32 | 1.53 | 1.46 |
| Category | DBH | Competition Index | |||
|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||
| Machine Learning Tree Selection System | Scenario 1 | 29.21 | 6.51 | 1.29 | 0.53 |
| Scenario 2 | 29.71 | 6.63 | 1.34 | 0.59 | |
| Scenario 3 | 30.06 | 6.28 | 1.31 | 0.53 | |
| Scenario 4 | 30.25 | 6.09 | 1.34 | 0.53 | |
| Expert Selection | 29.26 | 5.93 | 1.41 | 0.61 | |
| Category | Before Thinning | Expert Selection | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|---|---|
| Moran’s Index | 0.16 | 0.16 | −0.03 | −0.01 | −0.04 | −0.03 |
| Expected Index | −0.00 | −0.00 | −0.00 | −0.00 | −0.00 | −0.00 |
| Variance | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| z-score | 5.01 | 4.93 | −0.74 | −0.07 | −1.15 | −0.82 |
| p-value | 0.00 | 0.00 | 0.46 | 0.94 | 0.25 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Sim, W.; Lee, S.; Lee, J. Development and Evaluation of a Thinning Tree Selection System Using Optimization Techniques Based on Multi-Platform LiDAR. Forests 2025, 16, 1776. https://doi.org/10.3390/f16121776
Lee Y, Sim W, Lee S, Lee J. Development and Evaluation of a Thinning Tree Selection System Using Optimization Techniques Based on Multi-Platform LiDAR. Forests. 2025; 16(12):1776. https://doi.org/10.3390/f16121776
Chicago/Turabian StyleLee, Yongkyu, Woodam Sim, Sangjin Lee, and Jungsoo Lee. 2025. "Development and Evaluation of a Thinning Tree Selection System Using Optimization Techniques Based on Multi-Platform LiDAR" Forests 16, no. 12: 1776. https://doi.org/10.3390/f16121776
APA StyleLee, Y., Sim, W., Lee, S., & Lee, J. (2025). Development and Evaluation of a Thinning Tree Selection System Using Optimization Techniques Based on Multi-Platform LiDAR. Forests, 16(12), 1776. https://doi.org/10.3390/f16121776






