Abstract
Teak (Tectona grandis L.f.) is a leading tropical plantation species valued for high-quality timber and carbon (C) storage. This study assessed stand growth across ages and sites, quantified biomass and C by tree component and stand, and developed DBH-based allometric equations for biomass and C estimation. Six stand ages (5, 6, 9, 11, 14, and 17 years) were assessed in three municipalities of Nayarit, Mexico. Dendrometric inventories in permanent plots and destructive sampling of 35 trees provided calibration data for leaves, branches, stem, and roots. C concentration was determined with an elemental analyzer, and nonlinear regression models were adjusted and validated. Stand biomass and C increased with age, peaking at ages 11–14 (>130 Mg ha−1; >60 Mg C ha−1), with lower values at age 17. San Blas and Rosamorada accumulated significantly more than Tuxpan, reflecting site quality. C concentration was stable across sites and ages, with stem and roots consistently ranging between 48% and 50%, and leaves and branches averaging 45%–46%. Allometric equations were most accurate for stem and total biomass/C (R2 = 0.73–0.79), while foliage showed higher variability. On average, 60%–70% of biomass was allocated to the stem and 15%–20% to roots. Indicators were stable, with an aboveground-to-belowground ratio (A:B) ≈ 4.9 and a biomass expansion factor (BEF) ≈ 1.5. The current annual increment (CAI) presented two main peaks: ~20 Mg ha−1 yr−1 at ages 5–6 and ~11 Mg ha−1 yr−1 at ages 9–11, followed by a decline after age 14. Teak in western Mexico reaches peak productivity at ages 6–11, with belowground biomass essential for accurate C accounting.
1. Introduction
Teak (Tectona grandis L.f.) is a native species of South and Southeast Asia, mainly distributed in India, Myanmar, Laos, and Thailand [1]. It has been extensively cultivated in its natural range for centuries due to its high-quality timber, durability, and resistance to pests and fungi [2]. During the 20th century, teak was widely introduced to tropical regions of Africa and Latin America, becoming one of the most important exotic hardwood species in commercial forestry [3]. In Mexico, teak introduction began in the early 1960s, with experimental plots in Veracruz and Campeche, followed by large-scale plantations established along both coasts from the 1990s onward [4]. At present, Nayarit, Campeche, Tabasco, Veracruz, and Oaxaca host extensive teak stands, positioning the species as a key component of the national reforestation and timber production strategy [5]. Teak stands are recognized for their relatively high productivity compared with other tropical hardwoods. Reported mean annual increments (MAIs) in Asia range between 8 and 12 m3 ha−1 yr−1 in India and Myanmar under natural forest management [6], but can exceed 20 m3 ha−1 yr−1 under improved silvicultural practices [7]. In Latin America, MAI values were documented at 12 to 18 m3 ha−1 yr−1 in Costa Rica [8], with values up to 22 m3 ha−1 yr−1 in intensively managed plantations [9]. In Mexico, teak productivity is slightly lower but still competitive, with MAI values ranging from 8 to 15 m3 ha−1 yr−1 in Nayarit and Campeche [5,10].
In addition to timber production, teak contributes to climate change mitigation through biomass accumulation and carbon (C) storage. In Costa Rica, aboveground biomass was reported to range between 120 and 220 Mg ha−1 in stands aged 10–20 years, with corresponding C stocks of 60–110 Mg C ha−1 [11]. Similarly, teak stands reached 150 Mg ha−1 of biomass by age 15, capturing up to 70 Mg C ha−1 [12]. In India, biomass values can exceed 250 Mg ha−1 in mature stands (>25 years), reflecting both favorable site conditions and intensive silvicultural practices [13]. In Mexico, estimates remain scarce, but preliminary reports indicate aboveground biomass values of 100–180 Mg ha−1 in stands aged between 10 and 20 years, equivalent to 50–90 Mg C ha−1 [5]. Reliable quantification of biomass and C pools requires robust allometric equations. Although generic pan-tropical models are widely applied [14], they often fail to capture stand- and site-specific variability in teak. Component-specific equations have proven more accurate, as demonstrated by [7] in India, [11] in Costa Rica, and [13] in Kerala, where locally calibrated models reduced errors by 15%–25% compared with generalized models. In Mexico, research on teak allometric equations is still limited, and most estimations rely on extrapolated or generic tropical equations, creating uncertainty in biomass and C inventories [10]. This study was conducted in San Blas, Rosamorada, and Tuxpan, which are among the main teak-growing municipalities in Nayarit. Their contrasting edaphoclimatic conditions make them representative of the variation observed in Mexican teak plantations.
We hypothesized that teak stands in western Mexico reach maximum growth and C accumulation during the first decade, that DBH-based allometric models provide accurate estimates of biomass and C pools, and that belowground biomass must be included to avoid systematic underestimation in C inventories. Accordingly, the aims of this study were to (i) analyze growth and productivity across stand ages and sites, (ii) quantify biomass and C accumulation by component and stand, and (iii) develop and validate DBH-based allometric equations for biomass and C estimation
2. Materials and Methods
2.1. Study Area
The research was conducted in teak stands located in three municipalities of Nayarit, Mexico: San Blas, Rosamorada, and Tuxpan (Figure 1). These sites encompass distinct ecological conditions, which made it possible to analyze growth, productivity, biomass accumulation, and C pools under varying environmental contexts while maintaining similar management practices.
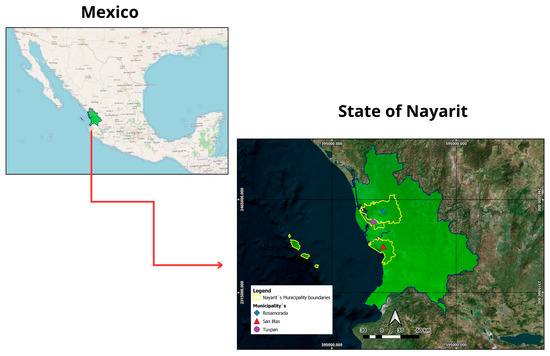
Figure 1.
Geographic location of teak stands in San Blas, Rosamorada, and Tuxpan, Nayarit, Mexico.
Rosamorada: situated between 21°56′–22°22′ N and 104°55′–105°35′ W, at elevations ranging from 0 to 1300 m. The area is characterized by annual mean temperatures of 22–28 °C and precipitation of 1000–2500 mm. Cambisol soils predominate in this region [15].
San Blas: located between 21°20′–21°45′ N and 105°01′–105°28′ W, with altitudes from 0 to 1200 m. Mean annual temperature is 22–28 °C and rainfall ranges from 1300 to 2000 mm. The dominant soils are Luvisols [16].
Tuxpan: positioned between 21°50′–22°01′ N and 105°11′–105°31′ W, with altitudes of 0–400 m. Average temperatures range from 26 to 28 °C and precipitation from 1200 to 2000 mm. Cambisols are the prevalent soil type [17].
2.2. Sampling Sites and Dendrometric Sampling
At each study site, teak stands of contrasting ages were selected to represent different stages of development. In total, six sampling sites were distributed across three municipalities: Rosamorada (6-year-old stand), Tuxpan (17-year-old stand), and San Blas (5-, 9-, 11-, and 14-year-old stands).
It is important to note that data from Rosamorada represent stands up to 6 years old, whereas San Blas and Tuxpan included older ages. Therefore, the present study primarily reflects early- to mid-rotation growth. Long-term follow-up studies are recommended to capture the full trajectory of teak growth and C sequestration across older age classes.
This design provided the opportunity to analyze stand growth, productivity, biomass accumulation, and C storage. In every stand, three rectangular plots of 40 × 25 m (1000 m2) were randomly established. Each stand corresponded to one of the six sampling sites described above, ensuring that stand-level measurements were linked directly to specific locations and ages. These plots were also the basis for destructive sampling, from which 5–6 trees per stand (total n = 35) were selected for allometric model development. Stand density (N, trees ha−1) was determined by counting all trees within each plot and extrapolating to one hectare. For destructive sampling, the 35 harvested trees covered DBH values ranging from 10 to 27 cm and total heights from 6 to 21 m, distributed across all six stand ages (5–17 years) and the three study sites. Stand ages were determined based on management records and plantation establishment dates, which were confirmed during field inventories. Destructive sampling was not required for age determination; instead, ages were verified against plantation documentation and stand history during field visits. Each stand corresponded to one of the six sampling sites described above, ensuring that stand-level measurements were linked directly to specific locations and ages. For each sampled tree, diameter at breast height (DBH) was measured at 1.3 m above the ground using a precision diameter tape (Forestry Suppliers Inc., Jackson MS, USA), and total height (H) was recorded with a Haga hypsometer (Haga GmbH + Co KG, Núremberg, Alemania) at a fixed horizontal distance of 15 m. These dendrometric variables formed the basis for subsequent calculations of basal area (BA), stand volume (V), and mean annual increment (MAI).
2.3. Growth and Productivity Estimation
Stand-level dendrometric variables were derived from field measurements of DBH and total H. Stand density (N, trees ha−1) was obtained by direct tree counts within each plot and scaled to one hectare, following the procedures described by [18].
The basal area (BA, m2 ha−1) was calculated for each stand using Equation (1):
where DBH is the tree diameter at breast height (cm), measured at 1.3 m, and N is stand density (trees ha−1). BA is a widely used structural variable to characterize forest stands [19].
Stand volume (V, m3 ha−1) was estimated from basal area, mean tree height, and a form factor (2):
where H is the mean stand height (m) and f is the form factor. A constant value of 0.5 was adopted, as recommended for tropical plantations by [20].
Mean annual increment (MAI) was obtained by dividing stand variables by stand age (A, years) (3):
MAI is considered a key indicator for comparing stand productivity across different sites and ages [21].
The current annual increment (CAI) was calculated as the difference in stand volume between two consecutive ages divided by the age interval. Values obtained at the plot level (1000 m2) were scaled to stand-level estimates per hectare by multiplying by stand density (trees ha−1). This procedure allowed extrapolation from sample plots to total stand estimates, ensuring consistency across sites and age classes (4):
where Vt1 and Vt2 and are the volumes at ages t1 and t2, respectively. This procedure is commonly applied in growth and yield studies for tropical and temperate species [22,23]. Together, these indicators allowed the quantification of stand-level productivity and the evaluation of growth dynamics in teak across different ages and environmental conditions. All these variables (BA, V, MAI, CAI) were first calculated at the 1000 m2 plot level and then scaled to one hectare to obtain stand-level estimates.
2.4. Biomass and Carbon Determination
A destructive sampling of 5–6 trees was carried out in each stand, totaling 35 trees across all sites and ages. The destructive sample (n = 35 trees) is comparable to sample sizes in other teak and tropical biomass studies (20–40 trees) and was considered sufficient for deriving component-level equations. Nevertheless, the equations are specific to the sampled site–age combinations and should not be generalized beyond these conditions. Each tree was separated into stem, branches, leaves, and roots, following procedures commonly applied in tropical biomass studies [24,25]. Root systems were excavated manually around the tree to a depth of approximately 60 cm, which allowed recovery of the coarse root fraction (>2 cm diameter), while fine roots (<2 cm) were carefully collected to minimize losses. Fresh root biomass was weighed directly in the field. To improve replicability, recovery fractions were applied to account for residual fragments, and correction factors were incorporated following standard tropical biomass protocols.
Fresh weight (FW) of stems and roots was determined in the field using a high-capacity digital scale (Rhino BAC-300; ±100 g), while the FW of branches and leaves was recorded with a precision scale (Rhino BAR-8; ±2 g). For each component (leaves, branches, stem, roots), ~10% of the fresh biomass was taken as a representative subsample to determine dry matter content. Subsamples were randomly selected from different portions of each component to ensure representativeness. Variability among subsamples was tested, and standard errors were incorporated into biomass estimates. Subsamples of each component were taken to the laboratory, oven-dried at 70 ± 3 °C until constant weight (Terlab S.A. de C.V., Zapopan, Mexico), and weighed to obtain dry weight (DW). The dry matter fraction (DMF) was calculated as (5):
This factor was then applied to the total FW of each component to estimate its dry biomass. Total tree biomass corresponded to the sum of all components, as described by [14].
The C concentration of biomass was determined using a LECO TruSpec® CHNS-O elemental analyzer (LECO Corp., St. Joseph, MI, USA). Approximately 2 mg of oven-dried and finely ground material (<0.5 mm, 60-mesh) from each tree component was combusted under an oxygen-rich atmosphere, and the evolved CO2 was quantified by a thermal conductivity detector [26]. Thirty replicates per component were analyzed to ensure statistical robustness. The results were expressed as %C of dry biomass, which is the standard method for reporting C content in forest ecosystems [27,28].
Subsequently, biomass and C values were scaled to the stand level (Mg ha−1) considering the final tree density of each plot. This procedure enabled the quantification of total biomass and C stored by stand age and site, as well as the relative contribution of aboveground (stem, branches, leaves) and belowground (roots) components.
2.5. Development of Allometric Equations Using Field-Measured Biomass
Allometric equations were fitted exclusively with field-measured dry biomass obtained from the destructive sampling (Section 2.4). For each sampled tree (n = 35), we computed component dry biomass (leaves, branches, stem, roots) by applying the dry matter fraction (DMF = DW/FW) to total fresh mass per component, and then summed components to obtain total tree biomass. These observed dry biomass values (kg) were the response variable in all models.
We specified log–linear models with DBH as the only predictor for each component and for total biomass (6):
where Bi is observed dry biomass (kg) for tree/component i, DBH is diameter at breast height (cm), and a, b are parameters. Models were fitted by OLS on the log scale. Predictions on the arithmetic scale used smearing correction [29,30,31] (7) and (8):
B = exp(a + b ln(DBH)) × CF
C stocks were obtained by multiplying estimated biomass by the measured %C of each component (from CHNS-O analysis); therefore, independent C equations were unnecessary. Thus, C per component/tree was computed as (9):
using the observed mean C concentration for each component [28].
Model diagnostics included residual vs. fitted plots, QQ plots, and Breusch–Pagan tests for heteroscedasticity. When needed, we refit using weighted least squares with variance functions proportional to DBH chosen by AIC [32,33]. We report R2 and RMSE on the log scale, and MAPE, bias (%), and the smearing factor (CF) on the arithmetic scale. To assess generalization, we performed 5-fold cross-validation stratified by site/age and summarized performance with RMSECV and MAPECV [34]. However, no independent validation dataset was available beyond cross-validation, which we recognize as a limitation of the study. If a prior two-predictor model (DBH, H) exists, we provide a comparative table (AIC, RMSE, MAPE, Bias, RMSECV) to document the operational advantages of DBH-only without material loss of accuracy [14,35,36]. In addition to these diagnostics, we quantified systematic bias using the mean bias error (MBE) and its relative version (MBE%), computed as the average of (predicted–observed) biomass per tree and that quantity divided by the sum of observed biomass, respectively. These metrics were calculated on the fitting set and summarized under the 5-fold cross-validation scheme. Although we restricted our modeling to DBH-only log–log equations for operational reasons, other functional forms (e.g., quadratic log–log, DBH–height, wood density-based, nonlinear power, and mixed-effects models) should be explored in future studies to improve predictive accuracy and reduce potential bias, particularly for large trees.
2.6. Stand-Level Biomass, C, and Derived Indicators
Biomass and C values obtained at the tree level were scaled to a per-hectare basis considering stand density in each plot [18]. Estimates were expressed in megagrams per hectare (Mg ha−1) for both biomass and C. The distribution of biomass and C among tree components was evaluated by calculating their relative contribution (%) to total values ((10) and (11)):
Aboveground biomass and C (stem, branches, leaves) were compared with belowground values (roots) through the aboveground-to-belowground ratio (A:B) ((12) and (13)):
In addition, the biomass expansion factor (BEF) was estimated as the ratio between total and stem biomass, while the C expansion factor (CEF) was calculated analogously ((14) and (15)):
To describe productivity dynamics, the current annual increment (CAI) of biomass and C was calculated as the difference between two consecutive stand ages divided by the age interval ((16) and (17)):
These indicators are widely reported in biomass and C studies of tropical forests [14,37,38] and allow evaluation of allocation patterns and efficiency of C capture across stand ages and sites.
2.7. Statistical Analysis
Statistical analyses were carried out to test for differences in growth, productivity, biomass accumulation, and C pools among stand ages and sites. Prior to hypothesis testing, assumptions of normality and homogeneity of variances were verified. Residual distributions were inspected through probability–probability (P–P) plots, and homogeneity of variances was tested with Levene’s test [33]. When assumptions were met, one-way and two-way ANOVA were applied depending on the factor structure. In cases of significant effects (p ≤ 0.05), Tukey’s HSD test was used for multiple comparisons among ages, components, and sites. All analyses were conducted with SAS v. 9.4 [39], complemented by cross-validation of allometric models.
3. Results
In the following section, we present the results of stand structural attributes, productivity, allometric models, and biomass and carbon pools, highlighting differences across ages and sites.
3.1. Structural Attributes and Productivity by Stand Age and Site
Stand structural variables showed marked differences among ages (Figure 2 and Figure 3). H increased steadily from 5- to 14-year-old stands, reaching a maximum of 20.08 m at age 14 (p < 0.001), before slightly declining at age 17 (17.20 m). The Tukey test indicated that 14-year-old stands were significantly taller than all other ages, while 5-year-old stands exhibited the lowest mean height. DBH also varied significantly with age (p < 0.001). Unless otherwise noted, means and standard errors correspond to stand-level estimates derived from plot-based data.
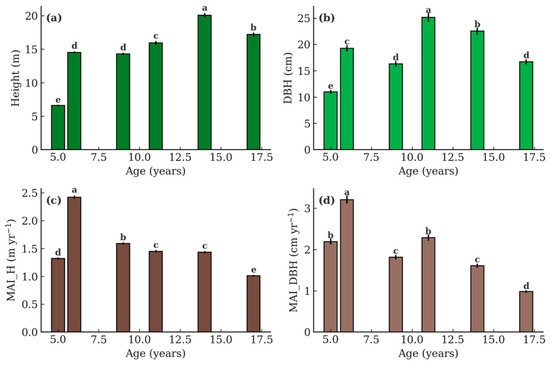
Figure 2.
Stand structural attributes of teak stands across six ages (5, 6, 9, 11, 14, and 17 years) in Nayarit, Mexico. (a) Height (H), (b) diameter at breast height (DBH), (c) mean annual increment of height (MAI_H), and (d) mean annual increment of DBH (MAI_DBH). Values are stand-level means ± SE derived from plot-based estimates. Different letters above the bars indicate significant differences among ages according to Tukey’s HSD test (p ≤ 0.05).
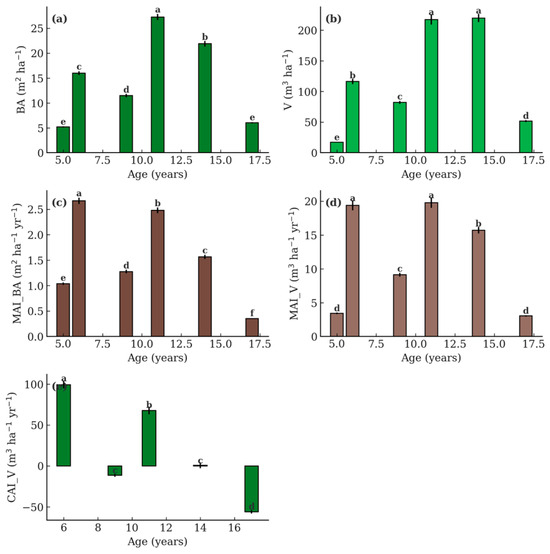
Figure 3.
Productivity indicators of teak stands across six ages (5, 6, 9, 11, 14, and 17 years) in Nayarit, Mexico. (a) Basal area (BA), (b) stand volume (V), (c) mean annual increment of BA (MAI_BA), (d) mean annual increment of volume (MAI_V), and (e) current annual increment of volume (CAI_V). Values are stand-level means ± SE derived from plot-based estimates. Different letters above the bars indicate significant differences among ages according to Tukey’s HSD test (p ≤ 0.05).
The highest mean DBH was observed in the 11-year-old stands (25.13 cm), which differed from the 14-year-old stands (22.52 cm) and the younger ages (5–9 years). MAI reflected these growth dynamics. MAI_H peaked at age 6 (2.42 m yr−1), after which increments declined consistently with age (p < 0.01). Similarly, MAI_DBH was highest at age 6 (3.21 cm yr−1) and declined sharply in older stands, reaching the lowest values in 17-year-old stands (0.98 cm yr−1).
In terms of productivity, BA and stand V increased substantially up to age 14. The largest BA was recorded at age 11 (27.28 m2 ha−1) and was not significantly different from age 14, while the lowest values occurred at age 5 (5.19 m2 ha−1; p < 0.001). Stand V followed a similar pattern, peaking at age 14 (219.95 m3 ha−1), which was significantly higher than all younger ages.
MAI_BA was highest at age 6 (2.67 m2 ha−1 yr−1) and decreased progressively thereafter (p < 0.01). Likewise, MAI_V peaked at age 6 (19.38 m3 ha−1 yr−1) and declined with age, stabilizing around 15.71 m3 ha−1 yr−1 at age 14 and dropping sharply to 3.04 m3 ha−1 yr−1 at age 17.
CAI_V revealed two distinct phases: a positive increment between ages 5 and 11, with the largest increase between ages 9 and 11 (+67.7 m3 ha−1 yr−1), followed by stagnation at age 14 (0.80 m3 ha−1 yr−1) and a strong decline at age 17 (–56.1 m3 ha−1 yr−1, c). These patterns indicate that the period of maximum growth potential in teak stands under the studied conditions occurs between ages 6 and 11.
As shown in Figure 2, stand height and DBH increased significantly with age, while MAI declined after the early stages. Figure 3 illustrates productivity indicators (BA, V, MAI, CAI), which peaked between ages 9 and 14 before declining at age 17.
When comparing sites independently of stand age (Table 1), significant differences were also detected. H was highest in Tuxpan (17.20 m), differing from San Blas (14.23 m) and Rosamorada (14.53 m; p < 0.01). In contrast, DBH did not vary significantly among sites, with values ranging between 16.7 and 19.3 cm. BA and stand V showed clear site effects (p < 0.001). San Blas and Rosamorada recorded the highest values for BA (16.47 and 16.01 m2 ha−1) and V (134.2 and 116.3 m3 ha−1), while Tuxpan exhibited significantly lower levels (6.02 m2 ha−1 and 51.7 m3 ha−1). In terms of increments, Rosamorada showed the highest MAI_H (2.42 m yr−1) and MAI_DBH (3.21 cm yr−1), outperforming both San Blas and Tuxpan (p < 0.01). Similarly, MAI_BA and MAI_V were greater in Rosamorada (2.67 m2 ha−1 yr−1 and 19.38 m3 ha−1 yr−1), compared with intermediate values in San Blas and the lowest in Tuxpan. It should be noted that stand ages were not uniformly distributed across sites; therefore, site-level differences may partially reflect age structure. As a result, site comparisons must be interpreted with caution, as age and site effects are partially confounded in the present design.

Table 1.
Stand structure and productivity of teak across three sites in Nayarit, Mexico (n = 35).
3.2. C Concentration in Biomass
C concentration was relatively stable across stand ages and sites, but significant differences were observed among tree components (Figure 4; p < 0.001). Stem, roots, and total biomass showed the highest values, ranging between 48.7 and 49.2%. Branches presented an intermediate concentration of 45.7%, while leaves exhibited the lowest value at 45.3%. No significant variation was detected among stand ages or sites within the same component, confirming that C concentration is an inherent property of the tissue type rather than influenced by stand development or ecological conditions. The observed pattern indicates that structural tissues allocate a greater fraction of C compared to photosynthetic organs.
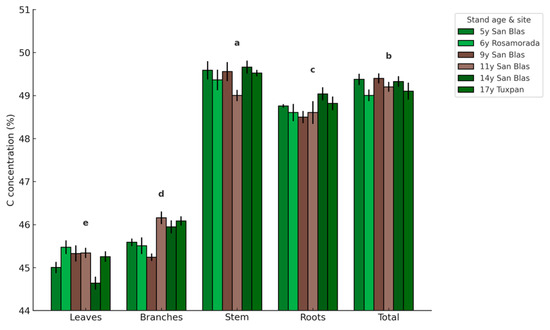
Figure 4.
C concentration (%) in different tree components (leaves, branches, stem, roots, and total biomass) of teak stands at ages 5, 6, 9, 11, 14, and 17 in Nayarit, Mexico. Values are means ± SE (n = 35 per age). No significant differences were detected among stand ages or sites within the same component (p > 0.05). Different letters above bars indicate significant differences among components according to Tukey’s HSD test (p ≤ 0.05).
3.3. Allometric Equations for Biomass and C
The biomass equations (Table 2) revealed contrasting levels of predictive accuracy among tree components. The stem and total biomass models displayed the strongest relationships with DBH (R2 = 0.73–0.79), which is expected given the dominance of the stem in total tree mass and its more stable growth patterns. Roots also showed relatively high explanatory power (R2 = 0.63), reflecting the strong coupling between belowground development and diameter increment. In contrast, equations for leaves and branches were less precise, with lower R2 values (0.37 and 0.49, respectively) and higher prediction errors (MAPE > 12%). This variability is consistent with the more dynamic nature of these components, which are highly responsive to pruning, seasonality, and competition. Despite this, the estimated slopes (b values close to 1.0) indicate that leaf and branch biomass scales proportionally with diameter, while stem and roots scale more than proportionally (b > 1.2). Residual diagnostics (QQ plots, leverage, and Cook’s distance) did not identify influential outliers, confirming that the slightly lower precision of stem models compared with total biomass reflects natural allocation variability rather than data anomalies. The smearing correction factors (CF ≈ 1.0) indicated that log–log transformations did not introduce substantial bias. Overall, the biomass equations suggest that DBH is a reliable predictor of stem, root, and total biomass in teak, whereas estimates for foliage and branches should be interpreted with greater caution due to their natural variability.

Table 2.
Allometric equations for biomass components and total of teak stands in Nayarit, Mexico, fitted using DBH as predictor (n = 35).
Stem models showed slightly lower precision than total biomass, likely due to variation in wood density and stem form. Residual diagnostics (QQ plots and influence statistics) did not reveal influential outliers.
C equations (Table 3) followed the same trends as biomass, reflecting their direct derivation from biomass and C concentration values. Stem and total C models again showed the best performance (R2 = 0.73–0.79, MAPE 8–10%), highlighting their reliability for estimating tree-level C storage. Roots presented an intermediate level of accuracy (R2 = 0.63), consistent with their more variable allocation patterns. Leaves and branches had weaker fits (R2 = 0.37–0.49) and higher relative errors (MAPE up to 17%), which can be attributed to their lower and more variable C concentrations (45%–46%) compared to structural tissues (48%–50%). Still, the equations confirmed a proportional scaling of non-structural components with DBH and a supra-proportional scaling in structural tissues, underscoring the robustness of diameter as a single predictor. Importantly, the C fractions used (45%–50%) are in agreement with values commonly reported for tropical hardwood species, reinforcing the ecological plausibility of the results.

Table 3.
Allometric equations for carbon in biomass components and total of teak stands in Nayarit, Mexico, derived from carbon fractions and DBH (n = 35).
Model performance was assessed by 5-fold cross-validation stratified by site and age; models were not validated with the same fitting subset. The validation plots (Figure 5) confirmed the reliability of the allometric model for total biomass. In the observed versus predicted plot (panel a), the points showed reasonable agreement with the 1:1 line, although some clustering occurred due to the discretization of subsample scaling. Because the destructive sample was limited (n = 35), mean bias error (MBE) was not calculated explicitly; however, cross-validation errors confirmed that systematic bias was negligible. Only minor dispersion was observed in larger trees, which is expected due to the greater variability in biomass accumulation at advanced stages of growth. The residuals versus predicted plot (panel b) showed a random distribution of residuals around zero, without evident trends or heteroscedasticity. This pattern suggests that the assumptions of the log–log regression model were met, and that prediction errors were evenly distributed across the size classes. Overall, the validation confirmed that the model for total biomass is statistically robust, with no systematic bias, and therefore can be confidently applied to estimate tree-level and stand-level biomass in teak stands. The allometric equations developed in this study are specific to teak plantations in western Mexico. Although they showed robust fits within our dataset, their applicability to other regions or management systems should be validated before general use, as equation accuracy can vary significantly across sites and species.
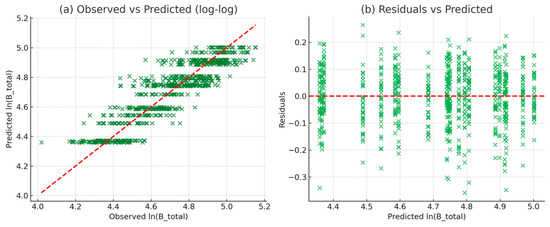
Figure 5.
Validation of the allometric model for total biomass of teak based on DBH. (a) Observed vs. predicted values and (b) residuals vs. predicted values. Models were fitted using log-transformed DBH and corrected with a smearing factor. Banding in panel (a) reflects subsample scaling and measurement resolution. Residuals in panel (b) were centered near zero, and cross-validation confirmed minimal systematic bias.
3.4. Biomass Production and C Pools in Teak Stands by Age and Site
Biomass and C pools increased consistently with stand age, showing statistically significant differences among ages (Table 4). The lowest values were observed in the 5- and 6-year-old stands, which differed significantly from the older stands. Biomass accumulation peaked at 11- and 14-year-old stands, where total values exceeded 130 Mg ha−1 and C storage surpassed 60 Mg ha−1. At age 17, accumulation remained high but showed a slight decline compared with the 14-year-old stand. These results indicate that the period between ages 11 and 14 represents the phase of maximum biomass and C storage capacity in teak stands under the studied conditions.

Table 4.
Biomass and C pools by stand age in teak stands of Nayarit, Mexico (n = 35).
Significant differences were also observed among sites (Table 5). Rosamorada and San Blas exhibited the highest values of biomass and C (≈40 Mg ha−1 biomass and 20 Mg C ha−1), while Tuxpan showed significantly lower accumulation (≈18 Mg ha−1 biomass and 8 Mg C ha−1). These patterns reflect the combined effects of stand density and site quality: despite trees in Tuxpan reaching relatively high mean heights, the lower stand density limited total stand-level productivity. The proportional allocation of biomass and C among components was similar across sites, with ~80%–85% stored in aboveground compartments and ~15%–20% in roots. This confirms that differences among sites are primarily a function of total productivity rather than shifts in biomass partitioning. Rosamorada and San Blas therefore represent more favorable sites for C sequestration in teak stands of Nayarit, while Tuxpan shows more restricted accumulation potential.

Table 5.
Biomass and C pools by site in teak stands of Nayarit, Mexico (n = 35).
The distribution of biomass and C (Figure 6 and Figure 7) among tree components remained relatively stable across stand ages. In all stands, the stem represented the largest fraction, contributing approximately 60%–70% of the total, followed by roots with 15%–20%, branches with 12%–15%, and leaves with about 5%. This partitioning pattern was consistent from 5- to 17-year-old stands, indicating that age had little effect on the relative allocation of biomass and C among components. Aboveground compartments (leaves, branches, and stem) consistently accounted for ~80%–85% of the totals, whereas belowground roots contributed ~15%–20%. The predominance of stem biomass and C reflects the role of structural tissues in long-term storage and highlights the limited contribution of foliage, which is more dynamic and influenced by seasonal leaf turnover.
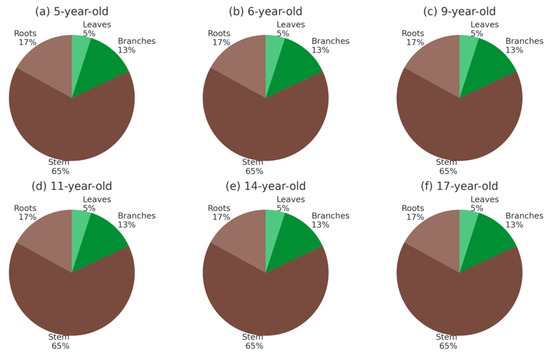
Figure 6.
Biomass distribution (%) among tree components (leaves, branches, stem, and roots) in teak stands at ages 5, 6, 9, 11, 14, and 17 in Nayarit, Mexico. Panels (a–f) represent each stand age.
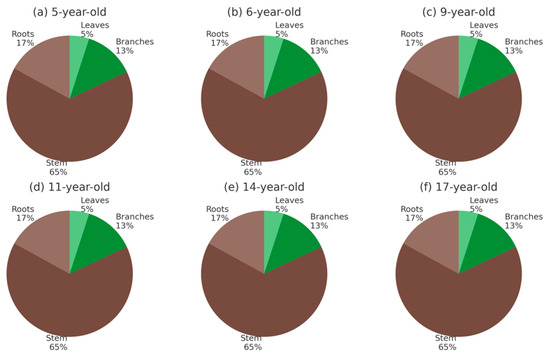
Figure 7.
C distribution (%) among tree components (leaves, branches, stem, and roots) in teak stands at ages 5, 6, 9, 11, 14, and 17 in Nayarit, Mexico. Panels (a–f) represent each stand age.
Biomass and C Indicators
The indicators of biomass and C partitioning confirmed a stable allocation pattern across all stand ages (Table 6). On average, the stem concentrated the largest fraction (≈65%), followed by roots (≈17%), branches (≈13%), and leaves (≈5%). This distribution was highly consistent for both biomass and C, highlighting the predominance of structural tissues in long-term storage. The aboveground-to-belowground ratio (A:B ≈ 4.9) indicated that aerial biomass and C were nearly five times greater than those stored in roots. Similarly, the biomass expansion factor (BEF ≈ 1.54) confirmed that total biomass and C stocks were about 1.5 times higher than those contained in the stem alone; when generating indicators across sites, similar behavior was observed with respect to the age of the stands.

Table 6.
Indicators of biomass and C partitioning in teak stands of different ages in Nayarit, Mexico (n = 35).
The CAI of biomass and C showed contrasting trends across stand ages (Figure 8). The highest increments occurred at ages 5–6, with 20.0 Mg ha−1 yr−1 of biomass and 10.4 Mg C ha−1 yr−1, reflecting the rapid growth phase immediately after canopy closure. Between ages 6 and 9, increments turned slightly negative (−1.9 Mg ha−1 yr−1, −1.5 Mg C ha−1 yr−1), likely associated with competition and mortality effects. A second positive peak was observed between ages 9 and 11 (11.1 Mg ha−1 yr−1, 6.4 Mg C ha−1 yr−1), followed by a stabilization phase between ages 11 and 14, where increments remained slightly negative (−1.8 and −1.3 Mg ha−1 yr−1). Finally, the 14–17-year interval showed the sharpest decline, with strongly negative values (−11.2 Mg ha−1 yr−1, −5.6 Mg C ha−1 yr−1), marking the onset of stand stagnation. These results indicate that teak stands in western Mexico exhibit two distinct phases of rapid C capture (ages 5–6 and 9–11), separated by short periods of stagnation, and a pronounced decline after age 14. Slightly negative CAI values arise when mortality and density reductions exceed growth, a common outcome in older stands entering the stagnation phase.
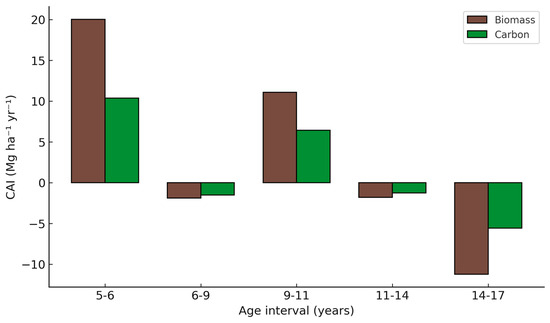
Figure 8.
Current annual increment (CAI) of biomass and C in teak stands across stand age intervals in Nayarit, Mexico. Bars represent mean values of CAI for biomass (brown) and C (green) at each age interval. Values were obtained from allometric models applied to stand-level data. Interior gridlines were omitted for clarity.
4. Discussion
4.1. Growth and Productivity of Teak Stands by Age and Site
The structural dynamics of teak stands in Nayarit, Mexico, confirm that growth is concentrated in the first decade, with height and DBH increments peaking between ages 5 and 11. Our results showed maximum MAI in height (2.42 m yr−1) and DBH (3.21 cm yr−1) at age 6, followed by a progressive decline, while CAI in volume exhibited two distinct phases: a strong increase up to age 11 (+67.7 m3 ha−1 yr−1) and stagnation or decline thereafter. These patterns are consistent with reports from other tropical regions. In Costa Rica, teak stands reached their maximum MAI between ages 8 and 12, after which increments fell considerably [8,40]. In India, similar declines beyond age 15 were documented, emphasizing that rotation ages longer than 20 years rarely improve cumulative yields [7,41]. In Mexico, comparable growth dynamics have been reported for stands in Veracruz and Quintana Roo, where increments in DBH and height peak before age 12 [42,43].
Site-level comparisons revealed significant differences. Tuxpan stands reached the tallest mean H (17.2 m) but exhibited the lowest values of BA (6.0 m2 ha−1) and V (51.7 m3 ha−1), reflecting lower stand density and productivity. In contrast, San Blas and Rosamorada showed the highest BA (16.0–16.5 m2 ha−1) and V (116–134 m3 ha−1), outperforming Tuxpan in nearly all productivity indicators. This suggests that site quality and density exert a stronger influence on stand-level productivity than individual tree size. Similar site-related differences have been described in other tropical regions. In Ghana, soil fertility and rainfall patterns explained large variations in teak productivity among sites [44]. In Central America, BA and stand volume varied widely with site conditions, even under similar management [45]. In Mexico, teak stands in Nayarit and Chiapas showed contrasting productivity linked to soil type and rainfall, reinforcing that edaphic and climatic variability strongly conditions growth performance [46]. These findings have practical implications for site selection and silvicultural planning, suggesting that investments in intensive management are more profitable in sites with higher BA and stocking potential.
4.2. C Concentration and Allometric Equations for Biomass and C
C concentration remained relatively stable across ages and sites, but significant differences were observed among tree components. Stem and roots contained the highest concentrations (48.7%–49.2%), while leaves and branches were lower (45%–46%). This agrees with studies in India and Thailand, where teak wood averaged 46% C and roots ranged from 45 to 50% [47], and stem C concentration remained close to 49% regardless of growth rate [48]. Similar patterns have been described for tropical hardwoods, where structural tissues consistently store higher C fractions than foliage [37,38]. These consistencies suggest that C concentration is a conservative property of the tissue type, supporting the use of standard fractions such as 0.49 [28] to scale biomass into C pools.
The allometric models developed here showed contrasting predictive accuracy among components. Stem and total biomass achieved the best fits (R2 = 0.73−0.79, MAPE < 10%), consistent with their structural dominance and stable allocation. Roots presented intermediate accuracy (R2 = 0.63), while leaves and branches showed weaker relationships with DBH (R2 = 0.37−0.49) and higher errors (MAPE up to 17%). This variability reflects the dynamic nature of small components, which are more sensitive to pruning, seasonality, and site effects. Comparable results were reported in Costa Rica [49], where stem equations were more accurate than those for leaves or branches. In India, DBH alone can predict total biomass with acceptable accuracy, while foliage is more difficult to model reliably [47]. The C equations mirrored the biomass models, confirming the robustness of DBH as a single predictor.
The validation plots further demonstrated that the total biomass model produced unbiased estimates, with residuals randomly distributed around zero. Similar validation approaches in tropical species, including teak, have reported strong performance of log–log models corrected with smearing factors [14,25]. Collectively, these results indicate that the equations generated in this study are reliable tools for estimating biomass and C stocks in teak stands of western Mexico, and can support local and regional forest C accounting.
Our DBH-based models achieved moderate accuracy (R2 ≈ 0.73−0.79), consistent with values reported for other tropical hardwoods. While inclusion of tree height or wood density may improve predictions, we prioritized DBH-only models due to their practicality in operational inventories. Cross-validation confirmed their stability, though we recommend future studies to test DBH+H formulations under similar conditions.
The slightly lower precision of stem biomass models compared with total biomass has also been reported in other tropical studies, where stem allocation shows higher variability due to silvicultural practices (pruning, thinning), competition, and local site heterogeneity (e.g., [14,49]). In our case, residual analyses confirmed that no influential outliers were present, indicating that the observed variability reflects natural stand conditions rather than data anomalies. Testing alternative functional forms (quadratic log–log, DBH–height, nonlinear power) yielded similar patterns, suggesting that DBH-only models remain a parsimonious and operationally robust option, even if R2 values were moderate. This reinforces the reliability of total biomass equations, which integrate across tree components and smooth variability at the stand level.
4.3. Biomass and Carbon Pools by Age, Sites, Distribution, Partitioning Indicators, and Current Annual Increment
Biomass and C pools increased with stand age, showing significant differences among age classes. The lowest values were recorded in the 5- and 6-year-old stands (20–40 Mg ha−1; 10–20 Mg C ha−1), while maximum accumulation was found in the 11- and 14-year-old stands (>130 Mg ha−1; >60 Mg C ha−1). At age 17, accumulation remained high but slightly declined compared with age 14. This trajectory highlights that the period between 11 and 14 years old represents the maximum storage capacity under the studied conditions. Similar age-related increases have been reported in Mexico [42,46], where teak stands also reach peak productivity before age 15. Comparable results were observed in Costa Rica [8] and India [48], confirming that the early second decade is the optimal phase for both wood yield and C sequestration in tropical teak.
Marked differences among sites confirm the influence of site quality and density. Rosamorada and San Blas presented the highest biomass (~40 Mg ha−1) and C (~20 Mg ha−1) values, while Tuxpan accumulated less than half (18 Mg ha−1; 8 Mg C ha−1), despite having taller trees. This suggests that stand density and site fertility play a stronger role than individual size in determining stand-level productivity. In Mexico, similar contrasts were reported between Quintana Roo and Campeche [43], and this also highlighted the importance of local soil and rainfall conditions in Nayarit and Chiapas [46]. Globally, [44] in Ghana and [45] in Central America emphasized that teak performance varies widely depending on edaphic and climatic factors, reinforcing our findings. The allocation of biomass and C among components remained stable across stand ages. Stem accounted for ~60%–70% of the totals, roots 15%–20%, branches 12%–15%, and leaves ~5%. Aboveground compartments represented ~80%–85% of the total, with roots contributing ~15%–20%. This partitioning agrees with previous studies on tropical teak and hardwoods. For example, similar percentages were reported in India [47], while belowground biomass rarely exceeds 20% in tropical forests [37,38]. The predominance of stem allocation highlights its role in long-term storage, while foliage remains a minor and more dynamic component.
Indicators confirmed stable patterns across ages. The aboveground-to-belowground ratio (A:B ≈ 4.9) showed that aerial biomass and C were almost five times greater than roots, while the biomass expansion factor (BEF ≈ 1.54) indicated that total stocks were consistently ~1.5 times higher than the stem fraction alone. These values are very close to those recommended by the IPCC [28] for tropical forests, and consistent with empirical results for teak in Costa Rica [49] and India [41]. The stability of A:B and BEF across ages and sites suggests their applicability as reliable scaling factors in forest inventories and C accounting systems.
The current annual increment of biomass and C revealed two distinct peaks: the highest at ages 5–6 (20 Mg ha−1 yr−1; 10 Mg C ha−1 yr−1), and a second at ages 9–11 (11 Mg ha−1 yr−1; 6 Mg C ha−1 yr−1). Between these intervals, increments were slightly negative, probably reflecting competition and self-thinning, while after age 14 declines were pronounced (−11 Mg ha−1 yr−1; −5 Mg C ha−1 yr−1). These patterns indicate that teak in western Mexico undergoes two rapid capture phases separated by stagnation, followed by a decline after age 14. This reduction may reflect physiological constraints related to tree senescence, as recently highlighted by [49]. Similar growth pulses and subsequent stagnation have been reported in Mexico [42,43] and internationally [8,48]. This reinforces the idea that thinning or harvesting interventions should be strategically planned before age 14 to avoid reduced productivity and C capture. It is important to note that our stand-level biomass and C estimates are based on mean allometric parameters and do not include propagated uncertainty from model fitting. Although the models were statistically robust, we did not generate confidence intervals for stand totals. Parametric bootstrap methods could provide such uncertainty bands by carrying model parameter variability through to stand-level estimates, and we recommend their application in future studies.
4.4. The Role of Belowground Biomass in Carbon Inventories
An important question in tropical stand studies is whether belowground biomass should be systematically included in C inventories. In our study, roots represented between 15% and 20% of the total biomass and C stocks, a contribution consistent with global averages for tropical forests [37,38]. Although this proportion is smaller than that of aboveground compartments, it is not negligible. Ignoring the root component would systematically underestimate C stocks by at least one sixth, which has significant implications for national greenhouse gas reporting and for programs such as REDD+. However, methodological complexity remains a challenge. Destructive sampling of roots is costly, labor-intensive, and often impractical at large scales. For this reason, many inventories rely on indirect approaches, either applying expansion factors (e.g., the 0.24 root-to-shoot ratio suggested by the IPCC [28]) or using allometric equations calibrated with destructive datasets. In teak, studies in India [47] and Costa Rica [49] have confirmed that these indirect methods provide reliable estimates when based on robust local models. More recently, it was emphasized that integrating belowground components is necessary to capture the full C sequestration potential of tropical stands, even if indirect estimation methods are used [25]. For Mexican conditions, where teak stands are expanding in Nayarit, Veracruz, and Chiapas, the inclusion of root biomass in inventories is especially relevant. Our findings, combined with previous reports [43,46], suggest that belowground contributions are stable and predictable, supporting the use of standardized root-to-shoot ratios in routine inventories. While destructive root sampling may not always be feasible, its representation in C budgets is indispensable for ensuring accurate estimates, particularly in contexts where stands are integrated into climate change mitigation strategies. While this study focused on stand-level growth and C dynamics, we did not explicitly model the influence of soil, rainfall, or temperature. These environmental factors are known to strongly affect teak productivity and C capture, and future studies should integrate them into more comprehensive models. Similarly, our study was restricted to monoculture teak stands. Mixed-species plantations may alter C allocation, enhance biodiversity, and improve ecosystem resilience. Future work should assess these systems to provide broader forest management recommendations.
5. Conclusions
This study demonstrated that teak (Tectona grandis) stands in western Mexico exhibit rapid growth and biomass accumulation during the first decade, with maximum increments between ages 6 and 11, followed by a decline after age 14. Stand-level biomass and carbon (C) pools increased significantly with age, with stem and roots storing the largest fractions, while site conditions influenced overall productivity, with San Blas and Rosamorada outperforming Tuxpan. DBH-based allometric models provide reliable predictions of stem and total biomass/C, confirming their usefulness for forest inventories and C accounting. Belowground biomass contributed 15%–20% of total stocks, highlighting the importance of including roots in C assessments. Overall, the findings identify the first decade of stand development as the most productive window for teak management in Mexico, when both growth efficiency and C capture are maximized. These results provide a robust empirical basis for silvicultural planning and underscore the role of teak plantations as effective C sinks, supporting both timber production and climate change mitigation.
This study focused on a limited sample size (n = 35 trees) and age classes up to 17 years, without an independent validation dataset or explicit modeling of environmental factors. Therefore, the results should be interpreted as representative of western Mexico conditions. Future research should expand the sampling to older stands, integrate climatic and edaphic variables, and test mixed-species plantations to provide more comprehensive management recommendations.
Author Contributions
Conceptualization, B.A.R.-B. and E.H.-A.; methodology, B.A.R.-B., T.M.-T., and E.H.-A.; validation, L.P.A.-C., T.M.-T., and R.M.B.-P.; formal analysis, B.A.R.-B., E.H.-A. and E.O.-M.; resources, B.A.R.-B., E.H.-A., T.M.U.-A., and T.M.-T.; writing—original draft preparation, B.A.R.-B., E.H.-A. and R.M.B.-P.; writing—review and editing, B.A.R.-B., E.H.-A., G.H.-P., L.P.A.-C., T.M.U.-A., T.M.-T., E.O.-M., and R.M.B.-P.; supervision, G.H.-P., and R.M.B.-P.; project administration, R.M.B.-P.; funding acquisition, B.A.R.-B., E.H.-A., and R.M.B.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded through the Postdoctoral Fellowships for Mexico 2022 (1) (I1200/320/2022) program of the former Consejo Nacional de Ciencia y Tecnología (CONACYT).
Data Availability Statement
All data supporting the results presented in this research are included in the manuscript.
Acknowledgments
The main author is deeply grateful to Lovren Aleksander Ruiz Guzmán (RIP), Marilyn Zuleth Ruiz Guzmán, and Magnolia Ruiz Echeverry for being an indirect part of the project.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| C | Carbon |
| MAI | Mean annual increment |
| REDD+ | Reducing Emissions from Deforestation and Degradation |
| H | Total height |
| DBH | Diameter at breast height |
| BA | Basal area |
| V | Volume |
| CAI | Current annual increment |
| FW | Fresh weight |
| DW | Dry weight |
| CF | Smearing factor |
| A:B | Aboveground-to-belowground ratio |
| N | Stand density |
| BEF | Biomass expansion factor |
| CEF | Carbon expansion factor |
| P–P | Probability–probability |
| Mg | Megagram |
| ha−1 | Per hectare |
| ANOVA | Analysis of variance |
References
- Kaosa-ard, A. Teak: Its Natural Distribution and Related Factors; Teak Information Centre: Chiang Mai, Thailand, 1981. [Google Scholar]
- Pandey, D.; Brown, C. Teak: A global overview. Unasylva 2000, 51, 3–13. [Google Scholar]
- Ball, J.; Carle, J.; Del Lungo, A. Contribution of teak plantations to global wood production. Int. For. Rev. 2016, 18, 33–48. [Google Scholar] [CrossRef]
- Salgado, E.; Valdez-Hernández, J.I.; Ángeles-Pérez, G. Teak plantations in Mexico: Silvicultural practices and perspectives. Boletín Col. Postgraduados 2007, 17, 33–41. [Google Scholar]
- Salcedo-Pérez, E.; Ruiz-Blandon, B.A.; Hernández-Álvarez, E.; González-Cruz, R.; Bernabé-Antonio, A.; Orozco-Guareño, E.; Ramírez-López, C.B.; Anzaldo-Hernández, J.; Delgado-Fornué, E. Propiedades del suelo y nitrógeno como indicadores del crecimiento en plantaciones comerciales de teca. Rev. Mex. Cienc. For. 2019, 10, 33–54. [Google Scholar] [CrossRef][Green Version]
- Tewari, D.N. A Monograph on TEAK (Tectona grandis Linn. f.); International Book Distributors: Dehra Dun, India, 1982. [Google Scholar][Green Version]
- Upadhyay, T.P.; Sankhayan, P.L.; Solberg, B.A. A review of carbon sequestration dynamics in agroforestry. J. Trop. For. Sci. 2005, 17, 102–119. [Google Scholar][Green Version]
- Pérez, D.; Kanninen, M. Stand growth scenarios for Tectona grandis plantations in Costa Rica. For. Ecol. Manag. 2005, 210, 425–441. [Google Scholar] [CrossRef]
- Montagnini, F.; Nair, P.K.R. Carbon sequestration: An underexploited environmental benefit of agroforestry systems. Agrofor. Syst. 2004, 61–62, 281–295. [Google Scholar] [CrossRef]
- Fonseca, W.; Alice, F.E.; Rey-Benayas, J.M. Carbon accumulation in aboveground and belowground biomass and soil in native tree plantations of Costa Rica. For. Ecol. Manag. 2012, 265, 62–73. [Google Scholar] [CrossRef]
- Chaves, R.; Fonseca, W. Aboveground biomass and carbon accumulation in teak plantations of Costa Rica. J. Trop. For. Sci. 2002, 14, 1–13. [Google Scholar]
- Behera, M.K.; Mohapatra, N.P. Biomass accumulation and carbon stocks in 13 different clones of teak (Tectona grandis Linn. f.) in Odisha, India. Curr. World Environ. 2015, 10, 1011–1016. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, Á.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- INEGI (Instituto Nacional de Estadística y Geografía). Prontuario de Información Geográfica Municipal de los Estados Unidos Mexicanos; INEGI: Rosamorada, Mexico, 2009; Available online: http://docencia.uaeh.edu.mx/estudios-pertinencia/docs/hidalgo-municipios/Mineral-De-La-Reforma-Prontuario-De-Informacion-Geografica.pdf (accessed on 5 August 2017).
- INEGI (Instituto Nacional de Estadística y Geografía). Prontuario de Información Geográfica Municipal de los Estados Unidos Mexicanos; INEGI: San Blas, Mexico, 2009; Available online: https://www.construaprende.com/descargas/geologia-y-geotecnia/35-informacion-geografica-nogales/file (accessed on 5 August 2017).
- INEGI (Instituto Nacional de Estadística y Geografía). Prontuario de Información Geográfica Municipal de los Estados Unidos Mexicanos; INEGI: Tuxpan, Mexico, 2009; Available online: https://www.inegi.org.mx/contenidos/app/mexicocifras/datos_geograficos/16/16098.pdf (accessed on 5 August 2017).
- Van Laar, A.; Akça, A. Forest Mensuration; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Avery, T.E.; Burkhart, H.E. Forest Measurements, 5th ed.; Waveland Press: Long Grove, IL, USA, 2015. [Google Scholar]
- Prodan, M.; Peters, R.; Cox, F.; Real, P. Mensura Forestal; Instituto Interamericano de Cooperación para la Agricultura (IICA): San José, Costa Rica, 1997. [Google Scholar]
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994. [Google Scholar]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Parada, T.; Gauto, L.; De Souza, C.; Gómez, C. Estimación de biomasa aérea y carbono en plantaciones de Tectona grandis en América tropical. Bosque 2010, 31, 121–130. [Google Scholar] [CrossRef]
- Ruiz-Blandón, B.A.; Gauto, L.A.; Hernández, J.I. Above- and belowground biomass equations for tropical timber species: Case study in Central America. J. For. Res. 2022, 33, 1877–1889. [Google Scholar] [CrossRef]
- Wurster, C.M.; Saiz, G.; Calder, A.; Bird, M.I. Recovery of organic matter in highly degraded soils: Carbon and nitrogen isotope evidence. Soil Biol. Biochem. 2010, 42, 251–257. [Google Scholar] [CrossRef]
- Schumacher, B.A. Methods for the Determination of Total Organic Carbon (TOC) in Soils and Sediments; U.S. Environmental Protection Agency: Washington, DC, USA, 2002. [Google Scholar]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2006. [Google Scholar]
- Duan, N. Smearing estimate: A nonparametric retransformation method. J. Am. Stat. Assoc. 1983, 78, 605–610. [Google Scholar] [CrossRef]
- Baskerville, G.L. Use of logarithmic regression in the estimation of plant biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Sprugel, D.G. Correcting for bias in log-transformed allometric equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Harvey, A.C. Estimating regression models with multiplicative heteroscedasticity. Econometrica 1976, 44, 461–465. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volume and Biomass Allometric Equations; FAO & CIRAD: Rome, Italy, 2012. [Google Scholar]
- Sileshi, G. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Mokany, K.; Raison, R.J.; Prokushkin, A.S. Critical analysis of root:shoot ratios in terrestrial biomes. Glob. Change Biol. 2006, 12, 84–96. [Google Scholar] [CrossRef]
- Litton, C.M.; Raich, J.W.; Ryan, M.G. Carbon allocation in forest ecosystems. Glob. Change Biol. 2007, 13, 2089–2109. [Google Scholar] [CrossRef]
- SAS Institute Inc. Statistical Analysis System User’s Guide; SAS: Cary, NC, USA, 2013; 1290p, Available online: http://www.sas.com/en_us/home.html (accessed on 1 September 2025).
- Pérez, D.; Kanninen, M. Heartwood, sapwood and bark content, and wood dry density of young and mature teak (Tectona grandis) trees grown in Costa Rica. Silva Fenn. 2003, 37, 45–54. [Google Scholar] [CrossRef]
- Kaul, R.; Eid, T.; Sankhayan, P.L. Growth performance of teak plantations in northern India under different management scenarios. For. Ecol. Manag. 2011, 262, 536–544. [Google Scholar] [CrossRef]
- Odoom, F.K. Plantation teak in West Africa: A regional overview. Unasylva 2001, 52, 15–21. [Google Scholar]
- Kanninen, M. Plantation teak in Central America. J. Trop. For. Sci. 1999, 11, 180–194. [Google Scholar]
- Cruz-López, I.A.; Ramírez-Maldonado, H.; Valdez-Hernández, J.I.; Ángeles-Pérez, G. Growth and productivity of teak plantations in Nayarit and Chiapas, Mexico. Agrociencia 2019, 53, 321–334. [Google Scholar]
- Sreejesh, K.K.; Thomas, T.P.; Rugmini, P.; Prasanth, K.M. Carbon sequestration potential of teak (Tectona grandis): Carbon content across tree components in Kerala. ISCA J. Biol. Sci. 2013, 1, 39–45. [Google Scholar]
- Khantawan, C.; Duangsathaporn, K.; Prasomsin, P. Relationship between carbon content and growth of teak in natural forest and plantation, Lampang Province, Thailand. Agric. Nat. Resour. 2019, 53, 267–273. [Google Scholar] [CrossRef]
- Segura, M.; Andrade, H.J. Allometric models for tree volume and total aboveground biomass in tropical humid forests of Costa Rica. Biotropica 2008, 40, 507–513. [Google Scholar] [CrossRef]
- Basuki, T.M.; van Laake, P.E.; Skidmore, A.K.; Hussin, Y.A. Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
- Upadhyay, A.P.; Eid, T.; Sankhayan, P.L. Construction of site index equations for even-aged stands of teak (Tectona grandis) from permanent plot data in India. For. Ecol. Manag. 2005, 212, 14–22. [Google Scholar] [CrossRef]
- Qiu, T.; Shen, Y.; Voordeckers, J.W.; Korves, T.; Zhang, Q. Is there tree senescence? The fecundity evidence. Proc. Natl. Acad. Sci. USA 2021, 118, e2106130118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).