Abstract
This paper compares two methods, inferential statistics and Systems Dynamics, to study the evolution of individual happiness after a single dose of drug consumption. In an application case, the effect of alcohol and caffeine on happiness is analyzed through a single-case experimental design, with replication, involving two participants. Both inferential statistical analysis and Systems Dynamics methods have been used to analyze the results. Two scales were used to measure happiness—the Euphoria Scale (ES) and the Smiling Face Scale (SFS)—in trait and state format. A single-case experimental ABC design was used. Phase A had no treatment, and Phases B and C saw both subjects receiving 26.51 mL of alcohol and 330 mg of caffeine, respectively. The participants filled in a form with both scales in a state format every 10 min over a 3 h period, operating in each one of the three phases A, B and C. The main conclusion of the analysis performed is that both methods provide similar results about the evolution of individual happiness after single dose consumption. Therefore, the article shows that inferential statistics and the stimulus response model derived from the Systems Dynamics approach can be used in a complementary and enriching way to obtain prediction results.
1. Introduction
The main objective of this paper is to demonstrate that the inferential statistics method and the Systems Dynamics method can provide similar results when studying the short-term evolution of individual happiness because of a single drug dose. To achieve this, an application case, where drugs are alcohol and caffeine, is analyzed through a single-case experimental design with replication with two participants.
There is a scientific debate about whether happiness is a trait or a state (see [1] for a review). However, some authors go beyond this controversy by offering an inclusive proposal about the happiness nature: it is both a trait and a state [2]. We adopt this inclusive approach in this study.
If happiness has a state nature as well as a trait one, then we must be able to study its short-term and long-term dynamics, even because of a single eliciting stimulus in a single session, as a drug intake is. For instance, it has been demonstrated that, after a single dose intake of alcohol or caffeine, both stimuli can increase happiness and other feelings such as euphoria in the short term [3,4,5,6,7,8].
The relationship between alcohol and happiness depends on doses and lifestyle. In fact, moderate drinkers tend to be happier than abstainers and heavy drinkers [9,10], and also tend to reduce their depression and stress [11]. In addition, happiness and team cohesion are significant predictors of alcohol consumption in university sports people [12]. In a longitudinal study with a Russian sample, a hump-shaped relationship among men but not among women was obtained [13]. In addition, there exists a nonlinear relationship between alcohol and happiness showing that abstainers and occasional drinkers, as well as heavy and problem drinkers, are at risk of reaching high anxiety and depression levels [14].
On the other hand, the existence of individual differences inside the acute effects of both drugs (alcohol and caffeine) has been proved [15,16,17], as well as the existence of an interaction between personality, time of the day and caffeine, in such a way that in the morning of the first day of the experiment, low impulsive persons were hindered and high impulsive ones were helped by caffeine. This pattern reverses in the evening of this first day, and it reverses again in the evening of the second day [18]. Furthermore, previous findings of studies using a large single dose, such as increased alertness and anxiety, improved performance on simple and choice reactive tasks, or a cognitive vigilance, may be applicable to normal patterns of the effects of caffeine consumption [19].
Long-term dynamical effects of alcohol consumption have also been studied [20]: the result of a meta-analysis show that the positive effect intensity of alcohol consumption decreases over time. In fact, the study [20] proposes the construction of a mathematical model to study accurately this dynamical response. However, even the corresponding short-term dynamics have not been well described yet. Therefore, a mathematical dynamical model, the stimulus response model (SRM), is here presented to fill this gap. The SRM is capable of predicting and describing how the whole personality (the General Factor of Personality or GFP) changes during a single session in response to a single dose of caffeine or alcohol, and also how its responses vary between individuals [21,22]. However, it has not been applied to the study of happiness dynamics yet.
Then, this study applies the SRM to predict the evolution of a subject’s happiness in response to a single dose of alcohol or caffeine. In fact, the advantages of the SRM are as follows: (a) it is capable of reproducing happiness dynamically as a consequence of a single dose of a stimulus such as alcohol or caffeine; (b) it points out how much the obtained happiness response is due to the stimulus; and (c) it provides the changes in the happiness trait at short term. Therefore, it is possible with the SRM to go beyond the results of the inferential statistics methods traditionally used by the behavioral sciences, as demonstrated here.
In addition, the SRM is presented within the System Dynamics approach, proposed by Jay W. Forrester about the half twentieth century [23]. The System Dynamics approach includes, between other features, a diagram like the hydrodynamic ones as a help to analyze, understand and program the model equations that can be written as a system of coupled differential or finite difference ones (see Section 4 for details). In fact, the “hydrodynamic diagram” that System Dynamics uses is much more intuitive for a behavioral researcher than an abstract set of coupled differential equations (see Section 5 for the comparison with other approaches frequently used in behavioral sciences). Nevertheless, and only for pure mathematicians’ interest, the SRM can be described as a time function equation for the stimulus plus an integrodifferential equation for happiness.
Moreover, it is here demonstrated that the SRM reproduces accurately the happiness’ measures of the experimental design below presented. In this experimental design happiness is measured with two instruments: the Euphoria Scale (ES) and the Smiley Face Scale (SFS). Both scales are shown in this work to be a very good instrument to measure happiness in both trait and state aspects.
On the other hand, and as announced above, both inferential statistics and the SRM are used here to integrate the mathematical tools currently used in humanity sciences (inferential statistics) and other ones frequently used in natural sciences (dynamical systems). In addition, to set the significance of the individual differences in the alcohol/caffeine dynamical response, both the SRM outcomes and SRM parameters are obtained with uncertainty, i.e., with their corresponding confidence intervals and confidence levels. Therefore, the here called overall power parameter (opp), defined as a combination of four SRM parameters, provides those differences with the possibility to determine whether they are significant or not. The conclusion of the above-mentioned integration is that the analysis of the opp confidence intervals leads to the same conclusions about those differences as the classical inferential statistics (see Section 5 for details).
About the contents of the next sections, Section 2 is devoted to the experimental design methodology. Section 3 presents the results of the inferential statistics application to the experimental scores. Section 4 presents the SRM by using the methodology of Systems Dynamics, with the hydrodynamic diagram as the central qualitative tool to help understanding. In Section 5, the SRM is used to reproduce the dynamics present in the scores obtained in Section 4 by the experimental design presented in Section 2, as well as its main predictions. Section 5 presents the integration of the results from inferential statistics and those from the SRM. Section 6 introduces the conclusions of this paper, stressing the advantages of the System Dynamics approach over other methods used in behavioral sciences such as structural equations or time series analysis. Annex 1 ending this paper is a practical support to better understand the construction of a dynamical model such as the SRM.
2. Materials and Methods: Experimental Design Methodology
Two voluntary men participated in the experimental design. Both are workers from Valencia (Spain), with 54 and 68 years old, respectively. Both subjects gave their informed consent for inclusion before they participated in the study. The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethics Committee of Universitat de València (5 October 2009) (for caffeine) and by the Ethics Committee of Universidad Politécnica de Valencia (26 July 2012) (for alcohol). A single-case experimental ABC design was used. In Phase A the participants received no treatment. At the start of Phase B, both participants received 26.51 mL of alcohol and a slight food. In Phase C, both participants received 330 mg of caffeine. Two instruments to evaluate happiness were used:
- (1)
- The Euphoria Scale (ES) [24] in its trait-format (“Are you like this in general?”) and in its state format (“Are you like this at this moment?” or “do you feel so at this moment?”). ES is a 4-item Likert-type response scale with the following self-descriptive adjectives: cheerful, elated, exhilarated, and lively. Each adjective score goes from 0 (no effect) to 5 (maximum effect); therefore, the ES goes from 0 (no effect) to 20 (maximum effect). Note that it has been assumed that the ES can take even values lesser than 1 score but positive.
- (2)
- The Smiling Face Scale (SFS) is a 7-item Likert-type response scale that shows images from very sad to very happy faces, so it ranges from the most negative non-smiling face aspect (scored by 1) to positive smiling face aspect (scored by 7) [25,26]. Therefore, the SFS has been taken from 0 (to include the non-effect, such as in the ES) to 7 (maximum effect). Note that it has been assumed that the SFS can take even values lesser than 1 score but positive.
Both participants filled in the ES and the SFS forms in its trait format at the very beginning of this study (before consumption, as initial condition for Phases B and C), and every 10 min over a 3 h period, in each one of the three phases A, B and C. Therefore, in phase B, for instance, both participants drank 26.51 mL of alcohol before the first register and then completed the remaining registers (filling out the scales) without drinking any more alcohol. Thus, one register before taking the alcohol dose and 18 registers over the next 3 h are available (total 19 registers). The goal was to see how a single dose of alcohol affects the next three hours registers. Phase B was not repeated. A similar situation held for Phases A and C.
Firstly, an inferential statistic procedure was used to analyze the results. Then, the stimulus response model (SRM) was applied for data analysis showing its usefulness to model the dynamical effect of both drugs. In Section 5, Figures 2 and 3 show the data for both scales in the base line, while Figures 4–7 show the data for both scales jointly with the corresponding evolution curves predicted by the SRM, being these results interpreted and commented.
3. Inferential Statistics Results
Table 1 shows the descriptive statistics of the results of the experiment, mean and standard deviation, corresponding to the two participants in all the three previously mentioned phases. Participant 1 (P1) score is lower in the base line (BL), for alcohol and caffeine in both ES and SFS than Participant 2 (P2). Moreover, the statistical dispersion measure in all conditions and scales is higher in P1 than in P2.

Table 1.
Descriptive statistics for both participants in experimental design.
Two-way repeated measures ANOVA were performed to determine whether there are significant differences in mean scores in ES between the three conditions (BL, alcohol and caffeine) for each participant. See Table 2. We have used these parametric statistical tests for the score on the ES because the score on that scale is the sum of the scores of the 4 items considered in the Likert scale for measuring EUPHORIA (cheerful, elated, exhilarated, and lively), assuming that it is an approximately continuous variable. Although Likert scales are technically ordinal because they consist of a series of ordered categories, several authors have found consistent support for using them as approximately continuous. Then, ordinal variables with five or more categories can often be used as continuous without any harm to the analysis performed on them. This fact may result in several categories much higher than the ordinal Likert scales they are calculated from. Therefore, the fact of taking the sum or mean of two or more ordinal variables to create an approximately continuous variable is something that many researchers encounter when using surveys [27,28,29,30].

Table 2.
Two-Way repeated measures ANOVA of ES for two participants.
For the SFS analyses, as it is an ordinal single-item scale, we used the Friedman test for repeated measures and the Wilcoxon test of related samples to compare the three conditions (BL, alcohol and caffeine). The results are shown in the text (last paragraph of Section 3).
The total number of registers was 19 over the course of 3 h. A factor (experimental condition) was considered with three levels, corresponding to the three phases of the experiment: A = baseline; B = alcohol; C = caffeine, for the analysis of variance of these repeated measures. The 19 registers from the two scales in each phase of the experiment were considered as the dependent variable. Thus, the 19 registers from Phase A were compared with those of Phase B and Phase C, with 19 registers each one as well.
There exist significant effects of both alcohol and caffeine in ES for both participants. For example, for P1, there exist a significant effect of both drugs in ES (F(2, 36) = 27.771, p < 0.001, η2 = 0.607, β = 1.000). In general, a medium effect size has been obtained for Cohen’s value, but the power is maximum (1) in both participants. The numbers in parentheses are the degrees of freedom. In the case of F, the first number (2) corresponds to the degrees of freedom of the model and the second number (36) to the degrees of freedom of the residuals.
Pairwise multiple comparisons were performed with the Bonferroni adjust for mean differences and t-test between all conditions and for both participants. See Table 3.

Table 3.
Pairwise comparisons and t-test of EUPHORIA measures.
In general, the effects of both drugs are higher for the ES scores than for the BL ones, but the effect of alcohol is higher in P1 than in P2 on ES, and the contrary occurs for the caffeine effect.
For example, in P1 alcohol increases significantly the Euphoria (ES), where the pre-scores (Table 1) (BL, M = 3.84, SD = 1.068) were lower than the post-scores (M = 13.63, SD = 6.457) t(32) = −6.886, p < 0.001, CI95% (−2.252, −0.889), β = 1.000, while regarding caffeine, the pre-scores were also lower than the post-scores (M = 10.16, SD = 5.069) t(32) = −5.712, p < 0.001, CI95% (−1.919, −0.682), β = 1.000, but, as we can see with CI 95%, there is no significant difference between both conditions when we compare the effects of caffeine and alcohol.
As for SFS, we applied a Friedman test, as mentioned above. For P1, the result is significant (χ2 = 7.01, p < 0.05), as it is the case for P2 (χ2 = 7.01, p < 0.05). But the Wilcoxon paired samples test only shows significant results for the effect of alcohol on BL in P1 (Z = −2949, p < 0.05), and for the effect of caffeine on BL in P2 (Z = −2.941, p < 0.05). Thus, the results from the ES and SFS are similar for both participants.
4. The Stimulus Response Model (SRM)
Following Forrester’s methodology [23] for Systems Dynamics, the model to be built (the SRM) can be represented qualitatively by the hydrodynamic diagram (HD) that is showed in Figure 1. It summarizes the factors and patterns of the problem dynamics studied in the specialized literature or obtained from the scholars’ knowledge about the problem. In the case here studied, the problem dynamics is given by the individual happiness response to a stimulus (drug), whose knowledge can be taken from [17,21,22].
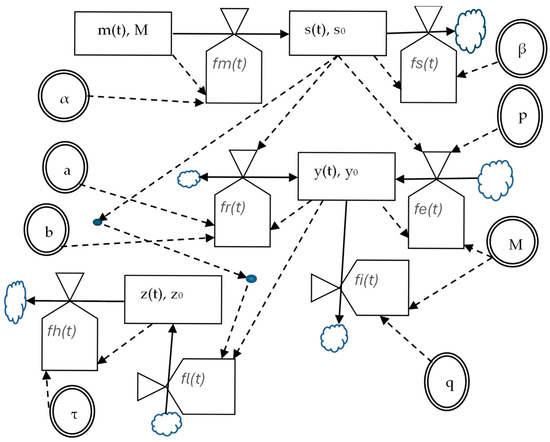
Figure 1.
Hydrodynamic diagram of stimulus response model (SRM). See Table 4 and Table 5 for meaning of variables inside icons. Symbols of HD in Figure 1 are shown in Appendix A.
However, before presenting the HD and deducing the equations from it, the variables considered, their symbols and their dimensions and units are presented in Table 4 for the input variables or parameters, and in Table 5 for the output variables. Note that the input variables or parameters are those not influenced causally for any other model variables, and, in general, can depend on time. In the model presented, they are constant, and their values are calibrated from real data with a genetic algorithm, i.e., an informatics program that finds the set of parameter values that provides the SRM dynamical prediction closest to the experimental scores, with their respective confidence intervals and corresponding confidence levels. The last two rows of Table 4 represent (for ES and for SFS) the initial happiness value and the initial drug in blood value, respectively. These values are not computed by the genetic algorithm, because the first one is the score of the participant before consumption (see below: y0 in Equation (12) or Equation (18)), and the second one is the amount of drug in blood before consumption, being always s0 = 0 because neither alcohol nor caffeine have been consumed since a long time ago for both participants.

Table 4.
Input variables of the SRM: symbols and dimensions.

Table 5.
Output variables of the SRM: symbols and dimensions.
The parameter that measures the global effect of the drug on an individual by the SRM is defined as a combination of the three power parameters and the inhibitor effect delay of Table 4, and it is here called as the overall power parameter: . Note that the three terms of have the same dimensions (T−1) and units (min−1).
In addition, the output variables of Table 5 depend causally on other model variables through the corresponding equations: every model output variable corresponds to a particular model equation deduced from the HD and the hypotheses stated about its variables.
Following Forrester’s methodology [23] for Systems Dynamics, the model to be built (the SRM) can be represented qualitatively by the hydrodynamic diagram (HD), as shown in Figure 1. It summarizes the factors and patterns of the problem dynamics studied in the specialized literature or obtained from the scholars’ knowledge about the problem. In the case here studied, the problem dynamics is given by the individual happiness response to a stimulus (drug), whose knowledge can be taken from [17,21,22].
Let us deduce the model equations from this diagram. Take into account for this deduction the variable dimensions and units presented in Table 4 and Table 5. First, to compute the drug in blood, , and the drug in digestive organs, , the following balance equations provided by the HD must be considered in finite differences form ( is a finite time increment):
However, Equations (1) and (2) can be written in the infinitesimal limit form ():
From now onwards, the balance equations for the level variables of the HD will be written in the infinitesimal limit form. Note from the HD the causal influences on the flows and . The hypothesis about how to compute them is provided by the drug chemical kinetics [21,22]:
Then, from (5) in (3) and (4), their initial values are added in the initial time :
Equations (6) and (7) provide the drug dynamics in organism, being α and β two parameters to be calibrated for both participants and phases. Both parameters depend on the individual personality and on the kind of drug. For alcohol in Phase B, they are calibrated in the intervals α [0.00118, 0.02050] and β [0.00462, 0.00533] following the literature about alcohol kinetics [22], and for caffeine in Phase C the corresponding intervals are α [0.00137, 0.091138] and β [0.00144, 0.00304] following the literature about caffeine kinetics [21].
Considering the balance equation in the infinitesimal limit form for the happiness level variable, in the HD:
Taking the literature about the subject as a base, the hypotheses about the mathematical patterns of the three flows considered in (8) are explained in the following paragraphs.
About the homeostatic control, fr(t), it is a control around the tonic or basal happiness b. It is assumed that the happiness state, y(t), tends to return to the tonic happiness when it is modified by a stimulus:
Parameter b in (9) represents the value to which the y(t) variable would tend asymptotically under the ideal case that no other stimulus would influence the individual happiness. The restriction to be considered in the calibration of parameter b is that its value must belong to the interval of the corresponding happiness scale: b 0, 20] for the ES and b (0, 7] for the SFS. Parameter a represents the strength or power of the above-mentioned asymptotic dynamics and its only restriction is that its value must be greater or equal to zero. Both parameter values also depend on the kind of drug and on the individual characteristics.
About the excitation effect, fe(t), it tends to increase happiness proportionally to the stimulus, s(t), and the present happiness, y(t), per unit of drug amount M:
Parameter p in (10) represents the strength or power of the excitation effect, and its value also depends on the kind of drug and on the individual characteristics. The only restriction for p is that its value must be greater or equal to zero. Note that the greater the value of p the greater the excitation effect of the considered drug on the individual happiness [21,22].
About the inhibitor effect, fi(t), assuming that it actuates with some delay, it tends to decrease happiness proportionally to the happiness delay, z(t), per unit of drug amount M:
Parameter q in (11) represents the strength or power of the inhibitor effect, and its value also depends on the kind of drug and on the individual characteristics. The only restriction for q is that its value must be greater or equal to zero. Note that the greater the value of q the greater the inhibitor effect of the considered drug on the individual happiness [21,22]. That is, the greater the values of p and q are the more intense is, respectively, the excitation effect and the inhibitor effect.
By substituting (9), (10) and (11) in (8), and adding the initial happiness value at the initial time :
Considering the balance equation in the infinitesimal limit form for the happiness delay level variable, , of the HD:
According to the literature about the subject [21,22], the hypotheses about the mathematical patterns of the two flows fh(t) and fl(t) that appear in (13) are the following.
About the happiness inhibitor delay, fh(t), it is a decreasing control about the happiness delay with a time parameter as follows:
The only restriction for parameter τ value in (14) is that it has to be positive. About the happiness excitation delay, fl(t), it tends to increase the happiness delay as the product of the present stimulus and happiness:
The initial value of in is zero due to it just starts to act when the stimulus arises from this instant. Therefore, considering this initial value and substituting (14) and (15) in (13):
Equations (6), (7), (12), and (16) define the stimulus response model (SRM) to study the short-term happiness dynamical response to a stimulus provided by a drug single dose, such as the here considered ones: alcohol and caffeine.
However, the SRM can be presented in a briefer way. On the one hand, the drug dynamics is given by (6) and (7); nevertheless, they define an independent subsystem of the SRM from which the drug in blood variable can be analytically found:
On the other hand, Equation (16) is a linear differential equation in ; therefore, it can be integrated and substituted into (12):
Equation (18) is an integrodifferential equation where the inhibitor effect arises explicitly with a continuous delay (the integral term). Both Equations (17) and (18) also define the SRM in a much more concise way. However, the complexity of (18) forces the researcher to find its solutions numerically. Consequently, it is more advantageous to find numerical solutions for happiness by using Equations (12) and (16), while the solutions for the drug in blood variable are found directly by (17) (see following section).
5. Dynamical Results of the Stimulus Response Model (SRM)
In order to fit the SRM dynamics presented in Section 4 to the scores obtained by the experimental design presented in Section 3, two questions must be answered: (1) how to achieve the SRM outcomes with uncertainty; and (2) how to achieve the best outcomes (also with uncertainty) of the model parameters of Table 4 to reproduce the dynamical patterns followed by the experimental design scores.
The answer for question (1) is that the outcomes of the stimulus response model are provided by Equation (17) for the drug in blood variable, , and by using the 4th order Runge–Kutta method for the numerical outcomes of the happiness variable, through Equations (12) and (16). However, these SRM outcomes do not present uncertainty. Therefore, to consider its uncertainty, the following steps are followed:
- (a)
- Once the SRM outcomes are obtained, the corresponding residuals are computed as the differences between the experimental scores and the SRM outcomes.
- (b)
- The p-value of the Anderson–Darling test is applied to the residuals to determine whether they are distributed as normal distributions of zero mean and sd standard deviation, N(0, sd), or not. Note that the H0 hypothesis is that the residuals follow such normal distribution. Subsequently, if the H0 hypothesis holds, the confidence interval for every SRM outcome is computed by the usual way, i.e., by the Student’s t distribution with a 0.05 signification level.
- (c)
- All corresponding figures present the experimental scores jointly with the SRM mean value line and the two limit lines corresponding to the confidence intervals.
The answer for question (2) is that a genetic algorithm, whose algorithmic bases can be found in [31], provides the model happiness responses with random residuals (i.e., the noise, considered as the influence of other sources different to the stimuli), as well as a sample of 40 relatively optimal sets of parameter values (those described in Table 4) that better fit the model outcomes to the experimental scores. To be more precise, the genetic algorithm of [31] just presents the set of values of each parameter that better fits the model outcomes. The genetic algorithm version used in this work is an advance on the [31] version that provides a sample of the best sets of parameter values to achieve the corresponding confidence intervals.
For better understanding of how the genetic algorithm works, a brief explanation is provided here (details can be found in [31]). The genetic algorithm tries to imitate natural selection. So, an individual is defined like a set of values for the parameters (genes) of the model and a population is defined as a set of individuals. Reproduction is defined as the creation of a new individual by choosing randomly a gene from every couple of genes one from each parent (may be with random mutation). Consanguinity is restricted to avoid too small differences between individuals. The SRM provides a fitting value for each individual of the considered population. The fitting method consists of calculating the quadratic sum (QS) of the differences between experimental scores and those provided by the SRM. The best fitting individuals (those with lesser values for QS) are chosen as reproducers to produce the next generation. Some immigrants may be considered. Summary: (1) The first population is determined by assigning randomly a value to each parameter (gene) inside a given scale. (2) Calculation of QS for each individual, ordering and selection of reproducers. (3) Random immigration. (4) Random reproduction (with consanguinity control and random mutation) up to completing population. (5) New ordering and selection. (6) Checking the end condition: if yes then exit routine else go to (3). The end condition is “no lesser QS values are observed”.
Once the samples of parameter values are obtained, the p-value of the Anderson–Darling test is applied to each sample to determine whether they are distributed as a N(m, sd), i.e., a normal distribution of m mean and sd standard deviation corresponding to each parameter. Note that the H0 hypothesis is that the samples follow a normal distribution. Subsequently, if the H0 hypothesis holds, the confidence intervals are computed in the usual way.
In addition, the results of the fitting process obtained through the genetic algorithm are evaluated by the determination coefficient values (), which measures the fitting degree between the experimental scores and the corresponding values provided by the SRM. Note that the SRM values here considered are those computed by the averages of the 40 size parameter samples, i.e., by the mean value of their confidence intervals. In addition, the measures the relation between the square covariance of both sets of data and the product of both variances, and it varies from 0 to 1, i.e., , such that the closer to the unit the better the fitting degree. The determination coefficient values are provided jointly with the p-value of the Anderson–Darling test with which the residuals are checked for being noise, i.e., a N(0, sd) or a normal distribution of zero mean and sd standard deviation between the experimental scores and the corresponding values given by the model. Note again that the H0 hypothesis is that the residuals follow a normal distribution.
It is important to emphasize the joint meaning of and the Anderson–Darling test: the value represents the part of scores’ dynamics explained by the SRM, and if, in addition, the residuals are demonstrated to be random by the Anderson–Darling test then it can be asserted that no other significant dynamical pattern is also assumed by the scores’ dynamics. Moreover, if a high value is associated with a low residual dispersion (do not confuse with the statistical dispersion of Section 3) and vice versa, then, in this case, the individual feels the drug effect accurately, and in the contrary case (low value that is associated with a high dynamical dispersion) the individual feels the drug effect not clearly.
Moreover, the production of the SRM numerical solutions as well as the above-described genetic algorithm is stated in a C++ program. The corresponding figures and Anderson–Darling test p-values have been obtained by the software MATHEMATICA 14.0.
Figure 2 (for Participant 1) and Figure 3 (for Participant 2) show the scores in low stimuli conditions for both participants in the experimental design in Phase A (base line), in both happiness scales. Note that both figures are far from seeming to represent noise. In fact, the Anderson–Darling test provides for both participants a p-value lesser than 0.01, i.e., it is not an orthodox noise N(m, sd), being m the average score. Therefore, either the outcomes follow a dynamical pattern produced by boring or the noise follows an unknown distribution. However, the dynamical patterns of happiness produced in Phase B and Phase C by alcohol and caffeine, respectively, are radically different, as it can be observed in the subsequent figures.
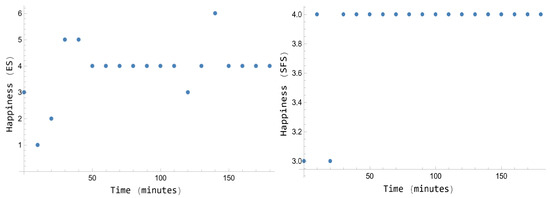
Figure 2.
ES scores (left) and SFS scores (right) for the base line for Participant 1.
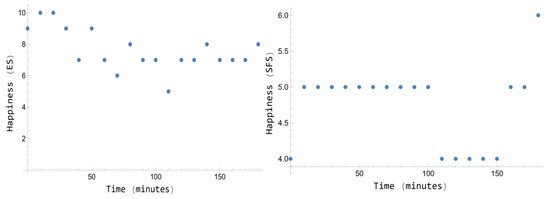
Figure 3.
ES scores (left) and SFS scores (right) for the base line for Participant 2.
Figure 4 presents the scores with uncertainty along time of the ES and SFS for Phase B of the experimental design of Participant 1, jointly with the curves predicted by the SRM because of 26.51 mL of alcohol dose. Note that for the ES response and for the SFS response , being the corresponding Anderson–Darling test of the residuals, respectively, 0.71 and 0.95, which provide us a conclusion: the SRM explains almost fully the scores’ dynamics of Participant 1, in other words, the prediction of the SRM for this participant is excellent, which implies that Participant 1 feels accurately the happiness response to the alcohol stimulus.
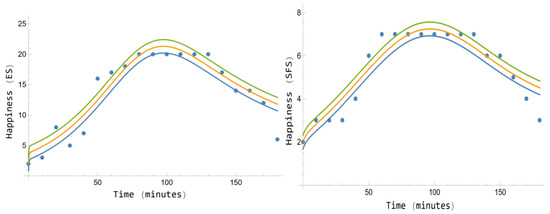
Figure 4.
Phase B, Participant 1. ES (left) and SFS (right) scores (dots) and curves with uncertainty predicted by the stimulus response model. For ES: , p-value = 0.71. For SFS: , p-value = 0.95.
In addition, Table 6 shows the parameter confidence intervals of the SRM provided by the genetic algorithm for Participant 1, except for the dose and the initial values that are known and then presented with their respective single values. The corresponding opp confidence intervals () obtained from Table 6 are (6.57082, 8.16833) min−1 for ES and (0.887418, 1.12422) min−1 for SFS (confidence level 0.95). In Section 6 these data are compared with those of Participant 2. In addition, note that the initial values for Participant 1 are very low for both happiness scales ( for both scales). About the initial values, according to the GFP theory [21,22], it is very important to emphasize that for happiness in both scales: the lower the initial value is, the more significant the dynamical responses will be, and vice versa. This is in correspondence with the high determination coefficients values obtained for both scales. Therefore, what the SRM predicts is that Participant 1 becomes happier after alcohol consumption than he usually uses to be, at least in the short term.

Table 6.
Parameters’ confidence intervals (0.95 confidence level) and values of the SRM provided by the genetic algorithm for ES and SFS for Participant 1 in Phase B (see dimensions and units in Table 4).
Figure 5 presents the scores with uncertainty of the ES and SFS for Phase B of the experimental design of Participant 2, jointly with the curves predicted by the SRM because of 26.51 mL of alcohol dose. Note that the scores’ residual dispersion is much higher than that of Participant 1. In fact, the low values of the determination coefficients, for ES and for SFS, announce this residual dispersion, although the Anderson–Darling test of the residuals (respectively, 0.46 and 0.70) shows us that the residuals are random. The conclusion from these data is very important: compared with Participant 1, the part of the data variability explained by the SRM for Participant 2 provides a very low happiness response to the alcohol stimulus.
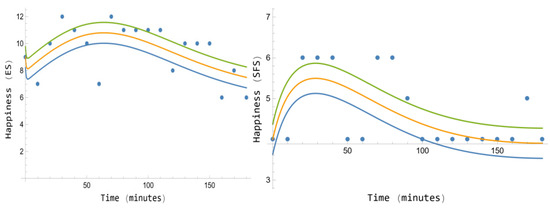
Figure 5.
Phase B, Participant 2. ES (left) and SFS (right) scores (dots) and curves with uncertainty predicted by the stimulus response model. For ES: , p-value = 0.46. For SFS: , p value = 0.70.
In addition, Table 7 shows the corresponding parameters’ confidence intervals of the SRM provided by the genetic algorithm for Participant 2, except for the dose and the initial values that are known and then presented with its respective single value. The corresponding opp confidence intervals () obtained from Table 7 are (4.46197, 6.20496) min−1 for ES and (0.18140, 0.25944) min−1 for SFS (confidence level 0.95). In Section 6 these data are compared with those of Participant 1. In this case, the model predictions must be taken more carefully, due to the low effect of alcohol on this participant happiness. However, it can be advanced, by comparing the respective opp intervals, that Participant 1 feels significantly more intensively the effect of alcohol consumption than Participant 2 for both happiness scales. In addition, note that the initial happiness values of Participant 2 are higher for both happiness scales than for Participant 1 ( for the ES and for the SFS). Following again the GFP theory [21,22], the higher the initial value the less significant the dynamical responses and vice versa. This is in correspondence with the lower determination coefficients values obtained for both scales.

Table 7.
Parameters’ confidence intervals (0.95 confidence level) and values of the SRM provided by the genetic algorithm for ES and SFS for Participant 2 in Phase B (see dimensions and units in Table 4).
Figure 6 presents the scores with uncertainty of ES and SFS for Phase C of the experimental design for Participant 1, jointly with the corresponding curves predicted by the SRM because of 330 mg of caffeine dose. Note that the determination coefficients are again very high for Participant 1. In fact, for ES and for SFS, due to the residual dispersion is very low. In addition, the Anderson–Darling tests for the residuals give, respectively, 0.35 and 0.43, i.e., the residuals are random. Again, the conclusion of these data is very important: Participant 1 also feels, in a very strong way, the happiness response to the caffeine stimulus.
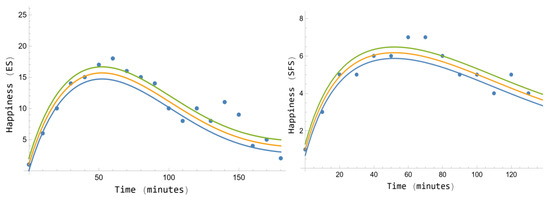
Figure 6.
Phase C, Participant 1. ES (left) and SFS (right) scores (dots) and curves with uncertainty predicted by the stimulus response model. For ES: , p value = 0.35. For SFS: , p value = 0.43.
In addition, Table 8 shows the parameters’ confidence intervals of the SRM provided by the genetic algorithm for Participant 1, except for the dose and the initial values that are known and then presented with its respective single value. The corresponding opp confidence intervals () obtained from Table 8 are (0.47382, 0.68607) min−1 for ES and (0.44504, 0.64521) min−1 for SFS (confidence level 0.95). In Section 6 these data are compared with those of Participant 2. In addition, note that the initial values of Participant 1 are very low for both happiness scales ( for both scales). About these values, the GFP theory [21,22] says that the lower the initial value the more significant the dynamical responses and vice versa, which is very important to be also emphasized for happiness in both scales. This is in correspondence with the high values obtained for the determination coefficients for both scales. Therefore, again for Participant 1, what the SRM predicts is that Participant 1 becomes happier after caffeine consumption than what he usually is, at least in the short term.

Table 8.
Parameters’ confidence intervals (0.95 confidence level) and values of SRM provided by genetic algorithm for ES and SFS for Participant 1 in Phase C (see dimensions and units in Table 4).
Figure 7 presents the scores with uncertainty of the ES and SFS for Phase C of the experimental design of Participant 2, jointly with the curves predicted by the SRM because of 330 mg of caffeine dose. Note that the scores’ residual dispersion is again much higher than that for Participant 1, in correspondence with the lower values of the determination coefficients, for ES and for SFS, although the Anderson–Darling test of the residuals (respectively, 0.80 and 0.25) indicate us that the residuals are random. The conclusion from these data is very important: compared with Participant 1, the part of the data variability explained by the SRM for Participant 2 provides in a very low way his happiness response to the caffeine stimulus.
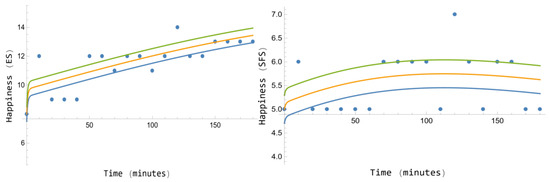
Figure 7.
Phase C, Participant 2. ES (left) and SFS (right) scores (dots) and curves with uncertainty predicted by the stimulus response model. For ES: , p value = 0.80. For SFS: , p value = 0.25.
In addition, Table 9 shows the parameters’ confidence intervals of the SRM provided by the genetic algorithm for phase C of Participant 2, except for the dose and the initial values that are known and then presented with its respective single values. The corresponding opp confidence intervals () obtained from Table 9 are (2.03852, 2.49726) min−1 for ES and (3.13283, 5.17100) min−1 for SFS (confidence level 0.95). In Section 6 these data are compared with those of Participant 1. In this case, the model predictions must be taken again very carefully, due to the low effect of the caffeine stimulus for participant happiness. However, although the part of the data variability explained by the SRM for Participant 2 provides in a very low way the happiness response to the caffeine stimulus, compared with Participant 1, it can be advanced, by comparing the respective opp intervals, that Participant 2 feels significantly more intensively the effect of caffeine consumption than Participant 1 for both happiness scales, despite the initial happiness values of Participant 2 are higher for both happiness scales than for Participant 1 ( for the ES and for the SFS).

Table 9.
Parameters’ confidence intervals (0.95 confidence level) and values of the SRM provided by the genetic algorithm for ES and SFS for Participant 2 in Phase C (see dimensions and units in Table 4).
A general conclusion of this section is that the SRM is a mathematical tool that predicts how much a stimulus (alcohol or caffeine) affects individual happiness along time as well as the happiness dynamics pattern of this change. In addition, the SRM highlights the individual differences between the responses to both drugs that the inferential statistics approach of Section 3 has discovered: (a) the jointly representation of the experimental scores with the SRM predictions in Phases B and C (Figure 4, Figure 5, Figure 6 and Figure 7); (b) the determination coefficients and the residual dispersion that this coefficient represents (the lower the determination coefficient the more residual dispersion); and (c) the significant differences between the overall power parameter (opp) confidence intervals. However, the individual differences between both participants are deeply explained in Section 6 in an integrated way with the inferential statistics results of Section 3.
6. Integration of Both Kinds of Results: Those from Inferential Statistics and Those from the Stimulus Response Model (SRM)
Consider the following Table 10 for the integration obtained in this section.

Table 10.
Overall power parameter () confidence intervals (0.95 confidence level), initial happiness values and determination coefficients of SRM provided by genetic algorithm for ES and SFS for Participants 1 and 2 in Phases B and C (see dimensions and units in Table 4).
6.1. Alcohol Effect
Considering the descriptive data of Table 1, the BL score is higher for P2 than for P1, for both the ES (M = 3.84 and M = 7.63, respectively) and the SFS (M = 3.89 and M = 4.58, respectively). With respect to the dynamic data (Table 6, Table 7, Table 8 and Table 9 and Figure 4, Figure 5, Figure 6 and Figure 7), the initial score in phases B and C (which in a certain way approximates the mean of the BL data), also follows this pattern of differences.
In the descriptive data (Table 1), the effect of alcohol on happiness is greater in P1 in relation to P2 in both ES and SFS, with a greater dispersion of the scores also for P1. In the dynamical data (Table 6, Table 7, Table 8 and Table 9 and Figure 4, Figure 5, Figure 6 and Figure 7), alcohol also produces a higher overall power parameter (opp) in P1 in relation to P2 in the two scales, as can be seen in the corresponding opp confidence intervals. Descriptive data and dynamic data are in the same line.
Regarding the contribution of each methodology, and the comparison of means between conditions (Table 3), the effect size (in absolute value) of the difference between BL and alcohol is higher for P1 than for P2 for ES (1.580 and 0.737, respectively) and for SFS (0.847 and 0.157, respectively). This result confirms everything stated in the previous paragraphs.
Regarding the contribution of the dynamic methodology, the prediction capacity of the model is excellent in P1 in both the ES and SFS (R2 = 0.87 and R2 = 0.88, respectively), while in P2 it is lower (R2 = 0.39 and R2 = 0.34, respectively), with a much greater dispersion of residuals in P2, although they are random, indicating that the effect has occurred. For P2, as we see in Table 3, β = 0.859 for ES and β = 0.097 for SFS, so that only ES registers the effect of alcohol. On the other hand, there is no intersection between confidence intervals for both participants, which means that the opp difference is significant statistically, with an overall power greater for P1, for both scales.
In summary, the effect of alcohol is clearly higher in P1 than in P2, and the higher statistical dispersion (of the scores) found in P1 with respect to P2 collected in Table 1, for both the ES (6.45 and 1.92, respectively) and the SFS (1.82 and 1.32, respectively) are now perfectly explained by their different pattern of change observed in Figure 4 and Figure 5. Now it can be well understood that since the statistical dispersion is higher in P1 than in P2, the inverse is true for the spread of the residuals, which means a better fitting of the model for P1 than for P2, which is illustrated by a greater R2.
6.2. Caffeine Effect
In the descriptive data (Table 1), the effect of caffeine is lower in P1 in relation to P2, for both ES (M = 10.16 and M = 11.53, respectively) and SFS (M = 4.58 and M = 5.53, respectively). Regarding the dispersion of the scores, it is greater in P1 than in P2 for both ES (DS = 5.06 and SD = 1.64, respectively) and SFS (DS = 1.53 and SD = 0.61, respectively).
Regarding the contribution of each methodology, and the comparison of means between conditions (Table 3), the effect size (in absolute value) of the difference between BL and caffeine is higher for P2 than for P1 for ES (1.577 and 1.310, respectively) and for SFS (0.805 and 0.470, respectively). This result confirms everything stated in the previous paragraphs.
Regarding the contribution of the dynamic methodology, the prediction capacity of the model is excellent in P1 in both the ES and SFS (R2 = 0.84 and R2 = 0.80, respectively), while in P2 it is lower (R2 = 0.51 and R2 = 0.10, respectively), with a much greater dispersion of residuals in P2, although they are random, indicating that the effect has occurred. In addition, there is no intersection between confidence intervals for both participants, which means that the opp difference is significant statistically, with an overall power greater for P2, for both scales.
Thus, the effect of caffeine is clearly lesser in P1 than in P2, but with a greater statistical dispersion (of the scores) in P1 than in P2 (collected in Table 1) both for ES (5.069 and 1.645, respectively) and for SFS (1.539 and 0.612, respectively). This is now perfectly explained by their different pattern of change observed in Figure 6 and Figure 7. Now it can be perfectly understood that since the statistical dispersion is greater in P1 than in P2, the inverse is true for the dispersion of the residuals: observe that the fitting degree of the model is greater in P1 than in P2, which is illustrated by higher R2. In other words, the trajectory (pattern of change) of the effect in P1 follows better the one predicted by the model than in P2.
6.3. Comparison Between the Effects of Alcohol and Caffeine
Regarding the comparison between the effects of alcohol and caffeine, the size of the difference in the scores of the effect of alcohol and caffeine in ES for P1 is 0.553 and for P2 is −0.670. And in SFS it is −0.470 for P1, while for P2 it is somewhat lower (−0.393), although this difference is not significant if we stick into the CI data (−0.856, 0.079). In summary, for ES, due to the size and sign of the effect, alcohol produces a higher effect than caffeine in P1 while in P2 the contrary occurs. As for SFS, the result is less conclusive. However, we can find a clearer result regarding opp. Thus, there is no intersection between the confidence intervals for both conditions (alcohol and caffeine) for both participants, which means that the opp difference is statistically significant, with higher overall power for alcohol than for caffeine in P1 and the reverse in P2.
In short, the two methodologies offer results that follow the same lines, but their interpretation is considerably enriched by putting both results together filling their respective gaps.
7. Discussion
Comparing the present approach with other approaches, on the one hand, Structural Equations Modeling (SEM), time series or network models (for instance) perhaps could fit the experimental data. However, we must consider that the SRM constitutes consolidated knowledge and its variables, parameters, and equations have a biological meaning. The SEM approach hardly could respect the hydrodynamic diagram of Figure 1 with the biological sense of its variables, parameters and structure. Note, for instance, that the drug (alcohol and caffeine) pharmacokinetics fits the balance equations of the System Dynamics approach that the hydrodynamic diagram provides. Then, the subsequent SRM equations are a natural continuation from the pharmacokinetics to the general pharmacodynamics represented by the SRM. In addition, the SRM approach considers the nonlinear dynamical equations that the SEM cannot represent.
On the other hand, network models and time series are considered as input–output models and do not provide any explanation of the biological mechanisms underlying personality dynamics after drug consumption. Again, for instance, the pharmacokinetics of the drug, the homeostatic control, the immediate excitation effect or the delayed inhibition effect, which defines the general pharmacodynamics represented by the SRM, i.e., the SRM nonlinear dynamical equations that the other models cannot represent.
A single-case experimental design with replication with two participants is used in this study. This fact leads us to a controversy about how to apply the statistical analysis to a single-case experimental design. In a classical book about this topic [32], the authors consider that ANOVA is not the most appropriate statistical analysis for the single-case experimental design. Nevertheless, being aware of the methodological limitations of this bold suggestion, this kind of analysis has been chosen because its results can illustrate very well the implicit dynamics in the effects of drugs, taking into account that the dynamical mathematical model can complement these results and facilitate both their humanistic and their natural scientific interpretations.
In fact, the results are clearly in the same vein. Starting from the two mathematical approaches, we can conclude that the difference between both participants in the experiment is evident: P1 presents more statistical dispersion (SD) than P2, but P2 presents more residual dispersion than P1, computed by the SRM predictions. In fact, this result of the SRM represents that P1 feels in a stronger way the dynamical response to both drugs than P2. However, the results provide random residuals in both cases, and so the SRM represents the deterministic predictive part of the dynamical responses.
As other studies pointed out [21,22], the model describes and predicts how the General Factor of Personality (GFP) changes in response to a single dose of caffeine or alcohol. This mathematical model predicts that the lower the GFP trait score is, the higher the response to both caffeine and alcohol intake will be, and better the corresponding model evolution curve will fit the data. Reading the Happiness scores, the relationship between the trait and the state evolution after a single dose intake of caffeine or alcohol is not the same as regarding the GFP in the previous studies. So, the difference between both participants is 10 and 14 points, respectively, for the Euphoria Scale, and the same score (5 points) for the Face Scale, and as we expected similar results in GFP and Happiness scores because they are closely related, this discrepancy should be studied in the future.
On the other hand, these results are consistent with the ones obtained for the GFP in the sense that the lower the initial score is the higher level will be achieved during the response to the drug intake. Likewise, the same thing happens regarding Happiness as this study reveals. So, the means of BL scores for P1 are 3.84 and 3.89 for the Euphoria Scale of Happiness and for the Face Scale, respectively, while for P2 they are 7.63 and 4.58 analogously. This result is coherent with the model prediction for the personality responses to drug intakes [21,22].
Finally, the individual differences between both participants observed by using the SRM parameter values can be highlighted. The overall power parameter (opp) sees the integration of four parameters involved in the three balance terms of Equation (12) or Equation (18): the homeostatic effect power (a), the excitation effect power (p) and the two parameters involved in the inhibition effect power, i.e., the inhibition effect power (q) and the inhibitor effect delay (). Their products have the same units of a and p (min−1). The addition of the four parameters as provides the sought global effect of the drug on an individual. In addition, due to the calibration has been performed with uncertainty, this global effect can be presented as a confidence interval for both participants. Comparing those confidence intervals significant individual differences can be found out. The conclusion is showed clearly in Table 10 by using the overall power parameter (opp) confidence intervals: the effect of alcohol consumption is significantly greater for Participant 1 than for Participant 2, and the effect of caffeine consumption is significantly greater for Participant 2 than for Participant 1. Moreover, as developed in Section 5, this result is in coherence with the inferential statistics. Therefore, one of the main goals of the present study is reached: that referred to the integration of the inferential statistics method, used classically in the behavioral sciences, and that known as System Dynamics, used for the modeling and simulation of complex systems.
This study has some limitations. We use a specific dose of drug, 26.51 mL of alcohol and 330 mg of caffeine, as a replication of doses used in previous research with group experimental design [21,22], but it would be better to calculate an individual dose taking into account the physical conditions of both participants. In addition, we presented a single-case experimental design with replications, but to increase the number of experimental subjects, it is necessary to test some of the considered hypothesis from an intra- and inter-individual experimental design. However, some considerations must be considered in this regard:
- This is not a case study but rather it is an experiment with control of variables, a single-case design with replication [28]. Thus, the data obtained in the baseline (phase A) are contrasted with two alternative treatments (phases B and C). This experimental design has given good results, in terms of its ability to describe and predict subjective measures of the effects produced by drugs, and in terms of the adjustment of dynamic mathematical models.
- The results of this study are consistent with previous studies using between-group designs that imply a larger number of participants and the same doses of both caffeine and alcohol [21,22]. In the first of these studies, 20 participants received 330 mg of caffeine, and in the second study, 28 participants received 26.51 g of alcohol.
- Although the two previous studies used different instruments than the one used here to measure the effect of drugs, there are some positive and significant statistical relationships between all of them. Thus, in the study about caffeine [21] the MAACL-R (Multiple Affect Adjective Checklist Revised) [33] was used, and in the study about alcohol [22] the GFP-FAS was used. In several studies it has been found that these scales are positively and significantly related to each and the Oxford Happiness Questionnaire (OHQ) [34]. Thus, the data obtained in this study are consistent with previous studies with large samples of participants and closely related subjective effects evaluation instruments. On the other hand, it can be argued that the results obtained in a single session cannot be extrapolated for a long-term effect, and that to increase euphoria in a session does not mean that happiness can increase and maintain itself in a stable way during life. As we pointed out above, the positive affect produced by alcohol consumption decreases along time, but it depends on the consumption pattern [20], what means that we can promote a moderate alcohol use as a therapeutic goal [22]. In addition, some authors [35,36] claim that happiness is associated with and precedes numerous successful outcomes, including marriage, friendship, income, work performance, and health. Then, the happiness–success link exists not only because success makes people happy, but also because positive affect engenders success.
Note, however, that this study is a first approach to the relationship between happiness and drug consumption. Considering that this subject can provide an upset social discussion due to somebody can understand that this paper suggests consuming drugs to reach short periods of happiness, we want to emphasize that its objective is the opposite: preventing consumers that drug consumption must be performed rationally. From this result, in future research, the objective could be to relate happiness with personality dynamics, such as it has been already performed with the General Factor of Personality dynamics [21,22].
The general conclusion that we can draw from this study is that inferential statistics and the SRM derived from the Systems Dynamics approach can be used in a complementary and enriching way to obtain prediction results. Particularly, it has been demonstrated that drugs such as alcohol and caffeine can increase happiness in a single session as measured by two different scales, ES and SFS.
Author Contributions
Conceptualization, S.A., A.C. and J.C.M.; methodology, S.A., A.C. and J.C.M.; software, S.A., A.C. and J.C.M.; validation, S.A., A.C. and J.C.M.; formal analysis, S.A., A.C., J.C.M. and P.D.R.; investigation, S.A., A.C. and J.C.M.; resources, S.A., A.C., J.C.M. and P.D.R.; data curation, S.A., A.C. and J.C.M.; writing—original draft preparation, S.A., A.C., J.C.M. and P.D.R.; writing—review and editing, S.A., A.C., J.C.M. and P.D.R.; visualization, S.A., A.C., J.C.M. and P.D.R.; supervision, S.A., A.C., J.C.M. and P.D.R.; project administration, S.A., A.C., J.C.M. and P.D.R.; funding acquisition, no funding. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable due to privacy and ethical restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
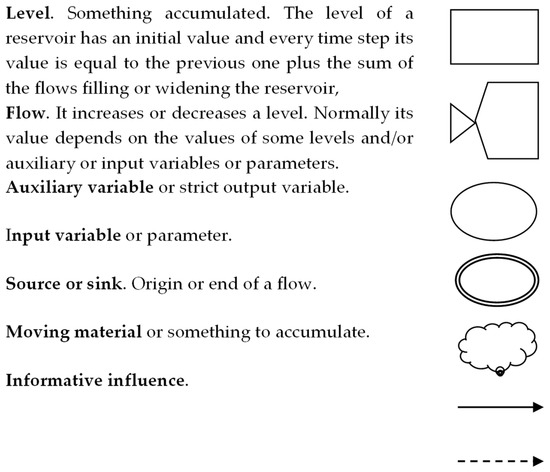
Figure A1.
Interpretation of the icons of the hydrodynamic diagram.
References
- Diener, E.; Larsen, R.J.; Emmons, R.A. Person x situation interactions: Choice of situations and congruence response models. J. Personal. Soc. Psychol. 1984, 47, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Stones, M.J.; Hadjistavopoulos, T.; Tuuko, H.; Kozma, A. Happiness has trait like and state like properties: A reply to Veenhoven. Soc. Indic. Res. 1995, 36, 129–144. [Google Scholar] [CrossRef]
- Geiger, B.B.; MacKerron, G. Can alcohol make you happy? A subjective wellbeing approach. Soc. Sci. Med. 2016, 2016, 156–184. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.; Sutherland, D.; Christopher, G. Effects of repeated doses of caffeine on mood and performance of alert and fatigued volunteers. J. Psychopharmacol. 2005, 19, 620–626. [Google Scholar] [CrossRef] [PubMed]
- Smit, H.J.; Rogers, P.J. Effects of low doses of caffeine on cognitive performance, mood and thirst in low and higher caffeine consumers. Psychopharmacology 2000, 152, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Warburton, D.M. Effects of caffeine on cognition and mood without caffeine abstinence. Psychopharmacology 1995, 119, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Childs, E.; de Wit, H. Subjective, behavioral, and physiological effects of acute caffeine in light, nondependent caffeine users. Psychopharmacology 2006, 185, 514–523. [Google Scholar] [CrossRef] [PubMed]
- Kuchinke, L.; Lux, V. Caffeine improves left hemisphere processing of positive words. PLoS ONE 2012, 7, e48487. [Google Scholar] [CrossRef] [PubMed]
- Cummins, R.A. The Wellbeing of Australians. Links with Exercise, Nicotine and Alcohol; Australian Unity Wellbeing Index, Survey 19; Australian Centre on Quality of Life, Deakin University: Geelong, VIC, Australia, 2008. [Google Scholar]
- Ventegodt, S. Liskvalitet I Danmark (Quality of Life in Denmark); Forskningscentrets Forlag: Copenhagen, Denmark, 1995. [Google Scholar]
- Lipton, R.I. The effect of moderate alcohol use on the relationship between stress and depression. Am. J. Public Health 1994, 84, 1913–1917. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; O’Brien, K.S.; Heim, D. Alcohol consumption in sportspeople: The role of social cohesion, identity and happiness. Int. Rev. Sociol. Sport 2013, 49, 278–293. [Google Scholar] [CrossRef]
- Massin, S.; Kopp, P. Is life satisfaction hump-shaped with alcohol consumption? Evidence from Russian panel data. Addict. Behav. 2014, 39, 803–810. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, B.; Korten, A.; Jorm, A.; Jacomb, P.; Christensen, H.; Henderson, A. Non-linear relationships in associations of depression and anxiety with alcohol use. Psychol. Med. 2000, 30, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Hammersley, R.; Finnigan, F.; Millar, K. Individual differences in the acute response to alcohol. Personal. Individ. Differ. 1994, 17, 497–510. [Google Scholar] [CrossRef]
- Yang, A.; Palmer, A.A.; de Wit, H. Genetics of caffeine consumption and responses to caffeine. Psychopharmacology 2010, 211, 245–257. [Google Scholar] [CrossRef] [PubMed]
- De Wit, H. Relationships Between Personality and Acute Subjective Responses to Stimulant Drugs. In Mind-Altering Drugs: The Science of Subjective Experience; Earleywine, M., Ed.; Oxford University Press: Oxford, UK, 2005; pp. 258–274. [Google Scholar]
- Revelle, W.; Humphreys, M.S.; Simon, L.; Gilliland, K. The interactive effect of personality, time of day, and caffeine: A test of the arousal model. J. Exp. Psychol. Gen. 1980, 109, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Brice, C.F.; Smith, A.P. Effects of caffeine on mood and performance: A study of realistic consumption. Psychopharmacology 2002, 164, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Tovmasyan, A.; Monk, R.L.; Heim, D. Towards an affect intensity regulation hypothesis: Systematic review and meta-analyses of the relationship between affective states and alcohol consumption. PLoS ONE 2022, 17, e0262670. [Google Scholar] [CrossRef] [PubMed]
- Caselles, A.; Micó, J.C.; Amigó, S. Dynamics of the General Factor of Personality in response to a single dose of caffeine. Span. J. Psychol. 2011, 14, 675–692. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Amigó, S.; Caselles, A.; Micó, J.C.; Sanz, M.T.; Soler, D. Dynamics of the general factor of personality: A predictor mathematical tool of alcohol misuse. Math. Methods Appl. Sci. 2020, 43, 8116–8135. [Google Scholar] [CrossRef]
- Forrester, J.W. Industrial Dynamics; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Kjellberg, A.; Bohlin, G. Self-reported arousal: Further development of a multifactorial inventory. Scand. J. Psychol. 1974, 15, 285–292. [Google Scholar] [CrossRef] [PubMed]
- Reynolds-Keefer, L.; Johnson, R.; Dickenson, T.; McFadden, L. Validity issues in the use of pictorial Likert scales. Stud. Learn. Eval. Innov. Dev. 2009, 6, 15–24. [Google Scholar]
- Hall, L.; Hume, C.; Tazzyman, S. Five Degrees of Happiness: Effective Smiley Face Likert Scales for Evaluating with Children. In Proceedings of the 15th International Conference on Interaction Design and Children, Manchester, UK, 21–24 June 2016; pp. 311–321. [Google Scholar]
- Johnson, D.R.; Creech, J.C. Ordinal measures in multiple indicator models: A simulation study of categorization error. Am. Sociol. Rev. 1983, 48, 398–407. [Google Scholar] [CrossRef]
- Norman, G. Likert scales, levels of measurement and the “laws” of statistics. Adv. Health Sci. Educ. 2010, 15, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, G.; Artino, A.R., Jr. Analyzing and Interpreting Data from Likert-Type Scales. J. Grad. Med. Educ. 2013, 5, 541–542. [Google Scholar] [CrossRef] [PubMed]
- Zumbo, B.D.; Zimmerman, D.W. Is the selection of statistical methods governed by level of measurement? Can. Psychol. 1993, 34, 390–400. [Google Scholar] [CrossRef]
- Caselles, A.; Soler, D.; Sanz, M.T.; Micó, J.C. A Methodology for Modeling and Optimizing Social Systems. Cybern. Syst. 2020, 51, 265–314. [Google Scholar] [CrossRef]
- Barlow, D.H.; Hersen, M. Single Case Experimental Designs. Strategies for Studying Behavior Change; Pergamon Press: New York, NY, USA, 1984. [Google Scholar]
- Zuckerman, M.; Lubin, B. Manual for the Multiple Affect Adjective Check List; EdITS/Educational and Industrial Testing Service: San Diego, CA, USA, 1965. [Google Scholar]
- Argyle, M.; Lu, L. The happiness of extraverts. Personal. Individ. Differ. 1990, 11, 1011–1017. [Google Scholar] [CrossRef]
- McIntosh, M.C.; Sanchez-Craig, M. Moderate drinking: An alternative treatment goal for early-stage problem drinking. Can. Med. Assoc. J. 1984, 131, 873–876. [Google Scholar] [PubMed] [PubMed Central]
- Lyubomirsky, S.; King, L.; Diener, E. The benefits of frequent positive affect: Does happiness lead to success? Psychol. Bull. 2005, 131, 803–855. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).