Abstract
This work presents a robust box-constrained nonlinear least-squares algorithm for accurately fitting the Jones–Wilkins–Lee (JWL) equation of state parameters, which describes the isentropic expansion of detonation products from high-energy materials. In the energetic material literature, there are plenty of methods that address this problem, and in some cases, it is not fully clear which method is employed. We provide a fully detailed numerical framework that explicitly enforces Chapman–Jouguet (CJ) constraints and systematically separates the contributions of different terms in the JWL expression. The algorithm leverages a trust-region Gauss–Newton method combined with singular value decomposition to ensure numerical stability and rapid convergence, even in highly overdetermined systems. The methodology is validated through comprehensive comparisons with leading thermochemical codes such as CHEETAH 2.0, ZMWNI, and EXPLO5. The results demonstrate that the proposed approach yields lower residual fitting errors and improved consistency with CJ thermodynamic conditions compared to standard fitting routines. By providing a reproducible and theoretically based methodology, this study advances the state of the art in JWL parameter determination and improves the reliability of energetic material simulations.
1. Introduction
Investigating highly energetic material behavior is critical for various applications, ranging from designing safer explosive devices to understanding high-energy astrophysical events. Central to this investigation is the accurate modeling of the energetic material detonation reaction products, where the Jones–Wilkins–Lee (JWL) equation of state (EoS) is a widely adopted model used to describe their behavior [1,2,3,4].
Upon detonation, an energetic material produces highly compressed and high-temperature gases and condensed products, with the density at the detonation wave front exceeding the original density of the explosive at the Chapman–Jouguet (CJ) state. This product mixture performs work on its surroundings under the hypothesis of an adiabatic process where no heat transfer occurs between the system and its environment [5]. The JWL EoS, hence, offers a semi-empirical description of the pressure–volume relationship of detonation products under isentropic conditions, valued for its relative simplicity and effectiveness.
The detonation energy can be evaluated using the JWL model, which assumes that the detonation products’ thermodynamics are entirely describable in a pressure–volume space. The CJ model of the detonation process assumes an instantaneous compression from ambient conditions to the CJ point, followed by expansion along the isentrope. Integrating the JWL equation yields the energy of the detonation products at any given relative volume.
The coefficients in the JWL EoS are crucial for accurate detonation modeling. These coefficients are typically derived from cylinder test data by matching wall velocity–time histories using finite element hydrocodes [6,7] and are subsequently refined through the nonlinear fitting of pressure–volume data [8]. Alternatively, theoretical evaluation involves thermochemical calculations to generate pressure–volume data along the expansion isentrope, fitting these data to the JWL equation to obtain the necessary coefficients.
Despite its broad application, heuristic (such as particle swarm algorithms) or empirical methods [9] are usually applied to find the JWL parameters; the literature lacks a comprehensive and explicit description of a robust numerical least squares fitting algorithm specifically applied to find the coefficients of the JWL EoS.
A detailed methodology for fitting the JWL EoS parameters using a nonlinear least squares (NLLS) approach [10] is presented. We provide a complete algorithmic framework for enforcing constraints at the CJ point, ensuring adherence to essential thermodynamic conditions. Furthermore, we delve into the distinct contributions of various terms in the JWL EoS, providing a granular analysis of their roles and impact on the overall equation. In this study, a Gauss–Newton method [11,12] combined with a trust-region strategy [13] is employed to achieve rapid and robust convergence. The proposed algorithm constructs a sequence of feasible iterates, incorporating a trust-region subproblem that effectively balances the trade-off between fast convergence and stability. By applying singular value decomposition (SVD) [14], our method ensures numerical robustness, particularly in overdetermined systems, which is crucial for accurate parameter estimation. In such a way, even if the rank of the coefficient matrix is not full-rank, the solution of the nonlinear least squares problem can be found.
The presented algorithm was implemented in HEMSim, a toolbox aimed at simulating highly energetic materials [15,16].
This article is structured as follows. We begin with an in-depth explanation of our fitting algorithm; this is followed by a theoretical overview of the JWL EoS, highlighting the significance of precise parameter fitting: the imposition of the CJ constraint and the treatment of different terms within the JWL expression are explained. Numerical results are presented to illustrate the effectiveness of our approach, with comparisons to published experimental data and other software simulations [5] validating the accuracy and robustness of the fitted parameters.
We conclude with a discussion on the sensitivity of the fitting process to initial conditions and parameter constraints, emphasizing the importance of the proposed algorithm.
2. Materials and Methods
2.1. Non-Linear Least Square Fitting Algorithm
Consider a set of data and a function
The residuals are vector-valued functions corresponding to the set of data possibly defined as follows:
- (absolute error) or
- (relative error)
Let be
Thus, R is a differentiable function, where n represents the number of unknowns (the dimension of x) and m is the number of data points, with .
The general box-constrained nonlinear least squares (NLLS) problem is defined as
where the vectors represent the lower and upper bounds, respectively, with , and the objective function is defined by the Euclidean norm of :
whose gradient is given by
with J being the Jacobian matrix of .
Given the constraints of the box-bounded domain, a diagonal scaling matrix D with non-zero elements is defined as follows:
in which denotes the th derivative of the function f.
The first-order necessary conditions for the optimality of problem (2), in the case of minima within the box or on its boundaries, are expressed as [11]
To solve problem (2), HEMSim implements a Gauss–Newton method enhanced with a trust-region strategy, combining the rapid convergence of Newton’s method with the robustness of the steepest descent approach.
The algorithm generates a sequence of feasible iterates defined by
At each iteration k, the trust-region subproblem centered at with radius involves defining a quadratic approximate model using a second-order Taylor expansion of f around with step s:
where and .
The trust-region strategy requires computing s by solving
To determine a feasible step , a trial solution to the trust-region subproblem is found.
By applying the stationary point condition to (7), the overdetermined system
is derived, and the minimum norm solution is given by
where is the Moore–Penrose pseudoinverse of , computed via singular value decomposition (SVD) [14]. This ensures the possibility of solving the problem even if the rank of is not maximum.
If , then
is used.
Otherwise, if the absolute minimum of lies outside the trust region, the solution to subproblem (8) is chosen as the projection of the solution of the unbounded problem onto the trust region boundary:
This problem can be solved exactly using Lagrange multipliers [17] or approximately by considering solutions in the subspace generated by the gradient of f, , to find the Cauchy point, which is the minimum of in the gradient direction within the trust region.
The scaled Cauchy step is defined by solving the constrained minimization problem inside the trust region within the box-boundary where the step s is constrained to lie on the direction given by the scaled gradient
Since the solution of the problem (13) is of the form [18], the initial is found being
ensuring it remains within the box constraints . If lies outside the current trust region, it is adjusted to stay on the trust region boundary by normalizing by the norm of the gradient:
To ensure the step is feasible, the maximum possible step length before meeting the box bound in the current gradient direction is computed, where is defined as
where all the s are defined as
leading to
Then, in the case that from (10) is outside the trust region, a dogleg step between and the Cauchy direction is computed. The classical Cauchy step , necessary for the construction of the dogleg step, is defined as
and if , a step is defined as
Otherwise, is a convex combination of and :
where is the positive root of the 2nd degree equation obtained, imposing that ,
The projected step is
where maps x into the box-bounded domain;
The projection map is employed at the very last step of the algorithm to achieve the best possible convergence ratio [18].
The first-order optimality conditions (5) are satisfied for each if meets the sufficient Cauchy decrease condition on the trust region model.
The trial step is accepted if meets condition (23). Otherwise, is computed as a convex combination of and :
with t chosen such that
At the end of the trust-region subproblem, the predicted reduction of and the actual reduction in f at are checked using
If the trial point reduces the objective function, is set, and the trust-region radius is updated, reducing it by a fixed fraction, ensuring it remains above a minimum value .
If does not satisfy (26), it is rejected and is reduced for improved model reliability. The algorithm fails if becomes smaller than .
Successful termination is achieved if one of the following conditions holds:
- , meaning that the residual scaled by the dimension of the problem is small;
- , meaning that a small gradient condition inside the box-bounded domain has been found;
- , meaning that the algorithm is not moving from the current iterate;
where and are prescribed tolerances, and is the machine tolerance.
2.2. JWL Equation of State for Isentropic Expansion
Detonation consists of a chemical transformation of the energetic material into products, accompanied by an extremely rapid transition of its potential energy into mechanical work. All this is caused by the compression and movement of the primary material or its products of decomposition.
To address issues involving the interaction of the explosion with the surrounding environment, such as the dispersion of detonation products into the air, underwater or ground explosions, the reflection of detonation waves from barriers, mass ejection, shell fragmentation, and cumulative jet formation, it is essential to understand the equation of state for the detonation products of condensed explosives. For these hydrodynamic flow scenarios, it is often sufficient to use a simplified equation of state for detonation products, which expresses the internal energy as a function of pressure and specific volume, excluding temperature.
A commonly used equation of this type is the one proposed by Jones, Wilkins, and Lee (JWL) [1]:
where
- p is the pressure measured in ;
- is the dimensionless volume, with
- –
- v is the reaction products mixture volume measured in ;
- –
- is the initial volume of the unreacted energetic compound with initial density ;
- are JWL coefficients that need to be determined by an NLLS algorithm.
- is the energy of the products released to the surroundings, as described in Section 2.3.
In applications, Equation (27) is usually expanded in a Taylor series around the isentrope expansion curve on the pressure–volume plane as follows:
For this reason, from (28) is often referred to as an isentropic (or adiabatic) expansion curve (for detonation products).
The contribution of individual terms of Equation (28) to the total pressure can be seen in Figure 1.
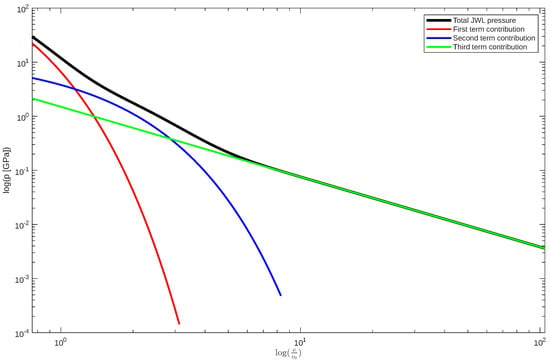
Figure 1.
Contributions of JWL terms to the total pressure; the black line is the total pressure given by the JWL Equation (28); the red line is the contribution from , the blue line is the contribution from , and green line is the contribution from .
For large dimensionless volumes, it is
with the exponential contribution terms being nearly zero; for large volumes, the JWL expression converges to the Poisson adiabatic Equation [19] for an ideal gas with an exponent .
For a volume ratio greater than 7, the JWL isentrope and the Poisson adiabatic equation are equivalent [20]. This consideration is later used in reducing the number of independent JWL coefficients to be determined.
2.3. JWL Energy of Detonation
Usually, the JWL equation is used to evaluate the energy released in the detonation process and compare it to the theoretical results. At the CJ state, under the assumption that the detonating compound is compressed instantly from the ambient temperature and atmospheric pressure up to the Rayleigh line to the CJ point, the energy of the shock wave compressing the unreacted material can be calculated by
or by using the detonation velocity (the shock wave speed):
where is the specific volume of detonation products at the CJ point, is the relative volume of detonation products at the CJ point, and is the pressure of detonation products at the CJ point.
The detonation energy is defined as the energy that the detonation reaction products have at an infinite volume:
To sum up, the energy is the work done by the shock in compressing the explosive, while the energy represents the chemical energy released by the detonation process.
The JWL equation for the internal energy of detonation products on the isentrope is obtained by integrating the JWL equation of state for pressure, leading to
The energy of detonation formula for any relative volume , as can be seen from the areas plotted in Figure 2, is given by
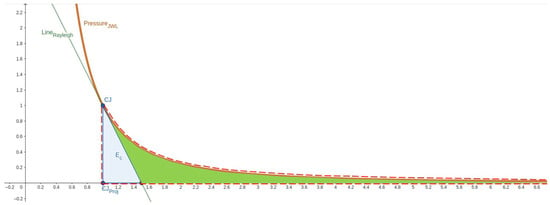
Figure 2.
The plot shows how to compute the detonation energy from the JWL curve and the Rayleigh line. The areas under the isentropic curve fitted by the JWL product EoS and the Rayleigh line, in fact, represent the work in the plane. The energy of compression given by the shock wave passage is represented by the triangular area under the Rayleigh line (blue); the chemical energy released is represented by the dashed red area under the JWL curve; , hence, is the difference (green) between the 2 areas.
Since at an infinite volume the energy on the isentrope equals zero, the detonation energy is as follows:
It is calculated as the difference between the internal energy of detonation products at the CJ point ) and the energy of shock compression of detonation products up to the C-J point .
2.4. JWL Fitting Methods
In the context of the CJ detonation theory [21], a complete JWL parameter set implicitly defines the detonation velocity , the detonation pressure , the relative volume at the CJ-condition , and and the JWL-parameter C. It is thereby common to provide instead of C because of the practical relevance of the usable detonation energy.
One of the primary methods for determining these constants is the cylinder test [22]; detailed descriptions of these experiment-based methods can be found in [7,23].
Over the years, several methods have been employed to fit JWL parameters [24,25]. The form of the JWL equation does not allow for the use of “brute force” fitting methods, since the coefficients are not independent. There is no optimal set of coefficients; an error in one of them can be easily compensated for by the “error” of others. Additional conditions can be applied by using the CJ theory.
One possibility is the one introduced by Baust in [9] that employs a global optimization method based on particle swarm to obtain a global minimum, given that the parameters are not independent.
A different approach comes from CTEv [26], in which the optimization is carried out through the minimization of the error function between the experimental points given by energy and reduced volumes and the expression for detonation energy
where coefficients , and C are fixed and computed at every step of the optimization loop by solving the linear system that enforces the constraints given from the knowledge of the point
Alternatively, the JWL constants can be derived from the expansion isentrope pressure–volume data obtained through thermochemical calculations: after determining the detonation parameters of the explosive material (the CJ point), it is possible to calculate the expansion isentrope of the product mixture at selected points on the plane, as described in [16]. These points are obtained by constraining the condition of constant entropy; . This method is employed in several other thermochemical codes aimed at energetic material simulations, such as CHEETAH 2.0 [27], EXPLO5 [5], and ZMWNI [20].
The isentrope data obtained by the thermochemical routines can then be used to determine the parameters of the JWL equation, minimizing the residual .
Generally, in this second approach, it is possible to exclude from the parameter set that needs to be determined by the minimization procedure and instead provide or to implicitly define from (32).
Therefore, one must take care to maintain consistency while providing redundant implicit parameters for the JWL that are just a necessity of the underlying CJ conditions. Very often, one finds in the literature that the JWL coefficients implicitly define detonation velocity or pressure that are not consistent with the provided experimental data.
Our methodology for the determination of coefficients is divided into two stages, which are described in the next subsections:
- In the first stage, the coefficients of the last term of the equation, C and , are determined using a linearization technique.
- In the second stage, the remaining four constants, , and , are identified using the NLLS algorithm described in Section 2.1.
2.5. Linearization of JWL’s Third Term and Least Square Fitting
The first stage is addressed by linearizing the JWL expression (28), considering only the third term (Poisson adiabatic) for reduced volume data taken after the threshold, set to . Taking the natural logarithm (denoted by ln) of the Equation (28) neglecting exponential terms, it is
By introducing the notation and , the above equation transforms into a linear form:
where and .
The constants and are determined using the linear least squares approximation method. First, to estimate the parameters C and of the JWL equation, the tail region of the dataset () is linearized, exploiting the logarithmic form of the JWL pressure Equation (33) for volumes significantly larger than the Chapman–Jouguet point, and fitted using the QR decomposition method.
The coefficient matrix M is created, consisting of a column of ones (intercept term) and as the second column:
Using the QR decomposition [17], the matrix M is factorized into an orthogonal matrix Q and a non-singular, upper triangular matrix R:
The coefficients of the linearized equation are computed by solving the triangular system:
The coefficients are then determined by taking the exponential of the intercept term
and inverting the formula for the slope
This approach efficiently isolates C and while minimizing numerical instability through the use of QR decomposition, which is particularly advantageous for overdetermined systems.
Afterwards, setting and starting from , the non-linear least square algorithm is applied to (2). The constants C and obtained by this procedure are then used as constraints in the second stage of the non-linear optimization aimed at determining the JWL isentrope coefficients.
2.6. Constraining the CJ Condition
In the second stage, it is assumed that at the Chapman–Jouguet (CJ) point, both the JWL curve and the constant entropy curve derived from thermochemical calculations converge to the same values and share identical derivatives. This condition ensures that the isentrope exponent, defined as the logarithm of the pressure with respect to the logarithm of the volume at fixed entropy,
has identical values at the CJ point for both curves. Using the detonation parameters at the CJ point, the isentrope exponent can be expressed as
where denotes the initial density of the explosive material and the pressure at the CJ point in . Therefore, at the CJ point, two key equations are obtained:
with being the dimensionless volume at the CJ point. From these equations, the constants A and B can be determined as functions of and , given fixed values of , C, and the CJ parameters obtained from the thermochemical code:
Thus, the JWL isentrope equation, substituting (43) in (28), can be written as
The values , and and the data coordinates on the isentrope are obtained from thermochemical calculations [16]. and are determined using the algorithm described in Section 2.1, which involves minimizing the function defined in (2) with
- ;
- is the pressure at any point obtained from the JWL Equation (28);
- is the pressure at point , on the constant entropy curve from thermochemical calculations.
3. Results and Discussion
The accuracy of the described approach, compared against different code results, is shown by considering the classical indicator
Several simulation runs were performed, comparing the open literature and personal communication results from three different software:
- CHEETAH version 2.0 [27], developed at Lawrence Livermore National Laboratory in the United States of America;
- ZMWNI [20], developed at the Faculty of Advanced Technologies and Chemistry at the Military University of Technology in Poland.
- EXPLO5 version 7.1 [5], developed by OZM Research s.r.o. in the Czech Republic.
Data points were taken from these programs to compare built-in ideal detonation code fitting routines with the approach described in Section 2.1. For coherence, CJ values obtained by detonation codes were used to constrain the objective function (44).
The first numerical test was performed against values from CHEETAH 2.0 [27] software. Isentropic reduced volume–pressure data for PETN (classic energetic compound) at maximum density obtained from CHEETAH 2.0 are presented in Table 1. As previously stated, it can be seen from the results in Table 2 that large deviations in JWL coefficients’ estimation are observed, even though the results for the detonation energy are similar. The error comparison shows a better accuracy in the fitting results.

Table 1.
Pressure () with respect to reduced volume data from CHEETAH 2.0 software for PETN with . Chapman–Jouguet (CJ) point values from CHEETAH 2.0 are , , .

Table 2.
Comparison of JWL parameters obtained using NLLS fitting and CHEETAH 2.0 built-in fitting solver. Even though the results for the coefficients differ, the value of detonation energy differs only by 0.9%.
The second test was performed against ZMWNI results stored in Table 3, taken from [20] for RDX. The authors employed a similar method for constraining CJ values and then fit the resulting cost function using a classic Powell method. The results are presented in Table 4, where it is shown again that, despite the differences in JWL parameters, the value of the detonation energy is equal up to five significant digits. Moreover, the error analysis demonstrates the major accuracy of the proposed approach.

Table 3.
Pressure () with respect to reduced volume data from ZMWNI software for RDX with . Chapman–Jouguet (CJ) point values from ZMWNI are , , .

Table 4.
Comparison of JWL parameters obtained using NLLS fitting and ZMWNI built-in fitting solver based on Powell’s method. It is worth noting that the value of the detonation energy is the same up to 5 significant digits.
The last numerical test that was performed against values of isentropic expansion taken from EXPLO5 simulation results available in Table 5. The authors do not describe in detail the fitting procedure implemented in the software: it is generically stated that both pressure and energy data are considered in the minimization process. It is worth noting that, unlike CHEETAH 2.0, ZMWNI, and other codes, EXPLO5 computes more than 50 points for a reduced volume, up to values near 900. The validity of the JWL EoS up to these values is uncertain when compared to volume ranges considered in the corresponding experimental setups. The results are summarized in Table 6. Even if the error from the EXPLO5 fitting is smaller than the one obtained by the proposed method, one should note that JWL coefficients coming from EXPLO5 do not fulfill CJ constraints (42).

Table 5.
Sixty-nine pressure values () with respect to reduced volume data from EXPLO for PETN with . Chapman–Jouguet (CJ) point values from EXPLO5 are , , .

Table 6.
Comparison of JWL parameters obtained using NLLS fitting and EXPLO5. Results for are comparable.
The plot in Figure 3 shows, qualitatively, a good agreement between the results from EXPLO5 and the described algorithm, being the isentropic data and the fitted curve practically overlapping.
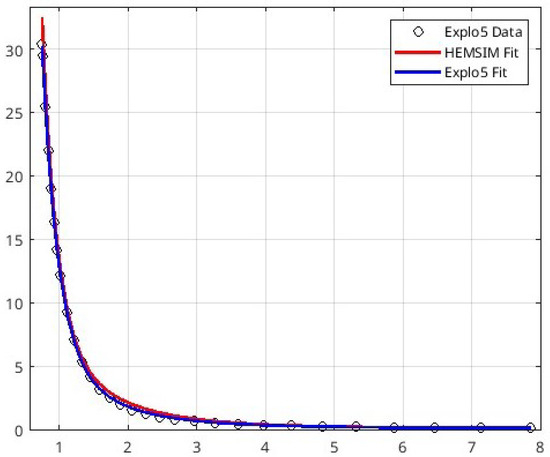
Figure 3.
Plot of isentropic data from EXPLO5 and the 2 fitting procedures from the latter software and the one presented in this work: qualitatively, the difference between the results is not appreciable.
4. Conclusions
The results presented in this study underscore the sensitivity of the JWL EoS parameter fitting process to the choices of algorithm and parameter constraints. The non-uniqueness of the fitting solution highlights the critical need for carefully imposed constraints, particularly at the Chapman–Jouguet (CJ) point, to ensure physically meaningful and accurate parameters. Our detailed algorithm, which includes the explicit imposition of the CJ constraints and the separate treatment of the different terms in the JWL EoS, demonstrates a robust approach to achieving reliable fits.
The sensitivity analysis from the open literature indicates that small variations in the input data or initial parameter guesses can lead to significant differences in the fitted parameters, emphasizing the importance of selecting appropriate ranges and constraints. These findings suggest that the success of the JWL EoS fitting is highly dependent on the specific choices made during the fitting process, including the handling of data and the definition of validity ranges for the parameters.
Additionally, it is important to recognize that the JWL EoS requires a constant Grüneisen gamma. This assumption can be problematic, as real materials often experience phase transitions, such as the transition between diamond and graphite, which introduce discontinuities and invalidate the constant gamma assumption. This further complicates the fitting process and requires careful consideration when applying the JWL EoS to materials undergoing such transitions.
Our comparative analysis with experimental data shows that, despite these sensitivities, the proposed algorithm can achieve high fidelity in modeling detonation phenomena when applied judiciously. However, users of the JWL EoS must remain cognizant of the potential for variability and the necessity of a methodical approach to parameter fitting.
By providing a clear and detailed methodology for JWL EoS parameter fitting, this work contributes to the field by offering a more reliable and efficient approach to detonation modeling.
In conclusion, this work provides a comprehensive methodology for the least-squares fitting of the JWL EoS parameters, offering clarity and guidance for future applications. By acknowledging and addressing the inherent sensitivities and potential for non-unique solutions, this study enhances the precision and reliability of detonation modeling, contributing valuable insights to the field.
Author Contributions
Conceptualization, Y.C. and A.C.; methodology, Y.C.; software, Y.C., A.C. and F.V.; validation, Y.C., A.C. and F.V.; formal analysis, Y.C. and S.B.; investigation, Y.C.; resources, Y.C.; data curation, Y.C. and A.C.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C., F.V. and S.B.; visualization, Y.C.; supervision, S.B. and F.V.; project administration, S.B. and Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
Yuri Caridi, Andrea Cucuzzella, Stefano Berrone, and Fabio Vicini are members of INdAM. The authors want to thank the INdAM-GNCS Project “Metodi numerici efficienti per problemi accoppiati in sistemi complessi” (CUP E53C24001950001). The authors also want to thank Sandra Pieraccini and Margherita Porcelli for their useful suggestions on the solver algorithm.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CJ | Chaptman–Jouguet |
| EoS | Equation of State |
| JWL | Jones–Wilkins–Lee |
| NLLS | Non-Linear Least Square |
References
- Lee, E.L.; Hornig, H.C.; Kury, J.W. Adiabatic Expansion Of High Explosive Detonation Products; Technical report; University of California Radiation Laboratory at Livermore: Livermore, CA, USA, 1968. [Google Scholar] [CrossRef]
- Cardoso, A.; Selesovsky, J.; Kunzel, M.; Kucera, J.; Pachman, J. Detonation Parameters of PlSEM Plastic Explosive. Cent. Eur. J. Energetic Mater. 2019, 16, 487–503. [Google Scholar]
- Farag, G.; Chinnayya, A. On the Jones-Wilkins-Lee equation of state for high explosive products. Propellants Explos. Pyrotech. 2024, 49, e202300223. [Google Scholar] [CrossRef]
- Castedo, R.; Natale, M.; López, L.M.; Sanchidrián, A.; Santos, A.; Navarro, J.; Segarra, P. Estimation of Jones-Wilkins-Lee parameters of emulsion explosives using cylinder tests and their numerical validation. Int. J. Rock Mech. Min. Sci. 2018, 112, 290–301. [Google Scholar] [CrossRef]
- Suceska, M. EXPLO5: Thermochemical Computer Code for Calculation of Detonation Parameters; OZM Research: Hrochův Týnec, Czechia, 2019. [Google Scholar]
- Elek, M.; Dzingalasevic, V.V.; Jaramaz, S.; Mickovic, M. Determination of detonation products equation of state from cylinder test: Analytical model and numerical analysis. Therm. Sci. 2015, 19, 35–48. [Google Scholar] [CrossRef]
- Souers, C.; Vitello, P.A.J. Detonation Energy Densities from the Cylinder Test; Technical report; Lawrence Livermore National Laboratory (LLNL): Livermore, CA, USA, 2015. [Google Scholar]
- Suceska, M.; Dobrilovic, M.; Bohanek, V.; Stimac, B. Estimation of Explosive Energy Output by EXPLO5 Thermochemical Code. Z. Für Anorg. Und Allg. Chem. 2020, 647, 231–238. [Google Scholar] [CrossRef]
- Baust, T. Improving the Design and Evaluation of PDV-Based Cylinder Test Experiments for JWL-Parameter Determination. Propellants Explos. Pyrotech. 2020, 45, 1344–1356. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Morini, B.; Porcelli, M. TRESNEI, a Matlab trust-region solver for systems of nonlinear equalities and inequalities. Comput. Optim. Appl. 2010, 51, 27–49. [Google Scholar] [CrossRef]
- Macconi, M.; Morini, B.; Porcelli, M. A Gauss–Newton method for solving bound-constrained underdetermined nonlinear systems. Optim. Methods Softw. 2009, 24, 219–235. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Golub, G.; Kahan, W. Calculating the Singular Values and Pseudo-Inverse of a Matrix. J. Soc. Ind. Appl. Math. Ser. B Numer. Anal. 1965, 2, 205–224. [Google Scholar] [CrossRef]
- Cucuzzella, A.; Caridi, Y.; Berrone, S.; Rondoni, L. MATLAB code for highly energetic material. In Proceedings of the III Aerospace PhD-Days: International congress of PhD students in Aerospace Science and Engineering, Bertinoro, Italy, 16–19 April 2023; Volume 33. [Google Scholar]
- Caridi, Y.; Cucuzzella, A.; Berrone, S. HEMSim: A new MATLAB software to simulate the behavior of highly energetic materials upon Chapman-Jouguet hypothesis. J. Energetic Mater. 2024, 1–16. [Google Scholar] [CrossRef]
- Quarteroni, A.; Saleri, F.; Gervasio, P. Scientific Computing with MATLAB and Octave; Springer: Berlin, Germany, 2006. [Google Scholar]
- Macconi, M.; Morini, B.; Porcelli, M. Trust-region quadratic methods for nonlinear systems of mixed equalities and inequalities. Appl. Numer. Math. 2009, 59, 859–876. [Google Scholar] [CrossRef]
- Engel, T.; Reid, P. Thermodynamics, Statistical Thermodynamics, Kinetics; Pearson: London, UK, 2005. [Google Scholar]
- Grys, S.; Trzciński, W. Calculation of Combustion, Explosion and Detonation Characteristics of Energetic Materials. Cent. Eur. J. Energetic Mater. 2010, 7, 97–113. [Google Scholar]
- Fickett, W.; Davis, W.C. Detonation Theory; Courier Corporation: Berkeley, CA, USA, 2012. [Google Scholar]
- Sanchidrián, J.; Castedo, R.; López, L.; Segarra, P.; Santos, A. Determination of the JWL Constants for ANFO and Emulsion Explosives from Cylinder Test Data. Cent. Eur. J. Energetic Mater. 2015, 12, 177–194. [Google Scholar]
- Weseloh, W.N. JWL in a Nutshell; Technical report; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 2014. [Google Scholar]
- Tarver, C.M. Jones-Wilkins-Lee (JWL) reaction product equations of state for overdriven PETN detonation waves. AIP Conf. Proc. 2020, 2272, 030031. [Google Scholar] [CrossRef]
- Tarver, C.M. Jones-Wilkins-Lee Unreacted and Reaction Product Equations of State for Overdriven Detonations in HMX- and TATB-based Plastic Bonded Explosives. J. Phys. Chem. 2020, 124, 1399–1408. [Google Scholar] [CrossRef] [PubMed]
- Selesovsky, J.J.; Pachman, J.; Kucera, J. Cylinder test of emulsion explosives: Possibilities of detonation pressure estimation. In Proceedings of the 24th New Trends in Research of Energetic Materials Conference, Skikda, Algeria, 16–17 November 2022. [Google Scholar]
- Fried, L.; Howard, W.; Souers, P. CHEETAH 2.0 User’s Manual; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1998. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).