Abstract
Time series anomaly detection in streaming environments faces persistent challenges due to concept drift, which gradually degrades model reliability. In this paper, we propose Anomaly Detection with Drift-Aware Ensemble-based Incremental Learning (ADDAEIL), an unsupervised anomaly detection framework that incrementally adapts to concept drift in non-stationary streaming time series data. ADDAEIL integrates a hybrid drift detection mechanism that combines statistical distribution tests with structural-based performance evaluation of base detectors in Isolation Forest. This design enables unsupervised detection and continuous adaptation to evolving data patterns. Based on the estimated drift intensity, an adaptive update strategy selectively replaces degraded base detectors. This allows the anomaly detection model to incorporate new information while preserving useful historical behavior. Experiments on both real-world and synthetic datasets show that ADDAEIL consistently outperforms existing state-of-the-art methods and maintains robust long-term performance in non-stationary data streams.
1. Introduction
Time series anomaly detection has become increasingly important with the rapid growth of sensors, IoT devices, and real-time monitoring systems. Anomalies often represent unexpected events that may lead to critical consequences, such as financial fraud, system malfunctions, or medical emergencies. Timely detection is essential to mitigate their potential impact, including economic loss, infrastructure disruption, and risks to human wellbeing [1,2].
Although traditional anomaly detection methods have demonstrated successes under static assumptions, their performance frequently declines as the data distribution changes over time. This phenomenon is known as concept drift [3]. This issue is particularly prevalent in streaming environments, where data rarely follows stationary patterns.
Edge computing scenarios further amplify these challenges. This is driven by the fact that full model retraining cannot satisfy the constraints on memory, latency, and energy consumption in edge deployments. Meanwhile, streaming data exhibits non-stationarity, which calls for frequent and costly model retraining. Many real-world applications, such as environmental monitoring, system health tracking, and automated metrics analysis, require timely and adaptive anomaly detection in streaming settings [4].
Unlike video anomaly detection, which identifies rare visual events in high-dimensional spatiotemporal data such as unexpected object movements [5], our work focuses on detecting anomalies in low-dimensional, non-visual time series, such as sensor readings and system logs. These two problem settings differ fundamentally in data modality. Video anomaly detection relies on structured visual data with both spatial and temporal continuity. In contrast, our setting involves sequential numerical data, where each observation is a single scalar value, such as temperature or voltage, recorded over time. This distinction in data modality leads to different definitions of anomalies and detection objectives. In video data, anomalies are defined as unexpected changes in motion or appearance. In contrast, our focus is on abrupt changes or deviations in temporal patterns of numerical data.
Ensemble-based methods have recently attracted increasing attention for addressing concept drift in streaming data environments [6,7,8]. In these methods, base detectors are designed to evolve over time or to be selectively replaced in response to distributional changes. This kind of model structure supports long-term adaptation without requiring full model retraining. However, ensemble frameworks specifically designed for unsupervised anomaly detection remain relatively limited. Most existing efforts target supervised classification tasks, and few have explored unsupervised ensemble designs for anomaly detection under non-stationary conditions.
Among unsupervised ensemble approaches, Isolation Forest [9] (iForest) has emerged as the most widely used model for anomaly detection. It is well recognized for its efficiency, scalability, and robustness in fully unsupervised settings, where labeled data is often unavailable. Its low computational overhead makes it even more attractive for edge computing applications, where resource constraints are critical. Nevertheless, iForest and its variants are typically built under static training assumptions and do not incorporate any inherent mechanisms for model adaptation. As a result, their detection performance tends to degrade over time when facing non-stationary data streams affected by concept drift.
Several methods have been proposed to support anomaly detection in data streams. For example, the Lightweight Online Detector of Anomalies (LODA) [10] is an ensemble-based approach using random projections and sparse histograms. It provides efficient scoring but lacks any form of model adaptation. MemStream [11] introduces a memory-augmented architecture that incrementally adapts to concept drift. However, updates in MemStream are based on recency of data alone, and there is no mechanism to explicitly detect drift intensity or monitor model degradation. These limitations suggest the need for a more robust adaptive framework. Such frameworks should detect concept drift proactively and perform updates efficiently and effectively. This is particularly important in unsupervised and resource-constrained streaming environments. To move toward this goal, several recent efforts have attempted to incorporate concept drift detection into anomaly detection frameworks such as Performance Weighted Probability Averaging Ensemble (PWPAE) [12] and Variational AutoEncoder for identifying Anomaly Sequences (VAEAS) [4]. However, the effectiveness of such systems is heavily dependent on the drift detection mechanism used.
Among the existing concept drift detection strategies, distribution- and performance-based methods are the most widely used due to their simplicity and generalizability [13,14]. Distribution-based methods monitor statistical changes in the data stream without data labels. However, they are often over-sensitive to minor distributional variations that do not actually impact model performance, leading to unnecessary updates and potential instability [13]. On the other hand, performance-based methods observe drift in the model behavior. Most of them use predictive accuracy or error rates to detect drift. However, they commonly require labeled data, which is rarely available in time series anomaly detection settings. Due to these limitations, neither of them alone is sufficient for robust, unsupervised drift detection in real-world anomaly detection tasks. This highlights the need for a hybrid approach that combines statistical sensitivity with structure-based performance evaluation.
Recent methods such as AEADF [15] have explored this direction by combining distribution-based and performance-based drift detection. However, AEADF relies on a fixed update strategy anchored to a static initial model, which limits its adaptability over time. Its drift detection also depends on histogram-based divergence measures and output-based performance evaluations, which may reduce stability and interpretability. These limitations motivate the development of a more flexible and robust hybrid framework.
To this end, this paper proposes a novel framework that incorporates hybrid drift detection and incremental model adaptation. The main contributions are summarized as follows:
1. A novel unsupervised anomaly detection framework: ADDAEIL
This paper introduces Anomaly Detection with Drift-Aware Ensemble-based Incremental Learning (ADDAEIL), an unsupervised framework for anomaly detection in non-stationary streaming time series. ADDAEIL incrementally updates its ensemble model by selectively replacing drift-affected base detectors. This enables the model to autonomously adapt to evolving data distributions while retaining useful historical knowledge. ADDAEIL is designed for long-term stability and efficient operation without full retraining. These characteristics make it well suited for deployment in resource-constrained environments, such as edge computing.
2. An automated hybrid drift detection mechanism
To robustly detect concept drift, a hybrid detection module is designed that integrates both distribution-based and performance-based concept drift detection approaches:
- (a)
- Distribution-based detection: Using robust statistical tests, the Kolmogorov–Smirnov (KS) test and Mann–Whitney U (MWU) test, ADDAEIL accurately captures both nuanced global shape and location shifts in data distributions across sliding windows.
- (b)
- Performance-based detection: ADDAEIL directly evaluates the distributional changes in path lengths of individual base detectors in iForest, as concept drift affects the decision paths within the tree structure and governs anomaly scoring. By analyzing these changes, it identifies which base detectors are most affected by concept drift from a structural perspective. This design provides a structure-based performance evaluation mechanism for drift detection without introducing any additional model training.
3. An adaptive model update strategy guided by drift intensit
The updating strategy is proposed, in which the update ratio is dynamically determined based on the intensity of the detected concept drift. The strategy automatically selects and replaces the base detectors whose structures are most significantly affected by the drift. This approach enables efficient incremental updates, making it well aligned with the computational constraints of edge computing applications.
The remainder of this paper is organized as follows: Section 2 reviews related work on time series anomaly detection under concept drift, highlighting existing limitations in adaptive learning, drift detection strategies, and ensemble model design in non-stationary streaming settings. Section 3 provides an overview of the ADDAEIL framework and shows the details of the important modules. Section 4 presents the comprehensive experiments and ablation studies with systematic evaluations across multiple datasets. Finally, Section 5 concludes the paper, summarizing key contributions and future research directions.
2. Related Work
2.1. Time Series Anomaly Detection Under Concept Drift
Anomaly detection in data streams is challenging due to concept drift, where the distribution of the data changes over time. Traditional anomaly detection approaches assume stationarity and are based on offline trained models. Thus, they suffer performance drops in real-world non-stationary scenarios [1,3].
Classical unsupervised methods such as iForest [9] and Empirical-Cumulative-distribution-based Outlier Detection (ECOD) [16] are unsupervised approaches assuming stationarity of data. Their performance will degrade when applied to non-stationary data. The state-of-the-art spectrum decomposition-based framework [17] achieves promising performance on stationary time series. However, this method assumes the data distribution remains the same. In practice, the data distribution rarely remains stationary in streaming scenarios, so this method cannot handle distributional drift.
To address these challenges, some partially adaptive methods have been proposed. LODA [10] applies random projections and histogram-based scoring to support streaming detection. Although its randomized features provide some robustness to minor drift, it lacks explicit drift detection and model adaptation. As a result, it functions as a static model throughout the deployment.
Several other approaches aim to improve adaptability in evolving environments. LSTM-VAE [18] model captures temporal dependencies and offers limited robustness to gradual drift, but lacks explicit mechanisms to detect or respond to distributional changes. Context-aware Domain Adaptation [19] tries to align the source and target domains using contextual information. However, these methods usually assume static and predefined domain boundaries, which are usually not satisfied in streaming scenarios where the drift is continuous and unstructured. MemStream [11] uses a memory buffer to update models online. However, the update process is driven by data recency. This method is not capable of monitoring drift intensity or model performance degradation, which can lead to delayed or suboptimal adaptation.
Although the above methods exhibit different levels of adaptability, none of them contains a concept drift detection component, which limits their responsiveness to large distributional changes.
Recently, there have been some attempts to introduce explicit concept drift detection to unsupervised anomaly detection. Most of these approaches focus on either distribution-based or performance-based evidence, while rarely combining the two. The PWPAE framework [12] follows a performance-based strategy. It uses detectors such as the Drift Detection Method (DDM) [20] and Adaptive Windowing (ADWIN) [21], which detect drift by tracking changes in prediction errors or output statistics. These methods usually rely on label data or assumptions of prediction stability, which are often not available in unsupervised scenarios.
In contrast, state-transition-aware anomaly detection under concept drifts (STAD) [22] employs a distribution-based approach by applying KS and AD tests within the latent space of an autoencoder. This enables the detection of subtle changes in data representation. However, STAD does not monitor the performance or internal structural alignment of the model. Its sensitivity to drift is limited by the encoder’s ability to consistently capture meaningful features.
VAEAS [4] introduces a dual-drift detection strategy by combining statistical testing and performance-based signals within the latent space. However, its statistical tests are conducted exclusively on encoded representations, assuming that the latent space fully reflects changes in the input distribution. If the encoder fails to adapt, important distributional shifts may go undetected. Consequently, despite its hybrid formulation, VAEAS lacks true distribution-level drift detection at the input level, and its effectiveness is constrained by the quality of latent representations.
In summary, many existing methods either rely on a single source of drift detection or ignore drift detection entirely. Few methods integrate both distribution-based and performance-based drift detection results in a fully unsupervised and interpretable framework. To address this gap, the proposed framework ADDAEIL introduces a hybrid, incremental adaptive strategy. It combines distribution-based drift scoring with structure-based performance evaluation to support efficient and reliable anomaly detection in evolving data streams.
2.2. Concept Drift Detection Strategies
As discussed in the previous section, concept drift has a large effect on anomaly detection performance in streaming applications. Although some detection approaches attempt to account for changing data distributions, their effectiveness is generally limited by the quality of the underlying drift detection method. In this section, we review the approaches used to detect concept drift, and then group methods into distributional, performance, and hybrid categories [3,23].
Distribution-based methods observe changes in the input data stream. Most distribution-based methods statistically model changes in data distributions across sliding windows. The KS test [24], the Kullback–Leibler (KL) divergence [25], and the MWU test [26] are commonly used for drift detection due to their simplicity, statistical foundation, and lack of dependence on labeled data [14,27]. Thus, they are often applied in unsupervised settings. However, these methods are vulnerable due to their sensitivity to even small distributional changes that have little impact on model performance. As a result, they often trigger unnecessary model updates and reduce stability in deployment.
Performance-based methods detect drift by observing changes in a model’s behavior, such as changes in prediction accuracy, error rates, or output scores. In supervised learning, these changes are usually tracked using labeled data over time [23,28]. However, in anomaly detection, which is often unsupervised, labeled data is usually unavailable in real-time. As such, the application of traditional performance-based methods is limited in practice.
To address the limitations of single-source drift detection, recent works have considered hybrid methods combining distributional and performance-based signals. For example, the AEADF framework [15] adopted a hybrid strategy: using Hellinger distance to measure distributional change and comparing the output of a local model (trained on the current window) with the output of the initial model to detect performance degradation.
Although this represents an important step towards practical hybrid drift detection, AEADF still suffers from several major limitations. Firstly, Hellinger distance is a histogram-based measure that works well on discrete distributions but is sensitive to the choice of bin size on continuous data. Poor choices of bin size may lead to unstable or even misleading results. At the same time, comparing the output of a local model (trained on the current window) with the output of the initial model brings additional computational overhead: a new local model needs to be trained for every incoming window. This may increase computational resource consumption and limit scalability in edge or streaming applications.
Therefore, although AEADF introduces the hybrid detection concept, its design suffers from both statistical instability and computational inefficiency. These limitations motivate the need for a more robust hybrid drift detection strategy.
2.3. Adaptive Ensemble Models and Incremental Learning
Adaptive ensemble models and incremental (continual) learning techniques have been increasingly explored to address concept drift in data streams. These approaches aim to maintain stable performance over time by enabling selective model updates without full retraining.
In adaptive ensembles, base detectors are designed to evolve over time or to be replaced selectively in response to distributional changes. Learn++.NSE [6] and Dynamic Weighted Majority (DWM) [29] are early examples of concept drift-aware ensemble methods. They adapt to drift by weighting or replacing classifiers based on recent performance. However, they rely on labeled data and are limited to supervised learning scenarios.
Recent research has extended ensemble adaptivity to streaming environments. DeepStreamEnsemble [7] combines deep feature extraction with Hoeffding Tree ensembles to detect and respond to drift. While it supports online adaptation, it requires labeled data after each drift event and is not designed for anomaly detection. Recurrent Adaptive Classier Ensemble (RACE) [8] addresses recurring drift by maintaining a pool of historical classifiers and reactivating them as needed. This approach also operates under a supervised setting and retrains models rather than updating them incrementally. Ensemble of Drift Feature Subspaces (EDFS) [30] targets anomaly detection in streaming settings using an ensemble-based strategy with entropy-guided pruning. Although the method emphasizes unsupervised detection, it still assumes access to occasional labels after drift for ensemble updating.
In summary, while these methods demonstrate the value of ensemble models for adapting to concept drift, they are limited in two key aspects. Most require supervision during adaptation, and few support incremental learning. The proposed ADDAEIL framework addresses these limitations by integrating fully unsupervised drift detection and incremental ensemble updates for streaming anomaly detection.
3. Methodology
3.1. Framework Overview
The proposed ADDAEIL is an unsupervised ensemble-based anomaly detection framework designed for streaming time series data under non-stationary conditions. Built upon the iForest architecture, ADDAEIL supports incremental concept drift-aware model updating. These characteristics make it particularly suitable for deployment in resource-constrained edge computing environments. An overview of the architecture is shown in Figure 1.
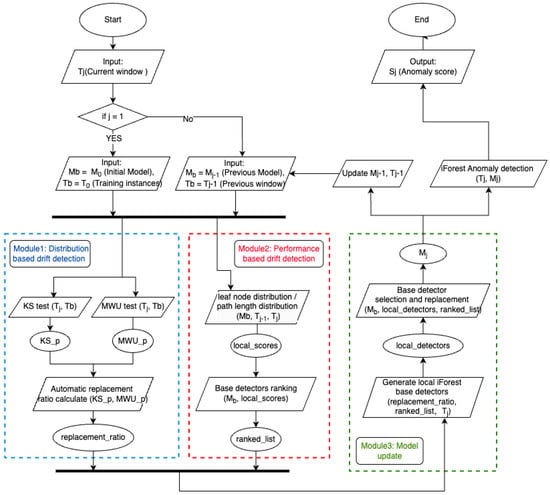
Figure 1.
Overview of the proposed framework ADDAEIL. The system integrates distribution-based and performance-based drift detection modules to guide selective updates to the iForest model.
The framework ADDAEIL operates under a sliding-window paradigm, where the time series data stream is processed in fixed-size windows. The initial model consists of N base detectors (i.e., decision trees in iForest), each trained on an initial historical training set . For each new window , the system first evaluates the presence and intensity of concept drift, based on both distribution and performance evaluation. It then incrementally updates the model based on the estimated drift level, ensuring incremental adaptation before performing anomaly detection.
To support adaptive learning without full retraining, a drift intensity-guided selective update strategy is implemented. First, module 1 (distribution-based drift detection) employs statistical hypothesis tests to estimate the level of distributional change, and maps this to a replacement ratio. Next, module 2 (performance-based drift detection) evaluates the path length distribution of each base detector. Concept drift affects the tree’s decision paths, and deviations in path length indicate which detectors are structurally degraded. From this perspective, the module ranks all base detectors by their level of structural misalignment. In module 3 (model update strategy), a subset of the most drift-affected detectors is replaced by new ones trained on , while the remaining detectors are retained. After the update, anomaly scores are computed by aggregating the outputs of all detectors in the updated model.
Each module plays a distinct role in enabling incremental, interpretable, and effective adaptation. Interpretability is ensured through transparent statistical tests and structure-based performance evaluation, which together clarify when and why model updates occur.
- Module 1: Distribution-based Drift Detection. In the distribution-based drift detection module, the KS test and MWU test are used to simultaneously capture shape and location shifts of the distribution across consecutive windows. The two tests act as complementary statistical measures for drift detection and jointly provide a more complete estimation of drift severity, which can be mapped to the replacement ratios. In other words, these tests can be used to estimate the replacement ratio for model updating according to the drift level in each window.
- Module 2: Performance-based Drift Detection. In the performance-based drift detection module, the internal structure of the iForest model is monitored to rank the base detectors according to their replacement priorities. Concept drift will have an impact on the result decision path of the tree structure in Isolation Forest. Analyzing path length deviation will give a very good indication of model performance degradation. Therefore, the framework provides a structure-based detector ranking without requiring additional model training during drift detection.
- Module 3: Model Update Strategy. For the model update strategy, a proportion of base detectors is replaced according to the replacement ratio estimated by the distribution-based drift detection module and the base detector ranking from the performance-based drift detection module. The remaining base detectors are preserved, which allows the framework to adaptively retain more useful historical knowledge.
Together, these modules form an effective and interpretable framework that delivers robust and efficient anomaly detection under evolving data distributions. In the following sections, each module is presented in more detail, including its mathematical formulation and algorithmic implementation.
3.2. Module 1: Distribution-Based Drift Detection
To detect the level of concept drift in streaming time series, this module compares the statistical properties of the current data window and the base window using robust, nonparametric hypothesis tests.
Let denote the base window and the current sliding window, each containing W standardized values from a univariate time series. The base window is updated adaptively as the most recent past window. This is denoted as , with as the initial training set. This design provides a consistent basis for drift detection by comparing the current window with the most recent window and supports incremental learning over streaming data.
The degree of change between and is quantified using two well-established nonparametric statistical tests:
- KS test [24]: The Kolmogorov–Smirnov (KS) test quantifies the maximum distance between the empirical cumulative distribution functions (ECDFs) of two samples:where and are the ECDFs of the base window and the current window , respectively. A larger value indicates a stronger distributional difference. The corresponding p-value is given bywhere is the complementary cumulative distribution function (CCDF) of the Kolmogorov distribution under the null hypothesis that both samples are drawn from the same distribution. It represents the probability of observing a KS statistic greater than or equal to . A smaller value indicates a stronger statistical rejection of the null hypothesis, suggesting that the two samples likely come from different distributions. The KS test is particularly sensitive to global changes in distribution shape (e.g., spread or skewness), but may be less responsive to subtle shifts in central tendency such as mean or median changes.
- MWU test [26]: The Mann–Whitney U (MWU) test evaluates whether two samples originate from the same distribution by comparing their central tendencies, particularly the median. The test is non-parametric and based on rank statistics. The U statistic is computed as follows:Here, and are the sums of ranks for elements in and , respectively, and are the sample sizes. The corresponding p-value is computed as follows:where is the cumulative distribution function (CDF) of the Mann–Whitney U distribution under the null hypothesis that both samples have equal medians. When the sample sizes are sufficiently large, can be approximated by a normal distribution. A smaller value indicates stronger evidence of a location shift (e.g., in the median), suggesting that concept drift may have occurred.The MWU test is particularly sensitive to changes in distribution center, making it complementary to the KS test, which is more responsive to differences in overall shape.
The combination of KS and MWU tests enhances the ability to comprehensively detect distributional changes. While MWU captures shifts in location, KS is sensitive to differences in overall distribution shape. Together, they offer a broader and more reliable assessment of distributional shifts, reducing the likelihood of missed changes in streaming data. The unified drift score is defined as follows:
We use equal-weighted averaging as a simple yet effective combination strategy, reflecting equal importance to shape and location changes. The resulting score lies in , with higher values indicating stronger evidence of drift.
We then compute a using linear interpolation:
In the implementation, these values are set as and . This ensures that the model is updated incrementally.
The lower bound is chosen to maintain a minimal level of incremental adaptation. Even in the absence of statistically significant drift, small updates allow the model to gradually incorporate new patterns from evolving data, supporting smooth incremental learning. The upper bound prevents excessive forgetting and model instability. Replacing more than 60% of base detectors at once could lead to overreaction to temporary fluctuations or noise in the data stream. By capping the update intensity, the model is able to retain sufficient historical knowledge and maintain robustness across consecutive windows.
The full procedure is summarized in Algorithm 1.
| Algorithm 1 Distribution-Based Drift Detection (Module 1) |
|
3.3. Module 2: Performance-Based Drift Detection
This module assesses the structural alignment of each base detector in by analyzing the change in its path length distributions between consecutive time windows. In iForest, the anomaly score of a sample is determined by the path length required to reach a leaf node. Concept drift alters the data distribution, which in turn affects the decision paths within the tree structures of Isolation Forest. As a result, analyzing deviations in path length distributions provides an effective signal of model degradation.
This effect can be visualized by comparing detector behavior before and after drift. Figure 2 illustrates this intuition using an example from a real-world time series. The left plot shows two consecutive windows before and after a drift event. The right plot compares the path length distributions of a single base detector on these two windows. After drift, the path lengths become more variable and the median shifts significantly, indicating that the detector has become misaligned with the new data.
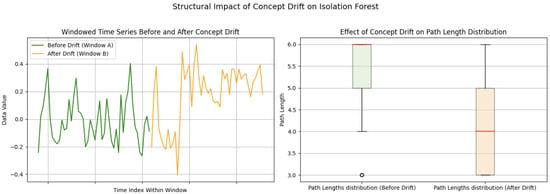
Figure 2.
Structural impact of concept drift on Isolation Forest. (Left) time series segments before and after the concept drift. (Right) Path length distributions before and after concept drift. Colored boxes represent distributions for Window A and Window B, with red lines indicating the medians. A clear shift is observed, reflecting detector misalignment.
To generalize this process across detectors, the following notation is defined: Let and denote the sets of path lengths observed from the i-th base detector when applied to the baseline window and the current window , respectively:
For each base detector , the MWU test is applied to assess whether the path length distributions have changed significantly. The resulting two-sided p-value quantifies the statistical evidence of change:
All base detectors are then ranked in ascending order of their values. Detectors with smaller are interpreted as being more affected by drift, and are given higher priority for replacement.
This structure-based performance evaluation strategy offers several practical advantages. First, it operates entirely unsupervised, without relying on ground truth labels or auxiliary models. Second, it directly monitors changes in internal model behavior. Specifically, it uses the distribution of path lengths, which fundamentally governs anomaly scoring in iForest. A shift in this distribution indicates that the partitioning structure of a base detector no longer matches the current data, signaling potential degradation.
By analyzing these changes at the structural level, ADDAEIL provides explainable insight into how individual detectors are affected by drift. This enables targeted model adaptation according to structure-based performance evaluation. The procedure is summarized in Algorithm 2.
| Algorithm 2 Performance-Based |
|
3.4. Module 3: Model Update Strategy
This module performs selective updates to the model in response to concept drift, as identified by the previous modules. It replaces only a subset of base detectors, avoiding full retraining and preserving valuable historical knowledge. This incremental update strategy enables the model to adapt over time while maintaining robustness under non-stationary conditions.
Given the replacement ratio computed by the distribution-based drift detection module (Module 1), the number of base detectors to be updated is determined as follows:
where N is the total number of base detectors in the model.
Then denotes the current model, consisting of N base detectors. These detectors are ranked in ascending order of p-values from Module 2, resulting in an ordered list:
The subset selected for replacement is defined as follows:
A new iForest consisting of K base detectors is trained on the current data window . These new detectors replace , while the remaining detectors are preserved. The updated model at time j is expressed as follows:
where contains the K base detectors newly trained on , which replace the drift-affected detectors in .
This update strategy offers stability of the model. Full retraining of all base detectors may lead to catastrophic forgetting and unnecessary computational burden. By contrast, the partial update strategy preserves a portion of prior knowledge while allowing drift-sensitive components to adapt. It also ensures efficiency adaptation by avoiding full model retraining and limiting updates to a smaller subset of base detectors. By adjusting the update strength in proportion to drift intensity and preserving unaffected detectors, the model adapts efficiently without overfitting to transient changes.
The procedure is outlined in Algorithm 3.
| Algorithm 3 Model Update Strategy (Module 3) |
|
4. Results
4.1. Experimental Setup
We conducted four sets of experiments to comprehensively evaluate the performance of proposed framework under non-stationary streaming scenarios.
Part I compares ADDAEIL with a variety of benchmark algorithms, including offline, semi-online, adaptive online methods, and deep learning-based models. Offline methods represent static detectors that do not respond to distributional changes. Semi-online methods support streaming inputs but lack explicit adaptation mechanisms. Adaptive online methods, by contrast, are capable of updating their models in response to evolving data. Deep learning-based models (e.g., LSTM-VAE and STAD) capture temporal dependencies or structural representations through complex architectures, typically requiring offline training. All the methods are evaluated under the same sliding-window protocol to ensure consistency.
In the case of LSTM-VAE, we implemented a standard architecture with an encoder–decoder and RepeatVector structure, trained with Adam (learning rate = 0.001) and a mean squared error loss. For other methods (including STAD), we used recommended settings from the original papers or default values provided by standard packages.
Part II presents an ablation study to assess the contribution of each core component in ADDAEIL. Three variants are tested against the proposed ADDAEIL framework:
- No Update: A static iForest trained only once on the initial data .
- Distribution-only: Where drift detection and updates are only conducted based on the results of the KS and MWU tests in module 1. The replaced base detectors are randomly selected from the base model.
- Performance-only: Where updates are conducted based on the results of the path-length-based detector in module 2. The replacement ratio is set to be fixed with the value 0.3.
- ADDAEIL (Proposed): The full version of the proposed framework, combining both drift detection results.
Part III conducts a sensitivity analysis of three key hyperparameters: the sliding window size W, the number of base detectors N, and the update ratio range . Each parameter is varied independently to examine its effect on model performance, while all other settings are held constant.
Part IV evaluates the practical deployment performance of the ADDAEIL framework in edge computing scenarios. To this end, we conducted experiments on the NVIDIA Jetson Orin NX 16 GB platform, measuring runtime efficiency and resource consumption on the CEMACS dataset. Metrics such as training time, per-window latency, maximum memory usage, and model size were collected to substantiate the framework’s suitability for deployment in resource-constrained environments.
In all four parts, the system is set to the fixed-size sliding-window setting. The first 30% of each time series is used as the initial training set and the remaining 70% is processed in an incremental fashion in windows of size . The base model is initialized with base detectors. The range of replacement ratio is set to be .
4.2. Datasets
Three widely adopted time series anomaly detection datasets were applied in the experiment. They cover both synthetic and real-world scenarios, and reflect a range of concept drift characteristics.
Yahoo A3 [31]: A synthetic dataset designed to simulate complex anomalies and incremental drift. Frequently used for evaluating drift-aware models.
Numenta Anomaly Benchmark (NAB) [32]: A benchmark for time series anomaly detection that contains 50 real and synthetic time series with labeled anomalies. It includes both sudden and incremental drift.
CEMACS [33]: Real-world ocean surface temperature data recorded every 30 min over two years. It shows mild but long-term drift.
To ensure consistent evaluation, a fixed window size of is used across all datasets. This size aligns with the temporal resolution and periodicity of the datasets (e.g., daily or sub-daily cycles), making it suitable for detecting both abrupt and slow-evolving drift.
The datasets used in our experiments are widely adopted in the literature for evaluating anomaly detection performance under evolving data distributions caused by concept drift [15,34,35,36,37]. Importantly, these datasets do not exclusively contain highly obvious anomaly points; some anomalies exhibit deviations that are relativity subtle and lie close to the typical variability range observed in normal data. For example, Figure 3 shows a time series from the Yahoo dataset. It illustrates two anomaly points: the first anomaly point exhibits a clear deviation from the normal data trend (a pronounced sudden drop), whereas the second anomaly point shows only a mild deviation, making it more difficult to distinguish it from natural fluctuations. This diversity of anomaly characteristics provides a valuable basis for comprehensively evaluating the capability of anomaly detection models under realistic streaming conditions.
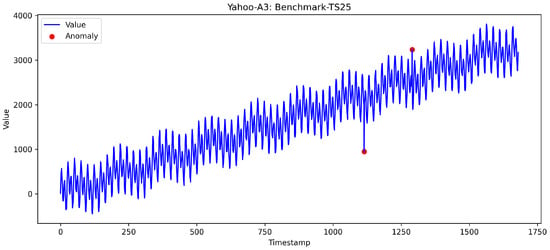
Figure 3.
Two anomaly points from the Yahoo-A3: Benchmark-TS25. The first point shows a pronounced sudden drop, while the second point shows a mild deviation, close to natural data fluctuations.
4.3. Evaluation Metrics
To comprehensively evaluate anomaly detection performance, four widely adopted metrics are used: Area Under the ROC Curve (AUC), F1-score, Precision, and Recall. These metrics are computed for each test window based on the predicted anomaly scores and ground-truth labels and are averaged over all windows in the test set.
- AUC: The metric measures the ability of a model to rank anomalies higher than normal instances, without assuming a decision threshold.
- F1-score: The geometric mean of Precision and Recall, reflecting the trade-off between the two when converting continuous anomaly scores to binary labels.
- Precision: The proportion of correctly identified anomalies among all anomalies detected.
- Recall: The proportion of true anomalies that have been detected by the model.
To convert the anomaly scores into binary labels, a threshold optimization strategy is adopted. For each test window, the threshold that maximizes the F1-score based on the ground-truth labels is computed, and the corresponding best F1 performance is reported. This approach enables reporting the best F1-score across different thresholding strategies and base classifiers, facilitating consistent comparisons across methods.
4.4. Model Performance Evaluation
ADDAEIL is evaluated against six representative benchmark methods covering a range of anomaly detection approaches, including static, semi-online, adaptive streaming, and deep learning-based methods. The key features of these methods are summarized in Table 1, and the results are presented in Table 2, which forms the basis for the following analysis.

Table 1.
Overview of baseline methods used in Experiment Part I: Model Performance Evaluation.

Table 2.
Performance comparison across benchmark datasets. Bold values indicate the best performance among all compared methods for each metric in each dataset.
- ECOD [16]: A recent static anomaly detector based on empirical copulas. Although not tailored for streaming scenarios, ECOD is widely used as an unsupervised baseline and reflects the performance of non-adaptive methods under evolving conditions.
- LODA [10]: A semi-online ensemble-based method that uses random projections and sparse histograms for lightweight anomaly scoring. While it does not update its model after deployment, it supports automatic bin sizing during training and offers some passive robustness to minor distributional changes.
- MemStream [11]: A streaming anomaly detector that adapts to new data through a memory buffer mechanism. It can handle concept drift at the data level but lacks structural modeling of detector degradation.
- LSTM-VAE [18]: A deep learning-based anomaly detector that employs an LSTM-based variational autoencoder for capturing temporal dependencies in time series data. Although capable of modeling complex sequential patterns, it requires offline training and lacks adaptation to evolving data distributions.
- STAD [22]: An anomaly detection approach that applies KS and AD tests within the latent space of an autoencoder to capture subtle changes in data representation under concept drift. However, it does not monitor the performance of the model or internal structural alignment, and its sensitivity to drift is limited by the feature representation capabilities of the encoder.
- AEADF [15]: An unsupervised ensemble-based anomaly detection framework for streaming time series with concept drift. It employs a hybrid drift detection mechanism combining histogram-based distributional comparison (e.g., Hellinger distance) and output-level evaluation. The framework uses a fixed update strategy anchored to a static initial model, without support for incremental model updates. This limits its adaptability to gradually evolving data streams.
- ADDAEIL (proposed): The proposed framework uses statistically grounded and structure-based drift detection, combined with an adaptive model update strategy. ADDAEIL enables incremental and interpretable adaptation in non-stationary streaming settings.
Table 2 provides the detailed evaluation metrics that support the subsequent dataset-specific analysis.
Yahoo Dataset: The Yahoo A3 dataset is challenging because it involves incremental concept drift. The data distribution changes gradually over time. It also contains some subtle anomalies, which are illustrated in Section 4.2. In this setting, static and semi-online methods like ECOD and LODA show clear weaknesses. ECOD is a non-adaptive static detector. It reaches an AUC of 0.66, but its F1-score of 0.52 and recall of 0.79 show reduced accuracy as the data evolves. LODA uses random projections and automatic binning. This gives it some resistance to small changes, but it cannot update itself. Its performance drops further, with an AUC of 0.54 and an F1-score of 0.18. These results show that static models do not work well when the distribution changes over time. To remain accurate and stable in non-stationary streams, models need to be able to update.
MemStream is built for streaming data and updates based on memory. However, it does not model the drift detection. Its updates are unguided and often replace components ineffectively. This leads to unstable performance and an F1-score of 0.075. Updating based only on recent data is not enough when the model’s internal structure no longer fits the current distribution. ADDAEIL addresses this by combining distribution-based testing with structure-based performance evaluation. It monitors path length distributions of base detectors to identify those most affected by drift. As a result, the model updates efficiently while preserving both accuracy and robustness.
Both deep learning-based methods, LSTM-VAE and STAD, perform poorly on the Yahoo dataset, with F1-scores of 0.53 and 0.52 and precision scores of 0.52 and 0.51, respectively. Although LSTM-VAE leverages the ability of LSTM to capture temporal dependencies and selectively forget irrelevant historical information, combined with VAE’s latent space modeling of data distributions, it lacks mechanisms to adapt to concept drift. Its reliance on a static, offline-trained model limits its adaptability to continuously evolving data streams, making it ill suited for scenarios with incremental drift where the data distribution changes gradually over time.
Similarly, STAD employs a state-transition framework, where upon detecting concept drift, it either reuses an existing autoencoder or retrains a new one. Although this design allows adaptation to abrupt changes, it lacks the ability to perform continuous or incremental updates. During incremental drift, STAD continues to use outdated models until performance drops below a threshold, at which point it retrains a completely new model and discards prior information. This non-incremental updating makes STAD unsuitable for handling gradual, continuous data shifts characteristic of incremental drift.
Both ADDAEIL and AEADF achieve high recall, with scores of 0.98 and 0.95. However, ADDAEIL reaches a higher precision of 0.75 compared to 0.54, leading to better overall performance. The key difference lies in their adaptation strategy. AEADF anchors its update decisions to a static reference model, which prevents timely adaptation to evolving data distributions. ADDAEIL uses performance-based evaluation and incrementally updates its model. This allows it to adapt more effectively as data evolves, maintaining reliability in non-stationary environments.
At the same time, ADDAEIL demonstrates a strong capability to detect subtle anomalies within evolving data streams. On the Yahoo dataset, it achieved a precision of 0.75 and a recall of 0.98, both outperforming all other methods. The high precision demonstrates ADDAEIL’s ability to accurately distinguish true anomalies from normal data fluctuations, effectively reducing false positives. Meanwhile, the high recall highlights its capacity to detect even subtle anomalies, minimizing false negatives and ensuring comprehensive coverage. Together, these results show that ADDAEIL effectively separates subtle anomalies from normal data, maintaining high detection accuracy even under incremental concept drifts.
NAB Dataset: The NAB dataset includes both sudden and incremental drift. This makes it hard for models to react quickly while staying stable. In this setting, ECOD and LODA do not adapt well to the changing distribution. Their F1-scores are low, at 0.59 and 0.38. This shows that adaptive update mechanisms are necessary when facing drifts in data.
MemStream also performs poorly, with an F1-score of only 0.0023. Its update process lacks structural guidance and is easily confused by sudden drift. Although it achieves a competitive AUC, this is misleading. NAB has a strong class imbalance, where anomalies make up only a small part of the data. In such cases, AUC alone often gives an overly optimistic view. F1, recall, and precision better reflect the model’s real detection ability.
ADDAEIL handles this setting much better. It achieves a strong F1-score of 0.61 and a precision of 0.58. This is due to its hybrid drift detection and update strategy, which adjusts based on drift intensity. By combining both distributional and structural detection results, ADDAEIL adapts well to both sudden and gradual drifts. It also avoids overreacting to small or temporary changes in the data.
Among deep learning-based methods, LSTM-VAE and STAD demonstrative some competitive performance on the NAB dataset. LSTM-VAE achieves an F1-score of 0.62 and a recall of 0.97, suggesting its ability to capture anomalies during abrupt drift. This is mainly due to its use of LSTM to model temporal dependencies, combined with the forget gate, which discards irrelevant historical information. STAD achieves an F1-score of 0.57, a precision of 0.54, and a recall of 0.93. Its state-transition mechanism allows it to respond to sudden and severe drift by identifying changes and retraining a new autoencoder. However, this full retraining process discards prior information, limiting its long-term adaptability.
Notably, although LSTM-VAE and STAD report F1-scores (0.62 and 0.57) comparable to ADDAEIL (0.61), their AUC values (0.81 and 0.76) are significantly lower than ADDAEIL’s (0.85). F1 reflects performance at a specific threshold, while AUC captures overall distinction across thresholds. LSTM-VAE relies on a static model that cannot maintain stable decision boundaries when data evolves, which leads to fluctuations in the ROC curve. STAD uses a discrete state switching and retraining mechanism that blurs decision boundaries, resulting in a lower AUC. In contrast, ADDAEIL achieves a higher AUC through continuous local updates and a combined structure–performance evaluation, maintaining robust distinction between normal and anomalous data.
Compared to AEADF, ADDAEIL gives more accurate and focused updates. AEADF compares outputs to a fixed base model, which becomes outdated over time. In contrast, ADDAEIL uses structure-based performance evaluation to identify which detectors are most affected by drift. It replaces only the components that require updating. As a result, it improves precision (0.58 vs. 0.48) while keeping high recall. These results show that ADDAEIL is effective in handling diverse and unpredictable drift in real-world data streams.
CEMACS Dataset: The CEMACS dataset, derived from ocean surface temperature measurements, exhibits relatively mild incremental drift driven primarily by seasonal variations. With a window size of , each window covers approximately two days, during which the short-term temperature changes are limited. As a result, the degree of drift between adjacent windows remains subtle, presenting a relatively stable streaming environment.
Under this setting, the performance differences across methods are less pronounced compared to datasets with stronger drift patterns. Most models achieve reasonably high AUC and F1-scores, indicating that even static or semi-adaptive methods can maintain acceptable performance in slowly evolving conditions. The two deep learning-based algorithms, LSTM-VAE and STAD, also demonstrate competitive capability in this scenario. However, ADDAEIL continues to outperform all the state-of-the-art methods, achieving the highest F1-score of 0.90 and maintaining both high recall and precision. This demonstrates that even in low-drift scenarios, ADDAEIL’s design enables it to preserve long-term accuracy through its effective and incremental adaptation strategy.
Unlike approaches that require full model retraining, ADDAEIL introduces minimal updates guided by statistical signals, allowing it to incorporate new data gradually while retaining useful historical knowledge. This balance between adaptability and stability is particularly important in real-world applications such as environmental monitoring, where drift is continuous but subtle. These results further validate the effectiveness of ADDAEIL’s detection and update mechanism in handling relatively stationary real-world scenarios.
Overall: Further analysis highlights the benefits of ADDAEIL across all three datasets. On both Yahoo A3 and NAB, which exhibit significant concept drift, the results show that ADDAEIL is able to achieve the highest recall while also improving precision and F1-score. This demonstrates that ADDAEIL can accurately track drifting data patterns and selectively update model components, which helps avoid underfitting (i.e., conservative updates when drift is present) as well as overreaction (i.e., aggressive updates when drift is absent). On CEMACS, where the degree of drift is relatively mild and gradual, ADDAEIL still achieves top performance without incurring excessive model changes.
The average results of all baselines over all datasets are reported in the last row in Table 2 and summarized in Figure 4. As expected, ADDAEIL obtains the highest F1-score of 0.76 and outperforms the next best baseline AEADF, which achieves 0.67. ADDAEIL also reaches the highest average precision of 0.75 and the highest AUC of 0.90. These results indicate that ADDAEIL can adapt to various forms of drift while maintaining strong window-level detection accuracy for both non-stationary and relatively stationary data streams. The hybrid drift detection enables ADDAEIL to combine the strengths of distribution-based and structure-based approaches, while its performance evaluation and proportional updating help avoid unnecessary model changes when no drift is present.
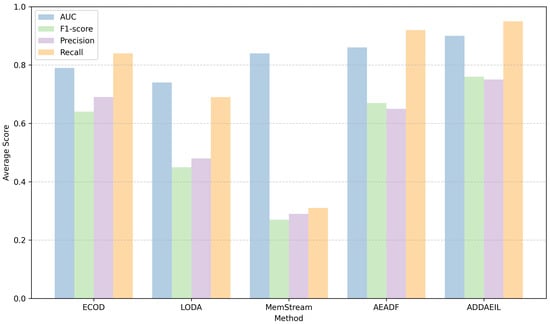
Figure 4.
Average AUC, F1-score, precision, and recall across datasets.
4.5. Ablation Study on Update Strategies
To evaluate the effectiveness of each core component in ADDAEIL, an ablation study was conducted involving three simplified variants: a static iForest model with no update, and two partial update strategies that use either path length-based detector ranking (Performance-only) or statistical test-based replacement ratio estimation (Distribution-only). These are compared against the full ADDAEIL framework. Results are presented in Table 3.

Table 3.
Ablation study on update strategies across benchmark datasets. Bold values indicate the best performance among all compared methods for each metric in each dataset.
As expected, the No Update baseline performs substantially worse than the other three variants across all datasets. Especially in non-stationary environments such as Yahoo and NAB, it achieves very low F1-scores of 0.31 and 0.47. This clearly demonstrates that in the presence of significant concept drift, static models become increasingly misaligned with the evolving data distribution. The lack of any adaptation mechanism leads to the accumulation of stale decision boundaries, particularly under highly non-stationary data streams where concept drift is pronounced. As the structural mismatch grows over time, detection accuracy deteriorates accordingly. In contrast, the other three variants all benefit from different model update strategies, highlighting the critical role of adaptive mechanisms in maintaining long-term model reliability under distributional shift.
Both the Performance-only and Distribution-only variants clearly outperform the static baseline. These results show that incremental updates are crucial in non-stationary settings. Both distribution- and performance-based concept drift detection mechanism can guide effective adaptation. On the Yahoo dataset, which exhibits gradual concept drift, the Performance-only variant achieves a higher F1-score of 0.74 than Distribution-only of 0.71. This suggests that structure-based performance evaluation is particularly effective under incremental drift. In such cases, subtle distributional changes may not trigger statistical tests but can still cause misalignment in the internal structure of base detectors.
Neither the performance-based nor the distribution-based variant achieves the best performance across all datasets or evaluation metrics. In contrast, ADDAEIL combines both types of drift detection. It uses statistical tests to determine update intensity and structure-based performance evaluation to rank which detectors should be replaced. This hybrid design yields consistently better results across all evaluation metrics. ADDAEIL achieves the highest average F1-score of 0.76, precision of 0.75, and AUC of 0.90, while maintaining a top-level recall of 0.95. These results demonstrate that both modules are complementary and essential. Together, they enable ADDAEIL to deliver robust, targeted, and interpretable adaptation under various types of concept drift.
4.6. Sensitivity Analysis on Key Hyperparameters
This subsection evaluates the robustness of ADDAEIL with respect to three key hyperparameters: the sliding window size W, the number of base detectors N, and the update ratio range . In each experiment, one parameter is varied while the others are fixed at their default values: , , and . The results on the Yahoo A3 dataset are summarized in Table 4.

Table 4.
Sensitivity analysis of ADDAEIL on Yahoo A3 dataset. Default setting: , , , and .
The results show that ADDAEIL remains stable across a range of parameter values. When adjusting the window size, the model achieves the highest F1-score (0.80) at , along with a slight increase in recall. In contrast, a larger window size () results in a minor drop in both recall and F1-score. This indicates that larger window sizes may slightly reduce model adaptability and accuracy, as long windows may encompass multiple or complex concept drifts, thereby increasing the difficulty for the model to promptly adapt to distributional changes.
The number of base detectors also shows limited influence on performance. All three configurations (, 100, and 200) yield nearly identical results. This suggests that the ensemble size can be flexibly adjusted to match resource constraints, without significantly compromising accuracy.
Adjusting the update ratio range likewise has only a modest effect. Increasing the maximum update rate to improves precision and F1-score slightly. Meanwhile, a more conservative setting () leads to a slight decrease in precision, from 0.77 to 0.74.
Overall, the results indicate that ADDAEIL is robust to variations in all three parameters. This robustness reduces the need for extensive hyperparameter tuning and supports practical deployment in streaming anomaly detection tasks.
4.7. Edge Computing Suitability
To validate the practical deployment potential of the proposed ADDAEIL framework in edge computing environments, we conducted a comprehensive evaluation of runtime efficiency and resource consumption on the NVIDIA Jetson Orin NX 16 GB platform. This platform is a compact and power-efficient computing module designed specifically for edge computing scenarios, featuring an 8-core Arm Cortex-A78AE v8.2 64-bit CPU (2 MB L2 + 4 MB L3) and 16 GB of 128-bit LPDDR5 memory (102.4 GB/s bandwidth), and operating within a 10 W–25 W power envelope.
The experiment was conducted on the CEMACS dataset, which features the longest time series in our dataset. The experimental results are summarized as follows:
- Training Time: 0.117 s.
- Latency per window (i.e., testing time): 0.15–0.21 s.
- Maximum Memory Usage: 340 MB.
- Model Size: 0.24 MB.
These results demonstrate that the ADDAEIL framework exhibits low resource consumption, with a maximum memory usage of 340 MB and a model size of 0.24 MB. The framework also supports efficient model initialization, achieving a training time of 0.117 s. These characteristics are critical for deployment in resource-constrained edge environments. The system maintains a consistent latency per window of 0.15 to 0.21 s across the long streaming sequence of the CEMACS dataset. This stability confirms that the system delivers consistent, timely anomaly detection outputs at a low computational cost.
For practical applications, the observed latency and resource requirements meet the real-time demands of edge computing scenarios. These scenarios include environmental monitoring, represented by the CEMACS dataset, and IT system monitoring and online analytics, represented by the NAB dataset. The system consistently maintains a response time of 0.15 to 0.21 s per window. This capability ensures that the framework can process real-time data streams effectively without compromising detection performance or requiring high-end computational resources.
5. Conclusions
This paper presents ADDAEIL, an incremental, unsupervised ensemble-based anomaly detection framework. It integrates distribution-based and performance-based drift detection, supported by an incremental updating strategy. ADDAEIL maintains interpretability and avoids full retraining by selectively replacing drift-affected base detectors. Each update decision is based on statistical tests and structure-based performance evaluation.
In contrast to traditional static or semi-adaptive methods, which operate within a fixed model structure, ADDAEIL continuously evolves its ensemble based on data-driven drift evaluation. This hybrid design enhances robustness and efficiency, making it well suited for edge computing environments. Compared to deep learning-based approaches such as LSTM-VAE and STAD, which rely on offline-trained models or threshold-triggered retraining, ADDAEIL provides superior adaptability and stability in evolving data streams. This design ensures precise anomaly detection in both sudden and incremental drift scenarios.
ADDAEIL is evaluated on both synthetic and real-world benchmarks. The experimental results show that, compared with existing baselines, ADDAEIL is superior on all evaluation metrics. For example, ADDAEIL obtains the highest average F1-score (0.76), AUC (0.90), and precision (0.75), while maintaining high recall (0.95). An ablation study is also conducted to validate the effectiveness of combining both drift detection modules.
While the current framework is limited to univariate time series, extending ADDAEIL to multivariate inputs is a promising direction. The base iForest model natively supports multivariate data; however, adapting the drift detection modules poses additional challenges. In particular, current statistical tests (e.g., KS and MWU) are univariate and would need to be replaced or extended with multivariate distributional comparison techniques such as Maximum Mean Discrepancy (MMD), multivariate KL divergence, or copula-based approaches. Moreover, evaluating structural drift in high-dimensional decision trees introduces further complexity in performance-based detection.
Author Contributions
Conceptualization, D.L.; methodology, D.L.; software, D.L.; validation, D.L., N.-K.C.N. and K.I.-K.W.; formal analysis, D.L.; investigation, D.L.; writing—original draft preparation, D.L.; writing—review and editing, D.L., N.-K.C.N. and K.I.-K.W.; supervision, N.-K.C.N. and K.I.-K.W.; project administration, K.I.-K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This project was (partially) supported by Te Hiranga Rū QuakeCoRE, an Aotearoa New Zealand Tertiary Education Commission-funded Centre. This is QuakeCoRE publication number 1068.
Data Availability Statement
The data that support the findings of this study will be publicly available in a suitable repository upon publication.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cook, A.A.; Misirli, G.; Fan, Z. Anomaly Detection for IoT Time-Series Data: A Survey. IEEE Internet Things J. 2020, 7, 6481–6494. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Lu, J.; Liu, A.; Dong, F.; Gu, F.; Gama, J.; Zhang, G. Learning under Concept Drift: A Review. IEEE Trans. Knowl. Data Eng. 2019, 31, 2346–2363. [Google Scholar] [CrossRef]
- Li, J.; Malialis, K.; Panayiotou, C.G.; Polycarpou, M.M. Unsupervised Incremental Learning with Dual Concept Drift Detection for Identifying Anomalous Sequences. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar]
- Chen, Y.; Liu, Z.; Zhang, B.; Fok, W.; Qi, X.; Wu, Y.C. Mgfn: Magnitude-contrastive glance-and-focus network for weakly-supervised video anomaly detection. AAAI Conf. Artif. Intell. 2023, 37, 387–395. [Google Scholar] [CrossRef]
- Elwell, R.; Polikar, R. Incremental learning of concept drift in nonstationary environments. IEEE Trans. Neural Netw. 2011, 22, 1517–1531. [Google Scholar] [CrossRef]
- Chambers, L.; Gaber, M.M.; Ghomeshi, H. Deepstreamensemble: Streaming adaptation to concept drift in deep neural networks. Int. J. Mach. Learn. Cybern. 2025, 16, 3955–3976. [Google Scholar] [CrossRef]
- Museba, T.; Nelwamondo, F.; Ouahada, K.; Akinola, A. Recurrent adaptive classifier ensemble for handling recurring concept drifts. Appl. Comput. Intell. Soft Comput. 2021, 2021, 5533777. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Pevný, T. Loda: Lightweight on-line detector of anomalies. Mach. Learn. 2016, 102, 275–304. [Google Scholar] [CrossRef]
- Bhatia, S.; Jain, A.; Srivastava, S.; Kawaguchi, K.; Hooi, B. Memstream: Memory-based streaming anomaly detection. In Proceedings of the ACM Web Conference 2022, Virtual, 25–29 April 2022; pp. 610–621. [Google Scholar]
- Yang, L.; Manias, D.M.; Shami, A. Pwpae: An ensemble framework for concept drift adaptation in iot data streams. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Bayram, F.; Ahmed, B.S.; Kassler, A. From concept drift to model degradation: An overview on performance-aware drift detectors. Knowl.-Based Syst. 2022, 245, 108632. [Google Scholar] [CrossRef]
- Agrahari, S.; Singh, A.K. Concept drift detection in data stream mining: A literature review. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 9523–9540. [Google Scholar] [CrossRef]
- Li, D.; Nair, N.; Kevin, I.; Wang, K.; Sakurai, K. Ensemble based unsupervised anomaly detection with concept drift adaptation for time series data. In Proceedings of the 2024 IEEE Smart World Congress (SWC), Nadi, Fiji, 2–7 December 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 434–441. [Google Scholar]
- Li, Z.; Zhao, Y.; Hu, X.; Botta, N.; Ionescu, C.; Chen, G. Ecod: Unsupervised outlier detection using empirical cumulative distribution functions. IEEE Trans. Knowl. Data Eng. 2022, 35, 12181–12193. [Google Scholar] [CrossRef]
- Lei, T.; Gong, C.; Chen, G.; Ou, M.; Yang, K.; Li, J. A novel unsupervised framework for time series data anomaly detection via spectrum decomposition. Knowl.-Based Syst. 2023, 280, 111002. [Google Scholar] [CrossRef]
- Lin, S.; Clark, R.; Birke, R.; Schönborn, S.; Trigoni, N.; Roberts, S. Anomaly detection for time series using vae-lstm hybrid model. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4322–4326. [Google Scholar]
- Lai, K.H.; Wang, L.; Chen, H.; Zhou, K.; Wang, F.; Yang, H.; Hu, X. Context-aware domain adaptation for time series anomaly detection. In Proceedings of the 2023 SIAM International Conference on Data Mining (SDM), Paul Twin Cities, MN, USA, 27–29 April 2023; pp. 676–684. [Google Scholar]
- Gama, J.; Medas, P.; Castillo, G.; Rodrigues, P. Learning with drift detection. In Proceedings of the Advances in Artificial Intelligence–SBIA 2004: 17th Brazilian Symposium on Artificial Intelligence, Sao Luis, Brazil, 29 September–1 October 2004; Springer: Berlin/Heidelberg, Germany, 2004. Proceedings 17. pp. 286–295. [Google Scholar]
- Bifet, A.; Gavalda, R. Learning from time-changing data with adaptive windowing. In Proceedings of the 2007 SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007; pp. 443–448. [Google Scholar]
- Li, B.; Gupta, S.; Müller, E. State-transition-aware anomaly detection under concept drifts. Data Knowl. Eng. 2024, 154, 102365. [Google Scholar] [CrossRef]
- Gama, J.; Žliobaitė, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A survey on concept drift adaptation. ACM Comput. Surv. (CSUR) 2014, 46, 1–37. [Google Scholar] [CrossRef]
- Berger, V.W.; Zhou, Y. Kolmogorov–smirnov test: Overview. In Wiley Statsref: Statistics Reference Online; Wiley: Cambridge, MA, USA, 2014. [Google Scholar]
- Joyce, J.M. Kullback-Leibler Divergence. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin, Germany, 2011; pp. 720–722. [Google Scholar] [CrossRef]
- MacFarland, T.W.; Yates, J.M. Mann–Whitney U Test. In Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer: Cham, Switzerland, 2016; pp. 103–132. [Google Scholar] [CrossRef]
- Goldenberg, I.; Webb, G.I. Survey of distance measures for quantifying concept drift and shift in numeric data. Knowl. Inf. Syst. 2019, 60, 591–615. [Google Scholar] [CrossRef]
- Cerqueira, V.; Gomes, H.M.; Bifet, A.; Torgo, L. STUDD: A student–teacher method for unsupervised concept drift detection. Mach. Learn. 2023, 112, 4351–4378. [Google Scholar] [CrossRef]
- Kolter, J.Z.; Maloof, M.A. Dynamic weighted majority: An ensemble method for drifting concepts. J. Mach. Learn. Res. 2007, 8, 2755–2790. [Google Scholar]
- Korycki, L.; Krawczyk, B. Unsupervised drift detector ensembles for data stream mining. In Proceedings of the 2019 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Washington, DC, USA, 5–8 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 317–325. [Google Scholar]
- Laptev, N.; Amizadeh, S. Yahoo Anomaly Detection Dataset S5. 2015. Available online: https://www.researchgate.net/publication/336315311_Unsupervised_Drift_Detector_Ensembles_for_Data_Stream_Mining (accessed on 6 May 2025).
- Lavin, A.; Ahmad, S. Evaluating real-time anomaly detection algorithms–the Numenta anomaly benchmark. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 38–44. [Google Scholar]
- Jamshidi, E.J.; Yusup, Y.; Kayode, J.S.; Kamaruddin, M.A. Detecting outliers in a univariate time series dataset using unsupervised combined statistical methods: A case study on surface water temperature. Ecol. Inform. 2022, 69, 101672. [Google Scholar] [CrossRef]
- Ahmad, S.; Lavin, A.; Purdy, S.; Agha, Z. Unsupervised real-time anomaly detection for streaming data. Neurocomputing 2017, 262, 134–147. [Google Scholar] [CrossRef]
- Gu, M.; Fei, J.; Sun, S. Online anomaly detection with sparse Gaussian processes. Neurocomputing 2020, 403, 383–399. [Google Scholar] [CrossRef]
- Vázquez, F.I.; Hartl, A.; Zseby, T.; Zimek, A. Anomaly detection in streaming data: A comparison and evaluation study. Expert Syst. Appl. 2023, 233, 120994. [Google Scholar] [CrossRef]
- Ding, C.; Zhao, J.; Sun, S. Concept drift adaptation for time series anomaly detection via transformer. Neural Process. Lett. 2023, 55, 2081–2101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).