Neural Network Based Approach to Recognition of Meteor Tracks in the Mini-EUSO Telescope Data
Abstract
:1. Introduction
2. Mini-EUSO Experiment
3. Meteor and Background Signals
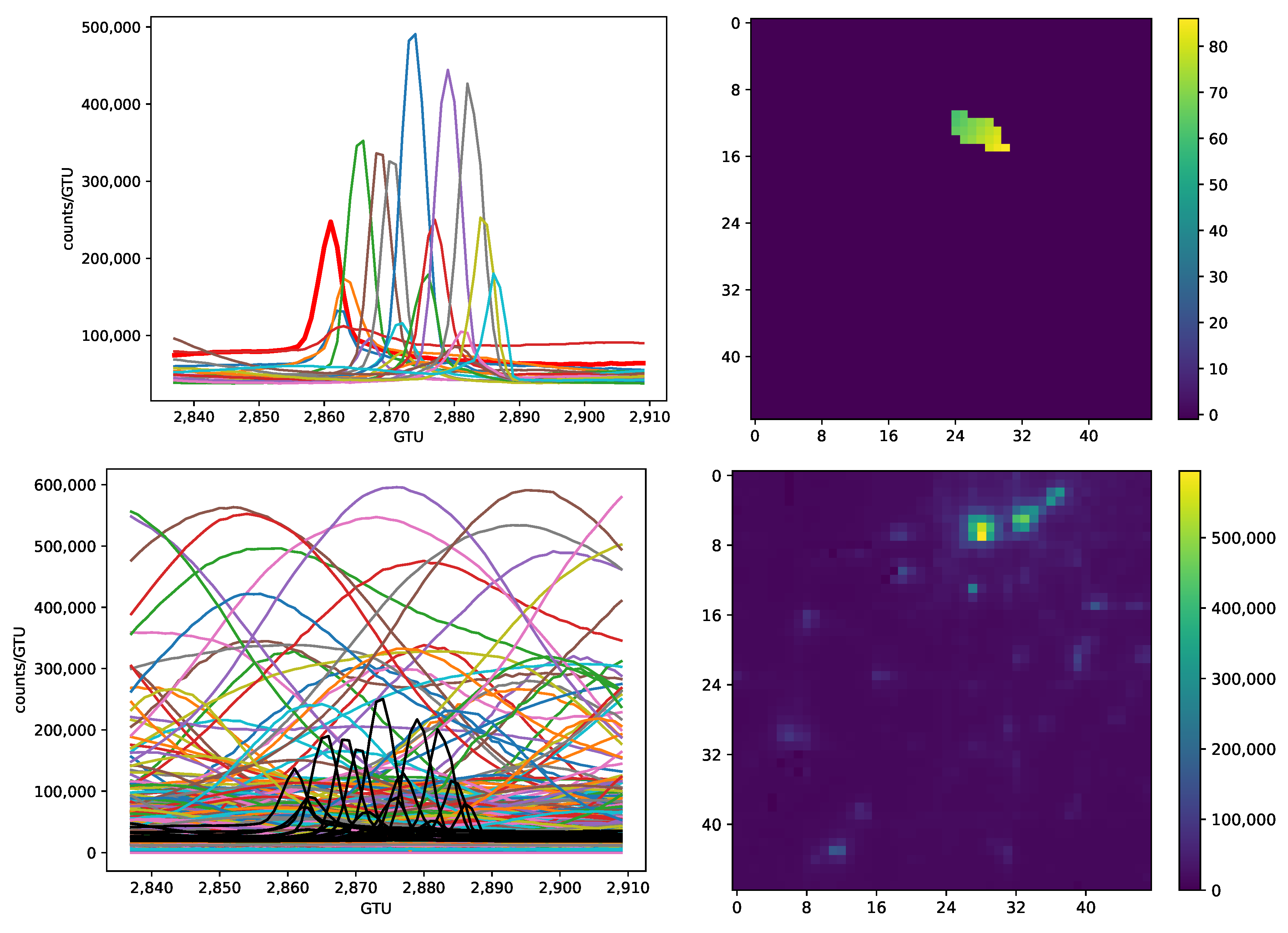
- A signal produced by a meteor in a pixel has a shape resembling the bell-like curve similar to the probability density function of the normal distribution.
- Meteor signals produce quasi-linear tracks in the focal surface.
- The number of hit (“active”) pixels in more than 75% of meteor tracks is ≤5, so that their footprints on the focal surface are small.
- Peaks of a meteor signal shift from one pixel to another (except for arrival directions close to nadir).
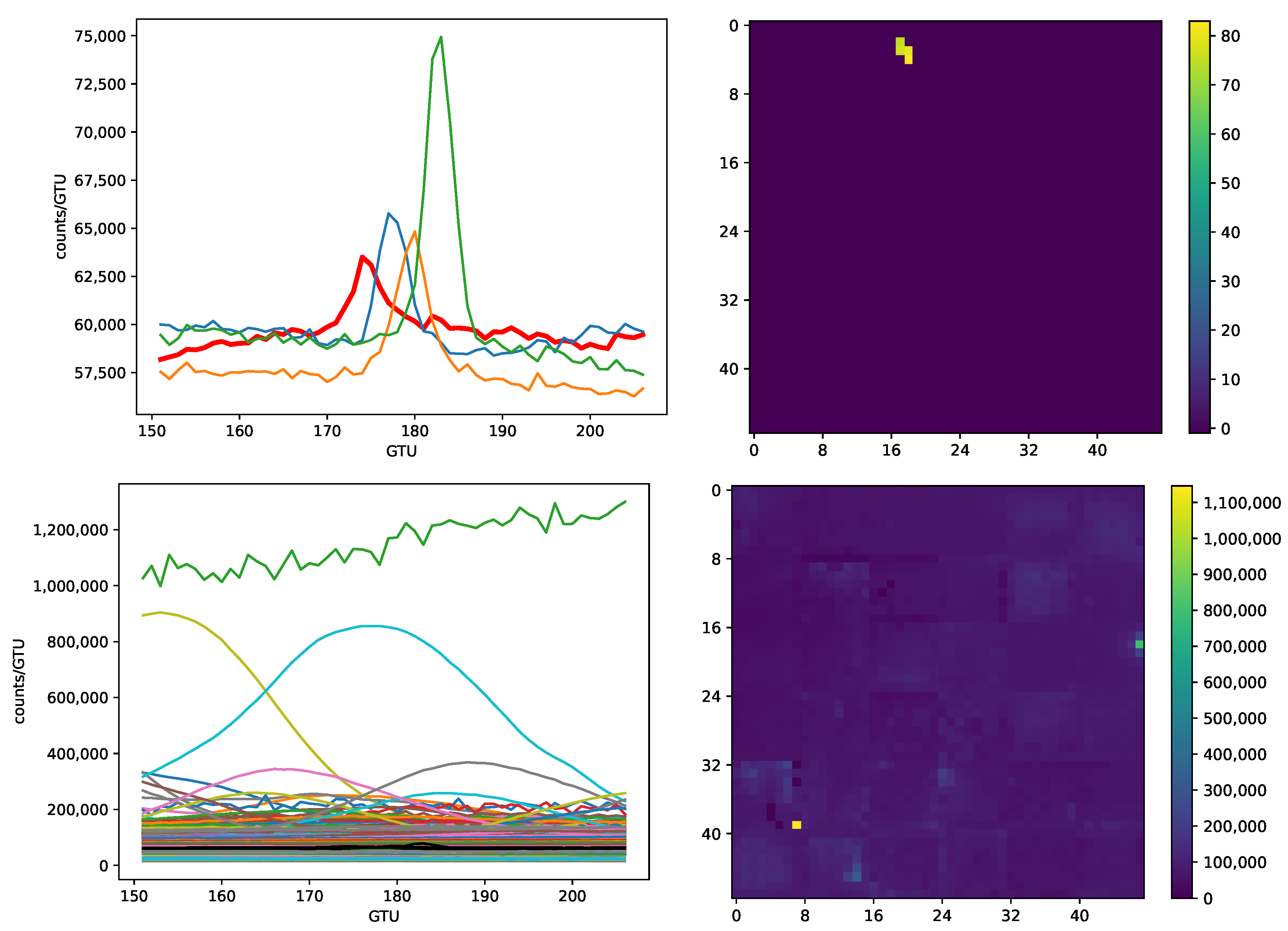
- There are multiple signals in the data with the shape similar to that of meteors but simultaneously illuminating large areas of the FS.
- Meteors are often registered on strong and quickly varying background illumination.
- The amplitude of a meteor signal is typically lower than amplitudes of some other signals in the FoV of Mini-EUSO registered simultaneously with the meteor.
- In some cases, it is impossible to judge unequivocally if a signal originated from a meteor or another source.
4. Results
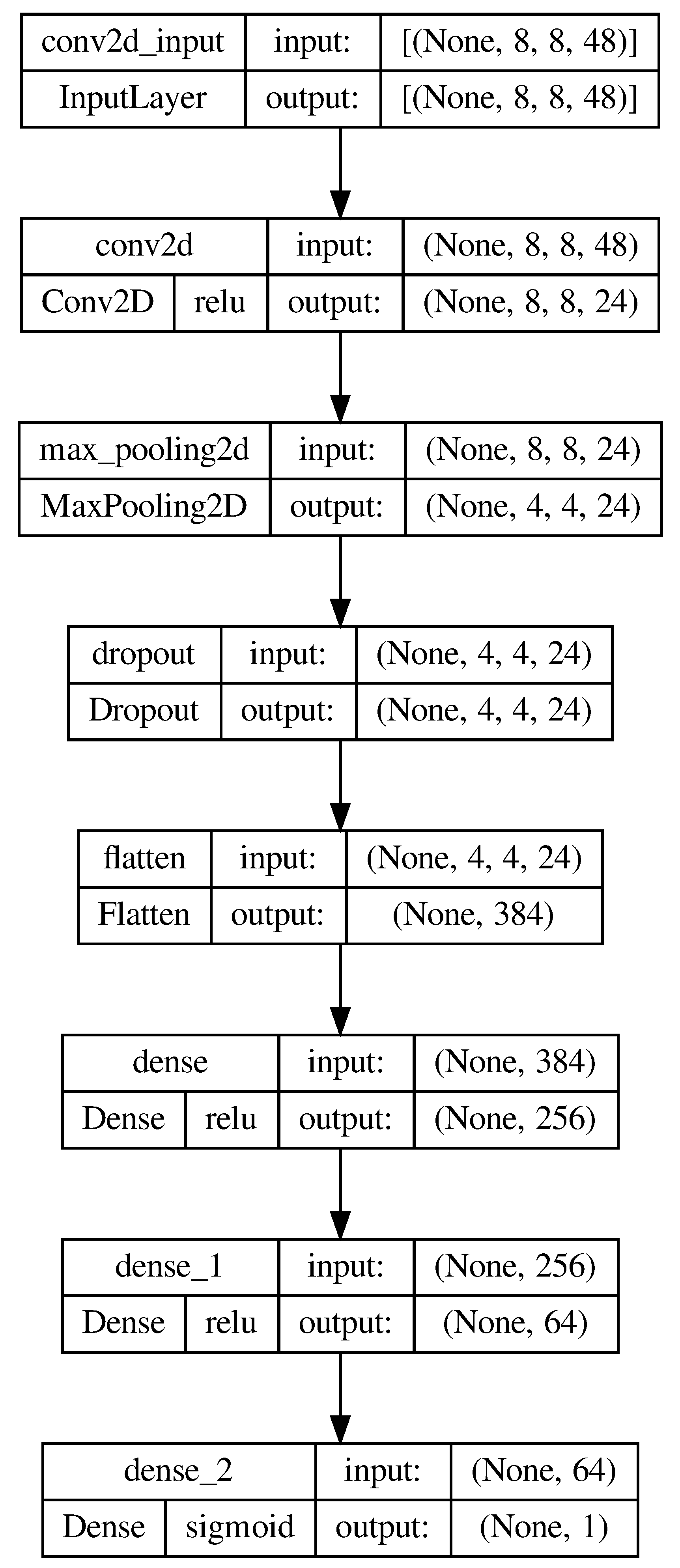
4.1. Recognition of Meteor Data Samples
4.2. Active Pixel Selection
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| AUC | Area under the curve |
| CNN | Convolutional neural network |
| EC | Elementary cell |
| FoV | Field of view |
| FS | Focal surface |
| ISS | International space station |
| MAPMT | Multi-anode photomultiplier |
| MCC | Matthews correlation coefficient |
| MLP | Multi-layer perceptron |
| PR | Precision-recall |
| PSF | Point spread function |
| ROC | Receiver operating characteristic |
| UHECR | Ultra-high energy cosmic ray |
| UV | ultraviolet |
References
- Adams, J.H., Jr.; Ahmad, S.; Albert, J.N.; Allard, D.; Anchordoqui, L.; Andreev, V.; Anzalone, A.; Arai, Y.; Asano, K.; Ave Pernas, M.; et al. The JEM-EUSO instrument. Exp. Astron. 2015, 40, 19–44. [Google Scholar] [CrossRef]
- Adams, J.H., Jr.; Ahmad, S.; Albert, J.N.; Allard, D.; Anchordoqui, L.; Andreev, V.; Anzalone, A.; Arai, Y.; Asano, K.; Ave Pernas, M.; et al. The JEM-EUSO mission: An introduction. Exp. Astron. 2015, 40, 3–17. [Google Scholar] [CrossRef]
- Bertaina, M.E. An overview of the JEM-EUSO program and results. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 15–22 July 2021; Volume 395, p. 406. [Google Scholar] [CrossRef]
- Benson, R.; Linsley, J. Satellite observation of cosmic ray air showers. In Proceedings of the 17th International Cosmic Ray Conference, Paris, France, 13–25 July 1981; Volume 8, pp. 145–148. [Google Scholar]
- Adams, J.H., Jr.; Ahmad, S.; Albert, J.N.; Allard, D.; Anchordoqui, L.; Andreev, V.; Anzalone, A.; Arai, Y.; Asano, K.; Ave Pernas, M.; et al. Science of atmospheric phenomena with JEM-EUSO. Exp. Astron. 2015, 40, 239–251. [Google Scholar] [CrossRef]
- Klimov, P.A.; Panasyuk, M.I.; Khrenov, B.A.; Garipov, G.K.; Kalmykov, N.N.; Petrov, V.L.; Sharakin, S.A.; Shirokov, A.V.; Yashin, I.V.; Zotov, M.Y.; et al. The TUS Detector of Extreme Energy Cosmic Rays on Board the Lomonosov Satellite. Space Sci. Rev. 2017, 212, 1687–1703. [Google Scholar] [CrossRef]
- Khrenov, B.A.; Klimov, P.A.; Panasyuk, M.I.; Sharakin, S.A.; Tkachev, L.G.; Zotov, M.Y.; Biktemerova, S.V.; Botvinko, A.A.; Chirskaya, N.P.; Eremeev, V.E.; et al. First results from the TUS orbital detector in the extensive air shower mode. J. Cosmol. Astropart. Phys. 2017, 9, 6. [Google Scholar] [CrossRef]
- Adams, J.H., Jr.; Ahmad, S.; Albert, J.N.; Allard, D.; Anchordoqui, L.; Andreev, V.; Anzalone, A.; Arai, Y.; Asano, K.; Ave Pernas, M.; et al. JEM-EUSO: Meteor and nuclearite observations. Exp. Astron. 2015, 40, 253–279. [Google Scholar] [CrossRef]
- Abdellaoui, G.; Abe, S.; Acheli, A.; Adams, J.; Ahmad, S.; Ahriche, A.; Albert, J.N.; Allard, D.; Alonso, G.; Anchordoqui, L.; et al. Meteor studies in the framework of the JEM-EUSO program. Planet. Space Sci. 2017, 143, 245–255. [Google Scholar] [CrossRef]
- Adams, J.H.; Ahmad, S.; Allard, D.; Anzalone, A.; Bacholle, S.; Barrillon, P.; Bayer, J.; Bertaina, M.; Bisconti, F.; Blaksley, C.; et al. A Review of the EUSO-Balloon Pathfinder for the JEM-EUSO Program. Space Sci. Rev. 2022, 218, 3. [Google Scholar] [CrossRef]
- Abdellaoui, G.; Abe, S.; Adams, J.; Ahriche, A.; Allard, D.; Allen, L.; Alonso, G.; Anchordoqui, L.; Anzalone, A.; Arai, Y.; et al. EUSO-TA—First results from a ground-based EUSO telescope. Astropart. Phys. 2018, 102, 98–111. [Google Scholar] [CrossRef]
- Bacholle, S.; Barrillon, P.; Battisti, M.; Belov, A.; Bertaina, M.; Bisconti, F.; Blaksley, C.; Blin-Bondil, S.; Cafagna, F.; Cambiè, G.; et al. Mini-EUSO Mission to Study Earth UV Emissions on board the ISS. Astrophys. J. Suppl. Ser. 2021, 253, 36. [Google Scholar] [CrossRef]
- Casolino, M.; Adams, J., Jr.; Anzalone, A.; Arnone, E.; Arnone, D.; Barghini, S.; Bartocci, M.; Battisti, R.; Bellotti, M.; Bertaina, F.; et al. The Mini-EUSO telescope on board the International Space Station: Launch and first results. In Proceedings of the 37th International Cosmic Ray Conference—PoS(ICRC2021), Berlin, Germany, 15–22 July 2021; Volume 395, p. 354. [Google Scholar] [CrossRef]
- Marcelli, L.; Barghini, D.; Battisti, M.; Blaksley, C.; Blin, S.; Belov, A.; Bertaina, M.; Bianciotto, M.; Bisconti, F.; Bolmgren, K.; et al. Integration, qualification, and launch of the Mini-EUSO telescope on board the ISS. Rend. Lincei. Sci. Fis. Nat. 2023, 34, 23–35. [Google Scholar] [CrossRef]
- Casolino, M.; Barghini, D.; Battisti, M.; Blaksley, C.; Belov, A.; Bertaina, M.; Bianciotto, M.; Bisconti, F.; Blin, S.; Bolmgren, K.; et al. Observation of night-time emissions of the Earth in the near UV range from the International Space Station with the Mini-EUSO detector. Remote Sens. Environ. 2023, 284, 113336. [Google Scholar] [CrossRef]
- Scotti, V.; Osteria, G.; JEM-EUSO Collaboration. The EUSO-SPB2 mission. Nucl. Instrum. Methods Phys. Res. A 2020, 958, 162164. [Google Scholar] [CrossRef]
- Cummings, A.; Eser, J.; Filippatos, G.; Olinto, A.V.; Venters, T.M.; Wiencke, L. EUSO-SPB2: A sub-orbital cosmic ray and neutrino multi-messenger pathfinder observatory. arXiv 2022, arXiv:2208.07466. [Google Scholar]
- Eser, J.; Olinto, A.V.; Wiencke, L. Overview and First Results of EUSO-SPB2. In Proceedings of the 38th International Cosmic Ray Conference—PoS(ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 397. [Google Scholar] [CrossRef]
- Klimov, P.; Battisti, M.; Belov, A.; Bertaina, M.; Bianciotto, M.; Blin-Bondil, S.; Casolino, M.; Ebisuzaki, T.; Fenu, F.; Fuglesang, C.; et al. Status of the K-EUSO Orbital Detector of Ultra-High Energy Cosmic Rays. Universe 2022, 8, 88. [Google Scholar] [CrossRef]
- POEMMA Collaboration; Olinto, A.V.; Krizmanic, J.; Adams, J.H.; Aloisio, R.; Anchordoqui, L.A.; Anzalone, A.; Bagheri, M.; Barghini, D.; Battisti, M.; et al. The POEMMA (Probe of Extreme Multi-Messenger Astrophysics) observatory. J. Cosmol. Astropart. Phys. 2021, 2021, 7. [Google Scholar] [CrossRef]
- Barghini, D.; Battisti, M.; Belov, A.; Edoardo Bertaina, M.; Bisconti, F.; Capel, F.; Casolino, M.; Ebisuzaki, T.; Gardiol, D.; Klimov, P.; et al. Meteor detection from space with Mini-EUSO telescope. In Proceedings of the European Planetary Science Congress, EPSC2020–800, Online, 21 September–9 October 2020. [Google Scholar] [CrossRef]
- Barghini, D.; Battisti, M.; Belov, A.; Bertaina, M.E.; Bertone, S.; Bisconti, F.; Capel, F.; Casolino, M.; Cellino, A.; Ebisuzaki, T.; et al. Analysis of meteors observed in the UV by the Mini-EUSO telescope onboard the International Space Station. In Proceedings of the European Planetary Science Congress, EPSC2021–243, Online, 13–24 September 2021. [Google Scholar] [CrossRef]
- Zotov, M.; Sokolinskii, D. A Neural Network Approach for Selecting Track-like Events in Fluorescence Telescope Data. Bull. Rus. Acad. Sci. Phys. 2023, 87, 1054–1057. [Google Scholar] [CrossRef]
- Vrábel, M.; Genci, J.; Bobik, P.; Bisconti, F. Machine Learning Approach for Air Shower Recognition in EUSO-SPB Data. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 24 July–1 August 2019; Volume 36, p. 456. [Google Scholar] [CrossRef]
- Szakács, P.; Vrábel, M.; Genči, J. Classification of EUSO-SPB data using convolutional neural networks (CNNs). In Electrical Engineering and Informatics X, Proceedings of the Faculty of Electrical Engineering and Informatics of the Technical University of Košice; Technical University of Košice: Staré Mesto, Slovakia, 2019; pp. 262–267. [Google Scholar]
- Filippatos, G.; Battisti, M.; Bertaina, M.E.; Bisconti, F.; Eser, J.; Osteria, G.; Sarazin, F.; Wiencke, L.; JEM-EUSO Collaboration. Expected Performance of the EUSO-SPB2 Fluorescence Telescope. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 15–22 July 2022; p. 405. [Google Scholar] [CrossRef]
- Montanaro, A.; Ebisuzaki, T.; Bertaina, M. Stack-CNN algorithm: A new approach for the detection of space objects. J. Space Saf. Eng. 2022, 9, 72–82. [Google Scholar] [CrossRef]
- Ruiz-Hernandez, O.I.; Sharakin, S.; Klimov, P.; Martínez-Bravo, O.M. Meteors observations by the orbital telescope TUS. Planet. Space Sci. 2022, 218, 105507. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Ferri, C.; Hernández-Orallo, J.; Modroiu, R. An experimental comparison of performance measures for classification. Pattern Recognit. Lett. 2009, 30, 27–38. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q. On the performance of Matthews correlation coefficient (MCC) for imbalanced dataset. Pattern Recognit. Lett. 2020, 136, 71–80. [Google Scholar] [CrossRef]
- Zotov, M. Application of Neural Networks to Classification of Data of the TUS Orbital Telescope. Universe 2021, 7, 221. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 30 April 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
| Test Session | 5 | 6 | 7 | 8 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|
| Training meteor chunks | 91,060 | 72,124 | 95,924 | 81,188 | 80,724 | 88,456 | 89,228 | 86,820 |
| Testing meteor chunks | 1712 | 6446 | 474 | 4180 | 4274 | 2341 | 2148 | 2772 |
| Testing meteors | 65 | 280 | 18 | 186 | 193 | 106 | 90 | 130 |
| Test Session | 5 | 6 | 7 | 8 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|
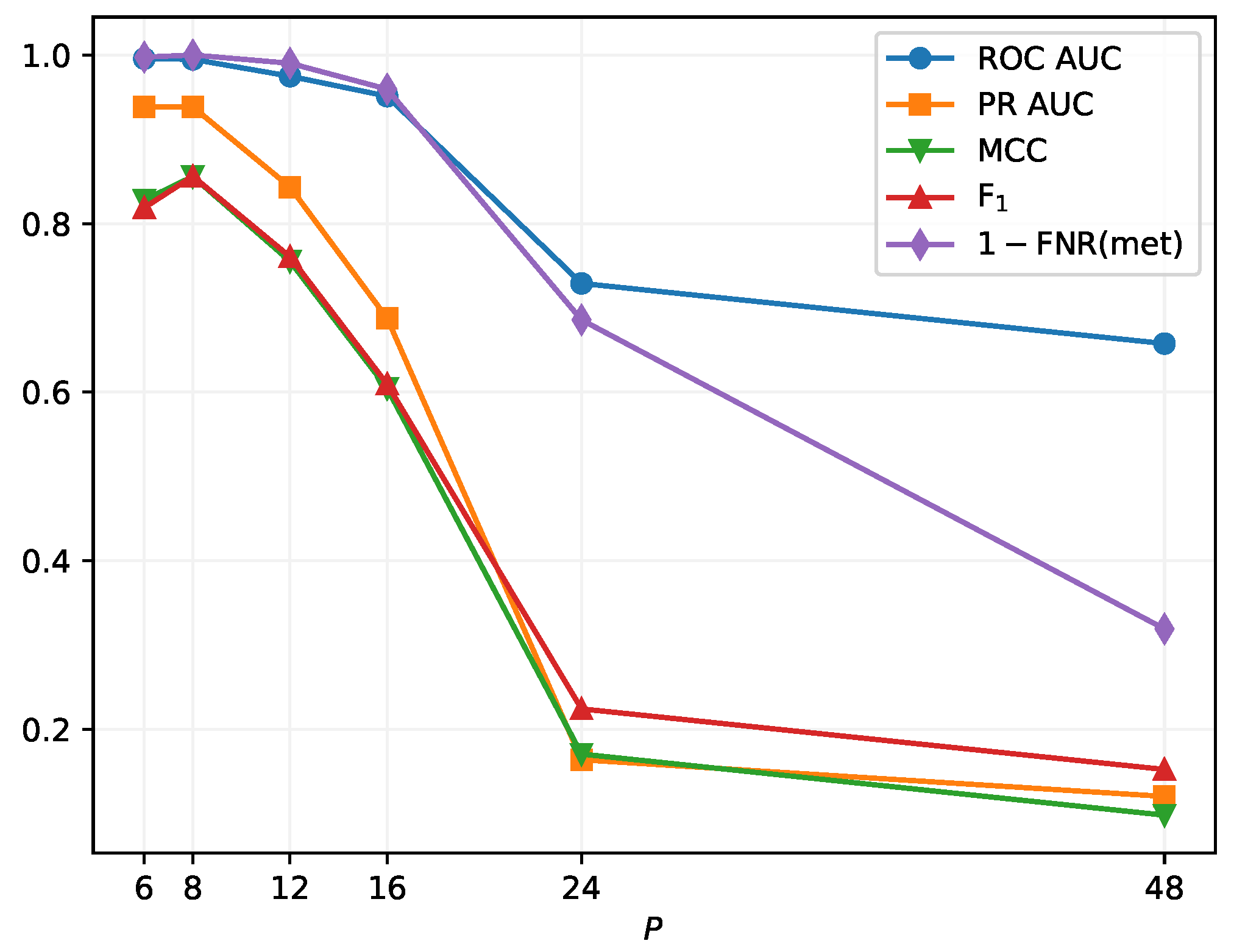
| ROC AUC | 0.992 | 0.994 | 0.999 | 0.993 | 0.994 | 0.998 | 0.993 | 0.996 |
| PR AUC | 0.937 | 0.955 | 0.876 | 0.933 | 0.946 | 0.973 | 0.931 | 0.956 |
| MCC | 0.872 | 0.894 | 0.732 | 0.857 | 0.888 | 0.921 | 0.782 | 0.901 |
| F1 | 0.873 | 0.901 | 0.718 | 0.863 | 0.892 | 0.922 | 0.776 | 0.904 |
| FNR (met) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Test Session | 5 | 6 | 7 | 8 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|
| ROC AUC | 0.992 | 0.995 | 0.993 | 0.994 | 0.996 | 0.993 | 0.995 | 0.995 |
| PR AUC | 0.899 | 0.932 | 0.877 | 0.916 | 0.932 | 0.887 | 0.936 | 0.928 |
| MCC | 0.790 | 0.841 | 0.744 | 0.826 | 0.847 | 0.812 | 0.809 | 0.835 |
| F1 | 0.794 | 0.845 | 0.737 | 0.832 | 0.852 | 0.814 | 0.810 | 0.840 |
| Mean IoU | 0.808 | 0.853 | 0.773 | 0.843 | 0.861 | 0.829 | 0.825 | 0.850 |
| FNR (pxl) | 2/422 | 2/1428 | 0/80 | 7/928 | 5/958 | 0/492 | 0/457 | 2/630 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zotov, M.; Anzhiganov, D.; Kryazhenkov, A.; Barghini, D.; Battisti, M.; Belov, A.; Bertaina, M.; Bianciotto, M.; Bisconti, F.; Blaksley, C.; et al. Neural Network Based Approach to Recognition of Meteor Tracks in the Mini-EUSO Telescope Data. Algorithms 2023, 16, 448. https://doi.org/10.3390/a16090448
Zotov M, Anzhiganov D, Kryazhenkov A, Barghini D, Battisti M, Belov A, Bertaina M, Bianciotto M, Bisconti F, Blaksley C, et al. Neural Network Based Approach to Recognition of Meteor Tracks in the Mini-EUSO Telescope Data. Algorithms. 2023; 16(9):448. https://doi.org/10.3390/a16090448
Chicago/Turabian StyleZotov, Mikhail, Dmitry Anzhiganov, Aleksandr Kryazhenkov, Dario Barghini, Matteo Battisti, Alexander Belov, Mario Bertaina, Marta Bianciotto, Francesca Bisconti, Carl Blaksley, and et al. 2023. "Neural Network Based Approach to Recognition of Meteor Tracks in the Mini-EUSO Telescope Data" Algorithms 16, no. 9: 448. https://doi.org/10.3390/a16090448
APA StyleZotov, M., Anzhiganov, D., Kryazhenkov, A., Barghini, D., Battisti, M., Belov, A., Bertaina, M., Bianciotto, M., Bisconti, F., Blaksley, C., Blin, S., Cambiè, G., Capel, F., Casolino, M., Ebisuzaki, T., Eser, J., Fenu, F., Franceschi, M. A., Golzio, A., ... Wiencke, L. (2023). Neural Network Based Approach to Recognition of Meteor Tracks in the Mini-EUSO Telescope Data. Algorithms, 16(9), 448. https://doi.org/10.3390/a16090448











