Abstract
This paper establishes a novel fractional-order version of a recently expanded form of the Susceptible-Exposed-Infectious-Recovery (SEIR) Mpox model. This model is investigated by means of demonstrating some significant findings connected with the stability analysis and the vaccination impact, as well. In particular, we analyze the fractional-order Mpox model in terms of its invariant region, boundedness of solution, equilibria, basic reproductive number, and its elasticity. In accordance with an effective vaccine, we study the progression and dynamics of the Mpox disease in compliance with various scenarios of the vaccination ratio through the proposed fractional-order Mpox model. Accordingly, several numerical findings of the proposed model are depicted with the use of two numerical methods; the Fractional Euler Method (FEM) and Modified Fractional Euler Method (MFEM). Such findings demonstrate the influence of the fractional-order values coupled with the vaccination rate on the dynamics of the established disease model.
1. Introduction
Mathematical modeling has turned into an invaluable tool in revealing the behaviors of infectious diseases and formulating effective control strategies. Mpox, a viral disease with similarities to smallpox, has attracted considerable attention in the field of epidemiological models due to its potential impact on human health. As the Mpox disease is a viral zoonotic infection, it might transmit from animals to people. In addition, it might transmit from the environment to a person, as it can transmit from one person to another [1]. In 2022, the Mpox disease began to spread like a pandemic in numerous countries all over the world. It is spreading now in some African countries [2,3].
To gain deeper insights into the transmission dynamics and develop accurate predictive models for Mpox, many researchers have increasingly explored the utilization of fractional calculus. Fractional calculus offers a promising tool for highlighting the intricate characteristics of infectious disease dynamics, as it allows for the incorporation of memory-dependent and non-local effects. Traditional models often suppose an instantaneous mixing by assuming that past interactions have no influence on future outcomes. So, from this point, the notion of fractional calculus might be utilized as an alternative to these models, as it can enable one to formulate a model of long-range dependence with extra freedom of fractional-order values. This would enable a more realistic representation of the spread and evolution of the disease; see [4].
In the context of Mpox, fractional calculus can potentially enhance our understanding of various epidemiological factors such as transmission rates, recovery rates, and the impact of interventions. By incorporating fractional derivatives and integrals into the modeling framework, researchers can address the non-local nature of interactions and the presence of memory effects in disease transmission. These effects can reflect the persistence of immunity, delayed responses to interventions, or even other temporal dependencies; see [5]. Developing a fractional calculus-based model for Mpox involves considering fractional differential equations that can describe the growth of the diseased population over time. The fractional-order derivatives correspond to the memory or long-range dependence, which might be observed in the transmission of disease. Accurate estimation of the fractional-order value requires a combination of empirical evidence, fitting the model to available data, and a deep understanding of the underlying epidemiological processes [6]. The utilization of fractional calculus in modeling Mpox has the potential to yield valuable insights into the disease’s dynamics and control strategies. Incorporating memory effects and non-local interactions in modeling the disease can provide a more accurate representation of its spread and evolution over time. Furthermore, such modeling can assist public health officials in evaluating and optimizing intervention strategies, estimating the impact of vaccination programs, and assessing the effectiveness of different control measures [7].
In this study, we aim to explore the application of fractional calculus in modeling Mpox transmission dynamics. By introducing fractional-order derivatives and considering memory-dependent effects, we attempt to enhance our understanding of the disease’s behavior and provide valuable tools for policymakers and health care professionals in their efforts to mitigate and control Mpox outbreaks. For this purpose, a novel fractional-order version of the SEIR model is established in light of operating the Caputo operator. This model is analyzed with the help of proposing certain novel stability results, including the investigation of its invariant region, equilibria, Basic Reproductive Number (BRN), elasticity, and boundedness of solution, which is observed by using the Adomian decomposition method. Additionally, we also solved this model numerically using the Fractional Euler Method (FEM) and Modified Fractional Euler Method (MFEM) [8] for the aim of revealing the influence of the fractional-order values and the vaccination rate on the dynamics of the model at hand. In summary, this paper is arranged in the following manner. In the next part, some key definitions and basic concepts associated with fractional calculus are recalled briefly, whereas the formulation of the Mpox illness model is proposed in Section 3. In Section 4, we study the stability analysis of the Mpox model. In Section 5, we solve the proposed fractional-order Mpox model using the FEM and MFEM, followed by the conclusion of this work.
2. Preliminary Concepts
In this part, we recall fundamental descriptions and theorems related to fractional calculus, including the Riemann–Liouville integral and derivative, the Caputo derivative, and other relevant concepts [9].
Definition 1.
The Riemann–Liouville integral operator of the function of fractional-order can be expressed by
In the following content, we list below some properties of the Riemann–Liouville integral operator:
Definition 2.
The Caputo fractional derivative operator of the function of fractional-order can be expressed by
Herein, we also list in what follows, some further properties of the Caputo derivative operator:
- For a constant c, we have .
- For , we have
- For constants a and b, is a linear operator, i.e.,
In the same regard, it is important to remember the following basic property:
where such that .
Definition 3.
The Caputo operator might be outlined in terms of the Riemann–Liouville integral operator along the following lines:
where and .
Definition 4
([9]). The two parameters of the Mittag-Leffler function can be expressed as
where and .
Theorem 1
([9]). Assume , for and . Then, the function might be expanded about in the following manner:
, where .
3. Mpox Model
Mathematical models are extensively engaged in simulating the dynamics and the transmission of infectious diseases. In accordance with an effective vaccine, we study the progression and dynamics of the Mpox disease in compliance with various scenarios of the vaccination rate through a compartmental model of the type SEIR. In this paper, we consider the intervention of vaccination playing a significant role as a parameter, impacting on the model’s dynamics. The equilibrium of the disease-free state will be determined, and then its stability with computing the BRN will be examined in Section 4.
The diagram of the compartment model, including the vaccination rate for the aimed Mpox model, is shown in Figure 1, in which the total of the susceptible population is denoted by S, the total of the exposed population is denoted by E, the total of the infected population is denoted by I, and, finally, the total of the recovery population by R.
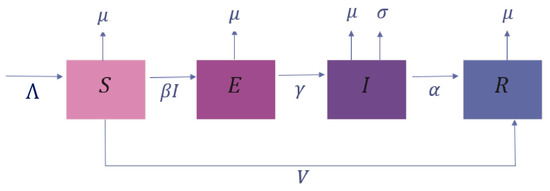
Figure 1.
The compartment model, including vaccination rate.
In the same context, Figure 1 exhibits the parameters () that are responsible for the dynamics of the considered model. These parameters are outlined in Table 1.

Table 1.
Model parameters.
It is noteworthy that the rate of transmission indicates the transmission’s contact from S to E as a result of interacting with I cases. Additionally, indicates the period of incubation, whereas indicates the period of recovery. In light of the aforementioned considerations, the conventional Mpox model might be described in the following manner [10]:
with initial conditions
For more clarification, model (10) is established in accordance with particular conditions, which might be stated as follows:
- The contact transmission parameter does not take into account some factors, like climate, age, marital status, or gender.
- All of the model’s parameters have no negative values.
- Inter-individual relations within society are distinguished by uniformity and homogeneity. This is because of the inherited suppositions for all of the model’s states in which all persons have the same parameter value of the contact transmission regardless of their situations, such as their health circumstances or age.
- The size of population N is considered constant at any time, and it meets the following equality:
- In the proposed model, the demography is taken into account, in which the natural death and natural birth are incorporated.
- System (10) satisfies the following property:where h is a function depending only on N [11]. To see this, one can observeNow, due to , we obtainWith the use of separation of variables, we can haveorBy using , we obtain
4. Stability Analysis
Herein, we aim to examine the primary properties of model (19) in view of various aspects including the invariant region, boundedness of solution, equilibrium point, BRN, and its elasticity.
4.1. The Invariant Region
This subsection intends to study the non-negativity of the solution of model (19). For instance, the solution of model (19) will be validated in accordance with the positive values of the initial conditions. For this purpose, we suppose for all non-negative values of t that the domain of the desired solution has the following form:
where . One could observe that all model parameters have non-negative values (i.e., ). Now, in order to show the non-negativity of the solution of model (19), we recall the following two results, which would pave the way to achieve our first target.
Lemma 1
([12,13]). (Generalized Mean Value Theorem). Suppose that and , where , then we have:
where , .
Remark 1
([12,13]). Suppose that and , where . In view of the above Lemma, one can conclude that, if , , then will be a non-decreasing vector-valued function, while if , , then such a function will be a non-increasing one.
Theorem 2.
There exists a unique solution of system (19), subject to the initial condition , and this solution will remain in .
Proof.
Tracking the necessary results deduced by the author in [13] leads us to identify, for definite, a unique solution on for system (19), subject to the initial condition . On the other hand, in order to show that the domain is indeed the positively invariant region, we have to observe the following assertions:
This validates that the solution of system (19) is non-negative over the domain given in (20). □
4.2. Boundedness of Solution
It was reported in [14] that the boundedness of the solution is regarded as a very important trait of this type of population model, with infectious diseases. In the epidemic population models, the solutions must be bounded, as unbounded solutions are physically meaningless. In what follows, we propose to show that the solution given at any specific time for system (19) is bounded by , as assumed previously in (20). For this purpose, we should note that
where N is given in (12). Accordingly, we can have
Under the assumed conditions in the domain reported in (20), one could observe that , which yields the following inequality:
In order to solve the above inequality analytically with the initial conditions
we use the so-called Adomian decomposition method (or simply ADM), as it is very suitable in this case. To see this, we first operate on both sides of the inequality (23) to obtain
or
Now, in view of the ADM, the general solution of inequality (25) might be supposed as =. This would immediately yield
which consequently implies
Thus, based on (26), we can obtain, for instance, as follows:
In the same way, we can obtain
If we continue in this manner, we obtain
Now, due to the solution having the form , then, with the help of using the Mittag-Leffler function, we can gain
Consequently, with the use of our assumptions in (20), we can deduce
Therefore, the solution of system (19) is bounded by the term as , and hence this system is well-posed over its domain .
4.3. The Disease-Free Equilibrium (DFE)
The DFE is the case in which society is clear of the Mpox illness. Such a point is , where is the initial susceptible state, is the initial exposed state, is the initial infected state, and is the initial recovered state. Thus, finding a solution for model (19), while considering and , leads us to the following DFE:
where and .
4.4. The BRN
The BRN is regarded a very significant index used to indicate the harshness of the infectious illness. It can be employed to describe the occurrence of the pandemic and the potential of outbreak. This index is regarded as an epidemiological measure to determine the hazard of the infectious transmission. With the aim of computing the BRN, we use the next-generation matrix method (NGMM), which was suggested in [15] and afterward developed in [16]. Such a method has been broadly employed for evaluating the BRN in a number of epidemiological models. Additionally, for the purpose of finding the BRN, we employ the NGMM by taking into account the exposed and infected classes. Afterward, we break down , in which and . This, consequently, gives
Now, by computing the Jacobian matrices of Q and G at declared in (29), we obtain
Thus, we can evaluate by finding the spectral radius of the (NGMM) . In other words, we have
4.5. Local Sensitivity and Elasticity Analysis of
In the field of epidemiological models, the parameters’ values have a vital role in computing . Under the assumption that all parameters are retained at specific values (estimated) including the parameter , we call this measure “local sensitivity” [17]. In such a measure, the formula used to evaluate the effect of changing one parameter on is written as
However, although this method does not consider a simultaneous changing of all parameters, it is influenced highly by the values of and . Hence, a better indicator will be the elasticity which is defined by the change in the quantity of , as a percentage, due to the value change of the parameter , as a percentage. The formula of elasticity is written as
where a positive elasticity indicates an increment in in terms of the parameter , while a negative elasticity indicates a decrement in , in terms of the parameter .
From Equation (32) of and using the elasticity Equation (34), we investigate the elasticity for all parameters of the model. From this point of view, we can calculate the local elasticity of in relation to the vaccination rate () as
Since the value of indicates the vaccination rate, then the increment of this rate leads to the decrement of and, thus, negatively affects the spreading of the disease. To see this, we plot Figure 2 based on the data reported in Table 2. This figure clearly shows the influence of the vaccination rate v on and, hence, confirms our aforesaid claim.
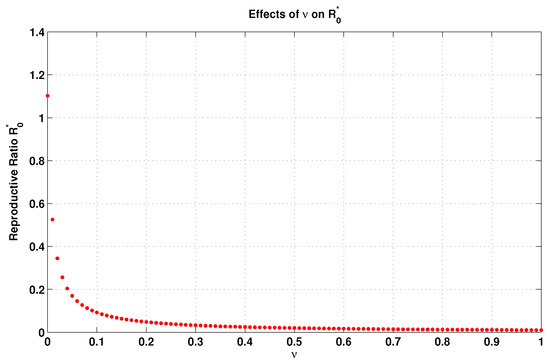
Figure 2.
Influence of the vaccination rate v on .

Table 2.
The parameters of the fractional-order Mpox model.
On the other hand, the local elasticity of , in relation to the contact transmission rate (), can be computed as
Thus, the increment of the transmission rate by leads to a rise in . This is the case of spreading infectious diseases due to the increment in personal contact and communications between individuals and due to the pathogen specifications. However, we plot Figure 3 on the basis of the same values reported in Table 2, but here we take and allow to be varied from 0.045 to 0.18. Such a figure also shows the influence of the transmission rate on , which completely coincides with our algebraic calculations mentioned previously.
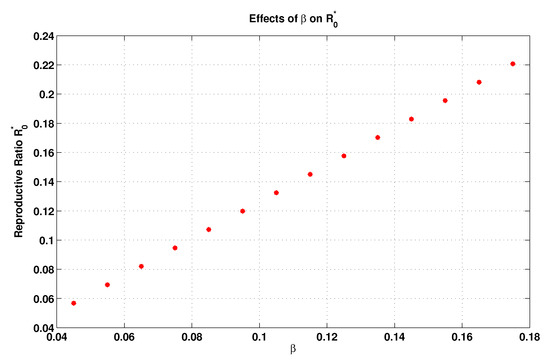
Figure 3.
Influence of the transmission rate on .
In the same manner, the local elasticity of , in relation to the transmission rate () from the I state to the R state, can be computed as
The inversevalue of , which is , is the recovery period. So, the increment in (decrement in recovery period) leads to a decrement in . This reflects the movement rate rise from the I state to the R state, and, consequently, the individuals become immunized. This would negatively affect the spreading of disease. Now, by taking and , and by keeping the remaining parameters as they are in Table 2, except for changing within the interval , we plot Figure 4, which shows the influence of the transmission rate on as well. This also confirms our assertion discussed previously.
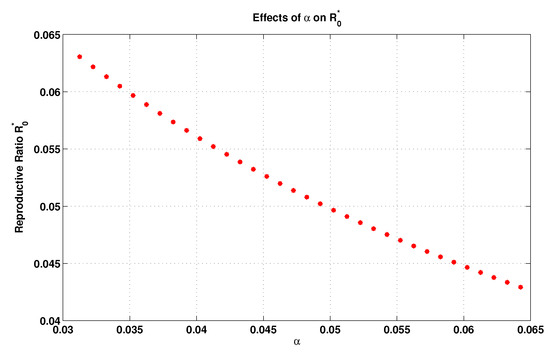
Figure 4.
Influence of the transmission rate on .
It should be mentioned here, that based on the data reported in Table 2, we can easily compute the BRN as , and due to this value being less than 1, then one can deduce that the Mpox illness will not promptly spread.
5. Numerical Findings
In the following content, we intend to employ two numerical methods (the FEM and MFEM) to obtain approximate solutions of the fractional-order Mpox system (19). In fact, these methods represent two fractional versions of the conventional Euler method. One can refer to [8] for the purpose of obtaining a comprehensive view about such methods. In this context, Theorem 1 can lay the foundation to recall the FEM and MFEM, which are considered for the following fractional problem:
To address problem (38), we assume as the interval over which we wish to obtain the desired numerical solution. In general, we are not capable to find , which represents the analytical solution to the problem at hand. As an alternative, we can establish a set of points , and then employ them in finding the approximate solution [8,18]. For simplification purposes, we divide into k sub-intervals with through , for . Now, we assume that , , and are continuous on . Therefore, by means of Theorem 1, one might expand about as
for some . Thus, if we substitute instead of t in (39), we obtain
for some . Now, if one chooses too small, then the last term of (40) can be eliminated to obtain
Actually, Equation (41) represents the primary formula of the FEM. In the same regard, if one substitutes
instead of (41), the result of will be consequently yielded. In other words, we obtain
for . Equation (42) represents the main formula of the MFEM that would be compared next with the FEM’s formula. In what follows, we attempt to implement only the MFEM on the fractional-order Mpox system (19), as the FEM is similar to the MFEM. To do so, we reconsider such a system again as
where
More precisely, with the aim of generating in relation to the compartment S, one should suppose that , , and are all continuous on . From this perspective, if we assume that
so that
then, with the use of (42), one might obtain
for .
In a similar manner, the aforesaid approach might be applied for the remaining classes to obtain their approximate solutions. In the long run, we can infer the following approximations of model (19):
where are already outlined in (44), .
In the following content, we propose to depict certain numerical findings that demonstrate the dynamics of the fractional-order Mpox system (19). In this connection, we consider Table 3, which takes very close data to certain available data captured out of the Indian community, on the basis of reference [19,20].

Table 3.
Parameters of system (19) [19].
On the basis of the previous discussion, we compare, in Figure 5, Figure 6, Figure 7 and Figure 8, between several MFEMs’ solutions for the I and E of system (19), in accordance with several fractional-order values of . The primary goal of these simulations is to notice the impact of the vaccination rate on the exposed and infected states.
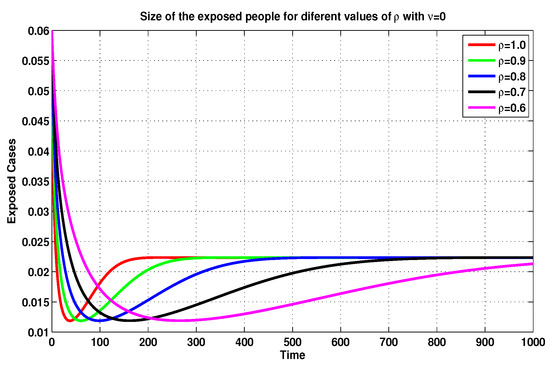
Figure 5.
Exposed sizes of system (19) for through MFEM with .
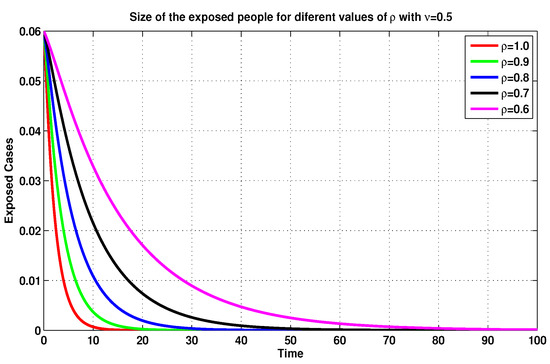
Figure 6.
Exposed sizes of system (19) for through MFEM with .
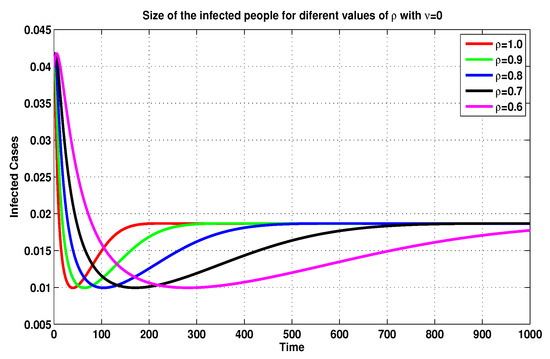
Figure 7.
Infected sizes of system (19) for through MFEM with .
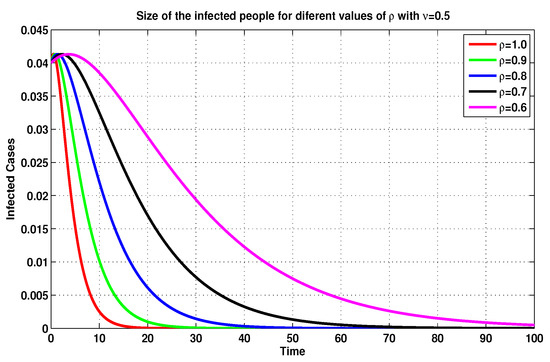
Figure 8.
Infected sizes of system (19) for through MFEM with .
For further description and in accordance with , we simulate, once again, the infected and exposed sizes of system (19), as shown in Figure 9 and Figure 10, by using the MFEM with and without consideration of the vaccination rate . Accordingly, one might obviously notice that, if the vaccination rate is raised, then the amounts of the exposed and infected states are reduced, validating the impact of such a rate on the model at hand.
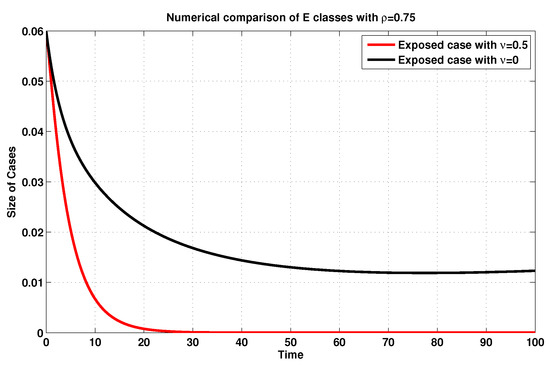
Figure 9.
Exposed sizes of system (19) for with and without considering .
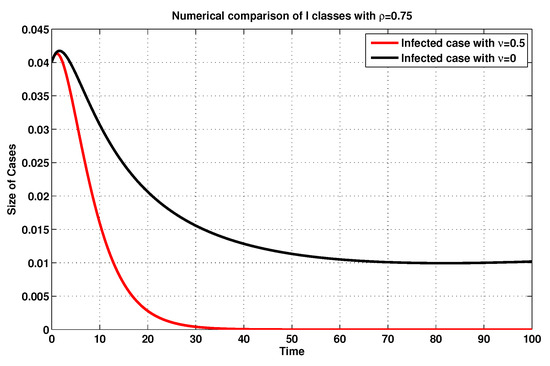
Figure 10.
Infected sizes of system (19) for with and without considering .
For the same connection, it was demonstrated in [8] that the MFEM is a modified numerical scheme for the FEM. Thus, with the aim of validating the numerical results generated by using the MFEM, we make some comparisons between its numerical results and the FEM’s numerical results (see Figure 11, Figure 12, Figure 13 and Figure 14).
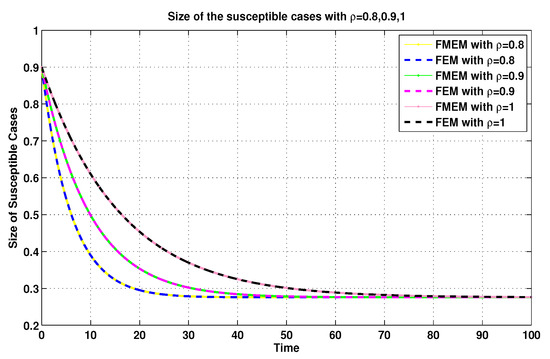
Figure 11.
Susceptible sizes of system (19) for using FEM and MFEM.
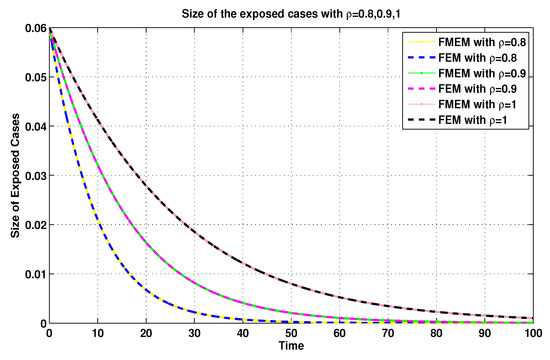
Figure 12.
Exposed sizes of system (19) for using FEM and MFEM.
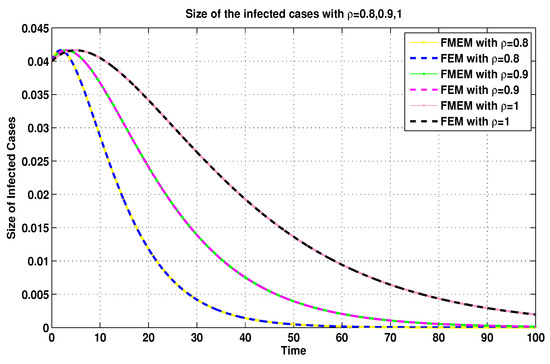
Figure 13.
Infected sizes of system (19) for using FEM and MFEM.
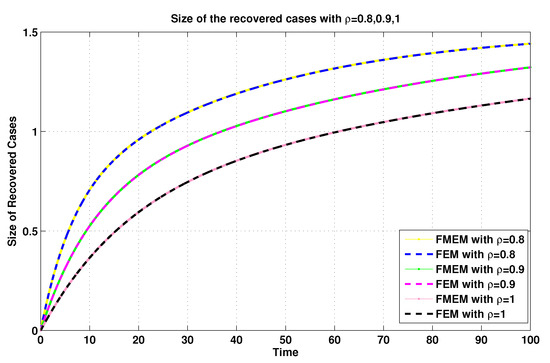
Figure 14.
Recovered sizes of system (19) for using FEM and MFEM.
In the same regard, for the purpose of showing the validity of the domain reported in Section 4.1 and the validity of the boundedness of solution of system (19) discussed in Section 4.2, one can easily check, based on the data reported in Table 3, that the sum of all classes satisfies the inequality declared in (20). In other words, one can check
This bound is further confirmed numerically by plotting the sum of according to different fractional-order values, as shown in Figure 15.
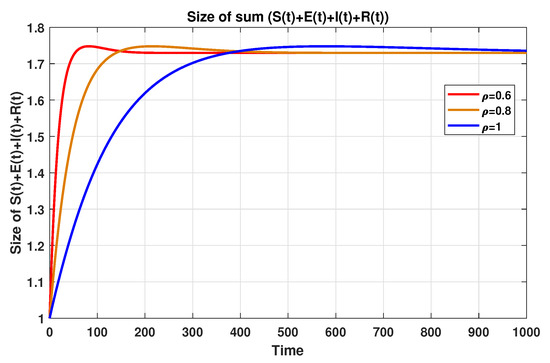
Figure 15.
The sizes of for using MFEM.
6. Conclusions
In this study, a novel fractional-order version of Mpox disease has been established in light of the Caputo operator. Accordingly, several innovative findings connecting to the stability analysis have been addressed. In the same connection, the proposed Mpox model has been numerically solved with the use of the FEM and MFEM. As a consequence of concentrating on the numerical findings, we can obviously notice that the behavior of the proposed fractional-order Mpox model is affected by performing any variation in the value of the fractional-order. This enables us to gain more extra degrees of freedom for the established model. In addition, we observe that the behavior of the MFEM’s solutions is completely coincided with the FEM’s ones, confirming the validity of the computational methods used in this work. Based on these solutions, it can be clearly concluded that, if the rate of vaccination is raised, then the exposed and infectious sizes are reduced gradually, confirming the influence of this rate. More precisely, if the vaccination aspect is regarded, then the infectious and exposed cases will vanish in the long run. This will consequently cause Mpox illness to be under control eventually.
Author Contributions
Conceptualization, I.M.B. and I.H.J.; methodology, A.A.A. and M.A.; software, S.B.A.-S.; validation, K.M.; formal analysis, I.M.B.; investigation, A.A.A. and M.A.; resources, S.B.A.-S.; data curation, I.H.J.; writing—original draft preparation, K.M.; writing—review and editing, I.M.B.; visualization, A.A.A. and M.A.; supervision, I.H.J.; project administration, S.B.A.-S.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to Arab Open University for funding this research through AOU research fund No. AOURG-2023-008.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Arab Open University and Al-Zaytoonah University for providing the necessary scientific research supplies to implement the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Suvvari, T.K.; Ghosh, A.; Lopinti, A.; Islam, M.A.; Bhattacharya, P. Hematological manifestations of Monkeypox virus (MPOX) and impact of human MPOX disease on blood donation—What we need to know? New Microbes New Infect. 2023, 52, 101108. [Google Scholar] [CrossRef] [PubMed]
- Adetifa, I.; Muyembe, J.-J.; Bausch, D.G.; Heymann, D.L. Mpox neglect and the smallpox niche: A problem for Africa, a problem for the world. Lancet 2023, 401, 1822–1824. [Google Scholar] [CrossRef]
- Sam-Agudu, N.A.; Martyn-Dickens, C.; Ewa, A.U. A global update of mpox (monkeypox) in children. Curr. Opin. Pediatr. 2023, 35, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Alotaibi, N.D. A fractional-order SIRD model with time-dependent memory indexes for encompassing the multi-fractional characteristics of the COVID-19. Chaos Solitons Fractals 2021, 143, 110632. [Google Scholar] [CrossRef] [PubMed]
- Stuart, C.I.J.M.; Takahashi, Y.; Umezawa, H. On the stability and non-local properties of memory. J. Theor. Biol. 1978, 71, 605–618. [Google Scholar] [CrossRef]
- Peter, O.J.; Oguntolu, F.A.; Ojo, M.M.; Oyeniyi, A.O.; Jan, R.; Khan, I. Fractional order mathematical model of monkeypox transmission dynamics. Phys. Scr. 2022, 97, 084005. [Google Scholar] [CrossRef]
- Rexma Sherine, V.; Chellamani, P.; Ismail, R.; Avinash, N.; Xavier, G.B.A. Estimating the Spread of Generalized Compartmental Model of Monkeypox Virus Using a Fuzzy Fractional Laplace Transform Method. Symmetry 2022, 14, 2545. [Google Scholar] [CrossRef]
- Batiha, I.M.; Bataihah, A.; Al-Nana, A.A.; Alshorm, S.; Jebril, I.H.; Zraiqat, A. A numerical scheme for dealing with fractional initial value problem. Int. J. Innov. Comput. Inf. Control 2023, 19, 763–774. [Google Scholar] [CrossRef]
- Kilbas, A.A. Theory and Application of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Almuzini, M.; Batiha, I.M.; Momani, S. A study of fractional-order monkeypox mathematical model with its stability analysis. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications (ICFDA), Ajman, United Arab Emirates, 14–16 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Garba, S.M.; Gumel, A.B.; Lubuma, J.M.-S. Dynamically-consistent non-standard finite difference method for an epidemic model. Math. Comput. Model. 2011, 53, 131–150. [Google Scholar] [CrossRef]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Chaos Solitons Fractals 2020, 138, 109826. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, Z.; Ahmed, N.; Baleanu, D.; Adel, W.; Rafiq, M.; Aziz-ur Rehman, M.; Alshomrani, A.S. Positivity and boundedness preserving numerical algorithm for the solution of fractional nonlinear epidemic model of HIV/AIDS transmission. Chaos Solitons Fractals 2020, 134, 109706. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Morio, J. Global and local sensitivity analysis methods for a physical system. Eur. J. Phys. 2011, 32, 1577. [Google Scholar] [CrossRef]
- Zraiqat, A.; Paikrayb, S.K.; Duttac, H. A Certain Class of Deferred Weighted Statistical B-Summability Involving (p,q)-Integers and Analogous Approximation Theorems. Filomat 2019, 33, 1425–1444. [Google Scholar]
- Statisticstimes.com. Countries by GDP Growth. 2020. Available online: https://statisticstimes.com (accessed on 15 March 2023).
- van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
