A Pattern Recognition Analysis of Vessel Trajectories

Abstract

The automatic identification system (AIS) facilitates the monitoring of ship movements and provides essential input parameters for traffic safety. Previous studies have employed AIS data to detect behavioral anomalies and classify vessel types using supervised and unsupervised algorithms, including deep learning techniques. The approach proposed in this work focuses on the recognition of vessel types through the “Take One Class at a Time” (TOCAT) classification strategy. This approach pivots on a collection of adaptive models rather than a single intricate algorithm. Using radar data, these models are trained by taking into account aspects such as identifiers, position, velocity, and heading. However, it purposefully excludes positional data to counteract the inconsistencies stemming from route variations and irregular sampling frequencies. Using the given data, we achieved a mean accuracy of 83% on a 6-class classification task.

1. Introduction

The automatic identification system (AIS) serves as a vital monitoring apparatus for maritime vessel surveillance. It supplies essential input parameters that feed into naval traffic simulation models. These models are instrumental in conducting maritime risk analysis and devising strategies for incident prevention. The AIS enables the monitoring of maritime movements via the electronic exchange of navigational data between various entities. This system interlinks vessels, onboard transmitters, ground stations, and satellites, fostering a comprehensive network for efficient tracking. These data include information that is relevant to traffic safety. Although the exchange of AIS data is legally mandatory only for larger vessels, the usage is on the rise, enabling the deduction of various levels of contextual information, from the characterization of ports and offshore platforms to the spatial and temporal distribution of routes.

Numerous studies have harnessed AIS data to examine anomalies in ship behaviors, intending to pinpoint potential navigational threats. Unsupervised anomaly detection algorithms have been employed, using Ornstein–Uhlenbeck stochastic processes based on the analysis of historical routes [1], or identifying outliers derived from the clustering of behaviors and trajectories [2]. Other studies have concurrently used infrared images to discriminate noise, irrelevant objects, and suspicious vessels [3]. Recently, deep learning techniques have been applied, with models aimed at classifying suspicious trajectories using convolutional neural networks (CNNs) and generative-discriminative learning algorithms [4].

Within the specific context of vessel classification aimed at tracking fishing activities, and more broadly, in the pursuit of augmenting maritime situational awareness (MSA), supervised multiclass methodologies have been implemented. These methodologies employed several algorithms, frequently including random forest models [5,6,7] and light gradient-boosting machine (Light GBM) [8], to distinguish between different types of vessels. In the latter case, a classification model was effectively implemented using 60-dimensional feature vectors as input, although its application was confined to just three distinct categories of vessels. These feature vectors encapsulated various metrics derived from AIS trajectory data, such as the mean, first quartile, median, third quartile, standard deviation, and coefficient of dispersion associated with changes in speed, course, longitude, latitude, and displacement.

From the studies examined so far, it emerges that current approaches mainly rely on the creation of a single, albeit complex, neural network to which the entire task of recognition is delegated. From an innovative perspective, this paper proposes an alternative strategy rooted in the idea of building an ecosystem of neural networks, diverse in both topological and mathematical terms, and not based exclusively on gradient descent or decision trees. In this regard, each network is purposefully designed to focus on a particular statistical subset of ship trajectories, resulting in an enhancement in performance.

More specifically, this study has focused on the need to provide the Italian Navy with an accurate and efficient solution for monitoring and classifying ship trajectories, employing AIS signals in the context of the Mediterranean Sea. A significant problem arises when ships refuse to respond to AIS signals or provide potentially misleading responses, making it difficult for the Navy to correctly identify the type of ship and its intention. In this context, a solution was needed that allowed the Navy to filter and prioritize its interventions, enabling it to focus resources on cases that presented higher levels of risk or suspicion. This involved the development of a system capable of distinguishing, for example, between a fishing boat and a cruise ship based solely on trajectories, thereby improving the efficiency and effectiveness of the Navy’s monitoring and response operations.

The approach presented here aims to recognize the type of vessel among N possible classes using adaptive algorithms specifically trained for this purpose. The data considered for the feature vector include the identifier, position, instantaneous velocity, and heading of each vessel. The adaptive algorithms have been trained using data acquired from radars on multiple vessels (after excluding the identifiers). Positional data are not included as vessels may follow new routes that are not present in the database, making the algorithm less reliable. Additionally, changes in vessel positions have been eliminated due to variations in sampling frequency, which could result in unreliable acceleration and deceleration data.

2. Materials and Methods

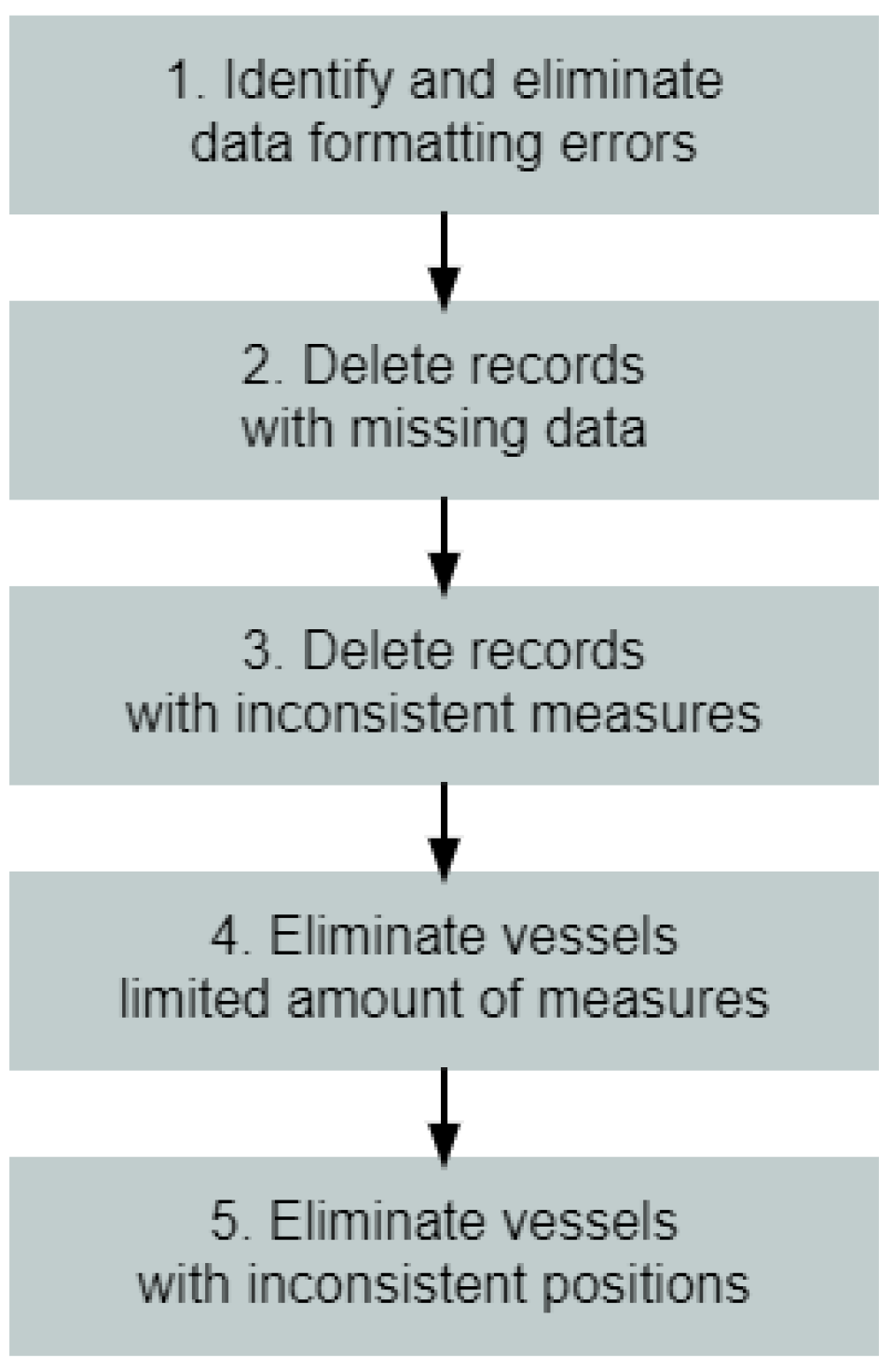
The experiments that were conducted during the search are summarized in three steps: (A) data preparation; (B) experimentation; (C) results analysis. The first step, data preparation, is structured in additional three phases: (A.I) data cleaning; (A.II) data pre-processing; (A.III) model definition;

2.1. A.I—Data Cleaning

To ensure a reliable dataset for the experiments, the following data-cleaning procedure was implemented (Figure 1):

Following this process, the analysis sample comprises 3669 vessels, each with a minimum of 100 consecutive radar detection points. Furthermore, in accordance with the Navy’s approval, six distinct vessel classes have been identified (N = 6), serving as the targets for intelligent recognition by the adaptive models (

Table 1. Number of vessels belonging to each of the six classes, before and after data cleaning. The maximum, minimum, and average readings of each class and the standard deviation from the averages are also shown.

Data	PAX-TMP	TM	TMC	TMO	TU	TUG	TOT
No. Vessels	871	1074	576	2857	849	303	6522
No. Vessels (no. pts ≥ 100)	502	634	323	1717	304	194	3669
Min Route Distance	103	101	101	101	100	100	100
Max Route Distance	4774	5315	3550	4813	3610	4985	4985
No. Routes-avg	1240.08	1143.85	873.88	950.60	570.01	1280.52	~
No. Routes-std dev	956.32	971.77	602.44	650.53	495.49	937.40	~

). Note that it was not possible to measure the acceleration of naval vessels as their positions were detected at non-uniform time intervals.

2.2. A.II—Data Pre-Processing

The strategic objective of this experiment is to represent each vessel through the statistical profile of its route. In the dataset provided by the Navy, there are only two variables that characterize the route of a vessel: the velocity and direction of the bow at the time of radar detection. This is regardless of the stretch of sea crossed.

For example, by dividing the variable “velocity” into regular intervals (bins), you can measure how often the velocity of each vessel falls within each of them, during its journey. With an appropriate transformation, one can define the general probability with which a vessel can be found in each of these intervals. By establishing a defined number of intervals (bins) for each variable that characterizes the vessel’s navigation, the statistical profile of each vessel’s route can be established through the use of the probability density function.

Utilizing these intervals, we decided to characterize the only two variables available in the database for each vessel: Punctual velocity and direction at every radar detection point along the route. However, it is important to note that these measurements are taken in an unsystematic manner, rather than following a strict sampling plan.

A new variable is introduced to the statistical profile of the route of each vessel: delta velocity.

Table 2. A total of 67 variables that will be used to rewrite the database of 3669 vessels.

ID	Variable Name	Code	Calculation	No. Intervals
1	Punctual velocity	$v\left(t\right)$	Available	22
2	Delta direction bow	$r(t,t-1)$	$\left|r\right(t)-r(t-1\left)\right|$	19
3	Delta velocity	$dv(t,t-1)$	$v\left(t\right)-v(t-1)$	23
4	Global average velocity			1 value
5	Global velocity variance			1 value
6	Global velocity variance with			1 value
Total variables				67

illustrates the variables that define the statistical profile of the route of each vessel, according to the pre-processing strategy adopted in experimentation no. 3.

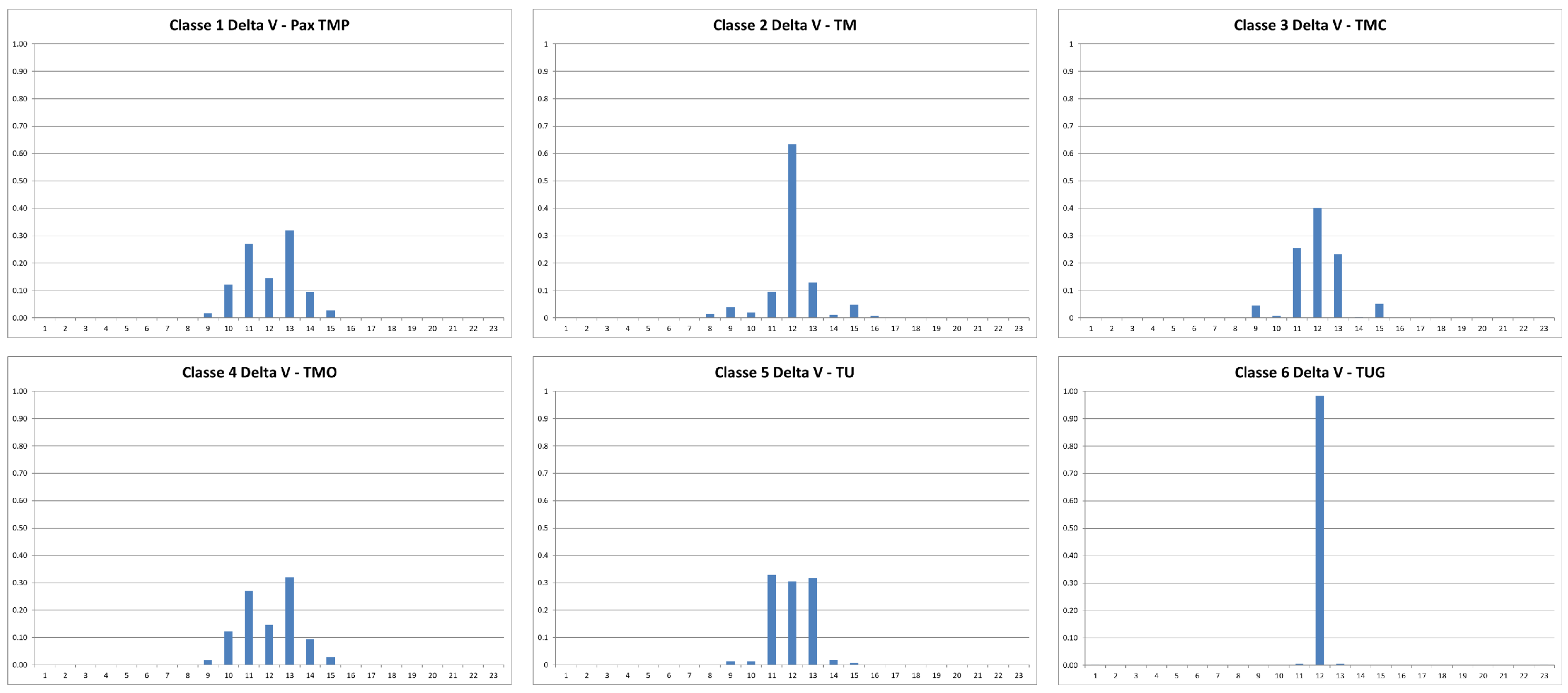
For illustrative purposes, we provide the statistical profile of the velocity, $v\left(t\right)$, of the change of route, $r(t,t-1)$, and of the dynamic delta of the velocity, $dv(t,t-1)$, of a vessel randomly selected for each class. This is to give an idea of the type of input that the adaptive algorithms must manage to define an analysis model that allows the automatic classification of unknown vessels. See Figure 2, Figure 3 and Figure 4.

Although Figure 2, Figure 3 and Figure 4 represent examples of vessels randomly chosen in the database, it is evident that these new variables should provide a reliable portrait of the navigation style of each of the six types of vessels. In the following paragraphs, we will measure the accuracy and precision of this third pre-processing strategy.

2.3. A.III—Model Definition

To address the complexities in this classification problem, we propose a new approach, denoted as ’Take One Class at a Time’ (TOCAT). This classification strategy operates on two fundamental principles during the training/testing stage:

(a) Breakdown of a multinomial classification (1 of N) into N independent binary classifications (1 of 2). Each class is treated separately: all records of the focus class are assigned target 1 while all records belonging to other classes are assigned target 0. The advantage of this system is that even when faced with a high number of classes N, these are reduced to N binary classification processes. Therefore, instead of having a single process that must decide the class membership of a record to N possible classes, there will be N processes, each specialized in a single class, which must decide whether the record is of that class or not;

(b) Free identification of the best algorithm for each class. As each class is treated separately, each will be reviewed by multiple Machine Learning methods to select the type of algorithm and structure that obtains the best predictive result in testing. This procedure, which allows for the selection of a different algorithm for each class, can improve the overall performance of the system.

TOCAT, therefore, is not tied to a specific algorithm, but draws on a variety of algorithms to tackle individual bimodal classifications. At the end of the training/testing stage, each class will be associated with the algorithm that achieved the best result, as assessed by the values of Sensitivity and Specificity on the confusion matrix. Only the algorithm with the best performance will be used for the recall stage on new records.

The output of the recall stage of the TOCAT system, in which unclassified new input records are assigned a target by the N networks, is complex. Each network specialized in a single target is called to respond; thus, there may be conflicts in the assignments. This feature is an advantage when it is important to identify ambiguous records that need to be reported by the system. Therefore, using the TOCAT strategy, it is possible for each new pattern to be attributed a fuzzy membership (from 0 to 1) with each of the N Classes.

For the training phase, many adaptive algorithms are used (machine learning and artificial neural networks). The results of these algorithms were finally filtered by a neural meta-network [9,10], which significantly exceeded the results of the best basic algorithm. The different algorithms were implemented through two types of Software, accredited for scientific research: (a) Supervised ANNs (version 27.5, Semeion, 1999–2017); (b) Meta Net Multi Train (version 3.5, Semeion, 2010–2015).

For the experimental phase, a set of algorithms was utilized to explore and analyze the data. Some of the algorithms are commonly used in the literature (kNN [11,12], naive Bayes [13,14,15,16,17], majority vote [9,10,18]), while the remaining algorithms have been specifically developed by Semeion for pattern recognition. The objective was to compare the effectiveness and efficiency of the algorithms and determine which ones would yield the most accurate and reliable results: (a) backpropagation (Bp) [19,20,21]; (b) deep learning (Deep) [22,23,24]; (c) adaptive vector quantization (AVQ) [25,26,27,28]; (d) kNN [11,12]; (e) meta Bayes (Mb) [29]; (f) Conic Net [30]; (g) Sine Net (Sn) [31]; (h) bimodal (Bm) [32]; (i) majority vote (Mv) [9]; (j) naive Bayes [13,14,15,16,17]; (k) supervised contractive map (SVCm) [32]. 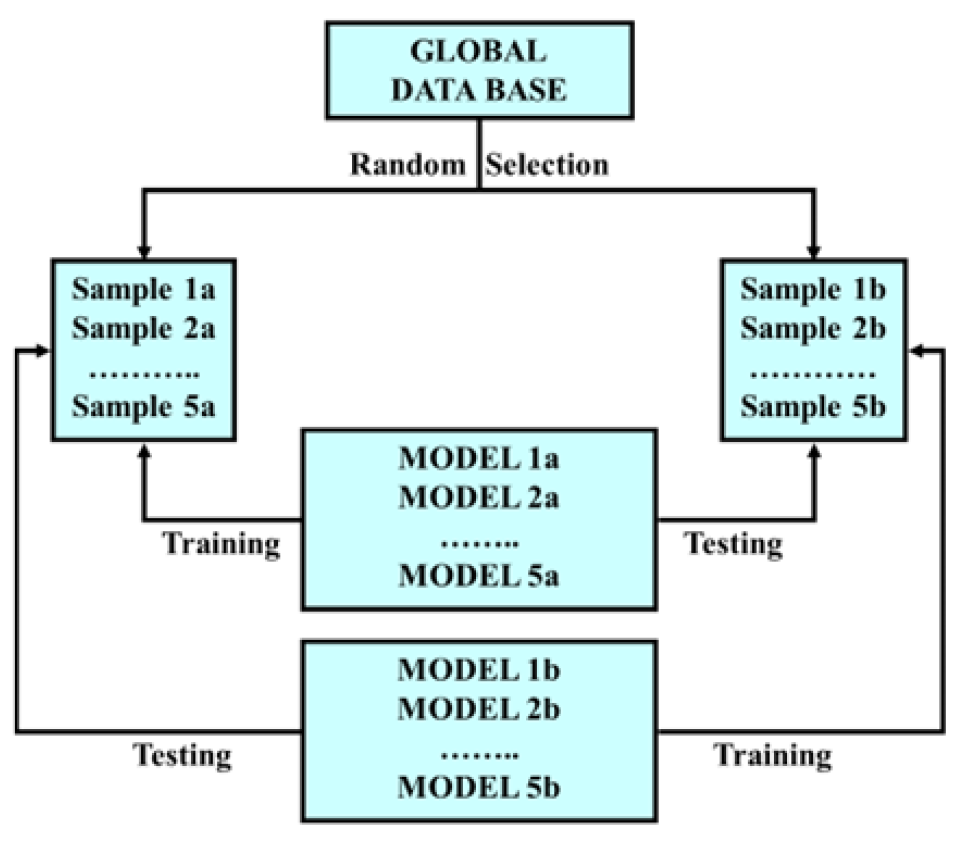The validation protocol used for all the algorithms is the training–testing protocol [33,34,35] (Figure 5: Validation protocol—5 × 2 CV (training–testing)).

In this experiment, three classification lines are used: (a) Classification 1 of 5: The attempt is to automatically classify each vessel in one of the five possible classes. In this specific case, class 2 (TM9) is excluded, as the results appear to be difficult to interpret and potentially confusing. This complexity arises from the indiscriminate inclusion of vastly different types of vessels within this class. (b) Classification 1 of 6: The attempt is to automatically classify each vessel in one of the six classes provided; (c) Classification “Take One Class at a Time” (TOCAT): Adaptive algorithms are trained to recognize when each vessel belongs or not to a specification of the six possible classes, and the operation is repeated by placing one class at a time in relation to all the others. This procedure generates six different datasets, each of which is subjected to two-class validation (focused class versus other classes).

3. Results

3.1. Exploratory Analysis

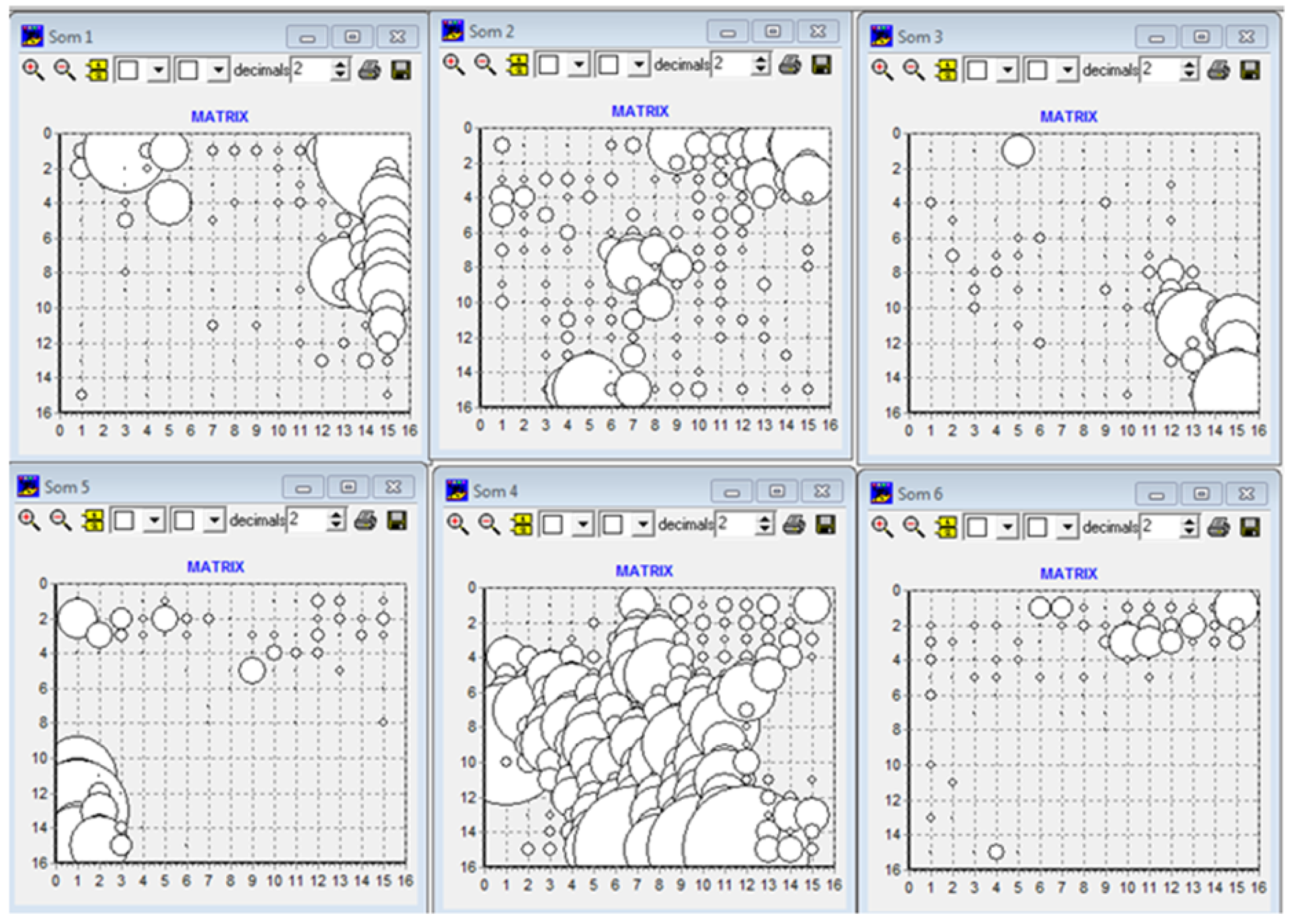
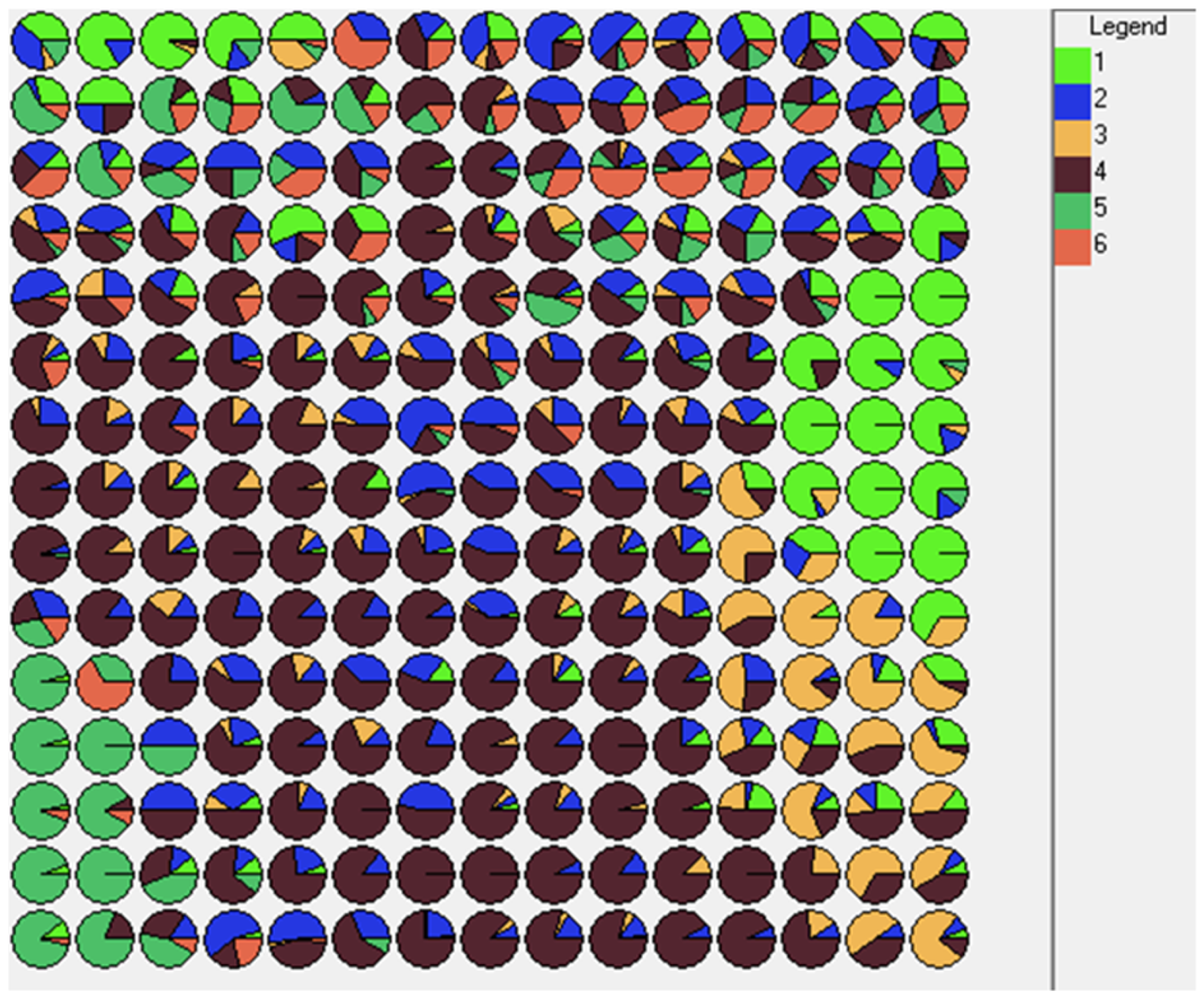
At this juncture, an unsupervised neural network is deployed once more to discern the extent to which our pre-processing step can spontaneously segregate the database into the six distinct vessel classes. A self-organizing map (SOM) [28] is used for this purpose with a square grid of 15 × 15, capable of generating 225 codebooks, where each codebook represents a similar group of vessels; Figure 6 shows the results of the SOM software.

Figure 6 illustrates a more defined spontaneous separation of vessels into the six targeted classes for classification, compared to the outputs produced by previous pre-processing strategies. Class 2 (TM) remains the most difficult to characterize and therefore to be separated from the others. In all cases, even with this pre-processing strategy, the definition of the classification model is very complex due to the notable non-linear separability of some classes.

Figure 7 shows the projection grid of the SOM with the overlap percentage of vessels of different classes in each of the 225 codebook cells.

The results of the analysis using SOMs highlight the potential of the selected set of variables. Each class is distributed in specific areas of the map, even though the resulting overlaps between classes make it difficult to obtain an accurate classification system that can be used in operational mode.

3.2. Results Analysis

3.2.1. Classification with Five Classes

Table 3. Results of the classifications on 5 classes. Class 2 (TM) is excluded.

Adaptive Algorithms	PAX-TMP	TMC	TMO	TU	TUG	A.Mean	W.Mean	Error	SW
Mb	0.7602	0.6757	0.9468	0.8593	0.6591	0.7802	0.8622	193	Sem. no. 55
Mv	0.6878	0.6622	0.885	0.837	0.7614	0.7667	0.818	255	Sem. no. 55
DeepSn	0.6742	0.6554	0.8702	0.8148	0.7727	0.7575	0.8051	273	Sem. no. 12
kNN_N1	0.6471	0.7365	0.9345	0.8667	0.5682	0.7506	0.8387	226	Sem. no. 12
DeepBp	0.6109	0.6959	0.8307	0.7852	0.8295	0.7504	0.7773	312	Sem. no. 12
DeepBm	0.7376	0.6351	0.8863	0.8222	0.6591	0.7481	0.8158	258	Sem. no. 12
K-CM	0.6471	0.723	0.9333	0.8593	0.5682	0.7461	0.8358	230	Sem. no. 12
DeepConic	0.6968	0.6216	0.8764	0.837	0.6818	0.7427	0.8051	273	Sem. no. 12
Bm	0.6968	0.6892	0.8591	0.8222	0.6364	0.7407	0.798	283	Sem. no. 12
Sn	0.6516	0.7095	0.8739	0.8667	0.5909	0.7385	0.803	276	Sem. no. 12
Conic	0.6561	0.6081	0.8826	0.8519	0.6932	0.7384	0.803	276	Sem. no. 12
Bp	0.7104	0.7162	0.8467	0.8148	0.5909	0.7358	0.7923	291	Sem. no. 12

shows the results of classifications one of five.

3.2.2. Classification with Six Classes

Table 4. Results of the classification on 6 classes.

Adaptive Algorithms	PAX-TMP	TM	TMC	TMO	TU	TUG	A.Mean	W.Mean	Error	SW
kNN_1	63.89%	50.95%	75.51%	86.79%	80.95%	42.16%	66.71%	73.45%	481	Sem. no. 12
Bm	71.43%	21.84%	67.35%	84.91%	78.91%	55.88%	63.39%	68.49%	571	Sem. no. 12
Conic	68.65%	38.61%	67.35%	81.72%	71.43%	45.10%	62.14%	68.32%	574	Sem. no. 12
DeepBp	71.83%	37.97%	61.90%	76.53%	79.59%	34.31%	60.36%	65.84%	619	Sem. no. 12
SVCm	71.83%	27.53%	63.95%	83.96%	72.79%	41.18%	60.21%	67.49%	589	Sem. no. 12
DeepConic	59.52%	37.34%	63.95%	77.48%	71.43%	42.16%	58.65%	64.40%	645	Sem. no. 12
AVQ	50.00%	33.86%	71.43%	81.72%	74.83%	30.39%	57.04%	64.68%	640	Sem. no. 12
Naive Bayes	11.11%	0.32%	41.50%	75.83%	0.68%	97.06%	37.75%	45.97%	979	Sem. no. 12

shows the results obtained by repeating the experiment with all six classes. In this case, the use of the meta-network is ineffective.

The outcomes of this experiment hold merit academically, but their practical applicability remains limited.

3.2.3. Class Classification of TOCAT

In this experiment, we present results from the six one-of-two classifications (class vs. other classes) to determine the sensitivity and specificity for each classification, as detailed in (

Table 5. Classification of Class 1: PAX-TMP.

ANN	Class1	Others	A.Mean	W.Mean	Errors
Conic(C1)	81.12%	91.03%	86.08%	89.65%	185
DeepConic(C1)	80.32%	91.61%	85.97%	90.04%	178
DeepBm(C1)	80.32%	91.61%	85.97%	90.04%	178
FFBp(C1)	79.92%	90.57%	85.25%	89.09%	195
DeepBp(C1)	78.71%	93.50%	86.11%	91.44%	153
DeepSn(C1)	76.31%	92.65%	84.48%	90.37%	172
kNN(C1)	74.30%	95.77%	85.04%	92.78%	129

,

Table 6. Classification of Class 2: PAX-TM.

ANN	Class1	Others	A.Mean	W.Mean	Errors
Conic(C2)	72.03%	70.01%	71.02%	70.35%	539
DeepConic(C2)	68.81%	70.74%	69.77%	70.41%	538
DeepBp(C2)	64.95%	75.71%	70.33%	73.87%	475
FFBm(C2)	62.70%	76.05%	69.37%	73.76%	477
DeepBm(C2)	62.06%	77.24%	69.65%	74.64%	461
kNN(C2)	58.52%	93.56%	76.04%	87.57%	226

,

Table 7. Classification of Class 3: TMC.

ANN	Class1	Others	A.Mean	W.Mean	Errors
Deep_Conic(C3)	76.36%	88.70%	82.53%	87.57%	223
FFBm(C3)	75.76%	90.67%	83.21%	89.30%	192
Conic(C3)	73.94%	93.43%	83.69%	91.64%	150
Conic(C3)	72.73%	93.25%	82.99%	91.36%	155
DeepBp(C3)	71.52%	92.69%	82.11%	90.75%	166
kNN(C3)	70.30%	98.16%	84.23%	95.60%	79

,

Table 8. Classification of Class 4: TMO.

ANN	Class1	Others	A.Mean	W.Mean	Errors
kNN(C4)	88.71%	87.34%	88.03%	87.99%	218
FFBp(C4)	84.52%	82.74%	83.63%	83.58%	298
DeepBm(C4)	85.10%	81.17%	83.14%	83.03%	308
DeepBp(C4)	84.52%	80.65%	82.58%	82.48%	318

,

Table 9. Classification of Class 5: TU.

ANN	Class1	Others	A.Mean	W.Mean	Errors
DeepBm(C5)	88.00%	88.11%	88.06%	88.10%	207
DeepBp(C5)	81.33%	93.90%	87.62%	92.82%	125
Conic(C5)	80.67%	96.42%	88.54%	95.06%	86
kNN(C5)	80.00%	98.93%	89.47%	97.30%	47
FFBp(C5)	80.00%	97.67%	88.84%	96.15%	67
DeepConic(C5)	79.33%	96.92%	88.13%	95.40%	80

and

Table 10. Classification of Class 6: TUG.

ANN	Class1	Others	A.Mean	W.Mean	Errors
Conic(C6)	88.24%	80.51%	84.37%	80.95%	346
DeepBm(C6)	84.31%	76.14%	80.23%	76.60%	425
DeepConic(C6)	63.73%	91.66%	77.69%	90.09%	180
DeepBp(C6)	65.69%	89.26%	77.48%	87.94%	219
FFBp(C6)	65.69%	88.62%	77.15%	87.33%	230
kNN(C6)	53.92%	98.72%	76.32%	96.20%	69

).

Table 11. The best algorithms of the 6 classifications with the TOCAT procedure.

Classes		Algorithm	Sensibility	Specificity	A.Mean	W.Mean	Errors
Class 1	PAX-TMP	Conic	81.12%	91.03%	86.08%	89.65%	185
Class 2	TM	Conic	72.03%	70.01%	71.02%	70.35%	539
Class 3	TMC	DeepConic	76.36%	88.70%	82.53%	87.57%	223
Class 4	TMO	kNN_1	88.71%	87.34%	88.03%	87.99%	218
Class 5	TU	DeepBm	88.00%	88.11%	88.06%	88.10%	207
Class 6	TUG	Conic	88.24%	80.51%	84.37%	80.95%	346
Average × Class			82.41%	84.28%	83.35%	84.10%	286.33

summarizes, in an overview, the results of the best algorithms in each of the 6 classifications

4. Discussion

Significant findings have emerged. Firstly, the study highlighted the potential of an approach that involves transforming a sparse and incomplete dataset of vessel paths into a consistent set of features that could be universally applicable across all types of vessels, despite variations in the number of observations. While the individual techniques employed to convert vessel trajectories into fixed features were not new, the innovation lay in their combined application, resulting in the transformation of temporal flows into spatial features, derived from highly heterogeneous data.

The second significant result was the development of the TOCAT (take one class at a time) research design. While the TOCAT strategy itself is not entirely new, as it is already used in support vector machine algorithms [36,37] for multinomial classifications, our innovative application of this processing strategy was significant. Existing methods typically rely on the development of a singular, albeit sophisticated, convolutional or recurrent neural network, which shoulders the full responsibility of recognition. The TOCAT strategy, however, hinges on the concept of creating a diversified ecosystem of neural networks, varying both topologically and mathematically, which is not strictly reliant on gradient descent or decision trees. Each of these networks is adept at specializing in a statistical niche within the vessels’ trajectories.

By utilizing different artificial neural networks (ANNs) and machine learning techniques for distinct “one of two” classification tasks, we achieved diverse mathematical and topological representations for each ANN used. This diversity enhanced classification accuracy, as each “one of two” classification tasks could leverage a specific ANN suitable for recognizing a particular class of vessels. The efficacy of this mathematical “biodiversity” in improving the final results represents an important milestone in this work. In summary, the collective integration of small, distinct artificial systems outperformed a single large ANN attempting to comprehend the entire scope independently.

5. Conclusions

This paper proposes a novel approach to vessel classification, using the normalization of sparse and incomplete vessel trajectory data into a universal set of features, which is applicable despite varying observation numbers. Our model utilizes the TOCAT (take one class at a time) design, a strategy typically used in support vector machine algorithms, but uniquely applied in this study to individual ’one versus rest’ classification tasks using a variety of diverse artificial neural networks (ANNs). We derived distinct mathematical and topological representations from vessel trajectory data for each ’one versus rest’ classification task, leveraging the proven capabilities of specific ANNs for recognizing certain vessel classes. The findings, which show a mean accuracy of 83% in a six-class classification task, suggest that the collaborative employment of these specialized ANNs could potentially outperform a single, larger ANN assigned to the entire classification task. During the experiments, we also pinpointed several critical aspects tied to data processing: primarily, the need for statistical sampling of the AIS signals from each vessel’s trajectories. This method enables a robust estimation of vital parameters such as the vessel’s speed, deceleration, and acceleration. Furthermore, as anticipated, the analysis highlights the importance of avoiding the use of overly complex algorithms, especially when the number of input variables is limited and the samples have not been collected through robust sampling procedures. Future research endeavors may explore the scalability and generalizability of the proposed approaches and extend their applications to other domains beyond vessel recognition and comparisons with the most recent techniques existing in the field.