Enhancing Metaheuristic Optimization: A Novel Nature-Inspired Hybrid Approach Incorporating Selected Pseudorandom Number Generators

Abstract

In this paper, a hybrid nature-inspired metaheuristic algorithm based on the Genetic Algorithm and the African Buffalo Optimization is proposed. The hybrid approach adaptively switches between the Genetic Algorithm and the African Buffalo Optimization during the optimization process, leveraging their respective strengths to improve performance. To improve randomness, the hybrid approach uses two high-quality pseudorandom number generators—the 64-bit and 32-bit versions of the SIMD-Oriented Fast Mersenne Twister. The effectiveness of the hybrid algorithm is evaluated on the NP-hard Container Relocation Problem, focusing on a test set of restricted Container Relocation Problems with higher complexity. The results show that the hybrid algorithm outperforms the individual Genetic Algorithm and the African Buffalo Optimization, which use standard pseudorandom number generators. The adaptive switch method allows the algorithm to adapt to different optimization problems and mitigate problems such as premature convergence and local optima. Moreover, the importance of pseudorandom number generator selection in metaheuristic algorithms is highlighted, as it directly affects the optimization results. The use of powerful pseudorandom number generators reduces the probability of premature convergence and local optima, leading to better optimization results. Overall, the research demonstrates the potential of hybrid metaheuristic approaches for solving complex optimization problems, which makes them relevant for scientific research and practical applications.

1. Introduction

Optimization is a fundamental principle in science and technology that involves finding the optimal solution to a given problem [1]. In computer science, optimization is widely used, including in the development of algorithms for task scheduling in operating systems. These algorithms aim to optimize the allocation of system resources, such as Central Process Unit (CPU) time and memory, to improve system utilization and performance. As a result, they contribute to higher efficiency, shorter response times, and higher throughput [2]. Mathematically, optimization problems involve finding the best solution to a given problem, usually seeking the maximum or minimum within certain constraints or conditions [3]. Such problems consist of an objective function that evaluates the quality, performance, or value of the solution and constraints to be satisfied. Real-world optimization problems often fall into the category of NP (Non-deterministic Polynomial time) problems, which require the use of non-deterministic algorithms for their solution. However, the resource-intensive nature of finding the optimal solution makes them impractical. To address this challenge, the use of metaheuristics proves to be highly beneficial. The authors in [4] have given a definition of metaheuristic algorithms in computer science and mathematical optimization as follows:

In computer science and mathematical optimization, a metaheuristic is a higher-level procedure or heuristic that aims to find, generate, or select a heuristic (partial search algorithm) that can provide a sufficiently good solution to an optimization problem, especially in the presence of incomplete or imperfect information or limited computational capacity.

Metaheuristic algorithms, unlike numerical optimization methods, offer no guarantee of finding a global optimal solution. However, they provide faster and computationally efficient satisfying solutions. Metaheuristics are popular, because they are easy to understand, implement, and very powerful [5]. These algorithms use stochastic optimization techniques that introduce randomness into the solutions. They undergo exploration (randomization of variable values) and exploitation (exploration of the solution space around high quality solutions). The random nature of metaheuristics means that a superior performance on one problem is no guarantee of similar results on other problems, which is known as the No Free Lunch (NFL) theorem [6]. For this reason, new metaheuristic algorithms are constantly being introduced in the scientific literature [7].

Nature-inspired metaheuristic algorithms are widely recognized and appreciated for their ability to model natural behaviors and optimize objective functions. The development of such algorithms began in 1975 with the proposal of a genetic algorithm [8], mimicking natural selection and genetics. Numerous new nature-inspired metaheuristic algorithms have emerged in the literature since then. In engineering fields, these metaheuristic algorithms are used for various applications, such as optimizing data clustering [9], determining an accurate diagnosis of patients in medicine [10], solving planetary gear problems and the crashworthiness of cars [11], solving optimization problems in the tire industry [12], optimizing threshold-based image segmentation [13], solving optimization problems in computer science [14], reducing carbon emissions [15], etc.

For real-world problems of significant scale, it becomes clear that the approach of relying only on a single metaheuristic algorithm is limited [7]. When using a single algorithm to solve different optimization problems, it becomes clear that the algorithm reaches its limits in certain problems that do not correspond to its strengths. Premature convergence and the tendency toward local optima are widely known as the main limitations of metaheuristic algorithms that can occur when solving a particular optimization problem. For this reason, not only new metaheuristic algorithms are constantly presented in the literature, as mentioned above, but also hybrid metaheuristic algorithms, which are developed by combining several well-known metaheuristic algorithms. These hybrid solutions aim to improve the optimization process for specific problems by mitigating the weaknesses of each algorithm and leveraging their respective strengths [16]. By integrating these algorithms into a new hybrid approach, it becomes possible to adapt and apply them to a broader range of optimization problems [17]. In [18], the authors introduced a taxonomy that categorizes potential hybrid metaheuristic solutions, resulting in the identification of four fundamental approaches to hybridization. One of the four main approaches is the high-level relay hybrid (HRH) solution, in which two metaheuristics are executed in sequence. This HRH solution will be the basis for our new hybrid metaheuristic algorithm. It is important to define the rules by which each metaheuristic is executed in this sequential execution. In this work, hybrid metaheuristics will not have the usual sequential execution of two algorithms, but a special adaptive switch will be introduced within the optimization process between each metaheuristic, according to the results obtained in the last iteration during the optimization.

A very important component of any metaheuristic algorithm, including the hybrid algorithm, is the pseudorandom number generator (PRNG), which is used at all stages of randomization within the optimization process. PRNGs are simple deterministic algorithms that generate deterministic sequences of numbers that appear random [19]. Due to the finite number of states in a PRNG, it is inevitable that the generator will eventually return to a previous state and repeat the sequence after a finite number of steps [20]. If the PRNG does not have a large period in which to repeat the random number sequence, the algorithm may end up in a local optimum due to the poor quality of the PRNG. There is a considerable number of scientific papers [7,9,10,11,12,13,14,15,21,22,23,24,25,26,27,28,29,30,31,32] that introduces a hybrid metaheuristic algorithm based on two or more existing algorithms, but to the best of our knowledge, no hybrid solution mentions the PRNG used for randomization. Therefore, it is assumed that randomization uses random functions implemented by default in the programming language used to implement the metaheuristic algorithm. In [20], it was proven that different PRNGs have a direct impact on the optimization results of a given metaheuristic approach. Therefore, it is very important which PRNG is used in the randomization phase of a single metaheuristic algorithm, as well as a hybrid metaheuristic solution. In our hybrid solution, we will pay special attention to the use of a particular PRNG in the randomization phase, according to the results of testing single PRNGs in [19]. In this way, the probability of premature convergence or staying in the local optimum will be reduced.

In this paper, we propose a hybrid nature-inspired metaheuristic solution based on two algorithms: Genetic Algorithm (GA) and African Buffalo Optimization (ABO) [33]. In addition, we introduce the adaptive switch method as part of the hybrid algorithm, which allows dynamic switching between GA and ABO during the optimization process. Unlike the traditional sequential execution, only one algorithm (e.g., ABO) can be executed in several consecutive iterations based on the performance of the single algorithm in the previous iteration. It is worth noting that this hybrid approach can be applied to combine any two-metaheuristic nature-inspired algorithms. In our specific hybrid solution, GA was chosen as a well-established nature-inspired metaheuristic, while ABO represents a more modern nature-inspired metaheuristic. Furthermore, to incorporate randomization within the optimization process, we utilize two PRNGs, namely the 64-bit and 32-bit versions of the SIMD-Oriented Fast Mersenne Twister (SFMT) [34]. These PRNGs have demonstrated exceptional performance and quality, as evidenced by their top rankings in a comprehensive evaluation of various PRNGs in [20]. As mentioned, using high-quality PRNGs enhances the optimization process by reducing the probability of premature convergence of the metaheuristic algorithm and mitigating the risk of getting trapped in local optima.

To evaluate the effectiveness of our proposed hybrid metaheuristic, we will evaluate its performance on the NP-hard Container Relocation Problem (CRP) [35], which is also one of the NP-complete problems. The CRP, also referred to as the Block Relocation Problem (BRP), is an engineering optimization problem that involves reshuffling containers within a container terminal stacking area to minimize the number of reshuffles required for retrieving specific containers. This paper focuses on evaluating our hybrid algorithm using a test set of restricted CRPs, as described in [36], which is considered the most relevant test set for evaluating CRP solution models. The restricted CRP, a subproblem of the CRP, specifically involves reshuffling only those containers that block the retrieval of the desired containers. We selected the restricted CRP for evaluation because of its higher complexity compared to the standard CRP. The results of our novel hybrid algorithm, which includes adaptive switches and the selected PRNGs, are compared with individual GA and ABO algorithms that use standard and only one PRNG. Moreover, the optimization results of our new algorithm were compared with the optimization method from [36], for which, to the best of our knowledge, the best optimization results were obtained by CRPs. Our new algorithm achieved the best optimization results for the tested CRPs. Moreover, our algorithm outperforms the individual algorithms from GA and ABO, proving that the implementation of such a hybrid solution is justified in scientific research.

The paper is divided into five interdependent sections. Section 2 contains a literature review of hybrid nature-inspired metaheuristic approaches and an examination of various PRNGs discussed in the literature. Section 3 presents the basic terminology of the algorithms GA and ABO, which are integral parts of our hybrid metaheuristic. In addition, both the 64-bit and 32-bit versions of SFMT pseudorandom generator are described in this section. The proposed hybrid nature-inspired metaheuristic algorithm is then presented in Section 4. Section 5 presents the evaluation of our new algorithm using the most challenging test instances of restricted CRPs. Finally, Section 6 provides a conclusion.

2. Literature Review

In the literature, there is a large number of proposed metaheuristic algorithms inspired by nature. Additionally, many authors have been working on modified versions of these algorithms. Recently, there has been a notable increase in the number of hybrid approaches among the proposed algorithms. These hybrid approaches typically combine two or more metaheuristic algorithms inspired by nature. By doing so, the optimization process for specific problems can be improved by addressing the weaknesses of each algorithm while capitalizing on their respective strengths. The first part of this review will focus on hybrid algorithms based on at least two nature-inspired metaheuristics. Scientific papers from the last ten years containing the terms hybrid, nature-inspired, and metaheuristics were considered. These papers were retrieved from the Web of Science (WoS) database [37], which is considered the most valued scientific database in the academic community. The second part of this review will shift its focus toward PRNGs and their impact on the quality of the optimization process.

In [10], a model for more accurate detection of melanoma on skin was presented. A hybrid metaheuristic algorithm consisting of a combination of Bat Algorithm (BA) [38] and Artificial Bee Colony (ABC) [39] is proposed to determine the optimal values of a set of parameters to improve the contrast and brightness of the image in order to better detect melanomas on the skin. In the search for optimal parameter values, first BA and then ABC are performed sequentially. Nowhere in the paper is it mentioned which PRNG was used to randomize the selected algorithm solutions.

The authors in [11] proposed a novel hybrid metaheuristic algorithm (HAHA-SA) based on the artificial Hummingbird Algorithm (AHA) [40] and Simulated Annealing (SA) [41]. New HAHA-SA was applied to solve three constrained real-world design problems (planar ten-bar truss problem, planetary gear train problem, and car crashworthiness problem) to prove its quality. The authors did not mention how the hybrid algorithm was developed (parallel or sequential architecture or something else). It is also not stated which PRNG was used to randomize the selected algorithm solutions.

In [9], a new hybrid metaheuristic algorithm based on the Water Cycle Algorithm (WCA) [42] and the Hookes and Jeeves Algorithm (H–J) [43] was presented. This novel hybrid algorithm was used for solving optimization problems in data clustering. The optimization process starts with the iterative execution of the WCA algorithm for the selected problem. If the WCA algorithm does not find a better solution in five consecutive iterations, the H–J algorithm is included in the optimization process, which then replaces the WCA algorithm. This paper also did not mention which PRNG is used to generate random solutions. For example, it would be possible, in case the WCA algorithm does not find a better solution in five consecutive iterations, to change the PRNG and thus avoid the local optimum and improve the optimization process for the given problem.

In addition, two hybrid algorithms were proposed in [12] by combining a “newer” algorithm (e.g., the Red Deer Algorithm (RDA) [44] or the Whale Optimization Algorithm (WOA) [45]) and an “older”, well-known algorithm (e.g., the Genetic Algorithm (GA) [8] or SA) to solve a problem of designing a supply chain network under uncertainty in the tire industry. The hybrid version called HWISA, which combines the WOA and SA algorithms in the search for the optimal solution, proved to be highly successful in solving this problem. In HWISA, SA is used in local search (intensification) throughout the optimization process with WOA. It is not mentioned in this paper which PRNG is used to generate random solutions.

The selection of optimal thresholds in threshold-based image segmentation is proposed in [13] using a multi-stage hybrid metaheuristic algorithm. This hybrid algorithm is a combination of three metaheuristic algorithms: Particle Swarm Optimization (PSO) [46], Ant Colony Optimization (ACO) [47], and ABC. The algorithm consists of 3 steps that are executed sequentially. First, PSO is used to search for optimal thresholds, then ABC is used, and finally the ACO algorithm is used. It is not stated in the paper which PRNG was used in the execution of the metaheuristic algorithms.

In [7], the ABC was hybridized with the GA to optimize parameter identification of an Escherichia coli-fed batch process model. First, the ABC algorithm is used to initialize the initial population for a given number of iterations. The resulting population is used as the initial population of GA and yields a population that is much closer to the optimal solutions than a randomly generated initial population. As in the previous related works, no mention is made of the PRNG utilized in the optimization process.

The authors in [14] propose three hybrid metaheuristics based on the Grey Wolf Optimizer (GWO) [48] and WOA to optimize the dimensionality reduction process, an important solution to the dimensionality problem encountered in most machine learning methods. The first hybrid algorithm is executed in a sequential order, such that GWO is executed first, followed by WOA. In the second hybrid algorithm, the optimization process randomly switches between two algorithms at each iteration. The third algorithm implements an adaptive switching mechanism between the GWO and WOA based on the number of improved solutions within the population from the previous iteration. If the count of improved solutions in the population fails to surpass the designated threshold, the algorithm is replaced in the subsequent iteration. This third approach is closest to our new hybrid metaheuristic algorithm, which alternates the execution of the two algorithms during the optimization process, but in this approach, the selected PRNG that was used for the randomization phase is not mentioned.

A hybrid metaheuristic algorithm based on a combination of the Ant Lion Optimizer (ALO) [49] and Jaya [50] algorithms was presented in [21]. The algorithm is divided into two phases. In the first phase, ALO and Jaya are run in parallel to obtain better solutions, which are then used in the second phase of the hybrid algorithm. In the second phase of the algorithm, solutions are selected from the population of the ALO and Jaya algorithms for each subsequent iteration, depending on the quality of each solution (value of the fitness function) in the previous iteration. This paper also does not mention the use of a specific PRNG that can improve the optimization results in the metaheuristic algorithm.

In [15], a novel hybrid metaheuristic combining WOA and SA algorithms is proposed as a solution for reducing carbon emissions in a production distribution network. In this hybrid algorithm, SA is integrated with WOA, and instead of spiraling updates of positions in WOA, a local search based on SA is performed. In this way, the phases of intensification and diversification of WOA are improved. Again, there is no mention of the selected PRNG used in the randomization phase of the proposed algorithm.

The authors in [22] proposed three hybrid algorithms for solving the optimization problem of maximizing the reliability of information retrieval in wireless multimedia sensor networks. The hybrid algorithms are based on GA and SA, where the branch-and-bound (B&B) algorithm [51] is used in the phases of the optimization process within GA or SA for a better optimization process. The use of the selected PRNG for the randomization process is also not mentioned in this paper.

In [23], a hybrid metaheuristic based on the Cultural Algorithm (CA) [52] and Differential Evolution (DE) [53] was proposed. In each iteration, the participation ratio for both algorithms is calculated, which determines the influence of each algorithm on the optimization process. Also, the PRNG used for randomization in the optimization process is not specified in this paper.

The hybrid metaheuristic approach based on the Mean Gray Wolf Optimizer (MGWO) [54] and WOA is proposed in [24]. In this hybrid algorithm, WOA is extended by a spiral equation from MGWO with the aim of achieving a balance between the exploitation and exploration phases. As in all previous works, the authors of this hybrid algorithm do not specify which PRNG is used for randomization.

The authors in [25] presented the Hybrid Flower Pollination Algorithm (HFPA), which is used for the optimal design of wideband digital differentiators and digital integrators with infinite impulse response. This hybrid algorithm is based on the PSO and Flower Pollination Algorithm (FPA) [55] algorithms. In this hybrid solution, PSO and FPA are run sequentially, with the best solutions of the PSO algorithm as the initial solutions for the FPA algorithm. The paper does not specify which PRNG was used.

In [26], three nature-inspired metaheuristics were combined in a new hybrid approach to solve constrained problems in numerical and engineering optimization. These metaheuristics are PSO, GA, and Symbiotic Organisms Search (SOS) [56]. The optimization process starts with GA, where better solutions have a higher probability of advancing to the second optimization stage as input solutions for the PSO algorithm. The principle is similar when moving from the PSO algorithm to SOS, where better solutions have a higher chance of being part of the initial population in SOS. It is not known which PRNG is chosen for the randomization phases within the hybrid algorithm.

The mean Gbest Particle Swarm Optimization (MGBPSO) [27] and Gravitational Search Algorithm (GSA) [57] were combined into a novel hybrid metaheuristic approach in [27] to improve the solution for function optimization in search space. GSA and MGBPSO are executed in parallel, and the results of both algorithms are incorporated into the optimization result. In this way, the strengths of each algorithm are effectively utilized in the hybrid version, namely the exploitation phase of the MGBPSO algorithm and the exploration phase of the GSA algorithm. The PRNG used in the new hybrid algorithm is not mentioned in this paper.

The authors in [28] proposed a hybrid variant of the ABC algorithm, where the functionality of the exploitation phase is enhanced by a newly proposed simple local search technique (SLST). The SLST technique improves the local search in the search space during the process of intensifying good solutions. Again, the selected PRNG was not mentioned in the paper.

In [29], two hybrid metaheuristic approaches are proposed. Both approaches are based on ACO and FPA algorithms. In the first version of the hybrid algorithm, the FPA algorithm was integrated with the ACO algorithm to improve the exploration phase. In the second version of the hybrid algorithm, ACO and FPA are executed sequentially and completely independently. It is not known which PRNG was used for the randomization process within the proposed algorithms.

A new hybrid metaheuristic based on PSO and Harmony Search Algorithm (HS) [58] is proposed in [30]. In this algorithm, HS and PSO are executed sequentially. HS is executed first, and its solution population represents the solution population for each iteration of the PSO algorithm. The PRNG used is not specified.

The authors in [31] propose novel hybrid metaheuristic based on GA and ACO for optimizing the resource levelling problem. The main idea behind the integration of ACO and GA is to use the ACO algorithm, which focuses on discovering a high-quality local solution. Then, the algorithm GA uses the solution obtained from ACO to search for the global optimum. The PRNG used in the optimization process was also not mentioned in this paper.

In [32], a new hybrid nature-inspired metaheuristic approach for optimizing course scheduling in universities was proposed using ABC with Hill Climbing Optimizer (HCO) [59]. HCO is integrated with ABC in the exploration phase to provide better search in the search space. The specific PRNG used in this new hybrid algorithm is not specified.

There are also a large number of hybrid algorithms in the literature that combine a nature-inspired algorithm with a deterministic method, as in [60,61,62,63]. As mentioned earlier, we restrict ourselves here to reviewing the literature that contains hybrid solutions that combine two nature-inspired metaheuristic algorithms.

To summarize the hybrid nature-inspired metaheuristics found in the literature, we note that all hybrid solutions adhere to predefined rules within the optimization process. In particular, the third version of the hybrid algorithm described in [14] introduces an adaptive switch between algorithms during optimization. This switch allows to select the algorithm that gives the best results for the given optimization problem, thus improving the overall optimization process. In this work, we follow a similar approach by evaluating the number of improved solutions in the current iteration compared to the previous one. In addition, our approach includes an evaluation of the overall quality of the current population compared to the previous population and whether the current population successfully found the best global solution. It is important to note that the adaptive switch in our approach is not activated immediately; instead, the currently selected algorithm in the hybrid model is assigned a certain number of iterations to explore and possibly discover better solutions.

In none of the hybrid nature-inspired algorithms described so far do the authors mention the specific pseudorandom number generators (PRNGs) used during the randomization phase of the optimization process. Therefore, it can be assumed that standard PRNGs already implemented in the programming languages, such as rand() [64] or random() [64], were used. However, it is important to note that the choice of PRNG can significantly affect the quality of the optimization results of a metaheuristic algorithm, as confirmed in the study [20]. The above study provides a detailed analysis of the optimization results of five metaheuristic nature-inspired algorithms (Salp Swarm algorithm [65], Regenerate Genetic Algorithm [66], Particle swarm optimization [67], Artificial Bee Colony [39], and Backtracking Search Optimization [68]) for specific test sets. In particular, the study focused on the use of different PRNGs to define the initial population in each algorithm. The performance of the algorithms was evaluated by testing them on two different numerical benchmark sets and by applying them to nine real-world problems. The results of the study show that the use of different PRNGs indeed affects the results of the optimization process of each of the five selected algorithms. Thus, the quality of the PRNGs themselves is very important for the randomization phase.

This was also proven in [19], where an extensive analysis of 29 existing PRNGs was performed to determine the quality of each PRNG. These include PRNGs from all three classifications into which PRNGs are divided: linear congruential generator, linear feedback shift register, and cellular automation. Empirical tests for PRNGs attempt to demonstrate the non-randomness of the particular PRNG. Both types of empirical tests used to test PRNGs are included in this analysis: blind tests and graphical tests. Of the blind or statistical tests, the well-known tests Diehard [69], TestU01 [70], and NIST [71] were used in this analysis. Of the graphical tests, the Lattice test and the space–time diagram [72] were selected. The 64-bit and 32-bit versions of the SFMT pseudorandom number generator (hereafter referred to as SFMT-64 and SFMT-32) were found to be the best PRNGs. These PRNGs are used in our hybrid algorithm for all stages of randomization within the optimization process. In addition, the standard PRNGs commonly used when writing program code in a particular programming language, rand() and random(), ranked 23rd and 24th, respectively, out of 29 PRNGs tested. It can be assumed that SFMT-64 and SFMT-32 affect the quality of the solutions found for the given optimization problem, which will be proven in Section 5.

3. Basic Components of the New Hybrid Metaheuristic Algorithm

In this section, we briefly review the basic components of our novel hybrid metaheuristic algorithm, whose optimization process is explained in detail in Section 4. First, we introduce the Genetic Algorithm (GA) and the African Buffalo Optimization (ABO) as nature-inspired algorithms that are integral parts of our hybrid solution. It is important to note that our hybrid metaheuristic algorithm can be adapted with minimal changes to combine some other metaheuristic algorithms in its optimization process. As mentioned before, in this work, the combination of GA as the most famous representative of nature-inspired metaheuristics with ABO as one of the representatives of the “newer” nature-inspired metaheuristic algorithms was chosen. We then discuss the SFMT-64 and SFMT-32 pseudorandom number generators, which are used to generate random numbers at all stages of the optimization process.

3.1. Genetic Algorithm (GA)

As stated before, GA is a nature-inspired metaheuristic that simulates the process of natural selection. The optimization process using GA starts with the definition of a random sample set of potential solutions, called the initial population. Each solution within this population is called a chromosome and consists of a set of genes. These genes collectively represent a potential solution to the given optimization problem. A fitness function is used to evaluate the efficiency of each chromosome. In subsequent generations, GA applies the core mechanisms of natural selection such as selection, crossover, and mutation to improve the solutions. In selection, certain chromosomes from the previous population are selected for the next generation. Normally, chromosomes with a better fitness function have a higher probability of being included in the next generation. In crossover, two chromosomes are combined to produce a more favorable chromosome for the next generation. Crossover of efficient chromosomes produces offspring chromosomes with improved characteristics (genes). Mutation changes genes within a chromosome to find better solutions and avoid remaining in the local optimum during the optimization process. Algorithm 1 shows the pseudocode for GA.

Algorithm 1. The pseudocode of GA

3.2. African Buffalo Optimization (ABO)

The behavior of African buffaloes in the vast forests and savannahs of Africa served as inspiration for the African Buffalo Optimization (ABO) algorithm. Since African buffaloes have always been known to be highly organized and remarkably successful herbivores [73], this metaheuristic algorithm attempts to leverage the natural intelligence of buffaloes to produce high-quality metaheuristics. A notable feature is their remarkable memory capacity, which allows buffaloes to retain knowledge of their routes over great distances for thousands of miles across the landscape. In the algorithm, when changing the position (solution) of each buffalo, the best previous position of that buffalo is always included in the calculation to simulate the remarkable memory capacity of these animals. Moreover, they communicate effectively through their vocalizations, especially their distinctive “waaa” calls, which serve a variety of purposes, such as signaling danger or finding a good food source. This behavior is introduced in the algorithm in such a way that the calculation of the new position (solution) of each buffalo also considers the position (solution) of the current best buffalo, towards which the other buffaloes of the herd are also moving. By implementing this previously described behavior of continuously updating the position of each buffalo based on its own historical best position and the current position of the overall best buffalo within the herd, the algorithm ABO successfully solves the problem of premature convergence or stagnation during the optimization process, allowing for a comprehensive exploration of the search space. This was proven in [74], where this algorithm obtained excellent results on the test sets of the well-known Travel-Salesman optimization problem. Algorithm 2 shows the pseudocode for ABO.

Algorithm 2. The pseudocode of ABO

The main formula (Algorithm 2, line 15) within the ABO algorithm that determines the parameter mk that affects the new position of an individual bison (solution) relative to its historical best position (that individual’s best solution) and relative to the current best position (the global best solution) is as follows:

$$mk=mk+\mathit{lp}1*({bg}_{max}-P_j)+\mathit{lp}2*({PLocal}_{max,j}-P_j),$$

(1)

where P_j is the current position (solution) of buffalo j, bg_max is the global best solution, and PLocal_max,j is the historical best position (solution) of buffalo j. The parameter mk is used to determine the new position P_j of buffalo j (Algorithm 2, line 16). The parameters lp1 and lp2 determine whether bison follows its best position or the position of the best global solution. In each iteration of the ABO algorithm, the global best solution and the historical best solution of each bison must also be updated if there has been a change. Then, the process is repeated until the condition for the termination of the algorithm is met.

3.3. SFMT Pseudorandom Number Generators

The SFMT pseudorandom number generator is recognized as one of the leading PRNGs. In this subsection, both the 64-bit (SFMT-64) and 32-bit (SFMT-32) versions are described. These PRNGs play an important role in our hybrid algorithm, as they serve as the main source of randomness throughout the optimization process. As mentioned earlier, SFMT-64 and SFMT-32, which were among the best-performing PRNGs in a comparative study by [20], proven to be clearly superior solutions compared to commonly used standard PRNGs such as rand() and random(). For this reason, they were selected as part of our hybrid solution in this paper.

3.3.1. SFMT-64 Pseudorandom Number Generator

As mentioned earlier, SFMT-64 is a PRNG that belongs to the SFMT family of PRNGs. This PRNG efficiently generates random numbers of high quality. The period of SFMT-64, as the part in its name implies (64), is 2¹⁹⁹³⁷ − 1, which gives a large and practically infinite sequence of random numbers. A PRNG of this quality will improve the randomization phase within the optimization process of our hybrid solution. Algorithm 3 shows the pseudocode for the SFMT-64 pseudorandom number generator.

Algorithm 3. The pseudocode of SFMT-64

The SFMT-64 algorithm begins by defining the required constants, state variables, and period parameters. It then initializes the generator with a given seed value by populating the state array and setting the parameter values. After initialization, it starts generating the next random number. When a predefined threshold is crossed, the algorithm performs a series of bitwise operations on the state array, making the necessary updates to the values that make it up. The algorithm then retrieves the next random number from the state array by referring to the current index and then incrementing it. The resulting random number presented as output embodies a 64-bit pseudorandom value.

3.3.2. SFMT-32 Pseudorandom Number Generator

The pseudorandom number generator SFMT-32 is very similar to the pseudorandom number generator SFMT-64. The basic logic and flow of SFMT-32 are the same as SFMT-64, the main difference being the data types for state variables and generated number variables. SFMT-64 uses unsigned 64-bit integers for state variables and generated numbers, while SFMT-32 uses unsigned 32-bit integers. In the Java programming language, which we will use in evaluating our new hybrid metaheuristic solution that uses SFMT-32 and SFMT-64 in the randomization phase, a 64-bit unsigned integer corresponds to the unsigned long data type, and a 32-bit unsigned integer corresponds to the unsigned data type.

3.3.3. SFMT-64 vs. SFMT-32

Due to its larger state size and longer period, SFMT-64 exhibits better statistical properties and higher randomness compared to SFMT-32. It achieves a higher degree of uniform distribution and reduces the correlation between the generated numbers, leading to the generation of higher quality random sequences. However, it should be noted that SFMT-64 requires more memory and computational resources due to its larger state size.

The choice between SFMT-64 and SFMT-32 depends on the specific requirements of the application. If a longer time period and higher quality random numbers are of utmost importance, SFMT-64 is the preferred option. On the other hand, if considerations such as memory usage and computational efficiency are paramount, SFMT-32 can still provide satisfactory random number generation performance. Therefore, in the evaluation in Section 5, we will use SFMT-64 and SFMT-32 equally to obtain the highest quality randomization phase in the optimization process in the shortest possible time.

4. The Architecture of the Novel Hybrid Metaheuristic Algorithm

In this section, we present our new hybrid metaheuristic algorithm whose architecture successfully combines two basic metaheuristic algorithms by using selected PRNGs for randomization phases within the basic metaheuristic algorithms.

As stated before, the use of a single metaheuristic algorithm is insufficient to solve real-world problems of significant scale. It becomes clear that the effectiveness of the algorithm is limited when it is confronted with different optimization problems that do not correspond to its strengths. The usual drawbacks of metaheuristic algorithms, such as premature convergence and the tendency to local optimization, are widely recognized limitations that arise when solving specific optimization problems with single metaheuristic algorithm.

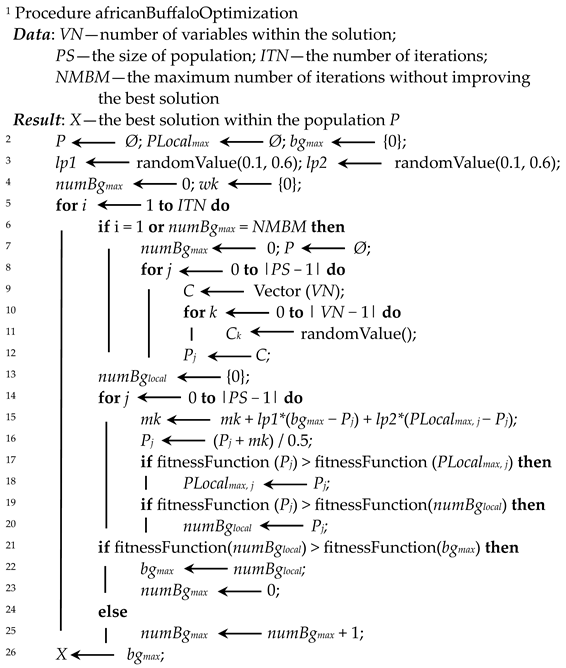
In this work, we have chosen to combine the GA (Genetic Algorithm) and ABO (African Buffalo Optimization) algorithms with the use of the SFMT-64 and SFMT-32 pseudorandom number generators for the random generation phase. It is important to note that this hybrid solution can be easily adapted to use any two metaheuristic algorithms with minor modifications specific to each algorithm. Of course, the number of iterations of the algorithm and the number of possible solutions in an iteration must be the same for both algorithms so that the hybrid solution can simply activate a particular metaheuristic algorithm in a particular optimization phase. Algorithm 4 shows the pseudocode of our new hybrid metaheuristic algorithm.

As input to the algorithm should be included all parameters that are important for both GA and ABO. The number of variables within the solution is here called VN (variable numbers) and also represents the number of genes within the chromosome (solution) in GA and the number of variables within the solution in ABO. PS represents the population size in each iteration of the algorithm. ITN represents the number of iterations of the hybrid algorithm (in GA, it is referred to as the evolution number). The mutation rate in GA is represented by MP and the selection rate in GA by SP. The new parameter is MCI, which gives the maximum number of consecutive iterations for which a single algorithm can be run without improving the overall quality of the solution population. This parameter is the most important part of the new hybrid model, as it is used to determine when to activate a particular individual algorithm within the hybrid solution. When the number of consecutive iterations without quality improvement within the solution population reaches the number of MCI for the same individual algorithm, then the current metaheuristic individual algorithm is deactivated, and another metaheuristic individual algorithm is activated (lines 12–13). The number of consecutive iterations without quality increase within the solution population is stored in the consecutiveIterations variable. After activating the other individual algorithm, the consecutiveIterations variable is set to 0, and the count of consecutive iterations without quality increase within the population is restarted (line 14). In addition to the consecutiveIterations variable being reset to 0 in the above case, the value of the consecutiveABO variable is also set to 0 (line 15) when the switch between algorithms occurs. The variable consecutiveABO is an integral part of the algorithm ABO but must be set to 0 here during the adaptive switch between two algorithms so that, when the algorithm ABO is restarted (immediately after the adaptive switch or after the execution of GA), the value of this variable is set to 0 again.

Based on the value of the variable ITN, the number of iterations to be performed in the hybrid algorithm is determined (lines 5–36). In the first iteration, an initial population of solutions must be randomly generated, with which the optimization process begins (lines 6–11).

Before starting the optimization phase with the single algorithm (GA or ABO), the current overall quality of the population should be calculated at the beginning of each iteration (lines 16–18). The overall quality of each population is defined by the sum of the values of the fitness functions of all solutions within the population, which is set by the variable sumFitnessCurrent. This variable sumFitnessCurrent actually represents the quality of the population obtained in the last iteration. The smaller/larger sumFitnessCurrent is (depending on whether the minimum or maximum of the function is sought), the better the population of solutions. Also, at the beginning of each iteration, the best previous population sumFitnessPrevious should be specified, to which the current population will be compared. This variable sumFitnessPrevious contains the highest quality of the sum of fitness functions over successive iterations within which the quality of the population has not improved. In the case that sumFitnessCurrent at the beginning of the iteration is better than sumFitnessPrevious over the entire period of successive iterations, without any improvement in the quality of the population, the variable sumFitnessPrevious is set to the value of sumFitnessCurrent (lines 19–20). This is also an indicator that the quality of the population has improved in the previous iteration, so the number of successive iterations without improvement in the quality of the population starts again at 0, which will be explained later in detail.

Algorithm 4. The pseudocode of a novel hybrid metaheuristic algorithm

Also, the variable bestSolutionPrevious, which represents the best solution of all populations so far, is set based on the variable bestSolution (line 21), in which the best solution so far was found. The variable bestSolutionPrevious helps to identify in which iteration a better solution than the current best one was found. This information indicates that the individual algorithm currently running in the optimization process is finding good solutions and that the algorithm in the optimization process will remain active for future iterations of the hybrid algorithm.

Thus, the parameters that determine whether a particular individual algorithm is activated/deactivated in an optimization iteration are the sum of the fitness functions of all solutions within the population and the best solution found in the current iteration. After executing the active individual metaheuristic algorithm (lines 23–26), the first step is to check whether there is a solution in the population of the current iteration that is better than the current best solution bestSolution (lines 27–28). If it exists, the variable bestSolution is updated. If the variable bestSolution has been updated, then the best solution of the current population is better than the best solution of all previous populations (bestSolutionPrevious), so the variable consecutiveIterations is set to 0 (lines 35–36). In this way, the activated individual algorithm is run in a larger number of iterations, since this algorithm finds better solutions in contrast to the previous iteration. The same is the case when the sum of fitness functions of all solutions of the current population sumFitnessCurrent (lines 32–34) is of higher quality than the sum of fitness functions of all solutions of the previous population sumFitnessCurrent (lines 35–36). Therefore, the individual algorithm that gives better quality results at a certain point of the optimization process is executed in a larger number of iterations than the other individual algorithm. As mentioned before, if during the execution of the current individual algorithm for a certain number of iterations (defined by MCI) no qualitatively better population is found, the hybrid algorithm deactivates the current individual algorithm and activates the other individual algorithm (lines 12–13).

In order for GA and ABO to work together, an additional change had to be made for GA to store the best solutions obtained during the optimization process for each solution within the population. ABO has implemented this functionality of storage, so this functionality should have been implemented during optimization iterations where GA is active. This is solved by marking the solutions within the population with indices from 0 to PS − 1, which do not change, while the best local solutions are stored in the variable PLocal_max, according to the same indices. The memory of the best solution found during GA or during ABO is updated after the execution of the individual algorithm (lines 29–31). Finally, the best solution (stored in the variable bestSolution) is used as a result of the optimization process in our hybrid metaheuristic algorithm. 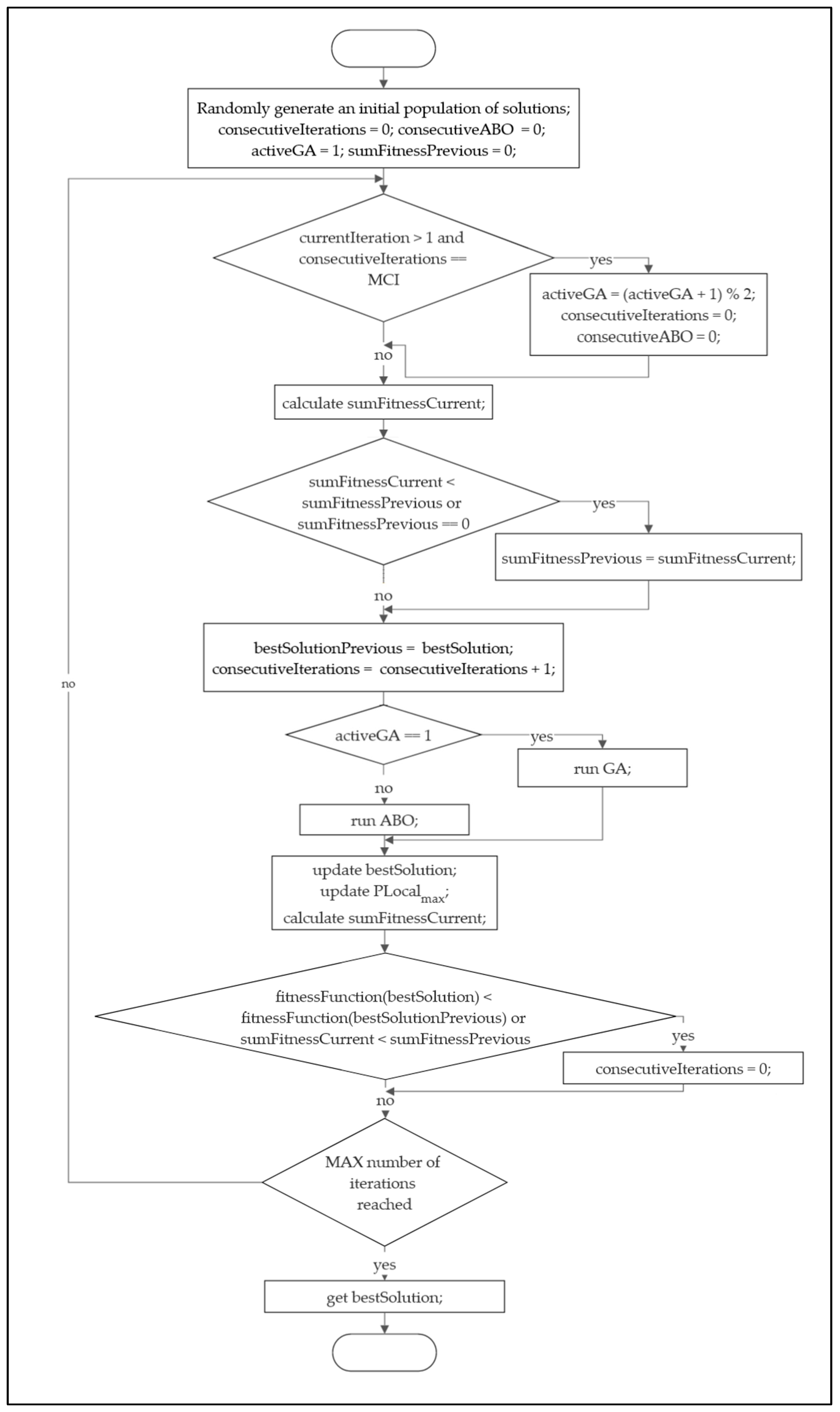Figure 1 shows the flowchart of our new hybrid algorithm.

5. Evaluation and Discussion

For this evaluation, we used a 64-bit Windows 11 operating system with an 11th generation Intel^® Core™ i7-11700 CPU 2.50 GHz processor and 16 GB RAM. The hybrid metaheuristic algorithm described in the previous section, along with the individual metaheuristic algorithms GA and ABO, was implemented in Java using the NetBeans 15 integrated development environment (IDE). No Java library was used for the implementation of all algorithms that are part of the evaluation (GA, ABO, novel hybrid algorithm). Instead, all implementations were created manually from scratch, so the program code for GA and ABO is practically identical to the program code of the hybrid algorithm that uses GA and ABO. Of course, with the necessary changes to the individual algorithms within the hybrid algorithm to make this hybrid solution work.

In this evaluation, we test our new hybrid algorithm on the NP-hard Container Relocation Problem (CRP) using the test set from [36]. As mentioned in the introduction, the main focus of the CRP is to determine an optimal relocation sequence that allows all containers to be retrieved within the designated bay in the container terminal at the port, given their respective priorities and to achieve this goal with as few reshuffles (additional relocations) as possible. The test set consists of restricted CRP, where only the containers blocking the next container to be shipped, may be relocated, which is a much more difficult problem than if other containers may also be relocated (unrestricted CRP) with the goal of minimizing the number of additional relocations. Also, the test set from [36] contains two-dimensional CRPs consisting of one bay with a certain number of columns (stacks) and rows (tiers). The example of a two-dimensional CRP can be seen in Figure 2.

This test set was selected for testing because it contains CRPs with a maximum occupancy of one bay. Thus, in each CRP problem, the maximum possible number of containers is found with respect to the size of the bay. This further complicates the problem and adds weight to the evaluation of our new hybrid algorithm combining GA and ABO together with SFMT-64 and SFMT-32. Considering the number of rows (tiers) R and the number of columns (stacks) C in the bay, the total number of containers that can be placed in the bay is obtained from the formula in [36]:

$$N=C\times R-(R-1),$$

(2)

where N represents the total number of containers in the bay. This ensures that there is a sufficient number of free container positions within the bay to which blocking containers can be shifted.

The evaluation was done for CRPs of different size of the bay. The size of the bay for the first “group” of CRPs has the number of columns (stacks) 3, while the size of the rows (tiers) is 3, 4, 5 and 6, respectively. There are four other “groups” of CRPs with the same row sizes of 3, 4, 5, and 6, and the column sizes are 4, 5, 6, and 7, respectively. Thus, the number of CRPs with different column and row sizes is 20. Each CRP for each bay size (e.g., 3 × 4) consists of 40 different test instances with different layout containers within the bay. The maximum tested bay size (6 × 7) meets the specifications of the latest technological RTG cranes in terms of actual bay sizes in port container terminal.

The results of our new hybrid algorithm, which combines the GA and ABO algorithms with SFMT PRNGs for the randomization phase, are compared with the results of the individual algorithms GA and ABO, and with the results of the Beam Search Algorithm (BSA) [36], which, to our knowledge, represents the best results for this large and relevant test set of CRPs.

For these tests comparing the best possible results of our new hybrid GA + ABO, GA and ABO, certain parameters were established throughout the evaluation process.

Table 1. The setup of new hybrid metaheuristic algorithm GA + ABO, GA, and ABO for resolving CRPs.

Parameter	Value
Number of iterations	500
Population size	15,000
The maximum number of consecutive iterations in the single algorithm without improving best solution	15
Number of variables within the solution	12 × #containers within particular CRP
The selection rate from previous iteration within GA	0.75
The rate of mutation in GA	0.10
The maximum number in ABO without improving the best solution	5
The value of factor lp1 in ABO	0.5
The value of factor lp2 in ABO	0.3
Ratio of use of SFMT-64 and SFMT-32	50/50

shows all the parameters and their corresponding values. After a large number of tests, it was determined that these parameter values were the most appropriate to obtain the best possible results with the hybrid GA + ABO, GA, and ABO. No algorithm achieved better results with a larger number of iterations than 500, as well as with a larger number of solutions within the population, which was set to 15,000. Through a large number of experiments, the other parameter values in the table, which are important for the execution of the algorithms themselves, proven to be the best for solving this test set.

The optimization results obtained with the algorithms GA, ABO, BSA and our new hybrid algorithm for the test set with 20 different sized CRPs are shown in

Table 2. Optimization results of the test set with 20 different sized CRPs obtained with GA, ABO, BSA and the new hybrid algorithm.

Rows × Columns	No. of Containers	New Hybrid GA + ABO	BSA [36]	ABO	GA
3 × 3 4 × 3 5 × 3 6 × 3	7 9 11 13	3.30 5.67 8.40 11.50	3.38 5.67 8.40 11.50	3.30 5.67 8.40 11.58	3.30 5.67 8.40 11.50
3 × 4 4 × 4 5 × 4 6 × 4	10 13 16 19	4.85 8.42 12.25 15.62	4.85 8.43 12.20 15.60	4.85 8.49 12.27 15.63	4.85 8.42 12.25 15.62
3 × 5 4 × 5 5 × 5 6 × 5	13 17 21 25	5.75 10.98 15.58 21.05	5.75 11.00 15.60 21.10	5.76 10.98 15.62 21.48	5.75 10.98 15.60 21.15
3 × 6 4 × 6 5 × 6 6 × 6	16 21 26 31	7.65 12.02 19.32 26.02	7.65 12.00 19.30 26.10	7.65 12.05 19.67 27.25	7.65 12.02 19.35 26.15
3 × 7 4 × 7 5 × 7 6 × 7	19 25 31 37	8.95 15.47 21.35 31.05	8.95 15.50 21.40 31.00	8.95 15.50 22.48 34.98	8.95 15.48 21.42 31.62
Total sum of average relocations		265.20	265.38	272.56	266.13

.

The numbers in bold indicate the best results for a given test set, taking into account the different bay sizes within the CRPs. Compared to the individual algorithms GA and ABO, our novel hybrid algorithm achieved the best result independently or shared the best result with GA or ABO. For the bay sizes 5 × 5, 6 × 5, 4 × 6, 5 × 6, 6 × 6, 4 × 7, 5 × 7, 6 × 7, our hybrid algorithm achieved the best results not sharing with ABO or GA. Thus, it can be concluded that this hybrid variant of the algorithm is very successful in solving the mentioned optimization problems and achieves better results than the individual variants of the algorithms. Thus, the combination of GA and ABO together with the introduction of the pseudorandom number generators SFMT-64 and SFMT-32 led to an improvement in the optimization results. It can also be seen that our hybrid algorithm and the individual algorithms GA and ABO give similar results for CRP with a smaller bay size. As soon as the size of the bay in CRPs increases (i.e., there is a larger number of containers in the bay and the problem becomes more complicated), it can be seen that the hybrid algorithm finds much better solutions than the individual algorithms GA and ABO. For CRPs with a larger bay size, the quality of the hybrid approach and the proposed adaptive switch method, which exploits the best features of GA and ABO together with better PRNGs, consequently leading to much better optimization results, comes into play. Furthermore, this can also be confirmed by examining the optimization results of the BSA algorithm, which to the best of our knowledge has so far produced the best results for this test data set.

Our new hybrid algorithm achieved better overall results than the BSA algorithm. Except for the test instances where BSA and our hybrid algorithm performed equally well (4 × 3, 5 × 3, 6 × 3, 3 × 4, 3 × 5, 3 × 6, 3 × 7), the hybrid algorithm outperformed BSA on 8 test instances (3 × 3, 4 × 4, 4 × 5, 5 × 5, 6 × 5, 6 × 6, 4 × 7, 5 × 7), while BSA achieved better results on 5 test instances (5 × 4, 6 × 4, 4 × 6, 5 × 6, 6 × 7). The overall result of the average additional relocations (referred to as the total sum of average relocations in Table 2) for all test instances shows that our hybrid algorithm achieves better results than BSA (265.20 vs. 265.38), which puts it at the top of the optimization results for this test set, again proving the high quality of this hybrid algorithm.

Apart from the fact that it is very important that an algorithm finds the best possible solution, it is also very important that the algorithm does so in as few iterations as possible to save time and the consumption of resources needed to run the optimization algorithm. The more iterations an algorithm requires to arrive at a satisfactory solution, the longer the activity of the processor and memory, and consequently the power consumption increases. In addition, the prolonged execution of the algorithm can lead to increased cooling requirements of the computer components to maintain temperature control, causing additional energy consumption through cooling processes such as fan operation. Thus, it is not only necessary to find a good enough solution, but also to use an algorithm that finds a good enough solution faster, thus minimizing execution time, processor activity, and cooling requirements, thereby decreasing power consumption during algorithm execution. Understanding these differences in energy efficiency is critical to developing greener computing practices.

Our new hybrid algorithm, using the SFMT-64 and SFMT-32 pseudorandom number generators, converges to better solutions faster than the individual algorithms GA and ABO. As mentioned earlier, this reduces the execution time of the algorithm, the use of the required resources, and consequently the power consumption. Accordingly, an analysis of the effectiveness of GA, ABO and our new hybrid GA + ABO was performed in terms of the number of iterations of the metaheuristic algorithms and the size of the population in each iteration. For this analysis, the parameter values from Table 1 were used, focusing on different values for the number of iterations of the algorithm ITN (100, 200, 500) and the population size PS (number of solutions) within an iteration (100, 500 and 1000). Thus, considering three different values for the number of iterations and for the population size, 9 different tests were performed for GA, ABO and our new hybrid algorithm for each of the above 20 different sized CRPs. Given the small number of iterations and the size of the population, the optimization results will not be the best possible for each algorithm. Therefore, for each individual test, 10 iterations of the execution of each algorithm were performed and the average value obtained by each algorithm was taken. It is important to emphasize again that the goal of these tests is to find out which of the algorithms finds better solutions in the test sets faster. Therefore, smaller values were chosen for both the number of iterations and the population size.

Table 3. The results of CRP test instances for column dimensions 3–4 and all row dimensions 3–6 for tests with different combination values of the population size and number of iterations obtained by the proposed hybrid algorithms and the individual algorithms GA and ABO.

	GA + ABO	GA	ABO		GA + ABO	GA	ABO
ITN × PS		3 (row) × 3 (col)		ITN × PS		3 (row) × 4 (col)
100 × 100	3.30	3.30	3.30	100 × 100	4.85	4.85	4.85
100 × 500	3.30	3.30	3.30	100 × 500	4.85	4.85	4.85
100 × 1000	3.30	3.30	3.30	100 × 1000	4.85	4.85	4.85
200 × 100	3.30	3.30	3.30	200 × 100	4.85	4.85	4.85
200 × 500	3.30	3.30	3.30	200 × 500	4.85	4.85	4.85
200 × 1000	3.30	3.30	3.30	200 × 1000	4.85	4.85	4.85
500 × 100	3.30	3.30	3.30	500 × 100	4.85	4.85	4.85
500 × 500	3.30	3.30	3.30	500 × 500	4.85	4.85	4.85
500 × 1000	3.30	3.30	3.30	500 × 1000	4.85	4.85	4.85
		4 (row) × 3 (col)				4 (row) × 4 (col)
100 × 100	5.67	5.67	5.67	100 × 100	8.42	8.42	8.42
100 × 500	5.67	5.67	5.67	100 × 500	8.42	8.42	8.42
100 × 1000	5.67	5.67	5.67	100 × 1000	8.42	8.42	8.42
200 × 100	5.67	5.67	5.67	200 × 100	8.42	8.42	8.42
200 × 500	5.67	5.67	5.67	200 × 500	8.42	8.42	8.42
200 × 1000	5.67	5.67	5.67	200 × 1000	8.42	8.42	8.42
500 × 100	5.67	5.67	5.67	500 × 100	8.42	8.42	8.42
500 × 500	5.67	5.67	5.67	500 × 500	8.42	8.42	8.42
500 × 1000	5.67	5.67	5.67	500 × 1000	8.42	8.42	8.42
		5 (row) × 3 (col)				5 (row) × 4 (col)
100 × 100	8.4	8.4	8.4	100 × 100	12.25	12.3	12.35
100 × 500	8.4	8.4	8.4	100 × 500	12.25	12.25	12.33
100 × 1000	8.4	8.4	8.4	100 × 1000	12.25	12.25	12.31
200 × 100	8.4	8.4	8.4	200 × 100	12.25	12.26	12.36
200 × 500	8.4	8.4	8.4	200 × 500	12.25	12.25	12.31
200 × 1000	8.4	8.4	8.4	200 × 1000	12.25	12.25	12.28
500 × 100	8.4	8.4	8.4	500 × 100	12.25	12.25	12.32
500 × 500	8.4	8.4	8.4	500 × 500	12.25	12.25	12.3
500 × 1000	8.4	8.4	8.4	500 × 1000	12.25	12.25	12.28
		6 (row) × 3 (col)				6 (row) × 4 (col)
100 × 100	11.5	11.5	11.61	100 × 100	15.62	16.01	15.85
100 × 500	11.5	11.5	11.60	100 × 500	15.62	15.71	15.68
100 × 1000	11.5	11.5	11.58	100 × 1000	15.62	15.73	15.71
200 × 100	11.5	11.5	11.60	200 × 100	15.62	15.86	15.75
200 × 500	11.5	11.5	11.60	200 × 500	15.62	15.74	15.69
200 × 1000	11.5	11.5	11.58	200 × 1000	15.62	15.66	15.63
500 × 100	11.5	11.5	11.60	500 × 100	15.62	15.75	15.71
500 × 500	11.5	11.5	11.60	500 × 500	15.62	15.64	15.63
500 × 1000	11.5	11.5	11.58	500 × 1000	15.62	15.65	15.63

shows the average test results of our new hybrid algorithm GA + ABO and the individual algorithms GA and ABO, for column (stacks) sizes 3 and 4 and all possible row (tier) sizes from 3 to 6 with different combinations of the number of iterations ITN of the individual algorithm along with the population size PS of each iteration.

It can be seen that for a small number of rows and columns, all three algorithms work similarly and converge to the best possible solutions as fast as possible. Therefore, for CRP problems with a smaller number of columns and rows, it is not necessary to run metaheuristic algorithms with a large number of iterations and a large population size of each iteration (as in the evaluation section in Table 2). The first significant differences in results are observed for test instances of size 6 (rows) × 4 (columns), where our hybrid algorithm immediately converges to the best possible solution even for the combination of ITN and PS 100 × 100, while GA and ABO converge to better solutions (not the best) only when the parameters of ITN and PS are higher. Although this table shows test instances with a smaller number of containers, there is little indication of how the result turns out for larger test instances of CRP, where our new hybrid algorithm achieved the best results.

The average test results of our new hybrid algorithm GA + ABO and the individual algorithms GA and ABO, for column (stacks) size 5 and all possible row (tier) sizes from 3 to 6 with different combinations of the number of iterations ITN of the individual algorithm along with the population size PS of each iteration can be seen in

Table 4. The results of CRP test instances for a column dimension of 5 and all row dimensions 3–6 for tests with different combination values of population size and number of iterations obtained by the proposed hybrid algorithms and the individual algorithms GA and ABO.

	GA + ABO	GA	ABO		GA + ABO	GA	ABO
ITN × PS		3 (row) × 5 (col)		ITN × PS		5 (row) × 5 (col)
100 × 100	5.75	5.75	5.84	100 × 100	15.58	15.99	15.91
100 × 500	5.75	5.75	5.84	100 × 500	15.58	15.73	15.88
100 × 1000	5.75	5.75	5.85	100 × 1000	15.58	15.68	15.68
200 × 100	5.75	5.75	5.85	200 × 100	15.58	15.84	15.84
200 × 500	5.75	5.75	5.83	200 × 500	15.58	15.68	15.68
200 × 1000	5.75	5.75	5.85	200 × 1000	15.58	15.60	15.65
500 × 100	5.75	5.75	5.85	500 × 100	15.58	15.70	15.74
500 × 500	5.75	5.75	5.83	500 × 500	15.58	15.60	15.64
500 × 1000	5.75	5.75	5.86	500 × 1000	15.58	15.60	15.63
		4 (row) × 5 (col)				6 (row) × 5 (col)
100 × 100	10.98	11	11.01	100 × 100	21.25	22.075	23.01
100 × 500	10.98	10.98	10.98	100 × 500	21.15	21.61	22.53
100 × 1000	10.98	10.98	10.98	100 × 1000	21.09	21.51	22.34
200 × 100	10.98	10.98	10.99	200 × 100	21.23	21.79	22.75
200 × 500	10.98	10.98	10.98	200 × 500	21.09	21.34	22.35
200 × 1000	10.98	10.98	10.98	200 × 1000	21.06	21.20	22.25
500 × 100	10.98	10.98	10.98	500 × 100	21.09	21.33	22.60
500 × 500	10.98	10.98	10.98	500 × 500	21.06	21.18	22.11
500 × 1000	10.98	10.98	10.98	500 × 1000	21.05	21.15	22.03

.

Here we can already see how our new hybrid algorithm with the pseudorandom number generators SFMT-64 and SFMT-32 achieves very good optimization results for these test instances in fewer iterations and with a smaller population size within an iteration. For the test instances of 3 × 5 and 4 × 5, the difference between the hybrid algorithm and the individual algorithms GA and ABO is not so large, but for the sizes of CRPs of 5 × 5 and 6 × 5, the quality of our new hybrid solution can be observed. For the size of 5 × 5, our hybrid algorithm already converges to the best solution when combining ITN and PS 100 × 100, while GA and ABO do not reach the best solution even when combining ITN and PS 500 × 1000. In this way, the hybrid GA + ABO can save computer resources, shorten the algorithm execution time and consequently reduce power consumption, which is one of the main tasks in all industries including computer science nowadays.

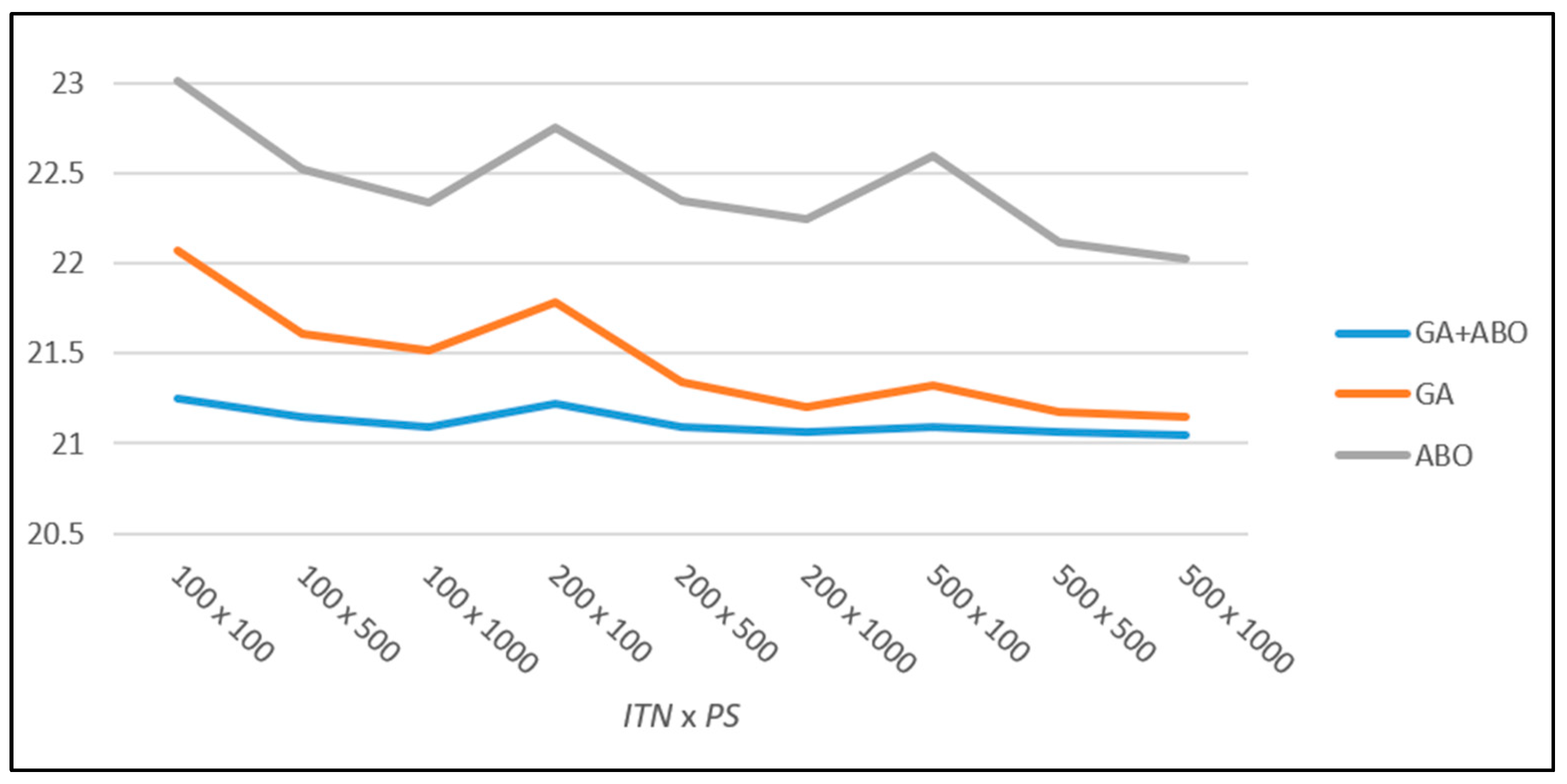
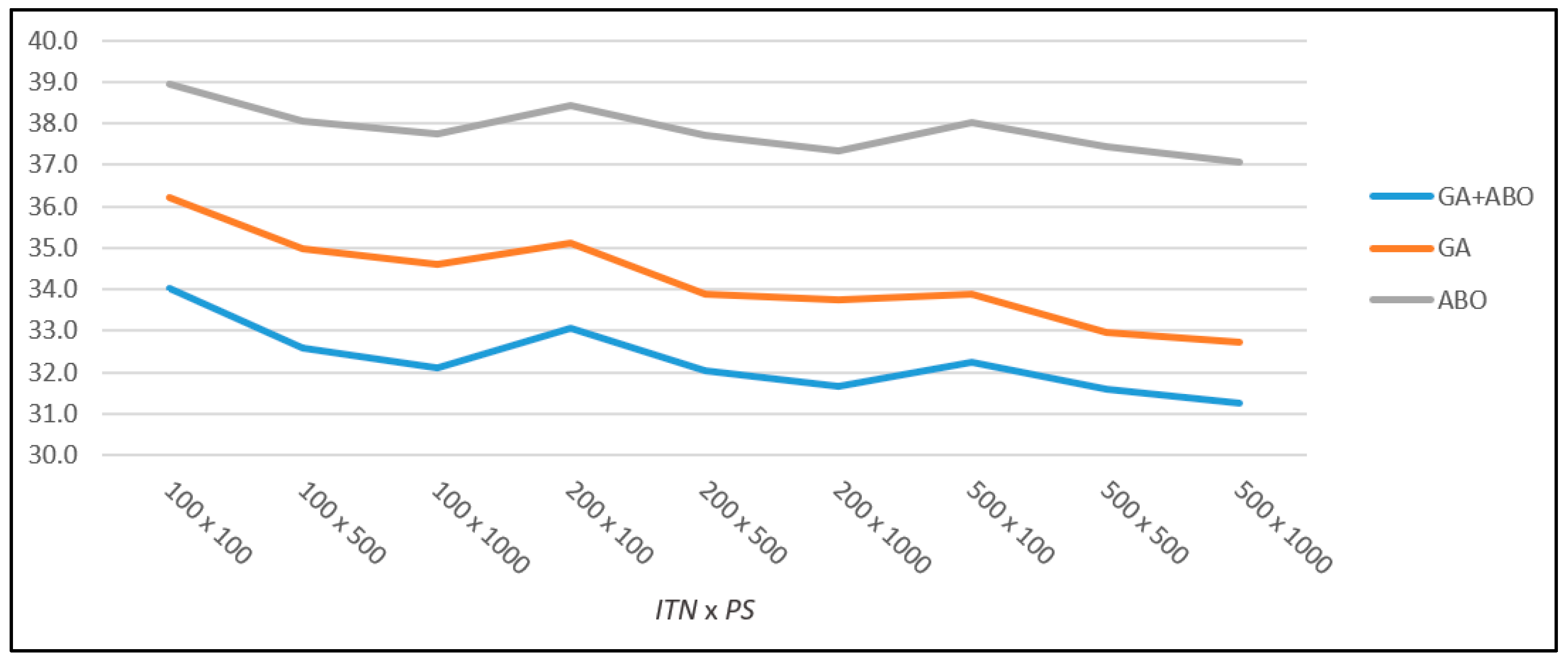
Moreover, our hybrid algorithm proven to be the best even with a CRP size of 6 × 5. It very quickly reached solutions that were close to the best solution (reached in Table 2), while the individual algorithms GA and ABO converged more slowly to better solutions. This difference in convergence is better seen in Figure 3, where the graph shows the average test results of our new hybrid algorithm GA + ABO and the individual algorithms GA and ABO for a CRP size of 6 × 5. There you can see a significant difference in the results obtained for different combinations of ITN and PS. The optimization results for the single algorithms GA and ABO decrease slightly as ITN and PS increase. The same happens with the hybrid GA + ABO, except that our algorithm converges very quickly to very good solutions for these test instances, which is already visible for the combination of ITN and PS of 100 × 100.

For CRPs with 6 columns, the difference in optimization results is even larger.

Table 5. The results of CRP test instances for a column dimension of 6 and all row dimensions 3–6 for tests with different combination values of population size and number of iterations obtained by the proposed hybrid algorithms and the individual algorithms GA and ABO.

	GA + ABO	GA	ABO		GA + ABO	GA	ABO
ITN × PS		3 (row) × 6 (col)		ITN × PS		5 (row) × 6 (col)
100 × 100	7.65	7.65	7.68	100 × 100	19.54	21.00	21.34
100 × 500	7.65	7.65	7.65	100 × 500	19.35	20.43	20.74
100 × 1000	7.65	7.65	7.65	100 × 1000	19.34	20.18	20.56
200 × 100	7.65	7.65	7.65	200 × 100	19.44	20.79	21.15
200 × 500	7.65	7.65	7.65	200 × 500	19.32	20.18	20.54
200 × 1000	7.65	7.65	7.65	200 × 1000	19.32	19.98	20.28
500 × 100	7.65	7.65	7.65	500 × 100	19.32	20.44	20.91
500 × 500	7.65	7.65	7.65	500 × 500	19.32	19.93	20.31
500 × 1000	7.65	7.65	7.65	500 × 1000	19.32	19.78	20.06
		4 (row) × 6 (col)				6 (row) × 6 (col)
100 × 100	12.02	12.24	12.23	100 × 100	27.19	28.93	30.88
100 × 500	12.02	12.06	12.09	100 × 500	26.64	27.90	29.56
100 × 1000	12.02	12.06	12.08	100 × 1000	26.25	27.63	29.45
200 × 100	12.02	12.20	12.16	200 × 100	26.95	28.14	30.04
200 × 500	12.02	12.06	12.09	200 × 500	26.35	27.33	29.28
200 × 1000	12.02	12.05	12.06	200 × 1000	26.20	27.04	29.08
500 × 100	12.02	12.09	12.09	500 × 100	26.69	26.99	29.61
500 × 500	12.02	12.05	12.06	500 × 500	26.21	26.71	29.03
500 × 1000	12.02	12.02	12.06	500 × 1000	26.10	26.46	28.68

shows the average test results of our new hybrid algorithm and the individual algorithms GA and ABO, for columns (stacks) of size 6 for tests with different combination values of the ITN and the PS of each iteration.

For a CRP with a size of 3 × 6, there is no difference in the optimization results but already for a CRP with a size of 4 × 6, it can be seen that our hybrid algorithm reaches its best possible result already in the tests with the combination values of ITN and PS 100 × 100, while the individual GA reaches its best possible result only in the tests with the combination values of ITN and PS 500 × 1000. 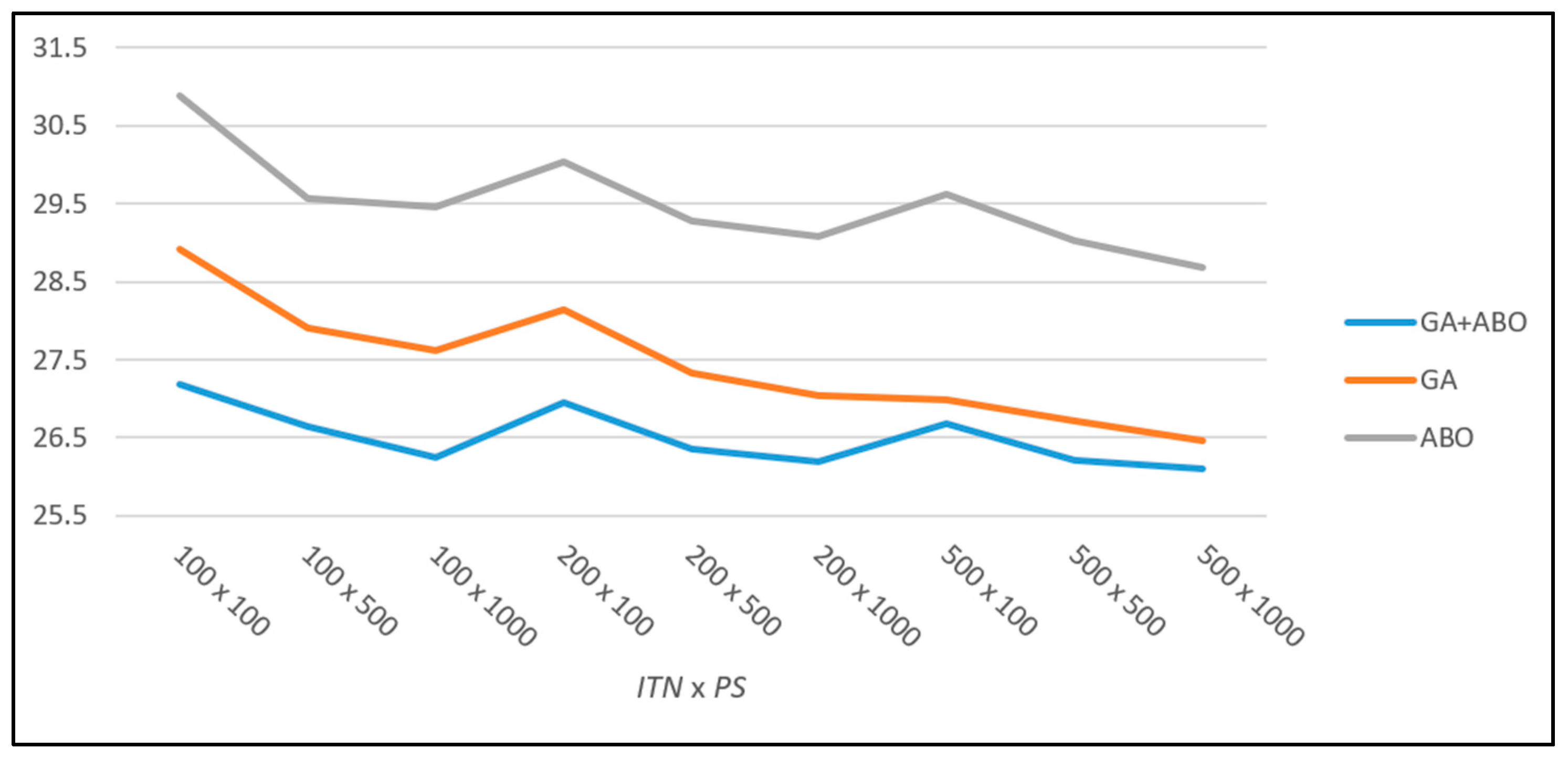The individual ABO does not reach its best result of 12.05, even in the tests with the combination of ITN and PS 500 × 1000. The biggest difference in convergence to the best optimization results is seen in CRP with a size of 6 × 6, which graphical representation can be seen in Figure 4. For the tests where the values of ITN and PS are smaller, a significant difference in convergence to better solutions can be seen. In the tests with ITN and PS 500 × 1000, it can be seen that GA converges to GA + ABO, while the individual results of ABO are much weaker. Again, this shows that the new hybrid algorithm can achieve very good solutions in less time and with fewer resources, while reducing the power consumption to solve this optimization problem.

The final comparison of optimization results of our new algorithm with individual GA and ABO was performed for CRPs with seven columns, which is the most complex set of test instances of CRPs for realistic bay sizes in a port container terminal. This is where the difference in optimization results is greatest for the algorithms compared.

Table 6. The results of CRP test instances for a column dimension of 7 and all row dimensions 3–6 for tests with different combination values of the population size and number of iterations obtained by the proposed hybrid algorithms and the individual algorithms GA and ABO.

	GA + ABO	GA	ABO		GA + ABO	GA	ABO
ITN × PS		3 (row) × 7 (col)		ITN × PS		5 (row) × 7 (col)
100 × 100	8.95	8.96	8.95	100 × 100	21.75	24.14	24.18
100 × 500	8.95	8.95	8.95	100 × 500	21.51	23.34	23.61
100 × 1000	8.95	8.95	8.95	100 × 1000	21.43	23.05	23.41
200 × 100	8.95	8.95	8.95	200 × 100	21.59	23.71	23.81
200 × 500	8.95	8.95	8.95	200 × 500	21.43	23.18	23.25
200 × 1000	8.95	8.95	8.95	200 × 1000	21.39	22.83	23.11
500 × 100	8.95	8.95	8.95	500 × 100	21.44	23.34	23.44
500 × 500	8.95	8.95	8.95	500 × 500	21.41	22.75	22.98
500 × 1000	8.95	8.95	8.95	500 × 1000	21.35	22.46	22.73
		4 (row) × 7 (col)				6 (row) × 7 (col)
100 × 100	15.50	16.06	15.95	100 × 100	34.01	36.20	38.95
100 × 500	15.47	15.75	15.88	100 × 500	32.59	34.98	38.05
100 × 1000	15.47	15.61	15.68	100 × 1000	32.11	34.59	37.74
200 × 100	15.47	15.94	15.89	200 × 100	33.05	35.11	38.43
200 × 500	15.47	15.65	15.65	200 × 500	32.03	33.89	37.71
200 × 1000	15.47	15.58	15.68	200 × 1000	31.66	33.76	37.33
500 × 100	15.47	15.68	15.83	500 × 100	32.25	33.88	38.03
500 × 500	15.47	15.56	15.60	500 × 500	31.58	32.95	37.45
500 × 1000	15.47	15.50	15.55	500 × 1000	31.25	32.73	37.06

shows the average test results of our new hybrid algorithm and the individual algorithms GA and ABO for columns (stacks) of size 7 for tests with different combination values of the ITN and the PS of each iteration.

In this table, one can already see the difference in the results for the test instance with four rows, where our hybrid algorithm again proved to be the best. For the test instances with five and six rows, the difference in results is even more pronounced. Figure 5 shows the graphical average test results of our hybrid algorithm GA + ABO and the individual algorithms GA and ABO for a CRP size of 6 × 7 with different combinations of the number of iterations ITN and the population size PS.

In this table, one can already see the difference in the results. In this most complex CRP, it can be seen that our hybrid algorithm achieves better results when the values of ITN and PS increase. In this test instance, no algorithm immediately achieves anywhere near the best results. However, a large difference in convergence to better solutions can be seen between all three algorithms. Again, the hybrid algorithm achieves the best results, followed by the individual GA and then ABO.

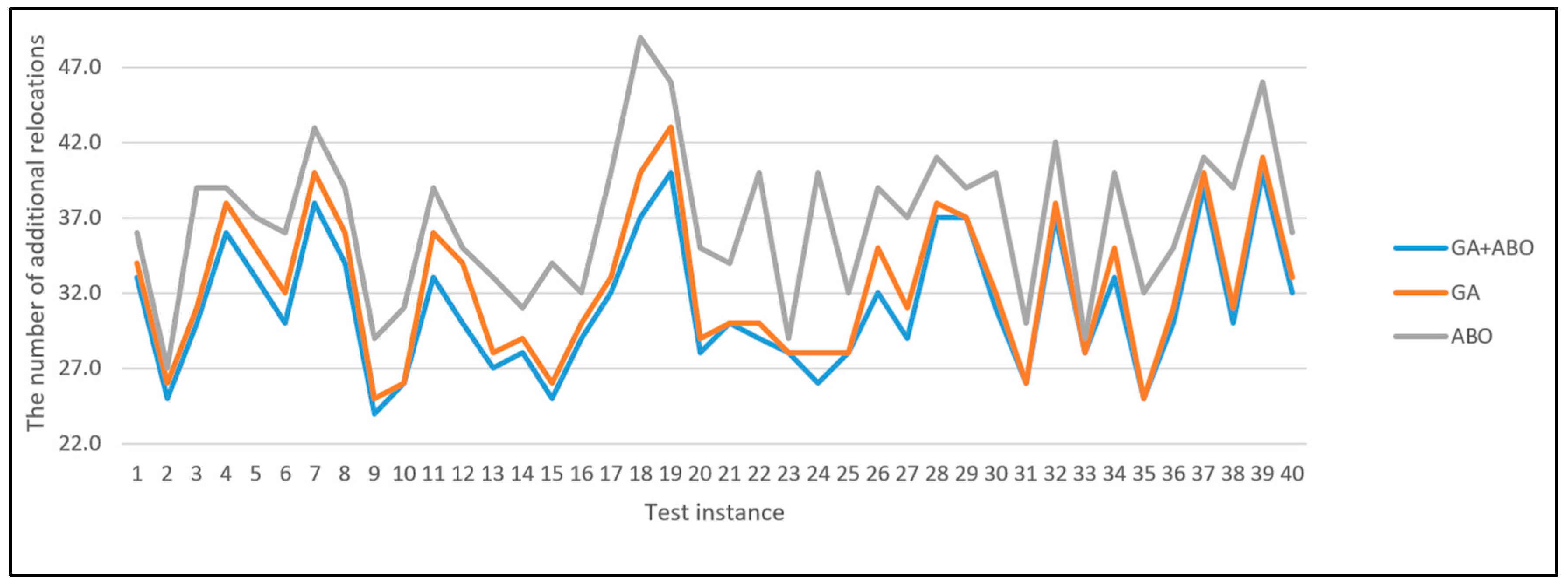
In addition, Figure 6 shows a comparison of the optimization results (the number of additional relocations) of the algorithms GA + ABO, GA, and ABO based on each of the 40 test instances of the large CRP test set with size 6 × 7 for the parameter values ITN and PS 500 × 1000.

In this figure, you can see the difference in the results of the compared algorithms for individual test instances that have different arrangements of containers within the bay. For some instances, all three algorithms give the same results, but in most instances, it can be seen that hybrid GA + ABO gives the best results (the smallest number of additional relocations).

It is also interesting to compare the times required for the compared algorithms to achieve the same optimization result for each of the 40 test instances. This time comparison gives a clear picture of how much faster GA + ABO finds very good solutions for a given CRP. For the tests from Table 2, we did not report the execution time because we set the maximum parameter values (Table 1) so that the results were as good as possible for all three algorithms, but the execution time was very slow for all of them. However, our hybrid algorithm achieved its best solutions much faster (before reaching the maximum number of iterations) than any of GA and ABO during this test. Therefore, the timing data for tests in Table 2 is not relevant for comparing these three algorithms. Thus, to be sure that GA + ABO solves the problems faster than GA and ABO, we performed the following test to determine how quickly all three algorithms achieve the same specified high-quality solution for CRP test instances with a bay size 6 × 7. In this evaluation of the time required to retrieve a given optimization result, the solutions obtained from GA are set as the reference results that the algorithms must retrieve. Since ABO provided the worst optimization results and may not be able to retrieve the optimization reference results obtained by GA for some of the 40 test instances, we include it in this test and stop the evaluation for a particular test instance if the time to retrieve the best result exceeds 60 s. We did not use the results of ABO as reference results for this evaluation, because we believe that GA + ABO and GA would very quickly reach the solution obtained by ABO for this 6 × 7 test set, so the difference between the algorithms would not be noticeable. The size of the population PS remains the same (1000), while the number of iterations ITN depends on the time at which each algorithm reaches the reference result for each of the individual 40 test instances. For each algorithm and for each of the 40 test instances, 10 tests were performed to determine the average retrieval time of the reference result for each algorithm for all 40 test instances.

Table 7. Average time to obtain GA reference results with the hybrid GA + ABO, GA, and ABO for all 40 test instances of CRP with a bay size 6 × 7.

Test Instance	GA + ABO	GA	ABO
1	6.3	22.0	N/A
2	1.7	5.0	45.3
3	3.3	6.3	N/A
4	5.0	18.0	49.2
5	6.0	17.0	N/A
6	2.0	3.7	N/A
7	3.7	10.7	N/A
8	3.3	6.0	53.1
9	6.3	8.7	N/A
10	1.7	5.7	N/A
11	3.0	9.0	N/A
12	1.0	2.3	43.8
13	4.0	8.0	N/A
14	0.7	4.3	N/A
15	5.3	8.7	N/A
16	1.0	9.7	39.7
17	3.3	18.3	N/A
18	2.7	6.3	N/A
19	1.7	5.0	36.9
20	1.3	5.0	N/A
21	3.3	12.3	N/A
22	16.3	20.3	N/A
23	3.3	9.7	25.4
24	5.0	13.7	N/A
25	3.7	9.7	N/A
26	3.0	6.3	N/A
27	1.0	3.7	N/A
28	4.0	15.7	N/A
29	9.0	46.7	N/A
30	2.3	10.7	N/A
31	1.3	3.3	42.6
32	15.3	20.3	49.7
33	3.0	2.7	20.5
34	4.0	23.3	55.7
35	5.3	9.7	N/A
36	8.7	12.7	N/A
37	2.0	5.0	10.9
38	1.0	7.3	N/A
39	6.3	15.7	N/A
40	1.7	6.7	N/A
Average time	4.1	10.9	N/A

shows the average time to obtain GA reference results with the hybrid GA + ABO, GA, and ABO for all 40 test instances of CRP with a bay size 6 × 7.

We can see how our hybrid algorithm outperforms GA and ABO in speed of convergence to the best solutions. ABO is very slow here, although it finds very good solutions for a large number of iterations, but here, we limited ourselves to obtaining GA reference results within 60 s for each of the 40 test instances. The hybrid algorithm achieved the best time for 39 out of 40 test instances of CRP with the size 6 × 7. Moreover, the average time of all average times (4.1) of the hybrid algorithm is more than two times faster than the average time of the single GA algorithm (10.9). At this point, it should be noted that the difference in the performance of the algorithms would be even greater if the reference results for which the retrieval time is requested were set to the values achieved by our hybrid algorithm in tests using a combination of ITN and PS 500 × 1000 values. Also, it is important to emphasize that the high-quality PRNGs SFMT-64 and SFMT-32 used in our hybrid algorithm have much higher temporal complexity than standard PRNGS like random() or rand() used in individual GA and ABO. However, by using SFMT-64 and SFMT-32 in the randomization phase, the best solutions were reached much earlier. It can be concluded that the quality of SFMT-64 and SFMT-32 exceeded the temporal complexity of these PRNGs and fully justified their inclusion in our hybrid algorithm. Moreover, after each iteration within the optimization phase, our hybrid algorithm must compute the quality of the obtained solutions from the previous iteration to determine which single algorithm to use in the next iteration. This should further slow down our algorithm. Considering that our algorithm is much faster than the single GA and ABO, it is proven that our hybrid algorithm takes advantage of the best features of GA and ABO in searching the solution space and obtains much better results in much less time using high-quality PRNGs.

In conclusion, the scientific research of hybrid algorithms using the best features of individual algorithms is justified. Moreover, the use of better PRNGs leads to better randomization in the optimization process and thus to better solutions in less time. In this way, time and resources are saved and so is the consumption of electrical energy, which is important today for several reasons, including reducing resource consumption, protecting the environment, reducing greenhouse gas emissions, and ensuring long-term sustainability and stability in the energy sector.

6. Conclusions and Future Studies

Optimization plays an important role in science and technology today, as it aims to find the best solution to problems. In computer science, it is particularly important to develop algorithms that produce high-quality results with as few resources as possible. Real-world optimization problems, which are often NP-hard, benefit from the use of metaheuristics because they provide computationally efficient solutions to complex challenges. Today, metaheuristic algorithms are well established in computer science and mathematical optimization, providing faster and computationally efficient solutions. However, using only one metaheuristic algorithm to solve a particular optimization problem sometimes leads to premature convergence and local optima and can reduce the quality of the optimization. To overcome this limitation, hybrid metaheuristic algorithms are developed by combining multiple metaheuristic algorithms to exploit their respective strengths and mitigate weaknesses.

In this paper, a new hybrid nature-inspired metaheuristic algorithm based on GA and ABO is proposed for optimizing real-world problems. The dynamic switching mechanism between GA and ABO within the optimization process allows the algorithm to adapt to different problem characteristics and improve the overall performance. In contrast to the traditional sequential execution, an adaptive switch is incorporated into the hybrid algorithm that dynamically selects either GA or ABO based on their performance in the previous iteration. This innovative adaptive approach contributes to higher efficiency and robustness in solving complex optimization problems. Moreover, this hybrid algorithm can be easily modified to base the optimization process on two other metaheuristic algorithms. Moreover, one of the features of this new hybrid algorithm is the use of selected PRNGs in the randomization process. To improve the performance of the hybrid algorithm, two high quality PRNGs, SFMT-64 and SFMT-32, were used, which had a significant impact on the ability of the algorithm to avoid premature convergence and local optima, leading to better optimization results.

The hybrid algorithm was evaluated on the NP-hard CRP problem, focusing on a restricted CRP due to its higher complexity. The experimental results show the effectiveness of the proposed hybrid solution, outperforming the individual algorithms GA and ABO, which use standard PRNGs. The hybrid algorithm also achieves the best optimization results for the tested CRPs and outperforms state-of-the-art optimization methods.

In the future, it would be interesting to test this new hybrid algorithm with some other individual nature-inspired metaheuristic algorithms, not only GA and ABO built into the hybrid algorithm. In this way, for any optimization problem in engineering, one could find a suitable pair of algorithms whose properties correspond to the optimization problem to be solved. Moreover, this hybrid algorithm could be extended to three or more algorithms which activation within the hybrid algorithm is implemented by a dynamic switching mechanism as in this work. Moreover, the dynamic switching mechanism could be improved by introducing some new performance methods of the individual algorithm that evaluate how well the currently active individual algorithm has performed in previous iterations. Furthermore, by refining the dynamic switching mechanism based on real-time performance evaluations, the hybrid algorithm has the potential to dynamically adjust and refine its algorithmic composition during runtime, increasing its efficiency and effectiveness in solving optimization tasks in a variety of domains. As for the CRP problem we used to evaluate our hybrid algorithm in this paper, it would be interesting to generate a restricted 3D CRP with the maximum occupancy of containers inside the bay and, in this way, additionally evaluate this new hybrid algorithm together with other solutions from the literature.