Abstract
Industrial projects are plagued by uncertainties, often resulting in both time and cost overruns. This research introduces an innovative approach, employing Reinforcement Learning (RL), to address three distinct project management challenges within a setting of uncertain activity durations. The primary objective is to identify stable baseline schedules. The first challenge encompasses the multimode lean project management problem, wherein the goal is to maximize a project’s value function while adhering to both due date and budget chance constraints. The second challenge involves the chance-constrained critical chain buffer management problem in a multimode context. Here, the aim is to minimize the project delivery date while considering resource constraints and duration-chance constraints. The third challenge revolves around striking a balance between the project value and its net present value (NPV) within a resource-constrained multimode environment. To tackle these three challenges, we devised mathematical programming models, some of which were solved optimally. Additionally, we developed competitive RL-based algorithms and verified their performance against established benchmarks. Our RL algorithms consistently generated schedules that compared favorably with the benchmarks, leading to higher project values and NPVs and shorter schedules while staying within the stakeholders’ risk thresholds. The potential beneficiaries of this research are project managers and decision-makers who can use this approach to generate an efficient frontier of optimal project plans.
1. Introduction
Uncertainty is a common challenge in project management and scheduling, which causes many projects to go over budget and miss their deadlines [1]. According to a report that analyzed over 50,000 projects from 1000 organizations, more than half of the projects (56%) had cost overruns, and 60% of them were delayed [2]. According to a 2021 publication by the Project Management Institute, projects worldwide exceed their budget and schedule by 38% and 45%, respectively [3]. The same report also reveals that the products or services delivered by the projects failed to meet the expectations of 44% of customers, implying that the projects did not provide the value that customers anticipated. This situation has prompted researchers in recent years to develop new frameworks for project management that can better deliver value and handle uncertainty.
This paper addresses three new problems in project management and scheduling. The problems account for uncertainty by using stochastic activity durations and are formulated as chance-constrained mixed integer programs (MIPs). The problems also use a multimode setting, where each activity has one or more modes or options from which to choose. Therefore, the solution to the problem involves selecting one mode for each activity.
The first challenge that this study tackles is a new application of Lean Project Management (LPM), which is a widely used framework to deal with the issue of schedule and cost overruns. The aim of LPM is to maximize value (also referred to as benefit in the literature) and minimize waste in the shortest possible time.
The value of a project is determined by a set of attributes that vary according to stakeholders’ preferences. These attributes may include aspects such as design aesthetics, features, functions, reliability, size, speed, availability, and so on [4]. We follow the approach proposed in [5], which defines an objective function that captures the value from the perspective of the customers and stakeholders. In Section 6, we offer an example of how to compute the value of a project.
We present a new LPM approach that can handle uncertain activity durations. Unlike previous studies on project scheduling that did not consider project value, we aim to maximize the value of the project while avoiding cost and schedule overruns. We use reinforcement learning (RL) algorithms to generate a stable project plan that meets the desired threshold for schedule and budget violation probabilities.
We present an MIP model that adopts a multimode approach. Each mode has data on the project scope, such as fixed and resource costs and stochastic duration parameters, and on the product scope, i.e., value parameters. The mode selection affects not only the project cost, duration, and probabilities of meeting the schedule and budget (through the stochastic duration parameters), but also the project value. Hence, the optimal activity modes both stabilize the project plan and maximize the project value. In Section 6, we illustrate this with a small project example where each activity mode has value and duration parameters. We explain how to compute the project value using these parameters and how to plot an efficient frontier to balance value, on-time, and on-budget probabilities.
We use a novel approach to solve the problem by applying a heuristic based on RL, which we explain in Section 5. RL-based heuristics are known for finding fast solutions in various applications with uncertain environments. The type of heuristic we propose is uncommon in the project scheduling domain in general and has never been used for our type of problem. We use this approach because solving chance-constrained MIPs is often impractical and time-consuming during the project planning stage. For example, when planning a new product development project, multiple project tradespace alternatives are usually created and solved, and the solution time of these alternatives is crucial. Decision makers can use our approach to plot an efficient frontier with the optimal project plans for given probabilities of meeting the schedule and budget.
The second challenge that we explore in this paper is a new formulation of Critical Chain Buffer Management (CCBM), which is a well-known framework that addresses uncertainty and the issue of project overruns. The usual procedure for generating a schedule within this framework is to use an appropriate scheduling method to find a baseline schedule that is optimal or near optimal for the problem with fixed activity durations and then apply a buffer sizing technique to add time buffers—namely, a project buffer (PB) and feeding buffers (FBs).
In this paper, we focus on solving the chance-constrained CCBM problem. We present a mixed-integer linear programming (MILP) model for the multimode problem and propose an RL-based algorithm to solve it. We demonstrate that solving the chance-constrained CCBM problem produces shorter project durations than solving the deterministic-constrained problem and then adding time buffers. We also prove that our RL-based method is effective in creating CCBM schedules compared with established benchmarks.
The third challenge that we address in this paper is building a novel model that integrates uncertainty and chance constraints with two of the most important objectives in project management: the maximization of the project’s net present value (NPV) and project value. The maximization of the project NPV (max-NPV) problem is highly relevant in the current context. Decision makers need to compare different project alternatives, make go/no go decisions, and decide which projects will be in their project portfolio [6]. Nevertheless, it is well known that the evaluation of a project should not only depend on financial factors; a project can have a high NPV but fail to deliver the expected value to customers and other stakeholders. As mentioned earlier, project value is becoming an essential factor in project management.
Most studies have investigated the max-NPV problem and project value separately instead of integrating them. We argue that considering both goals together provides a more comprehensive assessment of a project when evaluating different project options. We propose a new formulation of the optimization problem that combines both NPV and project value, which we call the tradeoff between project value and NPV (TVNPV). We design RL-based algorithms to solve the TVNPV problem and explore the tradeoff between attaining both objectives.
Each of the three challenges is critical because they help to solve different aspects of the situation pointed out above: the high percentage of time and cost overruns, caused in part by project uncertainty, and the failure to deliver value to stakeholders. The LPM challenge tackles value and adopts due date and budget chance constraints to avoid overruns. CCBM focuses directly on the robust minimum duration project plans to avoid delays. TVNPV takes a more holistic approach and deals both with the financial objective in the context of risk by maximizing a robust formulation of the NPV and satisfying stakeholders’ needs and expectations by maximizing value.
Our study presents several novel contributions. Firstly, in terms of problem formulation, we introduce three new models: an LPM one, a CCBM one, and a TVNPV one. Our LPM is the first model to maximize a value function with chance constraints. Our CCBM model is novel since it tackles the chance-constrained problem directly and addresses multimode problems, which is rare in the literature. The TVNPV model considers project value and NPV in tandem for the first time and introduces the concept of robust NPV. Secondly, in terms of solution methods, we apply RL to the three problems. This heuristic approach is seldom employed within the realm of project management and has yet to be applied to similar problems of this nature.
The rest of the paper is organized as follows: Section 2 provides a literature review of the relevant research in the field. Section 3 gives a brief overview of the materials and methods used in this study and provides a method flowchart. Section 4 presents the quantitative models that are used in the paper. Section 5 describes the RL solution that is proposed in this paper. Section 6 provides an example of how the RL solution can be applied. Section 7 describes the experimental setting used to evaluate the RL solution. Section 8 presents the results of the experiments. Section 9 discusses the results and their implications. Finally, Section 10 concludes the paper with a summary of the main findings and suggestions for future research.
2. Literature Review
We now review the key publications related to the three research tracks related to this paper: project value management, CCBM, and the max-NPV problem.
2.1. Project Value Management
Value management is a common theme in LPM research. Some researchers use qualitative methods to explore various aspects of value, such as frameworks for defining and measuring value [7,8,9,10,11], mechanisms for creating value [12], challenges for decommissioning projects [13], and implications of offshore projects [14].
Other researchers use quantitative methods to assess value in terms of stakeholder preferences and attributes [4,15,16]. Some of them apply quality function deployment (QFD), a technique that translates customer needs into engineering requirements [17], to project management [18,19,20]. We use QFD to determine project value by using value parameters in the activity modes, as shown in an example in Section 6.
Another line of research in project value integrates the project scope and the product scope by extending the concept of activity modes to include value parameters in addition to cost and duration. The mode selection affects the project value. Cohen and Iluz [21] propose to maximize the ratio of effectiveness to cost, while [22] aligns the activity modes with the architectural components. Some studies also demonstrate the use of simulation-based training for LPM implementation [23,24]. Balouka et al. [5] develop and solve an MIP that maximizes the project value in a deterministic multimode project scheduling problem. We build on their work by modeling and solving the problem with stochastic activity durations, which is more realistic but also more challenging, as uncertainty can lead to delays and overruns that affect the optimal mode selection.
LPM suggests using schedule buffers to prevent schedule overruns [25], but it does not recommend any specific buffering methods (we review the literature on this topic in the next section). Previous studies on project scheduling with robustness or stability, however, have not considered project value. In this study, we develop and solve a new LPM model that maximizes project value and avoids cost and schedule overruns. We create a stable project plan that keeps the probabilities of violating the schedule and budget below a desired level.
Our method for achieving stability is similar to the buffer scheduling framework because, when we select activity modes, we create a time gap between the baseline project duration and its due date. This time gap will cushion activity delays to meet the on-schedule and on-budget probabilities set by the decision makers. Hoel and Taylor [26] suggest using Monte Carlo simulation to set the size of a baseline schedule’s buffer. We advance their work by directly searching for a baseline schedule that gives us the highest value under the desired on-schedule and on-budget probabilities. Our solution method is based on simulation, which supports our approach.
Project scheduling and its solutions, both exact, using MILP, and heuristic, using methods such as genetic algorithms (GAs), have been extensively studied in the literature. Value functions in project scheduling are a novel concept, introduced by [5]. No one has ever shown the combination of value functions and chance constraints.
2.2. CCBM
There is a large body of literature on CCBM scheduling and buffer sizing methods for single-mode projects. Some studies use fuzzy numbers to model uncertainty. For example, ref. [27] uses fuzzy numbers to estimate the uncertainty of project resource usage and determine the size of the PB with resource constraints. Zhang et al. [28] used an uncertainty factor derived from fuzzy activity durations and other factors to calculate the PB. Ma et al. [29] used fuzzy numbers to create a probability matrix with all possible combinations of realized activity durations.
Other recent studies use probability density functions (PDFs) to represent uncertainty in activity duration. For instance, ref. [30] uses an approximation technique for the convolution to combine activity-level PDFs and model project-level variability. Zhao et al. [31] used classical methods for sizing the FBs and proposed a two-stage rescheduling approach to solve resource and precedence conflicts and prevent critical chain breakdown and non-critical chain overflow. Ghoddousi et al. [32] extended the traditional root square error method (RSEM) [33] to develop a multi-attribute buffer sizing method. Bevilacqua et al. [34] used goal programming to minimize duration and resource load variations and insert the PB and FBs using RSEM. Ghaffari and Emsley [35] showed that some multitasking can reduce buffer sizes by releasing resource capacity. Hu et al. [36] considered a modified CCBM approach with two types of resources: regular resources available until a cutoff date and irregular emergency resources available after that date. Hu et al. [37] focused on creating a new project schedule monitoring framework using a branch-and-bound algorithm and RSEM for scheduling and buffering. Salama et al. [38] combined location-based management with CCBM in repetitive construction projects and introduced a new resource conflict buffer. Zhang et al. [39] calculated the PB using the duration rate and network complexity of each project phase and monitored the buffer dynamically for each phase.
Some researchers also use information flow between project activities. For example, Zhang et al. [40] proposed optimal sequencing of the critical chain activities based on the information flow and the coordination cost, aiming to reduce duration fluctuation and buffering. Zhang et al. [41] used two factors to calculate the PB using the design structure matrix: physical resource tightness and information flow between activities. Information flows are also used in [42], whose work is extended in [43]. In their studies, they considered rework risks and a rework buffer in scheduling.
There are few publications on CCBM buffer sizing and scheduling for multimode projects. Some recent publications include [44], which uses work content in resource-time units to generate activity modes and compares two types of CCBM schedules. Peng et al. [45] combined mode selection rules and activity priority rules (PRs) for scheduling multimode projects with CCBM. Ma et al. [46] used three modes—urgent, normal, and deferred—to level multiple resources and add five metrics to the RSEM buffer calculation formula. Buffer management is also studied in contexts other than CCBM. A discussion of those methodologies falls outside the scope of this paper; some examples are [47,48,49,50,51,52,53,54,55].
Previous research has some drawbacks. Researchers mostly focused on using PDFs either to compute the buffers for a schedule that was already built based on fixed activity durations or to assess the buffered schedule using simulation, rather than finding a time-buffered schedule by solving the chance-constrained CCBM problem. Few researchers have explored RL applications in project scheduling, despite the proven effectiveness of RL-based methods in dealing with uncertain environments, as mentioned above. Lastly, there is little research on multimode CCBM problems. This study, hoping to address some of these gaps, focuses on solving the chance-constrained CCBM problem. We present an MILP model for the multimode problem and propose an RL-based algorithm to solve it. We conduct experiments with two objectives: (1) To examine the chance-constrained CCBM problem and compare the obtained project duration with the traditional method in which the deterministic-constrained problem is first solved and then the time buffers are inserted; (2) To evaluate the effectiveness of our RL-based method in the generation of CCBM schedules compared with established benchmarks.
2.3. Max-NPV Problem
Extensive research has been conducted regarding the max-NPV problem. Russell [56] conducted an investigation into the deterministic problem, employing a linearization technique that approximated the objective function through the first terms of the Taylor expansion. Subsequently, a wealth of additional studies have contributed to the existing body of knowledge on the max-NPV problem. Notably, ref. [57] demonstrated its NP-hardness, while [58] proposed a precise solution approach tailored to smaller projects as well as a Lagrangian relaxation method coupled with a decomposition strategy for more extensive problems. Additionally, ref. [57] devised a methodology that involved grouping activities together, and in a subsequent publication [59], they further expanded their work to encompass capital constraints and various cash outflow models. Klimek [60] explored projects characterized by payment milestones and investigated diverse scheduling techniques, including activity right-shift, backward scheduling, and left-right justification.
The deterministic max-NPV problem, when extended to accommodate multiple modes, presents a multimode variant of the original problem. Chen et al. [61] successfully achieved optimal solutions for projects containing up to 30 activities and three modes by utilizing a network flow model. Building upon the scheduling technique mentioned earlier in [57], ref. [62] further expanded their approach to incorporate multimode projects and diverse payment models for cash inflows. The examination of these payment models continued in the context of the max-NPV discrete time/cost tradeoff problem. In this regard, ref. [63] compared the impact of three distinct solution representations by integrating them into an iterated local search algorithm. Additionally, ref. [64] addressed a bi-objective optimization problem, aiming to balance the NPV between the contractor and the client.
The stochastic max-NPV problem serves as another extension to the original deterministic max-NPV problem, introducing random variables for activity durations and cash flows. Wiesemann and Kuhn [65] provided an in-depth review of the early literature on this subject. In their study, Creemers et al. [66] focused on maximizing the expected value of NPV (eNPV) while considering variable activity durations, the risk associated with activity failure, and different approaches or modules to mitigate this risk. Resource constraints, however, are not taken into account in their analysis. Similarly, ref. [6] explored the notion of a general project failure risk that diminishes as project progress is made. They also considered activity-specific risks. It is worth noting that completing earlier activities sooner not only eliminates the risk of failure, thereby improving the eNPV, but also potentially accelerates costs, consequently worsening the eNPV. Incorporating weather condition modeling into stochastic durations, ref. [67] introduced decision variables in the form of gates. These gates dictate when resources become available for specific activities, allowing for a more comprehensive analysis of the problem at hand.
In the study conducted by [68], optimal solutions on a global scale were identified for the stochastic NPV problem. Specifically, the focus was on activity durations that followed a phase-type distribution, deterministic cash flows, and the absence of resource constraints. Expanding on these findings, the authors further applied them to determine the optimal sequence of stages in multistage sequential projects characterized by stochastic stage durations. In doing so, exact expressions in closed form were derived for the moments of NPV, with the utilization of a three-parameter lognormal distribution to accurately approximate the distributions of NPV [69]. Additionally, it was demonstrated that this problem is equivalent to the least-cost fault detection problem, which was established by [69] and [70]. Hermans and Leus [71] contributed to the field by presenting a novel and efficient algorithm. Their research specifically pertains to Markovian PERT networks, where activities are exponentially distributed and no resource constraints exist. Interestingly, their findings reveal that the optimal preemptive solution also solves the non-preemptive case. Zheng et al. [49] investigated the max-eNPV problem, considering stochastic activity durations, utilizing two proactive scheduling time buffering methods, and incorporating two reactive scheduling models. The goal of their research was to explore different approaches to tackling this problem effectively. Liang et al. [72] proposed time-buffer allocation as a means to address the max-eNPV problem. They introduced the expected penalty cost as a measure of solution robustness, aiming to enhance the reliability of the proposed solutions. Lastly, ref. [73] delved into the consideration of uncertainty in both activity duration and cash flow while simultaneously incorporating two objectives: maximizing eNPV and minimizing NPV risk. Notably, their model does not include resource constraints.
3. Materials and Methods
The method flowchart is shown in Figure 1. The situation of project delays, cost overruns, and reduced value (Section 1) motivated the researchers to model three challenges that help solve different aspects of the situation: LPM, CCBM, and TVNPV. Each of these challenges is modeled by introducing mathematical programming formulations (Section 4) and novel RL-based solutions (Section 5). The challenges are illustrated in an example (Section 6). Experiments were designed, and datasets were prepared by supplementing the well-known PSPLIB datasets with relevant information for each model (Section 7). Data analysis was performed on the results (Section 8).
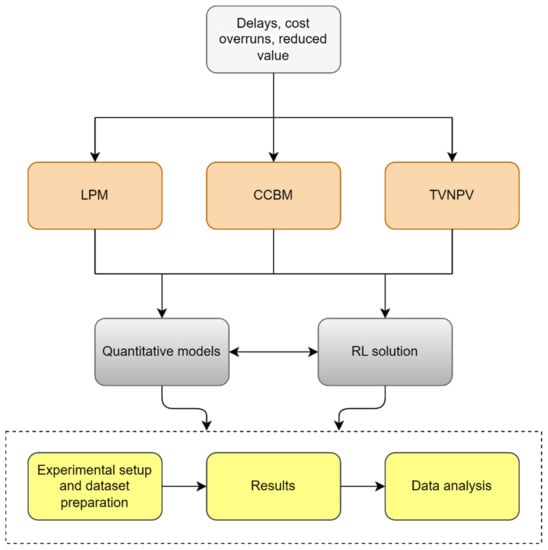
Figure 1.
Method flowchart.
4. Quantitative Models
In this section, we present the mathematical models representing our three problems.
4.1. LPM
Our LPM deterministic model is formulated as a MIP, aiming to maximize the project value while considering duration and cost constraints. We now provide an overview of our notation, model, and explanations of its objectives and constraints.
We consider a project consisting of J activities, where each activity j can be executed in one of modes and is preceded by a set of immediate predecessors . Executing activity j in mode m requires a duration and incurs a fixed cost . Additionally, there are K renewable resources available, each with a unit cost per period. Resource k is consumed by activity j in mode m at a rate of units. The project is constrained by a due date D and a budget C. We assume that if the project adheres to the budget constraint, the required resources can be readily acquired. Similar assumptions regarding resource availability can be found in studies on time-cost tradeoff problems and recent project scheduling research [73,74,75,76,77].
The project encompasses V different value attributes, denoted by the parameter which represents the value of attribute v for activity j executed in mode m. Decision variable corresponds to the value of attribute v for activity j when executed in its selected mode. To determine the project value for each attribute v, we define the function which takes into account the individual attribute values and the function , which calculates the project value based on the attribute values.
Within our model, the binary decision variable indicates whether activity j is performed in mode m. Additionally, decision variable denotes the starting time of activity j, where j ranges from 0 to . In this context, denotes a project milestone that has only one mode and does not have any duration, cost, resources, or value. It functions as the starting point of the project. Conversely, represents another milestone signifying the project’s end.
The model itself is:
subject to:
Objective (1) aims to maximize the project value, which is a specific function of the chosen modes. Constraints (2) are responsible for determining the value attributes based on the selected modes. Constraints (3) introduce the binary decision variable that indicates the chosen mode for each activity. These constraints ensure that exactly one mode is selected for each activity. Constraint (4) sets the beginning of the project as the starting time for milestone 0. Constraint (5) ensures that the project is completed within the specified due date. Constraints (6) ensure that an activity cannot start before its immediate predecessor is finished. Constraint (7) restricts the fixed and resource costs to be within the project budget. Lastly, constraints (8) and (9) are integrality and nonnegativity constraints.
In the case of a model with stochastic activity durations, constraints (5) and (7) cannot be guaranteed with certainty. Hence, we need to model them as chance constraints. A common approach to solving such stochastic programs is using a scenario approach (SA), which was introduced by [78] and applied in several project scheduling papers [79,80,81]. The idea behind SA is to generate S samples or scenarios representing the possible outcomes of the random variables in the constraints, such as the activity durations. These samples replace the deterministic scenario. If our objective function is linear, the resulting SA program becomes a MILP, which can be solved using commercial solvers. We employ this method as a benchmark in the computational experiments presented in Section 7 (a discussion of SA falls outside the scope of this paper; more details on this topic can be found in [78]).
To continue our presentation of the LPM model, we must now introduce additional notation and constraints and provide an explanation for the SA formulation of our problem. We can define parameters S and to represent the number of scenarios sampled and the duration of activity j in mode m for scenario s, respectively. Parameters and are established as the desired probabilities of the project finishing within the due date and on budget, while parameters and serve as upper limits for the project’s delay and budget overrun. Let decision variable represent the starting time of activity j in scenario and let binary decision variables and indicate whether the project finishes within the due date and on budget, respectively, in scenario s. In the SA model, the objective function (1) and constraints (2) and (3) remain unchanged while replace in constraints (9). Constraints (10) through (15) provided below replace constraints (4) to (7).
Constraints (10) define the project’s starting time as the beginning of milestone 0 across all scenarios. Constraints (11) maintain the project’s completion within the due date () or within the specified upper bound (). To meet the desired probability, constraint (12) guarantees that the proportion of scenarios completing within the due date aligns accordingly. In each scenario, constraints (13) ensure that no activity can commence before its immediate predecessor concludes. Constraints (14) enforce the project’s adherence to the budget () or the specified upper limit (). Constraint (15) ensures that the fraction of scenarios completed within the budget aligns with the desired probability. Lastly, constraints (16) and (17) represent the integrality and nonnegativity conditions, respectively.
Our LPM model is highly relevant and applicable to project management in several ways. Firstly, the objective function and the chance constraints aim to maximize project value while meeting the deadline and staying within budget—a key objective for project managers. Secondly, the LPM model considers uncertainties in activity durations, which is a common challenge in project management. By incorporating stochastic duration parameters, the model provides a more realistic representation of project timelines and allows project managers to make more informed decisions. Thirdly, the model adopts a multimode approach that considers the impact of mode selection on project cost, duration, and value. This allows project managers to optimize project outcomes by selecting the most appropriate mode for each activity. Finally, the LPM model provides a framework for decision-making that can help project managers balance project schedule, cost, and value.
4.2. CCBM
Traditionally, the CCBM scheduling approach begins by creating a baseline schedule that minimizes the project duration based on deterministic estimates of activity durations such as the median or mean values [82]. This involves solving the resource-constrained project scheduling problem (RCPSP) or its multimode extension. Due to the NP-hard nature of the problem [83], heuristic methods are commonly used, especially for larger projects.
Once a baseline schedule is established, the PBs and FBs are inserted using a buffer-sizing technique such as the methods discussed in Section 2.2. The aim is to create a stable schedule that can be evaluated using robustness measures described in relevant literature, such as the standard deviation of project length, stability cost, and timely project completion probability [44].
The on-time probability not only serves as an indicator of schedule robustness but also plays a role in buffer calculation. Hoel and Taylor [26] proposed the use of Monte Carlo simulation to determine the cumulative distribution function (CDF) for project completion time, thereby determining the size of the PB. For example, if we aim for a 95% probability of completing the project on schedule, the PB would be the difference between the project duration at the 95th percentile and the duration of the baseline schedule.
Let us go one step further. If we directly search for the shortest time-buffered schedule that meets the desired on-time probability, we can identify a schedule with the same probability but a shorter duration. This leads us to the chance-constrained CCBM problem, where we consider multimode projects. In this problem formulation, we not only search for the schedule but also determine the activity modes that result in the shortest project duration while meeting the desired on-time probability. This duration encompasses the baseline schedule, nominal (deterministic) activity durations, and the PB. In this paper, we define project delivery as this time-buffered project duration, which represents the deadline we can meet (i.e., deliver the project) with the desired on-time probability.
To model our chance-constrained CCBM problem, we adopt a MILP approach using the flow-based formulation described in [84], extending it to accommodate multimode projects. We handle the chance constraints using SA as in the LPM model but require additional parameters and decision variables that were not present there.
There are K distinct renewable resources available, each having a total availability of units. When activity j is executed in mode m, it requires units of resource k. For a given scenario s, the earliest start time for activity j is denoted as , while represents the latest start time.
The project delivery is represented by decision variable . Project milestones 0 and have a singular mode, zero duration, and no resource requirements. Binary decision variable is employed to indicate if activity j commences after the completion of activity i, taking a value of 1 in such cases. The flow variable models the amount of resource k transferred from activity i to activity j.
Our chance-constrained CCBM model incorporates constraints (3), (8), (12), and (16) from the LPM model. Moving forward, we will present the model, followed by an explanation of the objective function and the remaining constraints.
subject to:
The objective function (18) is designed to minimize the project’s delivery time. Constraints (19) indicate whether a scenario is completed within the desired timeframe. Constraints (20) and (21), derived from previous works [84,85], prevent cycles of 2 or 3 or more activities. Constraints (22) enforce the precedence relationships between activities. Constraints (23) establish the relationship between continuous activity start time variables and binary sequencing variables. Constraints (24) define upper and lower bounds for activity start times. Constraints (25), drawing from [85], establish a connection between the continuous resource flow variables, binary sequencing variables, and mode variables.
Outflow constraints (26) guarantee that all activities, except for milestone transfer their resources (when finished with them) to other activities. Inflow constraints (27) ensure that all activities, except for milestone 0, receive their resources from other activities. Constraints (28) set bounds on the flow variables based on the maximum resource consumption modes.
It is important to note that the general constraints (25) and (28) can be reformulated as MIP constraints using linear and special-ordered set constraints, along with auxiliary variables [86]. Commercial solvers such as Gurobi automatically handle the equivalent formulation (in [85], these constraints are also handled by the solver).
Once the MILP is solved, constructing a schedule follows a straightforward approach. The project is represented as an activity-on-node (AON) network, with arcs connecting activities j to their immediate predecessors . If resources flow from activity i to j, j cannot start before i finishes, making i an immediate predecessor of j. Hence, we add arcs between activities wherever . This construction, referred to as a resource flow network [87], can be achieved by simply adding i to . Finally, we schedule all activities using the “early start” approach, where each activity commences when its immediate predecessor concludes.
For the baseline schedule, the activity duration used is typically the most likely duration based on a three-point estimate. After the completion of the last activity, the PB is inserted, calculated as the difference between the project delivery time and the baseline duration. An example illustrating this approach can be found in Section 6.
To insert FBs, we adopt the method proposed by [26] and applied in subsequent works, e.g., [88,89] (the latter employing the method as an upper bound for the buffers). In this approach, activities are scheduled using an “early start” strategy, and the FB is determined based on the free float of the activity that merges into the critical chain, ensuring that no new resource conflicts arise from the insertion of FBs. Thus, since we initiate all activities as early as possible, we can disregard the size of FBs in our problem.
Our CCBM model is extremely significant for project management applications, especially for addressing uncertainties and risks in project scheduling. The objective function and chance constraints allow the project manager to produce time-buffered project plans that minimize the project delivery date while staying within the stakeholders’ risk threshold. In the Introduction, we discussed the importance of this topic, and in Section 2.2, we discussed the limitations of existing scheduling methods. In Section 8, we demonstrate the effectiveness of the proposed CCBM model in producing shorter project durations compared with established benchmarks.
4.3. TVNPV
In line with Section 4.2, we utilize the flow-based formulation introduced by [84] and extend it to encompass multimode projects, NPV, value functions, and chance constraints. The primary objective of the TVNPV model is to maximize the robust project NPV and the project value. To address the chance constraints, we employ SA. We now describe additional parameters and decision variables that are not present in the LPM and CCBM models.
Within the problem context, we have K distinct renewable resources, each associated with a unit cost per period. Additionally, activity j executed in mode m incurs a fixed cash inflow or outflow consisting of fixed costs and payments received. For convenience, we assume that payments are received or made at the end of each activity. To avoid gaps between activities and prevent indefinitely postponing activities with negative cash flows, two main approaches exist in the literature: (1) utilizing a deadline [57] and (2) assuming a sufficiently large payout at the end of the project to offset the gains from postponing activities impacting project completion [66]. In this paper, we adopt the latter approach.
When aiming to minimize project duration, a common measure of robustness is the timely project completion probability [44]. In our problem, we adapt this concept and introduce the decision variable rNPV to represent the robust NPV. It signifies the project NPV achieved with a probability of at least γ. Thus, instead of evaluating the robustness of a given schedule, we search directly for a schedule with the desired level of robustness.
Several parameters are defined within the model. serves as an upper bound for rNPV. denotes the discount rate, while and represent the earliest and latest finish times for activity j in scenario s, respectively. Additionally, acts as an upper bound for the project’s duration.
To represent the finish time of activity j in scenario s, we introduce the decision variable . Binary variable takes the value 1 if the scenario NPV is greater than rNPV. Moreover, decision variable represents the discount factor for activity j in scenario s, and serves as an upper bound for the discount factor.
Objective function weights and are included to determine the tradeoff between rNPV and the project value. By solving the MIP for different values of and we can identify the efficient frontier that balances these objectives.
To linearize two sets of constraints, we introduce additional variables. Binary variables are assigned a value of 0 for all and 1 for all . Variables replace the products . The model incorporates constraints (2), (3), (8), (20)–(22), and (25)–(28) from the LPM and CCBM models.
We now present the model, providing an explanation of the objective function, followed by an overview of the remaining constraints. Subsequently, we will discuss the linearization of the nonlinear constraints.
subject to:
The primary objective of the model, captured in the objective function (29), is to maximize a weighted sum of the project’s rNPV and its overall value. This approach, known as the weighted-sum method, is widely employed in multi-objective optimization [90] and has been utilized in various project scheduling studies, e.g., [72,91,92].
To ensure the robustness of the project’s NPV, constraints (30) are introduced, which evaluate whether a scenario’s NPV surpasses the project’s rNPV. Inspired by [93], we adopt a discrete discount factor in constraints (31). Constraint (32) is employed to monitor the fraction of scenarios that yield the desired rNPV, enforcing this fraction to remain above a predetermined threshold.
The interdependence between the continuous activity finish time variables and the binary sequencing variables is established through constraints (33). Additionally, constraints (34) provide necessary bounds for the activity’s finish times.
Constraints (30) pose a challenge due to the nonlinearity arising from the product of the discount factor and the indicator variable, . To address this nonlinearity, we replace constraints (30) with constraints (35) that involve auxiliary variables, denoted as . To ensure the equivalence of and , constraints (36)–(39) are introduced to maintain the relationship between these variables within the model.
To replace the exponential discount factor from constraints (31), we introduce linear constraints (40) into the model. Additionally, we incorporate the following constraints into the model:
- Constraints (41) establish a connection between the binary variables and .
- Constraints (42) ensure that an activity can only have a single finish time.
- Constraints (43) impose bounds on as the predecessor will always have a value of 1 before its successor.
- Constraints (44) and (45) fix the value of for finish times occurring before the early finish and after the late finish, respectively.
- Finally, constraints (46) determine the fixed value for the initial milestone.
We can use a commercial solver to solve the MIP if the value function of the project is linear because the constraints are linearized, as explained before. This method is our benchmark for the computational experiments that we present in Section 7.
Our TVNPV model is very useful and suitable for project management in various aspects. Firstly, the objective function and the chance constraints aim to maximize both project value and NPV. This is a new and useful tool for decision-making because it allows the generation of project plans on the efficient frontier with different optimal combinations of value and NPV. Secondly, the uncertainties in activity durations and the chance constraints enable the calculation of a robust NPV according to the stakeholders’ tolerance for risk. Additionally, the model employs a multimode approach that evaluates the impact of mode selection on project cost, duration, resources, and value.
5. The RL Solution
RL has demonstrated remarkable achievements in various domains, ranging from mastering backgammon at a level comparable to the world’s best players [94] to successfully landing unmanned aerial vehicles (UAVs) [95], defeating top-ranked contestants in Jeopardy! [96], and achieving human-level performance in Atari games [97]. These accomplishments highlight the effectiveness of RL in dealing with uncertain environments. Inspired by this success, we apply RL to the formulations described in Section 4. While RL-based heuristics have been employed in project scheduling [98,99], to the best of our knowledge, no previous work has addressed multimode problems with chance constraints using RL.
The RL framework begins by placing an agent in a state denoted as S. The agent takes an action denoted as A and transitions to state receiving a reward denoted as . Subsequently, the agent performs action moves to state and receives reward and the pattern continues. Hence, the agent’s life trajectory can be represented as and so on. To guide the agent’s behavior in each state, a policy denoted as is followed, instructing the agent which action to take. The objective of the RL problem is to learn a policy that maximizes the agent’s cumulative reward. Additionally, we introduce an action-value function denoted as which estimates the reward for taking action A in state S and subsequently following policy .
By applying the RL model to the formulations outlined in Section 4, we define a state as a project activity denoted by j. The agent takes action by selecting a mode and additionally, in CCBM and TVNPV, a start time for activity j, and then proceeds to the next activity. After determining modes and start times for all activities the agent can calculate its reward . As the agent receives rewards, it learns the action-value function and the corresponding policy to be followed.
In this study, we utilize Monte Carlo control (MCC), an RL method based on [100]. MCC leverages Monte Carlo simulation to estimate CDFs for the activity durations, which are used in reward calculations. The algorithms for each of the three problems consist of a main procedure in which multiple functions are called. This section presents the main procedures along with a high-level explanation. The pseudocode and detailed explanations for each function can be found in Appendix A.
The LPM main procedure is shown in Algorithm 1. The iterative process comprises three key steps:
- Policy calculation: The policy is a table of the probabilities of the agent taking each action. In our case, this means selecting a mode for each activity. We employ a technique called ε-greedy policies, where we examine the action-value table and assign a probability ε of picking a random mode for an activity. Otherwise, we pick the mode with the highest action-value.
- Reward computation: We use the policy to select the modes and then compute the reward for this action. In LPM, we model the reward as the project value, calculated by the project-specific value function. For an example of a value function, see Section 6.
- Action-value update: The reward obtained by this choice of modes is used to update the action-value table. To calculate the new action-values, we either average all the rewards obtained for this specific mode choice (RL1) or use a constant-step formula (RL2). For more details on these action-value update variants, see Appendix A.
| Algorithm 1: Main MCC procedure for LPM. |
| initialize_action_values from Algorithm A1 |
| while not stopping criterion: |
| calculate_policy from Algorithm A2 |
| calculate_reward from Algorithm A3 |
| update_action_values_RL1 from Algorithm A4 or update_action_values_RL2 from Algorithm A5 |
If the stopping criterion is not met, the policy is recalculated based on the updated action-values, initiating a new iteration of the cycle.
The main procedure for the CCBM model is shown in Algorithm 2. Focusing on the features that differ from the previous LPM–RL algorithm, in CCBM, an action consists of selecting a start time for an activity in addition to the mode. Regarding the reward, we construct an early-start resource-feasible baseline schedule and model the reward as the reciprocal of the delivery date, defined in Section 4.2.
| Algorithm 2: Main procedure for MCC for CCBM and TVNPV. |
| initialize_action_values from Algorithm A6 |
| while not stopping criterion: |
| calculate_policy from Algorithm A7 |
| choose_mode_start from Algorithm A8 |
| calculate_reward from Algorithms A9 and A10 |
| update_action_values_RL1 from Algorithm A4 or update_action_values_RL2 from Algorithm A5 |
Finally, regarding the TVNPV RL algorithm, the difference between it and the previous CCBM is the reward calculation. The reward is the objective function value, which is the weighted sum between rNPV and project value. Instead of an early-start schedule, the project activities are scheduled according to the selected start-time action. This way, we account for cash inflows and outflows, since in the latter case, it is advantageous to postpone an activity instead of starting it early.
6. Example
To provide a concrete illustration of our problem and the RL solution approach, let us consider as an example the development of a radar system, drawn from a real-world project. In Figure 2, we present the project’s AON network, while Table 1 provides a list of the project’s five activities, each with two available modes. The table includes the optimistic, most likely, and pessimistic durations (O, ML, and P) of the activities, their respective fixed costs (FC), the required resources per period for each mode (engineers, E, and technicians, T), the value parameters, and the income received upon activity completion.
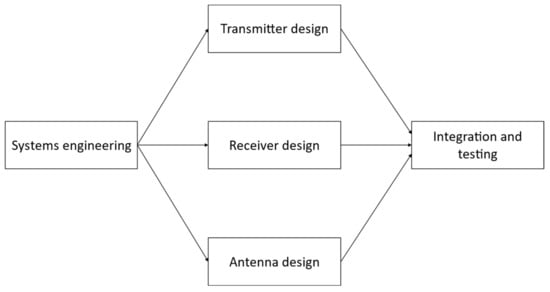
Figure 2.
Project network diagram.

Table 1.
Summary of data for radar development.
It is worth noting that three of the five activities exhibit negative cash flows, i.e., fixed and resource costs, while the remaining two activities yield positive cash flows due to the generated income. This example effectively illustrates how value is defined and measured in practice. The needs and expectations of project stakeholders are translated into value attributes such as range, quality, and reliability (R, Q, and Re, respectively, as shown in Table 1). These attributes are determined by the value parameters associated with each activity mode. Additionally, it is important to consider the resource unit costs per period, which amount to USD 100 for engineers and USD 50 for technicians.
In the context of the radar system, we employ the radar equation [101] for computing the radar range [21]. The quality and reliability of the radar system are also considered, as they depend on technical parameters such as transmitter power and antenna gain. These parameters, in turn, are contingent upon the technological alternatives available for each mode. The selection of a mode for the project plan not only determines its value but also has a significant impact on cost and NPV, effectively integrating both components of project value.
The equation for calculating radar range involves the variables (transmitter power), (receiver sensitivity), and (antenna gain). These parameters are extracted from the corresponding activities in Table 1—namely, transmitter design, receiver design, and antenna design. Similarly, the equation for radar quality incorporates the impact of various factors denoted by , and which represent systems engineering, transmitter, receiver, antenna, and integration effects on quality, respectively. Likewise, the equation for radar reliability considers the contributions of antenna design, integration effort, transmitter reliability, and receiver reliability, represented by and respectively. Finally, the project value is determined by computing a weighted sum of the three value attributes, a widely used technique in multi-attribute utility theory [102] expressed as . We now illustrate this example within the context of the three challenges presented in this paper: LPM, CCBM, and TVNPV.
6.1. LPM
Here we address the optimization of activity modes and start times to maximize the project value while ensuring a 95% probability of meeting both the schedule and budget requirements. The project is characterized by a due date of 17 time periods and a budget of USD 39,800. To achieve our objective, we employed the RL1 algorithm and terminated the iterations when no further improvement in the maximum project value was observed over the last 100 iterations.
To facilitate analysis and comparison, we normalized the project values on a scale of 0 to 100, following the approach outlined by [5]. The solution obtained from the algorithm is presented in the form of a Gantt chart (Figure 3). It is important to note that the activity durations shown on the Gantt chart correspond to the most likely (nominal) durations (Table 1). For example, for the activity “systems engineering”, mode “large team”, the most likely duration is four time periods.

Figure 3.
LPM: Gantt chart of radar project plan. The arrows indicate predecessor activities.
The project plan resulting from this optimization approach achieved a project value of 58.365, which, after normalization, corresponds to a value of 100. The nominal cost associated with this plan is USD 31,900. Furthermore, the probability of completing the project on time is 100%, while the probability of staying within the budget stands at 99%.
As outlined in Section 5, our search process is guided by learning and updating the action-value table, which subsequently leads to the recalculation of the ε-greedy policy. To illustrate this approach, we provide an overview of the action-value evolution in Table 2, showcasing the progression from the initial optimistic values to the latest iteration.

Table 2.
LPM: evolution of action-values for the radar project.
One significant advantage of our solution is its ability to support decision-making by generating an efficient frontier of project plans that incorporate the inherent uncertainty of project durations. This empowers tradeoff analysis, enabling the selection of the optimal plan based on a careful balance between risk and value considerations.
To exemplify the practical application of our approach, let us consider a scenario in our radar project example where the decision-makers aim to reduce the budget by USD 13,300, adjust the due date to 18 time periods, and ascertain the achievable value for the stakeholders. The efficient frontier for this particular case is depicted in Figure 4.
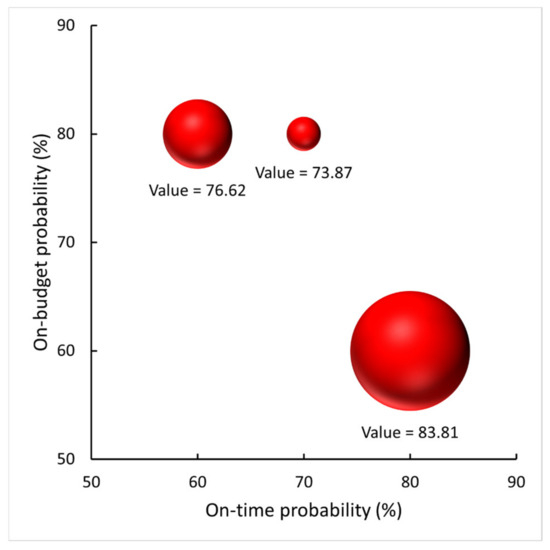
Figure 4.
LPM: efficient frontier for radar project. Due date: 18 time periods; budget: USD 26,500.
When examining the scenario where the on-time probability stands at 80% and the on-budget probability at 70%, it becomes apparent that the project is deemed infeasible. If, however, the decision-makers are willing to accept a lower on-budget probability of 60%, it becomes possible to achieve the maximum value, approximately 83. This observation highlights the substantial impact of a constrained budget on the project’s capacity to provide value to stakeholders. It underscores the significance of incorporating stochastic activity durations to accurately portray the value that the project can deliver to its stakeholders.
6.2. CCBM
In this and Section 6.3, we consider a scenario where there are 11 engineers and four technicians available to work on the project. Our goal is to find the shortest project duration that satisfies a given probability β of completing the project on time. Gantt charts illustrating the project activities, selected modes, FBs, and PBs are presented in Figure 5, Figure 6 and Figure 7. These charts showcase the solutions achieved for different desired probabilities, namely, 90%, 95%, and 100%. The baseline schedule activity durations correspond to the most likely durations from Table 1.
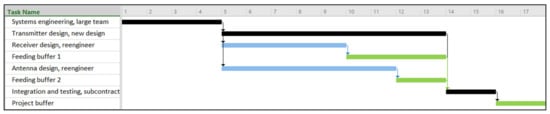
Figure 5.
CCBM: Gantt chart for 90% on-time probability. The arrows indicate predecessor activities. The FBs and PBs appear in green, while the critical chain activities are highlighted in black.

Figure 6.
CCBM: Gantt chart for 95% on-time probability. The arrows indicate predecessor activities. The FBs and PBs appear in green, while the critical chain activities are highlighted in black.

Figure 7.
CCBM: Gantt chart for 100% on-time probability. The arrows indicate predecessor activities. The FBs and PBs appear in green, while the critical chain activities are highlighted in black.
As anticipated, the lower the level of risk we are willing to tolerate, indicated by a higher on-time probability, the longer the duration of the buffered project grows. It is intriguing to observe the progressive improvement in solutions achieved by our RL agent. In our RL model, we defined the reward as the reciprocal of the project duration. Figure 8 displays the learning curves for both variants of action-value updating, RL1 and RL2, focusing on a 95% on-time probability. At the initial stages of the curves, the influence of optimistic initial values (described in Section 5) is evident: despite discovering the minimum delivery duration early on, the agent continued to explore randomly, under the impression that it might obtain a better reward by pursuing alternative actions, given the artificially inflated values in the action-value list. Eventually, the delivery duration stabilized at 18 time periods. As we employed ε-greedy policies (outlined in Section 5), the agent occasionally explored, resulting in intermittent deviations from the minimum delivery duration.
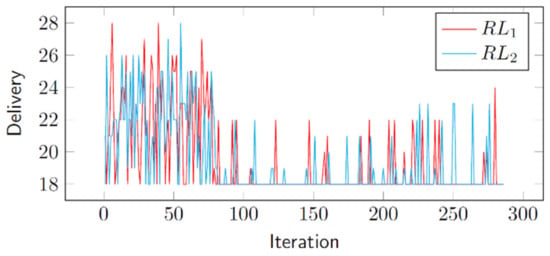
Figure 8.
CCBM learning curves for RL1 and RL2: 95% on-time probability.
6.3. TVNPV
We aim to address the problem by considering different weights, w1 and w2, and obtaining the efficient frontier for a 95% probability of rNPV. The resulting frontier, consisting of four non-dominated points, is depicted in Figure 9. Decision makers can perform a tradeoff analysis to select the solution that best aligns with stakeholders’ needs and requirements.
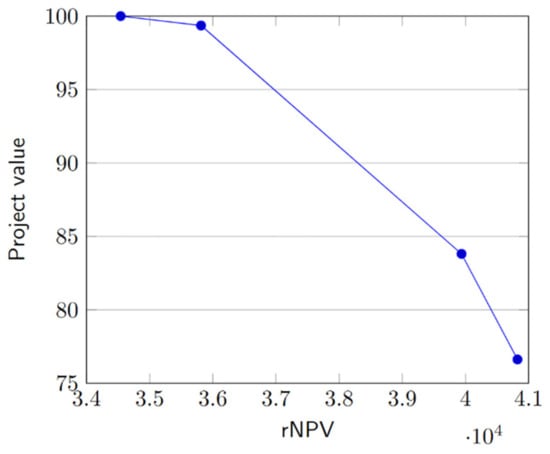
Figure 9.
TVNPV: efficient frontier for radar project.
As discussed in Appendix A.3, rNPV is determined iteratively by simulating the NPV CDF. In Figure 10, the CDF plot illustrates the rNPV for the point (76.62, 40,772) in Figure 9. With the decision makers’ chosen solution, a baseline schedule can easily be constructed using the process outlined in Algorithm A10 and explained in Appendix A.3. The resulting Gantt chart is presented in Figure 11. Figure 12 showcases the learning curves for both RL1 and RL2, demonstrating how our action-value updating variants evolve over time.
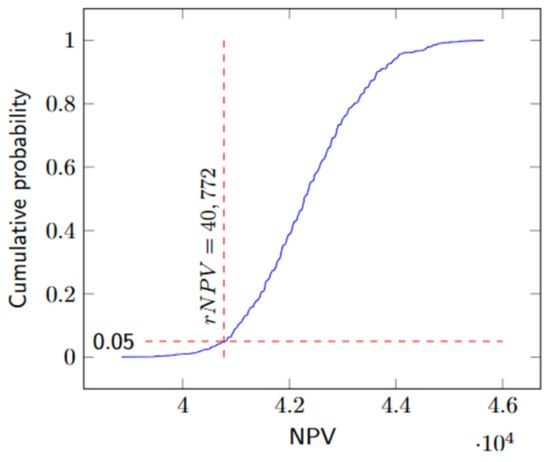
Figure 10.
NPV CDF plot.

Figure 11.
TVNPV: Gantt chart for a project with value = 76.62 and rNPV = 40,772. The arrows indicate predecessor activities.
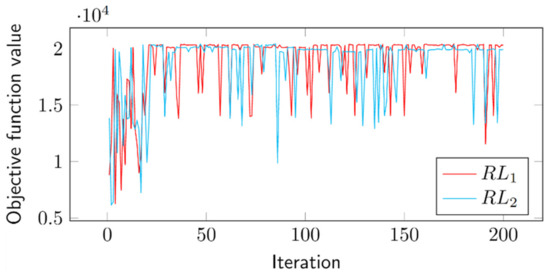
Figure 12.
TVNPV learning curves for RL1 and RL2: 95% rNPV probability, w1 = w2 = 0.5.
7. Experimental Setting
The experiments were conducted to validate the effectiveness of our RL procedure in solving the formulations outlined in Section 4. We utilized the PSPLIB dataset [103], which consists of 535 project instances with 10 activity projects and three activity modes per project. This dataset is widely recognized as the standard in the literature on multimode project management [104].
To generate scenarios and simulate runs, we employed three-point estimates for activity mode durations. Specifically, we defined the dataset’s duration as the most likely duration, with the optimistic duration set at half this value and the pessimistic duration set at 2.25 times the most likely duration. These multipliers align with the characteristic right-skewed distribution of activity durations in project management [47]. Realized durations were randomly drawn from a triangular distribution, a common approach in project simulation [105], and rounded to the nearest integer.
Our RL algorithms were executed using two different methods for updating the action values, RL1 and RL2, as described in Section 5. We maintained the same probability of a random action (ε = 0.1) and constant step-size parameter (α = 0.1) as specified in [100]. To solve the MILP problems in the benchmarks, we employed the Python interface for Gurobi solver version 9.0. All algorithms were implemented in Python.
The experiments were conducted on a computer equipped with an Intel(R) Core(TM) i7-7700 CPU 3.60 GHz and 8 GB RAM. For data analysis, we performed pairwise comparisons of the objective function values generated by each method. We utilized JMP statistical software to calculate the p-values for Wilcoxon signed rank (WSR) tests with a significance level of 0.05.
Below, we provide specific details of the experimental design for each of the three problems discussed in this paper.
7.1. LPM
We compared the project values obtained from our variants to those of two benchmarks: a genetic algorithm (GA) and a solution for our MILP problem (Section 4.1). GAs are widely used for solving project scheduling problems [106], which motivated our selection of a GA as a benchmark. We used the specialized GA proposed by [5] with minor modifications, as it is specifically designed for value functions and closely aligned with our problem. The GA parameters included a population size of 500, percentiles for elite and worst solutions, and a mutation probability of 0.1.
Since the GA fitness function in [5] was designed for deterministic problems only, we developed a new fitness function suitable for our stochastic settings (details in Appendix A). To ensure a fair comparison, we terminated RL1 and RL2 at the point when the GA converged according to its published stopping criterion, i.e., when the best value remained unchanged for two consecutive generations. We generated additional data for the PSPLIB instances based on our problem specifications and adjusted the sample size according to the runtime (additional details in Appendix B).
7.2. CCBM
We employed two methods as benchmarks for the CCBM problem. Firstly, we solved our MILP from Section 4.2. Secondly, we utilized the best combination of mode-selecting and activity-selecting PRs reported by [45] (details in Appendix C). We conducted 1000 scenarios for both chance constraints using the solver (CS) and chance-constrained RL1 and RL2 (CRL1 and CRL2). For deterministic constraints using the solver (DS), we modified the model by removing specific constraints and scenario indexes as follows: Constraints (23) became and constraints (24) became . For CS, owing to the increased runtime, we set a 30-minute limit. In the deterministic-constrained RL1 and RL2 (DRL1 and DRL2) approaches, the calculate_reward function (refer to Algorithm A9) yielded the reciprocal of the project duration without any simulation runs, denoted as . The stopping criterion for RL1 and RL2 was set to 1000 iterations after visiting all states with optimistic initial values.
7.3. TVNPV
We selected two benchmarks for the TVNPV problem. Firstly, we solved the MILP problem described in Section 4.3. Secondly, we employed a tabu search (TS) as proposed by [107] (see Appendix D for more details about our TS implementation). We opted for a TS because, in [107], it produced smaller maximal relative deviations from the best solutions than simulated annealing. The stopping criterion for all RL methods was set to 1000 iterations after visiting all states with optimistic initial values. To determine when to stop the process for TS, we established a criterion based on the maximum amount of time elapsed between RL1 and RL2 for each corresponding instance. Our intention was to provide TS with a runtime equal to or greater than RL’s runtime.
The objective function was evaluated using equal weights (w1 = w2 = 0.5), and we set the desired probability (γ) of the project, yielding an rNPV of 0.95. The cash flows for activity modes were randomly generated from uniform distributions ranging from 0 to 10, with a final payment of 10 at the end. The value attributes and parameters were set up following the approach used in LPM (see Appendix B).
Table 3 provides a summary of the benchmarks and stopping criteria for each of the three problems.

Table 3.
Benchmarks and stopping criteria for the experiments.
8. Results
In this section, we report the results of our computational experiments for each of the three problems addressed in this paper.
8.1. LPM
In Table 4, which compares the average percent decrease from the optimal project value for linear objective functions, RL1 and RL2 exhibited values that were on average closer to SA than GA. Notably, RL2 outperformed RL1. Despite the SA solutions not necessarily being optimal, they consistently outperformed both GA and RL. It is, however, worth noting that, in addition to its long running times, SA generated a substantial proportion of infeasible solutions. These solutions, when simulated on test sets, failed to reach the on-budget or on-schedule proportion of 0.95, as demonstrated in Appendix E.

Table 4.
Average decrease (%) from SA.
To examine the performance of RL1, RL2, and GA, refer to Table 5. While GA outperformed RL1, RL2 demonstrated superiority over GA with stronger statistical significance. The results validate the effectiveness of our RL-based algorithm as a valuable substitute for GA during the project planning phase, particularly when dealing with the generation and resolution of multiple tradespace alternatives within the constraints of runtime.

Table 5.
Performance of RL1, RL2, and GA. Average GA running time to reach stopping criterion: 48.01 s.
8.2. CCBM
As outlined in the Introduction, our experiments were carried out with two primary objectives:
- To showcase that addressing the chance-constrained CCBM problem directly results in shorter project durations compared with the approach of solving the deterministic-constrained problem and subsequently incorporating time buffers.
- To establish the efficacy of our RL-based method in generating CCBM schedules in comparison to established benchmarks.
In relation to the first objective, the chance-constrained methods consistently produced project durations that were shorter than their deterministic-constrained counterparts. Table 6 illustrates the percentage difference in project delivery between the chance-constrained models and their deterministic counterparts (only the optimal CS solutions, where the Gurobi MIPGap parameter was less than 0.1, were taken into consideration).

Table 6.
Chance-constrained methods compared with deterministic-constrained counterparts: Difference in project delivery.
As far as the second objective is concerned, we see that CRL1 had the best performance compared with the benchmarks. As Table 7 indicates, CRL1 achieved the lowest delivery times. All the other methods, including CS for the optimal group, had significantly longer delivery times than CRL1, as confirmed by WSR tests for pairwise comparisons with a p-value = 0.000. CRL2 also performed better than all the other methods except CRL1 and CS for the optimal group, with a p-value = 0.000.

Table 7.
CRL1 compared with the other chance-constrained methods: Difference in project delivery.
8.3. TVNPV
Strong evidence supporting the appropriateness of the RL methods was discovered. The findings from the pairwise comparison are presented in Table 8, which displays the average percent difference and WSR p-value for each method pair.

Table 8.
Performance of RL1, RL2, SA, and TS.
Among the methods, RL1 demonstrated the closest alignment with the solver values for the objectives. Additionally, RL1 outperformed all other methods, with the exception of the solver itself. In comparison to RL2, TS yielded more favorable outcomes. It is important to note that, as in Section 8.2, only SA solutions with a maximum gap of 0.1 between the lower and upper objective bounds were considered. Solutions with larger gaps were deemed inferior, and including them would have skewed the results.
9. Discussion
During the LPM experiments, we observed that RL generated higher project values, which is noteworthy considering the well-established proficiency of GA, particularly for 10-activity projects, demonstrated in a study with value maximization in a deterministic setting [5]. One potential explanation for this result could be attributed to the RL algorithm’s inherent nature, whereby the agent takes immediate actions and receives corresponding rewards, thus continually learning the policy throughout each iteration.
In contrast, GA operates in a more randomized manner. Initially, it generates a population of solutions, evaluates each one, and attempts to enhance them through the random mixing of pairs. Discovering optimal solutions through this process takes time for two primary reasons. Firstly, we must await the completion of the entire population’s generation and evaluation. Secondly, the fitness value of each solution holds minimal influence on the quality of solutions generated in subsequent iterations, implying that it is not effectively utilized for learning.
As stated in the Introduction, LPM aims to create value and minimize waste in the shortest amount of time. One of the main practical implications of our LPM model is the ability it offers project managers to generate alternative solutions and conduct tradeoff analysis, considering different risk levels in terms of time and cost overruns. Each solution generated is an implementable project schedule with the selected mode for each activity, maximizing the project value according to the stakeholders’ risk threshold.
Our CCBM experiments yielded compelling results, demonstrating that shorter schedules can be obtained by directly solving the chance-constrained model instead of resorting to solving the deterministic model and subsequently incorporating time buffers (Objective 1). This outcome aligns with our expectations. By addressing the chance-constrained problem directly and considering the actual realization of activity durations, we make informed decisions on modes and start times that satisfy the true objective of minimizing the delivery date. In our context, the project duration encompasses the desired on-time probability, including the PB that ensures project completion within the specified timeframe. To the best of our knowledge, no previous work on CCBM scheduling has adopted this outlook.
Furthermore, our investigation revealed that the RL approach produces schedules that are competitive when compared with well-established benchmarks (Objective 2). Notably, CRL1 achieved shorter durations than CS, even in cases where CS discovered an optimal solution. This finding can be explained by the fact that CS identifies an optimal solution based on a specific sample of scenarios, while a different set of realized durations may lead to an even shorter schedule. Smaller 10-activity projects, as anticipated, allow for a faster and more comprehensive exploration of the search space. CRL1 excelled in determining optimal start-time and mode combinations as well as exploring a greater number of realized duration instances.
We note that the CS runtimes tend to be considerably longer than those of CRL1, as evident from the distributions shown in Figure 13. This observation further suggests that relying solely on MILP solver-based solutions may not be the most advantageous option. In fact, the time limit masks the 75th percentile for CS, suggesting that it is likely much higher and further supporting the idea that alternative approaches, such as CRL1, offer more compelling options.
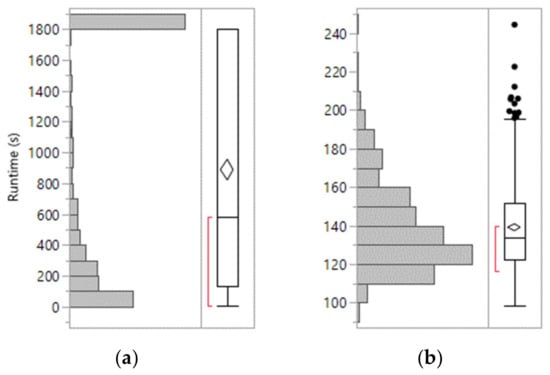
Figure 13.
(a) Box plot illustrating the runtime distribution of CS. The maximum runtime value corresponds to the 30-min time limit. (b) Box plot for CRL1 runtime. The center line in each box represents the median for the runtimes. The bottom and top of the box show the 25th and 75th percentiles. The whiskers extend to the minimum and maximum runtime values, excluding outliers. The data points that fall beyond the whiskers are outliers. The top and bottom of the diamonds are a 95% confidence interval for the mean. The middle of each diamond is the sample average. The bracket outside of each box identifies the shortest half, which is the densest 50% of the runtimes.
The performance of PR, which yielded comparatively lower-quality outcomes, was anticipated. Given that PR does not actively search for or learn solutions, it is relatively easier to discover superior solutions through RL or MILP approaches.
It was interesting to see that CRL1 outperformed CRL2. We had a different expectation regarding CRL2 because it uses a constant-step action-value update that assigns more weight to the recent actions and less weight to the earlier actions. This way, it could learn faster from the better decisions that are made later in the process, as it did in the LPM experiments. In the CCBM challenge, however, CRL2 did not meet our expectations, and we need to investigate further the possible causes and potential improvements for CRL2.
One of the main implications of our study is the usefulness for project managers of directly solving the chance-constrained CCBM problem. By achieving a lower project delivery time with the desired probability of on-time completion, they could have a competitive edge in securing contracts. Our RL-based algorithm can handle this problem and generate appealing solutions.
Turning our attention to TVNPV, our experimental results confirm the validity of RL as a valuable approach for analyzing the tradeoff between project value and NPV, particularly when compared with established benchmarks. The RL agent in our methodology effectively captures signals, represented as rewards, at each iteration to assess solution quality and promptly takes actions accordingly. This enables an informed search process from the outset, leveraging real-time information. In contrast, TS operates as a neighborhood search algorithm with a memory mechanism to avoid local optima but does not utilize acquired information during the search to guide its subsequent steps. Evidently, this limitation hampers TS’s ability to explore more promising regions of the search space earlier, potentially explaining the superior performance of RL1 over TS. Although TVNPV is a new model and no previous method has been applied to solve it, TS has been extensively used in max-NPV problems, as seen in [49,59,72,107]. Our results indicate the great potential for the application of RL in this area, which has up until now been tackled by heuristics [60].
As anticipated, the solver consistently produced the best results. It is worth noting, however, that, as mentioned in Section 4.2, RCPSP-derived problems are NP-hard, imposing significant computational time constraints on solver-based methods. Even for 10-activity projects, the solver failed to find an incumbent solution within the allotted 30-min limit for 33% of the projects.
In line with the CCBM experiments, RL1 exhibited superior performance compared with RL2, which is an interesting observation. In conclusion, our findings strongly suggest that employing the RL method for analyzing the project value versus NPV tradeoff can be a valuable tool for project managers. The near-optimal solutions generated through this approach can be used to construct an efficient frontier that captures the relationship between project value and rNPV, enabling decision-makers to conduct a thorough tradeoff analysis and select project plans that satisfactorily meet stakeholders’ requirements.
10. Conclusions
This paper presents a novel approach for LPM that maximizes value while ensuring adherence to minimum on-schedule and on-budget probabilities defined by decision makers. The proposed model employs a stochastic programming formulation with an SA approach. To achieve fast solutions during the project planning stage, we apply RL methods with two variations for action-value updates. A comprehensive experiment is conducted, comparing both RL variants against two benchmarks: a GA and a commercial solver solution.
The experimental results highlight the potential of RL methods as an appealing alternative to GA for generating high-quality solutions within shorter timeframes. Notably, RL2 outperforms RL1 in the LPM experiments. While SA yields higher objective values, it also produces a higher proportion of infeasible solutions when tested with datasets, along with extended running times that are typical of large MILP problems known to be NP-hard [108].
Our research offers valuable insights for decision-makers by enabling the plotting of an efficient frontier that showcases the best project plans for specific on-schedule and on-budget probabilities. It is crucial to consider the risk of activity durations when evaluating project plan options. Using deterministic activity durations could lead to an inflated estimation of the project value, which could result in stakeholder dissatisfaction, as demonstrated in Appendix F.
Our model has some limitations, despite its advantages. We assume that the project can obtain the resources it needs as long as it meets the budget constraint; however, this may not always be true, and resource constraints may still be an issue even if there is enough money to hire/acquire the resources. The TVNPV model addresses this problem by incorporating resource constraints.
Additionally, we explore a novel formulation of CCBM, specifically the multimode chance-constrained CCBM problem. We propose an MILP formulation for this problem and apply SA to handle the chance constraints. Our innovative use of RL provides a solution for this formulation, and experimental validation reinforces its efficacy.
Further, our research emphasizes the significance of solving the chance-constrained problem directly to derive a PB tailored to the desired on-schedule probability. The results demonstrate that solving the chance-constrained CCBM problem leads to shorter project durations compared with incorporating time buffers in a baseline schedule generated by the deterministic approach. We also confirm that our RL method yields competitive schedules compared with traditional approaches such as PR and MILP solutions. This contribution empowers decision-makers with the potential to achieve shorter schedules while maintaining the same on-time probabilities.
Finally, we explore the tradeoff between project value and NPV within a stochastic multimode framework. We propose a MIP formulation utilizing a flow-based model with a project-specific value function and a robust NPV decision variable. Robustness is addressed through chance constraints, which are tackled using SA. Leveraging linearization techniques, we develop MILP models that can be efficiently solved by commercial solvers for small projects with linear value functions.
To solve the MIP formulation, we leverage RL and present an illustrative example. The conducted experiment yields satisfactory results, demonstrating the suitability of RL for solving our proposed formulation. The practical significance of our contribution lies in identifying the efficient frontier that allows decision makers to make focused tradeoffs between different project plan alternatives based on robust NPV and project value, representing the project scope and product scope, respectively. This thorough evaluation facilitates informed decision-making.
Future research will explore alternative RL techniques to enhance the search for optimal schedules in larger projects, where action-value tables become impractical due to their size. Methods such as function approximation and neural networks hold untapped potential for their application in project scheduling. In the former, the action-value table is replaced by a function; in the latter, interconnected processing nodes substitute for the table. In both cases, we can have a more compact representation that requires less memory while using sophisticated representations to approximate the action-value function, even in high-dimensional spaces.
Author Contributions
Conceptualization, C.S. and A.S.; methodology, C.S. and Y.T.H.; software, C.S.; validation, C.S.; formal analysis, C.S.; investigation, C.S.; resources, Y.T.H. and A.S.; data curation, C.S.; writing—original draft preparation, C.S.; writing—review and editing, Y.T.H.; visualization, C.S.; supervision, Y.T.H. and A.S.; project administration, C.S., Y.T.H. and A.S.; funding acquisition, Y.T.H. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Israel Science Foundation, grant number 2550/21, and the Bernard M. Gordon Center for Systems Engineering at the Technion.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
| AON | Activity-On-Node |
| CCBM | Critical Chain Buffer Management |
| CDF | Cumulative Distribution Function |
| CRL | Chance-Constrained Reinforcement Learning—A method that applies RL to the problem with chance constraints |
| CS | Chance-Constrained Solver—A method that solves the MILP problem with chance constraints |
| DRL | Deterministic-constrained Reinforcement Learning—A method that applies RL to the problem with deterministic constraints |
| DS | Deterministic-constrained Solver—A method that solves the MILP problem with deterministic constraints |
| eNPV | Expected Net Present Value |
| FB | Feeding Buffer |
| GA | Genetic Algorithm |
| LPM | Lean Project Management |
| MCC | Monte Carlo Control |
| MILP | Mixed-Integer Linear Program |
| MIP | Mixed Integer Program |
| NPV | Net Present Value |
| PB | Project Buffer |
| Probability Density Function | |
| PR | Priority Rule |
| QFD | Quality Function Deployment |
| RCPSP | Resource-Constrained Project Scheduling Problem |
| RL | Reinforcement Learning |
| RL1 | Reinforcement Learning Algorithm Employing Average Rewards |
| RL2 | Reinforcement Learning Algorithm Employing Constant Step |
| rNPV | Robust Net Present Value |
| RSEM | Root Square Error Method |
| SA | Scenario Approach |
| TS | Tabu Search |
| TVNPV | Tradeoff between Project Value and its Net Present Value |
| WSR | Wilcoxon Signed Rank |
Appendix A. Functions Used in the Main RL Procedures
Appendix A.1. LPM
Table A1 summarizes our notation for RL, in addition to the notation utilized in the quantitative models. Subsequently, we present the pseudocode and provide a comprehensive explanation of our MCC method.

Table A1.
Additional notation for the LPM–RL method.
Table A1.
Additional notation for the LPM–RL method.
| ε-greedy policy, decision-making rule | |
| Value of choosing mode m for activity j under ε-greedy policy π | |
| Probability of selecting mode m for activity j under ε-greedy policy π | |
| Reward for selecting mode m for activity j under ε-greedy policy π | |
| Probability of random action in ε-greedy policy | |
| Selected mode for activity j | |
| Nj | Number of times mode mj is selected for activity j |
| Step-size parameter |
In Algorithm A1, we illustrate the initial phase of our approach, where we initialize the action-value table with intentionally overestimated values, employing a technique referred to as optimistic initial values [100]. The purpose of this strategy is to promote exploration in the early stages. Initially, the modes with the highest action-values are chosen, resulting in the agent receiving a reward that may be lower than anticipated. This, in turn, encourages the agent to select other modes with optimistically high action-values in subsequent iterations.
| Algorithm A1: Initialization of the action-value list. |
| def initialize_action_values : |
| for |
| for : |
| large number |
| return |
When performing the policy calculation (Algorithm A2), we address a well-known challenge in RL and other search methodologies, namely, the tradeoff between exploration and exploitation. Opting for a purely greedy policy, where we select the mode with the highest action-value for each activity, may lead us to quickly find a solution but potentially overlook a superior solution achievable through a different combination of modes. Conversely, employing a random policy would result in pure exploration without any learning. To strike a balance, we utilize a technique called ε-greedy policies, described in Section 5.
Moving forward, we use the policy to select modes and then compute the reward for this action (Algorithm A3). The function’s main concept is that a feasible project plan gets the reward of the project value, which is our optimization goal; otherwise, it gets a zero reward as a penalty. The plan is feasible only if it meets or exceeds the decision-makers’ requirements for finishing on time and on budget with certain probabilities.
We utilize two distinct approaches for updating the action-values, as described by [100]. The first method, known as average rewards (RL1), involves calculating the action-values by taking the average of the rewards obtained each time a particular mode is selected for an activity. To prevent the accumulation of large lists and the associated increase in memory usage and runtime, we adopt an incremental approach for computing the averages. The variable Nj in Algorithm A4 represents the number of times that mode was selected for the activity.
| Algorithm A2: Policy calculation. |
| def calculate_policy : |
| for |
| x |
| return |
| Algorithm A3: Reward calculation. |
| def calculate_reward |
| simulate large number of project runs |
| if |
| return |
| else: |
| return |
| Algorithm A4: Action-value update using average rewards (RL1). |
| def update_action_values_RL1 |
| for |
| return |
The second method, referred to as constant step (RL2), aims to leverage the learning process by assigning exponentially higher weight to the most recent actions, which are expected to be more optimal. The constant α in Algorithm A5 represents the step parameter used in this method.
| Algorithm A5: Action-value update using constant step (RL2). |
| def update_action_values_RL2 |
| for |
| return |
Appendix A.2. CCBM
In addition to the notation presented in Table A1, the RL algorithm for CCBM incorporates the notation provided in Table A2.

Table A2.
Additional notation for the CCBM RL method.
Table A2.
Additional notation for the CCBM RL method.
| Value of choosing mode m and start time t for activity j under ε-greedy policy π | |
| Probability of choosing mode m and start time t for activity j under ε-greedy policy π | |
| Reward for choosing mode m and start time t for activity j under ε-greedy policy π | |
| Chosen start time for activity j | |
| Most likely duration of activity j in chosen mode | |
| Quantity of resources of type k needed to execute activity j in chosen mode | |
| Set of activities executed in parallel to activity j | |
| Nj | Number of times mode mj and start time tj are chosen for activity j |
As in LPM, we begin by initializing the list of action-values (Algorithm A6). Each action consists of selecting an activity mode and start time. We divide the time interval from zero to the latest possible start of the activity into 10 equal segments and use them as the start times. We then use the action-value list to compute the policy (Algorithm A7).
| Algorithm A6: Initialization of the action-value list. |
| def initialize_action_values : |
| for |
| for |
| for |
| return |
| Algorithm A7: Policy calculation. |
| def calculate_policy : |
| for |
| return |
We then follow the policy to select an action for each activity (Algorithm A8), which involves choosing a mode and a start time based on the probabilities in the policy table. To ensure that the start times respect the precedence relations, we shift each activity to the right by adding the finish time of its immediate predecessor to its chosen start time. This means that if activity j has a start time of we move it to start at plus the finish time of its immediate predecessor. We use the most likely duration of each activity in its selected mode to calculate the finish times. Finally, we arrange all activities in ascending order of their adjusted start times, resulting in a precedence-feasible list of activities and their modes.
| Algorithm A8: Choose activity mode and start time. |
| def choose_mode_start : |
| for |
| if |
| else: |
| return |
We note that choosing different start times for the actions is equivalent to choosing different precedence combinations between the activities. The range of possible start times from zero to the upper bound allows for more flexibility and diversity in starting or delaying each activity, which can lead to a better and richer search space for solutions. Moreover, by adjusting the activity list to be precedence-feasible, we avoid wasting time on infeasible solutions or losing potentially good solutions.
The next step in the algorithm is to compute the reward for the actions taken (Algorithm A9). We first construct the early-start baseline schedule by taking each activity from the list and placing it at the earliest possible time. We start with the finish time of the most immediate predecessor, and if there are not enough resources, we shift the activity to the right repeatedly until we reach the next scheduled activity finish time where there are enough resources. Once we have the schedule, we calculate the project delivery date. For instance, if the decision-makers want a 95% probability of completing the project on time, we simulate the baseline schedule 1000 times, sort the finish times, and take the 950th element of the finish time list as the delivery date. Since our goal is to minimize the delivery date, we define the reward as to follow the RL idea of maximizing the reward.
| Algorithm A9: Reward calculation. |
| def calculate_reward |
| for |
| return |
The final step in the algorithm is to update the action-values using the RL1 and RL2 methods. These methods are almost the same as those in Appendix A.1, with only two changes: we use instead of as the arguments for the functions, and we substitute with and with .
Appendix A.3. TVNPV
In this section, we focus on the calculate_reward function (Algorithm A10) for TVNPV, which is different from the one for CCBM as it uses rNPV instead of the project delivery date. The other RL functions for TVNPV are identical to those for CCBM, as described in Appendix A.2. We first explain how we insert each activity into the baseline schedule. We do this for each activity in sequence. We start by finding the interval between the earliest possible start that respects the precedence relations and the latest finish time of the activities already scheduled. We divide this interval into 10 equal parts and then place the activity according to its start time in the policy list. For instance, if is the third start time in the policy list, we use the third part of the interval, rounding it to the closest finish time of an activity. If there are not enough resources, we keep moving the activity to the right until we reach the next finish time of a scheduled activity where there are enough resources. Once we have the schedule, we calculate the value of the objective function. To calculate rNPV, we simulate the NPV CDF. For example, if the decision makers want a 95% probability of achieving the rNPV, we simulate the baseline schedule 1000 times, sort the NPVs, and take the 50th element of the NPV list as the rNPV. We define the reward as the value of the objective function.
| Algorithm A10: Reward calculation. |
| def calculate_reward |
| for activity mode in sorted |
Appendix B. A New Fitness Function for the Stochastic GA
We modified the fitness function of the GA that we used for comparison because it was designed only for deterministic problems. Our stochastic datasets required a different approach. We defined the fitness value of a solution I as
where . A solution I is the chosen mode for each activity. This formula penalizes an infeasible solution by measuring the difference between the actual and the desired on-budget proportion. This scaled penalty helps the best infeasible solutions become feasible through crossover. Moreover, the formula ensures that no infeasible solution has a higher fitness value than a feasible one, as [5] did.
Appendix C. LPM Experiment Data Generation and Sample Sizes
To create more data for the PSPLIB instances that matched our problem specifications, we randomly assigned resource unit costs and activity mode fixed costs from a uniform distribution within the ranges of (5, 50) and (0, 14,000), respectively, following the method of [5]. We calculated the budgets for each project by taking the average of the project costs, with all modes having the highest cost (fixed and resource) and all modes having the middle cost. Similarly, we computed the due dates for each project by taking the average of the project duration, with all modes having the longest duration and all modes having the middle duration.
We had two value attributes (V = 2) with relative weights of 0.6 and 0.4. We also defined an additive project value function Fv for each attribute in the linear objective function. Thus, the objective function was . We randomly selected the value parameters Vjmv from a uniform distribution within the interval (0, 10).
We set the desired probability of being on schedule and on budget to 0.95 and ran each solution 1000 times for each project to estimate the percentage of scenarios that met these criteria. Unlike our model, the model in [5] does not have hard due date constraints; rather, it has penalty costs instead. Therefore, we used a very high penalty cost for violating the due date in our GA code, making it impossible to generate a feasible schedule that exceeded the due date.
We employed our SA model (Section 4.1) with 1000 scenarios to match the 1000 project simulation runs for the GA and RL.
Appendix D. Mode and Activity PRs Employed in the CCBM Experiment
A comprehensive assessment was conducted by [45] to evaluate a set of 60 PRs for mode selection and activity selection across diverse datasets. The analysis revealed that the combination of PRs resulting in the shortest project durations consisted of selecting modes based on the least total resource usage (LTRU) and activities based on the greatest resource demand (GRD). Detailed formulas for LTRU and GRD can be found in [45].
To streamline the problem, we initially transformed the multimode scenario into a single-mode scenario by implementing the LTRU PR. Subsequently, we utilized the GRD PR in conjunction with the widely recognized serial schedule generation scheme [109] to generate the project schedule.
Appendix E. The TS Algorithm Used in This Paper
We used the TS method from [107] as a comparison. We made some changes to fit the formulation in Section 4.3:
- We replaced the original pure NPV objective with the objective function (29) from Section 4.3.
- TS was for deterministic problems only. For our stochastic problem, we followed the RL algorithms to compute the objective function: we ran 1000 project simulations as shown in Algorithm A10 and described in Appendix A.3.
- We did not use any penalty functions because all our solutions were feasible.
TS is not discussed in depth in this paper. For more details on this topic, see [107].
Appendix F. Proportion of Infeasible Solutions
In Table A3, we present the percentage of solutions that were deemed infeasible. Each solution underwent 10,000 simulation runs, with randomly generated activity durations drawn according to the distributions and parameters outlined in Appendix B. If fewer than 95% of the simulation runs were completed within the specified time frame or budget, the solution was classified as infeasible. For each algorithm, we recorded the proportion (P) of the 535 solutions that fell into this category, along with the corresponding Newcombe confidence interval (CI) for the proportion of infeasible solutions (calculated using [110]).
Analyzing the results depicted in Table A3, it becomes evident that SA exhibited a significantly higher proportion of infeasible solutions compared with RL, which nullified its advantage of higher values.

Table A3.
Confidence interval for proportion of infeasible solutions, 95% confidence level.
Table A3.
Confidence interval for proportion of infeasible solutions, 95% confidence level.
| RL1 | RL2 | SA | |||
|---|---|---|---|---|---|
| P | CI | P | CI | P | CI |
| 0.09 | [0.07, 0.12] | 0.09 | [0.06, 0.11] | 0.37 | [0.33, 0.41] |
Appendix G. Comparing Deterministic to Stochastic Project Values
The significance of incorporating project risk by utilizing stochastic activity durations is highlighted in Table A4. The table presents a pairwise comparison of project values between the deterministic and stochastic versions. In the deterministic version, the most likely durations were used instead of three-point estimates. Consequently, project runs were not simulated in the GA and RL algorithms, and the MILP was solved without generating scenarios. Across all algorithms, the project value objectives in the deterministic version exhibit a significant increase compared with their counterparts in the stochastic version.

Table A4.
WSR test p-values comparing deterministic to stochastic project values. The alternative hypothesis is that deterministic values are greater.
Table A4.
WSR test p-values comparing deterministic to stochastic project values. The alternative hypothesis is that deterministic values are greater.
| GA | RL1 | RL2 | MILP | |
|---|---|---|---|---|
| p-value | 0.000 | 0.000 | 0.000 | 0.000 |
References
- De Meyer, A.; Loch, C.H.; Pich, M.T. Managing Project Uncertainty: From Variation to Chaos. MIT Sloan Manag. Rev. 2002, 43, 60–67. [Google Scholar] [CrossRef]
- The Standish Group. CHAOS Report. 2015. Available online: https://standishgroup.com/sample_research_files/CHAOSReport2015-Final.pdf (accessed on 20 July 2023).
- Project Management Institute. Beyond Agility: Flex to the Future. 24 March 2021. Available online: https://www.pmi.org/learning/library/beyond-agility-gymnastic-enterprises-12973 (accessed on 20 July 2023).
- Browning, T.R. Planning, Tracking, and Reducing a Complex Project’s Value at Risk. Proj. Manag. J. 2019, 50, 71–85. [Google Scholar] [CrossRef]
- Balouka, N.; Cohen, I.; Shtub, A. Extending the Multimode Resource-Constrained Project Scheduling Problem by Including Value Considerations. IEEE Trans. Eng. Manag. 2016, 63, 4–15. [Google Scholar] [CrossRef]
- Zhao, W.; Hall, N.G.; Liu, Z. Project Evaluation and Selection with Task Failures. Prod. Oper. Manag. 2020, 29, 428–446. [Google Scholar] [CrossRef]
- Chih, Y.Y.; Zwikael, O. Project Benefit Management: A Conceptual Framework of Target Benefit Formulation. Int. J. Proj. Manag. 2015, 33, 352–362. [Google Scholar] [CrossRef]
- Badewi, A. The Impact of Project Management (PM) and Benefits Management (BM) Practices on Project Success: Towards Developing a Project Benefits Governance Framework. Int. J. Proj. Manag. 2016, 34, 761–778. [Google Scholar] [CrossRef]
- Ul Musawir, A.; Serra, C.E.M.; Zwikael, O.; Ali, I. Project Governance, Benefit Management, and Project Success: Towards a Framework for Supporting Organizational Strategy Implementation. Int. J. Proj. Manag. 2017, 35, 1658–1672. [Google Scholar] [CrossRef]
- Serra, C.E.M.; Kunc, M. Benefits Realisation Management and Its Influence on Project Success and on the Execution of Business Strategies. Int. J. Proj. Manag. 2015, 33, 53–66. [Google Scholar] [CrossRef]
- Zwikael, O.; Chih, Y.-Y.; Meredith, J.R. Project Benefit Management: Setting Effective Target Benefits. Int. J. Proj. Manag. 2018, 36, 650–658. [Google Scholar] [CrossRef]
- Laursen, M. Project Networks as Constellations for Value Creation. Proj. Manag. J. 2018, 49, 56–70. [Google Scholar] [CrossRef]
- Invernizzi, D.C.; Locatelli, G.; Grönqvist, M.; Brookes, N.J. Applying Value Management When It Seems That There Is No Value to Be Managed: The Case of Nuclear Decommissioning. Int. J. Proj. Manag. 2019, 37, 668–683. [Google Scholar] [CrossRef]
- Mishra, A.; Sinha, K.K.; Thirumalai, S. Project Quality: The Achilles Heel of Offshore Technology Projects? IEEE Trans. Eng. Manag. 2017, 64, 272–286. [Google Scholar] [CrossRef]
- Browning, T.R.; Deyst, J.J.; Eppinger, S.D.; Whitney, D.E. Adding Value in Product Development by Creating Information and Reducing Risk. IEEE Trans. Eng. Manag. 2002, 49, 443–458. [Google Scholar] [CrossRef]
- Browning, T.R. A Quantitative Framework for Managing Project Value, Risk, and Opportunity. IEEE Trans. Eng. Manag. 2014, 61, 583–598. [Google Scholar] [CrossRef]
- Dinçer, H.; Yüksel, S.; Martínez, L. Balanced Scorecard-Based Analysis about European Energy Investment Policies: A Hybrid Hesitant Fuzzy Decision-Making Approach with Quality Function Deployment. Expert Syst. Appl. 2019, 115, 152–171. [Google Scholar] [CrossRef]
- Cordeiro, E.C.; Barbosa, G.F.; Trabasso, L.G. A Customized QFD (Quality Function Deployment) Applied to Management of Automation Projects. Int. J. Adv. Manuf. Technol. 2016, 87, 2427–2436. [Google Scholar] [CrossRef]
- Liu, A.; Hu, H.; Zhang, X.; Lei, D. Novel Two-Phase Approach for Process Optimization of Customer Collaborative Design Based on Fuzzy-QFD and DSM. IEEE Trans. Eng. Manag. 2017, 64, 193–207. [Google Scholar] [CrossRef]
- Lo, S.M.; Shen, H.-P.; Chen, J.C. An Integrated Approach to Project Management Using the Kano Model and QFD: An Empirical Case Study. Total Qual. Manag. Bus. Excell. 2016, 28, 1584–1608. [Google Scholar] [CrossRef]
- Cohen, I.; Iluz, M. When Cost–Effective Design Strategies Are Not Enough: Evidence from an Experimental Study on the Role of Redundant Goals. Omega (Westport) 2015, 56, 99–111. [Google Scholar] [CrossRef]
- Masin, M.; Dubinsky, Y.; Iluz, M.; Shindin, E.; Shtub, A. EMI: Engineering and Management Integrator. In Complex Systems Design & Management; Springer International Publishing: Cham, Switzerland, 2016; pp. 143–155. [Google Scholar]
- Cohen, I.; Iluz, M.; Shtub, A. A Simulation-Based Approach in Support of Project Management Training for Systems Engineers. Syst. Eng. 2014, 17, 26–36. [Google Scholar] [CrossRef]
- Shtub, A.; Iluz, M.; Gersing, K.; Oehmen, J.; Dubinsky, Y. Implementation of Lean Engineering Practices in Projects and Programs through Simulation Based Training. PM World J. 2014, 3, 1–13. [Google Scholar]
- Oehmen, J. (Ed.) The Guide to Lean Enablers for Managing Engineering Programs; Joint MIT-PMI-INCOSE Community of Practice on Lean in Program Management: San Diego, CA, USA, 2012. [Google Scholar]
- Hoel, K.; Taylor, S.G. Quantifying Buffers for Project Schedules. Prod. Inventory Manag. J. 1999, 40, 43–47. [Google Scholar]
- Zhang, J.; Song, X.; Díaz, E. Critical Chain Project Buffer Sizing Based on Resource Constraints. Int. J. Prod. Res. 2017, 55, 671–683. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, S.; Diaz, E. A New Buffer Sizing Approach Based on the Uncertainty of Project Activities. Concurr. Eng. 2015, 23, 3–12. [Google Scholar] [CrossRef]
- Ma, G.; Gu, L.; Li, N. Scenario-Based Proactive Robust Optimization for Critical-Chain Project Scheduling. J. Constr. Eng. Manag. 2015, 141, 04015030. [Google Scholar] [CrossRef]
- Poshdar, M.; González, V.; Raftery, G.; Orozco, F.; Romeo, J.; Forcael, E. A Probabilistic-Based Method to Determine Optimum Size of Project Buffer in Construction Schedules. J. Constr. Eng. Manag. 2016, 142, 4016046. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, N.; Tian, W. A Two-Stage Approach for the Critical Chain Project Rescheduling. Ann. Oper. Res. 2020, 285, 67–95. [Google Scholar] [CrossRef]
- Ghoddousi, P.; Ansari, R.; Makui, A. A Risk-Oriented Buffer Allocation Model Based on Critical Chain Project Management. KSCE J. Civ. Eng. 2016, 21, 1536–1548. [Google Scholar] [CrossRef]
- Newbold, R.C. Project Management in the Fast Lane; CRC Press: Boca Raton, FL, USA, 1998; ISBN 9780429258152. [Google Scholar]
- Bevilacqua, M.; Ciarapica, F.E.; Mazzuto, G.; Paciarotti, C. Robust Multi-Criteria Project Scheduling in Plant Engineering and Construction. In Handbook on Project Management and Scheduling Vol. 2; Springer International Publishing: Cham, Switzerland, 2015; pp. 1291–1305. ISBN 9783319059150. [Google Scholar]
- Ghaffari, M.; Emsley, M.W. The Impact of Good and Bad Multitasking on Buffer Requirements of CCPM Portfolios. J. Mod. Proj. Manag. 2016, 4, 91–95. [Google Scholar] [CrossRef]
- Hu, X.; Demeulemeester, E.; Cui, N.; Wang, J.; Tian, W. Improved Critical Chain Buffer Management Framework Considering Resource Costs and Schedule Stability. Flex. Serv. Manuf. J. 2017, 29, 159–183. [Google Scholar] [CrossRef]
- Hu, X.; Cui, N.; Demeulemeester, E.; Bie, L. Incorporation of Activity Sensitivity Measures into Buffer Management to Manage Project Schedule Risk. Eur. J. Oper. Res. 2016, 249, 717–727. [Google Scholar] [CrossRef]
- Salama, T.; Salah, A.; Moselhi, O. Integration of Linear Scheduling Method and the Critical Chain Project Management. Can. J. Civ. Eng. 2018, 45, 30–40. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, S.; Diaz, E. Dynamic Monitoring and Control of a Critical Chain Project Based on Phase Buffer Allocation. J. Oper. Res. Soc. 2018, 69, 1966–1977. [Google Scholar] [CrossRef]
- Zhang, J.; Song, X.; Chen, H.; Shi, R. Optimisation of Critical Chain Sequencing Based on Activities Information Flow Interactions. Int. J. Prod. Res. 2015, 53, 6231–6241. [Google Scholar] [CrossRef]
- Zhang, J.; Song, X.; Díaz, E. Project Buffer Sizing of a Critical Chain Based on Comprehensive Resource Tightness. Eur. J. Oper. Res. 2016, 248, 174–182. [Google Scholar] [CrossRef]
- Zhang, J.; Song, X.; Chen, H.; Shi, R. Determination of Critical Chain Project Buffer Based on Information Flow Interactions. J. Oper. Res. Soc. 2016, 16, 1146–1157. [Google Scholar] [CrossRef]
- Ma, G.; Hao, K.; Xiao, Y.; Zhu, T. Critical Chain Design Structure Matrix Method for Construction Project Scheduling under Rework Scenarios. Math. Probl. Eng. 2019, 2019, 1595628. [Google Scholar] [CrossRef]
- Tian, W.; Demeulemeester, E. Railway Scheduling Reduces the Expected Project Makespan over Roadrunner Scheduling in a Multi-Mode Project Scheduling Environment. Ann. Oper. Res. 2014, 213, 271–291. [Google Scholar] [CrossRef]
- Peng, W.; Huang, M.C.; Yongping, H. A Multi-Mode Critical Chain Scheduling Method Based on Priority Rules. Prod. Plan. Control 2015, 26, 1011–1024. [Google Scholar] [CrossRef]
- Ma, G.; Wang, A.; Li, N.; Asce, M.; Gu, L.; Ai, Q. Improved Critical Chain Project Management Framework for Scheduling Construction Projects. J. Constr. Eng. Manag. 2014, 140, 04014055. [Google Scholar] [CrossRef]
- Ma, Z.; Demeulemeester, E.; He, Z.; Wang, N. A Computational Experiment to Explore Better Robustness Measures for Project Scheduling under Two Types of Uncertain Environments. Comput. Ind. Eng. 2019, 131, 382–390. [Google Scholar] [CrossRef]
- Ning, M.; He, Z.; Wang, N.; Liu, R. Metaheuristic Algorithms for Proactive and Reactive Project Scheduling to Minimize Contractor’s Cash Flow Gap under Random Activity Duration. IEEE Access 2018, 6, 30547–30558. [Google Scholar] [CrossRef]
- Zheng, W.; He, Z.; Wang, N.; Jia, T. Proactive and Reactive Resource-Constrained Max-NPV Project Scheduling with Random Activity Duration. J. Oper. Res. Soc. 2018, 69, 115–126. [Google Scholar] [CrossRef]
- Davari, M.; Demeulemeester, E. Important Classes of Reactions for the Proactive and Reactive Resource-Constrained Project Scheduling Problem. Ann. Oper. Res. 2019, 274, 187–210. [Google Scholar] [CrossRef]
- Torabi Yeganeh, F.; Zegordi, S.H. A Multi-Objective Optimization Approach to Project Scheduling with Resiliency Criteria under Uncertain Activity Duration. Ann. Oper. Res. 2020, 285, 161–196. [Google Scholar] [CrossRef]
- Li, H.; Demeulemeester, E. A Genetic Algorithm for the Robust Resource Leveling Problem. J. Sched. 2016, 19, 43–60. [Google Scholar] [CrossRef]
- Bakry, I.; Moselhi, O.; Zayed, T. Optimized Scheduling and Buffering of Repetitive Construction Projects under Uncertainty. Eng. Constr. Archit. Manag. 2016, 23, 782–800. [Google Scholar] [CrossRef]
- Ghoddousi, P.; Ansari, R.; Makui, A. An Improved Robust Buffer Allocation Method for the Project Scheduling Problem. Eng. Optim. 2017, 49, 718–731. [Google Scholar] [CrossRef]
- Wichmann, M.G.; Gäde, M.; Spengler, T.S. A Fuzzy Robustness Measure for the Scheduling of Commissioned Product Development Projects. Fuzzy Sets Syst. 2019, 377, 125–149. [Google Scholar] [CrossRef]
- Russell, A.H. Cash Flows in Networks. Manag. Sci. 1970, 16, 357–373. [Google Scholar] [CrossRef]
- Leyman, P.; Vanhoucke, M. A New Scheduling Technique for the Resource-Constrained Project Scheduling Problem with Discounted Cash Flows. Int. J. Prod. Res. 2015, 53, 2771–2786. [Google Scholar] [CrossRef]
- Gu, H.; Schutt, A.; Stuckey, P.J.; Wallace, M.G.; Chu, G. Exact and Heuristic Methods for the Resource-Constrained Net Present Value Problem. In Handbook on Project Management and Scheduling Vol. 1; Springer International Publishing: Cham, Switzerland, 2015; pp. 299–318. ISBN 9783319054438. [Google Scholar]
- Leyman, P.; Vanhoucke, M. Capital- and Resource-Constrained Project Scheduling with Net Present Value Optimization. Eur. J. Oper. Res. 2017, 256, 757–776. [Google Scholar] [CrossRef]
- Klimek, M. Techniques of Generating Schedules for the Problem of Financial Optimization of Multi-Stage Project. Appl. Comput. Sci. 2019, 15, 18. [Google Scholar] [CrossRef]
- Chen, M.; Yan, S.; Wang, S.-S.; Liu, C.-L. A Generalized Network Flow Model for the Multi-Mode Resource-Constrained Project Scheduling Problem with Discounted Cash Flows. Eng. Optim. 2015, 47, 165–183. [Google Scholar] [CrossRef]
- Leyman, P.; Vanhoucke, M. Payment Models and Net Present Value Optimization for Resource-Constrained Project Scheduling. Comput. Ind. Eng. 2016, 91, 139–153. [Google Scholar] [CrossRef]
- Leyman, P.; Van Driessche, N.; Vanhoucke, M.; De Causmaecker, P. The Impact of Solution Representations on Heuristic Net Present Value Optimization in Discrete Time/Cost Trade-off Project Scheduling with Multiple Cash Flow and Payment Models. Comput. Oper. Res. 2019, 103, 184–197. [Google Scholar] [CrossRef]
- Zhang, Z.-X.; Chen, W.-N.; Jin, H.; Zhang, J. A Preference Biobjective Evolutionary Algorithm for the Payment Scheduling Negotiation Problem. IEEE Trans. Cybern. 2020, 51, 6105–6118. [Google Scholar] [CrossRef]
- Wiesemann, W.; Kuhn, D.; Rustem, B. Maximizing the Net Present Value of a Project under Uncertainty. Eur. J. Oper. Res. 2010, 202, 356–367. [Google Scholar] [CrossRef]
- Creemers, S.; De Reyck, B.; Leus, R. Project Planning with Alternative Technologies in Uncertain Environments. Eur. J. Oper. Res. 2015, 242, 465–476. [Google Scholar] [CrossRef]
- Kerkhove, L.P.; Vanhoucke, M. Optimised Scheduling for Weather Sensitive Offshore Construction Projects. Omega 2017, 66, 58–78. [Google Scholar] [CrossRef]
- Creemers, S. Maximizing the Expected Net Present Value of a Project with Phase-Type Distributed Activity Durations: An Efficient Globally Optimal Solution Procedure. Eur. J. Oper. Res. 2018, 267, 16–22. [Google Scholar] [CrossRef]
- Creemers, S. Moments and Distribution of the Net Present Value of a Serial Project. Eur. J. Oper. Res. 2018, 267, 835–848. [Google Scholar] [CrossRef]
- Creemers, S. Two Sequencing Problems: Equivalence, Optimal Solution, and State-of-the-Art Results. SSRN Electron. J. 2017. [Google Scholar] [CrossRef]
- Hermans, B.; Leus, R. Scheduling Markovian PERT Networks to Maximize the Net Present Value: New Results. Oper. Res. Lett. 2018, 46, 240–244. [Google Scholar] [CrossRef]
- Liang, Y.; Cui, N.; Wang, T.; Demeulemeester, E. Robust Resource-Constrained Max-NPV Project Scheduling with Stochastic Activity Duration. OR Spectr. 2019, 41, 219–254. [Google Scholar] [CrossRef]
- Rezaei, F.; Najafi, A.A.; Ramezanian, R. Mean-Conditional Value at Risk Model for the Stochastic Project Scheduling Problem. Comput. Ind. Eng. 2020, 142, 106356. [Google Scholar] [CrossRef]
- Bianco, L.; Caramia, M.; Giordani, S. A Chance Constrained Optimization Approach for Resource Unconstrained Project Scheduling with Uncertainty in Activity Execution Intensity. Comput. Ind. Eng. 2019, 128, 831–836. [Google Scholar] [CrossRef]
- Tantisuvanichkul, V. Optimizing Net Present Value Using Priority Rule-Based Scheduling; The University of Manchester: Manchester, UK, 2014. [Google Scholar]
- Briand, C.; Ngueveu, S.U.; Šůcha, P. Finding an Optimal Nash Equilibrium to the Multi-Agent Project Scheduling Problem. J. Sched. 2017, 20, 475–491. [Google Scholar] [CrossRef]
- Xiong, J.; Liu, J.; Chen, Y.; Abbass, H.A. A Knowledge-Based Evolutionary Multiobjective Approach for Stochastic Extended Resource Investment Project Scheduling Problems. IEEE Trans. Evol. Comput. 2014, 18, 742–763. [Google Scholar] [CrossRef]
- Calafiore, G.; Campi, M.C. Uncertain Convex Programs: Randomized Solutions and Confidence Levels. Math. Program. 2005, 102, 25–46. [Google Scholar] [CrossRef]
- Gutjahr, W.J. Bi-Objective Multi-Mode Project Scheduling under Risk Aversion. Eur. J. Oper. Res. 2015, 246, 421–434. [Google Scholar] [CrossRef]
- Lamas, P.; Demeulemeester, E. A Purely Proactive Scheduling Procedure for the Resource-Constrained Project Scheduling Problem with Stochastic Activity Durations. J. Sched. 2016, 19, 409–428. [Google Scholar] [CrossRef]
- Tian, J.; Hao, X.; Gen, M. A Hybrid Multi-Objective EDA for Robust Resource Constraint Project Scheduling with Uncertainty. Comput. Ind. Eng. 2019, 130, 317–326. [Google Scholar] [CrossRef]
- Herroelen, W.; Leus, R.; Demeulemeester, E. Critical Chain Project Scheduling: Do Not Oversimplify. Proj. Manag. J. 2002, 33, 48–60. [Google Scholar] [CrossRef]
- Blazewicz, J.; Lenstra, J.K.; Kan, A.H.G.R.G.R. Scheduling Subject to Resource Constraints: Classification and Complexity. Discret. Appl. Math. (1979) 1983, 5, 11–24. [Google Scholar] [CrossRef]
- Artigues, C.; Koné, O.; Lopez, P.; Mongeau, M. Mixed-Integer Linear Programming Formulations. In Handbook on Project Management and Scheduling Vol.1; Springer International Publishing: Cham, Switzerland, 2015; pp. 17–41. [Google Scholar]
- Balouka, N.; Cohen, I. A Robust Optimization Approach for the Multi-Mode Resource-Constrained Project Scheduling Problem. Eur. J. Oper. Res. 2019, 291, 457–470. [Google Scholar] [CrossRef]
- Gurobi Constraints. Available online: https://www.gurobi.com/documentation/9.1/refman/constraints.html (accessed on 21 February 2021).
- Lambrechts, O.; Demeulemeester, E.; Herroelen, W. Time Slack-Based Techniques for Robust Project Scheduling Subject to Resource Uncertainty. Ann. Oper. Res. 2011, 186, 443–464. [Google Scholar] [CrossRef]
- Peng, W.; Huang, M. A Critical Chain Project Scheduling Method Based on a Differential Evolution Algorithm. Int. J. Prod. Res. 2014, 52, 3940–3949. [Google Scholar] [CrossRef]
- Van de Vonder, S.; Demeulemeester, E.; Herroelen, W.; Leus, R. The Use of Buffers in Project Management: The Trade-off between Stability and Makespan. Int. J. Prod. Econ. 2005, 97, 227–240. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization. In Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; Edmund, K., Burke, G.K., Eds.; Springer: Boston, MA, USA, 2014; pp. 403–449. ISBN 978-1-4614-6939-1. [Google Scholar]
- Bomsdorf, F.; Derigs, U. A Model, Heuristic Procedure and Decision Support System for Solving the Movie Shoot Scheduling Problem. OR Spectr. 2008, 30, 751–772. [Google Scholar] [CrossRef]
- Liang, Y.; Cui, N.; Hu, X.; Demeulemeester, E. The Integration of Resource Allocation and Time Buffering for Bi-Objective Robust Project Scheduling. Int. J. Prod. Res. 2020, 58, 3839–3854. [Google Scholar] [CrossRef]
- Etgar, R.; Shtub, A.; Leblanc, L.J. Scheduling Projects to Maximize Net Present Value—The Case of Time-Dependent, Contingent Cash Flows. Eur. J. Oper. Res. 1997, 96, 90–96. [Google Scholar] [CrossRef]
- Barto, A.G. Reinforcement Learning: Connections, Surprises, Challenges. AI Mag. 2019, 40, 3–15. [Google Scholar] [CrossRef]
- Polvara, R.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R. Autonomous Vehicular Landings on the Deck of an Unmanned Surface Vehicle Using Deep Reinforcement Learning. Robotica 2019, 37, 1867–1882. [Google Scholar] [CrossRef]
- Ferrucci, D.; Levas, A.; Bagchi, S.; Gondek, D.; Mueller, E.T. Watson: Beyond Jeopardy! Artif. Intell. 2013, 199–200, 93–105. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Jędrzejowicz, P.; Ratajczak-Ropel, E. Reinforcement Learning Strategy for Solving the MRCPSP by a Team of Agents. In Intelligent Decision Technologies; Neves-Silva, R., Jain, L., Howlett, R., Eds.; Springer: Cham, Switzerland, 2015; pp. 537–548. [Google Scholar]
- Wauters, T.; Verbeeck, K.; De Causmaecker, P.; Vanden Berghe, G. A Learning-Based Optimization Approach to Multi-Project Scheduling. J. Sched. 2015, 18, 61–74. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018; ISBN 9780262039246. [Google Scholar]
- Skolnik, M.I. Radar Handbook; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Sarin, R.K. Multi-Attribute Utility Theory. In Encyclopedia of Operations Research and Management Science; Springer: Boston, MA, USA, 2013; pp. 1004–1006. [Google Scholar]
- Kolisch, R.; Sprecher, A. PSPLIB–A Project Scheduling Problem Library. Eur. J. Oper. Res. 1997, 96, 205–216. [Google Scholar] [CrossRef]
- Vanhoucke, M.; Coelho, J. A Tool to Test and Validate Algorithms for the Resource-Constrained Project Scheduling Problem. Comput. Ind. Eng. 2018, 118, 251–265. [Google Scholar] [CrossRef]
- Iluz, M.; Moser, B.; Shtub, A. Shared Awareness among Project Team Members through Role-Based Simulation during Planning—A Comparative Study. Procedia Comput. Sci. 2015, 44, 295–304. [Google Scholar] [CrossRef]
- Pellerin, R.; Perrier, N.; Berthaut, F. A Survey of Hybrid Metaheuristics for the Resource-Constrained Project Scheduling Problem. Eur. J. Oper. Res. 2020, 280, 395–416. [Google Scholar] [CrossRef]
- Mika, M.; Waligóra, G.; Weglarz, J. Simulated Annealing and Tabu Search for Multi-Mode Resource-Constrained Project Scheduling with Positive Discounted Cash Flows and Different Payment Models. Eur. J. Oper. Res. 2005, 164, 639–668. [Google Scholar] [CrossRef]
- Sierksma, G.; Zwols, Y. Linear and Integer Optimization, 3rd ed.; Chapman and Hall/CRC: New York, NY, USA, 2015; ISBN 9780429159961. [Google Scholar]
- Kolisch, R. Serial and Parallel Resource-Constrained Project Scheduling Methods Revisited: Theory and Computation. Eur. J. Oper. Res. 1996, 90, 320–333. [Google Scholar] [CrossRef]
- Lowry, R. VassarStats: Website for Statistical Computation. Available online: http://vassarstats.net/ (accessed on 13 August 2019).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).