Abstract
The increasing popularity of cruise tourism has led to the need for effective planning and management strategies to enhance the city tour experience for cruise passengers. This paper presents a deep reinforcement learning (DRL)-based planner specifically designed to optimize city tours for cruise passengers. By leveraging the power of DRL, the proposed planner aims to maximize the number of visited attractions while considering constraints such as time availability, attraction capacities, and travel distances. The planner offers an intelligent and personalized approach to city tour planning, enhancing the overall satisfaction of cruise passengers and minimizing the negative impacts on the city’s infrastructure. An experimental evaluation was conducted considering Naples’s fourteen most attractive points of interest. Results show that, with 30 state variables and more than possible states to be explored, the DRL-based planner converges to an optimal solution after only 20,000 learning steps.
1. Introduction
Over the course of several decades, numerous port cities throughout Europe have made significant investments in the renovation of their waterfront areas and the revitalization of their historic centers. As a consequence of these efforts, these cities have emerged as highly desirable tourist destinations and have established themselves as prominent players within the global tourist industry rankings [1]. For instance, several cities, such as Venice and Barcelona, serve as home ports for a plethora of shipping enterprises. Several other cities, including Lisbon, Genoa, and Naples, have directed their attention towards enhancing cultural offerings to establish themselves as prominent ports along key cruise itineraries [2]. Cities are progressively implementing marketing strategies aimed at attracting a greater volume of cruise passengers.
As a consequence, in recent years, European port cities have experienced an influx of mass tourism driven by the emergence of increasingly larger cruise ships and low-cost tourism. This phenomenon, commonly known as touristification, severely threatens these destinations’ sustainability [3,4]. The World Tourism Organization UNWTO [5] defines this tourist overcrowding or overtourism as “the impact of tourism on a destination, or parts thereof, that excessively influences the perceived quality of life of citizens and/or quality of visitor experiences in a negative way”.
The phenomenon of cruise tourism has been identified as a noteworthy source of concern in urban centers such as Amsterdam, Barcelona, Naples, and Venice. The significant number of visitors that converge on the cities within prescribed schedules leads to congestion in transportation infrastructure and the preeminent attraction sites. Consequently, the impact of cruise tourism on urban spaces and their associated facilities has emerged as a critical issue [2]. Among several strategies, intelligent and adaptive planning of touristic itineraries, which propose alternative itineraries considering the city’s dynamic situation and unexpected events such as a public transportation strike, a protest, traffic, or points-of-interest congestion, may help mitigate tourist overcrowding.
In this direction, this paper proposes an autonomous dynamic planner for touristic itineraries in the smart city context designed to enhance the quality of the tourists’ experience following the prevailing conditions of the urban environment. We propose a new autonomous dynamic planner that seeks to find the best route for a one-day cruise traveler. From a tourist’s perspective, the objective is to maximize the number of points of interest (PoIs) to be visited during both the outbound and return journey with the view.
The proposed autonomous dynamic planner aims to define the optimal path of a one-day cruise tourist, maximizing as many points of interest as possible in the outer and back routes. At the same time, the proposed planner considers the hard time constraints of the cruise and the dynamic city conditions affecting the travel time from one PoI to another and their current receptivity. In so doing, real-time information from the city, such as traffic information, availability of public resources, and reception capacity of tourist attraction sites, are included in the planner. Moreover, the planner is designed to adapt the city itinerary to several unexpected events to improve the tourist-positive experience of the city and mitigate the contemporary tourist overcrowding of congested city areas and points of interest. The proposed dynamic planner is mainly based on a deep reinforcement learning (DRL) algorithm that employs run-time information during the learning process.
An experimental evaluation was carried out to assess the proposed approach’s performance in providing alternative itineraries under hard time constraints. A deeper analysis and an evaluation of itinerary planning performance are also addressed, outlining new experiments and more detailed results than the pilot experiment reported in [6]. A use-case scenario of a cruise landing in Naples was examined by considering the most important fourteen attractions of the city. The adaptation of the proposed approach was evaluated by simulating unexpected events during the city itinerary.
The rest of the paper is organized as follows. Section 2 discusses some related works. Section 3 introduces some background on reinforcement learning and the deep Q-network (DQN). Section 4 introduces the problem addressed in this paper. Section 5 reports the planner, its training, and performance. Finally, experimental results and conclusions are presented in Section 6 and Section 7, respectively.
2. Literature Analysis
Most of the works in the literature focus on providing solutions to plan tours that maximize the tourist travel experience [7]. The tourist tour planning problem is difficult to address due to the diversity of involved objectives and preferences that cannot always be expressed as linear combinations, making classic optimization approaches unfeasible. These problems have been proven to be NP-hard [8], so heuristic techniques are adopted to solve them.
Genetic algorithms are well-established heuristic approaches to solve such search and optimization problems. When considering the time to visit and user preferences over the points of interest, the itinerary planning can be formulated as a multi-objective optimization problem, as in [9] where an adaptive genetic algorithm is proposed.
A genetic algorithm was also proposed in [10] to generate tourist itineraries that include not only touristic attractions but also restaurants, with the additional constraint that they should be visited at lunch or dinner time.
In [11], the authors propose a novel automatic planning method based on a genetic algorithm to suggest multiple itineraries that satisfy the specific preferences of tourists while spending the least time on roads, visiting highly-rated PoIs, and visiting diverse PoIs. The proposed algorithm provides multiple optimized itineraries for the tourists so that they can choose their most preferred one.
Solutions proposed for the team orienteering problems are adopted for generating itinerary plans as a path connecting a set of nodes with the constraint of not exceeding a budget score expressed in terms of time and cost, as in [12].
In [13], an algorithm is proposed to recommend personalized tours taking into account user preferences, the popularity of PoIs derived from geotagged photographs, and constraints on the duration and the starting and end point of the tour.
The dispatch of cruise passengers arriving on the same day in a destination city to different city locations is addressed in [14], where a decision support system is proposed to organize their transportation from the port. The system computes the itinerary for the number of arriving passengers by taking into account their tourist needs and specific city events that may prevent their access to specific city areas.
In [15], the itinerary planning problem is addressed with a deep variational Q-network that includes a reward scheme of route score, similar to our approach, but it considers the user’s preferences to compute a personalized tour.
A multi-objective reinforcement learning approach for trip recommendation is proposed in [16] that considers dynamic user preferences and the trip diversity and popularity that may enhance the user travel experience.
In [17], an interactive multi-objective framework is introduced to generate personalized tourist walking itineraries, with the objective of minimizing the total distance and maximizing user satisfaction when visiting the selected PoIs. The itinerary planning problem is formulated according to the multi-objective prize-collecting vehicle routing problem (MO-PCVRP), and the optimizations are performed by an algorithm that considers preferences progressively introduced during the optimization process.
In [18], a framework named GRM-RTrip for personalized trip recommendation is proposed, where the trip consists of an ordered sequence of PoIs that maximize user satisfaction, considering time and geographical restrictions. It relies on a graph-based representation model to learn PoI–PoI transition probability using graph networks. A Q-based reinforcement learning algorithm is used to compute the personalized trip.
In [19], a deep neural network approach is proposed to compute travel route planning as a prediction of a sequence of PoIs. The prediction relies on learning user preferences, PoI attributes, and historical route data. The proposed approach can be applied to generate three types of planning, i.e., next-point recommendation, general route planning, and must-visit planning.
The reported approaches do not consider that planning a touristic tour for cruise passengers requires considering not only user satisfaction but also aspects that involve the destination city due to the massive number of passengers that disembark simultaneously. The approach proposed in the present work differs from the reported works mainly because it does not search for an optimal itinerary meeting the user’s preferences. Still, it computes itineraries compliant with the dynamic nature of constraints. The considered constraints are the capacity of PoIs and the maximization of the number of visited PoIs to avoid overcrowding and to allow cruise passengers to visit as many PoIs as possible with the available time before returning to the port. Both constraints vary because the capacity of PoIs may depend on specific and unexpected circumstances occurring in the city, and the number of PoIs to be visited depends on the time needed to transit from one PoI to another variable for traffic conditions.
This is why it is crucial to consider that the selection of each PoI heavily impacts the selection of the successive PoIs since the time spent visiting the computed sequence of PoIs drives the choice of the rest of the tour to meet the time constraints imposed by the cruise departure. Approaches that rely on immediate rewards for selecting each PoI [20] are not feasible in our case since long-term rewards should be considered. In order to take into account long-term rewards, a reinforcement learning approach that considers these variable constraints is proposed with the purpose of limiting the negative effects of tourist itineraries of cruise passengers in the destination city. In addition, since these kinds of tours are devoted to large groups of tourists, personal user preferences are not taken into account as in the mentioned approaches, only the popularity of the PoI as given by touristic information available on the destination city.
3. Reinforcement Learning Background
Reinforcement learning (RL) is a powerful machine-learning technique to solve problems involving sequential decision-making. In RL, an artificial agent, a controller, interacts with an uncertain environment to maximize long-term rewards. The agent learns an optimal policy by selecting and executing actions that lead to state transitions and influence the environment. Each state transition is associated with a numerical reward, which can be positive or negative. RL provides a framework for training agents to achieve goals through interactions with their environment. The concept of RL is extensively discussed in the book “Reinforcement Learning” by [21].
The agent’s primary objective in reinforcement learning is maximizing the cumulative rewards it receives. The agent achieves this by following a policy consisting of stimulus–response rules, mapping each environment state to a set of possible actions. The policy can be implemented using a lookup table or more complex computations such as search processes. The policy guides the agent’s decision-making process and ensures the system’s proper functioning. However, a major challenge in RL is that the agent often interacts with an environment with considerable uncertainty. This uncertainty relates to the changes in the state of the environment and the rewards associated with those state transitions. The agent must navigate this uncertain environment to learn and make optimal decisions that lead to the highest possible rewards.
In the context of reinforcement learning, an RL task is formally defined as a Markov decision process (MDP). The MDP is represented as a tuple, , where S is a finite set of states, A is a finite set of actions, R is a reward function, P represents the state transition probability, and is a discount factor, which ranges between 0 and 1. The Markov property assumes that the future state depends solely on the current state and is independent of previous states. The MDP describes the dynamics of the environment, specifying the available actions, the possible states, and the transition probabilities.
For any given state–action pair (), the probability of transitioning to a particular next state and receiving a reward is denoted as . This probability captures the stochastic nature of the environment. In the context of RL, the objective is to maximize the cumulative sum of rewards from a given time step t to the final time step T, denoted as . The goal is to find the optimal policy that maximizes this cumulative reward.
Often, such a function is referred to as a discounted return:
where 0 ≤ ≤ 1 is the discount rate enabling a trade-off between two needs, the attempt to achieve the maximum cumulative reward and the desire to gain a sufficient benefit within a reasonable time. A policy is a probability distribution over actions and states.
Given the policy and the return , the action-value function (s,a) of an MDP is the expected return reward from state s, selecting action a, and following .
The optimal action-value function (s,a) is defined as the maximum value function of all policies, and it is the one that allows the highest return reward to be achieved:
Q-learning is a commonly used algorithm to determine the optimal action-value function, denoted as . It utilizes a two-dimensional array known as a Q-table, which stores information about state–action pairs. Each cell (i, j) in the Q-table represents the estimated value, denoted as q(i, j), that can be achieved by selecting action j in state i. During the learning process, the Q-table is updated iteratively based on the agent’s interactions with the environment. The agent explores different actions, observes the resulting rewards and next states, and updates the corresponding Q-values in the table accordingly. Through this process, the Q-table gradually converges towards the optimal action-value function, , which reflects the maximum expected rewards for each state–action pair.
Deep Reinforcement Learning
In the case of high-dimensional problems, it is intractable to manage Q-tables. So, deep reinforcement learning (DRL) [22] is used since deep neural networks can automatically find compact low-dimensional representations (features) of high-dimensional data (e.g., images, text, and audio). In DRL, deep neural networks are employed to approximate the value function or policy function used in reinforcement learning algorithms. The deep network can process high-dimensional input, such as raw sensory data, and learn complex mappings from states to actions or state values. This enables the agent to make decisions based on raw sensory input without requiring explicit feature engineering. In DRL, one of the most used approaches is based on deep Q-networks (DQNs) [23] relying on Q-learning methods where Q-tables are replaced with neural networks for approximating Q-values for each action-state pair. DRL has achieved remarkable successes in various domains, including game playing, robotic control, autonomous driving, and resource management. By leveraging the power of deep neural networks and reinforcement learning, DRL enables agents to learn directly from raw sensory input and acquire sophisticated decision-making capabilities in complex and dynamic environments.
4. Adaptive Cruise Tourist Itinerary Planning Problem
The adaptive cruise tourist itinerary planning problem is similar to the more general tourist trip design problem (TTDP) [24]. This generic class of problems comprises a set of candidate points of interest (PoIs) together with their associated attributes (e.g., type, location, timetable), travel time between PoIs, user-dependent functions relative to PoIs (e.g., satisfaction, expected duration), the trip time span, and the daily time limit. A daily schedule that meets the constraints imposed by POI properties and maximizes user satisfaction is expected to be proposed in a quality TTDP solution. The problem addressed in this paper is more challenging since the specific constraints to be considered for cruise passengers and city needs may change during the itinerary. An exemplification of the posed problem is illustrated in Figure 1. It shows a scenario in which the planned itinerary can not be fulfilled or is no longer deemed the optimal choice. This may happen for many unexpected reasons, such as a public transportation strike, a protest and/or unplanned building works preventing the transit in specific areas of the city, or overcrowding of a tourist attraction at a specific time. In this situation, a static planner is useless, and a human expert should re-plan a novel itinerary based on their experience, with no certainty that it will be the best.
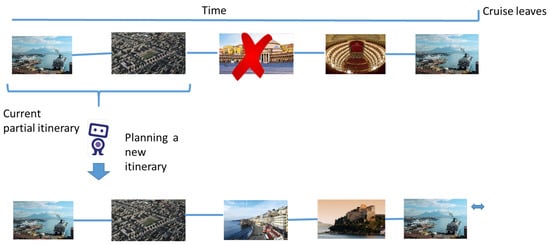
Figure 1.
Dynamically planning a novel sub-optional route.
This paper proposes a DRL-based planner able to plan itineraries automatically through different points of interest that may dynamically change according to city conditions. The DRL agent can generalize the planning process to optimize and plan novel itineraries from any partial ones. Mainly, an itinerary is defined as a sequence of PoIs under temporal and physical constraints, where temporal means that the duration time of an itinerary must not exceed a fixed duration time depending on the cruise departure, and physical means that each PoI has a specified capacity and visiting time which must be taken into account at the time of choosing the PoIs.
During the itinerary, changes in the city conditions may occur, affecting both the current receptivity of a PoI in correlation with its capacity and the time to travel from one PoI to another in relation to the city traffic conditions. This dynamic information on the city is assumed to be gathered through a sensor layer and notifications services (e.g., Google TrafficTM), which collect and process raw sensor data and signals from the environment.
This paper refers to the city of Naples as a use-case scenario. The itineraries are built considering a set of Naples tourist attractions for fourteen points of interest. A touristic itinerary in Naples entails sequentially visiting various attractions, ultimately returning to the cruise. Each point of interest has a maximum number of people it can hold and a specific amount of time it takes to finish a visit. According to the problem, the greater the number of places tourists visit during a tour, the more enjoyable it is. However, the planner must consider overcrowding of attractions and ensure that the tourists have time to return to the port before departure.
5. Methods and Methodology
The Intelligent Planner
The planner was implemented as a self-learning agent utilizing the deep Q-network (DQN) algorithm. To train this agent, an environment was created that simulates the dynamics of the city. This environment considers essential parameters for evaluating the reward and planning touristic itineraries.
- Stay time (T) represents the time passing from the disembarkation of the tourists from the ship up to the boarding after the tour. In our scenario, it was assumed that the tourists have up to 480 min (8 h) for their city tour;
- Current residual capacity——is the residual reception capacity of the touristic attraction is determined by subtracting the current occupancy from the maximum nominal capacity. In our case, Naples has 14 suggested tourist attraction locations, denoted as N. We collected data on the average occupancy of each location, representing the mean number of museum visitors at each hour. These mean values are varied on an episode-by-episode basis using a uniform distribution with a variance of .
- Traveling time——is the time needed by a bus to move from the to the location. Starting from a fixed baseline, for modeling the distances between each PoI, these values are varied according to a casual distribution with to emulate different traffic conditions (Figure 2);
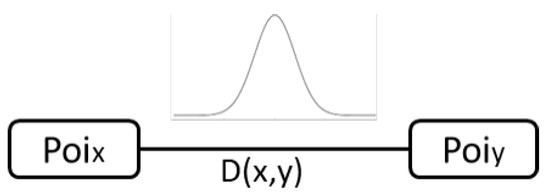 Figure 2. Overview of distance modeling between two PoIs.
Figure 2. Overview of distance modeling between two PoIs. - Visiting time——is the mean time required for a tourist to visit the touristic attraction. In our case, these values are kept constant during the agent’s training.
- Current position (Bpos) is the current position of the bus;
- Cruise status (Cstatus) is the cruise ship status that may be or if tourists are brought back to the port on time for boarding or not;
- Bus tourists (NTourists) are tourists that will take the cruise bus for the city tour.
- Time to visit (Time) is the available time after a PoI is chosen.
- City PoIs (C_PoIs) is a list of relevant points of interest of the city to be visited.
- PoIs visited (PoI_Visited) is a list that takes into account the current visited PoIs.
The main characteristics underlying the behavior of the proposed adaptive planner are founded on the pseudo-code shown in Algorithm 1 and encompass the following ones:
- -
- A set of states where s is a vector containing the following information:
- -
- A set of actions consisting of selecting a PoI from a list of PoIs:
- -
- A reward r the agent receives for its choice evaluated according to the following rule:where represents the importance of a given city’s tourist attraction. This reward function allows the agent to obtain a positive cumulative reward if and only if it avoids overcrowded places and composes an itinerary that brings the tourists back to the port before the ship’s departure. Conversely, the agent is subjected to a penalty commensurate with the adverse effects generated by its decision.
As the penalty’s severity increases, the agent’s motivation to engage in specific actions is diminished.
- -
- Experience replay memory (RM) allows the agent to store its experiences, for performing Q-learning and updating its neural network.
- -
- Target Network : As is common in the DQN algorithm, the agent uses two DNNs to stabilize its learning process. The first one is the main neural network, represented by the weight vector , and it is used to estimate the Q-values for the current state s and action a: . The second one is the target neural network, parameterized by the weight vector , and it will have the exact same architecture as the main network but will be used to estimate the Q-values of the next state and action .
Hence, the agent chooses an appropriate itinerary according to Algorithm 1. After the first initialization phase for the replay buffer RM, Q-network, and target Q-network, the algorithm works in accordance with the following steps:
- -
- For each learning process step, the agent collects dynamic information from the environment, then the agent selects an action according to an -greedy policy. Namely, it chooses a random PoI with probability ; otherwise, it picks the PoI with the highest expected future reward according to .
- -
- According to this choice, episode-by-episode, the agent collects rewards and observations from the environment. Then, it stores the transition in its experience replay memory (RM) and collects a random batch of transitions from the RM.
- -
- For each transition k, the agent sets the future rewards and performs gradient descent concerning the loss function to update Q. The loss function is defined as the squared error between the Q-value and the target Q-value.
- -
- Every C step, the weights of the main network are copied into the target network, thus transferring the learned knowledge from one to the other.
To introduce a variability factor in the training of the planner, a few of the variables states are randomly initiated each round.
| Algorithm 1: Deep Q-network algorithm |
| Initialize experience replay memory (RM); Initialize Q(s,a) with random weights ; Initialize target with = Q; repeat Initialize sequence and pre-processed sequence repeat Collect environment information Either choose randomly with probability or choose Get and Store transition in the RM Sample random mini-batch of transitions from the RM if episode ends at step k+1 then = else = end Have a gradient descent step on ( − Q(, , )) Every C steps set until t = 1, T; until Episode = 1, M; |
6. Experimental Results and Discussions
The DQN agent for the experimentation is based on a multi-layer perception composed of an input layer (512 neurons), four hidden layers (256, 128, 64, and 32 neurons), and an output layer that allows the agent to select the following location to visit among fifteen possible destinations (1 to 14 for an attraction location, 0 for the port). As stated before, this paper refers to the city of Naples as a use-case scenario. The itineraries were built considering a set of fourteen points of interest.
Figure 3 shows an example of the planning process. Initially, the agent starts from the initial state providing the first PoI. Next, the state, and all the parameters (e.g., time to visit, current position of the bus, the current status of the cruise) are updated following the selected PoI. The process continues until the agent completes the recent trials, which means that the agent finds a correct itinerary or fails due to exceeding the temporal constraints (i.e., stay time). When the trial ends, the agent restarts the process starting from the initial state to find other news itineraries. In each trial, the trade-off between exploration and exploitation changes according to the treading of the values of the epsilon decay, and, consequently, the agents look for novel itineraries.
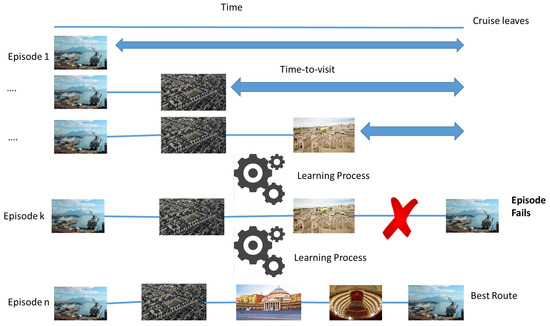
Figure 3.
Learning the best route.
It is worth recalling that since the aim of the agent is to maximize the total reward, it is important to find an itinerary that maximizes the number of the PoIs and, at the same time, minimizes the value of time-to-visit. Figure 4 shows a trial that produces a good itinerary, counting six PoIs by providing a view of the values of the parameters during the several planning steps and the resulting output plan. It is worth noting that the parameter time takes into account the total time currently spent, and the parameter visit is a list that considers the current visited PoIs. At the end of the learning process, the agent aims to define the most extended sequence of PoIs, minimizing the value of time-to-visit.
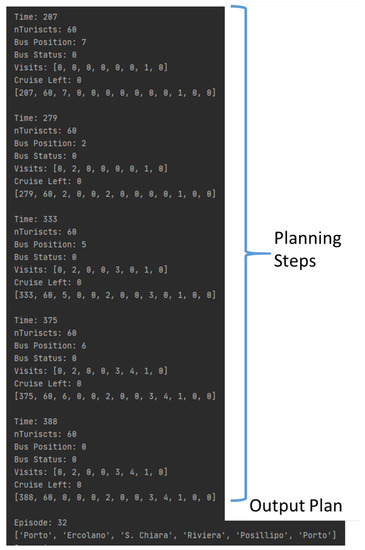
Figure 4.
Step-by-step planning definition process.
To evaluate the proposed approach, several experiments were conducted. Table 1 reports an overview of reward performance in different experiments in which the number of training episodes was changed. The results demonstrate how the agent planned itineraries in several tests. The first and second column of Table 1 report the maximum reward values achieved during the training and testing. The two values are comparable, demonstrating the effectiveness of training. The last column reports the residual time of a planned itinerary resulting in the testing step. It is possible to reduce this value as the number of training episodes increases. Since the planner’s objective is to provide the longest path saving as much time as possible, these results confirm the quality of the training.

Table 1.
Overview of planner performance with testing data.
To provide a deeper analysis of this point, Figure 5 shows an example of the reward-epsilon trend during training. As proof of the effectiveness of the learning process, at the top of Figure 5, it can be seen that the reward’s mean values increase as the number of episodes increases.
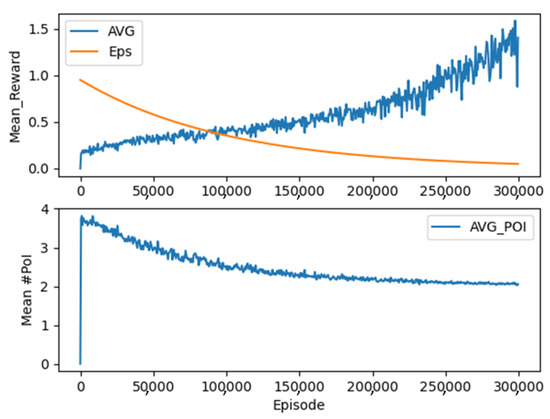
Figure 5.
Trend of reward during training.
The orange line represents the values of the epsilon decay which estimates the trade-off between exploration and exploitation. At the beginning of the training process, the value of the epsilon is 1, meaning that the agent learns to maximize the exploration. In this stage, the agents choose the PoIs to include in the itinerary with greedy behavior to produce the most extended itineraries. As the number of epochs increases, the epsilon value decreases, and consequently, the agent emphasizes exploitation. Since the mean values of the reward increase, it proves that the agent is learning to achieve a complete itinerary without making errors. At the end of the training process, the epsilon value is close to zero.
Table 2 and Figure 6 provide a view of the achieved result, focusing on the plan’s length. At the end of the training, results show that the planner could provide a path ranging from two PoIs to four PoIs because of the setting provided to model both the environments and the agent.

Table 2.
Overview of reward performance by number of PoIs.
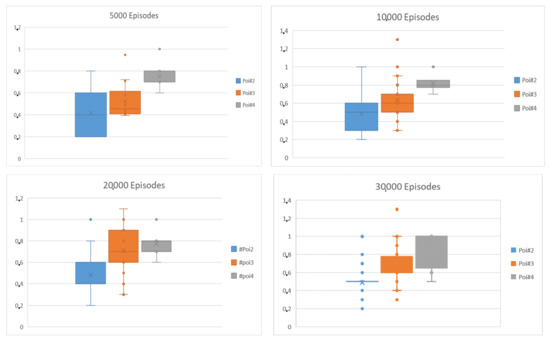
Figure 6.
Overview of reward performance with reference to the number of PoIs in the itinerary.
Table 2 reports the mean, variance, and maximum reward value for each setting. Notably, that these values increase as long as the number of episodes increases. Figure 6 reports a box chart graphically demonstrating the different settings in terms of minimum reward value, first (lower) quartile, median, third (upper) quartile, and maximum reward value. The most uniform distribution appears to be achieved by the 20,000-episode setting, and the reward distribution with a path length of 3 PoIs appears to expose the fairness rewards distribution.
Finally, Figure 7 reports one example of applying the dynamic re-planning of the agent’s output when an unexpected event happens. We simulated the occurrence of a public transportation strike as a uniform probability distribution. When the probability overcomes a fixed threshold in this study, set to 0.3, the events are triggered. The first PoI is the National Museum of Naples, and the next PoI is the Riviera di Chiaia, but a strike is taking place, so the agents have to re-plan a new itinerary and forward the tourist to Posilipo and then to the port.
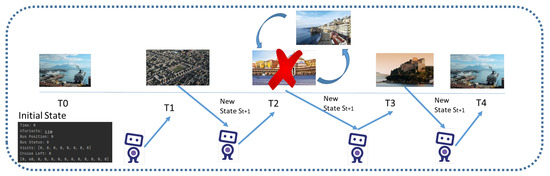
Figure 7.
Planning an itinerary with unexpected events.
In the simulation, each PoI is scheduled individually, and each time the agent provides the best PoIs to maximize the time to visit. However, a strike is taking place, and consequently, the agent has to provide a novel PoI that produces a sub-optional itinerary.
With the aim of providing an honest discussion, the following reports a few limitations of the achieved results: The main issue concerns the fixed number of PoIs adopted for the planner’s training. We designed only fourteen PoIs for experimental reasons, a number which could be higher in a real use-case scenario.
Another issue is training the agent with a high number of episodes; Table 1 reports that the performance does not increase with the number of episodes. Indeed, moving from 20,000 episodes to 30,000 means an increased rate equal to 33%; the testing reward does not improve.
This aspect suggests that the training process should be optimized to improve performance as the number of episodes increases, or the learning process should be stopped early to save time.
7. Conclusions
This paper addresses the problem of planning onshore touristic itineraries for cruise passengers in the context of a smart city. Planning touristic itineraries for cruise passengers presents specific challenges due to the arrival of a high number of people visiting a city for a limited time that may cause overcrowding of tourist attractions and, at the same time, the necessity to consider unforeseen events occurring in the city that may prevent a planned tour from taking place. This is a complex problem considering the high number of variables to be taken into account. This paper proposes a planner of onshore touristic itineraries for cruise passengers. The planner is based on a deep reinforcement learning approach, allowing one to compute a city tour composed of PoIs spread in the destination city by considering more than 230 state variables and more than possible states with 14 PoIs. The proposed approach provides encouraging results since it computes tours by maximizing the number of PoIs to be visited in the available time window and at the same time by avoiding regrettable situations for cruise passengers, such as visiting overcrowded locations or not returning to the port in time for cruise departure. Results show that after around 20,000 episodes, the average number of visited PoIs stabilizes.
In addition, the adoption of deep reinforcement learning allows our solution to learn to dynamically define alternative itineraries in case events happen in the city that interfere with the original plan. This point is another contribution brought by our solution with respect to state-of-the-art methods. Most works for itinerary planning provide a solution to statically plan the optimal route/itinerary at the designated time. Therefore, in case of unexpected events, the planning must be repeated. However, our solution can adapt to unexpected events and provide a novel itinerary without repeating the training process.
Future works will extend the proposed approach to plan itineraries for multiple cruises arriving at the same time in a destination city so as to distribute passengers in different locations to further limit overcrowding conditions.
Author Contributions
The individual contribution of authors follows: Conceptualization, C.D.N.; methodology, G.P., P.R. and L.S.; software, G.P. and L.S.; writing—original draft preparation, C.D.N. and P.R.; writing—review and editing, C.D.N., G.P., P.R. and L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial intelligence |
| DQN | Deep Q-network |
| DRL | Deep reinforcement learning |
| MDP | Markov decision process |
| PoI | Point of interest |
| RL | Reinforcement learning |
References
- Giovinazzi, O.; Moretti, M. Port cities and urban waterfront: Transformations and opportunities. TeMA-J. Land Use Mobil. Environ. 2009, 2, 57–64. [Google Scholar]
- Andrade, M.J.; Costa, J.P.; Jiménez-Morales, E. Challenges for european tourist-city-ports: Strategies for a sustainable coexistence in the cruise post-COVID context. Land 2021, 10, 1269. [Google Scholar] [CrossRef]
- Sequera, J.; Nofre, J. Shaken, not stirred: New debates on touristification and the limits of gentrification. City Taylor Fr. J. 2018, 22, 843–855. [Google Scholar] [CrossRef]
- Sequera, J.; Nofre, J. Touristification, transnational gentrification and urban change in Lisbon: The neighbourhood of Alfama. Urban Stud. 2020, 57, 3169–3189. [Google Scholar] [CrossRef]
- Cheung, K.S.; Li, L.H. Understanding visitor–resident relations in overtourism: Developing resilience for sustainable tourism. J. Sustain. Tour. 2019, 27, 1197–1216. [Google Scholar] [CrossRef]
- Coronato, A.; Di Napoli, C.; Paragliola, G.; Serino, L. Intelligent Planning of Onshore Touristic Itineraries for Cruise Passengers in a Smart City. In Proceedings of the 2021 17th International Conference on Intelligent Environments (IE), Dubai, United Arab Emirates, 21–24 June 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Zhou, X.; Su, M.; Liu, Z.; Hu, Y.; Sun, B.; Feng, G. Smart Tour Route Planning Algorithm Based on Naïve Bayes Interest Data Mining Machine Learning. ISPRS Int. J. Geo-Inf. 2020, 9, 112. [Google Scholar] [CrossRef]
- Cohen, R.; Katzir, L. The Generalized Maximum Coverage Problem. Inf. Process. Lett. 2008, 108, 15–22. [Google Scholar] [CrossRef]
- Yochum, P.; Chang, L.; Gu, T.; Zhu, M. An Adaptive Genetic Algorithm for Personalized Itinerary Planning. IEEE Access 2020, 8, 88147–88157. [Google Scholar] [CrossRef]
- Wibowo, B.S.; Handayani, M. A Genetic Algorithm for Generating Travel Itinerary Recommendation with Restaurant Selection. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 427–431. [Google Scholar]
- Huang, T.; Gong, Y.J.; Zhang, Y.H.; Zhan, Z.H.; Zhang, J. Automatic Planning of Multiple Itineraries: A Niching Genetic Evolution Approach. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4225–4240. [Google Scholar] [CrossRef]
- Kobeaga, G.; Merino, M.; Lozano, J.A. An efficient evolutionary algorithm for the orienteering problem. Comput. Oper. Res. 2018, 90, 42–59. [Google Scholar] [CrossRef]
- Lim, K.H.; Chan, J.; Leckie, C.; Karunasekera, S. Personalized Trip Recommendation for Tourists Based on User Interests, Points of Interest Visit Durations and Visit Recency. Knowl. Inf. Syst. 2018, 54, 375–406. [Google Scholar] [CrossRef]
- Di Napoli, C.; Santamaria, P.M.; Rossi, S. A web-based multi-agent decision support system for a city-oriented management of cruise arrivals. Intell. Syst. Account. Financ. Manag. 2017, 24, 62–72. [Google Scholar] [CrossRef]
- Chen, S.; Chen, B.H.; Chen, Z.; Wu, Y. Itinerary Planning via Deep Reinforcement Learning. In Proceedings of the 2020 International Conference on Multimedia Retrieval. Association for Computing Machinery, Dublin, Ireland, 8–11 June 2020; pp. 286–290. [Google Scholar]
- Chen, L.; Zhu, G.; Liang, W.; Wang, Y. Multi-objective reinforcement learning approach for trip recommendation. Expert Syst. Appl. 2023, 226, 120145. [Google Scholar] [CrossRef]
- Trachanatzi, D.; Rigakis, M.; Marinaki, M.; Marinakis, Y. An interactive preference-guided firefly algorithm for personalized tourist itineraries. Expert Syst. Appl. 2020, 159, 113563. [Google Scholar] [CrossRef]
- Chen, L.; Cao, J.; Tao, H.; Wu, J. Trip Reinforcement Recommendation with Graph-Based Representation Learning. ACM Trans. Knowl. Discov. Data 2023, 17, 1–20. [Google Scholar] [CrossRef]
- Huang, F.; Xu, J.; Weng, J. Multi-Task Travel Route Planning with a Flexible Deep Learning Framework. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3907–3918. [Google Scholar] [CrossRef]
- Gao, Q.; Trajcevski, G.; Zhou, F.; Zhang, K.; Zhong, T.; Zhang, F. DeepTrip: Adversarially Understanding Human Mobility for Trip Recommendation. In Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, SIGSPATIAL ’19, Chicago, IL, USA, 5–8 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 444–447. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Gavalas, D.; Konstantopoulos, C.; Mastakas, K.; Pantziou, G. A survey on algorithmic approaches for solving tourist trip design problems. J. Heuristics 2014, 20, 291–328. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).