Hierarchical Modelling for CO2 Variation Prediction for HVAC System Operation
Abstract
1. Introduction
- Propose a hierarchical framework, including Convolutional Neural Networks (CNNs), transfer learning, and supervised learning that accurately predicts CO2 variations to serve as proxy estimators of occupancy and provide feedback about the utility of the current ventilation system controls;
- Utilize a novel time-series-to-image data transformation strategy that reflects the time-correlation aspect of time-series data in general and environmental sensory data in particular;
- Evaluate and compare the proposed approaches with state-of-the-art approaches applied to the same dataset in terms of prediction accuracy using different history and future time windows;
- Evaluate the proposed approach to different office spaces using transfer learning and re-tuning techniques.
2. Related Work
- Utility: Their work predicts CO2 concentrations, such that a value of concentration can drastically vary from one spatial setting to another. For example, a specific prediction value can be interpreted differently in a room with two or 12 people. Mapping CO2 concentrations to occupancy represents a physical modelling exercise, which varies depending on the studied space. Both these aspects are addressed when predicting the future variations of CO2 concentrations.
- Feature Engineering: When linked to occupancy, the pressure feature is indicative of invasive airflow introduced by the occupants entering or leaving a specific space. This detail is overlooked by excluding this feature from the feature engineering step. Their methodology involves a tedious feature engineering step, resulting in many extracted features;
- Results: Their reported results are not categorized based on the capacities of each room. This factor is instrumental because of the drastic changes in the relationship between environmental features in different spatio-temporal modalities.
- Transferability: This aspect is missing among most of the state-of-the-art methods. The developed models lack the structural disposition for fine-tuning, which jeopardises their utility in multi-zonal spaces of different capacities or different buildings. This characteristic is instrumental when encountering an environment with a limited amount of data.
3. Data Preliminaries
3.1. Dataset Description
- Data from different sensors in each room are aggregated;
- Gaps of less than two minutes are interpolated;
- Continuous data samples of high variability in CO2 levels are extracted as testing set to evaluate the developed methodology.
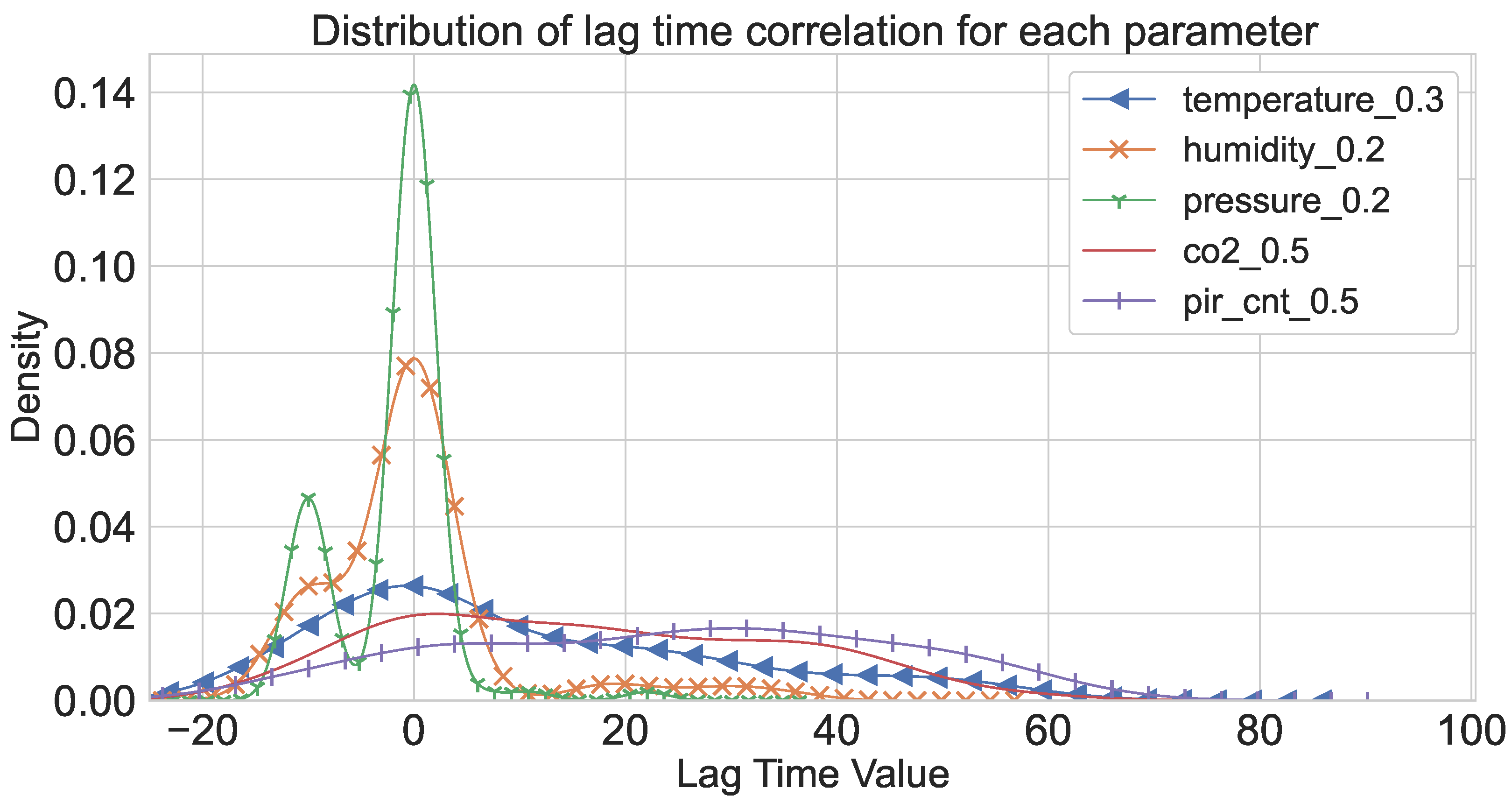
3.2. Exploratory Data Analysis
- –
- is the expectation
- –
- is the mean of
- –
- is the mean of C
- –
- is the standard deviation of
- –
- is the standard deviation of C
4. Method: Hierarchical Model for CO2 Variation Predictions (HMCOVP)
4.1. Time-Series to Image Transformation
4.2. Individual Learners
4.3. Ensemble Learner
5. Experimental Setup
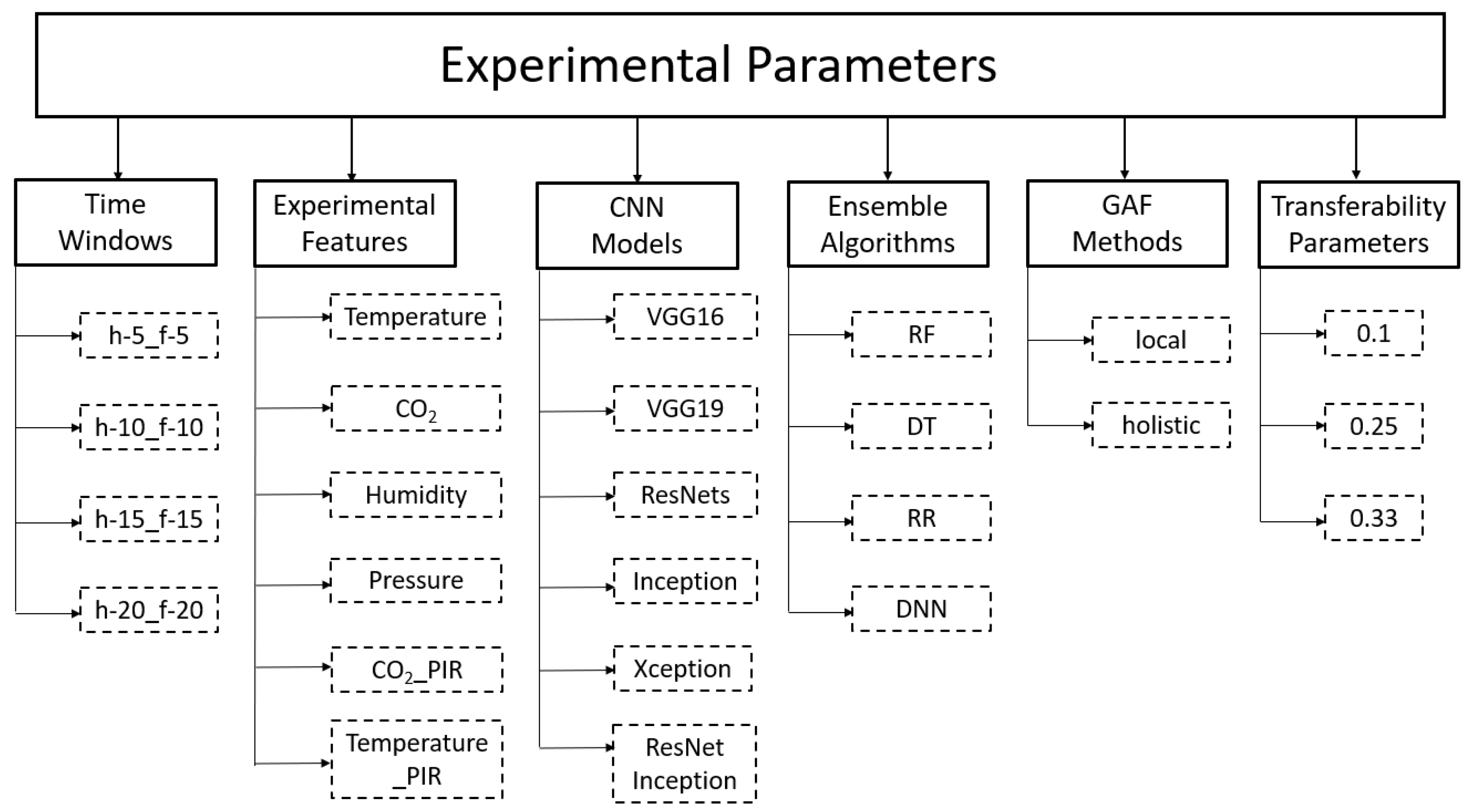
5.1. Experimental Parameters
5.2. Experimental Procedure
5.3. Evaluation Metrics
5.4. Implementation
6. Results and Discussion
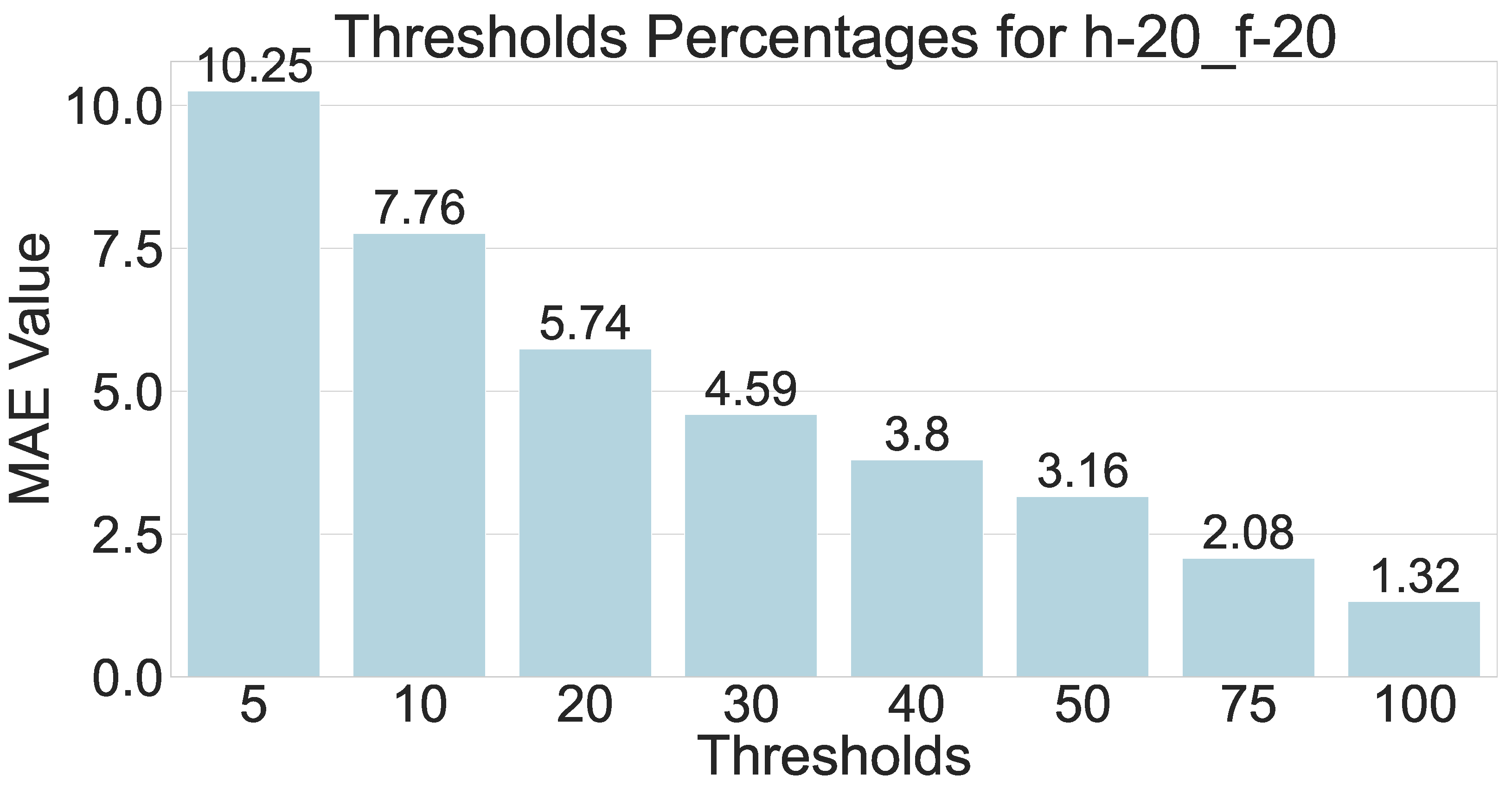
6.1. Parameter Selection
6.2. HMCOVP vs. FECOP vs. 1D CNN
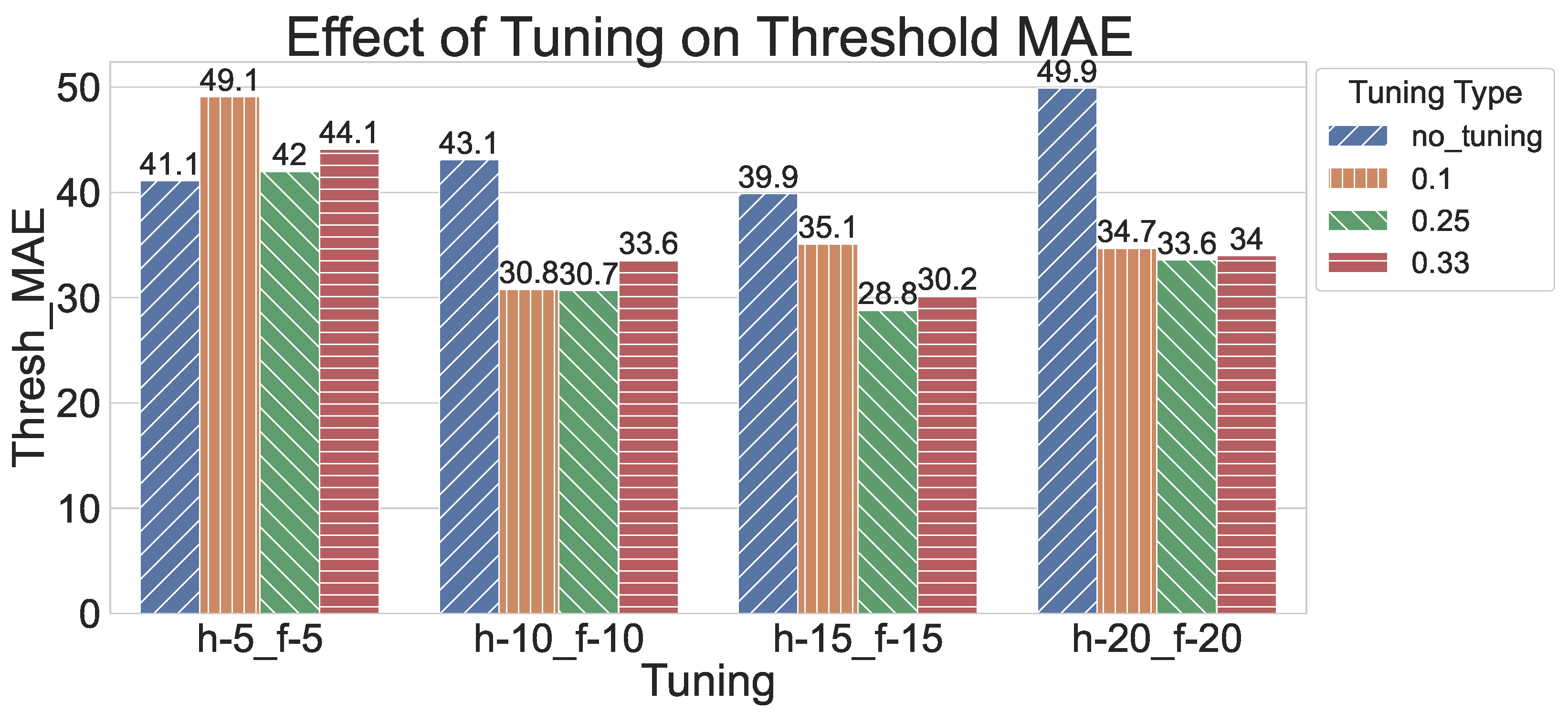
6.3. Transferability Assessment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- The Rockefeller Foundation and Deutsche Bank Group. Building Retrofit Paper—Final 3-1-12 vEDIT. Rockefellerfoundation. Available online: https://www.rockefellerfoundation.org/wp-content/uploads/United-States-Building-Energy-Efficiency-Retrofits.pdf (accessed on 16 May 2020).
- Berardi, U. Building energy consumption in US, EU, and BRIC countries. Procedia Eng. 2015, 118, 128–136. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Satish, U.; Mendell, M.J.; Shekhar, K.; Hotchi, T.; Sullivan, D.; Streufert, S.; Fisk, W.J. Is CO2 an indoor pollutant? Direct effects of low-to-moderate CO2 concentrations on human decision-making performance. Environ. Health Perspect. 2012, 120, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Tandoc, M.C.; Mack, M.L.; Siegel, J.A. Indoor CO2 concentrations and cognitive function: A critical review. Indoor Air 2020, 30, 1067–1082. [Google Scholar] [CrossRef]
- Lewis, D. Why indoor spaces are still prime COVID hotspots. Nature 2021, 592, 22–25. [Google Scholar] [CrossRef] [PubMed]
- Berry, G.; Parsons, A.; Morgan, M.; Rickert, J.; Cho, H. A review of methods to reduce the probability of the airborne spread of COVID-19 in ventilation systems and enclosed spaces. Environ. Res. 2022, 203, 111765. [Google Scholar] [CrossRef]
- World Health Organization. A Conceptual Framework for Action on the Social Determinants of Health; World Health Organization: Geneva, Switzerland, 2010. [Google Scholar]
- Xin, J.; Duan, Q.; Jin, K.; Sun, J. A reduced-scale experimental study of dispersion characteristics of hydrogen leakage in an underground parking garage. Int. J. Hydrogen Energy 2023, 48, 16936–16948. [Google Scholar] [CrossRef]
- Mallach, G.; St-Jean, M.; MacNeill, M.; Aubin, D.; Wallace, L.; Shin, T.; Van Ryswyk, K.; Kulka, R.; You, H.; Fugler, D.; et al. Exhaust ventilation in attached garages improves residential indoor air quality. Indoor Air 2017, 27, 487–499. [Google Scholar] [CrossRef]
- Cao, S.; Chen, X.; Zhang, L.; Xing, X.; Wen, D.; Wang, B.; Qin, N.; Wei, F.; Duan, X. Quantificational exposure, sources, and health risks posed by heavy metals in indoor and outdoor household dust in a typical smelting area in China. Indoor Air 2020, 30, 872–884. [Google Scholar] [CrossRef]
- Liao, W.; Liu, X.; Kang, N.; Song, Y.; Wang, L.; Yuchi, Y.; Huo, W.; Mao, Z.; Hou, J.; Wang, C. Associations of cooking fuel types and daily cooking duration with sleep quality in rural adults: Effect modification of kitchen ventilation. Sci. Total Environ. 2023, 854, 158827. [Google Scholar] [CrossRef]
- Cakyova, K.; Figueiredo, A.; Oliveira, R.; Rebelo, F.; Vicente, R.; Fokaides, P. Simulation of passive ventilation strategies towards indoor CO2 concentration reduction for passive houses. J. Build. Eng. 2021, 43, 103108. [Google Scholar] [CrossRef]
- Metcalf, G.E.; Weisbach, D. The design of a carbon tax. Harv. Environ. Law Rev. 2009, 33, 499. [Google Scholar] [CrossRef]
- Act, E.P. Energy Policy Act of 2005; US Congress: Washington, DC, USA, 2005.
- Esrafilian-Najafabadi, M.; Haghighat, F. Occupancy-based HVAC control systems in buildings: A state-of-the-art review. Build. Environ. 2021, 197, 107810. [Google Scholar] [CrossRef]
- Kleiminger, W.; Mattern, F.; Santini, S. Predicting household occupancy for smart heating control: A comparative performance analysis of state-of-the-art approaches. Energy Build. 2014, 85, 493–505. [Google Scholar] [CrossRef]
- Zou, H.; Zhou, Y.; Yang, J.; Spanos, C.J. Towards occupant activity driven smart buildings via WiFi-enabled IoT devices and deep learning. Energy Build. 2018, 177, 12–22. [Google Scholar] [CrossRef]
- Scislo, L.; Szczepanik-Scislo, N. Air quality sensor data collection and analytics with iot for an apartment with mechanical ventilation. In Proceedings of the 2021 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Cracow, Poland, 22–25 September 2021; Volume 2, pp. 932–936. [Google Scholar]
- Sun, K.; Zhao, Q.; Zou, J. A review of building occupancy measurement systems. Energy Build. 2020, 216, 109965. [Google Scholar] [CrossRef]
- Naylor, S.; Gillott, M.; Lau, T. A review of occupant-centric building control strategies to reduce building energy use. Renew. Sustain. Energy Rev. 2018, 96, 1–10. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, C.; Xie, L. Building occupancy estimation and detection: A review. Energy Build. 2018, 169, 260–270. [Google Scholar] [CrossRef]
- Li, C.; Cui, C.; Li, M. A proactive 2-stage indoor CO2-based demand-controlled ventilation method considering control performance and energy efficiency. Appl. Energy 2023, 329, 120288. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, R.; Zhu, Q.; Masood, M.K.; Soh, Y.C.; Mao, K. Building occupancy estimation with environmental sensors via CDBLSTM. IEEE Trans. Ind. Electron. 2017, 64, 9549–9559. [Google Scholar] [CrossRef]
- Räsänen, P.; Koivusaari, J.; Kallio, J.; Rehu, J.; Ronkainen, J.; Tervonen, J.; Peltola, J. VTT SCOTT IAQ Dataset. 2020. Available online: https://zenodo.org/record/3774723#.ZGOobXbMKUk (accessed on 16 June 2022).
- Dong, B.; Andrews, B.; Lam, K.P.; Höynck, M.; Zhang, R.; Chiou, Y.S.; Benitez, D. An information technology enabled sustainability test-bed (ITEST) for occupancy detection through an environmental sensing network. Energy Build. 2010, 42, 1038–1046. [Google Scholar] [CrossRef]
- Candanedo, L.M.; Feldheim, V. Accurate occupancy detection of an office room from light, temperature, humidity and CO2 measurements using statistical learning models. Energy Build. 2016, 112, 28–39. [Google Scholar] [CrossRef]
- Masood, M.K.; Soh, Y.C.; Jiang, C. Occupancy estimation from environmental parameters using wrapper and hybrid feature selection. Appl. Soft Comput. 2017, 60, 482–494. [Google Scholar] [CrossRef]
- Shaer, I.; Shami, A. Sound Event Classification in an Industrial Environment: Pipe Leakage Detection Use Case. In Proceedings of the International Wireless Communications and Mobile Computing (IWCMC), Dubrovnik, Croatia, 30 May–3 June 2022; pp. 1212–1217. [Google Scholar]
- Kallio, J.; Tervonen, J.; Räsänen, P.; Mäkynen, R.; Koivusaari, J.; Peltola, J. Forecasting office indoor CO2 concentration using machine learning with a one-year dataset. Build. Environ. 2021, 187, 107409. [Google Scholar] [CrossRef]
- Golestan, S.; Kazemian, S.; Ardakanian, O. Data-driven models for building occupancy estimation. In Proceedings of the Ninth International Conference on Future Energy Systems, Karlsruhe, Germany, 12–15 June 2018; pp. 277–281. [Google Scholar]
- Stjelja, D.; Jokisalo, J.; Kosonen, R. Scalable Room Occupancy Prediction with Deep Transfer Learning Using Indoor Climate Sensor. Energies 2022, 15, 2078. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Piette, M.A.; Pritoni, M. Inferring occupant counts from Wi-Fi data in buildings through machine learning. Build. Environ. 2019, 158, 281–294. [Google Scholar] [CrossRef]
- Laaroussi, Y.; Bahrar, M.; El Mankibi, M.; Draoui, A.; Si-Larbi, A. Occupant presence and behavior: A major issue for building energy performance simulation and assessment. Sustain. Cities Soc. 2020, 63, 102420. [Google Scholar] [CrossRef]
- Yu, L.; Sun, Y.; Xu, Z.; Shen, C.; Yue, D.; Jiang, T.; Guan, X. Multi-agent deep reinforcement learning for HVAC control in commercial buildings. IEEE Trans. Smart Grid 2020, 12, 407–419. [Google Scholar] [CrossRef]
- Wang, Y.; Velswamy, K.; Huang, B. A long-short term memory recurrent neural network based reinforcement learning controller for office heating ventilation and air conditioning systems. Processes 2017, 5, 46. [Google Scholar] [CrossRef]
- Barandas, M.; Folgado, D.; Fernandes, L.; Santos, S.; Abreu, M.; Bota, P.; Liu, H.; Schultz, T.; Gamboa, H. TSFEL: Time series feature extraction library. SoftwareX 2020, 11, 100456. [Google Scholar] [CrossRef]
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time series feature extraction on basis of scalable hypothesis tests (tsfresh–a python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Imaging time-series to improve classification and imputation. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Osaku, D.; Gomes, J.F.; Falcão, A.X. Convolutional neural network simplification with progressive retraining. Pattern Recognit. Lett. 2021, 150, 235–241. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 1–40. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 16 May 2023).
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]


| History (Minutes) | Future (Minutes) | Training Data Testing Data |
|---|---|---|
| h-5 | f-5 | 334,677 74,730 |
| h-10 | f-10 | 332,667 74,514 |
| h-15 | f-15 | 330,657 74,300 |
| h-20 | f-20 | 328,647 74,085 |
| History and Future Time Window (in Minutes) | Ensemble Algorithm | CNN Model | CNN FCL | Method | MAE |
|---|---|---|---|---|---|
| h-5_f-5 | RR | VGG_16 | [64] | holistic | 1.61 |
| DT | Resnet_152 | [256] | local | 0.65 | |
| RF | VGG_16 | [512] | holistic | 0.4 | |
| NN | Resenet_152 | [512, 256] | holistic | 1.3 | |
| h-10_f-10 | RR | VGG_19 | [4096] | local | 3.25 |
| DT | VGG_19 | [512] | local | 0.84 | |
| RF | Resnet_152 | [128, 64] | local | 0.765 | |
| NN | Resnet_101 | [256, 128] | local | 2.63 | |
| h-15_f-15 | RR | VGG_16 | None | local | 5.54 |
| DT | Resnet_152 | [256, 128] | local | 0.98 | |
| RF | Xception | None | local | 1.22 | |
| NN | Resnet_101 | [256] | local | 4.48 | |
| h-20_f-20 | RR | Resnet_50 | [128] | holistic | 6.07 |
| DT | Resnet_101 | [128, 64] | local | 1.18 | |
| RF | VGG_19 | [4096] | holistic | 0.84 | |
| NN | Resnet_50 | [128, 64] | local | 4.91 |
| h&f | Ensemble | CNN Model | CNN FCL | Method | Thresh_MAE |
|---|---|---|---|---|---|
| h-5_f-5 | DT | Xception | [512] | local | 0.11 |
| h-10_f-10 | DT | Resnet_50 | [128, 64] | local | 0.6 |
| h-15_f-15 | DT | Resnet_152 | [256, 128] | local | 1.0 |
| h-20_f-20 | DT | Resnet_101 | [128, 64] | local | 1.49 |
| Parameter | Thresh_MAE | Training Time (min) | ||||
|---|---|---|---|---|---|---|
| Methodologies | HMCOVP | FECOP | 1D-CNN | HMCOVP | FECOP | 1D-CNN |
| h-5_f-5 | 10.14 | 40.89 | 2331.11 | 229.69 | 2.1 | 36.5 |
| h-10_f-10 | 14.48 | 52.52 | 8969.98 | 360.34 | 2.275 | 22.62 |
| h-15_f-15 | 19.37 | 66.83 | 9201.81 | 716.54 | 2.83 | 19.16 |
| h-20_f-20 | 27.74 | 77.21 | 10,128.83 | 381.78 | 3.62 | 17.84 |
| Parameters | Thresh_MAE | Time/Instance (ms) | ||
|---|---|---|---|---|
| Methodologies | HMCOVP | FECOP | HMCOVP | FECOP |
| h-5_f-5 | 41.11 | 49.35 | 6.24 | 0.67 |
| h-10_f-10 | 43.14 | 52.4 | 6.48 | 1.14 |
| h-15_f-15 | 39.90 | 55.9 | 14.64 | 2.16 |
| h-20_f-20 | 49.93 | 54.2 | 10.44 | 1.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaer, I.; Shami, A. Hierarchical Modelling for CO2 Variation Prediction for HVAC System Operation. Algorithms 2023, 16, 256. https://doi.org/10.3390/a16050256
Shaer I, Shami A. Hierarchical Modelling for CO2 Variation Prediction for HVAC System Operation. Algorithms. 2023; 16(5):256. https://doi.org/10.3390/a16050256
Chicago/Turabian StyleShaer, Ibrahim, and Abdallah Shami. 2023. "Hierarchical Modelling for CO2 Variation Prediction for HVAC System Operation" Algorithms 16, no. 5: 256. https://doi.org/10.3390/a16050256
APA StyleShaer, I., & Shami, A. (2023). Hierarchical Modelling for CO2 Variation Prediction for HVAC System Operation. Algorithms, 16(5), 256. https://doi.org/10.3390/a16050256








