Abstract
Road traffic accidents are a significant public health issue, accounting for almost 1.3 million deaths worldwide annually, with millions more experiencing non-fatal injuries. A variety of subjective and objective factors contribute to the occurrence of traffic accidents, making it difficult to predict and prevent them on new road sections. Artificial neural networks (ANN) have demonstrated their effectiveness in predicting traffic accidents using limited data sets. This study presents two ANN models to predict traffic accidents on common roads in the Republic of Serbia and the Republic of Srpska (Bosnia and Herzegovina) using objective factors that can be easily determined, such as road length, terrain type, road width, average daily traffic volume, and speed limit. The models predict the number of traffic accidents, as well as the severity of their consequences, including fatalities, injuries and property damage. The developed optimal neural network models showed good generalization capabilities for the collected data foresee, and could be used to accurately predict the observed outputs, based on the input parameters. The highest values of r2 for developed models ANN1 and ANN2 were 0.986, 0.988, and 0.977, and 0.990, 0.969, and 0.990, accordingly, for training, testing and validation cycles. Identifying the most influential factors can assist in improving road safety and reducing the number of accidents. Overall, this research highlights the potential of ANN in predicting traffic accidents and supporting decision-making in transportation planning.
1. Introduction
Road traffic accidents represent one of the leading causes of death worldwide. According to the World Health Organization (WHO) [1], almost 1.3 million people die in road traffic accidents, while almost 50 million suffer non-fatal injuries. The leading cause of death of children and young people between 5 and 29 years is road traffic crashes. The serious problem is that 93% of fatalities come from the low-income and middle-income countries in development. Except for human suffering, road traffic accidents significantly influence the economy, costing countries up to 3% of their Gross Domestic Product (GDP).
The occurrence of traffic accidents can be related to a variety of factors. Some of these factors are subjective: driver knowledge, training level, experience, the influence of alcohol, drugs, etc., while others are objective, such as: road volume (annual average daily traffic volume—AADT), road geometry (curvature, slopes, lane width, shoulder width), type of road (freeway or two-lane road), road conditions (pavement quality and potential damage of pavement surface), weather conditions (wind, ice, snow, rain, etc.), cars maintenance, speed limits, frequency of police controls, etc. An increase in a number of road vehicles leads to heavier traffic volume on almost all roads, which increases the chances of collision between vehicles. On the other hand, the same traffic volume on the freeway and the two-lane roads has a different possibility of collision.
This variety of factors makes complicated efforts to predict the number of traffic accidents for new roads or reconstruction of existing roads. In order to predict the number of traffic accidents in the near future on the existing or the newly planned/built road section, it is necessary to know what factors will mostly influence the occurrence of a road traffic accident. Objective factors that cannot be easily changed in the future are recognized as: the type of road, road geometry and AADT (which will likely to be increased in the future). Other factors can be changed (pavement can be repaired, weather conditions are subject to daily change, car maintenance can be improved by frequent checks, speed limits can also be adapted, etc.).
The classical machine learning models such as: artificial neural network (ANN), random forest regression (RFR), support vector machine (SVM), extreme learning machine (ELM), K-nearest neighbors (KNN) and decision tree (DT) are extensively used in modelling in various branches of science. The SVM is a widely used discriminant technique based on the statistical learning theory, well recognized for its strong generalization ability. The optimal network is obtained by exploring the balance between the complexity of the model and the training error [2,3]. The ELM designs a single-layer feedforward network by randomly generating the input weights and biases of the hidden layers [4].
The vast variety of state-of-the-art machine learning techniques is suitable for sequence data like ensemble learning models, such as: XGBoost [5] and LightGBM [6] and CatBoost. XGBoost model exerts its advantages, especially for high prediction accuracy and interpretability. LightGBM model enables large amounts of data and GPU training. The LightGBM models are proven to be more accurate and faster than XGBoost. Furthermore, data fusion enables stronger forecasting accuracy, according to the integration of gradient boosting-based categorical attributes supported by the CatBoost algorithm [7]. Applying artificial neural networks has proved its feasible feature in recent years by predicting and presenting desired results although limited data sets. Obtained results illustrate that the variables such as highway width, head-on collision, type of vehicle at fault, ignoring lateral clearance, following distance, inability to control the vehicle, violating the permissible velocity, and deviation to the left by drivers are the most influential aspects that can raise traffic accidents in urban roads.
This paper provides two ANN models for the assessment of traffic accidents on the state roads of the Republic of Serbia and the Republic of Srpska (Bosnia and Herzegovina) using objective factors that can be easily determined.
Literature Review
Predicting traffic accidents and understanding the factors that influence traffic safety has been the focus of numerous studies in various regions. These studies have employed different tools and methodologies to investigate the relationship between specific factors and the occurrence of accidents [8]. In the Highway Safety Manual, Chapter 10 explicitly addresses the prediction model for rural two-lane, two-way roads, emphasizing the impact of traffic volume (AADT) through safety performance functions (SPF) and project geometry and traffic management characteristics through crash modification factor (CMF) [9].
The major subject of the paper [10] was to determine which parameter has the greatest influence on the occurrence of traffic accidents. Several studies have examined the influence of specific factors on traffic accidents on two-lane rural roads. Vogt and Bared [11] researched Minnesota and Washington to analyze the geometric characteristics leading to accidents. Fitzpatrick et al. [12] focused on the difference in traffic crashes between two-lane and four-lane highways in Texas. Geedipally et al. [13] identified that head-on crashes were affected by AADT, percentage of trucks, and shoulder width. Cardoso [14] developed an accident prediction model for curves and tangents on two-lane roads in Portugal. This research defined an accident prediction model for curves and tangents, as well as for roads with paved and unpaved shoulders. Two-lane rural roads were the main subject of Harwood et al. [15] research. In his research, a prediction algorithm was developed. Mayora et al. [16] analyzed almost 3500 km of two-lane rural roads in Spain (region of Valencia and West Castile) in a five-year period.
The article by Cafiso et al. [17] analyzed about 170 km of two-lane rural roads in Italy over a period of 5 years; in this paper variables such as: curvature (radius, length), tangent length, cross-section elements (lane width and shoulder width and type). Research on traffic accidents in Ghana was presented in Ackaah and Salifu [18] paper. The model for prediction developed in this research was GLM (Generalized Linear Model) with a Negative Binomial error structure. In India, Dinu and Veeraragavan [19] developed a model for accident prediction with random parameters. Variables for the model were: traffic volume (veh/h), length (km), percent of buses, trucks, cars, and two-wheelers, as well as shoulder width and curvature (horizontal and vertical). Turner et al. [20] developed accident prediction models for two-lane rural roads in New Zealand. A total of 6800 km of state roads was analyzed. The developed model created a relationship between a number of accidents and traffic volume, road geometry, cross-section, road surfacing, roadside hazards, and driveway density. For different types of accidents was developed different linear models. A combination of three different statistical methods was developed in a paper written by Deublein et al. [21]. Models used were: (1) gamma-updating of the occurrence rates of injury accidents and injured road users, (2) hierarchical multivariate Poisson-lognormal regression analysis, and (3) Bayesian inference algorithms. Influence parameters were: traffic volume, percentage of trucks and buses, speed, curvature and the number of lanes. Other machine learning methods are attempted for traffic systems to aid in transportation planning, including LSTM/RNN often used for sequence modeling and prediction [22,23], CNN used for image and video processing tasks [24,25], and broader machine learning for traffic accident analysis [26].
Research in Malaysia conducted by Hosseinpour et al. [27] analyzed 448 segments of state roads over five years. Input variables was: horizontal curvature, terrain type, heavy-vehicle percent, and access points Traditional crash prediction models, such as generalized linear regression model, are unable to take into account multilevel data design [28]. Artificial Neural Network (ANN) approach was given in Çodur and Tortum [28] paper. Bayesian Network with Rough Sets for traffic accident analysis was the subject of research in Xiaoxia et al. [29] paper. In their paper, Olmuş and Erbaş [30] analyzed traffic accidents by using Log-Linear Models. Bayesian Neural Network was the subject of research in Marković et al. [31] paper. Milenković et al. [32] analyzed the impact of road and traffic characteristics on the occurrence of traffic accidents with fatalities on state roads in Serbia. A regression analysis was used for data analysis, which was the first attempt at this type of analysis in Serbia. Tubić et al. [33] made a calculation of traffic accident costs for major roads in the Republic of Serbia, with the costs per kilometer. Some of the influencing factors on the occurrence of traffic accidents were presented in the paper by Marković et al. [34].
Overall, the influence of different factors on traffic safety and the occurrence of traffic accidents has been widely studied, with many researchers focusing on the impact of traffic volume, project geometry, traffic management characteristics, and other related factors. These studies have resulted in the development of various accident prediction models and methods for analyzing and predicting traffic accidents. These studies, each employing specific tools and methodologies, have contributed to our understanding of the factors influencing traffic accidents. However, there is a need to investigate the prediction of accidents in the Republic of Serbia and the Republic of Srpska (Bosnia and Herzegovina) using objective factors. By utilizing Artificial Neural Network models, this study aims to predict traffic accidents accurately and determine their severity based on factors such as road length, terrain type, road width, average daily traffic volume, and speed limit. The findings from this research will provide insights for improving road safety and supporting decision-making in transportation planning.
As to our knowledge, this paper is the first to implement artificial neural networks to predict traffic accidents in the Republic of Serbia and the Republic of Srpska (Bosnia and Herzegovina) using objective factors: road length, terrain type, road width, average daily traffic volume, and speed limit.
2. Methodology
For this research, detailed analysis of parameters influencing the occurrence of traffic accidents was done. AADT data was collected from automatic traffic counters in the Republic of Serbia [35] and the Republic of Srpska (Bosnia and Herzegovina) [36]. Total of 191 road sections in the Republic of Serbia and 180 road sections were selected in the Republic of Srpska. Table 1 shows the number of road sections at each road type.

Table 1.
Number of road sections selected for analysis in Serbia and Republic of Srpska.
The collected data were marked as follows:
- Section Length (km)-SL,
- Annual average daily traffic volume -AADT (veh/day),
- Terrain type-TT (type 1-level, type 2-rolling, type 3-mountainous),
- Curvature (curve 1-minimal, curve 2-severe, curve 3-serpentine),
- Lane width (5–6 m, >6 m),
- Speed limit-SPL (100–130 km/h, 130 km/h for freeways).
Figure 1, Figure 2 and Figure 3 illustrate the roads networks of the Republic of Srpska and the Republic of Serbia, respectively.
Figure 1.
Road sections in the Republic of Serbia.
Figure 2.
Highway networks in the Republic of Srpska.
Figure 3.
Main roads of the Republic of Srpska.
The number of traffic accidents-TA was extracted from the Road Traffic Safety Agency data (Republic of Serbia), for each section using GPS location and characteristics of each accident [37] For the Republic of Srpska, data on traffic accidents was acquired from official reports [38].
2.1. Statistical Analysis
2.1.1. ANN Modeling
A multi-layer perceptron (MLP) structural models, consisting of three layers (input, hidden, and output) were implemented for modelling the artificial neural network models (ANN) for prognostication the number of traffic accidents, based on the road conditions. In the first ANN model (ANN1), the length of the road section, road section type (level—1, rolling—2 and mountainous—3), curvatures in the road (no significant bends—1, severe—2, serpentines—3), road width (>6 m, 5–6 m and <5 m) and AADT were used for prediction of the number of traffic accidents in state roads (1st class), and state roads (2nd class), in the Republic of Srpska and two-way roads in the Republic of Serbia. The ANN2 model was used for the prediction of the number of traffic accidents, and also the consequences of traffic accidents including the number of: fatalities—F, disabling injury—DI, evident injury—EI, and property damage only -PDO in the highways of the Republic of Serbia, according to the length of the road section, road section type (plain—1, hill—2 and mountain—3), speed limit (130 km/h, 100–130 km/h and <100 km/h) and AADT. The length of the road section, road section type, curves in the road, road width and speed limit were used as categorical variables. The number of crashes, and also F, DI, EI and PDO were employed as numerical variables for the ANN1 and ANN2 modelling.
Considering the literature references, the ANN models were widely accepted as comprehensively suitable for the solution of nonlinear problems [39,40,41]. Prior to the ANN model building, input and output variables were standardized to augment the exactness of ANN model’s results. Throughout the iterative process, input data were consistently submitted to the ANN network [42,43]. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm was employed as an iterative tool for solving unconstrained nonlinear optimization in the course of ANN model building.
Figure 4 shows the flowchart of the research conducted with the aim of determining the most appropriate ANN model in terms of predictive ability, but also in terms of the error rate of each model. The present study is characterized by the comparative evaluation of different artificial neural networks (ANN), with the aim of predicting the number of traffic accidents, as well as the severity of their consequences, including fatalities, injuries and property damage through using objective factors that can be easily determined, such as road length, terrain type, road width, average daily traffic volume, and speed limit.
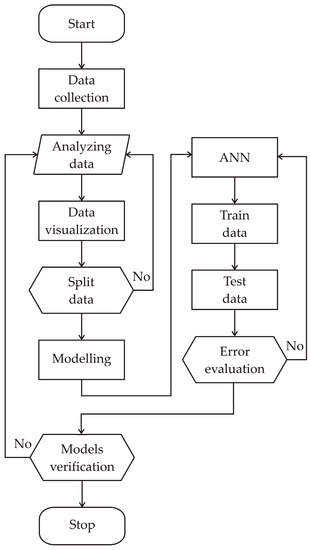
Figure 4.
Flowchart of the conducted research.
The collected data for ANN modelling was randomly partitioned into training, cross-validation, and testing data (with shares of 70%, 15%, and 15% of collected data, respectively). A series of 100,000 different MLP configurations were studied, through the training cycle, by changing the number of neurons in hidden layer (between 5 and 10) applying random preliminary values of weights and biases for the ANN model, and testing different activation functions for hidden and the output layer (such as hyperbolic tangent, logistic sigmoidal, exponential or identity). Using identity function the activation level from the input is passed on directly as the output of the neurons. Logistic uses the logistic sigmoid S-shaped function, with output in the range 0 to +1. The hyperbolic tangent function (tanh) is a symmetric S-shaped (sigmoid) function, whose output lies in the range −1 to +1. It often performs better than the logistic sigmoid function due to its symmetry. Exponential uses the negative exponential activation function.
The optimization setup included the minimization of the square error. It is assumed that the successful training was reached when learning and cross-validation curves approached zero.
The coefficients involved with the hidden layer (weights and biases) were split up in matrices W1 and B1. Moreover, coefficients connected to the output layer were combined with matrices W2 and B2. It is feasible to describe the neural network models by utilizing matrix record (Y is the matrix of the output variables (the number of traffic accidents for ANN1, and the number of traffic accidents, EI, DI, F and PDO for ANN2), f1 and f2 are transfer functions in the hidden and output layers, accordingly, and X is the matrix of input variables) the length of the road section, road section type, curves in the road, road width and AADT for ANN1 and the length of the road section, road section type, speed limit and AADT for ANN2 [44,45]:
Weight coefficients in the ANN models (elements of matrices W1 and W2 and vectors B1 and B2) were defined thought determination of the ANN models [34,35]. The widely-applied BFGS algorithm, was utilized to consolidate the convergence in resolving the solution of non-linear problem [46].
2.1.2. Global Sensitivity Analysis
Yoon’s interpretation method was used to determine the relative influence of the length of the road section, road section type (plain—1, hill—2 and mountain—3), curvatures in the road (minimal—1, severe—2, serpentines—3), road width (>6 m, 5–6 m and <5 m) and AADT on the number of traffic accidents for ANN 1 model. Furthermore, the influence of the length of the road section, road section type (plain—1, hill—2 and mountain—3), speed limit (130 km/h, 100–130 km/h and <100 km/h) and AADT on the number of traffic accidents, and also traffic accident consequences including EI, DI, F and PDO was also studied for the ANN2 model. This calculation was performed according to the weight coefficients of the erected ANN models [47,48,49].
The computation of ANN models was performed applying StatSoft Statistica, ver. 10.0, Palo Alto, CA, USA. The following equation was used to estimate the direct influence of the input parameters on the output variables, according to the weighting coefficients within the ANN models [50,51]:
where w—presents the weights of the ANN models, i—input variable, j—output variable, k—hidden neuron, n—number of hidden neurons, m—number of inputs.
2.1.3. The Accuracy of the Model
The statistical validation of the developed non-linear models was explored using standard computational tests, including: the coefficient of determination (r2), reduced chi-square (χ2), mean bias error (MBE), root mean square error (RMSE), mean percentage error (MPE), according to the following equations [52]:
where xexp,i were collected values and xpre,i were the model anticipated values, N and n are the number of observations and constants, accordingly.
3. Results and Discussion
The complete collected data for the Republic of Srpska and the Republic of Serbia used for ANN models’ calculations are shown in Tables S1 and S2. The average section length, the annual average daily traffic and the average number of traffic accidents values for road 1—Republic of Srpska state road 1st class, road 2—Republic of Srpska state road 2nd class, and road 3—Serbia two-lane road are presented in Table 2.

Table 2.
The average data for roads 1–3.
In Table 3 are given the average values for high ways in the Republic of Serbia for the average number of traffic accidents, section length, evident injury, disabling injury, fatality, property damage and the number of traffic accidents.

Table 3.
The average data for roads 4.
3.1. Cluster Analysis
Figure 5 depicts the results of a cluster analysis performed on the observed samples. The analysis employed the complete linkage algorithm and the City block (Manhattan) distances to assess the proximity of the samples. The City block distances, displayed on the abscissa axis, are a measure of the average difference between the dimensions of the tested samples [53,54]. The linkage distance, also shown on the abscissa axis, between the main clusters was substantial, approximately 60,000. The dendrogram generated by the cluster analysis revealed the presence of seven main clusters, as seen in Figure 5. The cluster analysis was performed according to the Table S2, which shows the data regarding AADT, section length, terrain type, speed limit, evident injury, disabling injury, fatality, property damage and traffic accident. The cluster analysis was applied to show the similarities in observed parameters between samples. Cluster 1 comprised of sites 1, 72, 57, 58, 59, 71, 60, 62, 61, and 70, Cluster 2 included sites 2, 55, 12, 14, 13, 53, 56, 3, 6, 52, 54, 4, 51, 73, 7, 8, 67, 69, 5, 9, 50, and 68, and Cluster 3 consisted of sites 10, 65, 11, 27, 64, 45, 47, 46, 75, 76, 28, 74, 66, and 49. Cluster 4 included 15, 16, 17, 37, 38, 39, 18, 40, 34, 35, 19, and 22. Cluster 5 included 26, 77, 44, 41, 48, 42, and 43. Cluster 6 included 20, 25, 32, 33, 36, 21, 78, and 24, Cluster 7 included 23, 31, 30, 29, and 63.
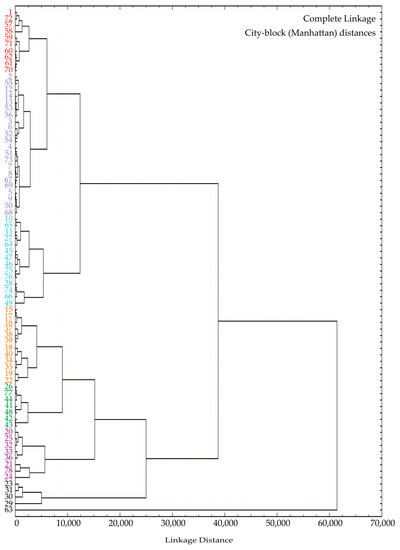
Figure 5.
Cluster analysis of observed sections.
3.2. Color Correlation Analysis
The color correlation analysis was used to examine the connections between observed samples (Figure 6). A color correlation diagram was created to show the significance of the correlation coefficients between the different variables and the responses. Positive correlations are represented by blue color and negative correlations are represented by red color, while the size of the circles indicates the strength of the correlation [55].
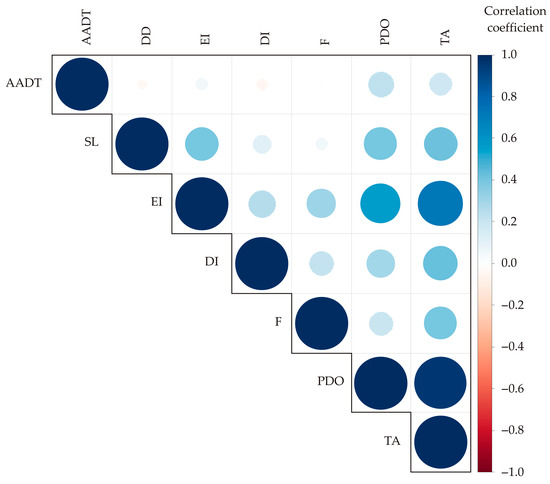
Figure 6.
Color correlation diagram between the parameters of the independent variables and the observed responses.
According to correlation analysis, positive relations between section length, evident injury, and also between section length and property damage only and section length and the number of traffic accidents were observed (correlation coefficients reached r = 0.398, statistically significant at p ≤ 0.001; r = 0.393, p ≤ 0.001 and r = 0.411, p ≤ 0.001, respectively). Positive correlation between the number of evident injuries and fatalities, property damage only and the number of traffic accidents were noticed (r = 0.309, p ≤ 0.01; r = 0.563, p ≤ 0.001 and r = 0.728, p ≤ 0.001, accordingly). Furthermore, a positive correlation between the number of traffic accidents and disabling injury, fatality and property damage only were established (r = 0.427, p ≤ 0.01; r = 0.393, p ≤ 0.001 and r = 0.955, p ≤ 0.001, respectively).
According to Sun and Yang [56], the expansion in the rate of highway mileage and the number of motor vehicle drivers would increase the traffic accidents death rate. Furthermore, in China, Sun et al. [57] found a significant correlation between car ownership, traffic accident fatality, traffic asset, urban residents, and property losses only of traffic accidents; especially, car ownership and urban population are positively correlated with direct property losses [58].
3.3. Principal Component Analysis
The Principal Component Analysis (PCA) was used to explore the relationships between different samples. The results of the PCA analysis are depicted in Figure 7. The proximity of spots in the PCA graphic indicates similarity in patterns [59]. The direction of the vectors in the factor space reveals the trends of the observed variables, while the length of the vectors represents the strength of the correlation between the fitting value and the variable [60]. By examining Figure 7, one can efficiently determine the correlation between the content of various compounds and the obtained compound content, as the angles between corresponding variables reflect the degree of correlation, with smaller angles corresponding to stronger correlations. The first three PCs demonstrated 74.38% of the total variance in the recorded data. The first PC explained 44.52%, the second 15.62% and the third 14.24% of the total variance between the collected data. The projection of the variables in the factor plane indicated that SL (9.3% based on correlation), EI (20.5%), DI (7.6%), PDO (24.9%) and TA (30.4%) contributed most negatively to the first principal component PC1. F (11.3%) and DI (16.2%) contributed positively to the second principal component PC2, while AADT (66.8%), and contributed negatively to PC2. The third principal component was most positively influenced by: F, AADT and DI (32.0%; 13.5%; and 8.6%, accordingly), while SL contributed negatively to PC3 coordinate (44.1%).
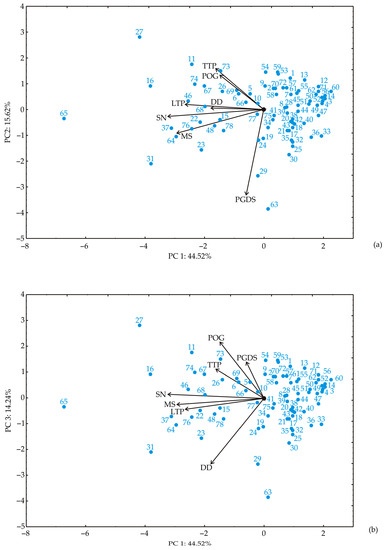
Figure 7.
The PCA biplot diagram, depicting the relationships among AADT, SL, EI, DI, F, PDO, MS, and TA: (a) PC 1 and PC 2, (b) PC 1 and PC 3.
3.4. ANN Models
In research by Kouziokas [61], several ANN models were developed to forecast road accidents. A few parameters were considered to optimize the anticipation of road accidents by building the optimal predicting model (considering the number of neurons in the hidden layers and the nature of the transfer functions). The relative performance indicators of the deep neural network (DNN), gene expression programming (GEP), and regular negative binomial model (RENB) models suggest that the DNN model delivered the best accuracy compared to GEP and RENB models and arised in the lowest root mean squared error, Singh et al. [62].
According to these references, the ANN model simulation was developed in this study. The structure and outcomes of an artificial neural network heavily rely on the initial assumptions of matrix parameters such as biases and weight coefficients. These parameters are crucial in building and fitting the ANN to experimental data. Furthermore, the performance of the ANN model can also be affected by the number of neurons in the hidden layer. To mitigate this problem, each topology was subjected to 100,000 runs to avoid any random correlation caused by initial assumptions and random weight initialization. By following this approach, the ANN model achieved the highest r2 value during the training cycle when using nine hidden neurons (Figure 8a).
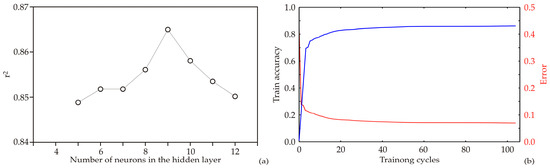
Figure 8.
ANN1 calculation: (a) The dependence of the r2 value of the number of neurons in the hidden layer in the ANN1 model, (b) Training results per epoch.
The ANN1 model was trained for 100 epochs, and the training results, i.e., train accuracy and error (loss), are presented in Figure 5b. The training accuracy increased with the number of training cycles increment until the 40–50th epoch, when it reached almost constant value. More than 50 epochs for training would possibly cause high overfitting, and 60 epochs would be enough to achieve high model accuracy without any risk of overfitting (Figure 8b) Similar results were obtained for ANN2 model.
The acquired optimal neural network models showed good generalization capabilities for the collected data foresee, and could be used to accurately predict the observed outputs, based on the input parameters. The number of neurons for ANN1 model was: 9 (network MLP 13-9-1) to obtain the highest values of r2 (the r2 values for prediction of output variables were 0.986, 0.988 and 0.977, for training, testing and validation cycles, respectively). On the other hand, the number of neurons for ANN2 model was: 8 (network MLP 6-8-5) to obtain the highest values of r2 (the r2 values for prediction of output variables were 0.990, 0.969, and 0.990, for training, testing and validation cycles, respectively).
Table 4 presents the elements of matrix W1 and vector B1 (presented in the bias row). Table 5 presents the elements of matrix W2 and vector B2 (bias) for the hidden layer used for calculation within the ANN1 model. In contrast, Table 6 presents the elements of matrix W1 and vector B1 (presented in the bias row). Table 7 presents the elements of matrix W2 and vector B2 (bias) for the hidden layer, used for calculation within ANN1 acquired using Equation (1).

Table 4.
The weight coefficients and biases W1 and B1 for ANN1.

Table 5.
The weight coefficients and biases W2 and B2 for ANN1.

Table 6.
The weight coefficients and biases W1 and B1 for ANN2.

Table 7.
The weight coefficients and biases W2 and B2 for ANN2.
3.5. The Accuracy of the Model
To numerically verify the displayed models accuracy coefficient of determination (r2), reduced chi-square (χ2), mean bias error (MBE), root mean square error (RMSE), and mean percentage error (MPE) were calculated, Table 8 and Table 9 In addition, the models feature fit were examined, and the residual analysis results are presented in Table 10 and Table 11. The results show that the ANN models had a minor lack of fit tests, which implies that the models satisfactorily predicted the values of the analyzed parameters.

Table 8.
The “goodness of fit” tests for the developed ANN1 model.

Table 9.
The residual analysis for the developed ANN1 model.

Table 10.
The “goodness of fit” tests for the developed ANN2 model.

Table 11.
The residual analysis for the developed ANN2 model.
The residual analysis of the developed model was additionally conducted. Skewness evaluates the variation of the distribution from normal symmetry. A skewness other than zero indicates the asymmetrical distribution, even though typical distributions are ideally symmetrical. The “peakedness” of distribution is assessed by kurtosis. When the kurtosis is greater than zero, the distribution is flatter or more peaked than predicted; the kurtosis of the normal distribution is zero. A high r2 suggests that the variation was evaluated and that the data fit adequately to the suggested model Beattie and Esmonde-White [63], Rupp et al. [64], Šovljanski et al. [65], Najafi et al. [60].
The coefficient of determination (0.987), the mean relative percent error (42.476), the root mean square error (2.975) and the reduced chi-square (8.953) were the evaluated values of developed ANN. According to these results, it was confirmed that obtained ANN model was statistically significant and in agreement with experimental results, Table 8.
The mean and the standard deviation of residuals have also been analyzed. The mean of residuals for the ANN1 model was equal to 0.144, and the standard deviation was 2.299. The skewness parameter showed minimal deviations from a normal distribution, 0.977, while the kurtoisis parameter showed almost neglecting the difference in “peakedness” compared to a normal distribution, 9.151, Table 9.
The coefficients of determination for EI, DI, F, PDO, and TA were between 0.987 and 0.999, the mean relative percent errors (between 3.085 and 18.815), the root mean square errors (between 0.201 and 1.545) and the reduced chi-square (between 0.041 and 2.460) were the evaluated values of developed ANN. According to these results, it was confirmed that obtained ANN model was statistically significant and in agreement with experimental results, Table 10.
The mean of residuals for the ANN2 model for EI, DI, F, PDO, and TA parameters were between −0.004÷0.063, while the standard deviations were between 0.202 and 1.554. The skewness parameters for these variables showed minimal deviations from a normal distribution, between 0.756 and 7.276, while the kurtosis parameters showed almost neglecting the difference in “peakedness” compared to a normal distribution, between 0.338 ÷ 59.253, Table 11.
3.6. Global Sensitivity Analysis—Yoon’s Interpretation Method
In this section, the influence of input variables, on the relative importance of the number of traffic accidents for ANN1, and the number of evident injuries, disabling injury, fatality, property damage only and traffic accidents for ANN2 were studied. According to Figure 9, section length was the most influential parameter on the number of traffic accidents with an approximately relative importance of 40.19%, Figure 6a. On the other hand, section length was the most influential parameter positively affecting the number of evident injuries (50.00%), disabling injury (39.87%), fatality (47.50%), property damage only (48.88%), and the number of traffic accidents (48.79%), Figure 9b–f. One potential avenue of inquiry in the study of traffic accidents is the influence of objective factors, such as stress, fatigue, sleepiness, and health issues, on driver behavior. Longer road sections may exacerbate these factors, leading to increased accident rates. Indeed, research has shown that the impact of these factors is amplified on lengthier roadways. For instance, a study by Chen et al. [66] found a significant association between road length and driver fatigue, indicating that longer roads may pose greater risks to driver safety.
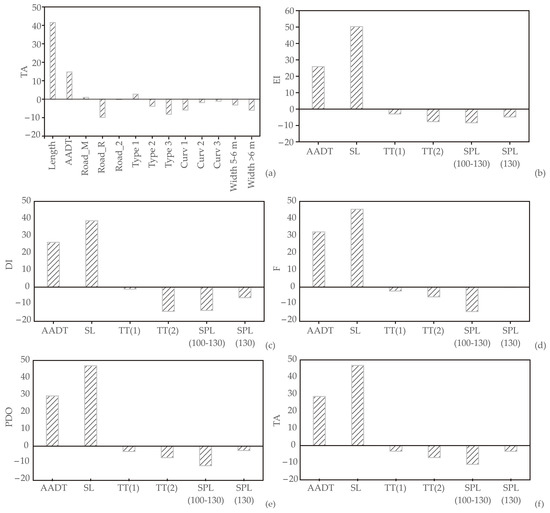
Figure 9.
The relative importance of the section length, AADT, Road 1–3, Type 1–3, Curv 1–3, Width 5–6, and Width ≥ 6 on: (a) TA, and the relative importance of the AADT, SL, TT1, TT2, SPL 100–130 and SPL 130 on: (b) EI, (c) DI, (d) F, (e) PDO, and (f) TA.
According to sensitivity analysis, performed by Chakraborty et al. [46], the approaching speed of the motorized vehicle has the most significant influence on fatal pedestrian crashes. ‘Logarithm of average daily traffic’ volume is found to be the second most sensitive variable.
Artificial neural networks proved to be useful in numerous real-world implementations, particularly where results and data are not same all the time and are altered by the occurrence of irregular changes [67].
4. Conclusions
In conclusion, the correlation analysis conducted in this study revealed several positive correlations between various factors related to traffic accidents on common roads in the Republic of Serbia and the Republic of Srpska (Bosnia and Herzegovina). The findings indicate that section length has a significant positive correlation with the number of traffic accidents, evident injury, and property damage. These results suggest that addressing section length and its impact on traffic accidents could be a key factor in reducing the number of accidents and their severity on roads. Further research is needed to explore other potential factors that contribute to these correlations and to develop effective interventions to prevent and mitigate the negative consequences of traffic accidents.
The results show that the developed ANN models had a minor lack of fit tests, which implies that the models satisfactorily predicted the values of the analyzed parameters. The first ANN model can be used for predicting the number of traffic accidents, while the second one can be also used in predicting traffic accident outcomes.
The Global Sensitivity Analysis recognized average daily traffic volume and section length as the most influential parameter affecting the number of traffic accidents and their fatal and mild consequences. Finally, the results suggest that the understanding of influential factors can help improve road safety and reduce the number of accidents. Future research in the field of transport safety promoting artificial intelligence could focus on developing and testing newer deep learning models that are capable of better handling complex and diverse data types. The algorithm is currently limited to the Republic of Serbia and the Republic of Srpska, but it needs to be validated in urban settings in other countries to appeal to its generality.
Future studies could explore the parameters like road safety authorities, local authorities, vicinities of hospitals, etc, that could affect the safety of traffic in this region. The development of more advanced and efficient algorithms for processing large datasets could be a major area of focus in future research on data science and big data analytics approach in traffic. Future research on traffic accidents could explore the use of advanced modeling techniques to better understand and predict the impacts of different parameters.
Possible future directions for research that emerge from this article include the following: The complexity of urban roads and highways topologies and operation mechanisms should be further investigated to leverage the performance of traffic accident predictors. The adaptability of ANN models for large-scale networks should be investigated in future research. More effective representations of the traffic network, as well as more efficient training strategies, should be applied to acquire a more suitable accuracy of the ANN models. This would increase the chance of the ANN models being used in real-time applications.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/a16050257/s1. Table S1: Collected data for 1–3 road type (-1-RS state road (1st class), 2-RS state road (2nd class), 3-Serbia two lane). Table S2: Collected data for road 4 (Serbia highways).
Author Contributions
Conceptualization, N.R. and D.G.; methodology, N.R. and D.G.; software, L.P. and B.L.; validation, D.G. and N.R.; formal analysis, B.A. and T.Đ.; investigation, B.A. and T.Đ.; resources, N.R. and D.G.; data curation, L.P. and B.L.; writing—original draft preparation, D.G., N.R., L.P. and B.L.; writing—review and editing, N.R., D.G., L.P. and B.L.; visualization, M.P.; supervision, M.P.; project administration, N.R.; funding acquisition, B.L., L.P. and M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science, Technological Development and Innovations of the Republic of Serbia, grant numbers 451-03-47/2023-01/200051, 451-03-47/2023-01/200134, and 451-03-47/2023-01/200017.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The research data available from authors upon email request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- WHO. World Health Organization—Road Traffic Injuries. 2023. Available online: https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries (accessed on 11 February 2023).
- Benos, L.; Tagarakis, A.C.; Dolias, G.; Berruto, R.; Kateris, D.; Bochtis, D. Machine learning in agriculture: A comprehensive updated review. Sensors 2021, 21, 3758. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Ding, F.; Wang, Y. A novel multi-innovation gradient support vector machine regression method. ISA Trans. Press 2022, 130, 343–359. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Peng, G.; De Baets, B. Embedding metric learning into an extreme learning machine for scene recognition. Expert Syst. Appl. 2022, 203, 117505. [Google Scholar] [CrossRef]
- Su, J.; Wang, Y.; Niu, X.; Shaa, S.; Yu, J. Prediction of ground surface settlement by shield tunneling using XGBoost and Bayesian optimization. Eng. Appl. Artif. Intel. 2022, 114, 105020. [Google Scholar] [CrossRef]
- Jawad, M.; Ghulam-e, M.; Muhammad, A. Accurate estimation of tool wear levels during milling, drilling and turning operations by designing novel hyperparameter tuned models based on LightGBM and stacking. Measurement 2022, 190, 110722. [Google Scholar]
- Dutta, J.; Roy, S. Occupancy Sense: Context-based indoor occupancy detection & prediction using CatBoost model. Appl. Soft Comput. 2022, 119, 108536. [Google Scholar]
- Mehdizadeh, A.; Cai, M.; Hu, Q.; Alamdar Yazdi, M.A.; Mohabbati-Kalejahi, N.; Vinel, A.; Rigdon, S.E.; Davis, K.C.; Megahed, F.M. A review of data analytic applications in road traffic safety. Part 1: Descriptive and predictive modeling. Sensors 2020, 20, 1107. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). Highway Safety Manual, 1st ed.; AASHTO: Washington, DC, USA, 2010; Volume 2. [Google Scholar]
- Glavić, D.; Mladenović, M.; Stevanović, A.; Tubić, V.; Milenković, M.; Vidas, M. Contribution to Accident Prediction Models Development for Rural Two-Lane Roads in Serbia. Promet 2016, 28, 415–424. [Google Scholar] [CrossRef]
- Vogt, A.; Bared, J. Accident Models for Two-Lane Rural Segments and Intersections. Transp. Res. Rec. 1998, 1635, 18–29. [Google Scholar] [CrossRef]
- Fitzpatrick, K.; Schneider, W.H.; Park, E.S. Comparisons of Crashes on Rural Two-Lane and Four-Lane Highways in Texas; Texas Department of Transportation: Austin, TX, USA, 2009.
- Geedipally, S.R.; Sunil, P.; Dominique, L. Examination of Methods to Estimate Crash Counts by Collision Type. J. Transp. Res. Board 2010, 2165, 12–20. [Google Scholar] [CrossRef]
- Cardoso, J.L. Design Consistency and Signing of Curves on Interurban Single Carriageway Roads; LNEC: Lisabon, Portugal, 2001. [Google Scholar]
- Harwood, D.; Council, F.; Hauer, E.; Hughes, W.; Vogt, A. Prediction of the Expected Safety Performance of Rural Two-Lane Highways; Federal Highway Administration: McLean, VA, USA, 2000.
- Pardillo-Mayora, J.M.; Llamas-Rubio, L. Relevant Variables for Crash Rate Prediction in Spain’s Two Lane Rural Roads. In Proceedings of the 82nd Transportation Research Board Annual Meeting, Washington, DC, USA, 12–16 January 2003. [Google Scholar]
- Cafiso, S.; Graziano, A.D.; Silvestro, G.D.; Cava, G.L.; Persaud, B. Development of comprehensive accident models for two-lane rural highways using exposure, geometry, consistency and context variables. Accid. Anal. Prev. 2010, 42, 1072–1079. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.; Salifu, M. Crash prediction model for two-lane rural highways in the Ashanti region of Ghana. IATSS Res. 2011, 35, 34–40. [Google Scholar]
- Dinu, R.; Veeraragavan, A. Random parameter models for accident prediction on two-lane undivided highways in India. JSR 2011, 42, 39–42. [Google Scholar] [CrossRef]
- Turner, S.; Singh, R.; Nates, G. The Next Generation of Rural Road Crash Prediction Models: Final Report; NZ Transport Agency: Wellington, New Zealand, 2012.
- Deublein, M.; Schubert, M.; Adey, B.T.; Köhler, J.; Faber, M.H. Prediction of road accidents: A Bayesian hierarchical approach. Accid. Anal. Prev. 2013, 51, 274–291. [Google Scholar] [CrossRef] [PubMed]
- Afrin, T.; Yodo, N. A Long Short-Term Memory-based correlated traffic data prediction framework. Knowl.-Based Syst. 2022, 237, 107755. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, W.; Wushour, S. Traffic accident prediction based on LSTM-GBRT model. J. Control Sci. Eng. 2020, 2020, 4206919. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, C.; Wen, J.; Xiao, X.; Chen, Z. A grey convolutional neural network model for traffic flow prediction under traffic accidents. Neurocomputing 2022, 500, 761–775. [Google Scholar] [CrossRef]
- Zheng, M.; Li, T.; Zhu, R.; Chen, J.; Ma, Z.; Tang, M.; Cui, Z.; Wang, Z. Traffic accident’s severity prediction: A deep-learning approach-based CNN network. IEEE Access 2019, 7, 39897–39910. [Google Scholar] [CrossRef]
- Wen, X.; Xie, Y.; Jiang, L.; Li, Y.; Ge, T. On the interpretability of machine learning methods in crash frequency modeling and crash modification factor development. Accid. Anal. Prev. 2022, 168, 106617. [Google Scholar] [CrossRef]
- Huang, H.; Abdel-Aty, M. Multilevel data and Bayesian analysis in traffic safety. Accid. Anal. Prev. 2010, 42, 1556–1565. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Yahaya, A.S.; Farh, A. Exploring the effects of roadway characteristics on the frequency and severity of head-on crashes: Case studies from Malaysian Federal Roads. Accid. Anal. Prev. 2014, 62, 209–222. [Google Scholar] [CrossRef] [PubMed]
- Çodur, M.Y.; Tortum, A. An Artificial Neural Network Model for Highway Accident Prediction: A Case Study of Erzurum, Turkey. Promet 2015, 27, 217–225. [Google Scholar] [CrossRef]
- Xiong, X.; Chen, L.; Liang, J. Analysis of Roadway Traffic Accidents Based on Rough Sets and Bayesian Networks. Promet 2018, 30, 71–81. [Google Scholar] [CrossRef]
- Olmuş, H.; Erbaş, S. Analysis of Traffic Accidents Caused by Drivers by Using Log-Linear Models. Promet 2012, 24, 495–504. [Google Scholar] [CrossRef]
- Marković, N.; Pešić, D.; Antić, B.; Lazarević, M. Identifying contributing factors on occurrence traffic accidents applying in-depth studies and Bayesian neural networks. J. Road Traffic Eng. 2019, 65, 29–38. [Google Scholar] [CrossRef]
- Milenković, M.; Glavić, D.; Kocić, A.; Petković, M. Impact of road and traffic characteristics on the traffic accidents. J. Road Traffic Eng. 2017, 63, 5–12. [Google Scholar]
- Tubić, V.; Antić, B.; Graovac, D. Traffic accidents costs on state roads of the first order. J. Road Traffic Eng. 2019, 65, 35–43. [Google Scholar] [CrossRef]
- Marković, N.; Pešić, D.; Kovač, M.; Smailović, E. Determination the influence of road factors on the occurrence of traffic accidents with dead pedestrians on the territory of Belgrade by independent estimates. J. Road Traffic Eng. 2021, 67, 41–49. [Google Scholar]
- P.E. Roads of Serbia. Traffic Counting. 2022. Available online: https://www.putevi-srbije.rs/index.php/%D0%B1%D1%80%D0%BE%D1%98%D0%B0%D1%9A%D0%B5-%D1%81%D0%B0%D0%BE%D0%B1%D1%80%D0%B0%D1%9B%D0%B0%D1%98%D0%B0 (accessed on 10 January 2023).
- P.E. Roads of Republic of Srpska. Traffic Counting. 2022. Available online: https://www.putevirs.com/index.php?jezik=sr&idm=12&idpm=14&meni=%D0%91%D0%B5%D0%B7%D0%B1%D1%98%D0%B5%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D1%81%D0%B0%D0%BE%D0%B1%D1%80%D0%B0%D1%9B%D0%B0%D1%98%D0%B0&stavka=%D0%91%D1%80%D0%BE%D1%98%D0%B0%D1%9A%D0%B5-%D1%81%D0%B0% (accessed on 5 January 2023).
- Road Traffic Safety Agency. Traffic Accident GIS Base. 2022. Available online: https://www.abs.gov.rs/%d1%81%d1%80/analize-i-istrazivanja/baza-podataka (accessed on 10 January 2023).
- Ministry of Internal Affairs of the Republic of Srpska. Number of Traffic Accidents and Casualties by Road Section; ICT Administration: Banja Luka, Bosnia and Herzegovina, 2021.
- Liu, S.; Chang, R.; Zuo, J.; Webber, R.J.; Xiong, F.; Dong, N. Application of artificial neural networks in construction management: Current status and future directions. Appl. Sci. 2021, 11, 9616. [Google Scholar] [CrossRef]
- Pang, Z.; Niu, F.; O’Neill, Z. Solar radiation prediction using recurrent neural network and artificial neural network: A case study with comparisons. Renew. Energy 2020, 156, 279–289. [Google Scholar] [CrossRef]
- Pezo, L.; Lončar, B.; Šovljanski, O.; Tomić, A.; Travičić, V.; Pezo, M.; Aćimović, M. Agricultural Parameters and Essential Oil Content Composition Prediction of Aniseed, Based on Growing Year, Locality and Fertilization Type—An Artificial Neural Network Approach. Life 2022, 12, 1722. [Google Scholar] [CrossRef]
- Brandić, I.; Pezo, L.; Bilandžija, N.; Peter, A.; Šurić, J.; Voća, N. Artificial neural network as a tool for estimation of the higher heating value of miscanthus based on ultimate analysis. Mathematics 2022, 10, 3732. [Google Scholar] [CrossRef]
- Ruškić, N.; Mirović, V.; Marić, M.; Pezo, L.; Lončar, B.; Nićetin, M.; Ćurčić, L. Model for Determining Noise Level Depending on Traffic Volume at Intersections. Sustainability 2022, 14, 12443. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering, 8th ed.; California State Polytecnic University, John Wiley & Sons Inc.: Hoboken, NJ, USA, 2019; ISBN 978-1-119-47422-7. [Google Scholar]
- Chakraborty, A.; Mukherjee, D.; Mitra, S. Development of pedestrian crash prediction model for a developing country using artificial neural network. Int. J. Inj. Control Saf. Promot. 2019, 26, 283–293. [Google Scholar] [CrossRef] [PubMed]
- Rezaie Moghaddam, F.; Afandizadeh, S.; Ziyadi, M. Prediction of accident severity using artificial neural networks. Int. J. Civ. Eng. 2011, 9, 41–48. [Google Scholar]
- Demir, H.; Demir, H.; Lončar, B.; Pezo, L.; Brandić, I.; Voća, N.; Yilmaz, F. Optimization of Caper Drying Using Response Surface Methodology and Artificial Neural Networks for Energy Efficiency Characteristics. Energies 2023, 16, 1687. [Google Scholar] [CrossRef]
- Rajković, D.; Jeromela, A.M.; Pezo, L.; Lončar, B.; Grahovac, N.; Špika, A.K. Artificial neural network and random forest regression models for modelling fatty acid and tocopherol content in oil of winter rapeseed. J. Food Compos. Anal. 2023, 115, 105020. [Google Scholar] [CrossRef]
- Kai, Z.; Xin, X.; Hong-Xing, L.; Yi-Peng, X.; Zhen-Chun, L.; Ping, J. Optimization method of first-arrival waveform inversion based on the L-BFGS algorithm. Appl. Geophys. 2021, 18, 515–524. [Google Scholar] [CrossRef]
- Puntarić, E.; Pezo, L.; Zgorelec, Ž.; Gunjača, J.; Kučić Grgić, D.; Voća, N. Prediction of the Production of Separated Municipal Solid Waste by Artificial Neural Networks in Croatia and the European Union. Sustainability 2022, 14, 10133. [Google Scholar] [CrossRef]
- Yoon, Y.; Swales, G.; Margavio, T.M. Comparison of Discriminant Analysis versus Artificial Neural Networks. J. Oper. Res. Soc. 2017, 44, 51–60. [Google Scholar] [CrossRef]
- Voća, N.; Pezo, L.; Jukić, Ž.; Lončar, B.; Šuput, D.; Krička, T. Estimation of the storage properties of rapeseeds using an artificial neural network. Ind. Crops Prod. 2022, 187, 115358. [Google Scholar] [CrossRef]
- Ćurčić, L.; Lončar, B.; Pezo, L.; Stojić, N.; Prokić, D.; Filipović, V.; Pucarević, M. Chemometric Approach to Pesticide Residue Analysis in Surface Water. Water 2022, 14, 4089. [Google Scholar] [CrossRef]
- Aćimović, M.; Zeremski, T.; Šovljanski, O.; Lončar, B.; Pezo, L.; Zheljazkov, V.D.; Pezo, M.; Šuput, D.; Kurunci, Z. Seasonal Variations in Essential Oil Composition of Immortelle Cultivated in Serbia. Horticulturae 2022, 8, 1183. [Google Scholar] [CrossRef]
- Sun, H.; Yang, G.Y. The combined measurement and correlation analysis of deaths in traffic accidents. J. Yanbian Univ. 2018, 44, 239–245. [Google Scholar]
- Sun, L.L.; Chen, T.; Zhao, J.; Wu, Q.; Zhao, H. Analysis of the influencing factors of traffic accident losses and their regional features in China-a study based on the panel data of 31 provinces from 2004 to 2015. Southwest Univ. 2019, 41, 114–123. [Google Scholar]
- Chen, J.; Wang, Q.; Huang, J. Motorcycle ban and traffic safety: Evidence from a quasi-experiment at Zhejiang, China. J. Adv. Transp. 2021, 2021, 7552180. [Google Scholar] [CrossRef]
- Soni, A.; Al-Sarayreh, M.; Reis, M.M.; Smith, J.; Tong, K.; Brightwell, G. Identification of cold spots using non-destructive hyperspectral imaging technology in model food processed by coaxially induced microwave pasteurization and sterilization. Foods 2020, 9, 837. [Google Scholar] [CrossRef] [PubMed]
- Najafi, Z.; Zare, K.; Mahmoudi, M.R.; Shokri, S.; Mosavi, A. Inference and Local Influence Assessment in a Multifactor Skew Normal Linear Mixed Model. Mathematics 2022, 10, 2820. [Google Scholar] [CrossRef]
- Kouziokas, G.N. Neural network-based road accident forecasting in transportation and public management. In Data Analytics: Paving the Way to Sustainable Urban Mobility: Proceedings of 4th Conference on Sustainable Urban Mobility (CSUM2018), Skiathos Island, Greece, 24–25 May 2018; Springer International Publishing: Berlin, Germany, 2019; pp. 98–103. [Google Scholar]
- Singh, G.; Pal, M.; Yadav, Y.; Singla, T. Deep neural network-based predictive modeling of road accidents. Neural Comput. Appl. 2020, 32, 12417–12426. [Google Scholar] [CrossRef]
- Beattie, J.R.; Esmonde-White, F.W. Exploration of principal component analysis: Deriving principal component analysis visually using spectra. Appl. Spectrosc. 2021, 75, 361–375. [Google Scholar] [CrossRef]
- Rupp, D.E.; Schmidt, J.; Woods, R.A.; Bidwell, V.J. Analytical assessment and parameter estimation of a low-dimensional groundwater model. J. Hydrol. 2009, 377, 143–154. [Google Scholar] [CrossRef]
- Šovljanski, O.; Tomić, A.; Pezo, L.; Ranitović, A.; Markov, S. Prediction of denitrification capacity of alkalotolerant bacterial isolates from soil—An artificial neural network model. J. Serb. Chem. Soc. 2020, 85, 1417–1427. [Google Scholar] [CrossRef]
- Chen, C.-F.; Chen, C.-H.; Chung, Y.-Y.; Chen, S.-L.; Chen, C.-C. Association between road length and driver fatigue on monotonous two-lane highways. Accid. Anal. Prev. 2016, 97, 118–125. [Google Scholar]
- Halim, Z.; Kalsoom, R.; Bashir, S.; Abbas, G. Artificial intelligence techniques for driving safety and vehicle crash prediction. Artif. Intell. Rev. 2016, 46, 351–387. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).