Learning from Imbalanced Datasets: The Bike-Sharing Inventory Problem Using Sparse Information †
Abstract
1. Introduction
- The inventory problem is formulated as a classification problem that can be easily solved using decision trees (or any other state-of-the-art classifier);
- While traditional classifiers over-represent the majority class, this paper presents a novel resampling technique that better leverages data and provides better estimates for rare observations;
- The proposed algorithm can be used to compute both an upper-bound and a lower-bound value for the bike-sharing inventory problem, thus yielding to different possible configurations;
- Although mainly based on historical data, the proposed approach can also be used to solve the inventory problem for new stations, for which historical information is not available;
- The proposed model is easily implementable into an ITS-based decision support system for also supporting bike-sharing companies in a day-to-day framework, thus helping in improving operations.
2. Related Research
2.1. The Inventory Problem and the Rebalancing Problem
2.2. Learning from Imbalanced Datasets
2.3. Discussion
3. Methodology
3.1. Benchmark Values from Historical Data
3.2. The Inventory Problem as a Classification Problem Using Machine Learning
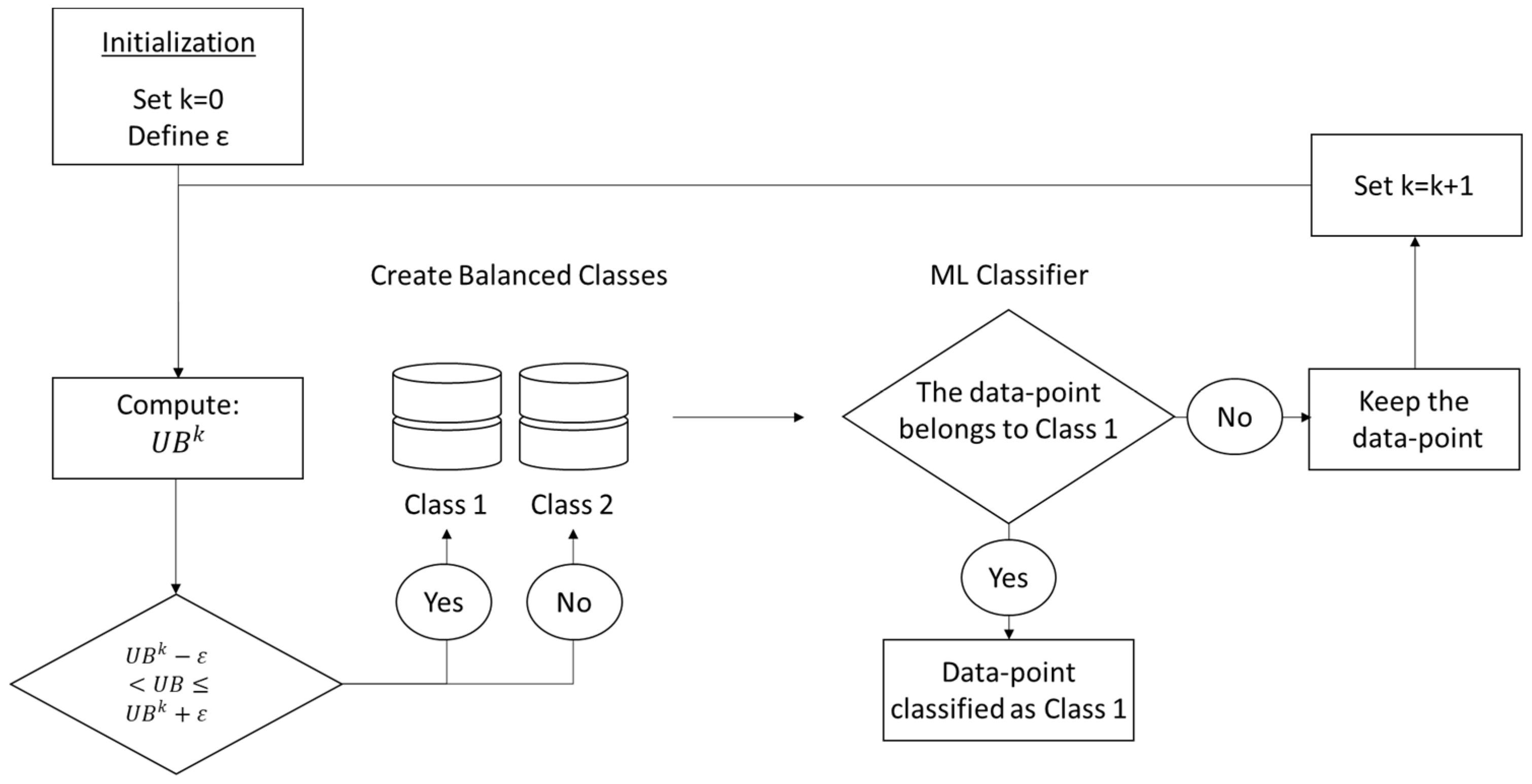
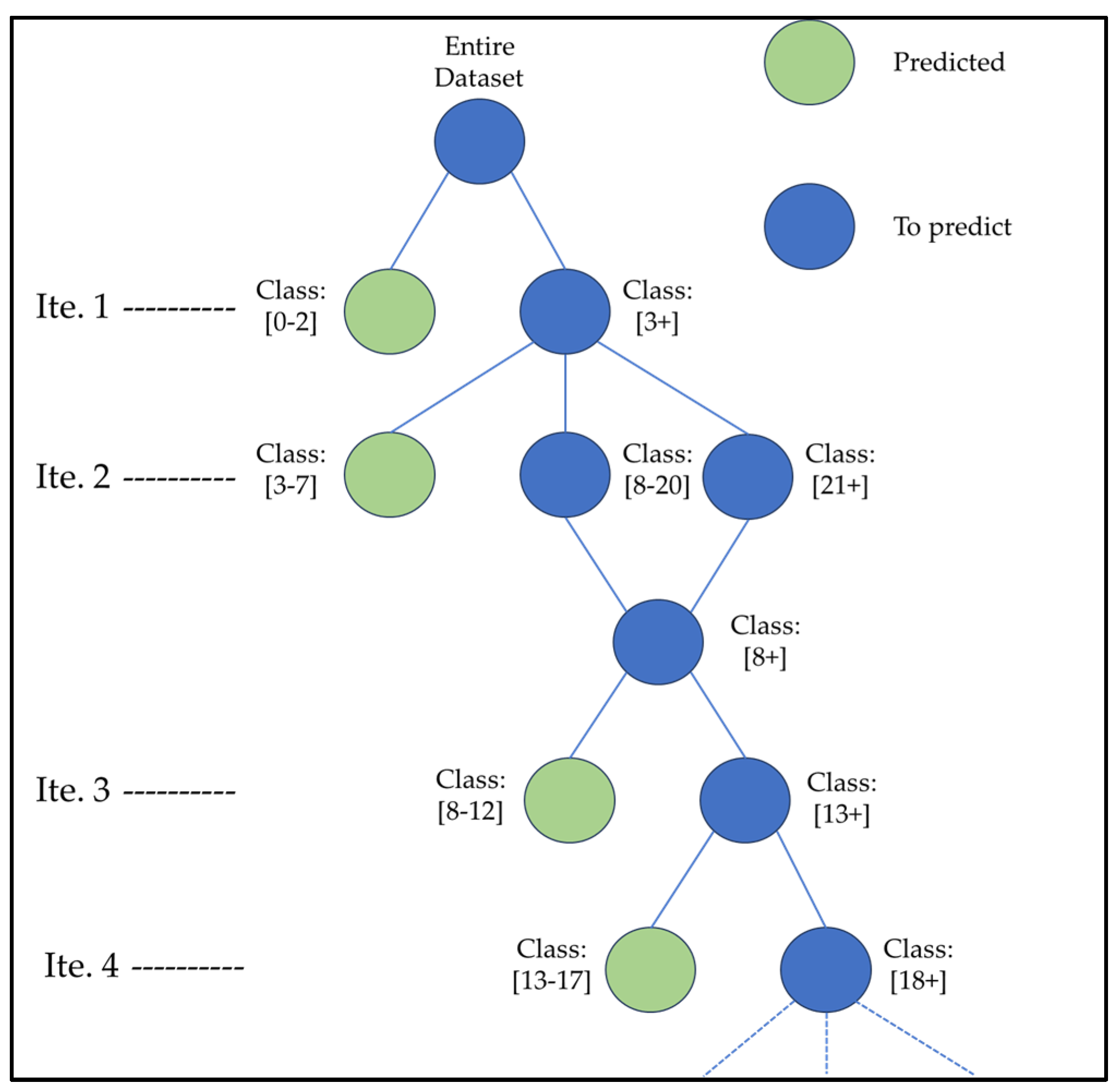
3.3. Iterative Resampling and Data Imbalance
| Algorithm 1: Iterative Resampling Technique |
| Procedure: resampling (X, Y, ε, k, E) ForUB in Y if Else If Set n = Split in n classes If Set n = )/Len Split in n classes Return (X, Class) |
| Algorithm 2: Iterative ML Classifier |
Set , k, E Set k = 0 While is not empty: , k, E) For : Set k = k + 1 |
4. Numerical Results
4.1. Case Study
- The prediction for new stations by adopting the best classifier as a result of the first point, again combining it with a standard resampling technique (BorderlineSMOTE) or with the iterative resampling approach;
- The first results in terms of predictions in a day-to-day framework as a result of applying Equation (9).
4.2. Data Imbalance
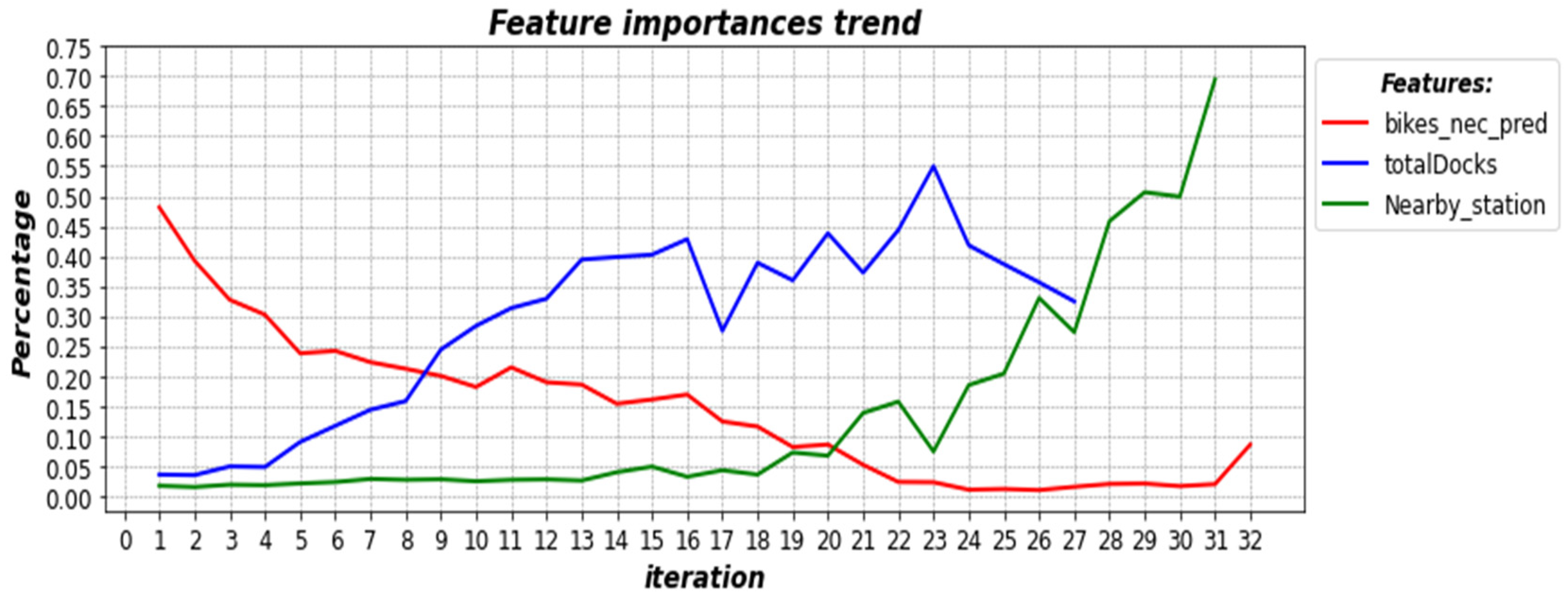
4.3. Resampling and Feature Importance
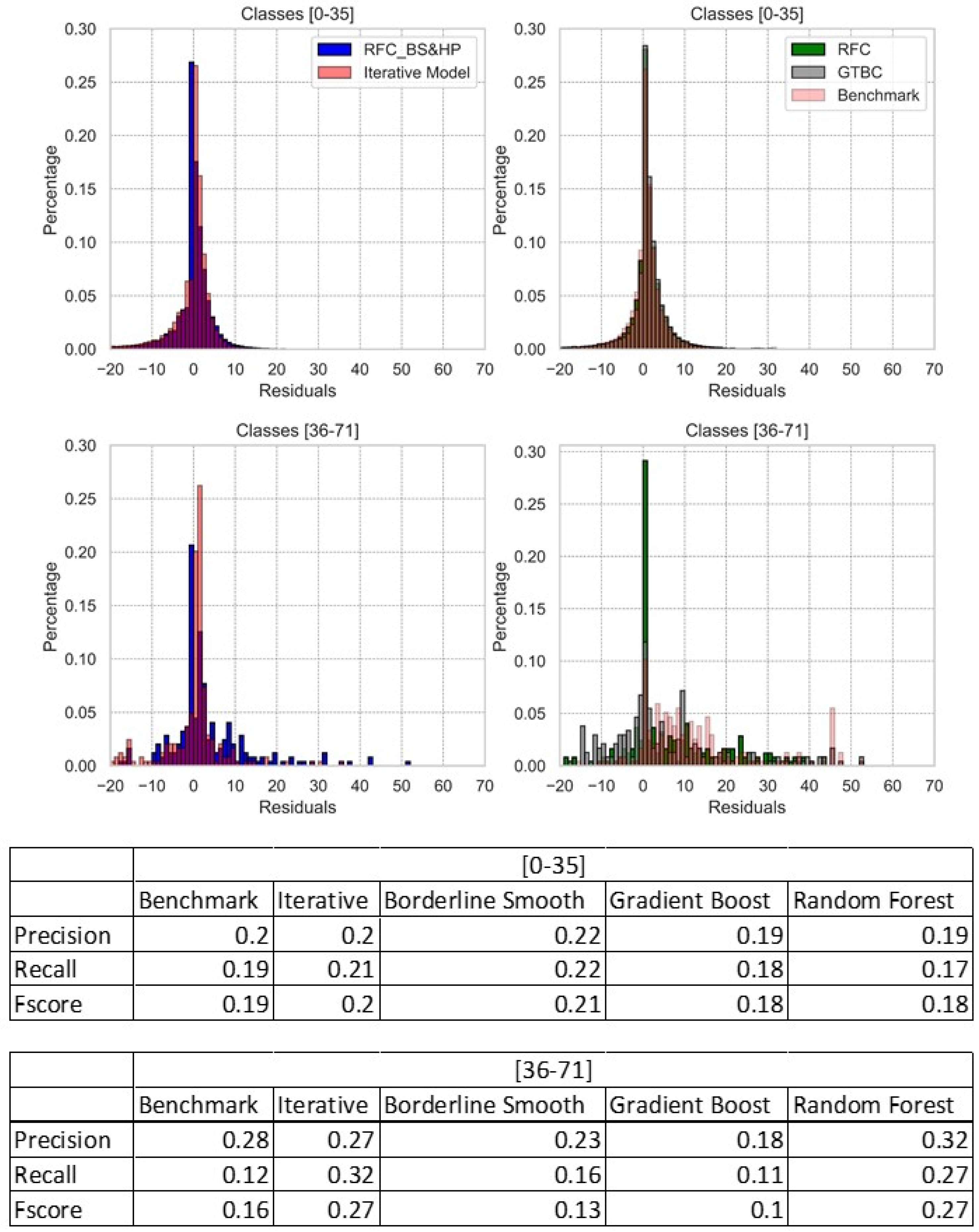
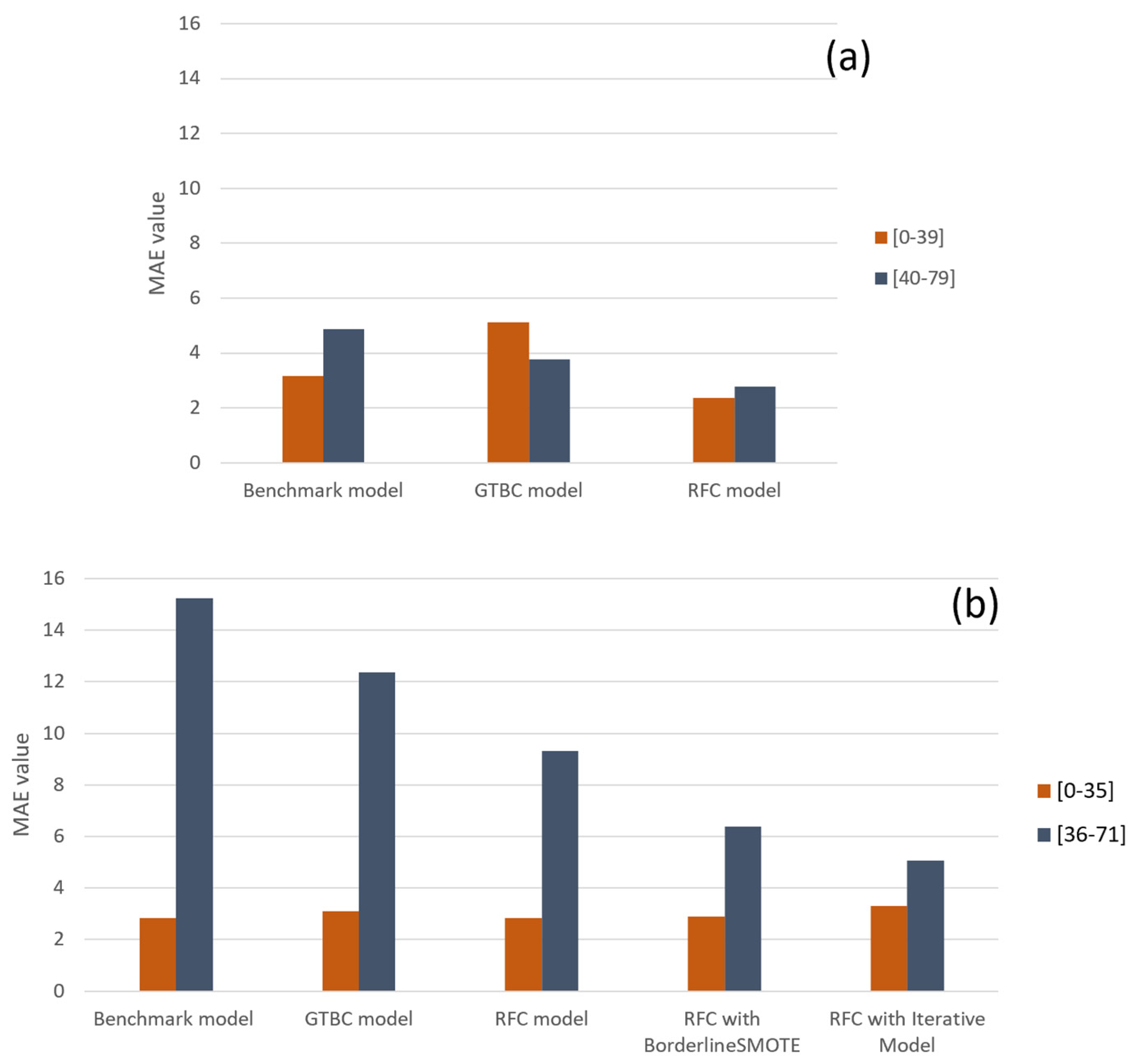
4.4. Prediction of the Upper Bound and Lower Bound for Existing Stations
4.5. Predicting New Stations Using Only Exogenous Variables
4.6. Prediction Based on a Day-to-Day Approach
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loaiza-Monsalve, D.; Riascos, A.P. Human Mobility in Bike-Sharing Systems: Structure of Local and Non-Local Dynamics. PLoS ONE 2019, 14, e0213106. [Google Scholar] [CrossRef]
- Lahoorpoor, B.; Faroqi, H.; Sadeghi-Niaraki, A.; Choi, S.-M. Spatial Cluster-Based Model for Static Rebalancing Bike Sharing Problem. Sustainability 2019, 11, 3205. [Google Scholar] [CrossRef]
- Fricker, C.; Gast, N.; Mohamed, H. Mean Field Analysis for Inhomogeneous Bike Sharing Systems. Discret. Math. Theor. Comput. Sci. 2012. Available online: https://dmtcs.episciences.org/3006/pdf (accessed on 23 June 2023). [CrossRef]
- Cruz, F.; Subramanian, A.; Bruck, B.P.; Iori, M. A Heuristic Algorithm for a Single Vehicle Static Bike Sharing Rebalancing Problem. Comput. Oper. Res. 2017, 79, 19–33. [Google Scholar] [CrossRef]
- Regue, R.; Recker, W. Proactive Vehicle Routing with Inferred Demand to Solve the Bikesharing Rebalancing Problem. Transp. Res. Part E Logist. Transp. Rev. 2014, 72, 192–209. [Google Scholar] [CrossRef]
- Legros, B. Dynamic Repositioning Strategy in a Bike-Sharing System; How to Prioritize and How to Rebalance a Bike Station. Eur. J. Oper. Res. 2019, 272, 740–753. [Google Scholar] [CrossRef]
- Datner, S.; Raviv, T.; Tzur, M.; Chemla, D. Setting Inventory Levels in a Bike Sharing Network. Transp. Sci. 2019, 53, 62–76. [Google Scholar] [CrossRef]
- Ashqar, H.I.; Elhenawy, M.; Almannaa, M.H.; Ghanem, A.; Rakha, H.A.; House, L. Modeling Bike Availability in a Bike-Sharing System Using Machine Learning. In Proceedings of the 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Naples, Italy, 26–28 June 2017; pp. 374–378. [Google Scholar]
- Ruffieux, S.; Spycher, N.; Mugellini, E.; Khaled, O.A. Real-Time Usage Forecasting for Bike-Sharing Systems: A Study on Random Forest and Convolutional Neural Network Applicability. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; pp. 622–631. [Google Scholar]
- Ceccarelli, G.; Cantelmo, G.; Nigro, M.; Antoniou, C. Machine Learning from Imbalanced Data-Sets: An Application to the Bike-Sharing Inventory Problem. In Proceedings of the 2021 7th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Heraklion, Greece, 16–17 June 2021; pp. 1–6. [Google Scholar]
- Laporte, G.; Meunier, F.; Calvo, R.W. Shared Mobility Systems. 4OR 2015, 13, 341–360. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Hadjicostantinou, E.; Iori, M.; Novellani, S. The Bike Sharing Rebalancing Problem: Mathematical Formulations and Benchmark Instances. Omega 2014, 45, 7–19. [Google Scholar] [CrossRef]
- Santos, G.G.D.; Correia, G.H.D.A. Finding the Relevance of Staff-Based Vehicle Relocations in One-Way Carsharing Systems through the Use of a Simulation-Based Optimization Tool. J. Intell. Transp. Syst. 2019, 23, 583–604. [Google Scholar] [CrossRef]
- Pal, A.; Zhang, Y. Free-Floating Bike Sharing: Solving Real-Life Large-Scale Static Rebalancing Problems. Transp. Res. Part C Emerg. Technol. 2017, 80, 92–116. [Google Scholar] [CrossRef]
- Chemla, D.; Meunier, F.; Calvo, R.W. Bike Sharing Systems: Solving the Static Rebalancing Problem. Discret. Optim. 2013, 10, 120–146. [Google Scholar] [CrossRef]
- Erdoğan, G.; Battarra, M.; Calvo, R.W. An Exact Algorithm for the Static Rebalancing Problem Arising in Bicycle Sharing Systems. Eur. J. Oper. Res. 2015, 245, 667–679. [Google Scholar] [CrossRef]
- Kloimüllner, C.; Papazek, P.; Hu, B.; Raidl, G.R. Balancing Bicycle Sharing Systems: An Approach for the Dynamic Case. In Evolutionary Computation in Combinatorial Optimisation; Lecture Notes in Computer, Science; Blum, C., Ochoa, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 73–84. [Google Scholar]
- Chen, P.; Hsieh, H.; Su, K.; Sigalingging, X.K.; Chen, Y.; Leu, J. Predicting Station Level Demand in a Bike-Sharing System Using Recurrent Neural Networks. IET Intell. Transp. Syst. 2020, 14, 554–561. [Google Scholar] [CrossRef]
- Wang, B.; Vu, H.L.; Kim, I.; Cai, C. Short-Term Traffic Flow Prediction in Bike-Sharing Networks. J. Intell. Transp. Syst. 2022, 26, 461–475. [Google Scholar] [CrossRef]
- Xu, C.; Ji, J.; Liu, P. The Station-Free Sharing Bike Demand Forecasting with a Deep Learning Approach and Large-Scale Datasets. Transp. Res. Part C Emerg. Technol. 2018, 95, 47–60. [Google Scholar] [CrossRef]
- Nair, R.; Miller-Hooks, E. Fleet Management for Vehicle Sharing Operations. Transp. Sci. 2011, 45, 524–540. [Google Scholar] [CrossRef]
- Schuijbroek, J.; Hampshire, R.; van Hoeve, W.-J. Inventory Rebalancing and Vehicle Routing in Bike Sharing Systems. Eur. J. Oper. Res. 2017, 257, 992–1004. [Google Scholar] [CrossRef]
- O’Mahony, E.; Shmoys, D.B. Data Analysis and Optimization for (Citi) Bike Sharing. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, AAAI’15, Austin, TX, USA, 25–30 January 2015; AAAI Press: Washington, DC, USA, 2015; pp. 687–694. [Google Scholar]
- Rudloff, C.; Lackner, B. Modeling Demand for Bikesharing Systems: Neighboring Stations as Source for Demand and Reason for Structural Breaks. Transp. Res. Rec. 2014, 2430, 1–11. [Google Scholar] [CrossRef]
- Ploeger, J.; Oldenziel, R. The sociotechnical roots of smart mobility: Bike sharing since 1965. J. Transp. Hist. 2020, 41, 134–159. [Google Scholar] [CrossRef]
- Moran, M.E.; Laa, B.; Emberger, G. Six scooter operators, six maps: Spatial coverage and regulation of micromobility in Vienna, Austria. Case Stud. Transp. Policy 2020, 8, 658–671. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Song, Y. Factors affecting bike-sharing behaviour in Beijing: Price, traffic congestion, and supply chain. Ann. Oper. Res. 2019, 1–16. [Google Scholar] [CrossRef]
- Jin, Y.; Ruiz, C.; Liao, H. A simulation framework for optimizing bike rebalancing and maintenance in large-scale bike-sharing systems. Simul. Model. Pract. Theory 2022, 115, 102422. [Google Scholar] [CrossRef]
- Jamali, I.; Bazmara, M.; Jafari, S. Feature Selection in Imbalance Data Sets. Int. J. Comput. Sci. Issues 2013, 9, 42. [Google Scholar]
- Orriols-Puig, A.; Bernadó-Mansilla, E. Evolutionary Rule-Based Systems for Imbalanced Data Sets. Soft Comput. 2009, 13, 213–225. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from Imbalanced Data: Open Challenges and Future Directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Liu, X.-Y. On Multi-Class Cost-Sensitive Learning. Comput. Intell. 2010, 26, 232–257. [Google Scholar] [CrossRef]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Ganganwar, V. An Overview of Classification Algorithms for Imbalanced Datasets. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 42–47. [Google Scholar]
- Wang, J.; Xu, M.; Wang, H.; Zhang, J. Classification of Imbalanced Data by Using the SMOTE Algorithm and Locally Linear Embedding. In Proceedings of the 2006 8th international Conference on Signal Processing, Guilin, China, 16–20 November 2006; Volume 3. [Google Scholar]
- Dal Pozzolo, A.; Caelen, O.; Johnson, R.A.; Bontempi, G. Calibrating Probability with Undersampling for Unbalanced Classification. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 159–166. [Google Scholar]
- Liu, X.-Y.; Wu, J.; Zhou, Z.-H. Exploratory Undersampling for Class-Imbalance Learning. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2009, 39, 539–550. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Chen, H.; Li, C.; Yang, W.; Liu, J.; An, X.; Zhao, Y. Deep Balanced Cascade Forest: A Novel Fault Diagnosis Method for Data Imbalance. ISA Trans. 2021, 126, 428–439. [Google Scholar] [CrossRef] [PubMed]
- Cantelmo, G.; Kucharski, R.; Antoniou, C. Low-Dimensional Model for Bike-Sharing Demand Forecasting That Explicitly Accounts for Weather Data. Transp. Res. Rec. 2020, 2674, 132–144. [Google Scholar] [CrossRef]
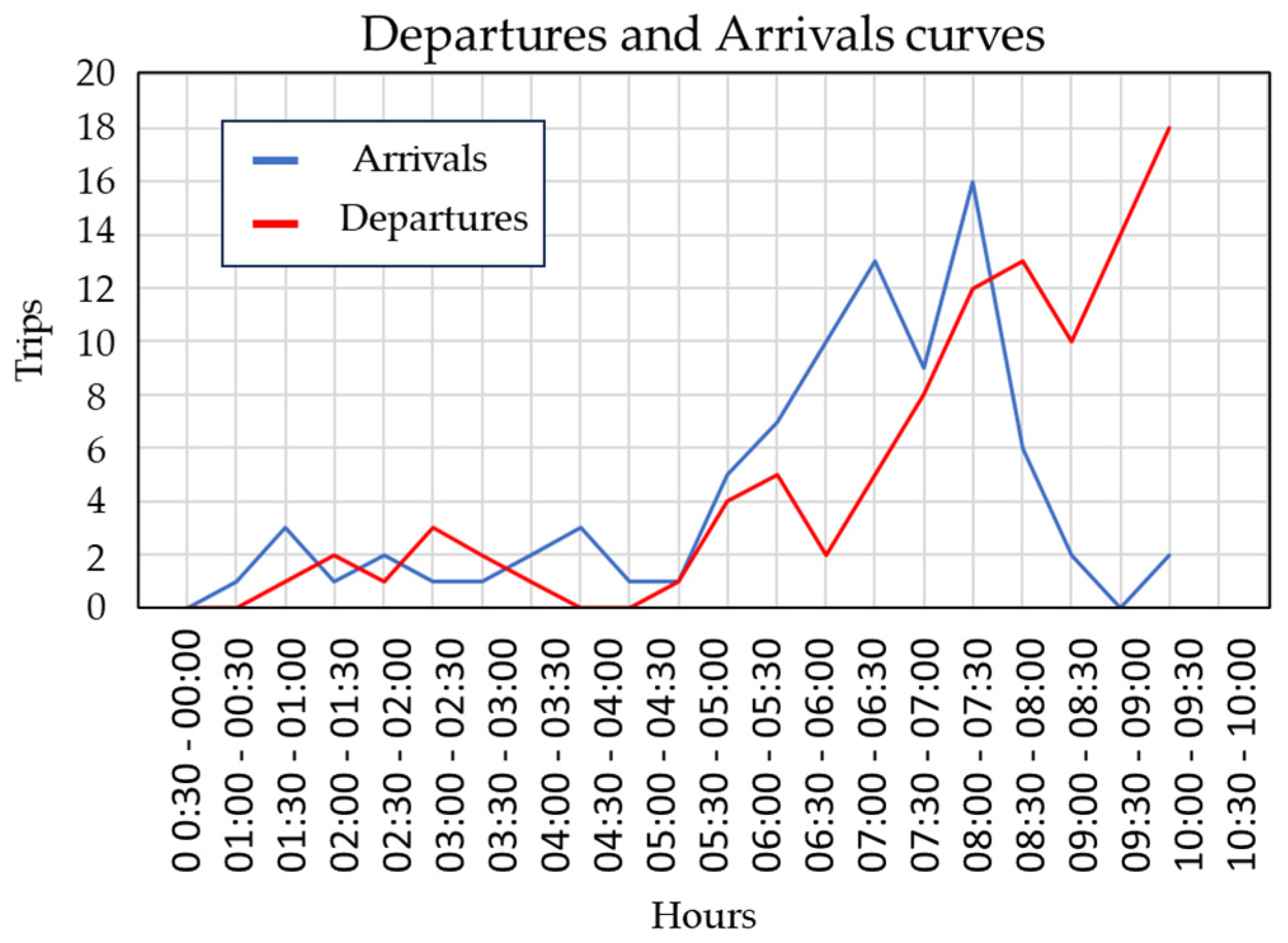
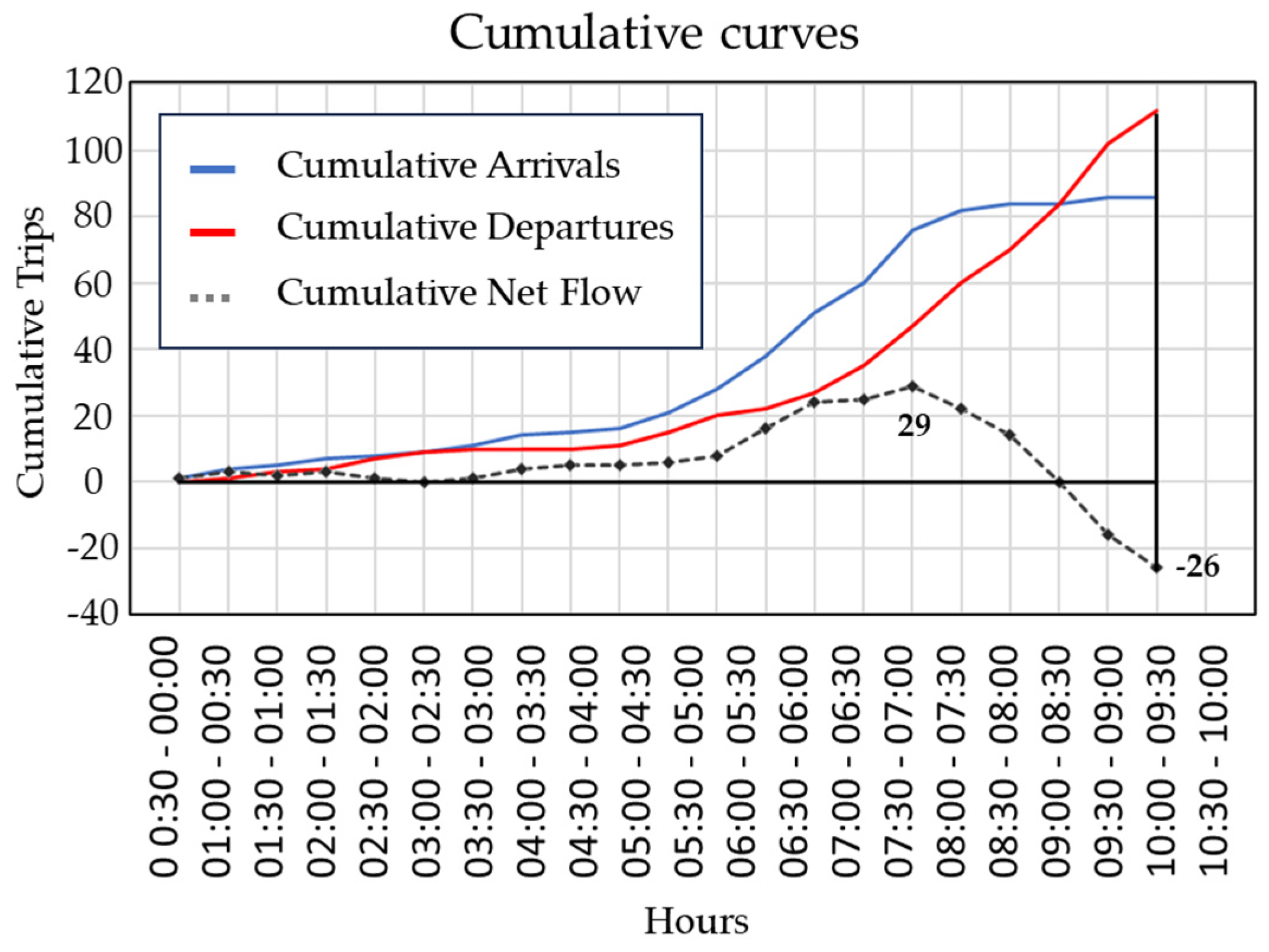
| Feature Type | Characterization | [Unit] |
|---|---|---|
| Exogenous | Month | |
| Weekday | ||
| Season | ||
| Capacity of the station | [number of bikes] | |
| Nearby stations | [number] | |
| Station location (inside/outside Manhattan) | [binary] | |
| Endogenous | Average number of departures/arrivals observed in the previous two months, in the same referenced period | [number] |
| Number of departures/arrivals at the station in the previous day | [number] | |
| Departure/arrival trip duration observed at the station the previous two months | [seconds] | |
| Average LB (or UB) observed in the previous two months, in the same referenced period and at the same station | [number of bikes] | |
| Behavioral * | Average temperature (current day) | [Classes from 1(Low) to 10 (High)] |
| Average temperature (day before) | [Classes from 1(Low) to 10 (High)] | |
| Variability of the temperature (current day), as the difference between the maximum and minimum registered | [Classes from 1(Low) to 5 (High)] | |
| Variability of the temperature (day before), as the difference between the maximum and minimum registered | [Classes from 1(Low) to 5 (High)] | |
| Precipitation (current day) | [Classes 0 (Null) and from 1(Low) to 5 (High)] | |
| Precipitation (day before) | [Classes 0 (Null) and from 1(Low) to 5 (High)] | |
| Snow depth (current day) | [Classes 0 (Null) and from 1(Low) to 5 (High)] | |
| Snow depth (day before) | [Classes 0 (Null) and from 1(Low) to 5 (High)] | |
| Dependent variable | Bikes LB (or UB) | [number of bikes] |
| Number of Bikes | Upper-Bound Distribution [%] | Lower-Bound Distribution [%] |
|---|---|---|
| (0–10) | 6.2 | 83.1 |
| (11–20) | 18.6 | 10.4 |
| (21–30) | 39.2 | 4.5 |
| (31–40) | 19.2 | 1.5 |
| (41–50) | 11.3 | 0.3 |
| (>50) | 5.5 | 0.2 |
| Lower-Bound Models | MAE (0–35) | MAE (36–71) |
|---|---|---|
| RFC | 4.85 | 37.83 |
| RFC with BorderlineSMOTE | 6.68 | 9.07 |
| RFC with Iterative Model | 8.41 | 8.36 |
| RFC with BorderlineSMOTE | RFC with Iterative Model | |||
|---|---|---|---|---|
| Correlation Cut | MAE (0–35) | MAE (36–71) | MAE (0–35) | MAE (36–71) |
| 0.1 | 6.66 | 10.67 | 8.18 | 8.19 |
| 0.3 | 6.68 | 9.07 | 8.41 | 8.36 |
| 0.5 | 6.73 | 8.94 | 8.31 | 8.43 |
| 0.7 | 6.66 | 9.40 | 8.16 | 8.51 |
| 1 | 6.66 | 8.81 | 8.19 | 8.44 |
| 1.2 | 10.45 | 21.39 | 11.43 | 8.17 |
| Lower-Bound Models | MAE (0–39) | MAE (40–79) |
|---|---|---|
| RFC with Iterative Model | 3.27 | 4.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceccarelli, G.; Cantelmo, G.; Nigro, M.; Antoniou, C. Learning from Imbalanced Datasets: The Bike-Sharing Inventory Problem Using Sparse Information. Algorithms 2023, 16, 351. https://doi.org/10.3390/a16070351
Ceccarelli G, Cantelmo G, Nigro M, Antoniou C. Learning from Imbalanced Datasets: The Bike-Sharing Inventory Problem Using Sparse Information. Algorithms. 2023; 16(7):351. https://doi.org/10.3390/a16070351
Chicago/Turabian StyleCeccarelli, Giovanni, Guido Cantelmo, Marialisa Nigro, and Constantinos Antoniou. 2023. "Learning from Imbalanced Datasets: The Bike-Sharing Inventory Problem Using Sparse Information" Algorithms 16, no. 7: 351. https://doi.org/10.3390/a16070351
APA StyleCeccarelli, G., Cantelmo, G., Nigro, M., & Antoniou, C. (2023). Learning from Imbalanced Datasets: The Bike-Sharing Inventory Problem Using Sparse Information. Algorithms, 16(7), 351. https://doi.org/10.3390/a16070351









