Neural Network Entropy (NNetEn): Entropy-Based EEG Signal and Chaotic Time Series Classification, Python Package for NNetEn Calculation
Abstract
1. Introduction
- The concept of computing NNetEn is introduced.
- Investigating the effect of input dataset (Stage 2) in NNetEn value by considering the SARS-CoV-2-RBV1 dataset.
- Proposing the R2 Efficiency and Pearson Efficiency as new time series features related to NNetEn.
- Python package for NNetEn calculation is developed.
- The results of the separation of synthetic and real EEG signals using NNetEn are presented.
- The synergistic effect of using NNetEn entropy along with traditional entropy measures for classifying EEG signals is demonstrated.
2. Materials and Methods
2.1. Description of Datasets
- Dataset 1: The MNIST dataset contains handwritten numbers from ‘0’ to ‘9’ with 60,000 training images and 10,000 testing images. Each image has a size of 28 × 28 = 784 pixels and is presented in grayscale coloring. This dataset is well balanced since the number of vectors of different classes is approximately the same. The distribution of elements in each class is given in Table 1.
| Classes | Number of Training Images | Number of Testing Images |
|---|---|---|
| 0 | 5923 | 980 |
| 1 | 6742 | 1135 |
| 2 | 5958 | 1032 |
| 3 | 6131 | 1010 |
| 4 | 5842 | 982 |
| 5 | 5421 | 892 |
| 6 | 5918 | 958 |
| 7 | 6265 | 1028 |
| 8 | 5851 | 974 |
| 9 | 5949 | 1009 |
| Total | 60,000 | 10,000 |
- Dataset 2: The SARS-CoV-2-RBV1 dataset contains information on 2648 COVID-19 positive outpatients and 2648 COVID-19 negative outpatients (control group), for 5296 patients, as described by Huyut, M.T. and Velichko in [36]. A data vector containing 51 routine blood parameters is included in this dataset. The dataset can be classified into two classes using binary methods such as COVID positive or normal control (NC). We used the entire dataset for both training and testing. As a result, the training and test sets coincided, and the resulting accuracy is equivalent to the accuracy on the training data.
- Dataset 3: This dataset contains records of EEG signals recorded at the AHEPA General Hospital of Thessaloniki’s 2nd Department of Neurology [46]. This dataset consists of electroencephalograms of 88 patients divided into three groups: controls (29 people), Alzheimer’s disease patients (36 people), and dementia patients (23 people). In order to record EEG, the authors of the dataset used a Nihon Kohden EEG 2100 device with 19 electrodes (channels) located on the head according to the 10–20 scheme: Fp1, Fp2, F7, F3, Fz, F4, F8, T3, C3, Cz, C4, T4, T5, P3, Pz, P4, T6, O1, O2. Each channel’s signal was digitized at a sampling rate of 500 Hz. The duration of EEG recordings ranged from 5 min to 21.3 min. A resting EEG was recorded with the eyes closed.
2.2. Performance Metrics
- Classification Accuracy (Acc): Based on [26], we proposed to use the classification accuracy, which is as follows for multiclass classification:where TP(Ci,i) indicates the number of true positive classified elements in class i.
- R2 Efficiency (R2E):
- Pearson Efficiency (PE):
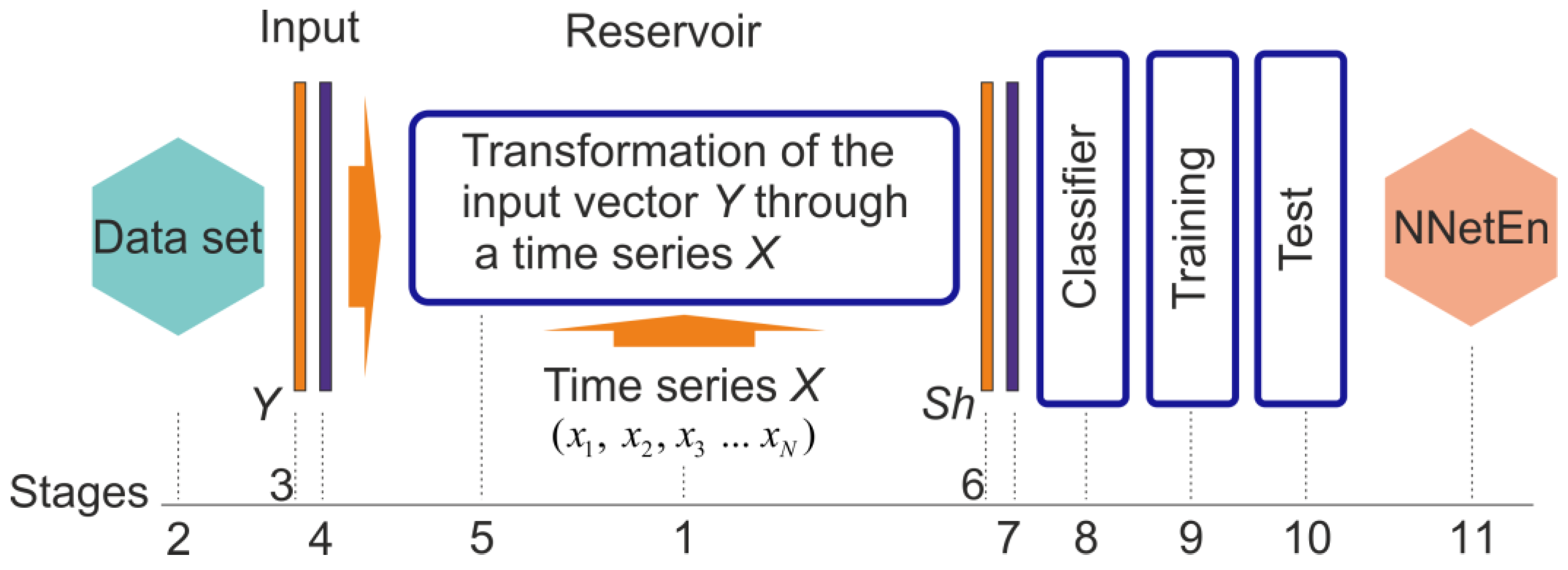
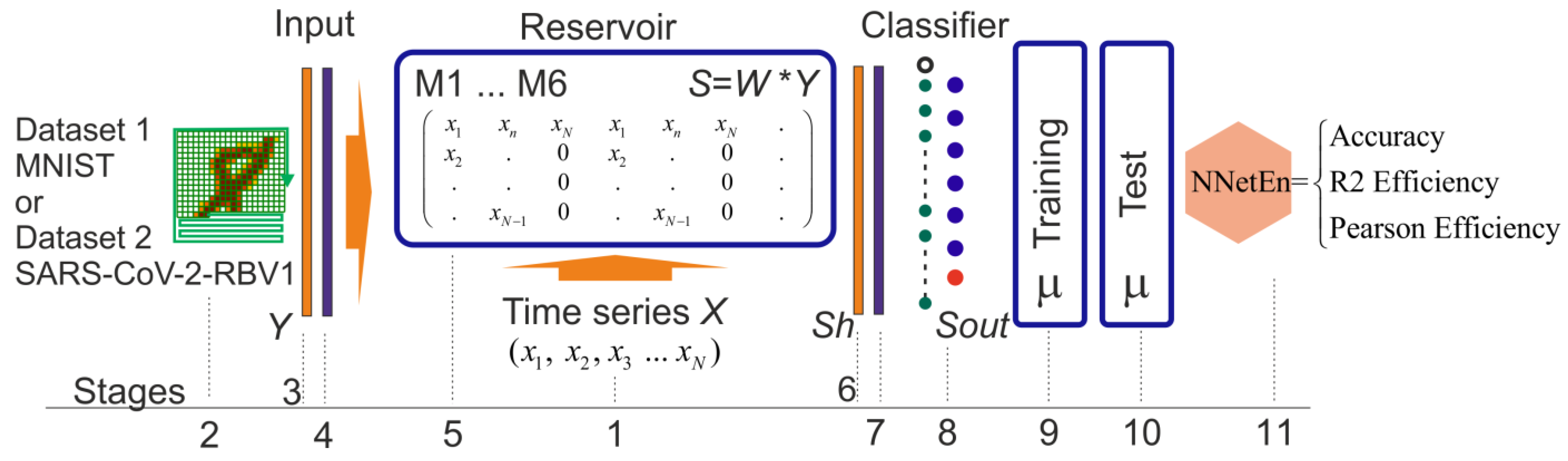
2.3. NNetEn Calculation
| (a) | (b) |
|
|
2.4. Entropy Settings Options in Python
- SVDEn (m = 2, delay = 1);
- PermEn (m = 4, delay = 2);
- SampEn (m = 2, r = 0.2∙d, τ = 1), where d is standard deviation of the time series;
- CoSiEn (m = 3, r = 0.1, τ = 1);
- FuzzyEn (m = 1, r = 0.2∙d, r2 = 3, τ = 1), where d is standard deviation of the time series and r2 is fuzzy membership function’s exponent;
- PhaseEn (K = 3, τ = 2);
- DistEn (m = 3, bins = 100, τ = 1);
- BubbleEn (m = 6, τ = 1);
- GridEn (m = 10, τ = 1);
- IncEn (m = 4, q = 6, τ = 1);
- AttnEn has no parameters;
2.5. Generation of Synthetic Time Series
2.6. Signal Separation Metrics
2.6.1. Statistical Analysis of Class Separation
2.6.2. Calculation of the Accuracy of Signal Classification by Entropy Features
- In the first stage, hyperparameters were selected using Repeated K-Fold cross-validation (RKF). In order to accomplish this, the original dataset was divided into K = 5 folds in N = 5 ways. The K-folds of each of the N variants of partitions were filled differently with samples. In addition, the distribution of classes in each K-fold approximated the distribution in the original dataset. Next, the classifier hyperparameters were selected at which the average accuracy of the classifier on the validation set was maximized. As a result of using a large number of training and validation sets, repeated K-Fold cross-validation allows minimize the overfitting of the model.
- As a second step, we used the hyperparameter values obtained in the first stage and performed RKF cross-validation (K = 5) in a similar manner to the first stage, but using different N = 10 partitions. As a result, the ARKF is calculated by averaging N partitioned scores. We used ARKF as a metric to assess signal separation.
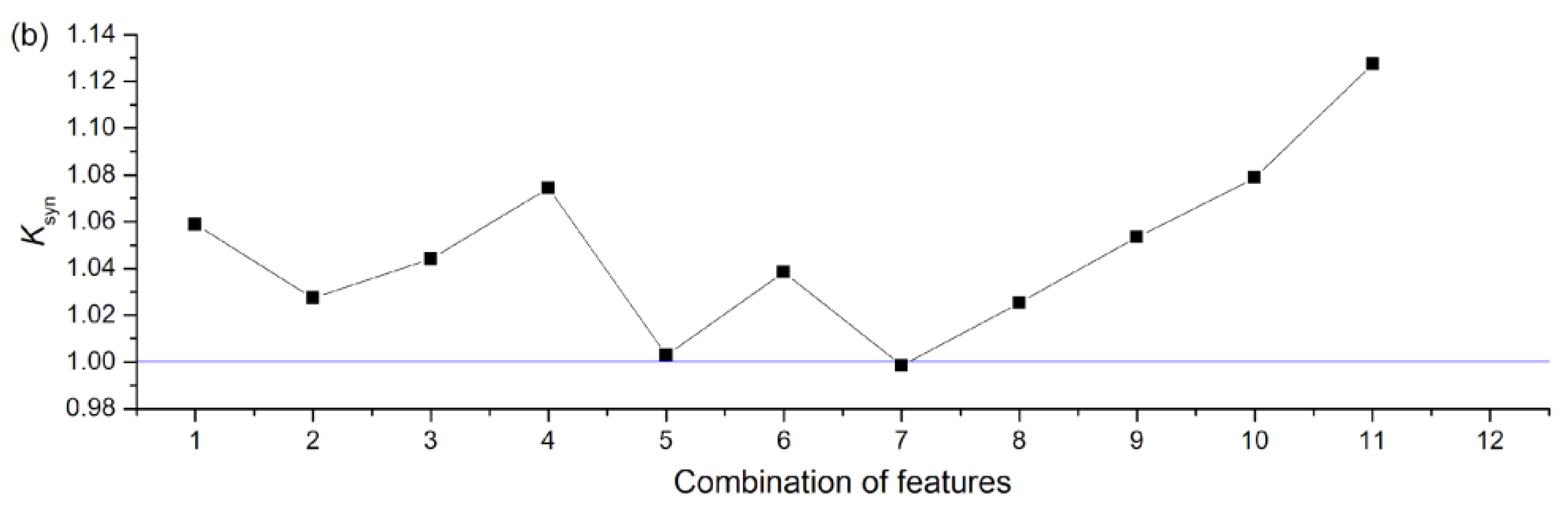
2.6.3. Synergy Effect Metric
2.7. Python Package for NNetEn Calculation
2.7.1. General Requirements
- NumPy
- Numba
2.7.2. Function Syntax
| pip install NNetEn |
| > > > from NNetEn import NNetEn_entropy > > > NNetEn = NNetEn_entropy(database = ‘D1’, mu = 1) |
- database— (default = D1) Select dataset, D1—MNIST, D2—SARS-CoV-2-RBV1
- mu— (default = 1) usage fraction of the selected dataset μ (0.01, …, 1).
| > > > value = NNetEn.calculation(time_series, epoch = 20, method = 3, metric = ’Acc’, log = False) |
- time_series—input data with a time series in numpy array format.
- epoch— (default epoch = 20). The number of training epochs for the LogNNet neural network, with a number greater than 0.
- method— (default method = 3). One of 6 methods for forming a reservoir matrix from the time series M1, …, M6.
- metric —(default metric = ‘Acc’). See Section 2.2 for neural network testing metrics. Options: metric = ‘Acc’, metric = ‘R2E’, metric = ‘PE’ (see Equation (6)).
- log— (default = False) Parameter for logging the main data used in the calculation. Recording is done in log.txt file
3. Numerical Results and Discussion
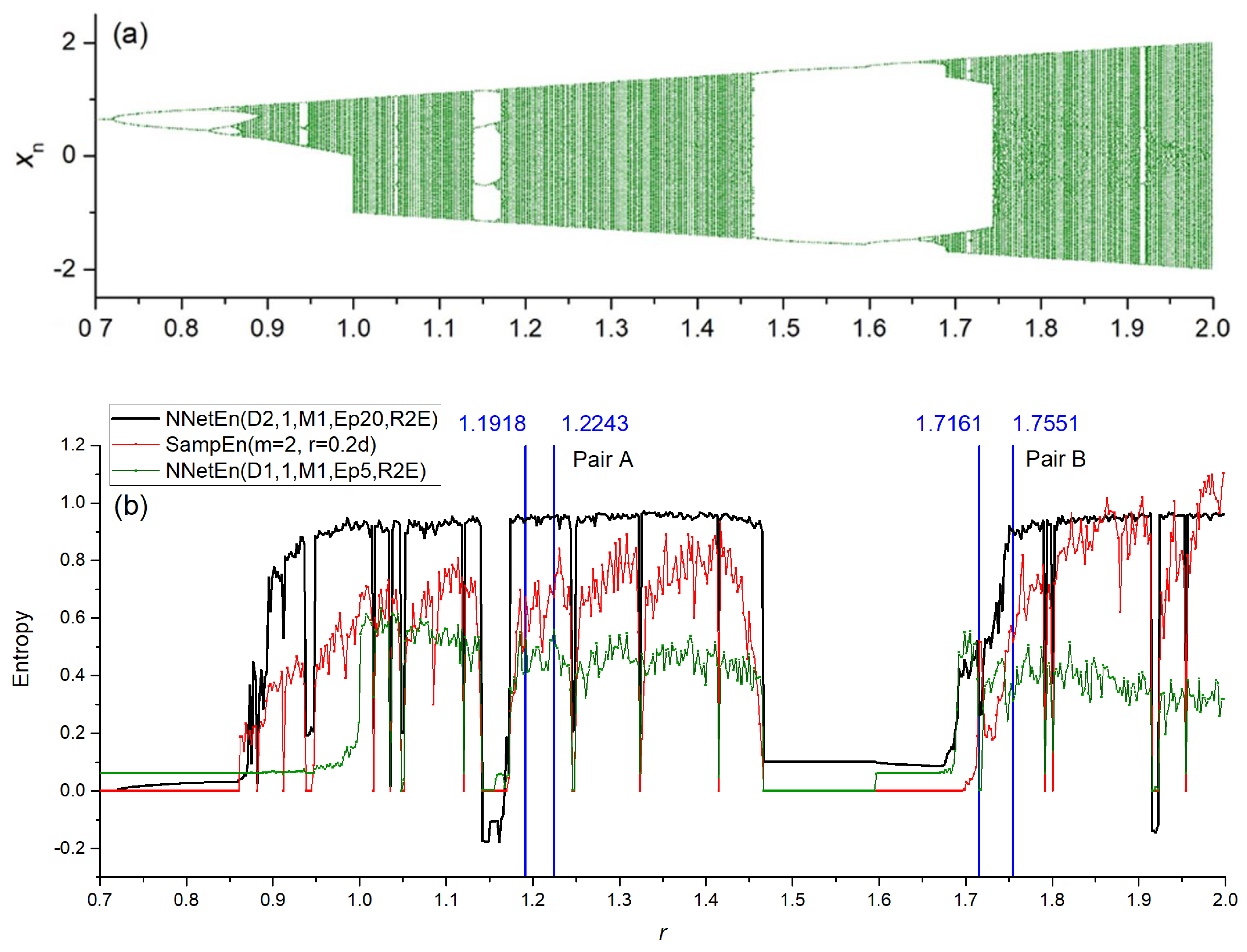
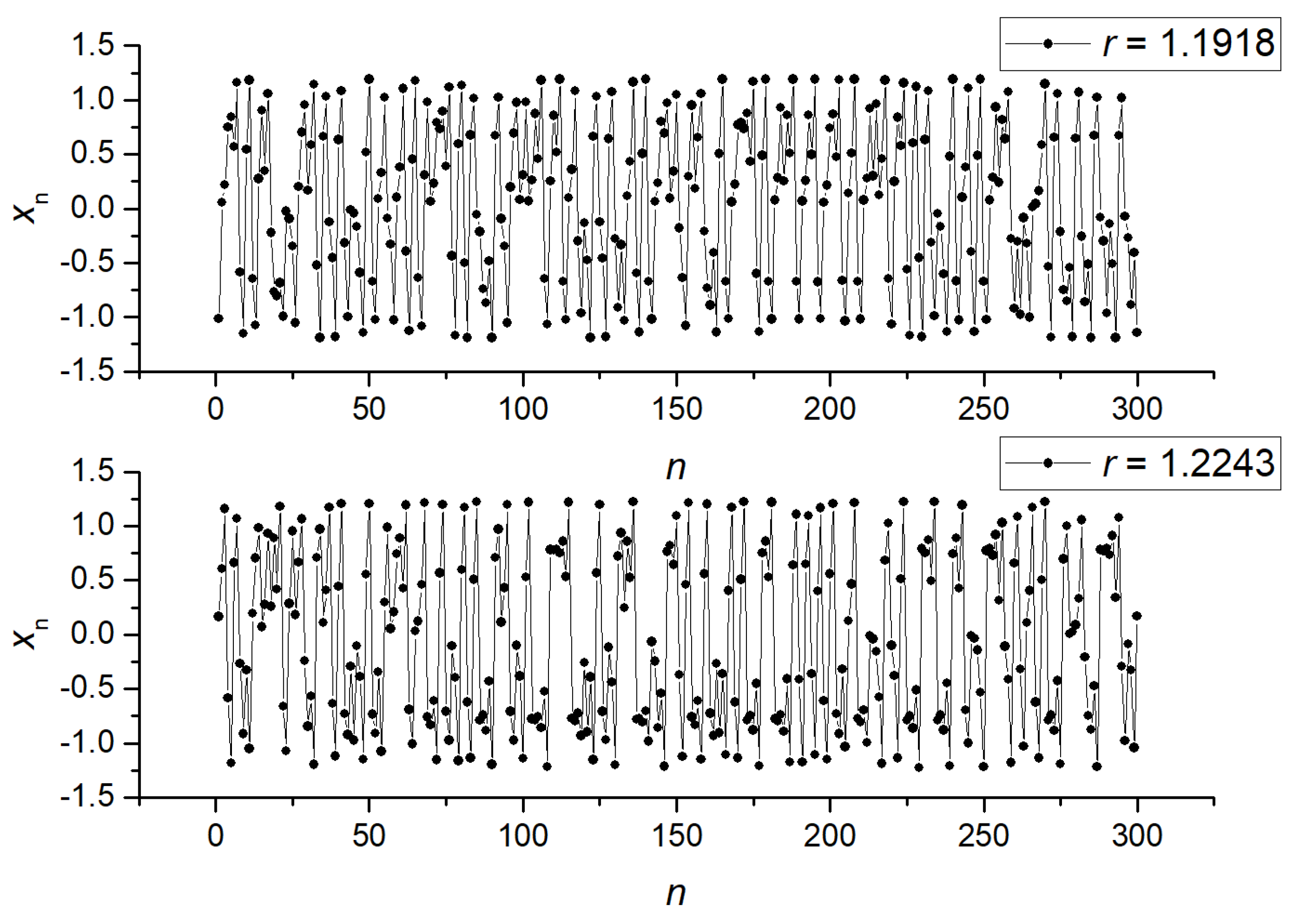
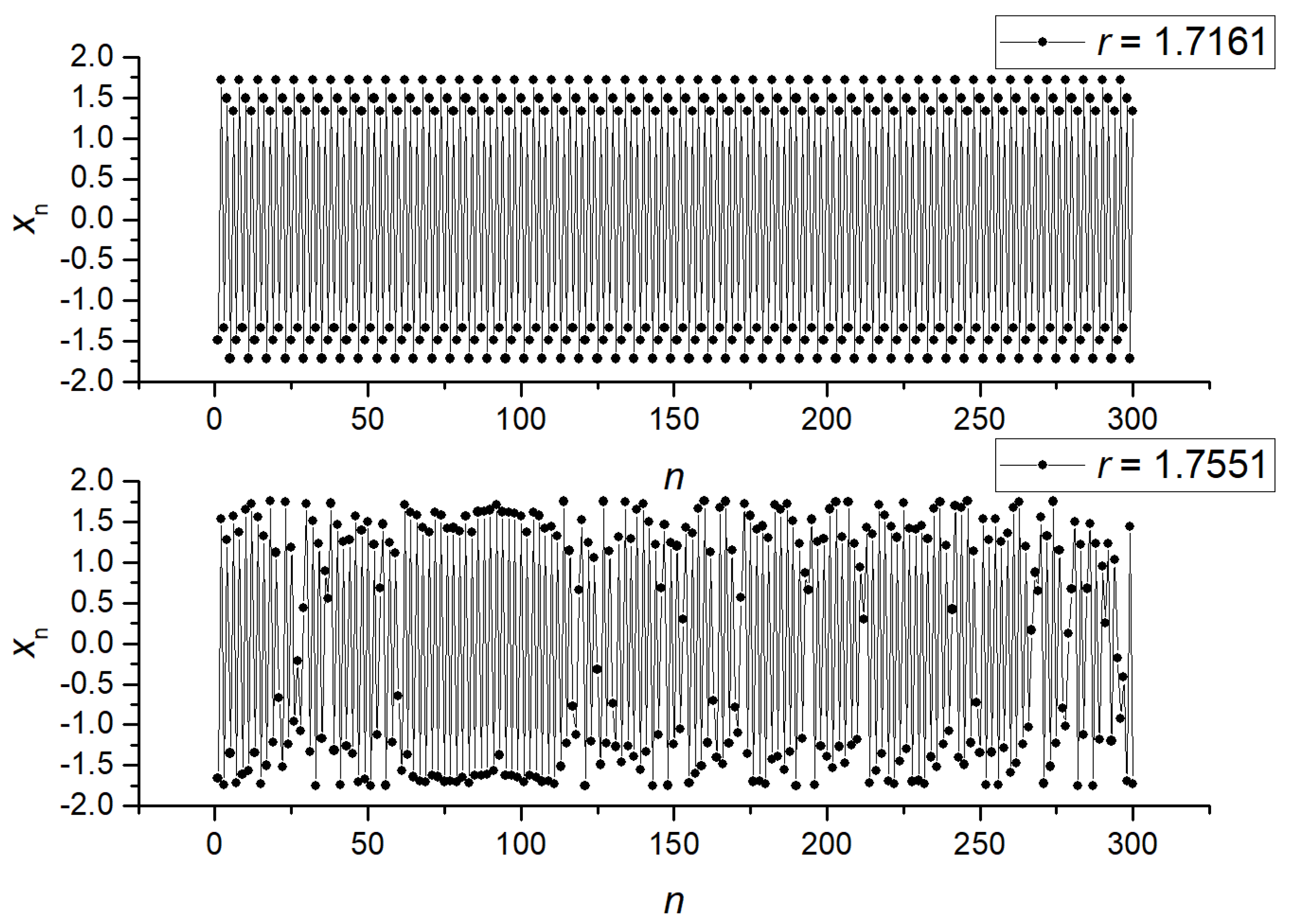
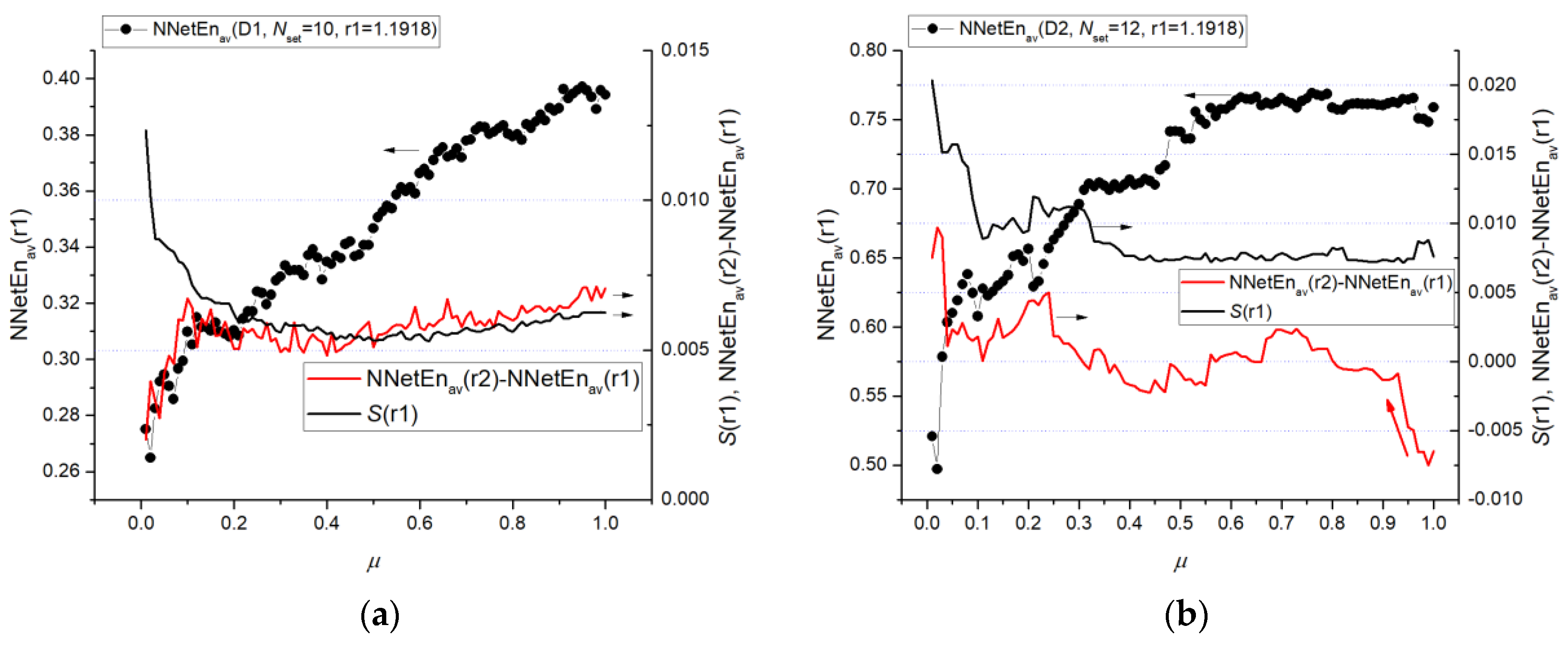
3.1. Separation of Synthetic Signals
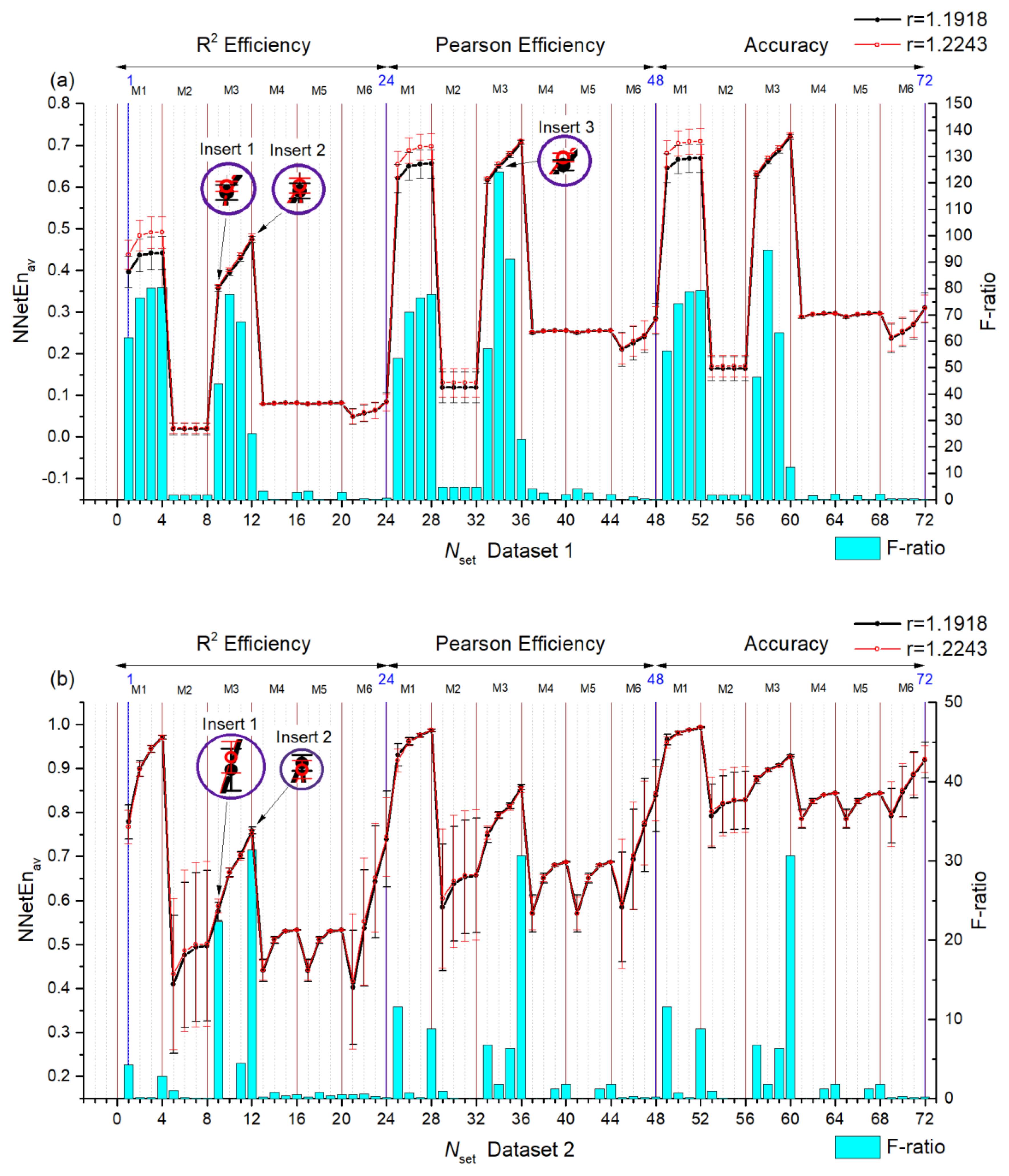
3.2. Entropy Combinations
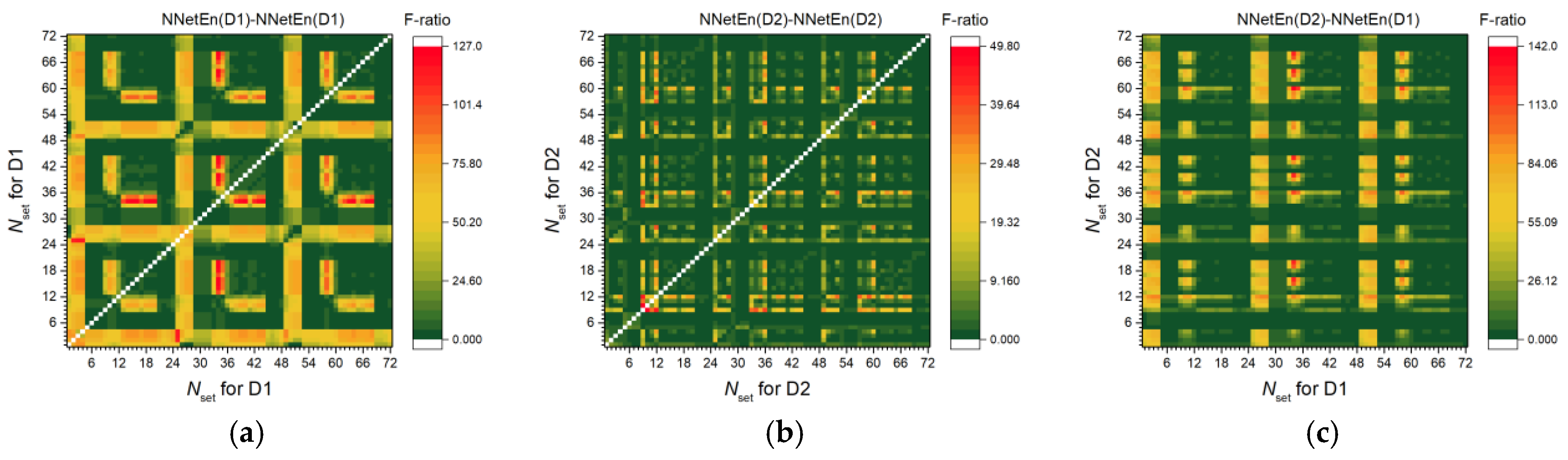
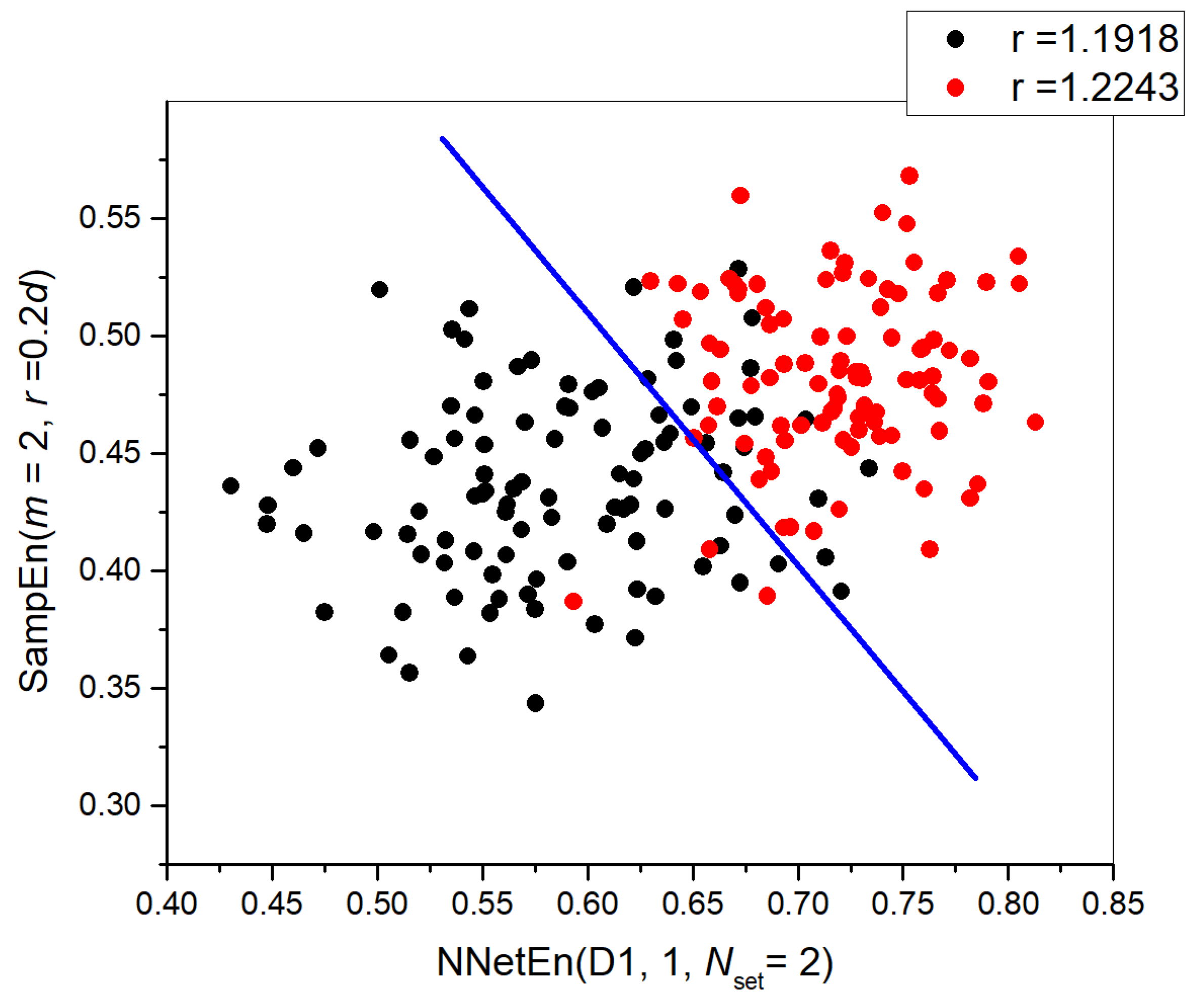
3.2.1. Entropy Difference NNetEn as a Feature for Signal Separation
3.2.2. NNetEn as a Paired Feature in Signal Classification
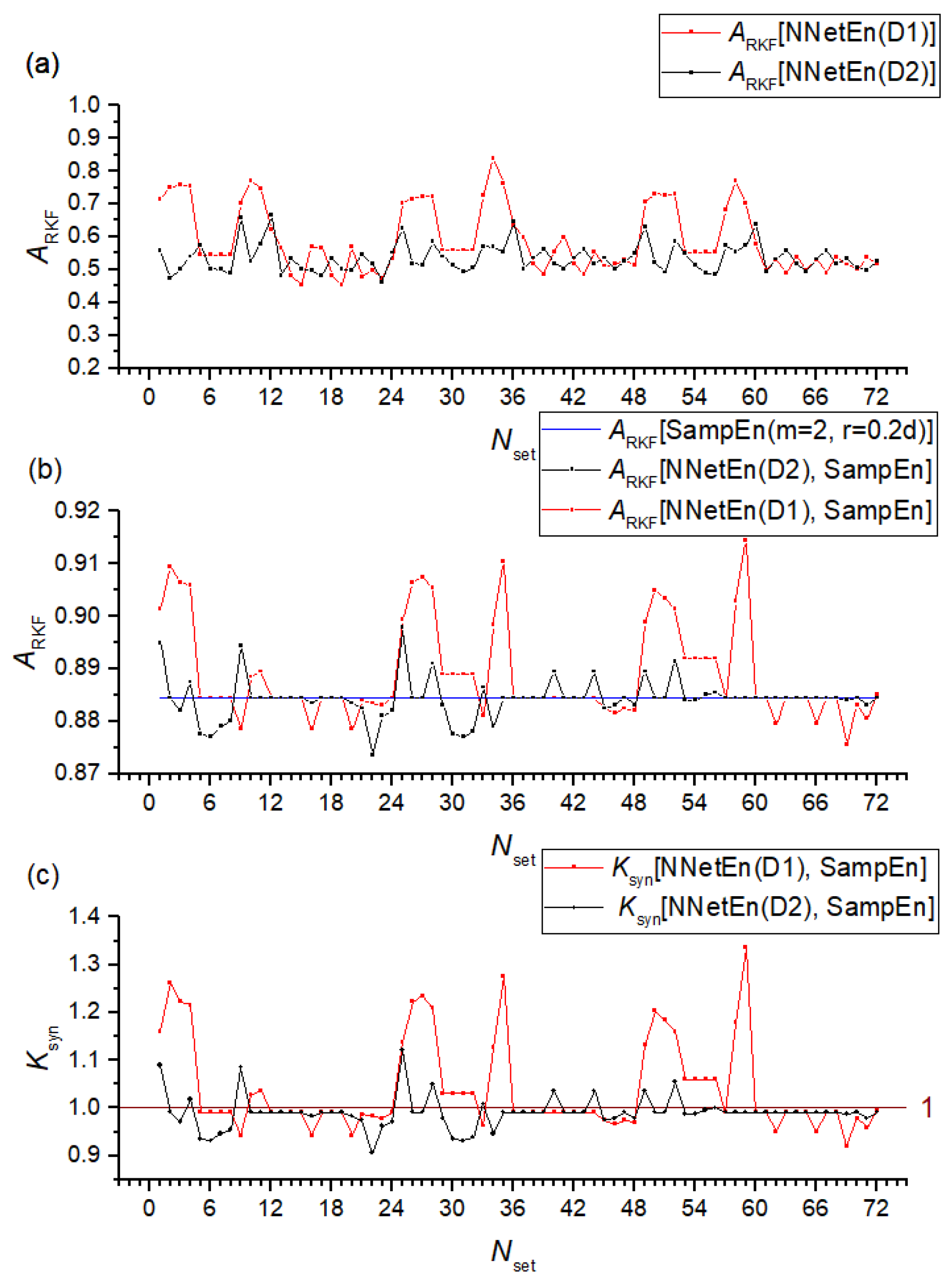
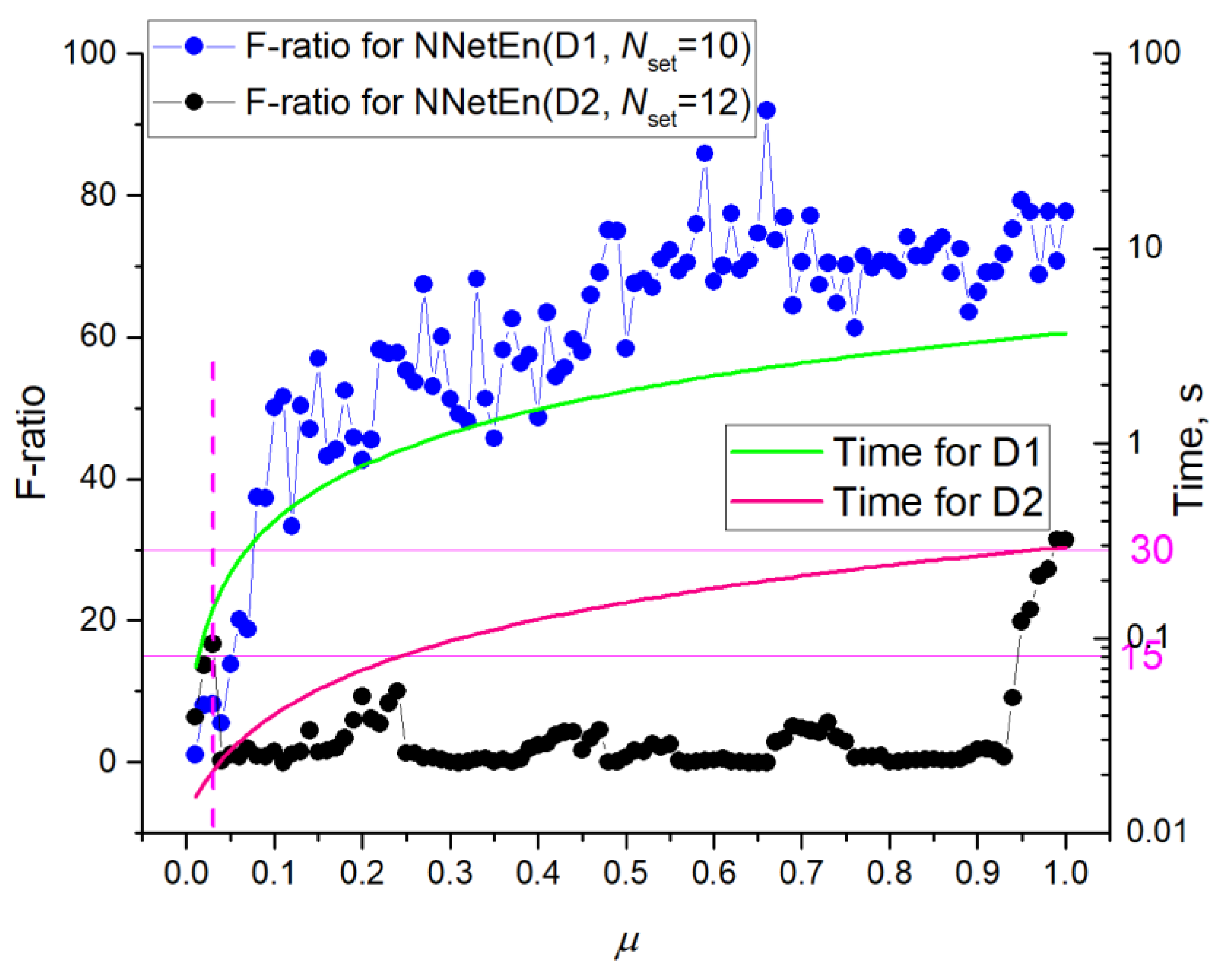
3.3. Dependence of F-Ratio and Algorithm Speed on Dataset Size
3.4. EEG Signal Separation
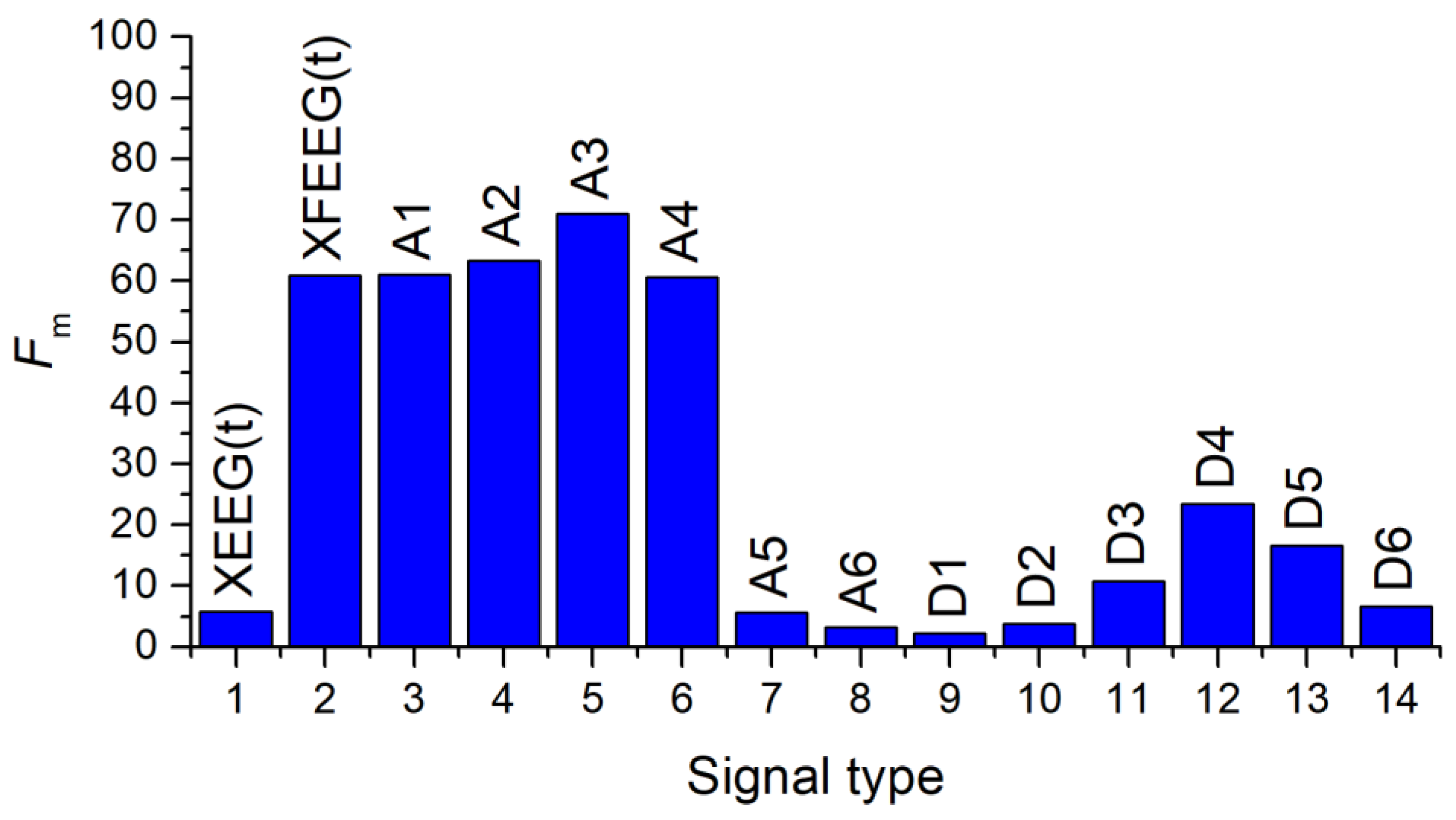
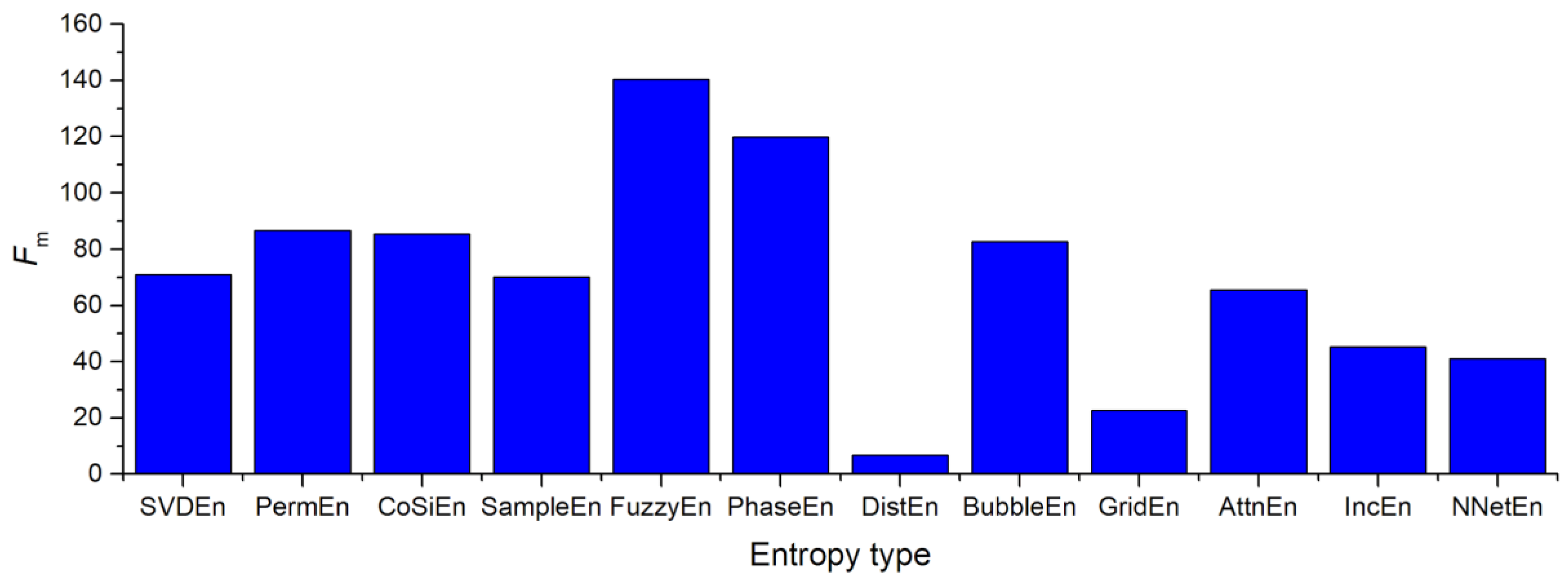
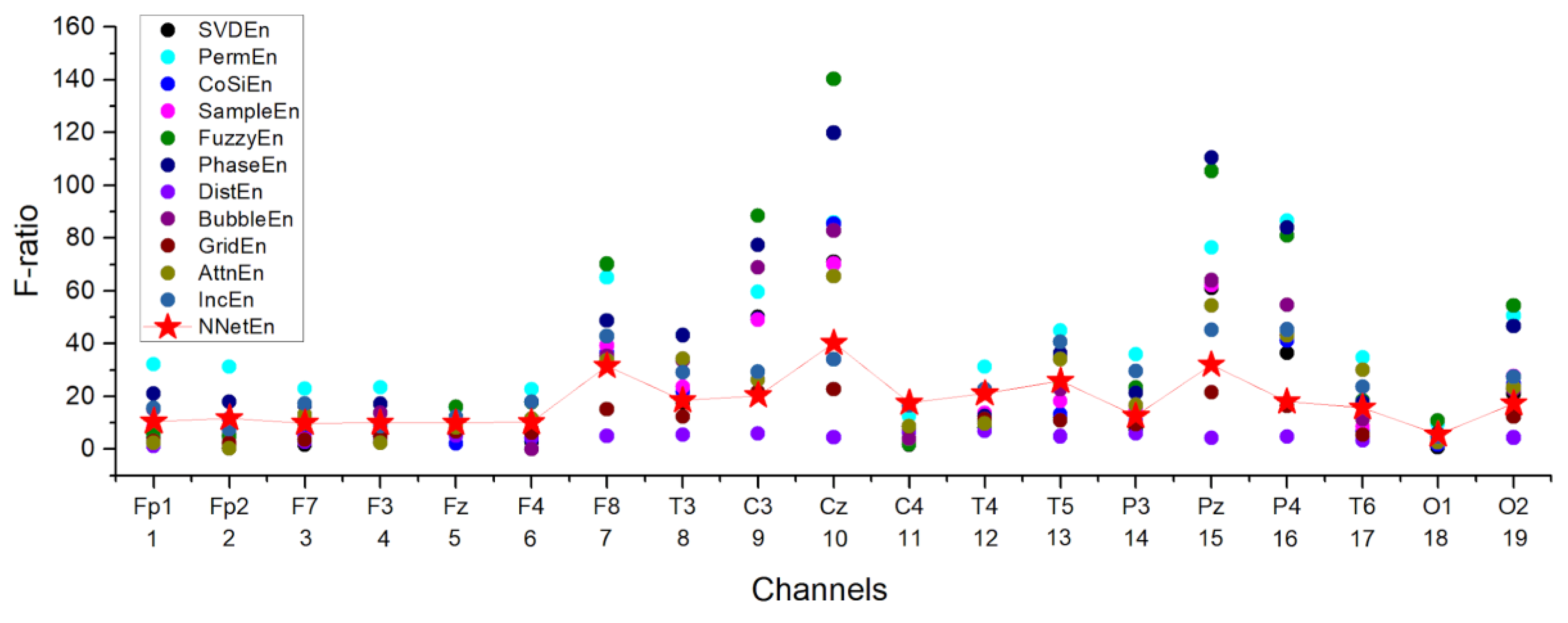
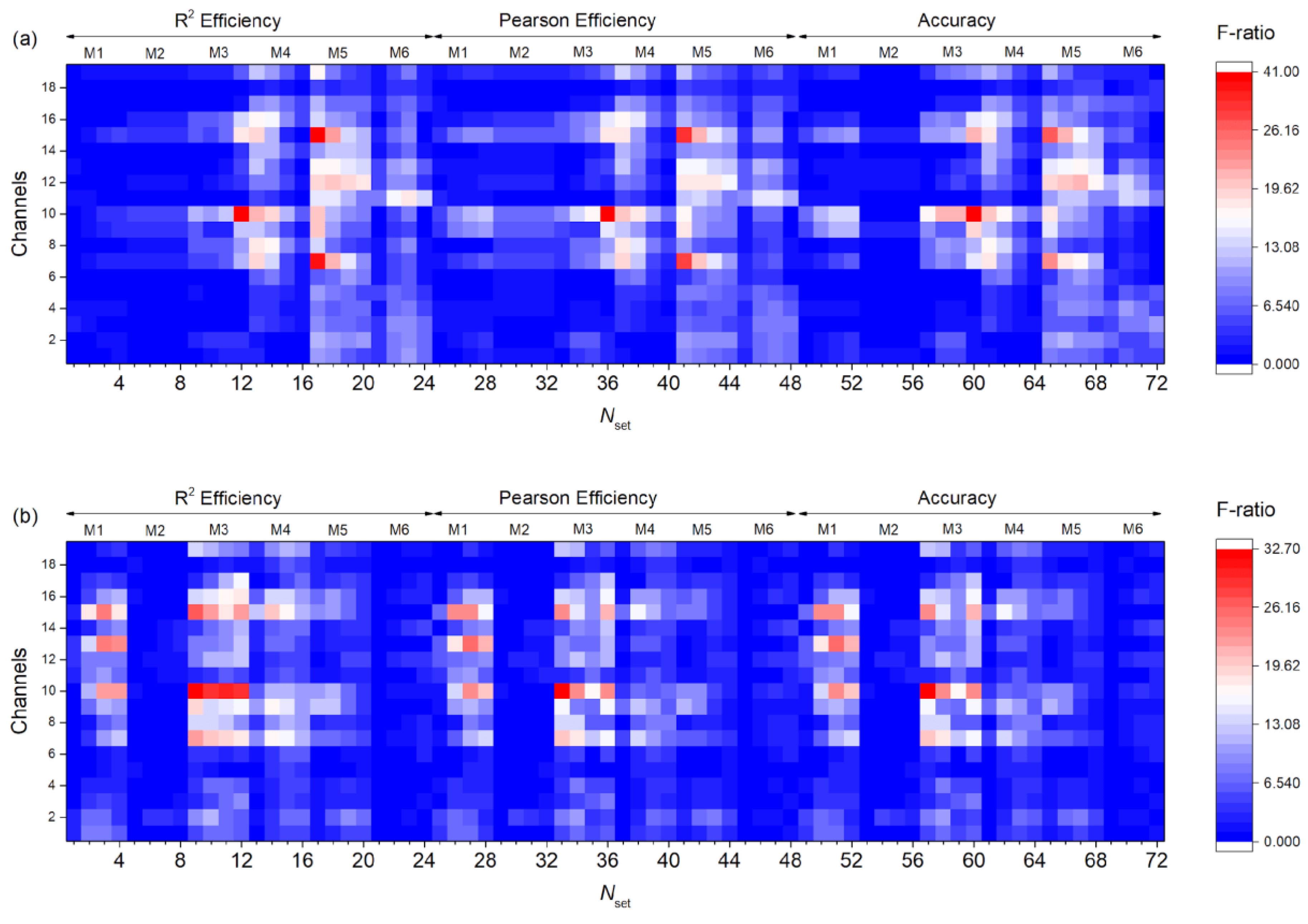
3.4.1. Selection of the Most Informative Component of the EEG Signal
3.4.2. Influence of the Entropy Calculation Method on the Separation of EEG Signals
3.5. Features of the Python Execution of the NNetEn Algorithm
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ribeiro, M.; Henriques, T.; Castro, L.; Souto, A.; Antunes, L.; Costa-Santos, C.; Teixeira, A. The Entropy Universe. Entropy 2021, 23, 222. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, T.; Parentani, R. Horizon Entropy. Found. Phys. 2003, 33, 323–348. [Google Scholar] [CrossRef]
- Bejan, A. Discipline in thermodynamics. Energies 2020, 13, 2487. [Google Scholar] [CrossRef]
- Bagnoli, F. Thermodynamics, entropy and waterwheels. arXiv 2016, arXiv:1609.05090, 1–18. [Google Scholar] [CrossRef]
- Karmakar, C.; Udhayakumar, R.K.; Li, P.; Venkatesh, S.; Palaniswami, M. Stability, consistency and performance of distribution entropy in analysing short length heart rate variability (HRV) signal. Front. Physiol. 2017, 8, 720. [Google Scholar] [CrossRef]
- Yang, F.; Bo, H.; Tang, Q. Approximate Entropy and Its Application to Biosignal Analysis. Nonlinear Biomed. Signal Process. 2000, 22, 72–91. [Google Scholar]
- Bakhchina, A.V.; Arutyunova, K.R.; Sozinov, A.A.; Demidovsky, A.V.; Alexandrov, Y.I. Sample entropy of the heart rate reflects properties of the system organization of behaviour. Entropy 2018, 20, 449. [Google Scholar] [CrossRef]
- Tonoyan, Y.; Looney, D.; Mandic, D.P.; Van Hulle, M.M. Discriminating multiple emotional states from EEG using a data-adaptive, multiscale information-theoretic approach. Int. J. Neural Syst. 2016, 26, 1650005. [Google Scholar] [CrossRef]
- Nezafati, M.; Temmar, H.; Keilholz, S.D. Functional MRI signal complexity analysis using sample entropy. Front. Neurosci. 2020, 14, 700. [Google Scholar] [CrossRef]
- Chanwimalueang, T.; Mandic, D.P. Cosine Similarity Entropy: Self-Correlation-Based Complexity Analysis of Dynamical Systems. Entropy 2017, 19, 652. [Google Scholar] [CrossRef]
- Simons, S.; Espino, P.; Abásolo, D. Fuzzy Entropy analysis of the electroencephalogram in patients with Alzheimer’s disease: Is the method superior to Sample Entropy? Entropy 2018, 20, 21. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.-B.; Chen, W.-T.; He, W.-X.; Liu, H. Complexity analysis of the biomedical signal using fuzzy entropy measurement. Appl. Soft Comput. 2011, 11, 2871–2879. [Google Scholar] [CrossRef]
- Chiang, H.-S.; Chen, M.-Y.; Huang, Y.-J. Wavelet-Based EEG Processing for Epilepsy Detection Using Fuzzy Entropy and Associative Petri Net. IEEE Access 2019, 7, 103255–103262. [Google Scholar] [CrossRef]
- Patel, P.; Raghunandan, R.; Annavarapu, R.N. EEG-based human emotion recognition using entropy as a feature extraction measure. Brain Inform. 2021, 8, 20. [Google Scholar] [CrossRef]
- Hussain, L.; Aziz, W.; Alshdadi, A.; Nadeem, M.; Khan, I.; Chaudhry, Q.-A. Analyzing the Dynamics of Lung Cancer Imaging Data Using Refined Fuzzy Entropy Methods by Extracting Different Features. IEEE Access 2019, 7, 64704–64721. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, K.; Zheng, D.; Liu, C.; Hou, Y. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 2015, 53, 77–87. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Manis, G.; Aktaruzzaman, M.; Sassi, R. Bubble Entropy: An entropy almost free of parameters. IEEE Trans. Biomed. Eng. 2017, 64, 2711–2718. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, A.; Xu, N.; Xue, J. Increment entropy as a measure of complexity for time series. Entropy 2016, 18, 22. [Google Scholar] [CrossRef]
- Banerjee, M.; Pal, N.R. Feature selection with SVD entropy: Some modification and extension. Inf. Sci. 2014, 264, 118–134. [Google Scholar] [CrossRef]
- Li, S.; Yang, M.; Li, C.; Cai, P. Analysis of heart rate variability based on singular value decomposition entropy. J. Shanghai Univ. Engl. Ed. 2008, 12, 433–437. [Google Scholar] [CrossRef]
- Yan, C.; Li, P.; Liu, C.; Wang, X.; Yin, C.; Yao, L. Novel gridded descriptors of poincaré plot for analyzing heartbeat interval time-series. Comput. Biol. Med. 2019, 109, 280–289. [Google Scholar] [CrossRef] [PubMed]
- Rohila, A.; Sharma, A. Phase entropy: A new complexity measure for heart rate variability. Physiol. Meas. 2019, 40, 105006. [Google Scholar] [CrossRef]
- Yang, J.; Choudhary, G.I.; Rahardja, S.; Franti, P. Classification of interbeat interval time-series using attention entropy. IEEE Trans. Affect. Comput. 2023, 14, 321–330. [Google Scholar] [CrossRef]
- Velichko, A.; Heidari, H. A Method for Estimating the Entropy of Time Series Using Artificial Neural Networks. Entropy 2021, 23, 1432. [Google Scholar] [CrossRef]
- Velichko, A. Neural network for low-memory IoT devices and MNIST image recognition using kernels based on logistic map. Electronics 2020, 9, 1432. [Google Scholar] [CrossRef]
- Heidari, H.; Velichko, A.A. An improved LogNNet classifier for IoT applications. J. Phys. Conf. Ser. 2021, 2094, 32015. [Google Scholar] [CrossRef]
- Heidari, H.; Velichko, A.; Murugappan, M.; Chowdhury, M.E.H. Novel techniques for improving NNetEn entropy calculation for short and noisy time series. Nonlinear Dyn. 2023, 111, 9305–9326. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C. MNIST Handwritten Digit Database. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 9 November 2018).
- Li, G.; Liu, F.; Yang, H. Research on feature extraction method of ship radiated noise with K-nearest neighbor mutual information variational mode decomposition, neural network estimation time entropy and self-organizing map neural network. Measurement 2022, 199, 111446. [Google Scholar] [CrossRef]
- Heidari, H. Biomedical Signal Analysis Using Entropy Measures: A Case Study of Motor Imaginary BCI in End Users with Disability BT—Biomedical Signals Based Computer-Aided Diagnosis for Neurological Disorders; Murugappan, M., Rajamanickam, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 145–164. ISBN 978-3-030-97845-7. [Google Scholar]
- Velichko, A.; Wagner, M.P.; Taravat, A.; Hobbs, B.; Ord, A. NNetEn2D: Two-Dimensional Neural Network Entropy in Remote Sensing Imagery and Geophysical Mapping. Remote Sens. 2022, 14, 2166. [Google Scholar] [CrossRef]
- Boriskov, P.; Velichko, A.; Shilovsky, N.; Belyaev, M. Bifurcation and Entropy Analysis of a Chaotic Spike Oscillator Circuit Based on the S-Switch. Entropy 2022, 24, 1693. [Google Scholar] [CrossRef] [PubMed]
- Oludehinwa, I.A.; Velichko, A.; Ogunsua, B.O.; Olusola, O.I.; Odeyemi, O.O.; Njah, A.N.; Ologun, O.T. Dynamical complexity response in Traveling Ionospheric Disturbances across Eastern Africa sector during geomagnetic storms using Neural Network Entropy. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030630. [Google Scholar] [CrossRef]
- Huyut, M.T.; Velichko, A. Diagnosis and Prognosis of COVID-19 Disease Using Routine Blood Values and LogNNet Neural Network. Sensors 2022, 22, 4820. [Google Scholar] [CrossRef] [PubMed]
- Miltiadous, A.; Tzimourta, K.D.; Giannakeas, N.; Tsipouras, M.G.; Afrantou, T.; Ioannidis, P.; Tzallas, A.T. Alzheimer’s disease and frontotemporal dementia: A robust classification method of EEG signals and a comparison of validation methods. Diagnostics 2021, 11, 1437. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Dang, W.; Wang, X.; Hong, X.; Hou, L.; Ma, K.; Perc, M. Complex networks and deep learning for EEG signal analysis. Cogn. Neurodyn. 2021, 15, 369–388. [Google Scholar] [CrossRef] [PubMed]
- Murugappan, M.; Murugappan, S. Human emotion recognition through short time Electroencephalogram (EEG) signals using Fast Fourier Transform (FFT). In Proceedings of the 2013 IEEE 9th International Colloquium on Signal Processing and its Applications, Kuala Lumpur, Malaysia, 8–10 March 2013; pp. 289–294. [Google Scholar]
- Amin, H.U.; Malik, A.S.; Ahmad, R.F.; Badruddin, N.; Kamel, N.; Hussain, M.; Chooi, W.-T. Feature extraction and classification for EEG signals using wavelet transform and machine learning techniques. Australas. Phys. Eng. Sci. Med. 2015, 38, 139–149. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E.W. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. Based Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Gopika Gopan, K.; Neelam, S.; Dinesh Babu, J. Statistical feature analysis for EEG baseline classification: Eyes Open vs Eyes Closed. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 2466–2469. [Google Scholar]
- Hosseini, M.-P.; Hosseini, A.; Ahi, K. A Review on Machine Learning for EEG Signal Processing in Bioengineering. IEEE Rev. Biomed. Eng. 2021, 14, 204–218. [Google Scholar] [CrossRef]
- Markoulidakis, I.; Rallis, I.; Georgoulas, I.; Kopsiaftis, G.; Doulamis, A.; Doulamis, N. Multiclass Confusion Matrix Reduction Method and Its Application on Net Promoter Score Classification Problem. Technologies 2021, 9, 81. [Google Scholar] [CrossRef]
- Nath, R.K.; Thapliyal, H.; Caban-Holt, A. Machine learning based stress monitoring in older adults using wearable sensors and cortisol as stress biomarker. J. Signal Process. Syst. 2022, 94, 513–525. [Google Scholar] [CrossRef]
- Miltiadous, A.; Tzimourta, K.D.; Afrantou, T.; Ioannidis, P.; Grigoriadis, N.; Tsalikakis, D.G.; Angelidis, P.; Tsipouras, M.G.; Glavas, E.; Giannakeas, N.; et al. A Dataset of 88 EEG Recordings From: Alzheimer’s Disease, Frontotemporal Dementia and Healthy Subjects. 2023. Available online: https://openneuro.org/datasets/ds004504/versions/1.0.4 (accessed on 1 May 2023).
- Flood, M.W.; Grimm, B. EntropyHub: An open-source toolkit for entropic time series analysis. PLoS ONE 2021, 16, e0259448. [Google Scholar] [CrossRef] [PubMed]
- Vallat, R. AntroPy: Entropy and Complexity of (EEG) Time-Series in Python. Available online: https://github.com/raphaelvallat/antropy (accessed on 26 April 2023).
- Numba: A High Performance Python Compiler. Available online: https://numba.pydata.org/ (accessed on 26 April 2023).
- Obukhov, Y.V.; Kershner, I.A.; Tolmacheva, R.A.; Sinkin, M.V.; Zhavoronkova, L.A. Wavelet ridges in EEG diagnostic features extraction: Epilepsy long-time monitoring and rehabilitation after traumatic brain injury. Sensors 2021, 21, 5989. [Google Scholar] [CrossRef] [PubMed]
- Motamedi-Fakhr, S.; Moshrefi-Torbati, M.; Hill, M.; Simpson, D.; Bucks, R.S.; Carroll, A.; Hill, C.M. Respiratory cycle related EEG changes: Modified respiratory cycle segmentation. Biomed. Signal Process. Control 2013, 8, 838–844. [Google Scholar] [CrossRef]



| Tools Used for Calculation | Time (s) Dataset 1, μ = 1 | Time (s) Dataset 2, μ = 1 |
|---|---|---|
| Delphi | 6.14 | 0.085 |
| Python (NumPy + Numba) | 3.7 | 0.293 |
| Python (NumPy) | 11.5 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velichko, A.; Belyaev, M.; Izotov, Y.; Murugappan, M.; Heidari, H. Neural Network Entropy (NNetEn): Entropy-Based EEG Signal and Chaotic Time Series Classification, Python Package for NNetEn Calculation. Algorithms 2023, 16, 255. https://doi.org/10.3390/a16050255
Velichko A, Belyaev M, Izotov Y, Murugappan M, Heidari H. Neural Network Entropy (NNetEn): Entropy-Based EEG Signal and Chaotic Time Series Classification, Python Package for NNetEn Calculation. Algorithms. 2023; 16(5):255. https://doi.org/10.3390/a16050255
Chicago/Turabian StyleVelichko, Andrei, Maksim Belyaev, Yuriy Izotov, Murugappan Murugappan, and Hanif Heidari. 2023. "Neural Network Entropy (NNetEn): Entropy-Based EEG Signal and Chaotic Time Series Classification, Python Package for NNetEn Calculation" Algorithms 16, no. 5: 255. https://doi.org/10.3390/a16050255
APA StyleVelichko, A., Belyaev, M., Izotov, Y., Murugappan, M., & Heidari, H. (2023). Neural Network Entropy (NNetEn): Entropy-Based EEG Signal and Chaotic Time Series Classification, Python Package for NNetEn Calculation. Algorithms, 16(5), 255. https://doi.org/10.3390/a16050255










