CTprintNet: An Accurate and Stable Deep Unfolding Approach for Few-View CT Reconstruction
Abstract
1. Introduction
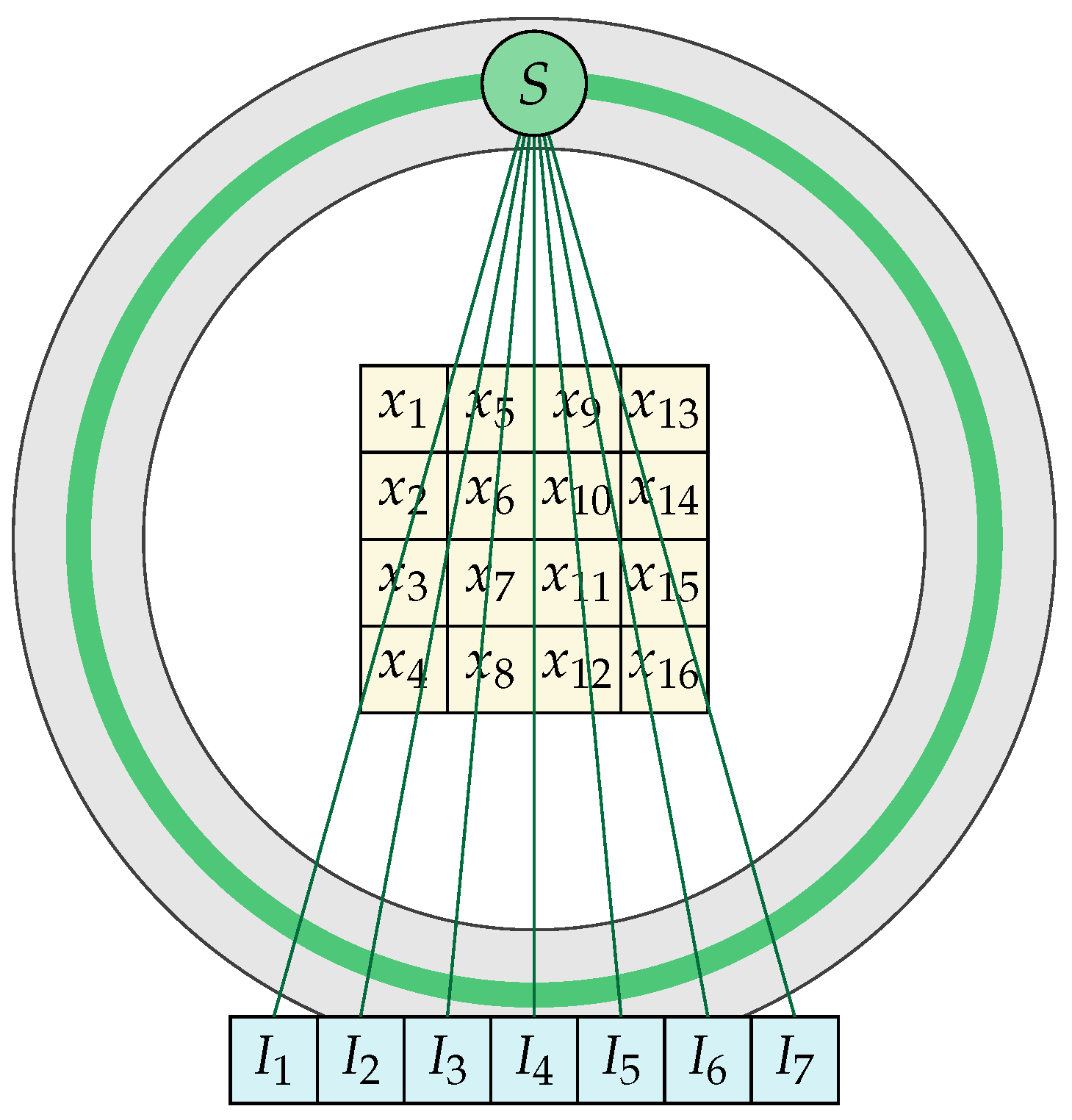
2. The Numerical Model
3. Proximal Interior Point Method for CT Reconstruction
| Algorithm 1: Proximal interior point algorithm. |
|
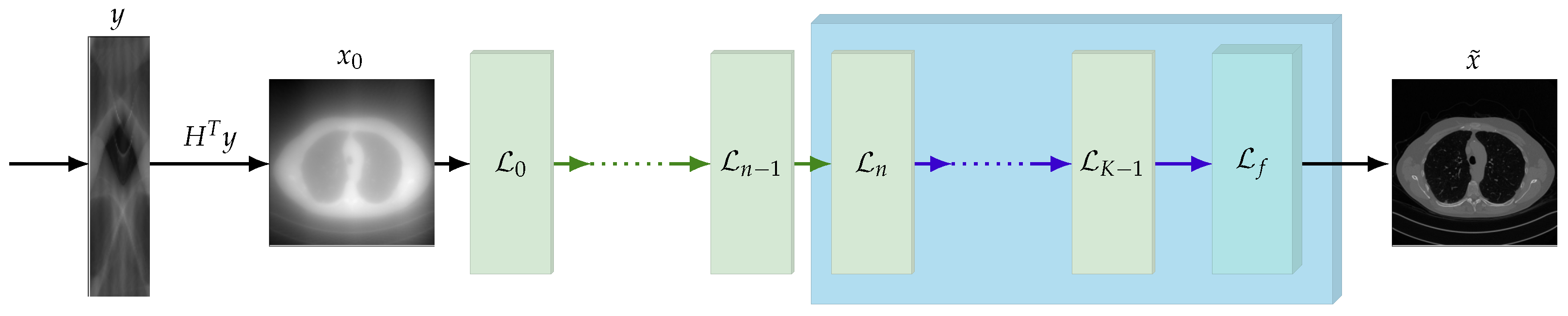
4. CTprintNet
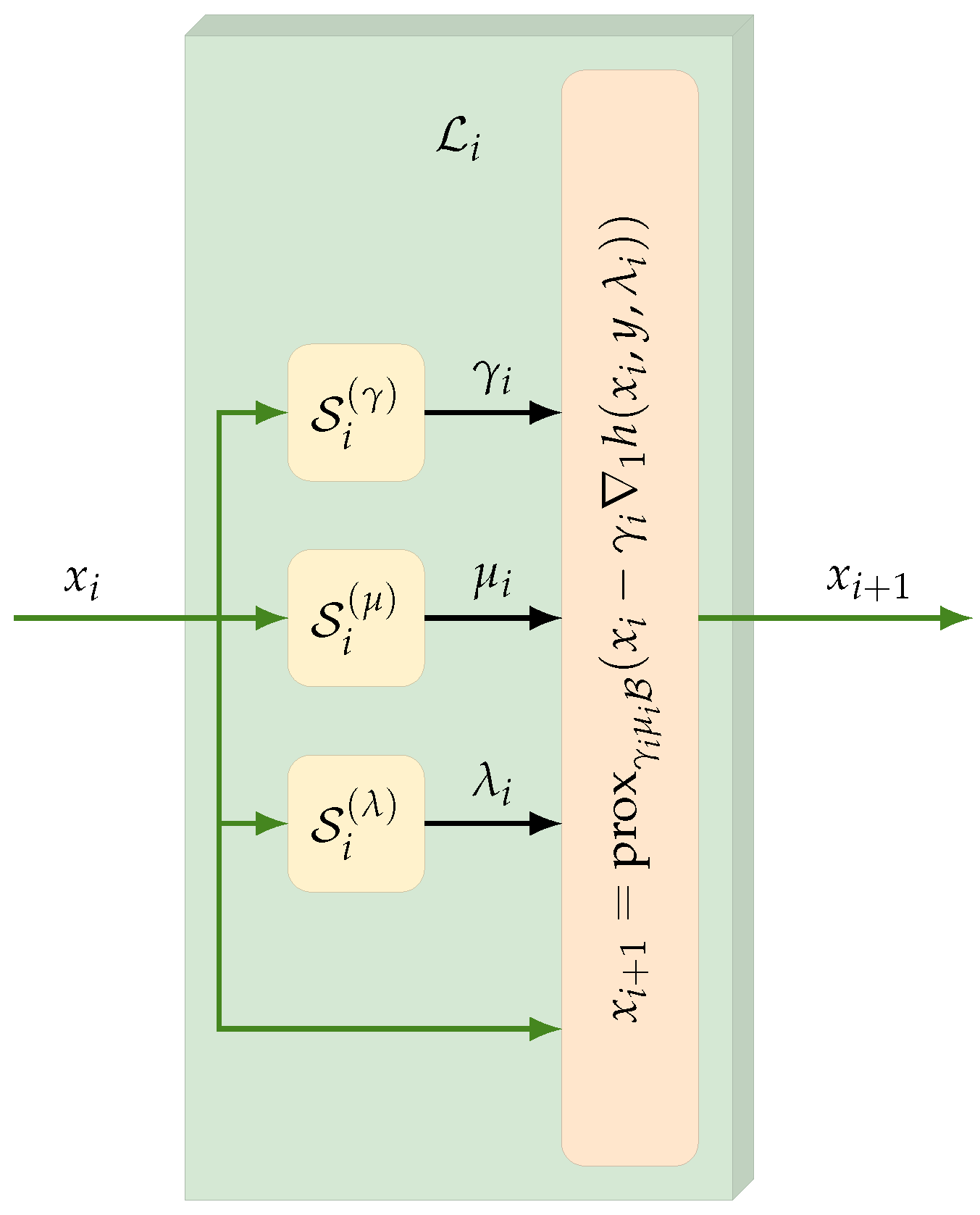
4.1. CTprintNet Architecture
- •
- Since the step size must be positive, this constraint is imposed by estimating the step size aswhere is a scalar parameter of the architecture learned during the training and the function is defined as
- •
- The barrier parameter is computed by twice alternating a convolutional layer and an average pooling layer, followed by a fully connected layer and a final Softplus activation function;
- •
- The regularization parameter is estimated as follows:where is the standard deviation of the concatenated spatial gradients of , are scalars learned by the architecture, and is the absolute value of the diagonal coefficients of the first-level Haar wavelet decomposition of y. The rationale behind this choice is to provide an initial guess from the ratio between the estimated data fidelity magnitude and the regularizer magnitude (represented by the noise level and the gradient variations, respectively), suitably adjusted by two learned constants.
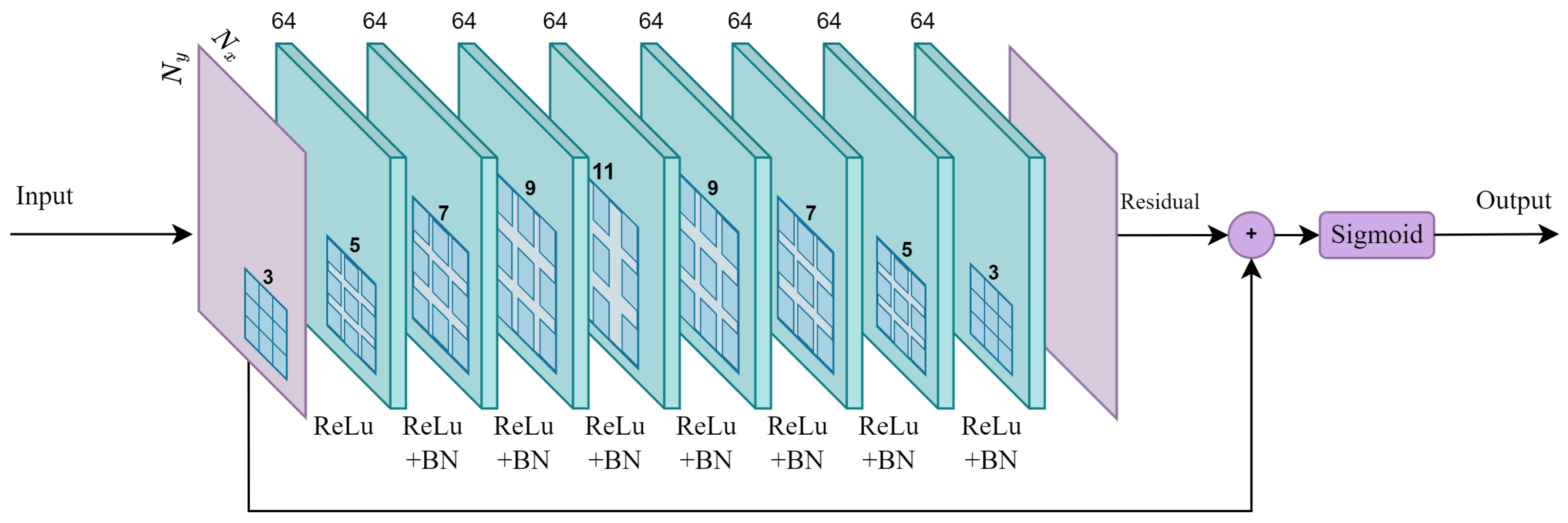
4.2. Forward/Backward Operators and Hyper-Parameter Setting
5. Results and Discussion
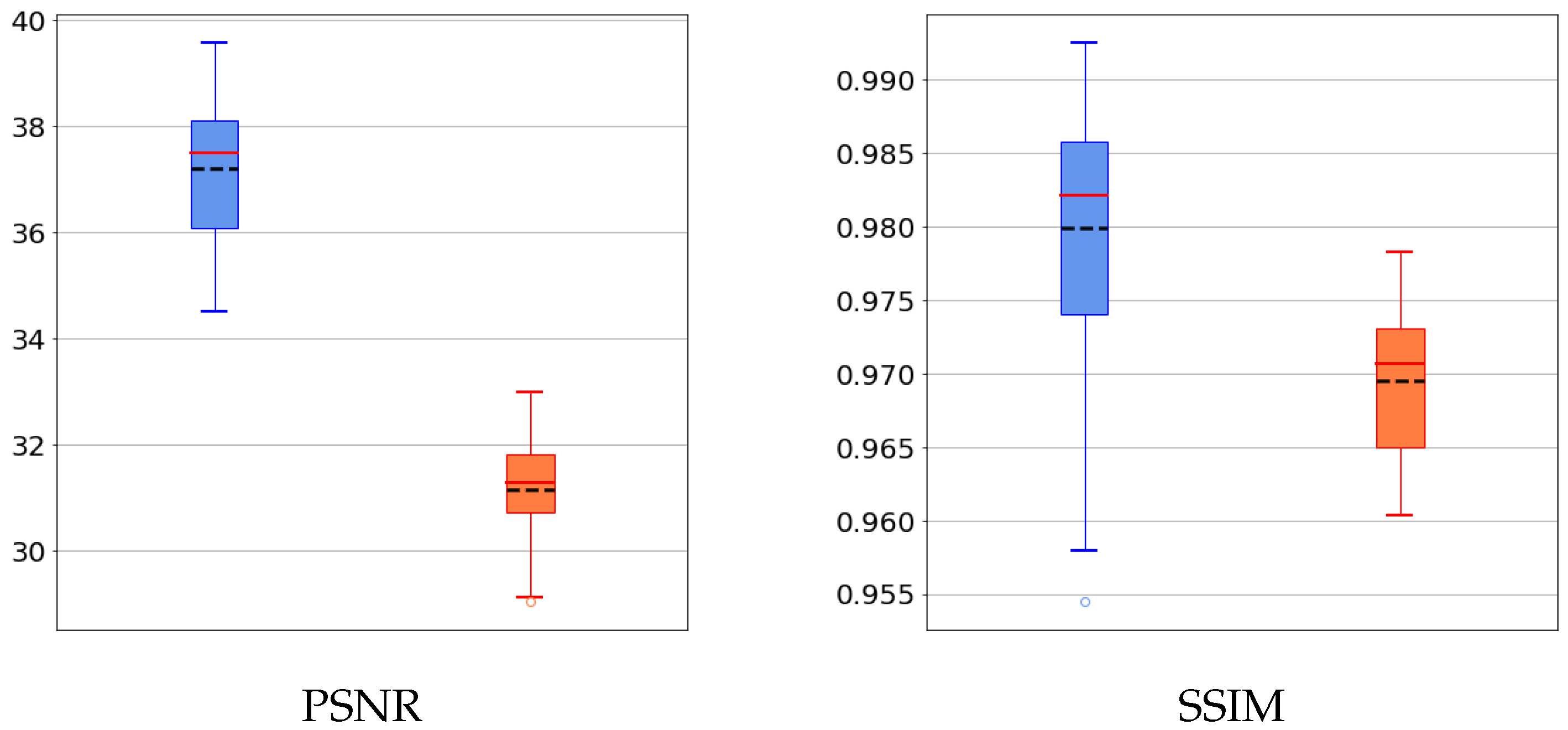
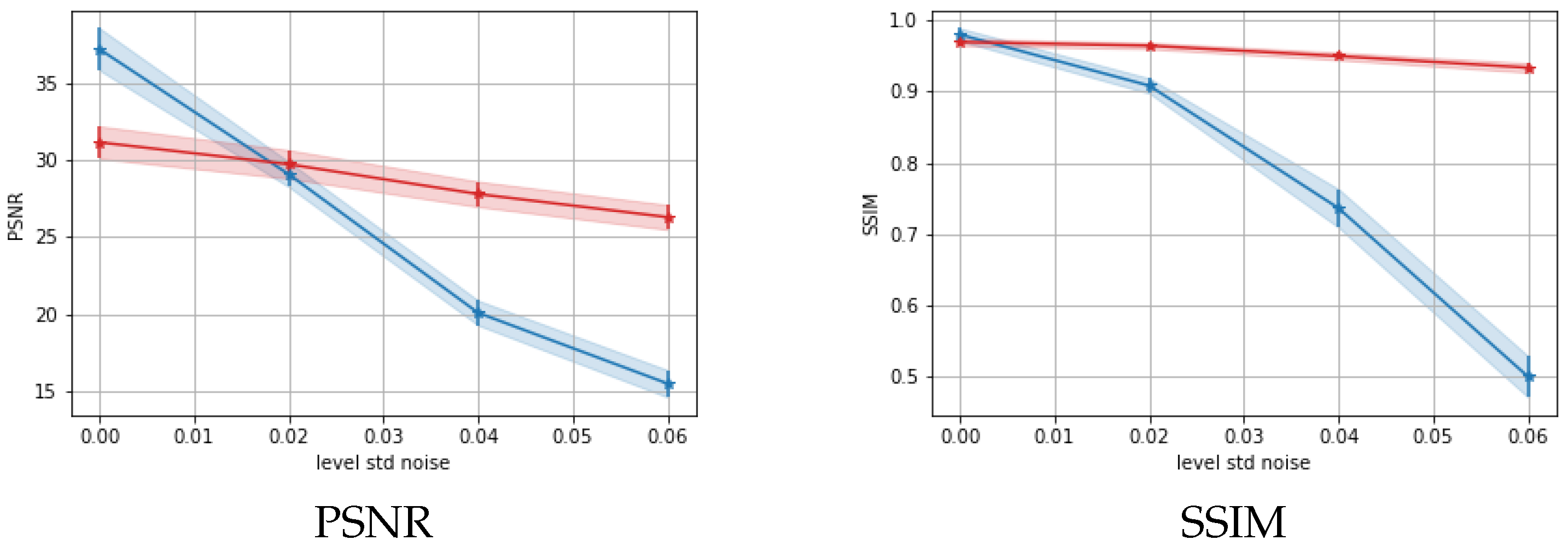
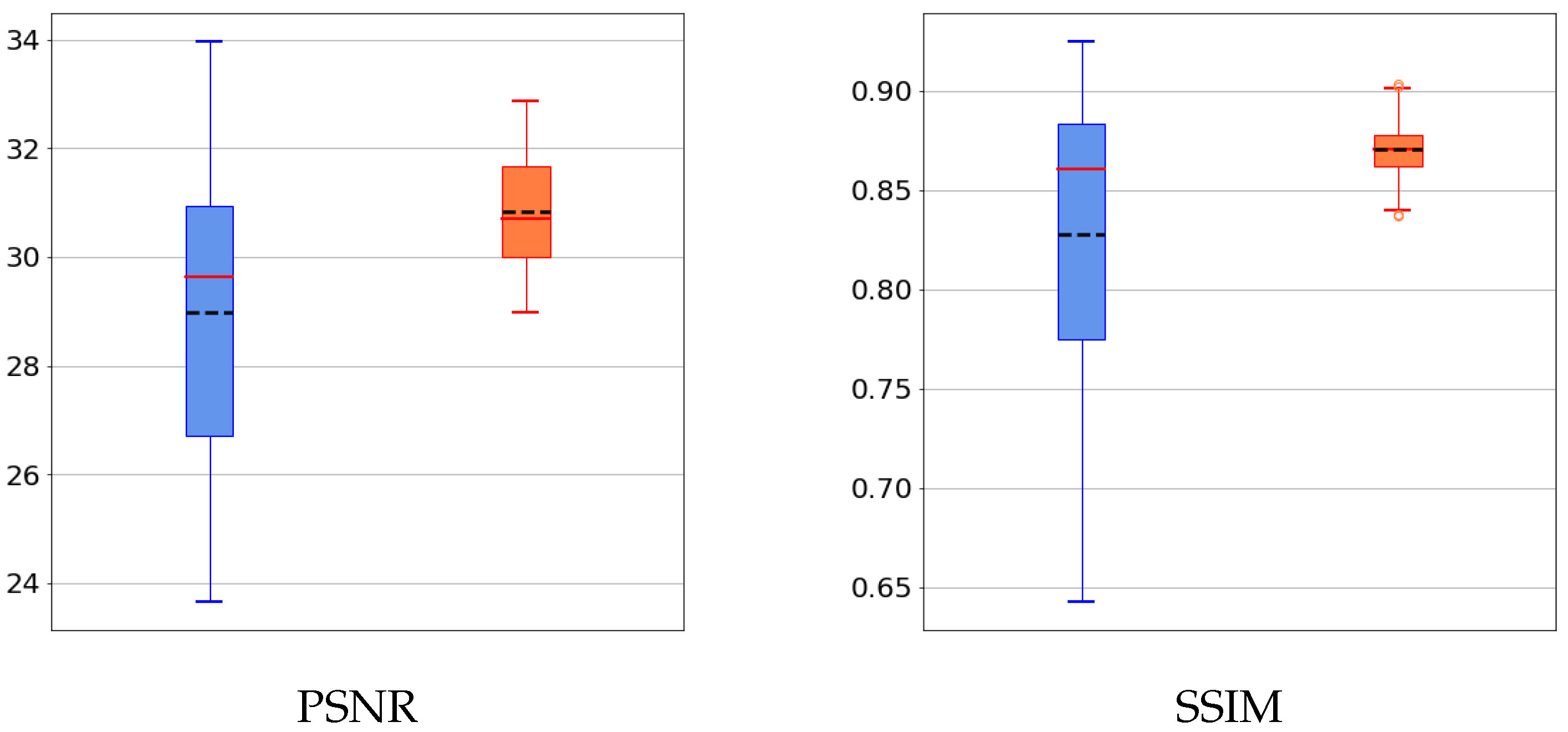
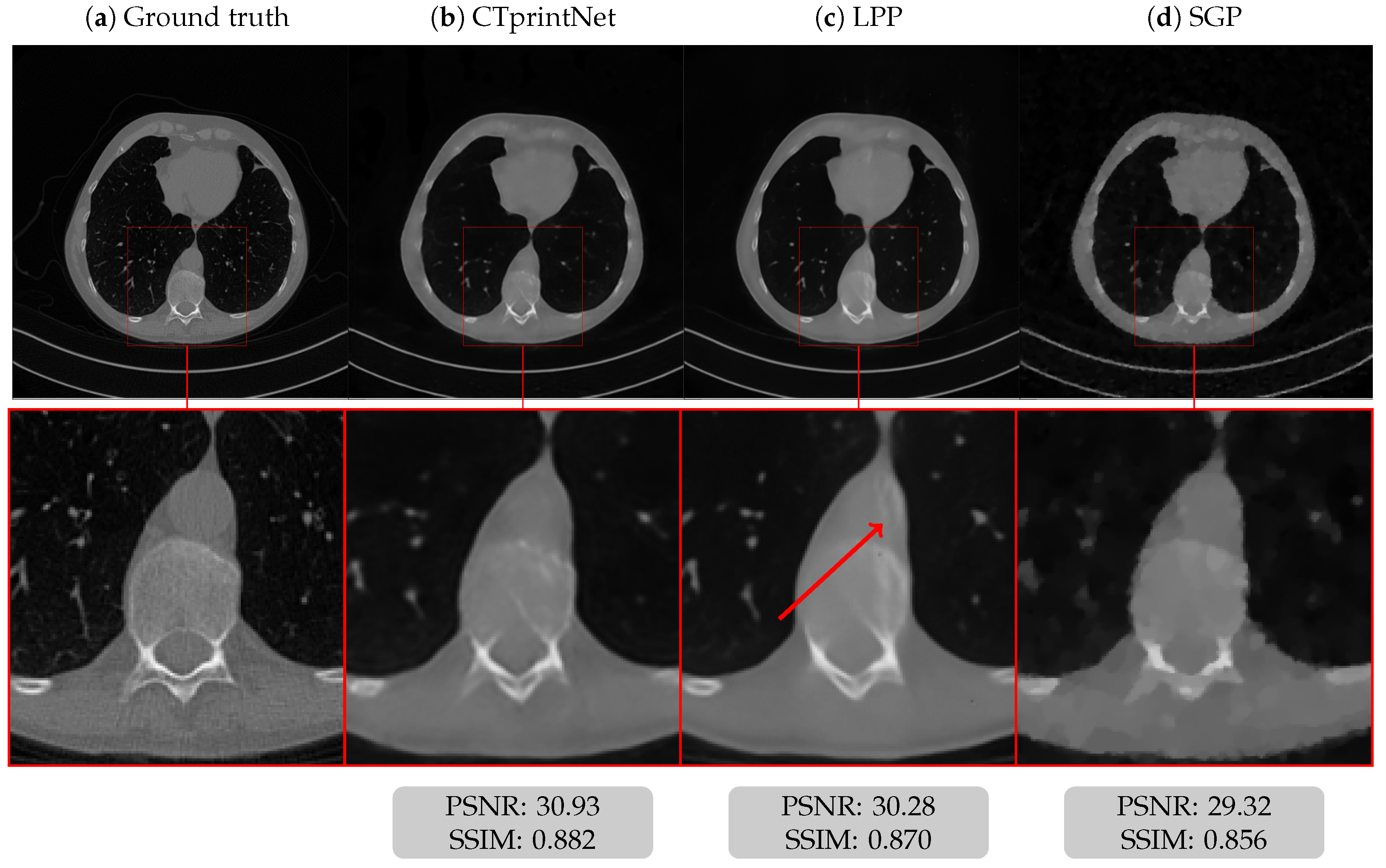
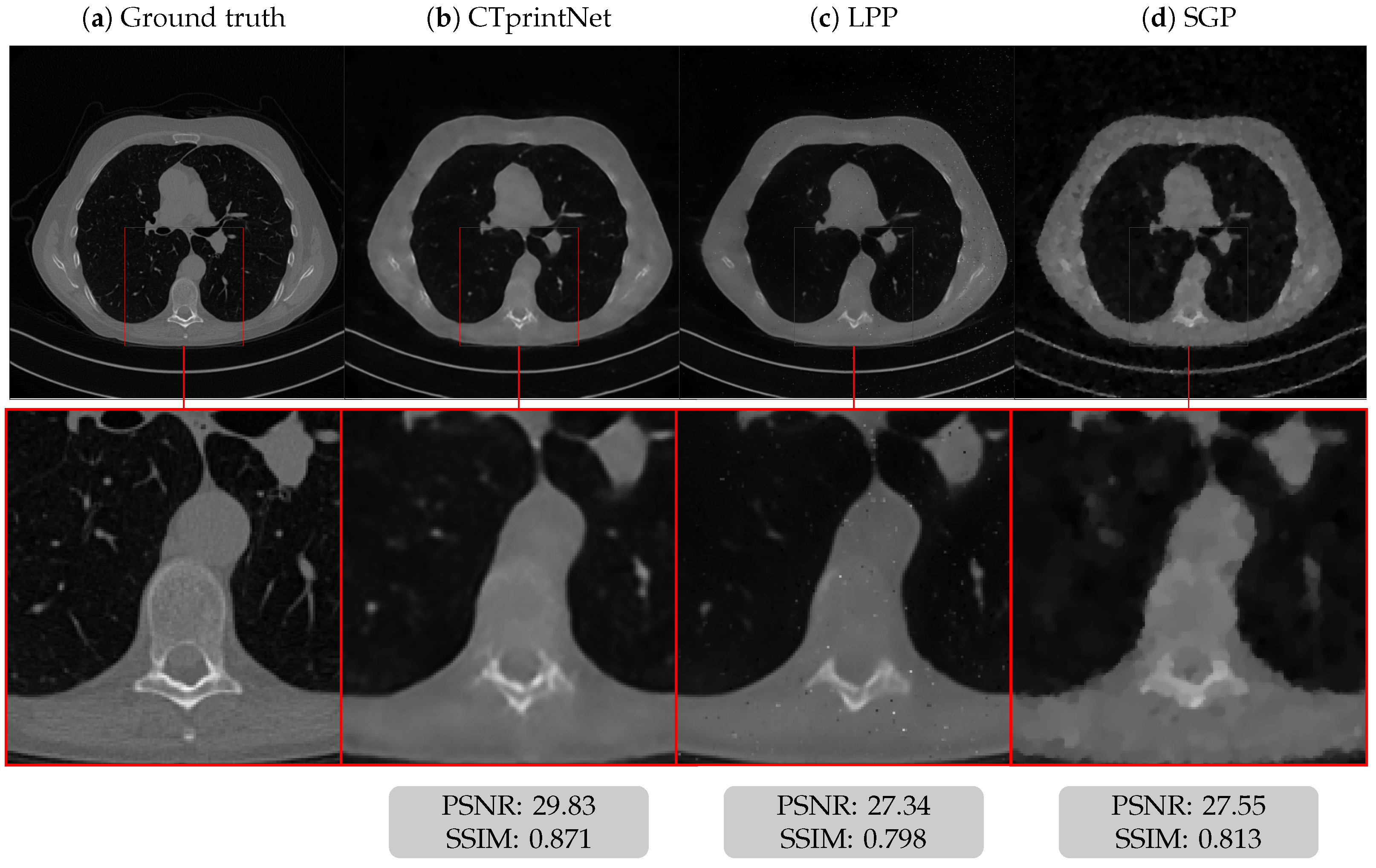
5.1. Results on a Synthetic Dataset
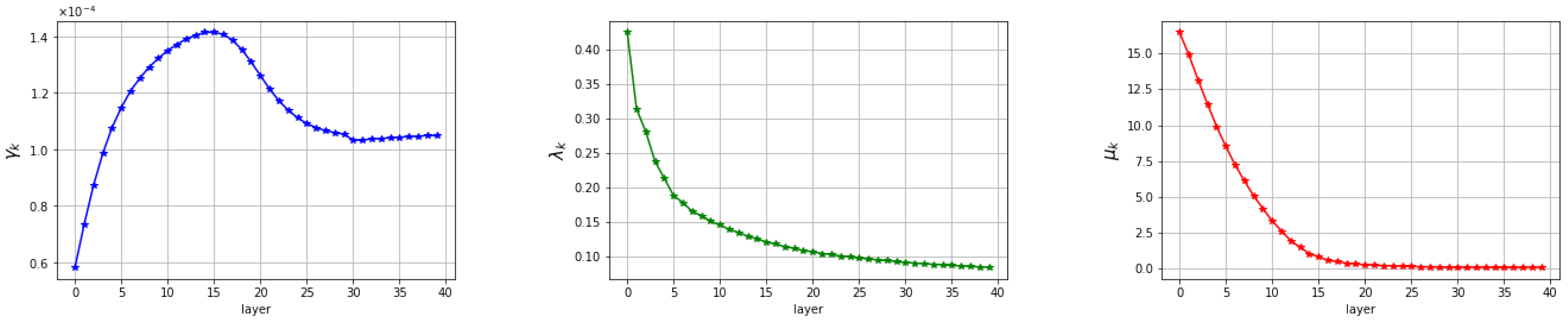
5.2. Discussion of the Learned Parameters
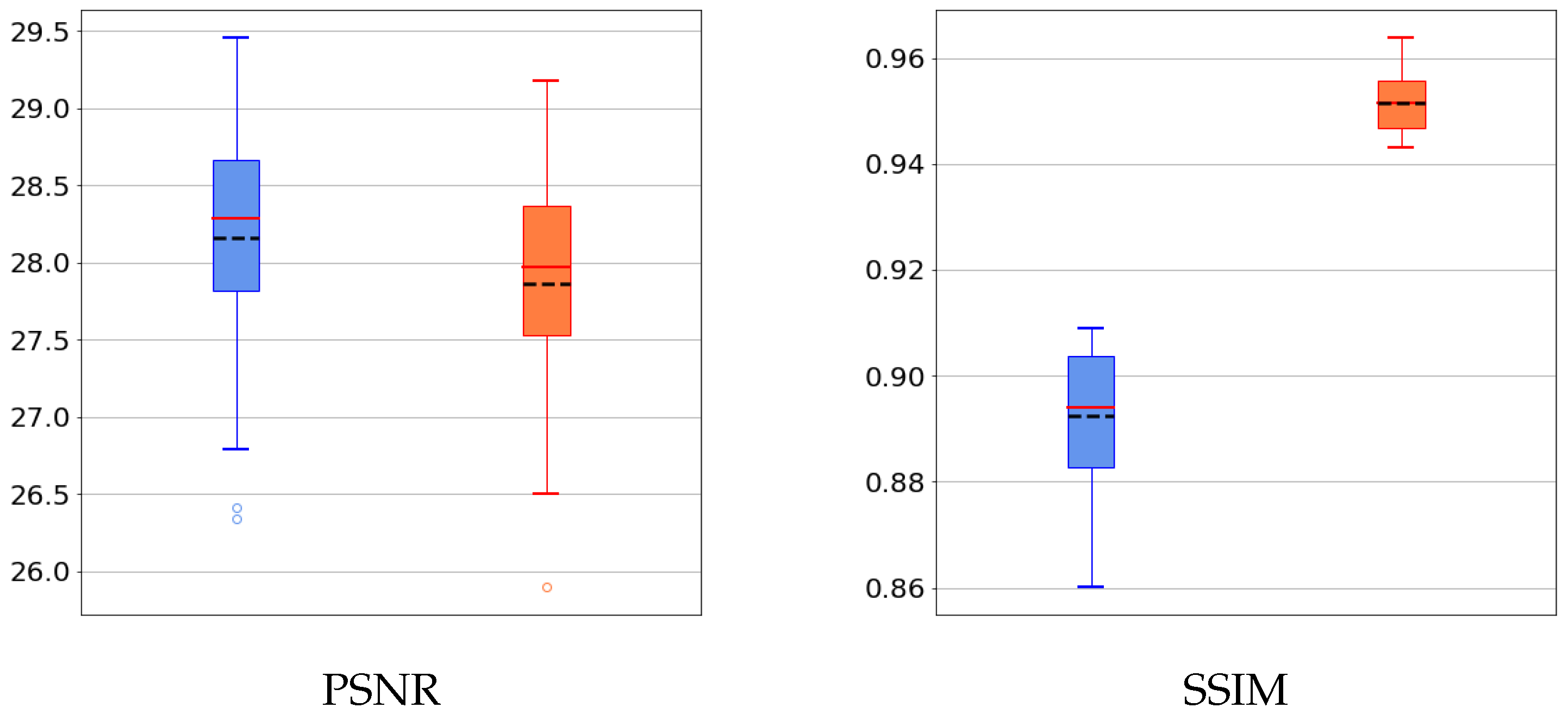
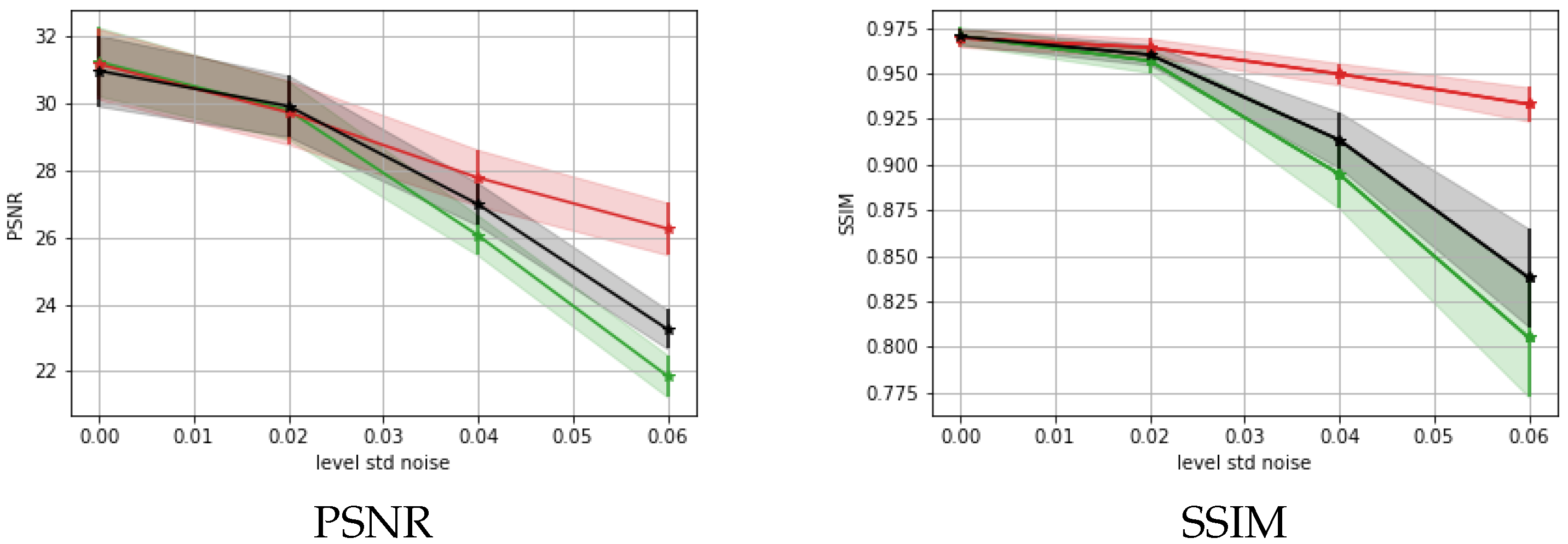
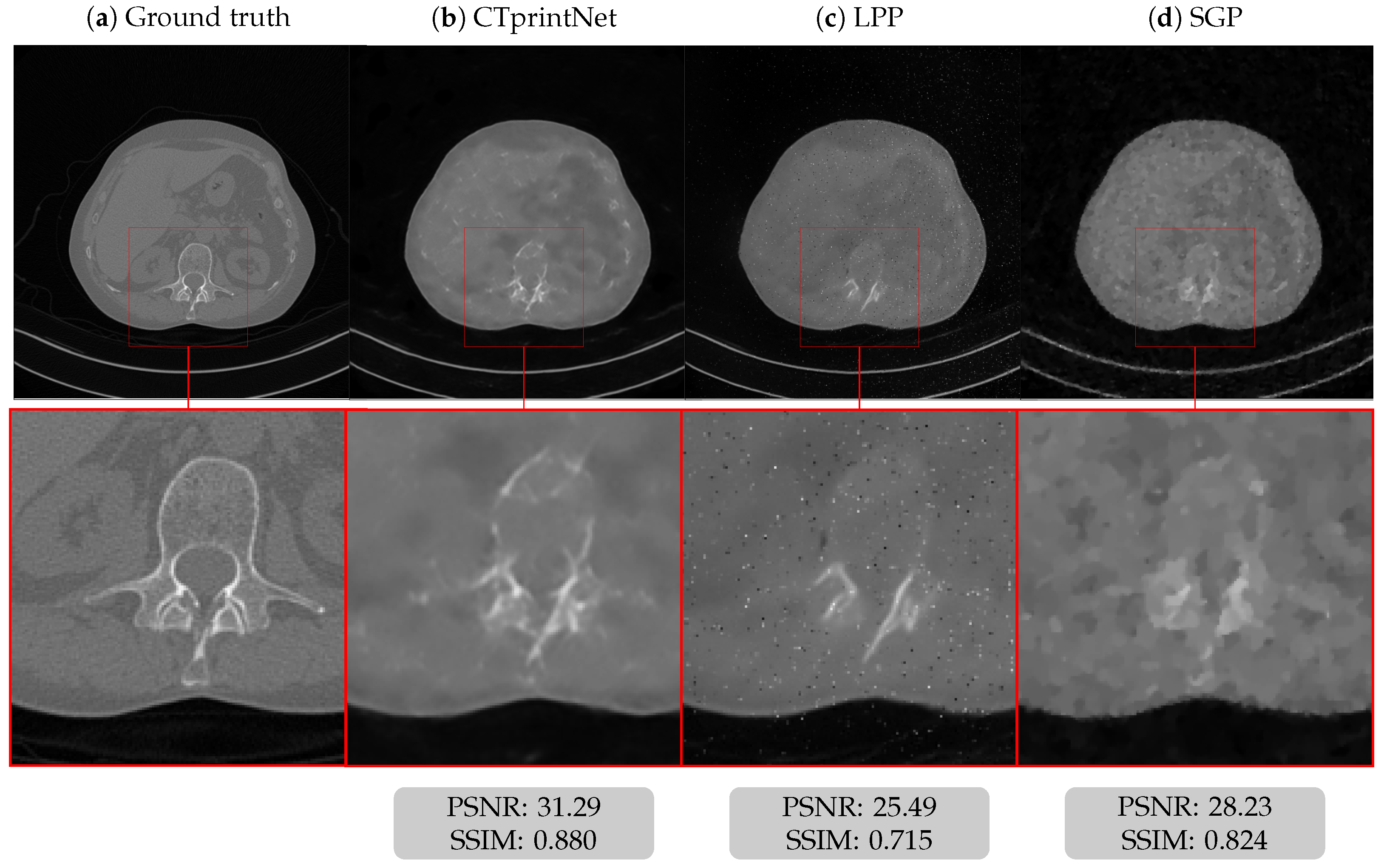
5.3. Results on a Realistic Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNNs | Convolutional neural networks |
| COULE | Contrasted overlapping uniform lines and ellipses |
| CT | Computed tomography |
| DNNs | Deep neural networks |
| FBP | Filtered back-projection |
| FBPIP | Forward–backward proximal interior point |
| GPUs | Graphics processing units |
| MSE | Mean square error |
| PSNR | Peak signal-to-noise ratio |
| SGP | Scaled gradient projection method |
| SSIM | Structural similarity index measure |
| TV | Total variation |
| WTV | Weighted total variation |
References
- Candès, E.J.; Romberg, J.K.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Süzen, M.; Giannoula, A.; Durduran, T. Compressed sensing in diffuse optical tomography. Opt. Express 2010, 18, 23676–23690. [Google Scholar] [CrossRef] [PubMed]
- Montefusco, L.B.; Lazzaro, D.; Papi, S.; Guerrini, C. A fast compressed sensing approach to 3D MR image reconstruction. IEEE Trans. Med. Imaging 2011, 30, 1064–1075. [Google Scholar] [CrossRef]
- Rostami, M.; Michailovich, O.V.; Wang, Z. Image Deblurring Using Derivative Compressed Sensing for Optical Imaging Application. IEEE Trans. Image Process. 2012, 21, 3139–3149. [Google Scholar] [CrossRef] [PubMed]
- Mohan, N.; Stojanovic, I.; Karl, W.C.; Saleh, B.E.A.; Teich, M.C. Compressed sensing in optical coherence tomography. In Proceedings of the Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing XVII; Conchello, J.A., Cogswell, C.J., Wilson, T., Brown, T.G., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2010; Volume 7570, p. 75700L. [Google Scholar]
- Uğur, S.; Arıkan, O. SAR image reconstruction and autofocus by compressed sensing. Digit. Signal Process. 2012, 22, 923–932. [Google Scholar] [CrossRef]
- Hauptmann, A.; Hämäläinen, K.; Harhanen, L.; Kallonen, A.; Niemi, E.; Siltanen, S. Total variation regularization for large-scale X-ray tomography. Int. J. Tomogr. Simul. 2014, 25, 1–25. [Google Scholar]
- He, J.; Wang, Y.; Ma, J. Radon inversion via deep learning. IEEE Trans. Med. Imaging 2020, 39, 2076–2087. [Google Scholar] [CrossRef]
- Antun, V.; Renna, F.; Poon, C.; Adcock, B.; Hansen, A.C. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc. Natl. Acad. Sci. USA 2020, 117, 30088–30095. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Kalra, M.K.; Lin, F.; Chen, Y.; Liao, P.; Zhou, J.; Wang, G. Low-dose CT with a residual encoder-decoder convolutional neural network. IEEE Trans. Med. Imaging 2017, 36, 2524–2535. [Google Scholar] [CrossRef] [PubMed]
- Morotti, E.; Evangelista, D.; Loli Piccolomini, E. A green prospective for learned post-processing in sparse-view tomographic reconstruction. J. Imaging 2021, 7, 139. [Google Scholar] [CrossRef] [PubMed]
- Gupta, H.; Jin, K.H.; Nguyen, H.Q.; McCann, M.T.; Unser, M. CNN-based projected gradient descent for consistent CT image reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1440–1453. [Google Scholar] [CrossRef] [PubMed]
- Lunz, S.; Öktem, O.; Schönlieb, C.B. Adversarial Regularizers in Inverse Problems. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; NIPS’18. pp. 8516–8525. [Google Scholar]
- Chang, J.R.; Li, C.L.; Póczos, B.; Vijaya Kumar, B.; Sankaranarayanan, A.C. One Network to Solve Them All—Solving Linear Inverse Problems Using Deep Projection Models. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5889–5898. [Google Scholar]
- Monga, V.; Li, Y.; Eldar, Y.C. Algorithm Unrolling: Interpretable, Efficient Deep Learning for Signal and Image Processing. IEEE Signal Process. Mag. 2021, 38, 18–44. [Google Scholar] [CrossRef]
- Gregor, K.; LeCun, Y. Learning Fast Approximations of Sparse Coding. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; ICML’10. pp. 399–406. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1828–1837. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 521–538. [Google Scholar] [CrossRef] [PubMed]
- Bertocchi, C.; Chouzenoux, E.; Corbineau, M.C.; Pesquet, J.C.; Prato, M. Deep unfolding of a proximal interior point method for image restoration. Inverse Probl. 2020, 36, 034005. [Google Scholar] [CrossRef]
- Adler, J.; Öktem, O. Solving ill-posed inverse problems using iterative deep neural networks. Inverse Probl. 2017, 33, 124007. [Google Scholar] [CrossRef]
- Adler, J.; Öktem, O. Learned Primal-Dual Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1322–1332. [Google Scholar] [CrossRef]
- Xiang, J.; Dong, Y.; Yang, Y. FISTA-Net: Learning a fast iterative shrinkage thresholding network for inverse problems in imaging. IEEE Trans. Med. Imaging 2021, 40, 1329–1339. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Chen, Y.; Zhang, J.; Zhang, W.; Sun, H.; Lv, Y.; Liao, P.; Zhou, J.; Wang, G. LEARN: Learned Experts’ Assessment-Based Reconstruction Network for Sparse-Data CT. IEEE Trans. Med. Imaging 2018, 37, 1333–1347. [Google Scholar] [CrossRef]
- Savanier, M.; Chouzenoux, E.; Pesquet, J.C.; Riddell, C. Deep Unfolding of the DBFB Algorithm with Application to ROI CT Imaging with Limited Angular Density; Technical Report hal-03881278; Inria Saclay: Palaiseau, France, 2022. [Google Scholar]
- Bubba, T.A.; Galinier, M.; Lassas, M.; Prato, M.; Ratti, L.; Siltanen, S. Deep Neural Networks for Inverse Problems with Pseudodifferential Operators: An Application to Limited-Angle Tomography. SIAM J. Imaging Sci. 2021, 14, 470–505. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Kao, C.M.; Pan, X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J. X-ray Sci. Technol. 2006, 14, 119–139. [Google Scholar]
- Landi, G.; Piccolomini, E.L. An efficient method for nonnegatively constrained Total Variation-based denoising of medical images corrupted by Poisson noise. Comput. Med. Imaging Graph. 2012, 36, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.C.; Jørgensen, J.H. Total variation and tomographic imaging from projections. In Proceedings of the 36th Conference Dutch-Flemish Numerical Analysis Communities Woudschouten, Zeist, The Netherlands, 5–7 October 2011. [Google Scholar]
- Siltanen, S.; Kolehmainen, V.; Järvenpää, S.; Kaipio, J.P.; Koistinen, P.; Lassas, M.; Pirttilä, J.; Somersalo, E. Statistical inversion for medical X-ray tomography with few radiographs: I. General theory. Phys. Med. Biol. 2003, 48, 1437–1463. [Google Scholar] [CrossRef] [PubMed]
- Wright, M.H. Interior methods for constrained optimization. Acta Numer. 1992, 1, 341–407. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; CMS Books on Mathematics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Chaux, C.; Combettes, P.L.; Pesquet, J.C.; Wajs, V.R. A variational formulation for frame-based inverse problems. Inverse Probl. 2007, 23, 1495. [Google Scholar] [CrossRef]
- Elfving, T.; Hansen, P.C. Unmatched Projector/Backprojector Pairs: Perturbation and Convergence Analysis. SIAM J. Sci. Comput. 2018, 40, A573–A591. [Google Scholar] [CrossRef]
- Chouzenoux, E.; Contreras, A.; Pesquet, J.C.; Savanier, M. Convergence Results for Primal-Dual Algorithms in the Presence of Adjoint Mismatch. SIAM J. Imaging Sci. 2023, 16, 1–34. [Google Scholar] [CrossRef]
- Bonettini, S.; Prato, M. New convergence results for the scaled gradient projection method. Inverse Probl. 2015, 31, 1196–1211. [Google Scholar] [CrossRef]
- Loli Piccolomini, E.; Morotti, E. A model-based optimization framework for iterative digital breast tomosynthesis image reconstruction. J. Imaging 2021, 7, 36. [Google Scholar] [CrossRef]
- Loli Piccolomini, E.; Coli, V.L.; Morotti, E.; Zanni, L. Reconstruction of 3D X-ray CT images from reduced sampling by a scaled gradient projection algorithm. Comput. Optim. Appl. 2018, 71, 171–191. [Google Scholar] [CrossRef]
- Bubba, T.A.; Labate, D.; Zanghirati, G.; Bonettini, S. Shearlet-based regularized reconstruction in region-of-interest computed tomography. Math. Model. Nat. Phenom. 2018, 13, 34. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Cascarano, P.; Sebastiani, A.; Comes, M.C.; Franchini, G.; Porta, F. Combining Weighted Total Variation and Deep Image Prior for natural and medical image restoration via ADMM. In Proceedings of the 2021 21st International Conference on Computational Science and Its Applications (ICCSA), Cagliari, Italy, 13–16 September 2021; pp. 39–46. [Google Scholar]
- Bortolotti, V.; Brown, R.J.S.; Fantazzini, P.; Landi, G.; Zama, F. Uniform Penalty inversion of two-dimensional NMR relaxation data. Inverse Probl. 2016, 33, 015003. [Google Scholar] [CrossRef]

| Parameters | |||
|---|---|---|---|
| epochs | 5 | 10 | 50 |
| batchsize | 8 | 8 | 5 |
| learning rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loli Piccolomini, E.; Prato, M.; Scipione, M.; Sebastiani, A. CTprintNet: An Accurate and Stable Deep Unfolding Approach for Few-View CT Reconstruction. Algorithms 2023, 16, 270. https://doi.org/10.3390/a16060270
Loli Piccolomini E, Prato M, Scipione M, Sebastiani A. CTprintNet: An Accurate and Stable Deep Unfolding Approach for Few-View CT Reconstruction. Algorithms. 2023; 16(6):270. https://doi.org/10.3390/a16060270
Chicago/Turabian StyleLoli Piccolomini, Elena, Marco Prato, Margherita Scipione, and Andrea Sebastiani. 2023. "CTprintNet: An Accurate and Stable Deep Unfolding Approach for Few-View CT Reconstruction" Algorithms 16, no. 6: 270. https://doi.org/10.3390/a16060270
APA StyleLoli Piccolomini, E., Prato, M., Scipione, M., & Sebastiani, A. (2023). CTprintNet: An Accurate and Stable Deep Unfolding Approach for Few-View CT Reconstruction. Algorithms, 16(6), 270. https://doi.org/10.3390/a16060270







