Discovering Non-Linear Boolean Functions by Evolving Walsh Transforms with Genetic Programming ^†

Abstract

Stream ciphers usually rely on highly secure Boolean functions to ensure safe communication within unsafe channels. However, discovering secure Boolean functions is a non-trivial optimization problem that has been addressed by many optimization techniques: in particular by evolutionary algorithms. We investigate in this article the employment of Genetic Programming (GP) for evolving Boolean functions with large non-linearity by examining the search space consisting of Walsh transforms. Especially, we build generic Walsh spectra starting from the evolution of Walsh transform coefficients. Then, by leveraging spectral inversion, we build pseudo-Boolean functions from which we are able to determine the corresponding nearest Boolean functions, whose computation involves filling via a random criterion a certain amount of “uncertain” positions in the final truth table. We show that by using a balancedness-preserving strategy, it is possible to exploit those positions to obtain a function that is as balanced as possible. We perform experiments by comparing different types of symbolic representations for the Walsh transform, and we analyze the percentage of uncertain positions. We systematically review the outcomes of these comparisons to highlight the best type of setting for this problem. We evolve Boolean functions from 6 to 16 bits and compare the GP-based evolution with random search to show that evolving Walsh transforms leads to highly non-linear functions that are balanced as well.

1. Introduction

The importance of cryptography methods is critical in several applications that involve performing communication and exchanging messages and data. Thanks to these techniques, data exchanges are executed in a safe way even within unsafe communication channels on which, in general, malicious actors are potentially listening. Symmetric cryptography is a particular type of cryptography in which the communication is protected with encryption and decryption by means of a shared secret key that should be known only by the participants involved in the communication [1].

A typical problem in the cryptography field consists of guaranteeing the confidentiality of communication in the presence of passive attackers that can eavesdrop on the exchanged messages. To this end, symmetric ciphers can be employed to encrypt the exchanged messages so that an attacker is not able to gain information about the original messages on the basis of the encrypted ones. In this context, stream ciphers represent a particular class of symmetric ciphers for which each message is elaborated as a whole and combined with other messages by means of bit-wise operations.

In many stream-cipher-based architectures, an important building block is represented by Boolean functions with a specific number n of variables. A Boolean function that exhibits high-quality cryptography properties (e.g., non-linearity and balancedness) is essential for guaranteeing high security standard for a given stream cipher. However, discovering Boolean functions with good security properties is, in practice, a complex optimization problem that has been largely studied in the literature. In particular, Evolutionary Computation (EC) methods have been shown to be promising techniques [2,3,4,5,6,7,8,9].

Among the safety properties that can be used to characterize a Boolean function, non-linearity is certainly one of the most important ones. Despite the large number of research works that have investigated how to devise Boolean functions that are characterized by large non-linearity [3,5,7,9,10,11], the optimal non-linearity, in the cases for which this value is theoretically known, has still not been reached yet (especially for real-world Boolean functions where n is large) [12]. For this reason, novel approaches to this problem are important for finding and addressing the best exploration strategy.

In this setting, the evolutionary-based optimization method and the Boolean function representation are both important factors. Especially, a Boolean function can be mainly represented in three ways: with a truth table, with the algebraic normal form (ANF), or with the Walsh transform [13]. By performing different combinations of algorithms and representations, it is possible to discover new and hopefully better ways of exploring the search space.

In this article, we delve into the usage of Genetic Programming (GP) in a way that we can design an algorithm that evolves Boolean functions represented by their corresponding Walsh transforms. This approach appears to be particularly promising since the Walsh transform can be easily and indirectly represented by a GP-based tree while encoding regularities among the different Walsh coefficients. Moreover, the optimization of Walsh transforms enables us to explore a different fitness landscape that may be hopefully more promising with respect to the desired objectives.

We evolve symbolic trees representing Walsh transforms to maximize their non-linearity. Specifically, for each evolved Walsh transform, we retrieve the corresponding Walsh spectrum from which, through spectral inversion, we generate a pseudo-Boolean function. Given a pseudo-Boolean function, we compute the nearest Boolean one while trying to improve the balancedness of the final solution as best as possible. To this end, we exploit the “uncertain” inputs of the pseudo-Boolean function in which we have to non-deterministically choose the binary values that should be mapped to the target truth table.

In this work, we try to provide an answer to the following research questions:

RQ1. 

Can we easily obtain balanced solutions?

RQ2. 

Can we leverage a GP-based evolution to discover solutions with higher non-linearity than random search?

RQ3. 

What are the implications of changing the tree syntactical structure as regards our fitness function?

We test and compare different combinations of function sets and terminal sets for the structure of the Walsh-transform-based tree. Additionally, we analyze the trend of the percentage of uncertain positions when computing the nearest Boolean function. We provide a review of all these comparisons to highlight the best type of setting for a Walsh-transform-based search-space exploration. Results show that by leveraging GP to evolve Walsh transforms, it is possible to outperform random search, meaning that the evolutionary process and the type of chosen representation are both effective at providing a high-quality exploration strategy, which, consequently, deserves further research effort. Furthermore, the discovered solutions appear also to be balanced thanks to the balancedness-preserving strategy adopted during the nearest Boolean function computation.

We detail the main contributions of this manuscript:

(i).

We show how we can evolve Walsh Transforms with GP to maximize non-linearity by using spectral inversion.

(ii).

We show how we can discover balanced solutions with an effective balancedness-preserving strategy when computing the nearest Boolean functions from the corresponding pseudo-Boolean ones.

(iii).

We demonstrate that, even with a small population size and with a low number of generations, GP is able to outperform RS if we choose the correct function set and terminal set.

(iv).

We provide an analysis for explaining why certain types of function and terminal set combinations perform poorly by inspecting the percentages of uncertain positions.

In Section 2, we analyze the current literature regarding optimization of Boolean functions for building secure stream ciphers. In Section 3, we describe the application domain by analyzing stream ciphers and Pseudo-Random Generators (PRG) in Section 3.1 and Boolean function representations in Section 3.2. In Section 4, we describe our proposed evolutionary-based approach. In Section 5, we describe our experimental phase and present the results. In Section 6, we inspect the obtained results and provide an answer to the research questions.

2. Related Works

Applying a brute-force-based optimization method in order to identify, with respect to a certain quality criterion, the best Boolean function is inconceivable when the number of variables (n) is larger than five. On the other hand, stream ciphers usually leverage Boolean functions with n greater than 13 [14]. Therefore, designing and constructing Boolean functions that are characterized by sound security features requires more intelligent approaches than a purely random one. In the literature, this problem has been addressed by leveraging different types of strategies.

Algebraic constructions, such as the Rothaus construction [15] and the McFarland construction [16], are adopted to build classes of Bent functions [17]. Li et al. [18] introduced a method to generate n-variable Boolean functions with optimal algebraic immunity and computed a lower bound of the number of Boolean functions with optimal algebraic immunity. Chen et al. [19] proposed two classes of symmetric Boolean functions with optimum algebraic immunity for which both the algebraic degree and the non-linearity are also determined. Tu et al. [20] presented a combinatorial conjecture about binary strings that, if correct, enables the discovers of two classes of Boolean functions with optimal algebraic immunity: Bent functions and balanced functions, with the latter having an optimal algebraic degree and the best non-linearity.

Heuristic-based optimization approaches have been applied to seek good-quality Boolean functions with respect to given security objectives. Burnett et al. [21] optimized the non-linearity of a starting Boolean function with incremental changes. Moreover, they provided a method that discovers resilient Boolean functions by progressively concatenating valid Walsh spectra. Clark et al. [13] optimized functions that intrinsically exhibit good cryptography properties and tried to transform the most-promising ones to Boolean functions that preserve the original properties. In [22], Clark et al. optimized good-quality Boolean functions by using a Simulated Annealing algorithm [23]. Lopez et al. [24] presented a novel diversity-aware meta-heuristic for non-linearity maximization of Boolean functions that exploits a cost function that adopts the Walsh–Hadamard Transform (WHT) to gather useful information for the task at hand.

Evolutionary Computation (EC) techniques serve as auspicious substitutes to more traditional optimization methods when it comes to searching for Boolean functions that possess certain security features. Aguirre et al. [11] investigated a multi-objective evolutionary approach to discover balanced functions with similar characteristic that satisfy multiple criteria such as non-linearity. Knevzevic et al. [25] provided a survey describing the usage of evolutionary algorithms in both the symmetric and asymmetric cryptography fields. Millan et al. used Genetic Algorithms (GAs) to discover balanced Boolean functions that satisfy both correlation immunity and the strict avalanche criterion [26], and they employed the same type of algorithm to identify Boolean functions with large non-linearity [3]. Asthana et al. [10] presented a GA-based scheme to build Boolean functions that satisfy balancedness, correlation immunity, algebraic degree, and non-linearity properties. Mariot et al. [2] adopted GA to evolve plateaued Boolean functions [27] by using the spectral inversion technique introduced in [13] and thus by representing the chromosome of an individual as a permutation of a three-valued Walsh spectrum. Morevoer, Mariot et al. [28] implemented a Particle Swarm Optimizer for generating Boolean functions with good cryptography properties. Particularly, this Particle Swarm Optimizer updates the particle positions while preserving their Hamming weights in a way that the generated functions remain balanced. Additionally, it exploits hill-climbing to further improve non-linearity and correlation immunity. Behera et al. [29] applied GA with the integration of a process based on hybrid local search for determining Boolean functions composed of good characteristics of auto-correlation and also non-linearity. Dimovski et al. [30] proposed a hill-climbing method that incorporates a GA to search for highly non-linear Boolean functions.

Miller et al. [4] presented an empirical study on how to adopt Cartesian Genetic Programming (CGP), i.e., a variant of Genetic Programming (GP) [31], to spot general-purpose Boolean functions. Picek et al. [5] resumed the work of Miller et al. [4] and investigated how much more effective CGP is than GP when it comes to learning highly non-linear Boolean functions. They further investigated GA and GP with different mutation operators and initialization procedures [32]. CGP was also investigated by Hrbacek et al. [33] to routinely build Bent functions with up to 16 variables. Husa et al. [34] implemented a parallelized version of Linear GP to discover Bent functions instead of using CGP, and they focused their research work on learning functions that are as large as possible. Moreover, they proposed a comparative study wherein GP, Linear GP, and CGP are compared with respect to the task of building Boolean functions with an even number of inputs and that can exhibit high-quality non-linearity, algebraic degree, balancedness, and correlation immunity [35]. Picek et al. [6] highlighted that among evolutionary algorithms, GP exhibits high qualitative performance when it comes to discovering both Boolean functions that provide non-linearity in filter and combiner generators and Boolean functions with sound correlation immunity and a Hamming weight that is as small as possible. Moreover, Picek et al. [36] analyzed the landscape of results obtained by integrating algebraic and EC-based approaches for searching for secure Boolean functions. Carlet et al. [37] also explored a method that tries to combine evolutionary algorithms with known algebraic constructions. Specifically, they analyzed a recent generalization of the Hidden Weight Boolean Function construction, and they showed that evolutionary algorithms can meaningfully improve the cryptography properties of functions based on this construction. Mariot et al. [8] proposed several evolutionary algorithms to evolve Hyper-Bent functions, which provide better security towards approximation attacks. They showed that these specific types of functions are extremely difficult to evolve because of their rarity and complexity. Moreover, they [7] applied GA and GP to evolve Boolean functions that satisfy the perfect balancedness property. Specifically, they used these evolutionary techniques to evolve two different types of solution encodings: the truth table and weight-wise balanced representations. Carlet et al. [9] tried to evolve Boolean constructions by leveraging GP to build balanced functions with high non-linearity. Finally, Rovito et al. [38] proposed a work in which they represented Boolean functions by using Walsh-transform-based representations, and they evolved these representations with GP to discover non-linear functions with good balancedness properties.

We introduce an algorithm based on GP with which we evolve Boolean functions represented by their corresponding Walsh transforms in order to maximize non-linearity and preserve balancedness as best as possible. Specifically, we resume the work in [38] and provide an in-depth experimental analysis of various types of symbolic Walsh-transform-based representations.

3. Cryptography Overview

Cryptography is the set of methodologies, practices, tools, and algorithms that facilitates the safe management and transmission of data while being in a not-safe channel. While there exist different types of cryptography, our main focus is symmetric cryptography—i.e., a type of cryptography wherein we have two entities that are interacting within an unsafe channel by employing a key (private and only shared between them). A public cipher adopts the key along with a message and safely performs the encryption and decryption of it [1]. In this section, we are going to briefly explore how a stream cipher works, along with its main construction, its building blocks, and how it can be represented.

3.1. PRG-Based Stream Cipher Design

In the context of symmetric cryptography (Figure 1), we are interested in making the interaction safe despite the eventual presence of eavesdroppers—i.e., our security requirement matches the confidentiality of the communication. This means that without having the secret key, it is computationally infeasible to retrieve the original content of an encrypted message or a single component of it. In this scenario, we assume an unsafe communication channel in which there is a passive attacker, i.e., a malicious actor that can retrieve the encrypted message and process it but, at the same time, cannot alter the communication itself [1].

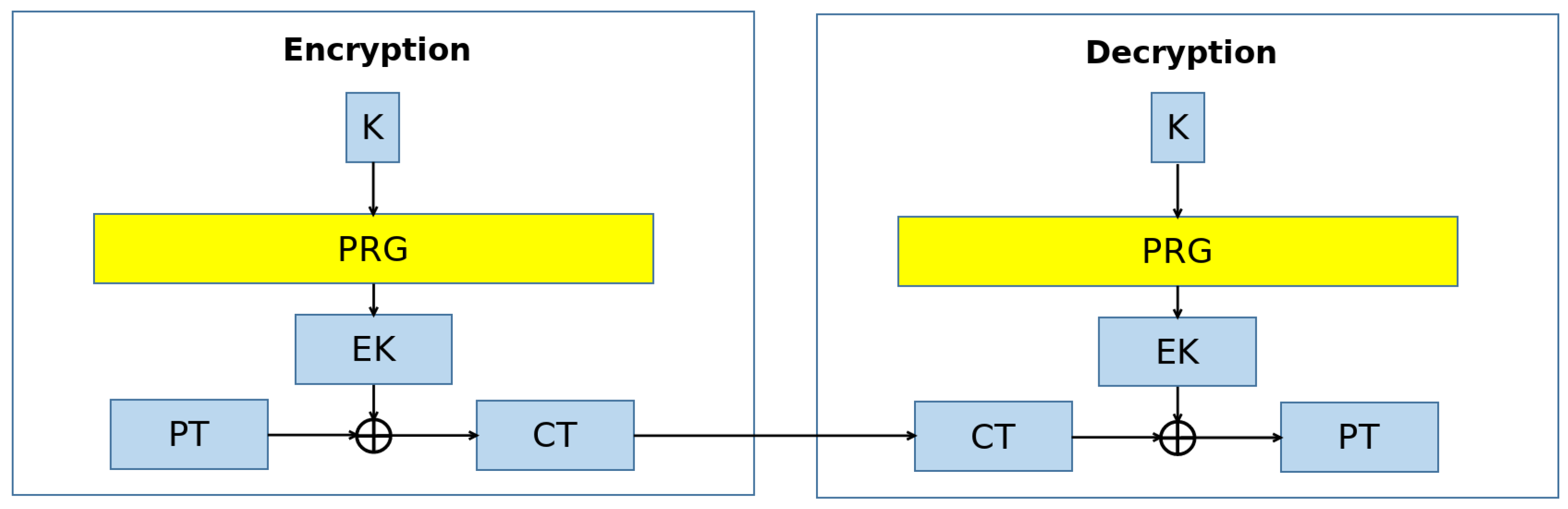
We focus our attention on stream ciphers, which are symmetric ciphers for which a message is treated as a single block. A One-Time Pad (OTP) is an example of a stream cipher that satisfies Shannon’s perfect secrecy definition, which states that an encrypted message must reveal no information about any bit of the corresponding plain-text message [39]. Given a plain-text message and a shared secret key, the encryption is performed by applying a bit-wise XOR operator between the plain-text message and a shared secret key. Similarly, the decryption is performed by applying the same operation between the encrypted message and the secret key. This implies that the secret key length must be as long as the length of the exchanged messages. Furthermore, in order to keep the OTP safe, the same secret key must not be reused across different message exchanges.

The aforementioned requirements pose practical limitations to the adoption of the OTP in real-world scenarios. To this end, a Pseudo Random Generator (PRG) can be employed to adapt the OTP construction when the length of the secret key is smaller than the length of the message. Specifically, a PRG is a public, deterministic, and efficient algorithm that, given a binary string called the “seed”, is able to generate a much longer, seemingly random binary string [40,41]. By adopting a PRG, it is possible to build the Vernam stream cipher [42] (Figure 2), which basically consists of an OTP for which the secret key is expanded by a PRG to match the length of the message. A Vernam stream cipher is considered to be confidentially safe if and only if the PRG is safe, i.e., unpredictable. To this end, several PRG architectures have been implemented.

The Linear Feedback Shift Register (LSFR) [43] is an example of a construction that can be adopted within a PRG architecture. This registry essentially outputs a single bit at every clock cycle starting from a given seed (a binary string). For instance, given a state represented by the current seed stored in the registry, at every clock cycle, the most-significant bit is returned as output; then, the registry performs a left-shift operation, and the least-significant bit is populated with bit-wise XOR operations performed on a subset of the seed. This way, if the registry works for t clock cycles, it will generate a t-bit long binary string. The Content Scramble System (CSS) [44] is an example of an unsafe stream cipher that leverages LSFR. This statement highlights the fact that LSFR alone does not suffice to build secure stream ciphers.

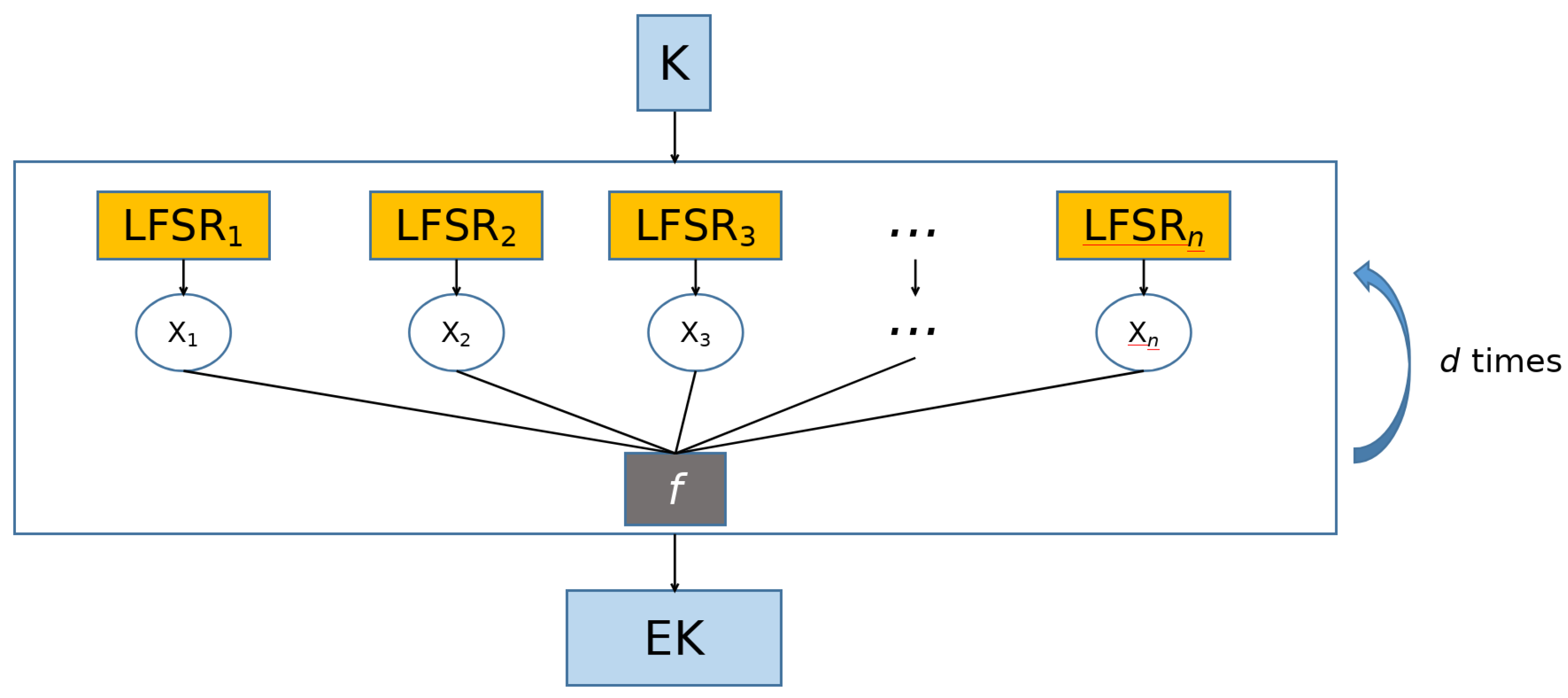
A potentially unpredictable PRG can be constructed by using a combination of n LSFRs and an n-variable Boolean function. This architecture is called the Combiner model [14] (Figure 3). The seed is an s-bit long binary string. It is processed in parallel by n LSFRs, which consequentially output an n-bit long binary string at each clock cycle (one bit for each LSFR). An n-variable Boolean function f is thus applied to this binary string, and a single bit is generated. Hence, if the Combiner model works for d clock cycles, it will generate a d-bit long binary string. The safety of the Combiner model relies entirely upon the safety of the Boolean function that processes the output of the LFSRs, i.e., the Combiner model is an unpredictable PRG if and only if the Boolean function exhibits highly secure cryptography properties. We are going to analyze these properties in the next section.

3.2. Boolean Function and Walsh Transforms

Let $\mathbb{B}=\{0,1\}$ be a set of binary values for which zero stands for False and one stands for True. Let ⊕ be the sum operator defined over $\mathbb{B}$, and ∧ is the product operator. Specifically, ⊕ is the logical XOR operator (the output bit is one if and only if the input bits are not equal), and ∧ is the logical AND operator (the output bit is one if and only if both the input bits are one). A Boolean function can be formalized as $f:{\mathbb{B}}^n\to \mathbb{B}$. Given n, $2^n$ is the total number of n-bit long binary strings, and thus the set of all possible values of f has a size of $2^{2^n}$. Provided that, searching for an f with a defined set of desired properties is already infeasible when n is greater than five [14]. Secure cryptography systems usually employ Boolean functions with at least 13 variables. From now on, we are going to use n to denote the number of variables of a Boolean function and f to denote a generic Boolean function. Moreover, we are going to use the terms “binary string” and “binary vector” interchangeably.

We can formulate an f of n variables with: an ${\mathbf{\Omega }}_f\in {\mathbb{B}}^{2^n}$ point holding the truth table of f, a multivariate polynomial called the Algebraic Normal Form (ANF) of f (defined as the sum of products over $\mathbb{B}$), or a Walsh transform [13]. Particularly, let $\mathbf{w}·\mathbf{x}={⨁}_{i=1}^n{\mathbf{w}}_i\wedge {\mathbf{x}}_i$ be the dot product defined over ${\mathbb{B}}^n$: a Walsh Transform is formulated as $\widehat{F}:{\mathbb{B}}^n\to \mathbb{R}$. More precisely:

$$\widehat{F}\left(\mathbf{w}\right)=\sum _{\mathbf{x}\in {\mathbb{B}}^n}f\left(\mathbf{x}\right){(-1)}^{\mathbf{w}·\mathbf{x}}$$

(1)

From the application of $\widehat{F}$ to all the $\mathbf{w}\in {\mathbb{B}}^n$, we obtain the Walsh spectrum of f, i.e., the vector of Walsh coefficients ${\mathbf{S}}_f\in {\mathbb{R}}^{2^n}$. Given a generic ${\mathbf{S}}_f$, it is possible to build ${\widehat{\mathbf{\Omega }}}_f\in {\mathbb{Z}}^{2^n}$, which is the polar-form version of the truth table of f. We retrieve that from the application of the Inverse Walsh Transform ${\widehat{F}}^{-1}:{\mathbb{B}}^n\to \mathbb{R}$:

$${\widehat{F}}^{-1}\left(\mathbf{x}\right)=2^{-n}\sum _{\mathbf{w}\in {\mathbb{B}}^n}\widehat{F}\left(\mathbf{w}\right){(-1)}^{\mathbf{w}·\mathbf{x}}$$

(2)

There is no guarantee that calling Equation (2) by providing a generic spectrum ${\mathbf{S}}_f$ as input leads to a Boolean function, specifically, a truth table in polar form. Generally, Equation (2) outputs a polar-form-based pseudo-Boolean function $\tilde{f}:{\mathbb{B}}^n\to \mathbb{R}$. Basically, the polar form is a truth table consisting only of −1 (True) and 1 (False).

For a given pseudo-Boolean function $\tilde{f}$, there are potentially many nearest Boolean functions that can be computed starting from the pseudo-Boolean one. We are mainly interested in computing only one (f) of all the possible nearest Boolean functions in polar form of a given pseudo-Boolean function. The classical approach consists of defining f as follows:

$$f\left(\mathbf{x}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\tilde{f}\left(\mathbf{x}\right)>0\hfill \\ -1\hfill & \mathrm{if}\tilde{f}\left(\mathbf{x}\right)<0\hfill \\ -1or1\mathrm{at}\mathrm{random}\hfill & \mathrm{if}\tilde{f}\left(\mathbf{x}\right)=0\hfill \end{array}\right.$$

(3)

When $\tilde{f}\left(\mathbf{x}\right)=0$, we say that there is uncertainty with $\tilde{f}$ as regards the computation of the truth value of $\mathbf{x}$. In Equation (3), the uncertain positions are filled by adopting a random criterion (i.e., unbiased uncertainty filling). Mind that uncertain positions could also be filled by leveraging other types of strategies. Clearly, selecting how uncertain cases are managed directly influences the way function f is defined.

Once the nearest Boolean function f is computed, the corresponding Walsh spectrum can be obtained by applying Equation (1). We are interested in discovering Boolean functions with good security properties. Especially, we focus our research work on building secure Boolean functions with respect to non-linearity and balancedness.

Let $w_H:{\mathbb{B}}^n\to \mathbb{N}$ be the Hamming weight of a given binary vector, i.e., the number of values equal to 1 contained in it. The Hamming weight of f can be calculated by applying the Hamming weight to ${\mathbf{\Omega }}_f$, i.e., the truth table of f. A Boolean function f is balanced if and only if $\widehat{F}\left(0\right)=0$, i.e.,

$$\left|\{b\in {\mathbf{\Omega }}_f|b=0\}\right|=\left|\{b\in {\mathbf{\Omega }}_f|b=1\}\right|$$

Under this condition, $w_H\left(f\right)=2^{n-1}$. We define the balancedness degree of a Boolean function as

$$\mid \left|\{b\in {\mathbf{\Omega }}_f|b=0\}\right|-\left|\{b\in {\mathbf{\Omega }}_f|b=1\}\right|\mid$$

The truth table is more balanced when this balancedness degree is lower. We are interested in balanced Boolean functions since non-balanced functions are characterized by some statistical bias, which, eventually, attackers may try to use.

The Hamming-based distance between two binary vectors of equal size is the number of positions for which the corresponding bits are not equal. The non-linearity of f can be formalized as the Hamming-based distance between f and linear functions [14]:

$$\overline{\ell }\left(f\right)=2^{n-1}-\frac{1}{2}\underset{\mathbf{w}\in {\mathbb{B}}^n}{max}\left|\widehat{F}\left(\mathbf{w}\right)\right|$$

(4)

The non-linearity $\overline{\ell }$, when n is even, is bounded by the Covering Radius bound ($U_n^{\mathrm{crb}}$) [45], which states that $\overline{\ell }\le 2^{n-1}-2^{\frac{n}{2}-1}$. When n is odd, the maximum non-linearity of n-variable Boolean functions is lower bounded by $2^{n-1}-2^{\frac{n-1}{2}}$ ($L_n^{\overline{\ell }}$) and upper bounded by $2\lfloor 2^{n-2}-2^{\frac{n}{2}-2}\rfloor$ ($U_n^{\overline{\ell }}$) [46]. A Boolean function with large non-linearity can more easily defend itself from attacks based on fast-correlation [12].

4. Proposed Approach

We adopt tree-based Genetic Programming (GP) [31] to evolve symbolic formulae. Especially, these formulae, or trees, express Walsh transforms of generic pseudo-Boolean functions, from which it is possible to discover actual Boolean functions. Specifically, a generic individual, or solution, can be adopted for calculating the Walsh transform coefficients. From now on, we are going to use the terms “tree” and “formula” interchangeably.

A GP-based symbolic tree has a specific structure. In particular, a given tree is related to a specific function set and a specific terminal set. The function set contains the (mathematical) operators that can be used to fill the internal nodes of a tree. The terminal set contains the values that can be used to fill the leaves of the tree, which are typically variables and constants. 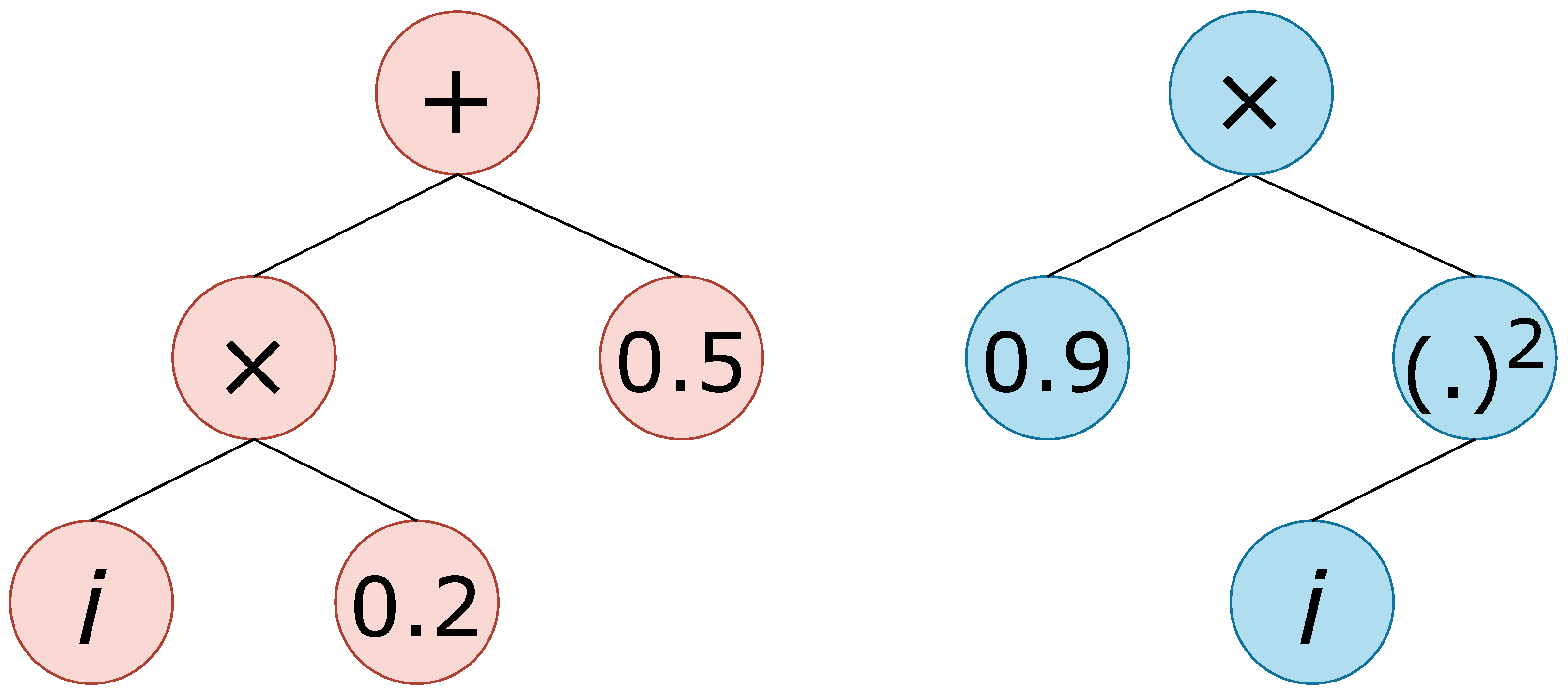In this work, we resume the tree configuration that has already been explored in [38] and provide a more in-depth comparison among different types of symbolic configurations. Specifically, we explore two types of function sets:

$$\mathsf{F}\mathsf{1}=\{+,\times ,{(.)}^2\}$$

$$\mathsf{F}\mathsf{2}=\{+,-,\times ,{\%}^{*},\mathtt{even},\mathtt{odd}\}$$

The module operator ${\%}^{*}$ is protected to avoid cases in which the denominator is equal to zero:

$${\%}^{*}(a,b)=\mathtt{sign}\left(b\right)(a\%(\left|b\right|\mathrm{if}b\ne 0\mathrm{else}1\left)\right)$$

The even function outputs 1 if the input value is an even number and 0 otherwise. On the other hand, the odd function outputs 1 if the input value is an odd number and 0 otherwise.

The input of a Walsh transform is a binary string of size n. For this purpose, we examine in-depth three variations of the input encoding. This results in three different types of terminal sets:

• A terminal set of one variable representing an integer between 0 and $2^n-1$, i.e., the integer encoded by a given binary string of size n ($\mathsf{N}$);
• A terminal set of n variables representing the binary positions of the input string ($\mathsf{B}$);
• A terminal set of n variables representing the binary positions of the input string in polar form ($\mathsf{P}$).

For each terminal set, we additionally test an extension that includes ephemeral random constants uniformly sampled between −1 and 1 ($\mathsf{ERC}$).

The combination of a specific function set and a specific terminal set provides us with a particular tree structure, which we are going to denote with the notation ${\mathcal{S}}_{\langle \mathrm{function}\_\mathrm{set}\rangle }^{\langle \mathrm{terminal}\_\mathrm{set}\rangle }$. For instance, ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$ refers to a structure with $\mathsf{F}\mathsf{1}$ as the function set and $\mathsf{N}$ as the terminal set, ${\mathcal{S}}_{\mathsf{F}\mathsf{2}}^{\mathsf{P},\mathsf{ERC}}$ refers to a structure with $\mathsf{F}\mathsf{2}$ as the function set and $\mathsf{P}$ with the addition of ephemeral random constants as the terminal set. Two examples of trees are shown in Figure 4.

Under these conditions, a tree represents a generic $\widehat{F}$. A generic tree can thus be applied to each $\mathbf{w}\in {\mathbb{B}}^n$ in a way so that a Walsh spectrum ${\widehat{S}}_f\in {\mathbb{Z}}^{2^n}$ can be retrieved. Precisely, the spectrum potentially contains real values that are eventually rounded to their corresponding integers. Then, by using the spectral inversion technique, Equation (2) can be applied to ${\widehat{S}}_f$ to obtain, in general, a pseudo-Boolean function $\widehat{f}$. The nearest Boolean function can be computed starting from $\widehat{f}$ by leveraging different strategies. These strategies differ among each other on the criterion that is adopted to assign the entries of ${\mathbf{\Omega }}_f$, where $\widehat{f}\left(\mathbf{w}\right)=0$ (large uncertainty on how to assign those entries). We explore two approaches, which we describe as follows:

(1)

Unbiased uncertainty filling: the nearest Boolean function is retrieved with Equation (3). This approach was already explored in [13].

(2)

Biased (toward balancedness) uncertainty filling: a strategy that was presented in [38] to propose a technique that tries to improve or, eventually, preserve the balancedness when computing nearest Boolean functions. This strategy is based on the idea that uncertain positions can be exploited for the purpose of balancing ${\mathbf{\Omega }}_f$. Let ${\widehat{\mathbf{\Omega }}}_f$ be the polar-form-based truth table of $\widehat{f}$. Let:

$$\begin{array}{c}\hfill v_1=\left|\{b\in {\widehat{\mathbf{\Omega }}}_f|b<0\}\right|\\ \hfill v_0=\left|\{b\in {\widehat{\mathbf{\Omega }}}_f|b>0\}\right|\\ \hfill u=\left|\right\{b\in {\widehat{\mathbf{\Omega }}}_f|b=0\}|\end{array}$$

Our purpose is to discover ${\mathbf{u}}^{*}\in {\{-1,1\}}^u$, i.e.:

$${\mathbf{u}}^{*}=arg\underset{\mathbf{u}\in {\{-1,1\}}^u}{min}|(v_1+u_1)-(v_0+u_0)|$$

where

$$\begin{array}{c}\hfill u_1=\left|\{b\in \mathbf{u}|b=-1\}\right|\\ \hfill u_0=\left|\{b\in \mathbf{u}|b=1\}\right|\end{array}$$

Obviously, the balancedness degree is not affected by the way −1 and 1 are sorted in ${\mathbf{u}}^{*}$. Hence, a given type of ${\mathbf{u}}^{*}$ can be computed deterministically (e.g., ${\mathbf{u}}^{*}=[-1^{u_1},1^{u_0}]$), and in order to enhance diversity, a random permutation of it can be performed. Finally, we obtain ${\mathbf{u}}_p^{*}\in {\{-1,1\}}^u$, i.e., a permutation of ${\mathbf{u}}^{*}$ retrieved by performing a random shuffle of it. We leverage ${\mathbf{u}}_p^{*}$ to assign the uncertain entries of ${\mathbf{\Omega }}_f$ as follows:

$$f\left(\mathbf{x}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\tilde{f}\left(\mathbf{x}\right)>0\hfill \\ -1\hfill & \mathrm{if}\tilde{f}\left(\mathbf{x}\right)<0\hfill \\ {\mathbf{u}}_p^{*}\left[ind\left(\mathbf{x}\right)\right]\hfill & \mathrm{if}\tilde{f}\left(\mathbf{x}\right)=0\hfill \end{array}\right.$$

(5)

where ${\mathbf{u}}_p^{*}\left[ind\left(\mathbf{x}\right)\right]$ is the value in ${\mathbf{u}}_p^{*}$ located at the position given by $ind\left(\mathbf{x}\right)$, where the latter represents an integer between 0 and $u-1$. Specifically, the $ind$ function is defined only for uncertain binary strings with respect to $\widehat{f}$ and provides the ranking in which these strings appear in ${\widehat{\mathbf{\Omega }}}_f$.

Once the truth table ${\mathbf{\Omega }}_f$ of the nearest Boolean function of $\widehat{f}$ is computed, Equation (1) can be applied to obtain the associated Walsh spectrum $S_f$. The fitness function is a single-objective function consisting of the non-linearity $\overline{\ell }$ Equation (4) evaluated on $S_f$. The optimization algorithm is set to maximize as much as possible the fitness function.

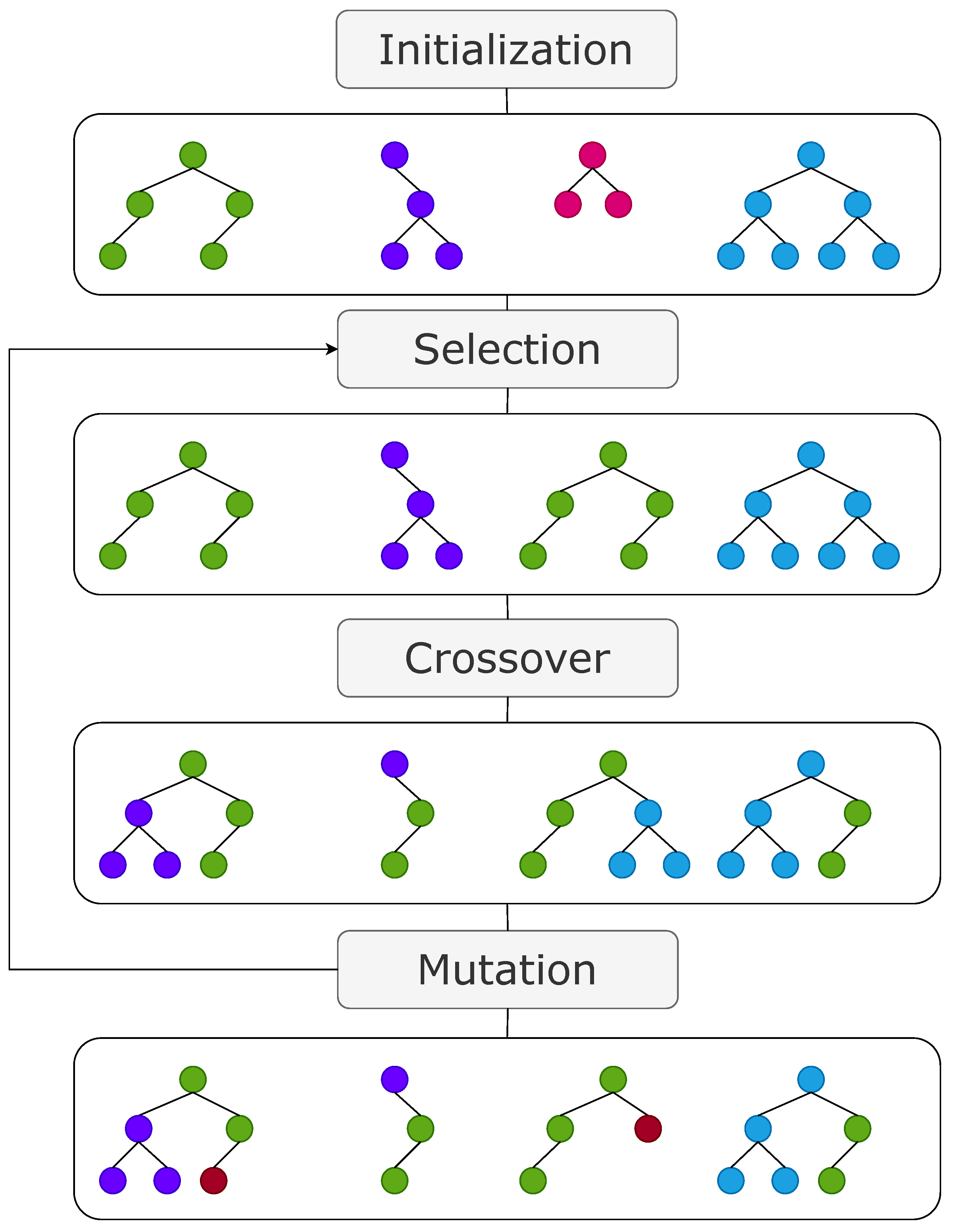
The optimization algorithm is tree-based GP [31] with a single-objective fitness function. We briefly describe the main steps of GP when evolved solutions represent symbolic formulae or trees:

• Initialization: generate an initial population of random symbolic formulae representing mathematical expressions and evaluate their fitness;
• Selection: choose symbolic formulae from the current population as parents for the next generation based on their fitness, with some randomness to maintain diversity;
• Crossover (Recombination): create new symbolic formulae by swapping sub-parts of two parent formulae, combining them to form offspring;
• Mutation: introduce random changes to offspring formula, which may involve adding, removing, or modifying sub-parts. Then, perform a novel evaluation of the fitness of the offspring and go back to the selection step so that the next generation begins.

These steps are the core of GP (Figure 5), where symbolic formulae are evolved and refined over multiple generations to approximate or represent desired symbolic relationships or mathematical expressions. In our specific context, these symbolic formulae are refined to identify a representation of the Walsh transform characterized by a large non-linearity.

5. Experimental Phase

We divide our experimental phase into three steps:

(1)

We analyze the distribution of the best solutions discovered at the end of the evolution with GP and Random Search (RS) and check whether GP is meaningfully better than RS;

(2)

We analyze the balancedness degree of the best solutions discovered at the end of the evolution, and we compare the results with the biased strategy and the unbiased strategy;

(3)

We perform an in-depth analysis of the mean percentage of uncertain positions in the discovered pseudo-Boolean functions to provide a justification of the obtained results.

We set RS as the baseline and compare it to GP. We set n with values from 6 to 16 and test both uncertainty filling strategies. We perform 30 repetitions with different seeds for RS and GP for each composition of uncertainty filling criterion, n, and tree structure.

We set a GP run with a number of generations of 5 and a population size of 500. Our fitness function is the non-linearity, and our problem is a maximization one. The selection procedure is based on tournaments of size 5, the crossover operator is a sub-tree crossover (executed with probability 0.80), and the mutation operator is a sub-tree mutation (executed with probability 0.30). We set an RS process with a sampling of 2500 random formulae (the sample size equals the fitness evaluations of GP). In particular, an RS process consists of a random generation of 2500 formulae, where the formula with the highest non-linearity is selected. The maximum depth is always 5 to limit the size of the trees (the depth of the root is 0).

Python 3.9 and Pymoo [47] are used for the implementation: BooleanCryptoGP, accessed on 10 September 2023.

5.1. Non-Linearity Distribution

An important component of this type of experimental evaluation consists of demonstrating that by leveraging the proposed approach, it is possible to exploit the advantages of a GP-based exploration, which should be, given the context, more effective than a simple RS-based method, even when the population size and number of generations are small.

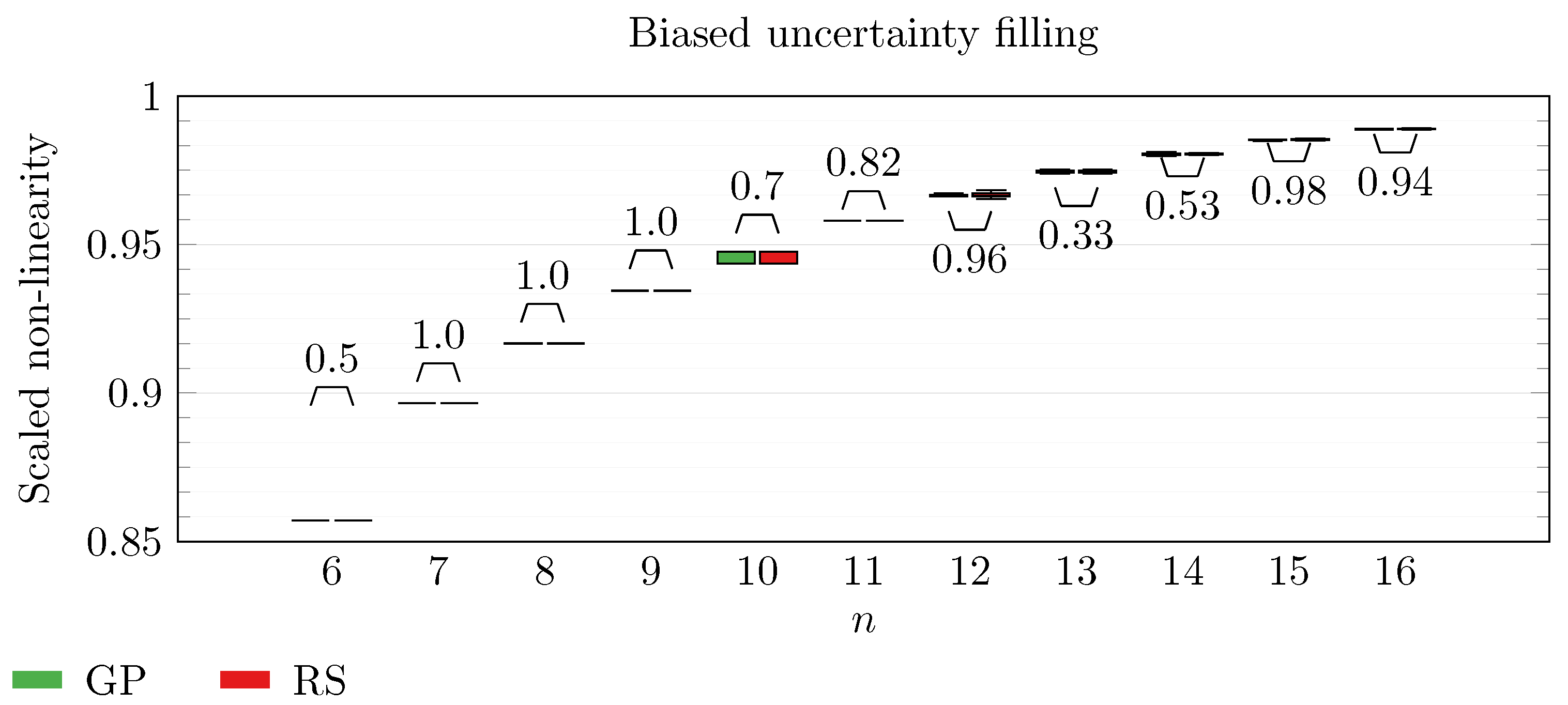
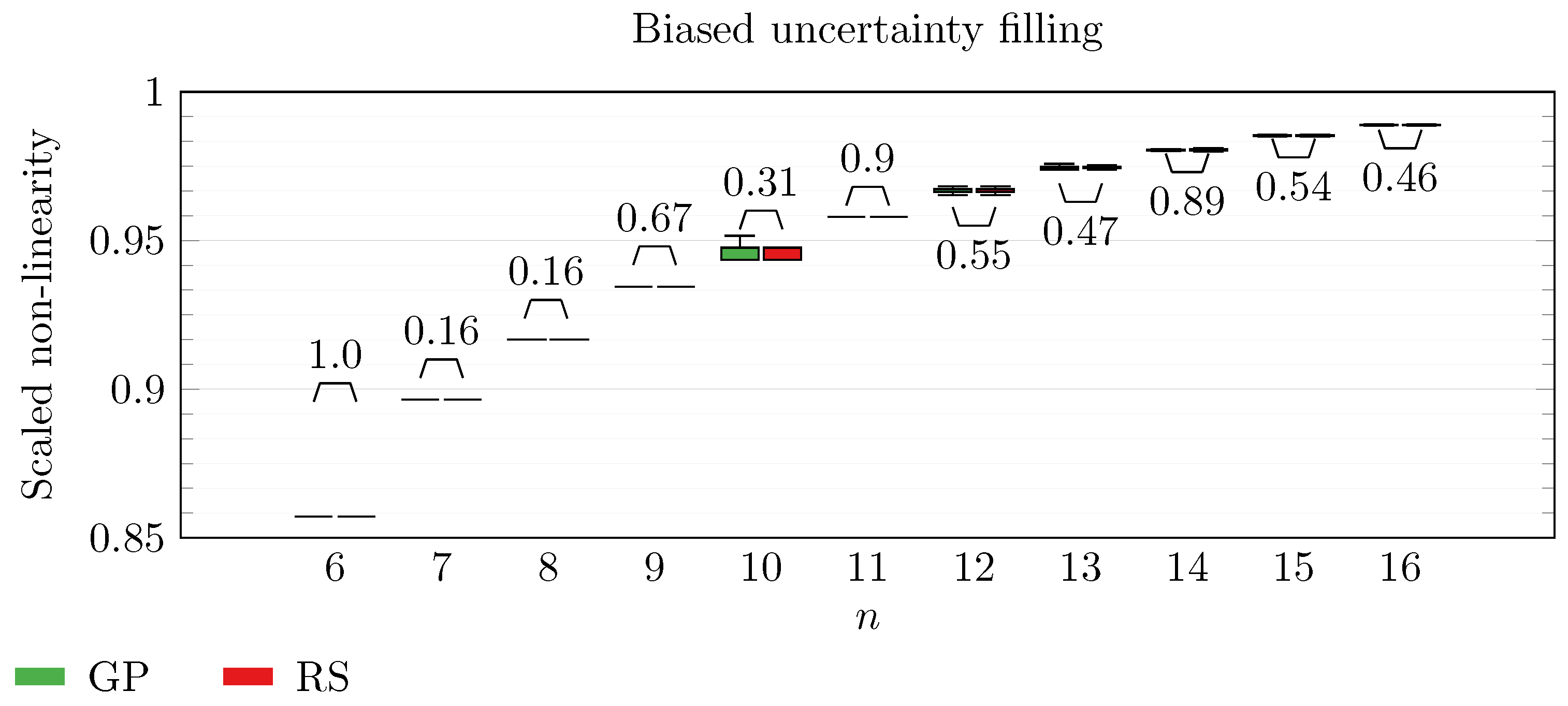
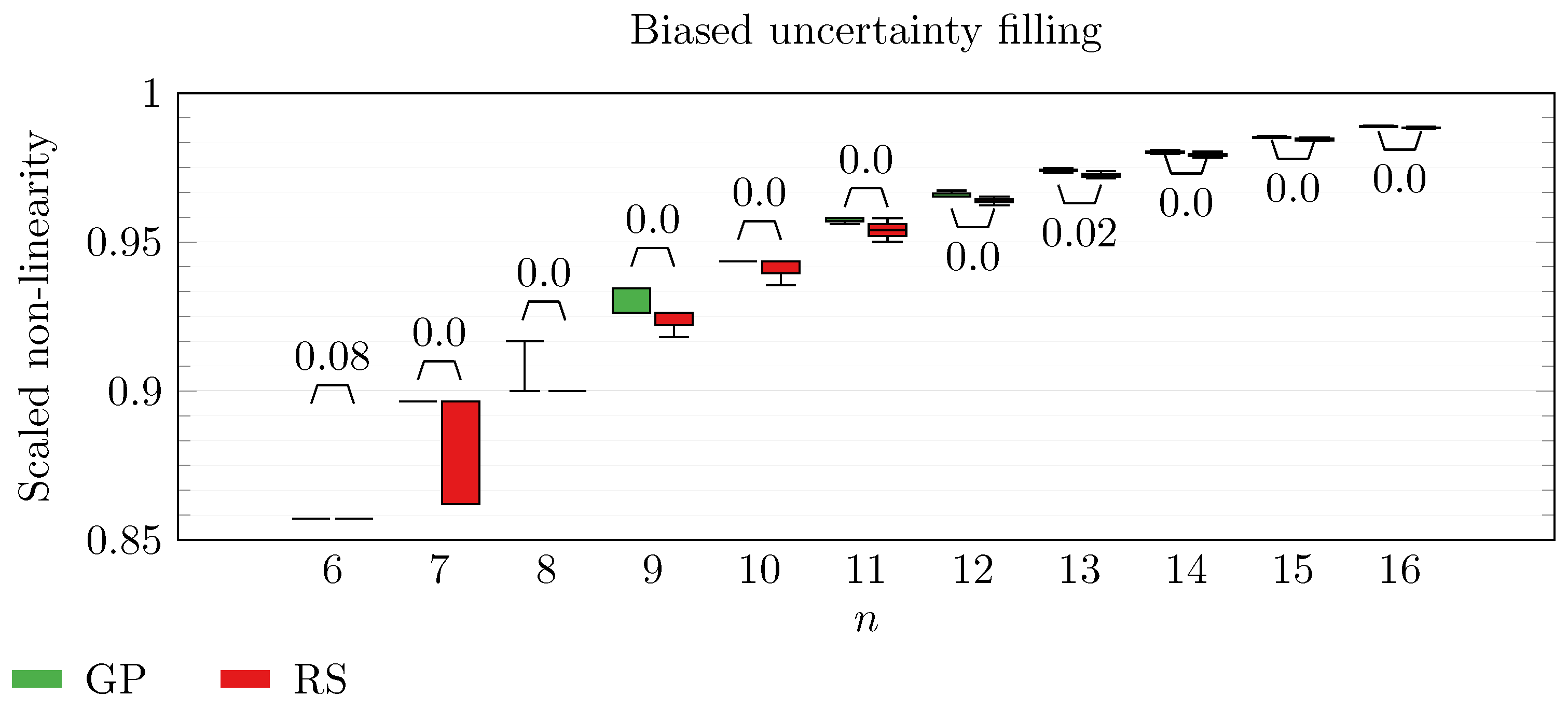
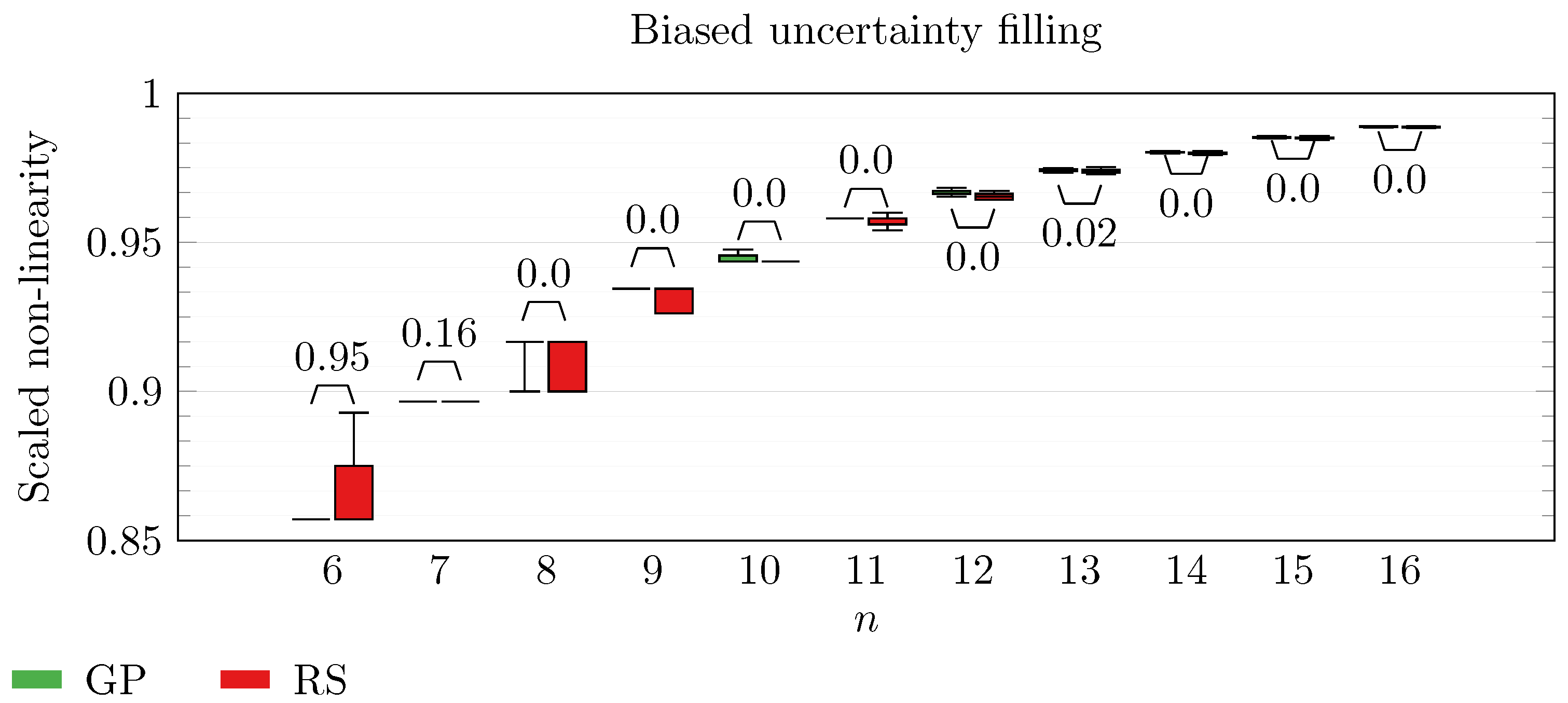
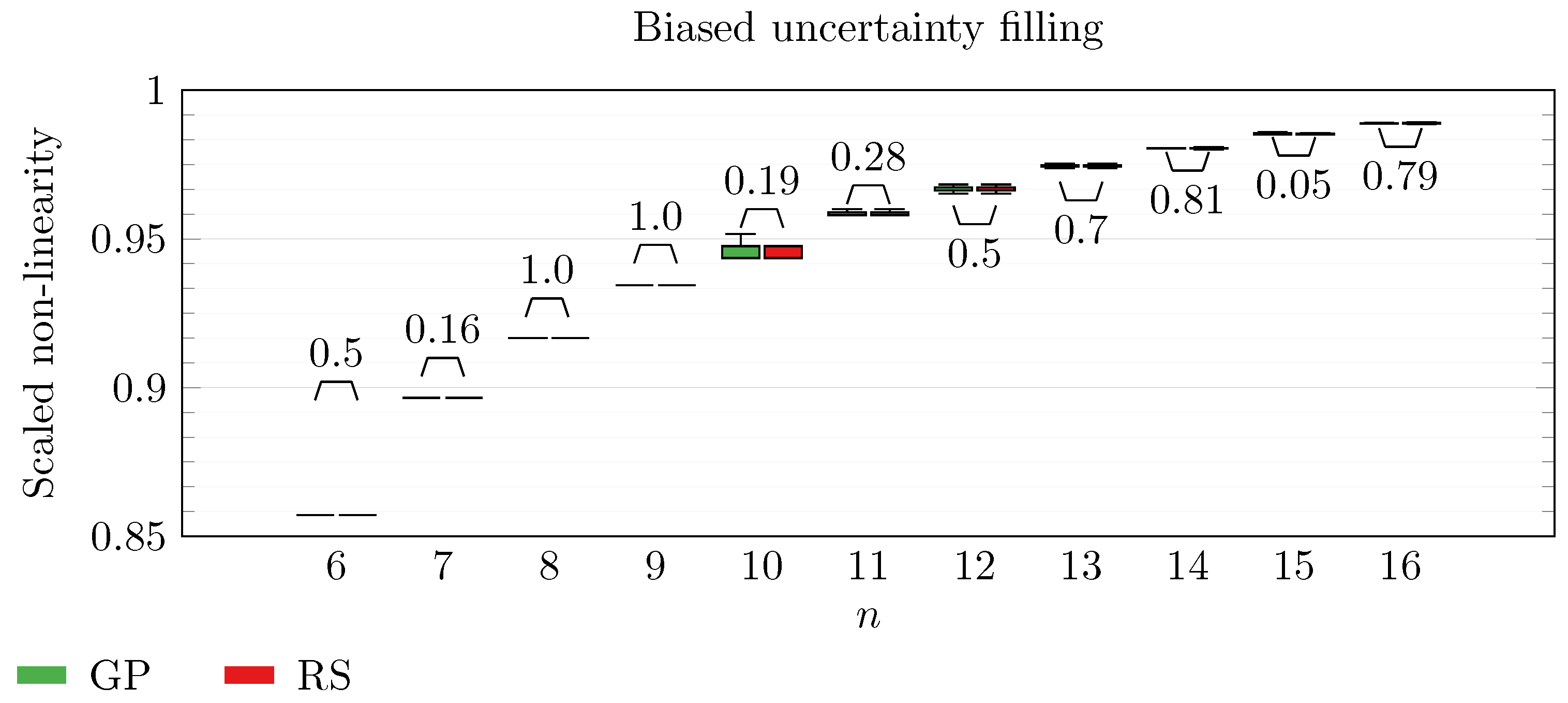
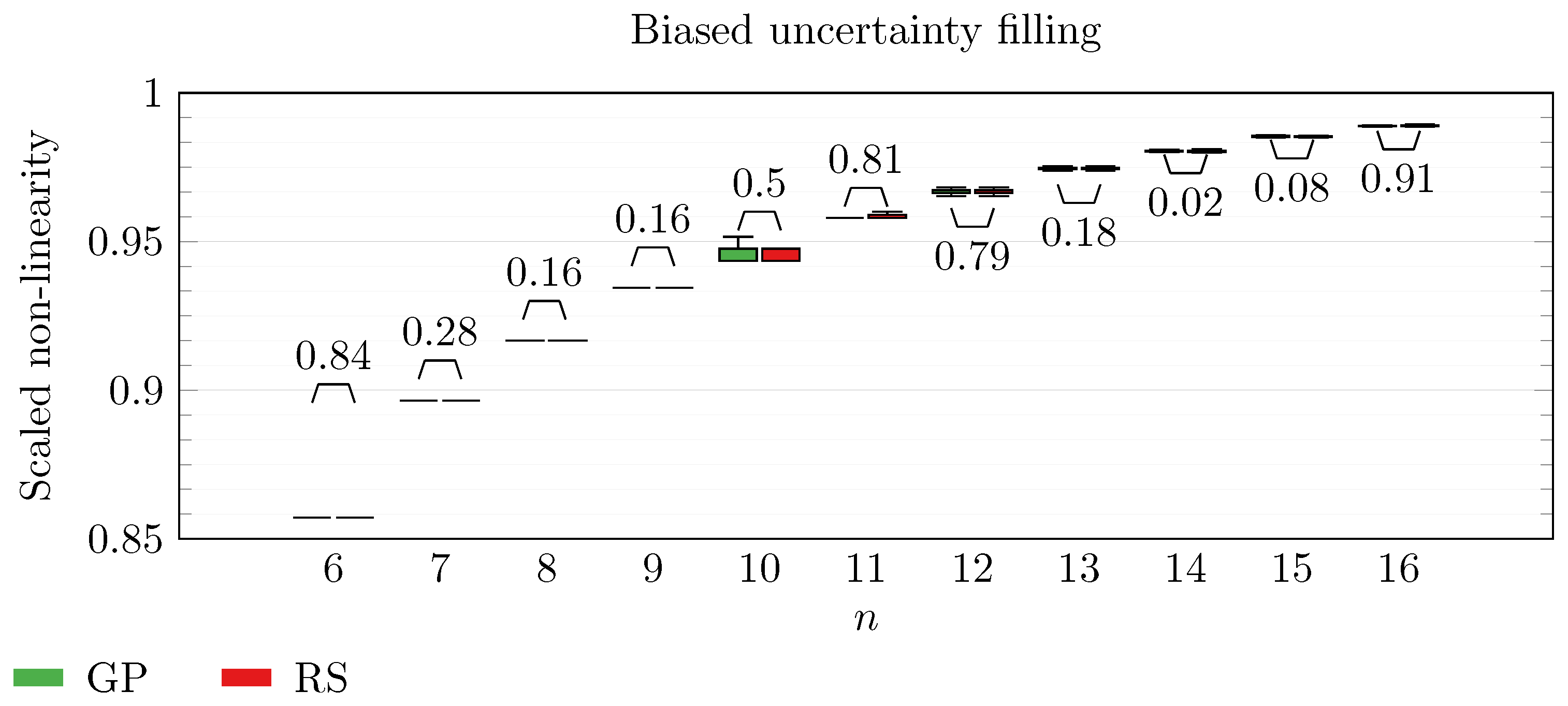
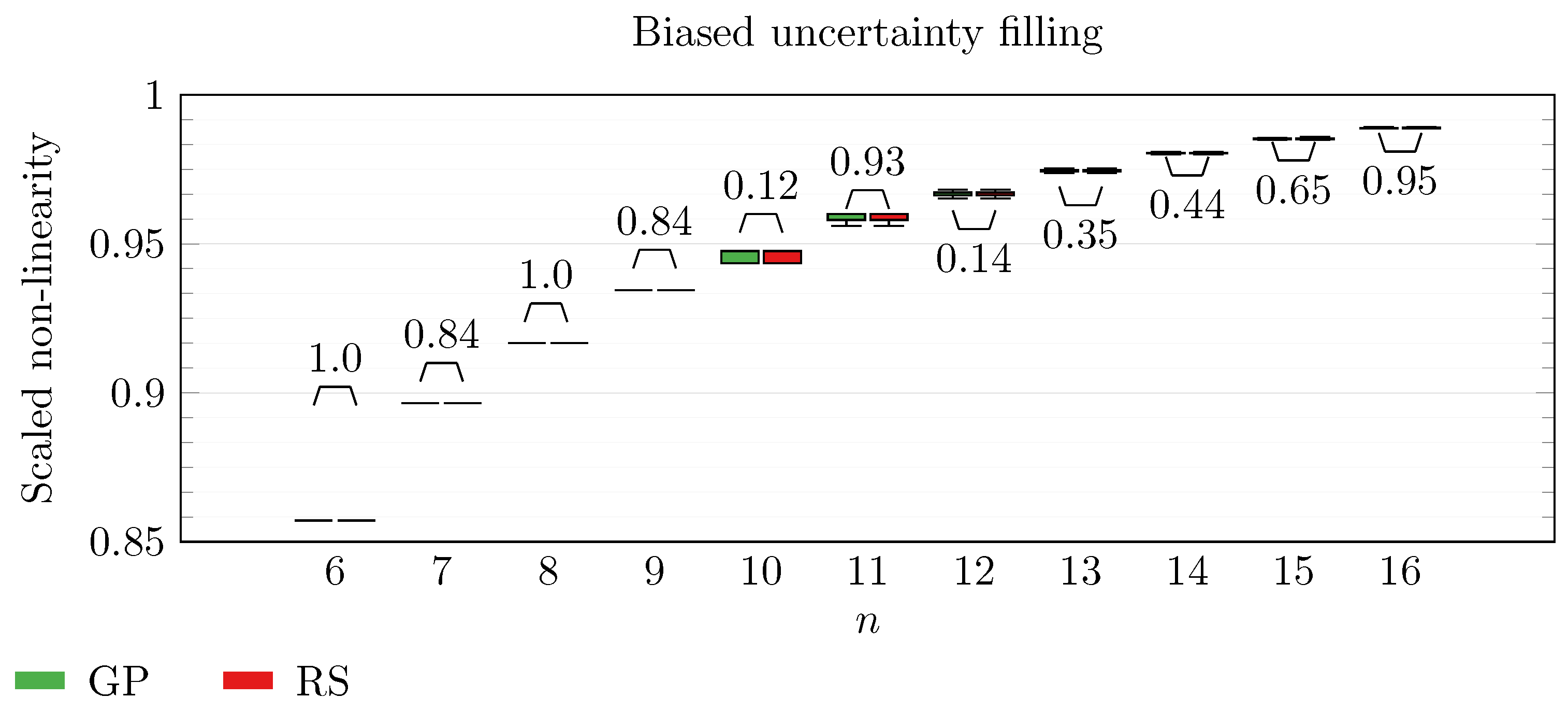
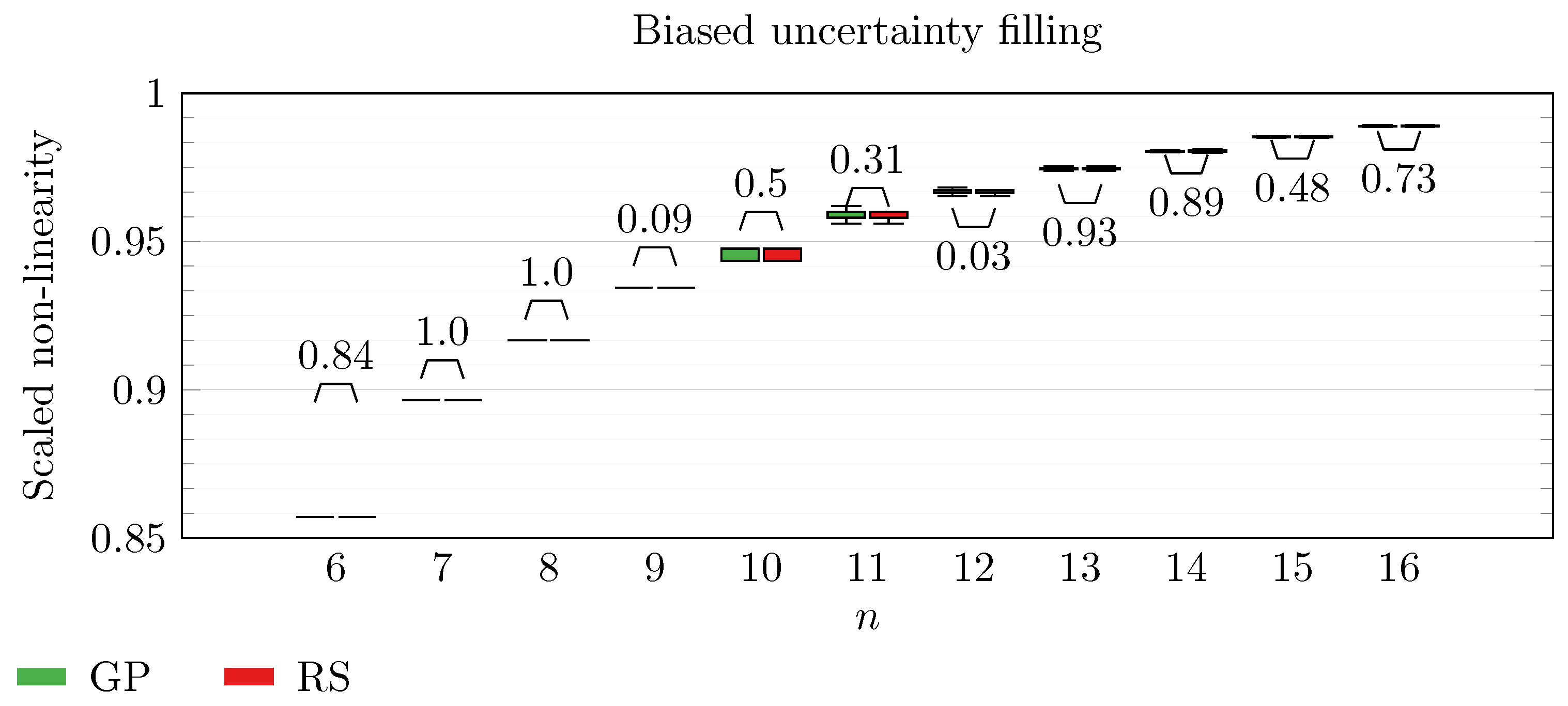
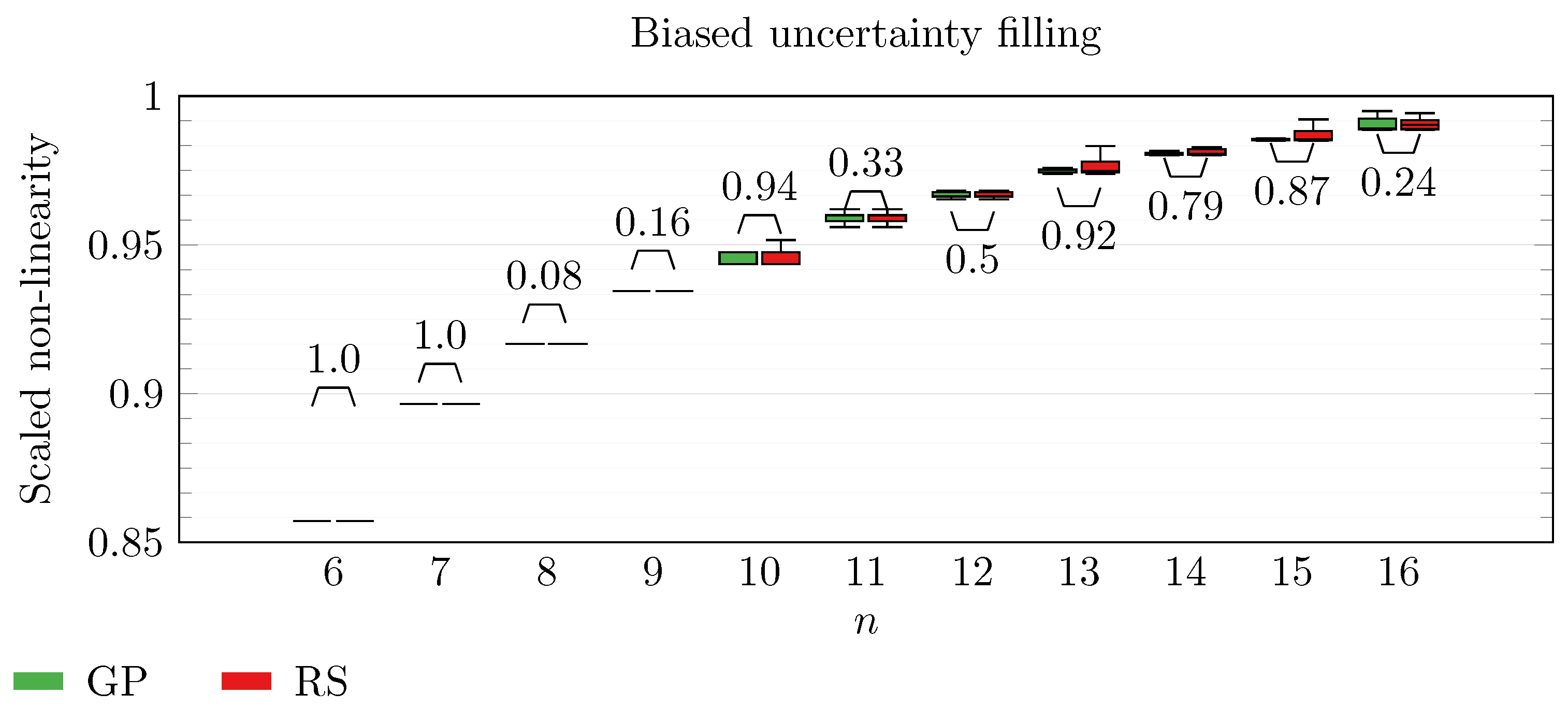
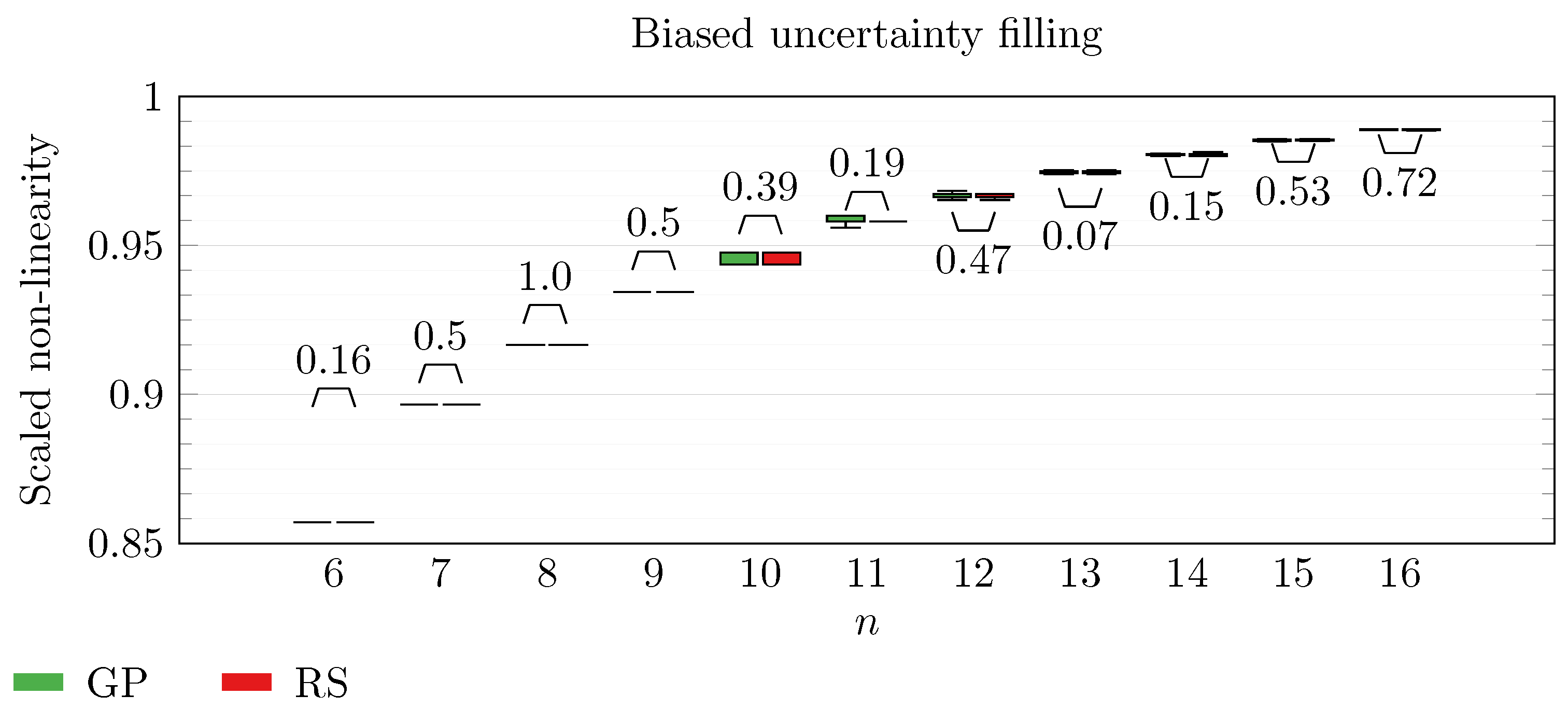
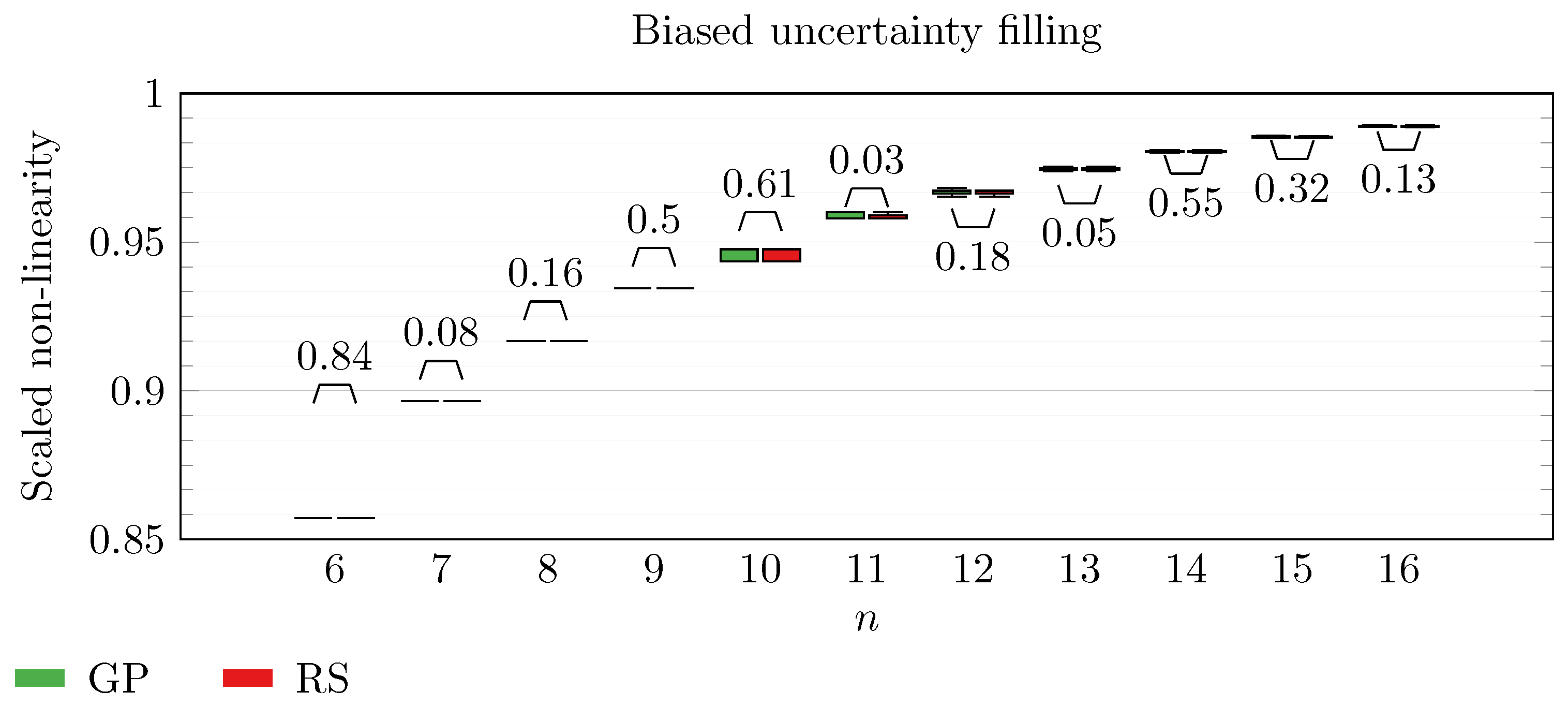
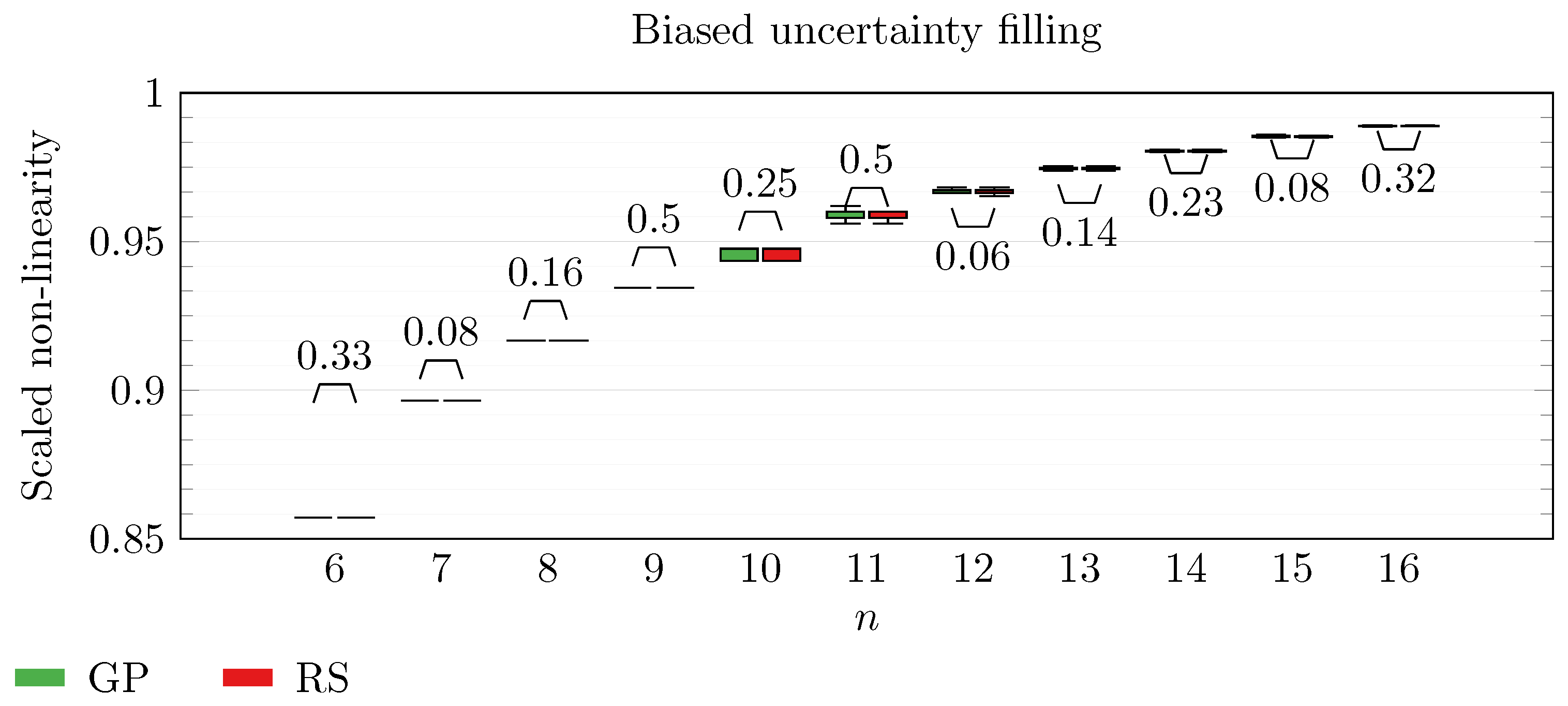
We operate a comparison of the distribution of non-linearity of the best individuals identified with RS and with full GP evolution. In this experiment, we adopt the biased uncertainty filling method. In the following box-plots (Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17), we show the results of this experiment, and we attach for each n the p-value of a Wilcoxon signed-rank test [48] performed on non-linearity values across all the repetitions. To make the plot readable, scaling between 0 and $U_n^{\overline{\ell }}$ is executed on each non-linearity value.

By inspecting the box-plots, we can easily observe that ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$ are the only Walsh transform symbolic representations that are able to take advantage of a GP evolution to reach better non-linearity values than RS (Figure 8 and Figure 9). All the other tested symbolic representations provide us with a negative result in which the corresponding GP evolution is not meaningfully better than RS.

This type of analysis highlights that ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$ are the configurations that, for this problem, provide the best results, and thus it is likely that future research efforts should focus on these types of configurations. As a final notice, we can see that the non-linearity tends to improve as n increases in all the box-plots.

5.2. Balancedness Degree

In this step, we provide an analysis of the balancedness degree of the best individuals identified with GP. In this phase, we employ the balancedness-preserving uncertainty filling criterion, and the aim consists of proving that this criterion is meaningfully better than the standard unbiased one as regards discovering balanced Boolean functions. For each tested uncertainty filling criterion and n, we perform the comparison of the distribution of balancedness degree across 30 repetitions. Particularly, we execute a Wilcoxon signed-rank test [48] for each n with the purpose of making a comparison between the balancedness degrees achieved from the two approaches.

We perform this experiment with ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$, i.e., the only symbolic configurations that are promising as regards the formulated problem. The results are presented in

Table 1. Table that details the mean ($\mu$) and standard deviation ($\sigma$) of the balancedness degree belonging to the best individuals. The p-values of the Wilcoxon test [48] are detailed as well. The results are based on GP with ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ as the tree structure.

n	Biased	Unbiased	p-Value
	$\mu \pm \sigma$	$\mu \pm \sigma$
6	0.53 ± 2.0	7.53 ± 2.12	0.0
7	0.0 ± 0.0	9.86 ± 5.34	0.0
8	0.0 ± 0.0	15.67 ± 6.95	0.0
9	0.0 ± 0.0	24.03 ± 10.42	0.0
10	0.0 ± 0.0	34.03 ± 19.28	0.0
11	0.0 ± 0.0	37.96 ± 21.88	0.0
12	0.0 ± 0.0	62.84 ± 44.66	0.0
13	0.0 ± 0.0	78.07 ± 42.94	0.0
14	0.0 ± 0.0	94.27 ± 67.75	0.0
15	0.0 ± 0.0	137.8 ± 107.01	0.0
16	0.0 ± 0.0	278.87 ± 185.31	0.0

and

Table 2. Table that details the mean ($\mu$) and standard deviation ($\sigma$) of the balancedness degree belonging to the best individuals. The p-values of the Wilcoxon test [48] are detailed as well. The results are based on GP with ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$ as tree structure.

n	Biased	Unbiased	p-Value
	$\mu \pm \sigma$	$\mu \pm \sigma$
6	0.0 ± 0.0	7.03 ± 2.36	0.0
7	0.0 ± 0.0	9.89 ± 4.07	0.0
8	0.0 ± 0.0	17.47 ± 8.2	0.0
9	0.0 ± 0.0	26.22 ± 11.89	0.0
10	0.0 ± 0.0	34.8 ± 17.59	0.0
11	0.0 ± 0.0	46.48 ± 29.98	0.0
12	0.0 ± 0.0	50.8 ± 38.46	0.0
13	0.0 ± 0.0	95.2 ± 69.43	0.0
14	0.0 ± 0.0	101.38 ± 60.62	0.0
15	0.0 ± 0.0	178.51 ± 128.97	0.0
16	0.0 ± 0.0	304.38 ± 218.25	0.0

.

The results demonstrate that by employing the biased uncertainty filling method, we have a high probability of discovering balanced solutions. We stress that balanced Boolean functions are preferable for constructing secure stream ciphers because of their resistance to statistical-bias-based attacks. For this reason, we believe that employing a biased uncertainty filling approach is almost mandatory when adopting these types of optimization techniques based on spectral inversion. As a matter of fact, by adopting an unbiased uncertainty filling method, we would probably end up with a totally unbalanced function, which should be absolutely avoided for safety concerns.

5.3. Uncertainty Position Percentage

In this step, we perform an in-depth analysis of the results obtained in the previous experimental steps to provide an explanation of and a justification for the negative results highlighted in Section 5.1. As we have already explained in Section 4, when applying spectral inversion to a symbolic formula representing a generic Walsh transform, we obtain a pseudo-Boolean function, which is basically a pseudo-truth table in polar form containing integer values. These values may be either strictly negative, strictly positive, or zero. We have explained that, since the output of spectral inversion is a function in polar form, negative values are mapped to True and positive values are mapped to False. On the other hand, zero values are said to be “uncertain” positions, which need to be filled via a random criterion (i.e., an uncertainty filling strategy, such as the ones proposed in Section 4).

In a setting like this one, if the percentage of uncertain positions in the pseudo-truth table is high, then the nearest Boolean function is computed almost entirely at random. This is not beneficial for the fitness optimization, since in this way, we lose the advantages of an actual evolution and end up with a standard random-search-based method that adds no intelligence to the way the fitness landscape is explored.

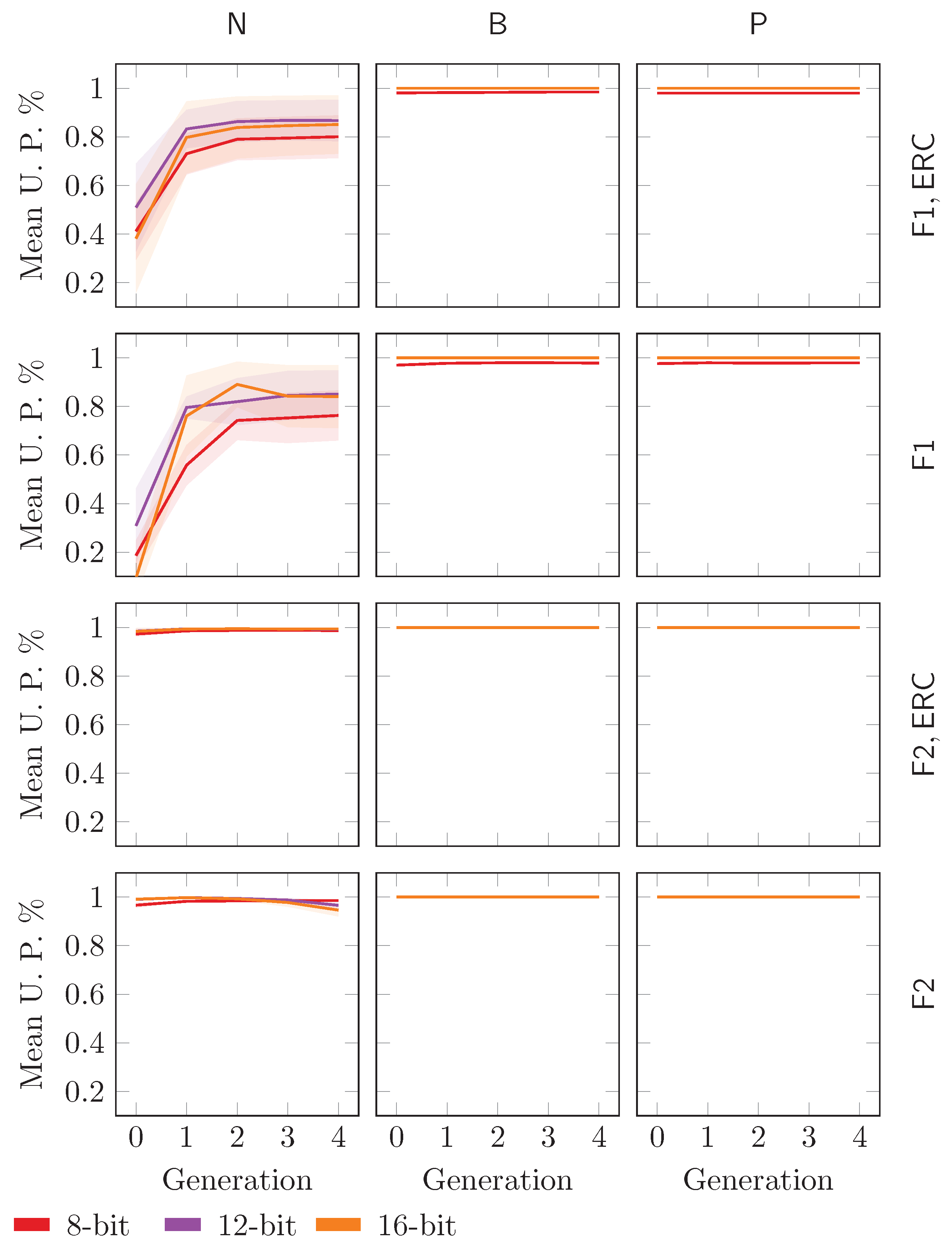
To this end, we analyze the mean uncertainty position percentage of the pseudo-truth tables corresponding to the individuals in the population across the executed generations and repetitions. We perform this experiment with n equal to 8 bit, 12 bit, and 16 bit. We test all the symbolic representations for the Walsh transform. We adopt the biased uncertainty filling strategy. The trend of the mean uncertainty position percentage is presented in Figure 18 (shaded area represents variance).

The plot shows that in almost all the cases, the mean uncertainty position percentage is approximately 1.0 for the whole evolution, meaning that the method resembles a random-search-based technique. Interestingly, we can see that the trend is lower only for ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$, i.e., the only tree structures that have been shown to outperform RS. This means that if we use a configuration that is different from ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$, then we identify pseudo-Boolean functions with an extremely high percentage of uncertain entries, which are, consequently, assigned with non-deterministic choices. These choices clearly invalidate the whole evolution. ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$ are clearly the only configurations that provide pseudo-Boolean functions that can be actually improved by an evolution based on GP, since the percentage of uncertain entries is not so high that the individual is entirely built at random.

6. Discussion

Following, we recap the research questions presented in Section 1 and try to provide an answer to them based on the observed results:

RQ1. 

Can we easily obtain balanced solutions?

We demonstrate that by using the proposed biased uncertainty filling method, we are able through a GP evolution to discover solutions that are balanced. This is of paramount importance since unbalanced functions have a statistical bias that can be exploited by attackers. Therefore, it is essential to guarantee a high chance of building balanced solutions when using the proposed spectral inversion technique.

RQ2. 

Can we leverage a GP-based evolution to discover solutions with higher non-linearity than random search?

We show that by using GP, we are able to discover better solutions than RS even if we set a small population size and a low number of generations, provided that we use a specific type of symbolic tree structure. In this case, it seems that the (scaled) non-linearity is usually larger than 0.90. This means that by employing ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$ as tree structures along with GP and biased uncertainty filling, the proposed technique has the potential to identify Boolean functions characterized by a large non-linearity. Therefore, performing an exploration of the search space composed by Walsh transforms is potentially an interesting approach. As a further remark, we stress that for the numbers of bits that have been extensively studied in a way for which the optimal non-linearity has been derived [12], given the complexity of the problem, GP is still unable to reach the optimal non-linearity.

RQ3. 

What are the implications of changing the tree syntactical structure as regards our fitness function?

We provide an analysis of why with certain types of symbolic representations the GP-based method is not able to perform better than random search. We find the justification of this phenomenon in the percentage of uncertain positions in the pseudo-truth tables obtained through spectral inversion. To this end, by analyzing the mean uncertainty position percentage across the executed generations, we show that when the tree structure is different from ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N},\mathsf{ERC}}$ and ${\mathcal{S}}_{\mathsf{F}\mathsf{1}}^{\mathsf{N}}$, the percentage of uncertain positions in the pseudo-truth tables constructed during the evolution is so high that the corresponding nearest functions are basically built at random, making the evolution ineffective and no different from a simple random search. On the other hand, when the percentage of uncertain positions is lower, then there is a portion of these pseudo-truth tables that actually take advantage of the GP evolution, leading to better solutions than random search.

This article provides a comprehensive analysis of how to design and implement Boolean functions that can serve as components for safe stream ciphers. In particular, as we have already seen in Section 3.1, we only need a safe Boolean function to build a confidentiality-safe stream cipher that can be adopted in real-world applications. As a matter of fact, we can adopt a Vernam cipher with PRG so that we do not need a key that is as long as the exchanged message. This is an almost mandatory requirement as regards cipher applicability in real-world tasks. Moreover, we can employ the Combiner model as PRG to guarantee confidentiality of the communication. However, this holds true if and only if we provide to the Combiner model a Boolean function characterized by good safety features. With our proposed approach, it is indeed possible to build Boolean functions that should respect those types of features. We can run our evolutionary process, retrieve the best solution, and plug that solution into a Combiner model that is employed as PRG in a Vernam cipher. In this way, we obtain a confidentiality-safe stream cipher that can be adopted in real-world problems for securing communications against eavesdroppers.

As a final analysis, we try to discuss possible validity threats when they apply in our context. All our experiments are executed on computational resources internal to the university. The only goal of our experiments is to assess the validity of a hypothesis. In our specific case, we run several repetitions (with different random seeds) of a heuristic optimization algorithm that performs calculations that are based on both deterministic and non-deterministic choices. Therefore, the internal validity is ensured by the fact that we set our random seeds to ensure reproducibility with a dedicated Python environment wherein dependencies and versions are detailed. Moreover, we perform several (30) repetitions that are statistically meaningful for our hypothesis. Changing the Python version or versions of some of the installed packages is unlikely to change the values of the results since non-deterministic choices are controlled by built-in Python libraries based on our fixed random seeds.

As regards the external validity, the only possible limitation consists of analyzing a re-implementation of our code with, for instance, a different coding language. Even in this case, the results may vary a little bit, but since we assess the validity of our hypothesis with statistical tests performed on many repetitions, we believe the final conclusions are unlikely to vary.

7. Conclusions

In this article, we introduce an evolutionary-based approach that discovers potentially balanced Boolean functions characterized by good non-linearity by performing an exploration of the search space composed by Walsh transforms, i.e., particular Boolean function representations. In our method, a Walsh transform is a symbolic formula with a given functions set and terminal set that can be evolved by leveraging GP. In addition, we present and analyze an effective balancedness-preserving strategy that enables us to obtain balanced Boolean functions when computing the nearest Boolean functions starting from the corresponding pseudo-Boolean ones.

In our experimental phase, we study and implement different types of Walsh-transform-based representations by using different combinations of the function set and the terminal set. We test these representations by performing several GP runs and RS runs. We perform a rigorous comparison between GP and RS and try to figure out whether the space determined by evolving Walsh transforms with GP represents an encouraging strategy for the purpose of devising Boolean functions that can build confidentiality-safe stream ciphers. For this particular problem, the results show that the convergence is faster for GP than the baseline based on RS, and this is evident even with a small population size with a low number of generations, making the proposed approach a promising one that deserves further research effort. However, we demonstrate that this result is possible only if a specific type of combination of function set and terminal set is adopted.

To this end, we provide a comprehensive analysis regarding the uncertain positions of the pseudo-Boolean functions that are built with spectral inversion. We show that for the majority of the tree syntactical structures, the percentage of uncertain positions is so high that the corresponding Boolean functions are basically constructed completely at random, making the whole evolution useless. On the other hand, we show that if the proper function set and terminal set are selected, then the percentage of uncertain positions is low enough to make the evolution be beneficial for the maximization of the non-linearity and the selection of better solutions as generations are executed.

This leads to possible future work in which larger populations can be adopted to seek higher non-linearity values, and a comprehensive benchmark of these types of evolutionary methods for Boolean function optimization can be formalized to help point out the best exploration strategy. This way, it should be possible to check the effectiveness of these techniques when a larger search space is explored. The goal in this case would consist of figuring out whether a higher and unknown non-linearity can be discovered. Finally, a strict comparison among these methods may help to highlight the technique that has the fastest convergence and the exploration strategy that appears to be the most promising for the task of maximizing the non-linearity of Boolean functions.