Abstract
Artificial neural networks have changed many fields by giving scientists a strong way to model complex phenomena. They are also becoming increasingly useful for solving various difficult scientific problems. Still, people keep trying to find faster and more accurate ways to simulate dynamic systems. This research explores the transformative capabilities of physics-informed neural networks, a specialized subset of artificial neural networks, in modeling complex dynamical systems with enhanced speed and accuracy. These networks incorporate known physical laws into the learning process, ensuring predictions remain consistent with fundamental principles, which is crucial when dealing with scientific phenomena. This study focuses on optimizing the application of this specialized network for simultaneous system dynamics simulations and learning time-varying parameters, particularly when the number of unknowns in the system matches the number of undetermined parameters. Additionally, we explore scenarios with a mismatch between parameters and equations, optimizing network architecture to enhance convergence speed, computational efficiency, and accuracy in learning the time-varying parameter. Our approach enhances the algorithm’s performance and accuracy, ensuring optimal use of computational resources and yielding more precise results. Extensive experiments are conducted on four different dynamical systems: first-order irreversible chain reactions, biomass transfer, the Brusselsator model, and the Lotka-Volterra model, using synthetically generated data to validate our approach. Additionally, we apply our method to the susceptible-infected-recovered model, utilizing real-world COVID-19 data to learn the time-varying parameters of the pandemic’s spread. A comprehensive comparison between the performance of our approach and fully connected deep neural networks is presented, evaluating both accuracy and computational efficiency in parameter identification and system dynamics capture. The results demonstrate that the physics-informed neural networks outperform fully connected deep neural networks in performance, especially with increased network depth, making them ideal for real-time complex system modeling. This underscores the physics-informed neural network’s effectiveness in scientific modeling in scenarios with balanced unknowns and parameters. Furthermore, it provides a fast, accurate, and efficient alternative for analyzing dynamic systems.
1. Introduction
In many scientific and engineering fields, understanding and predicting a wide range of complex events is all about understanding and predicting dynamical systems. These systems often employ ordinary differential equations (ODEs) to describe and model the intricate relationships inherent in various natural and artificial processes. One such common usage is seen in compartmental models, extensively used across fields such as ecology [1], epidemiology [2], chemical engineering [3], mathematical biology [4], and economics. These models require careful estimation of numerous unknown parameters for their validity, often derived from data collected from experiments or real-world observations. This process, termed calibration of the dynamical system, constitutes a challenging optimization problem due to its iterative nature and potential convergence issues. It is also important to keep the gap between observed data and model forecasts as small as possible. This makes the accurate estimation of parameters a key step in developing models. Moreover, the need for dynamical system models with accurate parameter estimates in chemical process engineering has surged due to process optimization and control technology advancements [5]. However, the difficulties associated with parameter estimation become compounded in models, such as ODEs or differential-algebraic equations (DAEs), that exhibit non-linearity in parameters. While many system identification techniques such as the Gauss-Newton method [6], multiple shooting, recursive estimation [7], maximum likelihood estimation, Markov chain Monte Carlo-based Bayesian inference [8,9], finite element methods [10], and collocation methods [11] are available for learning parameters and solving dynamical systems, each has limitations, including high computational costs, reliance on initial guesses, and limitations with time-varying parameters. Despite the challenges, the role of parameter estimation in model accuracy and predictability remains paramount, calling for continued innovation and research in this fundamental mathematical field.
Artificial intelligence (AI), particularly the implementation of deep neural networks (DNNs), has experienced a significant increase in applications for analyzing and interpreting complex systems [12,13]. This is especially true for dynamical systems, which present complex interactions requiring sophisticated analytic tools. Although these AI models have demonstrated remarkable efficacy in data fitting and short-term prediction tasks, their implementation may need to be improved due to certain obstacles. One major barrier is that it takes work for AI models to understand the underlying structures of a dynamic system’s activities. The resulting AI model predictions and real system behaviors may be at odds with one another. Additionally, the performance of these models is heavily reliant on the quantity and quality of input data, potentially resulting in inadequate insights when the data fails to portray the system’s dynamics. Artificial neural networks (ANNs) have gained popularity as an AI model because of their potential to overcome common problems in the field, such as the necessity of massive training datasets and high processing costs. It has been proposed that ANNs can be used to pioneering effect in estimating parameters in systems of differential equations. The advent of ANNs traces back to the 1940s, primarily attributed to the research article by McCulloch and Pitts [14]. However, it is only in recent years that ANNs and DNNs have seen widespread acceptance and use, owing to significant advancements in computational capabilities and data storage. DNNs, essentially ANNs with multiple hidden layers, have seen a surge in application across different sectors, including computer vision, image processing [15], pattern recognition [16], and cybersecurity [17]. The architecture of DNNs allows them to capture more variance, contributing to their success.
The effectiveness of compartmental models, which are often described by systems of ordinary differential equations, and the effectiveness of AI models in understanding and predicting the behaviors of dynamical systems have been demonstrated. However, they are not without their weaknesses. Researchers are increasingly gravitating toward combining compartmental and AI models to improve their abilities to analyze and predict the behavior of dynamical systems. The recent emergence of physics-informed neural networks (PINNs) has demonstrated a promising stride in integrating differential equations into neural networks [18]. This allows the networks to fit the data accurately, learn the parameters, and adhere to the equations. This approach employs neural networks to simulate nonlinear systems while minimizing the necessary data and limiting the model’s search space with pre-existing knowledge, such as a system of differential equations. Since this development, physics-informed neural networks (PINNs) have been routinely employed as a method for nonlinear function approximation. These networks have exhibited impressive capabilities in tackling diverse scientific computing tasks across multiple fields. Moreover, various research initiatives have utilized the PINNs framework for modeling and scrutinizing dynamic systems. Oluwasakin et al. introduced the logistic-informed neural network (LINN), inspired by the physics-informed neural network (PINN), to specifically predict the number of individuals infected by the COVID-19 Omicron variant. The major benefit of using LINN in their study lies in its ability to incorporate logistic growth behavior directly into the neural network, resulting in predictions that align well with the natural growth pattern of an epidemic. This method provides more accurate and reliable forecasts for the Omicron variant spread, crucial for timely and effective public health responses and resource allocation. By integrating logistic growth principles, LINN ensures that the model’s predictions are not only data-driven but also grounded in epidemiological knowledge [19]. The PINN algorithm was used to learn the epidemiological parameters of a model for COVID-19 vaccine efficacy [20]. Long et al. applied PINN to identify and predict the time-varying parameter of the susceptible (S), infected (I), recovered (R), and death (D) (SIRD model) [21], Olumoyin et al. used the epidemiological-informed neural network (EINN), which was developed through PINN, to learn the time-varying transmission rate for the COVID-19 pandemic in various mitigation scenarios [22]. Thus, this paper seeks to make the following significant contributions:
- We employ physics-informed neural networks (PINNs) to learn the unknown time-varying parameters within systems of differential equations.
- Although the application of PINNs in modeling dynamic systems is well-established, our work introduces novel approaches that substantially augment the existing methodology. Firstly, we present a unique assumption where the right-hand side function of a dynamical system is posited to have an equal number of parameters and equations. This hypothesis is pivotal because it implies the existence of an exact solution for the system, a scenario rarely considered in the existing literature. By demonstrating this principle, we provide a foundational understanding that can be leveraged for more accurate modeling of certain types of dynamical systems. Secondly, we address the more complex situation where the number of parameters does not align with the number of equations in the dynamical system. Here, we focus on developing and optimizing network architectures that significantly enhance the convergence speed. This innovation results in improved computational efficiency and elevates the accuracy in estimating time-varying parameters. Our approach is particularly effective in complex systems where traditional models struggle with computational load and accuracy.
- We thoroughly compare parameters obtained using physics-informed neural networks (PINNs) and those derived from fully connected deep neural networks (DNNs). To assess the effectiveness of both methodologies, we focus on two key aspects: computational efficiency and accuracy. Computational efficiency is evaluated based on the time and resources required to achieve convergence, while accuracy is measured in terms of the fidelity of the parameters to known or established values. We employ a suite of established error metrics, including mean absolute error (MAE), root mean square error (RMSE), and mean squared error (MSE), to evaluate the performance of the proposed method rigorously. These metrics provide a comprehensive view of the method’s accuracy and reliability in different scenarios. The evaluation process is designed to validate the efficacy of PINNs in modeling dynamical systems and offer insights into how they compare with traditional DNN approaches. By analyzing the results through these error metrics, we can draw informed conclusions about the practicality of employing PINNs for complex dynamical systems, particularly regarding their ability to provide precise and computationally efficient solutions.
- We show that employing the PINN algorithm to this specific problem becomes computationally more efficient as the number of layers increases, outperforming DNNs in terms of computational time. This finding suggests that PINNs can provide faster processing rates for complex computational tasks, providing a substantial advantage for time-sensitive applications.
The paper is organized as follows: Section 2 discusses the systems of ordinary differential equations used in the study. Section 3 explores the neural network used for analysis. Section 4 examines error metrics for model performance assessment. Section 5 analyzes computational simulations of dynamical systems. Finally, Section 6 concludes the paper, summarizing the study’s main findings and key points.
2. Systems of Ordinary Differential Equation
Consider a dynamical system characterized by n ordinary differential equations encompassing m undetermined parameters (see also, [12]).
These equations make up the mathematical model that describes the system’s behavior being studied, with m parameters that define the system’s characteristics. In this context, = [, , , ..., ] is a vector field composed of n components. Further, let = [, , ..., ] be the vector encompassing the unknown parameters, and be the initial condition. On the right-hand side of (1), we have the vector-valued function
not necessarily linear, consisting of n components designated as
with k = 1, ..., n. The data for the model equation will be represented by .
Using the data measured at P distinct time points for the given model, for , our goal is to develop physics-informed neural network (PINN) algorithm that estimates both the unidentified parameters and the solution across all time points t. Understanding the value and change of these parameters over time can give useful information about the system’s dynamic behavior, which can be used to improve predictive models and solutions.
3. Artificial Neural Network
Artificial neural networks, commonly referred to as neural networks (NNs), are computational models inspired by the biological neural networks present within the human brain [14]. These systems can learn to carry out tasks by processing a range of examples, typically without explicit, task-specific programming. While there are numerous types of artificial neural networks, this discussion primarily focuses on deep neural networks (DNNs) and physics-informed neural networks (PINNs).
3.1. Deep Neural Networks
Deep neural networks are a type of artificial neural network with multiple layers between the input and output layers. These layers, known as hidden layers, allow DNNs to learn high-level features from the input data. DNNs are a cornerstone of deep learning and are widely used for tasks such as image recognition, speech recognition, natural language processing, and many other applications. Consider a deep neural network with similar architecture in [12].
where denotes the predicted solution, are the input, is the activation function, and are the weight, and the bias, respectively. Using the DNN approach to solve and identify the parameters of the dynamical system (2.1), we find the best network parameters representing the biases and weights network that minimizes the loss function. In a DNN, the loss function is typically a measure of the discrepancy between the predictions of the network and the true output values from the training data.
and
where are the output values, are the predicted output values, and n is the number of instances.
3.2. Physics-Informed Neural Network
Physics-informed neural networks represent an advanced machine-learning technique that integrates knowledge from physical principles to provide a robust approximation of function and parameter identification. PINNs have emerged as a powerful tool among data-driven deep neural networks due to their versatility in solving inverse and forward problems [18]. A PINN is a differential system solver discovering the system parameters directly from the available data. Alternatively, it can simulate the differential system when the parameters are already known. Interestingly, PINNs are not restricted to a specific neural network architecture and can utilize architectures like feed-forward neural networks (FNNs) as their foundational framework. PINNs utilize conventional deep learning methodologies, employing standard activation functions and optimization techniques. However, the unique feature of PINNs lies in their sophisticated loss function, composed of boundary conditions, initial values, and physical restrictions. This formulation ensures that the output from the neural network adheres strictly to the underlying system of differential equations by integrating residuals from these equations into the loss function. This algorithm holds immense promise, primarily due to its ability to tackle complex, non-linear systems and process vast quantities of noisy or incomplete data. Furthermore, the duality of PINNs in managing both forward and inverse problems allows them to fit observational data effectively and generate reliable predictions based on identified parameters. Physics-informed neural networks represent a critical leap forward in machine learning. PINNs offer a dynamic and comprehensive approach to data approximation and system parameter identification by amalgamating conventional deep-learning techniques with physical principles embodied in differential equations.
3.3. Parameter Identification of Dynamical Systems Model Using PINN
Let us consider a dynamical system (1). The goal is to use the PINN approach to solve and identify the parameters of the dynamical system model. This can be conducted by finding the best network parameters , representing the biases and weights network that minimizes the loss function. We offer a physics-informed neural network shown in Figure 1, with two networks to do this. The first network outputs are , which admits t as the input data. The second network learns the parameters from the data. The following loss function was minimized.
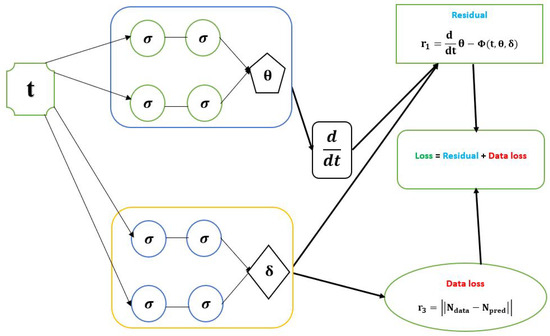
Figure 1.
Schematic diagram of the PINN with the parameters of a dynamical system of ODE model.
is called the training loss and is called the residual loss. in the total training datasets. We define the following:
where
and
The network is trained to minimize ; an optimizer such as Adams is the most optimal weight and bias that would minimize . The neural network also obtains the optimal values for the model parameters. The represents the loss function’s training data. We identify the parameter by solving Equation . When trying to address the problem , we can categorize it into two possible scenarios:
Scenario 1: In this particular instance, we assume the right-hand side function of a dynamical system (1) has an equal number of parameters and equations. This scenario shows that a solution exists. In other words, there is an exact solution [12].
Scenario 2: In this context, the number of parameters does not match the number of dynamical system equations [12].
Remark 1.
It is important to underscore that the number of networks can exceed two, contingent upon the intricacies of the dynamical system and the parameters involved.
The implementation of physics-informed neural networks (PINNs) is carried out using Python. Its simplicity and extensive library ecosystem make it an ideal choice for developing sophisticated models like PINNs. Key to our implementation is TensorFlow, which offers robust tools for building and training neural network models. TensorFlow’s compatibility with Python and its efficient handling of large-scale numerical computations enable the effective construction of PINN architectures. Additionally, we employ NumPy, a Python library that supports large, multi-dimensional arrays and matrices, along with a collection of high-level mathematical functions to operate on these arrays. This is crucial for handling the numerical aspects inherent in PINN development. We also utilize Pandas, a library for data manipulation and analysis. Pandas provides structures and functions that are ideal for modifying numerical tables and time series, making it useful for preprocessing and organizing the data that neural networks need to learn. The synergy of these libraries in Python creates a powerful toolkit for developing and implementing PINNs.
The source code in Figure 2 provides a comprehensive example of physics-informed neural network implementation, illustrating the practical application of parameter identification in dynamical systems. This Python-based code features a custom PINN class, which encompasses the complete workflow of constructing, training, and deploying the neural network for predictive analysis. At the core of this class is the initialization method, which is responsible for configuring the network’s layers, weights, and biases. This setup is facilitated by the initialize_NN function, leveraging TensorFlow’s robust computational power for efficient network architecture development. The functions neural_net and neural_net1 each articulate distinct network structures tailored for specific segments of the model. The train and loss functions represent the heart of the learning process, where TensorFlow’s optimization algorithms are utilized to refine the network by minimizing the loss function. This method effectively enables the network to learn the intricacies of the dynamical system under study. Finally, the predict function demonstrates the practical use of the trained network in generating predictions for new datasets. This implementation not only showcases the coding aspects of PINNs but also exemplifies the fusion of theoretical principles with their practical application in advanced computational modeling.

Figure 2.
PINN source code.
4. Error Metrics
This section discusses the error metrics used for data-driven simulations, examining when and why specific metrics should be employed. These error metrics provide valuable insights into the accuracy and performance of data-driven models, such as physics-informed neural networks (PINNs). By evaluating the models based on these metrics, researchers can determine the quality of their predictions and compare the effectiveness of different approaches. In the context of learning the time-varying parameters for dynamical systems, it is important to consider the specific characteristics of the problem and the goals of the analysis when selecting the appropriate error metrics. For instance, if symbolizes the actual data and represents the data predicted by the model, these error metrics are applied in our data-driven simulations:
- Mean absolute error (MAE): a significant advantage of using the mean absolute error (MAE) is its relevance to quantile regression. MAE represents an average of absolute differences between predicted and actual values. The formula for mean absolute error is given by:
- Root mean squared error (RMSE): RMSE is in the same units as the predicted variable, providing a straightforward interpretation of the model’s prediction error magnitude. The formula for root mean squared error is given by:
- Mean squared error (MSE): mean squared error (MSE) measures the amount of error in the models. It assesses the average squared difference between the observed and predicted values.
5. Computational Simulations of Dynamical Systems
This section explores physics-informed neural networks (PINNs) for parameter identification and solution in various dynamical systems. Parameter identification is crucial, especially when working with ordinary differential equations (ODEs), as each model is essentially unique. ODEs showcase their practicality when the parameters are correctly determined, emphasizing this methodology’s significance. The identification of parameters becomes evident as we develop a model employing ordinary differential equations (ODEs) to elucidate the fundamental occurrences. These parameters include different characteristics of the modeled system, such as rate constants, initial conditions, and coefficients, defining the form, rate of change, and stability of the solution. The parameters that make up an ODE can also determine the computational techniques used to solve it and have a big impact on the quality of the solution. Consequently, parameter identification is crucial for making insightful predictions and adequately assessing the simulation of the modeled dynamical system. We consider five benchmark problems derived from the existing literature in our discussion. For each example, we will specify the choice of neurons, the number of hidden layers, activation functions, and other network parameters. Two of these five problems have an exact analytical solution, which will be leveraged to validate the model’s accuracy. In addition, the relative error metric showing the fitting accuracy of each dynamical system using the PINN algorithm will be provided.
5.1. First-Order Irreversible Chain Reactions
First-order irreversible chain reactions are a type of chemical reaction where a reactant undergoes a series of transformations to form a product, with the process continuing in a chain-like manner. A common example of such a reaction is the decomposition of hydrogen peroxide (HO) in the presence of an iodide ion as a catalyst. One of the most fundamental studies on chain reactions was conducted by Polanyi and Wigner [23], who published a series of papers in the 1920s and 1930s on the theory of chain reactions. Consider the subsequent first-order irreversible chain reactions [24,25].
The first step is a first-order reaction where species transforms into species at a rate determined by the rate constant . The second is another first-order reaction where species transforms into species at a rate determined by the rate constant . In both steps, the reaction rate depends on the concentration of a single reactant (either A or B), which is characteristic of first-order reactions and characterized by the following model:
where and symbolize the concentrations of chemical species and , respectively and , denote the rate constants which are the parameters required to be learned. Given that , and , then the observed data and are given in Table 1. The data was taken from reference [12].

Table 1.
Observed values of and at different time points.
The analytical solution of is given as follows:
and the analytical derivatives of (7) are given by:
The PINNs approach to solve and identify the parameters of the first-order irreversible chain reactions model is performed by finding the best network parameters, , which represents the biases and weights network that minimizes the loss function. We offer a physics-informed neural network (PINN) shown in Figure 3 with three networks to do this. The first network outputs are and , which admits t as the input data. The second and third networks learn the parameters and from the data. The neural network also obtains the optimal values for the model parameters. The and represent the loss function’s training data. Finally, the first-order irreversible chain reaction model parameters’ mean value was obtained using PINN with one layer of 40 neurons, 90,000 epochs, sigmoid activation function used, and learning rate. The PINN Algorithm 1 for learning the optimal parameters of the first-order irreversible chain reactions model (6) is shown above.
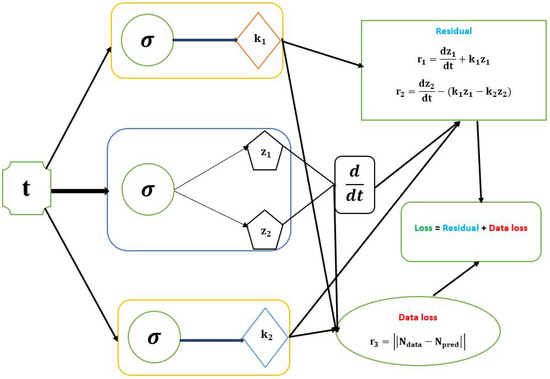
Figure 3.
Schematic diagram of the PINN with the parameters of first-order irreversible chain reactions model.
We define the residual loss and training loss as follows:
where
and
Two distinct scenarios were examined in the study of the first-order irreversible chain reactions model, with results detailed in Figure 4, Figure 5, Figure 6 and Figure 7. For Scenario 1, the system was solved using Equation (10) at and , while for Scenario 2, it was solved at and . Figure 4 shows the obtained solution of the actual output and the predicted output of the first-order irreversible chain reactions model from the data. The phase space plot of the actual output of species against species and the predicted output of species against species is shown in Figure 5. This visualization provides insight into the relationships and behaviors of the species involved. Figure 6 shows the learned time-varying parameter and values of the first-order irreversible chain reaction models, shedding light on how these parameters change over time in the first-order irreversible chain reaction models. The curve appears to have an oscillatory behavior, and the oscillation frequency seems consistent throughout the curve. Upon examining the amplitude of oscillations over time, there is a noticeable variation in amplitude. While there are some fluctuations, there appears to be an amplitude increase toward the end of the interval. Considering the observations, a potential functional form for the curve could be a simple sinusoidal oscillation with a constant offset. A common form for such a function is:
where A is the amplitude, determines the frequency, is the phase shift, and C is the vertical shift (which should be close to 5, given the curve’s behavior). The curve appears to have an initial rise, followed by a decrease, then stabilizes after a certain time. It appears to resemble an exponential decay combined with an exponential rise. A potential functional form for such a curve could be:
where a and c are the amplitudes of the respective exponential terms, b and d are the rate constants for the decaying and rising terms, and e is a constant offset.
| Algorithm 1 PINN algorithm for learning the parameters of the first-order irreversible chain reactions model |
|
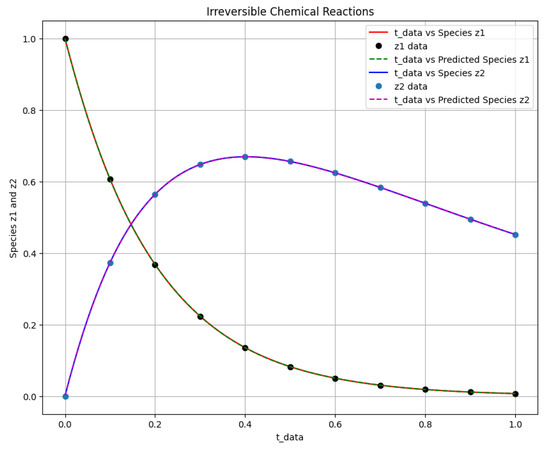
Figure 4.
The first-order irreversible chain reactions solution of the actual output of species against and the predicted output of species against .
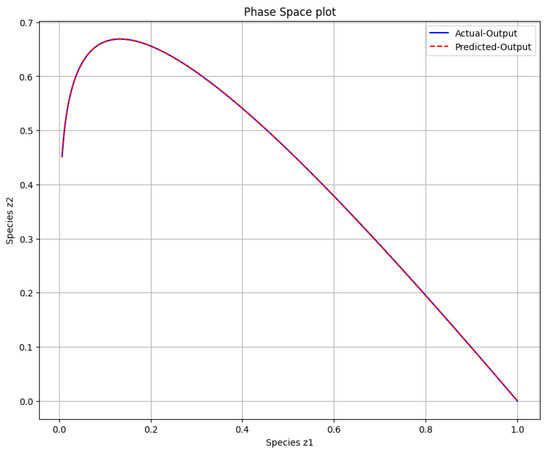
Figure 5.
The phase space plot of the actual output of species against species and the predicted output of species against species .
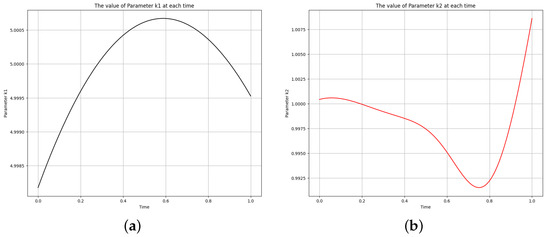
Figure 6.
The learned time-varying parameter values of the first-order irreversible chain reactions model. (a) Time-varying parameter . (b) Time-varying parameter .
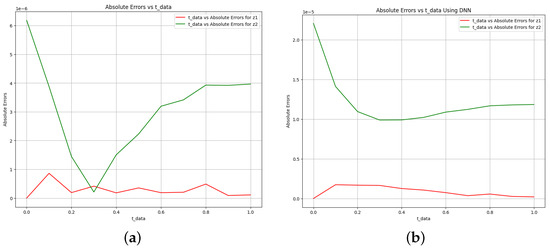
Figure 7.
Absolute error plot between the data, PINN solution, and DNN solution. (a) Absolute error plot using PINN. (b) Absolute error plot using DNN.
Table 2 shows the obtained time-varying parameters and error metrics through the approaches described in Scenario 1 and Scenario 2. We observe that Scenario 1 proved more accurate than Scenario 2. The accuracy of the PINN technique is evaluated by comparing the predicted concentrations of and with the actual values obtained from the data. These metrics provide insights into the fitting accuracy of the PINN technique. The results of the simulations show that the PINN algorithm can accurately predict the concentrations and learn the time-varying parameters of the first-order irreversible chain reactions model. The obtained time-varying parameter values are close to the true values, and the error metrics indicate high accuracy and good fitting of the model to the data.

Table 2.
Comparison of the two approaches using PINN.
In addition, we compared the results we achieved using physics-informed neural networks to those obtained using deep neural networks, as shown in Table 3 and Table 4. This comparison study used a setup of 90,000 epochs and one hidden layer containing 40 neurons, with processing time measured in seconds.

Table 3.
Comparison of obtained results using PINN vs. DNN through the approaches described in Scenario 1. The table demonstrates a significant 67.7% improvement in computational efficiency when employing PINNs compared to DNNs, highlighting the enhanced performance and time-saving capabilities of PINNs in dynamic system modeling.

Table 4.
Comparison of obtained error results using PINN vs. DNN. This table presents a detailed analysis of the error metrics for both PINN and DNN models across two variables, and . The results highlight the superior accuracy of PINNs, as evidenced by significantly lower error values across all metrics compared to DNNs, underscoring the effectiveness of PINNs in dynamic system modeling.
Figure 7 explores the model’s accuracy by showing the absolute error between the target and the predictions. Specifically, Figure 7a indicates that the absolute error is bounded by 1 when using PINN, while Figure 7b reveals that the error is bounded by 1 using DNN. This comparative analysis highlights the difference in accuracy between the two techniques, PINN and DNN, used in the modeling process. Finally, the results show that the PINN technique achieves comparable or better parameter estimation accuracy than the DNN technique. Additionally, the PINN technique exhibits faster computation times, making it an efficient choice for solving and identifying parameters in dynamical systems.
Furthermore, we also conducted a detailed investigation on the impact of augmenting the number of layers in the network called shallow vs. deep layers. Specifically, we focused on network architectures consisting of one, two, and three hidden layers, implemented using physics-informed neural networks. Subsequently, we compared the results obtained with deep neural networks. The respective outcomes of these analyses are succinctly presented in Table 5. The results indicate that the PINN with one hidden layer achieves good accuracy, and increasing the number of layers does not significantly improve performance. Interestingly, the three hidden layer PINN model showed a lower computation time (9 s) than the two layer model (13 s). There are various reasons for this unexpected outcome. Firstly, the increased depth (three layers) might enable more efficient learning and quicker convergence to a solution, thereby reducing the required epochs for training. Although the table shows more epochs for the two-layer configuration than the three-layer one, the actual computation time (CPU time) is less for the latter. This suggests that each epoch in the three-layer configuration is computationally less expensive.

Table 5.
Comparison of PINN vs. DNN based on shallow vs. deep layers through the approaches described in Scenario 1. This table details the accuracy of parameter estimation ( and ) and computational performance across various network depths. Notably, it showcases the increasing computational efficiency of PINNs over DNNs, with improvements of , and for different layer configurations. These findings emphasize the enhanced efficiency and adaptability of PINNs in handling complex dynamical systems, especially in deeper network architectures.
Moreover, the three-layer network might better capture the complexities of the modeled dynamical system, leading to more efficient computation per epoch. This is indirectly supported by parameter estimation accuracy ( and ), which are very close to their ideal values in the three-layer setup, indicating a high-quality learning process. Therefore, the reduction in computation time for the three-layer networks compared to the two-layer ones can be attributed to more efficient learning per epoch, potentially due to better representation and processing of the complex relationships in the data by the deeper network architecture.
5.2. Brusselator Model
The Brusselator model is a simple mathematical model for the behavior of chemical oscillations. Ilya Prigogine and Lefever first proposed it in 1968 [26]. The model comprises two chemical species, U and V, that interact through non-linear differential equations. The equations describe how the concentrations of the two species change over time, taking into account chemical reactions, diffusion, and other factors. The Brusselator is known for its ability to make complex, self-sustaining oscillations in the concentrations of the two chemical species. As a result, it has been used to study a wide range of phenomena in chemistry, biology, and physics, including patterns of gene expression and the behavior of simple electronic circuits [27,28]. The Brusselator model is useful in various fields because it is a simple yet rich model that can exhibit a wide range of complex behaviors.
The Brusselator reaction is a simple model of autocatalytic chemical reactions, which is a chemical reaction catalyzed by one of the products of the reaction. The reaction has been used as a model to study the emergence of self-organizing behavior in chemical systems [29]. It has been applied to various fields, including chemistry, physics, biology, and engineering. The Brusselator reaction consists of the following:
The overall reaction is with intermediary species U and V. A and B are reactants while C and D are products. During the chemical reaction, suppose the concentration reactant A and B are kept constant; therefore, the ordinary differential equation version of the Brusselator is given below:
where and are the concentrations of the two chemical species involved in the reaction, and and are the time-varying parameters that control the system’s behavior. The Brusselator model exhibits various dynamic behaviors, depending on the values of the a and b parameters [26]. They demonstrated that the system could exhibit stable, steady states, oscillations, and chaotic behavior. Finally, the parameters of the Brusselator system are also important in understanding the behavior of real-world chemical systems, which can be modeled using similar equations. Understanding how the parameters of such a system affect its behavior can provide insights into the underlying chemical reactions and help predict and control the system’s behavior.
Our primary aim is to learn the time-varying parameters of the Brusselator model. Here, we used synthetic data that was generated by randomizing the numerical solution of the Brusselator model derived from an ODE-solver on the Brusselator model, where we assumed the initial conditions for the first species and the second species variables to be and , respectively. We choose and . This problem was solved on the time interval , where T = 30. We used a grid with points on the time interval, and every second-time step, the numerical solution vector is taken to obtain the observation or synthetic data. We use the PINN architecture shown in Figure 1 with three networks to learn the time-varying parameters of the Brusselator model. The first network outputs are and , which admits t as the input data. The second and third networks learn the parameters and from the data. We define the residual loss and training loss which was minimized as follows:
where
and
The time-varying parameters of the Brusselator model were obtained after using PINN and the approach of Scenario 2 with three hidden layers, 64 neurons per layer, 50,000 epochs, the tanh activation function was used, and the learning rate was . The PINN Algorithm 2 is an excellent choice for learning the optimal parameters of the Brusselator model. The maximum parameter value a was solved at and parameter b at . Figure 8 shows the obtained solution of the actual and predicted output of the Brusselator model after the parameters were learned with the same initial condition used to generate the data. The phase space plot of the actual output of species against species and the predicted output of species against species is shown in Figure 9.
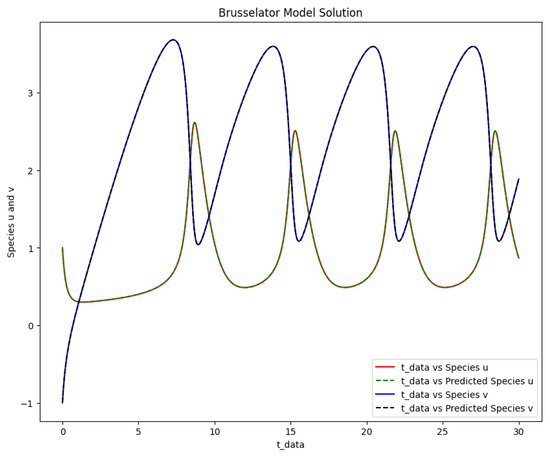
Figure 8.
The Brusselator model solution of the actual output of species u,v against and the predicted output of species u,v against .
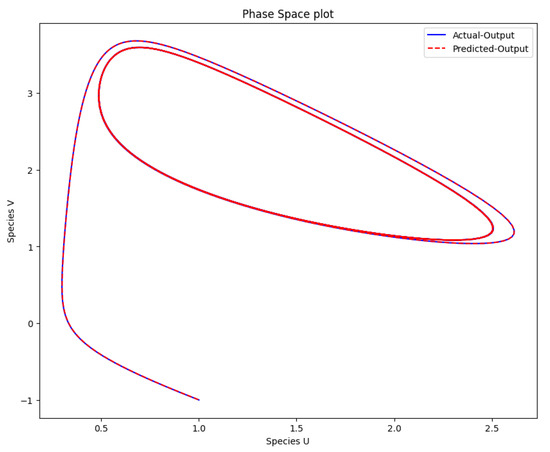
Figure 9.
The phase space plot of the actual output of species u against species v and the predicted output of species u against species v.
Figure 10 shows the learned time-varying parameter values of and of the Brusselator model. The curve appears to oscillate with an overall decreasing trend. A potential functional form for this curve is:
where is the constant coefficient, its value will determine the growth or decay rate. Since is negative in (16), the function represents decay, and if positive, the function represents growth. The magnitude of will determine how fast this growth or decay occurs. The curve also appears to oscillate with an overall increasing trend. Since is positive in (17), the function represents growth, and if negative, the function represents decay. is a time-dependent function that appears as the exponent of the exponential term. It plays a crucial role in determining the behavior of the curve over time. Table 6 shows the parameters and error metrics obtained through the approaches described in Scenario 2. The results showed that the PINN algorithm successfully learned the parameters of the Brusselator model. The obtained parameter values were close to the true values used to generate the synthetic data. The accuracy of the predictions was evaluated using various error metrics, such as mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE). The error metrics indicated a high level of accuracy in the predictions, with very small errors.
| Algorithm 2 PINN algorithm for learning the parameters of the Brusselator model |
|
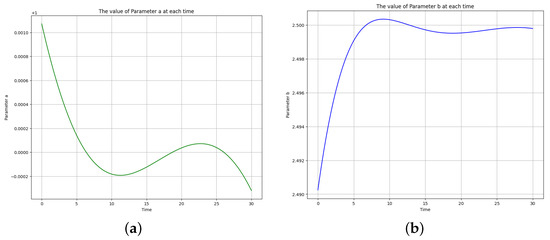
Figure 10.
The learned time-varying parameter values of the Brusselator model. (a) Time-varying parameter a. (b) Time-varying parameter b.

Table 6.
The optimal parameter estimation and the error metrics using PINN.
Furthermore, we conducted a comparison between the results obtained using physics-informed neural networks (PINN) and those obtained through deep neural networks (DNN), as detailed in Table 7 and Table 8. This comparative analysis was carried out under the specific setup of 50,000 epochs, three hidden layers containing 64 neurons, and employing the tanh activation function. Processing time, measured in seconds, was also considered in this comparison. The study revealed that PINN not only achieved faster processing times than DNN but also showed that the optimal parameters learned through PINN were closer to the actual values than those determined by DNN. This emphasizes the efficiency and accuracy advantages of PINN in this particular application.

Table 7.
Comparison of obtained results using PINN vs. DNN through the approaches described in Scenario 1. This table illustrates the accuracy in parameter estimation and the significant computational efficiency improvement of 88.7% with PINNs over DNNs, highlighting the robustness and speed of PINNs in complex system modeling.

Table 8.
Comparison of obtained error results using PINN vs. DNN.
In addition, the model’s accuracy is further illustrated in Figure 11, where the absolute error between the target and predictions made by physics-informed neural networks (PINN) and deep neural networks (DNN) is presented. The comparative analysis demonstrates that the error was significantly reduced when PINN was utilized instead of DNN. This discrepancy highlights the difference in accuracy between the two techniques employed in the modeling process. Furthermore, the results demonstrate that PINN matches but often exceeds DNN regarding parameter estimation accuracy. Finally, faster computation times make PINN an especially efficient choice for solving and pinpointing parameters in dynamical systems.
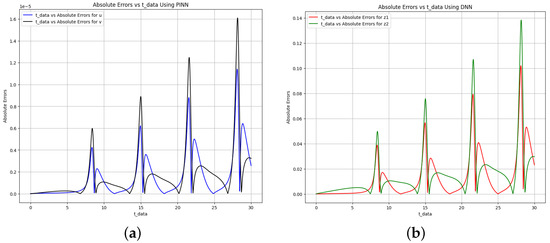
Figure 11.
Absolute error plot between the data, PINN solution, and DNN solution for the Brusselator model. (a) Absolute error plot using PINN. (b) Absolute error plot using DNN.
Finally, an analysis of data-driven simulations for training with varying numbers of epochs, such as 30,000, 40,000, and 50,000, using three layers with 64 neurons on the Brusselator model to learn time-varying parameters is presented in Table 9. The overall loss decreases as the number of epochs increases from 30,000 to 50,000. This indicates that the model benefits from a longer training duration, refining its weights and biases more effectively to minimize the difference between its predictions and the actual data. Therefore, increasing the number of epochs generally leads to a decrease in loss and better performance in predicting the parameters of u and v.

Table 9.
Analysis of the Brusselator model using different epochs.
5.3. Biomass Transfer
Biomass transfer involves the movement of organic material from one organism to another within an ecosystem. This concept is key to understanding the flow of energy within an ecosystem, as energy is transferred from producers (like plants) to primary consumers (like herbivores) and then on to secondary and tertiary consumers (like carnivores and omnivores). Imagine a forest in Europe populated by one or two species of trees. We pick out some of the eldest among them, those on the brink of their life cycle and anticipated to wither in the coming years. We then observe their journey from living, thriving trees to becoming lifeless entities. Over time, these deceased trees decompose and topple due to natural seasonal changes and biological influences. Ultimately, these fallen trees transform into nutrient-rich humus, completing their life cycle [30]. Differential equations are often used to model biomass transfer as they can describe the rate of change of a quantity (in this case, biomass) over time.
Let us consider the dynamical system model of a biomass transfer
where variable , and is defined by
and the variable and c are the parameters required to be estimated. Given that , , and the initial conditions of , then the observed data [12] are given in Table 10.

Table 10.
Observed values of and at different time points.
The analytical solution of is given as follows:
The PINN approach to solve and identify the parameters of the biomass transfer model is made by finding the best network parameters, , representing the biases and weights network that minimizes the loss function. Following a similar procedure in the previous application, we offer PINN with four networks to do this. The first network outputs are , and , which admits t as the input data. The second, third and fourth networks learn the parameters , and from the data.
We define the residual loss and training loss as follows:
where
and
The neural network obtains the optimal values for the model parameters. The , and represent the loss function’s training data. The training process minimizes the residual loss, which measures the discrepancy between the model predictions and the actual differential equations, and the training loss, which measures the discrepancy between the model predictions and the observed data. Finally, the biomass transfer model’s time-varying parameters were obtained using PINN with one layer of 10 neurons, 71,800 epochs, the tanh activation function, and a learning rate of . The PINN Algorithm 3 for learning the optimal parameters of the biomass transfer model is shown below.
| Algorithm 3 PINN algorithm for learning the parameters of the biomass transfer model |
|
The time-varying parameters , , and are obtained using the above two scenarios. The corresponding Equation system was solved at , , and for parameters , and c, and Figure 12 shows the obtained exact solution and the predicted output of the biomass transfer model. The 3D surface plot of the actual output of species and and the predicted output of species and is shown in Figure 13. Figure 14 shows the learned time-varying parameter values of the biomass transfer model for different inputs of , and . The a, b, and c curves look like quadratic functions. The plot of the absolute error between the target and the predictions is shown in Figure 15. Table 11 shows the parameters and error metrics obtained through the approaches described in Scenarios 1 and 2. We observe that Scenario 1 proved more accurate than Scenario 2. The results demonstrate that the PINN approach yields accurate parameter estimates and predictions for the biomass transfer model. The obtained parameters are close to their true values, and the error metrics indicate high accuracy and performance.
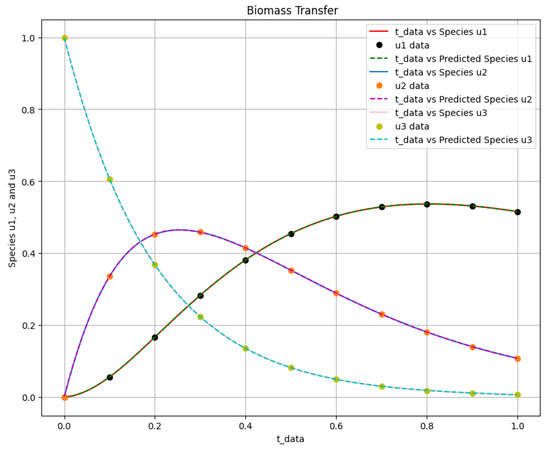
Figure 12.
The biomass transfer exact solution and the predicted output of species against .
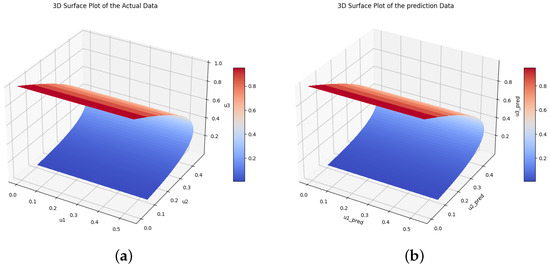
Figure 13.
The true and the predicted values of species and . (a) The true values of species U. (b) The predicted values of species U.
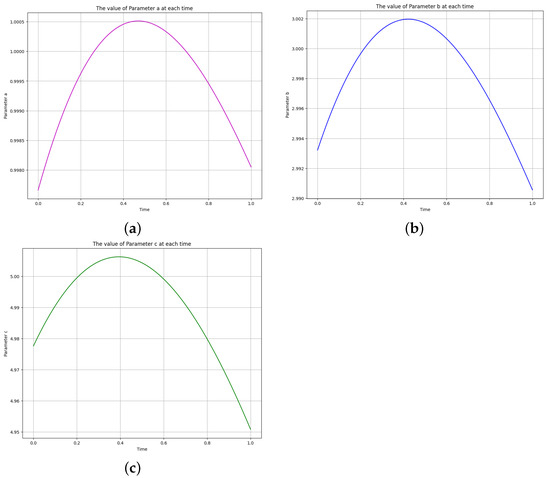
Figure 14.
The learned time-varying parameter values of the biomass transfer model. (a) Time-varying parameter a. (b) Time-varying parameter b. (c) Time-varying parameter c.
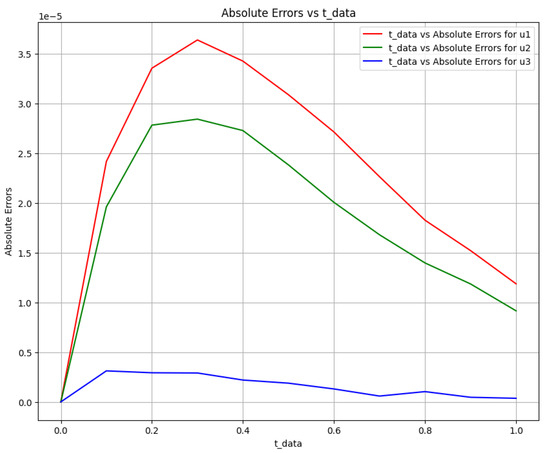
Figure 15.
Absolute error plot between the data and PINN solution.

Table 11.
Comparison of the two approaches using PINN.
In addition, the results obtained from the physics-informed neural networks approach are compared with the values and results reported in the literature using deep neural networks [12]. This comparative study was conducted with a configuration of 71,800 epochs and one hidden layer containing 10 neurons. The results are shown in Table 12. The PINN approach outperforms the DNN approach in terms of accuracy and computational efficiency, as evidenced by comparing results and CPU times in Table 12. Furthermore, Table 13 presents a comparative analysis between physics-informed neural networks and deep neural networks, illustrating the differences in their performance across shallow and deep layers. The CPU time of PINN for one, two, and three layers with 40 neurons are 9, 9, and 6 s, while for DNN is 20, 19, and 16 s [12]. The data presented in Table 13 demonstrates that the PINN approach outperforms the DNN approach in terms of accuracy and computational efficiency, as evidenced by comparing results and CPU times, especially in both shallow and deep-layer processing capabilities. Specifically, for a network with one layer of 40 neurons, the PINN model was 55% more efficient than the DNN model. Similarly, for two layers of 40 neurons each, the efficiency improvement was 52.63%, and for three layers, it increased to 62.5%. These results highlight the potential of PINNs in providing faster computational solutions, particularly as the network complexity increases, making them highly suitable for real-time complex system modeling.

Table 12.
Comparison of obtained results using PINN vs. reported in the literature using DNN.

Table 13.
Comparison of PINN vs. reported in the literature using DNN [12] based on shallow vs. deep layers.
Finally, applying physics-informed neural networks in modeling biomass transfer shows promising results in accurately learning time-varying parameters and predicting the ecosystem’s behavior. The PINN approach offers advantages over traditional and other neural network approaches, making it a valuable tool for studying complex ecological systems.
5.4. Lotka-Volterra Model
The Lotka-Volterra model is a model of the evolution of a prey-predator system. A prey-predator system is a completion where one species, called the predator, has more impact (winning), and the other species, less impact (losing), called the prey. James Lotka and Vito Volterra proposed the Lotka-Volterra model in 1925 and 1926 [31,32]. If is the prey population and the predator population at time t, then the ordinary differential equation of the Lotka-Volterra model is
where variable and represents
The parameters are non-negative.
The Lotka-Volterra model has an adequate system model up to some parameters that need to be determined. To solve the Lotka-Volterra model, you can use numerical methods or analytical techniques. A physics-informed neural network approach is proposed in this case. The PINN combines neural networks with physical laws or equations to learn the model’s time-varying parameters from data. Following the same PINN architecture shown in Figure 3, we offer a PINN algorithm with five networks to do this. The first network outputs are and , which admits t as the input data. The second, third, fourth, and fifth networks learn the parameters , , and from the data. We define the residual loss and training loss as follows to quantify the discrepancy between the model predictions and the actual data. The PINN algorithm minimizes the combined loss function to learn the optimal parameters and obtain the solution of the Lotka-Volterra model.
where
and
To generate our measurement data, we numerically solve (23) and (24), utilizing an initial condition of . We selected parameter values as follows: , and . The problem was resolved over a period delineated by the interval , where T is set to 13, a duration that approximately encapsulates one cycle. We employ a points grid within this temporal scope. Our measurement data is procured by extracting the numerical solution vector at every alternate time step. As a result of this method, we obtain a dataset where [33]. Finally, the Lotka-Volterra model parameters were obtained using PINN and the approaches from Scenario 2 with three hidden layers, 64 neurons per layer, 50,000 epochs, the sigmoid activation function, and a learning rate of . The PINN Algorithm 4 for learning the optimal parameters of the Lotka-Volterra model is shown below.
After the parameters were learned using the same initial condition used to produce the data, the results that are obtained are then compared with the true values of the parameters and the actual data. Figures are provided to visualize the predicted prey and predator populations, the phase space plot, and the absolute error between the target and predicted values. The tables present the initial and obtained parameters and error metrics such as MAE, MSE, and RMSE.
| Algorithm 4 PINN algorithm for learning the parameters of Lotka-Volterra model |
|
Figure 16 displays the resulting solution of the actual and predicted output of the Lotka-Volterra model. Figure 17 shows the phase space plot of the anticipated output of species versus species and the actual output of species against species . Figure 18 displays the Lotka-Volterra model’s learned time-varying parameter values for various inputs of and .
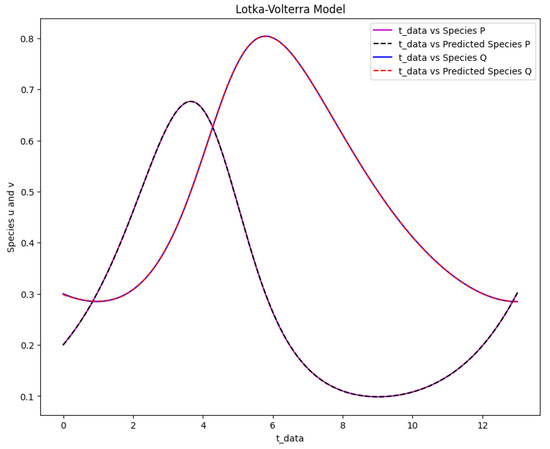
Figure 16.
The Lotka-Volterra model solution for the real output of species P and Q against time data and the predicted output of species P and Q against time data.
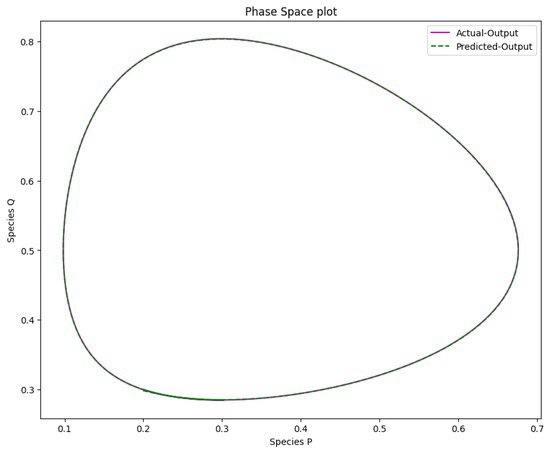
Figure 17.
The phase space plot of the actual output of species P against species Q and the predicted output of species P against species Q of the Lotka-Volterra model.
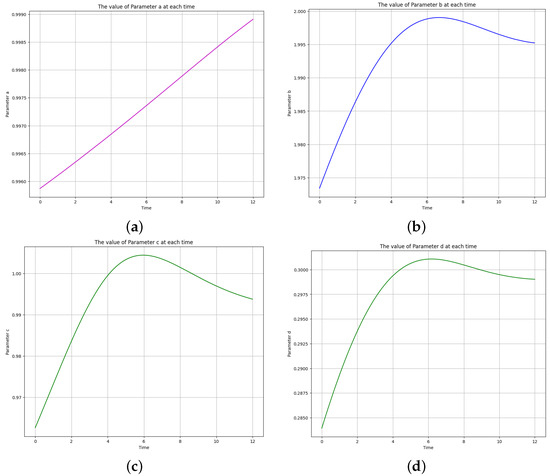
Figure 18.
The learned time-varying parameter values of the Lotka-Volterra model. (a) Time-varying parameter a. (b) Time-varying parameter b. (c) Time-varying parameter c. (d) Time-varying parameter d.
The learned time-varying parameters are , , , and . It was observed that the functional form of the curve of is linear, while the functional forms of , , and are
where B, C and D are the amplitude, determines the frequency, is the phase shift, and K is the vertical shift (which should be close to the initial values, given the curve’s behavior).
Figure 19 plots the absolute error between the target and the Lotka-Volterra model’s predictions. Table 14 and Table 15 show the initial and the obtained parameters for the Lotka-Volterra model and the error metrics through the approaches described in Scenario 2.
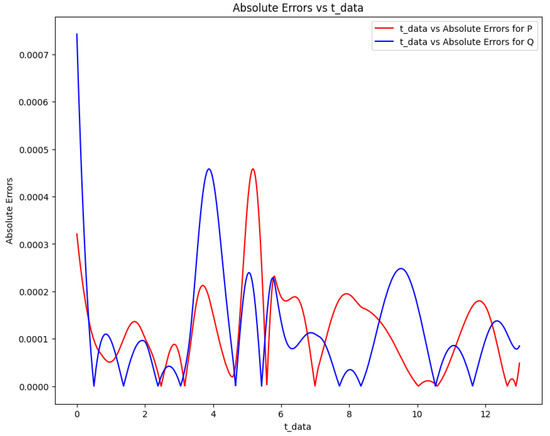
Figure 19.
Absolute error plot between the data and PINN solution of the Lotka-Volterra model.

Table 14.
The parameter estimation of the Lotka-Volterra model.

Table 15.
The error metrics of the Lotka-Volterra model.
Furthermore, our findings, obtained through the utilization of physics-informed neural networks (PINN), were compared with those reported in scholarly literature employing deep neural networks (DNN) [33]. As illustrated in Table 16, this comparison involved using a single hidden layer encompassing 20 neurons and a sigmoid activation function over a training span of 50,000 epochs. The comparison shows that PINNs perform better than DNNs regarding parameter estimation for the Lotka-Volterra model.

Table 16.
Comparison of the obtained results using PINN vs. those reported in the literature using DNN for the Lotka-Volterra model.
5.5. SIR Model
The SIR model is a widely used mathematical model in epidemiology to understand the spread of infectious diseases within a population. It divides the population into three compartments: susceptible (S), infected (I), and recovered (R). In this model, individuals can transition between these compartments by interacting with infected others [2,34]. The SIR model assumes that the population size is constant, meaning no births, deaths, or migrations occur during the disease outbreak. Additionally, it assumes that individuals in the population mix randomly, and there is a homogeneous mixing pattern. A set of ordinary differential equations can describe the dynamics of the SIR model. Let us denote the number of susceptible individuals as , the number of infected individuals as , and the number of recovered individuals as . The following equations give the rates of change of these compartments over time:
where variable , , , N, and represents
The continuity equation is given by
where the initial conditions are denoted by and , where represents time in days and is the start date of the pandemic in the model. The SIR model provides insights into the dynamics of an infectious disease outbreak, such as the peak number of infected individuals, the duration of the epidemic, and the overall fraction of the infected population. These quantities depend on the model parameters and values. It is important to note that the SIR model makes several simplifying assumptions. For instance, it assumes that the population is well-mixed, which may be false. We aim to learn the time-varying parameter and of the SIR model from real-life data (COVID-19) using PINN. Following the same procedure as in the previous application, we present PINN Algorithm 5 with three networks to do this. The first network outputs are , and , which admits t as the input data. The second and third networks learn the parameters and from the data, where and represent the biases and weights of the network that minimize the loss function.
| Algorithm 5 PINN algorithm for learning the parameters of the SIR model |
|
We define the residual loss and training loss as follows:
where
Here, we use data from Italy [35] starting from the date of the first reported cases to the day before vaccination data were reported, which is from 31st of January to 11 December 2020. We take the total population N to be × in Italy. Cubic spline interpolation generates 2000 training points from the cumulative infection and recovered data. The cumulative infections and recovered data are matched against the cumulative and recovered learned solutions. Algorithm 5 was implemented using publicly available COVID-19 data [35]. The parameters of the data using the SIR model and the learned cumulative infection and recovered data were obtained after using PINN and the approach of Scenario 2 with five hidden layers, 64 neurons per layer, 100,000 epochs, the tanh activation function was used, and a learning rate of . Figure 20 shows the learned solution of the SIR model, comparing the actual and predicted outputs of the infected and recovered populations. The cumulative data aligns closely with an exponential function. Figure 21 displays the learned values of and using PINN. The phase space plot in Figure 22 illustrates the relationship between the actual and predicted infected and recovered populations.
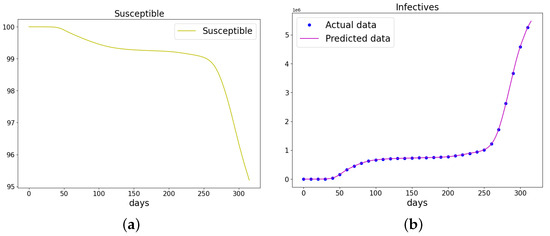
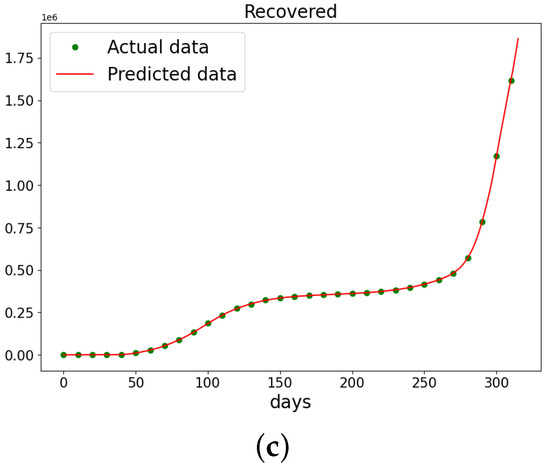
Figure 20.
The data and the learned SIR model using PINN Algorithm 5 on COVID-19 data. (a) The susceptible graph. (b) The data and the learned infectives. (c) The data and the learned recovered population.
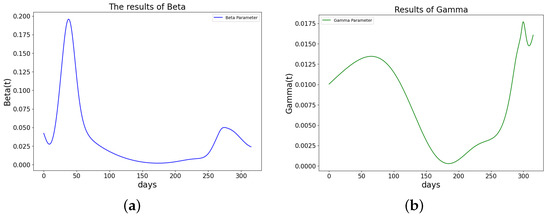
Figure 21.
The learned parameters of SIR model using PINN Algorithm 5 on COVID-19 data. (a) The learned . (b) The learned .
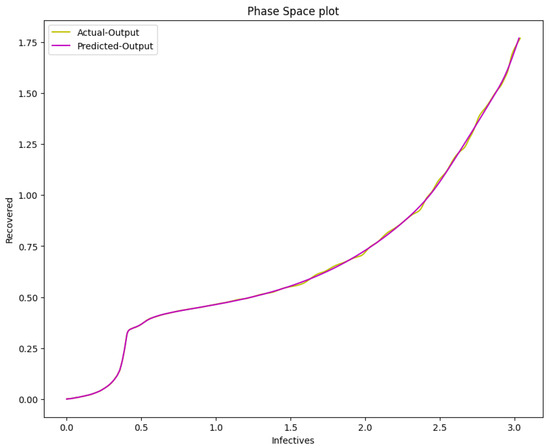
Figure 22.
The phase space plot of the actual output of I against R and the predicted output of I against R of the SIR model from the COVID-19 data.
Figure 23 depicts the absolute error between the target and predicted values of the SIR model using PINN. Table 17 summarizes the error metrics for the SIR model, indicating the accuracy of the PINN solution. The graph displays the absolute errors for two datasets, “I” and “R” over time. After day 250, there is a noticeable spike in errors for both datasets. This surge might be attributed to data inconsistencies, external factors impacting the measurements, or potential limitations in the predictive model if one was used. Additionally, increased variability in the data or unforeseen shifts in the underlying system around day 250 could also be factors. A thorough examination of the data collection process and any external events during that period is essential for a definitive conclusion. The metrics include mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE). These metrics show that the PINN solution closely approximates the COVID-19 data, demonstrating the approach’s effectiveness. Finally, learning time-varying parameters from real-life data using PINN enhances our understanding of disease dynamics and can aid in making informed decisions regarding public health interventions. This approach can be applied to various infectious diseases, allowing for more accurate modeling and prediction of their spread. Combining the SIR model and PINN presents a valuable tool for studying and managing epidemics.
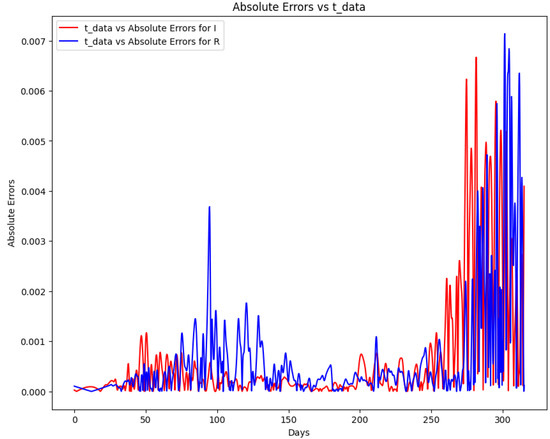
Figure 23.
Absolute error plot between the COVID-19 data and the PINN solution of the SIR model.

Table 17.
The error metrics of the SIR model.
6. Conclusions
This study has systematically explored the capabilities of physics-informed neural networks in modeling dynamic systems, marking a significant contribution to the field. Our research has highlighted the enhanced computational efficiency and accuracy of physics-informed neural networks, especially when compared to traditional deep neural networks. Physics-informed neural networks are very good at staying consistent with basic scientific laws because they use physical principles directly in the learning process. This is very important when working with complex dynamic systems. The novel contributions of this research lie in optimizing physics-informed neural networks for scenarios where the number of unknowns corresponds to the number of undetermined parameters. This approach has not only streamlined the process of dynamic system modeling but has also opened new avenues for research in this field. The application of our methodology to real-world scenarios, such as the COVID-19 pandemic model, further validates its practicality and relevance.
Quantitative comparisons have been a cornerstone of this study, providing clear evidence of the superiority of physics-informed neural networks over deep neural networks. We have demonstrated this through various error metrics. Additionally, computational efficiency has been quantitatively assessed, revealing that physics-informed neural networks significantly improve processing speed, an aspect critical for real-time applications. Finally, our results show that physics-informed neural networks have a lot of potential as strong, fast, and accurate scientific modeling tools that can deal with the complexities of dynamic systems. This research opens up new possibilities for future studies. It shows how important it is to keep looking into and improving complex neural network designs for use in science. A key area for future work is to determine how to learn the time-dependent parameters of stiff dynamical systems.
The code for the work can be found on github (accessed on 23 November 2023).
Author Contributions
All the authors have contributed equally to the conceptualization, software, validation, writing the original draft preparation, and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qureshi, S.; Yusuf, A. Mathematical modeling for the impacts of deforestation on wildlife species using Caputo differential operator. Chaos Solitons Fractals 2019, 126, 32–40. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Dua, V. An artificial neural network approximation based decomposition approach for parameter estimation of system of ordinary differential equations. Comput. Chem. Eng. 2011, 35, 545–553. [Google Scholar] [CrossRef]
- Ning, X.; Jia, L.; Wei, Y.; Li, X.; Chen, F. Epi-DNNs: Epidemiological priors informed deep neural networks for modeling COVID-19 dynamics. Comput. Biol. Med. 2023, 158, 106693. [Google Scholar] [CrossRef] [PubMed]
- Varziri, M.S.; Poyton, A.A.; McAuley, K.B.; McLellan, P.J.; Ramsay, J.O. Selecting optimal weighting factors in iPDA for parameter estimation in continuous-time dynamic models. Comput. Chem. Eng. 2008, 32, 3011–3022. [Google Scholar] [CrossRef]
- Kalogerakis, N.; Luus, R. Improvement of Gauss-Newton method for parameter estimation through the use of information index. Ind. Eng. Chem. Fundam. 1983, 22, 436–445. [Google Scholar] [CrossRef]
- Voss, H.; Timmer, J.; Kurths, J. Nonlinear dynamical system identification from uncertain and indirect measurements. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2004, 14, 1905–1933. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, W.; Wu, X.; Ruktanonchai, C.W.; Liu, H.; Wang, J. Untangling the changing impact of non-pharmaceutical pharmaceutical interventions and vaccination on European Covid-19 trajectories. Nat. Commun. 2022, 13, 3106. [Google Scholar] [CrossRef]
- Xue, L.; Jing, S.; Miller, J.C.; Sun, W.; Li, H.; Estrada-Franco, J.G.; Hyman, J.M.; Zhu, H. A data-driven network model for the emerging COVID-19 epidemics in Wuhan, Toronto, and Italy. Math. Biosci. 2020, 326, 108391. [Google Scholar] [CrossRef]
- Viguerie, A.; Lorenzo, G.; Auricchio, F.; Baroli, D.; Hughes, T.J.; Patton, A.; Reali, A.; Yankeelov, T.E.; Veneziani, A. Simulating the spread of COVID-19 via a spatially-resolved susceptible-exposed-infected-recovered-deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 2021, 111, 106617. [Google Scholar] [CrossRef]
- Baden, N.; Villadsen, J. A family of collocation-based methods for parameter estimation in differential equations. Chem. Eng. J. 1982, 23, 1–13. [Google Scholar] [CrossRef]
- Temesgen, D.T.; Chimdessa, S.Y.; Carlos, F.P. Parameter Estimation for Dynamical Systems Using a Deep Neural Network. Appl. Comput. Intell. Soft Comput. 2022, 2022, 2014510. [Google Scholar]
- Temesgen, D.T. Deep neural network for system of ordinary differential equations: Vectorized algorithm and simulation. Mach. Learn. Appl. 2021, 5, 100058. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comput. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- Dixit, P.; Silakari, S. Deep learning algorithms for cybersecurity applications: A technological and status review. Comput. Sci. Rev. 2021, 39, 100317. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Oluwasakin, E.O.; Khaliq, A.Q.M. Driven Deep Learning Neural Networks for Predicting the Number of Individuals Infected by COVID-19 Omicron Variant. Epidemiologia 2023, 4, 420–453. [Google Scholar] [CrossRef]
- Torku, T.K.; Khaliq, A.Q.M.; Furati, K.M. Deep-Data-Driven Neural Networks for COVID-19 Vaccine Efficacy. Epidemiologia 2021, 2, 564–586. [Google Scholar] [CrossRef]
- Long, J.; Khaliq, A.; Furati, K. Identification and prediction of time-varying parameters of COVID-19 model: A data-driven deep learning approach. Int. J. Comput. Math. 2021, 98, 1617–1632. [Google Scholar] [CrossRef]
- Olumoyin, K.; Khaliq, A.; Furati, K. Data-Driven Deep-Learning Algorithm for Asymptomatic COVID-19 Model with Varying Mitigation Measures and Transmission Rate. Epidemiologia 2021, 2, 471–489. [Google Scholar] [CrossRef] [PubMed]
- Eyring, H.; Polanyi, M.Z. Simple gas reactions. J. Phys. Chem. B 1931, 12, 279–311. [Google Scholar]
- Esposito, W.R.; Floudas, C.A. Global optimization for the parameter estimation of differential-algebraic systems. Ind. Eng. Chem. Res. 2002, 39, 1291–1310. [Google Scholar] [CrossRef]
- Katare, S.; Bhan, A.; Caruthers, J.M.; Delgass, W.N.; Venkatasubramanian, V. A hybrid genetic algorithm for efficient parameter estimation of large kinetic models. Comput. Chem. Eng. 2004, 28, 2569–2581. [Google Scholar] [CrossRef]
- Prigogine, I.; Lefever, R. Symmetry breaking instabilities in dissipative systems II. J. Chem. Phys. 1968, 48, 1665–1700. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, Z. Turing-Hopf bifurcation analysis and normal form of a diffusive Brusselator model with gene expression time delay. Chaos Solitons Fractals 2021, 152, 111478. [Google Scholar] [CrossRef]
- Domguia, U.S.; Tchakui, M.V.; Herve, S.; Woafo, P. Theoretical and Experimental Study of an Electromechanical System Actuated by a Brusselator Electronic Circuit Simulator. Vib. Acoust. 2017, 139, 061017. [Google Scholar] [CrossRef]
- Field, R.J.; Noyes, R.M. Oscillations in chemical systems. IV. Limit cycle behavior in a model of a real chemical reaction. Chem. Phys. 1974, 60, 1877–1884. [Google Scholar] [CrossRef]
- Gustafson, G.B. Differential Equations and Linear Algebra, Undergraduate Mathematics Science and Engineerin; Amazon Kindle Direct Publishing: Seattle, WA, USA, 2022; pp. 1–1729. ISBN 9798705491124/9798711123651. [Google Scholar]
- Lotka, A.J. Elements of Physical Biology; Williams and Wilkins Company: Philadelphia, PA, USA, 1925. [Google Scholar]
- Volterra, V. Variazionie fluttuazioni del numero d’individui in specie animali conviventi. Mem. R. Accad. Naz. Lincei 1926, 2, 31–113. [Google Scholar]
- Borzì, A. Modelling with Ordinary Differential Equations: A Comprehensive Approach; Taylor and Francis Group, LLC: Abingdon, UK, 2020; Volume 1, pp. 1–387. [Google Scholar]
- Fred, B.; Carlos, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012; Volume 40, pp. 1–4. [Google Scholar]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).