Abstract
In today’s competitive world, it is essential to provide a new method through which maximum efficiency can be created in the production and supply cycle. In many production environments, sending goods directly from the producer to the consumer brings many problems. Therefore, an efficient transport system should be established between producers and consumers. Such a system is designed in the field of supply chain management knowledge. Supply chain management is the evolutionary result of warehousing management and is one of the important infrastructural foundations of business implementation, in many of which the main effort is to shorten the time between the customer’s order and the actual delivery of the goods. In this research, the supply chain consists of three levels. Suppliers are placed on the first level, cross-docks on the second level, and factories on the third level. In this system, a number of suppliers send different raw materials to several different cross-docks. Each channel is assigned to a cross-dock for a specific product. The main goal of this article is to focus on optimizing the planning of incoming and outgoing trucks with the aim of minimizing the total operation time within the supply chain. The arrival rate of goods from suppliers to the cross-dock is stochastic with a general probability distribution. On the other hand, the time required to prepare and send the goods is random with a general probability distribution. The service time in each cross-dock depends on the number of its doors. Therefore, each cross-dock can be modeled as a G/G/m queueing system where m represents the number of doors. The mathematical model of the research has been developed based on these assumptions. Since the problem is NP-hard, the time to solve it increases drastically with the increase in the dimensions of the problem. Therefore, three metaheuristics, including multi-objective water flow, non-dominated sorting genetic, and a multi-objective simulated annealing algorithm have been used to find near-optimal solutions to the problem. After adjusting the parameters of the algorithms using the Taguchi method, the results obtained from the algorithms were analyzed with a statistical test and the performance of the algorithms was evaluated. The results vividly demonstrate that non-dominated sorting genetics is the best of all.
1. Introduction
A growing tendency to optimize the distribution network in order to decrease logistics costs, which aims to ensure the optimum location of facilities, reduce inventory and transportation expenses, verifies the necessity for distribution and supply chain management. On the other hand, the efficient control of the physical flow of goods is the most significant factor in reducing costs in the supply chain. Accordingly, many companies try to develop their distribution strategies to achieve their material flow’s efficient management. The presence of a middle center seems necessary to link producers and customers within a supply chain system. Cross-docking is a method for distribution management and goods transportation leading to warehousing cost reduction via the direct transfer of cargo from input vehicles to output vehicles without storage. Hence, product storage and recycling costs are reduced by applying cross-dock systems and even by synchronizing input and output vehicle flows [1]. In a cross-dock system, the main target is to remove storage and reduce the over-transportation of goods. Therefore, the existing product in the warehouse is stored for a short time [2]. The Material Handling Industry of America defines a cross-dock as a warehouse focused on transferring goods from a vehicle to another vehicle [2]. A cross-dock acts more as an inventory coordinator than as filling a warehousing role, shifting the focus from supply chain management to demand–supply management [3]. Galbert et al. (2008) presented a model based on customers’ perspectives for the optimal use of cross-docking and concluded that lower demand variability and higher stock costs exacerbate the effects of cross-docking. On the other hand, supply chain management can be divided into three categories of supply chain designing, planning, and control [4].
The performance level includes scheduling problems, warehouse door allocation, transportation within doors, and vehicle routing. The tactical level examines problems in cross-dock layout design and the strategic level evaluates problems related to cross-dock networks. Yu (2002) [5] examines three different models based on the number of available doors, the vehicle loading pattern of doors, and the existence or absence of temporary storage. Magableh et al. (2005) [6] expanded a simulation method of cross-docks in order to evaluate the existing risk value in product transportation and showed the operation within a cross-dock facility in a dynamic environment and with the existence of demand growth. Ley and Elfayoumy (2007) [7] examined a model without a temporary warehouse and unlimited transportation systems, and for solving their minimization objective function they calculated the distance from the discharging site to the loading site. Yu and Egbelu (2008) [8] presented a mixed integer programming model with cross-docks including an entrance door and an exit door and combined it with product allocation problems. This model was more flexible than unpredictable events. Chen and Lee (2009) [9] considered the cross-dock scheduling problem in which an operation is performed based on a two-machine flow shop. The first machine discharges input products and the second machine loads an input vehicle. Vahdani and Zandieh (2010) [10] scheduled input and output vehicles in cross-docks using the imperialist competitive Algorithm.
Agustina et al. (2010) [1] presented a mixed integer linear programming algorithm aiming at minimizing system delivery costs, taking into consideration product combinations and delivery windows. Dondo and Cerda (2015) [11] examined vehicle routing problems and presented a reciprocating method, finding a near optimum solution. Shahin Moghadam et al. (2014) [12] considered vehicle routing and scheduling in a cross-docks customer-supplier network in which a set of homogenous vehicles transfer products from suppliers to customers using cross-docks. Ahmadizar et al. (2015) [13] evaluated a model consisting of a two-vehicle routing level with cross-docks. Yu et al. (2016) [14] considered one type of product and cross-dock with homogenous capacity vehicles in which vehicles start the loading operation at different points at various times. Amini and Tavakkoli-Moghaddam (2016) [15] studied truck scheduling problems in cross-docks with the assumption of truck failure. The truck failure rate was modeled by Poisson distribution and used three metaheuristic algorithms to solve it.
Ahmadizar et al. (2015) [14] introduced a model that considers two-level vehicle routing along with cross-docking. Cóccola et al. (2015) [16] proposed a truncated branch and price solution algorithm to take care of a sensible issue including the satisfaction of a rundown of transportation demands. Utama et al. (2016) [17] introduced the constructed optimization model based on the water flow algorithm (WFA) to address the intermittent street gridlock issue. Hasani Goodarzi et al. (2018) [18] proposed a pickup and drop-off issue for the cross-docking technique, in which shipments from providers to retailers are directly cross-docked. Ahkamiraad and Wang (2018) [19] presented a MILP model of an exceptional multiple cross-docked VRP. Baniamerian et al. (2018) [20] proposed a vehicle routing and scheduling issue with cross-docking and time windows in a three-echelon store network. Molavi et al. (2018) [21] introduced truck scheduling in a two-touch cross-dock with hard due dates for outbound trucks. Fonseca et al. (2018) [22] proposed a Lagrangian metaheuristic methodology for the cross-dock scheduling issue with parallel docks.
Gelareh et al. (2018) [23] proposed eight new MIP models and exhibited the numerical identicalness of every one of the 11 models, along with thoroughly demonstrating a portion of their properties. Musavi et al. (2018) [24] introduced a bi-objective model for a green truck scheduling and routing problem at a cross-docking framework. Nassief et al. (2018) [25] introduced two new MIP mathematical formulations for cross-dock door assignment problems (CDAPs). Shaelaie et al. (2018) [26] considered a production network including the multi-provider and a solitary client. They explored the impact of joining on parts transport. Baniamerian et al. (2019) [27] proposed a practical version of a vehicle routing problem with cross-docking. They planned three metaheuristic algorithms, namely a hybrid GA with modified VNS, ABC, and SA to solve large-scale problems.
Seyedi et al. (2019) [28] created five heuristic algorithms for managing the truck planning issue in a cross-docking framework. Rijal et al. (2019) [29] proposed an integrated scheduling and assignment of trucks at unit-load cross-dock terminals with mixed service mode dock doors. They created an adaptive large neighborhood search algorithm for the integrated problem. Corsten et al. (2019) [30] proposed an optimization model, which coordinated the planning tasks of truck and workforce scheduling in a cross-dock for a solitary working day. Dulebenets (2019) [31] concentrated on a truck scheduling problem at a cross-docking facility. They proposed a delayed start parallel evolutionary algorithm to solve the issue. Rahbari et al. (2019) [32] extended the applicability of the cross-dock to disperse perishable items. Hadipour et al. (2019) [33] proposed a bi-objective mathematical model to improve the dependability of a confounded framework. They utilized distinctive repetition systems with part blending in every subsystem. Khorshidian et al. (2019) [34] proposed a bi-objective mathematical model to coordinate truck scheduling and transportation planning in a cross-docking framework in a forward/invert coordination organization.
Fard and Vahdani (2019) [35] proposed a bi-objective optimization model for the issue of scheduling, the succession of trucks, and the task of trucks and forklifts to the doors in a multi-door cross-dock with flexible doors. Hasani Goodarzi et al. (2020) [36] considered a vehicle routing problem with cross-docking and parting pickup. They introduced a new bi-objective mixed-integer linear programming model and a multi-objective evolutionary algorithm to find high-quality solutions. Movassaghi and Avakh Darestani (2020) [37] presented a mixed-integer, non-linear programming model to solve cross-dock scheduling problems. Hasani Goodarzi and Zegordi (2020) [38] considered an inventory-routing problem in a distribution network in which kanban is utilized as a way to execute a just-in-time strategy.
Ardakani et al. (2020) [39] proposed the truck-to-door sequencing problem. They focused on optimizing truck-to-door sequencing with the intention of rehashing the truck holding pattern in inbound trucks in order to minimize makespan. Nogueira et al. (2020) [40] proposed an approach dependent on the parallel machine environment for the cross-docking issue. Nikzamir and Baradaran (2020) [41] proposed a novel healthcare waste location-routing problem with another point of view in medical services coordination organization. They considered a stochastic essence for the discharge of defilement. Shahabi-Shahmiri et al. (2021) [42] proposed a new multi-objective mixed-integer programming (MIP) model for the scheduling and routing of heterogeneous vehicles conveying transient products across various cross-docking frameworks. Castellucci et al. (2021) [43] incorporated network scheduling with cross-docks and 3D stacking constraints. They proposed an effective logic-based decomposition Benders system.
Hasani Goodarzi et al. (2021) [44] developed a dependable organization of cross-docks by considering interruption and unwavering quality issues to support against the heterogeneous danger of cross-dock frustration. Hasani Goodarzi et al. (2021) [45] concentrated on a vehicle routing problem in a multi-product multi-door cross-docking framework. They introduced an M/M/c queue model to consider the random arrivals of trucks at cross-docks. Yu et al. (2021) [46] presented the heterogeneous armada vehicle routing problem with multiple cross-docks (HF-VRPMCD). They proposed an adaptive neighborhood simulated annealing (ANSA) heuristic for solving HF-VRPMCD. Theophilus et al. (2021) [47] concentrated on a truck scheduling problem at a cross-docking terminal. They displayed the product decay using an exponential function. Qiu et al. (2021) [48] presented a mixed integer programming model for the two-echelon production routing problems with satellites. They proposed a branch-and-cut algorithm with substantial disparities and a metaheuristic. Smith et al. (2022) [49] introduced the multi-tiered vehicle routing problem with global cross-docking (MTVRPGC). Table 1 shows reviewed articles in the domain of cross-docks for this research.

Table 1.
Reviewed Articles on cross-docks. For this work.
Despite the strong desire to research cross-docks, provide a new concept of modeling, and design different algorithms, this field still faces many shortcomings, which are mainly related to the extension of existing models to approach real-world problems. As a result, the main motivation of this article is to present a model that reduces the time of product transfer and increases the quality of the system’s performance, and also causes integration in the entire supply chain system.
As can be seen, most of the researches have considered the problem by assuming the accuracy of the input parameters. Few studies have considered warehouse entry and service rates to be probable. In all these researches, the probability distribution of entering the warehouse and the probability distribution of the service rate in the warehouse follow the exponential or normal process. Therefore, it can be claimed that none of the researches have examined and modeled the warehouse service rate and warehouse entry rate with a general probability distribution. Therefore, this research intends to model and optimize cross-docks by considering the entry and service rates with the distribution of general probability in warehouses. In this case, each warehouse is modeled as a G/G/m queue system, where m represents the number of doors. Issues such as warehouse location will also be considered during modeling.
In spite of the fact that cross-docks attracted much attention in a practical approach, the main reason behind the existence of these shortcomings is the complexity in solving the problem and improving the solution methods to enhance the quality of the solution and the solution time. Therefore, in this paper, we aim to minimize operational time and cost simultaneously and use metaheuristic algorithms to overcome these deficiencies. Thus, this paper is trying to present an analytical model for the cross-docking concept using queue theory. Regarding the proposed model, minimizing material transportation costs and customer waiting time is a determined mathematical target. On the other hand, considering a general probability distribution for warehouse servicing rate and entrance rate, along with location–allocation problems, is one of the innovative aspects of this paper. In practical scope, the proposed model is far closer to real-world problems because of considering uncertainty.
This paper’s structure is as follows: in the second section, we define the conceptual supply chain model. In the third section, we present the proposed mathematical programming model considering the probable warehouse servicing rate and entrance rate and evaluate the proposed solution method. In the fourth section, we analyze the related results to the presented solutions, and finally, in the fifth section, we discuss conclusions and suggestions for future research.
2. Methods and Modeling
In this paper, the design of the distribution network includes three levels in which the first level is allocated to suppliers, the second level to cross-docks, and the third level to factories. In this system, there are several suppliers that transfer different raw materials to several cross-docks. Each channel is allocated to a cross-dock for a special product. Then, these materials are transferred to factories in the least possible time. The entrance rate of items from supplier to cross-docks is probable and follows a general probability distribution. On the other hand, item startup and delivery within cross-docks are also probable and follow a general probability distribution. Service time in each warehouse depends on the number of existing doors; therefore, we can model each warehouse in the form of a G/G/m queue system where m stands for the number of doors (Figure 1).
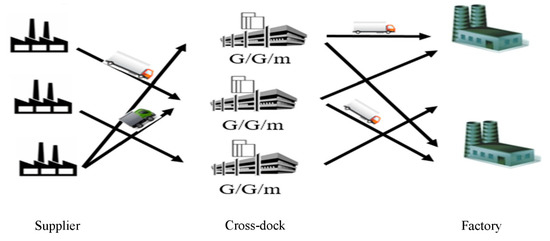
Figure 1.
Three-level structure in the supply chain.
The first level includes several suppliers and each supplier tries to meet distribution network requirements by offering various products.
- Suppliers’ locations are not predetermined and their final location is selected from among several potential locations.
- The manufactured items by suppliers are transferred to the warehouse by different transportation vehicles.
- This level includes costs related to suppliers and items transferred from suppliers to warehouses.
- The second level includes cross-docks or distribution centers.
- Warehouse locations are not determined in advance and are chosen from among several potential locations.
- There are several servers in each warehouse in charge of receiving, packaging, and sending items.
- Warehouses are of cross-dock type and items are sent as soon as they are packaged. Hence, storage costs are neglected.
- Location costs are fixed and unique and determined based on warehouse location.
- The third level includes a factory which is in charge of producing the final product.
- Factory location is not predetermined and the final location is selected from among several potential locations.
Regarding examined features in the desirable distribution network, decisions are made as follows:
Location decisions
- Which potential suppliers should be established so that related costs are minimized?
- Which potential warehouses should be established so that related costs are minimized?
- Which potential factories should be established so that related costs are minimized?
- Allocation decisions
- Which active suppliers should be chosen by warehouses for supplying their desired products so that total cost is minimized?
- Which active warehouses should be chosen by factories for supplying their desired products so that total cost is minimized?
- Which transportation vehicle should be selected for transferring products between suppliers and warehouses?
- Which transportation vehicle should be selected for transferring products between warehouses and factories?
Related decisions to warehouse planning
How many servers should exist in each established warehouse to respond to product transfer and packaging so that costs are minimized?
The proposed model assumptions are as follows:
- The discharging process for input vehicles follows first in first out. It means that the first input vehicle that enters the cross-docks area is allocated to a free entrance door if there is any; otherwise, it will wait in the area.
- Door capacities are the same in each warehouse.
- Input and output trucks are not allowed to exit the warehouse and interrupt their respective services until the discharging and loading processes are over.
- Servicing time (load discharging) in each door is probable and follows a general probability distribution.
- Warehouses and factories are capacitated.
Decision-making variables are as follows in term of concept:
- Supplier locations
- Cross-dock locations
- Factory locations
- Allocating suppliers to warehouses
- Allocating warehouses to factories
- Determining item transportation between suppliers and warehouses
- Determining item transportation between warehouses and factories
- Determining the number of existing doors in each warehouse
Considering the decision-making variables, the indices and parameters in this model are found in Table 2.

Table 2.
Indices and parameters.
Dependents and independent variables of the research model are embedded at Table 3.

Table 3.
Dependent and independent decision variables.
The first objective function is Equation (1) which aims at minimizing location-fixed costs, transportation costs, and cross-dock costs.
The second objective function tries to minimize the transfer time of products from supplier to cross-dock and from cross-dock to factory and also includes product waiting time in the cross-docks. Regarding the fact that the entrance rate to each cross-dock and service rate in each cross-dock follow a general probability distribution, the average product waiting time at the cross-dock is calculated using Equation (2).
where stands for probability in cross-dock j which is calculated as (3):
In this equation, is the issued demand to cross-dock j which is defined as (4):
The second objective function is based on Equation (5), in which its first part is related to the transfer time from supplier to cross-dock, its second part is related to transfer time and its third part is related to waiting time and the presence of goods at the cross-dock.
Model constraints are defined as follows:
Constraint sets (6)–(8) ensure the maximum number of permitted suppliers, cross-docks, and factories in order to avoid facility overlap. Constraint (9) insures that the number of existing servers in each cross-dock doesn’t exceed the predetermined allowed number. Constraint sets (10)–(15) control the dependence between independent and dependent decision variables. Constraint (16) selects a vehicle for transferring products between the supplier and the cross-dock. Constraint (17) selects a vehicle for transferring products from a cross-dock to a factory. Constraint (18) insures that the servicing ability in cross-docks is more than the entrance rate to cross-docks, i.e., the productivity rate is less than 1. Constraint sets (19)–(20) control decision-making variable values. Since the proposed model is regarded as NP-hard, the necessity of expanding efficient algorithms is verified. To do that, in this paper, we use non-dominated sorting genetic algorithms (NSGA-II), a multi-objective simulated annealing algorithm, and a multi-objective water flow algorithm to solve it.
2.1. Genetic Algorithm
The genetic algorithm uses a two-phase mechanism to define the solution. In the first phase, solutions are generated as coded items, and then, in the second phase, the coded solutions are decoded and show decision-making variable values as the result. Chromosome encryption and decryption methods for the proposed problem, which includes 8 potential distribution centers, 6 potential cross-docks, 5 potential factories, and 10 vehicle types are as follows: The first section shows the location of the suppliers. This section consists of a 1*P vector, where P is the maximum number of allowed suppliers. All of the vector digits are in (0, 1) intervals. To encrypt data, first, all of the numbers are multiplied by the potential number of suppliers and rounded up, and locations 5, 6, and 7 are selected to place the supplier. To determine which location is finally selected to place the supplier, the second section of the encrypted chromosome is multiplied by the number of potential nodes, and locations 5 and 6 are selected for the placing supplier. The third section determines the appropriate vehicles for good transferring from suppliers to cross-docks. This part includes a 1*P vector, where P is the maximum number of vehicles and all of the numbers are between 0 and 1. To decrypt the numbers, at first, all of the numbers are multiplied by the maximum number of transportation vehicles and rounded upwardly, and vehicles 4, 2, and 6 are selected to transfer materials from suppliers to cross-docks.
The fourth section represents appropriate places for locating cross-docks. This part includes a 1*P vector, where P is the maximum number of allowed cross-docks and all of the numbers are between 0 and 1. To decrypt numbers, at first, all of the numbers are multiplied by the maximum number of cross-docks and rounded upwardly, and then, vehicles 1, 4, and 8 are selected to transfer materials from cross-docks to factories. The seventh section, which represents factory locations consists of 1*P vector, where P is the maximum number of allowed cross-docks and all of the numbers are between 0 and 1. To decrypt numbers, at first, all of the numbers are multiplied by the number of potential factories and rounded upwardly, and then, factories are located in 3, 6, and 5. To determine which location is finally chosen for placing suppliers, the eighth section of the chromosome is multiplied by the number of potential points, and the supplier is located in places 3 and 4. To determine which goods (1) from which supplier and with which vehicle and (2) from which cross-dock to which factory and with which vehicle should be transferred, the obtained results by previous phases are placed in a separate matrix as Table 4. Regarding the first column, products are transferred from supplier 5, by vehicle 4 to cross-dock 3, and then, by vehicle 8 from cross-dock 3 to factory 4.

Table 4.
Goods transfer pattern within supply chains levels.
The ninth section determines each cross-dock server. This section consists of a 1*P vector, where P is the number of potential cross-docks and acquires one of the values from 0 to 1. To decrypt numbers, all of them are multiplied by the maximum number of servers and rounded upwardly, and then, 1, 2, and 5 servers are located in cross-docks. In the next step, the selection of the parent population that is affected by crossover and mutation operators is performed based on a crowded tournament selection operator. In mutation, each person’s chromosome is changed individually and without any need to be merged with another person’s chromosome based on probability rules. In this paper, we use the number of generations as the break condition, and its size is determined by parameter tuning based on Maghsoudloo et al. (2016).
2.2. Multi-Objective Simulated Annealing Algorithm (MOSA)
In the present paper, at first, a large number of stochastic solutions are generated and their objective functions are determined. Then, we calculate the existing standard deviation in the obtained results and use them to determine the initial temperature. In the proposed algorithm, we used 1.5 times more than the existing standard deviation in initial solutions to determine the initial solution. For each target, a separate temperature is needed. The temperature reduction trend is determined as a linear equation . The maximum number of produced solutions in each temperature is used as a basis for examining the balance condition in that degree. MOSA has two loops. The number of iterations in the internal loop is determined based on parameter tuning and the number of iterations in the external loop is determined based on the number of iterations just like NSGA-II.
2.3. Multi-Objective Water Flow Algorithm (MOWFA)
This algorithm includes four main operators: 1. motion and flow division; 2. flow integration; 3. water evaporation; 4. raining. The structure of presenting the MOWFA algorithm solution and determining the fitness level is the same as NSGA-II and is stochastic. At the beginning of the water flow algorithm, we assume there is only one flow with the stochastic location. Flow division depends on the liquid power. The divided sub-branches are located in the vicinity of the main flow location. When a water flow divides to several sub-branches, flow density is also divided into several sub-branches. When more than two water flows move toward a common space, all of them are merged into a flow with the most mass and kinetic energy. If we call the existing flow i, and other flows which join to it j, after merging them, the flow j is removed and the new flow volume and speed are updated. Using an integration operator, the extra elements of the solution won’t affect object function values anymore and extra search is avoided. If there is no improvement after several phases, flow loses its kinetic energy, evaporates, and randomly falls to another space that has one or more common features with this space (like rain). The break condition in MOWFA is the number of iterations as those of NSGA-II and MOSA algorithms.
3. Discussion and Results Evaluation
After a brief review of the multi-objective metaheuristic algorithms criteria, the optimum values of algorithm parameters are determined via parameter tuning. Then, the obtained results of the three metaheuristic algorithms are evaluated and compared with each other using 32 random samples. Calculations are performed using a laptop with 4 GB RAM and a 2 duo 3.2 GHz processor, Core i5. We also used Minitab17 software for parameter tuning and MATLAB 2010 software for algorithm programming. In this paper, evaluation criteria include mean ideal distance (MID) which is used to calculate the average distance of Pareto solutions from a Cartesian coordinate system. The less the MID, the more the algorithm efficiency will be. MID is calculated as Equation (21).
where m is the number of objectives and is the value of jth objective function. The spread of the non-dominance solution (SNS) shows the dispersion of Pareto queue solutions from their qualities. According to Asef et al. (2014) SNS is calculated from Equation (22) in which :
Maximum spread or diversity in a bi-objective mode equals the Euclidean distance between two boundary solutions in the target space. The more this criterion, the best the answer. Equation (23) represents the computational trend of this criterion:
The NOEF criterion or number of evaluating functions represents the speed of the algorithm running. The only difference is that this criterion is more practical and obvious than the computational time criterion and its size is not related to the computer system.
The next step is to tune the parameters which is impossible without an experiment design. To achieve this, we used the Taguchi method which uses an orthogonal array (OA) to measure the effect of one factor on the average and determine the deviation from the average. One of the best advantages of the orthogonal array is that for each level of a factor, all the other factor levels are repeated equally, thus, we can repeat the results of experiments. Another advantage of the orthogonal array is its expense efficiency. Furthermore, in the Taguchi method, experimental data’s difference or response variable variance values are examined and the signal-to-noise ratios (S/N) are used to simplify its concept. In the first step of parameter tuning, the studied parameters are identified and their levels are determined. One of the fundamental parameters is the number of iterations, which depends on the size of the problems. In this paper, the number of iterations is determined via 5IJ, where I is the number of suppliers and J is the number of cross-docks. Other parameters and search domains of their levels are presented in Table 5. This parameter is evaluated in five levels, and finally, the best level is selected.

Table 5.
Controllable parameters and their levels.
The number of required experiments for the factors above equals . However, regarding time and cost, this kind of experiment is not affordable. Accordingly, we get help from fractional iteration plans. In this problem, the freedom degree is set to 1 for the total average and 4 for each five level factors. Therefore, the total of freedom degrees equals . Thus, we have to select an array with at least 13 rows, and the L25 orthogonal array meets this requirement. The designed array structure and experiment results for NSGA-II, MOSA, and MOWFA are presented in Table 5. MID is considered a response variable. Each experiment is repeated three times and MID values are considered a basis for experimental results. Figure 2 demonstrates how the S/N criterion values are changed for different algorithm levels. The levels in which the S/N criterion has reached its maximum are optimum levels. It represents the MOWFA algorithm, and the best level of population size is its third level. Therefore, the appropriate population size for MOWFA is 30. The optimum levels of two other factors of MOWFA are also evaluated in the domain and for the M0 factor, the third, and for V0 the fourth levels are chosen. Figure 3 demonstrates the related results to the MOSA algorithm. The best level of population size is placed within the evaluated domain and is its third level. Therefore, the appropriate population size for MOWFA is 30. Thus, the appropriate population size for MOSA is 20. The optimum level of two other factors is also evaluated in the domain and for both factors i.e., for the inner loop and alpha, the third level is chosen. Figure 4 shows the related results to the NSGA-II algorithm. The best level of population size is placed within the evaluated domain and is its third level. Therefore, the appropriate population size for NSGA-II is 100. The optimum levels of two other factors of NSGA-II are also evaluated in the domain and for both Pcross Pmute factors the second levels are chosen. These real values are presented in Table 5.
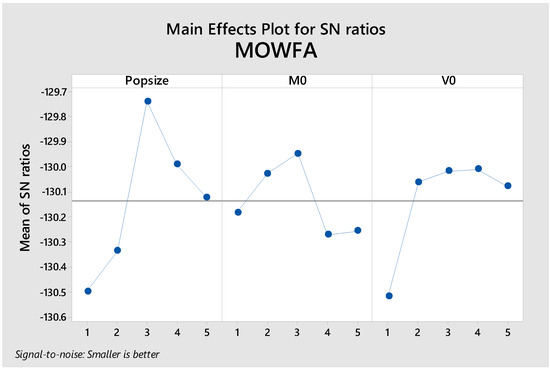
Figure 2.
S/N changes for MOWFA factors.
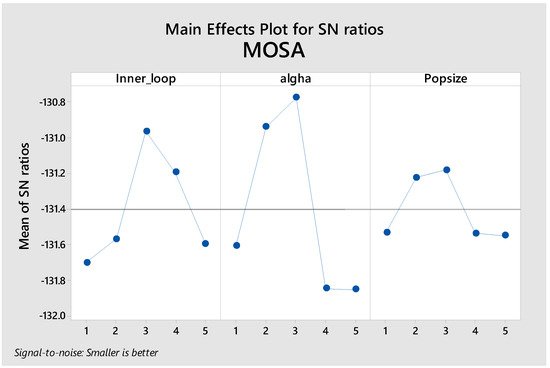
Figure 3.
S/N changes for MOSA factors.
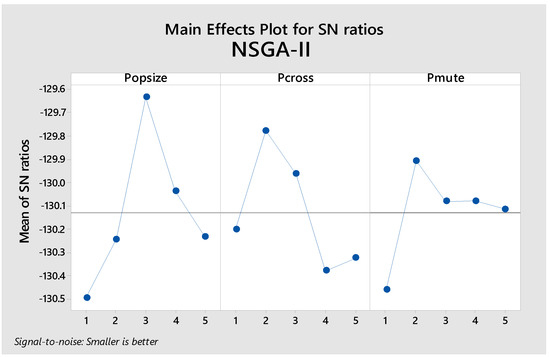
Figure 4.
S/N changes for NSGA-II factors.
Now, we use small problems to evaluate algorithm efficiency to find a globally optimum solution. All of the examples are optimized using GAMS software and the obtained solutions from GAMS are compared with the obtained solutions of the proposed algorithms.
To do that, at first we produce 10 random samples with 2 suppliers, 3 factories, and 3 vehicles and compare the obtained MID from GAMS and the obtained MID from the mentioned algorithms. All of the obtained results from GAMS are limited to 2000 s. If we don’t reach the global optimum solution in the proposed time, the software stops, and the local optimum solution with its related GAP is presented. Regarding the obtained results, it can be seen that NSGAII’s distance from the globally optimum solution is 2.174928, MOSA’s, 2.254297, and MOWFA’s, 2.805116 percent.
The confidence interval of 95% for algorithms is also illustrated in Figure 5. According to the fact that intervals cross each other, we can statistically conclude that the obtained results from metaheuristic algorithms are equal to the obtained results from GAMS. Therefore, the proposed algorithms are capable of finding globally optimum solutions and are also an appropriate case for large-scale problems.
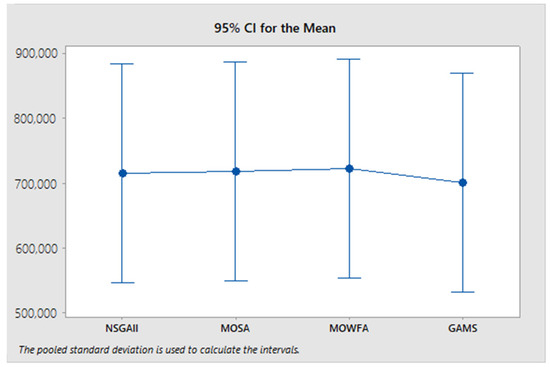
Figure 5.
Confidence interval of 95% for algorithms MID.
After proving algorithm efficiency, large-scale problems are applied to evaluate algorithm performance in finding near-optimum solutions for large-scale problems. To analyze the results, we selected 32 samples which are placed in four categories regarding the number of suppliers, cross-docks, factories, and transportation vehicles. The first group includes problems with 3 suppliers, 4 cross-docks, 5 factories, and 7 transportation vehicles. The second group includes problems with 6 suppliers, 5 cross-docks, 7 factories, and 9 transportation vehicles. The third group includes problems with 8 suppliers, 7 cross-docks, 9 factories, and 11 transportation vehicles, and the fourth group includes problems with 10 suppliers, 9 cross-docks, 11 factories, and 13 transportation vehicles. Eight random samples are generated for each group. Then, the performance of the proposed algorithms is evaluated based on comparison criteria. In Figure 6, the proposed criteria are calculated and illustrated for all of the generated random problems. Additionally, Figure 6 represents algorithm efficiency in the SNS criterion. Since the less the SNS, the better it is, NSGA-II has the best performance among all the other algorithms. Furthermore, in smaller size problems, all of the algorithm’s efficiencies are similar to each other.
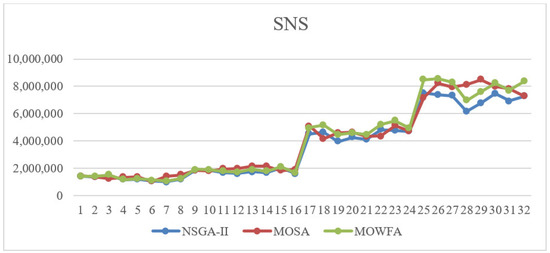
Figure 6.
Comparison of the proposed algorithm efficiency in SNS.
Figure 7 illustrates the proposed algorithm performance for the MID criterion. Approximately, in all of the sample problems, NSGA-II performs better and reaches high-quality solutions.
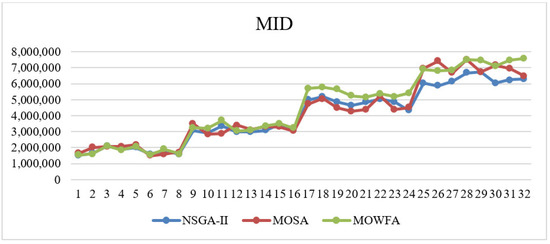
Figure 7.
Comparison of the proposed algorithm efficiency in MID.
Figure 8 shows algorithm efficiency for the Diversity criterion. NSGA-II still stands on the first stage for this criterion.
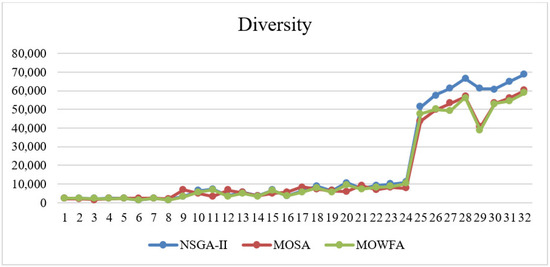
Figure 8.
Comparison of the proposed algorithms efficiency in Diversity.
Figure 9 illustrates the superiority of the proposed NSGA-II to MOSA and MOWFA when running speed is considered. According to this Figure 9, the MOSA algorithm has a similar performance to NSGA-II in small-size problems. However, when the size of the problem increases, the performance of NSGA-II is far better than the two other algorithms, especially MOWFA.
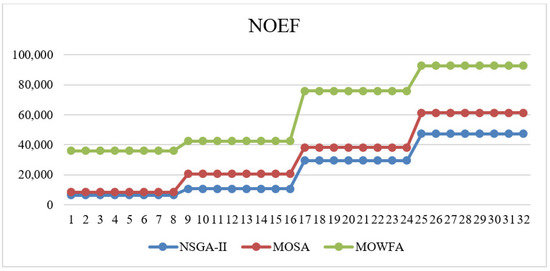
Figure 9.
Comparison of the proposed algorithms efficiency in NOEF.
In order to evaluate and compare more precisely, statistical analyses are used. At first, we normalize all the obtained results using relative percentage division (RPD). The RDP value shows the gap between each algorithm solution and the best-obtained solutions. We can calculate RPD as Equation (24):
where i is the algorithm number and j is the example number. To determine algorithm efficiency, we use the confidence interval of 95%. The obtained results are illustrated in Figure 10. The results show that in the SNS criterion, the NSGA-II algorithm performs significantly better than the two other algorithms. Although the MOSA and MOWFA algorithms are similar to each other in terms of results, the MOSA and NSGA-II algorithms are also similar in terms of MID. In this criterion, MOWFA has the worst performance. In the Diversity criterion, NSGA-II performs far better than MOFA and MOWFA. MOSA and MOFA are also similar to each other in terms of statistics. However, MOSA performs better than MOWFA. In the computational time criterion, MOWFA performs worse than the other two algorithms. In this criterion, NSGA-II has the best performance.
RPDij = (solij − solj,min)/solj,min
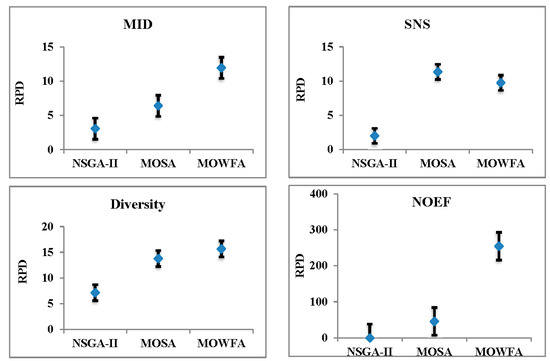
Figure 10.
Confidence intervals of 95% for algorithms RPD in different criteria.
4. Conclusions and Suggestions for Future Work
Modeling and optimizing the supply chain in order to locate an optimum material transferring system has attracted many researchers’ attention. In this paper, the supply chain has three levels including suppliers, cross-docks, and factories. Raw materials are transferred to several cross-docks via several suppliers. Each channel is inclusively for a special product in a cross-dock. Goods entrance rate from supplier to cross-docks is stochastic and follows a general probability distribution. On the other hand, we assume that startup and delivery time in cross-docks are stochastic and follow a general probability distribution. Service time in each cross-dock depends on the number of existing doors; therefore, we can consider each cross-dock as the G/G/m queue system in which m is the number of doors. The mathematical model is expanded by considering variables and their relations. Our main aim is to present an analytical model using the cross-docks and queue theory technique. Thus, the minimization of two main objectives is evaluated; the former is to minimize materials transferring whereas the latter is to minimize customer waiting time.
Regarding the fact that the proposed model is NP-hard, three metaheuristics including multi-objective water flow, non-dominated sorting genetic, and multi-objective simulated annealing algorithm are used to optimize the proposed model. After tuning the algorithm parameters via the Taguchi method, the obtained results from the algorithms are analyzed by statistical test and the algorithm efficiencies are evaluated. The results vividly demonstrate that in terms of SNS, MID, and Diversity criteria, NSGA-II has higher efficiency than the other two algorithms. Furthermore, the MOSA algorithm performs better than MOWFA in the NOEF criterion. Regarding the resulted tables obtained from algorithms solutions, we can surely conclude that NSGA-II performs highly better than MOSA and MOWFA and reaches better solutions. Examining and analyzing the obtained results from analysis and variance tests prove this claim.
In this paper, we evaluated fundamental costs which are related to transportation and cross-docks. As a result, the most important impact of this research is to identify factors that have high costs. This can help organizations reduce their costs. The special suggestions that this research has for future researchers are derived from the current needs in today’s world. If transportation paths are of high significance, routing problems can be added as a scope for future research. Some other assumptions can be added to the model such as operational storage expenses for products and considering time limitations and distance for each route. Designing another model which is able to plan all of the events in a cross-dock can be considered another practical scope for future research. Replacing metaheuristic algorithms with simulation methods and neural networks and also evaluating other metaheuristic algorithms is another way to enlarge our knowledge in this scope.
Author Contributions
All authors contributed to the study concept and methodology. Material preparation, data collection and analysis were performed by P.R. The supervision and leading the work was conducted by S.A.D. The first draft of the manuscript was written by P.R. All corrections and editing are done by M.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors have no competing interest to declare that are relevant to the content of this article.
Ethical Approval
The authors have no relevant ethical approval to disclose for this article.
References
- Agustina, D.; Lee, C.; Piplani, R. A Review: Mathematical Modles for Cross Docking Planning. Int. J. Eng. Bus. Manag. 2010, 2, 47–54. [Google Scholar] [CrossRef]
- Van Belle, J.; Valckenaers, P.; Cattrysse, D. Cross-docking: State of the art. J. Omega 2012, 40, 827–846. [Google Scholar] [CrossRef]
- Apte, U.M.; Viswanathan, S. Effective Cross Docking for Improving Distribution Efficiencies. Int. J. Logist. Res. Appl. 2000, 3, 291–302. [Google Scholar] [CrossRef]
- Bachlaus, M.; Pandey, M.K.; Mahajan, C.; Shankar, R.; Tiwari, M.K. Designing an integrated multi-echelon agile supply chain network: A hybrid taguchi-particle swarm optimization approach. J. Intell. Manuf. 2008, 19, 747–761. [Google Scholar] [CrossRef]
- Yu, W. Operational Strategies for Cross Docking Systems. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2002. [Google Scholar]
- Magableh, G.; Rossetti, M.; Mason, S. Modeling and Analysis of a Generic Cross-Docking Facility. In Proceedings of the 37th Winter Simulation Conference, Orlando, FL, USA, 4 December 2005; pp. 1613–1620. [Google Scholar] [CrossRef]
- Ley, S.; Elfayoumy, S. Cross Dock Scheduling Using Genetic Algorithms. In Proceedings of the 2007 International Symposium on Computational Intelligence in Robotics and Automation, Jacksonville, FL, USA, 20–23 June 2007; pp. 416–420. [Google Scholar] [CrossRef]
- Yu, W.; Egbelu, P.J. Scheduling of inbound and outbound trucks in cross docking systems with temporary storage. Eur. J. Oper. Res. 2008, 184, 377–396. [Google Scholar] [CrossRef]
- Chen, F.; Lee, C.-Y. Minimizing the makespan in a two-machine cross-docking flow shop problem. Eur. J. Oper. Res. 2009, 193, 59–72. [Google Scholar] [CrossRef]
- Vahdani, B.; Zandieh, M. Scheduling trucks in cross-docking systems: Robust meta-heuristics. Comput. Ind. Eng. 2010, 58, 12–24. [Google Scholar] [CrossRef]
- Dondo, R.; Cerdá, J. The heterogeneous vehicle routing and truck scheduling problem in a multi-door cross-dock system. Comput. Chem. Eng. 2015, 76, 42–62. [Google Scholar] [CrossRef]
- Moghadam, S.S.; Ghomi, S.F.; Karimi, B. Vehicle routing scheduling problem with cross docking and split deliveries. Comput. Chem. Eng. 2014, 69, 98–107. [Google Scholar] [CrossRef]
- Ahmadizar, F.; Zeynivand, M.; Arkat, J. Two-level vehicle routing with cross-docking in a three-echelon supply chain: A genetic algorithm approach. Appl. Math. Model. 2015, 39, 7065–7081. [Google Scholar] [CrossRef]
- Yu, V.F.; Jewpanya, P.; Redi, A.A.N.P. Open vehicle routing problem with cross-docking. Comput. Ind. Eng. 2016, 94, 6–17. [Google Scholar] [CrossRef]
- Amini, A.; Tavakkoli-Moghaddam, R. A bi-objective truck scheduling problem in a cross-docking center with probability of breakdown for trucks. Comput. Ind. Eng. 2016, 96, 180–191. [Google Scholar] [CrossRef]
- Cóccola, M.; Mendez, C.; Dondo, R.G. A branch-and-price approach to evaluate the role of cross-docking operations in consolidated supply chains. Comput. Chem. Eng. 2015, 80, 15–29. [Google Scholar] [CrossRef]
- Utama, D.N.; Zaki, F.A.; Munjeri, I.J.; Putri, N.U. A water flow algorithm based optimization model for road traffic engineering. In Proceedings of the International Conference on Advanced Computer Science and Information Systems (ICACSIS), Malang, Indonesia, 15–16 October 2016; pp. 591–596. [Google Scholar] [CrossRef]
- Hasani Goodarzi, A.; Nahavandi, N.; Zegordi, S.H. A Multi-Objective Imperialist Competitive Algorithm for Vehicle Routing Problem in Cross-docking Networks with Time Windows. J. Ind. Syst. Eng. 2018, 11, 1–23. [Google Scholar]
- Ahkamiraad, A.; Wang, Y. Capacitated and multiple cross-docked vehicle routing problem with pickup, delivery, and time windows. Comput. Ind. Eng. 2018, 119, 76–84. [Google Scholar] [CrossRef]
- Baniamerian, A.; Bashiri, M.; Zabihi, F. Two phase genetic algorithm for vehicle routing and scheduling problem with cross-docking and time windows considering customer satisfaction. J. Ind. Eng. Int. 2018, 14, 15–30. [Google Scholar] [CrossRef]
- Molavi, D.; Shahmardan, A.; Sajadieh, M.S. Truck scheduling in a cross docking systems with fixed due dates and shipment sorting. Comput. Ind. Eng. 2018, 117, 29–40. [Google Scholar] [CrossRef]
- Fonseca, G.B.; Nogueira, T.H.; Ravetti, M.G. A hybrid Lagrangian metaheuristic for the cross-docking flow shop scheduling problem. Eur. J. Oper. Res. 2018, 275, 139–154. [Google Scholar] [CrossRef]
- Gelareh, S.; Glover, F.; Guemri, O.; Hanafi, S.; Nduwayo, P.; Todosijević, R. A comparative study of formulations for a cross-dock door assignment problem. Omega 2018, 91, 102015. [Google Scholar] [CrossRef]
- Musavi, M.M.; Tavakkoli-Moghaddam, R.; Rayat, F. A bi-objective model for pickup and delivery pollution routing problem with integration and consolidation shipments in cross-docking system. Iran. J. Oper. Res. 2018, 8, 2–14. [Google Scholar] [CrossRef][Green Version]
- Nassief, W.; Contreras, I.; Jaumard, B. A comparison of formulations and relaxations for cross-dock door assignment problems. Comput. Oper. Res. 2018, 94, 76–88. [Google Scholar] [CrossRef]
- Shaelaie, M.-H.; Ranjbar, M.; Jamili, N. Integration of parts transportation without cross docking in a supply chain. Comput. Ind. Eng. 2018, 118, 67–79. [Google Scholar] [CrossRef]
- Baniamerian, A.; Bashiri, M.; Tavakkoli-Moghaddam, R. Modified variable neighborhood search and genetic algorithm for profitable heterogeneous vehicle routing problem with cross-docking. Appl. Soft Comput. 2019, 75, 441–460. [Google Scholar] [CrossRef]
- Seyedi, I.; Hamedi, M.; Tavakkoli-Moghaddam, R. Truck Scheduling in a Cross-Docking Terminal by Using Novel Robust Heuristics. Int. J. Eng. 2019, 32, 296–305. [Google Scholar]
- Rijal, A.; Bijvank, M.; de Koster, R. Integrated scheduling and assignment of trucks at unit-load cross-dock terminals with mixed service mode dock doors. Eur. J. Oper. Res. 2019, 278, 752–771. [Google Scholar] [CrossRef]
- Corsten, H.; Becker, F.; Salewski, H. Integrating truck and workforce scheduling in a cross-dock: Analysis of different workforce coordination policies. J. Bus. Econ. 2019, 90, 207–237. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Delayed Start Parallel Evolutionary Algorithm for just-in-time truck scheduling at a cross-docking facility. Int. J. Prod. Econ. 2019, 212, 236–258. [Google Scholar] [CrossRef]
- Rahbari, A.; Nasiri, M.M.; Werner, F.; Musavi, M.; Jolai, F. The vehicle routing and scheduling problem with cross-docking for perishable products under uncertainty: Two robust bi-objective models. Appl. Math. Model. 2019, 70, 605–625. [Google Scholar] [CrossRef]
- Hadipour, H.; Amiri, M.; Sharifi, M. Redundancy allocation in series-parallel systems under warm standby and active components in repairable subsystems. Reliab. Eng. Syst. Saf. 2019, 192, 106048. [Google Scholar] [CrossRef]
- Khorshidian, H.; Shirazi, M.A.; Ghomi, S.M.T.F. An intelligent truck scheduling and transportation planning optimization model for product portfolio in a cross-dock. J. Intell. Manuf. 2019, 30, 163–184. [Google Scholar] [CrossRef]
- Fard, S.S.; Vahdani, B. Assignment and scheduling trucks in cross-docking system with energy consumption consideration and trucks queuing. J. Clean. Prod. 2019, 213, 21–41. [Google Scholar] [CrossRef]
- Goodarzi, A.H.; Tavakkoli-Moghaddam, R.; Amini, A. A new bi-objective vehicle routing-scheduling problem with cross-docking: Mathematical model and algorithms. Comput. Ind. Eng. 2020, 149, 106832. [Google Scholar] [CrossRef]
- Movassaghi, M.; Avakh Darestani, S. Cross-docks scheduling with multiple doors using fuzzy approach. Eur. Transp. 2020, 79, 2. [Google Scholar] [CrossRef]
- Goodarzi, A.H.; Zegordi, S.H. Vehicle routing problem in a kanban controlled supply chain system considering cross-docking strategy. Oper. Res. 2020, 20, 2397–2425. [Google Scholar] [CrossRef]
- Ardakani, A.; Fei, J.; Beldar, P. Truck-to-door sequencing in multi-door cross-docking system with dock repeat truck holding patter. Int. J. Ind. Eng. Comput. 2020, 11, 201–220. [Google Scholar] [CrossRef]
- Nogueira, T.H.; Coutinho, F.P.; Ribeiro, R.P.; Ravetti, M.G. Parallel-machine scheduling methodology for a multi-dock truck sequencing problem in a cross-docking center. Comput. Ind. Eng. 2020, 143, 106391. [Google Scholar] [CrossRef]
- Nikzamir, M.; Baradaran, V. A healthcare logistic network considering stochastic emission of contamination: Bi-objective model and solution algorithm. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102060. [Google Scholar] [CrossRef] [PubMed]
- Shahabi-Shahmiri, R.; Asian, S.; Tavakkoli-Moghaddam, R.; Mousavi, S.M.; Rajabzadeh, M. A routing and scheduling problem for cross-docking networks with perishable products, heterogeneous vehicles and split delivery. Comput. Ind. Eng. 2021, 157, 107299. [Google Scholar] [CrossRef]
- Castellucci, P.B.; Costa, A.M.; Toledo, F. Network scheduling problem with cross-docking and loading constraints. Comput. Oper. Res. 2021, 132, 105271. [Google Scholar] [CrossRef]
- Goodarzi, A.H.; Diabat, E.; Jabbarzadeh, A.; Paquet, M. An M/M/c queue model for vehicle routing problem in multi-door cross-docking environments. Comput. Oper. Res. 2021, 138, 105513. [Google Scholar] [CrossRef]
- Goodarzi, A.H.; Zegordi, S.H.; Alpan, G.; Kamalabadi, I.N.; Kashan, A.H. Reliable cross-docking location problem under the risk of disruptions. Oper. Res. 2021, 21, 1569–1612. [Google Scholar] [CrossRef]
- Yu, V.F.; Jewpanya, P.; Redi, A.P.; Tsao, Y.-C. Adaptive neighborhood simulated annealing for the heterogeneous fleet vehicle routing problem with multiple cross-docks. Comput. Oper. Res. 2021, 129, 105205. [Google Scholar] [CrossRef]
- Theophilus, O.; Dulebenets, M.A.; Pasha, J.; Lau, Y.-Y.; Fathollahi-Fard, A.M.; Mazaheri, A. Truck scheduling optimization at a cold-chain cross-docking terminal with product perishability considerations. Comput. Ind. Eng. 2021, 156, 107240. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, D.; Du, Y.; Liu, J.; Pardalos, P.M.; Qiao, J. The two-echelon production routing problem with cross-docking satellites. Transp. Res. Part E Logist. Transp. Rev. 2021, 147, 102210. [Google Scholar] [CrossRef]
- Smith, A.; Toth, P.; Bam, L.; van Vuuren, J. A multi-tiered vehicle routing problem with global cross-docking. Comput. Oper. Res. 2022, 137, 105526. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).