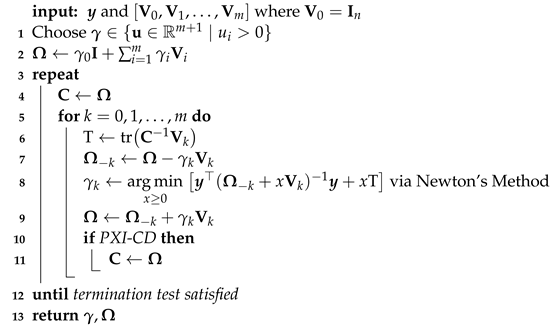Coordinate Descent for Variance-Component Models

Abstract

Variance-component models are an indispensable tool for statisticians wanting to capture both random and fixed model effects. They have applications in a wide range of scientific disciplines. While maximum likelihood estimation (MLE) is the most popular method for estimating the variance-component model parameters, it is numerically challenging for large data sets. In this article, we consider the class of coordinate descent (CD) algorithms for computing the MLE. We show that a basic implementation of coordinate descent is numerically costly to implement and does not easily satisfy the standard theoretical conditions for convergence. We instead propose two parameter-expanded versions of CD, called PX-CD and PXI-CD. These novel algorithms not only converge faster than existing competitors (MM and EM algorithms) but are also more amenable to convergence analysis. PX-CD and PXI-CD are particularly well-suited for large data sets—namely, as the scale of the model increases, the performance gap between the parameter-expanded CD algorithms and the current competitor methods increases.

1. Introduction

Linear models that contain both fixed and random effects are referred to as variance components or linear-mixed models (LMMs). They arise in numerous applications, such as genetics [1], biology, economics, epidemiology and medicine. A broad coverage of existing methodologies and applications of these models can be found in the textbooks [2,3].

In the simplest variance component setup, we observe a response vector $y\in {\mathbb{R}}^n$ and a predictor matrix $\mathbf{X}\in {\mathbb{R}}^{n\times p}$ and assume that $y$ is an outcome of a normal random variable $\mathit{Y}\sim \mathcal{N}(\mathbf{X}\mathit{\beta },\mathbf{\Omega })$, where the covariance is of the form,

$$\mathbf{\Omega }=\sum _{i=0}^m{\gamma }_i{\mathbf{V}}_i\in {\mathbb{R}}^{n\times n},{\gamma }_i\ge 0.$$

The matrices ${\mathbf{V}}_0,\dots ,{\mathbf{V}}_m$ are fixed positive semi-definite matrices, and ${\mathbf{V}}_0$ is non-singular. The unknown mean effects $\mathit{\beta }=({\beta }_1,\dots ,{\beta }_p)$ and variance component parameters $\mathit{\gamma }=({\gamma }_0,\dots ,{\gamma }_m)$ can be estimated by maximizing the log-likelihood function,

$$L(\mathit{\beta },\mathit{\gamma })=-\frac{1}{2}lndet\mathbf{\Omega }-\frac{1}{2}{\left(y-\mathbf{X}\beta \right)}^{\top }{\mathbf{\Omega }}^{-1}\left(y-\mathbf{X}\beta \right).$$

(1)

If $\mathbf{\Omega }$ is known, the maximum likelihood estimator (MLE) for $\mathit{\beta }$ is given by

$$\widehat{\mathit{\beta }}={\left({\mathbf{X}}^{\top }{\mathbf{\Omega }}^{-1}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\top }{\mathbf{\Omega }}^{-1}y.$$

To simplify the MLE estimate for $\mathit{\gamma }$, one can adopt the restricted MLE (REML) method [4] to remove the mean effect in the likelihood expression by projecting $y$ onto the null space of $\mathbf{X}$. Let $\nu =n-p$ and suppose we have the QR decomposition,

$$\mathbf{X}=\left[\begin{array}{cc}{\mathbf{Q}}_{\left[p\right]}& {\mathbf{Q}}_{\left[\nu \right]}\end{array}\right]\left[\begin{array}{c}\mathbf{R}\\ {\mathbf{0}}_{\nu \times p}\end{array}\right],$$

where $\mathbf{R}$ is an $p\times p$ upper triangular matrix, ${\mathbf{0}}_{\nu \times p}$ is an $\nu \times p$ zero matrix, ${\mathbf{Q}}_{\left[p\right]}$ is an $n\times p$ matrix, ${\mathbf{Q}}_{\left[\nu \right]}$ is $n\times \nu$, and ${\mathbf{Q}}_{\left[p\right]}$ and ${\mathbf{Q}}_{\left[\nu \right]}$ both have orthogonal columns. If we take the Cholesky decomposition $\mathbf{L}{\mathbf{L}}^{\top }$ of the matrix ${\mathbf{Q}}_{\left[\nu \right]}^{\top }{\mathbf{V}}_0{\mathbf{Q}}_{\left[\nu \right]}$, then the transformation, ${\mathbf{L}}^{-1}{\mathbf{Q}}_{\left[\nu \right]}^{\top }:{\mathbb{R}}^n\mapsto {\mathbb{R}}^{\nu }$ removes the mean from the response, and we obtain $y^{\prime }:={\mathbf{L}}^{-1}{\mathbf{Q}}_{\left[\nu \right]}^{\top }y\sim \mathcal{N}(\mathbf{0},{\mathbf{\Omega }}^{\prime })$, where ${\mathbf{\Omega }}^{\prime }:={\gamma }_0\mathbf{I}+{\sum }_{i=1}^m{\gamma }_i{\mathbf{V}}_i^{\prime }\in {\mathbb{R}}^{\nu \times \nu }$ and ${\mathbf{V}}_i^{\prime }:={\mathbf{L}}^{-1}{\mathbf{Q}}_{\left[\nu \right]}^{\top }{\mathbf{V}}_i{\mathbf{Q}}_{\left[\nu \right]}{\mathbf{L}}^{-\top }$. After this transformation, the restricted likelihood $-\frac{1}{2}lndet{\mathbf{\Omega }}^{\prime }-\frac{1}{2}{\left(y^{\prime }\right)}^{\top }{\left({\mathbf{\Omega }}^{\prime }\right)}^{-1}{y}^{\prime }$ will not depend on $\mathit{\beta }$.

Henceforth, and without loss of generality, we assume that such a transformation has been performed so that we can focus on minimizing an objective function of the form:

$$-2L\left(\mathit{\gamma }\right)=lndet\mathbf{\Omega }+y^{\top }{\mathbf{\Omega }}^{-1}y.$$

(2)

There exists extensive literature on optimization methods for the log-likelihood expression (2), including Newton’s Method [5], Fisher Scoring Method [6], the EM and MM Algorithms [7,8,9]. Newton’s method is known to scale poorly as n, or the number of variance components $m+1$, increase due the cost of $O\left(m{n}^3\right)+O\left(m^3\right)$ flops required to invert a Hessian matrix at each update. Both the EM and MM algorithms have simple updating steps; however, numerical experience shows that they are slow to identify the active set $\{i:{\widehat{\gamma }}_i=0\}$, where $\widehat{\mathit{\gamma }}$ is the MLE.

One class of algorithms yet to be applied to this problem are coordinate-descent (CD) algorithms. These algorithms successively minimize the objective function along coordinate directions and can be effective when the optimization for each sub-problem can be made sufficiently simple. Furthermore, only few assumptions are needed to prove that accumulation points of the iterative sequence are stationary points of the objective function. CD algorithms have been used to solve optimization problems for many years, and their popularity has grown considerably in the past few decades because of their usefulness in data science and machine learning tasks. Further in-depth discussions of CD algorithms can be found in the articles [10,11,12].

In this paper, we show that a basic implementation of CD is costly for large-scale problems and does not easily succumb to standard convergence analysis. In contrast, our novel coordinate-descent algorithm called parameter-expanded coordinate descent (PX-CD) is computationally faster and more amenable to theoretical guarantees.

The PX-CD is computationally cheaper to run than the basic CD implementation because the first and second derivatives for each sub-problem can be evaluated efficiently with the conjugate gradient (CG) algorithm [13], whereas the basic CD implementation requires repeat Cholesky factorizations for each coordinate update, each with a complexity of $O\left(n^3\right)$. Further to this, it is often the case that the ${\mathbf{V}}_i$ are low-rank, and we can take advantage of this by employing the well-known Woodbury matrix identity or QR transformation within PX-CD to reduce the computational cost of each univariate minimization.

In PX-CD, the extended parameters are treated as a block of coordinates, which is updated at each iteration by searching through a coordinate hyper-plane rather than single-coordinate directions. We provide an alternate version of PX-CD, which we call parameter expanded-immediate coordinate descent (PXI-CD), where the extended coordinate block is updated multiple times within each cycle of the original parameters. We observe numerically that, for large-scale models, the number of iterations needed to converge greatly offsets the additional computational cost for each coordinate cycle. As a result, the overall convergence time is better than that of the PX-CD.

From a theoretical point of view, we show that the accumulation points of the iterative sequence generated by both the PX-CD and PXI-CD are coordinate-wise minimum points of (2).

We remark that the improved efficiency of the PX-CD algorithm is similar to the well-known superior performance of the PX-DA (parameter-expanded data-augmentation) algorithm [14,15] in the Markov-chain Monte Carlo (MCMC) context—namely, the PX-DA algorithm is often much faster to converge than a basic data-augmentation Gibbs algorithm. This similarity is also the reason for using the same prefix “PX” in our nomenclature.

The remainder of the paper is structured as follows. In Section 2, we describe the basic implementation of CD and provide examples for which it performs unsatisfactorily. In Section 3, we introduce the PX-CD and PXI-CD and show that accumulation points of the iterations are coordinate-wise minima for the optimization. We then discuss their practical implementation and detail how to reduce the computational cost when the ${\mathbf{V}}_i$ are low-rank. We also extend the PX-CD algorithm for penalized estimation to perform variable selection. Then, in Section 4, we provide numerical results when ${\mathbf{V}}_i$ are computer simulated and when ${\mathbf{V}}_i$ are constructed from a real-world genetic data set. We have made our code for these simulations available on GitHub (https://github.com/anantmathur44/CD-for-variance-components) (accessed on 1 July 2022).

2. Basic Coordinate Descent

Recall that, after the REML procedure to remove the mean effect, we have $\mathbf{Y}\sim \mathcal{N}(\mathbf{0},\}\}\mathbf{\Omega })$ and $\mathbf{\Omega }={\sum }_{i=0}^m{\gamma }_i{\mathbf{V}}_i$, where ${\mathbf{V}}_0={\mathbf{I}}_n$. We thus seek to compute:

$$\begin{array}{cc}\hfill \widehat{\mathit{\gamma }}& =\underset{\mathit{\gamma }}{arg\; min}G(\mathbf{\Omega }),{\gamma }_i\ge 0,i=0,1\dots ,m\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill G(\mathbf{\Omega })& :=y^{\top }{\mathbf{\Omega }}^{-1}y+lndet\mathbf{\Omega }.\hfill \end{array}$$

(4)

CD can be applied to solve this problem by successively minimizing G along coordinate directions. There is significant scope for variation in the way components are selected to be updated. In the most conventional way the algorithm cycles through the parameters in the order ${\gamma }_0\to {\gamma }_1\to \cdots \to {\gamma }_m$ and updates each in turn. This version, known as cyclic coordinate descent, is shown in Algorithm 1.    

Algorithm 1 Cyclic CD for $G(\mathbf{\Omega })$.

    If we choose to minimize along one coordinate at a time, then the update of a parameter consists of a line search along the selected coordinate direction—that is, if the selected parameter is component k, then the new parameter value is updated as

$${\gamma }_k^{(t+1)}\leftarrow \underset{x\ge 0}{arg\; min}G\left({\sum }_{i=0}^{k-1}{\mathit{\gamma }}_i^{(t+1)}{\mathbf{V}}_i+{\sum }_{i=k+1}^m{\mathit{\gamma }}_i^{\left(t\right)}{\mathbf{V}}_i+x{\mathbf{V}}_k\right).$$

2.1. Implementation

 The non-trivial component of Algorithm 1 is to compute the line search,

$$\underset{x\ge 0}{arg\; min}G({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k),$$

where ${\mathbf{\Omega }}_{-k}:=\mathbf{\Omega }-{\gamma }_k{\mathbf{V}}_k$. When ${\mathbf{\Omega }}_{-k}$ is invertible, this step can be simplified to a one-dimensional algebraic expression that can be numerically solved without repeated evaluations of the terms $y^{\top }({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)y$ and $lndet({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)$. The simplification is achieved using the Generalized Eigenvalue Decomposition (GEV) [13] to decompose $({\mathbf{V}}_k,{\mathbf{\Omega }}_{-k})\to ({\mathbf{D}}_k,{\mathbf{U}}_k)$ such that,

$${\mathbf{V}}_k{\mathbf{U}}_k={\mathbf{\Omega }}_{-k}{\mathbf{U}}_k{\mathbf{D}}_k\mathrm{and}{\mathbf{U}}_k^{\top }{\mathbf{\Omega }}_{-k}{\mathbf{U}}_k={\mathbf{I}}_n,$$

where ${\mathbf{D}}_k\in {\mathbb{R}}^{n\times n}$ is a diagonal matrix with non-negative entries and ${\mathbf{U}}_k\in {\mathbb{R}}^{n\times n}$ is invertible. Using the above expressions we obtain the factorized expression, ${\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k={\mathbf{U}}_k^{-\top }\left(\mathbf{I}+x\mathbf{D}\right){\mathbf{U}}_k^{-1}$. Therefore, we can express the inverse and log-determinant terms in $G({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)$ as,

$$\begin{array}{cc}\hfill {\left({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k\right)}^{-1}& ={\mathbf{U}}_k{({\mathbf{I}}_n+x{\mathbf{D}}_k)}^{-1}{\mathbf{U}}_k^{\top },\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill lndet\left({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k\right)& =lndet\left({\mathbf{I}}_n+x{\mathbf{D}}_k\right)-2lndet{\mathbf{U}}_k.\hfill \end{array}$$

(6)

From (4), we have that,

$$G({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)=y^{\top }{\mathbf{U}}_k{({\mathbf{I}}_n+x{\mathbf{D}}_k)}^{-1}{\mathbf{U}}_k^{\top }y+lndet({\mathbf{I}}_n+x{\mathbf{D}}_k)+\mathrm{const}.$$

Let ${\mathit{\alpha }}_k={\mathbf{U}}_k^{\top }y$ and ${\mathit{d}}_k=\mathrm{diag}\left({\mathbf{D}}_k\right)$. Then, the function to be minimized at the k-th component is of the form,

$$g_k\left(x\right):=G({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)=\sum _{j=1}^n\frac{{\alpha }_{k,j}^2}{d_{k,j}x+1}+ln(1+d_{k,j}x)+\mathrm{const}.$$

(7)

where $d_j\ge 0$ for all j. Unless $n=1$, in general, there is no closed-form expression for the minimum. We thus resort to a numerical method, such as Newton’s method or the Golden-section search method. With the above simplification the majority of the cost is attributed to the GEV, which has a time complexity of $O\left(14n^3\right)$. Alternatively, one could employ iterative methods without prior simplification of $g_k\left(x\right)$ via the GEV. In that case, however, evaluation of $g_k\left(x\right)$ and its derivatives at each step requires one full Cholesky factorization, costing $O\left(n^3\right)$. Either way, for problems where n is large, basic CD is too costly per one update.

2.2. Convergence

An interesting question is whether the sequence generated in Algorithm 1 converges to a local minimum of the objective function (3) (which is assumed to have a global minimum). To make a general point about the convergence theory, take $\mathcal{C}$ to be the set of limit points of a coordinate-descent sequence $\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}$. It is well-known [16,17] that the following existence and uniqueness assumption:

$$g_k\left(x\right)=G({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)\mathrm{has} \mathrm{a} \mathrm{unique} \left(\mathrm{global}\right) \mathrm{minimizer} \mathrm{for}x\ge 0$$

(8)

is one of the simplest sufficient conditions that ensures the set $\mathcal{C}$ is not empty and contains only singletons. Assuming that the existence and uniqueness assumption holds for a given coordinate-descent algorithm and ${\mathit{\gamma }}^{*}\in \mathcal{C}$ then, by construction, ${\mathit{\gamma }}^{*}$ is a global coordinate-wise minimum of (3)—that is, one cannot reduce the value of the objective function by moving along each of the coordinate directions (that is, $G({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)\ge G({\mathbf{\Omega }}_{-k}+{\gamma }_k^{*}{\mathbf{V}}_k)$ for each k and all $x\ge 0$).

Even if ${\mathit{\gamma }}^{*}\in \mathcal{C}$ is a coordinate-wise minimum, it may not be a local minimum of (3). It may well be a saddle point of (3). For example, the function $f({\gamma }_1,{\gamma }_2)={\gamma }_1^2+{\gamma }_2^2-5{\gamma }_1{\gamma }_2$ does not have a local minimum at zero ($f(\gamma ,\gamma )=-3{\gamma }^2$ indicating that a minimum does not even exist); however, it has a coordinate-wise minimum at $({\gamma }_1,{\gamma }_2)=(0,0)$.

Thus, it is important to remember that the set of local minima of the optimization problem (3) is a subset of $\mathcal{C}$ because $\mathcal{C}$ may contain coordinate-wise minima, which are still saddle points of (3). One positive aspect is that the saddle points found by any coordinate-descent algorithm (under the existence and uniqueness assumption) are a subset of all the saddle points of (3) because they are constrained to be coordinate-wise minima. Stated another way, the set $\mathcal{C}$ consists of either local minimizers or saddle points that look like coordinate-wise minimizers.

Either way, there is simply no guarantee that any of our coordinate-descent procedures in this paper will converge to a strict local minimum of (3), see [16,18] for more in-depth discussions. Of course, this is an issue for any of the existing optimization algorithms for (3) (MM and EM algorithms simply being a special case of coordinate descent, and Newton’s method known for convergence only when initialized near a local minimum), and thus it should not be viewed as a particular disadvantage of our proposals.

Unfortunately, the existence and uniqueness assumption (8) cannot be used to deal with the convergence of the basic CD Algorithm 1. This is because $g_k\left(x\right)$ can exhibit multiple local minima, as illustrated next.

Suppose $n=2$, then from Equation (7), we have

$$g_k\left(x\right)=\frac{{\alpha }_{k,1}^2}{d_{k,1}x+1}+ln(1+d_{k,1}x)+\frac{{\alpha }_{k,2}^2}{d_{k,2}x+1}+ln(1+d_{k,2}x)+\mathrm{const}.$$

In Figure 1, we observe two minimizers for $g_k\left(x\right)$ when ${\mathit{\alpha }}_k=(1.2,3)$ and ${\mathit{d}}_k=(10,0.2)$, respectively. This implies that the existence and uniqueness assumption does not hold for the basic implementation of CD, and we cannot ensure that accumulation points of the sequence $\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}$ are coordinate-wise minima of G.

Figure 1. Two local minima: $(0.11,10.26)$ and $(14.35,8.66)$ obtained for $g_k\left(x\right)$ when ${\alpha }_{k,1}=1.2$, ${\alpha }_{k,2}=3$, $d_{k,1}=10$ and $d_{k,2}=0.2$.

Example 1 (Sufficient Conditions for a Unique Minimum).

In this example, we show that strong conditions are needed for the existence and uniqueness assumption to hold, making the basic CD Algorithm 1 less than attractive. Suppose $\delta :=\frac{1}{n}{\sum }_{j=1}^n{\alpha }_{k,j}^2>1$ and there is a constant $d>0$ such that $d_{k,j}=d$ for all $j=1,\dots ,n$. In that case, we have

$$g_k\left(x\right)=\frac{n\delta }{dx+1}+nln(1+dx)+\mathrm{const}.$$

Therefore, the first and second derivatives of $g_k\left(x\right)$ are, respectively, given by

$$g_k^{\prime }\left(x\right)=\frac{nd}{(1+dx)}\left(1-\frac{\delta }{(1+dx)}\right)\mathrm{and}{g}_k^{″}\left(x\right)=-\frac{n{d}^2}{{(1+dx)}^2}\left(1-\frac{2\delta }{(1+dx)}\right).$$

Since $d>0$, it easy to see that the equation $g_k^{\prime }\left(x\right)=0$ has a unique (positive) solution, which is $x_1^{*}=\frac{\delta -1}{d}$. Similarly, the solution of $g_k^{″}\left(x\right)=0$ is $x_2^{*}=\frac{2\delta -1}{d}$, which is greater than $x_1^{*}$.

Since $g_k^{″}\left(x\right)>0$ for every $x\in [0,x_2^{*})$, $g_k\left(x\right)$ is (strictly) convex over $[0,x_2^{*})$. As a result, since $0<x_1^{*}<x_2^{*}$, $g_k\left(x\right)$ exhibits a global minimum at $x_1^{*}$.

3. Parameter-Expanded CD

Since the basic CD Algorithm 1 is both expensive per coordinate update and is not amenable to standard convergence analysis [16,17], we consider an alternative called the parameter-expanded CD or PX-CD. We argue that our novel coordinate-descent algorithm is both faster to converge and also amenable to simple convergence analysis because the existence and uniqueness assumption holds. This constitutes our main contribution.

In the PX-CD, we use the supporting hyper-plane (first-order Taylor approximation) to the concave matrix function $f\left(\mathbf{A}\right)=lndet\mathbf{A}$, where $\mathbf{A}\succ \mathbf{0}$. The supporting hyper-plane gives the bound [9]:

$$lndet\mathbf{A}\le lndet\mathbf{C}+tr\left({\mathbf{C}}^{-1}(\mathbf{A}-\mathbf{C})\right),$$

where $\mathbf{C}\in {\mathbb{R}}^{n\times n}$ is an arbitrary PSD matrix, and equality is achieved if and only if $\mathbf{C}=\mathbf{A}$. Replacing the log-determinant term in G with the above upper bound, we obtain the surrogate function,

$$H(\mathbf{\Omega },\mathbf{C}):=y^{\top }{\mathbf{\Omega }}^{-1}y+\sum _{i=0}^m{\gamma }_i\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_i\right)+lndet\left(\mathbf{C}\right)-n\ge G(\mathbf{\Omega }).$$

(9)

The surrogate function H has $\mathbf{C}$ as an extra variable in our optimization, which we set to be of the form:

$$\mathbf{C}=\sum _{i=0}^m{\tilde{\gamma }}_i{\mathbf{V}}_i,$$

where $\tilde{\mathit{\gamma }}=\left({\tilde{\gamma }}_0,{\tilde{\gamma }}_1,\dots ,{\tilde{\gamma }}_m\right)$ are latent parameters. Similar to the MM algorithmic recipe [9], we then jointly minimize the surrogate function H with respect to both $\mathit{\gamma }$ and $\tilde{\mathit{\gamma }}$ using CD.

The most apparent way of selecting our coordinates is to cyclically update in the order:

$${\gamma }_0\to {\gamma }_1\to \cdots \to {\gamma }_m\to \tilde{\mathit{\gamma }},$$

where the last update is a block update of the entire block $\tilde{\mathit{\gamma }}$. In other words, the expanded parameters $\tilde{\mathit{\gamma }}$ are treated as a block of coordinates that is updated in each cycle by searching through the coordinate hyper-plane rather than the single-coordinate directions. We refer to a full completion of updates in a single ordering as a “cycle” of updates. Suppose the initial guess for the parameters are $({\mathit{\gamma }}^{\left(0\right)},{\tilde{\mathit{\gamma }}}^{\left(0\right)})$, then, at the end of cycle t, we denote the updated parameters as $({\mathit{\gamma }}^{\left(t\right)},{\tilde{\mathit{\gamma }}}^{\left(t\right)})$. In Theorem 1, we state that under certain conditions, the sequence ${\left\{({\mathit{\gamma }}^{\left(t\right)},{\tilde{\mathit{\gamma }}}^{\left(t\right)})\right\}}_{t\ge 0}$ generated by PX-CD has limit-points, which are coordinate-wise minima for G.

Let ${\mathbf{\Omega }}^{\left(t\right)}={\sum }_{i=0}^m{\gamma }_i^{\left(t\right)}{\mathbf{V}}_i$ be the updated covariance matrix after the $m+1$ original parameters have been updated in cycle t. Then, as the inequality in (9) achieves equality if and only if $\mathbf{C}=\mathbf{\Omega }$ the update for the expanded block parameters $\tilde{\mathit{\gamma }}$ in cycle t is,

$${\tilde{\mathit{\gamma }}}^{\left(t\right)}=\underset{\tilde{\mathit{\gamma }}}{arg\; min}H({\mathbf{\Omega }}^{\left(t\right)},\sum _{i=0}^m{\tilde{\gamma }}_i{\mathbf{V}}_i)={\mathit{\gamma }}^{\left(t\right)}.$$

In practice, we simply store ${\mathbf{C}}^{\left(t\right)}={\mathbf{\Omega }}^{\left(t\right)}$ at the end of each cycle.

Minimizing H with respect to the k-th component of the original parameter $\mathit{\gamma }$ yields a function of the form:

$$h_k\left(x\right):=H({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k,\mathbf{C})=y^{\top }{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}y+x\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)+\mathrm{const}.,x\ge 0.$$

(10)

One of the main advantages of the PX-CD procedure over the basic coordinate descent in Algorithm 1 is that the optimization along each coordinate has a unique minimum.

Lemma 1.

$h_k\left(x\right)$ has a unique minimizer for $x\ge 0$.

Proof. 

We now show that on $[0,\infty )$, the function $h_k\left(x\right)$ is either strictly convex or a linear function with a strictly positive gradient.

We first consider the case where ${\mathbf{\Omega }}_{-k}$ is invertible. From [13], we have the GEV decomposition: $({\mathbf{V}}_k,{\mathbf{\Omega }}_{-k})\to ({\mathbf{D}}_k,{\mathbf{U}}_k)$ where ${\mathbf{D}}_k\in {\mathbb{R}}^{n\times n}$ is a diagonal matrix with non-negative entries and ${\mathbf{U}}_k\in {\mathbb{R}}^{n\times n}$ is invertible. In a similar fashion to the simplified basic CD expression (7), let ${\mathit{\alpha }}_k={\mathbf{U}}_k^{\top }y$ and ${\mathit{d}}_k=\mathrm{diag}\left({\mathbf{D}}_k\right)$. Then, $h_k\left(x\right)$ can be simplified to,

$$h_k\left(x\right)=\sum _{j=1}^n\frac{{\alpha }_{k,j}^2}{d_{k,j}x+1}+x\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)+\mathrm{const}.$$

(11)

We then obtain the first and second derivatives,

$$h_k^{\prime }\left(x\right)=-\sum _{j=1}^n\frac{{\alpha }_{k,j}^2{d}_{k,j}}{{(d_{k,j}x+1)}^2}+\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right),h_k^{″}\left(x\right)=\sum _{j=1}^n\frac{2{\alpha }_{k,j}^2{d}_{k,j}^2}{{(d_{k,j}x+1)}^3}.$$

(12)

where $d_j\ge 0$. If there exists j such that ${\alpha }_{k,j}{d}_{k,j}\ne 0$, then $h^{″}\left(x\right)>0$ for $x\ge 0$. Then, h is strictly convex and attains a unique global minimizer $x^{*}\in [0,\infty )$. Suppose that ${\alpha }_{k,j}{d}_{k,j}=0$ for $j=1,\dots ,n$ then $h_k^{\prime }\left(x\right)=\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)$. If we can show that $\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)>0$, then $h_k\left(x\right)$ is strictly increasing on $[0,\infty )$, and $x^{*}=0$ is the unique global minimizer for $x\in [0,\infty )$.

We note that the matrix ${\mathbf{C}}^{-1}$ is positive-definite since $\mathbf{C}={\sum }_{i=0}^m{\tilde{\gamma }}_i{\mathbf{V}}_i$ is invertible and positive semi-definite. Therefore, the symmetric square root factorization, ${\mathbf{C}}^{-1}={\mathbf{C}}^{-1/2}{\mathbf{C}}^{-1/2}$ exists, and

$$\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)=\mathrm{tr}\left({\mathbf{C}}^{-1/2}{\mathbf{V}}_k{\mathbf{C}}^{-1/2}\right),$$

due to the invariant cyclic nature of the trace. The matrix ${\mathbf{C}}^{-\frac{1}{2}}{\mathbf{V}}_k{\mathbf{C}}^{-\frac{1}{2}}$ is positive semi-definite as ${\mathbf{z}}^{\top }{\mathbf{C}}^{-1/2}{\mathbf{V}}_k{\mathbf{C}}^{-1/2}\mathbf{z}={\parallel {\mathbf{V}}_k^{1/2}{\mathbf{C}}^{-1/2}\mathbf{z}\parallel }_2^2\ge 0$ for all $\mathbf{z}\in {\mathbb{R}}^n$. Since ${\mathbf{C}}^{-\frac{1}{2}}{\mathbf{V}}_k{\mathbf{C}}^{-\frac{1}{2}}$ is a non-zero matrix and positive-semi-definite, $\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)>0$ and $h_k\left(x\right)$ has a strictly positive slope, which implies that $x^{*}=0$ is the unique global minimizer for $x\in [0,\infty )$.

Consider the case $\dim \left(\mathrm{span}\{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_m\}\right)=r<n$. Assuming ${\gamma }_0>0$, then ${\mathbf{\Omega }}_{-k}$ will be invertible except when $k=0$. When ${\mathbf{\Omega }}_{-0}$ is singular, a simplified expression in the form of (11) may be difficult to find. Instead, we take the singular value decomposition (SVD) of the symmetric matrix ${\mathbf{\Omega }}_{-0}$,

$${\mathbf{\Omega }}_{-0}={\mathbf{Q}}^{\top }\mathbf{\Lambda }\mathbf{Q},\mathbf{\Lambda }=\left[\begin{array}{cc}\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_r)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right],$$

where ${\lambda }_1,\dots ,{\lambda }_r>0$ are the real-positive eigenvalues of ${\mathbf{\Omega }}_{-k}$, and the matrix $\mathbf{Q}\in {\mathbb{R}}^{n\times n}$ is orthogonal. Then, we can express the inverse as

$${\left({\mathbf{\Omega }}_{-0}+x\mathbf{I}\right)}^{-1}=\mathbf{Q}{(\mathbf{\Lambda }+x{\mathbf{I}}_n)}^{-1}{\mathbf{Q}}^{\top }.$$

If we assume $y\notin \mathrm{span}\{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_m\}$, then $\mathit{\alpha }={\mathbf{Q}}^{\top }y\ne \mathbf{0}$. Then,

$$h_0\left(x\right)=\sum _{j=1}^r\frac{{\alpha }_j^2}{{\lambda }_j+x}+\sum _{j=r+1}^n{\alpha }_j^2{x}^{-1}+x\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)+\mathrm{const}.$$

(13)

and

$$h_0^{″}\left(x\right)=\sum _{j=1}^r\frac{2{\alpha }_j^2}{{({\lambda }_j+x)}^3}+\sum _{j=r+1}^n\frac{2{\alpha }_j^2}{x^3}>0,$$

when $x>0$. Therefore, $h_0\left(x\right)$ still attains a unique minimizer as the function is strongly convex for $x>0$.   □

The result of this lemma ensures the existence and uniqueness condition (8), and thus we can ensure that accumulation or limit points of the CD iteration are also coordinate-wise minimal points. The details of the optimization follow.

3.1. Univariate Minimization via Newton’s Method

Unlike the basic CD Algorithm 1, for which each coordinate update costs $O\left(n^3\right)$, here we show that a coordinate update for the PX-CD algorithm costs only $O\left(j{n}^2\right)$ for some constant j where typically $j\ll n$.

The function $h_k\left(x\right)$ can be minimized via the second-order Newton’s method, which numerically finds the root of $h_k^{\prime }\left(x\right)$. The basic algorithm starts with an initial guess $x_0$ of the root, and then

$$x_{n+1}=x_n-h_k^{\prime }\left(x_n\right){\left[h_k^{″}\left(x_n\right)\right]}^{-1},$$

(14)

are successive better approximations. The algorithm can be terminated once successive iterates are sufficiently close together. The first and second derivatives of h are given as

$$\begin{array}{cc}\hfill h_k^{\prime }\left(x\right)& =-y^{\top }{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}{\mathbf{V}}_k{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}y+\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill h_k^{″}\left(x\right)& =2y^{\top }{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}{\mathbf{V}}_k{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}{\mathbf{V}}_k{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}y,\hfill \end{array}$$

(16)

where we used differentiation of a matrix inverse, which implies that

$$\frac{\partial {({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}}{\partial x}=-{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}\frac{\partial ({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}{\partial x}{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}.$$

Similar to the basic CD implementation, computing the algebraic expression in (11) via GEV is expensive. Evaluating (15) and (16) by explicitly calculating ${({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}$ is also expensive for large n and is of time complexity $O\left(n^3\right)$. Instead, we utilize the conjugate gradient (CG) algorithm [13] to efficiently solve linear systems. At each iteration of Newton’s method, we approximately solve,

$$({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)\mathit{b}=y,({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)\mathit{c}={\mathbf{V}}_k\mathit{b},$$

(17)

and store the solution in $\mathit{b}$ and $\mathit{c}$, respectively, via CG algorithm. Generally, $\parallel \mathit{b}-{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}y\parallel$ and $\parallel \mathit{c}-{({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k)}^{-1}{\mathbf{V}}_k\mathit{b}\parallel$ can be made small with $l\ll n$ iterations, where each iteration requires a matrix-vector-multiplication operation with a $n\times n$ matrix. The CG algorithm has complexity $O\left(l{n}^2\right)$ and can be easily implemented with standard Linear Algebra packages. With the stored approximate solutions, we evaluate the first and second derivatives as

$$h_k^{\prime }\left(x\right)=-{\mathit{b}}^{\top }{\mathbf{V}}_k\mathit{b}+\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right),h_k^{″}\left(x\right)=2{\mathit{b}}^{\top }{\mathbf{V}}_k\mathit{c}.$$

(18)

Before initiating Newton’s method, we can check if k is in the active constraint set $\{k:{\widehat{\gamma }}_k=0\}$. Following from Lemma 1, if $h_k^{\prime }\left(0\right)\ge 0$, then $h_k\left(x\right)$ is non-decreasing on $[0,\infty )$. Then, $h_k\left(0\right)$ is the global minimum for $x\in [0,\infty )$, and we let ${\gamma }_i^{(t+1)}=0$ if we are in cycle $t+1$ of PX-CD. If $h_k^{\prime }\left(0\right)<0$, we initiate Newton’s method at the current value of the variance component, $x_0={\gamma }_k^{\left(t\right)}$. If $\dim \left(\mathrm{span}\{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_m\}\right)<n$, we require ${\gamma }_0>0$ so that $\mathbf{\Omega }$ is invertible.

In this case, $k=0$ cannot be in the active constraint set and we immediately initiate Newton’s method at the starting point $x_0={\gamma }_0^{\left(t\right)}$. In rare cases $h_k^{\prime }\left(x\right)$ is sufficiently flat at $x_n$ and (14) may significantly overstep the location of the minimizer and return an approximation $x_{n+1}<0$. In this case, we dampen the step size until $x_{n+1}>0$.

3.2. Updating Regime

We now consider an alternative to the cyclic ordering of updates. Suppose we update the block $\tilde{\mathit{\gamma }}$ after every co-ordinate update—that is, the updating order of one complete cycle is

$${\gamma }_0\to \tilde{\mathit{\gamma }}\to {\gamma }_1\to \tilde{\mathit{\gamma }}\to \dots \to {\gamma }_m\to \tilde{\mathit{\gamma }}.$$

This ordering regime satisfies the “essentially cyclic” condition whereby, in every stretch of $2(m+1)$ updates, each component is updated at least once. We refer to CD with this ordering as parameter expanded-immediate coordinate descent (PXI-CD).

In practice, this ordering implies updating the matrix $\mathbf{C}$ after every update made to each ${\gamma }_k$. Since the expression for $h_k^{\prime }\left(x\right)$ requires one to evaluate $\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)$ and $\mathbf{C}$ is updated after every coordinate, we must re-compute ${\mathbf{C}}^{-1}$ for each k. This implies that each cycle in PXI-CD will be more expensive than PX-CD. However, we observe that in situations where ${\mathbf{V}}_i$ is full rank and n is sufficiently large, the number of cycles needed to converge is significantly less than that required for PX-CD and basic CD.

This results in PXI-CD being the most time-efficient algorithm when the scale of the problem is large. In Section 3.3, we show that, when ${\mathbf{V}}_i$ is low-rank, re-computing $\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{V}}_k\right)$ comes at no additional-cost through the use of the Woodbury matrix identity. However, in this particular scenario, where ${\mathbf{V}}_k$ are low-rank, the performance gain from PXI-CD is not as significant as when ${\mathbf{V}}_i$ are full rank, and both PXI-CD and PX-CD show similar performance. Algorithm 2 summarizes both PX-CD and PXI-CD methods to obtain $\widehat{\mathit{\gamma }}$.

Algorithm 2 PX-CD and PXI-CD for $G(\mathbf{\Omega })$

As mentioned previously, the novel parameter-expanded coordinate-descent algorithms, PX-CD and PXI-CD, are both amenable to standard convergence analysis.

Theorem 1 (PX-CD and PXI-CD Limit Points).

For both PX-CD and PXI-CD in Algorithm 2, let ${\{{\mathit{\gamma }}^{\left(t\right)},{\tilde{\mathit{\gamma }}}^{\left(t\right)}\}}_{t\ge 0}$ be the coordinate-descent sequence. Then, either $G\left({\sum }_k{\gamma }_k^{\left(t\right)}{\mathbf{V}}_k\right)\to -\infty$, or every limit-point of ${\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}}_{t\ge 0}$ is a coordinate-wise minimum of (3). If we further assume that $y\notin \mathrm{span}\{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_m\}<n$, then the sequence ${\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}}_{t\ge 0}$ is bounded and $G\left({\sum }_k{\gamma }_k^{\left(t\right)}{\mathbf{V}}_k\right)\to -\infty$ is ruled out.

Proof. 

Recall that $\mathbf{\Omega }={\sum }_{i=0}^m{\gamma }_i{\mathbf{V}}_i$ and $\mathbf{C}={\sum }_{i=0}^m{\tilde{\gamma }}_i{\mathbf{V}}_i$. Denote $(x_1,\dots ,x_{m+1}):=\mathit{\gamma }$ and ${\mathbf{x}}_{m+2}:=\tilde{\mathit{\gamma }}\in {\mathbb{R}}^{m+1}$ as well as $\mathbf{x}:=(x_1,\dots ,x_{m+1},{\mathbf{x}}_{m+2})\in {\mathbb{R}}^{2(m+1)}$. We can rewrite the optimization problem (3) in the penalized form:

$$f\left(\mathbf{x}\right):=f_0\left(\mathbf{x}\right)+\sum _{k=1}^{m+1}{f}_k\left(x_k\right)+f_{m+2}\left({\mathbf{x}}_{m+2}\right),$$

where $f_0\left(\mathbf{x}\right):=H(\mathbf{\Omega },\mathbf{C})$ and

$$f_k\left(x\right):=\left\{\begin{array}{cc}0,\hfill & x\ge 0\hfill \\ \infty ,\hfill & x<0\hfill \end{array}\right.,k=1,\dots ,m+1,f_{m+2}\left(\mathbf{x}\right):=\left\{\begin{array}{cc}0,\hfill & \mathbf{x}\in [\mathbf{0},\infty ]\hfill \\ \infty ,\hfill & \mathbf{x}\notin [\mathbf{0},\infty )\hfill \end{array}\right..$$

We can then apply the results in [18], which state that every limit point of ${\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}}_{t\ge 0}$ is a coordinate-wise minimum provided that:

• Each function $x_k\mapsto f\left(x\right)$, $k=1,\dots ,m+1$ and $x_{m+2}\mapsto f\left(x\right)$ has a unique minimum. For $k=1,\dots ,m+1$ this has already been verified in Lemma 1. For $x_{m+2}\mapsto f\left(x\right)$, we simply recall that $H(\mathbf{\Omega },\mathbf{C})\ge G(\mathbf{\Omega })$ with equality achieved if and only if $\mathbf{C}=\mathbf{\Omega }$, or equivalently $x_{m+2}=(x_1,\dots ,x_{m+1})$.
• Each $f_k,k=1,\dots ,m+2$ is lower semi-continuous. This is clearly true for $k=1,\dots ,m+1$ because, at the point of discontinuity, we have ${lim\; inf}_{x\to 0}{f}_k\left(x\right)\ge f_k\left(0\right)=0$. For $f_{m+2}$, we simply check that $\{x:f_{m+2}\left(x\right)\le c\}$ for a given $c\in \mathbb{R}$ is a closed set.
• The domain of $f_0$ is a Cartesian product and $f_0$ is continuous on its domain. Clearly, the domain is the $2(m+1)$ Cartesian product $\mathcal{D}:=[0,\infty )\times \cdots \times [0,\infty )$ and $f_0$ is continuous on its effective domain $\{x\in \mathcal{D}:f(x)<\infty \}$.
• The updating rule is essentially cyclic—that is, there exists a constant $T\ge m+2$ such that every block in $(x_1,\dots ,x_{m+1},x_{m+2})$ is updated at least once between the r-th iteration and the $(r+T-1)$-th iteration for all r. In our case, each block is updated at least once in one iteration of Algorithm 2 so that we satisfy the essentially cyclic condition. In the PXI-CD, we actually update $(m+1)$ times the block $x_{m+2}$.

Thus, we can conclude by Proposition 5.1 in [18] that either $f_0\left({\mathit{\gamma }}^{\left(t\right)}\right)\to -\infty$ or the limit points of ${\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}}_{t\ge 0}$ are coordinate-wise minima of $H(\mathbf{\Omega },\mathbf{C})$.

If we further assume that $y\notin \mathrm{span}\{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_m\}<n$, then we can show that set $\{\mathit{\gamma }\ge \mathbf{0}:f_0\left(\mathit{\gamma }\right)\le f_0\left({\mathit{\gamma }}^{\left(0\right)}\right)\}$ is compact, which ensures that the sequence ${\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}}_{t\ge 0}$ is bounded and rules out the possibility that ${lim}_t{f}_0\left({\mathit{\gamma }}^{\left(t\right)}\right)=-\infty$. To see that this is the case, note that $G(\mathbf{\Omega })$ provides a lower bound to $H(\mathbf{\Omega },\mathbf{C})$, and this is sufficient to show that $\{\mathit{\gamma }\ge \mathbf{0}:G\left({\sum }_k{\gamma }_k{\mathbf{V}}_k\right)\le c\}$ is compact for any $c\in \mathbb{R}$ under the assumption that ${\mathbf{V}}_0:=\mathbf{I}$ and $y\notin \mathrm{span}\{{\mathbf{V}}_1,\dots ,{\mathbf{V}}_m\}<n$. However, these are precisely the conditions of Lemma 3 in [9], which ensure that $\{\mathit{\gamma }\ge \mathbf{0}:L(\mathit{\gamma })\ge c\}$ is compact for a likelihood $L\left(\gamma \right):=-G\left({\sum }_k{\gamma }_k{\mathbf{V}}_k\right)$.

Finally, note that since we update the entire block $\tilde{\mathit{\gamma }}$ simultaneously (in both PX-CD and PXI-CD), this means that a coordinate-wise minimum of $H(\mathbf{\Omega },\mathbf{C})$ is also a coordinate-wise minimum for $G(\mathbf{\Omega })$.   □

We again emphasize that, as with all the competitor methods, the theorem does not guarantee convergence of the coordinate-descent sequence ${\left\{{\mathit{\gamma }}^{\left(t\right)}\right\}}_{t\ge 0}$ or that the convergence will be to a local minimum. The only thing we can say for sure is that, when the sequence converges, then the limit will be a coordinate-wise minimum (which could be a saddle point in some special cases). Nevertheless, our numerical experience in Section 4 is that the sequence always converges to a coordinate-wise minimum and that the coordinate-wise minimum is in fact a (local) minimum.

3.3. Linear Mixed Model Implementation

We now show that, for Linear Mixed Models (LMM), we can reduce the computational complexity of each sub-problem to $O\left(j{d}^2\right)$, for some constants $j\ll n$ and $d<n$. As shown in Section 3.1, solving each univariate sub-problem can be simplified to implementing Newton’s method, where at each Newton’s update, we solve two n-dimensional linear systems.

In settings where $\mathrm{rank}\left(\mathbf{V}i\right)<n$, for $i=1,\dots ,m$, we are able to reduce the dimensions of the linear system that is required to be solved. To see this, let us first specify the general variance-component model (also known as the general mixed ANOVA model) [19]. Suppose,

$$y=\mathbf{X}\beta +{\mathbf{Z}}_1{\mathbf{b}}_1+\cdots +{\mathbf{Z}}_m{\mathbf{b}}_m+\mathit{ϵ},$$

(19)

where $\mathbf{X}$ is an $n\times p$ matrix of known fixed numbers, $p\le n$; $\mathit{\beta }$ is an $p\times 1$ vector of unknown constants; ${\mathbf{Z}}_i$ is a full-rank $n\times c_i$ matrix of known fixed numbers, $c_i\le n$; ${\mathbf{b}}_i$ is an $c_i\times 1$ vector of independent variables from $\mathcal{N}(0,{\gamma }_i)$, which are unknown and $\mathit{ϵ}$ is an $n\times 1$ vector of independent errors from $\mathcal{N}(0,{\gamma }_0)$ that are unknown. In this setup, ${\gamma }_0,\dots ,{\gamma }_m$, are the variance component parameters that are to be estimated, ${\mathbf{V}}_i={\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }$ and $\mathbf{\Omega }={\gamma }_0\mathbf{I}+\mathbf{Z}\mathbf{\Sigma }{\mathbf{Z}}^{\top }$, where

$$\mathbf{Z}=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{Z}}_1& {\mathbf{Z}}_2& \cdots & {\mathbf{Z}}_m\\ \mid & \mid & & \mid \end{array}\right],\mathbf{\Sigma }=\mathbf{block}\mathbf{diag}({\gamma }_1{\mathbf{I}}_{c_1},\dots ,{\gamma }_m{\mathbf{I}}_{c_m}).$$

We now provide two methods that take advantage of ${\mathbf{V}}_i$ being low-rank. Let,

$$c:=\sum _{i=1}^m\mathrm{rank}\left({\mathbf{V}}_i\right)=\sum _{i=1}^m{c}_i.$$

In the first method, we utilize a QR factorization that reduces the computational complexity when $c<n$, i.e., the column rank of $\mathbf{Z}$ is less than n. In the second method, we use the Woodbury matrix identity to reduce the complexity when $c_i<n$ for $i=1,\dots ,m$, i.e., the column rank of each of the matrices ${\mathbf{Z}}_i$ is less than n.

3.3.1. QR Method

The following QR factorization can be viewed as a data pre-processing step that allows all PX-CD and PXI-CD computations to be c-dimensional instead of n-dimensional. The QR factorization only needs to be computed once initially with a cost of $O\left(c{n}^2\right)$ operations. Let the QR factorization of $\mathbf{Z}\in {\mathbb{R}}^{n\times c}$ be

$$\mathbf{Z}=\stackrel{\mathbf{Q}}{\overbrace{\left[\begin{array}{cc}{\mathbf{Q}}_{\left[c\right]}& {\mathbf{Q}}_{[n-c]}\end{array}\right]}}\left[\begin{array}{c}\mathbf{R}\\ \mathbf{0}\end{array}\right],\mathbf{R}=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{R}}_1& {\mathbf{R}}_2& \cdots & {\mathbf{R}}_m\\ \mid & \mid & & \mid \end{array}\right],$$

where $\mathbf{R}$ is an $c\times c$ upper triangular matrix, $\mathbf{0}$ is an $(n-c)\times c$ zero matrix, ${\mathbf{Q}}_{\left[c\right]}$ is an $n\times c$ matrix, ${\mathbf{Q}}_{[n-c]}$ is $n\times (n-c)$, and ${\mathbf{Q}}_{\left[c\right]}$ and ${\mathbf{Q}}_{[n-c]}$ both have orthogonal columns. The matrix $\mathbf{R}$ is partitioned such that the number of columns in ${\mathbf{R}}_i$ is equal to the number of columns in ${\mathbf{Z}}_i$. Let $\tilde{y}={[{\tilde{y}}_{\left[c\right]},{\tilde{y}}_{[n-c]}]}^{\top }={\mathbf{Q}}^{\top }y$, where ${\tilde{y}}_{\left[c\right]}$ are the first c elements of $\tilde{y}$ and ${\tilde{y}}_{[n-c]}$ are the last $n-c$ elements of $\tilde{y}$. Then,

$$\begin{array}{c}\hfill H(\mathbf{\Omega },\mathbf{C})={\tilde{y}}_{\left[c\right]}^{\top }{\tilde{\mathbf{\Omega }}}^{-1}{\tilde{y}}_{\left[c\right]}+\sum _{i=0}^m{\gamma }_i\mathrm{tr}\left({\tilde{\mathbf{C}}}^{-1}{\tilde{\mathbf{V}}}_i\right)+lndet\left(\mathbf{C}\right)-n+\alpha ,\end{array}$$

where we define: ${\tilde{\mathbf{V}}}_i:={\mathbf{R}}_i{\mathbf{R}}_i^{\top }$, ${\tilde{\mathbf{V}}}_0:={\mathbf{I}}_c$, $\tilde{\mathbf{\Omega }}:={\sum }_{i=0}^m{\gamma }_i{\tilde{\mathbf{V}}}_i$, $\tilde{\mathbf{C}}:={\sum }_{i=0}^m\widetilde{{\gamma }_i}{\tilde{\mathbf{V}}}_i$ and $\alpha :={\gamma }_0{\widetilde{{\gamma }_0}}^{-1}(n-c)+{\gamma }_0^{-1}{\tilde{y}}_{[n-c]}^{\top }{\tilde{y}}_{[n-c]}$. The details of this derivation are provided in the Appendix A. To implement PX-CD or PXI-CD after this transformation we run Algorithm 2 with inputs ${\tilde{\mathbf{V}}}_0,\dots ,{\tilde{\mathbf{V}}}_m\in {\mathbb{R}}^{c\times c}$ and ${\tilde{y}}_{\left[c\right]}\in {\mathbb{R}}^{c\times 1}$. In this simplification of H, we have the additional term $\alpha$, which is dependent on ${\gamma }_0$. Therefore, when we update the parameter ${\gamma }_0$ and implement Newton’s method we must also add

$$\frac{\partial \alpha }{\partial {\gamma }_0}={\widetilde{{\gamma }_0}}^{-1}(n-c)-{\gamma }_0^{-2}{\tilde{y}}_{[n-c]}^{\top }{\tilde{y}}_{[n-c]}\mathrm{and}\frac{{\partial }^2\alpha }{\partial {\gamma }_0^2}=2{\gamma }_0^{-3}{\tilde{y}}_{[n-c]}^{\top }{\tilde{y}}_{[n-c]}$$

to the corresponding derivatives derived for Newton’s method in Section 3.1.

3.3.2. Woodbury Matrix Identity

Alternatively, if c is large (say $c>n$) but individually $c_i<n$, for $i=1,\dots ,m$, we can use the Woodbury identity to reduce each linear system to $c_k$ dimensions (instead of n dimensions) when updating the component ${\gamma }_k$. Suppose we are in cycle $t+1$ of either PX-CD or PXI-CD and we wish to update the parameter ${\gamma }_k$, where $k\ne 0$, then we can simplify the optimization,

$${\gamma }_k^{(t+1)}=\underset{x\ge 0}{arg\; min}{h}_k\left(x\right),h_k\left(x\right)=H({\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k,\mathbf{C}),$$

by viewing ${\mathbf{\Omega }}_{-k}+x{\mathbf{V}}_k=\mathbf{\Omega }+(x-{\gamma }_k^{\left(t\right)}){\mathbf{Z}}_k{\mathbf{Z}}_k^{\top }$ as a low-rank perturbation to the matrix $\mathbf{\Omega }$. The Woodbury identity gives the expression for the inverse,

$${\left[\mathbf{\Omega }+(x-{\gamma }_k^{\left(t\right)}){\mathbf{Z}}_k{\mathbf{Z}}_k^{\top }\right]}^{-1}={\mathbf{\Omega }}^{-1}-(x-{\gamma }_k^{\left(t\right)}){\mathbf{\Omega }}^{-1}{\mathbf{Z}}_k{\left[{\mathbf{I}}_{c_k}+(x-{\gamma }_k^{\left(t\right)}){\mathbf{Z}}_k^{\top }{\mathbf{\Omega }}^{-1}{\mathbf{Z}}_k\right]}^{-1}{\mathbf{Z}}_k^{\top }{\mathbf{\Omega }}^{-1},$$

(20)

which contains the unperturbed inverse matrix ${\mathbf{\Omega }}^{-1}$ and the inverse of a smaller $c_k\times c_k$ matrix. In this implementation of PXI-CD and PX-CD we re-compute and store the matrix ${\mathbf{\Omega }}^{-1}$ after each coordinate update. Let $\mathit{w}:={\mathbf{Z}}_k^{\top }{\mathbf{\Omega }}^{-1}y$, then the line search along the k-th component ($k\ne 0$) of the function H simplifies to

$$\begin{array}{cc}\hfill h_k\left(x\right)& =-(x-{\gamma }_k^{\left(t\right)}){\mathit{w}}^{\top }{\left[{\mathbf{I}}_{c_k}+(x-{\gamma }_k^{\left(t\right)}){\mathbf{Z}}_k^{\top }{\mathbf{\Omega }}^{-1}{\mathbf{Z}}_k\right]}^{-1}\mathit{w}+x\mathrm{tr}\left({\mathbf{C}}^{-1}{\mathbf{Z}}_k{\mathbf{Z}}_k^{\top }\right)+\mathrm{const}.\hfill \end{array}$$

When implementing PXI-CD, there is no additional cost when using the Woodbury identity, as the update $\mathbf{C}\leftarrow \mathbf{\Omega }$ is made after every coordinate update and the trace term in the line search can be evaluated cheaply because ${\mathbf{\Omega }}^{-1}$ is known. We can now implement Newton’s method to find the minimum of $h_k\left(x\right)$. Let

$$\mathbf{B}:={\mathbf{Z}}_k^{\top }{\mathbf{\Omega }}^{-1}{\mathbf{Z}}_k,\mathbf{M}:={\mathbf{I}}_{c_k}+(x-{\gamma }_k^{\left(t\right)})\mathbf{B}.$$

If we then solve the $c_k$-dimensional linear systems $\mathbf{M}\mathit{d}=\mathit{w}$ and $\mathbf{M}\mathit{f}=\mathbf{B}\mathit{d}$ with CG and store the solution in the vectors $\mathit{d}$ and $\mathit{f}$, respectively, we can evaluate the first and second derivatives of $h_k\left(x\right)$ as

$$h_k^{\prime }\left(x\right)=-{\mathit{w}}^{\top }\mathit{d}+(x-{\gamma }_k^{\left(t\right)}){\mathit{d}}^{\top }\mathbf{B}\mathit{d}+\mathrm{tr}\left(\mathbf{B}\right),h_k^{″}\left(x\right)=2{\mathit{d}}^{\top }\mathbf{B}\mathit{d}+2(x-{\gamma }_k^{\left(t\right)}){\mathit{d}}^{\top }\mathbf{B}\mathit{f},$$

(21)

and implement the Newton steps (14). The derivation of these derivative expressions are provided in Appendix B. After each coordinate k is updated we evaluate and store the updated inverse covariance matrix,

$${\mathbf{\Omega }}^{-1}\leftarrow {\left[\mathbf{\Omega }+({\gamma }_k^{(t+1)}-{\gamma }_k^{\left(t\right)}){\mathbf{Z}}_k{\mathbf{Z}}_k^{\top }\right]}^{-1},$$

using (20), where we invert a smaller $c_k\times c_k$ matrix only. When $k=0$, no reduction in complexity can be made as the perturbation to $\mathbf{\Omega }$ is full-rank and we update ${\gamma }_0$ as we did in Section 3.1. If $c={\sum }_{i=1}^m{c}_i<n$, then we can use an alternate form of the Woodbury identity,

$${\mathbf{\Omega }}^{-1}={\gamma }_0^{-1}\left[\mathbf{I}-\mathbf{W}{({\gamma }_0\mathbf{I}+{\mathbf{W}}^{\top }\mathbf{W})}^{-1}{\mathbf{W}}^{\top }\right],$$

where $\mathbf{W}:=\mathbf{Z}{\mathbf{\Sigma }}^{1/2}$ to update ${\mathbf{\Omega }}^{-1}$ after ${\gamma }_0$ has been updated. If $c>n$, we invert the full $n\times n$ updated matrix covariance to obtain ${\mathbf{\Omega }}^{-1}$ using a Cholesky factorization at cost $O\left(n^3\right)$. This $O\left(n^3\right)$ cost for updating ${\gamma }_0$ is a disadvantage for this implementation if $c>n$; however, numerical simulations suggest that, when $c_i\ll n$ for $i=1,\dots ,m$, the Woodbury implementation is the fastest implementation.

3.4. Variable Selection

When the number of variance components is large, performing variable selection can enhance the model interpretation and provide more stable parameter estimation. To impose sparsity when estimating $\gamma$, a lasso or ridge penalty can be added to the negative log-likelihood [20]. The MM implementation [9] provides modifications to the MM algorithm such that both lasso and ridge penalized expressions can be minimized. We now show that, with PX-CD, we can minimize the penalized negative log-likelihood when using the ${\parallel ·\parallel }_1$ penalty. Consider the penalized negative log-likelihood expression,

$$G(\mathbf{\Omega })+\lambda \sum _{i=0}^m{\gamma }_i,{\gamma }_i\ge 0,\lambda >0.$$

We then have the surrogate function,

$$J(\mathbf{\Omega },\mathbf{C}):=H(\mathbf{\Omega },\mathbf{C})+\lambda \sum _{i=0}^m{\gamma }_i.$$

If we use PX-CD to minimize J, we need to repeatedly minimize the one-dimensional function along each co-ordinate, $j_k\left(x\right):=h_k\left(x\right)+\lambda x+\lambda {\sum }_{i\ne k}^m{\gamma }_i$. Here, we implement Newton’s method as before with the only difference now being that the derivative is increased by the constant $\lambda$,

$$j_k^{\prime }\left(x\right):=h_k^{\prime }\left(x\right)+\lambda .$$

It follows from Lemma 1 that $j\left(x\right)$ is either strictly convex or linear with strict positive gradient for $x\in [0,\infty )$. We check if $h_k^{\prime }\left(0\right)+\lambda \ge 0$ to determine if $j_k\left(0\right)$ is the global minimizer for $x\in [0,\infty )$. If it is, we let ${\gamma }_i^{(t+1)}=0$ if we are in cycle $t+1$. If $j_k^{\prime }\left(0\right)<0$, we initiate Newton’s method at the current value of the variance component $x_0={\gamma }_k^{\left(t\right)}$. The larger the parameter $\lambda$ is, the greater number of times this active constraint condition will be met, and therefore more variance components will be set to zero.

4. Numerical Results

In this section, we assess the efficiency of PX-CD and PXI-CD via simulation and compare them against the best current alternative method, the MM algorithm [9]. In [9] the MM algorithm is found to be superior to both the EM and Fisher Scoring Method in terms of performance. This superior performance was also described in [21].

In our experiments, we additionally include the Expectation–Maximization (EM) and Fisher-Scoring (FS) method in the small-scale problem only, where ${\gamma }_0=0.1$. We exclude the EM and FS method for more difficult problems, as they are too slow and unsuitable. The MM, EM and FS are executed with the Julia implementation in [9]. We provide results in three settings. First, we simulate data from the model (Section 3.3), where $c_i<n$, i.e., when the matrices ${\mathbf{V}}_i$ are low-rank. Secondly, we simulate when $c_i=n$, i.e., the matrices ${\mathbf{V}}_i$ are full-rank, and finally, we simulate data from model (Section 3.3), where the matrices ${\mathbf{V}}_i$ are constructed from a real data-set containing genetic variants of mice.

4.1. Simulations

For the following simulations, we simulate data from the model (Section 3.3). Since the fixed effects $\mathit{\beta }$ can always be eliminated from the model using the REML, we focus solely on the estimation of the variance component parameters. In other words, the value of $\mathit{\beta }$ in our simulations is irrelevant. In each simulation, we generate the fixed matrices ${\mathbf{V}}_i$ as

$${\mathbf{V}}_i=\frac{{\sum }_{j=1}^r{\mathbf{Z}}_{i,j}{\mathbf{Z}}_{i,j}^{\top }}{{∥{\sum }_{j=1}^r{\mathbf{Z}}_{i,j}{\mathbf{Z}}_{i,j}^{\top }∥}_F},$$

(22)

where ${\mathbf{Z}}_{i,j}\sim \mathcal{N}(\mathbf{0},{\mathbf{I}}_n)$ and ${\parallel ·\parallel }_F$ is the Frobenius matrix norm. The rank of each ${\mathbf{V}}_i$ is equal to the parameter r, which we vary.

In each simulation, for $k\ne 0$, we draw the m true variance components as ${\gamma }_k={(1+\rho )}^2$ where $\rho \sim \mathcal{N}(0,1)$. Then, we simulate the response from $y\sim \mathcal{N}(\mathbf{0},{\sum }_{i=0}^m{\gamma }_i{\mathbf{V}}_i)$ and estimate the vector $\widehat{\mathit{\gamma }}$. We vary the value of ${\gamma }_0$ from the set $\{0.1,1,10\}$ and keep $n=1000$.

4.1.1. Low-Rank

We now present the results for where ${\mathbf{V}}_i$ are generated as stated above and $r<n$. As ${\mathbf{V}}_i$ are low-rank, we run the Woodbury implementation of PXI-CD and exclude PX-CD as it has the same computational cost as PXI-CD for each update and exhibits almost identical performance. First, PXI-CD is run until the relative change $\left[L\left({\mathit{\gamma }}^{(t+1)}\right)-L\left({\mathit{\gamma }}^{\left(t\right)}\right)\right]/\left[\mid L\left({\mathit{\gamma }}^{\left(t\right)}\right)\mid +1\right]$ is less than ${10}^{-10}$ and we store the final objective value as $L^{*}$. We then run the algorithms MM, EM and FS and terminate once $L\left({\mathit{\gamma }}^{\left(t\right)}\right)>L^{*}$. We initialize all algorithms to start from the point ${\mathit{\gamma }}^{\left(0\right)}=\mathbf{1}$. Each simulation scenario is replicated 10 times. The mean running time is reported along with the standard error of the mean running time provided in parentheses.

The results of the low-rank simulations are given in Table 1, Table 2 and Table 3. The results indicate that, apart from the smallest scale problem when $r=m=20$, our PXI-CD algorithm outperforms the MM algorithm and significantly so that the scale of the model (both m and r) increases.

Table 1. The running times (s) when ${\mathbf{V}}_i$ are low-rank, $n=1000$, and ${\gamma }_0=0.1$.

		m
Method	$\mathit{r}$	20	50	75	100
PXI-CD	20	4.20 (0.07)	17.00 (1.18)	25.81 (1.57)	51.8 (5.09)
MM		1.89 (0.22)	42.54 (7.69)	220.06 (61.19)	845.2 (136.89)
EM		23.30 (0.52)	-	-	-
FS		91.80 (0.99)	-	-	-
PXI-CD	50	5.42 (0.16)	21.36 (0.85)	37.46 (2.72)	40.21 (2.97)
MM		95.63 (41.20)	203.24 (53.20)	584.76 (53.20)	1167.22 (114.38)
PXI-CD	100	8.96 (0.25)	30.17 (2.24)	28.26 (0.73)	45.65 (2.56)
MM		112.58 (21.48)	555.38 (82.01)	699.89 (90.55)	1327.54 (53.80)
PXI-CD	150	14.13 (0.63)	33.18 (4.67)	38.24 (1.54)	48.97 (2.08)
MM		122.44 (38.48)	628.24 (55.61)	929.67 (75.87)	1243.97 (84.30)

Table 2. The running times (s) when ${\mathbf{V}}_i$ are low-rank, $n=1000$, and ${\gamma }_0=1$.

		m
Method	$\mathit{r}$	20	50	75	100
PXI-CD	20	3.10 (0.08)	9.52 (0.28)	16.30 (0.43)	26.05 (0.77)
MM		3.11 (0.84)	117.40 (24.42)	280.31 (51.43)	719.32 (158.51)
PXI-CD	50	4.08 (0.11)	14.35 (0.76)	29.94 (1.33)	53.10 (3.7)
MM		157.98 (34.53)	501.60 (90.15)	546.56 (91.48)	1133.83 (129.96)
PXI-CD	100	6.00 (0.36)	25.34 (0.95)	61.69 (3.38)	73.23 (10.6)
MM		103.08 (31.4)	544.06 (61.35)	743.79 (104.67)	1254.97 (87.32)
PXI-CD	150	9.18 (0.45)	42.30 (2.08)	66.13 (8.3)	66.67 (10.2)
MM		176.80 (31.64)	498.12 (63.39)	986.87 (61.46)	1110.90 (105.59)

Table 3. The running times (s) when ${\mathbf{V}}_i$ are low-rank, $n=1000$, and ${\gamma }_0=10$.

		m
Method	$\mathit{r}$	20	50	75	100
PXI-CD	20	3.62 (0.10)	8.79 (0.20)	15.60 (0.41)	23.13 (0.91)
MM		10.17 (0.84)	318.53 (90.49)	648.64 (132.62)	839.24 (158.52)
PXI-CD	50	4.36 (0.09)	14.39 (0.4)	24.65 (0.97)	42.07 (1.13)
MM		184.03 (38.8)	473.58 (80.82)	648.33 (114.98)	1230.56 (128.79)
PXI-CD	100	6.53 (0.22)	26.07(1.51)	48.48 (2.48)	60.72 (5.33)
MM		124.68 (19.93)	511.66 (65.85)	880.53 (69.53)	1279.40 (81.93)
PXI-CD	150	10.15 (0.37)	35.34 (1.72)	66.94 (2.28)	103.89 (10.36)
MM		199.80 (33.17)	512.35 (49.97)	943.84 (84.24)	1244.32 (72.13)

4.1.2. Full-Rank

We now present the results when $\mathrm{rank}\left({\mathbf{V}}_i\right)=n=1000$. We implement the standard PX-CD, PXI-CD and MM algorithms, where either the Woodbury, or the QR method cannot be used. Initially, PX-CD is run until the relative change $\left[L\left({\mathit{\gamma }}^{(t+1)}\right)-L\left({\mathit{\gamma }}^{\left(t\right)}\right)\right]/\left[\mid L\left({\mathit{\gamma }}^{\left(t\right)}\right)\mid +1\right]$ is less than ${10}^{-10}$, and we store the final objective value as $L^{*}$. The other algorithms terminate once $L\left({\mathit{\gamma }}^{(t+1)}\right)>L^{*}$. For the following simulations, we consider one iteration of a CD algorithm as a single cycle of updates. Each simulation scenario is replicated 10 times. The mean running time and mean iteration number is reported with the standard error of the mean running time and mean iteration provided in parentheses.

The results of the full-rank simulations are given in Table 4, Table 5 and Table 6. PX-CD and PXI-CD both significantly outperform the MM and the basic CD algorithms in these examples. We observe that as the number of components m increases the problem becomes increasingly difficult for the MM algorithm. An intuitive explanation for this performance gap is that the CD algorithms are able to identify the active constraint set $\{k:{\widehat{\gamma }}_k=0\}$ in only a few cycles.

Table 4. The convergenceresults when ${\mathbf{V}}_i$ are full-rank, $n=1000$, and ${\gamma }_0=0.1$.

Method	m	Iterations	Time (s)	Objective
PX-CD	25	89.00 (2.90)	37.47 (1.71)	−1383.44
PXI-CD		146.90 (21.17)	97.49 (13.58)	−1383.44
CD		109.40 (17.52)	286.96 (19.83)	−1383.44
MM		3957.90 (300.77)	281.53 (21.03)	−1383.44
PX-CD	50	182.40 (11.34)	147.21 (10.64)	−1831.40
PXI-CD		73.10 (2.97)	104.42 (4.64)	−1831.40
CD		103.40 (6.18)	852.41 (70.22)	−1831.40
MM		10,240.40 (2140.25)	1557.79 (343.47)	−1831.40
PX-CD	100	279.10 (15.09)	376.18 (24.14)	−2143.93
PXI-CD		80.70 (2.97)	211.19 (8.58)	−2143.93
CD		164.00 (8.84)	2060.69 (155.37)	−2143.93
MM		12,171.90 (1526.30)	3482.30 (465.51)	−2143.93

Table 5. The convergence results when ${\mathbf{V}}_i$ are full-rank, $n=1000$, and ${\gamma }_0=1$.

Method	m	Iterations	Time (s)	Objective
PX-CD	25	82.60 (4.05)	32.00 (1.93)	−1707.53
PXI-CD		172.70 (7.08)	112.31 (5.15)	−1707.53
CD		116.90 (6.31)	279.61 (18.03)	−1707.53
MM		4313.90 (347.85)	303.13(24.3)	−1707.53
PX-CD	50	192.50 (8.89)	155.03 (8.11)	−1957.26
PXI-CD		103.00 (18.85)	147.79 (26.11)	−1957.26
CD		110.20 (4.53)	940.96 (58.0)	−1957.26
MM		15,860.80 (2872.82)	2488.70 (484.24)	−1957.26
PX-CD	100	313.60 (13.88)	423.78 (20.48)	−2203.61
PXI-CD		86.80 (3.06)	226.10 (8.51)	−2203.61
CD		185.60 (8.33)	2422.93 (143.76)	−2203.61
MM		12,820.60 (2102.69)	3792.45 (725.63)	−2203.61

Table 6. The convergence results when ${\mathbf{V}}_i$ are full-rank, $n=1000$, and ${\gamma }_0=10$.

Method	m	Iterations	Time (s)	Objective
PX-CD	25	75.20 (2.88)	25.74 (1.46)	−2603.51
PXI-CD		152.00 (6.98)	95.59 (5.12)	−2603.51
CD		38.50 (1.60)	172.03 (11.70)	−2603.51
MM		3616.90 (513.57)	254.87 (36.27)	−2603.51
PX-CD	50	143.70 (6.93)	108.55 (5.89)	−2668.99
PXI-CD		177.50 (28.72)	249.73 (39.38)	−2668.99
CD		79.80 (4.59)	668.65 (40.71)	−2668.99
MM		11,306.30 (1824.79)	1697.89 (275.36)	−2668.99
PX-CD	100	304.00 (12.39)	412.54 (19.01)	−2731.09
PXI-CD		87.40 (2.54)	230.54 (7.27)	−2731.09
CD		181.80 (7.63)	2697.20 (150.64)	−2731.09
MM		11,796.10 (1732.0)	3358.14 (521.92)	−2731.09

When ${\gamma }_0=0.1$ and ${\gamma }_0=1$ and m is large ($m=50$, $m=100$), PXI-CD is the fastest algorithm, even though it is computationally the most expensive per cycle. When ${\gamma }_0=10$ and $m=100$, PXI-CD is the fastest algorithm. In fact, as the problem size grows, the number of iterations that PXI-CD requires to converge is less than that of the basic CD. This simulation indicates that PXI-CD is well-suited to problems with large $m,n$ and when ${\mathbf{V}}_i$ are full-rank. The basic CD algorithm, while numerically the inferior compared to the PX-CD and PXI-CD algorithms still outperforms the MM algorithm in these simulations.

4.2. Genetic Data

We now present simulation results when ${\mathbf{Z}}_i$ are constructed from the https://openmendel.github.io/SnpArrays.jl/latest/#Example-data (accessed on 1 July 2022) mouse single nucleotide polymorphism (SNP) array data set available from the Open Mendel project [21]. The dataset consists of $\mathbf{Z}$, an $n\times c$ matrix consisting of c genetic variants for n individual mice. For this experiment, c = 10,200 and $n=500$. We artificially generate m different genetic regions by partitioning the columns of $\mathbf{Z}$ into ${\mathbf{Z}}_{i=1,\dots ,m}$ gene matrices, where ${\mathbf{Z}}_i\in {\mathbb{R}}^{n\times r}$. Then, we can compose our fixed matrices ${\mathbf{V}}_1,\dots ,{\mathbf{V}}_m$ as,

$${\mathbf{V}}_i=\frac{{\mathbf{Z}}_i{\mathbf{Z}}_i^{\top }}{{∥{\sum }_{j=1}^m{\mathbf{Z}}_j{\mathbf{Z}}_j^{\top }∥}_F}.$$

We simulate $\mathit{\gamma }$ and $y$ as we did in Section 4.1. In this case, $y$ mimics a vector of quantitative trait measurements of the n mice. This data set is well-suited for testing our method when m is large ($m>n$). In these cases, we observe that, when initialized at the same point, the MM and PXI-CD method converge to different solutions, i.e., they may converge to different stationary points. Therefore, we run all algorithms until the relative change $\left[L\left({\mathit{\gamma }}^{(t+1)}\right)-L\left({\mathit{\gamma }}^{(t+1)}\right)\right]/\left[\mid L\left({\mathit{\gamma }}^{\left(t\right)}\right)\mid +1\right]$ is less than ${10}^{-10}$. Since $r<n$, we implement PXI-CD utilizing the Woodbury identity. Each simulation scenario is replicated 10 times. The mean running time and mean iteration number are reported with the standard error of the mean running time and mean iteration provided in parentheses.

The results of the genetic study simulation are provided in Table 7. We observe that PXI-CD outperforms the MM algorithm for all values of m and r for this data set in both the number of iterations and running time until convergence. When $m>n$, we observe that the MM and PXI-CD method converge to noticeably different objective values. We suspect that this is because when $m>n$ the likelihood in (2) exhibits many more local minima. On average, PXI-CD converges to a more optimal stationary point when m is large and $m>n$.

Table 7. The running times (s)—mouse data.

Method	m	r	Iterations	Time (s)	Objective
PXI-CD	100	102	95.1 (9.9)	23.1 (2.66)	−43.6
MM			1580.2 (194.76)	108.7 (15.37)	−43.6
PXI-CD	200	51	180.0 (13.41)	58.8 (4.4)	−82.5
MM			2797.8 (401.1)	466.0 (88.95)	−82.6
PXI-CD	500	20	397.8 (53.73)	258.1 (34.56)	−100.3
MM			2700.8 (366.57)	1055.4 (179.97)	−106.6
PXI-CD	1000	10	434.7 (35.7)	507.5 (39.91)	−82.1
MM			3004.8 (343.61)	2329.4 (296.37)	−91.2

5. Conclusions

The MLE solution for variance-component models requires the optimization of a non-convex log-likelihood function. In this paper, we showed that a basic implementation of the cyclic CD algorithm is computationally expensive to run and is not amenable to traditional convergence analysis.

To remedy this, we proposed a novel parameter-expanded CD (PX-CD) algorithm, which is both computationally faster and also subject to theoretical guarantees. PX-CD optimizes a higher-dimensional surrogate function that attains a coordinate-wise minimum with respect to each of the variance component parameters. The extra speed is derived from the fact that required quantities (such as first and second-order derivatives) are evaluated via the conjugate-gradient algorithm.

Additionally, we propose an alternative updating regime called PXI-CD, where the expanded block parameters are updated immediately after each coordinate update. This new updating regime requires more computation for each iteration as compared to PX-CD. However, numerically, we observed that, for large-scale models, where the number of variance components $m+1$ is large and ${\mathbf{V}}_i$ are full-rank, the number of iterations needed to converge greatly offsets the additional computational cost per coordinate update cycle.

Our numerical experiments suggest that PX-CD and PXI-CD outperform the best current alternative—the MM algorithm. When the number of variance components m is large, we observed that PXI-CD was significantly faster than the MM algorithm and tended to converge to more optimal stationary points.

A potential extension of this work is to apply parameter-expanded CD algorithms to the multivariate-response variance-component model. Instead of the univariate response, one considers the multivariate response model with a $n\times d$ response matrix $\mathbf{Y}$. In this setup, $\mathbb{E}\left[\mathbf{Y}\right]=\mathbf{X}\mathbf{B}$ where $\mathbf{B}$ is a $p\times d$ matrix. The $nd\times nd$ covariance matrix is of the form

$$\mathbf{\Omega }=\mathrm{cov}\left(\mathrm{vec}\left(\mathbf{Y}\right)\right)=\sum _{i=0}^m{\mathbf{\Gamma }}_i\otimes {\mathbf{V}}_i,$$

where ${\mathbf{\Gamma }}_i$ are unknown $d\times d$ variance components and ${\mathbf{V}}_i$ are the known $n\times n$ covariance matrices. The challenging aspect of this problem is that each optimization with respect to a parameter ${\mathbf{\Gamma }}_i$ is not univariate but is rather a search over positive semi-definite matrices—itself, a difficult optimization problem.