Abstract
Evolutionary approaches are widely applied in solving various types of problems. The paper considers the application of EvolODE and EvolODES approaches to the identification of dynamic systems. EvolODE helps to obtain a model in the form of an ordinary differential equation without restrictions on the type of the equation. EvolODES searches for a model in the form of an ordinary differential equation system. The algorithmic basis of these approaches is a modified genetic programming algorithm for finding the structure of ordinary differential equations and differential evolution to optimize the values of numerical constants used in the equation. Testing for these approaches on problems in the form of ordinary differential equations and their systems was conducted. The influence of noise present in the data and the sample size on the model error was considered for each of the approaches. The symbolic accuracy of the resulting equations was studied. The proposed approaches make it possible to obtain models in symbolic form. They will provide opportunities for further interpretation and application.
1. Introduction
Nowadays, evolutionary algorithms are applied in solving problems of optimization, classification, clustering, forecasting, and regression in various practical fields [1,2,3,4].
In addition, evolutionary algorithms are an efficient tool for solving identification problems [5,6]. System identification is the process of constructing mathematical models of dynamic systems based on measurements that describe input and output variables of the process under consideration. One of the most informative ways to represent models of dynamical systems are differential equations and their systems [7,8]. This way of describing the processes makes it possible to present the relationship between variables in an interpretable form as well as to reflect the dynamics.
The problem of parametric identification is mainly solved with the help of evolutionary algorithms. Thus, evolutionary approaches to parametric identification are considered in the following papers [9,10].
Parametric identification determines the parameter values of a model with an already known structure. This class of models makes it possible to describe a lot of real processes. For example, there exist processes described by a homogeneous differential equation in economics, biology and chemistry [6].
The presented papers consider a genetic programming algorithm applied to construct a model in the form of an ordinary differential equation (ODE). However, they are all from a class of homogeneous equations. Consequently, the method is not universal due to its applicability to only one class of ODEs [11,12].
However, there is a need to identify processes with a previously unknown structure with the increasing complexity of technological processes. In this case, there is a need for automated methods to construct models of dynamic systems of arbitrary structure. The need to search for such models is faced by specialists in such fields as metallurgy, chemical industry and thermal power plants.
Various methods have been developed due to the current significance of the problem being solved. Nonparametric methods and artificial neural networks are of the greatest importance [13,14,15,16,17].
However, these methods are often unable to construct a model that reflects the true nature of the process in an understandable and interpretable form. The paper presents approaches to the identification of dynamical systems in the form of ODEs and their systems.
2. Materials and Methods
The paper solves an inverse problem of mathematical modelling. The inverse problem involves constructing a system model based on a sample of measurements of inputs and outputs. The approaches proposed in the paper fulfil the search for models in the form of ODEs and their systems. It is possible to apply a genetic programming algorithm to solve the inverse problem of mathematical modelling in order to construct a model in symbolic form. The application of the genetic programming algorithm becomes possible when considering the identification problem as a problem of symbolic regression [18].
2.1. The Evolutionary Approach EvolODE for the Identification of Dynamical Systems in the Form of an ODE
The authors’ approach based on a self-configuring genetic programming algorithm to identify a system in ODE form of arbitrary structure is presented in detail in [19]. The paper denotes this approach as EvolODE (evolutionary approach, ordinary differential equation).
Let us consider a statement of the problem in more detail and highlight the key features of the approach under consideration.
It is necessary to construct a model in ODE form of arbitrary order (1) based on the measurement data of the input xti and output yi characteristics of the process (where t is the number of inputs, i = 1, …, n, where n is sample size):
The authors propose to apply the genetic programming algorithm to construct models in ODE form. Consequently, the terminal set has been changed to encode an ODE in the form of a tree. Changes to the terminal set were made relative to the classical GP algorithm for solving the symbolic regression problem. The terminal set in the proposed approach was represented by a set of all input (x) and output (y) variables, a set of constants, and derivatives (). The root vertex is supplemented with information about the maximum order of the derivative for the current individual at the current iteration. The functional set is standard for the problem of symbolic regression. It contains a set of functions for constructing dependencies. Thus, Figure 1 shows an example of the ODE encoded as a tree.
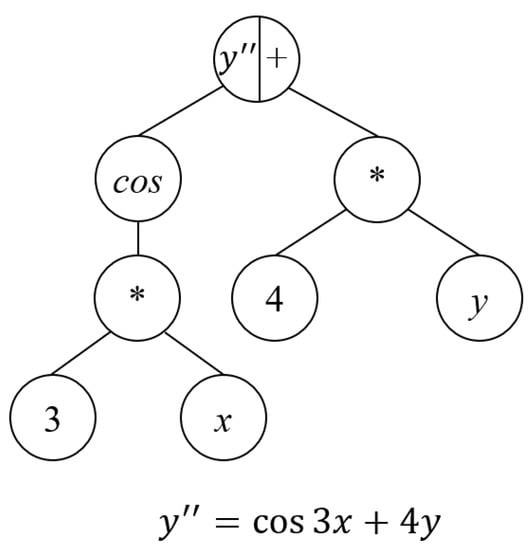
Figure 1.
Example of the ODE encoded as a tree.
The main stages of the evolutionary process of the EvolODE algorithm were also modified. Its scheme is presented in Figure 2:
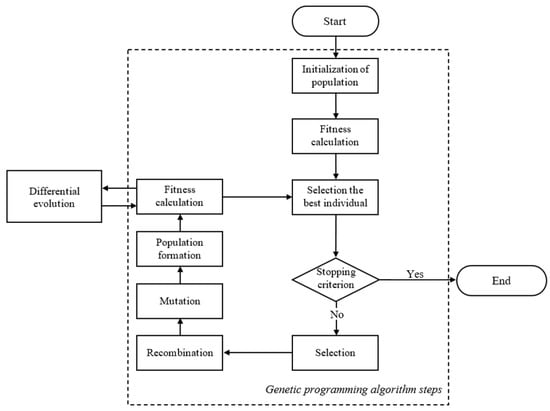
Figure 2.
Scheme of the evolutionary approach EvolODE for the identification of dynamical systems in the form of ODE.
The authors modified such steps of the genetic programming algorithm as the initialization, fitness calculation, and mutation to implement the proposed approach.
The population is generated at the initialization stage. Here, each individual encodes an ODE of the k-order not higher than K, where K is the maximum order of the derivative specified by a researcher. The algorithm determines an order for each individual automatically, but the value of the order does not exceed the value of K. Thus, the order of the equation is not fixed initially, but restricted.
The fitness calculation is carried out in accordance with Equations (2) and (3):
where n is the sample size, is the value of the individual at the i-th point, and yi represents values from the original sample.
The peculiarity is that mutation could be at the root node. The node contains the maximum order of the derivative for the given individual. In this case, the order of all derivatives included in the tree is randomly changed so that their order does not exceed a new maximum order of the derivative.
The authors of the paper chose the achievement by the algorithm of a given number of generations as a stop criterion.
The authors apply the method of differential evolution to optimize the numerical constants included in the equation and initial conditions [20]. The study presents the efficiency of a hybrid evolutionary approach that combines genetic programming and differential evolution [21].
The presented approach makes it possible to obtain a model of a dynamic system in ODE form of arbitrary structure.
2.2. The Evolutionary Approach EvolODES for the Identification of Dynamical Systems in the Form of an ODE System
An output of a dynamic system is often characterized by several variables in real processes. It is necessary to use the representation in the form of a system of ODEs to develop a model of such processes.
As provided by this problem statement, it is obligatory to construct a model in the form of an ODE system of arbitrary order (4) according to the measurement data of the input xti and output ysi characteristics of the process (where t is the number of input and output variables, i = 1, …, n, where n is sample size):
The order of ODE k will be considered as a limited K-value set by a user.
The paper presents a new approach based on the EvolODE evolutionary approach described above. Thus, according to the new proposed approach, a system of ODEs should be encoded by a set of trees (Figure 3).
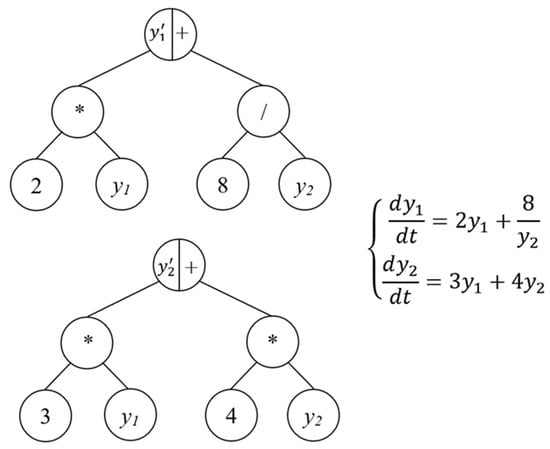
Figure 3.
Example of the ODE system encoded as a tree.
The evolutionary approach to the identification of dynamical systems in the form of a system of ODEs will be denoted as EvolODES (Evolutionary, Ordinary Differential Equations System).
The peculiarity of the proposed EvolODES approach is the implementation of a combination of several genetic programming algorithms (k genetic programming algorithms are required for k equations in the system) [22]. Each of them searches for one equation of the system. The number of equations n corresponds to the number of output variables in the data (Figure 4).
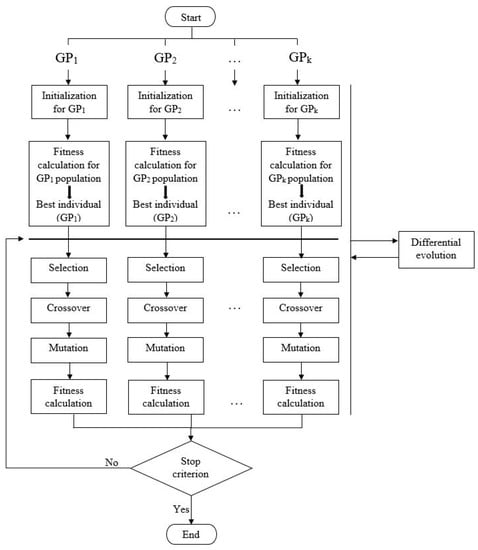
Figure 4.
Scheme of the evolutionary approach EvolDES for the identification of dynamical systems in the form of an ODE system.
Next, a population of individuals is generated by each genetic programming algorithm. Individuals are potential representations of each of the k ODEs in the system.
The fitness is calculated for all individuals of each population (one-time full enumeration of all possible combinations of individuals without regard to order). It is based on the obtained values in each population; the best individual is determined. The fitness calculation for each individual of each population is conducted by substitution into each of the equations of the system. The best individuals are selected as the remaining equations. The calculation is performed in accordance with Equations (5) and (6).
where n is the sample size, s is the number of equations, are values from the original sample, and is the value of the model.
According to the new approach, there are no restrictions on the number of ODEs included in the system, their order or their structure. The models obtained in symbolic form can be interpreted in the context of the subject area under consideration.
Both proposed approaches apply a self-configuring type of evolutionary algorithms (genetic programming and differential evolution) [19,21]. The success history adaptation algorithm is applied for genetic programming and differential evolution parameters containing numerical values [23]. The PDP method is applied for parameters with the selection of the type [24]. For the experiment, the authors determined the number of generations for differential evolution as 30. The population contains 10 individuals.
3. Results
Let us consider the proposed approaches in detail. Firstly, consider the efficiency on test tasks represented by ODEs and their systems.
The tasks presented in Table 1 were used to test the evolutionary approach of EvolDE. ODEs represent tasks of various types and orders. The exhaustive testing and study of the efficiency of this algorithm on tasks with some input variables and with input variables represented by functions are reflected in [25].

Table 1.
Test tasks for the evolutionary approach to the identification of dynamical systems in the form of an ODE.
Table 2 presents the results of identification according to the data generated by the tasks from Table 1. Data of different volumes were generated without noise and with noise for each task. Noise is distributed normally. The authors conducted 50 runs for each task. Table 2 shows the results by error values (averaged over 50 runs) depending on the sample size and the presence of noise in the data.

Table 2.
Testing results of the evolutionary approach to the identification of dynamical systems in the form of an ODE.
The authors consider the dependence of the rate of a chemical reaction on temperature to study the possibility of using this approach in solving applied tasks. A set of values describing the process for a chemical reaction is known. It is necessary to construct a model that describes a change in the rate of a chemical reaction depending on temperature.
It is necessary to estimate the dependence of the reaction rate constant on temperature for the reaction H2 + I2 → 2HI. A sample of temperature (T) and rate constant (k) values was applied to construct a model. The sample size was 12 points. As a result, the authors obtained a symbolic model. It corresponds to the well-known Arrhenius Equation (7):
where Ea is the activation energy, and R is the universal gas constant [26].
Figure 5 shows graphs corresponding to the original data and points obtained from the model. The mean squared error of the fit was 0.
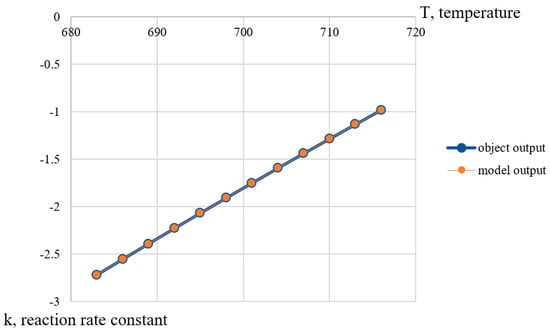
Figure 5.
Initial sample fit with the output of the obtained model of the change in the rate of a chemical reaction on temperature.
The tasks presented in Table 3 are applied to test the evolutionary approach of EvolDES. The systems of ODEs of various types and orders represented these tasks.

Table 3.
Test tasks for the evolutionary approach to the identification of dynamical systems in the form of an ODE system.
The analysis of the error of the obtained models was conducted in a similar way to the previous testing scheme. This depended on the amount of data and the presence of noise (Table 4).

Table 4.
Testing results of the evolutionary approach to the identification of dynamical systems in the form of an ODE system.
Let us consider the application of this approach in solving a practical task from the field of biology. Let values describing the change in the population size of predators and prey over time be given in some ecosystem. The sample size is 50 points. It is necessary to calculate the change in the number of prey and predator populations over time.
As a result, an expression was obtained represented by a system of differential equations.
The presented system corresponds to the best solution found among 50 runs. It corresponds to an error of 0.0019. The best solution was found 24 times from 50 runs. The averaged error over 50 runs was 0.0031.
The presented system of differential equations corresponds to the Holding–Tanner model. Generally, it is represented as follows [27]:
where x is the size of the predator population, y is the size of the prey population, is the predation coefficient, and a, b, f are positive parameters.
Figure 6 shows graphs corresponding to the original data and points obtained from the model represented by the system of differential Equation (8). The mean squared error of the fit is 0.
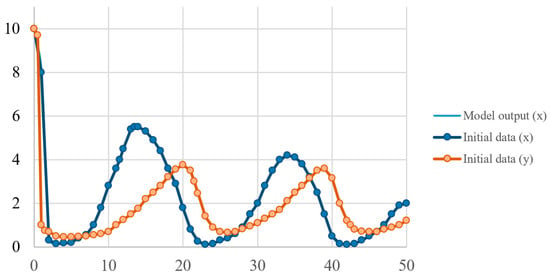
Figure 6.
Initial sample fit to the output of the obtained model of changes in the number of predators and prey over time.
4. Discussion
The authors conducted the study of two evolutionary approaches for constructing models of dynamical systems in the form of differential equations (EvolDE) and their systems (EvolDES). According to the results, we can observe high accuracy of the models obtained as a result of testing. Changing the sample size within presented limits does not have a significant effect on the error.
An important peculiarity of these approaches is the possibility of obtaining models in symbolic form. However, such representation is expected to be consistent with the true nature of the process. Therefore, it was determined that the models obtained as the identification of test tasks belong to three types: symbolically accurate (full compliance of the structure and parameters of the resulting equation or system with known true ones), symbolically conditionally accurate (the resulting structure corresponds to the known true one after performing the simplest mathematical operations), and approximate ones (solutions that do not belong to two previous types). Figure 7 and Figure 8 show the number of symbolically accurate, symbolically conditionally accurate, and approximate solutions for each of the 50 runs for each task. Figure 7 contains information about the results for the evolutionary approach to the identification of dynamical systems in the form of an ODE. Figure 8 contains information about the results for the evolutionary approach to the identification of dynamical systems in the form of ODE systems.
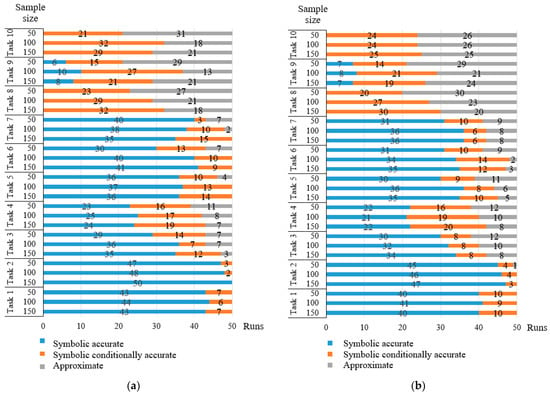
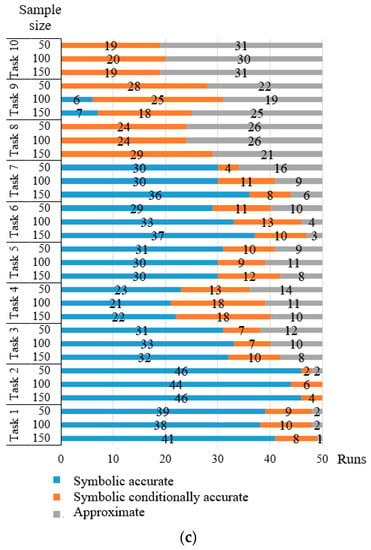
Figure 7.
Symbolic accuracy of the resulting ODEs: (a) Data without noise; (b) Data with 5% of noise; (c) Data with 10% of noise.
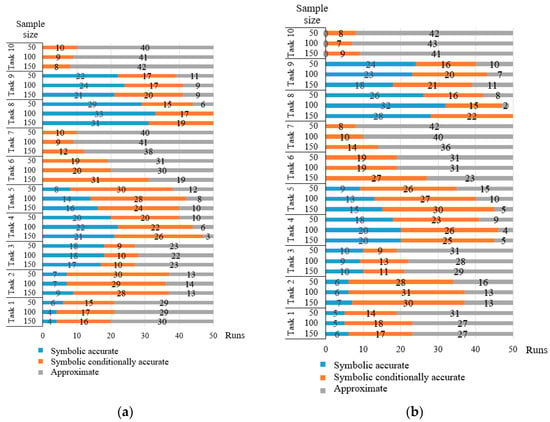
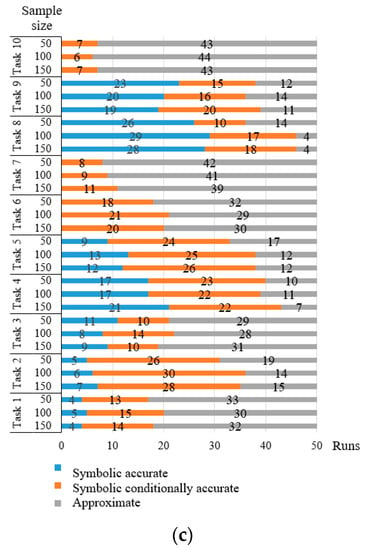
Figure 8.
Symbolic accuracy of the resulting ODE systems: (a) Data without noise; (b) Data with 5% of noise; (c) Data with 10% of noise.
The successful search for a structure that corresponds to the true nature of the process is also proven by the above models of processes from chemistry and biology.
The paper presents two evolutionary approaches that combine a genetic programming algorithm, differential evolution, and methods for the self-configuring parameters of evolutionary algorithms. The proposed approaches make it possible to identify dynamical systems in the form of ODEs and their systems. In the process of identification, both approaches automatically select the order, structure, and parameters of an ODE, both single and included in the system. The developed approaches make it possible to operate with systems in the form of ODEs of arbitrary order, a number of input and output variables.
Author Contributions
Conceptualization, E.S.; methodology, T.K. and E.S.; software, T.K.; validation, T.K. and E.S.; formal analysis, T.K. and E.S.; investigation, T.K. and E.S.; data curation, T.K.; writing—original draft preparation, T.K. and E.S.; writing—review and editing, T.K. and E.S.; visualization, T.K.; supervision, E.S.; project administration, T.K. and E.S.; funding acquisition, E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation within limits of state contract № FEFE-2020-0013.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nesmachnow, S.; Massobrio, R.; Arrechea, E.; Mumfordb, C.; Olivera, A.C.; Pablo, A.; Vidalc, O.J.; Tchernykhd, A. Traffic lights synchronization for Bus Rapid Transit using a parallel evolutionary algorithm. Int. J. Transp. Sci. Technol. 2019, 8, 53–67. [Google Scholar] [CrossRef]
- Tretyakova, A.; Seredynski, F. Application of evolutionary algorithms to maximum lifetime coverage problem in wireless sensor networks. In Proceedings of the IEEE 27th International Parallel and Distributed Processing Symposium Workshops and PhD Forum, IPDPSW, Boston, MA, USA, 20–24 May 2013. [Google Scholar] [CrossRef]
- Bagheri, S.; Wu, N.; Filizadeh, S. Application of artificial intelligence and evolutionary algorithms in simulation-based optimal design of a piezoelectric energy harvester. Smart Mater. Struct. 2020, 29, 105004. [Google Scholar] [CrossRef]
- Lee, S.-J.; Yoon, Y. Electricity Cost Optimization in Energy Storage Systems by Combining a Genetic Algorithm with Dynamic Programming. Mathematics 2020, 8, 1526. [Google Scholar] [CrossRef]
- Parmar, G.; Prasad, R.; Mukherjee, S. Order reduction of linear dynamic systems using stability equation method and GA. Int. J. Comput. Inf. Eng. 2007, 1, 26–32. [Google Scholar]
- Chen, Y.; Luo, Y.; Liu, Q.; Xu, H.; Zhang, D. Symbolic genetic algorithm for discovering open-form partial differential equations (SGA-PDE). Phys. Rev. Res. 2022, 4, 023174. [Google Scholar] [CrossRef]
- Cao, H.; Kang, L.; Chen, Y.; Yu, J. Evolutionary modeling of systems of ordinary differential equations with genetic programming. Genet. Program. Evol. Mach. 2000, 1, 309–337. [Google Scholar] [CrossRef]
- Cottineau, C.; Reuillon, R.; Chapron, P.; Rey-Coyrehourcq, S.; Pumain, D. A Modular Modelling Framework for Hypotheses Testing in the Simulation of Urbanisation. Systems 2015, 3, 348–377. [Google Scholar] [CrossRef]
- Ryzhikov, I.S. Automatic linear differential equation identification in analytical form. Vestnik SibSAU Aerosp. Tehnol. Control Syst. 2014, 1, 66–72. [Google Scholar]
- Ryzhikov, I.; Brester, C. Restart operator for optimization heuristics in solving linear dynamical system parameter identification problem. In Proceedings of the 11th International Joint Conference on Computational Intelligence, Vienna, Austria, 17–19 September 2019. [Google Scholar]
- Gaucel, S.; Keijzer, M.; Lutton, E.; Tonda, A. Learning Dynamical Systems Using Standard Symbolic Regression. Lect. Notes Comput. Sci. 2014, 8599, 25–36. [Google Scholar] [CrossRef]
- Iba, H. Inference of differential equation models by genetic programming. Inf. Sci. 2008, 178, 4453–4468. [Google Scholar] [CrossRef]
- Medvedev, A.V.; Tereshina, A.V.; Yareshenko, D.I. Nonparametric modelling of multidimensional memoryless processes. In Proceedings of the Twelfth International Conference Computer Data Analysis and Modeling: Stochastics and Data Science, Minsk, Belarus, 18–22 September 2019. [Google Scholar]
- Medvedev, A.V.; Chzhan, E.A. On Nonparametric Modelling of Multidimensional Noninertial Systems with Delay. Bull. South Ural State Univ. Ser. Math. Model. Program. Comput. Softw. 2017, 10, 124–136. [Google Scholar] [CrossRef]
- Sholokhova, A.A.; Ivanov, A.N. Modeling of dynamic systems based on polynomial neural networks. Model. Optim. Inf. Technol. 2017, 4, 23. [Google Scholar]
- Ballesteros, M.; Polyakov, A.; Efimov, D.; Chairez, I.; Poznyak, A.S. Non-parametric identification of homogeneous dynamical systems. Automatica 2021, 129, 109600. [Google Scholar] [CrossRef]
- Lee, C.-H.; Teng, C.-C. Identification and Control of Dynamic Systems Using Recurrent Fuzzy Neural Networks. IEEE Trans. Fuzzy Syst. 2000, 8, 349–366. [Google Scholar]
- Merta, J.; Brandejsky, T. Lifetime adaptation in genetic programming for the symbolic regression. Adv. Intell. Syst. Comput. 2019, 1047, 339–346. [Google Scholar]
- Karaseva, T.S. Automatic differential equations identification by self-configuring genetic programming algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2020, 734, 12093. [Google Scholar] [CrossRef]
- Das, S.S.; Mullick, S.S.; Suganthan, P.N. Recent Advances in Differential Evolution—An Updated Survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Karaseva, T.S.; Semenkina, O.E. Hybrid approach to the dynamic systems identification based on the self-configuring genetic programming algorithm and the differential evolution method. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1047, 12076. [Google Scholar] [CrossRef]
- Kazakovtsev, L.; Rozhnov, I.; Shkaberina, G. Self-configuring (1 + 1)-evolutionary algorithm for the continuous p-median problem with agglomerative mutation. Algorithms 2021, 14, 130. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Meyer-Nieberg, S.; Beyer, H.-G. Self-Adaptation in Evolutionary Algorithms. Parameter Setting Evol. Algorithm 2007, 54, 47–75. [Google Scholar]
- Karaseva, T.; Semenkin, E. On the automatic identification of differential equations using a hybrid evolutionary approach. In Proceedings of the 35th International Conference on Information Technologies (InfoTech 2021), Varna, Bulgaria, 16–17 September 2021. [Google Scholar] [CrossRef]
- The Effect of Temperature on the Rate of Chemical Reactions. Available online: http://chemnet.ru/rus/teaching/eremin/4.html (accessed on 13 June 2022).
- Gasull, A.; Kooij, R.; Torregrosa, J.E. Limit cycles in the Holling-Tanner model. Publ. Mat. 1997, 41, 149–167. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).