Abstract
In this study, a new approach for novelty and anomaly detection, called HPFuzzNDA, is introduced. It is similar to the Possibilistic Fuzzy multi-class Novelty Detector (PFuzzND), which was originally developed for data streams. Both algorithms initially use a portion of labelled data from known classes to divide them into a given number of clusters, and then attempt to determine if the new instances, which may be unlabelled, belong to the known or novel classes or if they are anomalies, namely if they are extreme values that deviate from other observations, indicating noise or errors in measurement. However, for each class in HPFuzzNDA clusters are designed by using the new evolutionary algorithm NL-SHADE-RSP, the latter is a modification of the well-known L-SHADE approach. Additionally, the number of clusters for all classes is automatically adjusted in each step of HPFuzzNDA to improve its efficiency. The performance of the HPFuzzNDA approach was evaluated on a set of benchmark problems, specifically generated for novelty and anomaly detection. Experimental results demonstrated the workability and usefulness of the proposed approach as it was able to detect extensions of the known classes and to find new classes in addition to the anomalies. Moreover, numerical results showed that it outperformed PFuzzND. This was exhibited by the new mechanism proposed for cluster adjustments allowing HPFuzzNDA to achieve better classification accuracy in addition to better results in terms of macro F-score metric.
1. Introduction
Novelty detection has been presented as a one-class problem where the main goal is to discriminate examples from the normal class and everything else that does not fit into the current understanding of normalcy. The learning phase for the novelty detection problem, formalized in such a way, is based only on examples from one class, which is also referred to as the normal concept. Therefore, in the application phase, the stream of new unlabelled examples can be classified as either normal (instance belongs to the normal concept, which was learned during the training phase) or unknown (instance does not belong to the normal concept). The unknown examples can indicate the presence of a new class, known as novelty, which was not learned in the training phase, or they can be anomalous data not belonging to any class. The latter can result from measurement errors, noise or other factors.
In this study, novelty detection is treated as a multi-class task, to be more specific, it is assumed that the normal concept may be composed not by one but by multiple classes. Moreover, new instances or test examples can also form multiple novel classes, or they can indicate new features of the known classes, or, lastly, they can be anomalies. It should be noted that the new classes result in a concept evolution [1], while new features of the known classes are the subject of the concept drift [2]. Thus, the decision model should be able to evolve to represent the new emergent classes or patterns.
Let us examine continuous data produced according to some probability distribution, which can change over time. These data are also denoted as data streams, and with data streams not only can novel concepts appear, but the known concepts can also evolve [3]. Thus, the dynamic nature of the normal and novel classes renders novelty detection a challenging task [4].
In this study, we propose a new algorithm, named HPFuzzNDA (Hybrid Possibilisitic Fuzzy approach with Automatically adjusted number of clusters), which is a modification of the Possibilistic Fuzzy multi-class Novelty Detector for continuous multi-class data stream problems [5]. The new approach employs the NL-SHADE-RSP algorithm [6], which is a modification of the well-known evolutionary algorithm L-SHADE [7]. Namely, NL-SHADE-RSP is used to design clusters for each known class and to determine the number of these clusters. It should be noted that the objective function for the NL-SHADE-RSP approach was the same as that proposed for the Possibilistic Fuzzy C-Means (PFCM) method [8]. Additionally, a new mechanism based on the fuzzy clustering similarity metric [9], the generalized soft C index metric [10] and mini-batch approach, is proposed to reduce the number of designed clusters where necessary.
Thus, the main contributions of this paper are as follows:
- NL-SHADE-RSP is able to design a more appropriate number of clusters for each class, normal or novel, which is supported by the experimental results, thus, the NL-SHADE-RSP algorithm presents a more flexible approach for clustering as it is not limited by a predefined number of clusters unlike the PFCM approach used for PFuzzND.
- For each class, the number of clusters is not fixed and can increase or decrease over time, so the final decision model can be simplified and vice versa, depending on the given dataset, and as a result, better classification results can be achieved.
- A new additional mechanism, proposed for the automated adjustment of the number of clusters, helps to increase the classification accuracy as the “borders” of clusters of different classes, and consequently, the “borders” of these classes, are better distinguished compared to the PFuzzND approach.
- The proposed algorithm is able to learn novel concepts or extensions of the known concepts as well as to detect anomalies that do not belong to any of the classes (known or novel) better than the original PFuzzND method, in terms of classification accuracy, macro F-score metric and the unknown rate measure [11], which is confirmed by the experimental results.
Thus, the paper is organized as follows. The main subjects of the related works are briefly explained in Section 2. The problem statement and our approach are presented in Section 3. The experimental methodology and setup as well as numerical results, obtained for different benchmark datasets, are described in Section 4. Finally, the discussion and conclusions (as well as the possibilities of future work) are given in Section 5 and Section 6, respectively.
2. Related Work
As was mentioned, in this paper, a new approach for novelty and anomaly detection is introduced. However, firstly, the distinction between these two terms should be given, and for this purpose the definitions presented in [12] are used.
In [12], two novelty detection learning scenarios were distinguished, namely the static and the dynamic scenarios. In the static scenario [13,14,15], the novelty detection problem is considered as a binary classification problem. Thus, a given dataset is composed by only one class and the designed model should be able to identify whether the newly arrived instance is normal or not, as the latter means that the novelty was detected [16,17].
The dynamic novelty detection, also known as evolving classes, future classes or novel class detection [11,18,19], can be formalized as a classification problem with an unknown number of labels. Therefore, the classifier has to determine whether the new instance belongs to one of the currently known classes or not. To be more specific, if the classifier is not sure whether the considered instance belongs to one of the known classes, then this instance should be stored in some external buffer [20,21]. The instances stored in the mentioned buffer are clustered when their number is sufficient, and later the obtained validated clusters are evaluated as either extensions of some known classes or novelties.
It should be noted that as the classes change over time, the classifier must be updated to be able to detect these changes. Thus, there are two possible outcomes of applying a given model for the dynamic novelty detection problem: concept evolution [4] and concept drift [22]. Concept evolution refers to the appearance of novel classes in dynamically updated datasets. Novel concepts should be determined as soon as they appear in data so that they can also be assimilated into the underlying concept for further detection of recurring novel class instances. The term concept drift refers to changes in the conditional distribution of the output or, in other words, target variable given the input features, while the distribution of the input features may stay unchanged [22]. Concept drift indicates that there are extensions of previously established classes, which should be considered for new incoming data instances.
In the case of anomaly detection, the data are labelled in two categories, namely the normal and anomalous categories, for example, in studies [23,24] patients with cancer and fraudulent credit-card transactions were considered as anomalies, respectively. It is assumed that anomalous instances are scarce due to the unbalanced distribution between normal and anomaly classes [25] and, thus, the anomaly detection learning scenario can be formalized as an unbalanced supervised classification problem.
Overall, the methods developed for novelty and anomaly detection can be divided into four groups:
- probabilistic methods [26,27,28,29];
- distance-based methods [30,31,32];
- reconstruction-based methods [33,34,35,36];
- deep learning methods [37,38,39,40].
Probabilistic novelty detection approaches are based on the idea that a statistical model can be designed using the training data, and then this model can be applied to estimate whether a new instance (or test sample) belongs to the same distribution or not. There are two basic models to follow when designing a statistical novelty detector: parametric and non-parametric models.
Parametric methods assume that the data come from a family of known distributions or are generated from an underlying parametric distribution [41,42,43]. The most commonly used form of distribution for continuous data is the Gaussian, but a mixture of other distributions, such as gamma, Poisson or Student’s t, can be used for more complex forms of data distribution modelling. For high dimensional data, the type of distribution has to be determined not only for one parameter, but for several interdependent parameters, thus, methods of parametric statistical novelty detection are of little use for these datasets [44]. Some well-known examples of parametric approaches include the Gaussian Mixture Models (GMM) [45] and Hidden Markov Models (HMM) [46].
Non-parametric methods do not make assumptions about the data distribution, and instead rely on estimating a distribution based on the data itself [47,48,49]. Non-parametric methods tend to be very powerful for problems that require adaptability, and those where the underlying distribution is naturally unknown. One of the most well-known non-parametric probabilistic approaches is the Parzen Windows estimator [50]. This method has been used for novelty detection in applications such as network intrusion detection [51], oil flow data [52], and mammography image analysis [53].
Distance-based methods, including clustering [54,55] or nearest-neighbour methods [56,57], represent other types of techniques that can be used for performing a task equivalent to that of estimating the probability density function of data. These methods rely on well-defined distance metrics to compute the distance or similarity measure between two data points. There are various works dedicated to this subject, for example, in [58] the authors proposed a Distance-based Angular Clustering Algorithm (DACA) for wireless networks, in [32] a novel two-phase heuristic approach for solving the problem of transporting vehicles equipped with (CVRP) was introduced. Moreover, in some cases, distance-based methods are used to pre-process data, namely, to determine the feature vectors, which are then used for other classifiers [59], etc.
Reconstruction-based approaches are frequently used in safety-critical applications for regression or classification purposes [36,60]. These types of methods can autonomously model the underlying data, and when new instances are presented to the system, the reconstruction error, defined as the distance between these instances and the output of the system, can be related to the novelty score.
Finally, deep learning for novelty and anomaly detection aims at learning feature representations or novelty/anomaly scores, respectively, via neural networks. A large number of deep learning methods have been introduced for novelty detection and they demonstrate significantly better performance than conventional approaches in addressing challenging detection problems in a variety of real-world applications [61,62,63,64,65]. Deep methods help largely improve the utilization of labelled normal data or some labelled anomaly data regardless of the data type, reducing the need for large-scale labelled data as in fully supervised settings [66]. This subsequently leads to more informed models and, thus, better recall rates. Deep methods are known for their ability to learn structures and relations from diverse types of data, such as high-dimensional tabular data, images, video, graphs, etc. However, deep learning approaches for novelty detection also have multiple disadvantages and weaknesses, which are explained in detail in the review [66].
A short summary of the various works related to the novelty and anomaly detection is presented in Table 1.

Table 1.
Summary of the related work: novelty and anomaly detection approaches.
Overall, previous research shows that most of the currently existing methods treat novelty and anomaly detection problems within the framework of one-class classification [67], in which one class (the specified normal or positive class) has to be distinguished from all other possibilities. However, there are some works that consider novelty detection as a multi-class task [68,69,70], but assume that more than one new class cannot appear interchangeably. In [11],, a short review of works related to anomalies and novelties in the context of dynamic multi-class settings is given. Thus, in this study, we introduce an approach that is able to treat the dynamic novelty detection learning scenario as a multi-class task as it performs classification on partially labelled data. During the examination of the unlabelled data, the proposed algorithm determines whether they form new classes or extensions of the known classes while being simultaneously able to distinguish anomalies that should be removed from a given dataset.
3. Proposed Approach
In this section, the proposed approach is described in detail. To do so, we have to explain how several algorithms work as they were used as the starting point for the new HPFuzzNDA method. Firstly, the description of the PFCM approach [8] is given as its objective function was used by the NL-SHADE-RSP [6] algorithm to design clusters for each class known at the time. Additionally, the main principles of the original PFuzzND algorithm [5] and our modification of the L-SHADE algorithm are presented.
3.1. Possibilistic Fuzzy C-Means Method
Let us consider clustering of a given dataset (where is the i-th data instance and p is the number of features describing instances) as a partitioning of X into subgroups such that each subgroup represents "natural" substructure in X. In [8], this partition of X, denoted as M, is a set of values that can be conveniently arrayed as two matrices and :
Equation (1) defines the set of possibilistic fuzzy partition of X. Here, U is the fuzzy matrix while T is the possibilistic one. Both matrices are mathematically identical, having entries between 0 and 1. These matrices are interpreted according to their entries. For the fuzzy matrix, U, each entry is taken as the membership of in the i-th cluster of M, and for the probabilistic matrix each entry is usually the (posterior) probability that, given , it came from cluster i. It should be noted that is a measure that shows how typical a given entry is for i-th cluster.
In [71], the authors explained why both possibilistic and fuzzy matrices should be used for clustering and in [8] they also listed the disadvantages of both Fuzzy C-Means (FCM) [72] and Possibilistic C-Means (PCM) [73] methods. Originally, there was a constraint on the typicality values (the sum of the typicality values over all data points in a particular cluster was set to 1). Thus, in [8] the authors relax this constraint, namely, in their algorithm, the row sum of typicality values is equal to 1, but the column constraint on the membership values is retained. This leads to the following optimization problem:
where is the set of cluster centres, , , and are algorithm’s parameters chosen by the end-user, is the standard Euclidean distance, and () is also a user-defined constant. In (2) , , , have the same meaning as membership values in FCM, and , , , have the same interpretation as typicality values in PCM. The PFCM approach is iterative, and U, T and V are updated over each iteration according to the rules presented in [8].
3.2. Possibilistic Fuzzy Multi-Class Novelty Detector
The PFuzzND approach [5] is used for the dynamic novelty detection learning scenario. It is an improved version of the Fuzzy multi-class Novelty Detector for data streams [74], which is a fuzzy generalization of the offline–online framework presented in [11] for the MINAS approach. All the mentioned algorithms can be divided into two stages. During the first stage, called offline, the model is built using a labelled training dataset. The second stage, during which new classes may emerge and disappear and the old classes may also drift, is referred to as the online or the prediction stage.
In the offline step of the PFuzzND algorithm, a decision model is learned from a labelled set of examples using the PFCM clustering method. To be more specific, for each known class a given number of clusters, , is designed, and this number is a user-defined parameter that can only increase (differently for each class) during the online stage until it reaches the maximum possible value . It also should be noted that is the same for all known classes during the offline phase, and each class cannot be divided into more than clusters. Furthermore, the maximum number of clusters, , that can be created for each class (normal or novel), is another user-defined parameter, which does not change during operation of the algorithm. Finally, it is assumed that generally only the portion of instances from the dataset are labelled, and, thus, they are used during the offline stage.
Thus, let us denote the number of the classes, known at the offline stage, as , then at the beginning of the online stage the decision model is defined as the set of clusters found for all different known classes. Additionally, an empty external set, called short memory, is created at the end of the offline phase. Examples labelled during the online stage as unknown are stored in the short memory for a time period , after this time limit, these instances are removed from the mentioned set. The latter can occur if it is established that they do not belong to the existing classes, and do not form novel classes either. Thus, these instances are considered as anomalies.
Moreover, there are four additional user-defined parameters for the online phase of the PFuzzND approach:
- The minimum number of instances (denoted as ) in the short memory to start the novelty detection procedure.
- The initial threshold, , to launch the classification process of the unlabelled instances.
- Two adaptation thresholds, and , used during the classification step.
During the online step, first, for each new instance, , its membership and typicality values related to all clusters, known at the moment, are calculated. Typicality values have more influence here as they are used to determine whether the instance will be labelled by one of the existing classes or will be marked as unknown. For this purpose, the highest typicality value of the j-th instance and the corresponding existing class, (), are determined. Subsequently, the maximum typicality values are found for all instances considered before the new one arrives (and these instances should belong to the class ), and the mean value of these typicalities is calculated. Let us denote this mean value as , where t is a timestamp, which shows how many instances were processed after the offline stage, and, therefore, is equal to 1 at the beginning of the online stage. If the highest typicality of the new instance, , is greater than the difference between the obtained mean value and the adaptation threshold , then the instance belongs to the class [5]. It should be noted that the highest typicality of the first instance processed after the offline phase is compared to the initial threshold .
If the instance is labelled, then its typicality value is used to update , while the PFCM approach is used to update the clusters of the class . Otherwise, the highest typicality of the new instance is compared to the difference between and the adaptation threshold . If the highest typicality is greater than the mentioned difference, then instance belongs to the class , but a new cluster with as its centroid should be created [5]. If instances belonging to the class are already divided into clusters, then the oldest cluster is removed and the new cluster with as its centre is generated instead of it.
If neither conditions are met, then the instance will be marked as unknown and stored in the short memory until the novelty detection step will not be executed. The latter happens if the number of instances marked as unknown reaches . In this case, firstly, the PFCM approach is applied to all the instances in the short memory and the pre-determined number of clusters is designed. After that, for each generated cluster its fuzzy silhouette [75] is calculated and if the obtained value is greater than 0 and the considered cluster is not empty, then this cluster is evaluated as the valid one. All validated clusters of short memory represent new patterns or novelties.
The next step of the novelty detection procedure consists of calculating the similarity between these validated clusters to the ones already existing (clusters belonging to the known classes), which is achieved by using the fuzzy clustering similarity metric introduced in [9]. Thus, the known cluster, that is the most similar to the examined cluster from the short memory, is determined. If the value of the mentioned metric for these two clusters is greater than (which is another parameter of the PFuzzND approach), then all instances from the examined cluster are labelled the same way as instances of the considered known cluster. Consequently, clusters of the corresponding class are updated by the PFCM algorithm. In this case, the known class has evolved, and we are referring to the concept drift. Otherwise, a new class is created, therefore, we should increment by one, and instances from the examined cluster are labelled as belonging to the new class.
If one of the short memory clusters is not validated, then it is discarded and its instances remain in the short memory until the model executes the novelty detection procedure again or decides to remove them all, which can happen if these instances are in the short memory for iterations.
3.3. Evolutionary Algorithms
Differential Evolution or DE is a well-known population-based algorithm introduced in [76] for real-valued optimization problems. DE maintains a population of solutions (also called individuals or target vectors) during the search process and the key idea of this algorithm comprises the usage of difference vectors calculated between the individuals in the current populations. These difference vectors are applied to the members of the population to generate mutant solutions. DE contains only three parameters, namely the population size , scaling factor for mutation F and crossover probability .
Generally, the initialization step is performed by randomly generating points , , , in the search space with uniform distribution within . Here, P is the dimensionality of the search space. Mutation, crossover and selection operators are then iteratively applied to the generated population. Originally, DE used the rand/1 mutation strategy [76]; however, most recent DE approaches, including L-SHADE [7], often use the current-to-pbest/1 strategy, which was initially proposed for the JADE algorithm [77]. The current-to-pbest strategy works as follows:
where is an index of one of the best individuals (the quality of individuals is estimated by their fitness values), k and l are randomly chosen indexes from the population, and scaling factor F is usually in the range . Indexes , k and l are generated in such a way that they are mutually different and are not equal to i.
The crossover operation is performed after mutation to generate a trial vector by combining the information contained in the target and mutant vectors. Specifically, during the crossover, the trial vector , , receives randomly chosen components from the mutant vector with probability as follows:
where is a randomly chosen index from , which is required to ensure that the trial vector is different from the target vector to avoid unnecessary fitness calculations.
After generating the trial vector , the bound constraint handling method is applied. Finally, the selection step is performed after calculating the fitness function value in the following way: if the trial vector outperforms or is equal to the parent in terms of fitness, then the target vector in the population is replaced by the trial vector .
3.3.1. L-SHADE Algorithm
The L-SHADE approach is a modification of the DE algorithm, firstly introduced in [7]. As previously mentioned, DE has three main parameters, and deciding upon which parameter to employ presents a difficult task, as they have an impact on the algorithm’s speed and efficiency. The L-SHADE algorithm uses a set of historical memory cells containing values to generate new parameter values F and for every mutation and crossover procedure. Mentioned parameter values are sampled using a randomly chosen memory index as follows:
where and are random numbers generated by Cauchy and normal distributions, respectively. The value is set to 0 or 1 if it spans outside the range , and the F value is set to 1 if or is generated again if . The values of F and , which caused an improvement to an individual, are saved into two arrays, and , together with the difference of the fitness value .
The memory cell with index h, incrementing from 1 to H every generation, is updated as follows:
where S is either or . Then, the previous parameter values are used to set the new ones in the following way:
In the last two formulas, c is an update parameter set to , and g is the current iteration number.
The L-SHADE algorithm uses the Linear Population Size Reduction (LPSR) approach to adjust the population size . To be more specific, it is recalculated at the end of each iteration, and the worst individuals are removed from the population. The new number of individuals depends on the available computational resources:
where and are the minimal and initial population sizes, respectively, is the current number of function evaluations, while is the maximal number of function evaluations.
Finally, L-SHADE uses an external archive A of inferior solutions. The archive, A, contains parent solutions rejected during selection operation, and is filled until its size reaches the predefined value . Once the archive is full, new solutions replace randomly selected ones in A. The current-to-pbest mutation (5) is changed to use the individuals from the archive so that the l index is taken either from the population or the archive A with a probability of . Additionally, the archive size, , decreases together with the population size in the same manner.
3.3.2. NL-SHADE-RSP Algorithm
The NL-SHADE-RSP algorithm is a modification of the L-SHADE approach, first introduced in [6]. It is a further development of the L-SHADE-RSP algorithm, presented in [78], which uses selective pressure for the mutation procedure. The effect of the selective pressure was studied in detail in [79]. The mutation strategy proposed for the L-SHADE-RSP approach is called current-to-pbest/r, and it is different from the original current-to-pbest strategy only with regard to the choosing of indexes k and l. To be more specific, for each individual i the probability is calculated in the following way:
where is the rank of the i-th individual. In addition, ranks , , were set as indexes of individuals in an array sorted by the fitness values, with largest ranks assigned to the best individuals. Finally, indexes k and l were chosen with the corresponding probabilities. In NL-SHADE-RSP, the same current-to-pbest/r strategy is used, however, the rank-based selective pressure is applied only to the index l, and only if it is chosen from the population, while the index k is chosen uniformly.
In contrast to the L-SHADE and L-SHADE-RSP approaches, in NL-SHADE-RSP the population size is reduced in a non-linear manner:
where is the ratio of the current number of fitness evaluations.
The external archive A is used for the index l in the current-to-pbest/r mutation procedure with probability , and in the NL-SHADE-RSP algorithm this probability is automatically adjusted. The latter is achieved by implementing the adaptation strategy, originally proposed for the IMODE algorithm [80]. Firstly, the probability should be within the range , and initially it is set to , unless the archive is empty. Then, the probability is calculated in the following way:
where is the amount of archive usage, which is incremented every time an offspring is generated using archive A, and are the fitness improvements achieved with and without archive, respectively. It should be noted that the new value of is checked to be within the range by applying the following rule:
In NL-SHADE-RSP, both binomial and exponential crossover operators are used with a probability of . The description of the exponential crossover is given in [6]. For exponential crossover, the Success-History Adaptation (SHA) is applied, but at the beginning of the generation, the crossover rates generated for each individual i are sorted according to fitness values, so that smaller crossover rate values are assigned to better individuals. For the binomial crossover, value is calculated in the following way:
Finally, the value for current-to-pbest/r mutation in NL-SHADE-RSP is controlled in the same way as in the jSO algorithm [81]:
Note that the following user-defined parameters were used: and . Furthermore, the parameter linearly decreases as it is performed in jSO.Detailed pseudo-code of the NL-SHADE-RSP algorithm is presented in [6].
3.4. The HFuzzNDA Approach
The HFuzzNDA algorithm, in contrast to the PFuzzND approach, has an additional parameter, namely the maximum possible number of clusters per class, denoted as . This parameter changes over time and is initially set to a minimal value (to be more specific, it is equal to 2). To calculate the new value, the following notations are used:
- First, we check how many instances are classified (this number is denoted as ); after the offline stage this number is equal to , and grows incrementally during the online stage (one new instance per iteration).
- Two new parameters are introduced, namely and ; controls the speed at which the value grows, and shows how much grows over each iteration.
- A given number of considered instances, denoted as , is saved after some number of iterations, right after the offline stage.
Thus, is updated as shown in Algorithm 1 (note that in Algorithm 1 the temporary variable only grows).
| Algorithm 1 update procedure |
|
Evolutionary and biology-inspired optimization algorithms are popular among researchers and are frequently used for anomaly and/or novelty detection. For example, in [82] the hybrid algorithm based on Fruit Fly Algorithm (FFA) and Ant Lion Optimizer (ALO), and in [83] the Farmland Fertility Algorithm were used, respectively, for feature selection to reduce the dimensionality of the data. Data, pre-processed in such a way, were later classified as normal or anomalous by using some well-known machine learning approaches (support vector machines, decision trees, k nearest neighbours). In this study, we did not apply an evolutionary algorithm as a pre-processing technique, instead it was used for clustering, namely, clusters’ centres were determined by the NL-SHADE-RSP algorithm. To be more specific, NL-SHADE-RSP determined centres of clusters belonging to each class and each individual represented the whole set of clusters’ centres; and no feature selection was applied. Thus, during the offline stage, the NL-SHADE-RSP approach is used to divide each known class into two clusters. For this purpose, function (2) is optimized and each individual represents the centres of the clusters. After that, the PFCM algorithm is used to obtain the membership U and typicality T matrices for these classes. The “age” of all clusters, designed during the offline stage, is recorded (they are considered as the oldest clusters).
The online stage starts with Algorithm 1 and then proceeds to check conditions, described for the PFuzzND approach, for each new instance iteratively. However, some changes were implemented to the online procedure. To be more specific, a new merging technique is applied to clusters to check if there is a need to decrease their number, and the NL-SHADE-RSP approach is used to refine clusters belonging to each class. The pseudo-code for the online stage is presented in Algorithm 2. Note that in Algorithm 2 is the current number of instances stored in short memory. Furthermore, the NL-SHADE-RSP approach can change the final number of clusters belonging to the considered class. To be more specific, it is executed for all possible variants of the for a given class from 2 to the current value of , and the best variant is chosen at the end of the optimization process.
| Algorithm 2 One iteration of the online phase |
|
The original PFuzzND algorithm allows an increase in the number of clusters belonging to each class, but not the other way around. Experiments showed that in some cases the instances belonging to the same class might be divided into an excessive number of clusters which can can lead to bad classification results. Thus, in this study, it is proposed to merge clusters belonging to the same class if they are similar to each other, which allows for a decrease in their number.
In [9], fuzzy similarity metric was introduced. It can be described in the following way: firstly, the dispersions of two considered clusters are calculated, then the dissimilarity between these clusters is determined and, finally, the sum of dispersions is divided by the dissimilarity value [9]. Each cluster’s dispersion is the weighted sum of distances between instances belonging to this cluster and its centre, averaged by the number of considered instances. Note that the membership values are used as weights. The dissimilarity between two clusters is the Euclidean distance between their centres.
In our study, the typicality values are used as the weight coefficients for calculating the similarity metric. We find two of the most similar clusters belonging to a given class, and determine if they should be merged by using the generalized soft C index metric [10] (here, we denote it as ). To use the latter, we have to conduct calculations for all instances that belong to the considered class. However, this can significantly slow the algorithm, so only a part (here, c is the class number and B is the batch size) of instances participate in calculating the values. The pseudo-code of the proposed merging procedure is demonstrated in Algorithm 3.
| Algorithm 3 The merging procedure |
|
Finally, during the novelty detection phase, instances stored in the short memory are divided into clusters using the NL-SHADE-RSP algorithm. The maximum possible number of short-memory clusters is set to the current value of . After that, membership and typicality matrices are determined. Then, the standard steps of the novelty detection procedure introduced for the PFuzzND approach are conducted.
The general scheme of the proposed approach is demonstrated in Figure 1.
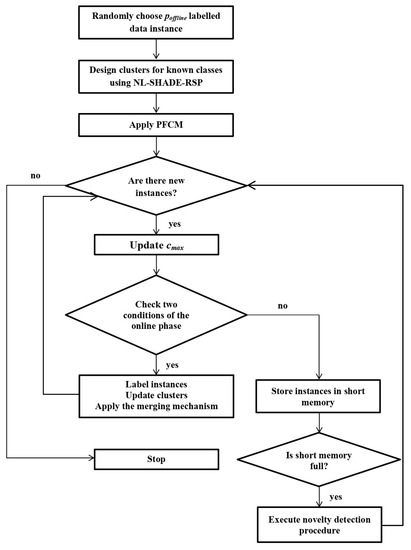
Figure 1.
The general scheme of the HPFuzzNDA approach.
4. Experimental Results
In order to verify the advantages of the proposed HPFuzzNDA algorithm, it was tested on a set of benchmark datasets, which were specifically generated to evaluate novelty detection algorithms and can be found in the corresponding repository [84]. The results obtained by the HPFuzzNDA approach for the benchmark datasets were compared against the results achieved by the PFuzzND algorithm. Only this comparison was performed for test problems due to the fact that PFuzzND outperformed the original FuzzND approach and the well-known MINAS algorithm, while the latter was the baseline for FuzzND [5].
Thus, firstly, the datasets and the evaluation metrics used in our experiments will be explained. Then, the obtained results and models will be presented.
4.1. Experimental Setup for Benchmark Problems
The performance of the proposed method was evaluated by using nine synthetic datasets named ,..., [84]. Table 2 presents the details of each dataset:

Table 2.
Benchmark datasets used in experiments.
- Column indicates the total number of examples for each dataset, respectively.
- Column indicates the number of features for each dataset, respectively.
- Column indicates the number of classes known at the offline phase.
- Column indicates the minimum total number of classes for each dataset (the difference between this number and the corresponding value from the column is the minimum number of novel classes that algorithms are expected to detect).
Both the PFuzzND and the proposed HPFuzzNDA approaches use possibilistic fuzzy clustering algorithm PFCM during offline and online phases. The parameters of the PFCM algorithm were the same for all conducted experiments and are listed in Table 3. The following notations are used in the table: and are constants responsible for the membership and the typicality values, a and b are constants that show the influence of the membership and the typicality values during the decision making step, is the maximum number of iterations for PFCM to generate a given number of clusters, and is the minimum difference between the objective function values calculated on two consequential iterations of the PFCM algorithm (if this difference was less than then calculations stopped).

Table 3.
Parameters of the PFCM algorithm.
It should be noted that the PFCM clustering method uses a specific parameter for each i-th cluster. All these parameters influence the typicality values, which in turn are necessary to determine the clusters’ centres. The parameters were introduced for the possibilistic clustering method PCM [73]. In this work, they were user-defined constants, while in [85] the authors proposed to calculate these values on each iteration of the clustering algorithm. In this study, experiments were conducted only for the iteratively calculated .
The same basic parameters were used during the offline and the online phases (including the novelty detection procedure) for both PFuzzND and HPFuzzNDA algorithms to make the comparison between them fair. As previously mentioned, was a constant for the PFuzzND approach, and it changed over time for HPFuzzNDA. All parameters are listed in Table 4. In the table, is the number of clusters that should be designed for the short memory; it is a user-defined parameter (constant) for PFuzzND and automatically adjusted for HPFuzzNDA.

Table 4.
Basic and newly introduced parameters of the PFuzzND and HPFuzzNDA approaches.
Additionally, the NL-SHADE-RSP also contains its own parameters. Most of them were taken from [6] as it was shown that they allow NL-SHADE-RSP to achieve the best optimization results. However, the following parameters were set during our experiments:
- ;
- ;
- initial = 25;
- .
Here, p is the number of features describing each instance from the dataset, and P is the number of variables optimized by the NL-SHADE-RSP algorithm.
It should be noted that for the original PFuzzND algorithm, parameters and are fixed during the offline phase and the novelty detection procedure, namely exactly these numbers of clusters are generated for each known class and short memory, respectively. Thus, initially the number of clusters is the same for all known classes, but can later be different for classes due to the procedures executed during the online phase. Moreover, in this study, the maximum number of clusters created for one class by PFuzzND is limited. Namely, this number cannot exceed 8 or be less than 2. Values for parameters used during the online stage (for both PFuzzND and HPFuzzNDA) were chosen according to the previously conducted experiments.
Experiments were evaluated using the incremental confusion-matrix, which evolves as soon as a new data point is classified [86]. This matrix is composed of rows and columns that represent known classes, concept drift of known classes and new classes (concept evolution), and finally unlabelled data instances (those removed from short memory). So, for each dataset, three values were calculated over 10 program runs: the accuracy, the macro F-score metric and the unknown rate measure [11]. The accuracy was calculated only for the labelled data instances (new classes were not considered), while the macro F-score values were calculated considering not only the examples classified with already existing labels but also with new class labels, determined by the algorithm during the novelty detection process.
4.2. Numerical Results for Benchmark Problems
The aim of the conducted experiments was to compare the HPFuzzNDA approach with the original PFuzzND algorithm. Thus, both algorithms were executed on all 9 datasets and repeated 10 times. Results obtained on all datasets are presented in Table 5. In these tables, results averaged by the number of program runs are shown, and means accuracy in % while denotes the macro F-score metric values (they are also given in %). Additionally, the values here should be multiplied by .

Table 5.
Results obtained by PFuzzND and HPFuzzNDA on benchmark problems.
Overall, the proposed method was able to detect class extensions at the classification step and adapt the model during the online phase. Moreover, the HPFuzzNDA algorithm could also detect the new classes which emerged along the online phase for datasets that had unlabelled instances (the latter is shown in the column with the unknown measure rate values). Generally, compared to the PFuzzND approach, the new HPFuzzNDA algorithm correctly classified instances more frequently.
Additionally, to compare the efficiency of HPFuzzNDA and PFuzzND the Mann–Whitney rank sum statistical test with significance level was used. Statistical tests were applied to the accuracy and macro F-score values, and obtained results are demonstrated in Table 6. It should be noted that in Table 6, the following notations are used:

Table 6.
Results of the Mann–Whitney rank sum statistical test.
- “+” means that HPFuzzNDA showed significantly better results than PFuzzND on a given problem;
- “−” means that HPFuzzNDA showed significantly poorer results than PFuzzND on a given problem;
- “=” means that there were no significant differences between results of the HPFuzzNDA and PFuzzND approaches for a given problem;
Thus, the HPFuzzNDA algorithm achieved significantly better results for four benchmark datasets and performed worse on only one dataset.
5. Discussion
For the first problem, both algorithms were able to detect the novel 4-th class. However, a portion of the instances originally belonging to the novel 4-th class, were considered as anomalies and discarded by both algorithms. The number of clusters, which were designed by HPFuzzNDA for normal classes, varied from five to nine, while for the novel class this number changed from two to six. In addition, all classes were divided into different numbers of clusters. Meanwhile, all normal and novel classes were divided into eight clusters by the PFuzzND approach, thus, the number of clusters increased to the maximum value and did not change thereafter. Figure 2 shows the example of results obtained on this dataset by both algorithms. Generally, PFuzzND achieves a lower accuracy and higher value of the unknown rate measure on . In Figure 2, it is evident that PFuzzND found more anomalies than HPFuzzNDA, but the latter was more successful while determining instances from normal classes.
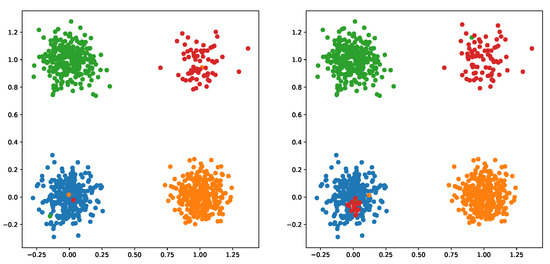
Figure 2.
Example of instances from the first dataset, classified by HPFuzzNDA (the left graph) and by PFuzzND (the right graph) algorithms. Red points belong to the novel class.
PFuzzND showed significantly better results compared to HPFuzzNDA only on the second dataset according to the Mann–Whitney test. Both algorithms were able to determine that there are only two normal classes and anomalies (novel classes were not detected, which is correct in the case of this dataset). The number of clusters that were designed by HPFuzzNDA for normal classes varied from 3 to 5, while it stayed at 8 by the end of PFuzzND work. Best results obtained for this dataset by both algorithms are presented in Figure 3. To be more specific, for the example demonstrated in Figure 3, PFuzzND’s accuracy was , while HPFuzzNDA correctly classified of the labelled data. Nevertheless, from this figure, it is clear that HPFuzzNDA was able to determine class extensions better than the PFuzzND approach. This might present a sign that for the second dataset it would perhaps be better to use HPFuzzNDA but with an initially increased number of clusters for classes.
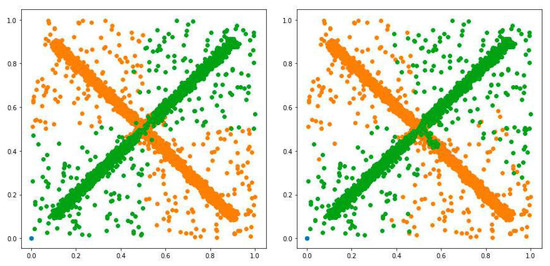
Figure 3.
Example of instances from the second dataset, classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms. Here, the best achieved results by both algorithms are presented. However, it is clear that class extension caused by the presence of unlabelled data was not detected correctly by PFuzzND.
According to the numerical results presented in the previous section, there is no significant difference between results obtained by both algorithms on , and . The fourth dataset is similar to the second as there are only two normal classes and anomalies. HPFuzzNDA mostly designed models with two clusters for each class, but PFuzzND still increased the number of clusters up to the maximum value causing an unnecessary partition of instances. Example of results obtained for is demonstrated in Figure 4.
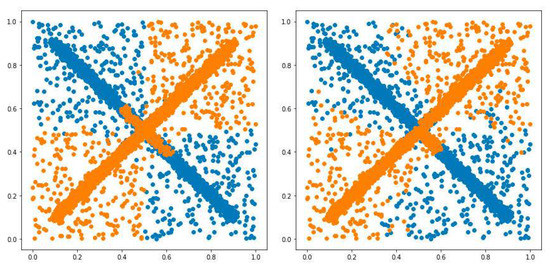
Figure 4.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
The 6-th and the 7-th datasets contain neither anomalies nor novel classes. HPFuzzNDA mostly forms four or five clusters for each normal class, while PFuzzND shows the same behaviour as it did for previously mentioned problems. It should be noted that both algorithms mistakenly marked some instances as anomalies for , but the number of “anomalies” found by the PFuzzND approach was much bigger compared to HPFuzzNDA. This fact is highlighted in Table 5, as the value of the unknown rate measure obtained by PFuzzND for is much greater than that obtained by HPFuzzNDA. Furthermore, slightly better accuracy was achieved by HPFuzzNDA on both datasets, and , due to the fact that PFuzzND was not always able to determine the “borders” between present classes. The latter can be clearly seen in Figure 5 and Figure 6.
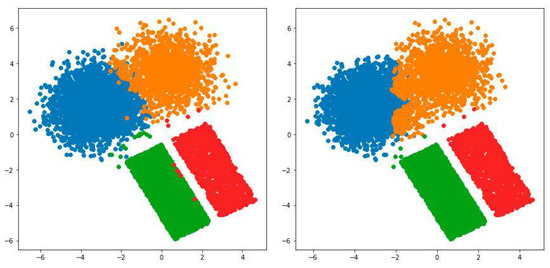
Figure 5.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
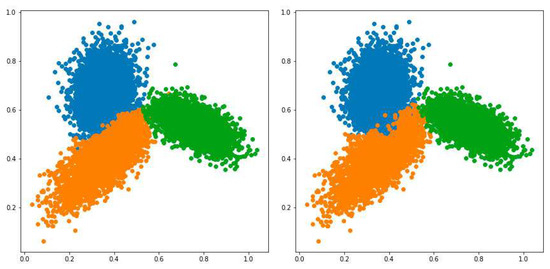
Figure 6.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
HPFuzzNDA significantly outperformed PFuzzND on , , and datasets. For the number of clusters varied from 4 to 9 for each class; for , and it changed from 2 to 4. It should be noted that PFuzzND constantly increased the number of clusters for each class until it reached the maximum value. Thus, it can be concluded that a lower number of clusters leads to better results for these datasets. The latter can be achieved by the proposed approach due to its flexibility and merging strategies.
According to the results from Table 5 and Table 6, HPFuzzNDA significantly outperformed PFuzzND in terms of accuracy and macro F-score, but unlike PFuzzND, it also had a non-zero unknown rate measure value. Figure 7 shows an example of the results obtained by both algorithms compared on . Again, it is obvious that PFuzzND could not determine the “borders” between normal classes, as instances that should have been marked as “green” were instead marked as “orange”. On the other hand, HPFuzzNDA classified a few instances as anomalies which were not present in this dataset. A similar situation can be seen in Figure 8 for . However, in the case of this dataset, PFuzzND also incorrectly marked instances as anomalies and the number of these instances was greater compared to the HPFuzzNDA approach.
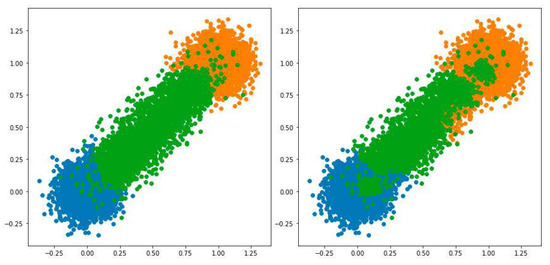
Figure 7.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
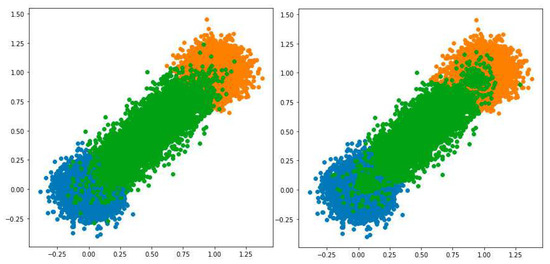
Figure 8.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
Examples of results obtained for the datasets and are presented in Figure 9 and Figure 10, respectively. According to results from Table 5 and Table 6, HPFuzzNDA significantly outperformed the original PFuzzND approach in terms of accuracy and macro F-score metric, which is obvious from the demonstrated figures. Moreover, both algorithms were able to determine that there were no anomalies in these datasets.
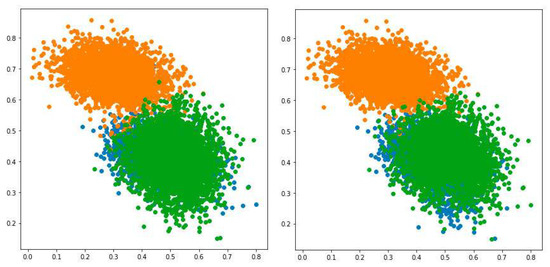
Figure 9.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
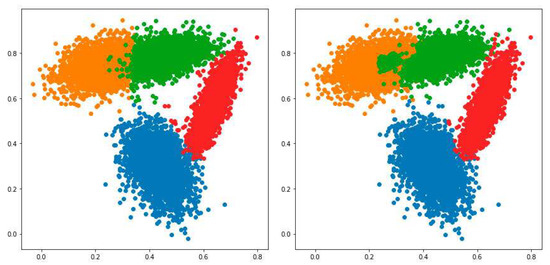
Figure 10.
Example of instances from the , classified by HPFuzzNDA (the left graph) and PFuzzND (the right graph) algorithms.
6. Conclusions and Future Work
In this study, a new HPFuzzNDA approach for novelty detection is introduced. It is able to classify data and determine anomalies better than the original PFuzzND algorithm owing to HPFuzzNDA’s use of an evolutionary algorithm, namely NL-SHADE-RSP, and a specific merging mechanism, which allows a more flexible partition of data instances into clusters. Experimental results demonstrated HPFuzzNDA’s workability and usefulness. The obtained numerical results confirmed the following:
- NL-SHADE-RSP is able to design a more appropriate number of clusters for each class, normal or novel, as it is not limited by the predefined number of clusters like the PFCM approach that is used for PFuzzND.
- The final decision model, designed by the proposed HPFuzzNDA approach, can be simplified or the other way around depending on the given dataset, and consequently, better classification results can be achieved.
- An adaptation strategy, proposed to control the number of clusters belonging to each class, allows increases in classification accuracy as the “borders” of clusters of different classes, and consequently, the “borders” of these classes, are better distinguished compared to the PFuzzND approach.
- The proposed algorithm is able to learn novel concepts or extensions of the known concepts and can better detect anomalies that do belong to any of the classes (known or novel) than the original PFuzzND method in terms of classification accuracy, macro F-score metric and the unknown rate measure.
However, we introduced several new parameters in this study for the HPFuzzNDA approach and did not attempt to adjust them, although it is clear that inadequate parameter choice can lead to poor classification results. Moreover, the new algorithm was tested only on synthetic datasets, which did not contain many features, and is thus not entirely representative of real-world problems. In addition, as previously mentioned in Section 3, the evolutionary algorithm NL-SHADE-RSP is used for determining the centres of all clusters. As a result, NL-SHADE-RSP may suffer from the curse of dimensionality when used for more complex data, as the number of features may increase significantly. Therefore, there is a need for a feature selection technique that should be applied before NL-SHADE-RSP to pre-process data and decrease the number of features describing each data instance.
Thus, the future work should be focused on the following:
- Execution of additional experiments to better understand the influence of each parameter (not only the parameters of the original PFuzzND approach but also the parameters introduced in this study).
- Development of adaptation strategies for the most important parameters determined during the conducted experiments.
- Introduction of the feature selection operator to reduce the dimensionality of the data.
- Application of the proposed algorithm for more complex datasets, for example, image or video data.
Author Contributions
Conceptualization, S.A. and V.S.; methodology, S.A.; software, S.A.; validation, S.A. and V.S.; formal analysis, Y.K.; investigation, S.A.; resources, Y.K.; data curation, Y.K.; writing—original draft preparation, S.A.; writing—review and editing, S.A. and V.S.; visualization, V.S.; supervision, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gurjar, G.S.; Chhabria, S. A review on concept evolution technique on data stream. In Proceedings of the 2015 International Conference on Pervasive Computing (ICPC), Pune, India, 8–10 January 2015; pp. 1–3. [Google Scholar]
- Gama, J.; Žliobaitė, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A survey on concept drift adaptation. ACM Comput. Surv. 2014, 46, 1–37. [Google Scholar] [CrossRef]
- Spinosa, E.J.; de Carvalho, A.P.D.L.F.; Gama, J. Novelty detection with application to data streams. Intell. Data Anal. 2009, 13, 405–422. [Google Scholar] [CrossRef]
- Gama, J. Knowledge Discovery from Data Streams, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Silva, T.P.; Arruda Camargo, H. Possibilistic approach for novelty detection in data streams. In Proceedings of the 2020 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. NL-SHADE-RSP algorithm with adaptive archive and selective pressure for CEC 2021 numerical optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Krakow, Poland, 28 June–1 July 2021; pp. 809–816. [Google Scholar]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Pal, N.R.; Pal, K.; Keller, J.M.; Bezdek, J.C. A possibilistic fuzzy C-means clustering algorithm. IEEE Trans. Fuzzy Syst. 2005, 13, 517–530. [Google Scholar] [CrossRef]
- Xiong, X.; Chan, K.L.; Tan, K.L. Similarity-driven cluster merging method for unsupervised fuzzy clustering. In Proceedings of the 20th Conference on Uncertainty in Artificial Intelligence, Banff, AB, Canada, 7–11 July 2004; pp. 611–618. [Google Scholar]
- Bezdek, J.C.; Moshtaghi, M.; Runkler, T.; Leckie, C. The generalized C index for internal fuzzy cluster validity. IEEE Trans. Fuzzy Syst. 2016, 24, 1500–1512. [Google Scholar] [CrossRef]
- de Faria, E.R.; de Leon Ferreira, A.C.P.; Gama, J. MINAS: Multiclass learning algorithm for novelty detection in data streams. Data Min. Knowl. Discov. 2016, 30, 640–680. [Google Scholar] [CrossRef]
- Carrenõ, A.; Inza, I.; Lozano, J.A.; Leckie, C. Analyzing rare event, anomaly, novelty and outlier detection terms under the supervised classification framework. Artif. Intell. Rev. 2020, 53, 3575–3594. [Google Scholar] [CrossRef]
- Pimentel, M.A.F.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Einardsdóttir, H.; Emerson, M.J.; Clemmensen, L.H.; Scherer, K.; Willer, A.; Bech, M.; Larsen, R.; Ersbøll, B.K.; Pfeiffer, F. novelty detection of foreign objects in food using multi-modal X-ray imaging. Food Control 2016, 67, 39–47. [Google Scholar] [CrossRef]
- Kafkas, A.; Montaldi, D. How do memory systems detect and respond to novelty? Neurosci. Lett. 2018, 680, 60–68. [Google Scholar] [CrossRef]
- Swarnkar, M.; Hubballi, N. OCPAD: One class Naive Bayes classifier for payload based anomaly detection. Expert Syst. Appl. 2016, 64, 330–339. [Google Scholar] [CrossRef]
- Luca, S.; Clifton, D.A.; Vanrumste, B. One-class classification of point patterns of extremes. J. Mach. Learn. Res. 2016, 17, 1–21. [Google Scholar]
- Masud, M.M.; Chen, Q.; Khan, L.; Aggarwal, C.C.; Gao, J.; Han, J.; Srivastava, A.; Oza, N.C. Classification and adaptive novel class detection of feature-evolving data streams. IEEE Trans. Knowl. Data Eng. 2013, 25, 1484–1497. [Google Scholar] [CrossRef]
- Mu, X.; Zhu, F.; Liu, Y.; Lim, E.P.; Zhou, Z.H. Social stream classification with emerging new labels. In Advances in Knowledge Discovery and Data Mining; Phung, D., Tseng, V.S., Webb, G.I., Ho, B., Ganji, M., Rashidi, L., Eds.; Springer: Cham, Switzerland, 2018; Volume 10937, pp. 16–28. [Google Scholar]
- Spinosa, E.J.; de Leon, F.; de Carvalho, A.P.; Gama, J. OLINDDA: A cluster-based approach for detecting novelty and concept drift in data streams. In Proceedings of the 2007 ACM Symposium on Applied Computing, Seoul, Korea, 11–15 March 2007; pp. 448–452. [Google Scholar]
- Zhu, Y.; Ting, K.M.; Zhou, Z.H. Multi-label learning with emerging new labels. IEEE Trans. Knowl. Data Eng. 2018, 30, 1901–1914. [Google Scholar] [CrossRef]
- Cejnek, M.; Bukovsky, I. Concept drift robust adaptive novelty detection for data streams. Neurocomputing 2018, 309, 46–53. [Google Scholar] [CrossRef]
- Miri Rostami, S.; Ahmadzadeh, M. Extracting predictor variables to construct breast cancer survivability model with class imbalance problem. J. AI Data Min. 2018, 6, 263–274. [Google Scholar]
- Fiore, U.; De Santis, A.; Perla, F.; Zanetti, P.; Palmieri, F. Using generative adversarial networks for improving classification effectiveness in credit card fraud detection. Inf. Sci. 2017, 479, 448–455. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection. ACM Comput. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Flexer, A.; Pampalk, E.; Widmer, G. Novelty detection based on spectral similarity of songs. In Proceedings of the 6th International Conference on Music Information Retrieval, London, UK, 11–15 September 2005; pp. 260–263. [Google Scholar]
- Putra, B.C.; Setiyono, B.; Sulistyaningrum, D.R.; Soetrisno; Mukhlash, I. Moving vehicle classification using pixel quantity based on Gaussian Mixture Models. In Proceedings of the 3rd International Conference on Computer and Communication Systems (ICCCS), Nagoya, Japan, 27–30 April 2018; pp. 254–257. [Google Scholar]
- Li, Z.; Liu, L.; Kong, D. Virtual machine failure prediction method based on AdaBoost-Hidden Markov Model. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019; pp. 700–703. [Google Scholar]
- Jo, T. String vector based KNN for text categorization. In Proceedings of the 20th International Conference on Advanced Communication Technology (ICACT), ChunCheon, Korea, 11–14 February 2018; p. 1. [Google Scholar]
- Mandhare, H.C.; Idate, S.R. A comparative study of cluster based outlier detection, distance based outlier detection and density based outlier detection techniques. In Proceedings of the 2017 International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 15–16 June 2017; pp. 931–935. [Google Scholar]
- Zhang, J.; Wang, H. Detecting outlying subspaces for high-dimensional data: The new task, and performance. Knowl. Inf. Syst. 2006, 10, 333–355. [Google Scholar] [CrossRef]
- Zhang, J. An efficient density-based clustering algorithm for the capacitated vehicle routing problem. In Proceedings of the International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 23–25 September 2017; pp. 465–469. [Google Scholar]
- Atkinson, H.V.; Gill, S.P.A. Modelling creep in nickel alloys in high temperature power plants. In Structural Alloys for Power Plants; Shirzadi, A., Jackson, S., Eds.; Woodhead Publishing: Cambridge, UK, 2014; pp. 447–478. [Google Scholar]
- Agarwal, K.; Pan, L.; Chen, X. Subspace-based optimization method for reconstruction of 2-D complex anisotropic dielectric objects. IEEE Trans. Microw. Theory Tech. 2010, 58, 1065–1074. [Google Scholar] [CrossRef]
- Zhao, F.; Li, P.; Li, Y.; Li, Y. The Li-ion battery State of charge prediction of electric vehicle using deep neural network. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 773–777. [Google Scholar]
- Chen, X. Subspace-based optimization method for solving inverse-scattering problems. IEEE Trans. Geosci. Remote Sens. 2010, 48, 42–49. [Google Scholar] [CrossRef]
- Marchi, E.; Vesperini, F.; Weninger, F.; Eyben, F.; Squartini, S.; Schuller, B. Non-linear prediction with LSTM recurrent neural networks for acoustic novelty detection. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 11–16 July 2015; pp. 1–7. [Google Scholar]
- Patel, V.M.; Chellappa, R.; Chandra, D.; Barbello, B. Continuous user authentication on mobile devices: Recent progress and remaining challenges. IEEE Signal Process. Mag. 2016, 33, 49–61. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, Q.; Wu, G.; Xu, Y.; Shibasaki, R.; Shao, X. Village building identification based on ensemble convolutional neural networks. Sensors 2017, 17, 2487. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Heras, J.A.; Donati, A. Novelty detection with deep learning. In Proceedings of the SpaceOps Conference, Marseilles, France, 28 May–1 June 2018; pp. 1–6. [Google Scholar]
- Mayrose, I.; Friedman, N.; Pupko, T. A gamma mixture model better accounts for among site rate heterogeneity. Bioinformatics 2005, 21, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, A.; Tanner, M. Modelling nonlinear count time series with local mixtures of Poisson autoregressions. Comput. Stat. Data Anal. 2007, 51, 5266–5294. [Google Scholar] [CrossRef]
- Svensén, M.; Bishop, C. Robust Bayesian mixture modelling. Neurocomputing 2005, 64, 235–252. [Google Scholar] [CrossRef]
- Fink, O.; Zio, E.; Weidmann, U. Novelty detection by multivariate kernel density estimation and growing neural gas algorithm. Mech. Syst. Signal Process. 2015, 50–51, 427–436. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Eddy, S. What is a hidden Markov model? Nat. Biotechnol. 2004, 22, 1315–1316. [Google Scholar] [CrossRef] [PubMed]
- Kruegel, C.; Vigna, G. Anomaly detection of web-based attacks. In Proceedings of the 10th ACM conference on Computer and communications security (CCS), Washington, DC, USA, 27–30 October 2003; pp. 251–261. [Google Scholar]
- Kruegel, C.; Mutz, D.; Robertson, W.; Valeur, F. Bayesian event classification for intrusion detection. In Proceedings of the 19th Annual Computer Security Applications Conference, Las Vegas, NV, USA, 8–12 December 2003; pp. 14–23. [Google Scholar]
- Mahoney, M.; Chan, P. Learning nonstationary models of normal network traffic for detecting novel attacks. In Proceedings of the 8th ACM International Conference on Knowledge Discovery and Data Mining (SIGKDD), Edmonton, AB, Canada, 23–26 July 2002; pp. 376–385. [Google Scholar]
- Lee, C.; Woo, S.; Rim, J. Parzen density estimator for complex pattern classification and high dimensional data analysis. In Proceedings of the 9th International Conference on Information, Intelligence, Systems and Applications (IISA), Zakynthos, Greece, 23–25 July 2018; pp. 1–5. [Google Scholar]
- Yeung, D.; Chow, C. Parzen-window network intrusion detectors. In Proceedings of the 16th International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002; pp. 385–388. [Google Scholar]
- Bishop, C. Novelty detection and neural network validation. In Proceedings of the IEEE Conference on Vision, Image and Signal Processing, Adelaide, SA, Australia, 19–22 April 1994; Volume 141, pp. 217–222. [Google Scholar]
- Tarassenko, L.; Hayton, P.; Cerneaz, N.; Brady, M. Novelty detection for the identification of masses in mammograms. In Proceedings of the 4th International Conference on Artificial Neural Networks, Cambridge, UK, 26–28 June 1995; pp. 442–447. [Google Scholar]
- Angiulli, F.; Pizzuti, C. Fast outlier detection in high dimensional spaces. In Proceedings of the 6th European Conference on Principles of Data Mining and Knowledge Discovery (PKDD), Helsinki, Finland, 19–23 August 2002; pp. 15–26. [Google Scholar]
- Bay, S.; Schwabacher, M. Mining distance-based outliers in near linear time with randomization and a simple pruning rule. In Proceedings of the 9th ACM International Conference on Knowledge Discovery and Data Mining (SIGKDD), Washington, DC, USA, 24–2 August 2003; pp. 29–38. [Google Scholar]
- Budalakoti, S.; Srivastava, A.; Akella, R.; Turkov, E. Anomaly Detection in Large Sets of High-Dimensional Symbol Sequences; Technical Report, NASATM-2006-214553; NASA Ames Research Center: Moffett Field, CA, USA, 2006. [Google Scholar]
- Clifton, D.; Bannister, P.; Tarassenko, L. A framework for novelty detection in jet engine vibration data. Key Eng. Mater. 2007, 347, 305–310. [Google Scholar] [CrossRef]
- Kumar, N.; Kaur, S. Distance based angular clustering algorithm (DACA) for heterogeneous wireless sensor networks. In Proceedings of the 2016 Symposium on Colossal Data Analysis and Networking (CDAN), Indore, Madhya Pradesh, India, 18–19 March 2016; pp. 1–5. [Google Scholar]
- Soylemez, O.F.; Ergen, B.; Soylemez, N.H. A 3D facial expression recognition system based on SVM classifier using distance based features. In Proceedings of the 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 15–18 May 2017; pp. 1–3. [Google Scholar]
- García-Rodríguez, J.; Angelopoulou, A.; García-Chamizo, J.; Psarrou, A.; Orts Escolano, S.; Morell Giménez, V. Autonomous growing neural gas for applications with time constraint: Optimal parameter estimation. Neural Netw. 2012, 32, 196–208. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 32, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In International Conference on Information Processing in Medical Imaging; Springer: Cham, Switzerland, 2017; pp. 146–157. [Google Scholar]
- Doersch, C. Tutorial on variational autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Pang, G.; Shen, C.; van den Hengel, A. Deep anomaly detection with deviation networks. KDD 2019, 353–362. [Google Scholar]
- Pang, G.; van den Hengel, A.; Shen, C.; Cao, L. Deep reinforcement learning for unknown anomaly detection. arXiv 2020, arXiv:2009.06847. [Google Scholar]
- Pang, G.; Yan, C.; Shen, C.; van den Hengel, A.; Bai, X. Self-trained deep ordinal regression for end-to-end video anomaly detection. arXiv 2020, arXiv:2003.06780. [Google Scholar]
- Moya, M.M.; Koch, M.W.; Hostetler, L.D. One-Class Classifier Networks for Target Recognition Applications; Technical Report; Sandia National Labs.: Albuquerque, NM, USA, 1993. [Google Scholar]
- Masud, M.M.; Chen, Q.; Khan, L.; Aggarwal, C.C.; Gao, J.; Han, J.; Thuraisingham, B.M. Addressing concept evolution in concept-drifting data streams. In Proceedings of the 10th IEEE International Conference on Data Mining (ICDM), Sydney, Australia, 14–17 December 2010; pp. 929–934. [Google Scholar]
- Masud, M.M.; Gao, J.; Khan, L.; Han, J.; Thuraisingham, B.M. Classification and novel class detection in concept-drifting data streams under time constraints. IEEE Trans. Knowl. Data Eng. 2011, 23, 859–874. [Google Scholar] [CrossRef]
- Al-Khateeb, T.; Masud, M.M.; Khan, L.; Aggarwal, C.; Han, J.; Thuraisingham, B.M. Stream classification with recurring and novel class detection using class-based ensemble. In Proceedings of the IEEE 12th International Conference on Data Mining (ICDM), Brussels, Belgium, 10–13 December 2012; pp. 31–40. [Google Scholar]
- Pal, N.R.; Pal, K.; Bezdek, J.C. A mixed C-means clustering model. In Proceedings of the IEEE 6th International Fuzzy Systems Conference, Barcelona, Spain, 1–5 July 1997; pp. 11–21. [Google Scholar]
- Bezdek, J.C. Pattern Recognition With Fuzzy Objective Function Algorithms; Plenum: New York, NY, USA, 1981. [Google Scholar]
- Krishnapuram, R.; Keller, J. A possibilistic approach to clustering. IEEE Trans. Fuzzy Syst. 1993, 1, 98–110. [Google Scholar] [CrossRef]
- Silva, T.P.; Schick, L.; Lopes, P.A.; Camargo, H.A. A fuzzy multiclass novelty detector for data streams. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Campello, R.J.; Hruschka, E.R. A fuzzy extension of the silhouette width criterion for cluster analysis. Fuzzy Sets Syst. 2006, 157, 2858–2875. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. LSHADE algorithm with rank-based selective pressure strategy for solving CEC 2017 benchmark problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. Selective pressure strategy in differential evolution: Exploitation improvement in solving global optimization problems. Swarm Evol. Comput. 2019, 50, 100463. [Google Scholar] [CrossRef]
- Sallam, K.M.; Elsayed, S.; Chakrabortty, R.K.; Ryan, M. Improved multi-operator differential evolution algorithm for solving unconstrained problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Brest, J.; Maucec, M.S.; Boskovic, B. Single objective real-parameter optimization algorithm jSO. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; pp. 1311–1318. [Google Scholar]
- Naseri, T.S.; Gharehchopogh, F.S. A feature selection based on the farmland fertility algorithm for improved intrusion detection systems. J. Netw. Syst. Manag. 2022, 30, 40. [Google Scholar] [CrossRef]
- Samadi Bonab, M.; Ghaffari, A.; Soleimanian Gharehchopogh, F.; Alemi, P. A wrapper-based feature selection for improving performance of intrusion detection systems. Int. J. Commun. Syst. 2020, 33, e4434. [Google Scholar] [CrossRef]
- Data Stream Repository. (n.d.). Computational Intelligence Group. Department of Computing. Federal University of Sao Carlos. Sao Carlos, Brazil. Available online: https://github.com/CIG-UFSCar/DS_Datasets (accessed on 24 August 2022).
- Krishnapuram, R.; Keller, J. The possibilistic c-means algorithm: Insights and recommendations. IEEE Trans. Fuzzy Syst. 1996, 4, 385–393. [Google Scholar] [CrossRef]
- de Faria, E.R.; Gonçalves, I.R.; Gama, J.; Carvalho, A.C.P.L.F. Evaluation of multiclass novelty detection algorithms for data streams. IEEE Trans. Knowl. Data Eng. 1996, 27, 2961–2973. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).