Matheuristics and Column Generation for a Basic Technician Routing Problem
Abstract
1. Introduction
2. Problem Statement and Related Work
2.1. Problem Statement and Notation
2.2. Related Problems in the Literature
2.2.1. Related Vehicle Routing Problems
2.2.2. Related Technician Routing Problems
2.3. Algorithms for Solving Related Problems
2.3.1. Solving Related Vehicle Routing Problems
2.3.2. Solving Technician Routing Problems
3. MILP Compact Formulations
3.1. First MILP Formulations
3.2. Four-Index MILP Formulation with Ordinality
4. Matheuristics Based on Compact MILP Formulations
4.1. MILP Neighborhoods for Local Optimizations
4.2. Greedy Heuristics Iterating along Technicians
| Algorithm 1. Greedy FO heuristics iterating along technicians |
Input: an order to iterate among technicians, a fixing strategy Initialization:x[i][j] for each technician i following : define the following sub MILP of (1)–(8): - removing technicians after i in - and applying variable fixing strategy to technicians before i in with x[i][j] values Solve the MILP and update assignment matrix in x end for return assignment matrix in x and the solution cost |
4.3. Greedy Heuristics Iterating among Jobs
| Algorithm 2. Greedy FO heuristic iterating along jobs |
Input: - an order to iterate among jobs, - n a maximal number of jobs for the insertion, - Insert, an insertion operator defined with variable fixing strategies Initialisation:x[i][j] , jobToPlan = , while jobs are iterated following : select , the n next jobs in jobToPlan following Insert optimally the jobs from in x calling Insert remove the n first jobs in jobToPlan following end while return assignment matrix in x and the solution cost |
- K-insertion with order reoptimization: Inserting k chosen jobs in the current planning MILP and allowing reoptimizing of the order of jobs of a given technician are equivalent to considering the variable fixing procedure for all the jobs j in the current planning;
- K-insertion without order reoptimization: By fixing current orders, k chosen jobs can be inserted in the current planning MILP with the previous variable fixing procedure and applying for the jobs and technicians of the current planning;
- 1-insertion without order reoptimization: The previous strategy with special case can be iterated easily without MILP computations. Indeed, considering the best insertion of a given job in the current planning makes at most possible insertions. Checking the feasibility of a sequence of job is an earliest date scheduling that applies only for improving costs in theses possibilities.
- Sorting the jobs by increasing the number of technicians that can process job j with skill constraints;
- Sorting the jobs by increasing value of the summed time windows where the technicians can process job j;
- Random sorting of jobs can be used to derive GRASP heuristics. We note that we can hybridize deterministic and random strategies with weighted sums to derive GRASP strategies from the deterministic order.
4.4. Local Branching Insertions of Jobs
| Algorithm 3. Best local insertion constructive heuristic |
Input: - n a maximal number of jobs for the insertion, - an optional and additional fixing strategy Initialization:x[i][j] = 0, jobToPlan = , foriter from 1 to : insert optimally n jobs of jobToPlan in x remove the inserted jobs from jobToPlan end for return assignment matrix in x and the solution cost |
4.5. VND Local Search Matheuristic
4.5.1. General Algorithm
| Algorithm 4. VND with MILP neighborhoods |
Input: an initial solutions, a set and order of neighborhoods to explore Initialization:currentSol = initSolution, initial neighborhood. while the stopping criterion is not met define the MILP with incumbent currentSol and the neighborhood ) define currentSol as warmstart currentSol = solveMILP(MILP,timeLimit( )) nextNeighborhood end while return CurrentSolution |
4.5.2. MILP Neighborhoods
- : For a given technician i, the neighborhood reoptimizes the routing of technician i considering any job j, even those that were planned in other routes. In other words, and are applied on the current solution x for all and for all .
- : For a given pair of technicians , the neighborhood reoptimizes only the routing of technicians i and considering only the jobs j planned in the current solution for i and and the jobs that are not assigned. In other words, the planning of the other technicians is not changed, and and are applied on the current solution x for all and for all .
- : For J a subset of jobs, planning is reoptimized fixing the assignments and the order of the jobs in . In other words, and are applied on the current solution x for all i and for all .
4.5.3. Sequence of MILP Neighborhoods
4.6. Parallel Heuristics
5. Dantzig–Wolfe Reformulation and CG Matheuristics
5.1. Extended Formulation and Column Generation
| Algorithm 5. Standard column generation algorithm |
Input: set of initial columns. do: solve RMP (31) with columns defined in store dual variables and and optimal cost from (31) for each technician : solve (35) to optimality with last values if then add the optimal column to end for while: columns are added in return the last cost of the RMP (31) |
5.2. POPMUSIC-CG Decomposition
| Algorithm 6. POPMUSIC column generation algorithm |
Input: set of initial columns. do: solve RMP (31) with columns defined in store dual variables and and optimal cost from (31) compute a partition of in small subsets for each subset : solve (36) with a matheuristic with last values for each column c with a negative reduced cost add the column to end for end for while: columns are added in return the last cost of the RMP (31) and updated set of columns |
5.3. Solving CG Sub-Problems
| Algorithm 7. Diversification of sub-problem solutions |
Input: - a subset of technician. - s a cyclic permutation of with order. - the dual variables of the last RMP computation. Initialization:, the columns to add in the RMP for each technician : Let , for to : solve (35) for technician with values and the remaining jobs in if the solution induces a column with a negative reduced cost add the column in remove the jobs of the column in end for: end for return |
5.4. How to Select Partitions of Sub-Problems?
5.4.1. Formulation as Clustering Problems
5.4.2. MILP Formulation with Two Technician by Cluster
5.4.3. Dealing with Heterogeneity of Sub-Problems
5.4.4. Related ML Techniques for Decomposition in Mathematical Programming
5.5. Tabu Search Intensification
| Algorithm 8. Tabu search intensification |
Input: - a subset of technicians - the current value in the RMP of dual variables - a set of initial columns with a negative reduced cost in (35) - an integer , a maximal number of TS iterations - an integer , a maximal number of assignment modifications TSintensification //Initialization: MILP, a MILP formulation for (35) related to technician i initial columns Taboo list of columns an integer to denote iterations //Loop to generate columns with negative reduced costs do: Add constraint (43) in MILP with columns of p Add constraint (42) in MILP with columns of p solve MILP remove constraint (43) in MILP with columns of p update p, the optimal columns in the last MIP update l adding the columns of p with a negative reduced cost in l while and ReducedCost returnl // the list of columns to add in the next RMP |
5.6. Dual Bounds Derived from CG
5.7. Primal CG Heuristics
- LAG_HEUR(): The continuous assignments implied by continuous relaxation of RMP can be repaired to obtain primal solutions, similarly with Lagrangian heuristics (the equivalence between CG iterations and Lagrangian relaxation is shown in previous section). Variable fixing strategies, fixing assignments with values 0 and/or 1, can be a first strategy. Once variables are fixed, straightforward B&B search or specific heuristics may apply in order to quickly obtain solutions;
- LAG_RINS(): RMP_INT_HEUR() and LAG_HEUR() can be combined in LAG_RINS(), a RINS lagrangian heuristic fixing common values in the continuous assignments and in the assignments of the primal solution given by RMP_INT_HEUR(). With such an approach, the initial solution from RMP_INT_HEUR() is still feasible for the RINS optimization for a better warmstarting of the Branch& Bound search or heuristics setting this initial solution.
5.8. Management of the CG Pool
5.9. Using Parallel Computing and a Many-Core Environment
6. Computational Results
6.1. Instance Characteristics, Benchmarks and Analysis Methodology
6.1.1. Instance Characteristics
6.1.2. Analysis Methodology
- Dataset with minimal speed () and maximal number of competences ;
- Dataset with maximal speed () and maximal number of competences ;
- Dataset with minimal speed () and no skill constraint ();
- Dataset with maximal speed () and no skill constraint ().
- Fail: The number of instances where the maximal number of jobs is not scheduled;
- BKS: The number of instances where the Best Known Solution (BKS) is reached;
- Mean: The average gap for all the considered instances of the primal solution to the BKS;
- : The standard deviation of the gaps between primal solution and BKS;
- Min: The minimum gaps between primal solution and BKS for all instances;
- Q1: The first quartile of the gaps between primal solutions and BKS;
- Med: The median (or second quartile) of the gaps between primal solutions and BKS;
- Q3: The third quartile of the gaps between primal solutions and BKS;
- Max: The maximum gaps between primal solution and BKS for all instances.
6.1.3. Implementation and Characteristics of MILP Solving
6.1.4. LocalSolver
6.1.5. Solving MILP Compact Formulations
6.2. MILP Formulations Results
6.2.1. Solving CG Sub-Problems
6.2.2. Results with Extended DW Reformulation
6.3. Results with Constructive Matheuristics
6.3.1. Constructive Matheuristics Iterating Technician by Technician
6.3.2. Constructive Matheuristics Iterating by Buckets of Jobs
6.3.3. CG Heuristics
6.4. Results with MILP-VND Local Search
6.5. Stabilization of CG Algorithm
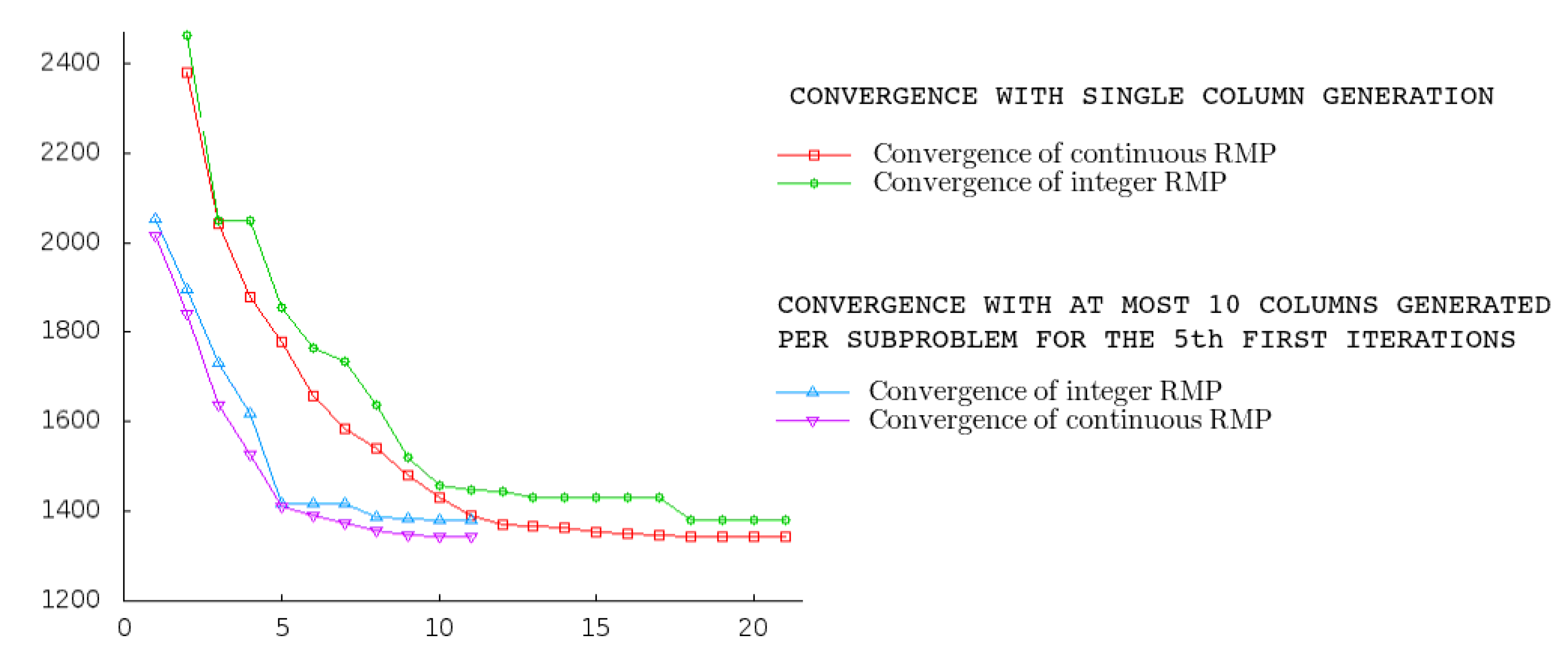
6.5.1. Impact of CG Initialization and Multi-Column Generation per Sub-Problem
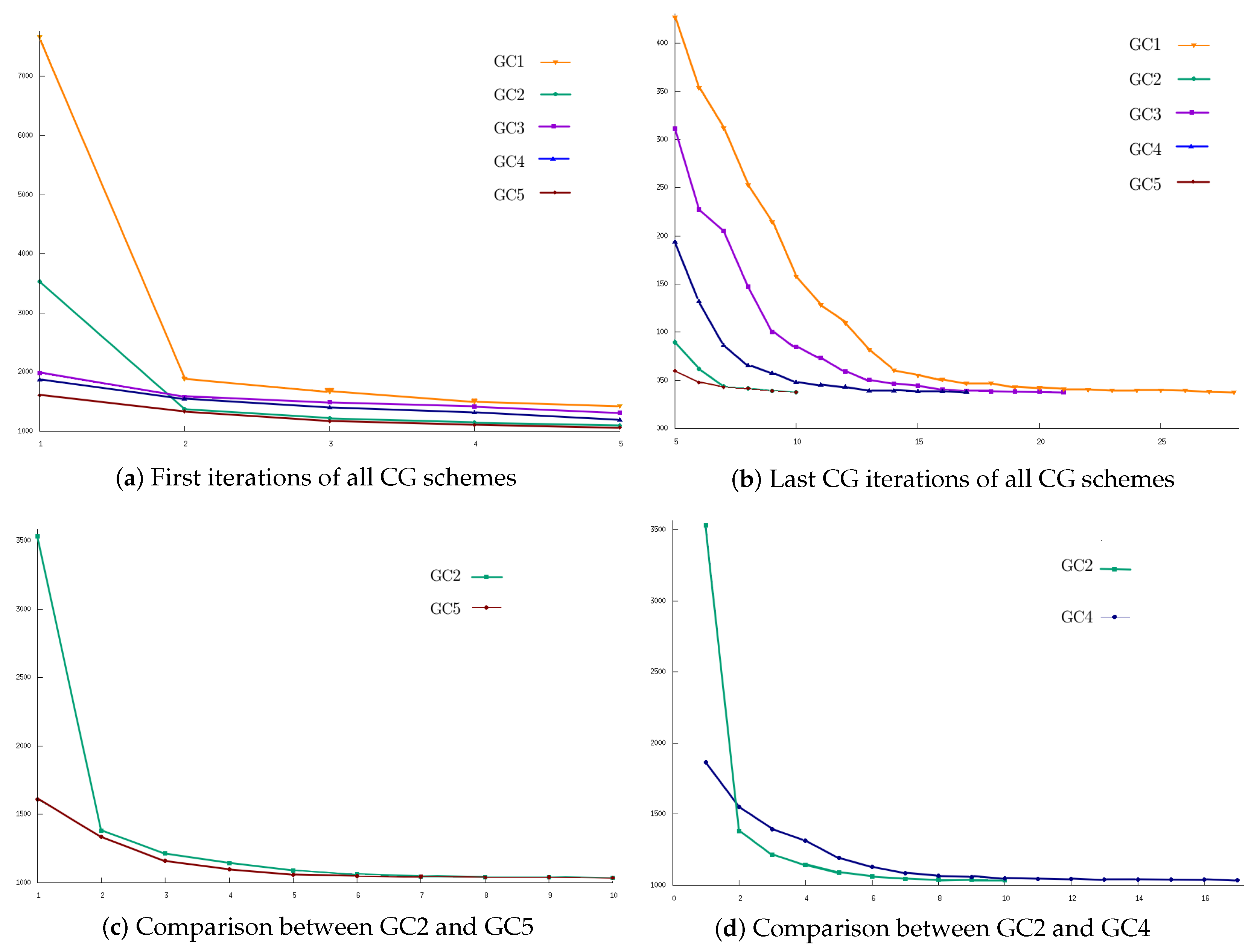
6.5.2. Impact of the Different CG Schemes and Stabilization Operators
- CG1: This is the standard CG scheme, as written in Algorithm 5;
- CG2: The standard CG scheme is followed by TS intensification to solve single technician sub-problems. It corresponds to Algorithm 8 with only partitions into singletons, with parameters and ;
- CG3: This is the POPMUSIC CG scheme without TS intensification, where sub-problems (36) are solved only using exact computations;
- CG4: This is the POPMUSIC CG scheme without TS intensification, where the sub-problems (36) are solved twice: Algorithm 7 provides the first solutions in a hierarchical manner, and a second phase optimizes the worst reduced cost (and, thus, balances the reduced costs) with a VND local search matheuristic, generating all the columns with a negatively reduced cost obtained from these two phases.
- CG5: This corresponds to the strategy CG4 with TS intensification activated with and .
7. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williams, H.P. Model Building in Mathematical Programming; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Blum, C.; Puchinger, J.; Raidl, G.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
- Jourdan, L.; Basseur, M.; Talbi, E.G. Hybridizing exact methods and metaheuristics: A taxonomy. Eur. J. Oper. Res. 2009, 199, 620–629. [Google Scholar] [CrossRef]
- Dupin, N.; Talbi, E. Matheuristics to optimize refueling and maintenance planning of nuclear power plants. J. Heuristics 2021, 27, 63–105. [Google Scholar] [CrossRef]
- Dupin, N.; Talbi, E. Parallel matheuristics for the discrete unit commitment problem with min-stop ramping constraints. Int. Trans. Oper. Res. 2020, 27, 219–244. [Google Scholar] [CrossRef]
- Talbi, E. Combining metaheuristics with mathematical programming, constraint programming and machine learning. Ann. Oper. Res. 2016, 240, 171–215. [Google Scholar] [CrossRef]
- Peschiera, F.; Dell, R.; Royset, J.; Haït, A.; Dupin, N.; Battaïa, O. A novel solution approach with ML-based pseudo-cuts for the Flight and Maintenance Planning problem. Spectr. 2021, 43, 635–664. [Google Scholar] [CrossRef]
- Riedler, M.; Jatschka, T.; Maschler, J.; Raidl, G. An iterative time-bucket refinement algorithm for a high-resolution resource-constrained project scheduling problem. Int. Trans. Oper. Res. 2020, 27, 573–613. [Google Scholar] [CrossRef]
- Dupin, N.; Talbi, E. Machine learning-guided dual heuristics and new lower bounds for the refueling and maintenance planning problem of nuclear power plants. Algorithms 2020, 13, 185. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014; Volume 18. [Google Scholar]
- Feillet, D. A tutorial on column generation and branch-and-price for vehicle routing problems. 4OR Q. J. Oper. Res. 2010, 8, 407–424. [Google Scholar] [CrossRef]
- Pessoa, A.; Sadykov, R.; Uchoa, E.; Vanderbeck, F. A generic exact solver for vehicle routing and related problems. Math. Program. 2020, 183, 483–523. [Google Scholar] [CrossRef]
- Danna, E.; Le Pape, C. Branch-and-price heuristics: A case study on the vehicle routing problem with time windows. In Column Generation; Springer: Berlin/Heidelberg, Germany, 2005; Volume 18, pp. 99–129. [Google Scholar]
- Doerner, K.F.; Schmid, V. Survey: Matheuristics for rich vehicle routing problems. In International Workshop on Hybrid Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 206–221. [Google Scholar]
- Archetti, C.; Speranza, M.G. A survey on matheuristics for routing problems. EURO J. Comput. Optim. 2014, 2, 223–246. [Google Scholar] [CrossRef]
- Furian, N.; O’Sullivan, M.; Walker, C.; Çela, E. A machine learning-based branch and price algorithm for a sampled vehicle routing problem. OR Spectrum 2021, 43, 693–732. [Google Scholar] [CrossRef]
- Morabit, M.; Desaulniers, G.; Lodi, A. Machine-Learning-Based Column Selection for Column Generation. Transp. Sci. 2021, 5, 815–831. [Google Scholar] [CrossRef]
- Dutot, P.F.; Laugier, A.; Bustos, A.M. Technicians and Interventions Scheduling for Telecommunications; Technical Report for France Telecom R&D: Paris, French, 2006. [Google Scholar]
- Gromicho, J.; van’t Hof, P.; Vigo, D. The VeRoLog verolog solver challenge 2019. J. Veh. Rout. Algorithms 2019, 2, 109–111. [Google Scholar] [CrossRef][Green Version]
- Cordeau, J.F.; Laporte, G.; Mercier, A. A unified tabu search heuristic for vehicle routing problems with time windows. J. Oper. Res. Soc. 2001, 52, 928–936. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G. A tabu search algorithm for the site dependent vehicle routing problem with time windows. INFOR Inf. Syst. Oper. Res. 2001, 39, 292–298. [Google Scholar] [CrossRef]
- Polacek, M.; Hartl, R.F.; Doerner, K.; Reimann, M. A variable neighborhood search for the multi depot vehicle routing problem with time windows. J. Heuristics 2004, 10, 613–627. [Google Scholar] [CrossRef]
- Feillet, D.; Dejax, P.; Gendreau, M.; Gueguen, C. An exact algorithm for the elementary shortest path problem with resource constraints: Application to some vehicle routing problems. Networks 2004, 44, 216–229. [Google Scholar] [CrossRef]
- Cappanera, P.; Gouveia, L.; Scutellà, M.G. Models and valid inequalities to asymmetric skill-based routing problems. EURO J. Transp. Logist. 2013, 2, 29–55. [Google Scholar] [CrossRef][Green Version]
- Cappanera, P.; Requejo, C.; Scutellà, M.G. Temporal constraints and device management for the Skill VRP: Mathematical model and lower bounding techniques. Comput. Oper. Res. 2020, 124, 105054. [Google Scholar] [CrossRef]
- Pessoa, A.; Sadykov, R.; Uchoa, E. Enhanced Branch-Cut-and-Price algorithm for heterogeneous fleet vehicle routing problems. Eur. J. Oper. Res. 2018, 270, 530–543. [Google Scholar] [CrossRef]
- Schwarze, S.; Voß, S. Improved load balancing and resource utilization for the skill vehicle routing problem. Optim. Lett. 2013, 7, 1805–1823. [Google Scholar] [CrossRef]
- Schwarze, S.; Voß, S. A bicriteria skill vehicle routing problem with time windows and an application to pushback operations at airports. In Logistics Management; Springer: Berlin/Heidelberg, Germany, 2015; pp. 289–300. [Google Scholar]
- Yan, X.; Xiao, B.; Xiao, Y.; Zhao, Z.; Ma, L.; Wang, N. Skill vehicle routing problem with time windows considering dynamic service times and time-skill-dependent costs. IEEE Access 2019, 7, 77208–77221. [Google Scholar] [CrossRef]
- Castillo-Salazar, J. and Landa-Silva, D.; Qu, R. Workforce scheduling and routing problems: Literature survey and computational study. Ann. Oper. Res. 2016, 239, 39–67. [Google Scholar] [CrossRef]
- Kovacs, A.; Parragh, S.; Doerner, K.; Hartl, R. Adaptive large neighborhood search for service technician routing and scheduling problems. J. Sched. 2012, 15, 579–600. [Google Scholar] [CrossRef]
- Xie, F.; Potts, C.; Bektaş, T. Iterated local search for workforce scheduling and routing problems. J. Heuristics 2017, 23, 471–500. [Google Scholar] [CrossRef]
- Pillac, V.; Gueret, C.; Medaglia, A. A parallel matheuristic for the technician routing and scheduling problem. Optim. Lett. 2013, 7, 1525–1535. [Google Scholar] [CrossRef]
- Mendoza, J.; Montoya, A.; Guéret, C.; Villegas, J. A parallel matheuristic for the technician routing problem with conventional and electric vehicles. In Proceedings of the 12th Metaheuristics International Conference, Municipality of Las Palmas, Spain, 19–24 February 2017. [Google Scholar]
- Chen, X.; Thomas, B.W.; Hewitt, M. The technician routing problem with experience-based service times. Omega 2016, 61, 49–61. [Google Scholar] [CrossRef]
- Pillac, V.; Guéret, C.; Medaglia, A. A fast reoptimization approach for the dynamic technician routing and scheduling problem. In Recent Developments in Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 347–367. [Google Scholar]
- Anoshkina, Y.; Meisel, F. Interday routing and scheduling of multi-skilled teams with consistency consideration and intraday rescheduling. EURO J. Transp. Logist. 2020, 9, 100012. [Google Scholar] [CrossRef]
- Bley, A.; Karch, D.; D’Andreagiovanni, F. WDM fiber replacement scheduling. Electron. Notes Discret. Math. 2013, 41, 189–196. [Google Scholar] [CrossRef]
- Pugliese, L.; Guerriero, F. A survey of resource constrained shortest path problems: Exact solution approaches. Networks 2013, 62, 183–200. [Google Scholar] [CrossRef]
- Sadykov, R.; Uchoa, E.; Pessoa, A. A bucket graph—Based labeling algorithm with application to vehicle routing. Transp. Sci. 2021, 55, 4–28. [Google Scholar] [CrossRef]
- Baldacci, R.; Battarra, M.; Vigo, D. Routing a heterogeneous fleet of vehicles. In The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–27. [Google Scholar]
- Baldacci, R.; Mingozzi, A. A unified exact method for solving different classes of vehicle routing problems. Math. Program. 2009, 120, 347. [Google Scholar] [CrossRef]
- Bettinelli, A.; Ceselli, A.; Righini, G. A branch-and-cut-and-price algorithm for the multi-depot heterogeneous vehicle routing problem with time windows. Transp. Res. Part C Emerg. Technol. 2011, 19, 723–740. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.Y.; Bräysy, O.; Hasle, G.; Løkketangen, A. Metaheuristics for the vehicle routing problem and its extensions: A categorized bibliography. In The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: Berlin/Heidelberg, Germany, 2008; pp. 143–169. [Google Scholar]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.; Gendreau, M.; Prins, C. A hybrid genetic algorithm with adaptive diversity management for a large class of vehicle routing problems with time-windows. Comput. Oper. Res. 2013, 40, 475–489. [Google Scholar] [CrossRef]
- Rizzoli, A.; Montemanni, R.; Lucibello, E.; Gambardella, L. Ant colony optimization for real-world vehicle routing problems. Swarm Intell. 2007, 1, 135–151. [Google Scholar] [CrossRef]
- Hurkens, C. Incorporating the strength of MIP modeling in schedule construction. RAIRO-Oper. Res. 2009, 43, 409–420. [Google Scholar] [CrossRef]
- Mancini, S. A real-life multi depot multi period vehicle routing problem with a heterogeneous fleet: Formulation and adaptive large neighborhood search based matheuristic. Transp. Res. Part C Emerg. Technol. 2016, 70, 100–112. [Google Scholar] [CrossRef]
- Taillard, E. A heuristic column generation method for the heterogeneous fleet VRP. RAIRO Oper. Res. 1999, 33, 1–14. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.; Gendreau, M.; Prins, C. A unified solution framework for multi-attribute vehicle routing problems. Eur. J. Oper. Res. 2014, 234, 658–673. [Google Scholar] [CrossRef]
- Pekel, E. Solving technician routing and scheduling problem using improved particle swarm optimization. Soft Comput. 2020, 24, 19007–19015. [Google Scholar] [CrossRef]
- Pereira, D.; Alves, J.; de Oliveira Moreira, M. A multiperiod workforce scheduling and routing problem with dependent tasks. Comput. Oper. Res. 2020, 118, 104930. [Google Scholar] [CrossRef]
- Cortés, C.E.; Gendreau, M.; Rousseau, L.; Souyris, S.; Weintraub, A. Branch-and-price and constraint programming for solving a real-life technician dispatching problem. Eur. J. Oper. Res. 2014, 238, 300–312. [Google Scholar] [CrossRef]
- Zamorano, E.; Stolletz, R. Branch-and-price approaches for the multiperiod technician routing and scheduling problem. Eur. J. Oper. Res. 2017, 257, 55–68. [Google Scholar] [CrossRef]
- Mathlouthi, I.; Gendreau, M.; Potvin, J. Branch-and-price for a multi-attribute technician routing and scheduling problem. SN Oper. Res. Forum 2021, 2, 1–35. [Google Scholar] [CrossRef]
- Penna, P.; Subramanian, A.; Ochi, L.S.; Vidal, T.; Prins, C. A hybrid heuristic for a broad class of vehicle routing problems with heterogeneous fleet. Ann. Oper. Res. 2019, 273, 5–74. [Google Scholar] [CrossRef]
- Graf, B. Adaptive large variable neighborhood search for a multiperiod vehicle and technician routing problem. Networks 2020, 76, 256–272. [Google Scholar] [CrossRef]
- Jagtenberg, C.; Maclaren, O.; Mason, A.; Raith, A.; Shen, K.; Sundvick, M. Columnwise neighborhood search: A novel set partitioning matheuristic and its application to the VeRoLog Solver Challenge 2019. Networks 2020, 76, 273–293. [Google Scholar] [CrossRef]
- Kheiri, A.; Ahmed, L.; Boyacı, B.; Gromicho, J.; Mumford, C.; Özcan, E.; Dirikoç, A. Exact and hyper-heuristic solutions for the distribution-installation problem from the VeRoLog 2019 challenge. Networks 2020, 76, 294–319. [Google Scholar] [CrossRef]
- Kastrati, V.; Ahmeti, A.; Musliu, N. Solving Vehicle Routing and Scheduling with Delivery and Installation of Machines using ILS. In Proceedings of the 13th International Conference on the Practice and Theory of Automated Timetabling-PATAT, Bruges, Belgium, 24–27 August 2021; Volume 1. [Google Scholar]
- Fırat, M.; Hurkens, C. An improved MIP-based approach for a multi-skill workforce scheduling problem. J. Sched. 2012, 15, 363–380. [Google Scholar] [CrossRef]
- Pokutta, S.; Stauffer, G. France Telecom workforce scheduling problem: A challenge. RAIRO Oper. Res. 2009, 43, 375–386. [Google Scholar] [CrossRef][Green Version]
- Estellon, B.; Gardi, F.; Nouioua, K. High-Performance Local Search for Task Scheduling with Human Resource Allocation. In International Workshop on Engineering Stochastic Local Search Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–15. [Google Scholar]
- Cordeau, J.F.; Laporte, G.; Pasin, F.; Ropke, S. Scheduling technicians and tasks in a telecommunications company. J. Sched. 2010, 13, 393–409. [Google Scholar] [CrossRef]
- Hashimoto, H.; Boussier, S.; Vasquez, M.; Wilbaut, C. A GRASP-based approach for technicians and interventions scheduling for telecommunications. Ann. Oper. Res. 2011, 183, 143–161. [Google Scholar] [CrossRef]
- Ascheuer, N.; Fischetti, M.; Grötschel, M. A polyhedral study of the asymmetric traveling salesman problem with time windows. Networks 2000, 36, 69–79. [Google Scholar] [CrossRef]
- Öncan, T.; Altınel, İ.K.; Laporte, G. A comparative analysis of several asymmetric traveling salesman problem formulations. Comput. 2009, 36, 637–654. [Google Scholar] [CrossRef]
- Fox, K.; Gavish, B.; Graves, S. An n-Constraint Formulation of the (Time-Dependent) Traveling Salesman Problem. Oper. Res. 1980, 28, 1018–1021. [Google Scholar] [CrossRef]
- Lindahl, M.; Sørensen, M.; Stidsen, T. A fix-and-optimize matheuristic for university timetabling. J. Heuristics 2018, 24, 645–665. [Google Scholar] [CrossRef]
- Fischetti, M.; Lodi, A. Local branching. Math Program. 2003, 98, 23–47. [Google Scholar] [CrossRef]
- Taillard, É.; Voss, S. POPMUSIC-Partial optimization metaheuristic under special intensification conditions. In Essays and Surveys in Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 613–629. [Google Scholar]
- Mancini, S. A combined multistart random constructive heuristic and set partitioning based formulation for the vehicle routing problem with time dependent travel time. Comput. Oper. Res. 2017, 88, 290–296. [Google Scholar] [CrossRef]
- Queiroga, E.; Sadykov, R.; Uchoa, E. A POPMUSIC matheuristic for the capacitated vehicle routing problem. Comput. Oper. Res. 2021, 136, 105475. [Google Scholar] [CrossRef]
- Du Merle, O.; Villeneuve, D.; Desrosiers, J.; Hansen, P. Stabilized column generation. Discret. Math. 1999, 94, 229–237. [Google Scholar] [CrossRef]
- Lazic, J.; Hanafi, S.; Mladenovic, N.; Urozevic, D. Variable Neighbourhood Decomposition Search for 0-1 Mixed Integer Programs. Comput. Oper. Res. 2010, 37, 1055–1067. [Google Scholar] [CrossRef]
- Desaulniers, G.; Lessard, F.; Hadjar, A. Tabu search, partial elementarity, and generalized k-path inequalities for the vehicle routing problem with time windows. Transp. Sci. 2008, 42, 387–404. [Google Scholar] [CrossRef]
- Desrosiers, J.; Lübbecke, M. A primer in column generation. In Column Generation; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–32. [Google Scholar]
- Dupin, N. Column generation for the discrete UC problem with min-stop ramping constraints. IFAC-PapersOnLine 2019, 52, 529–534. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.; Gendreau, M.; Lahrichi, N.; Rei, W. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Oper. Res. 2012, 60, 611–624. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Zuo, X. Solving multi-depot electric vehicle scheduling problem by column generation and genetic algorithm. Appl. Soft Comput. 2021, 112, 107774. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Li, K.; Lin, Z.; Yang, J.; Shen, X. A hybrid particle swarm optimization algorithm using adaptive learning strategy. Inf. Sci. 2018, 436, 162–177. [Google Scholar] [CrossRef]
- Nurcahyadi, T.; Blum, C. Adding Negative Learning to Ant Colony Optimization: A Comprehensive Study. Mathematics 2021, 9, 361. [Google Scholar] [CrossRef]
- Agra, A.; Christiansen, M.; Figueiredo, R.; Hvattum, L.; Poss, M.; Requejo, C. The robust vehicle routing problem with time windows. Comput. Oper. Res. 2013, 40, 856–866. [Google Scholar] [CrossRef]
- Jozefowiez, N.; Semet, F.; Talbi, E. Multi-objective vehicle routing problems. Eur. J. Oper. Res. 2008, 189, 293–309. [Google Scholar] [CrossRef]
- Glize, E.; Jozefowiez, N.; Ngueveu, S. An ε-constraint column generation-and-enumeration algorithm for Bi-Objective Vehicle Routing Problems. Comput. Oper. Res. 2021, 138, 105570. [Google Scholar] [CrossRef]
| I | Number of technicians (or equivalently vehicles). |
| J | Number of jobs (or equivalently customers, requests, or request location). |
| Index and set for nodes, a node is a technician depot or a job location. | |
| Index and set for customers, the jobs for the technicians. | |
| Index and set for technicians. | |
| Subset of jobs that technician can complete with skill constraints. | |
| Subset of nodes that technician can visit (depot and skill constraints). | |
| Duration (amount of time) of job . | |
| Cost penalization if job is not planned (or outsourcing cost). | |
| Upper bound for the number of jobs that technician can process. | |
| Distance from the location of node to the location of node . | |
| Transportation time from the location of node to the location of node . | |
| Working time window for technician , to leave and come back to the depot. | |
| Time window for the beginning of job . |
| (1)–(8) | (1)–(8) | (1)–(8) | (1)–(8) | (12)–(19) | (12)–(19) | (12)–(19) | (12)–(19) | (27)–(29) | |
|---|---|---|---|---|---|---|---|---|---|
| Bound | LP | nod1 | LP | nod1 | LP | nod1 | LP | nod1 | LP |
| Cuts | No | No | (10) | (10) | No | No | (21) | (21) | No |
| data_3_1_10 | 45.7% | 8.7% | 11.9% | 3.2% | 28.1% | 3.3% | 8.8% | 1.0% | 1.8% |
| data_3_5_10 | 43.4% | 0.0% | 9.7% | 0.0% | 23.4% | 0.0% | 8.0% | 0.0% | 0.0% |
| data_5_1_20 | 44.8% | 29.5% | 27.9% | 11.6% | 35.7% | 17.9% | 22.0% | 13.7% | 1.9% |
| data_5_3_20 | 52.7% | 30.3% | 30.8% | 17.7% | 39.0% | 19.9% | 22.7% | 15.5% | 0.6% |
| data_5_5_20 | 58.1% | 28.7% | 27.5% | 14.6% | 42.1% | 18.5% | 25.1% | 14.1% | 0.3% |
| data_8_1_20 | 40.5% | 20.6% | 20.8% | 10.6% | 32.6% | 10.6% | 16.8% | 7.8% | 1.3% |
| data_8_3_20 | 54.7% | 28.5% | 28.6% | 17.1% | 35.2% | 14.8% | 20.0% | 11.2% | 1.8% |
| data_8_5_20 | 60.6% | 26.7% | 25.9% | 11.2% | 39.7% | 8.1% | 21.3% | 1.6% | 0.5% |
| data_10_10_40 | 55.9% | 25.0% | 25.8% | 14.3% | 40.8% | 19.4% | 20.7% | 13.9% | 2.0% |
| data_15_10_40 | 55.6% | 18.9% | 19.6% | 10.7% | 35.8% | 11.0% | 13.4% | 6.3% | 0.6% |
| data_15_20_40 | 53.9% | 14.2% | 16.1% | 6.1% | 32.1% | 7.5% | 13.1% | 4.8% | 0.7% |
| (1)–(8) | (1)–(8) | (12)–(19) | (12)–(19) | |
|---|---|---|---|---|
| No Cuts | +(10) | No Cuts | +(21) | |
| 4_1_20_ex4 | 34.7 | 7.6 | 333.1 | 601.2 |
| 4_3_20_ex4 | 45.4 | 19.6 | 799.3 | 121.2 |
| 4_5_20_ex4 | 14.6 | 5.4 | 35.0 | 27.0 |
| 5_3_20_ex1 | 131.5 | 83.4 | >1200 | 955.5 |
| 5_3_20_ex2 | 21.3 | 24.9 | 224.8 | 86.2 |
| 5_3_20_ex3 | 34.7 | 14.4 | >1200 | 647.3 |
| 5_3_20_ex4 | 48.1 | 20.4 | 259.9 | 223.8 |
| 5_5_20_ex1 | 4.3 | 5.4 | 161.6 | 36.1 |
| 5_5_20_ex2 | 5.5 | 2.6 | 34.0 | 3.0 |
| 5_5_20_ex3 | 6.2 | 5.8 | 118.4 | 101.9 |
| 5_5_20_ex4 | 7.5 | 4.1 | 40.4 | 29.2 |
| 8_5_20_ex1 | 8.4 | 6.1 | 81.4 | 12.5 |
| 8_5_20_ex2 | 1.0 | 0.7 | 0.4 | 0.4 |
| 8_5_20_ex3 | 2.5 | 0.8 | 1.7 | 1.9 |
| 8_5_20_ex4 | 5.3 | 0.9 | 0.8 | 1.8 |
| 8_5_20_ex5 | 2.1 | 1.0 | 5.7 | 3.6 |
| 15_20_40_ex1 | 46.2 | 7.5 | 408.7 | 89.1 |
| 15_20_40_ex2 | 8.3 | 3.0 | 22.4 | 15.0 |
| 15_20_40_ex3 | 15.6 | 10.6 | 53.9 | 31.2 |
| 15_20_40_ex4 | 58.8 | 15.7 | 108.3 | 35.6 |
| 15_20_40_ex5 | 114.5 | 15.2 | 114.4 | 58.6 |
| 15_20_40_ex6 | 6.9 | 3.7 | 4.7 | 5.2 |
| 15_20_40_ex8 | 7.3 | 1.5 | 3.3 | 2.7 |
| Sort | Fix | Fail | BKS | Mean | min | Q1 | Med | Q3 | Max | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 job | nbTec | 7 | 0 | 21.54% | 11.49% | 5.48% | 12.83% | 20.72% | 28.36% | 44.57% | |
| 2 job | nbTec | 7 | 0 | 20.01% | 10.07% | 5.79% | 11.94% | 19.34% | 26.02% | 40.35% | |
| 8 job | nbTec | 5 | 0 | 16.59% | 8.27% | 2.74% | 10.90% | 16.15% | 21.26% | 34.56% | |
| 10 job | nbTec | 6 | 0 | 16.27% | 8.55% | 3.89% | 10.80% | 14.89% | 19.51% | 36.64% | |
| 1 job | timeJob | 2 | 0 | 28.61% | 15.62% | 7.91% | 17.65% | 26.14% | 36.95% | 66.30% | |
| 2 job | timeJob | 2 | 0 | 26.04% | 13.95% | 7.24% | 17.02% | 23.44% | 32.77% | 61.49% | |
| 5 job | timeJob | 2 | 0 | 23.68% | 12.12% | 5.10% | 15.19% | 21.39% | 32.85% | 47.61% | |
| 8 job | timeJob | 2 | 0 | 19.94% | 11.23% | 3.03% | 11.32% | 19.00% | 26.81% | 44.76% | |
| 10 job | timeJob | 1 | 0 | 19.74% | 11.37% | 5.61% | 11.95% | 16.47% | 24.33% | 51.71% | |
| 1 job | nbTec | 6 | 0 | 19.58% | 9.78% | 4.68% | 12.57% | 18.94% | 26.45% | 37.34% | |
| 2 job | nbTec | 6 | 0 | 18.68% | 9.43% | 5.64% | 11.61% | 17.29% | 24.25% | 39.60% | |
| 5 job | nbTec | 3 | 0 | 6.18% | 2.80% | 1.36% | 4.24% | 5.57% | 8.48% | 11.40% | |
| 8 job | nbTec | 7 | 0 | 20.83% | 11.35% | 3.63% | 13.83% | 20.07% | 26.22% | 48.52% | |
| 10 job | nbTec | 6 | 0 | 4.69% | 1.33% | 1.90% | 4.32% | 4.87% | 5.55% | 6.65% | |
| 1 job | timeJob | 2 | 0 | 27.12% | 15.91% | 6.69% | 16.09% | 24.29% | 35.62% | 64.39% | |
| 2 job | timeJob | 2 | 0 | 24.41% | 13.12% | 6.31% | 15.40% | 21.89% | 31.12% | 57.20% | |
| 5 job | timeJob | 4 | 0 | 21.85% | 11.40% | 4.87% | 13.97% | 18.85% | 29.41% | 44.54% | |
| 8 job | timeJob | 4 | 0 | 18.04% | 10.34% | 2.96% | 10.73% | 17.21% | 23.74% | 40.87% | |
| 10 job | timeJob | 6 | 0 | 18.34% | 10.74% | 5.30% | 11.10% | 15.80% | 22.09% | 45.33% | |
| 1 tic | 10 | 0 | 55.31% | 27.98% | 24.83% | 36.67% | 48.13% | 66.72% | 123.43% | ||
| 1 tic | 10 | 0 | 54.32% | 25.52% | 25.59% | 35.88% | 49.45% | 65.79% | 116.51% | ||
| Best | Constr | 1 | 0 | 13.17% | 8.99% | 1.84% | 7.57% | 11.97% | 17.20% | 38.70% |
| Fail | Mean | min | Q1 | Med | Q3 | Max | ||
|---|---|---|---|---|---|---|---|---|
| LocalSolver 30 s | 2 | 6.05% | 4.20% | 0.85% | 2.73% | 5.06% | 8.12% | 16.04% |
| LocalSolver 60 s | 2 | 4.50% | 3.51% | 0.64% | 2.11% | 3.58% | 6.38% | 14.41% |
| LocalSolver 300 s | 2 | 1.96% | 1.96% | 0.00% | 0.45% | 1.29% | 2.69% | 7.14% |
| LocalSolver 600 s | 2 | 1.03% | 1.01% | 0.00% | 0.14% | 0.90% | 1.57% | 3.51% |
| LocalSolver 900 s | 1 | 0.94% | 1.06% | 0.00% | 0.03% | 0.40% | 1.57% | 3.51% |
| RMP_INT_HEUR | 0 | 1.07% | 1.27% | 0.00% | 0.05% | 0.63% | 1.60% | 3.90% |
| LAG_HEUR | 0 | 0.73% | 1.01% | 0.00% | 0.01% | 0.34% | 1.06% | 3.46% |
| LAG_RINS | 0 | 0.20% | 0.34% | 0.00% | 0.00% | 0.04% | 0.25% | 1.18% |
| LAG_RINS+VND | 0 | 0.10% | 0.26% | 0.00% | 0.00% | 0.00% | 0.06% | 0.97% |
| 5 job,nbTec+VND | 0 | 1.90% | 2.29% | 0.00% | 0.23% | 0.92% | 2.80% | 7.31% |
| 5 job,timeJob+VND | 0 | 2.03% | 2.34% | 0.00% | 0.25% | 1.09% | 3.16% | 8.38% |
| 10 job,nbTec+VND | 0 | 2.38% | 2.67% | 0.00% | 0.51% | 1.57% | 3.47% | 10.38% |
| 10 job,timeJob+VND | 0 | 2.93% | 3.00% | 0.02% | 0.77% | 2.19% | 4.28% | 10.84% |
| init0+VND | 0 | 3.45% | 3.76% | 0.00% | 0.82% | 2.49% | 5.09% | 13.82% |
| Multi-start VND | 0 | 0.70% | 1.10% | 0.00% | 0.03% | 0.19% | 0.86% | 9.23% |
| For Dataset s(the Most Constrained Instances) | |||||||||
| Fail | BKS | Mean | min | Q1 | Med | Q3 | Max | ||
| LocalSolver 30 s | 2 | 0 | 13.68% | 9.93% | 2.43% | 6.47% | 10.78% | 19.09% | 35.86% |
| LocalSolver 60 s | 2 | 0 | 11.24% | 9.61% | 2.31% | 3.76% | 6.99% | 19.03% | 32.18% |
| LocalSolver 300 s | 2 | 0 | 5.36% | 5.78% | 1.30% | 1.96% | 3.35% | 6.96% | 24.52% |
| LocalSolver 600 s | 2 | 0 | 3.89% | 2.63% | 0.70% | 1.91% | 3.35% | 5.06% | 8.76% |
| LocalSolver 900 s | 1 | 1 | 2.99% | 2.37% | 0.00% | 1.68% | 2.49% | 2.95% | 8.26% |
| RMP_INT_HEUR | 0 | 6 | 1.09% | 1.32% | 0.00% | 0.00% | 0.50% | 1.82% | 3.66% |
| LAG_HEUR | 0 | 7 | 0.81% | 1.10% | 0.00% | 0.00% | 0.43% | 1.07% | 3.66% |
| LAG_RINS | 0 | 8 | 0.19% | 0.29% | 0.00% | 0.00% | 0.08% | 0.29% | 1.12% |
| LAG_RINS+VND | 0 | 15 | 0.08% | 0.27% | 0.00% | 0.00% | 0.00% | 0.00% | 1.12% |
| 5 job,nbTec+VND | 0 | 3 | 2.91% | 2.84% | 0.00% | 0.49% | 2.10% | 4.71% | 9.23% |
| 5 job,timeJob+VND | 0 | 2 | 3.60% | 3.59% | 0.00% | 0.70% | 2.66% | 5.56% | 14.32% |
| 10 job,nbTec+VND | 0 | 1 | 3.34% | 3.17% | 0.00% | 1.24% | 2.84% | 4.43% | 13.53% |
| 10 job,timeJob+VND | 0 | 0 | 4.71% | 3.57% | 0.09% | 2.33% | 4.13% | 7.03% | 11.67% |
| init0+VND | 0 | 2 | 5.91% | 6.04% | 0.00% | 1.11% | 4.44% | 10.46% | 20.91% |
| Multi-start VND | 0 | 4 | 1.71% | 2.33% | 0.00% | 0.11% | 0.66% | 2.49% | 9.23% |
| For Dataset s | |||||||||
| Fail | BKS | Mean | min | Q1 | Med | Q3 | Max | ||
| LocalSolver 30 s | 0 | 0 | 7.91% | 5.36% | 1.32% | 4.97% | 7.05% | 8.56% | 24.33% |
| LocalSolver 60 s | 0 | 0 | 5.02% | 3.06% | 0.79% | 2.94% | 4.80% | 6.55% | 13.50% |
| LocalSolver 300 s | 0 | 3 | 1.85% | 1.63% | 0.00% | 0.56% | 1.30% | 2.98% | 4.62% |
| LocalSolver 600 s | 0 | 5 | 1.20% | 1.45% | 0.00% | 0.03% | 0.77% | 1.77% | 4.62% |
| LocalSolver 900 s | 0 | 5 | 0.91% | 1.09% | 0.00% | 0.03% | 0.51% | 1.24% | 3.63% |
| RMP_INT_HEUR | 0 | 5 | 1.31% | 1.78% | 0.00% | 0.03% | 0.48% | 2.03% | 5.52% |
| LAG_HEUR | 0 | 7 | 0.87% | 1.45% | 0.00% | 0.00% | 0.13% | 1.02% | 4.76% |
| LAG_RINS | 0 | 9 | 0.14% | 0.18% | 0.00% | 0.00% | 0.06% | 0.25% | 0.59% |
| LAG_RINS+VND | 0 | 16 | 0.03% | 0.08% | 0.00% | 0.00% | 0.00% | 0.00% | 0.27% |
| 5 job,nbTec+VND | 0 | 7 | 1.29% | 1.99% | 0.00% | 0.00% | 0.40% | 1.78% | 7.42% |
| 5 job,timeJob+VND | 0 | 7 | 1.29% | 1.99% | 0.00% | 0.00% | 0.40% | 1.78% | 7.42% |
| 10 job,nbTec+VND | 0 | 8 | 1.80% | 3.17% | 0.00% | 0.00% | 0.17% | 2.24% | 12.66% |
| init0+VND | 0 | 7 | 0.77% | 1.03% | 0.00% | 0.00% | 0.22% | 0.95% | 3.16% |
| Multi-start VND | 0 | 12 | 0.29% | 0.55% | 0.00% | 0.00% | 0.00% | 0.33% | 2.06% |
| For Dataset S1 (the Less Constrained Instances) | |||||||||
| Fail | BKS | Mean | min | Q1 | Med | Q3 | Max | ||
| LocalSolver 30 s | 0 | 0 | 7.78% | 5.03% | 2.56% | 3.44% | 6.65% | 11.21% | 19.30% |
| LocalSolver 60 s | 0 | 0 | 6.35% | 4.67% | 0.83% | 2.97% | 5.24% | 7.46% | 15.81% |
| LocalSolver 300 s | 0 | 3 | 2.42% | 3.05% | 0.00% | 0.13% | 0.69% | 4.62% | 9.10% |
| LocalSolver 600 s | 0 | 6 | 1.71% | 2.59% | 0.00% | 0.00% | 0.32% | 1.56% | 7.52% |
| LocalSolver 900 s | 0 | 8 | 0.83% | 1.19% | 0.00% | 0.00% | 0.13% | 1.46% | 3.72% |
| RMP_INT_HEUR | 0 | 3 | 0.86% | 0.80% | 0.00% | 0.16% | 0.79% | 1.29% | 2.21% |
| LAG_HEUR | 0 | 5 | 0.35% | 0.41% | 0.00% | 0.02% | 0.17% | 0.67% | 1.36% |
| LAG_RINS | 0 | 11 | 0.17% | 0.31% | 0.00% | 0.00% | 0.00% | 0.13% | 0.86% |
| LAG_RINS+VND | 0 | 16 | 0.07% | 0.21% | 0.00% | 0.00% | 0.00% | 0.00% | 0.86% |
| 5 job,nbTec+VND | 0 | 9 | 0.67% | 0.91% | 0.00% | 0.00% | 0.05% | 0.89% | 2.53% |
| 5 job,timeJob+VND | 0 | 9 | 0.67% | 0.91% | 0.00% | 0.00% | 0.05% | 0.89% | 2.53% |
| 10 job,nbTec+VND | 0 | 8 | 0.99% | 1.21% | 0.00% | 0.00% | 0.47% | 1.87% | 3.86% |
| init0+VND | 0 | 11 | 0.68% | 1.51% | 0.00% | 0.00% | 0.00% | 0.72% | 5.98% |
| Multi-start VND | 0 | 15 | 0.07% | 0.19% | 0.00% | 0.00% | 0.00% | 0.00% | 0.74% |
| Instance | 1 col per Sub-Problem | Multicol | Multicol + Warm Start |
|---|---|---|---|
| data_3_5_10_ex1 | 24 | 7 | 4 |
| data_3_5_10_ex2 | 13 | 5 | 7 |
| data_3_5_10_ex3 | 8 | 5 | 5 |
| data_3_5_10_ex4 | 11 | 6 | 5 |
| data_8_5_20_ex1 | 21 | 9 | 7 |
| data_8_5_20_ex2 | 11 | 9 | 7 |
| data_8_5_20_ex3 | 38 | 15 | 12 |
| data_8_5_20_ex4 | 15 | 10 | 8 |
| data_15_20_40_ex1 | 21 | 13 | 13 |
| data_15_20_40_ex2 | 19 | 11 | 9 |
| data_15_20_40_ex3 | 17 | 10 | 14 |
| data_15_20_40_ex4 | 21 | 11 | 11 |
| data_10_3_50_ex1 | 54 | 21 | 22 |
| data_15_3_50_ex1 | 32 | 26 | 18 |
| Total | 324 | 168 | 150 |
| % iterations | 100 | 51.9% | 46.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dupin, N.; Parize, R.; Talbi, E.-G. Matheuristics and Column Generation for a Basic Technician Routing Problem. Algorithms 2021, 14, 313. https://doi.org/10.3390/a14110313
Dupin N, Parize R, Talbi E-G. Matheuristics and Column Generation for a Basic Technician Routing Problem. Algorithms. 2021; 14(11):313. https://doi.org/10.3390/a14110313
Chicago/Turabian StyleDupin, Nicolas, Rémi Parize, and El-Ghazali Talbi. 2021. "Matheuristics and Column Generation for a Basic Technician Routing Problem" Algorithms 14, no. 11: 313. https://doi.org/10.3390/a14110313
APA StyleDupin, N., Parize, R., & Talbi, E.-G. (2021). Matheuristics and Column Generation for a Basic Technician Routing Problem. Algorithms, 14(11), 313. https://doi.org/10.3390/a14110313







