Abstract
A major goal in pre-detonation nuclear forensics is to infer the processing conditions and/or facility type that produced radiological material. This review paper focuses on analyses of particle size, shape, texture (“morphology”) signatures that could provide information on the provenance of interdicted materials. For example, uranium ore concentrates (UOC or yellowcake) include ammonium diuranate (ADU), ammonium uranyl carbonate (AUC), sodium diuranate (SDU), magnesium diuranate (MDU), and others, each prepared using different salts to precipitate U from solution. Once precipitated, UOCs are often dried and calcined to remove adsorbed water. The products can be allowed to react further, forming uranium oxides UO3, U3O8, or UO2 powders, whose surface morphology can be indicative of precipitation and/or calcination conditions used in their production. This review paper describes statistical issues and approaches in using quantitative analyses of measurements such as particle size and shape to infer production conditions. Statistical topics include multivariate t tests (Hotelling’s ), design of experiments, and several machine learning (ML) options including decision trees, learning vector quantization neural networks, mixture discriminant analysis, and approximate Bayesian computation (ABC). ABC is emphasized as an attractive option to include the effects of model uncertainty in the selected and fitted forward model used for inferring processing conditions.
1. Introduction
References [1,2,3,4,5,6,7] describe pre-detonation nuclear forensics goals. Pre-detonation nuclear forensics focuses on determining the source and route of nuclear materials and devices prior to their use in an improvised nuclear device or radiological dispersal device. Baseline morphology and discussion of the technical production details for four precipitation conditions (ADU, AUC, SDU, and MDU) are provided in [1,2]. Subsequent studies have investigated the quantitative morphological variations for a selection of these materials due to processing, aging, and/or storage conditions [3,4,7]. One related inference goal is to determine factors that impact particle morphology, such as calcination temperature, production pathway involving UO3, U3O8, or UO2, at 400 °C, 800 °C, and 510 °C (in H2), respectively, and impurities for a given precipitation condition. Nuclear forensic analysis utilizes a suite of techniques to help elucidate the provenance for a nuclear material of interest. The analysis of surface morphology for particulate samples has been of great interest as a possible indicator of the synthetic conditions used to produce nuclear materials, such as uranium ore concentrates (UOCs). The technique of quantitative morphological analysis as applied to nuclear forensics is this paper’s focus.
This review paper illustrates statistical issues using 22 quantitative morphological metrics (Appendix A describes these 22 metrics) derived from the analysis of scanning electron microscopy images (SEM) of each segmented particle [2,4,5]. Figure 1 highlights some example SEM images acquired from nuclear materials. The left image is the raw unprocessed SEM image and the right image is the image following manual particle segmentation using the Morphological Analysis of Materials (MAMA) software [2,8,9,10]. Morphological features are proving to be useful signatures to infer the chemical processing histories (which relate to forensics goals [1,2,3]) of uranium oxides. Particle morphology analysis has recently been developed and applied with image analysis software to segment fully visible particles in SEM images and then compute attributes, such as circularity, area, perimeter, and ellipse aspect ratio of the segmented particles. One example of such software is MAMA, which performs segmentation and quantification. SEM images of nuclear materials can be difficult to segment due to overlapping particles, charging effects, and image clarity. Manual segmentation (locating, recognizing, and assigning boundaries to particles) requires significant time-consuming user inputs to only segment fully visible particles. An alternative automated segmentation method using a deep learning model (a U-net based on convolutional neural networks) was shown in [8] to effectively segment fully visible particles (see also Reference [11] for another segmentation option); however, this paper’s focus is on inferring processing conditions using currently-available segmentation software, such as MAMA, that can also provide the 22 quantitative particle morphological metrics.

Figure 1.
SEM image from the calcination of MDU at 400 °C. The left image contains the raw unprocessed image of the particle surface morphology at 50,00×. The image on the right was manually segmented using MAMA software. The blue regions were the individual particle features that had clearly defined boundaries and were used to quantitatively characterize the morphology of the material.
Figure 2 highlights representative SEM images of ADU, SDU, MDU, and AUC and the materials generated throughout the calcination and reduction pathway of each respective starting material. In [1,2], each of the ADU, AUC, MDU, and SDU conditions have three processing pathways involving UO3, U3O8, or UO2, at 400 °C, 800 °C, and 510 °C (in H2), respectively. The main inference goal is to use particle morphology to distinguish among ADU, AUC, MDU, and SDU processing routes. One open question is whether machine learning (ML) methods can clearly recognize ADU, AUC, MDU, SDU when all 3 pathways are represented in the data and also when only one pathway (baseline condition only, or either of the other two conditions) is represented in the data. Another inference goal is then to determine factors that impact particle morphology, such as calcination temperature, production pathway, and impurities for a given precipitation condition.

Figure 2.
Example SEM images, such as those used in [1,2], at the listed magnifications (right), for MDU, ADU, SDU, and AUC throughout the 400 °C (UO3), 800 °C (U3O8), and 510 °C (UO2) production pathways.
This paper focuses on ML options applied to the 22 MAMA measurements per particle to recognize ADU, AUC, MDU, and SDU precipitation conditions when 1, 2, or 3 pathways are represented in the data. Data from [2] are analyzed to estimate the correct classification rate (CCR) in recognizing ADU, AUC, SDU, and MDU. For completeness, it is noted here that data from [1] are vector representations of images (using unsupervised vector quantized variational autoencoding) either of length 256 or 1000 that are derived from each SEM image [1]. These vector representations of images have been shown to have a CCR of approximately 0.80 depending on the particular data subset used [1]. Because the CCR depends on the particular data subset analyzed, this paper does not directly compare the CCR when using the 256-length or 1000-length vectors from [1] for each image to the CCR when using 22-length MAMA measurements from each segmented particle from its respective SEM image. Instead, this paper reviews statistical issues in using the 22-length MAMA measurements per particle, and applies ML options to the 22-length MAMA measurements per segmented particle, with the ADU, AUC, MDU, and SDU precipitation conditions and the processing pathways involving UO3, U3O8, and UO2, at 400 °C, 800 °Cand 510 °C (in H2) all known (supervised learning).
Data from [2] are 22 morphological measurements produced from MAMA software (morphological analysis for material attribution) such as particle area, aspect ratio, and circularity (Appendix A). Data from [2] can be analyzed per particle or per image. Available data include 10s to 100s of MAMA measurements of particles per image, with a total of 9255 particle measurements (2258, 2436, 2263, and 2298 sets of 23 MAMA measurements of particles for ADU, AUC, SDU, and MDU, respectively). For ADU, there are 16, 12, and 14 images with an average of 47.3, 62.5, and 53.6 particles per image, for ADU1, ADU2, ADU3 (ADU1, ADU2, ADU3 denote pathways U3O8, UO2, or UO3, respectively). For AUC, there are 15, 8, and 10 images with an average of 57.7, 99.4, and 77.5 particles per image, for AUC1, AUC2, AUC3, respectively. For SDU, there are 8, 8, and 7 images with an average of 94, 94.5, and 107.9 particles per image, for SDU1, SDU2, SDU3, respectively. For MDU, there are 16, 19, and 18 images with an average of 46.9, 40.2, and 43.6 particles per image for MDU1, MDU2, MDU3, respectively. The results presented here are by particle because of the limited number of images for each precipitation condition and pathway [1,2,3,4,5].
This paper is organized as follows. Section 2 presents CCR results for nine ML methods. Section 3 relates the multivariate T2 test to LDA and illustrates impacts of model assumptions violations due to having multiple components (pathway, U3O8, UO2, or UO3, at 800 °C. 510 °C and 400 °C) per group (precipitation condition, ADU, ADU, SDU, MDU). Section 4 relates LDA to the multivariate T2 test to assess group separation. Section 5 provides more details regarding ABC in the context of experimental design. Section 6 summarizes this paper.
2. CCR Results
Results based on the 22 MAMA measurements [2] are given in Table 1 for nine ML options including decision trees, flexible discriminant analysis (FDA), mixture DA (MDA), linear DA (LDA), k-nearest neighbor, approximate Bayesian computation (ABC), learning vector quantization (LVQ), multivariate adaptive regression with splines (MARS), and support vector machines (SVM). When all three pathways are in the data, the CCRs (using 70% of the data to train and 30% of the data to test) for decision trees, MDA, LDA, FDA, k-nearest neighbor, LVQ, SVM, ABC, and MARS, are 0.83, 0.76, 0.74, 0.74, 0.81, 0.75, 0.76, 0.87, and 0.87, respectively. All analyses are done in R [12].

Table 1.
CCRs for 9 ML methods for recognizing ADU, AUC, SDU, and MDU with 3 pathways present in the data, or with 1 pathway present in the data. The boldface entries are the largest entries in each row, and all entries are repeatable to within approximately . Decision trees, MARS, and ABC have the highest CCRs.
When only pathway 1 is in the data for each of ADU, AUC, SDU, and MDU, the CCRs (again using 70% of the data to train and 30% of the data to test) for decision trees, MDA, LDA, FDA, k-nearest neighbor, LVQ, SVM, ABC, and MARS, are all increased, to 0.93, 0.82, 0.81, 0.81,0.85, 0.87, 0.83, 0.89, and 0.89, respectively. Precipitation conditions SDU and MDU are the most difficult to distinguish, so if SDU and MDU are merged into one group, reducing the number of groups from 4 to 3, then all methods have higher CCRs, some as large at 0.98. ML options 1–9 are described in Appendix B. In addition, LDA is discussed in Section 4, and ABC is discussed in Section 5 because the simulation framework used in ABC is helpful for including various sources of model uncertainty.
It is not surprising that the CCR decreases when all three pathways are represented in the data. Figure 3 plots principal coordinate (PC, [13]) 7 versus PC 4 for particles from the ADU, AUC, SDU, and MDU. PCs are coordinates from which the matrix of pairwise distances in the 22-dimensional space can be closely approximated. In Figure 3, there is qualitative evidence of moderately-good group separation, particularly considering that only two PCs are used (up to 22 PCs are available). Figure 4 is the same as Figure 3, but is for PC1, PC2, and PC4, and illustrates that using three PCs leads to better group separation than using the two PCs in Figure 3.
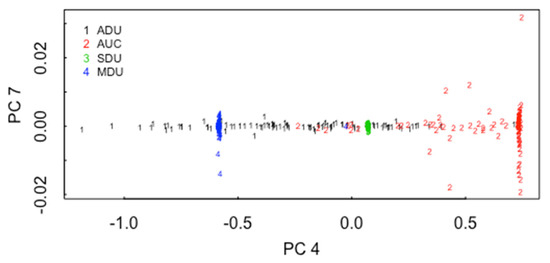
Figure 3.
Principal coordinate 7 versus PC 4 for particles from the ADU, AUC, SDU, and MDU.
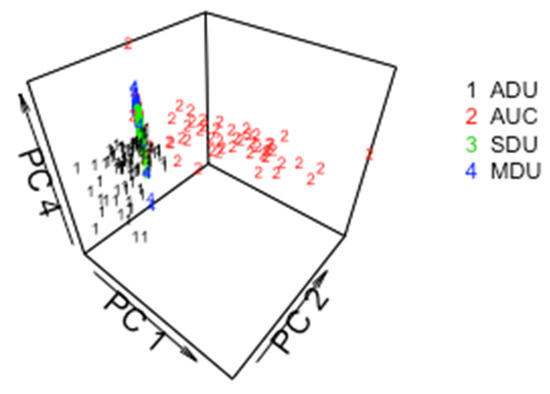
Figure 4.
PC 4 versus PC 1 and PC2 for particles from the ADU, AUC, SDU, and MDU.
Methods such as MDA have the potential to recognize clusters within the 4 precipitation conditions and thereby mitigate the decrease in classification accuracy [13,14]. Figure 5 plots the Bayesian information criterion (BIC) used in model-based clustering versus the number of clusters (“components”) in the ADU data with all three pathways (U3O8, UO2, UO3) present. There is modest evidence for 3–7 clusters within ADU. Figure 6a plots the case in which mclust is asked to find the best 3-cluster fit in 22 MAMA features in the ADU data (using MDS coordinates 7 and 3 as one good option to display the data in 2-dimensions). The three clusters are somewhat distinct, but the same types of plots for 4, 5, 6, or 7 clusters look equally plausible, and there are small sub-clusters in 2 of the 4 clusters. Figure 6b is the “true” clusters as defined by the three pathways. Note in comparing Figure 6a,b that some of U3O8 cases are clustered in the UO2 group. Figure 7 plots the raw MAMA feature 5 (perimeter of convex hull covering the particle) versus feature 1 (particle vector area) without transformation into PCs. Figure 8 plots the raw MAMA feature 3 (particle pixel area) versus feature 1 (particle vector area) and feature 2 (area of convex hull covering the particle) without transformation into PCs. Figure 9 plots the ADU, AUC, MDU, SDU data from [1] for UMAP coordinates 1 and 2. The UMAP coordinates are a uniform manifold approximation and projection for dimension reduction, which is used to reduce the dimension of either a 256-length vector or a 1000-length vector used to represent each image that are the derived image-based features from [1] using a vector quantized variational encoder. The CCR from the UMAP coordinates is approximately 0% to 10% smaller than those presented here for the MAMA features from [2], depending on the data subsets analyzed.
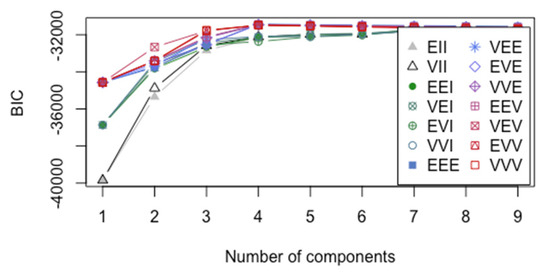
Figure 5.
The BIC versus the number of components for ADU with 3 pathways in the training data (U3O8, UO2, UO3). The legend describes different modeling assumptions regarding the data covariance matrix within each cluster, where “E” denotes “equal”, “I” denotes “identity” matrix (independent MAMA components), and “V” denotes “varying” features of the covariance matrix in the order volume, shape, orientation in an eigenvector decomposition. For example, EVI denotes equal volume, varying shape, and identity orientation among the groups, and VVV denotes varying volume, shape, and orientation among the groups.
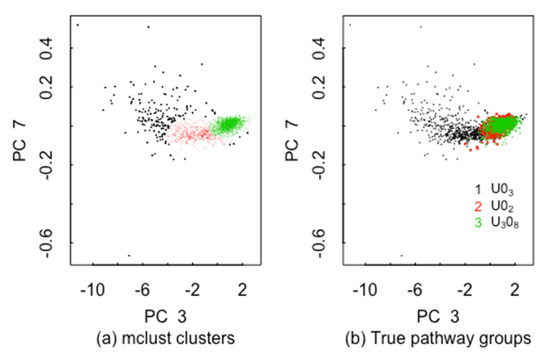
Figure 6.
(a) The 3 clusters found in the 22 MAMA features in the ADU data, (b) the 3 true groups (pathways) in the ADU data. Dimension reduction using MDS is used for plotting.
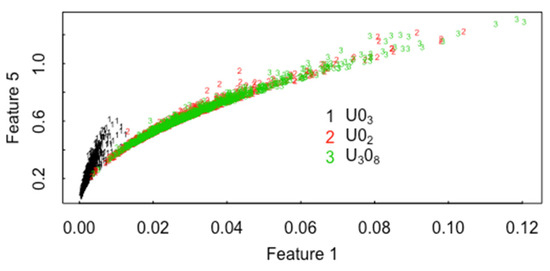
Figure 7.
MAMA feature 5 (perimeter of convex hull covering the particle) versus feature 1 (particle area).
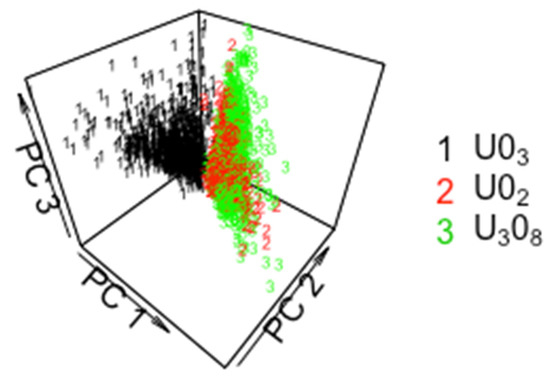
Figure 8.
The raw MAMA feature 3 (particle pixel area) versus feature 1 (particle vector area) and feature 2 (area of convex hull covering the particle) without transformation into PCs for ADU.
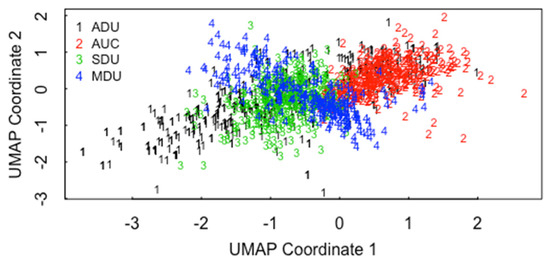
Figure 9.
UMAP coordinates 1 and 2 for the ADU, AUC, SDU, and MDU, data from [1].
3. Multivariate t-Test
If two groups of normally-distributed data have the same variance and possibly different means then the well-known univariate t statistic
where is the sample mean of group 1, is the sample mean of group 2, and is distributed as (at distribution with degrees of freedom. Therefore, the value of as computed in Equation (1) is compared to the quantiles of the t distribution with degrees of freedom to test whether the mean of group 1 is different from the mean of group 2 [15].
The precipitation condition could define group 1 as ADU and group 2 as AUC and other production, aging, and/or storage conditions could be varied to evaluate how robustly and reliably the ADU data could be distinguished from the AUC data. If the two groups cannot be assumed to have the same variance, then another version of the t statistic, such as Welch’s t [15], can be used. The normality assumption is not crucial, partly because the sample means and are usually approximately normal in distribution due to the central limit effect [15].
If the data are from the two groups are more than one dimension (a vector rather than a scalar), as for example in Figure 8, then Hotelling’s multivariate T statistic [16] generalizes Equation (1) to:
Figure 10 plots simulated group 1 and group 2 data for p = 2, with the true and estimated (from 100 observations per group) linear decision boundaries. The correlation is 0.5, and the true mean shift is 3 units in the direction of x1 only (a 3 unit mean shift to the east, and the standard deviation in both groups is (1).
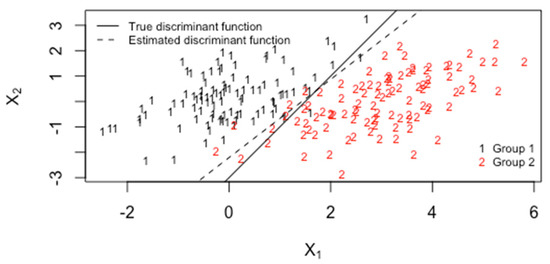
Figure 10.
The predictor versus with 100 observations per group, correlation 0.5 and mean shift of 3 units in the direction.
Figure 11 plots the estimated probability density function (pdf) of simulated values of from Equation (2) and the corresponding analytical probability density, . The R programming language is used for all figures, simulations, and calculations [12].
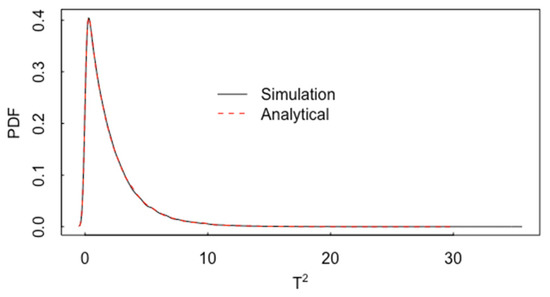
Figure 11.
The estimated pdf of simulated values of from Equation (2) and the corresponding analytical pdf, .
Not surprisingly, if the mean shift between group 1 and group 2 is due to a mean shift of only a subset of p variables, then the probability to detect the mean shift decreases as.
If then , where the non-centrality parameter of the F distribution is:
If in Equation (3) is fixed, for example, at , and the number of variables (predictors) p increases then the non-centrality parameter remains fixed, but p increases, which means that a mean shift from to becomes more difficult to detect. To illustrate, Figure 12 plots the detection probability to detect as p increases for . The MAMA software currently provides 22 particle measurements (such as convex hull area, pixel area, vector perimeter, ellipse perimeter, ellipse aspect ratio, circularity, etc.), some of which might not be useful to distinguish among groups, and Figure 12 indicates that using useless measurements can decrease the CCR. Therefore, Section 5 on ABC investigates whether variable screening based on t statistic values can increase the CCR.
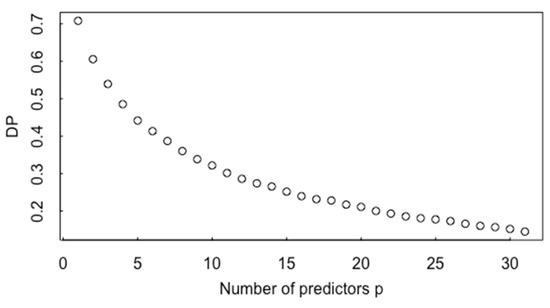
Figure 12.
The detection probability (DP) versus the number of predictors.
Figure 13 plots one example of the impact of nonnormality on the pdf for T2. In Figure 13, p = 2, and the pdf of T2 is plotted for normal data (with correlation 0.60 and n1 = n2 = 20) and for lognormal data, also with a correlation 0.60. The analytical result is the same as in Figure 11 for normal data. In this case, there is noticeable effect of non-normality on the pdf of T2. Figure 14 is the same as Figure 13 but for p = 15. Figure 15 is the same as Figure 14, but for and n1 = n2 = 200. The approach to approximate normality is somewhat slower as p increases.
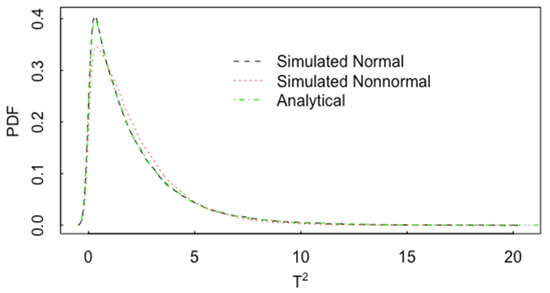
Figure 13.
The pdf of T2 for normal data with p = 2, (with correlation 0.60) and for lognormal data, also with a correlation 0.60 and n1 = n2 = 20.
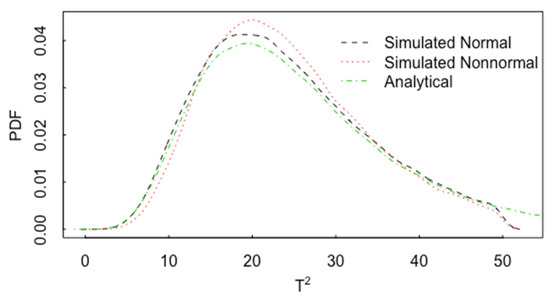
Figure 14.
The pdf of T2 for normal data (with correlation 0.60) and for lognormal data, also with a correlation 0.60, p = 15, and n1 = n2 = 20.
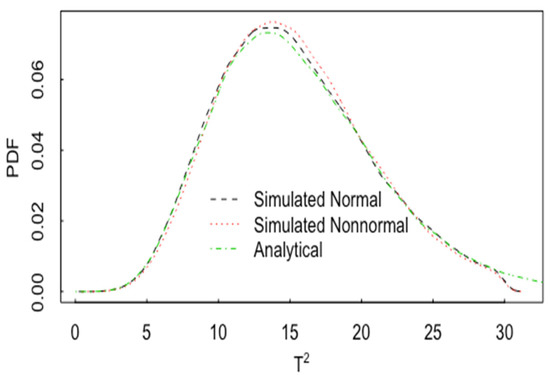
Figure 15.
The same as Figure 14, but for n1 = n2 = 200.
4. LDA
The multivariate T2 statistic uses the statistical distance between two sample means and leads to a simple and reasonably robust test, for example, of whether the ADU group mean is different from the AUC mean. Linear discriminant analysis (LDA) uses the statistical distance from a test observation to each of the ADU and AUC group means to assign the test observation to the ADU or AUC group. LDA is one of the oldest [12,13,15] and simplest pattern recognition methods (“supervised learning” in ML jargon) used to assign a group membership to a test case based on training data that has known group assignments.
Figure 16 plots simulated group 1 and group 2 data for p = 2, with the true and estimated (from 100 observations per group) linear decision boundaries. The correlation is 0.5, and the true mean shift is 3 units in the direction of x1 only (a 3-unit mean shift to the east, and the standard deviation in both groups is 1). The mean vector of group 1 is (0,0) and the mean vector of group 2 is (3,0). By appealing to likelihood ratio theory, or Bayes rule, the true linear decision boundary is computed using and the estimated linear decision boundary is computed using where [13,14,16].
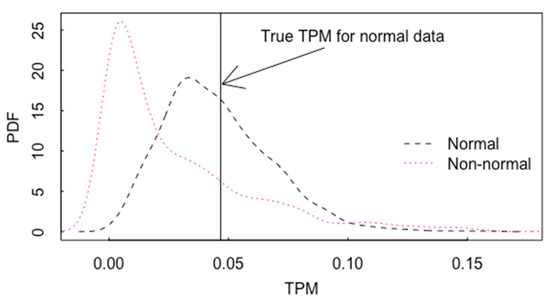
Figure 16.
The estimated pdf for TPM based on 105 sets of 100 simulated observations from each of group 1 and group 2, with the true TPM = 0.042, n1 = n2 = 20, 0.6 correlation between x1 and x2.
Similarly to using the non-centrality parameter in Section 3 to quantify the effect of a mean shift from to , the total probability of misclassification (TPM) by LDA (the probability that a group 1 item is classified as group 2, or a group 2 item is classified as group 1, TPM = 1−CCR), is given by the cumulative normal probability , where [16]. For the data in Figure 16, the true TPM = 0.042 and the estimated TPM is 0.045. Figure 16 plots the pdf for the estimated TPM based on 105 sets of 100 simulated observations per group, both for normal data and log normal data.
Of course, real data are rarely so close in distribution to multivariate normal (MVN). For example, Figure 17 plots 25 simulated observations from each of 4 clusters, where clusters 1 and 2 belong to group 1 and clusters 3 and 4 belong to group 2. ML methods such as learning vector quantization (LVQ [14]) or mixture discriminant analysis (MDA [14]) training are effective for this type of data. However, with more than p = 2 predictors, it is rarely so evident that clusters are present, so LDA, LVQ, and MDA are compared. MDA assigns a test case to the nearest cluster and corresponding group. Although real data rarely closely follow the LDA assumptions that the data are MVN with the same covariance matrix and possibly different means, LDA sometimes has a competitive CCR compared to other ML options such as MDA and LVQ.
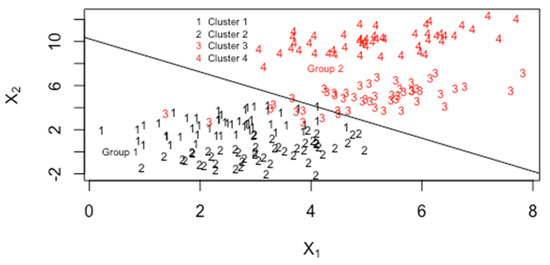
Figure 17.
Mixture data with clusters 1 and 2 in group 1 and clusters 3 and 4 in group 2.
Note that due to processing, aging, and/or storage conditions, clustering, such as in Figure 17, could occur and performance claims regarding how distinct group 1 is from group 2 depend on the relative frequency of each cluster. For example, cluster 4 in group 2 is quite distinct from all of group 1, but cluster 3 from group 2 is not distinct from cluster 2 of group 1. Therefore, performance claims regarding group separability could depend on the relative frequencies of the clusters in the training and testing data. Applying leave-one-out cross validation (CV) to 103 simulated observations in each of the four clusters in each group, the estimated TPM using either LDA or MDA is 0. Simply assuming MVN data in each group without clustering and applying , where
leads to an estimated TPM = 0.08, with in Equation (4), describing the T2 based measure of group separation. Somewhat surprisingly, the estimate 0.08 closely agrees with 1 − CCR = 0.08 (recall from previous paragraphs that CCR = 0.93 if clustering is ignored) in this case because is badly estimated due to ignoring the clustering within each group. In the case with the probability of 1, 2, 3, 4, 5, 6, or 7 clusters in each group calculated from BIC leads to an estimated TPM = 0.13 (CCR = 0.87, in good agreement with the CCR of 0.88 from the previous paragraph), with in Equation (4) describing the T2-based measure of group separation. Again, somewhat surprisingly, because is badly estimated due to ignoring the clustering within each group, the CCR is well estimated even if clustering is ignored. The true simulated distribution is a mixture of MVN clusters within each of the two groups, with either four clusters or a random number of clusters from 1 to 7 as modeled using BIC as estimated using mclust applied to the real data with ADU = group 1 and AUC = group 2. Real data can often be modeled effectively using mixtures, including mixtures of MVN distributions [17]; however, ignoring the mixture behavior and assuming one cluster per group can often lead to competitive performance. Recall that LDA assumes one MVN component per group while MDA allows one or more MVN components per group.
5. ABC
Because ABC is a versatile and robust option for many inverse problems [18,19,20,21,22,23], ABC is described in detail here. ABC can be used to evaluate candidate experimental designs, accommodate model uncertainty such as how many clusters could be present in each precipitation condition (ADU, AUC, SDU, MDU), and to provide a model-based summary of the data.
In any Bayesian approach [24], prior information regarding the magnitudes and/or relative magnitudes of any model parameter(s) can be provided. If the prior is “conjugate” for the likelihood, then the posterior is in the same likelihood family as the prior, in which case analytical methods are available to compute posterior prediction intervals for quantities of interest. So that a wide variety of priors and likelihoods can be accommodated, modern Bayesian methods do not rely on conjugate priors, but use numerical methods to obtain samples from approximate posterior distributions [24]. For numerical methods, such as Markov chain Monte Carlo [24], the user specifies a prior distribution (which need not be normal), for the parameters to be inferred, such as processing and aging conditions. The user must also specify a likelihood for the data given the model parameters. In contrast, ABC does not require a likelihood for the data; and, as in any Bayesian approach, ABC accommodates constraints on variances through prior distributions [18,19,20,21,22,23,24].
No matter what type of Bayesian approach is used, a well-calibrated Bayesian approach is defined here as an approach that satisfies several requirements. One calibration requirement is that in repeated applications of ABC for classification the actual correct classification probability should be closely approximated by the predicted correct classification probability. For example, if the average probability of the selected model is 0.90, then the actual CCR should be approximately 0.90. In applications of ABC for estimating a continuous-valued parameter (“regression”), one requirement is that in repeated applications of ABC, approximately 95% of the middle 95% of the posterior distribution for the parameter should contain the true value. That is, the actual coverage should be closely approximated by the nominal coverage. The nominal coverage is obtained by using the quantiles of the estimated posterior. For example, the 0.005 and 0.995 quantiles define the lower and upper limits of a 99% probability interval. A second requirement is that the true mean squared error (MSE) of the ABC-based estimate of the parameter should be closely approximated by the variance of the ABC-based posterior distribution of that parameter [22].
Denote the real data as y. Inference using ABC can be summarized as follows:
- (1)
- Sample from the prior
- (2)
- Simulate data from the model
- (3)
- If the distance , then accept as an observation from
Repeat steps 1–3 many times, usually 105 or more times. In step (2), the model can be analytical or, for example, a computer model. In ABC, the model has input parameters , has output data , and there is corresponding real data yobs. For the example below, the forward model has 1 parameter (the group membership, 1, 2, 3, or 4 for ADU, AUC, SDU, and MDU, respectively).
Synthetic data are generated from the model for many trial values of , and trial values are accepted as contributing to the estimated posterior distribution for | yobs if the distance d(yobs, y()) between yobs and y() is reasonably small. Alternatively, for most applications, it is necessary to reduce the dimension of yobs to a small set of summary statistics and accept trial values of if d(S(yobs), S(y()) < ε, where ε is a user-chosen threshold. Here, for example, is the 22 MAMA morphology measurements or transformations of them. Because trial values of are accepted if if d(S(yobs), S(y()) < ε, an approximation error to the posterior distribution arises that several ABC options [20,21] attempt to mitigate. Such options weight the accepted values by the actual distance d(S(yobs), S(y()) (abctools package in R [12]). In practice, the true posterior distribution is not known, so a method such as that in [22] using calibration checks, is needed in order to choose an effective value of the threshold ε.
ABC is used here for two main reasons:
- (A)
- ABC allows for comparison of the performance of candidate summary statistics such as the mean or quantiles of the particle attributes such as size and shape.
- (B)
- ABC allows for easy experimentation with the effects of EDA to choose a model and to include uncertainty in the estimated forward model (such as the number of mixture components in each of ADU, AUC, SDU, MDU) used to perform ABC.
5.1. ABC for ADU, AUC, SDU, MDU
ABC requires a forward model with source terms (such as group membership being ADU, AUC, SDU, or MDU) as inputs and observables such as any subset of the 22 MAMA features as outputs. For a test set of outputs, the most likely inputs can be inferred using steps 1, 2, and 3. The forward model can be simple or complicated, and can include empirical adjustments based on training data. For example, empirical measurements (training data) can be used to select a model (such as the number of mixture components in MDA) and estimate the chosen model parameters. Uncertainty arising from the model selection step [25] is often ignored; however, the effects of model selection can be easily including via ABC (Section 5.3).
This section uses subsets of the MAMA measurements as the model output and assigns the group membership as 1, 2, 3, or 4, for ADU, AUC, SDU, and MDU, respectively. The CCR of 0.87 in Table 1 corresponds to the choice of MAMA features 1–9, 11, 21, 22 (Vector area (μm2), Convex hull area (μm2), Pixel area (μm2), Vector perimeter (μm), Convex hull perimeter (μm), Ellipse perimeter (μm), ECD (μm), Major ellipse (μm), Minor ellipse (μm), Diameter aspect ratio, Grayscale mean, Gradient mean). Features 1–9, 11, 21, and 22 were chosen because these 12 features had the largest ratio of between-group variance to the within-group variance (as is done in LDA). The average probability assigned by ABC to the inferred group membership is 0.85, which is acceptably close to 0.87. If instead all 22 MAMA features are used, the CCR of ABC is approximately 0.82 instead of 0.87.
Note that this implementation of ABC for classification uses the actual data rather than an explicit forward model; therefore, this implementation of ABC is similar to a smooth version of k-nn in that it is based on using weighted distances from the test case to the training cases. In ABC applications below, the data is used to fit a model and uncertainty due to model selection [25] and parameter estimation is included.
5.2. ABC for the 3 Pathways in ADU, AUC, SDU, MDU
The same procedure as in Section 5.1 can be repeated for training data that includes only one of the three pathways (U3O8, UO2, or UO3, at 400 °C, 510 °C and 800 °C, for each of the four precipitation conditions. Recall from Table 1 that the nine ML methods each have larger CCR for the one-pathway per group training data (for any of the three pathways) than for the three-pathways per group training.
5.3. Model Uncertainty Accommodated by ABC for Inverse Problems in Forensics
Suppose that a model such as is fit to training data for one MAMA feature (or a transformation of several MAMA features), where for example is processing temperature and is humidity (not available in the data from [2] used here but experiments are ongoing that will have other processing conditions). The ABC framework is useful to evaluate the fitted forward model’s performance in the inverse problem consisting of using several responses to infer the value of . Design of experiments has traditionally focused on choosing effective values of that lead to low prediction error variance in each of , such as I-optimal designs [26,27,28,29,30,31]. A key task in nuclear forensics is the inverse problem, using future measured values of to infer the corresponding values of However, it is expected that good values of in training/calibration data that lead to competitively small prediction error variance in will also be good values for performing the inverse [26,27,28,29,30,31], because uncertainty in the fitted forward model is minimized subject to resource constraints (number of experiments). ABC is a good framework for including model uncertainty in addition to model parameter estimation uncertainty, as illustrated below.
A simulated example below uses q = 5 and p = 3 continuous-valued variables such as temperature, humidity and concentration of impurities. The ABC output (as in any Bayesian approach) is the estimated posterior for each of . Each candidate experimental design [26,27,28,29,30,31] such as central composite and Box-Behnken for fitting quadratic models can be evaluated in the ABC framework. The experimental design having the narrowest (smallest standard deviation) posterior probability density function (pdf) for (or any other processing parameter) as the least uncertainty, provided the ABC-based approximation is sufficiently accurate. Simulations such as those used below indicate that ABC is accurate, so ABC-based posterior widths corresponding to candidate experimental designs can be compared [26,27,28,29,30,31].
Figure 18 plots an example of the ABC-based estimated posterior pdf of for nominal measurement error standard deviations (SDs) in and in and for two times the nominal standard deviations. The SDs include measurement error and modeling error effects. Note from Figure 18 that measurement errors in the factors (“predictors”) leads to a mean shift when the SDs are multiplied by a factor of 2. Figure 18 also includes a well-chosen experimental design (central-composite design [28,29]) and a randomly chosen experimental design that has non-zero correlations among the 3 predictors. The posterior width for a few other experimental designs were also compared [28,29]. For example, the posterior standard deviation for is 0.023, 0.053, 0.028, 0.024, 0.023, 0.021 for a full 3-level factorial for with 33 runs plus 5 repeated runs at the central position (27 + 5 = 32 runs), then the same full factorial but with two times the nominal standard deviations in the measurements of and in , then a random reordering of each of the design-matrix columns (a random design), a Box–Behnken design with 16 runs, a central composite design with 20 runs, and a central composite design with 20 runs but with a linear fit only, respectively. Because of the quadratic and interaction terms in the model, the full factorial design does not have uncorrelated predictors, which is one reason the Box–Behnken or central composite designs lead to a similar posterior standard deviation for as does the full factorial design with more runs (32 runs compared to 20 runs).
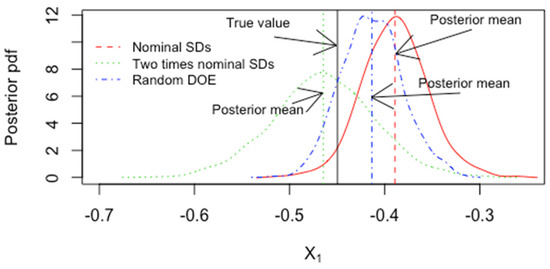
Figure 18.
The ABC-based posterior pdf for the factor both for nominal SDs and two times nominal SDs for the central composite design with 20 runs and for a random design.
Figure 18 plots the posterior for for the central composite design and for the random design. Recall that ABC is based on an approximate method, but the two ABC calibration checks for a continuously-valued parameter such as indicate that ABC is well calibrated with a choice of ε = 0.01. The two checks are that the nominal posterior intervals coverages agree with the actual coverages at 0.90, 095, and 0.99 levels, and the RMSE is well estimated by the posterior standard deviation. Therefore, the posterior standard deviations are good indications of inference quality and are a good basis to compare candidate experimental designs. In this case, the central composite design or the Box–Behnken designs are better than the full factorial because they achieve similar posterior width with fewer runs.
As pointed out in [27], ignoring estimation error in model parameters, one could use plug-in estimates of forward model parameters to compute the estimate
For example, if then the estimate are plugged into , ignoring their uncertainty, and ignoring the model selection process. Note the similarity of the plug-in approach to ABC in that ABC also seeks plausible values of that lead to small distance . However, the ABC framework makes it simple to include the effects of estimation error in model parameter estimates and to include the effects of model selection. Regarding model selection, a key assumption in experimental design is that the model form such as is known in advance and then good values of and can be calculated for minimizing prediction errors in (such as the I-optimal or the Box–Behnken designs [27,28,29]). In practice, if EDA suggests that some model form (perhaps nonlinear in the parameters or a segmented regression) is more appropriate than a low-order quadratic, then the strategy in [27] of using plug-in estimates of forward model parameters to compute the estimate in Equation (5) should be modified to account for the model selection step [25], as illustrated in the next two paragraphs in the classification context.
In practice, if EDA suggests that some model form (perhaps nonlinear in the parameters or a segmented regression) is more appropriate than a low-order quadratic, then the strategy in [27] of using plug-in estimates as illustrated in the next paragraph in the regression context and in the following two paragraphs in the classification context could be used, but it ignores model selection effects.
For ABC-based model selection effects in the regression context, first a model form such as is specified in the case of p = 3 continuous predictors , for each of q = 5 measured responses (such as 5 of the 22 MAMA measurements, or transformations of the MAMA measurements). Standard design of experiments assumes that the model form is known in advance, and effective training values of are selected in order to have good predictions of future y values at future values. In practice, EDA can suggest other candidate models and to keep this example short and simple, the impact of model selection will be illustrated when the true model is either (1) a 4-parameter model having only linear terms ( without interactions such as , or (2) is the full 10-parameter model model with parameters { ABC will then be implemented assuming the 4-parameter model, the 10-parameter, or using BIC to choose between the two models. ABC is implemented by simulating possible values and corresponding values for each set of { values simulated from their respective prior probability distributions. The measurement error variances in and are assumed here to have been well estimated by using small repeatability studies. The BIC for comparing regression models (1) and (2) fit to the same data is given by
where RSS in Equation (6) is the residual sum of squares , n is the number of observations (n = 20 for the central composite design as used to generate Figure 18 as in this example) and p is the number of model parameters (p = 10 for model 1 and p = 4 for model 2). Then for a randomly-generated test case, the ABC-based posterior standard deviations (SDs, repeatable to ) for are 0.046, 0.050, 0.064, respectively, if model 1 is the true and assumed model; the SDs are 0.054, 0.058, 0.077, respectively, if model 1 is the true and model 2 is the chosen model, and the SDs are 0.068, 0.043, 0.059, respectively, if model 1 is the true model and the model selection process is included in the training data for ABC, so model 1 is assumed with relative probability , which has an average value over 105 simulations of approximately 0.65 for each of the 5 responses in this example. The model selection process can be included in ABC by simulating from model 1 with 10 estimated parameters with the BIC-based model relative probability and by simulating from model 2 with relative probability . Such a simulation procedure is a representation of our state of knowledge after the n = 20 run central composite design, such as a BIC-based approximate 65% probability that model 1 is more appropriate than model 2 when model 1 is the correct model. For the same simulated test case as above, having true values Figure 19 plots the ABC-based posterior pdf for the factor ignoring the effects of model selection and including the effects of model selection, for the central composite design with 20 runs. The three cases plotted are: model 1 is the true model and (a) model 1 is always the chosen model, (b) model 2 is always the chosen model, and (c) BIC-based model selection chooses between model 1 and 2 in the ABC training data. It should be noted that the calibration checks indicate that ABC is working: the actual coverages of 0.99, 0.95, and 0.90 are the same as the nominal coverages, and the estimated RMSE is 0.05, in agreement with the observed average RMSE, using threshold ε = 0.01.
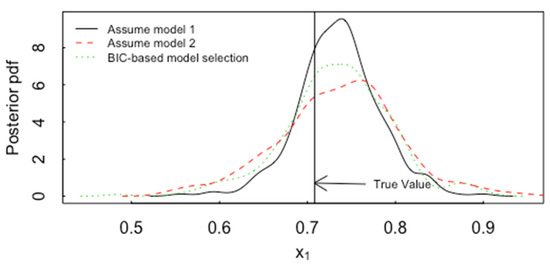
Figure 19.
The ABC-based posterior pdf for the factor if model 1 is the true model and model 1 is always the chosen model, if model 2 is always the chosen model, and if BIC-based model selection chooses between model 1 and 2 in the ABC training data. for the central composite design with 20 runs.
Although this is a simple model selection example, it illustrates how ABC can accommodate both model selection and parameter estimation effects. Alternatively, [25] used a smoothed bootstrap method to assess model selection effects, which were non-negligible even for the case of selecting among linear, quadratic, or higher order polynomials to fit a response, as done here.
For ABC-based model selection effects in the classification context, recall that Figure 5 plots the BIC used in model-based clustering versus the number of clusters (“components”) in the ADU data with all 3 pathways (U3O8, UO2, UO3) present. There is modest evidence for 3–7 clusters within ADU. Recall that Figure 6 is a two-dimensional plot of the identified clusters when the mclust function in R is asked to find 4 clusters. ABC can be implemented with a fixed number of clusters per group, or with the probability of 1, 2, 3, 4, 5, 6, or 7 clusters per group calculated from the BIC (with the relative model probability assumed to be well approximated by [14] and see below). In the case of distinguishing group 1 (ADU) from group 2 (AUC), the 4-cluster model has an ABC-based CCR estimate of 0.92 and the random-cluster model has an ABC-based CCR estimate of 0.88. The corresponding actual CCRs in simulated data are 0.93 and 0.88, in good agreement with prediction, and with the anticipated feature that the CCR is larger if the assumed forward model has a known number (4) of clusters in each group.
Returning to ABC applied to the 9255 sets of 22 MAMA measurements on particles, recall that the CCR in Table 1 is 0.87, which was for the case of using MAMA measurements {1–9, 23, 24} and using 70% of the data to train and 30% to test. If leave-one-out cross validation (CV, [14]) is used, the CCR is again 0.87. If model-based clustering (mclust in R) is use to model the data, and 3 clusters are selected for each of ADU, AUC, SDU, and MDU, then the ABC-based CCR is 0.93 (unrealistically high CCR due to over-simplified forward model in ABC). If instead the BIC-based probability of 1, 2, 3, 4, 5, 6, or 7 clusters is used, so that model uncertainty is accommodated in the forward model used by ABC, then the ABC-based CCR is 0.88, only 0.01 larger than that observed in real data, and lower than the over-simplified 3-clusters-per-group forward model. The BIC-based probability of a candidate model M, such as one with M = 1–7 clusters, is approximated as , with
where the model likelihood in Equation (7) depends on the assume parametric form and measures how well the model fits the data, p is the number of parameters, and n is the number of observations. The number of parameters in the clustering example, where k is the dimension of the data and there are k means, k variances, and k(k − 1)/2 covariances per cluster. There are other ways to approximate the probability of a candidate model, such as the integrated complete-data likelihood, but the point of this example is to illustrate how ABC can accommodate the model selection process, no matter what type of model selection [25] is used.
One goal for ABC applications is that the data model used in ABC lead to essentially the same CCR as that from using the real data within the ABC framework, in which case the fitted data model is a convenient model-based summary of the data.
6. Discussion and Summary
This review paper described statistical issues and approaches in using quantitative morphological measurements such as particle size and shape to infer production conditions. Statistical topics included multivariate T2 tests (Hotelling’s T2), design of experiments, and several machine learning (ML) options including decision trees, learning vector quantization neural networks, linear and mixture discriminant analysis, and approximate Bayesian computation (ABC). Particular emphasis was given to ABC because its simulation framework is effective for including effects of model selection and other sources of model uncertainty [25]. Any calibrated Bayesian approach is useful for comparing candidate experimental designs (which are in progress for 2022). For example, Figure 18 plotted the posterior probability distribution for inferred processing temperature in simulated data for a well-chosen experimental design (a full factorial design) and for a randomly-chosen design.
Author Contributions
Conceptualization: all, methodology: T.B., I.S., software: T.B., I.S.; analysis: T.B., I.S., writing: all, project administration: K.S. and M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NA22 in the office of nuclear nonproliferation under: LA21-ML-MorphologySignature-P86-NTNF1b.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Morphological Analysis of Materials (MAMA), Software Quantification Attributes
Appendix A briefly describes the 22 quantitative morphological attributes or features that are produced from the segmentation of particles within an image. See Appendix A in reference [30] for more details.
- 1
- Vector AreaThe area of the object calculated using the contour representation, but does not remove any holes. Due to the contour representation passing through the pixels of the perimeter of the object, generally slightly smaller than the pixel area representation.
- 2
- Convex Hull AreaThis is the area contained within the convex hull (convex polygon outline) of the segmented feature.
- 3
- Pixel AreaThis is the area of the object which does not include any holes. This metric is calculated by taking the total number of pixels encapsulated by the object boundary and multiplying by the micrometer/pixel scale.
- 4
- Vector PerimeterThe perimeter of the object using the object contour, calculates the length of the perimeter by summing the lengths of the segments between subsequent points around the boundary as determined by the cvFindCountours function in the OpenCV software.
- 5
- Convex Hull PerimeterThe perimeter of the convex hull of the object.
- 6
- Ellipse PerimeterThe calculated perimeter of the best-fitted ellipse around the boundary of the object using the cvFitEllipse function in the OpenCV software. The major and minor ellipse are extracted from these calculations.
- 7
- Equivalent Circular Diameter (ECD)This is the diameter of a perfect circle that has an area equivalent to the pixel area of the segmented feature. ECD = [4 ∗ (Pixel Area)/π)]1/2
- 8
- Major EllipseMajor ellipse axis calculated from the fitted ellipse from the ellipse perimeter calculations
- 9
- Minor EllipseMinor ellipse axis calculated from the fitted ellipse perimeter calculations
- 10
- Ellipse Aspect RatioThe ratio between the major ellipse and minor ellipse (Major ellipse/minor ellipse)
- 11
- Diameter Aspect RatioFollowing the assignment of a particle boundary to the object, the distance between all pairs of points on the boundary is calculated. The points with the greatest distance between them are assigned the maximum distance chord. Then the pair of points with the greatest distance between them that are within +/− 5 degrees of the orthogonal axis of the maximum distance chord are assigned as the longest orthogonal chord. The ratio of the maximum distance chord and the longest orthogonal chord is the diameter aspect ratio.
- 12
- CircularityA measure of how closely the object perimeter approaches a perfect circle (Circularity=1.0). Calculated from (4 ∗ π ∗ Pixel Area)/(Pixel Perimeter2).
- 13
- Perimeter ConvexityThe ratio of the convex hull perimeter and the object pixel perimeter.
- 14
- Area ConvexityThat ratio of the object area to the convex hull area.
- 15
- Hu Moment 1The image moment is a weighted average of the intensities of the image’s pixels by a set of functions that are invariant to scale, rotation, and translation. The 6 Hu moments were calculated using the cvMoments function in the OpenCV software. The Hu moments are particularly useful for shape matching and pattern recognition of objects from images.
- 16
- Hu Moment 2
- 17
- Hu Moment 3
- 18
- Hu Moment 4
- 19
- Hu Moment 5
- 20
- Hu Moment 6
- 21
- Grayscale meanThe mean of the grayscale intensity values extracted from the all pixels belonging to an object.
- 22
- Gradient MeanThe mean of the gradient magnitudes for each pixel location, which utilized the Sobel operator determined 2D approximate gradient at each pixel location.
Appendix B. ML Options Considered for Classification (as ADU, AUC, SDU, or MDU)
- 1
- Decision TreesCART (classification and regression trees) is among the most versatile and effect ML options, for a categorical response (classification) or continuous response (regression). The R implementation in rpart is versatile and allows recursive partitioning of the predictor space. In addition, Bayesian additive regression trees (BART) as implemented in gbart (generalized BART for continuous and binary outcomes) was applied, but had lower CCR than rpart in R.
- 2
- MDAMixture discriminant analysis as implemented in mclust in R allows several choices for modeling the within-group covariance matrices, as shown in Figure 5.
- 3
- LDA
- 4
- FDAFlexible discriminant analysis uses a mixture of linear regression models, and applies optimal scoring to transform the response variable so that the data are in a better form for linear separation, and multiple adaptive regression splines (MARS) to generate the discriminant surface
- 5
- k-nnNearest-neighbor classification records the group of each of the nearest k neighbors and uses majority rule voting. The choice of k is made by performance on the training data, usually using CV, and the choice of a distance measure to define distances among observations is usually made by trial and error.
- 6
- LVQLearning vector quantization is a neural-network based version of MDA.
- 7
- SVMSupport vector machines can be designed for classification or regression, and seek good class separation (margin) by using hyper-plane separation boundaries.
- 8
- ABCApproximate Bayesian Computation is described for classification in Section 5.
- 9
- MARSMultiple adaptive regression fits a piecewise linear model to capture any nonlinear relationships in the data by choosing cutpoints (knots, as used in spine fits) similar to step functions. MARS is somewhat similar to CART due to the piecewise fitting, and can be performed with categorical responses.
References
- Girard, M.; Hagen, A.; Schwerdt, I.; Gaumer, M.; McDonald, L.; Hodas, N.; Jurrus, E. Uranium Oxide Synthetic Pathway Discernment through Unsupervised Morphological Analysis. J. Nucl. Mater. 2021, 552, 152983. [Google Scholar] [CrossRef]
- Schwerdt, I.; Hawkins, C.; Taylor, B.; Brenkmann, A.; Martinson, S.; McDonald, L. Uranium Oxide Synthetic Pathway Discernment Through Thermal Decomposition and Morphological Analysis. Radiochim. Acta 2019, 107, 193–205. [Google Scholar] [CrossRef]
- Hanson, A.; Schwerdt, I.; Nizinski, C.; Nicholls, R.; Mecham, N.; Abbott, E.; Heffernan, S.; Olsen, A.; Klosterman, M.; Martinson, S.; et al. Impact of Controlled Storage Conditions on the Hydrolysis and Surface Morphology of Amorphous-UO3. ACS Omega 2021, 6, 8605–8615. [Google Scholar] [CrossRef]
- Schwerdt, I.; Olsen, A.; Lusk, R.; Heffernan, S.; Klosterman, M.; Collins, B.; Martinson, S.; Kirkham, T.; McDonald, L. Nuclear Forensics Investigation of Morphological Signatures in the Thermal Decomposition of Uranyl Peroxide. Talanta 2018, 176, 284–292. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Hyun, J.; Lee, K.; Lee, E.; Lee, K.; Song, K.; Moon, J. Effects of the Different Conditions of Uranyl and Hydrogen Peroxide Solutions on the Behavior of the Uranium Peroxide Precipitation. J. Hazard. Mater. 2011, 193, 52–58. [Google Scholar] [CrossRef] [PubMed]
- Olsen, A.; Richards, B.; Schwerdt, I.; Heffernan, S.; Lusk, R.; Smith, B.; Jurrus, E.; Ruggiero, C.; McDonald, L. Quantifying Morphological Features of α-U3O8 with Image Analysis for Nuclear Forensics. Anal. Chem. 2017, 89, 3177–3183. [Google Scholar] [CrossRef]
- Schwerdt, I.; Brenkmann, A.; Martinson, S.; Albrecht, B.; Heffernan, S.; Klosterman, M.; Kirkham, T.; Tasdizen, T.; McDonald, L. Nuclear Proliferomics: A New Field of Study to Identify Signatures of Nuclear Materials as Demonstrated on alpha-UO3. Talanta 2018, 186, 433–444. [Google Scholar] [CrossRef]
- Ly, C.; Olsen, A.; Schwerdt, I.; Porter, R.; Sentz, K.; McDonald, L.; Tasdizen, T. A New Approach for Quantifying Morphological Features of U3O8 for Nuclear Forensics Using a Deep Learning Model. J. Nucl. Mater. 2019, 517, 128–137. [Google Scholar] [CrossRef]
- Schwartz, D.; Tandon, L. Uncertainty in the USE of MAMA Software to Measured Particle Morphological Parameters from SEM Images; LAUR-17-24503; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2017.
- Gaschen, B.K.; Bloch, J.J.; Porter, R.; Ruggiero, C.E.; Oyen, D.A.; Schaffer, K.M. MAMA User Guide V2.0.1; LA-UR-16-25116; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2016.
- Wang, Z. A New Approach for Segmentation and Quantification of Cells or Nanoparticles. IEEE Trans. Ind. Inform. 2016, 12, 962–971. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org/ (accessed on 11 May 2021).
- Venables, W.; Ripley, B. Modern Applied Statistics with S-Plus; Springer: New York, NY, USA, 1999. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. Elements of Statistical Learning; Springer: New York, NY, USA, 2001. [Google Scholar]
- Miller, R. Beyond ANOVA: The Basics of Applied Statistics; Chapman and Hall: London, UK; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Johnson, R.; Wichern, D. Applied Multivariate Statistical Analysis, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1992. [Google Scholar]
- Burr, T.; Foy, B.; Fry, H.; McVey, B. Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes in Hyperspectral Imagery. Sensors 2006, 6, 1587–1615. Available online: http://www.mdpi.org/sensors/list06.htm#issue11 (accessed on 11 May 2021). [CrossRef]
- Burr, T.; Croft, S.; Favalli, A.; Krieger, T.; Weaver, B. Bottom-up and Top-Down Uncertainty Quantification for Measurements. Chemom. Intell. Lab. Syst. 2021, 209, 104224. [Google Scholar] [CrossRef]
- Burr, T.; Favalli, A.; Lombardi, M.; Stinnett, J. Application of the Approximate Bayesian Computation Algorithm to Gamma-Ray Spectroscopy. Algorithms 2020, 13, 265. [Google Scholar] [CrossRef]
- Blum, M.; Nunes, M.; Prangle DSisson, S. A Review of Dimension Reduction Methods in Approximate Bayesian Computation. Stat. Sci. 2013, 28, 189–208. [Google Scholar] [CrossRef]
- Nunes MPrangle, D. abctools: An R package for Tuning Approximate Bayesian Computation Analyses. R J. 2016, 7, 189–205. [Google Scholar] [CrossRef] [Green Version]
- Burr, T.; Skurikhin, A. Selecting Summary Statistics in Approximate Bayesian Computation for Calibrating Stochastic Models. BioMed Res. Int. 2013, 2013, 210646. [Google Scholar] [CrossRef] [Green Version]
- Burr, T.; Krieger, T.; Norman, C. Approximate Bayesian Computation Applied to Metrology for Nuclear Safeguards. J. Phys. Conf. Ser. 2018, 57, 50–59. [Google Scholar]
- Carlin, B.; John, B.; Stern, H.; Rubin, D. Bayesian Data Analysis; Chapman and Hall: London, UK; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Efron, B. Estimation and Accuracy after Model Selection. J. Am. Stat. Assoc. 2014, 109, 991–1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawson, J. Design and Analysis of Experiments in R; Chapman and Hall: London, UK; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Lewis, J.; Hang, A.; Anderson-Cook, C. Comparing Multiple Statistical Methods for Inverse Prediction in Nuclear Forensics Applications. Chemom. Intell. Lab. Syst. 2018, 17, 116–129. [Google Scholar] [CrossRef]
- Lu, L.; Anderson-Cook, C. Strategies for Sequential Design of Experiments and Augmentation. Qual. Reliab. Eng. 2020, 2020, 1740–1757. [Google Scholar] [CrossRef]
- Myers, R.; Montgomery, D. Response Surface Methodology; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Silvestrini RMontgomery, D.; Jones, B. Comparing Computer Experiments for the Gaussian Process Model Using Integrated Prediction Variance. Qual. Eng. 2013, 25, 164–174. [Google Scholar] [CrossRef]
- Thomas, E.; Lewis, J.; Anderson-Cook, A.; Burr, T.; Hamada, M.S. Selecting an Informative/Discriminating Multivariate Response for Inverse Prediction. J. Qual. Technol. 2017, 49, 228–243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).