Abstract
In this paper, a discrete moth–flame optimization algorithm for community detection (DMFO-CD) is proposed. The representation of solution vectors, initialization, and movement strategy of the continuous moth–flame optimization are purposely adapted in DMFO-CD such that it can solve the discrete community detection. In this adaptation, locus-based adjacency representation is used to represent the position of moths and flames, and the initialization process is performed by considering the community structure and the relation between nodes without the need of any knowledge about the number of communities. Solution vectors are updated by the adapted movement strategy using a single-point crossover to distance imitating, a two-point crossover to calculate the movement, and a single-point neighbor-based mutation that can enhance the exploration and balance exploration and exploitation. The fitness function is also defined based on modularity. The performance of DMFO-CD was evaluated on eleven real-world networks, and the obtained results were compared with five well-known algorithms in community detection, including GA-Net, DPSO-PDM, GACD, EGACD, and DECS in terms of modularity, NMI, and the number of detected communities. Additionally, the obtained results were statistically analyzed by the Wilcoxon signed-rank and Friedman tests. In the comparison with other comparative algorithms, the results show that the proposed DMFO-CD is competitive to detect the correct number of communities with high modularity.
1. Introduction
The analysis of complex networks in real-world applications such as social, biological, metabolic, and paper citation networks is receiving more attention from researchers and experts [1,2]. The structure and function of a real-world network can be studied by graph features such as small-world effect, power-law, or network transitivity [1,2]. An important issue in most real-world networks is to find the hidden structures. Community detection (CD) identifies these structures of a complex network, and the density of edges inside these structures is higher than their outside. The more similarity between the members of a community has been caused the community detection able to be used as a tool in the analysis of complex networks structure [3]. CD has a significant role in social network analysis, which includes the identification of friendship groups, relationship analysis, identify influential people, detect terrorist attacks, use in link-prediction, or identify classes in COVID-19 datasets [1,4,5].
Each network is mathematically represented by a graph consisting of nodes and edges, which the nodes are connected to each other by edges. To detect a community in a complex network, there are different criteria such as betweenness [2], modularity [6], node similarity [7], normalized cut [8], and partition entropy [9]. In addition, some algorithms detect the communities by approximate methods such as label propagation [10], which at first, a label is allocated to each node, and then the labels of some nodes, which are randomly selected, are propagated to other nodes. This method is continued until all nodes have most of their neighbor nodes’ labels. In addition, many community detection approaches determine communities by optimizing modularity that has been proposed by Newman in 2004 [11]. In this approach, algorithms attempt to reach the optimal value of the modularity by different methods [5,12,13,14].
Generally, detecting communities with modularity maximization in a network can be considered as an optimization problem [15]. Metaheuristic algorithms are shown to be effective approaches to solve complex problems in a reasonable time when compared with exact methods [16]. A wide variety of metaheuristic algorithms have been introduced such as differential evolution (DE) [17], particle swarm optimization (PSO) [18], cuckoo search (CS) [19], grey wolf optimizer (GWO) [20], salp swarm algorithm (SSA) [21], whale optimization algorithm (WOA) [22], and multi-verse optimizer (MVO) [23]. Due to the arising challenges and complexities in real-world problems, there is still a need to propose new or enhance the existed algorithms [24,25,26,27,28,29,30,31,32]. Although these algorithms are well suited for solving problems with continuous search space, some algorithms such as genetic algorithm (GA) [33] and ant colony optimization (ACO) [34] were proposed to solve problems over discrete spaces. In addition, different methods were employed to develop the discrete version of a continuous algorithm [35]. The metaheuristic algorithms are applied for solving complex problems in different applications such as parameter identification of solar cells [36], feature selection [37,38,39,40,41], scheduling and planning [42,43,44], disease diagnosis [45,46], clustering [47], medical applications [48,49,50], industrial applications [51,52,53,54,55], and engineering optimization [56,57].
To use metaheuristic algorithms in community detection, each solution must be modeled according to the requirements of CD’s problem, such that each solution can be represented to an N-dimensional vector with discrete values. The dimension of such a vector is equal to the number of network nodes and the value of each dimension depends on the type of solution representation that is used. Two representations that are utilized to represent the solution vectors are label-based representation and locus-based adjacency representation (LAR) [14]. In addition, the objective function has a critical role in CD which is a measurement for metaheuristic algorithms to determine the optimality of the detected communities. Modularity [6], community score [58], modularity density [59], and partition entropy [9] are some objective functions that are introduced into the CD problem. The community detection problem is solved by using metaheuristic algorithms that imitate the natural phenomenon such as [60,61,62].
The moth–flame optimization (MFO) [63] algorithm is designed to solve continuous optimization problems inspired by the moths’ navigation mechanism to fly at night. The moths fly toward the moon in a straight line by maintaining a fixed angle, which is an effective mechanism for navigating long distances. Therefore, when the moth flies toward the nearby artificial lights, this mechanism leads to flight in a spiral line. This behavior is mathematically modeled in the MFO algorithm to solve global optimization problems. The MFO algorithm is used in different applications such as feature selection [64], software defect prediction (SDP) [65], economic dispatch problem [66], optimal power flow [67], gene selection [68], classification [69], image segmentation [70], and photovoltaic energy generation system [71]. Although MFO is used to solve many problems, it still has insufficiencies, such as lack of population diversity [72], imbalance between exploitation and exploration [73], and premature convergence [74]. To improve the performance of the canonical MFO, enhanced or hybrid variants are proposed, such as in [74,75].
The main purpose of this paper is to adapt a continuous metaheuristic algorithm that can be used to solve community detection and provide competitive results. Therefore, in this paper, a discrete moth–flame optimization algorithm for community detection (DMFO-CD) is proposed. To implement the proposed DMFO-CD algorithm, first, the representation of the canonical MFO is altered such that can be applied on a discrete problem community detection by using locus-based adjacency representation (LAR). The initial population of solution vectors is created using LAR, which detects the communities without any prior knowledge. Then, the modularity function is used as the evaluation criterion to calculate the fitness of the solution vectors and evaluate them. Next, the DMFO-CD’s movement strategy is proposed by altering the canonical MFO’s movement strategy such that the main concept of MFO is maintained and suitable for solving community detection. Finally, after iterating the movement, evaluating, and updating the solution vectors, the detected communities are obtained. To adapt MFO using community detection, the position of moths and flames are modeled as solution vectors, which is represented using locus-based adjacency representation (LAR). The initialization process is performed by considering the network structure and the relation between the nodes. Then, the movement strategy is performed to move the moth’s solution vectors around flames and update their position. This movement is accomplished by an adapted strategy consisting of a single-point crossover between the moth’s solution vector and corresponding flame to imitate the distance calculated, the two-point crossover between the calculated distance and corresponding flame for movement strategy, and the single-point neighbor-based mutation to increase the exploration ability. To validate the proposed DMFO-CD algorithm, a set of experiments were conducted on eleven real-world networks. The results were compared with five well-known algorithms in community detection, including a discrete particle swarm optimization with particle diversity and mutation that (DPSO-PDM) [13], a genetic algorithm for community detection (GA-Net) [58], a genetic algorithm for detecting communities in large-scale complex networks (GACD) [14], an enhanced genetic algorithm for community detection (EGACD) [60], and a multi-objective evolutionary clustering algorithm (DECS) [76]. The performance of the proposed DMFO-CD algorithm was evaluated in terms of important evaluation criteria: modularity, normalized mutual information (NMI), and the number of detected communities. Moreover, the proposed algorithm was also statistically analyzed by Friedman [77] and Wilcoxon signed-rank tests [78]. The comparison of results proves that the DMFO-CD is able to detect the correct number of communities with better modularity than other comparative algorithms.
The rest of this paper is organized as follows: Section 2 presents a summary of the relevant works on community detection. Section 3 presents the mathematical model of the MFO algorithm. Section 4 contains the proposed DMFO-CD algorithm. The experimental evaluation of DMFO-CD is presented in Section 5. Finally, the conclusion and future works are given presented Section 6.
2. Related Work
Metaheuristics due to their acceptable performance in solving complicated real-world problems have been broadly used to find communities in complex networks. As shown in Figure 1, metaheuristic algorithms based on their inspiration can be classified into three categories [26]: evolutionary, swarm intelligence, and physics-based algorithms. In the related literature, almost all algorithms from the evolutionary category were used to solve the community detection problem. Despite the simplicity of swarm intelligence algorithms, they are less applied in this problem. In the following, some representative metaheuristic algorithms that are used to find communities in complex networks are described.
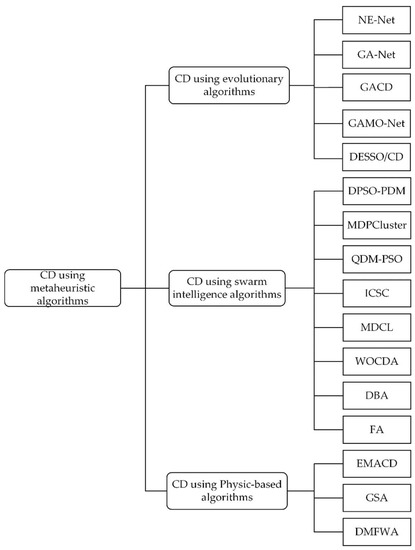
Figure 1.
A classification of metaheuristic algorithms used for community detection.
Evolutionary algorithms are inspired by the biological evolution process of the species in nature [24]. A population of individuals is iteratively processed by applying mutation, crossover, and selection operators to improve the individuals. The genetic algorithm (GA) is one of the well-known algorithms in this category, which was inspired by Darwin’s biological evolution theory. In [79], GA was employed to find the communities by optimizing the Newman modularity. In the proposed algorithm, a one-way crossing over operation is introduced in which two chromosomes are selected as parents, a node is randomly selected from one of the parents. Then, the community label is determined, all the nodes with the same label are found, and their labels are dedicated to another parent. In [58], GA-Net was proposed by Pizzuti, which is one of the state-of-the-art algorithms in community detection. GA-Net detects the communities by the use of GA and the community score (CS) as an objective function. CS measures the density of edges in each community and better partitioning leads to get a better CS.
Shi et al. [14] proposed GACD, in which a kind of genetic representation is introduced for use in community detection, which is called locus-based adjacency representation (LAR). In addition, the authors used a simple way of crossover and mutation based on their representation. In another work, Moradi et al. [60] proposed an enhanced genetic algorithm for community detection named EGACD by proposing a local search strategy. The proposed strategy is to improve the accuracy and increase the convergence speed up of the GACD algorithm. In EGACD, LAR is used to represent the individuals, and the modularity index is applied to calculate the fitness. In [62], the GAOMA-net algorithm was proposed by a special representation in which a memory and specific depth are dedicated to the network nodes. Then, the values of memory move by object migrating automata in depth, and the gene’s evolution is performed by the use of GA. GAOMA-net can overcome the GA’s premature convergence and accelerate the convergence. Liu et al. [76] proposed DECS to detect communities in evolving networks by adaptation of a genetic algorithm on community detection.
The second category is swarm intelligence algorithms, which imitate the animals’ behaviors such as the movement of birds’ flocks, the echolocation behavior of bats, or the navigation mechanism of moths at night. One of the most popular algorithms of this category is particle swarm optimization (PSO) [18], which imitates the behavior of bird flocks. In this algorithm, each bird is considered as a particle that is moved by its current, local-best, and global-best positions. Rahimi et al. [61] proposed a multi-objective particle swarm optimization algorithm for community detection in complex networks named MOPSO-Net in which the PSO algorithm is adapted as a discrete algorithm by a two-point crossover. At first, a crossover is performed between the current position and local-best position; then, a two-point crossover is performed between the resulted position and the global best position. Li et al. [13] developed an algorithm called DPSO-PDM with improvements in PSO that controls the motion of each particle relative to its difference from global best. With this strategy, when the particle diversity decreases, the algorithm tries to increase it and vice versa. Li et al. [80] proposed DESSO/CD, which is a hybridized version of an improved DE and social spider optimization (SSO) [81] algorithm. In the proposed algorithm, the population is initialized and moved by the SSO algorithm, the similarity of nodes is considered as local fitness function, and further improvement on population is performed by the improved DE.
Liu et al. [82] proposed DMFO algorithm, which is a new algorithm for clustering, with the equivalent aim of community detection. They adapted MFO by redesigning its movement strategies for a discrete algorithm and kernel k-means and ratio cut use as multi-objective functions. Zhao et al. [83] proposed ICSC, which is an improved CS algorithm to detect communities in protein-protein interaction networks. Zhang et al. [84] proposed a new algorithm named WOCDA to use on community detection with changes to the motion equation of WOA. The movement strategy of WOA is adapted by updating the node label with the label of most neighbor, one-way crossover, and updating the node label with a random neighbor’s label. The third category regards physics-based algorithms, which are inspired by physical rules in nature. Guendouz et al. [85] proposed a new algorithm by use of black hole optimization algorithm in CD problem. In this algorithm initialization, two new strategies, and evolution enhance the performance of the algorithm. Liu et al. [86] proposed the EMACD algorithm, which is an evolutionary algorithm based on membrane system for solving community detection problem. Kumar et al. [87] used graph embedding for low-level vector representation, which can keep the topological features of the network, and the communities are detected by a gravitational search algorithm and k-means.
3. The MFO Algorithm
The moth–flame optimization (MFO) algorithm is proposed by Mirjalili in 2015 [63], which is inspired by the moth’s navigation mechanism in nature. The moths by maintaining a fixed angle with the moon can fly long paths in a straight line during the night that is called transverse orientation. This mechanism is effective only when the light source is located in far distances, while flying toward nearby lights causes moths to move in a spiral path, as shown in Figure 2. In the MFO algorithm, moths update their position to reach the optimum solution by moving toward the flames in a spiral path. MFO is a population-based algorithm in which the positions of moths and flames are stored in MN × D and FN × D matrices as shown in Equations (1) and (2).
where N is the population number and D is the dimension of the problem. In the first iteration, F is the sorted moths’ population based on their calculated fitness. For other iterations, the M and F are merged and sorted based on their fitness such that their first N solutions are considered as new F. When the flames are identified, each moth is assigned to a flame and its position is updated with a logarithmic spiral equation as shown in Equation (3).
where S is a spiral function, Di is the distance of the i-th moth and j-th flame, which is described in Equation (4), t is a random number between in a range of [−1,1], and b is a constant number that identifies the shape of the spiral.

Figure 2.
Spiral movement of a moth around a flame.
To increase the exploitation ability of MFO, the number of flames is decreased in the course of iterations as calculated by Equation (5).
where T is the maximum number of iterations and l is the current iteration number.
4. DMFO-CD: Discrete Moth–Flame Optimization Algorithm for Community Detection
The purpose of the paper is to introduce a discrete moth–flame optimization algorithm for community detection (DMFO-CD) is explained in this section. The methodology for implementation of the proposed DMFO-CD algorithm shown in flowchart Figure 3 has two main steps: initialization and movement. This methodology is defined in the following sequence: In the initialization step, N moths are overspread to the restricted search space, and the fitness of each moth is calculated by considering the objective function. Thereafter, the moth population is sorted based on the obtained fitness and considered as the flame population. In the second step, moths are moved around flames by an adapted movement strategy to update their position. This process iterates until the terminating criterion is satisfied. In the following, the procedure of the proposed DMFO-CD algorithm is explained in detail.
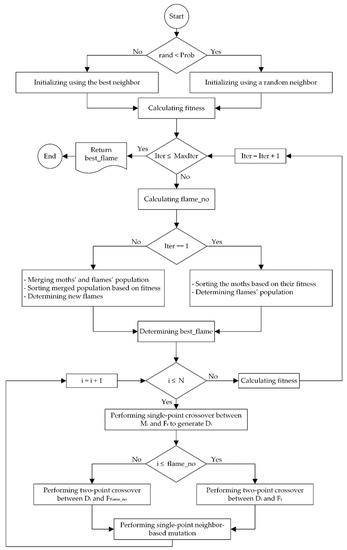
Figure 3.
The flowchart of DMFO-CD algorithm.
4.1. Initialization
In the initialization step, the locus-based adjacency representation (LAR) [14] is used to show the community structure of the network.
4.1.1. Representation
In our proposed DMFO-CD, the position of moths and flames are represented using LAR as solution vectors through which moth Mi and flame Fi are D-dimensional vectors Mi = {mi1, mi2, …, miD} and Fi = {fi1, fi2, …, fiD}, where D is the number of nodes in the network. If there exists an edge between nodes r and s in the network, then in the solution vector Mi, the value of mir is set by s, which means nodes r and s belong to a same community. Once the network is represented by LAR, those nodes that have connected to each other in any solution vector Mi construct a connected component. To detect the communities hidden in Mi, a decoding procedure is applied to detect candidate communities by tracking connected components. To illustrate using the LAR in DMFO-CD, consider graph G, as a network consisting of ten nodes depicted in Figure 4a, the solution vector Mi represented in Figure 4b. The communities decoded from the connected components are shown in Figure 4c,d.
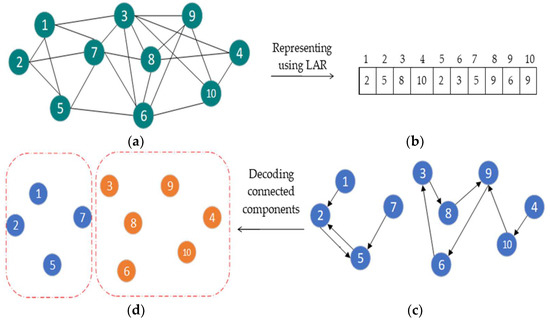
Figure 4.
The methodology of community detection: (a) original network; (b) solution vector Mi; (c) connected components constructed by Mi; (d) detected communities.
4.1.2. Initialization
To initialize the moths’ population using LAR, N solution vectors are generated and distributed in the search space. The initialization process randomly assigns one of the neighbor nodes or the best neighbor of the node [88] to dimension i. The best neighbor of node i is one of its neighbor nodes that has the most common neighbors. An example of finding the best node is shown in Figure 5. To find the best neighbor of node “3” in graph G each of its neighbor nodes is checked and then a node with the most common neighbors is selected. If there is more than one node with the most common neighbors, one of them is selected randomly. To initialize the moth’s position, when rand, a randomly generated number between 0 and 1, is less than the fixed parameter Prob (rand < Prob), a random neighbor is selected, otherwise (rand > Prob), the best neighbor of the node is assigned. This assignment guarantees that an existing connection in the network is kept in the initial population. Then, the fitness of each moth’s solution vector is calculated by considering the objective function, and the sorted moth population is considered as the flame population.

Figure 5.
The best neighbor selection: (a) the neighbor set of node 3; (b) the common neighbors of each neighbor of node 3.
4.2. Movement Strategy
In the continuous MFO, the moth flies around the flame in a spiral path as shown in Equation (2). Since community detection is a discrete problem, the canonical MFO must be adapted to detect communities of a network. Thus, in this paper, the canonical MFO is adapted by altering the distance calculation and the spiral flight movement. The proposed adaptation is performed by introducing: (1) a single-point crossover to calculate the distance, (2) a two-point crossover between the moth’s solution vector and corresponding flame for movement strategy, and (3) a single-point neighbor-based mutation to increase the exploration ability.
4.2.1. Distance Imitating Using Single-Point Crossover
In canonical MFO, the distance (Di) between the moth’s solution vectors and their corresponding flames is calculated using Equation (4). DMFO-CD imitates the distance calculating and generates Di by adapting a single-point crossover (⨞) operator [60]. The crossover operator is used to combine two parent solutions Mi and Fi and generates two new solutions Child1 and Child2 by Equation (6).
Then, the fitness of each generated child is calculated, and the one that has better fitness is selected as Di by Equation (7).
An example of generating new solutions using the single-point crossover is shown in Figure 6, where Figure 6a,b shows solution vectors Mi and Fi considered as parents. In Figure 6c, a crossover point is randomly selected. To produce Child1, the values of Fi from the beginning to the crossover point are copied and the rest values from the crossover point to the endpoint of Mi are considered. Child2 is produced in reverse order such that the first values are copied from Mi and then the values from the crossover point to the endpoint of Fi are considered. Then, as shown in Figure 6d, Child2 is selected as Di due to its better fitness.
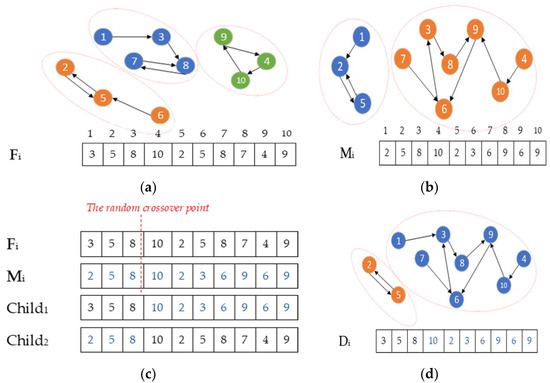
Figure 6.
Distance imitating using the single-point crossover: (a) solution vector Fi and its communities; (b) solution vector Mi and its communities; (c) generating Child1 and Child2; (d) Child2 with better fitness is selected as Di.
4.2.2. The Movement Strategy Using Two-Point Crossover
To adapt the MFO movement strategy, a two-point crossover (⨝) [61] is applied between Di and the corresponding flame. The corresponding flame of Mi is either Fi or Fflame_no in which flame_no is calculated by Equation (5). Regarding the canonical MFO, the moths update their position with respect to their corresponding flame by Equation (8).
In this two-point crossover, two points are randomly selected as crossover points, and the values of Di and the corresponding flame are combined to each other based on a crossover point to generate two new solutions MChild1 and MChild2. Then, the fitness of each child is calculated and the one that has better fitness is selected as Mi-tmp using Equation (9).
To better understand, an example of two-point crossover is provided in Figure 7 in which Figure 7a,b shows solution vectors of Fi and Di, and Figure 7c is a two-point crossover to generate MChild1 and MChild2. In Figure 7d, MChild2 is selected as Mi-tmp due to its better fitness.
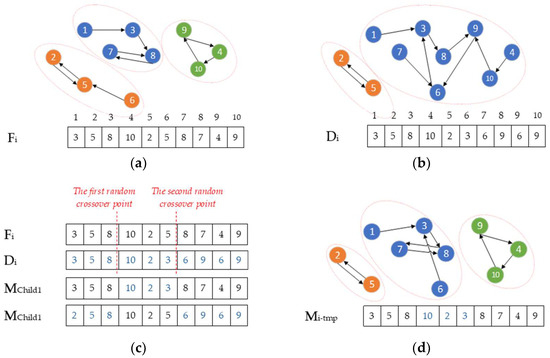
Figure 7.
Generating new solutions using the two-point crossover: (a) solution vector Fi and its communities; (b) solution vector Di and its communities; (c) generating MChild1 and MChild2; (d) MChild1 with better fitness is selected as Mi-tmp.
4.2.3. Single-Point Neighbor-Based Mutation
To increase the exploration ability of the DMFO-CD algorithm, a single-point neighbor-based mutation [58] is performed on all moths’ solution vectors. In this mutation, the solution vector Mi is updated such that each Mi-tmp a node is randomly selected, and its value is replaced by the number of a node selected randomly from its neighbor set. This limitation guarantees that the obtained solution vector Mi does not exit from the solution space. Figure 8 further illustrates the process of this mutation on Mi-tmp that results in Mi.
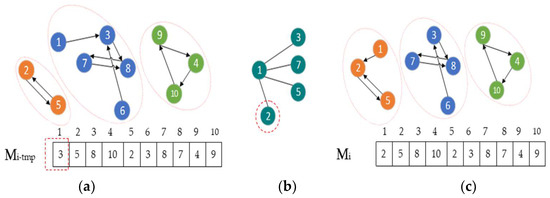
Figure 8.
Updating Mi using the single-point neighbor-based mutation: (a) randomly selecting a node; (b) randomly selecting a neighbor; (c) replacing value of selected node using its selected neighbor.
After updating all moths’ solution vectors, their fitness is calculated using a fitness function explained in the next section. Then, to determine the flames population for the next iteration, the current moths and flames populations are merged and sorted based on their fitness value. Thereafter, N best flames are selected as new flames. The pseudo-code of the proposed DMFO-CD is shown in Algorithm 1.
| Algorithm 1: Algorithm of the Proposed DMFO-CD | |
| Input: MaxIter (Maximum iterations), N (Number of moths), Prob, D (Number of network nodes) | |
| Output: best_flame | |
| Begin | |
| For i = 1: N | |
| For d = 1: D | |
| If rand < Prob | |
| Mi,d ← Initializing using a random neighbor | |
| Else | |
| Mi,d ← Initializing using the best neighbor | |
| End | |
| End | |
| End | |
| Calculating moths’ fitness | |
| Iter = 1 | |
| While Iter ≤ MaxIter | |
| flame_no ← round (N–Iter × (N-1/MaxIter)) | |
| If Iter == 1 | |
| Sorting the moths based on their fitness | |
| Determining flames’ population | |
| Else | |
| Merging moths’ and flames’ population | |
| Sorting merged population based on fitness | |
| Determining new flames | |
| End | |
| Determining best_flame | |
| For i = 1: N | |
| Di ← ⨞(Fi, Mi) | |
| If i ≤ flame_no | |
| Mi-tmp ← ⨝(Fi, Di) | |
| Else | |
| Mi-tmp ← ⨝(Fflame_no, Di) | |
| End | |
| Mi ← Single-point neighbor-based mutation (Mi-tmp) | |
| End | |
| Calculating moths’ fitness | |
| Iter = Iter + 1 | |
| End while | |
| Return best_flame | |
| End | |
4.3. Fitness Function
Fitness function measures the quality of partitioning of the network during the optimization process and converges the algorithm to detect optimum communities; therefore, fitness function plays a key role. In this study, the modularity Q, which was proposed by Newman et al. [11], is used to evaluate the fitness of moths. The greater value of modularity demonstrates the better quality of partitioning. Consider a network is partitioned into the k communities; thus, its modularity can be calculated by Equation (10) [60]:
where m is the number of edges, k is the number of detected communities, ls is the number of edges joining nodes of the community k, and ds is the sum of the degrees of the nodes belonging to the community k. In Equation (10), is the fraction of edges inside a community and its value represent the strength of that community, is the expected fraction of edges that could be in a random network without any community structure, and it represents the weakness of a community; therefore, the partitioning quality would be calculated by distracting these two terms.
5. Experimental Evaluation
The performance of the proposed DMFO-CD algorithm was evaluated on eleven real-world datasets, and the results were compared with five state-of-the-art algorithms in community detection, consisting of DPSO-PDM [13], GA-Net [58], GACD [14], EGACD [60], and DECS [76]. The proposed and comparative algorithms were implemented in MATLAB 2020b except for GA-Net and DECS; its executable MATLAB code [89,90] was used. All experiments were run on a CPU, Intel Core (TM) i7-3770 3.4GHz with 12.0 Gb real memory. The performance comparison was based on various metrics consisting of modularity (Q), normalized mutual information (NMI) [91], and the number of detected communities. The overall performance of the algorithms was statistically analyzed by two non-parametric statistical tests Friedman [77] and Wilcoxon signed-rank [78].
5.1. Datasets Description
The proposed DMFO-CD algorithm was tested on eleven real-world network datasets known as social networks consists of Zachary’s karate club (karate) [92], American College football (football) [2], Bottlenose Dolphins (dolphins) [93], co-purchase political books (polbooks) [94], WebKB network [95] includes four datasets, adjective Noun network (adjnoun) [12], Email-Eu-core network (email-Eu) [96], and DBLP network (dblp) [97]. The details and statistical information of the networks are described as follows.
Zachary’s karate club (karate) network is a friendship network that has been divided into two factions based on the conflict between the administrators of the club. In this study, an unweighted version of the network was used to detect the factions only based on the friendship relations. This network contains 34 nodes, 78 edges, and has two real communities as shown in Figure 9a.

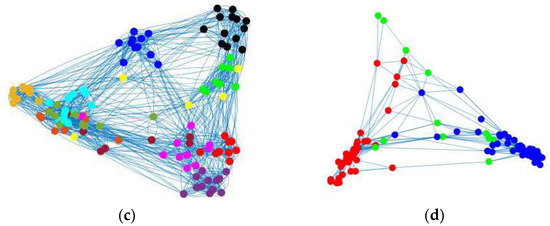
Figure 9.
The community structure of datasets network: (a) the Zachary’s karate club network; (b) the Bottlenose dolphins network; (c) the American college football network; (d) the Political books network.
Bottlenose dolphins (dolphins) network is about 62 dolphins that lived in Doubtful Sound, New Zealand and were collected by Lusseau et al. [93]. The members of this bottlenose dolphin’s community had been studied in a 7 years’ period and during that time they did not have any permanent migration or immigration. The observed community structure between these dolphins was temporally stable, which had not been seen in other bottlenose dolphins population. This dataset consists of 62 nodes, 159 undirected edges, and has two real communities as shown in Figure 9b.
American college football (football) network consists of 115 American football teams of Division IA colleges that have played with each other during a season in 2000 [2]. Nodes represent teams and edges represent the regular season games between the two teams. The network includes 115 nodes, 1226 edges, and is grouped into 12 teams as shown in Figure 9c.
Political books (polbooks) network contains 105 American political books that have sold on Amazon’s online store. The books purchased by a same person have been connected by an edge to each other. All books are divided by Newman [94] based on the descriptions and reviews posted on Amazon, into three classes of “liberal”, “neutral”, and “conservative”. This network includes 105 nodes, 441 edges, and three real communities as shown in Figure 9d.
WebKB network [95] consists of four datasets webkb-cornell, webkb-texas, webkb-washington, and webkb-wisconsin including of the webpages of computer science department of four universities Cornell University, University of Texas at Austin, University of Washington, and University of Wisconsin. In these datasets, each node represents a webpage, and each edge shows there is a hyperlink between two webpages. These webpages are classified into faculty, staff, student, project, and course. In addition, in these datasets, each university is considered as a separate dataset, with the Cornell University consisting of 195 nodes and 304 edges, University of Texas having 187 nodes and 328 edges, University of Washington having 265 nodes and 446 edges, and University of Wisconsin also having 265 nodes and 530 edges.
Adjective Noun (adjnoun) network dataset prepared by Newman [12] consists of the most common adjacent adjective and noun that are come in the novel David Copperfield by Charles Dickens. In this dataset, each node represents an adjective or noun, and each edge represents a pair of words that adjacent with each other. In addition, each word has one of adjective or noun class.
Email-Eu-core network consist of 1005 members’ email of European research institution [96]. In this network, dataset nodes represent institution members’ email and the edges determined which members sent at least one email to each other. Each member of this network belongs to one department of the institution, and this research institution has 42 departments. This network consists of 1005 nodes and 25,571 edges, and its real communities are 42.
DBLP network dataset is a co-authorship network of researchers in computer science [97]. This dataset includes of 10,824 authors that they connected to each other when they published at least one paper together. The authors who published in same journal or conference form a community. This network dataset has 10,824 nodes, 38,732 edges and 100 communities.
5.2. Evaluation Metrics
The performance of DMFO-CD is evaluated using metrics: several statistical values of modularity such as average (Qavg), standard deviation (Qstd) and optimal (Qmax) modularities, normalized mutual information (NMI), and the number of detected communities. The modularity measures the quality of detected communities and NMI measures the accuracy of the resulted partitioning. If R is the real partitioning of a network, then the NMI can be used to measure the similarity between R and the resulted partitioning M gained by the algorithm. The NMI of M and R is calculated by using Equation (11).
where is confusion matrix, CM and CR are the number of communities in partitioning M and R. Cij represents the number of common nodes between community i in partitioning M and community j in partitioning R. Ci and Cj are the number of elements in i and j rows in matrix C.
5.3. Performance Evaluation
In this subsection, the performance of the proposed DMFO-CD algorithm was experimentally evaluated, and the experimental results were compared with comparative algorithms. As shown in Table 1, the parameter settings of all comparative algorithms were considered the same as suggested values in their original works. All algorithms were evaluated to detect the communities of network dataset using 30 independent runs, except email-Eu and dblp network that were evaluated by using 10 runs; in each run, the maximum number of iterations (MaxIter) was set by 100. Similar to previous works [61] the population number (N) for karate, email-Eu, dblp, dolphins, all webkbs, adjnoun, football, and polbooks datasets were set by 100, 100, 100, 200, 200, 200, 400, and 400, respectively. The average modularity (Qavg), the standard deviation of modularity (Qstd), the optimal modularity (Qmax), the average NMI (NMIavg), and the number of detected communities (Cnumber) are used to report. The reported results are shown in Table 2 and Table 3, in which the best-obtained values are remarked in boldface.

Table 1.
Parameter settings.

Table 2.
The modularity results on eleven datasets.

Table 3.
The NMI and community number.
Table 2 and Figure 10 show the obtained modularity by DMFO-CD and comparative algorithms on eleven datasets. As per the results in Table 2 and Figure 10, DMFO-CD, GACD, and EGACD have the highest value of modularity and lowest distribution of modularity on karate network. In Figure 10, EGACD has the largest distribution of modularity than others, and GACD has the lowest average modularity that shows that they have the poorest performance on the dolphins network. The average modularity gained by GA-Net is better than EGACD and GACD; however, its distribution is near to GACD. The modularity of DMFO-CD is evident in that it is superior to other comparative algorithms for detecting communities of the dolphins network. As shown in Figure 10, GACD and EGACD have the lowest performance in the football dataset among other algorithms, while DMFO-CD and DPSO-PDM have better results than other algorithms. Figure 10 shows the results on polbooks network in which the GA-NET algorithm has the largest distribution and weak modularity, while in comparison to other algorithms, DMFO-CD has the best average modularity. Table 2 shows that DMFO-CD has mostly gained the best result of modularity among other comparative algorithms on webkb datasets. GACD and EGACD have the results near to DMFO-CD, and DPSO-PDM could not gain proper results in term of modularity. For adjnoun dataset, as shown in Figure 10, the proposed DMFO-CD has the best average of modularity than other comparative algorithms. GACD and EGACD after DMFO-CD have better results than DPSO-PDM, GA-Net, and DECS. In Table 2 the row of email-Eu represents the results of modularity on email-Eu dataset that DMFO-CD has the best results on it. DMFO-CD in compare with GA-Net and DECS has better performance and is near to EGACD. As shown in Figure 10, the performance of DMFO-CD in terms of modularity for dblp dataset is better than others, except for DPSO-PDM.
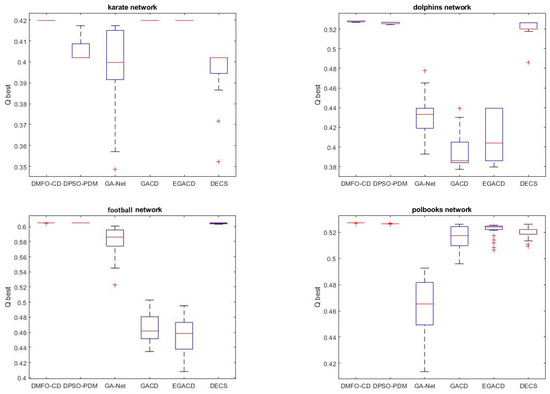
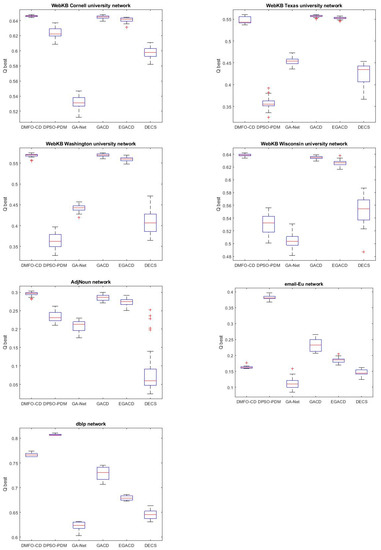
Figure 10.
The boxplot of modularity (Q).
The reported results show that the proposed DMFO-CD has the best performance in terms of modularity in the dolphins and polbooks datasets. In addition, DMFO-CD is competitive with GACD and EGACD on the karate dataset, and with DPSO-PDM and DECS on the football dataset. DMFO-CD in email-Eu dataset has a weak performance in terms of modularity; however, it is better than GA-Net and DECS. In dblp dataset, although DMFO-CD is not better than DPSO-PDM, it is better than other algorithms. Thus, DMFO-CD is able to provide superior and competitive results in comparison to the comparative algorithms in terms of modularity.
Table 3 shows the average NMI of values gained by GA-Net, GACD, EGACD, DPSO-PDM, DECS, and DMFO-CD in karate, dolphins, football, polbooks, webkb, and adjnoun datasets from 30 runs and email-Eu and dblp datasets from 10 independent runs. In Figure 11, the bar plot of gained NMI of all algorithms is shown on each dataset. In the karate dataset, although DMFO-CD in terms of NMI obtains better results than GA-Net and DPSO-PDM, all comparative algorithms detect four communities, except for DECS, which has better NMI than others and detects the more correct community number. In the dolphins dataset, DPSO-PDM gained the most value of average NMI. In the football dataset, DPSO-PDM and GA-Net have better performance than DMFO-CD, while DMFO-CD after GA-Net detects the correct number of communities. As shown in the fourth row of Table 3, in polbooks dataset, DMFO-CD and DPSO-PDM detect a more accurate and correct number of communities than the rest of the comparative algorithms. In webkb, network datasets GA-Net gained the best results of average NMI, while DMFO-CD could not gain proper results. In adjnoun dataset, GA-Net has the best result, but DMFO-CD has less good performance than other algorithms. In email-Eu dataset, DMFO-CD has the greatest value of NMI. The last row of Table 3 shows the results in dblp dataset in which DMFO-CD after GACD has the best average of NMI. Although in this experiment, DMFO-CD does not have the expected performance in terms of NMI, it practically detects the correct number of communities.
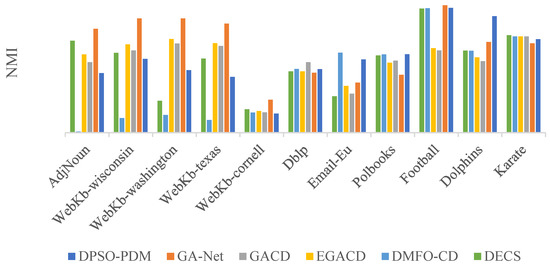
Figure 11.
The average NMI of real-world network datasets.
5.4. Convergence Evaluation
In this subsection, the DMFO-CD convergence behavior and speed are assessed and compared to the comparative algorithms except GA-net because it uses community score to calculate the fitness. Figure 12 shows the convergence curves of all algorithms on eleven datasets. These curves show the best modularity in every iteration for each algorithm over 30 runs on karate, dolphins, football, polbooks, four webkb datasets, and adjnoun networks and 10 runs on email-Eu and dblp networks. The convergence curves show that DMFO-CD on karate, dolphins, football, and polbooks datasets is better than GACD and EGACD, and is competitive with DPSO-PDM and DECS. In webkb datasets, the convergence curve of DMFO-CD follows closely GACD and EGACD, and in adjnoun dataset, DMFO-CD has the best convergence curve versus other comparative algorithms. In email-Eu dataset, DMFO-CD does not have a good convergence, but in dblp, it has the best performance after DPSO-PDM. The better convergence of DMFO-CD originates from the usage of the best neighbor in the initialization step. The convergence of the DMFO-CD is sped up when the best neighbor is used in the initialization step versus when the best neighbor is not used. Figure 13 shows this difference on four selected datasets.
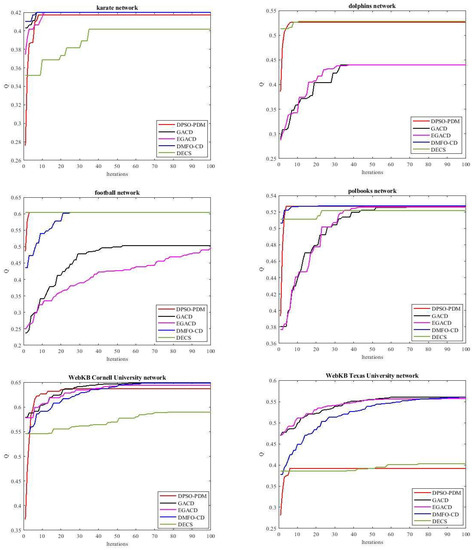
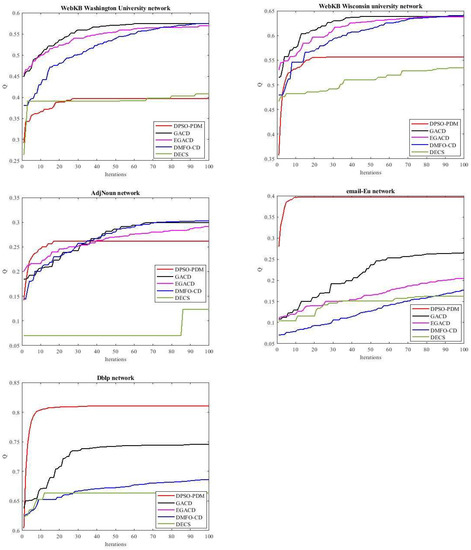
Figure 12.
Convergence curves of the proposed DMFO-CD and comparative algorithms.
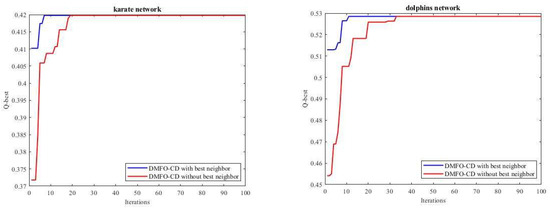
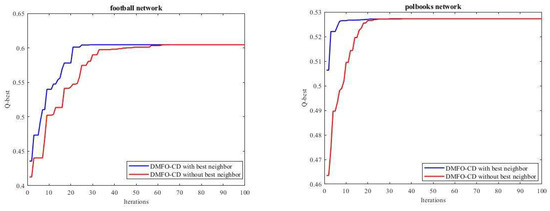
Figure 13.
Impact of using the best neighbor on convergence speed of DMFO-CD.
5.5. Statistical Analysis
In this subsection, the performance of the proposed DMFO-CD algorithm and comparative algorithms were statistically analyzed by two statistical tests, i.e., Friedman test [77] and Wilcoxon signed-rank test [78].
5.5.1. Friedman Test
The non-parametric Friedman test was conducted to prove the superiority of the proposed DMFO-CD algorithm statistically. The Friedman test (Ff) [77] is a non-parametric test using for multiple comparisons of different algorithms for all functions. This test is used to rank the DMFO-CD and comparative algorithms based on the achieved fitness by using Equation (12),
where k, n, and Rj are the number of algorithms, case tests, and the mean rank of the jth algorithm, respectively. For each pair of algorithms, it ranks from 1 (best result) to k (worst result) and then calculates the average ranks obtained in all problems to find the algorithms’ final rank. The Friedman test on modularity and NMI were calculate for all algorithms over 30 runs on karate, dolphins, football, polbooks, four webkb datasets, and adjnoun networks and over 10 runs on email-Eu and dblp networks. The gained results on modularity and NMI are tabulated in Table 4 and Table 5. Based on the overall ranking results, the DMFO-CD algorithm has better overall ranked on modularity and competitive rank compared with other stat × 10of-th × 10art algorithms.

Table 4.
The Friedman test on modularity.

Table 5.
The Friedman test on NMI.
5.5.2. Wilcoxon Signed-Rank Test
In order to verify the significant difference between DMFO-CD and other comparative algorithms, the Wilcoxon signed-rank test was employed [78]. This test is a non-parametric statistical test that requires two sets of random observations and two hypotheses. In this paper, the two sets of observations represent the obtained modularity values from each algorithm, i.e., the DMFO-CD algorithm and the compared one, over 30 runs on karate, dolphins, football, polbooks, all four webkb, adjnoun and 10 runs on email-Eu and dblp datasets. The null hypothesis (H0) was assumed that there is no significant difference between the mean values of the two observation sets (modularity values). While the alternative hypothesis (H1) is that there is a significant difference in the average values of the two sets. Table 6 presents the results of this test at significance level α = 0.05. The p value refers to the significant difference between each pair of algorithms (DMFO-CD and one other algorithm). The considerable difference exists only if p value < α. Therefore, the results prove that the null hypothesis is rejected on most of the networks.

Table 6.
The p values of Wilcoxon signed-rank test.
6. Conclusions and Future Works
In this study, a discrete moth–flame optimization algorithm for community detection (DMFO-CD) was proposed for complex networks. The solution vectors representation, the distance calculation, and the spiral flight movement of the MFO algorithm were adapted for community detection. This adaptation was performed by introducing a singl × 10point crossover to imitate the distance calculation, a two-point crossover to alter the movement strategy, and a singl × 10point neighbor-based mutation to increase the exploration ability. The performance of the DMFO-CD was experimentally evaluated on eleven real-world networks and compared with five well-known algorithms in community detection in terms of modularity, NMI, and the number of detected communities. The experimental results show that the proposed DMFO-CD can detect the correct number of communities with better modularity in comparison to other stat × 10of-th × 10art algorithms. The overall effectiveness of the proposed algorithm was also statistically analyzed using the Friedman and Wilcoxon signed-rank tests. To be more specific, the gained rank and p values by statistical tests show DMFO-CD has better overall rank on modularity and that the null hypothesis is rejected on most of the networks. The NMI gained by DMFO-CD shows that it can be focused on combining the local search strategy to detect more accurate communities in further studies. Furthermore, the single objective DMFO-CD algorithm can be extended such that it solves the multi-objective community detection.
Author Contributions
Conceptualization, M.H.N.-S.; Methodology, M.H.N.-S., E.M., S.T.; Software, M.H.N.-S., E.M., S.T.; Validation, M.H.N.-S., E.M., S.T., S.M.; Formal analysis, M.H.N.-S., E.M., S.T.; Investigation, M.H.N.-S., E.M., S.T.; Resources, M.H.N.-S., S.T., S.M.; Data curation, M.H.N.-S., E.M., S.T.; Writing, M.H.N.-S., E.M., S.T.; Original draft preparation, M.H.N.-S., E.M, S.T.; Writing—review and editing, M.H.N.-S., S.T., S.M.; Visualization, M.H.N.-S., E.M., S.T.; Supervision, M.H.N.-S.; Project administration, M.H.N.-S., S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atay, Y.; Koc, I.; Babaoglu, I.; Kodaz, H. Community detection from biological and social networks: A comparative analysis of metaheuristic algorithms. Appl. Soft Comput. 2017, 50, 194–211. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, F.; Cui, T.; Su, Y.; Niu, Y.; Zhang, X. A local information based multi-objective evolutionary algorithm for community detection in complex networks. Appl. Soft Comput. 2018, 69, 357–367. [Google Scholar] [CrossRef]
- El Mouden, Z.A.; Taj, R.M.; Jakimi, A.; Hajar, M. Towards Using Graph Analytics for Tracking Covid-19. Procedia Comput. Sci. 2020, 177, 204–211. [Google Scholar] [CrossRef]
- Sánchez-Oro, J.; Duarte, A. Iterated Greedy algorithm for performing community detection in social networks. Future Gener. Comput. Syst. 2018, 88, 785–791. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Liu, G.; Lao, S.-y. A genetic algorithm for community detection in complex networks. J. Cent. South Univ. 2013, 20, 1269–1276. [Google Scholar] [CrossRef]
- Shi, C.; Yan, Z.; Cai, Y.; Wu, B. Multi-objective community detection in complex networks. Appl. Soft Comput. 2012, 12, 850–859. [Google Scholar] [CrossRef]
- Žalik, K.R.; Žalik, B. Memetic algorithm using node entropy and partition entropy for community detection in networks. Inf. Sci. 2018, 445–446, 38–49. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in larg × 10scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wu, X.; Xu, S.; Qing, S.; Chang, P.-C. A novel complex network community detection approach using discrete particle swarm optimization with particle diversity and mutation. Appl. Soft Comput. 2019, 81, 105476. [Google Scholar] [CrossRef]
- Shi, C.; Yan, Z.; Wang, Y.; Cai, Y.; Wu, B. A Genetic Algorithm for Detecting Communities in Larg × 10scale Complex Networks. Advs. Complex Syst. 2010, 13, 3–17. [Google Scholar] [CrossRef]
- Newman, M.E.J. Detecting community structure in networks. Eur. Phys. J. B Condens. Matter 2004, 38, 321–330. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 74. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo Search via Levy Flights. arXiv 2010, arXiv:1003.1594. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A natur × 10inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. CCSA: Conscious Neighborhood-based Crow Search Algorithm for Solving Global Optimization Problems. Appl. Soft Comput. 2019, 85, 105583. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Faris, H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new natur × 10inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Banai × 10Dezfouli, M.; Nadimi-Shahraki, M.H.; Beheshti, Z. R-GWO: Representativ × 10based grey wolf optimizer for solving engineering problems. Appl. Soft Comput. 2021, 106, 107328. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Varaee, H. A fast multi-objective optimization using an efficient ideal gas molecular movement algorithm. Eng. Comput. 2017, 33, 477–496. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning; Addison-Wesle: Boston, MA, USA, 1988. [Google Scholar]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 1472, pp. 1470–1477. [Google Scholar]
- Taghian, S.; Nadimi-Shahraki, M.H.; Zamani, H. Comparative Analysis of Transfer Function-Based Binary Metaheuristic Algorithms for Feature Selection. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018. [Google Scholar]
- Oliva, D.; Cuevas, E.; Pajares, G. Parameter identification of solar cells using artificial bee colony optimization. Energy 2014, 72, 93–102. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H. Feature selection based on whale optimization algorithm for diseases diagnosis. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 1243–1247. [Google Scholar]
- Taghian, S.; Nadimi-Shahraki, M.H. A Binary Metaheuristic Algorithm for Wrapper Feature Selection. Int. J. Comput. Sci. Eng. (IJCSE) 2019, 8, 168–172. [Google Scholar]
- Mohmmadzadeh, H.; Gharehchopogh, F.S. An efficient binary chaotic symbiotic organisms search algorithm approaches for feature selection problems. J. Supercomput. 2021, 77, 9102–9144. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, W.; Jia, H.; Leng, X. Simultaneous Feature Selection and Support Vector Machine Optimization Using an Enhanced Chimp Optimization Algorithm. Algorithms 2021, 14, 282. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.; Abualigah, L.; Oliva, D.; Algamal, Z.Y.; Anter, A.M.; Ali Ibrahim, R.; Ghoniem, R.M.; Abd Elaziz, M. Boosting Arithmetic Optimization Algorithm with Genetic Algorithm Operators for Feature Selection: Case Study on Cox Proportional Hazards Model. Mathematics 2021, 9, 2321. [Google Scholar] [CrossRef]
- Dezfouli, M.B.; Shahraki, M.H.N.; Zamani, H. A Novel Tour Planning Model using Big Data. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar]
- Abualigah, L.M.; Diabat, A. A novel hybrid antlion optimization algorithm for multi-objective task scheduling problems in cloud computing environments. Clust. Comput. 2021, 24, 205–223. [Google Scholar] [CrossRef]
- Sa’ad, S.; Muhammed, A.; Abdullahi, M.; Abdullah, A.; Hakim Ayob, F. An Enhanced Discrete Symbiotic Organism Search Algorithm for Optimal Task Scheduling in the Cloud. Algorithms 2021, 14, 200. [Google Scholar] [CrossRef]
- Arjenaki, H.G.; Nadimi-Shahraki, M.H.; Nourafza, N. A low cost model for diagnosing coronary artery disease based on effective features. Int. J. Electron. Commun. Comput. Eng. 2015, 6, 93–97. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.-H. Swarm Intelligence Approach for Breast Cancer Diagnosis. Int. J. Comput. Appl. 2016, 151, 40–44. [Google Scholar] [CrossRef]
- Rahnema, N.; Gharehchopogh, F.S. An improved artificial bee colony algorithm based on whale optimization algorithm for data clustering. Multimed. Tools Appl. 2020, 79, 32169–32194. [Google Scholar] [CrossRef]
- Taghian, S.; Nadimi-Shahraki, M.H. Binary Sine Cosine Algorithms for Feature Selection from Medical Data. arXiv 2019, arXiv:1911.07805. [Google Scholar] [CrossRef]
- Fasihi, M.; Nadimi-Shahraki, M.H. Multi-class cardiovascular diseases diagnosis from electrocardiogram signals using 1-D convolution neural network. In Proceedings of the 2020 IEEE 21st International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 11–13 August 2020; pp. 372–378. [Google Scholar]
- Abualigah, L.; Diabat, A.; Sumari, P.; Gandomi, A.H. A Novel Evolutionary Arithmetic Optimization Algorithm for Multilevel Thresholding Segmentation of COVID-19 CT Images. Processes 2021, 9, 1155. [Google Scholar] [CrossRef]
- Zahrani, H.K.; Nadimi-Shahraki, M.H.; Sayarshad, H.R. An intelligent social-based method for rail-car fleet sizing problem. J. Rail Transp. Plan. Manag. 2021, 17, 100231. [Google Scholar]
- Fard, E.S.; Monfaredi, K.; Nadimi-Shahraki, M.H. An Area-Optimized Chip of Ant Colony Algorithm Design in Hardware Platform Using the Address-Based Method. Int. J. Electr. Comput. Eng. 2014, 4, 989–998. [Google Scholar] [CrossRef]
- Sayarshad, H.R. Using bees algorithm for material handling equipment planning in manufacturing systems. Int. J. Adv. Manuf. Technol. 2010, 48, 1009–1018. [Google Scholar] [CrossRef]
- Oliva, D.; Abd El Aziz, M.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Shaban, H.; Houssein, E.H.; Pérez-Cisneros, M.; Oliva, D.; Hassan, A.Y.; Ismaeel, A.A.; AbdElminaam, D.S.; Deb, S.; Said, M. Identification of Parameters in Photovoltaic Models through a Runge Kutta Optimizer. Mathematics 2021, 9, 2313. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Varaee, H. Enhanced IGMM optimization algorithm based on vibration for numerical and engineering problems. Eng. Comput. 2018, 34, 91–116. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Taghian, S.; Dezfouli, M. Enhancement of Bernstain-Search Differential Evolution Algorithm to Solve Constrained Engineering Problems. Int. J. Comput. Sci. Eng. 2020, 386–396. [Google Scholar] [CrossRef]
- Pizzuti, C. GA-Net: A Genetic Algorithm for Community Detection in Social Networks. In Parallel Problem Solving from Nature—PPSN X; Rudolph, G., Jansen, T., Beume, N., Lucas, S., Poloni, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5199, pp. 1081–1090. [Google Scholar]
- Li, Z.; Zhang, S.; Wang, R.-S.; Zhang, X.-S.; Chen, L. Quantitative function for community detection. Phys. Rev. E 2008, 77, 036109. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Parsa, S. An evolutionary method for community detection using a novel local search strategy. Phys. A Stat. Mech. Its Appl. 2019, 523, 457–475. [Google Scholar] [CrossRef]
- Rahimi, S.; Abdollahpouri, A.; Moradi, P. A multi-objective particle swarm optimization algorithm for community detection in complex networks. Swarm Evol. Comput. 2018, 39, 297–309. [Google Scholar] [CrossRef]
- Zarei, B.; Meybodi, M.R. Detecting community structure in complex networks using genetic algorithm based on object migrating automata. Comput. Intell. 2020, 36, 824–860. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel natur × 10inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Ewees, A.A.; Ibrahim, R.A.; Lu, S. Opposition-based moth-flame optimization improved by differential evolution for feature selection. Math. Comput. Simul. 2020, 168, 48–75. [Google Scholar] [CrossRef]
- Khurma, R.A.; Alsawalqah, H.; Aljarah, I.; Elaziz, M.A.; Damaševičius, R. An Enhanced Evolutionary Software Defect Prediction Method Using Island Moth Flame Optimization. Mathematics 2021, 9, 1722. [Google Scholar] [CrossRef]
- Elsakaan, A.A.; El-Sehiemy, R.A.; Kaddah, S.S.; Elsaid, M.I. An enhanced moth-flame optimizer for solving non-smooth economic dispatch problems with emissions. Energy 2018, 157, 1063–1078. [Google Scholar] [CrossRef]
- Taher, M.A.; Kamel, S.; Jurado, F.; Ebeed, M. An improved moth-flame optimization algorithm for solving optimal power flow problem. Int. Trans. Electr. Energy Syst. 2019, 29, e2743. [Google Scholar] [CrossRef]
- Dabba, A.; Tari, A.; Meftali, S.; Mokhtari, R. Gene selection and classification of microarray data method based on mutual information and moth flame algorithm. Expert Syst. Appl. 2021, 166, 114012. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharif, M.; Akram, T.; Damaševičius, R.; Maskeliūnas, R. Skin Lesion Segmentation and Multiclass Classification Using Deep Learning Features and Improved Moth Flame Optimization. Diagnostics 2021, 11, 811. [Google Scholar] [CrossRef]
- Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Dynamic harris hawks optimization with mutation mechanism for satellite image segmentation. Remote Sens. 2019, 11, 1421. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.-Q.; Li, L.-L.; Tseng, M.-L.; Liu, H.-M.; Yuan, D.-D.; Tan, R.R. An improved moth-flame optimization algorithm for support vector machine prediction of photovoltaic power generation. J. Clean. Prod. 2020, 253, 119966. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, X.; Liu, J. An Improved Moth-Flame Optimization Algorithm for Engineering Problems. Symmetry 2020, 12, 1234. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.; Nayak, J.; Naik, B.; Deng, Y. An Improved Moth-Flame Optimization algorithm with hybrid search phase. Knowl. Based Syst. 2020, 191, 105277. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Gaber, T.; Mokhtar, U.; Hefny, H. An improved moth flame optimization algorithm based on rough sets for tomato diseases detection. Comput. Electron. Agric. 2017, 136, 86–96. [Google Scholar] [CrossRef]
- Liu, F.; Wu, J.; Xue, S.; Zhou, C.; Yang, J.; Sheng, Q. Detecting the evolving community structure in dynamic social networks. World Wide Web 2020, 23, 715–733. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 196–202. [Google Scholar]
- Tasgin, M.; Herdagdelen, A.; Bingol, H. Community Detection in Complex Networks Using Genetic Algorithms. arXiv 2007, arXiv:0711.0491. [Google Scholar]
- Li, Y.-H.; Wang, J.-Q.; Wang, X.-J.; Zhao, Y.-L.; Lu, X.-H.; Liu, D.-L. Community Detection Based on Differential Evolution Using Social Spider Optimization. Symmetry 2017, 9, 183. [Google Scholar] [CrossRef] [Green Version]
- Cuevas, E.; Cienfuegos, M.; Zaldívar, D.; Pérez-Cisneros, M. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Syst. Appl. 2013, 40, 6374–6384. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Zhang, F.; Li, X.; Gao, C.; Liu, J. Multi-objective Discrete Moth-Flame Optimization for Complex Network Clustering. In Foundations of Intelligent Systems; Helic, D., Leitner, G., Stettinger, M., Felfernig, A., Raś, Z.W., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12117, pp. 372–382. [Google Scholar]
- Zhao, J.; Lei, X.; Wu, F.-X. Predicting Protein Complexes in Weighted Dynamic PPI Networks Based on ICSC. Complexity 2017, 2017, 4120506. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, Y.; Li, J.; Zhu, J.; Yang, C.; Yang, W.; Wen, C. WOCDA: A whale optimization based community detection algorithm. Phys. A Stat. Mech. Its Appl. 2020, 539, 122937. [Google Scholar] [CrossRef]
- Hamou, R.M. Handbook of Research on Biomimicry in Information Retrieval and Knowledge Management; Hamou, R.M., Ed.; IGI Global: Hershey, PA, USA, 2018. [Google Scholar]
- Liu, C.; Fan, L.; Liu, Z.; Dai, X.; Xu, J.; Chang, B. Community detection in complex networks by using membrane algorithm. Int. J. Mod. Phys. C 2018, 29, 1850003. [Google Scholar] [CrossRef]
- Kumar, S.; Panda, B.S.; Aggarwal, D. Community detection in complex networks using network embedding and gravitational search algorithm. J. Intell. Inf. Syst. 2020, 57, 51–72. [Google Scholar] [CrossRef]
- Pizzuti, C.; Socievole, A. A genetic algorithm for community detection in attributed graphs. In Proceedings of the International Conference on the Applications of Evolutionary Computation, Parma, Italy, 4–6 April 2018; pp. 159–170. [Google Scholar]
- Pizzuti. GA-NET is Genetic Algorithm to Find Communities in Complex Networks. Available online: http://staff.icar.cnr.it/pizzuti/codes.html (accessed on 20 September 2021).
- Wu, J. Detecting the Evolving Community Structure in Dynamic Social Networks. Available online: https://github.com/JiaWu-Repository/DECS (accessed on 20 September 2021).
- Danon, L.; Díaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. 2005, 2005, P09008. [Google Scholar] [CrossRef]
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef] [Green Version]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [Green Version]
- Craven, M.; McCallum, A.; PiPasquo, D.; Mitchell, T.; Freitag, D. Learning to Extract Symbolic Knowledge from the World Wide Web; Carnegi × 10Mellon Univ Pittsburgh pa School of Computer Science: Pittsburgh, PA, USA, 1998. [Google Scholar]
- Yin, H.; Benson, A.R.; Leskovec, J.; Gleich, D.F. Local higher-order graph clustering. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 555–564. [Google Scholar]
- Jia, Y.; Zhang, Q.; Zhang, W.; Wang, X. Communitygan: Community detection with generative adversarial nets. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 784–794. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).