Multi-Objective UAV Positioning Mechanism for Sustainable Wireless Connectivity in Environments with Forbidden Flying Zones
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions
- A smart UAV positioning mechanism for a sustainable UAV communication system is proposed, under certain constraints.
- A multiobjective optimization model is formulated, that is, minimizing the energy consumption of UAV, while maximizing the number of users covered.
- A weighting mechanism is developed to prioritize the two objectives given in the previous item over each other for different scenarios.
- Q-learning-based algorithm is used to find the optimal position of UAV. The convergence of the developed algorithm is first tested, followed by comparing its performance with the baseline k-means method in terms of number of users covered and energy consumption.
1.3. Organization of the Paper
2. System Model
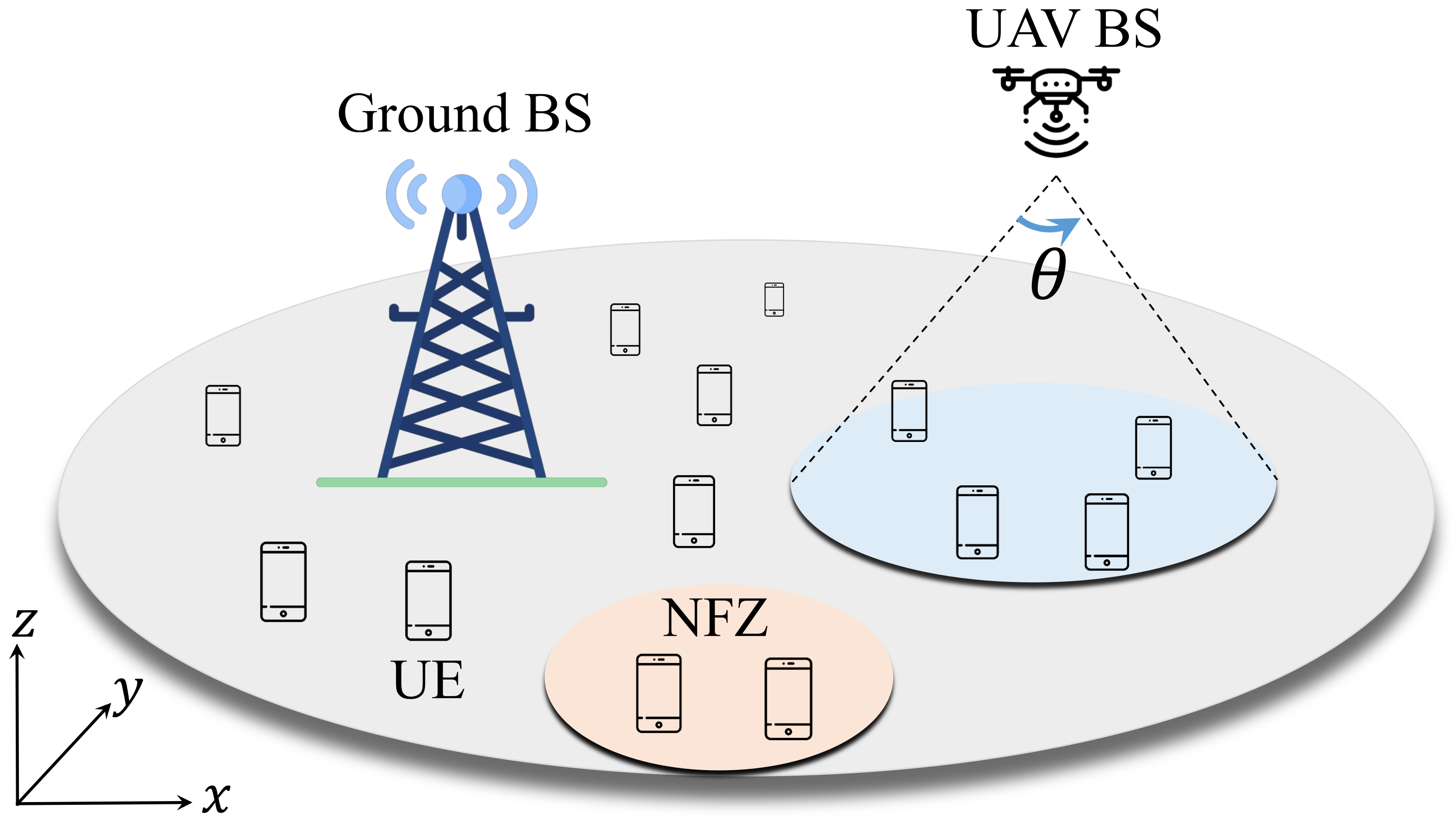
2.1. Scenario
2.2. Propagation Model
2.3. Energy Consumption Model
Communication Energy Consumption
2.4. Hovering Energy Consumption
2.5. Mobility Energy Consumption
3. Problem Formulation
3.1. Optimization Problem Formulation
3.1.1. Maximization of Number of Served Users
Explanations of Constraints in (20)
- : The altitude of the UAV () is regulated in many countries and regions, such that the maximum () and minimum () altitudes that UAVs can flight are determined. Therefore, in this work, the UAV is supposed to obey these limitations in terms of the altitude.
- : Since F is defined as the NFZ, it means that the UAV BS cannot fly over it. As such, this constraint confirms that the UAV BS is flying out of F, such that the projection of the UAV BS on the -plane, , is not within F.
- : The directivity angle of the antenna of the UAV BS can be at maximum (The use of an isotropic antenna is not a good idea for UAV BSs as they are serving to the users under them in terms of height, and there is no sense to provide a radiation above the UAV BS. Therefore, we assume that the maximum antenna angle for the UAV BSs should be ), but practically it should be less than that to have a better antenna gain. Though this could be normally not a hard constraint, in this work we deal with the case where the antenna angle is less than , thereby this becomes a constraint for the optimization problem.
- : Given that the maximum transmit power of the BSs are regulated, this constraint captures such regulations, meaning that the transmit power of the UAV BS has an upper bound.
3.1.2. Minimization of Energy Consumption
3.1.3. Multiobjective Problem Formulation
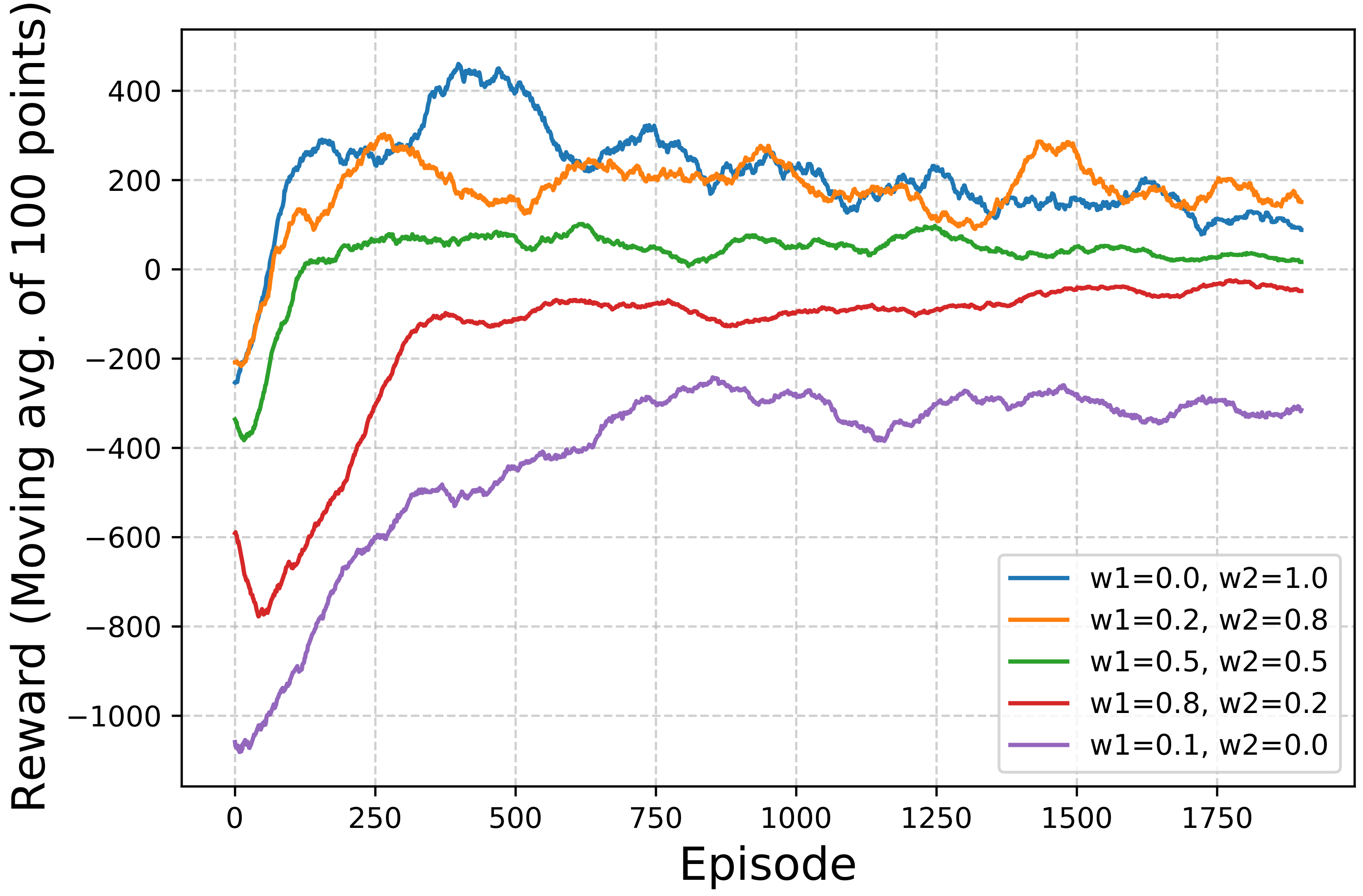
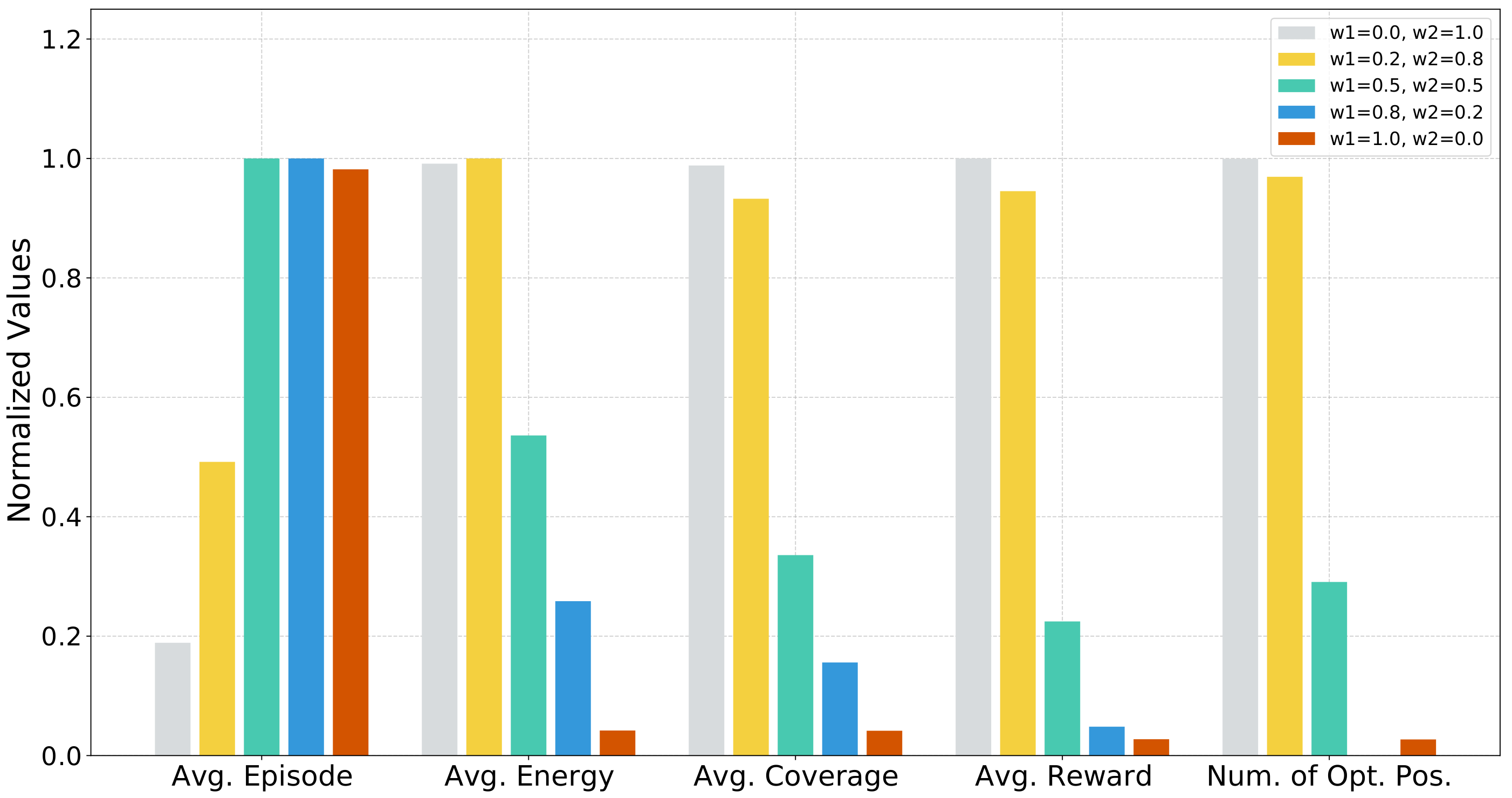
- To prioritize one objective over the other. For example, a mobile network operator may not be interested in the energy consumption much and focuses only on covering as much as users as possible for a short duration, and it would choose . On the other hand, if the operator ranks both objectives equally, then it would choose . Therefore, and allow the operators to rank the objectives according to their requirements.
- To make the units of both (unitless) and (in Joules) the same, since includes the summation of and . To this end, while is chosen to be unitless, is in ().
4. Proposed Q-Learning Based UAV Positioning Mechanism
| Algorithm 1:Q-learning algorithm [52] |
 |
4.1. Environment
4.2. Agent
4.3. Actions
- : Move up (in z direction)
- : Move down (in z direction)
- : Move left (in x direction)
- : Move right (in x direction)
- : Move forward (in y direction)
- : Move backward (in y direction)
- :Hold
4.4. States
4.5. Reward
- goes beyond the dimensions of the environment,
- flies on the NFZ,
- does not respect any other constraint in (23).
4.6. Policy
4.7. Q-Table Update
4.8. Initialization
4.9. Episodes
4.10. Stopping Criteria
4.11. Complexity
5. Performance Evaluation
5.1. Simulation Scenario
5.2. Benchmark and Metrics
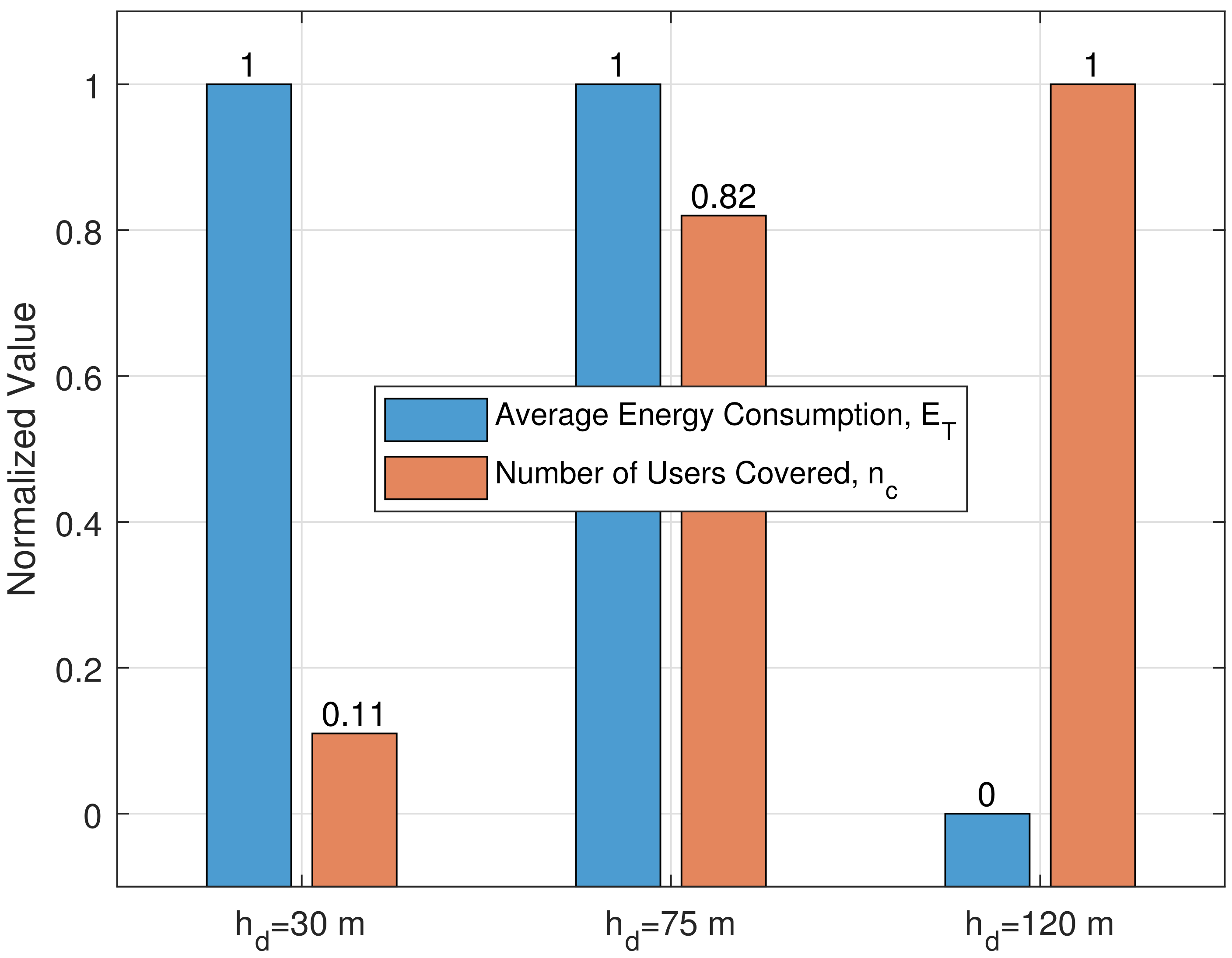
5.3. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ericsson. Ericsson Mobility Report; Technical report; Ericsson: Stockholm, Sweden, 2021. [Google Scholar]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A Survey on Enabling Technologies, Protocols, and Applications. IEEE Commun. Surv. Tutorials 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; De Silva, P.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A Tutorial Overview of Standards, Trials, Challenges, Deployment, and Practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Jameel, F.; Faisal; Haider, M.A.A.; Butt, A.A. Massive MIMO: A survey of recent advances, research issues and future directions. In Proceedings of the 2017 International Symposium on Recent Advances in Electrical Engineering (RAEE), Islamabad, Pakistan, 24–26 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Dai, L.; Rodriguez, J. Millimeter-Wave Massive MIMO Communication for Future Wireless Systems: A Survey. IEEE Commun. Surv. Tutorials 2018, 20, 836–869. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; MacCartney, G.R.; Molisch, A.F.; Mellios, E.; Zhang, J. Overview of Millimeter Wave Communications for Fifth-Generation (5G) Wireless Networks—With a Focus on Propagation Models. IEEE Trans. Antennas Propag. 2017, 65, 6213–6230. [Google Scholar] [CrossRef]
- 3GPP. 5G; NR; Base Station (BS) Radio Transmission and Reception. Technical Specification (TS) 38.104. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3202 (accessed on 1 September 2021).
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutorials 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Klaine, P.V.; Imran, M.A.; Onireti, O.; Souza, R.D. A Survey of Machine Learning Techniques Applied to Self-Organizing Cellular Networks. IEEE Commun. Surv. Tutorials 2017, 19, 2392–2431. [Google Scholar] [CrossRef]
- Zhang, C.; Patras, P.; Haddadi, H. Deep Learning in Mobile and Wireless Networking: A Survey. IEEE Commun. Surv. Tutorials 2019, 21, 2224–2287. [Google Scholar] [CrossRef]
- Morocho Cayamcela, M.E.; Lim, W. Artificial Intelligence in 5G Technology: A Survey. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 17–19 October 2018; pp. 860–865. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, M.; Zhou, Y.; Huang, Y.; Mao, S. Application of Machine Learning in Wireless Networks: Key Techniques and Open Issues. IEEE Commun. Surv. Tutorials 2019, 21, 3072–3108. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, L. Mobility Prediction: A Survey on State-of-the-Art Schemes and Future Applications. IEEE Access 2019, 7, 802–822. [Google Scholar] [CrossRef]
- Dogra, A.; Jha, R.K.; Jain, S. A Survey on beyond 5G network with the advent of 6G: Architecture and Emerging Technologies. IEEE Access 2020. [Google Scholar] [CrossRef]
- Lu, Y.; Zheng, X. 6G: A survey on technologies, scenarios, challenges, and the related issues. J. Ind. Inf. Integr. 2020, 19, 100158. [Google Scholar] [CrossRef]
- Ozturk, M.; Nadas, J.P.B.; Klaine, P.H.V.; Hussain, S.; Imran, M.A. Clustering Based UAV Base Station Positioning for Enhanced Network Capacity. In Proceedings of the 2019 International Conference on Advances in the Emerging Computing Technologies (AECT), Medina, Saudi Arabia, 8–10 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, L. Energy-Saving Deployment Algorithms of UAV Swarm for Sustainable Wireless Coverage. IEEE Trans. Veh. Technol. 2020, 69, 10320–10335. [Google Scholar] [CrossRef]
- de Paula Parisotto, R.; Klaine, P.V.; Nadas, J.P.B.; Souza, R.D.; Brante, G.; Imran, M.A. Drone Base Station Positioning and Power Allocation using Reinforcement Learning. In Proceedings of the 2019 16th International Symposium on Wireless Communication Systems (ISWCS), Oulu, Finland, 27–30 August 2019; pp. 213–217. [Google Scholar] [CrossRef]
- Wang, L.; Hu, B.; Chen, S. Energy Efficient Placement of a Drone Base Station for Minimum Required Transmit Power. IEEE Wirel. Commun. Lett. 2020, 9, 2010–2014. [Google Scholar] [CrossRef]
- Donevski, I.; Nielsen, J.J. Dynamic Standalone Drone-Mounted Small Cells. In Proceedings of the 2020 European Conference on Networks and Communications (EuCNC), Dubrovnik, Croatia, 16–17 June 2020; pp. 342–347. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Unmanned Aerial Vehicle With Underlaid Device-to-Device Communications: Performance and Tradeoffs. IEEE Trans. Wirel. Commun. 2016, 15, 3949–3963. [Google Scholar] [CrossRef]
- Becvar, Z.; Mach, P.; Nikooroo, M. Reducing Energy Consumed by Repositioning of Flying Base Stations Serving Mobile Users. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea, 25–28 May 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Qi, H.; Hu, Z.; Huang, H.; Wen, X.; Lu, Z. Energy Efficient 3-D UAV Control for Persistent Communication Service and Fairness: A Deep Reinforcement Learning Approach. IEEE Access 2020, 8, 53172–53184. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man, Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Xu, C.; Liao, X.; Tan, J.; Ye, H.; Lu, H. Recent Research Progress of Unmanned Aerial Vehicle Regulation Policies and Technologies in Urban Low Altitude. IEEE Access 2020, 8, 74175–74194. [Google Scholar] [CrossRef]
- Fotouhi, A.; Qiang, H.; Ding, M.; Hassan, M.; Giordano, L.G.; Garcia-Rodriguez, A.; Yuan, J. Survey on UAV Cellular Communications: Practical Aspects, Standardization Advancements, Regulation, and Security Challenges. IEEE Commun. Surv. Tutorials 2019, 21, 3417–3442. [Google Scholar] [CrossRef]
- Patané, G.M.M.; Valastro, G.C.; Sambo, Y.A.; Ozturk, M.; Hussain, S.; Imran, M.A.; Panno, D. Flexible SDN/NFV-based SON testbed for 5G mobile networks. In Proceedings of the 2019 IEEE/ACM 23rd International Symposium on Distributed Simulation and Real Time Applications (DS-RT), Cosenza, Italy, 7–9 October2019; pp. 1–8. [Google Scholar] [CrossRef]
- Sambo, Y.A.; Valastro, G.C.; Patané, G.M.M.; Ozturk, M.; Hussain, S.; Imran, M.A.; Panno, D. Motion Sensor-Based Small Cell Sleep Scheduling for 5G Networks. In Proceedings of the 2019 IEEE 24th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Limassol, Cyprus, 11–13 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile Unmanned Aerial Vehicles (UAVs) for Energy-Efficient Internet of Things Communications. IEEE Trans. Wirel. Commun. 2017, 16, 7574–7589. [Google Scholar] [CrossRef]
- Pang, Y.; Zhang, Y.; Gu, Y.; Pan, M.; Han, Z.; Li, P. Efficient data collection for wireless rechargeable sensor clusters in Harsh terrains using UAVs. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 234–239. [Google Scholar] [CrossRef]
- Liu, X.; Ansari, N. Resource Allocation in UAV-Assisted M2M Communications for Disaster Rescue. IEEE Wirel. Commun. Lett. 2019, 8, 580–583. [Google Scholar] [CrossRef]
- Bithas, P.S.; Michailidis, E.T.; Nomikos, N.; Vouyioukas, D.; Kanatas, A.G. A Survey on Machine-Learning Techniques for UAV-Based Communications. Sensors 2019, 19, 5170. [Google Scholar] [CrossRef] [PubMed]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Drone Small Cells in the Clouds: Design, Deployment and Performance Analysis. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Efficient Deployment of Multiple Unmanned Aerial Vehicles for Optimal Wireless Coverage. IEEE Commun. Lett. 2016, 20, 1647–1650. [Google Scholar] [CrossRef]
- Hayajneh, A.M.; Zaidi, S.A.R.; McLernon, D.C.; Ghogho, M. Drone Empowered Small Cellular Disaster Recovery Networks for Resilient Smart Cities. In Proceedings of the 2016 IEEE International Conference on Sensing, Communication and Networking (SECON Workshops), London, UK, 27–30 June 2016; pp. 1–6. [Google Scholar] [CrossRef][Green Version]
- Bor-Yaliniz, R.I.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an aerial base station in next generation cellular networks. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Kalantari, E.; Yanikomeroglu, H.; Yongacoglu, A. On the Number and 3D Placement of Drone Base Stations in Wireless Cellular Networks. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montréal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Košmerl, J.; Vilhar, A. Base stations placement optimization in wireless networks for emergency communications. In Proceedings of the 2014 IEEE International Conference on Communications Workshops (ICC), Sydney, NSW, Australia, 10–14 June 2014; pp. 200–205. [Google Scholar] [CrossRef]
- Zhan, P.; Yu, K.; Lee Swindlehurst, A. Wireless Relay Communications using an Unmanned Aerial Vehicle. In Proceedings of the 2006 IEEE 7th Workshop on Signal Processing Advances in Wireless Communications, Cannes, France, 2–5 July 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Mohamed, E.M.; Hashima, S.; Aldosary, A.; Hatano, K.; Abdelghany, M.A. Gateway Selection in Millimeter Wave UAV Wireless Networks Using Multi-Player Multi-Armed Bandit. Sensors 2020, 20, 3947. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for Multi-UAV Enabled Wireless Networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Jiang, F.; Swindlehurst, A.L. Optimization of UAV Heading for the Ground-to-Air Uplink. IEEE J. Sel. Areas Commun. 2012, 30, 993–1005. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Throughput Maximization for UAV-Enabled Mobile Relaying Systems. IEEE Trans. Commun. 2016, 64, 4983–4996. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Franco, C.D.; Ferreira, P.R.; Buttazzo, G.C. Energy-Aware Spiral Coverage Path Planning for UAV Photogrammetric Applications. IEEE Robot. Autom. Lett. 2018, 3, 3662–3668. [Google Scholar] [CrossRef]
- Shao, X.; Gong, Y.J.; Zhan, Z.H.; Zhang, J. Bipartite Cooperative Coevolution for Energy-Aware Coverage Path Planning of UAVs. IEEE Trans. Artif. Intell. 2021. [Google Scholar] [CrossRef]
- Yang, D.; Dan, Q.; Xiao, L.; Liu, C.; Cuthbert, L. An efficient trajectory planning for cellular-connected UAV under the connectivity constraint. China Commun. 2021, 18, 136–151. [Google Scholar] [CrossRef]
- Sun, G.; Li, J.; Liu, Y.; Liang, S.; Kang, H. Time and Energy Minimization Communications Based on Collaborative Beamforming for UAV Networks: A Multi-objective Optimization Method. IEEE J. Sel. Areas Commun. 2021. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, J.; Huang, J.; Zhang, X.; So, D.K.C.; Wong, K.K. Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks Based on Extended DDPG Algorithm. IEEE Trans. Commun. 2021. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication With Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Arani, A.H.; Hu, P.; Zhu, Y. Re-envisioning Space-Air-Ground Integrated Networks: Reinforcement Learning for Link Optimization. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv preprint arXiv:1606.01540.
| Parameter | Value |
|---|---|
| General | |
| Carrier frequency, | 1 GHz |
| Antenna directivity angle, | 60 |
| Minimum UAV height, | 30 m |
| Maximum UAV height, | 120 m |
| Urban Area | 250 × 250 m |
| Total number of users, | 100 |
| Height from ground for all UEs | 1.5 m |
| Speed of light, c | m/s |
| LoS | 1.6 dB |
| NLoS | 23 dB |
| Parameter of A2G path loss model, | 12.08 |
| Parameter of A2G path loss model, | 0.11 |
| Number of rotors, M | 4 |
| Fluid density of the air, | 1.2 Kg/m |
| Rotor disk radius, | 0.25 m |
| Weight of the frame | 1.5 Kg |
| Weight of the battery and payload | 2 Kg |
| Bandwidth | 180 kHz |
| Transmit power, | 30 dBm (1 W) |
| On-board circuit power, | 0.01 W |
| Duration of hovering of UAV, | 1 s |
| Duration to communication of UAV, | 1 s |
| Velocity of the UAV, v | 30 m/s |
| Angular velocity, | 40 rad/s |
| Drag coefficient | 0.025 |
| Rotor chord, | 0.022 m |
| Reference frontal area of the UAV | 0.192 m |
| -learning | |
| Discount rate, | 0.9 |
| Epsilon, | 1 |
| Epsilon decay, -decay | 0.95 |
| Learning rate, | 0.9 |
| Learning rate decay, -decay | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atli, İ.; Ozturk, M.; Valastro, G.C.; Asghar, M.Z. Multi-Objective UAV Positioning Mechanism for Sustainable Wireless Connectivity in Environments with Forbidden Flying Zones. Algorithms 2021, 14, 302. https://doi.org/10.3390/a14110302
Atli İ, Ozturk M, Valastro GC, Asghar MZ. Multi-Objective UAV Positioning Mechanism for Sustainable Wireless Connectivity in Environments with Forbidden Flying Zones. Algorithms. 2021; 14(11):302. https://doi.org/10.3390/a14110302
Chicago/Turabian StyleAtli, İbrahim, Metin Ozturk, Gianluca C. Valastro, and Muhammad Zeeshan Asghar. 2021. "Multi-Objective UAV Positioning Mechanism for Sustainable Wireless Connectivity in Environments with Forbidden Flying Zones" Algorithms 14, no. 11: 302. https://doi.org/10.3390/a14110302
APA StyleAtli, İ., Ozturk, M., Valastro, G. C., & Asghar, M. Z. (2021). Multi-Objective UAV Positioning Mechanism for Sustainable Wireless Connectivity in Environments with Forbidden Flying Zones. Algorithms, 14(11), 302. https://doi.org/10.3390/a14110302







